子集构造法
第05讲 子集

第5讲 子集本讲内容有子集、子集的个数、集合的划分及子集的应用。
设a 表示任意元素,B A ,表示两个集合。
若B a A a ∈⇒∈ ,则B A ⊆ ,即集合A 是集合B 的子集。
规定空集是任何集合的子集。
子集是由原集合中的部分元素构成。
对于由n 个元素组成的集合,它的每一个子集中元素的构成,都是对这n 个元素进行选择的结果。
由于对每一个元素的选择都有两种可能(选上或不选),因此,对这n 个元素共有n 2种不同选择结果,即由n 个元素组成的集合共有n 2个不同子集。
其中,不同的非空子集有12-n 个,不同的真子集有n 2个。
A 类例题例1 求集合}03|{2=++-∈=a ax x R x M 的子集的个数。
分析 欲求集合M 的子集的个数,可先求出集合M 的元素的个数。
例2 求满足},,,,{},{e d c b a P b a ⊆⊆的集合P 的个数。
分析 本题要求的是集合},,,,{e d c b a 中,必定含有元素b a ,的子集的个数,只要求出集合},,{e d c 的子集数。
例3 已知集合}7,6,5,4,3,2{=A ,对A X ⊆,定义)(X S 为X 中所有元素之和。
求全体)(X S 的总和S 。
分析 要求出全体)(X S 的总和S ,只要求出每个元素出现的次数。
情景再现1.设集合}14|),{(2+-==x x y y x A ,}12|),{(-==x y y x B 。
求集合B A 的子集的个数。
2.若数集},4,2,1{},2,1{}1,{2a a a ⊆⊆,则a 的值是_____。
3.设非空集合}7,6,5,4,3,2,1{⊆A ,且当A a ∈时,必有A a ∈-8,问:这样的A 共有多少个?B 类例题例4 在某次竞选中,各个政党共作出p 种不同的诺言)0(>p ,任何两个政党都至少有一种公共诺言,但没有两党作出完全相同的诺言。
试证明,政党的数目不多于12-p 个。
第三节 子集与集合的分划

第三节 子集与子集的分划一个集合可以写成若干个集合的并集,这是对集合分类讨论的常用方法.对于一个较为复杂的集合,我们在研究其性质时,往往可以划分成若干个小集合的并集进行研究,通过对这些小集合的性质的研究,可以达到化整为零、化繁为易的效果. 集合的分划反映了集合与子集之间的关系,这既是一类数学问题,也是数学中的解题策略——分类思想的基础,在近几年来的数学竞赛中经常出现,日益受到重视. 本讲主要介绍有关的概念、结论以及处理集合、子集与划分问题的方法.【基础知识】一.集合的分划1.集合分划的概念:把一个集合M 分成若干个非空子集:.,,,21n A A A 如果满足(1)),1(n j i A A j i ≤≤=φ ;(2) n i i M A1==,那么称这些子集的全体为集合M 的一个n -分划,其中每一个子集叫做集合M 的一个类.2.加法原理由集合分划的定义,容易证明有限的一个非常有用的性质:设.,,,21n A A A 是有限集n -分划,则∑==ni iA Card M Card 1)()(,这是一个基本的计数公式,被称为加法原理. 3.最小数原理(极端原理)最小数原理I:设M 是正整数集的一个非空子集,则M 中必有最小数.最小数原理II:设M 是实数集的一个有限的非空子集,则M 中必有最小数.推论:设M 是实数集的一个有限非空子集,则M 中必有最大数.二.子集族1.子集族的概念我们可以将某些集合取来作为元素构成一个新的集合,例如}},0}{1,0{},1{{*φ=A 就是含4个元素φ},0}{1,0{},1{的集合,特别地,将集合M 的若干个子集作为元素构成的集合*M叫做原集合的一个子集族.如上例中的*A 就是二元集}1,0{=A 的全部子集构成的子集族.子集族中所含原来集合的子集的数目叫做该子集族的阶.例如子集族*A 的阶为4,即.4||*=A2.C 族最简单的子集族是由有限集M 的全体子集所构成的子集族,简称为C 族.3.C 族的性质设n M =||,则集合M 的全体子集所构成的集合*M 的阶为.2n即.2||10*n n n n n C C C M =+++=4.R 族设(),Card A n =12,{,,}n M A A A = 是A 的一个子集族,若存在(21)k k m ≤≤-使得: (1)M 中任意k 个i A 都相交;(2)M 中任意(1)k +个i A 都不相交.则称M 为A 的一个指数为k 的R 族.定理:如果12,{,,}n M A A A = 是A 的一个指数为k 的R 族,()Card A n =,则.k m C n ≤5.K 族设A 为一个n 阶集合,12,{,,}n M A A A = 是A 的一个子集族.若M 中任何两个A 的子集i A 和j A 互不包含,即i j A A ⊄且j i A A ⊄,则称M 为集合A 的一个K 族.定理:设M 为n 阶集合A 的K 族中阶数最高者,则[]2().n n Card M C =上述两个定理的证明有一定的麻烦程度,我们将其放在习题中,请读者自己完成其证明过程. 本讲的内容没有因定的方法,难度也较大,有些问题甚至就是一些数学专业论文中的一些结果或著名的定理,初学者若感到较为困难,可以耐心地多看几遍,多做几遍本讲中的例题与习题就会有所收获.【典例精析】【例1】(第43届美国中学数学竞赛)设S 为集合}50,,2,1{ 的子集,并且S 中任意两个元素之和不能被7整除,那么S 中元素最多有多少个?〖分析〗对于两个不同的自然数n m ,,n m +不被7整除也就是n m +被7除的余数不为0.我们将集合}50,,2,1{ 按照其中元素被7除所得的余数相同与否进行归类,余数相同的组成一个集合,这样可得到7个子集.然后从这7个子集中适当地抽取满足题意的元素组成集合S 即可.【解法一】将集合}50,,2,1{ 中的元素按被7除所得的余数相同分为7个子集,即: }50,43,36,29,22,15,8,1{1=A ;}44,37,30,23,16,9,2{2=A ;}45,38,31,24,17,10,3{3=A ;}46,39,32,25,18,11,4{4=A ;}47,40,33,26,19,12,5{5=A ;}48,41,34,27,20,13,6{6=A ;}49,42,35,28,21,14,7{0=A .可知S 最多包含0A 的一个元素,而如果S 包含其它任何一个子集中一个元素时,则它可以包含这个子集中的所有元素;另外,S 不有同时包含61,A A 中的元素;同样,S 不能同时包含52,A A 和43,A A 中的元素.故S 中的元素最多有1+8+7+7=23个.【解法二】将{1,2,,50} 按照模7分成7类:1{1,8,15,22,29,36,43,50}K =;2{2,9,16,23,30,37,44}K =;3{3,10,17,24,31,38,45}K =;4{4,11,18,25,32,39,46}K =;5{5,12,19,26,33,40,47}K =;6{6,13,20,27,34,41,48}K =;0{7,14,21,28,35,42,49}K =.下面证明123{7}S K K K = 为满足要求的元素最多的集合.首先对,,a b S a b ∈≠有3种可能:(1),(13)i a b K i ∈≤≤,则2(mod7)a b i +≡,则a b +不能被7整除;(2),(13)i j a K b K i j ∈∈≤≠≤,则(mod 7)a b i j +≡+,则a b +不能被7整除;(3),7(13)i a K b i ∈=≤≤,则(mod 7)a b i +≡,则a b +不能被7整除.综上知,S 中任何两个元素之和不能被7整除.其次证明,若S 中添加1个元素c ,则必存在S 中的一个元素与c 的和能被7整除. 添加的c 有4种可能:(1)4c K ∈,则c 与3K 中的元素之和能被7整除;(2)5c K ∈,则c 与2K 中的元素之和能被7整除;(3)6c K ∈,则c 与1K 中的元素之和能被7整除;(4)0c K ∈,则c 与7的和能被7整除.综上知,S 中的元素不能再添加.所以S 中元素数目的最大值为:123()()()()123.Card S Crad K Card K Card K =+++=〖说明〗本题实际上是集合的划分问题,从以上的解答过程可以看出,利用余数构造集合的划分是解决本题的关键,也是解决集合问题的一种常用的手段. 解法二中,首先按模7的剩余类对集合{1,2,,50} 中的元素进行分类的想法是自然的.后面的解答中又进行了两次分类,但是这两个分类的理由已经蕴涵中最初的分类之中了.【例2】对于一个由非负整数组成的集合S ,定义)(n r s 为满足条件的有序对),(21s s 的对数: 2121,,s s S s S s ≠∈∈且.21n s s =+问:是否能将非负整数集分划为两个集合A 和B ,使得对任意n ,均有?)()(n r n r B A =〖分析〗整数有多种表示形式,其中二进制表示的每位数字只有0和1这两种选择.由于是将S 分划为两个集合A 、B ,对每个因定的n ,满足n s s =+21的非负整数对),(21s s 是有限的,用二进制来讨论),(21s s 在A 和B 中的分配情况似乎较有利.【解】存在上述分划.将所有二进制下数码1出现偶数个的非负整数归入集合A ,其余的非负整数归入B ,则A 、B 是非负整数N 的分划.注意到,对A 中满足A a a a a n a a ∈≠=+212121,,,的数对),(21a a ,由于21a a ≠,因此在二进制表示下1a 与2a 在该位上的数码,分别得到21,b b ,则B b b ∈21,且.,2121n b b b b =+≠这个将),(21a a 对应到),(21b b 的映射是一一对应的,因此).()(n r n r B A = 〖说明〗本题中构造一一映射成为求解的关键,这个构造使得我们将要求证的问题简单地转化成了二进制下的数码个数问题,这种方法在涉及到集合所有子集问题中很常见.【例3】(2007年全国高中数学联赛)已知A 与B 是集合}100,,2,1{ 的两个子集,满足A 与B 的元素个数相同,且B A 为空集,若A n ∈时总有B n ∈+22,则B A 的元素个数最多为( )A .62B .66C .68D .74【解】先证66)(≤B A Crad ,只须证33)(≤A Crad ,为此只须证若A 是}49,,2,1{ 的任一个34元子集,则必存在A n ∈,使得A n ∈+22,证明如下:将}49,,2,1{ 分成如下33个集合:}48,23{,},12,5{},8,3{},4,1{ 共12个; }38,18{},30,14{},22,10{},6,2{共4个; }49{,},29{},27{},25{ 共13个; }46{},42{},34{},26{共4个.由于A 是}49,,2,1{ 的34元子集,从而由抽屉原理可知上述33个集合中至少有一个2元子集中的数均属于A ,即存在A n ∈,使得A n ∈+22.如取}46,42,34,26,49,,29,27,25,18,14,10,2,23,,5,3,1{ =A ,}|22{A n n B ∈+=,则B A ,满足题设条件66)(=B A Crad .〖说明〗在我们的经验中,有些数学问题涉及的对象较为复杂,统一地解决有困难,于是就将这些对象分成“不重不漏”的若干类,然后再逐类的解决,这就是分类解决问题的方法.这种方法在竞赛中是常用的.【例4】(1995年全国高中数学联赛)设}1995,2,1{ =M ,M A ⊆且当A x ∈时A x ∉15,求)(A Card 的最大值.〖分析〗∴=⎥⎦⎤⎢⎣⎡,133131995 当133,,11,10,9 =k 时,k 与k 15不能同时在A 中..18701251995)(=-≤A Card 只需再构造一个集合A ,使得1870)(=A Card 即可.【解】由题设当133,,11,10,9 =k 时,k 与k 15不能同时在A 中.故至少有133-8=125个数不在集合A 中,即.18701251995)(=-≤A Card 另一方面,M 的子集A 可取}1995,,135,134{}8,,2,1{ 满足题意,此时.1870)(=A Card 故)(A Card 的最大值为1870.〖说明〗本题是要求满足一定条件的某个集合的子集的元素个数的最大值.先证明这个子集的元素个数不大于某个常数,然后再构造一个集合,它的元素个数正好是这个常数,此时这个常数就是我们所要求的最大值. 本题解答中得到x 与x 15)35,,10,9( =x 这两个数中至少有一个不属于A 是非常巧妙的一步,便得求解过程简单明了解.【例5】把n2个元素的集合分为若干个两两不交的子集,按照下述规则将某一个子集中某些元素挪到另一个子集:从前一子集挪到后一子集的元素个数等于后一子集的元素个数(前一子集的元素个数应不小于后一子集的元素个数),证明:可以经过有限次挪动,使得到的子集与原集合相重合.〖分析〗首先考虑到n 2是一个很特殊的数,其次我们发现若两个集合的元素个数除以2的若干次幂后若为奇数,那么,它们之间挪后就应为偶数这一事实,若还不能想到解答就试一下3,2==n n 时的情况,相信解答就不会难找到了.【证明】考虑含奇数个元素的子集(如果有这样的子集),因为所有子集所含元素的个数总和是偶数,所以具有奇数个元素的子集个数也是偶数,任意将所有含有奇数个元素的子集配成对,对每对子集按题目要求的规则移动:从较大的子集挪出一些元素,添加到较小的子集,挪出的元素个数为较小子集的元素个数,于是得到的所有子集的元素个数都是偶数,现在考虑元素个数不被4整除的子集,如果1=n ,则总共有两个元素,它们在同一个子集,因此设2≥n ,因为子集的元素个数的总数被4整除,因此这样的子集的个数为偶数,任意将这样的子集配成对,对每一对子集施行满足题目要求的挪动,于是得到的每个子集数均可被4整除,依此做下去,最后得到的每个子集元素个数均可被n 2整除,也就是只能有一个子集,它的元素个数为n 2,证毕.〖说明〗这道题的证明中隐含了一种单一变量在变化时变化方向相同这一性质,就这道题来说,一直在增加的就是各子集元素个数被2的多少次幂整除的这个幂次数,这是一大类问题,除了这种变化量,还要经常考虑变化中的不变量.【例6】(2005年全国高中数学联赛)设t s r ,,为整数,集合}0,222|{r s t a a t s r <<≤++=中的数由小到大组成数列}{n a : ,14,13,11,7,则=36a 【解】∵t s r ,,为整数且r s t <<≤0,∴r 最小取2,此时符合条件的数有122=C3=r ,t s ,可在2,1,0中取,符合条件有的数有323=C同理,4=r 时,符合条件有的数有624=C ;5=r 时,符合条件有的数有1025=C ;6=r 时,符合条件有的数有1526=C ;7=r 时,符合条件有的数有2127=C ;因此,36a 是7=r 中的最小值,即131********=++=a .〖说明〗在应用加法原理时,我们通常首先描述性地定义,即把问题分成互相排斥的若干情形,而这此情形包括了所有的可能.应用加法原理的技巧就在于要把被计数的集合S 划分成“不太多的易于处理的部分”.【例7】(2007年浙江省预赛题)设{}1,2,,65M = ,A M ⊆为子集.若33A =,且存在,x y A ∈,x y <,x y ,则称A 为“好集”.求最大的a M ∈,使含a 的任意33元子集为好集. 【解】令{}{}211,2,,44\2(21)1,2,,11P i i i i =+=+= ,33P =.显然对任意144i j ≤<≤,不存在3n ≥,使得21(21)j n i +=+成立.故P是非好集. 因此 21a ≤.下面证明:包含21的任意一个33元子集A一定为好集.设{}1232,,,,21A a a a = .若1,3,7,42,63中之一为集合A的元素,显然为好集. 现考虑1,3,7,42,63都不属于集合A.构造集合 {}12,4,8,16,32,64A =,{}25,10,20,40A =,{}36,12,24,48A =,{}49,18,36A =,{}511,22,44A =,{}613,26,52A =,{}714,28,56A =,{}815,30,60A =,{}917,34A = {}1019,38A =,{}1123,46A =,{}1225,50A =,{}1327,54A =,{}1429,58A =,{}1531,62A =,{}33,35,37,,61,65A '=由上可见,1215,,,A A A 每个集合中两个元素都是倍数关系.考虑最不利的情况,即A A '⊂,也即A '中16个元素全部选作A的元素,A中剩下16个元素必须从1215,,,A A A 这15个集合中选取16个元素.根据抽屉原理,至少有一个集合有两个元素被选,即集合A中至少有两个元素存在倍数关系.综上所述,包含21的任意一个33元子集A一定为好集,即a 的最大值为21.〖说明〗若),,,,(1111k c b a ,),,,,(2222k c b a ,……,),,,,(n n n n k c b a 这n 组数都具有相同的性质M (*N n ∈),则在研究与性质M 有关的问题时,我们可以只研究其中的一组数据,进面推得所有这n 组数据的性质.【例8】已知集合}10,9,8,7,6,5,4,3,2,1{,求该集合具有下列性质的子集的个数:每个子集至少含有2个元素,且每个子集中任意2个元素的差的绝对值大于1.〖分析〗虽然已知集合中只有10个元素,但是分类还是比较复杂的.如果将问题一般化,可能过构造递推式来解决.【解】设n a 是集合}10,9,8,7,6,5,4,3,2,1{的具有题设性质的子集的个数,考察集合 ,3,2,1{,}2,1,++n n n 具有题设性质的子集,可分为两类:(1)包含元素2+n 的子集有n a n +个,即每个},,2,1{n 与}2{+n 的并集,以及}2,1{+n ,}.2,{,},2,2{++n n n(2)不包含2+n 的子集有1+n a 个,即集合}1,,,3,2,1{+n n 的具有题设性质的子集的个数. 于是有递推式n a a a n n n ++=++12 ①显然3,141==a a (即}4,2{},4,1{},3,1{),代入①式得:73135=++=a ,4376++=a =14, .13384679,7972646,4661426,26571410987=++==++==++==++=a a a a 故满足题设条件的子集共有133个.【例9】证明:一个有限集的全体子集,可以按如下方式排成一行:(1)居中第一位是空集;(2)每个子集恰好在此行中出现一次;(3)每个子集中的元素或者是前一个子集添加一个元素或删除一个元素所得.〖分析〗从特殊情形入手,寻找规律.【解】我们可以先观察特殊情形:当1=n 时,显然可以排成}1{,φ;当2=n 时,子集共有422=个,可以排成}2{},2,1{},1{,φ;当3=n 时,子集共有823=个,不难排出如下一列子集:}1,3{},3}{3,2{},2{},2,1{},1{,φ,}.3,2,1{或}.3{},3,1{},3,2,1{},3,2{},2{},2,1{},1{,φ从后一种情形发现,若将后四个子集中的元素3删去,正好是前四个子集的一种逆排列,这种规律在2=n 时也正是如此.现以这种规律来看4=n 的情形:}4,3,2{},4,3,2,1{},4,3,1{},4,3{},3{},3,1{},3,2,1}{3,2{},2{},2,1{},1{,φ,}.4{},4,1{},4,2,1{},4,2{于是假设k n =时,已将k 2个子集按题设要求排成一列,那么当1+=k n 时,只需在已排好的k 2个子集中,分别添加元素1+k ,逆序排在这k 2个子集的后面形成1+=k n 的12+k 个子集的一种符合要求的排列.〖说明〗一个复杂的问题,也许一时找不到突破口,我们可以先将其退化成一个很简单的问题或者特殊问题,从中发现规律或者方法,从而找到一般问题的解法.这里运用了“进难则退,以退为进”的解题策略.【例10】(2007年北京高考试题)已知集合{})2(,,,,321≥=k a a a a A k 其中),,2,1(k i Z a i =∈,由A 中的元素构成两个相应的集合(){}A b a A b A a b a S ∈+∈∈=,,,,(){}A b a A b A a b a T ∈-∈∈=,,,,其中()b a ,是有序实数对,集合T S 和的元素个数分别为n m ,.若对于任意的A a A a ∉-∈,总有,则称集合A 具有性质P .(Ⅰ)检验集合{}3,2,1,0与{}3,2,1-是否具有性质P ,并对其中具有性质P 的集合写出相应的集合T S 和;(Ⅱ)对任何具有性质P 的集合A ,证明:()21-≤k k n ; (Ⅲ)判断n m 和的大小关系,并证明你的结论.【解】(Ⅰ)解:集合{}3,2,1,0不具有性质P ,{}3,2,1-具有性质P ,其相应的集合T S 和是()(){}()(){}3,2,1,2,1.3,3,1-=--=T S ;(Ⅱ)证明:首先由A 中的元素构成的有序实数对共有2k 个,因为()T a a A i i ∈∈,,0),,2,1(k i =,又因为当A a A a ∉-∈时,,所以当()()T a a T a a i j j i ∉∈,,时,),,2,1(k i =,于是集合T 中的元素的个数最多为()()121212-=-=k k k k n ,即()21-≤k k n . (Ⅲ)解:n m =,证明如下:①对于()S b a ∈,,根据定义()T b b a A b a A b A a ∈+∈+∈∈,,,从而,则如果()()d c b a ,,与是S 中的不同元素,那么d b c a ==与中至少有一个不成立,于是d c b a +=+与d b =中至少有一个不成立,故()b b a ,+与()d d c ,+也是T 中的不同元素.可见S 中的元素个数不多于T 中的元素个数,即n m ≤;②对于()T b a ∈,,根据定义()S b b a A b a A b A a ∈-∈-∈∈,,,从而,则如果()()d c b a ,,与是T 中的不同元素,那么d b c a ==与中至少有一个不成立,于是d c b a -=-与d b =中至少有一个不成立,故()b b a ,-与()d d c ,-也是S 中的不同元素.可见T 中的元素个数不多于S 中的元素个数,即m n ≤.由①②可知n m =.〖说明〗本题以集合为载体,涉及到它的性质,考查了考生的知识迁移能力和抽象思维能力.【例11】(2007年中国西部奥林匹克竞赛试题)已知{}1,2,3,4,5,6,7,8T =,对于,A T A ⊆≠∅,定义()S A 为A 中所有元素之和,问:T 有多少个非空子集A ,使得()S A 为3的倍数,但不是5的倍数?〖分析〗可按3的余加以分类,由于能被3整除且能被5整除的数必能被15整除,从而我们只需将能被15整除的数去掉即可.【解】对于空集∅,定义()0S ∅=.令012{3,6},{1,4,7},{2,5,8}T T T ===.对于A T ⊆,令001122,,A A T A A T A A T === ,则01212()()()()()()(mod3)S A S A S A S A Card A Card A =++≡-, 因此,3()S A 当且仅当12()()(mod3)Card A Card A ≡.有以下几种情况:111222()0,()0,()3,()0,()3,()0,Card A Card A Card A Card A Card A Card A ===⎧⎧⎧⎨⎨⎨===⎩⎩⎩111222()3,()1,()2,()3,()1,()2,Card A Card A Card A Card A Card A Card A ===⎧⎧⎧⎨⎨⎨===⎩⎩⎩ 从而满足3()S A 的非空子集A 的个数为20003303311223333333333332()1C C C C C C C C C C C C +++++-=87. 若3()S A ,5()S A ,则15()S A .由于()36S T =,故满足3()S A ,5()S A 的()S A 的可能值为15,30.而15=8+7=8+6+1=8+5+2=8+4+3=8+4+2+1=7+6+2=7+5+3=7+5+2+1 =7+4+3+1=6+5+4=6+5+3+1=6+4+3+2=5+4+3+2+1,36-30=6=5+1=4+2=3+2+1. 故满足3()S A ,5()S A ,A ≠∅的A 的个数为17.所以,所求的A 的个数为87-17=70. 〖说明〗本题从正面出发不容易解决,因此可以采用“正难则反”的思想,从而其反面出发,将不符合条件的元素减去,即可得到所求的答案.【例12】设{0,1,2,,29}A ⊆ 满足:对任何整数k 及A 中任意数a 、b (a 、b 可以相同),30a b k +-均不是两个相邻整数的积.试确定所含元素最多的集合A .〖分析〗因为当b a =时,230a k +均不是两个相邻整数的积,故我们只需考察2a 被30除的余数即可.【解】所求A 为{32|09}l l +≤≤.设A 满足题中条件且()Card A 最大.因为两个相邻整数的积被30除,余数为0,2,6,12,20,26,则对于a A ∀∈,有2a0,2,6,12,20,26(mod 30),即a 0,1,3,6,10,15,16,18,21,25,28,因此,{2,4,5,7,8,9,11,12,14,17,19,20,22,23,24,26,27,29}A ⊆,后一个集合可分拆成下列10个子集的并,其中每一个子集至多有一个元素包含在A 中:{2,4},{5,7},{8,12},{9,11},{14,22},{17,19},{20},{23,27},{24,26},{29}.故()10.Card A ≤若()10Card A =,则每个子集恰好有一个元素包含在A 中,因此20,29A A ∈∈.由20A ∈知12A ∉,从而8A ∈,这样4A ∉,22A ∉,24A ∉.因此2A ∈,14A ∈,26.A ∈ 由29A ∈知7A ∉,27A ∉从而5A ∈,23A ∈这样9A ∉,19A ∉.因此11A ∈,17A ∈. 综上所述,有{2,5,8,11,14,17,20,23,26,29}A =,此确定的A 确实满足要求.【赛向点拨】1.求解子集族的问题主要分为两类:求子集的阶,或确定属于子集族的原集合的全部子集.2.有关子集族的最值问题是竞赛中常见的问题,主要有三类题型:(1)求子集族阶的最值;(2)求子集族中的原集合的子集阶的最值;(3)求符合特定条件的集合元素的最值.3.在代数不等式中,有一类确定满足不等关系的量是否存在的问题,通常可以尝试用最小值原理解决.4.集合分类的标准不一,但基本原则都是每次分类必须是不重不漏,其理论依据就是最小值原理.【针对练习】 (A 组)1.已知集合A {2,3,7}且A 中至多有1个奇数,则这样的集合的共有( ).A .2个B .4个C .5个D .6个2.在集合M ={1,2,…,10}的所有子集中,有这样的一族不同的子集,它们两两的交集都不是空集,那么这族子集最多有( )A .102个B .92个C .210个D .29个3.集合S ={0,1,2,3,4,5},A 是S 的一个子集,当x A ∈时,若有1x A -∉且1x A +∉,则称x 为集合A 的一个“孤立元素”,那么S 的子集中无“孤立元素”且含有4个元素的集合的个数是( )A .4B .5C .6D .74.集合{1,2,3,,2,21}A n n =+ 的子集B 满足:对任意的,,x y B x y B ∈+∉,则集合B 中元素个数的最大值是( )A .1n +B .2n +C .3n +D .4n +5.10名学生按下面的规则组成运动队,规则是:①每人可报名参加任何一个运动队;②每个运动队都不能完全包含于或重合于另一个运动队.则最多可组成( )个队.A .410CB .510C C .510C +1D .410C6.(2006年山西省预赛题)集合A 中的元素均为正整数,具有性质:若A a ∈,则12-A a ∈,这样的集合共有 个. 7.已知集合{1,2,3,,31,3n n - 可以分成n 个互不相交的三元组{,,}x y z ,其中⊆3.x y z +=则满足上述要求的最小的正整数n 是 .8.设集合M ={1,2,…,1000},现对M 的任一非空子集X ,令X a 表示X 中最大数与最小数之和.则所有这样的X a 的算术平均值为 .9.设S 是一个有6个元素的集合,选取S 的两个子集(可以相同),使得这两个子集的并集是S ,选取的次序无关紧要,例如一对子集{,},{,,,,}a c b c d e f 与另一对子集{,,,,}b c d e f ,{,}a c 表示同一种取法.这样的取法共有 种.10.求集合B 和C ,使得{1,2,3,,10}B C = ,并且C 的元素乘积等于B 的元素之和.11.(2006年第17届希望杯高二试题)试确定所有的正整数k ,使得集合{2006,20061,20062,,2006}P k =+++ 可以分成两个互不相交的子集A 与B ,且A 中元素之和等于B 中元素之和.12.求证:集合{1,2,,1989} 可以划分为117个互不相交的子集(1,2,,117)i A i = 使得(1)每个i A 恰好有17个元素;(2)每个i A 中各元素之和相同.(B 组)1.已知A }2000,,2,1{ ⊆,且A 中任意两个数之差的绝对值不等于4或`7,求)(A Card 的最大值.2.设M 为n 阶集合A 的K 族中阶数最高者,则[]2().n n Card M C =3.如果12,{,,}n M A A A = 是A 的一个指数为k 的R 族,()Card A n =,则.k m C n ≤4.给出一个60×70的数表如下:12359602346061111213697012131470169701575870125859⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭其中每一行组成一个数的集合1270,,,A A A ,从这70个集合中取出k 个,若任7个的交集都是非空的,求k 的最大值.5.(2007年第七届中国西部奥林匹克竞赛试题)将n 个白子与n 个黑子任意地放在一个圆周上.从某个白子起,按顺时钟方向依次将白子标以1,2,,n .再从某个黑子起,按逆时钟方向依次将黑子标以1,2,,n . 证明:存在连续n 个棋子(不计黑白), 它们的标号所成的集合为{}1,2,,n .6.设}20,,2,1{ =M ,对于M 的任一9元子集S ,函数)(S f 取1到20之间的整数值.求证:不论f 是怎样的一个函数,总存在M 的一个10元子集T ,使得对所有的T k ∈,都有k k T f ≠-}){((}{k T -即T 对k 的差集).【参考答案】A 组1.D 解析:集合A 可有3在:第1类是空集;第2类是A 中不含奇数;第3类是A 中只有1个奇数,它们是,{2},{3},{7},{2,3},{2,7}.φ故应选D.2.B 解析:显然不含空集.按元素的多少把这族子集分成10类,设含i 个元素的子集为i A ,其个数为i a .易知01991210999 2.a a a C C C +++≤+++= 3.C 解析一:可将本题中满足条件的集合分成两类:一类是有4个连续整数的集合,共有3个:{0,1,2,3},{1,2,3,4},{2,3,4,5}.另一类是将4个元素分成两组,每组是连续的但组间不连续的集合,也有3个:{0,1,3,4},{0,1,4,5},{1,2,4,5}.故应选C.解析二:由题知满足条件的子集中的每个元素必有与之相邻的自然数,从而得到满足条件的子集为{0,1,2,3},{0,1,3,4},{0,1,4,5},{1,2,3,4},{1,2,4,5},{2,3,4,5}共6个.解析三:将S 中的元素分成5组:{0,1},{1,2},{2,3},{3,4},{4,5},则满足条件的4元子集的个数为2546C -=,故应选C.4.A 解析:首先{1,,3,5,,21}B n =+ 满足题意,且() 1.Card B n =+其次,设B 中最大元素为21k n =+,将1,2,,2n 分成n 组:(1,2),(2,21),,(,1)n n n n -+ .由抽屉原理可知,如果()2Card B n ≥+,则必有B 中两个元素在同一组,两数和等于21n +,这与已知矛盾,所以有()1Card B n ≤+.如果21k n <+,同理可得()1Card B n ≤+,所以集合B 中元素个数的最大值是 1.n +5.B 解析:根据定理n 阶集合的子集12,,n A A A 若满足i j A A ⊄且j i A A ⊄则m 的最大值为[]2.n n C ,代入本题即得.6.解:从集合A 的性质可得,A 必然是六个集合{1,11},{2,10},{3,9},{4,8},{5,7},{6},中某几个的并集,因此符合要求的A 共有16C +26C +36C +46C +56C +66C =62-1=63个 7. 5,8 解析:设第i 个三元子集组为{,,}i i i x y z 且3,1,2,,.i i i x y z i n +== 则有31113(31)4.2n n i i n n i z ==+==∑∑当n 为偶数时,8|3n ,所以8n ≥,得n 的最小值为8;当n 为奇数时,8|31n +,所以5,n ≥得n 的最小值为5.可验证5,8即为所求.例如当5n =时,集合{1,11,4},{2,13,5},{3,15,6},{9,12,7},{10,14,8}满足条件.8.1001 解析:构造子集{1001|}X x x X '=-∈,则所有非空子集分成两类X X '=和X X '≠.当X X '=时,必有X X M '==,于是X a =1001.当X X '≠时,设,x y 分别是X 中的最大数与最小数,则1001,1001x y --分别是X '中的最小数与最大数,于是,2002.X X a x y a x y '=+=--从而1001.2X X a a '+=因此,所求的X a 的算术平均数为1001. 9.435 解析:设,()().S A B Card A Card B =≤ 若()0Card A =,则()6Card B =,有1种取法;若()1Card A =,则()6,5Card B =,有1615666512C C C C +=种取法;类似地,可分别计算出()2,3,4,5,6Card A =时的取法.10.解:因为123105512012345++++=<=⨯⨯⨯⨯ ,所以集合C 中至多有4个元素,下面对()Card C 分成4种情况进行讨论.(1)若C 由一个元素构成,因为C 的元素乘积不超过10,B 的元素之和至少为55-10=45.故此情形不成立.(2)若C 由两个元素,x y 构成.设x y <,则有55xy x y =--,即(1)(1)56.x y ++=因为1111x y +<+≤,解得6,1x y ==,故{6,7},{1,2,3,4,5,8,9,10}C B ==.(3)若C 由三个元素x y z <<构成.由题设得55.xyz x y z =---当1x =时,解得4,10,y z ==因此{1,4,10},{2,3,5,6,7,8,9}C B ==;当2x =时,有253,yz y z ++=即(21)(21)107y z ++=为质数,无解;当3x ≥时,显然有3456055xyz x y z ≥⨯⨯=>---,无解. (4)若C 由四个元素x y z t <<<构成,必有1x =,否则xyzt ≥2×3×4×5=120>55.这时554,2.yzt y z t y z t =---≤<<如(3),当3y ≥时无解.故2,252y zt z t =++=.即(21)(21)105z t ++=,解得3,7z t ==,从而{1,2,3,7},{4,5,6,8,9,10}.C B == 综上可知B 、C 有3组解.11.解:当41()k m m Z +=-∈时,P 中共有4m 个元素,从第一个元素开始连续4个的第1,4两个数放入A 中,第2,3两个数放入B 中,可满足要求;当43()k m m Z +=-∈时,P 中各元素的和:(20062006)(1)2k k S +++=(4012)(21)k m =+-为奇数,不可能分成符合题意的两个子集;当42()k m m Z +=-∈时,(41)(22005)S m m =-+为奇数,结论同上;当4()k m m Z +=∈时,(41)(22006)S m m =++能分的必要条件是前21m +项和不在于2S ,即21(2006)(21)(41)(1003)m S m m m m +=++≤++,化简得:2210030m -≥,所以22.4m ≥≈或m ≤(舍去),由于m 是整数,所以23.m ≥ 当23m =时,共有93个元素,于是93479395363,190836,95418,2S S S === 9347954189536355,2S S -=-=934795473S S -=,所以93934755.2S S S --=即前47项的和比平均值少55,后46项的和比平均值多55,所以前后两部分要交换相差55的一组数,如2098-2043=55,将2098与2043交换,即A 中有2006,2007,…,2042,2004,2045,…,2052,2098;B 中有2053,2054,…,2097,2043.可使A 中元素之和等于B 中元素之和.当23m >时,前93个元素按上述方法分入A 、B 集,剩下元素个数是4的倍数,每相邻4个数中的第1,4位上的数放入A 中,第2,3位上的数放入B 中,可达到目的.综上,当41()k m m Z +=-∈或4(23,)k m m m Z +=≥∈时,可以将集合P 分成符合题意的两个子集.12.解:将集合{1,2,,1989} 中的数从小到大顺次分成17段,每段含117个数,从第4段数开始,将偶数段的数从小到大依次放入12117,,,A A A 中,并将奇数段的数从小到大依次放入这117个子集中,易见,所有集合中的14个元素之和都相等.于是问题归结为如何将前三段数{1,2,,351} 的每3个一组分别放入每个集合中,且使每组3个数之和都相等. 把这些数中3的倍数抽出来从大到小排好:{351,348,345,,6,3} 共117个数,依次放入12117,,,A A A 中.其余的234个数从小到大排列并分成两段,每段117个数,即{1,2,4,5,7,,173,175} 和{176,178,179,349,350} ,将这两段数分别顺次放入12117,,,A A A 之中便可以满足要求.事实上,若交这两段数中的数顺次相加,则其和为{177,180,183,186,,5 .由此可见,放入每个i A 的3个数之和都是528.B 组 1.解:注意到2000=11×181+9,我们取,911,711,611,411,111|{+++++=t t t t t t A 1810≤≤t , }Z t ∈,则A 中任意两个数之差不是4或7.事实上,若4|)()(11|=-+-a b r t 或7,这里}9,7,6,4,1{,∈b a ,而1810≤≤≤t r ,则当2≥-r t 时,显然不能成立;当1=-r t 时,应有4|)(11|=-+a b 或7,这一点只须直接验证即可知不能成立;当0=-r t ,与上面类似,也不能成立.所以)(A Card 的最大值1825⨯≥=910.另一方面,设A 是满足条件的集合,且)(A Card >910,这时存在t 使得集合r t x x +=11|{,}111≤≤r 中出现6个数减去t 11后都属于A ,说明1,2,……,11中,有6个数入选A ,我们证明这是不可能的.将1,2,……,11排成一个圆圈,例如:1,5,9,2,6,10,3,7,11,4,8(这里1和8首尾相连),则此圆圈上任意两个相邻的数的差的绝对值为4或7.从中任取6个数,,必有两个数相邻,从而1,2,……,11中不能同时有6个数入选A.矛盾!综上所述,)(A Card 的最大值为910.2.证明:记max{||,},min{||,}p x x M q x x M =∈=∈,其中||().x Card x =当p q =时,即M 中每个元素作为A 的子集含有A 中同样多的元素时,显然[]2(),n nCard M C ≤且当[]2n p q ==时取得最大,故此时结论成立. 下面只需证p q >的情形,记().D M p q =- 若2n p ≤,令{,}N X A X M =-∈,显然N 仍是A 的互不包含子集族,且()()Card N Crad M =, 令max{(),}2n Card X X N ∈>,故可设2n p >,即2 1.n p ≤- 设{:()},{{}:,}U X M Card X p V X a a X X U =∈==-∈∈,就是说U 是M 中恰好有A 中p 个元素的那些子集构成的集合,而V 是这样的集合:它的每一个元素也是A 的子集,这些元素是把U 中元素作为A 的子集删去1个元素得到的.任取,X U Y V ∈∈,若Y X ∈,则称X 与Y 为一对相关集,称X 与Y 互相相关.显然共有()pCard U 对相关集.另一方面,因为()1Card Y p =-,与Y 相关的集合均是把A 中某一个不属于Y 的元素添加到Y 中得到的,于是若记()m Y 为与Y 相关的集合个数,则()m Y ≤ (1)21(1).n p p p p --≤---=因为()Card V 个不同的Y ,故相关集对数不超过()pCard V ,于是()()pCard U pCard V ≤,即()().Card U Card V ≤记\()M M U V '= ,因M 是A 的互不包含的子集族,所以M '也是A 的互不包含的子集族,于是M '也是A 的K 族,且有()()()()().Card M Card M Card U Card V Card M '=-+≥ 而()()1D M D M '=-,将M 转换成M ',其元素个数并未减少,但()D M p q =-减少了1,经有限这种转换,即知()Card M 的最大值必在p q =时取到,此时M 中最多含有[]2n n C 个元素.3.证明:由(1)得M 中的每个子集(1)s A s n ≤≤都与M 中其余的1m -个子集中任意选出的1k -个子集相交,且至少有1个公共元素,而这种选法共有11k m C --种;由(2)得,11k m C --个元素两两不同.这样一来,s A 中至少有11k m C --个元素,而1m ii A = 至少有11k m mC --个元素(重复计算),但由(1)知其中每个元素重复了k 次,因为它同时属于k 个不同的子集,所以1mii A = 至少含有11k m m C k --个不同的元素.但是显然1m i i A A =⊆ ,故可得11,k m m C n k --≤即.k m C n ≤ 4.解:(这是个子集族的问题)设取出的k 个集合的第1个元素依次是12,,k a a a ,并记全集{1,2,,70}U = ,A ={12,,k a a a },则,().A U Card A k ⊆=若60k >,则存在一个a A ∈,使得110a ≤≤,且a 与U C A 中的每一个数的个位数都不相同,从而10(0,1,2,,6).U a n C A n +∉= 10(0,1,2,,6)a n A n ∴+∈= .∴所取出的k 个集合中,必存在7个集合1060,,,n n n A A A ++ 满足1060.U n U n U n C A C A C A U ++=∴1060.U n U n U n C A C A C A φ++= 这与已知矛盾,故60k ≤ ○1 ○1式的等号是成立的,例如1260,,A A A 均含有60个元素,显然任7个集合的交集都是非。
编译原理 第3章习题解答
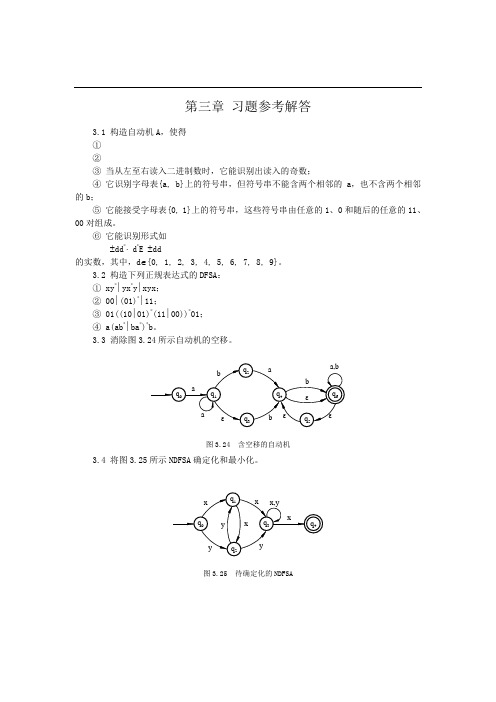
第三章习题参考解答3.1 构造自动机A,使得①②③当从左至右读入二进制数时,它能识别出读入的奇数;④它识别字母表{a, b}上的符号串,但符号串不能含两个相邻的a,也不含两个相邻的b;⑤它能接受字母表{0, 1}上的符号串,这些符号串由任意的1、0和随后的任意的11、00对组成。
⑥它能识别形式如±dd*⋅ d*E ±dd的实数,其中,d∈{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}。
3.2 构造下列正规表达式的DFSA:① xy*∣yx*y∣xyx;② 00∣(01)*∣11;③ 01((10∣01)*(11∣00))*01;④ a(ab*∣ba*)*b。
3.3 消除图3.24所示自动机的空移。
bεq1q2q3aba,bqaq6q4q5abεεε图3.24 含空移的自动机3.4 将图3.25所示NDFSA确定化和最小化。
xyqq1q2q4q3xyxyx,yx图3.25 待确定化的NDFSA3.5 设e、e1、e2是字母表∑上的正规表达式,试证明① e∣e=e;② {{e}}={e};③ {e}=ε∣e{e};④ {e1 e2} e1= e1{e2 e1};⑤ {e1∣e2}={{e1}{e2}}={{e1}∣{e2}}。
3.6 构造下面文法G[Z]的自动机,指明该自动机是不是确定的,并写出它相应的语言: G[Z]:Z→A0A→A0∣Z1∣03.7 设NDFSA M=({x, y},{a, b},f, x, {y}), 其中,f(x, a)={x, y}, f(x, b)={y}, f(y, a)=∅, f(y, b)={x, y}。
试对此NDFSA确定化。
3.8 设文法G[〈单词〉]:〈单词〉→〈标识符〉∣〈无符号整数〉〈标识符〉→〈字母〉∣〈标识符〉〈字母〉∣〈标识符〉〈数字〉〈无符号整数〉→〈数字〉∣〈无符号整数〉〈数字〉〈字母〉→a∣b〈数字〉→1∣2试写出相应的有限自动机和状态图。
集合 —— 子集

【概述】在集合论中,子集是一个较常用的概念,当给出一个集合 {0,1,2,...,n-1} 时,常需要生成所有的子集。
生成子集有三种方法:增量构造法、位向量法、二进制法其中,二进制法除了可以生成子集,还是一种集合的表示方法。
【子集生成算法】1.增量构造法每次选出一个元素放到集合中,然后打印当前集合,由于集合 A 中的元素不确定,因此每次递归调用都要输出当前集合,这样一来,递归的边界也不需要显示的确定,当无法继续添加元素时,即停止递归int A[N];void subset(int cur,int n){for(int i=0;i<cur;i++)//打印当前集合printf("%d ",A[i]);printf("\n");int num=cur?A[cur-1]+1:0;//确认当前元素最小可能值for(int i=num;i<n;i++){A[cur]=i;subset(cur+1,n);}}int main(){int n;scanf("%d",&n);subset(0,n);return 0;}2.位向量法位向量法是通过构造一个位向量 B[i],然后构建解答树,当 B[i]=1 时,说明 i 在子集 A 中int B[N];void subset(int cur,int n){if(cur==n){for(int i=0;i<cur;i++)//打印当前集合if(B[i])printf("%d ",i);printf("\n");return;}B[cur]=true;//选取当前元素subset(cur+1,n);B[cur]=false;//不选取当前元素subset(cur+1,n);}int main(){int n;scanf("%d",&n);subset(0,n);return 0;}3.二进制法二进制法除了用于生成集合子集外,还是一种集合的表示方法。
自动机理论 语言和计算导论课后习题答案

Basis: If y = ε, then the statement is δ-hat(q,x) = δ-hat(δ-hat(q,x),ε). This statement follows from the basis in the definition of δ-hat. Note that in applying this definition, we must treat δ-hat(q,x) as if it were just a state, say p. Then, the statement to be proved is p = δ-hat(p,ε), which is easy to recognize as the basis in the definition of δ-hat.
01 ->s d q1 *q0 q0 q1 q1 q2 q3 q2 q4 q0 q3 q1 q2 q4 q3 q4
dd d
Exercise 2.2.9
Part (a) is an easy induction on the length of w, starting at length 1.
Basis: |w| = 1. Then δ-hat(q0,w) = δ-hat(qf,w), because w is a single symbol, and δ-hat agrees with δ on single symbols.
Definition of δ-hat
δˆ 的定义
δˆ (q,xy)
y=za
Exercise 2.2.4(a)
编译原理作业20150515(答案)
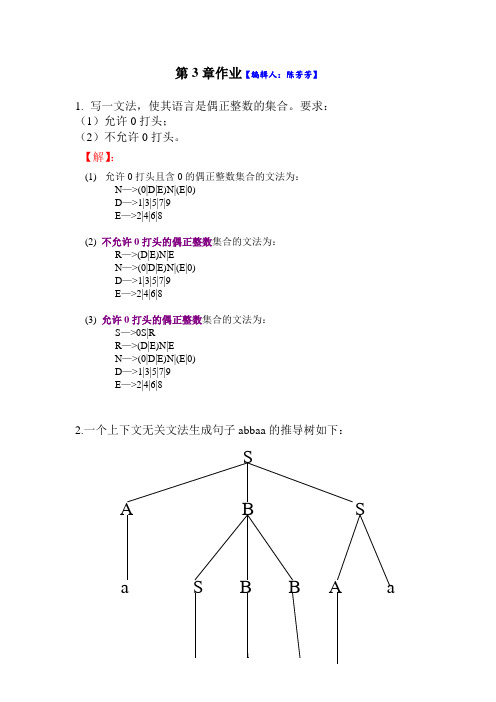
第3章作业【编辑人:陈芳芳】1.写一文法,使其语言是偶正整数的集合。
要求:(1)允许0打头;(2)不允许0打头。
【解】:(1)允许0打头且含0的偶正整数集合的文法为:N—>(0|D|E)N|(E|0)D—>1|3|5|7|9E—>2|4|6|8(2) 不允许0打头的偶正整数集合的文法为:R—>(D|E)N|EN—>(0|D|E)N|(E|0)D—>1|3|5|7|9E—>2|4|6|8(3) 允许0打头的偶正整数集合的文法为:S—>0S|RR—>(D|E)N|EN—>(0|D|E)N|(E|0)D—>1|3|5|7|9E—>2|4|6|82.一个上下文无关文法生成句子abbaa的推导树如下:SA B Sa S B B A aƐ b b a(1)给出该句子的相应的最左推导,最右推导。
(2)该文法的产生式集合P可能有哪些元素?(3)找出该句子的所有短语,简单短语,句柄。
【解】:(1)最左推导:S=>ABS=>aBS=>aSBBS=>aBBS=>abBS=>abbS=>abbAa=>abbaa最右推导:S=>ABS=>ABAa=>ABaa=>ASBBaa=>ASBbaa=>ASbbaa=>Abbaa=>abbaa (2) 产生式集合P:S—>ABS | Aa| ƐA—>aB—>SBB | b(3) 短语:a , Ɛ , b , bb , aa , abbaa直接短语:a , Ɛ , b句柄:a3、给出生成下述语言的上下文无关文法:(1){a n b n a m b m | n, m >= 0}(2){1n0m1m0n | n, m >= 0}【解】:(1)S—>AAA—>aAb | Ɛ(2)S—>1S0 | AA—>0A1 | Ɛ第4章课后作业1.构造一个状态数最小的DFA,它接受∑={0,1}上所有倒数第二个字符为1的字符串。
编译原理 NFA转DFA
实验一:利用子集法构造DFA一.实验目的掌握将非确定有限自动机确定化的方法和过程。
二.实验要求、内容及步骤实验要求:1.输入一个NFA,输出一个接受同一正规集的DFA;2.采用C++语言,实现该算法;3.编制测试程序;4.调试程序。
实验步骤:1.输入一个NFA关系图;2.通过一个转换算法将NFA转换为DFA;3.显示DFA关系图。
三.实验设备计算机、Windows 操作系统、Visual C++ 程序集成环境。
四.实验原理1.NFA-DFA转换原理:从NFA的矩阵表示中可以看出,表项通常是一状态的集合,而在DFA的矩阵表示中,表项是一个状态,NFA到相应的DFA的构造的基本思路是:DFA的每一个状态对应NFA的一组状态。
DFA使用它的状态去记录在NFA读入一个输入符号后可能到达的所有状态。
输入:一个NFA N输出:一个接受同样语言的DFA D方法:为D构造转换表Dtran,DFA的每个状态是NFA的状态集。
D的状态集合用Dstates表示。
D的开始状态为ε-closure(s0),s0是N的开始状态。
使用下列算法构造D的状态集合Dstates和转换表Dtran。
如果D的某个状态是至少包含一个N的接受状态的NFA状态集,那么它是D的一个接受状态。
2.子集构造法:初始时, ε-closure(S0) 是Dstates中唯一的状态且未被标记;while Dstates中存在一个未标记的状态T do begin标记T;for 每个输入符号a do beginU := ε-closure ( move (T, a) );if U 没在Dstates中then将U作为一个未被标记的状态添加到 Dstates.Dtran [ T, a ] := Uendend3.ε-closure的计算:将T中所有状态压入栈stack;将ε-closure (T) 初始化为T;while stack不空 do begin将栈顶元素t弹出栈;for 每个这样的状态u:从t到u有一条标记为ε的边do if u不在ε-closure ( T )中 do begin将u 添加到ε-closure ( T );将u压入栈stack中 endend五.程序设计1.总体设计2.子程序设计识别模块读入字符识别模块识别标识符识别分界符、运算符识别常数输出六.程序中的结构说明1.结构体Symbolrecord 结构体结构体成员名 成员属性Symbol[10] 用于存储关键字编码名 id用于存储关键字对应的编码读取字符字母识别标识符数字识别数字/识别注释打印并结束FTFTFTentrytype结构体结构体成员名成员属性idname[10] 用于存储识别后标识符名address 用于存储标识符的地址type 用于存储标识符的类型digittype结构体结构体成员名成员属性num 用于存储识别后的数字address 用于存储标识符数字的地址tokentype结构体结构体成员名成员属性id 用于存储被识别的类型名entry 用于存储标识符的地址idname[10] 用于存储被识别的标识符名2.符号编码表符号编码表符号名代码符号名代码Begin 0 } 14End 1 ( 15If 2 ) 16 Then 3 < 17 Else 4 <= 18for 5 = 19do 6 != 20while 7 > 21+ 8 >= 22- 9 := 23* 10 ‘’24/ 11 Id 25; 12 Const 26{ 133.重要函数介绍tokentype recogid(char ch)//识别标识符算法tokentype recogdig(char ch) ///识别数字函数tokentype recogdel(char ch) //识别算符和界符函数tokentype handlecom(char ch) //handlecom函数,识别注释函数void sort(char ch) //sort函数,读取文件内容,并根据读入内容调用不同的识别函数void scanner()//scanner函数,打开文件七.函数代码#include <stdio.h>#include <string.h>#include <ctype.h>#include <stdlib.h>;-----------------------定义单词编码表的数据结构-------------------- struct symbolrecord{ char symbol[10];int id;} ;;-------------------------定义符号表的数据结构---------------------- struct entrytype{ char idname[10];int address;int type;};;-------------------------定义常数表的数据结构---------------------- struct digittype{ int num;int address;};;---------------------------Token字的数据结构----------------------- struct tokentype{ int id;int entry;char idname[10];};FILE *fp; //源文件指针struct digittype d[10]; //定义常数表,个数指针struct entrytype a[40];int k=0,t=0;;---------------------------单词编码表初始化------------------------ struct symbolrecord s[26]={ "Begin",0,"End",1,"If",2,"Then",3, "Else",4, "for",5, "do",6,"while",7, "+",8,"-",9,"*",10,"/",11,";",12,"{",13,"}",14,"(",15,")",16,"<",17,"<=",18, "=",19,"!=",20, ">",21,">=",22, ":=",23, " ",24,"const",26 };;---------------------------识别标识符算法-------------------------- tokentype recogid(char ch){ tokentype tokenid;FILE *fs;int flag,fflag;char word[10]={0};int i,j;i=0;while(isalpha(ch)||isdigit(ch)){ word[i]=ch;ch=fgetc(fp);i=i+1;}ungetc(ch,fp);word[i]='\0';for(j=0;j<=8;j++){ flag=strcmp(word, s[j].symbol);if(flag==0) //是关键字{ tokenid.id=j;tokenid.entry=-1;break;} }if(flag!=0){ for(j=0;j<=k;j++){ fflag=strcmp(a[j].idname,word);if(fflag==0) //在符号表中可以找到{ tokenid.id=25;tokenid.entry=a[j].address;break;} }if(fflag!=0){ fs=fopen("symbol.txt","a"); //符号表中不存在的标识符 strcpy(a[k].idname, word);a[k].address=k;a[k].type=25;tokenid.id=25;tokenid.entry=k;for(j=0;j<9;j++)fprintf(fs,"%c",word[j]);fprintf(fs,"%c",'\t');fprintf(fs,"%d",a[k].address);fprintf(fs,"%c",'\t');fprintf(fs,"%d",a[k].type);fprintf(fs,"%c",'\n');fclose(fs);k=k+1;} }strcpy(tokenid.idname, word);//自行添加的return tokenid;};-----------------------------识别数字函数-------------------------- tokentype recogdig(char ch){ int flag;int i=0,j;int num=0;tokentype tokenid;while(isdigit(ch)){ num=(ch-48)+num*10;ch=fgetc(fp);i=i+1;}for(j=0;j<=t;j++)if(d[j].num==num){ flag=1;tokenid.id=26;tokenid.entry=d[j].address;break;}if(flag!=1){ d[t].num=num;d[t].address=t;tokenid.id=26;tokenid.entry=t;t=t+1;}sprintf(tokenid.idname, "%d", num);//int>>charreturn tokenid;};------------------------识别算符和界符函数------------------------- tokentype recogdel(char ch){ tokentype tokenid;switch(ch){ case'{':{ tokenid.id=13;strcpy(tokenid.idname, "{");//自行添加的}break;case'}':{ tokenid.id=14;strcpy(tokenid.idname, "}");}break;case';':{ tokenid.id=12;strcpy(tokenid.idname, ";");}break;case'=':{ tokenid.id=19;strcpy(tokenid.idname, "=");}break;case':':ch=fgetc(fp);if(ch=='=') tokenid.id=23; break;case'!':{ ch=fgetc(fp);if(ch=='=') tokenid.id=20;strcpy(tokenid.idname, "!="); } break;case'<':{ch=fgetc(fp);if(ch=='='){ tokenid.id=18;strcpy(tokenid.idname, "<=");}else{ tokenid.id=17;strcpy(tokenid.idname, "<");ungetc(ch,fp);}}; break;case'>':ch=fgetc(fp);if(ch=='='){tokenid.id=22;strcpy(tokenid.idname, ">=");}else { tokenid.id=21;strcpy(tokenid.idname, ">");ungetc(ch,fp);}; break;case'+':{ tokenid.id=8;strcpy(tokenid.idname, "+");}break;case'*':{ tokenid.id=10;strcpy(tokenid.idname, "*");}break;case'(':{ tokenid.id=15;strcpy(tokenid.idname, "(");}break;case')':{ tokenid.id=16;strcpy(tokenid.idname, ")");}break;}tokenid.entry=-1;return tokenid;};---------------------------handlecom函数--------------------------- tokentype handlecom(char ch){ tokentype tokenid;char ch1;int flag=0;if(ch!='*' ){ tokenid.id=25;tokenid.entry=-1;}else{ while(flag==0){ ch1=ch;ch=fgetc(fp);if((ch1='*')&&(ch='/'))flag=1;}}return tokenid;};---------------------------sort函数---------------------------- void sort(char ch){struct tokentype tokenword;FILE * fq = fopen("tokenfile.txt","a");if(isalpha(ch))tokenword=recogid(ch); //字母else if(isdigit(ch))tokenword=recogdig(ch); //数字else if(ch=='/')tokenword=handlecom(ch);elsetokenword=recogdel(ch);printf("%s\t%d\t%d\n",tokenword.idname,tokenword.id,tokenword.entry) ;fprintf(fq,"%d",tokenword.id);fprintf(fq,"%c",'\t');fprintf(fq,"%d",tokenword.entry);fprintf(fq,"%c",'\n');fclose(fq);};--------------------------scanner函数---------------------------- void scanner(){ char ch;fp=fopen("source.txt","r");ch=getc(fp);while(ch!=EOF){ if(!isspace(ch)){ sort(ch);}ch=fgetc(fp);}fclose(fp);};------------------------------主函数------------------------------ int main(){ int i;printf("输出token字如下:\n");printf("idname\ttype\taddress\n");scanner();printf("************************************\n");printf("输出符号表如下:\n");printf("%s\t%s\t%s\n","idname","address","type");for(i=0;i<=k-1;i++)printf("%s\t%d\t%d\n",a[i].idname,a[i].address,a[i].type);printf("************************************\n"); printf("输出常数表如下:\n");printf("%s\t%s\n","num","address");for(i=0;i<=t-1;i++)printf("%d\t%d\n",d[i].num,d[i].address);printf("\n\n");system("pause");}八.程序测试Source源文件程序截图main(){If a!=35end;do whileend;36}九.实验小结子集构造法的基本思想是构造得到的DFA的每个状态对应于NFA的一个状态集合。
表示集合的三种基本方法
表示集合的三种基本方法
表示集合的三种基本方法是:子集构造法、并集构造法和规格语法(set-builder notation)。
子集构造法是指一个集合可以由他的子集来构成,其中一个集合A包含所有的子集B,C,D,…,那么它就可以用A = {B, C, D, …}来表示。
这种方法也可以把一个复杂的集合分解成几个子集来构造,比如说有一个集合S,它可以由S1和S2构成,那么它可以用S = S1∪S2来表示,它的意思就是S1和S2的并集就是S。
并集构造法是指一个集合可以由它的并集来构成,其中一个集合A包含所有的子集B,C,D,…,那么它就可以用A = ∪{B, C, D, …}来表示。
这种方法可以把一个复杂的集合分解成几个子集来构成,比如说有一个集合S,它可以由S1,S2,S3构成,那么它可以用S = S1∪S2∪S3来表示,它的意思就是S1,S2,S3的并集就是S。
规格语法(set-builder notation)是一种比较抽象的表示方式,它可以用来表示一个集合的成员,比如说有一个集合S={x | x是偶数},那么可以用S={x | x为偶数}来表示,它的意思就是集合S包含所有的偶数。
总之,表示集合的三种基本方法是子集构造法、并集构造法和规格语法(set-builder notation)。
子集构造法
可以将一个复杂的集合分解成几个子集来构成;并集构造法可以将一个复杂的集合由它的并集来构成;规格语法(set-builder notation)可以用来表示一个集合的成员。
3 第三章 有限自动机资料
第一节 有限自动机
一、有限状态系统的概念 状态:状态是可以将事物区分开的一种标识。
具有离散状态的系统:如数字电路(0,1), 十 字路口的红绿灯。离散状态系统的状态数 是有限的. 具有连续状态的系统:比如水库的水位,室内 温度等可以连续变化,即有无穷个状态. 有限状态系统必然是离散状态系统(而且 状态数有限),因为只有有限个状态.
15
College of Computer Science & Technology, BUPT
设计有限自动机
自动机的设计是一个创造过程,没有简单的算法或过程。 技巧:假设自己是机器,思考如何去实现机器的任务。 为判断到目前为止所看到的字符串是否满足某个语言,须估 算出读一个字符串时需要记住哪些关键的东西。
L={x000y | x,y∈{0,1}*}
0, 1 0, 1
q0
0
q1
0
q2
0
q3
比较: 其相应的DFA:
1 1 0, 1
q0
0 1
q1
0
q2
0
q3
College of Computer Science & Technology, BUPT
22
二、NFA的状态转移函数
与 DFA 唯一不同之处 1.δ'(q, ε) = {q}
DFA接收的语言: 被DFA接收的字符串的集合. L(M) = ω ( q0 , ω) F 例:T = {0,1}
1 0 Start 1 0 2 1
接收含有奇数个0的任意串
13
College of Computer Science & Technology, BUPT
博弈论势函数的构造方法
博弈论中的势函数是用来衡量博弈过程中某个状态的稳定性和优劣程度的函数。
构造势函数的方法有很多种,其中一些常见的方法包括:
1. 集合覆盖法:通过将博弈状态空间分解成若干个互不相交的子集,并为每个子集构造一个势函数,然后将这些势函数进行线性组合得到整体的势函数。
2. 构造性方法:通过对博弈状态空间的特定结构进行深入分析,找到能够反映状态演化规律的变量,并构造满足一定条件的势函数。
3. 对偶势函数法:将博弈状态空间的一个势函数与另一个满足一定条件的势函数进行对偶组合,构造出新的势函数。
4. 梯度系统方法:利用梯度系统理论中的技巧,构造出满足一定条件的势函数。
这些方法都是为了在博弈论中寻找一个合适的势函数,以便分析博弈的稳定状态、演化路径等问题。
在具体应用时,选择合适的方法需要根据具体的博弈模型和问题进行综合考虑。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告
编译原理
课程名称
子集构造法
题目
信息与控制工程学院
院(系)
专业班级
姓名
学号
叶娜
指导教师
2017年 4 月 30 日。
目录
一、实验目的 (2)
二、实验要求、内容 (2)
三、实验设备 (2)
四、实验原理及步骤 (2)
五、程序源代码 (4)
六、存在的问题及体会 (5)
精选资料,欢迎下载。
一、实验目的
掌握将非确定有限自动机确定化的方法和过程
二、实验要求、内容
实验要求:
1.输入一个NFA,输出一个接受同一正规集的DFA
2.采用C++语言,实现该算法
3.编制测试程序
4.调试程序
实验步骤:
1. NFA关系图
2. 通过一个转换算法将NFA转换为DFA
3. 显示DFA关系图
三、实验设备
开发系统:Windows 10
开发工具:Visual Studio 2013
四、实验原理及步骤
1、NFA与DFA之间的联系
将NFA转换成等价的DFA的基本思想是让DFA的每一个状态对应NFA的一组状态,也就是说让DFA使用它的状态去记录在NFA读入一个输入符号后可能达到的所有状态,在读入输入符号之后,DFA处在a1a2......an那样一个状态,该状
精选资料,欢迎下载。
精选资料,欢迎下载
态表示这个NFA 的状态的一个子集T ,T 是从NFA 的开始状态沿着某个标记为a1a2......an 可以达到的那些状态构成的。
2、 DFA 的化简
得到新的DFA 之后,并没有完成任务,因为通过NFA 转化成DFA 不一定是最简单的,即有多余的状态可以删除,即NFA 转换成DFA 之后,还需要化简,确定化。
化简DFA 的基本思想是将它的状态分成一些互不相交的子集,每一个子集中的状态都不是等价的,不同子集中的状态可以由某个输入串来区别,最后将不能区别的每个子集用一个状态来做代表,具体方法如下:
(1)将M 的所有状态分成两个子集,即终态集和非终态集;
(2)考察每一个子集,若发现某子集中的状态不等价,将其划分为两个集合; (3)重复第(2)步,继续考察一得到的每一个子集,直到没有任何一个子集需要继续划分为止。
此时DFA 的状态被分为若干个互不相交的子集;
(4)从每个子集中选出一个状态做代表即可得到最简的DFA 。
3、流程图
总模块NFA 图结构
状态转换表
DFA 图结构
初始化状态转
换矩阵
状态转换操作
图3-1程序总框图。
开始
输入NFA,初
始化NFA
初步转化为DFA
重命名化简
结束
图4-2 功能图五、程序源代码
部分代码:
void child_method()
{
int m,n;
for(m=0;m<100;m++)
for(n=0;n<100;n++)
Dtran[m][n]='#';
for(m=0;m<100;m++)
DFA[m].flag=-1;
State S0,U;
S0.flag=0;
S0.count=1;
S0.H[0]=first;
State T;
T=closure(S0);
精选资料,欢迎下载。
T.mark=0;
T.flag=0;
DFA[numof_Dtran++]=T;
memset(useof_DFA,0,sizeof(useof_DFA));
int j=check_inDFA();
int k;
while(j!=-1)
{
useof_DFA[j]=1;
for(k=0;k<numof_char;k++)
{
U=closure(move(DFA[j],alpha[k]));
//if U不在DFA中
if(!check_whetherin_DFA(U))
{ U.mark=numof_Dtran;
DFA[numof_Dtran++]=U;
}
Dtran[DFA[j].mark][U.mark]=alpha[k];
}
j=check_inDFA();
}
}
六、存在的问题及体会
虽然在此之前学习了很多的编程语言,但是对于编程还不是那么熟练。
对于此次的编译原理实验,要求用子集构造法来求NFA转换为DFA的算法实现,由于在课上对于本节的知识点掌握的也只是表面,因而要用算法来实现对于我来说还是有些困难。
对于此次的程序首先需要实现NFA转换为DFA,其次就是NFA的确定化。
这两方面的实现都是有些难度,起初对于程序的实现毫无头绪,之后在同
精选资料,欢迎下载。
学与老师的讲解下有了相应的了解,然后再在网上查阅相关资料以及相关程序算法的博客,向同学请教,解读别人的算法,加深自己的理解。
经过长时间的调试之后,该程序终于得以成功实现。
经过此次的实验,更加加深了我对子集构造法NFA转换DFA相关算法的理解,也更加深刻地认识到上机实践的重要作用,同时使我对编译原理课程的进一步理解,理论与实践结合对于软件开发学习的重要性。
精选资料,欢迎下载。
Welcome !!!
欢迎您的下载,
资料仅供参考!
精选资料,欢迎下载。
