高考数学微专题突破 (28)
正余弦定理与三角形面积公式综合应用-高考数学微专题突破含详解
正余弦定理与三角形面积公式综合应用-高考数学微专题突破一、单选题1．在ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，已知(a ＋b －c )(a ＋b ＋c )＝3ab ，且c ＝4，则ABC 面积的最大值为（ ）A ．B ．C ．D2．已知ABC 三个内角A ，B ，C 及其对边a ，b ，c ，其中，角B 为锐角，b =且()222tan a c bB +-=， 则ABC ∆面积的最大值为（ ）A B C ．34D ．323．在ABC 中，内角A 、B 、C 的对边分别为a ，b ，c ，满足3c =，sin sin 2C c A a =，则ABC 面积的最大值为（ ）A B ．36C D 4．在△ABC 中，M 为BC 上一点，60,2,||4ACB BM MC AM ∠=︒==，则△ABC 的面积的最大值为（ ）A ．B ．C ．12D ．5．在ABC 中，a 、b 、c 分别为内角A 、B 、C 所对的边，且满足b c =，1cos cos bBa A-=，若点O 是ABC 外一点，()0AOB θθπ∠=<<，2OA =，1OB =，则平面四边形OACB 面积的最大值是（ ）A ．44+ BC ．3D ．426．ABC ∆中，已知6BA BC CA CB BC ⋅+⋅=，3A π=，则ABC ∆面积的最大值为（ ）A ．2B ．32C ．D ．47．在三角形ABC 中，已知2,45c C ==︒，则三角形ABC 面积的最大值为（ ）A．2+B ．4C 1D ．4+8．已知锐角ABC ∆的三个内角、、A B C 所对边分别为a b c ，，，若角、、A B C 成等差数列，b =ABC ∆的面积的取值范围（ ）A ．(B ．(C ．⎡⎣D ．⎡⎣9．在△ABC 中，内角△BAC ，△ABC ，C ∠所对的边分别为a ，b ，c ，a =c 且满足cos (cos )cos 0C BAC BAC ABC +∠-∠⋅∠=，若点O 是△ABC 外一点，24OA OB ==，则平面四边形OACB 的面积的最大值为（ ）A ．8+B ．4+C ．12D ．4-10．如图，在Rt△ABC 中，2C π∠=，6B π∠=，AC ＝4，D 在AC 上且AD ：DC ＝3：1，当△AED 最大时，△AED 的面积为（ ）A ．32B ．2C ．3D ．11．锐角ABC ∆的内角,,A B C 的对边分别为,,a b c ，已知sin sin5A C b Aa+=，22BA BC AB AC ⋅+⋅=．则ABC ∆面积的取值范围是（ ）A ．14,33⎛⎫⎪⎝⎭B ．C ．1,2D ．⎭12．在平面内，四边形ABCD 的B 与D ∠互补，1,30DC BC DAC ︒==∠=，则四边形ABCD 面积的最大值=（ ）A B 1 C ．12+ D ．213．在△ABC 中，a ，b ，c 分别为内角A ，B ，C 所对的边，b ＝c ，且满足sin sin B A ＝1cos cos BA-，若点O 是△ABC 外一点，△AOB ＝θ(0<θ<π)，OA ＝2OB ＝2，则平面四边形OACB 面积的最大值是( )A B C ．3 D 二、多选题14．ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，则下列说法正确的是（ ） A ．若A B >，则sin sin A B >B ．若30A =，4b =，3a =，则ABC 有两解 C ．若ABC 为钝角三角形，则222a b c +>D ．若60A =，2a =，则ABC 15．如图，ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ．若a b =，且)cos cos 2sin a C c A b B +=，D 是ABC 外一点，1DC =，3DA =，则下列说法正确的是（ ）A ．ABC 是等边三角形B ．若AC =A ，B ，C ，D 四点共圆C ．四边形ABCD 3D ．四边形ABCD 面积最小值为32- 三、填空题16．锐角ABC 中，内角A 、B 、C 所对的边分别为a 、b 、c ，a b c -=，且a =ABC 面积的取值范围是___________.17．如图，点A 是半径为1的半圆O 的直径延长线上的一点，OA =B 为半圆上任意一点，以AB 为一边作等边ABC ，则四边形OACB 的面积的最大值为___________.18．设ABC 的面积为S ，满足20S AC +⋅=.且||3BC =，若角B 不是最小角，则S 的取值范围是_________.19．在ABC 中，内角A 、B 、C 所对的边分别为a 、b 、c ，a c =且满cos cos )cos 0(C A A B +=若点O 是ABC 外一点，24OA OB ==，则四边形OACB 的面积的最大值为_______________.20．在锐角三角形ABC 中，sin 22C C =，cos cos c B b C +=ABC 的面积的取值范围为______．21．在三角形ABC 中，2AB =，且角A 、B 、C 满足()2712sin cos 2242C A B -=+，三角形ABC 的面积的最大值为M ，则M =______．22．如图所示，在平面四边形ABCD 中，AB BC =，60ABC ∠=，1CD =，2AD =，则四边形ABCD 的面积的最大值为______.23．如图，已知D 为ABC ∆内一点，4AC =，3AD BC ==，ACB ∠与ADB ∠互补，则ACD ∆与BCD ∆面积之和的最大值为_______.24．如图所示，点M ，N 分别在菱形ABCD 的边AD ，CD 上，422,,33AB ABC MBN π=∠=∠=面积的最小值为________．25．在ABC ∆中，三个内角,,A B C 所对的边为,,a b c ，且满足(cos cos )cos 122a Bb A B a b +=+，4c =，则ABC ∆的面积的最大值为__________．26．已知平面四点,,,A B C D 满足2,AB BC CD AD ====设ABD ∆，BCD∆的面积分别为1S ，2S ，则2212S S +的取值范围是__________.27．如图所示，在平面四边形ABCD 中，1AB =，2BC =，ACD △是以D 为顶点的等腰直角三角形，则BCD △面积的最大值为________．四、双空题28．如图，设ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，cos cos )2sin a C c A b B +=，且3CAB π∠=.若点D 是ABC 外一点，1CD =，3AD =，则当D ∠=______时，四边形ABCD 的面积的最大值为____________29．在圆内接四边形ABCD 中，60DAB ∠=︒，BD =，则ADB =∠________，若AC =BCD 面积的最大值为________.30．四边形ABCD 中，60BAD ∠=︒，120BCD ∠=︒，BC =5BD =，则cos BDC ∠=________，AB AC ⋅的最大值________.31．如图，在凸四边形ABCD 中，4,2,AD CD ABC ==为等边三角形，△若60D ︒∠=，则四边形ABCD 的面积为________________；△当D ∠变化时，四边形ABCD 的面积的最大值为_________________.五、解答题32．在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若2sin (2)sin (2)sin a A b c B b c C =+++.（1）求角A 的大小；（2）若a =ABC 面积的最大值.33．已知ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且sin sin 2A Ca b A +=． （1）求角B ；（2）若D 是AC 边的中点，且BD =ABC 面积的最大值．34．在锐角ABC 中，内角,,A B C 所对的边分别为,,a b c ，已知ABC 的面积2224b c a S +-=. （1）求A ；（2）作角B 的平分线交边AC 于点O ，记BOA △和BOC 的面积分别为12,S S ，求12S S 的取值范围.35．在四边形ABCD 中，A C ∠=∠，E 是AD 上的点且满足BED ∆与ABD ∆相似，34AEB π∠=，6DBE π∠=，6DE =.（1）求BD 的长度；（2）求三角形BCD 面积的最大值.36．ABC 中，内角,,A B C 所对的边分别为,,a b c ，已知(sin sin ,sin )a B A C =+，(sin sin ,b B A =-sin sin )C B -，且a b ⊥.（1）求角A 的大小； （2）若a =求__________.△求ABC 周长的最大值；△求ABC 面积的最大值.请考生在．△．和．△．中任选一个作答．．．．．．．，如两个都选，按第一个解答记分.）37．在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且向量()3,2sin m A =-，22cos 1,cos 22A n A ⎛⎫=- ⎪⎝⎭，且//m n ，A 为锐角．（△）求角A 的大小；（△）若2a =，求ABC 的面积的最大值．38．在锐角三角形ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若4sin s sin sin in C B a B C +=.（1）求角A 的大小；（2）若2sin 2sin b B c C bc +=，求ABC 面积的取值范围.39．现给出两个条件：△22cos c a B =，△()2cos cos b A C =，从中选出一个条件补充在下面的问题中，并以此为依据求解问题：（选出一种可行的条件解答，若两个都选，则按第一个解答计分）在ABC ∆中，,,a b c 分别为内角,,A B C 所对的边( ). （1）求A ； （2）若31a ，求ABC ∆面积的最大值.40．已知函数()22sin sin 6x x f x πωω⎛⎫=--⎪⎝⎭（x ∈R ，ω为常数且112ω<<），函数()f x 的图像关于直线x π=对称. （1）求函数()f x 的最小正周期；（2）在ABC ∆中，角A 、B 、C 的对边分别为a 、b 、c ，若1a =，3154f A ⎛⎫= ⎪⎝⎭，求ABC ∆的S 最大值.答案第1页，总40页参考答案1．B 【分析】根据已知条件，反凑余弦定理求得C ，再用余弦定理，借助基本不等式求得ab 的最大值，再利用面积公式即可求得结果. 【详解】由已知等式得a 2＋b 2－c 2＝ab ，则cos C ＝2222a b c ab+-＝2ab ab ＝12．由C △(0，π)，所以sin C又16＝c 2＝a 2＋b 2－ab ≥2ab －ab ＝ab ，则ab ≤16， 当且仅当4a b ==时，取得最大值. 所以ABC S＝12ab sin C ≤12故S max ＝． 故选：B ． 【点睛】本题考查利用余弦定理和基本不等式求面积的最大值，属基础题. 2．A 【分析】由余弦定理求得3B π=，且223ac a c =+-，再由三角形的面积公式和基本不等式可得选项. 【详解】由()222tan a c b β+-=得222tan 22a c b ac β⎛⎫+-= ⎪⎝⎭，所以cos tan ββ=，即sin B =，而02B π<<，所以3B π=，所以1sin 24ABCSac B ac ==，又因为222221cos 322a c b B ac a c ac +-==⇒=+-，所以22323ac a c ac =+-≥-，所以3ac ≤3ac ≤=故选：A. 【点睛】本题考查运用余弦定理解三角形，三角形的面积公式，以及运用基本不等式求最值，属于中档题. 3．B 【分析】由正弦定理结合二倍角公式可得1cos 22C =，进而可得23C π=，再由余弦定理结合基本不等式可得19ab ≤，再由三角形面积公式即可得解. 【详解】由正弦定理得sin sin sin sin 2C C A A =，所以2sin cos sin sin sin 222C C C A A =， 因为()0,A π∈，0,22C π⎛⎫∈ ⎪⎝⎭，所以sin 02C≠，sin 0A ≠， 所以1cos22C =，所以23C π=，23C π=， 由余弦定理得222222cos 3c a b ab C a b ab ab =+-=++≥，又c =133ab ≤即19ab ≤，当且仅当13a b ==时，等号成立，所以ABC 面积111sin 229362S ab C =≤⨯⨯=. 故选：B. 【点睛】本题考查了正弦定理边角互化的应用，考查了余弦定理结合基本不等式求三角形面积的最值，属于中档题. 4．A 【分析】由已知条件，令||AC a =，||BC b =，则在△ACM 中结合余弦定理可知48ab ≤，根据三角形面积公式即可求最大值【详解】由题意，可得如下示意图令||AC a =，||BC b =，又2BM MC =，即有1||||33b CM CB == △由余弦定理知：222||||||2||||cos AM CA CM CA CM ACB =+-∠2221216()332333a ab ab ab abb =+-⨯≥-=，当且仅当3a b =时等号成立△有48ab ≤△11sin 48222ABC S ab C ∆=≤⨯⨯=故选：A 【点睛】本题考查了正余弦定理，利用向量的知识判断线段的长度及比例关系，再由余弦定理并应用基本不等式求三角形两边之积的范围，进而结合三角形面积公式求最值 5．B 【分析】利用正弦定理边角互化思想化简得出c a =，进而可得出ABC 是等边三角形，利用余弦定理求得2c ，然后利用三角形的面积公式可得出四边形OACB 的面积关于θ的函数关系式，利用三角恒等变换化简函数解析式，结合正弦函数的基本性质可求得结果. 【详解】1cos cos b B a A -=，由正弦定理得sin 1cos sin cos B B A A-=，即cos sin sin sin cos A B A A B =-， 即()sin sin cos cos sin sin sin A A B A B A B C =+=+=，由正弦定理得a c =，又b c =，所以，ABC 为等边三角形，则2222cos 54cos c OA OB OA OB θθ=+-⋅=-，2112sin sin2ABCAOBOACB S SSθθθ=+=⨯⨯⨯+=平面四边形2sin 34πθ⎛⎫=-+⎪⎝⎭， 0θπ<<，2333πππθ∴-<-<， 当32ππθ-=时，即当56πθ=时，四边形OACB的面积取最大值84+. 故选：B. 【点睛】四边形的面积往往转化为两个三角形面积之和，从而所求问题转化为三角函数的有界性问题，结合条件易得结果. 6．A 【分析】利用平面向量数量积的运算得出a =利用正弦定理结合三角恒等变换思想将ABC ∆的面积化为以角B 为自变量的正弦型函数，进而可得出ABC ∆面积的最大值. 【详解】由()6BA BC CA CB BC BA AC BC BC BC ⋅+⋅=+=⋅=，得6a BC ==，由正弦定理sin sin sin b c a B C A ===22sin b Bc C⎧=⎪⎨=⎪⎩， 所以ABC ∆面积12sin sinsin 23Sbc A B C BB π⎛⎫===- ⎪⎝⎭)21cos 213sin 3sin cos sin2222B BB B B B B B ⎫-=+=+=+⎪⎪⎝⎭26B π⎛⎫=-+ ⎪⎝⎭，其中20,3B π⎛⎫∈ ⎪⎝⎭，72666B πππ∴-<-<，当262B ππ-=时，ABC ∆ 故选：A. 【点睛】本题考查三角形面积最值的计算，涉及平面向量数量积的运算以及正弦定理的应用，考查计算能力，属于中等题. 7．C 【分析】由余弦定理可得224a b +=，及24ab ≤，可得ab 的最大值，由1sin 2ABC S ab C ∆=可得三角形ABC 面积的最大值. 【详解】解：由余弦定理可得：2222cos 45o c a b ab =+-，可得：224a b +=，可得24ab ≤，可得2(24ab ≤=+=+a b =时，等式成立，由1sin 2ABC S ab C ∆=,可得三角形ABC 面积的最大值为：1(4122⨯+⨯=， 故选：C. 【点睛】本题主要考查利用余弦定义、基本不等式求三角形面积的最大值，属于中档题. 8．B 【分析】根据角、、A B C 成等差数列可得3B π=,再利用面积公式与正弦定理将ABC ∆的面积转换为关于角A 的三角函数式,最后根据A 的取值范围求解函数的范围即可. 【详解】因为角、、A B C 成等差数列,故2B A C B π=+=-,故3B π=.故外接圆直径24sin 2b R B === . 由面积公式与正弦定理有11sin 2sin 2sin sin 22ABCS ac B R A R C B ∆ 243sin sin 43sin sin 23sin 6sin cos 3A C A AA A A π31cos 23sin 223sin 236A A Aπ.又锐角ABC ∆中3B π=,故0022200322A A A C πππππ⎧⎧<<<<⎪⎪⎪⎪⇒⎨⎨⎪⎪<-<<<⎪⎪⎩⎩,即62A ππ<<. 故52,666Aπππ.1sin 2,162Aπ. 故23,3236A π.故选：B 【点睛】本题主要考查了利用面积公式、正弦定理以及三角恒等变换等公式表达三角形面积的解析式,进而根据角度的范围求解面积范围的问题.属于中档题. 9．A 【分析】利用cos cos()C BAC ABC =-∠+∠可整理条件为cos sin sin BAC ABC BAC ABC ∠∠=∠∠,即sin tan cos ABCABC ABC∠=∠=∠,则3ABC π∠=,进而可得△ABC 为等边三角形,设AOB θ∠=,利用三角形面积公式整理可得AOBABCOACB S SS=+四边形8sin 3πθ⎛⎫=-+ ⎪⎝⎭从而求得最值即可【详解】△cos (cos )cos 0C BAC BAC ABC +∠∠∠=, 且cos cos()C BAC ABC =-∠+∠,△cos cos cos cos BAC ABC BAC ABC C ∠∠-∠∠=-=cos()cos cos sin sin BAC ABC BAC ABC BAC ABC ∠+∠=∠∠-∠∠,cos sin sin BAC ABC BAC ABC ∠∠=∠∠, △△BAC 为三角形的内角,sin 0BAC ∠≠,△sin tan cos ABCABC ABC∠=∠=∠由(0,)ABC π∠∈得3ABC π∠=,又△a =c ,△△ABC 为等边三角形, 设AOB θ∠=,则0θπ<<,△AOBABCOACB S SS=+四边形211sin 22OA OB AB θ=⋅+⨯)22142sin 2cos 2OA OB OA OB θθ=⨯⨯⨯++-⋅4sin (164242cos )4θθ=++-⨯⨯⨯4sin 8sin 3πθθθ⎛⎫=-+=-+ ⎪⎝⎭△0θπ<<, △2333πππθ-<-<, △当32ππθ-=,即56πθ=时,sin 3πθ⎛⎫- ⎪⎝⎭取得最大值1,△平面四边形OACB 面积的最大值为8+. 故选：A 【点睛】本题考查余弦和角公式的应用,考查三角形面积最值问题,考查利用正弦型函数求最值【分析】根据条件得到AED AEC DEC ∠=∠-∠,然后设△AED ＝θ,△AEC ＝α,△DEC ＝β,用两角差的正切公式求出tanθ,再用基本不等式求出tanθ最大值,从而得到当△AED 最大时,△AED 的面积. 【详解】解:因为AD :DC ＝3:1,所以DC 14=AC ＝1, 所以S △AED ＝S △ACE ﹣S △DEC 12=AC •CE 12-DC •EC 12=AC •CE 12-•14AC •CE ＝AC •CE (113)288-=AC •EC . 因为AC ＝4,CE ≤CB ,而在Rt △ABC 中,,26C B ππ∠=∠=,AC ＝4,所以CB ＝,△AED ＝△AEC ﹣△DEC . 设△AED ＝θ,△AEC ＝α,△DEC ＝β,则tanθ＝tan (α﹣β)()211AC DCAC DC EC tan tan EC EC AC DC tan tan EC AC DCEC ECαβαβ--⋅-===-⋅+⋅+⋅2333444EC EC EC EC ==≤=++, 当且仅当EC 4EC=,即EC ＝2时,取等号, 所以tanθ的最大值为34,此时△AED 最大, 所以当△AED 最大时,△AED 的面积AEDS =38•4•2＝3. 故选:C . 【点睛】本题考查了三角形的面积公式和利用基本不等式求最值,考查了转化思想和计算能力,属中档题. 11．D 【分析】根据三角关系求出角B ，根据向量数量积求出边c ，作出三角形，数形结合求解.由题sin sin5A C b Aa+=，三角形ABC ∆中，A B C π++=，A C B π+=-， 结合正弦定理，sin sin sin 5sin B B A A π-=，sin sin 5BB π-=，B 为锐角， 所以5B B π-=，=6B π， 22BA BC AB AC⋅+⋅=，即cos cos ac B bcA +=，由射影定理：c = 作图：在1Rt ABC ∆中，12cos6BC π==在2Rt ABC ∆中，22cos6BC ==当点C 在线段12C C 之间（不含端点）时，三角形ABC ∆为锐角三角形，1122ABCSBC=⨯⨯∈⎭， 所以面积取值范围3⎭故选：D 【点睛】此题考查锐角三角形三内角和关系，正余弦定理，边角互化综合应用，重在数形结合思想. 12．B 【分析】根据正弦定理，可求得sin BAC ∠=，即角60BAC ︒∠=或120BAC ︒∠=，分类讨论，由BCD ABDS S S ∆=+，计算三角形的面积，利用均值不等式求最值即可.【详解】因为B 与D ∠互补，sin sin B D ∠=∠，且,,,A B C D 四点共圆.所以30CBD DAC ︒∠=∠=，在ADC 中，由正弦定理得sin sin AC DCD DAC=∠∠，在ABC 中，由正弦定理得sin sin AC BC B BAC =∠∠，所以sin sin BC DCBAC DAC=∠∠，得sin 2BAC ∠=，所以60BAC ︒∠=或120BAC ︒∠=. 设四边形ABCD 的外接圆半径为R ，则2sin DCR DAC=∠，解得1R =.（1）设,AB a AD b ==.当60BAC ︒∠=，则90BAD ︒∠=，故90BCD ︒∠=，此时11sin 9022BCDS︒=⨯=，且2BD =，在Rt △ABD 中，2242a b ab =+，所以2ab ≤，即112ABDSab =⨯. 所以四边形ABCD 面积31BCD ABDS S S∆=++，当且仅当a b =时，四边形ABCD 面1+ （2）当120BAC ︒∠=，则150BAD ︒∠=，故30BCD ︒∠=，所以11sin 302BCDS︒=⨯=.因为2sin BD R BAD =∠，所以1BD =，则在ABD △中由余弦定理得2212cos150a b ab ︒=+-，()2211a b=-+<，即ab <.所以11sin15024ABDS ab ab ︒=⨯=<，此时，四边形ABCD 面积31BCDABDS S S=+<<+.综上，四边形ABCD 面积的最大值等于12+， 故选：B. 【点睛】本题主要考查了正弦定理解三角形，三角形面积公式，均值不等式，属于难题. 13．A 【分析】根据正弦和角公式化简得ABC ∆ 是正三角形，再将平面四边形OACB 面积表示成θ 的三角函数，利用三角函数求得最值. 【详解】由已知得：sin cos sin sin cos ,B A A A B =- 即sin cos sin cos sin ,B A A B A +=所以sin()sin ,A B A += 即sin()sin sin ,C C A π-== 又因为0,0,A C ππ<<<< 所以,A C = 所以,a c =又因为,b c = 所以ABC ∆ 是等边三角形.所以21sin ,23ABC S AB AB AB π∆=⨯⨯= 在ABO ∆中，由余弦定理得2222cos 54cos ,AB AO BO AO BO θθ=+-⨯=- 且1sin sin ,2ABO S AO OB θθ∆=⨯⨯= 因为平面四边形OACB 面积为4cos )sin 2sin()3ABC ABO S S S πθθθ∆∆=+=-+=-+ 当56πθ= 时，sin()3πθ-有最大值1 ，此时平面四边形OACB ， 故选A.【点睛】本题关键在于把所求面积表示成角的三角函数，属于难度题.14．ABD【分析】利用正弦定理结合大边对大角定理可判断A 选项的正误；利用正弦定理可判断B 选项的正误；利用余弦定理可判断C 选项的正误；利用基本不等式、余弦定理结合三角形的面积公式可判断D 选项的正误.【详解】对于A 选项，若A B >，则a b >，由正弦定理可得sin sin a b A B=，所以，sin sin A B >，A 选项正确；对于B 选项，sin 4sin302b A ==，则sin b A a b <<，所以，ABC 有两解，B 选项正确；对于C 选项，若ABC 为钝角三角形且C 为钝角，则222cos 02a b c C ab+-=<，可得222a b c +<，C 选项错误；对于D 选项，由余弦定理与基本不等式可得2222242cos 2a b c bc A b c bc bc bc bc ==+-=+-≥-=，即4bc ≤，当且仅当2b c ==时，等号成立，所以，1sin 24ABC S bc A bc ==≤△，D 选项正确. 故选：ABD.【点睛】方法点睛：求三角形面积的最值是一种常见的类型，主要方法有两类：（1）找到边与边之间的关系，利用基本不等式来求解；（2）利用正弦定理，转化为关于某个角的三角函数，利用函数思想求解.15．AC【分析】利用三角函数恒等变换化简已知等式可求sin B ，再利用a b =，可知ABC 为等边三角形，从而判断A ；利用四点A ，B ，C ，D 共圆，四边形对角互补，从而判断B ；设AC x =，0x >，在ADC 中，由余弦定理可得2106cos x D =-，利用三角形的面积公式，三角函数恒等变换的，可求ABCD S 四边形，利用正弦函数的性质，求出最值，判断CD ．【详解】由正弦定理2sin ,2sin ,2sin a R A b R B c R C ===，(sin cos sin cos )2sin sin A C C A B B +=⋅，2sin ,sin B B =∴= a b =，B 是等腰ABC 的底角，(0,)2B π∴∈，,3B ABC π∴=∴△是等边三角形，A 正确；B 不正确：若,,,A BCD 四点共圆，则四边形对角互补，由A 正确知21,cos 32D D π∠==-，但由于1,3,DC DA AC ===22211cos 232DC DA AC D DA DC +-===-≠-⋅⋅， △B 不正确．C 正确，D 不正确：设D θ∠=，则2222cos 106cos AC DC DA DC DA θθ=+-⋅⋅=-，(106cos )ABC S θθ∴=-=△， 3sin 2ADC S θ=△，3sin 2ABC ADC ABCD S S S θθ∴=+=+四边形13(sin cos 2θθ=⋅-+，3sin()32πθ=-+，(0,),sin()(3πθπθ∈∴-∈，3ABCD S <≤四边形，△C 正确，D 不正确； 故选：AC.．【点睛】本题主要考查正弦定理，余弦定理，三角函数恒等变换，正弦函数的图象和性质在解三角形中的综合应用，考查计算能力和转化思想，属于中档题．16．11,2⎛+ ⎝⎦【分析】利用正弦定理、余弦定理可得出cos A 的值，可求得角A 的值，利用正弦定理、三角恒等变换思想可得出12242ABC S B π⎛⎫=-+ ⎪⎝⎭△，求出角B 的取值范围，利用正弦型函数的基本性质可求得ABC 面积的取值范围.【详解】由正弦定理可得a b c -==222a b c -=，可得222b c a +-=，所以，222cos 2b c a A bc +-==， 0A π<<，4A π∴=， 由正弦定理可得2sin sin sin b c a B C A===，2sin b B ∴=，2sin c C =，()11sin 2sin sin sin sin 224ABC S ac B C B B A B B B π⎛⎫===+=+ ⎪⎝⎭△)211cos 2cos sin sin cos sin sin sin 222B B B B B B B B -=+=+=+12242B π⎛⎫=-+ ⎪⎝⎭， 因为ABC 为锐角三角形，则0224B B ππππ⎧<<⎪⎪⎨⎪<+<⎪⎩，解得42B ππ<<，32444B πππ∴<-<，sin 2124B π⎛⎫<-≤ ⎪⎝⎭，则11122422B π⎛⎫<-+≤ ⎪⎝⎭. 因此，ABC面积的取值范围是11,2⎛ ⎝⎦.故答案为：⎛ ⎝⎦.【点睛】方法点睛：求三角形有关代数式的取值范围是一种常见的类型，主要方法有两类： （1）找到边与边之间的关系，利用基本不等式来求解；（2）利用正弦定理，转化为关于某个角的三角函数，利用函数思想求解.17．【分析】设AOB θ∠=，表示出ABC 的面积及OAB 的面积，进而表示出四边形OACB 的面积，并化简所得面积的解析式为正弦函数形式，再根据三角函数的有界性进行求解．【详解】四边形OACB 的面积OAB =△的面积ABC +△的面积，设AOB θ∠=，2222cos 31214AB OA OB OA OB θθθ∴=+-⋅⋅=+-⨯=-则ABC 的面积213sin 60cos 22AB AC θ=⋅⋅︒=OAB 的面积11sin 122OA OB θθθ=⋅⋅=⨯=，四边形OACB 的面积3cos 2θθ+13(sin )60)2θθθ=-︒，故当6090θ-︒=︒，即150θ=︒时，四边形OACB =故答案为：【点睛】方法点睛：应用余弦定理一定要熟记两种形式：（1）2222cos a b c bc A =+-；（2）222cos 2b c a A bc+-=，同时还要熟练掌握运用两种形式的条件.另外，在解与三角形、三角函数有关的问题时，还需要记住30,45,60︒︒︒等特殊角的三角函数值，以便在解题中直接应用.18．0,4⎛⎫ ⎪ ⎪⎝⎭【分析】先利用20S AC ⋅=解得角A ，然后利用余弦定理及基本不等式解得bc 的取值范围，再根据1sin 2S bc A =求解S 的取值范围. 【详解】由20S AC +⋅=得：sin cos 0bc A A +=，即sin A A =0,解得：[]tan 0A A π=∈，，所以23A π=.又||BC a ==222222cos a b c bc A b c bc =+-=++所以223b c bc ++=，又B 不是最小角，所以22323b c bc bc bc bc =++>+=，得1bc <，故11sin 122S bc A =<⨯=，又0S >，所以0S <<.故答案为：0,4⎛ ⎝⎭.【点睛】本题考查解三角形中三角形面积最值的计算问题，难度一般. 一般地，在△ABC 中，已知一角及其对边求三角形面积最值及周长最值，都采用余弦定理，结合基本不等式得出另外两边之积或两边之和的最值即可得到答案.19．8+【分析】由诱导公式、两角和的余弦公式化简已知的式子,由内角的范围、商的关系、特殊角的三角函数值求出B,结合条件判断出ABC 为等边三角形,设AOB θ∠=求出θ的范围,利用三角形的面积公式与余弦定理,表示出OACB S ,利用辅助角公式化简,由θ的范围和正弦函数的性质求出平面四边形OACB 面积的最大值.【详解】解:cos (cos )cos 0C A A B +-=，cos cos()C A B =-+cos cos cos cos()cos cos sin sin A B A B A B A B A B ∴=+=-cos sin sin A B A B =A 为三角形内角,sin 0A ≠, tanB ∴=∴由(0,)B π∈得,3B π=又a c =, ABC ∴为等边三角形设AOB θ∠=,则0θπ<<211||||sin ||222OACB AOB ABC S S S OA OB AB θ∴=+=⋅+⨯⨯)22142sin ||||2||||cos 24OA OB OA OB θθ=⨯⨯⨯++-⋅4sin 16224cos )4sin θθθθ=++-⨯⨯⨯=-+8sin 3πθ⎛⎫=-+ ⎪⎝⎭0θπ<<,2333πππθ∴-<-< ∴当32ππθ-=,即56πθ=时,sin 3πθ⎛⎫- ⎪⎝⎭取得最大值1,∴平面四边形OACB 面积的最大值为8+【点睛】本题主要考查了诱导公式、两角和的余弦公式、余弦定理、三角形面积公式以及正弦函数的性质，题目较为综合，涉及面较广，属于难题.20． 【分析】利用辅助角公式，结合锐角三角形特点可求得C ；利用余弦定理化简已知等式可求得a ；利用正弦定理和锐角三角形角的大小可确定,sin c B 的取值范围，代入三角形面积公式可得结果.【详解】由sin 22C C =+sin 222sin 23C C C π⎛⎫=-= ⎪⎝⎭sin 232C π⎛⎫∴-= ⎪⎝⎭， ABC 为锐角三角形，0,2C π⎛⎫∴∈ ⎪⎝⎭，22,333C πππ⎛⎫∴-∈- ⎪⎝⎭，3C π∴=，由余弦定理知：222222cos cos 22a c b a b c c B b C a a a+-+-+=+== ABC 为锐角三角形且3C π=，,62A ππ⎛⎫∴∈ ⎪⎝⎭，,62B ππ⎛⎫∈ ⎪⎝⎭， 1sin ,12A ⎛⎫∴∈ ⎪⎝⎭，1sin ,12B ⎛⎫∈ ⎪⎝⎭，由正弦定理知：sin sin sin a C c A A ==∈， 1sin sin 2ABC S ac B B ∴==∈．故答案为：. 【点睛】 本题考查利用正余弦定理求解三角形面积取值范围的问题，关键是能够熟练应用正余弦定理进行边角转化，从而求得所需的边和角的取值范围，代入三角形面积公式求得结果.21．3【分析】由已知利用三角函数恒等变换的应用化简已知等式可得24cos 4cos 10C C ++=，可求得23C π=，利用余弦定理，基本不等式可求ab 的最大值，进而根据三角形的面积公式即可求解．【详解】()28sin 2cos 272C A B =++，即()28sin 2cos 2702C A B -+-=，因为()()21cos 8sin 2cos 282cos 222C C A B C π--+=⋅-- ()2244cos 2cos 244cos 22cos 14cos 4cos 6C C C C C C =--=---=--+， 即24cos 4cos 10C C ++=，解得1cos 2C =-， 0C π<<，所以23C π=， 设a 、b 、c 分别为角A 、B 、C 的对边，由余弦定理得2222cos c a b ab C =+-，即224a b ab =++．又因为22423a b ab ab ab ab =++≥+=，即43ab ≤，当且仅当a b =时等号成立．所以三角形ABC 的面积1sin 2S ab C M ==≤=．【点睛】 本题主要考查了三角函数恒等变换的应用，余弦定理，基本不等式，三角形的面积公式在解三角形中的应用，考查了计算能力和转化思想，属于中档题．22．2+ 【分析】连接AC ，设D θ∠=，利用余弦定理得出2AC 关于θ的表达式，然后利用三角形的面积公式将四边形ABCD 的面积表示为关于θ的三角函数，并利用三角恒等变换思想化简函数解析式，利用正弦函数的有界性可求得结果.【详解】连接AC ，设D θ∠=，则0θπ<<，在ACD 中，2AD =，1CD =，D θ∠=，由余弦定理得2222cos 54cos AC AD CD AD CD θθ=+-⋅=-，AB BC =，60ABC ∠=，ABC ∴是等边三角形，则四边形ABCD 的面积为21sin 24ACD ABC S S S AD CD AC θ=+=⋅⋅+)sin 54cos sin 2sin 3πθθθθθ⎛⎫=-==- ⎪⎝⎭， 0θπ<<，2333πππθ∴-<-<，当32ππθ-=时，四边形ABCD 的面积取最大值24+.故答案为：24+. 【点睛】 本题考查四边形面积最值的计算，涉及余弦定理、三角形面积公式以及正弦函数基本性质的应用，解答的关键就是将面积表示为以某角为自变量的三角函数，考查计算能力，属于中等题.23．92 【分析】由已知得ACD BCD ABC ABD S S S S ∆∆∆∆+=-1134sin 3sin 22ACB BD ADB =⨯⨯∠-⨯⨯⨯∠，转化为求出BD 与ACB ∠关系，设BD x =，在,ABC ABD ∆∆中，用余弦定理分别求出AB ，建立BD 与ACB ∠关系，化简即可.【详解】设BD x =，由余弦定理2222cos 2524cos AB AC BC AC BC ACB ACB =+-⋅∠=-∠2222AB AD BD AD BDcos ADB =+-⋅∠229696x xcos ADB x xcos ACB =+-∠=++∠，则2252496cos ACB x xcos ACB -∠=++∠，整理得2624160x cos ACB x cos ACB +∠⋅+∠-=，解得46x cos ACB =-∠，或4x =-（舍去），于是ACD BCD ABC ABD S S S S S ∆∆∆∆=+=-1134sin 3sin 22ACB x ADB =⨯⨯∠-⨯⨯∠ ()36sin 46cos sin 2ACB ACB ADB =∠--∠∠ 9sin 22ACB =∠ 当4ACB π∠=时，ACD ∆与BCD ∆面积之和S 取得最大值92. 故答案为：92. 【点睛】 本题考查余弦定理解三角形、求面积的最值，解题的关键是利用方程思想将边角关系统一，意在考查直观想象、逻辑推理能力，属于中档题.24．12-【分析】设ABM θ∠=，由此表示出AMB ∠，BNC ∠，利用正弦定理求得BM ，BN ，再由三角形面积公式表示BMN 的面积，从而由三角函数性质求得最小值.【详解】设ABM θ∠=，由题意可知23AMB πθ∠=-，2362BNC πππθθ⎛⎫∠=--=+ ⎪⎝⎭． 在ABM 和BCN 中，由正弦定理，可得sin sin BM AB A AMB =∠，sin sin BN BC C BNC=∠，所以sin sin sin 3AB A BM AMB θ==∠- ⎪⎝⎭sin sin BC C BN BNC ==∠故131222sin cos 3BMN S BM BN πθθ=⋅=⋅⎛⎫- ⎪⎝⎭，其中06πθ．记()2211cos 211sin cos cos sin cos sin 23222222f πθθθθθθθθ+⎛⎫=-=+=+⋅ ⎪⎝⎭1111sin 2cos 2sin 222223πθθθ⎛⎫⎛⎫=+=++ ⎪ ⎪⎝⎭⎝⎭，当且仅当12πθ=时，()f θ取得12+，此时BMN S 取得最小值，故()min 3122BMN S ==-． 【点睛】本题考查由正弦定理解三角形进而表示面积，还考查了利用三角函数性质求最值，属于中档题.25【分析】根据题意，利用边化角公式和两角和与差，正弦公式化简求出2=3C π∠，结合余弦定理和基本不等式求出ab 最大值，最后利用三角形面积公式即可求出ABC ∆的面积的最大值. 【详解】解：由于(cos cos )cos 122a Bb A B a b +=+，4c =， 则：()sin cos cos sin cos 12sin sin 2A B A B B A B +=+，即：sin cos 12sin sin 2C B A B =+， 整理得：2sin cos =2sin sin =2sin cos 2sin cos sin C B A B B C C B B +++，即：2sin cos sin =0B C B +，()sin 2cos 1=0B C +，sin B >0，则1cos =-2C ，2=3C π∴∠， 由余弦定理得：2222cos e a b ab C =+-,22162cos a b ab C =+-，即：221623a b ab ab =+-≥，即：163ab ≤， 当且仅当a b =时，取等号， ab ∴最大值为163， 而ABC ∆的面积为S=1sin 2ab C ，则面积的最大值S=1162sin 233π⨯⨯=，. 【点睛】 本题考查正弦定理和余弦定理的应用，以及基本不等式求最值，还有三角形的面积公式，两角和与差，正弦公式，考查计算能力.26．(12,14⎤⎦【分析】cos 1A C -=，由三角形面积公式可得21S ，22S ，由24BD <<确定cos C 的取值范围后即可得解.【详解】在△ABD 中，2222cos 16BD AB AD AB AD A A =+-⋅⋅=-，在△BCD 中，2222cos 88cos BD BC CD BC CD C C =+-⋅⋅=-，所以1688cos A C -=-cos 1A C -=， 所以2222211sin 1212cos 4S AB AD A A =⋅⋅=-，2222221sin 44cos 4S BC CD C C =⋅⋅=-， 22222121212cos 44cos 8cos 8cos 12S S A C C C +=-+-=--+，因为24BD -<<，所以()288cos 16C BD -=∈-，解得1cos 1C -<<，所以(22221218cos 8cos 128cos 1412,142S S C C C ⎛⎫⎤+=--+=-++∈ ⎪⎦⎝⎭.故答案为：(12,14⎤⎦.【点睛】本题考查了余弦定理和面积公式的应用，考查了函数思想，属于中档题.27．1 【分析】设AC b =，ACB α∠=，ABC β∠=，则BCD ∆的面积12sin()sin()244S DC DC ππαα=⨯+=+，在ABC ∆中，运用余弦定理，表示出AC ，根据ACD ∆是以D 为顶点的等腰直角三角形，得到DC ，代入面积公式，利用三角函数即可求BCD ∆面积的最大值．【详解】在ABC ∆中，设AC b =，ACB α∠=，ABC β∠=在ABC ∆中，1AB =，2BC =，由余弦定理，可得24113cos ()44b b b bα+-==+，由3b b +≥=当且仅当b =即有cos α≥，由于(0,)απ∈ 则06πα<≤，利用余弦定理可得：2222cos AC BC AB BC AB β=+-⋅，化简得：254cos b β=-，又因为ACD ∆是以D 为顶点的等腰直角三角形，则2215=2cos 22DC b β=- ， 在ABC ∆中，由正弦定理可得：sin sin b AB βα=，即：sin sin b αβ=，则sin CD αβ=，由于2222cos (1sin )CD CD αα=- 222sin CD CD α=-221sin 2CD β=- 251=2cos sin 22ββ-- 21cos 2cos 22ββ=-+ 21(2cos )2β=-，即cos cos )CD αβ=- 所以BCD ∆的面积12sin()sin()244S DC DC ππαα=⨯+=+sin cos DC αα=+sin (2cos )222DC αβ=+⨯-(2cos )2222ββ=+- 11=sin cos 122ββ++)124πβ=++当=4πβ时，sin()4πβ+取最大值1，所以BCD ∆的面积的最大值为+12故答案为1+. 【点睛】 本题考查三角形面积的最值的求法，注意运用余弦定理和面积公式，同时考查不等式的运用，属于难题．28．56π 32+【分析】利用正弦定理边角互化结合B 的取值范围可求得3B π∠=，可判断出ABC 为等边三角形，利用余弦定理求得2106cos AC θ=-，利用三角形的面积公式可得出四边形ABCD 的面积关于θ的表达式，利用三角恒等变换思想结合正弦函数的有界性可求得四边形ABCD 面积的最大值及其对应的θ的值，即可得解.【详解】 ()3cos cos 2sin a C c A b B +=，)2sin cos cos sin 2sin A C A C B +=，所以，()()22sin B A C B B π=+=-=，3CAB π∠=，20,3B π⎛⎫∴∠∈ ⎪⎝⎭，可得sin 0B >，sin 2B ∴=，3B π∴∠=， 所以，ABC 为等边三角形，设D θ∠=，则0θπ<<，由余弦定理可得2222cos 106cos AC AD CD AD CD θθ=+-⋅=-，()21sin 106cos 23422ABC S AC πθθ==-=-△， 13sin sin 22ACD S AD CD θθ=⋅=△， 所以，四边形ABCD 的面积为3sin cos 3sin 22232ACD ABC S S S πθθθ⎛⎫=+=+-=-+ ⎪⎝⎭△△， 0θπ<<，2333πππθ∴-<-<，所以，当32ππθ-=时，即当56D πθ∠==时，四边形ABCD 的面积取最大值32+.故答案为：56π；3 【点睛】方法点睛：在解三角形的问题中，若已知条件同时含有边和角，但不能直接使用正弦定理或余弦定理得到答案，要选择“边化角”或“角化边”，变换原则如下：（1）若式子中含有正弦的齐次式，优先考虑正弦定理“角化边”；（2）若式子中含有a 、b 、c 的齐次式，优先考虑正弦定理“边化角”；（3）若式子中含有余弦的齐次式，优先考虑余弦定理“角化边”；（4）代数式变形或者三角恒等变换前置；（5）含有面积公式的问题，要考虑结合余弦定理求解；（6）同时出现两个自由角（或三个自由角）时，要用到三角形的内角和定理.29．90【分析】设AD t =，根据BD =，得到BD =，然后利用余弦定理解得2AB t =，由222AB AD BD =+得解；由AB 是圆的直径，则90ACB ∠=，设BAC θ∠=，表示cos AB θ=，BC θ=，cos BD θ=，60CBD θ∠=-，得到()()1sin 600602BCD S BD BC θθ=⋅⋅-<<，利用三角恒等变换化简为2tan S θ=-+⎭. 【详解】设AD t =，因为BD =，所以BD =，由余弦定理得：)2222cos 60t AB tAB =+-，解得2AB t =，所以222AB AD BD =+，所以90ADB ∠=，所以AB 是圆的直径，则90ACB ∠=，设BAC θ∠=，所以AB =，BC θ=，BD =，60CBD θ∠=-，所以()()1sin 600602ABC S BD BC θθ=⋅⋅-<<，()1sin 602θθ=⨯-，()2sin 60cos θθθ⨯-=，2212sin cos cos θθθθ-=，212tan θθ=-，2tan θ=-+⎭当tan 2θ=时，BCD面积取得最大值为故答案为：（1）90；（2）【点睛】本题主要考查余弦定理，三角恒等变换在平面几何中的应用，还考查了数形结合思想和运算求解的能力，属于中档题.30．4530 【分析】在BCD 中应用正弦定理得sin BDC ∠，然后得余弦值，根据60BAD ∠=︒，120BCD ∠=︒，得ABCD 是圆内接四边形，因此有BAC ADC ∠=∠是确定的角，这样只要求得ABC 面积的最大值即可得AB AC ⋅的最大值，而BC =A 到BC 的距离最大即可，它是线段BC 的中垂线与四边形ABCD 外接圆的交点时，得最大值．【详解】 BCD 中，sin sin BD BC BCD BDC =∠∠，△3sin 5BDC ∠==，BDC ∠为锐角，△4cos 5BDC ∠=，△60BAD ∠=︒，120BCD ∠=︒，△,,,A B C D 四点共圆，△BC =△当A 到BC 的距离最大时，ABC 面积最大，此时A 是边AB 的中垂线与外接圆的交点，设A '在BC 的中垂线上，O 是圆心，E 是BC 中点，则,,A O E '共线，A E BC '⊥，外接圆的直径为52sin sin1203BD R BCD ===∠︒，3OA OB OC '===，又12CE BE BC ===△OE ==A E OA OE ''=+= 11922A BC S BC A E ''=⋅=⨯=△，又113sin sin 2210A BC S AB AC BA C A B A C BDC A B A C ''''''''=⋅∠=⋅∠=⋅△， △3910A B A C ''⋅=，△30A B A C ''⋅=． 又113sin sin 2210ABC S AB AC BAC AB AC BDC AB AC =⋅∠=⋅∠=⋅， △AB AC ⋅的最大值是30． 故答案为：45；30【点睛】本题考查正弦定理，考查四点共圆，三角形面积公式，解题的关键是利用边BC 为定值，BAD ∠为定值，把问题转化为求ABC 面积的最大值，利用点在圆上，由圆的性质可三角形面积最大时点的位置，从而易求解．31． 8+。
2024年高考数学专项复习数列中的奇偶项问题(微专题)(解析版)
数列中的奇偶项问题(微专题)题型选讲题型一、分段函数的奇偶项求和1(深圳市罗湖区期末试题)已知数列a n中，a1=2，na n+1-n+1a n=1n∈N*.(1)求数列a n的通项公式；(2)设b n=a n+1,n为奇数,2a n+1,n为偶数，求数列bn的前100项和.1(2023·黑龙江大庆·统考三模)已知数列a n满足a1+3a2+⋯+2n-1a n=n．(1)证明：1a n是一个等差数列；(2)已知c n=119a n,n为奇数a n a n+2,n为偶数，求数列c n 的前2n项和S2n．2024年高考数学专项复习数列中的奇偶项问题（微专题）（解析版）2(2023·吉林·统考三模)已知数列a n满足a n=2n-2,n为奇数3n-2,n为偶数an的前n项和为S n．(1)求a1，a2，并判断1024是数列中的第几项；(2)求S2n-1．3(2023·安徽蚌埠·统考三模)已知数列a n满足a1=1，a2n+1=a2n+1，a2n=2a2n-1.(1)求数列a n的通项公式；(2)设T n=1a1+1a2+⋯+1a n，求证：T2n<3.4(2023·湖南邵阳·统考三模)记S n 为等差数列{a n }的前n 项和，已知a 3=5,S 9=81，数列{b n }满足a 1b 1+a 2b 2+a 3b 3+⋯+a n b n =n -1 ⋅3n +1+3.(1)求数列{a n }与数列{b n }的通项公式；(2)数列{c n }满足c n =b n ,n 为奇数1a n a n +2,n 为偶数，n 为偶数，求{c n }前2n 项和T 2n .5(2023·湖南岳阳·统考三模)已知等比数列a n 的前n 项和为S n ，其公比q ≠-1，a 4+a 5a 7+a 8=127，且S 4=a 3+93．(1)求数列a n 的通项公式；(2)已知b n =log 13a n ,n 为奇数a n,n 为偶数，求数列b n 的前n 项和T n ．2【2020年新课标1卷文科】数列{a n}满足a n+2+(-1)n a n=3n-1，前16项和为540，则a1=1(2021·山东济宁市·高三二模)已知数列{a n}是正项等比数列，满足a3是2a1、3a2的等差中项，a4=16．(1)求数列{a n}的通项公式；log，求数列{b n}的前n项和T n．(2)若b n=-1n⋅2a2n+12【2022·广东省深圳市福田中学10月月考】已知等差数列{a n}前n项和为S n，a5=9，S5=25.(1)求数列{a n}的通项公式及前n项和S n；(2)设b n=(-1)n S n，求{b n}前n项和T n.n n+13(2023·广东深圳·统考一模)记S n，为数列a n的前n项和，已知S n=a n2+n2+1，n∈N*．(1)求a1+a2，并证明a n+a n+1是等差数列；(2)求S n．1(2022·湖北省鄂州高中高三期末)已知数列a n满足a1=1，a n+a n+1=2n；数列b n前n项和为S n，且b1=1，2S n=b n+1-1.(1)求数列a n和数列b n的通项公式；(2)设c n=a n⋅b n，求c n前2n项和T2n.2(2022·湖北省鄂州高中高三期末)已知数列a n前n项和满足a1=1，a n+a n+1=2n；数列b n为S n，且b1=1，2S n=b n+1-1.(1)求数列a n的通项公式；和数列b n(2)设c n=a n⋅b n，求c n前2n项和T2n.数列中的奇偶项问题(微专题)题型选讲题型一、分段函数的奇偶项求和1(深圳市罗湖区期末试题)已知数列a n中，a1=2，na n+1-n+1a n=1n∈N*.(1)求数列a n的通项公式；(2)设b n=a n+1,n为奇数,2a n+1,n为偶数，求数列bn的前100项和.【解析】【小问1详解】∵na n+1-n+1a n=1,∴a n+1n+1-a nn=1n-1n+1,a n+1+1n+1=a n+1n，所以a n+1n是常数列，即a n+1n=a1+11=3,∴a n=3n-1；【小问2详解】由(1)知，a n是首项为2，公差为3等差数列，由题意得b2n-1=a2n-1=6n-4，b2n=2a2n+1=12n+4，设数列b2n-1，b2n的前50项和分别为T1，T2，所以T1=50b1+b992=25×298=7450，T2=50×b2+b1002=25×620=15500，所以b n的前100项和为T1+T2=7450+15500=22950；综上，a n=3n-1，b n的前100项和为T1+T2=7450+15500=22950.1(2023·黑龙江大庆·统考三模)已知数列a n满足a1+3a2+⋯+2n-1a n=n．(1)证明：1a n是一个等差数列；(2)已知c n=119a n,n为奇数a n a n+2,n为偶数，求数列c n 的前2n项和S2n．【答案】(1)证明见详解(2)S2n=2n-1n19+n34n+3【详解】(1)当n=1时，可得a1=1，当n≥2时，由a1+3a2+⋯+2n-1a n=n，则a1+3a2+⋯+2n-3a n-1=n-1n≥2，上述两式作差可得a n=12n-1n≥2，因为a1=1满足a n=12n-1，所以a n的通项公式为a n=12n-1，所以1a n=2n-1，因为1a n-1a n-1=2n-1-2n-3=2(常数)，所以1a n是一个等差数列．(2)c n=2n-119,n为奇数12n-12n+3,n为偶数 ，所以C1+C3+⋯C2n-1=1+5+9+⋯4n-319=2n-1n19，C2+C4+⋯C2n=1413-17+17-111+⋯+14n-1-14n+3=n34n+3所以数列c n的前2n项和S2n=2n-1n19+n34n+3．2(2023·吉林·统考三模)已知数列a n满足a n=2n-2,n为奇数3n-2,n为偶数an的前n项和为S n．(1)求a1，a2，并判断1024是数列中的第几项；(2)求S2n-1．【答案】(1)a1=12，a2=4；1024是数列a n的第342项(2)S2n-1=4n6+3n2-5n+116【详解】(1)由a n=2n-2,n为奇数3n-2,n为偶数可得a1=12，a2=4．令2n-2=1024=210，解得：n=12为偶数，不符合题意，舍去；令3n-2=1024，解得：n=342，符合题意．因此，1024是数列a n的第342项．(2)S2n-1=a1+a2+a3+a4+⋅⋅⋅+a2n-2+a2n-1=12+4+2+10+⋅⋅⋅+6n-8+22n-3=12+2+⋅⋅⋅+22n-3+4+10+⋅⋅⋅+6n-8=121-4n1-4+n-14+6n-82=164n-1+n-13n-2=4n6+3n2-5n+116．另解：由题意得a2n-1=22n-3，又a2n+1a2n-1=4，所以数列a2n-1是以12为首项，4为公比的等比数列．a2n=6n-2，又a2n+2-a2n=6，所以数列a2n是以4为首项，6为公差的等差数列．S2n-1为数列a2n-1的前n项和与数列a2n的前n-1项和的总和．故S2n-1=121-4n1-4+n-14+6n-82=164n-1+n-13n-2=4n6+3n2-5n+116.3(2023·安徽蚌埠·统考三模)已知数列a n满足a1=1，a2n+1=a2n+1，a2n=2a2n-1.(1)求数列a n的通项公式；(2)设T n=1a1+1a2+⋯+1a n，求证：T2n<3.【答案】(1)a n=2n+12-1,n为奇数, 2n2+1-2,n为偶数.(2)证明见解析.【详解】(1)由题意a2n+1=a2n+1=2a2n-1+1,所以a2n+1+1=2a2n-1+1,因为a1+1=2≠0,所以数列a2n-1+1是首项为2,公比为2的等比数列,所以a2n-1+1=2n,即a2n-1=2n-1,而a2n=2a2n-1=2n+1-2,所以a n=2n+12-1,n为奇数, 2n2+1-2,n为偶数.(2)方法一：由(1)得T2n=ni=11a2i-1+1a2i=32ni=112i-1=32ni=12i+1-12i-12i+1-1<32ni=12i+12i-12i+1-1=3ni=12i2i-12i+1-1=3ni=112i-1-12i+1-1=31-12n+1-1<3方法二：因为2n-1≥2n-1n∈N*,所以T2n=∑ni=11a2i-1+1a2i=32∑n i=112i-1≤32∑n i=112i-1=31-12n<34(2023·湖南邵阳·统考三模)记S n为等差数列{a n}的前n项和，已知a3=5,S9=81，数列{b n}满足a 1b 1+a 2b 2+a 3b 3+⋯+a n b n =n -1 ⋅3n +1+3.(1)求数列{a n }与数列{b n }的通项公式；(2)数列{c n }满足c n =b n ,n 为奇数1a n an +2,n 为偶数，n 为偶数，求{c n }前2n 项和T 2n .【答案】(1)a n =2n -1,b n =3n (2)T 2n =3⋅9n 8-116n +12-724【详解】(1)设等差数列{a n }的公差为d ，∵a 3=5S 9=81 ，即a 1+2d =59a 1+9×82d =81 ，∴a 1=1,d =2，∴a n =2n -1.∵a 1b 1+a 2b 2+a 3b 3+⋯+a n b n =n -1 ⋅3n +1+3，①∴a 1b 1+a 2b 2+⋯+a n -1b n -1=n -2 ⋅3n +3n ≥2 ，②所以①-②得，a n b n =2n -1 ⋅3n ，∴b n =3n n ≥2 .当n =1时，a 1b 1=3,b 1=3，符合b n =3n .∴b n =3n .(2)T 2n =c 1+c 2+c 3+⋯+c 2n ，依题有：T 2n =b 1+b 3+⋯+b 2n -1 +1a 2a 4+1a 4a 6+⋯+1a 2n a 2n +2.记T 奇=b 1+b 3+⋯+b 2n -1，则T 奇=3(1-32n )1-32=32n +1-38.记T 偶=1a 2a 4+1a 4a 6+⋯+1a 2n a 2n +2，则T 偶=12d 1a 2-1a 4 +1a 4-1a 6 +⋯+1a 2n -1a 2n +2=12d 1a 2-1a 2n +2=1413-14n +3 .所以T 2n =32n +1-38+1413-14n +3 =3⋅9n 8-116n +12-7245(2023·湖南岳阳·统考三模)已知等比数列a n 的前n 项和为S n ，其公比q ≠-1，a 4+a 5a 7+a 8=127，且S 4=a 3+93．(1)求数列a n 的通项公式；(2)已知b n =log 13a n ,n 为奇数a n,n 为偶数，求数列b n 的前n 项和T n ．【答案】(1)a n =3n (2)T n =18×3n +1-98-n +1 24,n 为奇数983n -1-n 24,n 为偶数【详解】(1)因为a n 是等比数列，公比为q ≠-1，则a 4=a 1q 3,a 5=a 1q 4，a 7=a 1q 6,a 8=a 1q 7，所以a 4+a 5a 7+a 8=a 1q 3+a 1q 4a 1q 6+a 1q 7=1q 3=127，解得q =3，由S 4=a 3+93，可得a 11-34 1-3=9a 1+93，解得a 1=3，所以数列a n 的通项公式为a n =3n ．(2)由(1)得b n =-n ,n 为奇数3n ,n 为偶数，当n 为偶数时，T n =b 1+b 2+⋅⋅⋅+b n =b 1+b 3+⋅⋅⋅+b n -1 +b 2+b 4+⋅⋅⋅+b n =-1+3+⋅⋅⋅+n -1 +32+34+⋅⋅⋅+3n=-n2⋅1+n -12×+91-9n 21-9=983n -1 -n 24；当n 为奇数时T n =T n +1-b n +1=983n +1-1 -n +1 24-3n +1=18×3n +1-98-n +1 24；综上所述：T n =18×3n +1-98-n +1 24,n 为奇数983n -1-n 24,n 为偶数.题型二、含有(-1)n 类型2【2020年新课标1卷文科】数列{a n }满足a n +2+(-1)n a n =3n -1，前16项和为540，则a 1=【答案】7【解析】a n +2+(-1)n a n =3n -1，当n 为奇数时，a n +2=a n +3n -1；当n 为偶数时，a n +2+a n =3n -1.设数列a n 的前n 项和为S n ，S 16=a 1+a 2+a 3+a 4+⋯+a 16=a 1+a 3+a 5⋯+a 15+(a 2+a 4)+⋯(a 14+a 16)=a 1+(a 1+2)+(a 1+10)+(a 1+24)+(a 1+44)+(a 1+70)+(a 1+102)+(a 1+140)+(5+17+29+41)=8a 1+392+92=8a 1+484=540，∴a 1=7.故答案为：7.1(2021·山东济宁市·高三二模)已知数列{a n }是正项等比数列，满足a 3是2a 1、3a 2的等差中项，a 4=16．(1)求数列{a n }的通项公式；(2)若b n =-1 n ⋅2a 2n +1log ，求数列{b n }的前n 项和T n ．【解析】(1)设等比数列{a n }的公比为q ，因为a 3是2a 1、3a 2的等差中项，所以2a 3=2a 1+3a 2，即2a 1q 2=2a 1+3a 1q ，因为a 1≠0，所以2q 2-3q -2=0，解得q =2或q =-12，因为数列{a n }是正项等比数列，所以q =2．因为a 4=16，即a 4=a 1q 3=8a 1=16，解得a 1=2，所以a n =2×2n -1=2n ；(2)解法一：(分奇偶、并项求和)由(1)可知，a 2n +1=22n +1，所以，b n =-1 n ⋅2a 2n +1log =-1 n ⋅222n +1log =-1 n ⋅2n +1 ，①若n 为偶数，T n =-3+5-7+9-⋯-2n -1 +2n +1 =-3+5 +-7+9 +⋯+-2n -1 +2n +1 =2×n2=n ；②若n 为奇数，当n ≥3时，T n =T n -1+b n =n -1-2n +1 =-n -2，当n =1时，T 1=-3适合上式，综上得T n =n ,n 为偶数-n -2,n 为奇数(或T n =n +1 -1 n -1，n ∈N *)；解法二：(错位相减法)由(1)可知，a 2n +1=22n +1，所以，b n =-1 n ⋅2a 2n +1log =-1 n ⋅222n +1log =-1 n ⋅2n +1 ，T n =-1 1×3+-1 2×5+-1 3×7+⋯+-1 n ⋅2n +1 ，所以-T n =-1 2×3+-1 3×5+-1 4×7+⋯+-1 n +1⋅2n +1 所以2T n =3+2[-1 2+-1 3+⋯+-1 n ]--1 n +12n +1 ，=-3+2×1--1 n -12+-1 n 2n +1 =-3+1--1 n -1+-1 n 2n +1=-2+2n +2 -1 n ，所以T n=n+1-1n-1，n∈N*2【2022·广东省深圳市福田中学10月月考】已知等差数列{a n}前n项和为S n，a5=9，S5=25.(1)求数列{a n}的通项公式及前n项和S n；(2)设b n=(-1)n S n，求{b n}前n项和T n.【答案】(1)a n=2n-1，S n=n2；(2)T n=(-1)n n(n+1)2.【解析】【分析】(1)利用等差数列的基本量，列方程即可求得首项和公差，再利用公式求通项公式和前n项和即可；(2)根据(1)中所求即可求得b n，对n分类讨论，结合等差数列的前n项和公式，即可容易求得结果.【详解】(1)由S5=5(a1+a5)2=5×2a32=5a3=25得a3=5.又因为a5=9，所以d=a5-a32=2，则a3=a1+2d=a1+4=5，解得a1=1；故a n=2n-1，S n=n(1+2n-1)2=n2.(2)b n=(-1)n n2.当n为偶数时：T n=b1+b2+b3+b4+⋯+b n-1+b n=-12+22+-32+42+⋯+-(n-1)2+n2=(2-1)×(2+1)+(4-3)×(4+3)+⋯+[n-(n-1)]×[n+(n-1)] =1+2+3+⋯+(n-1)+n=n(n+1)2.当n为奇数时：T n=b1+b2+b3+b4+⋯+b n-2+b n-1+b n=-12+22+-32+42+-(n-2)2+(n-1)2-n2=(2-1)×(2+1)+(4-3)×(4+3)+⋯+[(n-1)-(n-2)]×[(n-1)+(n-2)]-n2 =1+2+3+⋯+(n-2)+(n-1)-n2=(n-1)(1+n-1)2-n2=-n(n+1)2.综上得T n=(-1)n n(n+1)2题型三、a n+a n+1类型3(2023·广东深圳·统考一模)记S n，为数列a n的前n项和，已知S n=a n2+n2+1，n∈N*．(1)求a1+a2，并证明a n+a n+1是等差数列；(2)求S n．【解析】(1)已知S n=a n2+n2+1，n∈N*当n=1时，a1=a12+2，a1=4；当n=2时，a1+a2=a22+5，a2=2，所以a1+a2=6．因为S n=a n2+n2+1①，所以S n+1=a n+12+n+12+1②．②-①得，a n+1=a n+12-a n2+n+12-n2，整理得a n+a n+1=4n+2，n∈N*，所以a n+1+a n+2-a n+a n+1=4n+1+2-4n+2=4(常数)，n∈N*，所以a n+a n+1是首项为6，公差为4的等差数列．(2)由(1)知，a n-1+a n=4n-1+2=4n-2，n∈N*，n≥2．当n为偶数时，S n=a1+a2+a3+a4+⋯+a n-1+a n=n26+4n-22=n2+n；当n为奇数时，S n=a1+a2+a3+a4+a5+⋯+a n-1+a n=4+n-1210+4n-22=n2+n+2．综上所述，S n=n2+n,当n为偶数时n2+n+2,当n为奇数时1(2022·湖北省鄂州高中高三期末)已知数列a n满足a1=1，a n+a n+1=2n；数列b n前n项和为S n，且b1=1，2S n=b n+1-1.(1)求数列a n和数列b n的通项公式；(2)设c n=a n⋅b n，求c n前2n项和T2n.【答案】(1)a n=n,n=2k-1,k∈Zn-1,n=2k,k∈Z，bn=3n-1；(2)58n-59n8.【分析】(1)根据递推公式，结合等差数列的定义、等比数列的定义进行求解即可；(2)利用错位相减法进行求解即可.(1)n ≥2，a n -1+a n =2n -1 ，∴a n +1-a n -1=2，又a 1=1，a 2=1，n =2k -1(k 为正整数)时，a 2k -1 是首项为1，公差为2的等差数列,∴a 2k -1=2k -1，a n =n ，n =2k (k 为正整数)时，a 2k 是首项为1，公差为2的等差数列.∴a 2k =2k -1，∴a n =n -1，∴a n =n ,n =2k -1,k ∈Zn -1,n =2k ,k ∈Z，∵2S n =b n +1-1，∴n ≥2时，2S n -1=b n -1，∴2b n =b n +1-b n ，又b 2=3，∴n ≥2时，b n =3n -1，b 1=1=30，∴b n =3n -1；(2)由(1)得c n =n 3n -1,n =2k -1,k ∈Zn -1 3n -1,n =2k ,k ∈Z ，T 2n =1×30+3×32+5×34+⋅⋅⋅+2n -1 ⋅32n -2 +1×31+3×33+5×35+⋅⋅⋅+2n -1 ⋅32n -1 =41×30+3×32+5×34+⋅⋅⋅2n -1 ⋅32n -2 设K n =1×30+3×32+5×34+⋅⋅⋅2n -1 ⋅32n -2 ①则9K n =1×32+3×34+5×36+⋅⋅⋅+2n -1 ⋅32n ②①-②得-8K n =1+232+34+⋅⋅⋅+32n -2-2n -1 ⋅32n=5+8n -5 9n-4，K n =5+8n -5 9n 32，∴T 2n =58n -5 9n82(2022·湖北省鄂州高中高三期末)已知数列a n 满足a 1=1，a n +a n +1=2n ；数列b n 前n 项和为S n ，且b 1=1，2S n =b n +1-1.(1)求数列a n 和数列b n 的通项公式；(2)设c n =a n ⋅b n ，求c n 前2n 项和T 2n .【答案】(1)a n =n ,n =2k -1,k ∈Zn -1,n =2k ,k ∈Z，b n =3n -1；(2)58n -5 9n8.【解析】(1)根据递推公式，结合等差数列的定义、等比数列的定义进行求解即可；(2)利用错位相减法进行求解即可.(1)n ≥2，a n -1+a n =2n -1 ，∴a n +1-a n -1=2，又a 1=1，a 2=1，n =2k -1(k 为正整数)时，a 2k -1 是首项为1，公差为2的等差数列,∴a 2k -1=2k -1，a n =n ，n =2k (k 为正整数)时，a 2k 是首项为1，公差为2的等差数列.∴a 2k =2k -1，∴a n =n -1，∴a n =n ,n =2k -1,k ∈Zn -1,n =2k ,k ∈Z，∵2S n =b n +1-1，∴n ≥2时，2S n -1=b n -1，∴2b n =b n +1-b n ，又b 2=3，∴n ≥2时，b n =3n -1，b 1=1=30，∴b n =3n -1；(2)由(1)得c n =n 3n -1,n =2k -1,k ∈Zn -1 3n -1,n =2k ,k ∈Z ，T 2n =1×30+3×32+5×34+⋅⋅⋅+2n -1 ⋅32n -2 +1×31+3×33+5×35+⋅⋅⋅+2n -1 ⋅32n -1 =41×30+3×32+5×34+⋅⋅⋅2n -1 ⋅32n -2 设K n =1×30+3×32+5×34+⋅⋅⋅2n -1 ⋅32n -2 ①则9K n =1×32+3×34+5×36+⋅⋅⋅+2n -1 ⋅32n ②①-②得-8K n =1+232+34+⋅⋅⋅+32n -2-2n -1 ⋅32n=5+8n -5 9n-4，K n =5+8n -5 9n 32，∴T 2n =58n -5 9n8。
高三数学二轮复习专题突破课件：解析几何
A．[1，＋∞) B．[－1，－ )
3
C．( ，1]
4
4
D．(－∞，－1]
答案：B
解析：∵y＝kx＋4＋2k＝k(x＋2)＋4，所以直线过定点(－2，4)，曲线y＝
4 − x 2 变形为x2＋y2＝4(y≥0)，表示圆的上半部分，当直线与半圆相切时直线斜
3
率为k＝－ ，当直线过点(2，0)时斜率为－1，结合图象可知实数k的取值范围是
a=2
所以 ሺ2 − 3 − ሻ2 + 2 = 2 ，解得 b = 1 .
r=2
2 + ሺ1 − ሻ2 = 2
所以圆的方程为(x－2)2＋(y－1)2＝4.
4．[2023·广东深圳二模]过点(1，1)且被圆x2 ＋y2 －4x－4y＋4＝0所
x＋y－2＝0
截得的弦长为2 2的直线的方程为___________．
－2)的距离为 2 − 0 2 + 0 + 2 2 ＝2 2，由于圆心
α
2
5
＝
2 2 2 2
α
αபைடு நூலகம்
α ＝ 2sin cos ＝
2
2
与点(0，－2)的连线平分角α，所以sin ＝
10
α
6
， 所 以 cos ＝ ， 所 以 sin
4
2
4
10
6
15
2×
× ＝ .故选B.
4
4
4
r
＝
(2)[2023·河南郑州二模]若圆C1：x2＋y2＝1与圆C2：(x－a)2＋(y－b)2
解析：圆x2＋y2－4x－4y＋4＝0，即(x－2)2＋(y－2)2＝4，
圆心为(2，2)，半径r＝2，
利用频率直方图求中位数、众数、平均数-高考数学微专题突破含详解
高考数学微专题突破利用频率分布直方图求中位数、平均数、总数一、单选题1．某校为了解高二年级学生某次数学考试成绩的分布情况，从该年级的1120名学生中随机抽取了100名学生的数学成绩，发现都在[]80,150内现将这100名学生的成绩按照[)8090，，[)90100，，[)100110，，[)110120，，[)120130，，[)130140，，[]140150，分组后，得到的频率分布直方图如图所示，则下列说法正确的是（）A ．频率分布直方图中a 的值为0.040B ．样本数据低于130分的频率为0.3C ．总体的中位数（保留1位小数）估计为123.3分D ．总体分布在[)90100，的频数一定与总体分布在[)100110，的频数相等2．2020年，一场突如其来的“新型冠状肺炎”使得全国学生无法在春季正常开学，不得不在家“停课不停学”.为了解高三学生居家学习时长，从某校的调查问卷中，随机抽取n 个学生的调查问卷进行分析，得到学生可接受的学习时长频率分布直方图（如下图所示），已知学习时长在[)9,11的学生人数为25，则n 的值为（）A ．40B ．50C ．80D ．1003．某地工商局对辖区内100家饭店进行卫生检查并评分，分为甲、乙、丙、丁四个等级，其中分数在[)60,70，[)70,80，[)80,90，[]90,100内的等级分别为：丁、丙、乙、甲，对饭店评分后，得到频率分布折线图，如图所示，估计这些饭店得分的平均数是（）A ．80.5B ．80.6C ．80.7D ．80.84．下面是甲、乙两位同学高三上学期的5次联考数学成绩，现在只知其从第1次到第5次分数所在区间段分布的条形图（从左至右依次为第1至第5次），则从图中可以读出一定正确的信息是（）A ．甲同学的成绩的平均数大于乙同学的成绩的平均数B ．甲同学的成绩的方差大于乙同学的成绩的方差C ．甲同学的成绩的极差小于乙同学的成绩的极差D．甲同学的成绩的中位数小于乙同学的成绩的中位数5．下面是追踪调查200个某种电子元件寿命（单位:h)频率分布直方图，如图：其中300-400、400-500两组数据丢失，下面四个说法中有且只有一个与原数据相符，这个说法是①寿命在300-400的频数是90；②寿命在400-500的矩形的面积是0.2；③用频率分布直方图估计电子元件的平均寿命为：⨯+⨯+⨯+⨯+⨯1500.12500.153500.454500.155500.15④寿命超过400h的频率为0.3A．①B．②C．③D．④6．为了解某电子产品的使用寿命，从中随机抽取了100件产品进行测试，得到图示统计图.依据统计图，估计这100件产品使用寿命的中位数为（）A．218.25B．232.5C．231.25D．241.25 7．为了让学生了解社会，拓宽视野，丰富知识，提高社会实践能力和综合素质，哈三中团委组织学生参加了抽测一批棉花的纤维长度(单位：cm)的社会实践活动.利用所学习的数学知识，同学们作出了样本的频率分布直方图.现在，由于原始数据不全，只能通过直方图来估计这一批棉花的纤维长度的平均值(同一组数据用这组数据所在区间的中点的值代替).则估计的平均值为（）A．21.75B．22.25C．23.75D．20.75 8．为了了解某校九年级1600名学生的体能情况，随机抽查了部分学生，测试1分钟仰卧起坐的成绩(次数)，将数据整理后绘成如图所示的频率分布直方图，根据统计图的数据，下列结论错误的是（）A．该校九年级学生1分钟仰卧起坐的次数的中位数为26.25次B．该校九年级学生1分钟仰卧起坐的次数的众数为27.5次C．该校九年级学生1分钟仰卧起坐的次数超过30次的人数约有320人D．该校九年级学生1分钟仰卧起坐的次数少于20次的人数约有32人9．某地气象局把当地某月(共30天)每一天的最低气温作了统计，并绘制了如下图所示的统计图.记这组数据的众数为M，中位数为N，平均数为P，则（）A ．M N P <<B ．N M P <<C ．P M N <=D ．P N M<<10．在某次高中学科竞赛中，4000名考生的参赛成绩按[)40,50，[)50,60，[)60,70，[)70,80，[)80,90，[)90,100分成六组，其频率分布直方图如图所示，则下列说法中错误的是（）.A ．成绩在[)70,80内的考生人数最多B ．不及格（60分以下）的考生人数约为1000人C ．考生竞赛成绩平均分的估计值为70.5分D ．考生竞赛成绩中位数的估计值为75分11．在2019年某省普通高中学业水平考试（合格考）中，对全省所有考生的物成绩进行统计，可得到如图所示的频率分布直方图，其中分组的区间为[)40,50，[)50,60，[)60,70，[)80,90，[]90,100，90分以上为优秀，则下列说法中不正确的是（）A ．从全体考生中随机抽取1000人，则其中得优秀考试约有100人B ．若要全省的合格考通过率达到96%，则合格分数线约为44分C ．若同一组中数据用该组区间中间值作代表值，可得考试物理成绩的平均分约为70D ．该省考生物理成绩的中位数为75分第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题12．某中学举行电脑知识竞赛，现将高一参赛学生的成绩进行整理后分成五组，绘制成如图所示的频率直方图，已知图中从左到右的第一､二､三､四､五小组的频率分别是0.30，0.40，0.15，0.10，0.05.则估计高一参赛学生的成绩的众数､中位数分别为____________.13．某仪器厂从新生产的一批零件中随机抽取40个检测，如图是根据抽样检测后零件的质量（单位：g ）绘制的频率分布直方图，样本数据分为8组，分别为[)80,82，[)82,84，[)84,86，[)86,88，[)88,90，[)90,92，[)92,94，[]94,96，则样本的中位数在第______组14．某中学举行了一场音乐知识竞赛，将参赛学生的成绩进行整理后分为5组，绘制如图所示的频率分布直方图.根据频率分布直方图，同一组数据用该区间的中点值代替，估计这次竞赛的平均成绩为______分.三、双空题15．根据高二某班50名同学的数学成绩，绘制频率分布直方图如图所示，虽不小心将其中一个数据污染了，但依然可以推断这个被污染的数据为_________，该班同学的成绩众数为_________.16．中小学生的视力状况受到社会的广泛关注，某市有关部门从全市6万名高一学生中随机抽取了400名，对他们的视力状况进行一次调查统计，将所得到的有关数据绘制成频率分布直方图，如图所示.从左至右五个小组的频率之比依次是5∶7∶12∶10∶6，则这400名学生视力的众数为________，中位数为________.四、解答题17．有一种鱼的身体吸收汞，一定量身体中汞的含量超过其体重的61.0010-⨯的鱼被人食用后，就会对人体产生危害．某海鲜市场进口了一批这种鱼，质监部门对这种鱼进行抽样检测，在30条鱼的样本中发现的汞含量（乘以百万分之一）如下：0.070.340.950.98 1.020.98 1.37 1.400.39 1.021.44 1.580.54 1.080.710.70 1.20 1.24 1.62 1.681.85 1.300.810.820.84 1.39 1.262.200.91 1.31（1）完成下面频率分布表，并画出频率分布直方图；频率分布表：分组频数频率[)0,0.50[) 0.50,1.001 3[) 1.00,1.50[) 1.50,2.002 15[)2.00,2.5011 30合计301频率分布直方图：（2）根据频率分布直方图估算样本数据的平均值（保留小数点后两位，同一组中的数据用该组区间中点值代表），并根据频率分布直方图描述这批鱼身体中汞含量的分布规律．18．经历过疫情，人们愈发懂得了健康的重要性，越来越多的人们加入了体育锻炼中，全民健身，利国利民，功在当代，利在千秋．一调研员在社区进行住户每周锻炼时间的调查，随机抽取了300人，并对这300人每周锻炼的时间（单位：小时）进行分组，绘制成了如图所示的频率分布直方图：（1）补全频率分布直方图，并估算该社区住户每周锻炼时间的中位数（精确到0.1）；（2）若每周锻炼时间超过6小时就称为运动卫士，超过8小时就称为运动达人．现利用分层抽样的方法从运动卫士中抽取5人，再从这5人中抽取2人做进一步调查，求抽到的2人中恰有1人为运动达人的概率．19．经历过疫情，人们愈发懂得了健康的重要性，越来越多的人们加入了体育锻炼中，全民健身，利国利民，功在当代，利在千秋．一调研员在社区进行住户每周锻炼时间的调查，随机抽取了300人，并对这300人每周锻炼的时间（单位：小时）进行分组，绘制成了如图所示的频率分布直方图：（1）补全频率分布直方图，并估算该社区住户每周锻炼时间的中位数（精确到0.1）；（2）若每周锻炼时间超过6小时就称为运动卫士，超过8小时就称为运动达人．现利用分层抽样的方法从运动卫士中抽取10人，再从这10人中抽取3人做进一步调查，设抽到的人中运动达人的人数为X ，求随机变量X 的分布列及期望．20．某贫困地区经过不懈的奋力拼搏，新农村建设取得巨大进步，农民年收入也逐年增加，为了制定提升农民收入、实现2020年脱贫的工作计划，该地扶贫办统计了2019年50位农民的年收入并制成如图频率分布直方图：（1）根据频率分布直方图，估计这50位农民的平均年收入x （单位：千元，同一组数据用该组数据区间的中点值表示）；（2）为推进精准扶贫，某企业开设电商平台，让越来越多的农村偏远地区的农户通过经营网络商城脱贫致富．甲计划在A 店，乙计划在B 店同时参加一个订单“秒杀”抢购活动，其中每个订单由()*2,n n n N ≥∈个商品W 构成，假定甲、乙两人在A 、B 两店订单“秒杀”成功的概率分别为p 、q ，记甲、乙两人抢购成功的订单总数量、商品W 总数量分别为X 、Y ．①求X 的分布列及数学期望()E X ；②若27sin4n p n n ππ=-，sin4n q nπ=，求当Y 的数学期望()E Y 取最大值时正整数n 的值．21．某地处偏远山区的古镇约有人口5000人，为了响应国家号召，镇政府多项并举，鼓励青壮劳力外出务工的同时发展以旅游业为龙头的乡村特色经济，到2020年底一举脱贫．据不完全统计该镇约有20%的人外出务工，下图是根据2020年扶贫工作期间随机调查本地100名在外务工人员的年收入（单位：千元）数据绘制的频率分布直方图．（1）根据样本数据估计该镇外出务工人员的创收总额（同一组中的数据用该组区间的中点值为代表）；（2）完成脱贫任务后，古镇党政班子并不懈怠，决心带领全镇人民在奔小康道路上再上一个新台阶，出台了多项优惠政策，鼓励本地在外人员返乡创业，调查显示年收入在35千元（含35千元）以上的人中有60%的人愿意返乡投资创业，年收入在35千元以下的人中有40%的人愿意返乡投资创业，请从样本数据中完成下面的22⨯列联表，并判断能否在犯错误的概率不超过0.1的前提下认为“是否愿意返乡投资创业和年收入有关”．35千元（含35千元）以上35千元以下愿意返乡投资创业不愿意返乡投资创业附：()()()()()22n ad bc X a b c d a c b d -=++++，()20P X k ≥0.100.050.0250.0100k 2.7063.8415.0246.63522．某市为大力推进生态文明建设，把生态文明建设融入市政建设，打造了大型植物园旅游景区.为了了解游客对景区的满意度，市旅游部门随机对景区的100名游客进行问卷调查（满分100分），这100名游客的评分分别落在区间[)50,60，[)60,70，[)70,80，[)80,90，[]90,100内，且游客之间的评分情况相互独立，得到统计结果如频率分布直方图所示.（1）求这100名游客评分的平均值（同一区间的数据用该区间数据的中点值为代表）；（2）视频率为概率，规定评分不低于80分为满意，低于80分为不满意，记游客不满意的概率为p .（ⅰ）若从游客中随机抽取m 人，记这m 人对景区都不满意的概率为m a ，求数列{}m a 的前4项和；（ⅱ）为了提高游客的满意度，市旅游部门对景区设施进行了改进，游客人数明显增多，对游客进行了继续旅游的意愿调查，若不再去旅游记1分，继续去旅游记2分，每位游客有继续旅游意愿的概率均为p ，且这次调查得分恰为n 分的概率为n B ，求4B .23．2016年春节期间全国流行在微信群里发､抢红包，现假设某人将688元发成手气红包50个，产生的手气红包频数分布表如下：金额分组[)1,5[)5,9[)9,13[)13,17[)17,21[)21,25频数39171182（1）求产生的手气红包的金额不小于9元的频率；（2）估计手气红包金额的平均数(同一组中的数据用该组区间的中点值作代表)；（3）在这50个红包组成的样本中，将频率视为概率．①若红包金额在区间[]21,25内为最佳运气手，求抢得红包的某人恰好是最佳运气手的概率；②随机抽取手气红包金额在[)[]1,521,25⋃内的两名幸运者，设其手气金额分别为m ，n ，求事件“16m n ->”的概率．24．绿色已成为当今世界主题，绿色动力已成为时代的驱动力，绿色能源是未来新能源行业的主导．某汽车公司顺应时代潮流，最新研发了一款新能源汽车，并在出厂前对100辆汽车进行了单次最大续航里程（理论上是指新能源汽车所装载的燃料或电池所能够提供给车行驶的最远里程）的测试．现对测试数据进行分析，得到如图所示的频率分布直方图．（1）估计这100辆汽车的单次最大续航里程的平均值x （同一组中的数据用该组区间的中点值代表）；（2）根据大量的汽车测试数据，可以认为这款汽车的单次最大续航里程X 近似地服从正态分布()2,N μσ，经计算第（1）问中样本标准差s 的近似值为50．用样本平均数x作为μ的近似值，用样本标准差s 作为σ的估计值；（ⅰ）现从该汽车公司最新研发的新能源汽车中任取一辆汽车，求它的单次最大续航里程恰好在200千米到350千米之间的概率；（ⅱ）从该汽车公司最新研发的新能源汽车中随机抽取10辆，设这10辆汽车中单次最大续航里程恰好在200千米到350千米之间的数量为Y ，求()E Y ；（3）某汽车销售公司为推广此款新能源汽车，现面向意向客户推出“玩游戏，送大奖”活动，客户可根据抛掷硬币的结果，操控微型遥控车在方格图上行进，若遥控车最终停在“胜利大本营”，则可获得购车优惠券．已知硬币出现正、反面的概率都是12，方格图上标有第0格、第1格、第2格、…、第50格．遥控车开始在第0格，客户每掷一次硬币，遥控车向前移动一次，若掷出正面，遥控车向前移动一格（从k 到1k +），若掷出反面，遥控车向前移动两格（从k 到2k +），直到遥控车移到第49格（胜利大本营）或第50格（失败大本营）时，游戏结束．设遥控车移到第n 格的概率为(1,2,,50)n P n = ，其中01P =，试说明{}1n n P P --是等比数列，并解释此方案能否成功吸引顾客购买该款新能源汽车.参考数据：若随机变量ξ服从正态分布()2,N μσ，则()0.6827P μσξμσ-<+≈ ，(22)0.9545P μσξμσ-<+≈ ，(33)0.9973P μσξμσ-<+≈ .25．某地处偏远山区的古镇约有人口5000人，为了响应国家号召，镇政府多项并举，鼓励青壮劳力外出务工的同时发展以旅游业为龙头的乡村特色经济，到2020年底一举脱贫.据不完全统计该镇约有20%的人外出务工.下图是根据2020年扶贫工作期间随机调查本地100名在外务工人员的年收入(单位：千元)数据绘制的频率分布直方图.（1）根据样本数据怙计该镇外出务工人员的创收总额(同一组中的数据用该组区间的中点值为代表)；（2）假设该镇外出务工人员年收入服从正态分布()2,N μσ，其分布密度函数为22()2()x f x μσ--=，其中μ为样本平均值.若()f x 的最大值为10π，求σ的值；（3）完成脱贫任务后，古镇党政班子并不懈怠，决心带领全镇人民在奔小康道路上再上一个新台阶，出台了多项优惠政策，鼓励本地在外人员返乡创业.调查显示务工收入在[],2μσμσ++和[]2,3μσμσ++的人群愿意返乡创业的人数比例分别为15%和20%.从样本人群收入在[],3μσμσ++的人中随机抽取3人进行调查，设X 为愿意返乡创业的人数，求随机变量X 的分布列和数学期望.参考答案1．C 【分析】对于A :由频率分布直方图中所有小矩形面积之和为1，列出等式可求得a 的值，进而作出判断；对于B ：先计算高于130分的频率，然后再用1减去于高于130分的频率即可得到低于130分的频率，进而作出判断；对于C ：先计算[)80,120的频率和[)120130,的频率，再求出总体的中位数，进而作出判断；对于D ：根据样本分布在[)90,100的频数一定与样本分布在[)100,110的频数相等，总体分布在[)90,100的频数不一定与总体分布在[)100,110的频数相等作出判断即可.【详解】由频率分布直方图得：()0.0050.0100.0100.0150.0250.005101a ++++++⨯=，解得0.030a =，故A 错误；样本数据低于130分的频率为：()10.0250.005100.7-⨯+=，故B 错误；[)80,120的频率为：()0.0050.0100.0100.015100.4+++⨯=，[)120130,的频率为：0.030100.3⨯=，∴总体的中位数(保留1位小数)估计为：0.50.412010123.30.3-+⨯≈分，故C 正确；样本分布在[)90,100的频数一定与样本分布在[)100,110的频数相等，总体分布在[)90,100的频数不一定与总体分布在[)100,110的频数相等，故D 错误.故选：C .【点睛】本题考查频率分布直方图的应用，考查逻辑思维能力和计算能力，属于基础题.2．B 【分析】由频率分布直方图的性质，求得0.25x =，再结合频率分布直方图的频率的计算方法，即可求解.由频率分布直方图的性质，可得()20.050.150.051x +++=，解得0.25x =，所以学习时长在[)9,11的频率2520.5x n==，解得50n =.故选：B .【点睛】本题主要考查了频率分布直方图性质及其应用，其中解答中熟记频率分布直方图的性质是解答的关键，着重考查了数据分析能力，以及计算能力.3．A 【分析】根据频率分布折线图计算该组数据的平均数为650.15750.4850.2950.25⨯+⨯+⨯+⨯.【详解】由折线图可知，该组数据的平均数为650.15750.4850.2950.2580.5⨯+⨯+⨯+⨯=.故选：A.【点睛】此题考查根据频率分布折线图求平均数，关键在于熟练掌握平均数的求解公式.4．D 【分析】根据频数分布表中的数据，对选项中的命题进行分析，判断正误，即可得到本题答案.【详解】甲同学的成绩的平均数1051201201301401235x ++++<=，乙同学的成绩的平均数1051151251351451255y ++++>=，所以A 错误；甲同学的成绩从第1次到第5次变化波动比乙同学的成绩的变化波动更小一些，所以甲同学的成绩的方差小于乙同学的成绩的方差，所以B 错误；甲同学的成绩的极差介于()30,40之间，乙同学的成绩的极差介于()35,45之间，所以甲同学的成绩的极差不一定小于乙同学的成绩的极差，所以C 错误；甲同学的成绩的中位数介于()115,120之间，乙同学的成绩的中位数介于()125,130之间，所以D 正确.故选：D本题主要考查频数直方图的相关问题，其中涉及中位数、平均数、方差、极差的求解. 5．B【详解】若①正确，则300400-对应的频率为0.45，则400500-对应的频率为0.15，则②错误；电子元件的平均寿命为1500.12500.153500.454500.155500.15⨯+⨯+⨯+⨯+⨯，则③正确；寿命超过400h的频率为0.150.150.3+=，则④正确，故不符合题意；若②正确，则300400-对应的频率为0.4，则①错误；电子元件的平均寿命为1500.12500.153500.44500.25500.15⨯+⨯+⨯+⨯+⨯，则③错误；寿命超过400h的频率为0.20.150.35+=，则④错误，故符合题意.故选：B.6．C【分析】设中位数为x，根据中位数左边的频数为50列等式可求得x的值.【详解】设中位数为x，前2组的频数之和为25，前3组的频数之和为65，由题意可得20025405050x-+⨯=，解得231.25x=.故选：C.7．A【分析】利用频率分布直方图计算平均数的方法求解即可.【详解】所给数据频率之和为(0.010.070.080.020.02)51++++⨯=则估计的平均值为5(12.50.0117.50.0722.50.0827.50.0232.50.02) 4.35521.75⨯+⨯+⨯+⨯+⨯=⨯=故选：A8．D 【分析】根据样本估计总体的知识依次判断各个选项即可得到结果.【详解】对于A ，设中位数为x ，则()()0.020.065250.080.5x +⨯+-⨯=，解得：26.25x =，即该校九年级学生1分钟仰卧起坐的次数的中位数为26.25次，A 正确；对于B ，根据频率分布直方图知众数为：253027.52+=次，B 正确；对于C ，该校九年级学生1分钟仰卧起坐的次数超过30次的人数约有16000.045320⨯⨯=人，C 正确；对于D ，该校九年级学生1分钟仰卧起坐的次数少于20次的人数约有16000.025160⨯⨯=人，D 错误.故选：D.9．A 【分析】由统计图分别求出该月温度的中位数，众数，平均数，由此能求出结果．【详解】解：由统计图得：该月温度的中位数为565.52N +==，众数为5M =，平均数为1(233410566372829210) 5.9730P =⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯≈．∴M N P <<．故选：A ．10．D 【分析】A ．根据频率分布直方图中哪一组数据的频率除以组距的值最大进行分析；B ．先分析60分以下对应的频率，再利用总体数量乘以所求频率即可得到结果；C ．利用每组数据的组中值乘以对应频率并将每组计算结果相加即可得到结果；D ．分析频率为0.5时对应的横坐标的值即为中位数.【详解】A ．根据统计图可知：[)70,80对应的频率除以组距的值最大，即频率最大，所以人数最多，故正确；B ．不及格的频率为：()0.0100.015100.25+⨯=，所以不及格的人数约为40000.25=1000⨯人，故正确；C ．根据频率分布直方图可知平均数为：()450.01550.015650.02750.03850.015950.011070.5⨯+⨯+⨯+⨯+⨯+⨯⨯=，故正确；D ．前三组的频率之和为：()0.01+0.0150.02100.450.5+⨯=<，前四组的频率之和为：()0.01+0.0150.020.03100.750.5++⨯=>，所以中位数在第四组数据中，且中位数为：0.50.45701071.70.0310-+⨯≈⨯，故错误；故选：D.11．D 【分析】利用频率分布直方图的性质直接求解．【详解】解：对于A ，90分以上为优秀，由频率分布直方图得优秀的频率为0.010100.1⨯=，∴从全体考生中随机抽取1000人，则其中得优秀考试生约有：10000.1100⨯=人，故A 正确；对于B ，由频率分布直方图得[40，50)的频率为0.01100.1⨯=，[50，100)的频率为：10.10.9-=，∴若要全省的合格考通过率达到96%，则合格分数线约为44分，故B 正确；对于C ，若同一组中数据用该组区间中间值作代表值，可得考试物理成绩的平均分约为：450.01010550.01510650.02010750.03010850.01510950.0101070.5⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯=分，故C 正确；对于D ，[40，70)的频率为：(0.0100.0150.020)100.45++⨯=，[70，80)的频率为0.030100.3⨯=，∴该省考生物理成绩的中位数为：0.50.45701071.670.3-+⨯≈分，故D 错误．故选：D ．【点睛】本题考查频数、合格分数线、平均数、中位数的求法，考查频率分布直方图的性质等基础知识，考查运算求解能力，属于基础题．12．65，65【分析】频率分布直方图中最高矩形的中点横坐标即为众数，利用平分矩形面积可得中位数．【详解】由题图可知众数为65，又∵第一个小矩形的面积为0.3，∴设中位数为60+x ，则0.3+x ×0.04=0.5，得x =5，∴中位数为60+5=65.故答案为：65，6513．四【分析】计算前几组的频率之和，判断频率为0.5在哪个区间即可判断中位数.【详解】根据频率分布直方图可知，前三组的频率之和为()0.03750.06250.07520.350.5++⨯=<，前四组的频率之和为()0.03750.06250.0750.120.550.5+++⨯=>，则可以判断中位数在第四组.故答案为：四.【点睛】本题考查根据频率分布直方图判断中位数所在区间，属于基础题.14．67.【分析】本题根据频率分布直方图直接求平均数即可.【详解】解：这次竞赛的平均成绩为：0.03055100.04065100.01575100.01085100.005951067⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯=故答案为：67.【点睛】本题考查根据频率分布直方图求平均数，是基础题.15．0.016130【分析】利用频率分布直方图中所有矩形的面积之和为1可求得污染的数据;利用最高矩形底边的中点值可求得众数.【详解】设被污染的数据为a ，利用频率分布直方图中所有矩形的面积之和为1可得0.004100.02100.028100.03210101a ⨯+⨯+⨯+⨯+⨯=，解得0.016a =.由图可知，该班同学的成绩众数为130.故答案为：0.016，13016．4.7 4.75【分析】根据频率分布直方图，取最高矩形底边中点的横坐标即可求出众数，求出第三小组矩形的高，设中位数为x ，由()0.1250.175 4.5510.5x ++-⨯=，解方程即可求解.【详解】由图可知，众数为4.7，第五小组的频率为0.50.30.15⨯=从左至右五个小组的频率之比依次是5∶7∶12∶10∶6，可得第一小组的频率为50.150.1256⨯=，第二小组的频率为70.150.1250.1756⨯==，第三小组的频率为120.150.36⨯=，所以中位在第三小组，第三小组矩形面积为0.3，则第三小组的高为0.310.3=设中位数为x ，则()0.1250.175 4.5510.5x ++-⨯=，解得 4.75x =故答案为：4.7；4.75【点睛】本题考查了根据频率分布直方图求众数、中位数，考查了运算求解能力，属于基础题. 17．（1）填表见解析；作图见解析；（2）平均值为：1.08，答案见解析．【分析】（1）由样本数据，即可完善频率分布表中的数据，并画出频率直方图.（2）由（1）的频率直方图计算样本均值，进而描述汞含量分布规律.【详解】（1）由题设样本数据，则可得频率分布表如下，分组频数频率[)0,0.5031 10[)0.50,1.00101 3[)1.00,1.50122 5[)1.50,2.0042 15[)2.00,2.5011 30合计301（2）根据频率分布直方图估算平均值为：112210.250.75 1.25 1.75 2.25 1.0810351530⨯+⨯+⨯+⨯+⨯≈，分布规律：①该频率分布直方图呈中间高，两边低，大多数鱼身体中汞含量主要集中在区间[]0.5,1.5；②汞含量在区间[]1,1.5的鱼最多，汞含量在区间[]0.5,1的次之，在区间[]2,2.5的最少；③汞含量超过61.0010-⨯的数据所占比例较大，这说明这批鱼被人食用，对人体产生危害的可能性比较大．18．（1）作图见解析；中位数为4.3；（2）35．【分析】（1）设中位数为x ，则有()40.150.05x -⨯=，故可求中位数.（2）利用古典概型的概率公式可求概率.【详解】解：（1）第二组的频率为()120.150.0750.050.10.25-⨯+++=，故第二组小矩形的高为0.125频率分布直方图如图所示，由频率分布直方图可得，第一组和第二组的频率之和为0.20.250.450.5+=<，前三组的频率之和为0.20.250.30.750.5++=>，可知中位数在第三组，设中位数为x ，则有()40.150.50.450.05x -⨯=-=，解得134.33x =≈，所以该社区住户每周锻炼时间的中位数为4.3；。
高考数学专题突破：程序框图难题
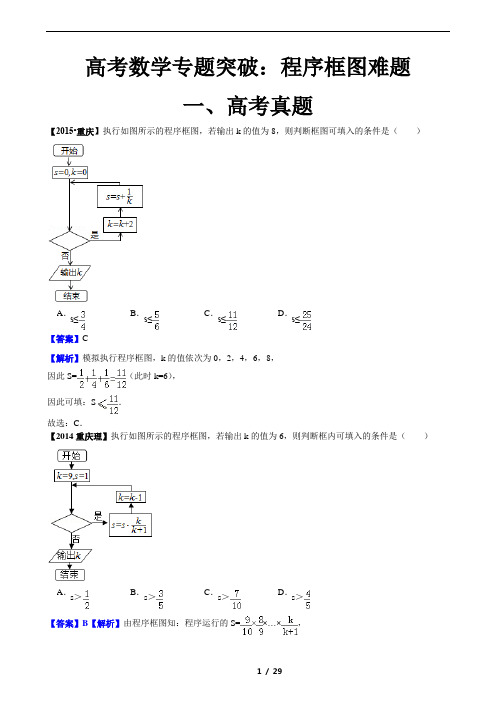
高考数学专题突破：程序框图难题一、高考真题【2015•重庆】执行如图所示的程序框图，若输出k的值为8，则判断框图可填入的条件是（）s≤【解析】模拟执行程序框图，k的值依次为0，2，4，6，8，因此S=（此时k=6），因此可填：S．故选：C．【2014重庆理】执行如图所示的程序框图，若输出k的值为6，则判断框内可填入的条件是（）＞＞【答案】B【解析】由程序框图知：程序运行的S=××…×，∵输出的k=6，∴S=××=，∴判断框的条件是S ＞，故选：C ．【2013课标全国Ⅱ理6】执行下面的程序框图，如果输入的N ＝10，那么输出的S ＝( )．A ．1111+2310+++ B ．1111+2!3!10!+++ C ．1111+2311+++ D ．1111+2!3!11!+++ 【答案】B【解析】由程序框图知，当k ＝1，S ＝0，T ＝1时，T ＝1，S ＝1； 当k ＝2时，12T =，1=1+2S ；当k ＝3时，123T =⨯，111+223S =+⨯； 当k ＝4时，1234T =⨯⨯，1111+223234S =++⨯⨯⨯；…； 当k ＝10时，123410T =⨯⨯⨯⨯ ，1111+2!3!10!S =+++，k 增加1变为11，满足k ＞N ，输出S ，所以B 正确．【2013重庆理8】执行如图所示的程序框图，如果输出s ＝3，那么判断框内应填入的条件是( )．A ．k ≤6B ．k ≤7C ．k ≤8D ．k ≤9 【答案】B【解析】由程序框图可知，输出的结果为s ＝log 23×log 34×…×log k (k ＋1)＝log 2(k ＋1)．由s ＝3，即log 2(k ＋1)＝3，解得k ＝7.又∵不满足判断框内的条件时才能输出s ，∴条件应为k ≤7.【2013江西理7】阅读如下程序框图，如果输出i ＝5，那么在空白矩形框中应填入的语句为( )．A ．S ＝2*i －2B ．S ＝2*i －1C ．S =2*iD ．S ＝2*i ＋4 【答案】C【解析】当i ＝2时，S ＝2×2＋1＝5；当i ＝3时，S ＝2×3＋4＝10不满足S ＜10，排除选项D ；当i ＝4时，S ＝2×4＋1＝9；当i ＝5时，选项A ，B 中的S 满足S ＜10，继续循环，选项C 中的S ＝10不满足S ＜10，退出循环，输出i ＝5，故选C.【2012陕西理】10. 右图是用模拟方法估计圆周率π的程序框图，P 表示估计结果，则图中空白框内应填入（ ）A ．1000N P =B ．41000N P =C ．1000M P =D ．41000M P =【答案】C 【解析】M 表示落入扇形的点的个数，1000表示落入正方形的点的个数， 则点落入扇形的概率为1000M ，由几何概型知，点落入扇形的概率为4π，则10004M P ==π，故选D【2012新课标理】如果执行右边和程序框图，输入正整数N （2N ≥）和实数1a ，2a ，…，N a ，输出A ，B ，则（ ）A 、AB +为1a ，2a ，…，N a 的和B 、2A B +为1a ，2a ，…，N a 的算术平均数C 、A 和B 分别是1a ，2a ，…，N a 中最大的数和最小的数D 、A 和B 分别是1a ，2a ，…，N a 中最小的数和最大的数【答案】C 【解析】由程序框图可知，A 表示1a ，2a ，…，Na 中最大的数，B 表示1a ，2a ，…，N a 中最小的数，故选择C 。
正余弦定理判定三角形形状-高考数学微专题突破含详解
正余弦定理判定三角形形状-高考数学微专题突破一、单选题1．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若22202c a b ab-->，则△ABC （ ） A ．一定是锐角三角形 B ．一定是直角三角形 C ．一定是钝角三角形D ．是锐角或直角三角形2．在ABC 中，若3sin b B =，cos cos A C =，则ABC 形状为（ ） A ．直角三角形 B ．等腰三角形 C ．等边三角形D ．等腰直角三角形3．若()()3a b c b c a bc +++-=，且sin 2sin cos A B C =，那么ABC 是（ ） A ．直角三角形 B ．等边三角形 C ．等腰三角形D ．等腰直角三角形4．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且2cos 22A b c c+=，则△ABC 是（ ） A ．直角三角形 B ．锐角三角形 C ．等边三角形 D ．等腰直角三角形5．在ABC 中，2sin 22C a ba-=，角A 、B 、C 的对边分别为a 、b 、c ，则ABC 的形状为（ ） A ．等边三角形 B ．等腰三角形 C ．等腰直角三角形 D ．直角三角形6．在ABC 中，若20AB BC AB ⋅+=，则ABC 的形状一定是（ ）A ．等边三角形B ．直角三角形C ．等腰三角形D ．等腰直角三角形7．若钝角三角形ABC 的三边长,8,()a b a b <成等差数列，则该等差数列的公差d 的取值范围是（ ） A ．(2,4)B ．(0,4)C ．(2,6)D ．(1,4)8．在ABC 中，a b c ，，分别是内角A B C ，，的对边，若222)4ABC a b c S +-=△（其中ABCS表示ABC 的面积），且角A 的平分线交BC 于E ，满足0AE BC ⋅=，则ABC 的形状是（ ） A ．有一个角是30的等腰三角形 B ．等边三角形 C ．直角三角形D ．等腰直角三角形9．已知ABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，满足222cos cos cos 1sin sin A B C A C -+=+，且sin sin 1A C +=，则ABC 的形状为（ ） A ．等边三角形B ．等腰直角三角形C ．顶角为120的非等腰三角形D ．顶角为120的等腰三角形10．已知a ，b ，c 分别为ABC 内角A ，B ，C 的对边，命题:p 若222a b c +>，则ABC 为锐角三角形，命题:q 若a b >，则cos cos A B <.下列命题为真命题的是（ ） A ．p q ∧B ．()p q ∨⌝C ．()()p q ⌝∧⌝D ．()p q ⌝∨11．在ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若直线cos cos 0bx y A B ++=,cos cos 0ax y B A ++=平行，则ABC 一定是（ ）A ．锐角三角形B ．等腰三角形C ．直角三角形D ．等腰或者直角三角形12．已知ABC ∆的三个内角,,A B C 所对的边分别为,,a b c ，满足222cos cos cos A B C -+1sin sin A C =+，且sin sin 1A C +=，则ABC ∆的形状为（ ） A ．等边三角形B ．等腰直角三角形C ．顶角为150的等腰三角形D ．顶角为120的等腰三角形13．ABC 中三个角的对边分别记为a 、b 、c ，其面积记为S ，有以下命题：△21sin sin 2sin B CS a A=；△若2cos sin sin B A C =，则ABC 是等腰直角三角形；△222sin sin sin 2sin sin cos C A B A B C =+-；△2222(+)sin ()()sin ()a b A B a b A B -=-+，则ABC 是等腰或直角三角形.其中正确的命题是( ) A ．△△△B ．△△△C ．△△△D ．△△△14．ABC ∆中，角A ，B ，C 所对应的边分别为a ，b ，c .已知222(cos cos )2cos a b a B b A ab B +-+=，则ABC ∆是（ ）A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．等腰或直角三角形15．在ABC ∆中，()()2222sin sin A B a b a b A B ++=--，则ABC ∆的形状是（ ） A ．等腰非直角三角形 B ．等腰直角三角形 C ．直角非等腰三角形D ．等腰或直角三角形16．对于ABC ∆，有如下四个命题:△若sin 2sin 2A B = ，则∆ABC 为等腰三角形， △若sin cos B A =，则∆ABC 是直角三角形△若222sin sin sin A B C +<，则∆ABC 是钝角三角形△若coscoscos222ab c AB C ==，则∆ABC 是等边三角形.其中正确的命题个数是 （ ） A ．1 B ．2C ．3D ．4二、多选题17．在△ABC 中，a 、b 、c 分别为△A 、△B 、△C 的对边，下列叙述正确的是（ ）A ．若sin sin a bB A = 则△ABC 为等腰三角形 B ．若cos cos a bB A= 则△ABC 为等腰三角形 C ．若ta ta a 0n n A t n B C ++>则△ABC 为锐角三角形 D ．若sin cos a b C c B =+，则△C 4π=18．已知ABC 的三个角A ，B ，C 的对边分别为a ，b ，c ，若cos cos A bB a=，则该三角形的形状是（ ） A ．等腰三角形 B ．直角三角形C ．等腰直角三角形D ．等腰或直角三角形19．已知△ABC 的内角A ､B ､C 所对的边分别为a ､b ､c ，下列四个命题中，正确的命题是（ ）A ．若2cos c aB =，则ABC 一定是等腰三角形B ．若()()2222sin()sin()a bA B ab A B +-=-+，则ABC 是等腰或直角三角形C ．若22tan tan a A b B=，则ABC 一定是等腰三角形D ．若2b a c =+，且2cos28cos 50B B -+=，则ABC 是等边三角形20．已知ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，下列说法中正确的有（ ） A ．若cos cos cos a b cA B C==，则ABC 一定是等边三角形 B ．若cos cos a A b B =，则ABC 一定是等腰三角形 C ．若cos cos b C c B b +=，则ABC 一定是等腰三角形 D ．若222a b c +<，则ABC 一定是钝角三角形 21．下列说法正确的有（ ）A ．在△ABC 中，a △b △c =sin A △sinB △sin CB ．在△ABC 中，若sin 2A =sin 2B ，则△ABC 为等腰三角形 C ．△ABC 中，sin A ＞sin B 是A ＞B 的充要条件D ．在△ABC 中，若sin A=12，则A=6π22．在ABC ∆中，下列命题正确的是（ ） A ．若A B >，则sin sin A B >B ．若sin 2sin 2A B =，则ABC ∆定为等腰三角形 C ．若cos cos a B b A c -=，则ABC ∆定为直角三角形D ．若三角形的三边的比是3:5:7，则此三角形的最大角为钝角 23．在ABC ∆中，以下结论正确的是____________A ．若222a b c >+，则ABC ∆为钝角三角形B ．若222a b c bc =++，则A 为120︒C ．若222a b c +>，则ABC ∆为锐角三角形D ．若::1:2:3A B C =，则::1:2:3a b c =三、填空题24．在ABC 中，满足cos cos a Ab B=的三角形是______________三角形. 25．在△ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，若cos A ＝12，b ＋c ＝2a ，则△ABC 的形状为________.26．若以3，4，x 为三边长组成一个锐角三角形，则x 的取值范围是____________．27．对于ABC ，有如下命题：△若sin2A ＝sin2B ，则ABC 为等腰三角形； △若sin A ＝cos B ，则ABC 为直角三角形；△若sin 2A +sin 2B +cos 2C ＜1，则ABC 为钝角三角形； △若满足C ＝6π，c ＝4，a ＝x 的三角形有两个，则实数x 的取值范围为(4,8)． 其中正确说法的序号是_____．28．已知ABC 的内角,,A B C 成等差数列，且,,A B C 所对的边分别为,,a b c ，则有下列四个命题： △3B π=；△若,,a b c 成等比数列，则ABC 为等边三角形； △若2a c =，则ABC 为锐角三角形；△若2AB AB AC BA BC CA CB =⋅+⋅+⋅，则3A C =.则以上命题中正确的有________________.( 把所有正确的命题序号都填在横线上 ). 29．设ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若22cos sin sin cos a A B b A B =，则ABC 的形状为______.30．在ABC 中，a b c ，，分别是角A B C ，，的对边，且a b c ，，成等差数列，sin A ，sin B ，sin C 成等比数列，则三角形的形状是________________．31．对于ABC ，有如下命题：()1若sin2sin2A B =，则ABC 一定为等腰三角形．()2若sin sin A B =，则ABC 一定为等腰三角形．()3若222sin sin cos 1A B C ++<，则ABC 一定为钝角三角形．()4若tan tan tan 0A B C ++>，则ABC 一定为锐角三角形．则其中正确命题的序号是______ .(把所有正确的命题序号都填上) 四、解答题32．在ABC 中，已知a 2tan B =b 2tan A ，试判断△ABC 的形状.33．ABC 中，sin sin sin b a Ba B A+=-，且()cos cos 1cos2A B C C -+=-，判断ABC 的形状．34．在ABC 中，若22tan :tan :,A B a b =试判断ABC 的形状.35．在ABC 中，已知22(cos cos )()cos a b B c C b c A -=-，试判断ABC 的形状36．已知a b c ，，为ABC ∆的内角A B C ，，的对边，满足sin sin 2cos cos sin cos B C B C A A +--=，函数()sin f x x ω= (0)ω>在区间0,3π⎡⎤⎢⎥⎣⎦上单调递增，在区间,π3π⎡⎤⎢⎥⎣⎦上单调递减. （1）证明：2b c a +=； （2）若()cos 9f A π=，证明ABC 为等边三角形．37．已知锐角三角形ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且tan A ． （1）求角A 的大小；（2）当a c 2＋b 2的最大值，并判断此时△ABC 的形状．38．在ABC 中，6BC =，点D 在BC 边上，且()2cos cos AC AB A BC C -⋅=. （1）求角A 的大小；（2）若AD 为ABC 的中线，且AC =AD 的长；（3）若AD 为ABC 的高，且AD =ABC 为等边三角形.39．在△cos 220B B +=，△2cos 2b C a c =-，△b a =三个条件中任选一个，补充在下面问题中，并加以解答．已知ABC ∆的内角A ，B ，C 所对的边分别是a ，b ，c ，若_____，且a ，b ，c 成等差数列，则ABC ∆是否为等边三角形？若是，写出证明；若不是，说明理由． 注：如果选择多个条件分别解答，按第一个解答计分．40．在ABC 中，内角A ，B ，C 对边的边长分别是a ，b ，c ，已知4c =，3C π=.（1）若ABC 的面积等于ABC 的形状，并说明理由； （2）若ABC 是锐角三角形，求ABC 周长的取值范围.参考答案1．C 【分析】由余弦定理确定C 角的范围，从而判断出三角形形状． 【详解】由22202c a b ab-->得－cos C >0，所以cos C <0，从而C 为钝角，因此△ABC 一定是钝角三角形. 故选：C ． 2．C 【分析】首先利用正弦定理化边为角求出sin A 的值，再结合A C =，以及三角形的内角和即可求出,B C ，进而可得正确选项.【详解】由正弦定理知：2sin b R B =，2sin a R A =，则3sin b B =可化为：32sin 2sin sin R B R A B ⨯=. 因为0180B << 所以sin 0B ≠，所以sin A =，可得60A =或120， 又因为cos cos A C =， 所以A C ∠=∠所以60A =，60C =，180606060B ∠=--=， 所以ABC 为等边三角形. 故选：C. 3．B 【分析】首先利用余弦定理求出A ，再由sin 2sin cos A B C =利用正弦定理将角化边，以及余弦定理将角化边可得b c =，即可判断三角形的形状；解：()()3a b c b c a bc +++-=，[()][()]3b c a b c a bc ∴+++-=，22()3b c a bc ∴+-=， 22223b bc c a bc ++-=，222b bc c a -+=，根据余弦定理有2222cos a b c bc A =+-， 222222cos b bc c a b c bc A ∴-+==+-，2cos bc bc A =，1cos 2A =， 60A ∴=︒，又由sin 2sin cos A B C =，则sin 2cos sin A C B=，即22222a a b c b ab +-=，化简可得，22b c =， 即b c =，ABC ∴是等边三角形故选：B ． 4．A 【分析】用降幂公式变形后利用余弦定理得边的关系，从而判断出三角形形状． 【详解】在△ABC 中，因为2cos22A b c c +=，所以1cos 1222A b c +=+，所以cos A ＝b c. 由余弦定理，知2222b c a bbc c+-=，所以b 2＋c 2－a 2＝2b 2，即a 2＋b 2＝c 2，所以△ABC 是直角三角形. 故选：A ． 5．D利用二倍角公式、正弦定理可得出sin sin cos B A C =，利用两角和的正弦公式可得出cos sin 0A C =，求出A 的值，即可得出结论.【详解】21cos sin 222C C a b a--==，cos b a C ∴=，由正弦定理可得sin sin cos B A C =， 所以，()sin cos sin sin cos cos sin A C A C A C A C =+=+，则cos sin 0A C =，0C π<<，则sin 0C >，cos 0A ∴=，0A π<<，2A π∴=，因此，ABC 为直角三角形.故选：D. 【点睛】方法点睛：在解三角形的问题中，若已知条件同时含有边和角，但不能直接使用正弦定理或余弦定理得到答案，要选择“边化角”或“角化边”，变换原则如下： （1）若式子中含有正弦的齐次式，优先考虑正弦定理“角化边”； （2）若式子中含有a 、b 、c 的齐次式，优先考虑正弦定理“边化角”； （3）若式子中含有余弦的齐次式，优先考虑余弦定理“角化边”； （4）代数式变形或者三角恒等变换前置；（5）含有面积公式的问题，要考虑结合余弦定理求解；（6）同时出现两个自由角（或三个自由角）时，要用到三角形的内角和定理. 6．B 【分析】先利用数量积运算化简得到2cos ac B c =，再利用余弦定理化简得解. 【详解】因为20AB BC AB ⋅+=， 所以2cos()0ac B c π-+=， 所以2cos ac B c =，所以22222a c b ac c ac+-⨯=，所以222b c a +=， 所以三角形是直角三角形. 故选：B 【点睛】方法点睛：判断三角形的形状，常用的方法有：（1）边化角；（2）角化边.在边角互化时常利用正弦定理和余弦定理. 7．A 【分析】设公差为d ，0d >，8,8a d b d =-=+，由最大角的余弦小于0得d 的一个范围，再由三线段长能构成三角形又可得d 的范围，两者结合可得结论． 【详解】由题意8b >，设公差为d ，0d >，8,8a d b d =-=+，设边长为8d +的边所对角为θ，则222(8)8(8)cos 028(8)d d d θ-+-+=<⨯⨯-，2>d ， 又888800d d d d -+>+⎧⎪->⎨⎪>⎩，即04<<d ，△24d <<． 故选：A ． 【点睛】易错点睛：本题考查由三角形形状求参数范围．三角形为钝角三角形，只要最大角为钝角即可．如果不能判断最大角，则需要分类讨论．解题中还不要忘记三条线段能构成三角形，否则出错． 8．B 【分析】由余弦定理和三角形面积公式结合已知得3A π=，由0AE BC ⋅=得AE BC ⊥，由角平分线得等腰三角形，从而得等边三角形的结论． 【详解】1sin 2ABCS ab C ==△，又2222cos a b c ab C +-=，12cos sin 2ab C ab C =，tan C =(0,)C π∈，所以3C π=，由0AE BC ⋅=得AE BC ⊥，又AE 是A 的平分线，所以AB AC =， 所以ABC 是等边三角形． 故选：B ． 【点睛】关键点点睛：本题考查三角形形状的判断．根据已知条件选择相应的三角公式是解题的关键，题中已知条件222)4ABC a b c S +-=△中，分子易与余弦定理联系在一起，然后结合三角形面积公式求解． 9．D 【分析】利用平方关系式和正弦定理得222122a cb ac +-=-，根据余弦定理求出120B =，再根据sin sin 1A C +=求出30A C ==，从而可得解.【详解】因为222cos cos cos 1sin sin A B C A C -+=+，所以2221sin (1sin )1sin 1sin sin A B C A C ---+-=+， 所以222sin sin sin sin sin A C B A C +-=-，根据正弦定理可得222a c b ac +-=-，即222122a cb ac +-=-，所以1cos 2B =-，因为0B π<<，所以120B =，所以60A C +=， 由sin sin 1A C +=得sin sin(60)1A A +-=， 得sin sin 60cos cos60sin 1A A A +-=，得1sin sin 12A A A +-=，得1sin 12A A +=， 得sin(60)1A +=，因为A 为三角形的内角，所以30A =，30C =， 所以ABC 为顶角为120的等腰三角形. 故选：D 【点睛】思路点睛：判断三角形形状从两个方面入手：△利用正余弦定理角化边，利用边的关系式判断形状，△利用正余弦定理边化角，利用角的关系式判断形状. 10．D 【分析】先利用余弦定理判断命题p 的真假，然后利用余弦函数的单调性判断命题q 的真假，再逐项判断含逻辑联结词的复合命题的真假. 【详解】因为222a b c +>，2222cos c a b ab C =+-，所以cos 0C >，所以C 为锐角，但角A ，B 不能确定，所以p 为假命题；若a b >，则A B >，因为cos y x =在(0,)π上单调递减，所以cos cos A B <，所以q 为真命题，所以p q ∧为假命题，()p q ∨⌝为假命题，()()p q ⌝∧⌝为假命题. 故选：D 【点睛】判断含逻辑联结词的复合命题的真假，首先可根据条件判断出原命题的真假，然后再根据逻辑联结词且、或、非判断复合命题的真假. 11．C 【分析】解法一根据直线的平行关系，结合正弦定理即可求得A 与B 的关系，根据直线平行又不重合的条件即可判断三角形形状；解法二根据直线平行关系得到cos cos 0b B a A -=，由余弦定理转化为边的表达式，进而利用因式分解可得a b 、的关系，根据平行又不重合的条件即可得三角形形状．【详解】解法一：由两直线平行可得cos cos 0b B a A -= 由正弦定理可知sin cos sin cos 0B B A A -=，即11sin 2sin 222A B = 又,(0,)A B π∈，且(0,)A B π+∈所以22A B =或22A B π=＋，即A B =或2A B π+=.若A B =，则a b =，cos cos A B =，此时两直线重合，不符合题意，舍去 故2A B π+=，则ABC 是直角三角形故选C.解法二：由两直线平行可得cos cos 0b B a A -=，由余弦定理得22222222b c a a c b a b bc ac+-+-⋅=⋅所以()()22222222a b c a b a c b +-=+- 所以()()()2222222cab a b a b -=+-所以()()222220a bab c -+-=所以a b =或222+=a b c若a b =，则两直线重合，不符合题意，故222+=a b c 则ABC 是直角三角形 故选C. 【点睛】本题考查了正弦定理与余弦定理在判断三角形形状中的应用，注意边角转化的应用，直线平行时不重合的条件限制，属于中档题． 12．D 【分析】先利用同角三角函数基本关系得222sin sin sin sin sin A C B A C +-=-，结合正余弦定理得222122a cb ac +-=-进而得B ,再利用sin sin 13A A π⎛⎫+-= ⎪⎝⎭化简得sin 13A π⎛⎫+= ⎪⎝⎭,得A值进而得C ,则形状可求 【详解】由题()2221sin 1sin 1sin 1sin sin A B C A C ---+-=+即222sin sin sin sin sin A C B A C +-=-，由正弦定理及余弦定理得222122a cb ac +-=-即()12cos ,0,23B B B ππ=-∈∴=故 sin sin 13A A π⎛⎫+-=⎪⎝⎭整理得sin 13A π⎛⎫+= ⎪⎝⎭ ，故,66A B ππ=∴=故ABC ∆为顶角为120的等腰三角形 故选D 【点睛】本题考查利用正余弦定理判断三角形形状，注意内角和定理，三角恒等变换的应用，是中档题 13．D 【分析】根据正弦定理、余弦定理、三角形面积公式、三角函数恒等变换对各个命题进行判断． 【详解】 由sin sin a b A B=得sin sin a B b A =代入in 12s S ab C =得21sin sin 2sin B CS a A =，△正确；若2cos sin sin B A C =sin()sin cos cos sin A B A B A B =+=+，△cos sin cos sin 0B A A B -=，in 0()s A B -=，△,A B 是三角形内角，△0A B -=，即A B =，ABC 为等腰三角形，△错；由余弦定理2222cos c a b ab C =+-，又sin sin sin a b cA B C==，△222sin sin sin 2sin sin cos C A B A B C =+-，△正确；2222(+)sin ()()sin ()a b A B a b A B -=-+，则2222sin()sin cos cos sin sin()sin cos cos sin a b A B A B A B a b A B A B A B ---==+++，△22sin cos cos sin a A Bb A B =，由正弦定理得22sin cos sin sin cos sin =A BA AB B，三角形中sin 0,sin 0A B ≠≠，则sin cos sin cos A A B B =，sin 2sin 2A B =，△22A B =或22A B π+=，△A B =或2A B π+=，△正确．故选：D ． 【点睛】本题考查正弦定理、余弦定理、三角形面积公式，考查三角形形状的判断，由正弦定理进行边角转化在其中起到了重要的作用，解题时注意体会边角转换． 14．B 【分析】由题，利用正弦定理和内角和定理化简可得2222cos a b c ab B +-=，再利用余弦定理可得cos cos B C =，可得结果.【详解】由题，已知()222+cos cos a b a B b A -+= 2cos ab B ，由正弦定理可得：()222sin sin sin cos cos sin 2sin sin cos A B A B A B A B B +-+= 即()222sin sin sin2sin sin cos A B A B A B B +-+=又因为()sin sin A B C +=所以222sin sin sin 2sin sin cos A B C A B B +-= 即2222cos a b c ab B +-=由余弦定理：2222cos a b c ab C +-= 即cos cos B C = 所以B C =所以三角形一定是等腰三角形 故选B 【点睛】本题考查了正余弦定理解三角形，解题的关键是在于正余弦的合理运用，属于中档题.【分析】由正弦定理可得22sin sin cos sin cos sin B A B A A B =，化为sin 2sin 2B A =， 由a b A B ≠⇒≠，进而可得结果. 【详解】()()2222sin sin A B a b a b A B ++=--, ()()()()2222sin sin a b A B a b A B ∴+-=-+化为22sin cos cos sin b A B a A B =，由正弦定理可得22sin sin cos sin cos sin B A B A A B =，sin cos sin cos B B A A =， sin 2sin 2B A =，,a b A B ≠∴≠，22,2B A A B ππ∴=-+=，ABC ∆是直角三角形，不是等腰三角形，故选C.【点睛】判断三角形状的常见方法是：（1）通过正弦定理和余弦定理，化边为角，利用三角变换得出三角形内角之间的关系进行判断；(2)利用正弦定理、余弦定理，化角为边，通过代数恒等变换，求出边与边之间的关系进行判断；（3）根据余弦定理确定一个内角为钝角进而知其为钝角三角形. 16．B 【详解】对于△sin 2sin 2A B =可推出A B =或2A B π+=，故不正确；△若100,10B A =︒=︒，显然满足条件，但不是直角三角形；△由正弦定理得2220a b c +-<，所以cos 0C <,是钝角三角形；△由正弦定理知sinsin sin 222A B C ==,由于半角都是锐角，所以222A B C==，三角形是等边三角形，故正确的有2个，选B. 17．ACD根据正余弦定理、三角形内角和性质，结合三角恒等变换有：A 可得a b =，B 可得A B =或2A B π+=，C 可得tan tan tan tan tan 0tanA B C A B C ++=>，D 中cos sin C C =，即可判断各选项正误. 【详解】A ：sin sin a b B A =有a bb a =，即22a b =，故△ABC 为等腰三角形，正确. B ：cos cos a bB A=有sin cos sin cos A A B B =，即sin 2sin 2A B =，0,A B π<<，所以A B =或2A B π+=，△ABC 不一定为等腰三角形，错误.C ：sin sin 11cos cos cos tan tan sin ()sin sincos cos cos cos cos cos cos cos cos tanA C C C A BB C C C A B C A B C A B C+++=+=⋅+=⋅=，所以△ABC 为锐角三角形，正确.D ：sin cos a b C c B =+知：sin sin()sin sin sin cos A B C B C C B =+=+，所以cos sin C C =，0C π<<，有△C 4π=，正确.故选：ACD 【点睛】关键点点睛：应用正弦定理边角互化及三角形内角和A B C π++=，两角和差公式等转化条件确定三角形形状. 18．D 【分析】在ABC 中，根据cos cos A b B a =，利用正弦定理得cos sin cos sin A B B A=，然后变形为sin 2sin 2A B =求解.【详解】在ABC 中，因为cos cos A bB a =， 由正弦定理得cos sin cos sin A BB A=， 所以sin cos sin cos A A B B =，即sin 2sin 2A B =， 所以22A B =或22A B π=-，解得A B =或2A B π+=.故ABC 是直角三角形或等腰三角形. 故选： D. 【点睛】本题主要考查利用正弦定理判断三角形的形状，还考查了运算求解的能力，属于基础题. 19．ABD 【分析】A ．利用正弦定理以及两角和的正弦公式进行化简并判断；B ．利用正弦定理以及两角和差的正弦公式进行化简并判断；C ．先进行切化弦，然后利用正弦定理进行化简并判断；D ．根据条件先求解出B ，然后利用正弦定理以及三角恒等变换计算出,A C 的值，从而判断出结果. 【详解】A ．因为2cos c aB =，所以()sin 2sin cos sinC A B A B ==+，所以sin cos sin cos A B B A =，所以tan tan A B =，所以A B =，所以ABC 为等腰三角形，故正确； B ．因为()()2222sin()sin()a bA B ab A B +-=-+，所以()()()()2222sin cos sin cos sin cos sin cos ab A B B A a b A B B A +-=-+，所以()()()()22222222sin cos sin cos a bab B A a b a b A B ⎡⎤⎡⎤-++=+--⎣⎦⎣⎦， 所以222sin cos 2sin cos a B A b A B =，所以222sin sin cos 2sin sin cos A B A B A B =， 所以sin 2sin 2B A =，所以2A B π+=或A B =，所以ABC 为等腰或直角三角形，故正确；C ．因为22tan tan a A b B =，所以22sin cos sin cos a A B b B A=，所以22sin cos sin cos a B A b A B =，所以22sin sin cos sin sin cos A B A B A B =，所以sin 2sin 2B A =，所以2A B π+=或A B =，所以ABC 为等腰或直角三角形，故错误；D ．因为2cos28cos 50B B -+=，所以24cos 8cos 30B B -+=，所以1cos 2B =或3cos 2B =（舍），所以3B π=，又因为2b a c =+，所以2sin sin sin B A C =+且23A C π+=，所以2sin sin 3A A π⎛⎫+-= ⎪⎝⎭所以3sin cos 22A A +=1sin cos 122A A +=，所以sin 16A π⎛⎫+= ⎪⎝⎭，所以3A π=，所以A B C ==，所以ABC 为等边三角形，故正确. 故选：ABD. 【点睛】本题考查利用正、余弦定理判断三角形形状，主要考查学生的转化与计算能力，难度一般.利用正、余弦定理判断三角形形状时，一定要注意隐含条件“A B C π++=”. 20．ACD 【分析】根据正弦定理，三角函数恒等变换的应用逐一判断各个选项即可． 【详解】 解：对于A ，若cos cos cos a b c A B C==，则sin sin sin cos cos cos A B CA B C ==，即tan tan tan A B C ==，即A B C ==，即ABC 是等边三角形，故正确；对于B ，若cos cos a A b B =，则由正弦定理得2sin cos 2sin cos r A A r B B =，即sin 2sin 2A B =，则22A B =或22180A B +=︒，即A B =或90A B +=︒，则ABC 为等腰三角形或直角三角形，故错误；对于C ，若cos cos b C c B b +=，所以sin cos sin cos sin B C C B B +=，所以sin()sin sin B C A B +==，即A B =，则ABC 是等腰三角形，故正确；对于D ，ABC 中，222a b c +<，又2222cos c a b ab C =+-，所以cos 0C <∴角C 为钝角，但ABC 一定是钝角三角形，故正确；故选：ACD ． 【点睛】本题考查正弦定理，三角函数恒等变换的应用，三角函数的图象与性质的应用等知识点，考查学生训练运用公式熟练变形的能力，属于中档题． 21．AC 【分析】由正弦定理，二倍角的正弦公式，逐一分析各个选项，即可求解. 【详解】 由正弦定理==2sin sin sin a b c R A B C= 可得：::2sin :2sin :2sin a b c R A R B R C = 即::sin :sin :sin a b c A B C =成立， 故选项A 正确；由sin 2sin 2A B =可得22A B =或22A B π+=， 即A B =或2A B π+=，则ABC 是等腰三角形或直角三角形， 故选项B 错误；在ABC 中，由正弦定理可得sin sin A B a b A B >⇔>⇔>，则sin sin A B >是A B >的充要条件， 故选项C 正确； 在△ABC 中，若sin A=12，则6A π=或5=6A π， 故选项D 错误. 故选：AC. 【点睛】本题考查了命题真假性的判断，正弦定理的应用，属于基础题. 22．ACD 【分析】选项A ，由三角形边角关系和正弦定理，可判断为正确；选项B ，由三角函数确定角的关系，要结合角范围，所以错误；选项C ，用正弦定理边化角，再将sin sin()C A B =+代入展开，整理可得cos 0A =，所以正确；选项D ，用余弦定理求出最大边所对的角，判断正确. 【详解】在ABC ∆中，若A B >，则a b >，因此sin sin A B >，A 正确； 若sin 2sin 2A B =，则22A B =或22A B π+=， 即A B =或2A B π+=，所以ABC ∆为等腰三角形或直角三角形，B 错误； 若cos cos a B b A c -=，则sin cos sin cos sin sin()A B B A C A B ⋅-⋅==+， 所以sin cos 0B A =，即cos 0A =，2A π=，所以ABC ∆定为直角三角形，C 正确；三角形的三边的比是3:5:7，设最大边所对的角为θ，则2223571cos 2352θ+-==-⨯⨯，因为0θπ<<，所以23πθ=，D 正确. 故选:ACD. 【点睛】本题考查正弦定理和余弦定理解三角形，以及判断三角形的形状，注意角的范围及三角形内角和等于0180，属于中档题. 23．AB 【分析】对各个结论利用余弦定理加以验证，得到正确的命题，即可得到答案 【详解】对于A ，由222cos 02b c a A bc+-=<，可知角A 为钝角，则ABC ∆为钝角三角形，故正确对于B ，由222a b c bc =++，结合余弦定理可知1cos 2A =-，120A ∴=︒，故正确 对于C ，由222a b c +>，结合余弦定理可知222cos 02a b c C ab+-=>，只能判断角C 为锐角，不能判断角A B ，的情况，所以ABC ∆不一定为锐角三角形，故错误对于D ，由::1:2:3A B C =可得30A =︒，60B =︒，90C =︒，则1::sin 30:sin 60:sin 90:1:2:32a b c =︒︒︒=≠，故错误 故选AB 【点睛】本题主要考查的知识点是余弦定理，解斜三角形及其应用，考查了计算能力和逻辑推理能力，难度一般 24．等腰 【分析】先利用正弦定理，再利用两角差的正弦公式化简整理即可得出结果. 【详解】 由cos cos a Ab B =， 得sin cos sin cos A AB B=， 即()sin cos sin cos sin 0A B B A A B -=-=， 因为0,0A B ππ<<<<， 所以0A B A B -=⇒=， 所以满足cos cos a A b B=的三角形是等腰三角形； 故答案为：等腰. 25．等边三角形 【分析】利用余弦定理求得,b c 的关系，从而得出三边关系，判断出三角形形状． 【详解】由余弦定理及cos A ＝12得2222b c a bc+-＝12，△b 2＋c 2－a 2＝bc .△b ＋c ＝2a ，△a ＝2b c +，△b 2＋c 2－22b c +⎛⎫ ⎪⎝⎭＝bc ，即(b －c )2＝0，△b ＝c ，于是a ＝b ＝c .△△ABC 为等边三角形. 故答案为：等边三角形．26．． 【分析】先求出x 的范围，然后由最大角的余弦大于0（最大边的平方小于两较小边的平方和）可得． 【详解】易知4343x -<<+，即17x <<，若4是最大边长，则22234x +>，x >4x <≤，若x 是最大边长，则22234x +>，5x <，所以45x <<，5x <<．故答案为：． 【点睛】关键点点睛：本题考查由三角形形状确定参数范围．首先三条线段能组成三角形的条件是：任一条线段长大于另两条线段长度的差且小于另两条线段长度的和．ABC 三边长分别为,,a b c ，由余弦定理得222cos 2a b c C ab +-=，因此C 为钝角222a b c ⇔+<，C 为直角222a b c ⇔+=，C 为锐角222a b c ⇔+>．27．△△ 【分析】举出反例可判断△、△；由同角三角函数的平方关系、正弦定理可得222a b c +<，再由余弦定理可判断△；由正弦定理可得8sin x A =，再由三角形有两个可得566A ππ<<且2A π≠，即可判断△；即可得解. 【详解】 对于△，当3A π=，6B π=时，满足sin 2sin 2A B =，此时△ABC 不是等腰三角形，故△错误；对于△，当23A π=，6B π=时，满足sin cos A B =，此时△ABC 不是直角三角形，故△错误；对于△，△222sin sin cos 1A B C ++<，△22222sin sin cos sin cos A B C C C ++<+， △222sin sin sin A B C +<，△根据正弦定理得222a b c +<，△222cos 02a b c C ab+-=<，()0,C π∈，△C 为钝角，△△ABC 为钝角三角形，故△正确；对于△，△,4,6C c a x π===，△根据正弦定理得481sin sin 2a c A C ===，△8sin x A =， 由题意566A ππ<<，且2A π≠，△1sin 12A <<，△48x ，即x 的取值范围为(4,8)，故△正确．故答案为：△△． 【点睛】本题考查了三角函数及解三角形的综合应用，考查了运算求解能力，合理转化条件是解题关键，属于中档题. 28．△△△ 【分析】△根据,,A B C 成等差数列，可得2=B A C +，再由+A B C π+=求解.△根据,,a b c 成等比数列，则2=b ac ，再由余弦定理结合△的结论求解.△根据2a c =，再由余弦定理结合△的结论求解.△根据2AB AB AC BA BC CA CB =⋅+⋅+⋅，利用数量积的运算得到0CA CB ⋅=求解. 【详解】因为ABC 的内角,,A B C 成等差数列， 所以2=B A C +，又+A B C π+=， 所以=3B π， 故△正确.因为,,a b c 成等比数列， 所以2=b ac ，由余弦定理得：22222=2cos b ac a c ac B a c ac =+-=+-， 所以2220+-=a c ac ， 即 ()20a c -=， 所以a c =，所以ABC 为等边三角形.故△正确.因为2a c =，由余弦定理得：22222222cos 423b a c ac B c c c c =+-=+-=，所以b =，所以222222cos 02b c a A bc +-===， 所以ABC 为直角三角形.故△错误. 因为2AB AB AC BA BC CA CB =⋅+⋅+⋅，则()22AB AB AC BC CA CB AB CA CB =⋅-+⋅=+⋅， 所以0CA CB ⋅=， 所以,26C A ππ==，所以3A C =.故△正确. 故答案为：△△△ 【点睛】本题主要考查余弦定理，等差中项，平面向量的数量积的定义，还考查了运算求解的能力，属于中档题.29．等腰三角形或直角三角形 【分析】由正弦定理统一为三角函数，化简即可求解. 【详解】由22cos sin sin cos a A B b A B = 及正弦定理，得sin 2sin 2A B =， 所以A B =或2A B π+=，故ABC 是等腰三角形或直角三角形. 故答案为：等腰三角形或直角三角形 【点睛】本题主要考查了正弦定理，二倍角公式，属于中档题. 30．等边三角形 【分析】由等差中项和等比中项性质可得2b a c =+，2sin sin sin B A C =⋅；根据正弦定理角化边可知2b ac =，与2b a c =+构成方程组化简可得2222a c b +=，从而配凑出cos B 和()20a c -=，得到a c =且3B π=，从而得到结果.【详解】由题意得：2b a c =+，2sin sin sin B A C =⋅由正弦定理可得：2b ac = ()2222222224a c a ac c a c b b ∴+=++=++=即2222a c b += 22222221cos 222a cb b b B ac b +--∴===()0,B π∈ 3B π∴=又22222a c b ac +== ()20a c ∴-= a c ∴=ABC ∆∴为等边三角形故答案为等边三角形 【点睛】本题考查解三角形中，三角形形状的判断问题，关键是能够利用正弦定理将角化边之后，配凑出余弦定理的形式和边长之间的关系，从而得到结果. 31．()2，()3，()4 【分析】三角形中首先想到内角和为π，每个内角都在()0，π内，然后根据每一个命题的条件进行判定 【详解】()122A B =或22A B π+=，ABC ∴为等腰或直角三角形() 2正确；()3由2221sin A sin B cos C ++<可得222sin A sin B sin C +<由正弦定理可得222a b c +<再由余弦定理可得0cosC <，C 为钝角，命题()3正确()()()()4tan 11tanA tanB A B tanAtanB tanC tanAtanB +=+-=--0tanA tanB tanC tanAtanBtanC ∴++=> ABC ∴全为锐角，命题()4正确故其中正确命题的序号是()2，()3，()4 【点睛】本题主要考查了借助命题考查三角形的有关知识，在运用正弦、正切解三角形时注意角之间的转化，三角形内角和为π，然后代入化简 32．ABC 为等腰三角形或直角三角形 【分析】设三角形外接圆半径为R ，根据a 2tan B =b 2tan A ，利用商数关系和正弦定理，变形为sin A cos A =sin B cos B ,再利用二倍角公式转化sin2A =sin2B ，得到角的关系判断. 【详解】设三角形外接圆半径为R ， 因为a 2tan B =b 2tan A ，所以22sin sin cos cos a B b AB A=， 所以22224sin sin 4sin sin cos cos R A B R B AB A =，所以sin A cos A =sin B cos B , 所以sin2A =sin2B ，则2A =2B 或2A +2B =π， 所以A =B 或A +B =2π. 所以ABC 为等腰三角形或直角三角形. 33．直角三角形 【分析】先利用正弦定理化简sin sin sin b a Ba B A+=-，得到22b a ab -=；再利用诱导公式，二倍角公式化简，最后利用两角和与差的余弦公式以及正弦定理得到2ab c =，即可得出结果. 【详解】 由sin sin sin a b B a b a B A a bb a++=⇒=--， 得22b a ab -=；由()cos cos 1cos2A B C C -+=-， 得()()2cos cos 2sin A B A B C --+=，2cos cos sin sin cos cos sin sin 2sin A B A B A B A B C +-+=， 22sin sin 2sin A B C ⋅=，2ab c =，又22b a ab -=，则222222b a c a c b -=⇒=+， 所以ABC 的形状为：直角三角形. 34．等腰三角形或直角三角形 【分析】解法一：利用正弦定理边化角，可得cos sin cos sin B AA B=，所以sin 2sin 2A B =，根据(0,)A B π∈、，可得22A B =或22A B π=-即可求得答案；解法二：利用正弦定理边化角，可得cos sin cos sin B A A B=，利用余弦定理，可得22222222a c b ac b c a bc+-+-=a b ，化简计算，即可得答案.【详解】解法一：由已知条件及正弦定理可得22sin cos sin cos sin sin A B AA B B=， 、(,)A B 0π∈，sin 0,sin 0A B ∴≠≠，cos sin cos sin B AA B∴=，即sin cos sin cos A A B B =， sin 2sin 2,22A B A B ∴=∴=或22A B π=-，A B ∴=或2A B π+=，所以ABC 为等腰三角形或直角三角形.解法二：由已知条件及正弦定理可得sin cos sin cos AA B B=22sin sin A B ，、(,)A B 0π∈，sin 0,sin 0A B ∴≠≠，即cos sin cos sin B AA B=， 由正弦定理和余弦定理可得22222222a c b ac b c a bc+-+-=a b，整理得4222240a a c b c b -+-=，即22222()()0a b a b c -+-=，22a b ∴=或2220a b c +-=，∴a b =或222+=a b c ，ABC ∴为等腰三角形或直角三角形.【点睛】解题的关键是熟练掌握正弦定理、余弦定理并灵活应用，易错点为sin 2sin 2A B =，可得2A =2B 或者22A B π+=，容易丢解，属基础题. 35．等腰三角形或直角三角形 【分析】根据22(cos cos )()cos a b B c C b c A -=-，利用正弦定理得到22sin (sin cos sin cos )(sin sin )cos A B B C C B C A -=-，然后利用二倍角公式和两角差的公式得到()()cos 2cos 2B A C A -=-求解. 【详解】。
高考数学微专题教学的目的价值及意义
高考数学微专题教学的目的价值及意义1.高考数学微专题教学，旨在通过对高中数学知识点的细致划分和深入剖析，帮助学生突破学习难点，提高解题能力。
其主要目的如下：•夯实基础知识：对基础概念、公式、定理进行系统梳理，确保学生对知识点的理解准确无误。
•提升解题技巧：通过精选例题和习题，讲解解题思路和方法，培养学生灵活运用知识的能力。
•突破思维瓶颈：针对高考数学中的易错点、难点，提供针对性的训练，帮助学生突破思维瓶颈。
•提高应试能力：针对高考题型进行专项训练，提高学生解题速度和准确率，增强应试信心。
•培养数学思维：通过探究性问题和开放性问题的设置，培养学生数学思维的严谨性和创造性。
2.高考数学微专题教学，是针对高考数学的特点和学生的实际情况，有针对性地进行教学的一种有效方式。
其价值主要体现在以下几个方面：•提高学习效率：将庞大的数学知识体系细化成一个个小专题，更有利于学生集中精力攻克难点。
•增强学习效果：通过针对性的训练，可以使学生的知识结构更加完善，解题能力得到显著提升。
•减轻学习负担：避免学生在复习时陷入盲目刷题的困境，而是有针对性地进行训练，减轻学习负担。
•增强应试信心：通过大量的练习和总结，学生可以建立起对高考数学的信心，从而在考场上发挥出最佳水平。
3.每个学生的学习基础和薄弱环节不同，高考数学微专题教学可以根据学生的实际情况，有针对性地进行教学，实现因材施教。
其意义主要在于：•查漏补缺：通过对学生进行诊断性测试，找出知识漏洞，有针对性地进行补救。
•巩固优势：对学生已掌握的知识点进行巩固和拓展，帮助学生建立知识体系。
•提升弱项：对学生薄弱环节进行重点训练，帮助学生克服困难。
•个性化指导：根据学生的学习特点和学习风格，提供个性化的学习指导。
总结高考数学微专题教学，是一种高效、灵活、针对性强的教学方式。
通过对知识点的细化和深入剖析，帮助学生更好地掌握数学知识，提高解题能力，最终在高考中取得优异成绩。
考向29 数列求和(重点)-备战2022年高考数学一轮复习考点微专题(新高考地区专用)
考向29 数列求和1．（2021·浙江高考真题）已知数列{}n a 满足)111,N 1nn na a n a *+==∈+.记数列{}n a 的前n 项和为n S ，则（ ） A ．100332S << B ．10034S << C ．100942S <<D ．100952S <<【答案】A 【分析】 显然可知，10012S >，利用倒数法得到21111124n n n n a a a a +⎛⎫==-⎪⎪⎭112n na a +<，由累加法可得24(1)n a n ≥+，进而由11n n na a ++局部放缩可得113n n a n a n ++≤+，然后利用累乘法求得6(1)(2)n a n n ≤++，最后根据裂项相消法即可得到1003S <，从而得解．【详解】 因为)111,N 1nn n a a n a *+==∈+，所以0n a >，10032S >． 由2111111241n n n n n n n a a a a a a ++⎛⎫==-⎪⎪+⎭ 21111122n n n n a a a a ++⎛⎫∴<⎪⎪⎭112n n a a +11122n n n a -+≤+=，当且仅当1n =时取等号，12412(1)3111n n n n n n a n a a a n n a n ++∴≥∴=≤=+++++ 113n n a n a n ++∴≤+，由累乘法可得6(1)(2)n a n n ≤++，当且仅当1n =时取等号，由裂项求和法得：所以10011111111116632334451011022102S ⎛⎫⎛⎫≤-+-+-++-=-< ⎪ ⎪⎝⎭⎝⎭，即100332S <<． 故选：A ． 【点睛】再由累加法可求得24(1)n a n ≥+，由题目条件可知要证100S 小于某数，从而通过局部放缩得到1,n n a a +的不等关系，改变不等式的方向得到6(1)(2)n a n n ≤++，最后由裂项相消法求得1003S <．2．（2011·全国高考真题（理））等比数列{}n a 的各项均为正数，且212326231,9a a a a a +==.（1）求数列{}n a 的通项公式；（2）设b n ＝log 3a 1＋log 3a 2＋…＋log 3a n ，求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和n T .【答案】（1）13n n a =；（2）21nn -+. 【分析】（1）根据题意列出方程组，求出首项与公比，即可求出等比数列的通项公式即可； （2）由a n ＝13n化简b n ＝log 3a 1＋log 3a 2＋…＋log 3a n，可得到bn 的通项公式，求出1n b 的通项公式，利用裂项相消法求和. 【详解】（1）设数列{a n }的公比为q , 由23a ＝9a 2a 6得23a ＝924a ,所以q 2＝19.由条件可知q ＞0,故q ＝13.由2a 1＋3a 2＝1得2a 1＋3a 1q ＝1,所以a 1＝13.故数列{a n }的通项公式为a n ＝13n. （2）b n ＝log 3a 1＋log 3a 2＋…＋log 3a n ＝－（1＋2＋…＋n ）＝－()12n n +.故()1211211n b n n n n ⎛⎫=-=-- ⎪++⎝⎭. 121111111122122311n n b b b n n n ⎡⎤⎛⎫⎛⎫⎛⎫+++=--+-++-=- ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎣⎦所以数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和为21nn -+1.非等差、等比数列的一般数列求和，主要有两种思想(1)转化的思想，即将一般数列设法转化为等差或等比数列，这一思想方法往往通过通项分解或错位相消来完成；(2)不能转化为等差或等比的特殊数列，往往通过裂项相消法、错位相减法、倒序相加法等来求和. 2.解答数列应用题的步骤(1)审题——仔细阅读材料，认真理解题意.(2)建模——将已知条件翻译成数学(数列)语言，将实际问题转化成数学问题，弄清该数列的特征、要求的是什么.(3)求解——求出该问题的数学解. (4)还原——将所求结果还原到实际问题中.1.特殊数列的求和公式 (1)等差数列的前n 项和公式： S n ＝n （a 1＋a n ）2＝na 1＋n （n －1）2d .(2)等比数列的前n 项和公式： S n ＝⎩⎪⎨⎪⎧na 1，q ＝1，a 1－a n q 1－q ＝a 1（1－q n ）1－q ，q ≠1.2.数列求和的几种常用方法 (1)分组转化法把数列的每一项分成两项或几项，使其转化为几个等差、等比数列，再求解. (2)裂项相消法把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵消，从而求得其和. (3)错位相减法如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，这个数列的前n 项和可用错位相减法求解. (4)倒序相加法如果一个数列{a n }的前n 项中与首末两端等“距离”的两项的和相等或等于同一个常数，那么求这个数列的前n 项和即可用倒序相加法求解. 【知识拓展】 数列应用题常见模型(1)等差模型：如果后一个量比前一个量增加(或减少)的是同一个固定值，该模型是等差模型，增加(或减少)的量就是公差.(2)等比模型：如果后一个量与前一个量的比是同一个固定的非零常数，该模型是等比模型，这个固定的数就是公比.(3)递推数列模型：如果题目中给出的前后两项之间的关系不固定，随项的变化而变化，应考虑a n 与a n ＋1(或者相邻三项等)之间的递推关系，或者S n 与S n ＋1(或者相邻三项等)之间的递推关系.1．（2021·南昌市豫章中学高三开学考试（理））已知数列{a n }的前n 项和S n 满足S n =n 2，记数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为T n ，n ∈N *.则使得T 20的值为（ ） A ．1939B ．3839C ．2041D ．40412．（2021·全国高三专题练习（理））设等差数列{a n }的前n 项和为S n ，且满足a 1＝2，S 7＝35，将a 3，a 7，a 11，a 15中去掉一项后，剩下的三项按原来的顺序恰为等比数列{b n }的前三项，则数列{a n b n }的前10项的和T 10＝（ ） A ．10⋅212B ．9⋅212C ．11⋅212D ．12⋅2123．（2021·南昌市豫章中学高二开学考试（理））已知数列{}n a 满足122a a +=，21cos n n a a n π+-=+，则数列{}n a 的前100项的和等于_______．4．（2022·全国高三专题练习）已知[]x 表示不超过x 的最大整数，例如：[2.3]2=，[]1.52-=-在数列{}n a 中，[]lg ,n a n n N +=∈，记n T 为数列{}n a 的前n 项和，则2021T = ___________.1．（2021·全国高三（文））已知数列{}n a 满足2110n n n a a a ++++=(*n N ∈)，且{}n a 中任何一项都不为1-，设数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和为n S ，若202220212022321a S a +=+，则1a 的值为（ ）A ．23B ．1C ．32D ．23-2．（2021·全国高三专题练习（文））我们把221nn F =+()0,1,2,n =⋅⋅⋅叫“费马数”（费马是十七世纪法国数学家）．设()2log 1n n a F =-，1,2,3,n =⋅⋅⋅，设数列{}n a 的前n 项和为n S ，则使不等式12320212n S S S S n +++⋅⋅⋅+>-成立的正整数n 的最小值是（ ）A ．8B ．9C ．10D ．1163．（2022·全国高三专题练习）设数列{a n }满足113,34n n a a a n +==-，若21485n n n n n b a a +++=，且数列{b n }的前n项和为n S ，则n S =（ ） A ．2169n n ⎛⎫- ⎪+⎝⎭B ．42369n n ++C ．1169n n ⎛⎫+ ⎪+⎝⎭D ．2169n n ⎛⎫+ ⎪+⎝⎭4．（2021·江苏南京师大附中）已知i 为虚数单位，则复数22019202012i 3i 2020i 2021i z =+++++的虚部为（ ）A ．1011-B ．1010-C ．1010D ．10115．（2021·浙江高三开学考试）设()f x 是定义在R 上的奇函数，满足()()2f x f x -=，数列{}n a 满足11a =-，且()1*121+⎛⎫=++∈ ⎪⎝⎭n n a a n n n N .则()22=f a （ ）A ．0B ．1-C ．21D ．226．（2022·全国高三专题练习（文））已知等差数列{}n a 中，35a =，公差大于0，且41a +是21a +与73a +的等比中项，设()*11n n n b n N a a +=∈⋅，则数列{}n b 的前2020项和为（ ） A ．20202021B ．10102021C ．20204039D ．202040417．（2021·全国高三）已知数列{}n a 满足2222122n n a a a a +=，11a =，22a =，则下列表达式2222235674222224152637485a a a a a a a a a a a a a a a ++++的值为____________． 8．（2022·全国高三专题练习）已知数列{}n a 满足11a =，21n n n a a a +=+，数列{}n b 的前n 项和n S ，1n n n a b a +=.若()100S k k Z <∈，则k 的最小值为_______________.9．（2021·云南昆明市·高三（文））已知等差数列{}n a 的前n 项和为n S ，33a =，5712a a +=． （1）求n a 及n S ； （2）令12n nb S =，求数列{}2nn b +的前n 项和n T ． 10．（2021·吉林长春市·高三（理））设数列{}n a 的前n 项和为n S ，()*11n n n a S S n N ++=-∈，11a=.（1）求证：数列1n S ⎧⎫⎨⎬⎩⎭是等差数列；（2）设2nn nb S =，求数列{}n b 的前n 项和n T .11．（2021·乐清市知临中学高三月考）已知数列{}n a 和{}n b 满足11a =，121n n a a +=+，且()()11112231N n n n n b n n n *+++=+++⨯⨯∈+. （1）求数列{}n a 和{}n b 的通项公式；（2）设数列{}n n a b 的前n 项和为n T ，求满足()()2111n n n T a b ≥+--的正整数n 的值. 12．（2021·全国）已知数列{}n a 为等差数列，11a =，2810a a +=. （1）求数列{}n a 的通项公式；（2）设数列112n a n n n c a a +=+，求数列{}n c 的前n 项和n T .1．（2012·四川高考真题（理））设函数()2cos f x x x =-，{}n a 是公差为8π的等差数列，125()()()5f a f a f a π++⋅⋅⋅+=，则2313[()]f a a a -=A ．0B ．2116π C ．218πD ．21316π 2．（2012·上海高考真题（理））设，. 在中，正数的个数是（ ） A ．25.B ．50.C ．75.D ．100.3．（2011·安徽高考真题（文））若数列{}n a 的通项公式是()()132nn a n =--，则1210a a a +++=（ ）A ．15B ．12C ．12-D ．15- 4．（2015·江苏高考真题）数列满足，且（），则数列的前10项和为_______．5．（2012·福建高考真题（理））数列{a n }的通项公式cos1,2n n a n π=+，前n 项和为S n ，则S 2012=___________ 6．（2021·全国高考真题）某校学生在研究民间剪纸艺术时，发现剪纸时经常会沿纸的某条对称轴把纸对折，规格为20dm 12dm ⨯的长方形纸，对折1次共可以得到10dm 12dm ⨯，20dm 6dm ⨯两种规格的图形，它们的面积之和21240dm S =，对折2次共可以得到5dm 12dm ⨯，10dm 6dm ⨯，20dm 3dm ⨯三种规格的图形，它们的面积之和22180dm S =，以此类推，则对折4次共可以得到不同规格图形的种数为______；如果对折n 次，那么1nk k S ==∑______2dm .7．（2015·天津高考真题（理））已知数列{}n a 满足212()*,1,2n n a qa q q n N a a +=≠∈==为实数，且1，，且233445,,a a a a a a 成等差数列.（Ⅰ）求q 的值和{}n a 的通项公式；（Ⅱ）设*2221log ,nn n a b n a -=∈N ，求数列{}n b 的前n 项和. 8．（2012·江西高考真题（理））已知数列{a n }的前n 项和21()2n S n kn k N *=-+∈,且S n 的最大值为8.（1）确定常数k ，求a n ；（2）求数列922n na -⎧⎫⎨⎬⎩⎭的前n 项和T n ． 9．（2014·浙江高考真题（理））已知数列和满足.若为等比数列，且（1）求与；（2）设．记数列的前项和为.（i ）求；（ii ）求正整数，使得对任意，均有． 10．（2013·安徽高考真题（文））设数列满足，,且对任意，函数满足(Ⅰ)求数列的通项公式；（Ⅱ）若，求数列的前项和.1．【答案】C 【分析】根据2n S n =联系到通项与前n 项和公式的关系11,1,2n nn S n a S S n -=⎧=⎨-≥⎩ ，求出 11111()22121n n a a n n +=--+，根据式子特点，求前n 项和用裂项相消法，即可求出T 20。
2022届高考数学一轮复习——微专题28-29函数的凹凸性、高斯函数
专题28 函数的凹凸性定义及拓展几何特征1 （形状特征）设函数 f 为定义在区间 I 上的函数，若对 (),a b 上任意两点 12x x 、, 恒有:(1) ()()121222f x f x x x f ++⎛⎫< ⎪⎝⎭, 则称 f 为 (),a b 上的凸函数; 曲线任意两点 1A 与 2A 之间的部分位于弦 12A A 的下方(2) ()()121222f x f x x x f ++⎛⎫> ⎪⎝⎭, 则称 f 为 (),a b 上的凹函数。
曲线任意两点 1A 与 2A 之间的部分位于弦 12A A 的上方。
几何特征 2 （切线斜率特征）设 12A A 是函数 ()y f x = 曲线上两点, 函数曲线 1A 与 2A 之间任一点 A 处切线的斜率: 凸函数的切线斜率特征是：切线的斜率 ()y f x = 随 x 增大而增大;凹函数的切线斜率特征是：切线的斜率 ()y f x = 随 x 增大而减小例 1、在 222,log ,,cos2x x y y y x y x ==== 这四个函数中，当 1201x x <<< 时,()()121222f x f x x x f ++⎛⎫> ⎪⎝⎭恒成立的函数的个数是 ( ) .0A .1B .2C .3D解: 运用数形结合思想, 考察各函数的图象，注意到对 ()12,0,1x x ∀∈, 且 121o x x <<<, 当 ()f x总 满足 ()()121222f x f x x x f ++⎛⎫> ⎪⎝⎭时, 函数 ()f x 在区间 ()0,1 上是凹函数。
其图象是 “上凸”的, 因此 否定 22,,cos2x y y x y x ===, 故选 B . 例 2 、如果一个函数 ()f x 在其定义区间内对任x y 、 都满足 ()()22f x f y x y f ++⎛⎫≤⎪⎝⎭, 则称这个函数是下凸函数, 下列函数: (1) ()2x f x =; (2) ()3;f x x = (3) ()()2log 0f x x x =>; (4)(),0,2,0x x f x x x <⎧=⎨≥⎩中是下凸函数的有（ ）. A. (1)(2) B. (2)(3) C. (3) (4) D. (1)(4)【答案】D例 3、已知函数 ()f x x x a =-, 若对任意 [][]12122,3,2,3,x x x x ∈∈≠, 恒有 ()()121222f x f x x x f ++⎛⎫> ⎪⎝⎭, 则实数a 的取值范围为______.【解析】根据题意, ()f x x x a =- 在 []2,3 上为凹函数（图像上表现为在 []2,3 上的函数 图象在两区间端点连线的上方)，数形结合可得 3a ≥专题29 高斯函数的性质和拓展1、有关概念对于任意实数x ，[]x 为不超过x 的最大整数, []y x =称为取整函数或叫高斯函数，并将{}[]y x x x ==- 称为小数部分函数，表示x 的小数部分。
2022-2023学年度高考数学专题突破《数列通项公式的多种妙解方式》含十六大经典题型附答案解析
数列通项公式的多种妙解方式经典题型一：观察法经典题型二：叠加法经典题型三：叠乘法经典题型四：待定系数法经典题型五：同除以指数经典题型六：取倒数法经典题型七：取对数法经典题型八：已知通项公式a n 与前n 项的和S n 关系求通项问题经典题型九：周期数列经典题型十：前n 项积型经典题型十一：“和”型求通项经典题型十二：正负相间讨论、奇偶讨论型经典题型十三：因式分解型求通项经典题型十四：其他几类特殊数列求通项经典题型十五：双数列问题经典题型十六：通过递推关系求通项(2022·全国·高考真题)记S n 为数列a n 的前n 项和，已知a 1=1,S n a n 是公差为13的等差数列．(1)求a n 的通项公式；(2)证明：1a 1+1a 2+⋯+1a n<2．【解析】(1)∵a 1=1，∴S 1=a 1=1,∴S 1a 1=1,又∵S n a n 是公差为13的等差数列，∴S n a n =1+13n -1 =n +23,∴S n =n +2 a n 3,∴当n ≥2时，S n -1=n +1 a n -13，∴a n =S n -S n -1=n +2 a n 3-n +1 a n -13,整理得：n -1 a n =n +1 a n -1,即a n a n -1=n +1n -1,∴a n =a 1×a 2a 1×a 3a 2×⋯×a n -1a n -2×a n a n -1=1×31×42×⋯×n n -2×n +1n -1=n n +1 2，显然对于n =1也成立，∴a n 的通项公式a n =n n +1 2；(2)1a n =2n n +1 =21n -1n +1 , ∴1a 1+1a 2+⋯+1a n=21-12 +12-13 +⋯1n -1n +1 =21-1n+1<2(2022·全国·高考真题(理))记S n为数列a n的前n项和．已知2S nn+n=2a n+1．(1)证明：a n是等差数列；(2)若a4,a7,a9成等比数列，求S n的最小值．【解析】(1)因为2S nn+n=2a n+1，即2S n+n2=2na n+n①，当n≥2时，2S n-1+n-12=2n-1a n-1+n-1②，①-②得，2S n+n2-2S n-1-n-12=2na n+n-2n-1a n-1-n-1，即2a n+2n-1= 2na n-2n-1a n-1+1，即2n-1a n-2n-1a n-1=2n-1，所以a n-a n-1=1，n≥2且n∈N*，所以a n是以1为公差的等差数列．(2)由(1)可得a4=a1+3，a7=a1+6，a9=a1+8，又a4，a7，a9成等比数列，所以a72=a4⋅a9，即a1+62=a1+3⋅a1+8，解得a1=-12，所以a n=n-13，所以S n=-12n+nn-12=12n2-252n=12n-2522-6258，所以，当n=12或n=13时S n min=-78．类型Ⅰ观察法：已知数列前若干项，求该数列的通项时，一般对所给的项观察分析，寻找规律，从而根据规律写出此数列的一个通项．类型Ⅱ公式法：若已知数列的前项和与a n的关系，求数列a n的通项a n可用公式a n=S1,(n=1)S n-S n-1,(n≥2)构造两式作差求解．用此公式时要注意结论有两种可能，一种是“一分为二”，即分段式；另一种是“合二为一”，即a1和a n合为一个表达，(要先分n=1和n≥2两种情况分别进行运算，然后验证能否统一)．类型Ⅲ累加法：形如a n+1=a n+f(n)型的递推数列(其中f(n)是关于n的函数)可构造：a n-a n-1=f(n-1)a n-1-a n-2=f(n-2)...a2-a1=f(1)将上述m2个式子两边分别相加，可得：a n=f(n-1)+f(n-2)+...f(2)+f(1)+a1,(n≥2)①若f(n)是关于n的一次函数，累加后可转化为等差数列求和；②若f(n)是关于n的指数函数，累加后可转化为等比数列求和；③若f(n)是关于n的二次函数，累加后可分组求和；④若f(n)是关于n的分式函数，累加后可裂项求和．类型Ⅳ累乘法：形如a n +1=a n ⋅f (n )a n +1a n=f (n )型的递推数列(其中f (n )是关于n 的函数)可构造：a n a n -1=f (n -1)a n -1a n -2=f (n -2)...a 2a 1=f (1)将上述m 2个式子两边分别相乘，可得：a n =f (n -1)⋅f (n -2)⋅...⋅f (2)f (1)a 1,(n ≥2)有时若不能直接用，可变形成这种形式，然后用这种方法求解．类型Ⅴ构造数列法：(一)形如a n +1=pa n +q (其中p ,q 均为常数且p ≠0)型的递推式：(1)若p =1时，数列{a n }为等差数列；(2)若q =0时，数列{a n }为等比数列；(3)若p ≠1且q ≠0时，数列{a n }为线性递推数列，其通项可通过待定系数法构造等比数列来求．方法有如下两种： 法一：设a n +1+λ=p (a n +λ)，展开移项整理得a n +1=pa n +(p -1)λ，与题设a n +1=pa n +q 比较系数(待定系数法)得λ=q p -1,(p ≠0)⇒a n +1+q p -1=p a n +q p -1 ⇒a n +q p -1=p a n -1+qp -1 ，即a n +q p -1 构成以a 1+qp -1为首项，以p 为公比的等比数列．再利用等比数列的通项公式求出a n +qp -1 的通项整理可得a n .法二：由a n +1=pa n +q 得a n =pa n -1+q (n ≥2)两式相减并整理得a n +1-a na n -a n -1=p ,即a n +1-a n 构成以a 2-a 1为首项，以p 为公比的等比数列．求出a n +1-a n 的通项再转化为类型Ⅲ(累加法)便可求出a n .(二)形如a n +1=pa n +f (n )(p ≠1)型的递推式：(1)当f (n )为一次函数类型(即等差数列)时：法一：设a n +An +B =p a n -1+A (n -1)+B ，通过待定系数法确定A 、B 的值，转化成以a 1+A +B 为首项，以A m n =n ！n -m !为公比的等比数列a n +An +B ，再利用等比数列的通项公式求出a n +An +B 的通项整理可得a n .法二：当f (n )的公差为d 时，由递推式得：a n +1=pa n +f (n )，a n =pa n -1+f (n -1)两式相减得：a n +1-a n =p (a n -a n -1)+d ，令b n =a n +1-a n 得：b n =pb n -1+d 转化为类型Ⅴ㈠求出 b n ，再用类型Ⅲ(累加法)便可求出a n .(2)当f (n )为指数函数类型(即等比数列)时：法一：设a n +λf (n )=p a n -1+λf (n -1) ，通过待定系数法确定λ的值，转化成以a 1+λf (1)为首项，以A m n =n ！n -m !为公比的等比数列a n +λf (n ) ，再利用等比数列的通项公式求出a n +λf (n ) 的通项整理可得a n .法二：当f (n )的公比为q 时，由递推式得：a n +1=pa n +f (n )--①，a n =pa n -1+f (n -1)，两边同时乘以q 得a n q =pqa n -1+qf (n -1)--②，由①②两式相减得a n +1-a n q =p (a n -qa n -1)，即a n +1-qa na n -qa n -1=p ，在转化为类型Ⅴ㈠便可求出a n .法三：递推公式为a n +1=pa n +q n (其中p ，q 均为常数)或a n +1=pa n +rq n (其中p ，q ， r 均为常数)时，要先在原递推公式两边同时除以q n +1，得：a n +1q n +1=p q ⋅a n q n +1q ，引入辅助数列b n (其中b n=a n q n)，得：b n +1=p q b n +1q 再应用类型Ⅴ㈠的方法解决．(3)当f (n )为任意数列时，可用通法：在a n +1=pa n +f (n )两边同时除以p n +1可得到a n +1p n +1=a n p n +f (n )p n +1，令an p n =b n ，则b n +1=b n +f (n )pn +1，在转化为类型Ⅲ(累加法)，求出b n 之后得a n =p n b n ．类型Ⅵ对数变换法：形如a n +1=pa q (p >0,a n >0)型的递推式：在原递推式a n +1=pa q 两边取对数得lg a n +1=q lg a n +lg p ，令b n =lg a n 得：b n +1=qb n +lg p ，化归为a n +1=pa n +q 型，求出b n 之后得a n =10b n.(注意：底数不一定要取10，可根据题意选择)．类型Ⅶ倒数变换法：形如a n -1-a n =pa n -1a n (p 为常数且p ≠0)的递推式：两边同除于a n -1a n ，转化为1a n =1a n -1+p 形式，化归为a n +1=pa n +q 型求出1a n的表达式，再求a n ；还有形如a n +1=ma n pa n +q 的递推式，也可采用取倒数方法转化成1a n +1=m q 1a n +mp形式，化归为a n +1=pa n +q 型求出1a n的表达式，再求a n ．类型Ⅷ形如a n +2=pa n +1+qa n 型的递推式：用待定系数法，化为特殊数列{a n -a n -1}的形式求解．方法为：设a n +2-ka n +1=h (a n +1-ka n )，比较系数得h +k =p ,-hk =q ，可解得h 、k ，于是{a n +1-ka n }是公比为h 的等比数列，这样就化归为a n +1=pa n +q 型．总之，求数列通项公式可根据数列特点采用以上不同方法求解，对不能转化为以上方法求解的数列，可用归纳、猜想、证明方法求出数列通项公式a n .(1)若数列{a n }的前n 项和为S n ，通项公式为a n ，则a n =S 1，n =1S n -S n -1，n ≥2，n ∈N ∗注意：根据S n 求a n 时，不要忽视对n =1的验证．(2)在数列{a n }中，若a n 最大，则a n ≥a n -1a n ≥a n +1 ，若a n 最小，则a n≤a n -1a n ≤a n +1 .经典题型一：观察法1.(2022·全国·高三专题练习)数列a n 的前4项为：12,15,18,111，则它的一个通项公式是( )A.12n -1B.12n +1C.13n -1D.13n +1【答案】C【解析】将12,15,18,111可以写成13×1-1,13×2-1,13×3-1,13×4-1，所以a n 的通项公式为13n -1；故选:C2.(2022·全国·高三专题练习(文))如图所示是一个类似杨辉三角的递推式，则第n 行的首尾两个数均为( )A.2nB.2n -1C.2n +2D.2n +1【答案】B【解析】依题意，每一行第一个数依次排成一列为：1，3，5，7，9，⋯，它们成等差数列，通项为2n -1，所以第n 行的首尾两个数均为2n -1.故选：B3.(2022·全国·高三专题练习)“一朵雪花”是2022年北京冬奥会开幕式贯穿始终的一个设计理念，每片“雪花”均以中国结为基础造型构造而成，每一朵雪花都闪耀着奥运精神，理论上，一片雪花的周长可以无限长，围成雪花的曲线称作“雪花曲线”，又称“科赫曲线”，是瑞典数学家科赫在1901年研究的一种分形曲线，如图是“雪花曲线”的一种形成过程：从一个正三角形开始，把每条边分成三等份，然后以各边的中间一段为底边分划向外作正三角形，再去掉底边，反复进行这一过程.若第一个正三角形(图①)的边长为1，则第5个图形的周长为___________.【答案】25627【解析】由题意知下一个图形的边长是上一个图形边长的13，边数是上一个图形的4倍，则周长之间的关系为b n =13⋅4⋅b n -1=43b n -1，所以{b n }是公比为q =43的等比数列，而首项b 1=3，所以b n =3⋅43n -1，当n =5时，“雪花”状多边形的周长为b 5=25627.故答案为：25627经典题型二：叠加法4.(2022·全国·高三专题练习)在数列{a n }中，已知a 1=1p ，a n +1=a n na n +1，p >0,n ∈N *.若p =1，求数列{a n }的通项公式.【解析】由题意，a n +1=a n na n +1 ，得：1a n +1-1a n=n ，运用累加法：1a 2-1a 1+1a 3-1a 2+⋯+1a n -1a n -1=1+2+⋯+n -1=n n -1 2，n ≥2∴1a n -1a 1=n n -1 2，即1a n =n n -1 2+p ，n ≥2 ，当p =1时，a n =2n 2-n +2，n ≥2 ，当n =1时，a n =1成立，所以a n =2n 2-n +25.(2022·全国·高三专题练习)已知数列a n 满足a n +1n +1-a n n =1n n +1n ∈N *，且a 1=1，求数列a n 的通项公式；【解析】因为a n +1n +1-a n n =1n n +1=1n -1n +1，所以a n n -a n -1n -1=1n -1-1n n ≥2 ，a n -1n -1-a n -2n -2=1n -2-1n -1，⋯a 22-a 11=1-12，所以累加可得a n n -a 1=1-1nn ≥2 ．又a 1=1，所以a n n =2n -1n，所以a n =2n -1n ≥2 ．经检验，a 1=1，也符合上式，所以a n =2n -1．6.(2022·全国·高三专题练习)已知数列a n 中，a 1=1中，a n +1=a n +n (n ∈N *)中，则a 4=________，a n =________.【答案】 7n 2-n +22【解析】依题意，n ∈N *，n ≥2，a n -a n -1=n -1，而a 1=1，则a n =a 1+(a 2-a 1)+(a 3-a 2)+⋯+(a n -a n -1)=1+1+2+⋯+(n -1)=1+1+n -12⋅n -1 =n 2-n +22，而a 1=1满足上式，所以a n =n 2-n +22，a 4=42-4+22=7.故答案为：7；n 2-n +22经典题型三：叠乘法7.(2022·全国·高三专题练习)在数列a n 中，a n +1=nn +2a n (n ∈N *)，且a 1=4，则数列a n 的通项公式a n =________.【答案】8n n +1【解析】由a n +1=n n +2a n ，得a n +1a n =nn +2，则a 2a 1=13，a 3a 2=24，a 4a 3=35，⋮a n a n -1=n -1n +1n ≥2 ，累乘得a n a 1=13×24×35×⋯×n -3n -1×n -2n ×n -1n +1=2n n +1，所以a n =8n n +1.故答案为：8n n +1 .8.(2022·全国·高三专题练习)设a n 是首项为1的正项数列，且(n +2)a n +12-na n 2+2a n +1a n =0(n ∈N *)，求通项公式a n =___________【答案】2n (n +1)【解析】由(n +2)a n +12-na n 2+2a n +1a n =0(n ∈N *)，得[(n +2)a n +1-na n ](a n +1+a n )=0，∵a n >0，∴a n +1+a n >0，∴(n +2)a n +1-na n =0 ，∴a n +1a n =nn +2，∴a n =a 1⋅a 2a 1⋅a 3a 2⋅a 4a 3⋅⋅⋅⋅⋅a n a n -1=1×13×24×35×⋅⋅⋅×n -2n ×n -1n +1=2n (n +1)(n ≥2)，又a 1=1满足上式，∴a n =2n (n +1).故答案为：2n (n +1).9.(2022·全国·高三专题练习)数列a n 满足：a 1=23，2n +2-1 a n +1=2n +1-2 a n n ∈N * ，则a n 的通项公式为_____________.【答案】a n =2n2n -1 2n +1-1【解析】由2n +2-1 a n +1=2n +1-2 a n 得，a n +1a n =2n +1-22n +2-1=2⋅2n -12n +2-1，则a n a n -1⋅a n -1a n -2⋅a n -2a n -3⋅⋅⋅a 2a 1=2⋅2n -1-12n +1-1⋅2⋅2n -2-12n -1⋅2⋅2n -3-12n -1-1⋅⋅⋅2⋅21-123-1=2n -1⋅32n +1-1 2n -1，即a n a 1=3⋅2n -12n -1 2n +1-1 ，又a 1=23，所以a n =2n 2n -1 2n +1-1.故答案为：a n =2n2n -1 2n +1-1.经典题型四：待定系数法10.(多选题)(2022·广东惠州·高三阶段练习)数列a n 的首项为1，且a n +1=2a n +1，S n 是数列a n 的前n 项和，则下列结论正确的是( )A.a 3=7 B.数列a n +1 是等比数列C.a n =2n -1 D.S n =2n +1-n -1【答案】AB【解析】∵a n +1=2a n +1，可得a n +1+1=2a n +1 ，又a 1+1=2∴数列a n +1 是以2为首项，2为公比的等比数列，故B 正确；则a n +1=2n ，∴a n =2n -1，故C 错误；则a 3=7，故A 正确；∴S n =21-2n1-2-n =2n +1-n -2，故D 错误.故选：AB .11.(2022·河南安阳·三模(文))已知数列a n 满足a n +1=2a n +12，且前8项和为506，则a 1=___________.【答案】32【解析】由题意得：∵a n +1=2a n +12∴a n +1+12=2a n +12 ，即a n +1+12a n +12=2∴数列a n +12 是以a 1+12为首项，2为公比的等比数列，记数列a n +12 的前n 项和为T n T 8=a 1+12 (1-28)1-2=a 1+12+a 2+12+a 3+12+⋯+a 8+12=(a 1+a 2+a 3+⋯a 8)+12×8=506+4=510解得：a 1=32故答案为：3212.(2022·河北衡水·高三阶段练习)已知数列a n 的前n 项和为S n ，且满足2S n +n =3a n ，n ∈N *．(1)求数列a n 的通项公式；(2)若b n =a 2n ，求数列b n 的前10项和T 10．【解析】(1)当n =1时，2S 1+1=3a 1，即2a 1+1=3a 1，解得a 1=1；当n ≥2时，∵2S n +n =3a n ，∴2S n -1+n -1=3a n -1，两式作差得2a n +1=3a n -3a n -1，即a n =3a n -1+1,a n +12=3a n -1+12，∴a n +12a n -1+12=3，又a 1+12=32，∴数列a n +12 是以32为首项，3为公比的等比数列，∴a n +12=32×3n -1=3n 2，a n =3n 2-12=123n -1 .(2)∵b n =a 2n ，则T 10=b 1+b 2+b 3+⋯+b 10=a 2+a 4+⋯+a 20=1232-1 +34-1 +⋯+320-1=1232+34+⋯+320 -10=12321-910 1-9-10 =911-8916．13.(2022·全国·高三专题练习)设数列a n 满足a 1=2，a n -2a n -1=2-n n ∈N * ．(1)求证：a n -n 为等比数列，并求a n 的通项公式；(2)若b n =a n -n ⋅n ，求数列b n 的前n 项和T n ．【解析】(1)因为a 1=2，a n -2a n -1=2-n n ∈N * ，所以a n =2a n -1+2-n ，即a n -n =2a n -1-n -1又a 1-1=2-1=1，所以a n -n 是以1为首项，2为公比的等比数列，所以a n -n =1×2n -1，所以a n =2n -1+n (2)由(1)可得b n =a n -n ⋅n =n ×2n -1，所以T n =1×20+2×21+3×22+⋯+n ×2n -1①，所以2T n =1×21+2×22+3×23+⋯+n ×2n ②，①-②得-T n =1+1×21+1×22+1×23+⋯+1×2n -1-n ×2n即-T n =1-2n1-2-n ×2n ，所以T n =n -1 ×2n +1；14.(2022·全国·高三专题练习)在数列a n 中，a 1=5，且a n +1=2a n -1n ∈N * .(1)证明：a n -1 为等比数列，并求a n 的通项公式；(2)令b n =(-1)n ⋅a n ，求数列b n 的前n 项和S n .【解析】(1)因为a n +1=2a n -1，所以a n +1-1=2a n -1 ，又a 1-1=4，所以a n +1-1a n -1=2，所以a n -1 是以4为首项，2为公比的等比数列.故a n -1=4×2n -1，即a n =2n +1+1.(2)由(1)得b n =(-1)n⋅2n +1+1 ，则b n =2n +1+1,n =2k ,k ∈N *-2n +1+1 ,n =2k -1,k ∈N* ，①当n =2k ,k ∈N *时，S n =-22-1 +23+1 -24+1 +⋯+-2n -1 +2n +1+1 =-22+23-24+25+⋯-2n +2n +1=22+24+⋯+2n =432n -1 ;②当n =2k -1,k ∈N *时，S n =S n +1-b n +1=432n +1-1 -2n +2+1 =-2n +2+73，综上所述，S n =432n -1 ,n =2k ,k ∈N*-2n +2+73,n =2k -1,k ∈N *经典题型五：同除以指数15.(2022·广东·模拟预测)已知数列a n 中，a 1=5且a n =2a n -1+2n -1n ≥2,n ∈N ∗ ，b n =a n -1n +1(1)求证：数列b n 是等比数列；(2)从条件①n +b n ，②n ⋅b n 中任选一个，补充到下面的问题中并给出解答．求数列______的前n 项和T n ．注：如果选择多个条件分别解答，按第一个解答计分．【解析】(1)因为a 1=5且a n =2a n -1+2n -1n ≥2,n ∈N ∗ ，所以当n ≥2时，a n -1=2a n -1-1 +2n ，所以a n -12n =a n -1-12n -1+1，即a n -12n -a n -1-12n -1=1所以a n -12n 是以a 1-12=2为首项，1为公差的等差数列，所以a n -12n =2+n -1 ×1=n +1，所以a n =n +1 2n+1，b n =a n -1n +1=n +1 2n+1-1n +1=2n因为b 1=a 1-11+1=2，n ≥2时，b n b n -1=2n 2n -1=2所以数列b n 是以2为首项，2为公比的等比数列．(2)选①：因为b n =2n ，所以n +b n =n +2n ，则T n =(1+2)+2+22 +3+23 +⋅⋅⋅+n +2n=1+2+3+⋅⋅⋅+n +2+22+23+⋅⋅⋅+2n=12n n +1 +21-2n 1-2=n 22+n2+2n +1-2选②：因为b n =2n ，所以nb n =n ⋅2n，则T n =1×21+2×22+⋅⋅⋅+n ×2n (i )2T n =1×22+2×23+⋅⋅⋅+n ×2n +1(ii )(i )-(ii )得-T n =1×21+22+23+⋅⋅⋅+2n -n ×2n +1T n =n ×2n +1-21-2n 1-2=n ×2n +1-2n +1+2=n -1 2n +1+216.(2022·全国·高三专题练习)已知数列a n 满足a 1=1，a n +1=2a n +3n ，求数列a n 的通项公式.【解析】由a n +1=2a n +3n 两边同除以3n +1得a n +13n +1=23⋅a n 3n +13，令b n =a n 3n ，则b n +1=23b n +13，设b n +1+λ=23(b n +λ)，解得λ=-1，b n +1-1=23(b n -1)，而b 1-1=-23，∴数列{b n -1}是以-23为首项，23为公比的等比数列，b n -1=-23 n ，得a n =3n -2n17.(2022·全国·高三专题练习)在数列a n 中，a 1=1，S n +1=4a n +2，则a 2019的值为( )A.757×22020B.757×22019C.757×22018D.无法确定【答案】A【解析】∵a 1=1，S n +1=4a n +2，∴S 2=a 1+a 2=4a 1+2，解得a 2=5.∵S n +1=4a n +2，∴S n +2=4a n +1+2，两式相减得，a n +2=4a n +1-4a n ，∴a n +2-2a n +1=2a n +1-2a n ，∴a n +1-2a n 是以a 2-2a 1=3为首项，2为公比的等比数列，∴a n +1-2a n =3×2n -1，两边同除以2n +1，则a n +12n +1-a n 2n=34，∴a n 2n 是以34为公差，a 121=12为首项的等差数列，∴a n 2n =12+n -1 ×34=3n -14，∴a n =3n -14×2n =3n -1 ×2n -2，∴a 2019=3×2019-1 ×22017=757×22020.故选：A .经典题型六：取倒数法18.(2022·全国·高三竞赛)数列a n 满足a 1=p ，a n +1=a 2n +2a n ．则通项a n =______．【答案】p +1 2n -1-1【解析】∵a n =a 2n -1+2a n -1，∴a n +1=a n -1+1 2=a n -2+1 22=⋯=a 1+1 2n -1=p +1 2n -1．即a n =p +1 2n -1-1．故答案为p +1 2n -1-119.(2022·全国·高三专题练习)已知数列a n 满足a 1=12，且a n +1=a n 3a n +1，则数列a n =__________【答案】13n -1【解析】由a n +1=a n 3a n +1两边取倒数可得1a n +1=1a n +3，即1a n +1-1a n=3所以数列1a n 是等差数列，且首项为2，公差为3，所以1a n=3n -1，所以a n =13n -1；故答案为：13n -120.(2022·全国·高三专题练习)数列a n 满足a n +1=a n 1+2a nn ∈N ∗，a 1=1，则下列结论错误的是( )A.2a 10=1a 3+1a 17B.21an是等比数列C.2n -1 a n =1D.3a 5a 17=a 49【答案】D 【解析】由a n +1=a n 1+2a n ，且a 1=1，则a 2=a 12a 1+1>0，a 3=a 21+2a 2>0，⋯，以此类推可知，对任意的n ∈N ∗，a n >0，所以，1a n +1=1+2a n a n =1a n +2，所以1a n +1-1a n =2，且1a 1=1，所以，数列1a n 是等差数列，且该数列的首项为1，公差为2，所以，1a n =1+2n -1 =2n -1，则2n -1 a n =1，其中n ∈N ∗，C 对；21a n +121a n=21an +1-1a n=22=4，所以，数列21an是等比数列，B 对；由等差中项的性质可得2a 10=1a 3+1a 17，A 对；由上可知a n =12n -1，则3a 5a 17=3×12×5-1×12×17-1=199，a 49=12×49-1=197，所以，3a 5a 17≠a 49，D 错.故选：D .21.(2022·全国·高三专题练习)已知数列a n 满足a 1=1，a n +1=a n 4a n +1，(n ∈N *)，则满足a n >137的n 的最大取值为( )A.7 B.8C.9D.10【答案】C【解析】因为a n +1=a n 4a n +1，所以1a n +1=4+1a n ，所以1a n +1-1a n =4，又1a 1=1，数列1a n是以1为首项，4为公差的等差数列．所以1a n =1+4(n -1)=4n -3，所以a n =14n -3，由a n >137，即14n -3>137，即0<4n -3<37，解得34<n <10，因为n 为正整数，所以n 的最大值为9；故选：C 经典题型七：取对数法22.(2022·湖南·长郡中学高三阶段练习)若在数列的每相邻两项之间插入此两项的积，形成新的数列，再把所得数列按照同样的方法不断构造出新的数列.现对数列1，2进行构造，第一次得到数列1，2，2；第二次得到数列1，2，2，4，2；依次构造，第n n ∈N * 次得到的数列的所有项的积记为a n ，令b n =log 2a n ，则b 3=___________，b n =___________.【答案】 143n +12【解析】设第n 次构造后得到的数列为1，x 1，x 2，⋯，x k ，2.则a n =2x 1x 2⋯x k ，则第n +1次构造后得到的数列为1，x 1，x 1，x 1x 2，x 2，⋯，x k -1x k ，x k ，2x k ，2.则a n +1=4x 1x 2⋯x k 3=4×a n 2 3=12a 3n ，∴b n +1=log 2a n +1=log 212a 3n=-1+3b n ，∴b n +1-12=3b n -12 ，又∵b 1=log 222=2，∴数列b n -12 是以32为首项，3为公比的等比数列，∴b n -12=32×3n -1=3n 2，b n =3n +12，b 3=14.故答案为：14；3n +1223.(2022·全国·高三专题练习(文))英国著名物理学家牛顿用“作切线”的方法求函数零点时，给出的“牛顿数列”在航空航天中应用广泛，若数列x n 满足x n +1=x n -f x nf x n，则称数列x n 为牛顿数列．如果函数f x =2x 2-8，数列x n 为牛顿数列，设a n =ln x n +2x n -2，且a 1=1，x n >2．数列a n 的前n 项和为S n ，则S n =______．【答案】2n -1【解析】∵f x =2x 2-8，∴f x =4x ，又∵x n +1=x n -f x n f x n=x n -2x n 2-84x n =x n 2+42x n ，∴x n +1+2=x n +2 22x n ，x n +1-2=x n -222x n，∴x n +1-2x n +1-2=x n +2x n -2 2，又x n >2∴ln x n +1+2x n +1-2=ln x n +2x n -2 2=2ln x n +2x n -2 ，又a n =ln x n +2x n -2，且a 1=1，所以a n +1=2a n ，∴数列a n 是首项为1，公比为2的等比数列，∴a n 的前n 项和为S n ，则S n =1×1-2n1-2=2n -1.故答案为：2n -1.经典题型八：已知通项公式a n 与前n 项的和S n 关系求通项问题24.(2022·江苏南通·高三开学考试)从条件①2S n =n +1 a n ，②a 2n +a n =2S n ,a n >0，③S n +S n -1=a n n ≥2 ，中任选一个，补充到下面问题中，并给出解答.已知数列a n 的前n 项和为S n ,a 1=1，___________.(1)求a n 的通项公式；(2)设b n =a n +1+12n +1，记数列b n 的前n 项和为T n ，是否存在正整数n 使得T n >83.【解析】(1)若选择①，因为2S n =n +1 a n ,n ∈N *，所以2S n -1=na n -1,n ≥2，两式相减得2a n =n +1 a n -na n -1，整理得n -1 a n =na n -1,n ≥2,即a n n =a n -1n -1,n ≥2，所以a n n 为常数列，而a n n =a 11=1，所以a n =n ；若选择②，因为a 2n +a n =2S n n ∈N *，所以a 2n -1+a n -1=2S n -1n ≥2 ，两式相减a 2n -a 2n -1+a n -a n -1=2S n -2S n -1=2a n n ≥2 ，得a n -a n -1 a n +a n -1 =a n +a n -1n ≥2 ，因为a n >0,∴a n +a n -1>0,∴a n -a n -1=1n ≥2 ，所以a n 是等差数列，所以a n =1+n -1 ×1=n ；若选择③，由S n +S n -1=a n n ≥2 变形得，S n +S n -1=S n -S n -1，所以S n +S n -1=S n +S n -1 S n -S n -1 ，由题意知S n >0，所以S n -S n -1=1，所以S n 为等差数列，又S 1=a 1=1，所以S n =n ,S n =n 2,∴a n =S n -S n -1=2n -1n ≥2 ，又n =1时，a 1=1也满足上式，所以a n =2n -1；(2)若选择①或②，b n =n +1+12n +1=n +22n +1，所以T n =3×12 2+4×12 3+5×12 4+⋯+n +2 ×12n +1,所以12T n =3×12 3+4×12 4+5×12 5+⋯+n +2 ×12n +2，两式相减得12T n =3×12 2+12 3+12 4+⋯+12 n +1-n +2 ×12n +2=34+181-12n -1 1-12-n +2 ×12 n +2=1-n +42n +2，则T n =2-n +42n +1，故要使得T n >83，即2-n +42n +1>83，整理得，n +42n +1<-23，当n ∈N *时，n +42n +1>0，所以不存在n ∈N *，使得T n >83.若选择③，依题意，b n =a n +1+12n +1=n +12n，所以T n =2×12+3×12 2+4×12 3+⋯+n +1 ×12n，故12T n =2×12 2+3×12 3+4×12 4+⋯+n +1 ×12 n +1，两式相减得：12T n =1+12 2+12 3+⋯+12 n -n +1 ×12 n +1=1+141-12n -1 1-12-n +1 ×12 n +1=32-n +32n +1，则T n =3-n +32n ，令T n =3-n +32n >83，则n +32n <13，即2n -3n -9>0，令c n =2n -3n -9，则c 1=-10<0，当n ≥2时，c n +1-c n =2n +1-3n +1 -9-2n -3n -9 =2n -3>0，又c 4<0,c 5>0，故c 2<c 3<c 4<0<c 5<c 6⋯，综上，使得T n >83成立的最小正整数n 的值为5.25.(2022·河南省上蔡第一高级中学高三阶段练习(文))记各项均为正数的等比数列a n 的前n 项和是S n ，已S n =a n +43a n +1-4n ∈N * .(1)求a n 的通项公式；(2)求数列na n 的前n 项和T n .【解析】(1)设等比数列a n 的公比为q .因为S n =a n +43a n +1-4n ∈N * ，所以当n =1时，a 1=a 1+43a 2-4，解得a 2=3；当n =2时，a 1+a 2=a 2+43a 3-4，则a 1=43a 3-4.因为a n 是等比数列，所以a 1a 3=a 22，即43a 3-4 a 3=9，整理得4a 23-12a 3-27=0，解得a 3=-32(舍去)或a 3=92.所以q =a 3a 2=32,a 1=a 2q=2，所以a n =2×32n -1.(2)由(1)得na n =2n ×32 n -1，所以T n =2×1+2×32+3×32 2+⋯+n -1 × 32 n -2+n ×32 n -1①则32T n =2×1×32+2×32 2+3×32 3+⋯+ n -1 ×32 n -1+n ×32 n ②①-②得-T n 2=2×1+32+32 2+323+⋯+ 32 n -1 -2n ×32 n=2×1-32 n1-32-2n ×32 n =-4+4-2n ×32 n ,所以T n =4n -8 ×32n+8.26.(2022·全国·高三专题练习)设数列{a n }的前n 项和为S n ，a n +1=-S n S n +1n ∈N * ，a 1=1. 求证：数列1S n是等差数列.【解析】∵-S n S n +1=a n +1=S n +1-S n ，S 1=1≠0，则S n ≠0，所以-1=S n +1-S nS n S n +1，有1S n +1-1S n=1，所以数列1S n 是以1为首项，1为公差的等差数列.经典题型九：周期数列27.(2022·上海中学高二期末)数列{x n }满足x n +1=x n -x n -1,n ≥2,n ∈N *,x 1=a ,x 2=b ，则x 2019=_________.【答案】b -a .【解析】由题干中递推公式，可得：x 1=a ，x 2=b ，x 3=x 2-x 1=b -a ，x 4=x 3-x 2=b -a -b =-a ，x 5=x 4-x 3=-a -(b -a )=-b ，x 6=x 5-x 4=-b -(-a )=a -b ，x 7=x 6-x 5=a -b -(-b )=a ，x 8=x 7-x 6=a -(a -b )=b ，x 9=x 8-x 7=b -a ，⋯∴数列{x n }是以6为最小正周期的周期数列．∵2019÷6=336⋯3，∴x 2019=x 3=b -a ．故答案为b -a .28.(2022·全国·高三专题练习)数列{a n }满足a 1=2，a 2=11-a 1，若对于大于2的正整数n ，a n =11-a n -1，则a 102=__________.【答案】12【解析】由题意知：a 2=11-2=-1,a 3=11--1 =12,a 4=11-12=2,a 5=11-2=-1，故{a n }是周期为3的周期数列，则a 102=a 3×34=a 3=12.故答案为：12.29.(2022·河南·模拟预测(文))设数列a n 满足a n +1=1+a n 1-a n ,且a 1=12，则a 2022=( )A.-2 B.-13C.12D.3【答案】D【解析】由题意可得：a 2=1+a 11-a 1=1+121-12=3，a 3=1+a 21-a 2=1+31-3=-2，a 4=1+a 31-a 3=1+-2 1--2 =-13，a 5=1+a 41-a 4=1-131+13=12=a 1，据此可得数列a n 是周期为4的周期数列，则a 2022=a 505×4+2=a 2=3.故选：D30.(2022·全国·高三专题练习)设数列a n 的通项公式为a n =-1 n 2n -1 ⋅cos n π2+1n ∈N * ，其前n 项和为S n ，则S 120=( )A.-60 B.-120C.180D.240【答案】D【解析】当n =4k -3，k ∈N *时，cos n π2=0，a 4k -3=1；当n =4k -2，k ∈N *时，cosn π2=-1，a 4k -2=2×4k -2 -1 ×-1 +1=-8k +6；当n =4k -1，k ∈N *时，cos n π2=0，a 4k -1=1；当n =4k ，k ∈N *时，cos n π2=1，a 4k =2×4k -1+1=8k .∴a 4k -3+a 4k -2+a 4k -1+a 4k =1+-8k +6 +1+8k =8，∴S 120=1204×8=240.故选：D 经典题型十：前n 项积型31.(2022·全国·高三专题练习)设数列a n 的前n 项积为T n ，且T n =2-2a n n ∈N * .(1)求证数列1T n 是等差数列；(2)设b n =1-a n 1-a n +1 ，求数列b n 的前n 项和S n .【解析】(1)因为数列a n 的前n 项积为T n ，且T n =2-2a n n ∈N * ，∴当n =1时，T 1=a 1=2-2a 1，则a 1=23，1T 1=32.当n ≥2时，T n =2-2T n T n -1⇒1=2T n -2T n -1，∴1T n -1T n -1=12，所以1T n 是以1T 1=32为首项，12为公差的等差数列；(2)由(1)知数列1T n =n +22，则由T n =2-2a n 得a n =n +1n +2，所以b n =1n +2 n +3=1n +2-1n +3，所以S n =13-14 +14-15 +⋯+1n +2-1n +3 =13-1n +3=n 3n +9.32.(2022·全国·高三专题练习)记T n 为数列a n 的前n 项积，已知1T n +3a n=3，则T 10=( )A.163B.154C.133D.114【答案】C 【解析】n =1,T 1=43,T n =a 1a 2a 3⋯a n ,则a n =T n T n -1(n ≥2)，代入1T n +3a n =3，化简得：T n -T n -1=13，则T n =n +33,T 10=133.故选:C .33.(2022·全国·高三专题练习)记S n 为数列a n 的前n 项和，b n 为数列S n 的前n 项积，已知2S n +b n =2，则a 9=___________.【答案】1110【解析】因为b n =S 1∙S 2∙⋯S n ，所以b 1=S 1=a 1，b n -1=S 1∙S 2∙⋯S n -1(n ≥2)，S n =b nb n -1(n ≥2), 又因为2S n +b n =2，当n =1时，得 a 1=23，所以b 1=S 1=a 1=23， 当n ≥2时， 2×b nb n -1+b n =2，即2b n =2b n -1+1，所以2b n 是等差数列，首项为2b 1=3，公差d =1， 所以2b n=3+(n -1)×1=n +2，所以b n =2n +2，满足 b 1=23，故b n =2n +2，即S 1∙S 2∙⋯S n =2n +2，所以S 1∙S 2∙⋯S n -1=2n +1(n ≥2)，两式相除得：S n =n +1n +2，所以S n -1=nn +1(n ≥2)，所以a n =S n -S n -1=n +1n +2-n n +1=1(n +1)(n +2)，所以a 9=111×10=1110.故答案为：1110.经典题型十一：“和”型求通项34.(2022·山西·太原市外国语学校高三开学考试)在数列a n 中，a 1=1，且n ≥2，a 1+12a 2+13a 3+⋯+1n -1a n -1=a n .(1)求a n 的通项公式；(2)若b n =1a n a n +1，且数列b n 的前项n 和为S n ，证明：S n <3.【解析】(1)因为n ≥2,a 1+12a 2+13a 3+⋯+1n -1a n -1=a n ，所以当n ≥3,a 1+12a 2+13a 3+⋯+1n -2a n -2=a n -1，两式相减，得1n -1a n -1=a n -a n -1，即nn -1a n -1=a n ，当n =2时，a 2=a 1=1，所以当n ≥3时，a n a n -1=nn -1，所以当n ≥3时，a n =a n a n -1×a n -1a n -2×⋯×a 3a 2×a 2=n n -1×n -1n -2×⋯×32×1=n2，当n =2时，上式成立；当n =1时，上式不成立，所以a n =1,n =1n2,n ≥2.(2)证明：由(1)知b n =1,n =14n (n +1),n ≥2当n ≥2时，b n =4n (n +1)=41n -1n +1 ，所以当n =1，S 1=1<3；当n ≥2时，S n =1+412-13 +413-14 +⋯+41n -1n +1=1+412-13+13-14+⋯+1n -1n +1 =1+412-1n +1 =3-4n +1<3.综上，S n <3.35.(2022·全国·高三专题练习)数列a n 满足a 1∈Z ，a n +1+a n =2n +3，且其前n 项和为S n .若S 13=a m ，则正整数m =( )A.99 B.103C.107D.198【答案】B【解析】由a n +1+a n =2n +3得a n +1-(n +1)-1=-a n -n -1 ，∴a n-n-1为等比数列，∴a n-n-1=(-1)n-1a1-2，∴a n=(-1)n-1a1-2+n+1，a m=(-1)m-1a1-2+m+1，∴S13=a1+a2+a3+⋯+a12+a13=a1+2×(2+4+⋯+12)+3×6=a1+102，①m为奇数时，a1-2+m+1=a1+102，m=103；②m为偶数时，-a1-2+m+1=a1+102，m=2a1+99，∵a1∈Z，m=2a1+99只能为奇数，∴m为偶数时，无解，综上所述，m=103.故选：B.36.(2022·黑龙江·哈师大附中高三阶段练习(理))已知数列a n的前n项和为S n，若S n+1+S n=2n2n∈N*，且a1≠0，a10=28，则a1的值为A.-8B.6C.-5D.4【答案】C【解析】对于S n+1+S n=2n2，当n=1时有S2+S1=2，即a2-2=-2a1∵S n+1+S n=2n2，∴S n+S n-1=2(n-1)2，(n≥2)两式相减得：a n+1+a n=4n-2a n+1-2n=-a n-2(n-1)，(n≥2)由a1≠0可得a2-2=-2a1≠0,∴a n+1-2na n-2(n-1)=-1(n≥2)即a n-2(n-1)从第二项起是等比数列，所以a n-2(n-1)=a2-2(-1)n-2，即a n=a2-2(-1)n-2+2(n-1)，则a10=a2-2+18=28，故a2=12，由a2-2=-2a1可得a1=-5，故选C.经典题型十二：正负相间讨论、奇偶讨论型37.(2022·河南·高二阶段练习(文))数列a n满足a1=1,a n+a n+1=3n n∈N*，则a2018=__________ _.【答案】3026【解析】∵a n+a n+1=3n，∴a n+1+a n+2=3n+1，得a n+2-a n=3，∵a1=1,a n+a n+1=3n n∈N*，∴a1+ a2=3⇒a2=2，所以a n的偶数项构成等差数列，首项为2，公差为3，∴a2018=a2+1008×3=2+3024= 3026.故答案为：302638.(2022·全国·高三专题练习)已知数列a n中，a1=1，a2=2，a n+2=-1n+1a n+2，则a18a19=( )A.3B.113C.213D.219【答案】D【解析】当n为奇数时，a n+2-a n=2，即数列a n中的奇数项依次构成首项为1，公差为2的等差数列，所以，a19=1+10-1×2=19，当n为偶数时，a n+2+a n=2，则a n+4+a n+2=2，两式相减得a n+4-a n=0，所以，a18=a4×4+2=a2=2，故a18a19=219，故选：D.39.(2022·广东·高三开学考试)已知数列a n满足a1=3，a2=2，a n+2=a n-1,n=2k-1 3a n,n=2k .(1)求数列a n的通项公式；(2)求数列a n的前2n项的和S2n.【解析】(1)当n为奇数时，a n+2-a n=-1，所以所有奇数项构成以a1=3为首项，公差为-1的等差数列，所以a n=3+(n-1)⋅-12=7-n2，当n为偶数时，a n+2=3a n，所以所有偶数项构成以a2=2为首项，公比为3的等比数列，所以a n=2×(3)n-2=2×3n-22，所以a n=7-n2,n=2k-1 2×3n-22,n=2k ；(2)S2n=a1+a2+⋯+a2n=a1+a3+a5+⋯+a2n-1+a2+a4+⋯+a2n=3n+(-1)⋅n(n-1)2+21-3n1-3=(7-n)n2+3n-1=-12n2+72n+3n-1.40.数列{a n}满足a n+2+(-1)n+1a n=3n-1，前16项和为540，则a2= ．【解析】解：因为数列{a n}满足a n+2+(-1)n+1a n=3n-1，当n为奇数时，a n+2+a n=3n-1，所以a3+a1=2，a7+a5=14，a11+a9=26，a15+a13=38，则a1+a3+a5+a7+a9+a11+a13+a15=80，当n为偶数时，a n+2-a n=3n-1，所以a4-a2=5，a6-a4=11，a8-a6=17，a10-a8=23，a12-a10=29，a14-a12=35，a16-a14=41，故a4=5+a2，a6=16+a2，a8=33+a2，a10=56+a2，a12=85+a2，a14=120+a2，a16=161+a2，因为前16项和为540，所以a2+a4+a6+a8+a10+a12+a14+a16=540-80=460，所以8a2+476=460，解得a2=-2．故答案为：-2．41.(2022•夏津县校级开学)数列{a n}满足a n+2+(-1)n a n=3n-1，前16项和为508，则a1= ．【解析】解：由a n+2+(-1)n a n=3n-1，当n为奇数时，有a n+2-a n=3n-1，可得a n-a n-2=3(n-2)-1，⋯a3-a1=3⋅1-1，累加可得a n-a1=3[1+3+⋯+(n-2)]-n-12=(n-1)(3n-5)4；当n为偶数时，a n+2+a n=3n-1，可得a4+a2=5，a8+a6=17，a12+a10=29，a16+a14=41．可得a2+a4+⋯+a16=92．∴a 1+a 3+⋯+a 15=416．∴8a 1+14(0+8+40+96+176+280+408+560)=416，∴8a 1=24，即a 1=3．故答案为：3．经典题型十三：因式分解型求通项42.(2022秋•安徽月考)已知正项数列{a n }满足：a 1=a ，a 2n +1-4a 2n +a n +1-2a n =0，n ∈N *．(Ⅰ)判断数列{a n }是否是等比数列，并说明理由；(Ⅱ)若a =2，设a n =b n -n ．n ∈N *，求数列{b n }的前n 项和S n ．【解析】解：(Ⅰ)∵a 2n +1-4a 2n +a n +1-2a n =0，∴(a n +1-2a n )(a n +1+2a n +1)=0，又∵数列{a n }为正项数列，∴a n +1=2a n ，∴①当a =0时，数列{a n }不是等比数列；②当a ≠0时，an +1a n=2，此时数列{a n }是首项为a ，公比为2的等比数列．(Ⅱ)由(Ⅰ)可知：a n =2n ，∴b n =2n +n ，∴S n =(21+22+⋯+2n)+(1+2+⋯+n )=2(1-2n )1-2+n (1+n )2=2n +1-2+n (n +1)2．43.(2022•怀化模拟)已知正项数列{a n }满足a 1=1，2a 2n -a n -1a n -6a 2n -1=0(n ≥2,n ∈N *)设b n =log 2a n ．(1)求b 1，b 2b 3；(2)判断数列{b n }是否为等差数列，并说明理由；(3){b n }的通项公式，并求其前n 项和为S n ．【解析】解：(1)a 1=1，2a 2n -a n -1a n -6a 2n -1=0，a n >0，可得(2a n +3a n -1)(a n -2a n -1)=0，则a n =2a n -1，数列{a n }为首项为1，公比为2的等比数列，可得a n =2n -1；b n =log 2a n =n -1，b 1=0，b 2b 3=1×2=2；(2)数列{b n }为等差数列，理由：b n +1-b n =n -(n -1)=1，则数列{b n }为首项为0，公差为1的等差数列；(3)b n =log 2a n =log 22n -1=n -1，前n 项和为S n =12n (0+n -1)=n 2-n2．44.(2022秋•仓山区校级月考)已知正项数列{a n }满足a 1=2且(n +1)a 2n +a n a n +1-na 2n +1=0(n ∈N *)(Ⅰ)证明数列{a n }为等差数列；(Ⅱ)若记b n =4a n a n +1，求数列{b n }的前n 项和S n ．【解析】(I )证明：由(n +1)a 2n +a n a n +1-na 2n +1=0(n ∈N *)，变形得：(a n +a n +1)[(n +1)a n -na n +1]=0，由于{a n }为正项数列，∴a n +1a n =n +1n，利用累乘法得：a n =2n (n ∈N *)从而得知：数列{a n }是以2为首项，以2为公差的等差数列．(Ⅱ)解：由(Ⅰ)知：b n=42n∙2(n+1)=1n(n+1)=1n-1n+1，从而S n=b1+b2+⋯+b n=1-1 2+12-13+13-15+⋯+1n-1-1n+1=1-1n+1=n n+1．经典题型十四：其他几类特殊数列求通项45.(2022·全国·高三专题练习)在数列{a n}中，已知各项都为正数的数列{a n}满足5a n+2+4a n+1-a n=0.(1)证明数列{a n+a n+1}为等比数列；(2)若a1=15，a2=125，求{a n}的通项公式.【解析】(1)各项都为正数的数列{a n}满足5a n+2+4a n+1-a n=0，得a n+1+a n+2=15(a n+1+a n)，即a n+1+a n+2 a n+a n+1=15所以数列{a n+a n+1}是公比为15的等比数列；(2)因为a1=15，a2=125，所以a1+a2=625，由(1)知数列{a n+a n+1}是首项为625，公比为15的等比数列，所以a n+a n+1=625×15n-1，于是a n+1-15n+1=-an-15 n=(-1)n a1-15，又因为a1-15=0，所以a n-15 n=0，即a n=15 n.46.(2022·湖北·天门市教育科学研究院模拟预测)已知数列a n满足a1=1,a2=6，且a n+1=4a n-4a n-1, n≥2,n∈N*.(1)证明数列a n+1-2a n是等比数列，并求数列a n的通项公式；(2)求数列a n的前n项和S n.【解析】(1)因为a n+1=4a n-4a n-1,n≥2,n∈N*所以a n+1-2a n=2a n-4a n-1=2(a n-2a n-1)又因为a2-2a1=4所以a n+1-2a n是以4为首项，2为公比的等比数列.所以a n+1-2a n=4×2n-1=2n+1变形得a n+12n+1-a n2n=1所以a n2n是以a12=12为首项，1为公差的等差数列所以a n2n=12+n-1=n-12，所以a n=(2n-1)2n-1(2)因为T n=1×20+3×21+5×22+⋅⋅⋅+(2n-1)2n-1⋯①所以2T n=1×21+3×22+5×23+⋅⋅⋅+(2n-1)2n⋯②①-②得：-T n=1+22+23+⋅⋅⋅+2n-1-(2n-1)2n=1+22(1-2n-1)1-2-(2n-1)2n所以T n=(2n-1)2n-2n+1+3=(2n-3)2n+347.(2022·内蒙古·赤峰红旗中学松山分校模拟预测(理))设数列{a n}的前n项和为S n，满足2S n=a2n+1a n n∈N*，则下列说法正确的是( )A.a2021⋅a2022<1B.a2021⋅a2022>1C.a2022<-22022D.a2022>22022【答案】A【解析】因为数列{a n}的前n项和为S n，满足2S n=a2n+1a n n∈N*，。
2020高考数学热点难点微专题五“隐圆”问题考点考向考题点拨(29张)
第13页
专题综述 典型例题 课后作业
热点难点微专题五 “隐圆”问题
2. 已知|O→A|＝|O→B|＝ 2，且O→A·O→B＝1，若点 C 满足|O→A＋O→B|＝1，则|O→C|的取值范 围是________． [ 6－1， 6＋1] 解析：O→A·O→B＝|O→A|×|O→B|×cos〈O→A，O→B〉＝1，cos〈O→A，O→B〉 ＝12，cos〈O→A，O→B〉＝π3.以 O 为坐标原点，OA 所在直线为 x 轴，建立平面直角 坐标系，则 O(0,0)，令 A( 2，0)，B 22， 26，令O→P＝O→A＋O→B＝32 2， 26，|O→P |＝ 6，|O→A＋O→B|＝|O→A＋O→B－O→C|＝|O→P－O→C|＝1，
－b23－522＋94≤12.
第19页
专题综述 典型例题 课后作业
热点难点微专题五 “隐圆”问题
6. 已知点 A(0,1)，B(1,0)，C(t,0)，点 D 是直线 AC 上的动点，若 AD≤2BD 恒成立， 则最小正整数 t 的值为________．
第20页
专题综述 典型例题 课后作业
第3页
专题综述 典型例题 课后作业
热点难点微专题五 “隐圆”问题
(3) 若直线 l：ax＋y－4a＝0 上存在相距为 2 的两个动点 A，B，圆 O：x2＋y2＝1 上存在点 C，使得△ABC 为等腰直角三角形(C 为直角顶点)，则实数 a 的取值范围 为________． (4) 在平面直角坐标系 xOy 中，已知圆 O：x2＋y2＝1，O1：(x－4)2＋y2＝4，动点 P 在直线 x＋ 3y－b＝0 上，过 P 分别作圆 O，O1 的切线，切点分别为 A，B.若满足 PB＝2PA 的点 P 有且只有 2 个，则实数 b 的取值范围是________．
立体几何中截面问题-高考数学微专题突破含详解
立体几何中截面问题-高考数学微专题突破一、单选题1．下列命题错误的是（ ）A ．圆柱的轴截面是过母线的截面中面积最大的一个B ．圆锥的轴截面是所有过顶点的截面中面积最大的一个C ．圆台的所有平行于底面的截面都是圆D ．圆锥所有的轴截面都是等腰三角形2．一正四面体木块如图所示，点P 是棱VA 的中点，过点P 将木块锯开，使截面平行于棱VB 和AC ，则下列关于截面的说法正确的是（ ）．A ．满足条件的截面不存在B ．截面是一个梯形C ．截面是一个菱形D ．截面是一个三角形3．已知正方体1111ABCD A B C D -，直线1AC ⊥平面α，平面α截此正方体所得截面中，正确的说法是（ ）A ．截面形状可能为四边形B ．截面形状可能为五边形C ．截面面积最大值为D ．截面面积最大值为24．球O 的截面把垂直于截面的直径分成1:3O 的体积为( )A ．16πB ．163πC ．323πD ．5．如图，在棱长为2的正方体1111ABCD A B C D -中，11A B 的中点是P ，过点1A 作与截面1PBC 平行的截面，则该截面的面积为( )A ．B ．C ．D ．46V ABC -中，40AVB BVC CVA ︒∠=∠=∠=，过点A 作截面则截面AEF ，则截面AEF 的周长的最小值为（ ）A B ．2 C ．3 D ．47．已知正方体1111ABCD A B C D -的棱长为2，1AC ⊥平面α.平面α截此正方体所得的截面有以下四个结论：①截面形状可能是正三角形①截面的形状可能是正方形①截面形状可能是正五边形①截面面积最大值为则正确结论的编号是（ ）A ．①①B ．①①C ．①①D ．①① 8．已知长方体1111ABCD A B C D -各个顶点都在球面上，8AB AD ==，16AA =，过棱AB 作该球的截面，则当截面面积最小时，球心到截面的距离为( )A ．3B ．4C ．5D ．69．过半径为2的球O 表面上一点A 作球O 的截面，若OA 与该截面所成的角是30，则截面的面积是( )A ．πB ．2πC ．3πD ．10．直三棱柱111ABC A B C -中，若22BC AB ==，1AA AC ==M 是11B C 中点，过AM 作这个三棱柱的截面，当截面与平面ABC 所成的锐二面角最小时，这个截面的面积为（ ）A ．2BC D11．在直三棱柱111ABC A B C -中，M 是1BB 上的点，3AB =，4BC =，5AC =，17CC =，过三点A 、M 、1C 作截面，当截面周长最小时，截面将三棱柱分成的两部分的体积比为（ ）．A ．34B ．45C ．910D ．101112．已知球O 是正三棱锥P ABC -的外接球，3,AB PA ==点E 在线段AC 上，且3AC AE =，过点E 作球O 的截面，则所得截面中面积最小的截面圆的面积是（ ） A ．2π B ．π C ．94π D ．74π 13．下列说法正确的是A ．平行于圆锥某一母线的截面是等腰三角形B ．平行于圆台某一母线的截面是等腰梯形C ．过圆锥顶点的截面是等腰三角形D ．过圆台上底面中心的截面是等腰梯形14．已知圆锥的底面半径和高相等，侧面积为，过圆锥的两条母线作截面，截面为等边三角形，则圆锥底面中心到截面的距离为（ ）A B C ．2 D 15．用一个平面截半径为25cm 的球，截面面积是2225cm π，则球心到截面的距离是（ ）A ．5cmB ．10cmC ．15cmD ．20cm 16．如图1-1-4所示的几何体：将它们按截面的形状分成两类时，下面分类方法正确的是（ ）A ．截面可能是圆和三角形两类B ．截面可能是圆和四边形两类C ．截面可能是圆和五边形两类D ．截面可能是三角形和四边形两类 17．在侧棱长为的正三棱锥中，，过 作截面，则截面的最小周长为（ ）A ．B ．4C ．6D ．1018．如图，三棱柱111ABC A B C -的所有棱长都为4，侧棱1AA ⊥底面ABC ，P ，Q ，R 分别在棱1AA ，AB ，11B C 上，2AP AQ ==，13B R =，过P ，Q ，R 三点的平面将三棱柱分为两部分，下列说法错误的是（ ）A．截面是五边形B ．截面面积为C ．截面将三棱柱体积平分D ．截面与底面所成的锐二面角大小为π3 19．过正四面体ABCD 的顶点A 作一个形状为等腰三角形的截面，且使截面与底面BCD 所成的角为75︒，这样的截面有（ ）A ．6个B ．12个C ．16个D ．18个 20．如图，正四棱锥S ABCD -的所有棱长都等于a ，过不相邻的两条棱,SA SC 作截面SAC ，则截面的面积为A ．232a B ．2a C ．212a D ．213a 21．棱长为a 的正方体，过上底面两邻边中点和下底面中心作截面，则截面图形的周长等于（ ）A ．2a + BC +D +b 22．在棱长为2的正方体1111ABCD A B C D -中，M 是棱11A D 的中点，过1C ，B ，M 作正方体的截面，则这个截面的面积为（ ）A ．35B ．35C ．92D ．98 23．棱锥被平行于底面的平面所截，当截面分别平分棱锥的侧棱、侧面积、体积时，相应截面面积为S 1、S 2、S 3，则（ ）A ．S 1<S 2<S 3B ．S 1>S 2>S 3C ．S 2<S 1<S 3D ．S 2>S 1>S 324．一个正方体内接于一个球，过球心作一个截面，如图所示，则截面的可能图形是（ ）A ．①①①B ．①①C ．①①①D ．①①① 25．如图是某几何体的三视图，则过该几何体顶点的所有截面中，最大截面的面积是（ ）A ．2BCD ．126．如图是某几何体的三视图，则过该几何体顶点的所有截面中，最大的截面面积是（ ）A ．2BC ．4D ．32π 27．已知球O 是正三棱锥A BCD -的外接球，底边3BC =，侧棱AB =E 在线段BD 上，且3BD DE =，过点E 作球O 的截面，则所得截面圆面积的取值范围是（ ）A ．5,44ππ⎡⎤⎢⎥⎣⎦B ．[]2,4ππC ．9,44ππ⎡⎤⎢⎥⎣⎦D ．11,44ππ⎡⎤⎢⎥⎣⎦28．如图所示，在棱长为 6的正方体1111ABCD A B C D -中，点,E F 分别是棱1111,C D B C 的中点，过,,A E F 三点作该正方体的截面，则截面的周长为（ ）A ．18+B ．C ．D ．10++二、多选题 29．正方体1111ABCD A B C D -的棱长为2，已知平面1AC α⊥，则关于α截此正方体所得截面的判断正确的是（ ）A ．截面形状可能为正三角形B ．截面形状可能为正方形C ．截面形状可能为正六边形D ．截面面积最大值为30．如图所示，有一正四面体形状的木块，其棱长为a ，点P 是ACD △的中心.劳动课上，需过点P 将该木块锯开，并使得截面平行于棱AB 和CD ，则下列关于截面的说法中正确的是（ ）A ．截面与侧面ABC 的交线平行于侧面ABDB ．截面是一个三角形C ．截面是一个四边形D ．截面的面积为24a 31．如图，已知四棱锥P ABCD -所有棱长均为4，点M 是侧棱PC 上的一个动点（不与点,P C 重合），若过点M 且垂直于PC 的截面将该四棱锥分成两部分，则下列结论正确的是（ ）A ．截面的形状可能为三角形、四边形、五边形B ．截面和底面ABCD 所成的锐二面角为4πC ．当1PM =时，截面的面积为D ．当2PM =时，记被截面分成的两个几何体的体积分别为()1212,>V V V V ，则123=V V32．如图，设正方体1111ABCD A B C D -的棱长为2，E 为11A D 的中点，F 为1CC 上的一个动点，设由点A ，E ，F 构成的平面为α，则（ ）A ．平面α截正方体的截面可能是三角形B．当点F 与点1C 重合时，平面α截正方体的截面面积为C ．点D 到平面α D ．当F 为1CC 的中点时，平面α截正方体的截面为五边形33．正方体的截面可能是（ ）A ．钝角三角形B ．直角三角形C ．菱形D ．正六边形三、双空题34．正方体1111ABCD A B C D -的棱长为1，点K 在棱11A B 上运动，过,,A C K 三点作正方体的截面，若K 为棱11A B 的中点，则截面面积为_________，若截面把正方体分成体积之比为2:1的两部分，则11A K KB =_______35．正方体1111ABCD A B C D -的棱长为2，点K 在棱11A B 上运动，过,,A C K 三点作正方体的截面，若K 与1B 重合，此时截面把正方体分成体积之比为(01)λλ<<的两部分，则λ=______；若K 为棱11A B 的中点，则截面面积为________．36．正方体1111ABCD A B C D -的棱长为2，M ，N ，E ，F 分别是11A B ，AD ，11B C ，11C D 的中点，则过EF 且与MN 平行的平面截正方体所得截面的面积为______，CE 和该截面所成角的正弦值为______．37．已知三棱锥P ABC -的四个顶点都在球O 的表面上，PA ⊥平面ABC ，6PA =，AB =2AC =，4BC =，则球O 的表面积为________；若D 是AB 的中点，过点D 作球O 的截面，则截面面积的范围是________．四、填空题38．如图所示，在棱长为2的正方体1111ABCD A B C D -中，11A B 的中点是P ，过点1A 作与截面1PBC 平行的截面，则截面的面积为__________.39．过半径为2的球O 表面上一点A 作球O 的截面，截面的面积为3π，则球心O 到该截面的距离为______40．已知正方体1111ABCD A B C D -的棱长为2，直线1AC ⊥平面α.平面α截此正方体所得截面有如下四个结论：①截面形状可能为正三角形；①截面形状可能为正方形；①截面形状不可能是正五边形；①截面面积最大值为其中所有正确结论的编号是______．41．体积为12的四面体ABCD 中，E F G 、、分别是棱AB BC AD 、、上的点，且2AE EB =，BF FC =，2AG GD =.过点E F G 、、作截面EFHG ，且点C 到此截面的距离为1.则此截面的面积是______.42．已知圆锥的底面半径和高相等，侧面积为4π，过圆锥的两条母线作截面，截面为等边三角形，则圆锥底面中心到截面的距离为____．43．在侧棱长为S ABC -中，40ASB BSC CSA ∠=∠=∠=︒，过点A 作截面AEF ，则截面最小的周长为______.44．过正四面体ABCD 的顶点A 作一个形状为等腰三角形的截面，且使截面与底面BCD 所成的角为75。
创新设计二轮理科数学配套PPT课件微专题28 解析几何中优化运算的方法
索引
可得 kAB·kCD＝y3Gy6H＝－1，
即yGyH＝－36， 所以 S△PGH＝21|PG|·|PH|＝12· 1＋k1A2 B|yG| · 1＋k12CD|yH|
＝18 2＋k12AB＋k12CD≥18 ＝18 2＋2＝36，
2＋|kAB2kCD|
曲线右支于 A，B 两点，且|A→F|＝λ|F→B|，则双曲线的离心率等于|（λ＋λ1－）1cos α|.
(3)过抛物线 y2＝2px(p＞0)的焦点 F 倾斜角为 θ 的直线交抛物线于 A，B 两点，
则两焦半径长为1－cpos θ，1＋cpos θ，|A1F|＋|B1F|＝p2，|AB|＝si2np2θ，S△AOB＝2spin2 θ.
索引
(2)过点P(m，0)(m>0)作互作垂直的两条直线l1，l2，它们与(1)中轨迹E分别交于 点A，B及点C，D，且G，H分别是线段AB，CD的中点，求△PGH面积的最小 值. 解 设A(x1，y1)，B(x2，y2)， 则有 y21＝12x1，y22＝12x2， 以上两式作差，并整理可得xy11－ －xy22＝y11＋2y2＝y6G. 即 kAB＝y6G，同理可得 kCD＝y6H，
3＝ 2
6 2.
索引
类型二 设而不求，整体推进
///////
核心归纳
在解决直线与圆锥曲线的相关问题时，通过设点的坐标，应用“点差法”或借 助根与系数的关系来进行整体处理，设而不求，避免方程组的复杂求解，简化 运算.
索引
例2 已知点M到点F(3，0)的距离比它到直线l：x＋5＝0的距离小2. (1)求点M的轨迹E的方程； 解 由题意知，点 M 到点 F(3，0)的距离与到直线 l′：x＋3＝0 的距离相等，结 合抛物线的定义，可知轨迹 E 是以 F(3，0)为焦点，以直线 l′：x＋3＝0 为准线 的抛物线，则知p2＝3，解得 p＝6，故 M 的轨迹 E 的方程为 y2＝12x.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
素养评析
(1)本例中
点O在以AB为直径的圆外
⇒
∠AOB为锐角
⇒
→→ OA·OB>0
⇒
x1x2＋y1y2>0
利用根与系数的关系与判别式可得到直线斜率的范围. (2)逻辑推理是得到数学结论、构建数学体系的重要方式，本例从条件出发与 已有知识结合，逐步推出相应的结论.对逻辑推理素养的培养有很好的帮助.
3 达标检测
反思感悟 判断直线与椭圆的位置关系，通过解直线方程与椭圆方程组成的方 程组，消去方程组中的一个变量，得到关于另一个变量的一元二次方程，则 Δ>0⇔直线与椭圆相交； Δ＝0⇔直线与椭圆相切； Δ<0⇔直线与椭圆相离.
跟踪训练 1 若直线 y＝kx＋1 与焦点在 x 轴上的椭圆x52＋ym2＝1 总有公共点， 则实数 m 的取值范围为_[_1_,_5_) _.
A.m>1
√B.m>1且m≠3
C.m>3
D.m>0且m≠3
解析
y＝x＋2， 由xm2＋y32＝1，
得(3＋m)x2＋4mx＋m＝0，
∵Δ＝(4m)2－4m(3＋m)>0，∴16m2－4m(3＋m)>0，
∴m>1或m<0.
又∵m>0且m≠3，∴m>1且m≠3.
1234
3.已知以F1(－2,0)，F2(2,0)为焦点的椭圆与直线x＋ 3y＋4＝0有且仅有一个公 共点，则椭圆的长轴长为__2__7__. 解析 由题意可设椭圆的方程为ax22＋a2y－2 4＝1(a>2)， 与直线方程 x＋ 3y＋4＝0 联立， 得 4(a2－3)y2＋8 3(a2－4)y＋(16－a2)(a2－4)＝0， 由 Δ＝0，得 a＝ 7， 所以椭圆的长轴长为 2 7.
(√) 4.设A是椭圆内一点，以A为中点的弦是唯一的.( × ) 5.直线 y＝k(x－a)与椭圆ax22＋by22＝1 的位置关系是相交.( √ )
2 题型探究
PART TWO
题型一 直线与椭圆的位置关系
例 1 已知直线 l：y＝2x＋m，椭圆 C：x42＋y22＝1.试问当 m 取何值时，直线 l
题型三 椭圆中的最值(或范围)问题
例3 已知椭圆4x2＋y2＝1及直线y＝x＋m. (1)当直线和椭圆有公共点时，求实数m的取值范围；
解
4x2＋y2＝1， 由
得 5x2＋2mx＋m2－1＝0，
y＝x＋m，
因为直线与椭圆有公共点，所以Δ＝4m2－20(m2－1)≥0，
解得－ 25≤m≤ 25.
这时直线l与椭圆C有两个公共点.
(2)有且只有一个公共点； 解 当 Δ＝0，即 m＝±3 2时， 方程①有两个相同的实数解，可知原方程组有两组相同的实数解. 这时直线l与椭圆C有且只有一个公共点. (3)没有公共点. 解 当 Δ<0，即 m<－3 2或 m>3 2时， 方程①没有实数解，可知原方程组没有实数解. 这时直线l与椭圆C没有公共点.
思考辨析 判断正误
SIKAOBIANXIPANDUANZHENGWU
1.若直线的斜率一定，则当直线过椭圆的中心时，弦长最大.( √ ) 2.在椭圆上的所有点中，长轴的端点到椭圆中心的距离最大，短轴的端点到椭 圆中心的距离最小.( √ ) 3.在椭圆的焦点弦中，当弦与长轴垂直时弦最短，当弦与长轴重合时弦最长.
(2)当P点恰好为线段AB的中点时，求l的方程.
反思感悟 处理直线与椭圆相交的关系问题的通法是通过解直线与椭圆构成 的方程.利用根与系数的关系或中点坐标公式解决，涉及弦的中点，还可使用 点差法：设出弦的两端点坐标，代入椭圆方程，两式相减即得弦的中点与斜 率的关系.
跟踪训练 2 已知椭圆 ax2＋by2＝1(a>0，b>0 且 a≠b)与直线 x＋y－1＝0 相交于 A，B 两点，C 是 AB 的中点，若|AB|＝2 2，OC 的斜率为 22，求椭圆的方程.
1234
(2)若过左焦点F1且倾斜角为45°的直线l与椭圆C交于P，Q两点，求线段PQ的长. 解 由已知得，直线l的斜率k＝tan 45°＝1，而F1(－2,0)， 所以直线 l 的方程为 y＝x＋2，代入方程x92＋y52＝1， 得5x2＋9(x＋2)2＝45，即14x2＋36x－9＝0， 设 P(x1，y1)，Q(x2，y2)，则 x1＋x2＝－178，x1x2＝－194， 则|PQ|＝ 1＋k2|x1－x2|＝ 1＋12× x1＋x22－4x1x2
PART THREE
1.点 A(a,1)在椭圆x42＋y22＝1 的内部，则 a 的取值范围是
√A.－ 2<a< 2
B.a<－ 2或 a> 2
C.－2<a<2
D.－1<a<1
解析 由题意知a42＋12<1，解得－ 2<a< 2.
1234
2.直线 y＝x＋2 与椭圆xm2＋y32＝1 有两个公共点，则 m 的取值范围是
1234
4.已知椭圆C的两个焦点是F1(－2,0)，F2(2,0)，且椭圆C经过点A(0， 5). (1)求椭圆C的标准方程； 解 由已知得，椭圆 C 的焦点在 x 轴上，可设椭圆的方程为ax22＋by22＝1(a>b>0)， (0， 5)是椭圆短轴上的一个顶点，可得 b＝ 5， 由题意可得 c＝2，故 a＝ b2＋c2＝3， 则椭圆 C 的标准方程为x92＋y52＝1.
跟踪训练3 已知椭圆C：x2＋2y2＝4. (1)若点P(a，b)是椭圆C上一点，求a2＋b2的取值范围； 解 由题意得a2＋2b2＝4， 则a2＝4－2b2， ∴a2＋b2＝4－2b2＋b2＝4－b2， ∵b∈[－ 2， 2]，∴4－b2∈[2,4]. 故a2＋b2∈[2,4]，a2＋b2的取值范围为[2,4].
(2)设O为原点，若点A在直线y＝2上，点B在椭圆C上，且OA⊥OB，求|AB|的最
小值.
解 设A(t,2)，B(x0，y0)，x0≠0.∵OA⊥OB， ∴O→A·O→B＝0， ∴tx0＋2y0＝0，∴t＝－2xy00. 又∵x20＋2y20＝4，∴0<x20≤4. ∴|AB|2＝(x0－t)2＋(y0－2)2＝x220＋x802＋4≥4＋4＝8， 当且仅当x220＝x820，即 x20＝4 时等号成立， ∴|AB|的最小值为 2 2.
与椭圆 C：
(1)有两个公共点；
y＝2x＋m，
解 直线 l 的方程与椭圆 C 的方程联立，得方程组x42＋y22＝1，
得9x2＋8mx＋2m2－4＝0.
消去 y， ①
方程①的判别式Δ＝(8m)2－4×9×(2m2－4)＝－8m2＋144.
当 Δ>0，即－3 2<m<3 2时，
方程①有两个不同的实数解，可知原方程组有两组不同的实数解.
消去 y，得关于 x 的一元二次方程.
当Δ＞0时，方程有 两个不同解 ，直线与椭圆 相交 ； 当Δ＝0时，方程有 两个相同解 ，直线与椭圆 相切 ； 当Δ＜0时，方程 无解 ，直线与椭圆 相离 .
知识点三 弦长公式 设直线方程为 y＝kx＋m(k≠0)，椭圆方程为ax22＋by22＝1(a>b>0)或ay22＋bx22＝1 (a>b>0)，直线与椭圆的两个交点为 A(x1，y1)，B(x2，y2)， 则|AB|＝ x1－x22＋y1－y22，
解析 ∵直线y＝kx＋1过定点M(0,1)， ∴要使直线与该椭圆总有公共点，则点M(0,1)必在椭圆内或椭圆上，
0<m<5， 由此得052＋1m2≤1，
解得 1≤m<5.
题型二 直线与椭圆的相交弦问题
例 2 已知椭圆3x62＋y92＝1 和点 P(4,2)，直线 l 经过点 P 且与椭圆交于 A，B 两点. (1)当直线 l 的斜率为12时，求线段 AB 的长度；
反思感悟 解析几何中的综合性问题很多，而且可与很多知识联系在一起出 题，例如不等式、三角函数、平面向量以及函数的最值问题等.解决这类问题 需要正确地应用转化思想、函数与方程思想和数形结合思想.其中应用比较多 的是利用方程根与系数的关系构造等式或函数关系式，这其中要注意利用根 的判别式来确定参数的限制条件.
(2)求被椭圆截得的最长弦所在的直线方程. 解 设直线与椭圆交于A(x1，y1)，B(x2，y2)两点， 由(1)知5x2＋2mx＋m2－1＝0， 所以 x1＋x2＝－25m，x1x2＝15(m2－1)， 所以|AB|＝ x1－x22＋y1－y22
＝ 2x1－x22＝ 2[x1＋x22－4x1x2] ＝ 242m52－54m2－1＝52 10－8m2. 所以当m＝0时，|AB|最大，此时直线方程为y＝x.
位置关系 P在椭圆外 P在椭圆上 P在椭圆内
满足条件 ax202＋by202>1 ax202＋by202＝1 ax202＋by202<1
知识点二 直线与椭圆的位置关系
直线 y＝kx＋m 与椭圆ax22＋by22＝1(a＞b＞0)的位置关系的判断方法：
y＝kx＋m， 联立ax22＋by22＝1，
解 由题意得2a＝4，即a＝2，
又点 P1， 23在椭圆 C 上， ∴14＋43b2＝1，即 b2＝1， ∴椭圆 C 的方程为x42＋y2＝1，焦点 F1(－ 3，0)，F2( 3，0).
(2)直线l过定点M(0,2)，且与椭圆C交于不同的两点A，B，若原点O在以线段 AB为直径的圆外，求直线l的斜率k的取值范围.
∴|AB|＝ x1－x22＋kx1－kx22
＝ 1＋k2 x1－x22
＝ 1＋k2 x1＋x22－4x1x2，
或|AB|＝ 1ky1－1ky22＋y1－y22 ＝ 1＋k12 y1－y22
＝ 1＋k12 y1＋y22－4y1y2. 其中，x1＋x2，x1x2或y1＋y2，y1y2的值，可通过由直线方程与椭圆方程联立消 去y(或x)后得到关于x(或y)的一元二次方程求得.