高考文科数学一轮复习分层练习第二章函数的图象
高考数学一轮复习第2章《函数》2：函数的图象.doc
课时作业12 函数的图象时间：45分钟 分值：100分一、选择题(每小题5分，共30分)1．函数f (x )＝1x－x 的图象关于 ( )A ．y 轴对称B ．直线y ＝－x 对称C ．坐标原点对称D ．直线y ＝x 对称∵f (x )＝－f (－x )，∴f (x )＝1x－x 是奇函数．∴f (x )的图象关于坐标原点对称． 答案：C2．若函数f (x )＝(k －1)a x －a －x (a >0且a ≠1)在R 上既是奇函数，又是减函数，则g (x )＝log a (x ＋k )的图象是 ( )解析：由函数f (x )＝(k －1)a x－a －x(a >0且a ≠1)在R 上为奇函数知，k －1＝1，即k ＝2. 又f (x )为减函数，∴0<a <1. ∴g (x )＝log a (x ＋2)(0<a <1)． 答案：A3．如果函数y ＝f (x )的图象如图1，那么导函数y ＝f ′(x )的图象可能是 ( )图1解析：y ＝f (x )的单调变化情况为增、减、增、减，因此y ＝f ′(x )的符号变化情况为大于零、小于零、大于零、小于零．故选A. 答案：A图24．已知甲、乙两车由同一起点同时出发，并沿同一路线(假定为直线)行驶．甲车、乙车的速度曲线分别为v 甲和v 乙(如图2所示)．那么对于图中给定的t 0和t 1，下列判断中一定正确的是 ( )A ．在t 0时刻，两车的位置相同B ．t 0时刻后，乙车在甲车前面C ．在t 1时刻，甲车在乙车前面D ．t 1时刻后，甲车在乙车后面答案：C5．设a <b ，函数y ＝(x －a )2(x －b )的图像可能是( )解析：当x >b 时，y >0，由数轴穿根法可知，从右上向左下穿，奇次穿偶次不穿可知，只有C 正确． 答案：C图36．如图3，当参数λ＝λ1，λ2时，连续函数y ＝x1＋λx(x ≥0)的图像分别对应曲线C 1和C 2，则 ( ) A ．0<λ1<λ2 B ．0<λ2<λ1 C ．λ1<λ2<0 D ．λ2<λ1<0 解析：如果λ<0，定义域不可能为[0，＋∞)，排除C 、D. 又∵C 2的图象在C 1的图象的上方，∴x 1＋λ2x >x 1＋λ1x ⇒1＋λ2x <1＋λ1x ⇒λ2<λ1.故选B.答案：B二、填空题(每小题5分，共7．如果函数y ＝f (x )满足f (x )＝f (2－x )，那么函数y ＝f (x )的图象关于直线x ＝__________对称．解析：f (x )＝f (2－x )⇔f [1－(1－x )]＝f [1＋(1－x )]⇔f (1－x )＝f (1＋x )．∴函数y ＝f (x )的图象关于直线x ＝1对称．答案：18．已知最小正周期为2的函数y ＝f (x )，当x ∈[－1,1]时，f (x )＝x 2，则函数y ＝f (x )(x ∈R )的图象与y ＝|log 5x |的图象的交点个数为__________．解析：由图4可知有5个交点．图4答案：5个图59．已知f (x )是定义域为(－∞，0)∪(0，＋∞)上的奇函数，在区间(0，＋∞)上单调递增，当x >0时，f (x )的图象如图5所示：若x ·[f (x )－f (－x )]<0，则x 的取值范围是__________．解析：∵f (x )为奇函数，∴x ·[f (x )－f (－x )]＝2x ·f (x )<0. 又f (x )在定义域上的图象如题图， ∴取值范围为(－3,0)∪(0,3)． 答案：(－3,0)∪(0,3)10．若函数f (x )＝log 2|ax －1|的图象的对称轴为x ＝2，则非零实数a 的值是__________．解析：∵函数f (x )的图象的对称轴为x ＝2，∴f (2＋x )＝f (2－x )，即|a (2－x )－1|＝|a (2＋x )－1|，∵a ≠0，∴2a －1＝0，∴a ＝12.答案：12三、解答题(共50分)11．(15分)分别画出下列函数的图象：(1)y ＝|lg x |；(2)y ＝2x ＋2；(3)y ＝x 2－2|x |－1.解：(1)y ＝⎩⎪⎨⎪⎧lg x (x ≥1)－lg x (0<x <1)(2)将y ＝2x 的图象向左平移2个单位．图6(3)y ＝⎩⎪⎨⎪⎧x 2－2x －1 (x ≥0)x 2＋2x －1 (x <0).12．(15分)已知函数f (x )＝log 2(x ＋1)，将y ＝f (x )的图象向左平移1个单位，再将图象上所有点 的纵坐标伸长到原来的2倍，横坐标不变，得到函数y ＝g (x )的图象． (1)求y ＝g (x )的解析式及定义域；(2)求函数F (x )＝f (x －1)－g (x )的最大值．解：(1)f (x )＝log 2(x ＋1)――→左1y ＝log 2(x ＋2)――→纵坐标伸长到原来的2倍y ＝2log 2(x ＋2)，即g (x )＝2log 2(x ＋2)，∵x ＋2>0. ∴x >－2.∴定义域为(－2，＋∞)．(2)∵F (x )＝f (x －1)－g (x )＝log 2x －2log 2(x ＋2)＝log 2x (x ＋2)2(x >0)＝log 2x x 2＋4x ＋4＝log 21x ＋4x＋4≤log 218＝－3，∴当x ＝2时，F (x )max ＝－3.13．(已知函数f (x )＝x ＋log 3x4－x.(1)求f (x )＋f (4－x )的值；(2)猜想函数f (x )的图象具有怎样的对称性，并给出证明．解：(1)f (x )＋f (4－x )＝x ＋log 3x4－x＋4－x ＋log 34－x 4－(4－x )＝4＋log 3x 4－x＋log 34－x x ＝4.(2)关于点P (2,2)对称．证明：设Q (x ，y )为函数f (x )＝x ＋log 3x4－x图象上的任一点，若点Q 关于点P 的对称点为Q 1(x 1，y 1)，则⎩⎪⎨⎪⎧ x ＋x 1＝4，y ＋y 1＝4⇒⎩⎪⎨⎪⎧x 1＝4－x ，y 1＝4－y ，f (x 1)＝x 1＋log 3x 14－x 1＝4－x ＋log 34－x x ＝4－x －log 3x 4－x ＝4－y ＝y 1，∴函数y ＝f (x )的图象关于点P (2,2)对称．。
届高考数学一轮复习讲义第二章函数图象-.ppt
函数图象与解析式的对应 关系
例 2 已知函数 f(x)＝lg |x|，g(x)＝－x2＋1，则函数 f(x)·g(x) 的图象只可能是______．(填序号)
f(x)·g(x)＝－(x2－1)lg|x|是偶函数，从 f(x)·g(x)的性质入手进 行判断．
解析 f(x)g(x)＝－(x2－1)lg|x|是偶函数，图象不可能是①③. 又 f(x)·g(x)＝－(x2－1)lg|x|无最小值，所以只可能是④.
要点梳理
忆一忆知识要点
(2)对称变换 ①y＝f(－x)与 y＝f(x)的图象关于 y 轴对称． ②y＝－f(x)与 y＝f(x)的图象关于 x 轴 对称． ③y＝－f(－x)与 y＝f(x)的图象关于 原点 对称． (3)翻折变换 ①作 y＝f(x)的图象，将图象位于 x 轴下方的部分以 x 轴为对 称轴翻折到上方，其余部分不变，得到 y＝|f(x)|的图象； ②作 y＝f(x)在 y 轴上及 y 轴右边的图象部分，并作 y 轴右边 的图象关于 y 轴对称的图象，即得 y＝f(|x|)的图象．
(2)因 y＝1＋x－3 1，先作出 y＝3x的图象，将其图象向右平移 一个单位，再向上平移一个单位，即得 y＝xx＋－21的图象，如 图②.
(3)先作出 y＝log2x 的图象，再将其图象向下平移一个单位， 保留 x 轴上方的部分，将 x 轴下方的图象翻折到 x 轴上方， 即得 y＝|log2x－1|的图象，如图③.
可以用描点作图，也可以用图象变换法作图．
解 (1)∵y＝|lg x|＝l－g lxg，xx，≥01<，x<1. ∴函数 y＝|lg x|的图象如图①； (2)将函数 y＝2x 的图象向左平移 2 个单位即可得出函数 y＝ 2x－2 的图象，如图②；
2024届高考数学一轮复习+第二章《函数》第六节+函数的图象 +课件
A. B. C. D.
（5） ；
⑤
[解析] 的图象是由 的图象先向下平移1个单位长度，再将其 轴下方的图象翻折到 轴上方后得到的.如图⑤.
（6） .
⑥
[解析] 的图象是由 的图象关于原点对称得到的.如图⑥.
考点二 函数图象的识别
角度1 知式识图
例2 （2021天津，3，5分）函数 的图象大致为( )
（1） 当 时,函数 与 的图象相同.( )
×
（2） 函数 与 （ 且 ）的图象相同.( )
×
（3） 函数 与 的图象关于原点对称.( )
×
（4） 若函数 满足 ,则函数 的图象关于直线 对称.( )
√
（5） 将函数 的图象向右平移1个单位长度得到函数 的图象.( )
[解析] 设 ，则 ，故排除B;设 ，当 时， ，所以 ，故排除C;设 ，则 ，故排除D.
方法感悟辨识函数图象的入手点（1）从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置.（2）从函数的奇偶性，判断图象的对称性.（3）从函数的单调性，判断图象的变化趋势.（4）从函数的特征点，排除不符合要求的图象.
×
2. （新教材改编题）在 内将某种药物注射进患者的血液中，在注射期间，血液中的药物含量呈线性增加；停止注射后，血液中的药物含量呈指数衰减，能反映血液中药物含量 随时间 变化的图象是( )
A. B. C. D.
图②
[解析] 将函数 的图象向左平移一个单位长度，再将 轴下方的图象翻折到 轴上方，即可得到函数 的图象，如图②实线部分.
（3） .
图③
[解析] 且该函数为偶函数，先用描点法作出 上的图象，再根据对称性作出 上的图象，得图象如图③实线部分.
高三新高考一轮复习(人教A版)第2章第6节函数的图像课件
x＝13；
当 x∈12，＋∞时，由 f(x)＝2x－1＝12，解得 x＝34. 画出当 x≥0 时函数 f(x)的图象如图所示，
结合图象可得，当 x≥0 时，不等式 f(x)≤12的解集为
x
|13≤x≤34.
因为函数 f(x)为偶函数，
所以当 x＜0 时，
不等式 f(x)≤12的解集为x |－34≤x≤－13，
解析 (1)y＝f(－x)的图象向左平移1个单位得到y＝ f(－1－x)，故(1)错.
(2)两种说法有本质不同，前者为函数自身关于y轴对 称，后者是两个函数关于y轴对称，故(2)错.
(3)令f(x)＝－x，当x∈(0，＋∞)时，y＝|f(x)|＝x， y＝f(|x|)＝－x，两函数图象不同，故(3)错.
(2)设函数 f(x)＝2x，则如图所示的函数图象对应的函数解 析式是( C )
A.y＝f(|x|)
B.y＝－|f(x)|
C.y＝－f(－|x|)
D.y＝f(－|x|)
解析(2)题图中是函数 y＝－2－|x|的图象，
即函数 y＝－f(－|x|)的图象.故选 C.
►规律方法 函数图象的辨识
(1)从函数的定义域，判断图象的左右位置；从函数 的值域，判断图象的上下位置.
伸 y＝ 0＜a＜1，横坐标伸长为原来 图象
缩 变
f(x) 的图
的1a倍，纵坐标不变
换 象 a＞1，纵坐标伸长为原来的
a 倍，横坐标不变；
y ＝ __a_f(_x_)_ 的
0＜a＜1，纵坐标缩短为原来 图象
的 a 倍，横坐标不变
x轴下方部分翻折到上方，x __y_＝__|f_(x_)_|_的
翻 y＝ 轴及上方部分不变
基础自测
(安徽专用)高考数学一轮复习 第二章函数2.8函数的图象及其变换试题 新人教A版
由数形结合可知：
0＜k＜1或1＜k＜kOC，
∴0＜k＜1或1＜k＜2.
三、解答题
11．解：由(1)知，－3≤x≤1，－2≤x＋1≤2，故f(x)的定义域是[－2,2]．
由(3)知，f(x)在[－2,0)上是增函数．
综合(2)和(4)知，f(x)在(0,2]上也是增函数，且f(－1)＝f(1)＝0，f(0)＝0.
6．C解析：由图象可知，函数f(x)为奇函数且关于直线x＝1对称；对于②，因为f(1＋x)＝f(1－x)，所以f[1＋(x＋1)]＝f[1－(x＋1)]，即f(x＋2)＝f(－x)．
故①②正确，选C.
7．C解析：当直线l：x＝t(0≤t≤ )从左向右移动的过程中，直线l左侧阴影部分的 面积f(t)随l的单位移动距离的改变量开始逐渐增大，当到达中点t＝ 时，面积f(t)随l的单位移动距离的改变量最大，而后面积f(t)随l的单位移动距离的改变量逐渐减小，故选C.
A．f(x)＝x＋
B．f(x)＝x－
C．f(x)＝x2－
D．f(x)＝x2＋
3．下列函数图象中不正确的是( )．
4．如果函数f(x)＝ax＋b－1(a＞0，且a≠1)的图象经过第 一、二、四象限，不经过第三象限，那么一定有( )．
A．0＜a＜1且b＞0 B．0＜a＜1且0＜b＜1
C．a＞1且b＜0D．a＞1且b＞0
课时作业11 函数的图象及其变换
一、选择题
1．已知函数y＝f(x)与函数y＝lg 的图象关于直线y＝x对称，则函数y＝f(x－2)的解析式为( )．
A．y＝10x－2－2 B． y＝10x－1－2
C．y＝10x－2D．y＝10x－1
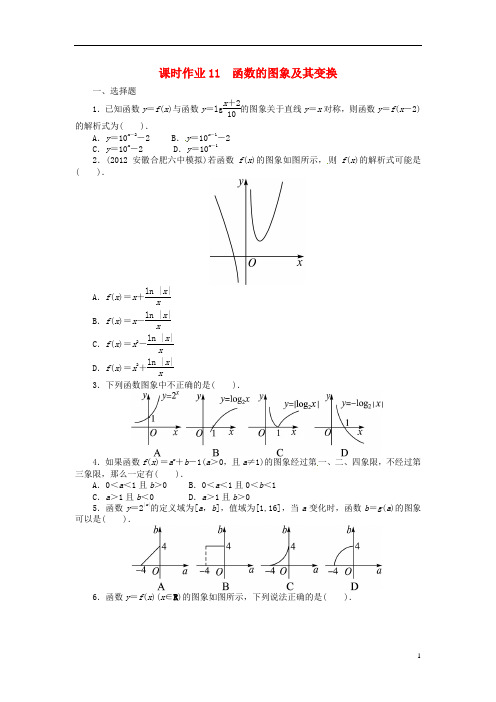
2．(2012安徽合肥六中模拟)若函数f(x)的图象如图所示， 则f(x)的解析式可能是( )．
届高考数学一轮复习讲义第二章函数图象
[难点正本 疑点清源] 1．一个函数的图象关于原点对称与两个函数的图象关于原
点对称 一个函数的图象关于原点对称与两个函数的图象关于原 点对称不是一回事．函数 y＝f(x)的图象关于原点对称是 自身对称，说明该函数为奇函数；而函数 y＝f(x)与函数 y＝－f(－x)图象关于原点对称，是两个函数的图象对称．
5．已知函数 f(x)＝x－x 1. (1)画出 f(x)的图象； (2)指出 f(x)的单调区间． 解 (1)∵f(x)＝x－x 1＝(x－x－1)1＋1＝1＋x－1 1， ∴f(x)的中心在(1,1)．如图．
(2)f(x)的单调减区间为(－∞，1)、(1，＋∞)．
作函数的图象
例 1 分别画出下列函数的图象： (1)y＝|lg x|； (2)y＝2x＋2； (3)y＝xx＋＋23； (4)y＝x2－2|x|－1.
答案 ④
探究提高
寻找图象与函数解析式之间的对应关系的方法： (1)知图选式： ①从图象的左右、上下分布，观察函数的定义域、值域； ②从图象的变化趋势，观察函数的单调性； ③从图象的对称性方面，观察函数的奇偶性； ④从图象的循环往复，观察函数的周期性． 利用上述方法，排除、筛选错误与正确的选项．
(2)知式选图： ①从函数的定义域，判断图象左右的位置；从函数的值域， 判断图象的上下位置； ②从函数的单调性，判断图象的变化趋势； ③从函数的奇偶性，判断图象的对称性； ④从函数的周期性，判断图象的循环往复． 利用上述方法，排除、筛选错误与正确的选项．
a
答案 ④
函数图象的应用
例 3 已知函数 f(x)＝x|m－x| (x∈R)，且 f(4)＝0. (1)求实数 m 的值； (2)作出函数 f(x)的图象； (3)根据图象指出 f(x)的单调递减区间； (4)根据图象写出不等式 f(x)>0 的解集．
高考数学一轮复习第二章函数2-7函数的图象课件文新人教版
③若函数y=f(x)的图象关于点(a,b)成中心对称⇔f(a+x)=2b-f(a-x)
⇔f(x)=2b-f(2a-x);
④若函数y=f(x)定义域为R,且满足条件f(a+x)+f(b-x)=c(a,b,c为
+
常数),则函数 y=f(x)的图象关于点 2 , 2 对称.
C.y=f(-|x|)
B.y=|f(x)|
D.y=-f(|x|)
关闭
当 x<0 时,图②的图象与图①相同,选项 C 中的
y=f(-|x|)=
C
(-), ≥ 0,
符合,故选 C.
(), < 0
关闭
解析
答案
-13知识梳理
双基自测
1
2
3
4.函数y=ln|x|-x2的图象大致为(
4
)
关闭
令y=f(x)=ln|x|-x2,其定义域为(-∞,0)∪(0,+∞),
2.7
函数的图象
-2知识梳理
双基自测
1
2
3
1.利用描点法作函数图象的流程
-3知识梳理
双基自测
1
2
3
2.函数图象间的变换
(1)平移变换
y=f(x)-k
对于平移,往往容易出错,在实际判断中可熟记口诀:左加右减,上
加下减.
-4知识梳理
双基自测
1
2
3
(2)对称变换
函数y=-f(-x)的图象
-5知识梳理
因为f(-x)=ln|x|-x2=f(x),
所以函数y=ln|x|-x2为偶函数,其图象关于y轴对称,故排除B,D,当x→+∞时,
高考文数学一轮复习课件第二章第七节函数的图象
命题方向二 解不等式
典例6 已知奇函数f(x)在(-∞,0)上是减函数,若f(-2)=0,则xf(x)<0的解集为
(B) A.(-2,0)∪(0,2) C.(-1,0)∪(2,+∞)
B.(-∞,-2)∪(2,+∞) D.(-∞,-2)∪(0,2)
解析 由题意得函数f(x)的大致图象如下,
因为xf(x)<0,所以函数f(x)的图象应在第二、四象限,所以不等式的解集为 (-∞,-2)∪(2,+∞),故选B.
规律总结 函数图象的识辨可从以下方面入手 1.由函数的定义域判断图象的左右位置;由函数的值域判断图象的上下位置; 2.由函数的单调性判断图象的变化趋势; 3.由函数的奇偶性判断图象的对称性; 4.由函数的周期性判断图象的循环往复; 5.由特殊点排除不符合要求的图象.
2-1
(1)函数y=
2
2x3 x 2-
规律总结 利用函数图象的直观性求解相关问题,关键在于准确作出函数图象,根据函数 解析式的特征和图象的直观性先确定函数的相关性质,特别是函数图象的对 称性,然后解决相关问题.
3-1 已知函数f(x)为R上的偶函数,当x≥0时, f(x)单调递减,若f(2a)>f(1-a),则a
的取值范围是 ( C )
解析
lg x(x 1),
(1)y=-lg x(0 x
1)
的图象如图①.
(2)将y=2x的图象向左平移2个单位长度即可得到y=2x+2的图象,如图②.
(3)y= x 2 =1+ 3 ,先作出y= 3 的图象,再将其图象向右平移1个单位长度,向上
x-1 x-1
x
平移1个单位长度,即得到y= x 2 的图象,如图③.
2021版高考文科数学(人教A版)一轮复习高效演练分层突破：第二章 第7讲 函数的图象 Word版解析
[基础题组练]1．小明骑车上学，开始时匀速行驶，途中因交通堵塞停留了一段时间后，为了赶时间加快速度行驶，与以上事件吻合得最好的图象是()解析：选C.小明匀速行驶时，所得图象为一条直线，且距离学校越来越近，故排除A.因交通堵塞停留了一段时间，与学校的距离不变，故排除D.后来为了赶时间加快速度行驶，故排除B.2．(2020·河北衡水中学第二次调研)函数y＝(2x－1)e x的图象大致是()解析：选A.因为x趋向于－∞时，y＝(2x－1)e x<0，所以C，D错误；因为y′＝(2x＋1)e x，所以当x<－12时，y′<0，y＝(2x－1)e x在(－∞，－12)上单调递减，所以A正确，B错误，故选A.3.(2020·江西七校第一次联考)设f(x)是定义在R上的周期为3的周期函数，如图表示该函数在区间(－2，1]上的图象，则f(2 018)＋f(2 019)＝()A．2B．1C．－1 D．0解析：选C.因为函数f(x)是定义在R上的周期为3的周期函数，所以f(2 018)＝f(2 018－673×3)＝f(－1)，f(2 019)＝f(2 019－673×3)＝f(0)，由题图知f(－1)＝－1，f(0)＝0，所以f(2 018)＋f(2 019)＝f(－1)＋f(0)＝－1.4.(2020·甘肃酒泉敦煌中学一诊)已知奇函数f(x)在x≥0时的图象如图所示，则不等式xf(x)<0的解集为()A．(1，2)B．(－2，－1)C．(－2，－1)∪(1，2) D．(－1，1)解析：选C.因为函数f(x)是奇函数，所以图象关于原点对称，补全当x<0时的函数图象，如图．对于不等式xf(x)<0，当x>0时，f(x)<0，所以1<x<2；当x<0时，f(x)>0，所以－2<x<－1，所以不等式xf(x)<0的解集为(－2，－1)∪(1，2)，故选C.5．已知函数y＝f(－|x|)的图象如图所示，则函数y＝f(x)的图象不可能是()解析：选C.函数y ＝f (－|x |)＝⎩⎪⎨⎪⎧f （－x ），x ≥0，f （x ），x <0，当x <0时，y ＝f (－|x |)＝f (x )，所以函数y ＝f (－|x |)的图象在y 轴左边的部分，就是函数y ＝f (x )的图象，故可得函数y ＝f (x )的图象不可能是C.6.如图，函数f (x )的图象是曲线OAB ，其中点O ，A ，B 的坐标分别为(0，0)，(1，2)，(3，1)，则f ⎝⎛⎭⎫1f （3）的值等于 ．解析：由图象知f (3)＝1，所以1f （3）＝1.所以f ⎝ ⎛⎭⎪⎫1f （3）＝f (1)＝2. 答案：27.若函数f (x )＝⎩⎪⎨⎪⎧ax ＋b ，x <－1，ln （x ＋a ），x ≥－1的图象如图所示，则f (－3)＝ ．解析：由题图可得a (－1)＋b ＝3，ln(－1＋a )＝0，得a ＝2，b ＝5，所以f (x )＝⎩⎪⎨⎪⎧2x ＋5，x <－1ln （x ＋2），x ≥－1，故f (－3)＝2×(－3)＋5＝－1. 答案：－18．设函数f (x )＝|x ＋a |，g (x )＝x －1，对于任意的x ∈R ，不等式f (x )≥g (x )恒成立，则实数a 的取值范围是 ．解析：如图，作出函数f (x )＝|x ＋a |与g (x )＝x －1的图象，观察图象可知：当且仅当－a ≤1，即a ≥－1时，不等式f (x )≥g (x )恒成立，所以a 的取值范围是[－1，＋∞)．答案：[－1，＋∞) 9．作出下列函数的图象． (1)y ＝x ＋2x －1；(2)y ＝|log 2(x ＋1)|.解：(1)因为y ＝x ＋2x －1＝1＋3x －1，先作出y ＝3x 的图象，将其图象向右平移1个单位长度，再向上平移1个单位长度，即得y ＝x ＋2x －1的图象，如图所示．(2)利用函数y ＝log 2x 的图象进行平移和翻折变换，图象如图实线所示．10．已知函数f (x )＝x |m －x |(x ∈R )，且f (4)＝0. (1)求实数m 的值； (2)作出函数f (x )的图象；(3)若方程f (x )＝a 只有一个实数根，求a 的取值范围． 解：(1)因为f (4)＝0，所以4|m －4|＝0，即m ＝4. (2)f (x )＝x |x －4|＝⎩⎪⎨⎪⎧x （x －4）＝（x －2）2－4，x ≥4，－x （x －4）＝－（x －2）2＋4，x <4，f (x )的图象如图所示．(3)从f (x )的图象可知，当a >4或a <0时，f (x )的图象与直线y ＝a 只有一个交点，即方程f (x )＝a 只有一个实数根，即a 的取值范围是(－∞，0)∪(4，＋∞)．[综合题组练]1．已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋2x －1，x ≥0，x 2－2x －1，x <0，则对任意x 1，x 2∈R ，若0<|x 1|<|x 2|，下列不等式成立的是( )A ．f (x 1)＋f (x 2)<0B ．f (x 1)＋f (x 2)>0C ．f (x 1)－f (x 2)>0D ．f (x 1)－f (x 2)<0解析：选D.函数f (x )的图象如图所示，且f (－x )＝f (x )，从而函数f (x )是偶函数，且在[0，＋∞)上是增函数． 又0<|x 1|<|x 2|， 所以f (x 2)>f (x 1)， 即f (x 1)－f (x 2)<0.2．已知函数f (x )＝x ＋1|x |＋1，x ∈R ，则不等式f (x 2－2x )<f (3x －4)的解集是 ．解析：由已知得，f (x )＝⎩⎪⎨⎪⎧1，x ≥0，－1－2x －1，x <0.其图象如图所示：由图可知，不等式f (x 2－2x )<f (3x －4)等价于⎩⎪⎨⎪⎧3x －4≥0，x 2－2x <0或⎩⎪⎨⎪⎧3x －4<0，x 2－2x <0，x 2－2x <3x －4，解得43≤x <2或1<x <43，所以所求的解集为(1，2)．答案：(1，2)3．已知函数f (x )＝|x |(x －a )，a >0， (1)作出函数f (x )的图象； (2)写出函数f (x )的单调区间；(3)当x ∈[0，1]时，由图象写出f (x )的最小值．解：(1)f (x )＝⎩⎪⎨⎪⎧x （x －a ），x ≥0，－x （x －a ），x <0，其图象如图所示．(2)由图知，f (x )的单调递增区间是(－∞，0)，⎝⎛⎭⎫a 2，＋∞；单调递减区间是⎝⎛⎦⎤0，a 2. (3)由图象知，当a2>1，即a >2时，所求最小值f (x )min ＝f (1)＝1－a ；当0<a2≤1，即0<a ≤2时，所求最小值f (x )min ＝f ⎝⎛⎭⎫a 2＝－a24. 综上，f (x )min ＝⎩⎪⎨⎪⎧－a 24（0<a ≤2），1－a （a >2）.4．已知函数f (x )＝2x ，x ∈R .(1)当m 取何值时，方程|f (x )－2|＝m 有一个解？两个解？ (2)若不等式[f (x )]2＋f (x )－m >0在R 上恒成立，求m 的取值范围．解：(1)令F (x )＝|f (x )－2|＝|2x －2|，G (x )＝m ，画出F (x )的图象如图所示，由图象看出，当m ＝0或m ≥2时，函数F (x )与G (x )的图象只有一个交点，即原方程有一个解；当0<m <2时，函数F (x )与G (x )的图象有两个交点，即原方程有两个解．(2)令f (x )＝t (t >0)，H (t )＝t 2＋t ，因为H (t )＝⎝⎛⎭⎫t ＋122－14在区间(0，＋∞)上是增函数， 所以H (t )>H (0)＝0.因此要使t 2＋t >m 在区间(0，＋∞)上恒成立，应有m ≤0，即所求m 的取值范围为(－∞，0]．。
(北京专用)高考数学一轮复习第二章函数第七节函数的图象课件文
5.(2018北京(běi jīnɡ)朝阳期中)已知函数logf1(x,)0= x若 1方, 程f(x)=m有2个
2 2x 1, x 1.
不相等的实数根,则实数m的取值范围是
1,
3 2
.
答案
1,
3 2
第十三页，共35页。
解析 函数f(x)的图象如图所示,要使方程f(x)=m有2个不相等的实数,即 函数f(x)的图象与函数y=m的图象有2个不同(bù tónɡ)的交点,只需1<m3≤ .
x
对于A,取x=-10和x=-1, f(-10)<f(-1),与图象不符. 对于B, f(-1)=0,与图象不符. 对于D, f(x)的定义域为(0,+∞),与图象不符. 故选C.
第二十二页，共35页。
方法技巧 函数图象识辨的常用方法 函数图象的识辨可从以下方面入手: (1)由函数的定义域判断图象的左右位置(wèi zhi);由函数的值域判断图象的上 下位置(wèi zhi); (2)由函数的单调性判断图象的变化趋势; (3)由函数的奇偶性判断图象的对称性; (4)由函数的周期性识辨图象; (5)由函数的特征点排除不符合要求的图象.
x
+1
2
2.
9 4
∴ 函y数=图象x x如12 12图22所94示,94x, .x
2, 2.
第十八页，共35页。
(2)将函数y=log2x的图象向左平移(pínɡ yí)1个单位,再将x轴下方的部分沿x 轴翻 折上去,即可得到函数y=|log2(x+1)|的图象,如图所示.
第十九页，共35页。
第十七页，共35页。
1-1 作出下列(xiàliè)函数的图象. (1)y=|x-2|·(x+1); (2)y=|log2(x+1)|.
高考数学(文通用)一轮复习课件：第二章第8讲函数的图象
第8讲第二章基本初等函数、导数及其应用函数的图象教材回顾▼夯实基础课本温故追根求源斓课舊理,1.利用描点法作函数图象其基本步骤是列表、描点、连线.首先：①确定函数的定义域；②化简函数解析式；③讨论函数的性质（奇偶性、单调性、周期性、对称性等）.其次：列表（尤其注意特殊点、零点、最大值点、最小值点、与坐标轴的交点等），描点，连线.2.利用图象变换法作函数的图象(1)平移变换(2)对称变换e ©、关于工轴对称一馆)®J =f(x) ------- J= __________ ;Q 0、关于V轴对称"―门®y =f(x)-------- > j= _________ ；③尸伽关^^=-D :④尸化>0且占1产心称尸上M(3)翻折变换伍、—、保留兀轴及上方图象_炉)|Qy 一几小将尢轴下方图象舖折上去y _ ---- ■✓gK _ f(保留y轴及右边图典,并作其_ /(Lrl)5=/(兀)关于丿轴对称為图象丿= --------- •(4)伸缩变换①丿=/(兀)«>1,横坐标缩短为原来的丄倍，纵坐标不变®y=f(x) “>1,纵坐标伸长为原来的"倍，横坐标不变 OVaVl,纵坐标缩短为原来的。
倍，横坐标不变y = a f(X) 0<«<1,横坐标伸长为原来的上倍，纵坐标不变y= /(心)要点整食,1.辨明两个易误点⑴在解决函数图象的变换问题时，要遵循“只能对函数关系式中的兀，y变换”的原则，如从f(-2x)的图象到/(—2r+1)的图象是向右平移*单位，其中是把兀变成x-|.(2)明确一个函数的图象关于J轴对称与两个函数的图象关于丁轴对称的不同，前者是自身对称，且为偶函数，后者是两个不同函数的对称关系.双基自测r1.函数J=xlx啲图象的形状大致是（A)2.（必修1 P112复习参考题A组T2）点P从点O出发，按逆时针方向沿周长为？的图形运动一周，O, P两点连线的距离V与点P走过的路程x的函数关系如图,那么点P所走的图形是（C ）A C D3.函数心)的图象向右平移1个单位长度, 所得图象与线j=e x关于y轴对称，则/(©=( ° )A.e x+1B. e-iC. e~x+1D.严解析：曲线y=e"关于丿轴对称的曲线为y=e~x f将尸「向左平移1个单位长度得到j=e_(x+1),即y(x)=e~x_1.4-为了得到函数丁=4><(|)的图象，可以把函数的图象向」―平移2 个单位长度.5.若关于兀的方程1x1=4—兀只有一个解，则实数4的取值范围是© +呵.解析：由题意a=lxl+x,2x兀> 0，"’图象如图所示，故要使a=\x\+x令y= lxl+x=0, x<0,只有一解，则a>0,即实数"的取值范围是(0, +°°).典例剖析护考点突破」考点一作函数的图象名师导悟以例说法作出下列函数的图象.（彷=严(2)j=llgxl；(3)丿=x+2 x— 1［解］⑴将y=2x的图象向左平移2个单位.图象如图所示.lg Xy兀Ml,—lgx, 0<x<l.图象如图所示.1-23 3(3)因为尸1+亠先作出尸三的图象，将其图象向右平X— 1 x兀+2 移1个单位，再向上平移1个单位，即得二;的图象，x— 1如图.移3个单位，再向上平移1个单位得到，如图所示.Q 互动探究将本例(3)的函数变为 =兀+2” 兀+3象如何? 解:y= x+2 兀+3x+3,该函数图象可由函数y=~^向左平函数图象的画法(1)直接法：当函数表达式(或变形后的表达式)是熟悉的基本函数时，就可根据这些函数的特征找出图象的关键点直接作出图象.(2)转化法：含有绝对值符号的函数，可脱掉绝对值符号，转化为分段函数来画图象.⑶图象变换法:若函数图象可由某个基本函数的图象经过平移、翻折、对称得到，可利用图象变换作出，但要注意变换顺序，对不能直接找到熟悉的基本函数的要先变形，并应注意平移变换的顺序对变换单位及解析式的影响.跟踪迦s 1作出下列函数的图象.(1)j=lx-2l(x+l)；(2)j=llog2(x+l)L解：(1)当 x^2,即 x —2^0 时, y = (x —2)(x+l)=x 2—x —2 壬-芬-召当xv2,即兀一2v0时， j = —(X —2)(x+l) = —X 2+X +2 图象可根据二次函数图象作出（如图）.(2)将函数j= Iog 2x 的图象向左平移一个单位，再将兀轴下~4f 毎2,_卜-芬+鲁,这是分段函数，每段函数的方的部分沿x轴翻折上去，即可得到函数y= llog2(x+1)1的图象，如图所示.WxW 兀且兀H0）的图象可能为（D ）Hl考点二识图与辨图 COS x(— 3T A C D⑵（2015•高考安徽卷）函数f（x）=-（兀十c）示，则下列结论成立的是（C ）A.B.C.D. «>O,avO,«<O,«<O,方>0,方>0,方>0c>0cvOcv㊁的图象如图所懈析］⑴函数/(x)=(x—|)cos x(—兀0W兀且兀HO)为奇函1 1 数，排除选项A，B；当x= Ji 时J(x)=(兀一7)cos Ji =-n<0,排除选项C,故选D.⑵函数定义域为{xlxH—c},结合图象知一c>0,所以cvO.令兀=0,得f(0)=£又由图象知/(0)>0,所以方>0.令/(x)=0,得兀=一¥，结合图象知一¥>0,所以X0.故选C.函数图象的识辨可从以下方面入手(1)从函数的定义域，判断图象的左右位置；从函数的值域, 判断图象的上下位置.(2)从函数的单调性，判断图象的变化趋势.(3)从函数的奇偶性，判断图象的对称性.(4)从函数的周期性，判断图象的循环往复.(5)从函数的特征点，排除不合要求的图象.跟刪练2.(1)函数心)=lo&bd+l(Ov“vl)的图象大致为(A )⑵在同一平面直角坐标系中，函数丁=心)和y=g(x)的图象关于直线y=x对称，现将丁=卓兀)的图象沿兀轴向左平移2 个单位，再沿y轴向上平移1个单位，所得图象是由两条线段组成的折线，如图，则函数y=f(x)^J 表达式为2x+2, —lWxWO,0VxW212解析：(1)由函数沧)的解析式可确定该函数为偶函数，图象关于y轴对称.设g(x)=logjxl,先画岀兀＞0时，g(x)的图象, 然后根据疏兀)的图象关于y轴对称画出xvO时巩兀)的图象，最后由函数g(Q的图象向上整体平移一个单位即得/⑴的图象，结合图象知选A.(2)设经过两次平移后所得图象对应的函数为h(x),贝？|X—1, —2WxW0, 世)=[2lir+l, OVxWl,—1, 0WxW2,所以g(x)=y 2<2x—4, 2V兀W3,2x+2, —lWxWO, 所以金)++, ov©・12考点三函数图象的应用(高频考点)函数的图象因其直观而形象地显示了函数的性质而成为高考命题的一个高频考点，常以选择题、填空题的形式出现.高考对函数图象应用问题的考查主要有以下五个命题角度: ⑴研究两图象的交点个数;(2)利用函数图象确定方程根的个数(下讲再举例);(3)利用函数图象研究函数性质；(4)利用函数图象研究不等式的解;(5)利用函数图象求参数的取值范围.興理3 (1)已知函数丿=心)的周期为2,当xe[—1, 1]时，f(x)=x2f那么函数丿=/(对的图象与函数J=llgxl的图象的交点共有(A )A. 10 个C. 8个B. 9个D. 1个⑵（2015•高考北京卷）如图，函数/*3）的图象为折线ACB,则不等式/（X）^lOg2（x+l）的解集是（° ）A.{xl— lVxWO}B.{xl—lWxWl}C・{xl— lVxW 1}D・{xl— 1V X W2}⑶函数J=log2bc+ll的单调递减区间为LT ）递增区间为［解析］(1)在同一直角坐标系中，分别作出J =/(x)和J = llg xl 的图象，如图，结合图象知，共有10个交点•(2)^ g (x)=j=log 2(x+l),知 g(Q 的定义域为(一 1，+~),作出函数巩兀）的图象如图.所以结合图象知不等式y （x ）^io g2（x+1）的解集为｛xi-i<兀Wl}・fx+j=2, ly = log 2 (x+1)1,♦ r作出函数y=lo 跆的图象，将其关于y 轴对称得到函数尸logzlxl 的图象，再将图象向左平移1个单位长度就得到函数y=io g2ix+i 的图象（如图所示）.由图知，函数j=i og2ix+ii 的单调递减区间为（一 8, -1）,单调递增区间为（一1, +QO ）.函数图象应用求解策略⑴研究函数性质:①根据已知或作出的函数图象，从最高点、最低点，分析函数的最值、极值；②从图象的对称性，分析函数的奇偶性；③从图象的走向趋势，分析函数的单调性、周期性；④从图象与兀轴的交点情况，分析函数的零点等.(2)研究不等式的解：当不等式问题不能用代数法求解，但其对应函数的图象可作出时，常将不等式问题转化为两函数图象的上、下关系问题，从而利用数形结合求解.23•⑴下列区间中，函数/(x)=llg(2-x)ffi 其上为4 3-D ・[1, 2)(2)(2015•高考安徽卷)在平面直角坐标系xOy中，若直线j=幷与函数y= \x —a\—l 的图象只有一个交点，则a 的值为通关练习增函数的是(D解析:(1)用图象法解决，将j=lg X的图象关于y轴对称得到尸lg(-x)的图象，再向右平移两个单位，得到尸lg[-(x-2)]的图象，将得到的图象在兀轴下方的部分翻折上来，即得到f(x)=llg(2-x)l的图象.由图象，在选项中的区间上/(兀)是增函数的显然只有D・⑵函数y= lx —a\— 1的图象如图所不，因为直线y= 2a与函数丿=lx—甸一1的图象只有一个交点，故2a= -1,解得"（2014-高考山东卷）已知函数Ax ）=lx-2I+1, g （x ）= g 若方程/（对=能）有两个不相等的实根，贝！I 实数k 的取值 范围是（A.(0,D. (2, +8)C. (1, 2) 拓展升华触类旁通 方法思想 数结合思想求参数的范围［解析］先作出函数f(x)=\x~2\+1的图象，如图所示，当直线g(x)=kx与直线AB平行时斜率为1,当直线g(x)=kx过A点时斜率为?故/3)=g(x)有两个不相等的实根时，k 澎感悟提高(1)本题求解利用了数形结合的思想，数形结合的思想包括“以形助数”或“以数辅形”两个方面，本题属于“以形助数”，是指把某些抽象的问题直观化、生动化, 能够变抽象思维为形象思维，解释数学问题的本质.本题首先作出/(x)=lx-2l+1的图象，再作出g(x)=kx 的图象，利用图象的交点情况确定k的取值范围.(2)有关恒成立问题，求方程根的个数问题常用数形结合思想求解.【跟对实数"和八定义运算“歔：a@b = b、a—b>l.设函数/(x)=(x2—2)®(x— l)xeR若函数y= f(x)~c的图象与工轴恰有两个公共点,则实数c的取值范昌是(B )A.(-1, 1]U(2, +8)B.(-2, -1]U(1, 2]C.(一8, -2)U(1, 2]D.[-2, -1]a9 a—bWl, 解析：因为a^b=\Jby a— b>l, 所以函数/（X）=（X2— 2）®（X—1）= [x2— 2, —1W X W2,[x— 1, x<— 1 或兀>2.作出函数图象如图.结合图象可知，当ce(-2, -1]U(1, 2]时，函数几Q与丿的图象有两个公共点,所以实数c的取值范围是(一2，-1]U(1, 2].闌1能训练▼轻松闯关* ［学生用书单独成册］以练促学强技提能点击链接本部分内容讲解结束闌1能训练▼轻松闯关* ［学生用书单独成册］以练促学强技提能。
高考数学一轮复习 第二章 第4讲 函数的图像资料(艺术班)
高考数学一轮复习 第二章 第4讲 函数的图像资料（艺术班）第4讲 函数的图像一、必记2个知识点1．利用描点法作函数图像其基本步骤是列表、描点、连线，具体为：首先：①确定函数的定义域；②化简函数解析式；③讨论函数的性质(奇偶性、单调性、周期性)；其次：列表(尤其注意特殊点、零点、最大值点、最小值点、与坐标轴的交点)； 最后：描点，连线．2．利用图像变换法作函数的图像 (1)平移变换：y ＝f (x )――――――――→a >0，右移a 个单位a <0，左移|a |个单位y ＝f (x －a )； y ＝f (x )―――――――――→b >0，上移b 个单位b <0，下移|b |个单位y ＝f (x )＋b .(2)伸缩变换：y ＝f (x )10111ωωωω<<>−−−−−−−−→，伸原的倍，短原的长为来缩为来 y ＝f (ωx )； y ＝f (x )――――――――――→A >1，伸为原来的A 倍0<A <1，缩为原来的A 倍y＝Af (x )．(3)对称变换：y ＝f (x )――――――→关于x 轴对称 y ＝－f (x )； y ＝f (x )――――――→关于y 轴对称y ＝f (－x )； y ＝f (x )――――――→关于原点对称y ＝－f (－x )． (4)翻折变换：y ＝f (x )――――――――――――→去掉y 轴左边图，保留y 轴右边图将y 轴右边的图像翻折到左边去y ＝f (|x |)； y ＝f (x )――――――――→留下x 轴上方图将x 轴下方图翻折上去y ＝|f (x )|. 二、必明2个易误区1．在解决函数图像的变换问题时，要遵循“只能对函数关系式中的x ，y 变换”的原则，写出每一次的变换所得图像对应的解析式，这样才能避免出错．2．明确一个函数的图像关于y 轴对称与两个函数的图像关于y 轴对称的不同，前者也是自身对称，且为偶函数，后者也是两个不同函数的对称关系． 三、必会2个方法1．数形结合思想借助函数图像，可以研究函数的定义域、值域、单调性、奇偶性、对称性等性质；利用函数的图像，还可以判断方程f (x )＝g (x )的解的个数、求不等式的解集等．2．分类讨论思想画函数图像时，如果解析式中含参数，还要对参数进行讨论，分别画出其图像．考点一作函数的图像(1)y ＝|lg x |； (2)y ＝2x ＋2； (3)y ＝x 2－2|x |－1.解：(1)y ＝⎩⎪⎨⎪⎧lg x ，x ≥1，－lg x ，0<x <1.图像如图1.(2)将y ＝2x的图像向左平移2个单位．图像如图2.(3)y ＝⎩⎪⎨⎪⎧x 2－2x －1，x ≥0，x 2＋2x －1，x <0.图像如图3.[类题通法]画函数图像的一般方法(1)直接法．当函数表达式(或变形后的表达式)是熟悉的基本函数时，就可根据这些函数的特征直接作出；(2)图像变换法．若函数图像可由某个基本函数的图像经过平移、翻折、对称得到，可利用图像变换作出，但要注意变换顺序．对不能直接找到熟悉的基本函数的要先变形，并应注意平移变换与伸缩变换的顺序对变换单位及解析式的影响．考点二 识图与辨图[典例] 2( )(2)(2012·湖北高考)已知定义在区间[0,2]上的函数y ＝f (x )的图像如图所示，则y ＝－f (2－x )的图像为( )[解析] (1)f (x )＝ln(x 2＋1)，x ∈R ，当x ＝0时，f (0)＝ln 1＝0，即f (x )过点(0,0)，排除B ，D.∵f (－x )＝ln[(－x )2＋1]＝ln(x 2＋1)＝f (x )，∴f (x )是偶函数，其图像关于y 轴对称，故选A.(2)法一：由y ＝f (x )的图像知f (x )＝⎩⎪⎨⎪⎧x 0≤x ≤1，11<x ≤2.当x ∈[0,2]时，2－x ∈[0,2]，所以f (2－x )＝⎩⎪⎨⎪⎧10≤x ≤1，2－x 1<x ≤2，故y ＝－f (2－x )＝⎩⎪⎨⎪⎧－10≤x ≤1，x －21<x ≤2.法二：当x ＝0时，－f (2－x )＝－f (2)＝－1；当x ＝1时，－f (2－x )＝－f (1)＝－1.观察各选项，可知应选B.[答案] (1)A (2)B[类题通法]识图常用的方法(1)定性分析法：通过对问题进行定性的分析，从而得出图像的上升(或下降)的趋势，利用这一特征分析解决问题；(2)定量计算法：通过定量的计算来分析解决问题；(3)函数模型法：由所提供的图像特征，联想相关函数模型，利用这一函数模型来分析解决问题． [针对训练]1．(2014·潍坊高三期末)函数y ＝x sin x 在[－π，π]上的图像是( )解析：选A 因为函数为偶函数，排除选项D ；f (π)＝0，排除选项C ；f ⎝ ⎛⎭⎪⎫π2＝π2，排除选项B.故选A.2.如图，函数f (x )的图像是曲线OAB ，其中点O ，A ，B 的坐标分别为(0,0)，(1,2)，(3,1)，则f ⎝⎛⎭⎪⎫1f 3的值等于________．解析：∵由图像知f (3)＝1，∴1f 3＝1.∴f ⎝⎛⎭⎪⎫1f 3＝f (1)＝2.答案：2考点三函数图像的应用角度一 1．(2014·日照一模)已知f (x )＝⎩⎪⎨⎪⎧|lg x |，x >0，2|x |，x ≤0，则函数y ＝2f 2(x )－3f (x )＋1的零点个数是________．解析：方程2f 2(x )－3f (x )＋1＝0的解为f (x )＝12或1.作出y＝f (x )的图像，由图像知零点的个数为5.角度二 求参数的取值范围2．对实数a 和b ，定义运算“⊗”：a ⊗b ＝⎩⎪⎨⎪⎧a ，a －b ≤1，b ，a －b >1.设函数f x ＝(x 2－2)⊗(x －1)，x ∈R .若函数y ＝f (x )－c 的图像与x 轴恰有两个公共点，则实数c 的取值范围是( )A ．(－1,1]∪(2，＋∞)B ．(－2，－1]∪(1,2]C ．(－∞，－2)∪(1,2]D ．[－2，－1]解析：选B ∵a ⊗b ＝⎩⎪⎨⎪⎧a ，a －b ≤1，b ，a －b >1，∴函数f (x )＝(x 2－2)⊗(x －1)＝⎩⎪⎨⎪⎧x 2－2，－1≤x ≤2，x －1，x <－1或x >2.结合图像可知，当c ∈(－2，－1]∪(1,2]时，函数f (x )与y ＝c 的图像有两个公共点，∴c 的取值范围是(－2，－1]∪(1,2]．课后作业[试一试]1.(2014·安徽“江南十校”联考)函数y ＝log 2(|x |＋1)的图像大致是( )解析：选B 首先判断定义域为R .又f (－x )＝f (x )．所以函数y ＝log 2(|x |＋1)为偶函数，当x >0时，y ＝log 2(x ＋1)．故选B. [练一练]2.若关于x 的方程|x |＝a －x 只有一个解，则实数a 的取值范围是________． 解析：由题意a ＝|x |＋x令y ＝|x |＋x ＝⎩⎪⎨⎪⎧2x ，x ≥0，0，x ＜0，图像如图所示，故要使a ＝|x |＋x 只有一解则a >0.答案：(0，＋∞)做一做3．函数y ＝x |x |的图像经描点确定后的形状大致是( )解析：选A y ＝x |x |＝⎩⎪⎨⎪⎧x 2，x >00，x ＝0－x 2，x <0为奇函数，奇函数图像关于原点对称．4．(2013·北京高考)函数f (x )的图像向右平移1个单位长度，所得图像与曲线y ＝e x关于y 轴对称，则f (x )＝( )A ．e x ＋1B ．e x －1C ．e－x ＋1D ．e－x －1解析：选D 与曲线y ＝e x关于y 轴对称的曲线为y ＝e －x，函数y ＝e －x的图像向左平移一个单位长度即可得到函数f (x )的图像，即f (x )＝e－(x ＋1)＝e－x －1.5.已知函数f (x )的图像如图所示，则函数g (x )＝2(x )的定义域是________．解析：当f (x )>0时，函数g (x )＝log2f (x )有意义，由函数f (x )的图像知满足f (x )>0的x ∈(2,8]． 答案：(2,8]6．设函数f (x )＝|x ＋a |，g (x )＝x －1，对于任意的x ∈R ，不等式f (x )≥g (x )恒成立，则实数a 的取值范围是________．解析：如图作出函数f (x )＝|x ＋a |与g (x )＝x －1的图像，观察图像可知：当且仅当－a ≤1，即a ≥－1时，不等式f (x )≥g (x )恒成立，因此a 的取值范围是[－1，＋∞)．答案：[－1，＋∞)7．函数f (x )＝2x 3的图像( ) A ．关于y 轴对称 B ．关于x 轴对称 C ．关于直线y ＝x 对称D ．关于原点对称解析：选D 显然函数f (x )＝2x 3是一个奇函数，所以其图像关于原点对称．8．函数y ＝⎩⎪⎨⎪⎧x 2，x <0，2x－1，x ≥0的图像大致是( )解析：选B 当x <0时，函数的图像是抛物线；当x ≥0时，只需把y ＝2x的图像在y 轴右侧的部分向下平移1个单位即可，故大致图像为B.9．为了得到函数y ＝2x －3－1的图像，只需把函数y ＝2x的图像上所有的点( )A ．向右平移3个单位长度，再向下平移1个单位长度B ．向左平移3个单位长度，再向下平移1个单位长度C ．向右平移3个单位长度，再向上平移1个单位长度D ．向左平移3个单位长度，再向上平移1个单位长度 解析：选A y ＝2x――――――――→向右平移3个单位长度y ＝2x －3――――――――→向下平移1个单位长度y ＝2x －3－1.故选A.10．(2013·四川高考)函数y ＝x 33x －1的图像大致是( )解析：选C 因为函数的定义域是非零实数集，所以A 错；当x <0时，y >0，所以B 错；当x →＋∞时，y →0，所以D 错，故选C..11.．函数f (x )＝x ＋1x图像的对称中心为________． 解析：f (x )＝x ＋1x ＝1＋1x ，把函数y ＝1x的图像向上平移1个单位，即得函数f (x )的图像．由y ＝1x的对称中心为(0,0)，可得平移后的f (x )图像的对称中心为(0,1)．答案：(0,1)12．已知函数f(x)＝2x，x∈R.当m取何值时方程|f(x)－2|＝m有一个解？两个解？解：令F(x)＝|f(x)－2|＝|2x－2|，G(x)＝m，画出F(x)的图像如图所示．由图像看出，当m＝0或m≥2时，函数F(x)与G(x)的图像只有一个交点，原方程有一个解；当0<m<2时，函数F(x)与G(x)的图像有两个交点，原方程有两个解．13．(2013·浙江高考)已知函数y＝f(x)的图像是下列四个图像之一，且其导函数y＝f′(x)的图像如图所示，则该函数的图像是( )解析：选B 由函数f(x)的导函数y＝f′(x)的图像自左至右是先增后减，可知函数y＝f(x)图像的切线的斜率自左至右先增大后减小．。
(江苏专用)新高考数学一轮复习 第二章 函数 2.8 函数的图象练习-人教版高三全册数学试题
2.8 函数的图象1．(2019·某某师X 大学附属中学月考)函数y ＝log 2|x |的图象大致是( )答案 C解析 函数y ＝log 2|x |为偶函数，作出x >0时y ＝log 2x 的图象，再作其关于y 轴对称的图象即得，故选C.2．已知函数f (x )＝⎩⎪⎨⎪⎧3x，x ≤1，13log x，x >1，则函数y ＝f (1－x )的大致图象是( )答案 D解析 方法一 先画出函数f (x )＝⎩⎪⎨⎪⎧3x，x ≤1，13log x，x >1的草图，令函数f (x )的图象关于y轴对称，得函数f (－x )的图象，再把所得的函数f (－x )的图象，向右平移1个单位，得到函数y ＝f (1－x )的图象(图略)，故选D.方法二 由已知函数f (x )的解析式，得y ＝f (1－x )＝⎩⎪⎨⎪⎧31－x，x ≥0，13log (1)x -，x <0，故该函数过点(0,3)，排除A ；过点(1,1)，排除B ；在(－∞，0)上单调递增，排除C.选D.3．将函数f (x )的图象向右平移1个单位长度，所得图象与曲线y ＝e x关于y 轴对称，则f (x )等于( ) A ．e x ＋1B ．e x －1C ．e－x ＋1D ．e－x －1答案 D解析 与曲线y ＝e x 关于y 轴对称的图象对应的函数为y ＝e －x ，将函数y ＝e －x的图象向左平移1个单位长度即得y ＝f (x )的图象，∴y ＝f (x )＝e －(x ＋1)＝e－x －1.4．(2019·某某中学调研卷)为了得到函数y ＝lg x ＋310的图象，只需把函数y ＝lg x 的图象上所有的点( )A ．向左平移3个单位长度，再向上平移1个单位长度B ．向右平移3个单位长度，再向上平移1个单位长度C ．向左平移3个单位长度，再向下平移1个单位长度D ．向右平移3个单位长度，再向下平移1个单位长度 答案 C 解析 ∵y ＝lgx ＋310＝lg(x ＋3)－1.∴选C.5．(2020·某某质检)已知函数f (x )是定义在R 上的奇函数，当x >0时，f (x )＝1－2－x，则不等式f (x )<－12的解集是( )A ．(－∞，－1)B ．(－∞，－1]C ．(1，＋∞)D ．[1，＋∞)答案 A解析 当x >0时，f (x )＝1－2－x>0. 又f (x )是定义在R 上的奇函数，所以f (x )<－12的解集和f (x )>12的解集关于原点对称，由1－2－x >12得2－x <12＝2－1，即x >1，则f (x )<－12的解集是(－∞，－1)．故选A.6．函数f (x )＝ax ＋b(x ＋c )2的图象如图所示，则下列结论成立的是( )A ．a >0，b >0，c >0B ．a <0，b >0，c >0C ．a <0，b >0，c <0D ．a <0，b <0，c <0 答案 C解析 由f (x )＝ax ＋b(x ＋c )2及图象可知，x ≠－c ，－c >0，则c <0.当x ＝0时，f (0)＝b c2>0，所以b >0， 当y ＝0时，ax ＋b ＝0⇒x ＝－b a>0. 所以a <0，选C.7．(多选)关于函数f (x )＝|ln|2－x ||，下列描述正确的有( ) A ．函数f (x )在区间(1,2)上单调递增 B ．函数y ＝f (x )的图象关于直线x ＝2对称 C ．若x 1≠x 2，但f (x 1)＝f (x 2)，则x 1＋x 2＝4 D ．函数f (x )有且仅有两个零点 答案 ABD解析 函数f (x )＝|ln|2－x ||的图象如图所示，由图可得，函数f (x )在区间(1,2)上单调递增，A 正确； 函数y ＝f (x )的图象关于直线x ＝2对称，B 正确；若x 1≠x 2，但f (x 1)＝f (x 2)，则x 1＋x 2的值不一定等于4，C 错误； 函数f (x )有且仅有两个零点，D 正确．8．(多选)(2019·某某浉河区校级月考)将函数f (x )的图象沿x 轴向左平移1个单位长度，得到奇函数g (x )的图象，则下列函数f (x )不能满足条件的是( ) A ．f (x )＝1x ＋1B ．f (x )＝ex －1－e1－xC ．f (x )＝x ＋2xD ．f (x )＝log 2(x ＋1)＋1答案 ACD解析 由题意知，f (x )必须满足两个条件： ①f (1)＝0，②f (1＋x )＝－f (1－x )． 对于选项A ，C ，D ，f (1)均不为0，不满足条件； 对于选项B ，f (1)＝e 0－e 0＝0，f (1＋x )＝e x －e －x，f (1－x )＝e －x －e x ＝－f (1＋x )．9．已知函数f (x )＝⎩⎪⎨⎪⎧sinπx ，0≤x ≤1，log 2020x ，x >1，若实数a ，b ，c 互不相等，且f (a )＝f (b )＝f (c )，则a ＋b ＋c 的取值X 围是__________． 答案 (2,2021)解析 函数f (x )＝⎩⎪⎨⎪⎧sinπx ，0≤x ≤1，log 2020x ，x >1的图象如图所示，不妨令a <b <c ，由正弦曲线的对称性可知a ＋b ＝1，而1<c <2020， 所以2<a ＋b ＋c <2021.10．已知f (x )是以2为周期的偶函数，当x ∈[0,1]时，f (x )＝x ，且在[－1,3]内，关于x 的方程f (x )＝kx ＋k ＋1(k ∈R ，k ≠－1)有四个实数根，则k 的取值X 围是__________．答案 ⎝ ⎛⎭⎪⎫－13，0解析 由题意作出f (x )在[－1,3]上的图象如图所示，记y ＝k (x ＋1)＋1，∴函数y ＝k (x ＋1)＋1的图象过定点A (－1,1)．记B (2,0)，由图象知，方程有四个实数根，即函数f (x )与y ＝kx ＋k ＋1的图象在[－1,3]内有四个交点， 故k AB <k <0，k AB ＝0－12－(－1)＝－13，∴－13<k <0.11．(2020·某某模拟)设a 为实数，且1<x <3，试讨论关于x 的方程x 2－5x ＋3＋a ＝0的实数解的个数．解 原方程即a ＝－x 2＋5x －3.作出函数y ＝－x 2＋5x －3＝－⎝ ⎛⎭⎪⎫x －522＋134(1<x <3)的图象，得当a >134或a ≤1时，原方程的实数解的个数为0；当a ＝134或1<a ≤3时，原方程的实数解的个数为1；当3<a <134时，原方程的实数解的个数为2.综上，a >134或a ≤1时有0个解；a ＝134或1<a ≤3时有1个解；3<a <134时有2个解．12．已知函数f (x )＝2x，x ∈R .(1)当实数m 取何值时，方程|f (x )－2|＝m 有一个解？两个解？ (2)若不等式f 2(x )＋f (x )－m >0在R 上恒成立，某某数m 的取值X 围．解 (1)令F (x )＝|f (x )－2|＝|2x－2|，G (x )＝m ，画出F (x )的图象如图所示．由图象可知，当m ＝0或m ≥2时，函数F (x )与G (x )的图象只有一个交点，即原方程有一个实数解；当0<m <2时，函数F (x )与G (x )的图象有两个交点，即原方程有两个实数解． (2)令f (x )＝t (t >0)，H (t )＝t 2＋t ，t >0，因为H (t )＝⎝ ⎛⎭⎪⎫t ＋122－14在区间(0，＋∞)上是增函数，所以H (t )>H (0)＝0.因此要使t 2＋t >m 在区间(0，＋∞)上恒成立，应有m ≤0，即所求m 的取值X 围为(－∞，0]．13．已知函数f (x －1)是定义在R 上的奇函数，且在[0，＋∞)上是增函数，则函数f (x )的图象可能是( )答案 B解析 函数f (x －1)的图象向左平移1个单位长度，即可得到函数f (x )的图象； ∵函数f (x －1)是定义在R 上的奇函数， ∴函数f (x －1)的图象关于原点对称，∴函数f (x )的图象关于点(－1,0)对称，排除A ，C ，D ，选B.14．已知函数f (x )的定义域为R ，且f (x )＝⎩⎪⎨⎪⎧2－x－1，x ≤0，f (x －1)，x >0，若方程f (x )＝x ＋a 有两个不同实根，则实数a 的取值X 围为________． 答案 (－∞，1)解析 当x ≤0时，f (x )＝2－x－1,0<x ≤1时，－1<x －1≤0，f (x －1)＝2－(x －1)－1.故x >0时，f (x )是周期函数，如图所示．若方程f (x )＝x ＋a 有两个不同的实数根，则函数f (x )的图象与直线y ＝x ＋a 有两个不同交点，故a <1，即a 的取值X 围是(－∞，1)．15．(2020·某某月考)函数y ＝f (x )的定义域为(－∞，－1)∪(1，＋∞)，其图象上任一点P (x ，y )满足x 2－y 2＝1，则给出以下四个命题：①函数y ＝f (x )一定是偶函数； ②函数y ＝f (x )可能是奇函数；③函数y ＝f (x )在(1，＋∞)上单调递增； ④若y ＝f (x )是偶函数，其值域为(0，＋∞)． 其中正确的序号为________． 答案 ②解析 由题意可得，函数y ＝f (x )的图象是双曲线x 2－y 2＝1的一部分． 由函数的定义可知，该函数的图象可能是如图所示的四种情况之一．其中，图(1)(4)表示的函数为偶函数，图(2)(3)表示的函数是奇函数，所以命题②正确，命题①错误；由图(2)(4)可知函数y ＝f (x )可以在区间(1，＋∞)上单调递减，故命题③错误； 由图(4)可知，该函数的值域也可能为(－∞，0)，所以命题④错误． 综上可知，填②.16．已知函数f (x )＝⎩⎪⎨⎪⎧－x 2＋x ，x ≤1，13log x，x >1，g (x )＝|x －k |＋|x －2|，若对任意的x 1，x 2∈R ，都有f (x 1)≤g (x 2)成立，某某数k 的取值X 围．解 对任意的x 1，x 2∈R ，都有f (x 1)≤g (x 2)成立，即f (x )max ≤g (x )min . 观察f (x )＝⎩⎪⎨⎪⎧－x 2＋x ，x ≤1，13log x，x >1的图象可知，当x ＝12时，函数f (x )max ＝14.因为g (x )＝|x －k |＋|x －2|≥|x －k －(x －2)|＝|k －2|， 所以g (x )min ＝|k －2|，所以|k －2|≥14，解得k ≤74或k ≥94.故实数k 的取值X 围是⎝ ⎛⎦⎥⎤－∞，74∪⎣⎢⎡⎭⎪⎫94，＋∞.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
[基础题组练]
1．小明骑车上学，开始时匀速行驶，途中因交通堵塞停留了一段时间后，为了赶时间加快速度行驶，与以上事件吻合得最好的图象是( )
解析：选C.小明匀速行驶时，所得图象为一条直线，且距离学校越来越近，故排除A.因交通堵塞停留了一段时间，与学校的距离不变，故排除D.后来为了赶时间加快速度行驶，故排除B.
2．(2020·河北衡水中学第二次调研)函数y ＝(2x －1)e x 的图象大致是( )
解析：选A.因为x 趋向于－∞时，y ＝(2x －1)e x <0，所以C ，D 错误；因为y ′＝(2x ＋1)e x ，所以当x <－12时，y ′<0，y ＝(2x －1)e x 在(－∞，－1
2)上是减少的，所以A 正确，B 错误，故
选A.
3.(2020·江西七校第一次联考)设f (x )是定义在R 上的周期为3的周期函数，如图表示该函数在区间(－2，1]上的图象，则f (2 018)＋f (2 019)＝( )
A ．2
B ．1
C ．－1
D ．0
解析：选C.因为函数f (x )是定义在R 上的周期为3的周期函数，所以f (2 018)＝f (2 018－673×3)＝f (－1)，f (2 019)＝f (2 019－673×3)＝f (0)，由题图知f (－1)＝－1，f (0)＝0，所以f (2 018)＋f (2 019)＝f (－1)＋f (0)＝－1.
4.(2020·甘肃酒泉敦煌中学一诊)已知奇函数f (x )在x ≥0时的图象如图所示，则不等式xf (x )<0的解集为( )
A ．(1，2)
B ．(－2，－1)
C ．(－2，－1)∪(1，2)
D ．(－1，1)
解析：选C.因为函数f (x )是奇函数，所以图象关于原点对称，补全当x <0时的函数图象，如图．对于不等式xf (x )<0，当x >0时，f (x )<0，所以1<x <2；当x <0时，f (x )>0，所以－2<x <－1，所以不等式xf (x )<0的解集为(－2，－1)∪(1，2)，故选C.
5．已知函数y ＝f (－|x |)的图象如图所示，则函数y ＝f (x )的图象不可能是( )
解析：选C.函数y ＝f (－|x |)＝⎩
⎪⎨⎪⎧f （－x ），x ≥0，f （x ），x <0，当x <0时，y ＝f (－|x |)＝f (x )，所以函数
y ＝f (－|x |)的图象在y 轴左边的部分，就是函数y ＝f (x )的图象，故可得函数y ＝f (x )的图象不可能是C.
6.如图，函数f (x )的图象是曲线OAB ，其中点O ，A ，B 的坐标分别为(0，0)，(1，2)，(3，1)，则f ⎝⎛⎭
⎫1
f （3）的值等于 ．
解析：由图象知f (3)＝1，所以1
f （3）＝1.所以f ⎝⎛⎭⎫1f （3）＝f (1)＝2.
答案：2
7.若函数f (x )＝⎩
⎪⎨⎪⎧ax ＋b ，x <－1，
ln （x ＋a ），x ≥－1的图象如图所示，则f (－3)＝ ．
解析：由题图可得a (－1)＋b ＝3，ln(－1＋a )＝0，得a ＝2，b ＝5，所以f (x )＝
⎩⎪⎨⎪⎧2x ＋5，x <－1
ln （x ＋2），x ≥－1，
故f (－3)＝2×(－3)＋5＝－1. 答案：－1
8．设函数f (x )＝|x ＋a |，g (x )＝x －1，对于任意的x ∈R ，不等式f (x )≥g (x )恒成立，则实数a 的取值范围是 ．
解析：如图，作出函数f (x )＝|x ＋a |与g (x )＝x －1的图象，观察图象可知：当且仅当－a ≤1，即a ≥－1时，不等式f (x )≥g (x )恒成立，所以a 的取值范围是[－1，＋∞)．
答案：[－1，＋∞) 9．作出下列函数的图象． (1)y ＝x ＋2
x －1；
(2)y ＝|log 2(x ＋1)|.
解：(1)因为y ＝x ＋2x －1＝1＋3x －1，先作出y ＝3
x 的图象，将其图象向右平移1个单位长度，
再向上平移1个单位长度，即得y ＝x ＋2
x －1
的图象，如图所示．
(2)利用函数y ＝log 2x 的图象进行平移和翻折变换，图象如图实线所示．
10．已知函数f (x )＝x |m －x |(x ∈R )，且f (4)＝0. (1)求实数m 的值； (2)作出函数f (x )的图象；
(3)若方程f (x )＝a 只有一个实数根，求a 的取值范围． 解：(1)因为f (4)＝0，所以4|m －4|＝0，即m ＝4. (2)f (x )＝x |x －4|
＝⎩
⎪⎨⎪⎧x （x －4）＝（x －2）2－4，x ≥4，
－x （x －4）＝－（x －2）2＋4，x <4， f (x )的图象如图所示．
(3)从f (x )的图象可知，当a >4或a <0时，f (x )的图象与直线y ＝a 只有一个交点，即方程f (x )＝a 只有一个实数根，即a 的取值范围是(－∞，0)∪(4，＋∞)．
[综合题组练]
1．已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋2x －1，x ≥0，x 2－2x －1，x <0，
则对任意x 1，x 2∈R ，若0<|x 1|<|x 2|，下列不等式
成立的是( )
A ．f (x 1)＋f (x 2)<0
B ．f (x 1)＋f (x 2)>0
C ．f (x 1)－f (x 2)>0
D ．f (x 1)－f (x 2)<0
解析：选D.函数f (x )的图象如图所示，
且f (－x )＝f (x )，从而函数f (x )是偶函数，且在[0，＋∞)上是增函数． 又0<|x 1|<|x 2|， 所以f (x 2)>f (x 1)， 即f (x 1)－f (x 2)<0.
2．已知函数f (x )＝x ＋1
|x |＋1，x ∈R ，则不等式f (x 2－2x )<f (3x －4)的解集是 ．
解析：由已知得，f (x )＝⎩
⎪⎨⎪
⎧1，x ≥0，－1－2
x －1，x <0.其图象如图所示：
由图可知，不等式f (x 2
－2x )<f (3x －4)等价于⎩⎪⎨⎪⎧3x －4≥0，x 2－2x <0或⎩⎪
⎨⎪⎧3x －4<0，
x 2－2x <0，
x 2
－2x <3x －4，
解得4
3
≤x <2
或1<x <4
3
，所以所求的解集为(1，2)．
答案：(1，2)
3．已知函数f (x )＝|x |(x －a )，a >0， (1)作出函数f (x )的图象； (2)写出函数f (x )的单调区间；
(3)当x ∈[0，1]时，由图象写出f (x )的最小值．
解：(1)f (x )＝⎩
⎪⎨⎪⎧x （x －a ），x ≥0，
－x （x －a ），x <0，
其图象如图所示．
(2)由图知，f (x )的递增区间是(－∞，0)，⎝⎛⎭⎫a 2，＋∞；递减区间是⎝⎛⎦⎤0，a
2. (3)由图象知，当a
2>1，即a >2时，所求最小值f (x )min ＝f (1)＝1－a ；
当0<a
2≤1，即0<a ≤2时，
所求最小值f (x )min ＝f ⎝⎛⎭⎫a 2＝－a
2
4
. 综上，f (x )min ＝⎩⎪⎨⎪⎧－a 2
4（0<a ≤2），1－a （a >2）.
4．已知函数f (x )＝2x ，x ∈R .
(1)当m 取何值时，方程|f (x )－2|＝m 有一个解？两个解？ (2)若不等式[f (x )]2＋f (x )－m >0在R 上恒成立，求m 的取值范围．
解：(1)令F (x )＝|f (x )－2|＝|2x －2|，G (x )＝m ，画出F (x )的图象如图所示，由图象看出，当m ＝0或m ≥2时，函数F (x )与G (x )的图象只有一个交点，即原方程有一个解；
当0<m <2时，函数F (x )与G (x )的图象有两个交点，即原方程有两个解． (2)令f (x )＝t (t >0)，H (t )＝t 2＋t ，
因为H (t )＝⎝⎛⎭⎫t ＋122
－1
4在区间(0，＋∞)上是增函数， 所以H (t )>H (0)＝0.
因此要使t 2＋t >m 在区间(0，＋∞)上恒成立，应有m ≤0，即所求m 的取值范围为(－∞，0]．。