期权平价公式
期权平价公式套利策略

期权平价公式套利公式
Kert c S p
其中S代表股票价格,C代表看涨期权价格, P代表看跌期图1.2
期权平价公式套利
Kert S p c
买入看涨期权,同时卖出看跌期权,做空股票,并将获 得的资金投入无风险投资 如果到期股票价格>K 行使看涨期权买入股票 如果到期股票价格<K 直接买入股票 最终利润大于零,实现了套利。
谢 谢 聆 听!
图1.2
期权平价公式套利
Kert S p c
借入资金(S+p-c),卖出看涨期权并购入看跌期权和对应的股 票 如果到期股票价格>K,用股票来实现看涨期权的交割,而 获得K的收入 如果到期股票价格<K,行使看跌期权来获得K的收入,还完 借入资金的本金和利息,最终的收益是大于零的。
图1.2
从平价公式的角度看期权常见策略
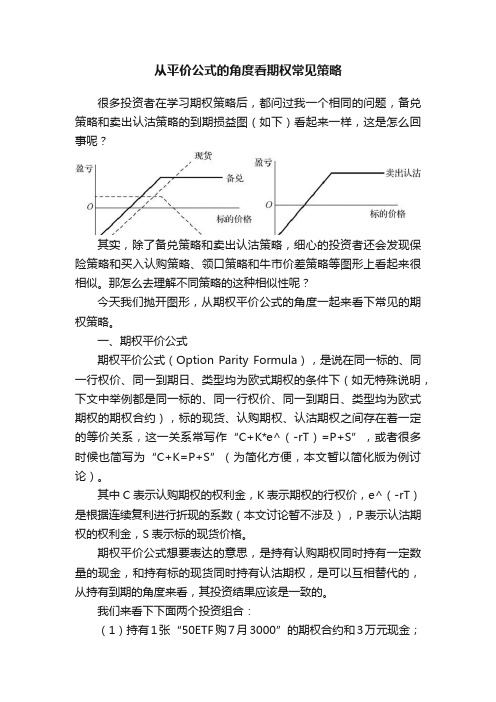
从平价公式的角度看期权常见策略很多投资者在学习期权策略后,都问过我一个相同的问题,备兑策略和卖出认沽策略的到期损益图(如下)看起来一样,这是怎么回事呢?其实,除了备兑策略和卖出认沽策略,细心的投资者还会发现保险策略和买入认购策略、领口策略和牛市价差策略等图形上看起来很相似。
那怎么去理解不同策略的这种相似性呢?今天我们抛开图形,从期权平价公式的角度一起来看下常见的期权策略。
一、期权平价公式期权平价公式(Option Parity Formula),是说在同一标的、同一行权价、同一到期日、类型均为欧式期权的条件下(如无特殊说明,下文中举例都是同一标的、同一行权价、同一到期日、类型均为欧式期权的期权合约),标的现货、认购期权、认沽期权之间存在着一定的等价关系,这一关系常写作“C+K*e^(-rT)=P+S”,或者很多时候也简写为“C+K=P+S”(为简化方便,本文暂以简化版为例讨论)。
其中C表示认购期权的权利金,K表示期权的行权价,e^(-rT)是根据连续复利进行折现的系数(本文讨论暂不涉及),P表示认沽期权的权利金,S表示标的现货价格。
期权平价公式想要表达的意思,是持有认购期权同时持有一定数量的现金,和持有标的现货同时持有认沽期权,是可以互相替代的,从持有到期的角度来看,其投资结果应该是一致的。
我们来看下下面两个投资组合:(1)持有1张“50ETF购7月3000”的期权合约和3万元现金;(2)持有1张“50ETF沽7月3000”的期权合约和10000份50ETF。
假设现在到了7月期权合约到期日,根据50ETF到期价格的不同,我们分情况来讨论:(1)到期50ETF价格高于3元,则组合1中认购合约是实值合约,此时会选择行权,交付3万元现金,然后收到10000份50ETF;组合2中认沽合约是虚值合约,到期失效即可,此时剩余10000份50ETF。
比较组合1、2,都是10000份50ETF,结果是一样的。
(2)到期50ETF价格低于3元,则组合1中认购期权是虚值合约,到期失效即可,此时剩余3万元现金;组合2中认沽合约是实值合约,此时会选择行权,交付10000份50ETF,然后收到3万元现金。
注会《财务成本管理》知识点:看跌期权估价平价定理

注会《财务成本管理》知识点:看跌期权估价平价定理
在套利驱动的均衡状态下,我们构建一个组合,针对具有相同执行价格和到期日的欧式看跌期权和欧式看涨期权,购进股票、购进看跌期权,同时售出看涨期权,该策略产生无风险收益,符合买卖权平价:
买入股票+买入看跌期权+出售看涨期权→无风险套利组合
则期初的净流出=S0+P-C
期权到期:
期权到期日合计都是执行价格x,则执行价格求现值就应该等于投资组合时的净流出S0+P-C
即:标的资产现行价格+看跌期权价格-看涨期权价格=执行价格的现值。
已知等式中的任何3个量,即可求得第4个量。
期权定价公式及其应用

企业风险管理
总结词
企业风险管理是期权定价公式的另一个重要应用领域,帮助企业识别、评估和管 理风险。
详细描述
期权定价公式在识别和管理企业风险方面发挥着重要作用。例如,通过使用期权 定价公式,企业可以评估和管理供应链风险、汇率风险和其他潜在风险。此外, 期权定价公式还可以帮助企业评估和管理投资项目的风险。
在房地产金融领域,二叉树模型被广 泛应用于可赎回房地产投资信托基金 (REITs)的定价。例如,某REIT发 行了一份额额为100万元的优先股, 并授予投资者在三年后以120万元赎 回的权利。投资者可以利用二叉树模 型计算该优先股在赎回日的市场价值 ,从而判断投资该REIT的潜在收益和 风险。
期权定价公式在投资决策中的应用案例
为了计算利率衍生品的价格,需要使用利率模型。常用的利率模型包括Vasicek模型、 Cox-Ingersoll-Ross模型等。这些模型可以模拟即期利率的动态变化,从而为利率衍生品 定价。
06
期权定价公式在实际操作 中的应用案例分析
基于Black-Scholes模型的期权定价案例
总结词
详细描述
应用案例
总结词
详细描述
应用案例
期权定价公式可以用于评估投资项目 的风险和潜在收益,指导投资者做出 更加明智的投资决策。
利用期权定价公式,投资者可以计算 出不同投资项目在不同时间点的预期 收益和风险。例如,对于一个具有重 大战略意义的项目,投资者可以选择 购买或出售相关资产的期权来对冲风 险。此外,投资者还可以利用期权定 价公式评估其他投资项目的潜在收益 和风险,如股票、债券、房地产等。
提高金融市场效率
期权定价公式的应用有助于提高 金融市场的信息传递和流通效率 ,使市场价格更及时、准确地反
期权入门基础知识单选题100道及答案解析

期权入门基础知识单选题100道及答案解析1. 期权是一种赋予期权买方在规定期限内按双方约定的价格()一定数量某种金融资产的权利的合约。
A. 买入B. 卖出C. 买入或卖出D. 以上都不对答案:C解析:期权买方有权在规定期限内按约定价格买入或卖出一定数量的某种金融资产。
2. 以下关于期权的说法,错误的是()A. 期权买方的风险有限B. 期权卖方的收益有限C. 期权买方需要支付权利金D. 期权卖方不需要支付保证金答案:D解析:期权卖方需要支付保证金。
3. 期权按照行权时间的不同,可以分为()A. 欧式期权和美式期权B. 看涨期权和看跌期权C. 实值期权、虚值期权和平值期权D. 场内期权和场外期权答案:A解析:按行权时间分,期权分为欧式期权和美式期权。
4. 欧式期权只能在()行权。
A. 期权到期日B. 期权到期日前的任何一天C. 期权到期日前一周D. 以上都不对答案:A解析:欧式期权只能在到期日行权。
5. 美式期权可以在()行权。
A. 期权到期日B. 期权到期日前的任何一天C. 只能在到期日前一周D. 以上都不对答案:B解析:美式期权在到期日前的任何一天都可行权。
6. 看涨期权的买方预期标的资产价格会()A. 上涨B. 下跌C. 不变D. 以上都有可能答案:A解析:看涨期权买方预期标的资产价格上涨。
7. 看跌期权的买方预期标的资产价格会()A. 上涨B. 下跌C. 不变D. 以上都有可能答案:B解析:看跌期权买方预期标的资产价格下跌。
8. 对于看涨期权,当标的资产价格()执行价格时,期权处于实值状态。
A. 高于B. 低于C. 等于D. 以上都不对答案:A解析:看涨期权,标的资产价格高于执行价格为实值。
9. 对于看跌期权,当标的资产价格()执行价格时,期权处于实值状态。
A. 高于B. 低于C. 等于D. 以上都不对答案:B解析:看跌期权,标的资产价格低于执行价格为实值。
10. 当标的资产价格等于执行价格时,期权处于()状态。
期权价格计算公式

期权价格计算公式股票的价格变化遵循一维维纳过程,其微分方程如下dz t s b dt t s a ds ),(),(+=式中:dz 的差分∆Z 满足如下条件的正态分布t z ∆=∈∆在一般情况下,ds 可用下式表示:sdz sdt ds σμ+=----------- (1)或表示为:dz dt sds σμ+= 式中:s μ股票价格的期望漂移率,μ 为一个恒定参数;2)(s σ为股票价格波动的方差, σ 为股票价格的波动率,可以通过观察股票价格的动态系列数据获得。
如果存在一个变量 G ,它是股票S 的一种衍生证卷,它的价格是S 和 t 的函数,G(s,t),那么,S 和G 都受到同一个基本的不确定性因素的影响。
根据ITO 定理,函数G 的行为遵循如下微分方程描述的过程:Sdz S G dt S S G t G S S G dG σσμ∂∂+∂∂+∂∂+∂∂=)21(2222 -------------(2)函数G 的漂移率为222221S SG t G S S G σμ∂∂+∂∂+∂∂ 方差为222)(S SG σ∂∂如果G 代表股票S 的一种期权,我们想用S 和G 构造一组风险中性的证卷组合。
为此,首先将公式(1)、(2)改写成对应的差分形式:z S t S S ∆+∆=∆σμ ---------------(3)z S SG t S G t G S S G G ∆∂∂+∆∂∂+∂∂+∂∂=∆σμ)21(22 ----------(4) 由于公式(3)、(4)中的z ∆t ∆=∈()是相同的维纳过程,只要证卷数量的搭配合理,整卷组合就可以消除z ∆。
恰当的证卷组合是:-1; 卖空一个期权S G∂∂+;买入期权价值变化对股票价格的敏感度,也就是他的偏微分那样多的股票。
定义这个证卷组合的价值为∏,表达式为S S G G ∏∂∂+-= ---------(5) t ∆时间后,这个证卷组合的价值变化为: S S G G ∆∂∂+∆-=∆∏ -----------(6)将(3)、(4)带入(6),消去z ∆,得:t S S G t G ∆∂∂-∂∂-=∆∏)21(2222σ ---------(7)由于这个证卷组合是风险中性的,所以,它的收益一定与任何一个无风险证卷的收益相同,就是∏∏∆=∆t r ---------(8)将(5)、(7)带入(8),得:t S SG G r t S S G t G ∆∂∂-=∆∂∂+∂∂)()21(2222σ 将上式进一步化简,得:rG S G S S G rS t G =∂∂+∂∂+∂∂222221σ --------(9)这就是获得诺贝尔奖的Black-Scholes 微分方程。
期权定价公式

期权定价公式期权定价公式是:期权价格=内在价值+时间价值。
期权定价模型,由布莱克与斯科尔斯在20世纪70年代提出。
该模型认为,只有股价的当前值与未来的预测有关;变量过去的历史与演变方式与未来的预测不相关。
模型表明,期权价格的决定非常复杂,合约期限、股票现价、无风险资产的利率水平以及交割价格等都会影响期权价格。
期权是购买方支付一定的期权费后所获得的在将来允许的时间买或卖一定数量的基础商品的选择权。
期权价格是期权合约中唯一随市场供求变化而改变的变量,其高低直接影响到买卖双方的盈亏状况,是期权交易的核心问题。
在国际衍生金融市场的形成发展过程中,期权的合理定价是困扰投资者的一大难题。
随着计算机、先进通讯技术的应用,复杂期权定价公式的运用成为可能。
简单期权定价模型。
我们把股价随机末态简化为两个等效的等概率量子态,要么50%的概率上涨到+1X的右边一个标准差处,要么50%的概率下跌到-1X的左边一个标准差处。
显然,对于认购期权,在-1X末态的行权收益是0;在+1X末态的行权收益是S*(1+σ)-K。
其中S是当前(初态)股价,K是到期日的行权价。
根据初态=末态期望值的原理,认购期权价格C=0.5*0+0.5*[S*(1+σ)-K]= 0.5*[S*(1+σ)-K]。
这对于平值和浅度虚值期权是适用的。
对于平值期权K=S,C=0.5*S*σ。
比如,当前股价S=3.3元,月波动率为σ=6%,那么行权价K=3.3元,剩余T=30天期限的平值认购期权价格就是,C=0.5*3.3*6%=0.0990元。
对于深度实值期权,当股价末态为-1X处,仍然会有行权收益。
所以,认购期权价格C=0.5*[S*(1-σ)-K]+0.5*[S*(1+σ)-K]=S-K。
比方说,对于深度实值期权实三K=3.0元,当股价从当前价S=3.3元下跌至末态(-1X处)ST=3.1元,仍然会有3.1-3.0=0.1元的行权收益。
所以,实三期权价格C=S-K=3.3-3.0=0.3元。
注册会计师考试财管知识点:常用公式期权价值评估

注册会计师考试财管知识点:常用公式期权价值评估纵观古往今来,凡成大事者,都有超乎常人的意志力、忍耐力。
2019年考试备考也是如此,需要我们保持充沛的精力,认真完成每天的学习计划,踏实学习,耐得住寂寞!小编今天为大家推送2019年注册会计师考试财管知识点。
记得学习吧1.多头看涨期权到期日价值=Max(0,股票市价﹣执行价格)2.空头看涨期权到期日价值=﹣Max(0,股票市价﹣执行价格)3.多头看涨期权到期日净损益=多头看涨期权到期日价值﹣期权价格4.空头看涨期权到期日净损益=空头看涨期权到期日价值+期权价格5.多头看跌期权到期日价值=Max(执行价格﹣股票市价,0)6.空头看跌期权到期日价值=﹣Max(执行价格﹣股票市价,0)7.多头看跌期权到期日净损益=多头看跌期权到期日价值﹣期权价格8.空头看跌期权到期日净损益=空头看跌期权到期日价值+期权价格9.保护性看跌期权:组合净损益=执行日组合收入﹣初始投资<1>到期股价(ST)<执行价格(X):组合净损益=执行价格﹣(股票买价+期权买价)<2>到期股价(ST)>执行价格(X):组合净损益=股票售价﹣(股票买价+期权买价)10.抛补看涨期权:组合净损益=执行日组合收入﹣初始投资<1>到期股价(ST)<执行价格(X):组合净损益=股票售价﹣股票买价+期权售价<2>到期股价(ST)>执行价格(X):组合净损益=执行价格﹣股票买价+期权售价11.多头对敲:组合净损益=执行日组合收入﹣初始投资<1>到期股价(ST)<执行价格(X):组合净损益=(执行价格﹣到期股价)﹣两种期权买价<2>到期股价(ST)>执行价格(X):组合净损益=(到期股价﹣执行价格)﹣两种期权买价12.空头对敲:组合净损益=初始投资收入﹣执行日组合损益<1>到期股价(ST)<执行价格(X):两种期权买价﹣(执行价格﹣到期股价)<2>到期股价(ST)>执行价格(X):两种期权买价﹣(到期股价﹣执行价格)13.期权价值=内在价值+时间溢价2019年注册会计师考试财管知识点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品文档
期权平价公式:
C+ KeA(-rT)=P+S
认购期权价格C与行权价K的现值之和等于认沽期权的价格P加上标的证券现价S Ke A(-rT) :
K乘以e的-rT次方,也就是K的现值。
e的-rT次方是连续复利的折现系数。
也可用exp( -rT )表示
贴现因子。
根据无套利原则推导:
构造两个投资组合。
1. 看涨期权C,行权价K,距离到期时间T。
现金账户KeA(-rT),利率r,期权到期时恰好变成行权价
K。
2. 看跌期权P,行权价K,距离到期时间T。
标的物股票,现价So
看到期时这两个投资组合的情况。
1. 股价St大于K:投资组合1,行使看涨期权C,花掉现金账户K,买入标的物股票,股价为St o投资
组合2,放弃行使看跌期权,持有股票,股价为St o
2. 股价St小于K:投资组合1,放弃行使看涨期权,持有现金投资组合2,行使看跌期
权,卖出标的物股票,得到现金K
3. 股价等于K:两个期权都不行权,投资组合1现金K,投资组合2股票价格等于K o
从上面的讨论我们可以看到,无论股价如何变化,到期时两个投资组合的价值一定相等,所
以他们的现值也一定相等。
根据无套利原则,两个价值相等的投资组合价格一定相等。
所以
我们可以得到C+KeA(-rT)=P+S。
换一种思路理解:C- P = S- KeA(-rT)
认购期权价格C与认沽期权的价格P的差等于证券现价与行权价K现值的差。
行权价K低于现货价格S 行权价K高于现货价格S
买入标的物
C
P
买入put
call
精品文档
1欢迎下载
欢迎您的下载,
资料仅供参考!
致力为企业和个人提供合同协议,策划案计划书,学习资料等等
打造全网一站式需求
2欢迎下载。
