实验设计与数据处理试题库
实验设计与数据处理

13125916机电硕1308班周晓易1.某工厂进行技术改造,以减少工业酒精中甲醇含量的波动。
原工艺生产的工业酒精中甲醇含量的总体方差为0.35.技术改造后,进行抽样检验,样品数为25个,结果样品甲醇含量的样本方差为0.15。
问技术改造后工业酒精中甲醇含量的波动性是否更小?(α=0.05)答:检验技术改造后工业酒精中甲醇含量的波动性是否更小,要使用χ2单侧(左侧)检验。
已知σ2=0.35,n=25,s2=0.15。
当α=0.05时,χ20.95(24)=CHIINV(0.95,24)=13.848,而χ2=24*0.15/0.35=10.286,χ20.95(24)>χ2,说明技术改革后产品中甲醇含量的波动较之前有显著减少。
2. A与B两人用同一种分析方法测定金属钠中铁的含量,测试结果分别为:A:8.0,8.0,10.0,10.0,6.0,6.0,4.0,6.0,6.0,8.0B:7.5,7.5,4.5,4.0,5.5,8.0,7.5,7.5,5.5,8.0试问A、B二人测定的铁的精密度是否有显著性差异?(α=0.05)解答如图:这里F>1,为右侧检验,这时F 单尾临界值>1,对于右侧检验,如果F<F 单尾临界,或者P(F<=f) 单尾>α,就可以认为第一组数据较第二组数据的方差没有显著增大,否则就认为第一组的数据较第二组的数据的方差有显著增大。
在本例中,由于P>0.05,所以A、B 二人测定的铁的精密度无显著性差异。
3. 用新旧工艺冶炼某种金属材料,分别从两种产品中抽样,测定试样中的杂质含量,结果如下:旧工艺:2.69, 2.28, 2.57, 2.30, 2.23, 2.42, 2.61, 2.64, 2.72, 3.02, 2.45, 2.95, 2.51新工艺:2.26, 2.25, 2.06, 2.35, 2.43, 2.19, 2.06, 2.32, 2.34试问新工艺是否更稳定,并检验两种工艺之间是否存在系统误差?(α=0.05)解答:由于s21<s22,故新工艺比旧工艺更稳定;又因为F<1,所以为左侧检验。
实验设计与数据处理第六章例题及课后习题答案
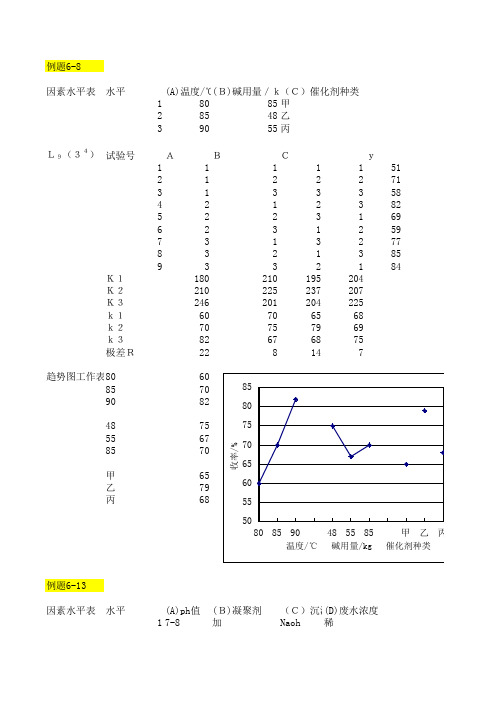
4
2
1
2
3
5
2
2
3
1
6
2
3
1
2
7
3
1
3
2
8
3
2
1
3
9
3
3
2
1
K1
142.51 173.93 218.76 211.49
K2
225.43 201.62 197.87 205.29
K3
257.97 250.36 209.28 209.13
k1
47.50333333 57.97667 72.92 70.4967
习题6.1
水平
(A)溶剂浓度(B、)反% 应温度/℃©保温时间/h
1
60
140
3
2
80
160
2
3
100
180
1
L9(34) 试验号
A
B
C
y
1
1
1
1
1 5.3
2
1
2
2
2
5
3
1
3
3
3 4.9
4
2
1
2
3 5.4
5
2
2
3
1 6.4
6
2
3
1
2 3.7
7
3
1
3
2 3.9
8
3
2
1
3 3.3
9
3
3
2
1 2.4
K1
A
B
1
1
2
1
3
2
4
2
5
3
实验设计与数据处理大作业及解答
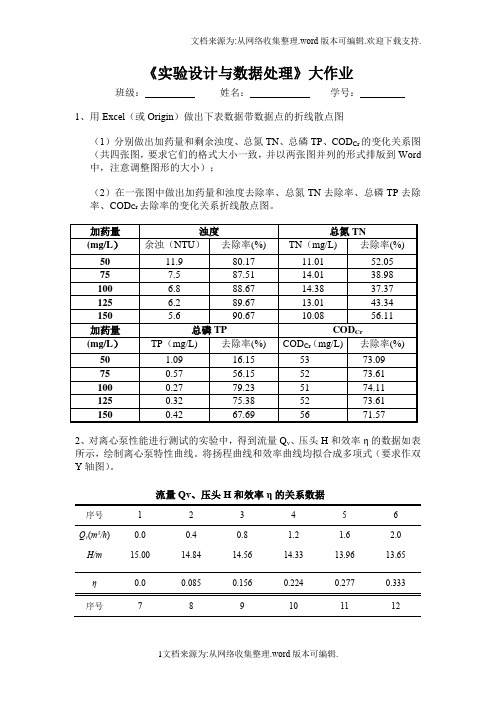
《实验设计与数据处理》大作业班级:姓名:学号:1、用Excel(或Origin)做出下表数据带数据点的折线散点图(1)分别做出加药量和剩余浊度、总氮TN、总磷TP、COD Cr的变化关系图(共四张图,要求它们的格式大小一致,并以两张图并列的形式排版到Word 中,注意调整图形的大小);(2)在一张图中做出加药量和浊度去除率、总氮TN去除率、总磷TP去除率、COD Cr去除率的变化关系折线散点图。
2、对离心泵性能进行测试的实验中,得到流量Q v、压头H和效率η的数据如表所示,绘制离心泵特性曲线。
将扬程曲线和效率曲线均拟合成多项式(要求作双Y轴图)。
流量Qv、压头H和效率η的关系数据序号123456Q v(m3/h) H/m0.015.000.414.840.814.561.214.331.613.962.013.65η0.00.0850.1560.2240.2770.333序号789101112Q v(m3/h) H/mη2.413.280.3852.812.810.4163.212.450.4463.611.980.4684.011.300.4694.410.530.4313、用分光光度法测定水中染料活性艳红(X-3B)浓度,测得的工作曲线和样品溶液的数据如下表:(1)列出一元线性回归方程,求出相关系数,并绘制出工作曲线图。
(2)求出未知液(样品)的活性艳红(X-3B)浓度。
4、对某矿中的13个相邻矿点的某种伴生金属含量进行测定,得到如下一组数据:试找出某伴生金属c与含量距离x之间的关系(要求有分析过程、计算表格以及回归图形)。
提示:⑴作实验点的散点图,分析c~x之间可能的函数关系,如对数函数y=a+blgx、双曲函数(1/y)=a+(b/x)或幂函数y=dx b等;⑵对各函数关系分别建立数学模型逐步讨论,即分别将非线性关系转化成线性模型进行回归分析,分析相关系数:如果R≦0.553,则建立的回归方程无意义,否则选取标准差SD最小(或R最大)的一种模型作为某伴生金属c与含量距离x之间经验公式。
工程实验设计数据处理试题整理

1、名词解释。
(1)数量数据:当试验结果表现为数量上的变化,由计数或测量所得到的数据称数量数据。
(2)算术平均值:一个样本内各个观察值的总和除以观察值总个数的商即为该样本的算术平均数,一般称为平均数或均数。
(3)方差:各因素或交互作用的偏差平方和除以各自相应的自由度。
(4)区域控制: 将试验处理按系统进行区组划分,使同一区组内的单元间环境因素保持一致,保证同一区组中局部范围内单元间误差的同质性,以便于消除系统误差。
区域控制又称划分区组。
(5)全面实验设计法:对各因素各水平排列组合成的全部试验处理都加以实施,称为全面试验。
(6)试验水平:在实验中,为了考察试验因素对试验指标的影响,必须使试验因素处于不同的状态,把因素所处的各种状态称为试验水平,简称水平或位级。
(7)Ln(m k)中各字母表示含义:L——表示正交表;n——试验次数(处理数);m——水平数;k——表的列数,即最多可以安排的因素数。
最多可安排k个因素,每个因素m水平,共做n次实验的等水平正交表。
(8)部分实施:在试验的全部组合处理中,选取有代表性的部分处理加以实施,称为部分实施。
(9)样本容量:样本容量又称“样本数”。
指一个样本的必要抽样单位数目。
(10)试验因素:在实验中,能对试验指标产生影响的原因或要素,都称为因素或因子。
通常也称为影响因素。
(11)试验处理:在试验中,不同因素的不同水平的搭配组合称为处理(12)极差:样本中最大值与最小值之差为极差。
(13)试验指标:在实验设计中,根据试验目的而选定的用来衡量试验效果的特征值。
2.简答(1)请回答,在实验设计中,为减少误差要遵循哪些原则,并解释其作用。
(2)(1)重复:即一种处理要重复两次以上。
设置重复的主要作用有两方面:一是估计试验误差:二是降低试验误差。
(3)(2)随机化:随机可以消除任何人为的主观偏性及各种干扰因子的影响,以保证获得处理效应及对误差有效无偏估计。
(4)(3)区域控制区域控制是将试验处理按系统进行区组划分,使同一区组内的单元间环境因素保持一致,保证同一区组中局部范围内单元间误差的同质性,以便于消除系统误差。
实验设计与数据处理第三四五章例题及课后习题答案

x3 13 19 25 10 16 22 28 133 19
y 1.5 0.33
3 0.336 1 0.294 2.5 0.476 0.5 0.209 2 0.451 3.5 0.482 14 2.578 2 0.368286
方程 1 1E-06 2 1E-06 3 2.32E-09 4 7.24E-11
0
系列1
5
10
15
0
SUMMARY OUTPUT
5
10
x
回归统计
Multiple
R
0.981636002
R Square
0.96360924
Adjusted
R Square 0.951478987
标准误差 0.643254553
观测值
9
方差分析
回归分析 残差 总计
df
SS
2 65.7395637
6 2.482658518
例4-5
试验号 x1 1 2 3 4 5 6 7
总和 平均
L11 L22 L33 L12 L23 L31
x2 1 1.4 1.8 2.2 2.6 3 3.4 15.4 2.2
4.48 252
7 16.8 10.5 1.4
L1y L2y L3y
检验线性 回归方程 的显著性 (1)F检 验
0.2404 0.564 0.5245
8 68.22222222
15
F0.01(2,6 )=10.92
MS
F
32.86978185 79.43851
0.41377642
Intercep t X Variable 1 X Variable 2
实验设计与数据处理(第二版部分答案)教学内容

实验设计与数据处理(第二版部分答案)试验设计与数据处理学院班级学号学生姓名指导老师第一章4、相对误差18.20.1%0.0182x mg mg ∆=⨯=故100g 中维生素C 的质量范围为:18.2±0.0182mg 。
5、1)、压力表的精度为1.5级,量程为0.2MPa ,则 max 0.2 1.5%0.003330.3758R x MPa KPax E x ∆=⨯==∆=== 2)、1mm 的汞柱代表的大气压为0.133KPa , 所以max 20.1330.1331.6625108R x KPax E x -∆=∆===⨯ 3)、1mm 水柱代表的大气压为gh ρ,其中29.8/g m s = 则:3max 339.8109.810 1.225108R x KPax E x ---∆=⨯∆⨯===⨯ 6.样本测定值3.48 算数平均值 3.421666667 3.37 几何平均值 3.421406894 3.47 调和平均值 3.421147559 3.38 标准差s 0.046224092 3.4 标准差σ 0.04219663 3.43 样本方差S 2 0.002136667总体方差σ20.001780556算术平均误差△ 0.038333333 极差R 0.117、S ₁²=3.733,S ₂²=2.303F =S ₁²/ S ₂²=3.733/2.303=1.62123而F 0.975 (9.9)=0.248386,F 0.025(9.9)=4.025994 所以F 0.975 (9.9)< F <F 0.025(9.9)两个人测量值没有显著性差异,即两个人的测量方法的精密度没有显著性差异。
分析人员A分析人员B8 7.5 样本方差1 3.733333 8 7.5 样本方差2 2.302778 10 4.5 Fa 值 0.248386 4.025994104F 值1.62123|||69.947|7.747 6.06p pd x =-=>6 5.56 84 7056 7.56 5.58 88.旧工艺新工艺2.69% 2.62%2.28% 2.25%2.57% 2.06%2.30% 2.35%2.23% 2.43%2.42% 2.19%2.61% 2.06%2.64% 2.32%2.72% 2.34%3.02%2.45%2.95%2.51%t-检验: 双样本异方差假设变量 1 变量 2平均0.025684615 2.291111111 方差0.000005861 0.031611111 观测值13 9 假设平均差0df 8t Stat -38.22288611P(T<=t) 单尾0t 单尾临界 1.859548033P(T<=t) 双尾0t 双尾临界 2.306004133F-检验双样本方差分析变量 1 变量 2平均0.025684615 2.291111111 方差0.000005861 0.031611111 观测值13 9 df 12 8 F 0.000185422P(F<=f) 单尾0F 单尾临界0.3510539349. 检验新方法是否可行,即检验新方法是否有系统误差,这里采用秩和检验。
试验设计与数据处理复习题
一、理论题1.根据研究目的确定的研究对象的全体称为总体(population),其中的一个研究单位称为个体(individual);总体的一部分称为样本(sample)。
通常把n≤30的样本叫小样本,n>30的样本叫大样本。
2.由总体计算的特征数叫参数(parameter), ;由样本计算的特征数叫统计量(statistic)。
常用希腊字母表示参数,例如用μ表示总体平均数,用σ表示总体标准差;常用拉丁字母表示统计量,例如用x表示样本平均数,用S表示样本标准差。
3. 准确性(accuracy)指在调查或试验中某一试验指标或性状的观测值与其真值接近的程度,精确性(precision)指调查或试验中同一试验指标或性状的重复观测值彼此接近的程度。
4. 高斯对数理统计和试验设计学科的主要贡献包括:1.建立了回归分析的最小二乘法;2.运用极大似然法及其他数学知识,推导出测量误差的概率分布公式,发现误差的高斯分布曲线,即今天的正态分布。
5.方差分析由R. 费雪于1918年首创, “方差分析法是一种在若干能相互比较的资料组中,把产生变异的原因加以区分开来的方法与技术”。
6.20世纪50年代,日本田口玄一将试验设计中应用最广的正交设计表格化;同一时期,我国著名数学家华罗庚积极倡导和普及“优选法”;在1978年我国数学家王元和方开泰首先提出了均匀设计。
7.两组精度不同的同一试验结果在计算加权平均数时权重通常由绝对误差平方倒数的比值来确定,即认为测量结果的可靠程度与测量次数成正比。
8.样本标准误差的无偏计算公式中分母的n-1来自于自由度的概念。
9. 实验最重要的因素是混杂问题。
所谓混杂是指,由于实验处理,针对你的假说所作的处理,导致的差异与其他因素可能导致的差异无法区分开来。
10. 重复是指在符合实验条件的空间和时间范围内,各组要有足够数量的例数。
重复非常必要,因为变异(差异)是生物体遗传固有的本质。
11. 生物数据中比正态分布更常见的是正偏斜,偏斜数据通常必须进行数据转换(例如对数和幂转换),以改善它们的正态性。
实验设计与数据处理
实验设计与数据处理第二次作业正交实验设计与数据处理姓名:班级:学号拟水平法:某啤酒厂实验期用不发芽的大麦制造啤酒新工艺的过程中,选择因素、水平及结果如下,不考虑交互作用,考察粉状粒越高越好,采用拟水平法将因素D的水平一136重复一次作为第二水平,(表一),按L9(34)安排实验,得到结果如表二,请分别进行直观分析、方差分析,并找出最好的工艺条件。
表一:因素水平表表二:实验设计及结果1.正交试验设计结果的直观分析法表三:试验方案及试验结果分析因素主次 C A B D优方案C1A3B3D1图一:趋势图2.正交试验设计结果的方差分析法表4正交实验的实验方案及结果分析试验号 A B C D粉状粒y i/%1 2 3 4 5 611122212312312323112331264.2553.2539.2544.2528.2553.25赤霉素浓度 /(mg/kg) 氨水浓度/% 吸氨量/g 底水/g粉状粒,y i /%⑴计算离差平方和: T=∑=91i iy=64.25+53.25+39.25+44.25+28.25+53.25+41.25+60.25+61.25=445.25 Q=∑=912i i y =64.252+53.252+39.252+44.252+28.252+53.252+41.252+60.252+61.252 =23179.06P=211⎪⎭⎫⎝⎛∑=n i i y n =T 2/n=445.252/9=22027.51SS T =21∑=-⎪⎭⎫ ⎝⎛-ni i y y =21121⎪⎭⎫ ⎝⎛-∑∑==n i i n i i y n y =Q-P=23179.06-22027.51=1151.55对于3水平正交实验的方差分析,由于r=3,所以任一列(第j 列)的离差平方和为:SS J =⎪⎭⎫⎝⎛∑=3123i i K n -PSS A =3/9(156.752+125.752+162.752)-22027.51=262.89 SS B =3/9(149.752+141.752+153.752)-22027.51=24.89 SS C =3/9(177.752+158.752+108.752)-22027.51=846.89因素D 的第一水平重复了6次,第二水平重复了3次,所以D 因素引起的离差平方和为:SS D =K12/6+K32/3-P=301.52/6+143.752/3-22027.51=10.89 误差的离差平方和为: SSe=SS T -(SS A +SS B +SS C +SS D )=1151.55-(262.89+24.89+846.89+10.89)=5.99 ⑵计算自由度:总自由度:dfT=n-1=9-1=8各因素自由度:dfA=dfB=dfC=r-1=3-1=2 dfD=2-1=1dfe=dfT-(dfA+dfB+dfC+dfD )=8-(2+2+2+1)=1 ⑶计算均方:(不考虑交互作用) MS A =SS A /dfA=262.89/2=131.445 MS B =SS B /dfB=24.89/2=12.445 MS C =SS C /dfC=846.89/2=423.45MS D=SS D/dfD=10.89/1=10.89MSe=SSe/dfe=5.99/1=5.99⑷计算F值:F A=MS A/MSe=131.445/5.99=21.94F B=MS B/MSe=12.445/5.99=2.08F C=MS C/MSe=423.45/5.99=70.69F D=MS D/MSe=10.89/5.99=1.82⑸F检验:查得临界值F0.10(2,1)=49.5,F0.10(1,1)=39.86,所以对于给定的显著性水平0.10,因素C对试验结果有显著影响。
实验设计与数据处理第八章例题及课后习题答案doc资料
0
428
0 1.162084
492
0 1.162084
512
0
0
509
0
0
Signific ance F
7.93E-05
Lower Upper 下限 上限
95%
95% 95.0% 95.0%
465.4405 471.5595 465.4405 471.5595
5.242078 12.93644 5.242078 12.93644
0.002795085 2.593838854 0.122018
例8-2
回归方程: 由该回归方程 中偏回归系数 绝对值的大 小,可以得到 各因素和交互 作用的主次顺 序为:
y=0.50475+0.00 975z1+0.03375z 2+0.00475z1z20.00575z3+0.00 725z1z3
0 0 -41.73590203
y=468.5+9.09z1 -26.56z2+z3
标准误差
t Stat P-value
1.10193312 425.1619191 1.84E-10
1.385649972 6.55956341 0.002794
1.385649972 -19.17042163 4.36E-05
SS 0.0091125
0.001626 0.0108635
MS
F
0.0091125 33.62546
0.000271
试验号
z1 1 2 3 4 5 6 7 8 9 10 11
z2 1 1 1 1 -1 -1 -1 -1 0 0 0
z3 1 1 -1 -1 1 1 -1 -1 0 0 0
《试验设计与数据处理》课程作业
《试验设计与数据处理》课程作业1.下表是采用不同提取方法测定的某有效成分提取率(%)的统计量,试根据这些数据用EXCEL画出柱状图并标注误差线,用选择性粘贴功能将柱状图过程演示:双击柱形图,打开误差线窗口,如下图选择“正负偏差”“线端”,误差量选择“自定义”,点击“指定值”,将标准误差输入正负错误值中。
2.在用原子吸收分光光度法测定镍电解液中微量杂质铜时,研究了乙炔和空气流量变化对铜在某波长上吸光度的影响,得到下表所示的吸光度数据。
试分析乙炔和空气流量对铜吸光度的影响。
实验分析:表中行代表的是乙炔流量,列代表的是空气流量,我们可以看到:F=28.61486>F –crit=3.490295且P-value=9.44E-06<0.01,所以乙炔的流量这个因素对铜的的吸光度的影响非常显著,而在空气流量中F<F-crit且P-value>0.01,所以空气因素对铜吸光度的影响不大。
过程演示:将数据输入Excel表格中,数据分析选择“无重复双因素分析”,具体操作如下图:3.为了研究铝材材质的差异对其在高温水中腐蚀性能的影响,用三种不同的铝材在相同温度的去离子水和自来水中进行了一个月的腐蚀试验,测得的腐蚀程度(μm)如下表所示。
试对铝材材质和水质对腐蚀程度进行方差分析,若显著则分别作多重比较。
方差分析:可重复双因素分析SUMMARY 去离子水自来水总计A1A2A3A4总计实验分析:由方差分析,铝材材质、水源及其交互作用对腐蚀程度均有较大的影响,主次因素从大到小为铝材材质>水源>交互作用。
A已显示同类子集中的组均值。
基于观测到的均值。
a. 使用调和均值样本大小= 6.000。
b. Alpha = .05。
过程演示:4.已知某物质的浓度C与沸点温度T之间关系如下表所示,试绘出散点图,配制出你认为最理想的回归方程式,进行显著性检验并求出该回归方程的标准误差。
SUMMARY OUTPUT:回归统计Multiple R 0.999753R Square 0.999505 Adjusted R Square -1.4标准误差0.089178观测值 1方差分析:df SS MS F回归分析7 80.36881 11.48126 10105.94残差 5 0.039763 0.007953总计12 80.408575.某物质在凝固时放出的热量Y(J/g)与4种化学成分X1、X2、X3、X4有关,试作y与X1、X2、X3、X4的线性回归分析:(1)试求出多元线性回归方程式;(2)对该方程式进行显著性检验,并判定影响热量的化学成分的主次顺序;(3)SUMMARY OUTPUT1234 (2)因P<0.05,故此方程显著。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、名词解释:(20分)1.准确度和精确度:同一处理观察值彼此的接近程度同一处理的观察值与其真值的接近程度2.重复和区组:试验中同一处理的试验单元数将试验空间按照变异大小分成若干个相对均匀的局部,每个局部就叫一个区组3回归分析和相关分析:对能够明确区分自变数和因变数的两变数的相关关系的统计方法:对不能够明确区分自变数和因变数的两变数的相关关系的统计方法4.总体和样本:具有共同性质的个体组成的集合从总体中随机抽取的若干个个体做成的总体5.试验单元和试验空间:试验中能够实施不同处理的最小试验单元所有试验单元构成的空间二、填空:(20分)1.资料常见的特征数有:(3空)算术平均数方差变异系数2.划分数量性状因子的水平时,常用的方法:等差法等比法随机法(3空)3.方差分析的三个基本假定是(3空)可加性正态性同质性4.要使试验方案具有严密的可比性,必须(2空)遵循“单一差异”原则设置对照5.减小难控误差的原则是(3空)设置重复随机排列局部控制6.在顺序排列法中,为了避免同一处理排列在同一列的可能,不同重复内各处理的排列方式常采用(2空)逆向式阶梯式7.正确的取样技术主要包括:()确定合适的样本容量采用正确的取样方法8.在直线相关分析中,用(相关系数)表示相关的性质,用(决定系数)表示相关的程度。
三、选择:(20分)1试验因素对试验指标所引起的增加或者减少的作用,称作(C)A、主要效应B、交互效应C、试验效应D、简单效应2.统计推断的目的是用(A)A、样本推总体B、总体推样本C、样本推样本D、总体推总体3.变异系数的计算方法是(B)4.样本平均数分布的的方差分布等于(A)5.t检验法最多可检验(C)个平均数间的差异显著性。
6.对成数或者百分数资料进行方差分析之前,须先对数据进行(B)A、对数B、反正弦C、平方根D、立方根7.进行回归分析时,一组变量同时可用多个数学模型进行模拟,型的数据统计学标准是(B)A、相关系数B、决定性系数C、回归系数D、变异系数8.进行两尾测验时,u0.10=1.64,u0.05=1.96,u0.01=2.58,那么进行单尾检验,u0.05=(A)9.进行多重比较时,几种方法的严格程度(LSD\SSR\Q)B10.自变量X与因变量Y之间的相关系数为0.9054,则Y的总变异中可由X与Y的回归关系解释的比例为(C)A、0.9054B、0.0946C、0.8197D、0.0089四、简答题:(15分)1.回归分析和相关分析的基本内容是什么?(6分)配置回归方程,对回归方程进行检验,分析多个自变量的主次效益,利用回归方程进行预测预报:计算相关系数,对相关系数进行检验2.一个品种比较试验,4个新品种外加1个对照品种,拟安排在一块具有纵向肥力差异的地块中,3次重复(区组),各重复内均随机排列。
请画出田间排列示意图。
(2分)3.田间试验中,难控误差有哪些?(4分)土壤肥力,小气候,相邻群体间的竞争差异,同一群体内个体间的竞争差异。
4随即取样法包括哪几种方式?(3分)简单随机取样法分层随机取样法整群简单随机取样法五、计算题(25分)1.研究变数x与y之间的关系,测得30组数据,经计算得出:x均值=10,y均值=20,l xy=60, l yy=300,r=0.6。
根据所得数据建立直线回归方程。
(5分)a=2 b=1.8 y=2+1.8 x2.完成下列方差分析表,计算出用LSR法进行多重比较时各类数据填下表:总体的株高(3分)4.9株番茄幼苗的平均株高为10cm,标准差为1cm,试对每株番茄幼苗株高作95%的区间估计、一、选择题(每题1分,共10分)1. 在正交实验设计中,试验指标是()A. 定量的B. 定性的C. 两者皆可2. 在正交实验设计中,定量因素各水平的间距是()A. 相等B. 不相等C. 两者皆可3. U7(74)中括号中的7表示()A. 最多允许安排因素的个数B. 因素水平数C. 正交表的横行数D. 总的实验次数4. 以下不属于简单比较法的缺点的是()A. 选点代表性差B. 无法考察交互作用C. 提供信息不够丰富D. 实验次数多5. L8(27)中的7代表()A. 最多允许安排因素的个数B. 因素水平数C. 正交表的横行数D. 总的实验次数6. 在L9(34)表中,有A,B,C三个因素需要安排。
则它们应该安排在()列A. 1,2,3B. 2,3,4C. 3,4,5D. 任意3列7. 三水平因素间的交互作用在正交表中需占用()列。
A. 5B. 4C. 3D. 28. 交互作用对实验结果的影响是()A. 增强B.减弱C.两者皆可能D.无影响9. 在一个正交实验中,因素A和B的水平数都为3,那么A和B的交互作用的自由度为()A. 6B. 1C. 4D. 210. 用L8(27)进行正交实验设计,若因素A和B安排在第1、2列,则A×B,应排在第()列。
A. 3B. 4C. 5D. 6二、判断题(每题1分,共10分)1. 在确定工艺条件时,对主要因素和次要因素均选取最优条件。
()2. 某列算出的极差的大小,反映了该列所排因素选取的水平变动对指标影响的大小。
()3. 在正交试验中,为了便于分析试验结果,凡遇到定性指标总把它加以定量化处理。
()4. 要考虑的因素及交互作用的自由度总和必须不大于所选正交表的总自由度。
()5. 正交实验中,若某号实验根据专业知识可以肯定其实验结果不理想,则可以略去不做。
()6. 多项式回归分析中,阶数越高,回归方程的精度越高。
()7. 在多元线性回归中,偏回归系数本身的大小直接反映了自变量的相对重要性。
()8. 对于拟水平正交试验,即使没有空白列,误差的离差平方和与自由度也不为零。
()9. 在同样的误差程度下,测得数据越多,计算出的离差平方和就越大。
()10. 拟水平法既可以对一个因素虚拟水平,也可以对多个因素虚拟水平。
()三、填空题(每空1分,共20分)1. 数据6.0×104μm的有位有效数字,测量仪器的最小刻度单位为。
2. 误差根据其性质或产生的原因,可分为、和。
3. 用正交表安排试验具有和的特征。
4. 多指标正交实验的分析方法有两种:和。
5. 单因素试验方差分析中,组间离差平方和反映了,组内离差平方和是反映。
6. 在一元线形回归分析中,回归平方和表示的是,残差平方和表示的是。
7. 某试验考虑A,B,C,D四个因素,每个因素取3个水平,并且考虑3个交互作用A×B,A×C,A×D,则应选择的合适正交表为,误差自由度为。
8. 在因素数为3,水平数为5的试验中,若采用正交设计来安排试验,则至少要做次试验,若采用均匀设计,则只需做次试验,若采用全面试验法,则需做次试验。
9. 精度为1.5级,量程为0.2MPa的弹簧管式压力表的最大绝对误差为kPa,今用其测得大约8kPa(表压)的空气压力,则其最大相对误差为。
四、计算题(共60分)1. 一种物质吸附另一种物质的能力与温度有关,在不同温度下测得吸附的重量及相关计算值如表所示。
试求:(1)吸附量y关于温度x的一元线性回归方程;(2)相关系数,回归平方和以及残差的标准误差;(3)若实际中需把y 控制在区间(10,13)内,则变量x应控制在什么区间内?(显著性水平0.05)(20分)2. 已知某合成试验的反应温度范围为340~420℃,通过单因素优选法得到:温度为400℃时,产品的合成率高,如果使用的是0.618法,试写出5个试验点的位置。
假设在试验范围内合成率是温度的单峰函数。
(10分)3. 对同一铜合金,有10个分析人员分别进行分析,测得其中铜(%)含量的数据为:62.20,69.49,70.30,70.35,70.82,71.03,71.22,71.25,71.33,71.38。
试用格拉布斯准则进行检验数据62.20是否应该被舍去?(α=0.05)(10分)4. 某工厂为了提高某产品的收率,根据经验和分析,选取反应温度(A )、碱用量(B )和催化剂种类(C )3个因素的3个水平进行正交试验,不考虑交互作用,试验方案及结果(收率/%)如表所示。
试用直观分析法确定因素主次和优方案,并画出趋势图。
(20分)一、填空题(共25分)1.根据误差产生的原因,误差可分为 随机 误差、 系统 误差和 过失 误差三大类。
其中 过失 误差是一种显然与事实不符的误差。
2.秩和检验法是用来检验A 、B 两组数据是否存在显著性差异的一种方法。
假设A 组数据无系统误差,如果A 与B 有显著性差异,则认为B 有 系统误差;如果A 与B 无显著性差异,则认为B 无 系统误差。
3.列出三种常用的数据图: 线图 、 条形图 、 圆形图 。
4.在回归分析中,设i y 、y 、i y 分别为试验值、算术平均值和回归值,则21()ni i i y y =-∑称为 残差 平方和,21()nii yy =-∑称为 回归 平方和。
5.在试验设计中,黄金分割法是在试验区间内取两个试验点,这两个试验点分别是该试验区间的 0.618 倍和 0.382 倍。
6.L 8(41×24)是一个 正交设计(或混合水平正交设计) 试验表,其中8是 试验次数 (或横行数) ,它可以安排4水平的因素 1 个, 2 水平的因素 4 个,共 5 个因素的试验。
二、简答题(共20分)1.回归分析的用途是什么?写出用Excel 软件进行回归分析时的操作步骤。
(10分)答:(1)回归分析是一种变量之间相关关系最常用的统计方法,用它可以寻找隐藏在随机性后面的统计规律。
通过回归分析可以确定回归方程,检验回归方程的可靠性等。
(2)用Excel 软件进行回归分析时的操作步骤是:① 从工具菜单中选择数据分析,则会弹出数据分析对话框,然后在分析工具库中选择回归选项,单击确定之后,弹出回归对话框。
② 填写回归对话框。
③ 填好回归对话框后,点击确定,即可得到回归分析的结果。
2.正交试验设计的基本步骤有哪些? (10分) 答:(1)明确试验目的,确定评价指标; (2)挑选因素,确定水平(3)选正交表,进行表头设计; (4)明确试验方案,进行试验,得到结果; (5)对试验结果进行统计分析; (6)进行验证试验,作进一步分析。
三、计算题(共30分)1.设间接测定值y 与直接测定值存在的关系为y = a x 1 x 2,如果x 1和x 2的相对误差分别为Δx 1/x 1和Δx 2/x 2,试计算y 的相对误差。
(8分) 解:(1)求误差传递系数:21y ax x ∂=∂ 12yax x ∂=∂ (4分) (2)求y 的相对误差:12112n i i i x x x y y y y y x y x y x y =∆∆∆∆∂∂∂=⋅=⋅+⋅∂∂∂∑=121221121212x x x xax ax ax x ax x x x ∆∆∆∆⋅+=+ (4分)2.已知因素A 和因素B 是影响试验结果的两个主要因素。
