苏北四市2018届高三第一次调研测试数学试题
江苏省苏北四市2018届高三第一次模拟考试

江苏省苏北四市2018 届高三第一次模拟考试数学参考答案及评分标准1. {-1,0,1}2. 13. (0,1]4. 135. 7506.78549.410.11.11 ..12. [ -1,+1] 13 . [-2,2]14. -15 . (1) 在△ABC中 ,由 cos A= ,得A为锐角 ,所以 sin A=-= ,所以 tan A== ,(2 分)所以 tan B=tan[( B-A)+A]= --(4 分) -==3.(6 分) -(2)在△ABC 中,由tan B=3,得 sin B=,cos B=,(8 分)所以 sin C=sin( A+B)=sin A cos B+ cos A sin B=.(10 分)由正弦定理=,得 b===15,(12 分)所以△ABC 的面积为 S= bc sin A= ×15×13×=78 .(14 分)16 . (1) 如图 , 取AB的中点P, 连接PM,PB1.因为 M,P 分别是 AB,AC 的中点,所以 PM∥BC,且 PM= BC.在直三棱柱 ABC- A1B1C1中,BC∥B1C1,BC=B 1C1,又因为N 是 1 1的中点,B C所以 PM∥B1N,且 PM=B1 N,(2 分)所以四边形 PMNB 1是平行四边形,所以∥ 1.(4分 ) MN PB因为 MN?平面 ABB1A1,PB1?平面 ABB1A1,所以 MN∥平面ABB1A1.(6分 )(2)因为三棱柱 ABC-A1B1C1为直三棱柱,所以 BB1⊥平面 A1B1C1,(第 16 题)又因为 BB1?平面 ABB1A1,所以平面 ABB1A1⊥平面 A1 B1C1 .(8 分)因为∠ABC=90°,所以 B1C1⊥B1A1,平面11∩平面1111A1, 1 1?平面111,ABB A ABC=B B C A B C所以 B1 C1⊥平面ABB1 A1 .(10 分)又因为 A1B?平面 ABB1A1,所以 B1 C1⊥A1B,即 NB 1⊥A1 B.如图 ,连接AB1,因为在平行四边形 ABB1 A1中,AB=AA1,所以 AB1⊥A1 B.又因为 NB 1∩AB1=B 1,且 AB1,NB 1?平面 AB1 N,所以 1 ⊥平面 1 ,(12 分)A B AB N因为 AN?平面 AB1N,所以 A1 B⊥AN.(14 分)(第 17题)17 . (1)如图 ,设AO交BC于点D,过点O作OE⊥AB,垂足为 E.在△AOE 中,AE=10cosθ,AB=2 AE=20cosθ,(2 分)在△ABD 中,BD=AB ·sinθ=20cosθ·sinθ,(4 分)所以S=· 2π·20sin ·cos ·20cos400π·sin cos 2θ.(6 分)θ θθ=θ(2)要使侧面积最大 ,由 (1)得 ,S=θθ=θ-θ.(8 分)400π sin cos 2400π(sin sin 3)设 f(x)=x-x3(0 <x<1),则 f' (x)=1 -3 x2,由 f' (x)=1-3x2=0,得 x= .当 x∈时,f'(x)>0;当 x∈时,f'(x)<0,所以 f(x)在区间上单调递增,在区间上单调递减,所以 f(x)在 x=时取得极大值,也是最大值,所以当 sin θ=时 ,侧面积S取得最大值.此时等腰三角形的腰长AB=20cos20 -=20 -=.θ=答: 侧面积S取得最大值时 ,等腰三角形的腰AB 的长度为cm .18 . (1) 设椭圆的方程为+ =1( a>b>0),由题意知解得所以椭圆的方程为+=1 .(2) 若AF=FC,由椭圆的对称性 , 知A,所以B--,此时直线BF的方程为 34 3 0.x- y-=--得 7 x2-6 x-13 =0,由解得 x=( x=-1 舍去 ),- -故== .-(3)设 A(x0,y0),则 B(-x0,-y0),直线 AF 的方程为 y=-(x-1),代入椭圆的方程+ =1,2-8-15+24 x =0 .得(15 -6 x ) x00因为0 是该方程的一个解,所以C 点的横坐标C-.x=x x =-又 C( x C,y C)在直线 y=-(x-1) 上 ,(11 分)(14 分)(2 分)(4 分)(6 分)(8 分)(10 分)(12 分)-所以 y C= -( x C-1) = -.同理 ,点D的坐标为,(14分 )--所以2=-= 1 ,k-= k--即存在 m= ,使得 k2 = k1 .(16分 ) 19 . (1) 函数h( x)的定义域为 (0,+∞).当 a= 1时, h(x)=f(x)-g(x)=x2 +x-ln x+2,所以 ()2 1-,(2 分) h' x = x+ - =所以当 0 <x<时 ,h'(x)<0;当 x> 时,h'(x)>0,所以函数h(x)在区间上单调递减,在区间上单调递增,所以当x=时,函数()取得极小值ln2, 无极大值.(4 分)h x+(2)设函数 f(x)上点( x1,f(x1))与函数 g(x)上点(x2,g(x2))处切线相同, 则(1)(2)-,f' x=g' x=-所以 2x1+a==--(6 分) -,所以 x1=-,代入-=11(ln2-a), +ax +- x得 - +ln x2+ -a-2=0 .(*)(8 分)设 F (x)= - +ln x+ -a- 2,则 F'( x)=- + + =- .不妨设 2+ax0-1=0( x0>0),则当 0<x<x0时 ,F'(x)<0;当 x>x 0时,F'(x) >0,所以 F(x)在区间(0,x0)上单调递减,在区间(x0,+∞)上单调递增,(10 分)代入 a= - = -2x 0 ,得 F (x )min =F ( x 0)= +2x 0 - +ln x 0-2 .设 G (x )=x 2 +2 x- +ln x-2, 则 G'(x ) =2 x+2+ + >0 对 x>0 恒成立 ,所以 ( )在区间 (0,)上单调递增 . 又G (1)=0,G x+∞所以当 0 <x ≤1 时 , G ( x )≤0,即当 0 0≤1 时, ( 0)≤0 .(12 分)<xF x又当 x=e a+2 时,F (x )= -+lne a+2 + -a-2 =- ≥0.(14 分)因此当 0 <x 0≤1 时,函数 F (x )必有零点 ,即当 0 <x 0≤1 时 ,必存在 x 2 使得 ( *)成立 ,即存在 x 1 ,x 2 使得函数 f (x )上点 (x 1 ,f (x 1))与函数 g (x )上点 (x 2, g ( x 2)) 处切线相同 .又由 2 x , 得y'=- 2 0,y= -- <所以 y= -2 x 在(0,1) 上单调递减 ,因此 a= -= -2x 0 ∈[-1,+∞),所以实数 a 的取值范围是 [-1,+∞).(16 分)20 .(1) 若 0, 4,则 n 4 n- 1( ≥2),λ=μ= S = a n所以 a n+1=S n+1 -S n =4( a n -a n- 1),即 a n+1-2a n =2(a n -2a n-1 ), 所以 b =2 b 1.(2 分)n n-又由12, 1 24 1,a = a +a = a得 a 2=3 a 1=6,a 2 -2 a 1 =2 ≠0, 即 b n ≠0,所以2,故数列 {n }是等比数列.(4 分)=b-(2) 若{a n }是等比数列 , 设其公比为 q (q ≠0),当 n= 2 时, S 2 =2λa 2+μa 1,即 a 1 +a 2=2λa 2+μa 1,得1+q=2λ q+μ; ①22当 n= 3 时, S 3 =3λa 3+μa 2,即 a 1 +a 2+a 3 =3 λa 3+μa 2,得 1+q+q =3λq +μq ; ②当 n= 4时, 4 4 43,即 1 2 3 4 4 43 ,得 1 23 4 32③S =λa +μaa +a +a +a= λa +μa +q+q +q = λq +μq .2②-①×q ,得 1 =λq ,③-②×q ,得 13 ,=λq解得 q=1,λ=1.代入① 式 ,得 0(8 分)μ=.此时 S n =na n (n ≥2),所以n1 2,数列 { n }是公比为 1的等比数列 ,a=a =a故 λ=1,μ=0.(10 分)(3) 若 a 2=3,由 a 1+a 2+2λa 2+μa 1, 得 5 =6λ+2μ,又,解得 , 1 (12 分)λ +μ= λ=μ=.由 a 1=2,a 2 =3,λ=,μ=1,代入 S n =λ na+μa n-1 ,得 a 3=4, 所以 a 1,a 2 ,a 3 成等差数列 .由 S n = a n +a n-1 ,得 S n+1 = a n+1 +a n ,两式相减 ,得 an+1 = an+1 - a +a -a n- 1 ,n n即( n-1)a n+1 -( n-2)a n -2a n-1 =0, 所以 na n+2 -(n-1) a n+1 -2a n =0,相减 ,得na n+ 2 2( 1) a n+1 ( 2) n 2 n 2n-10,- n- + n- a - a + a =所以 n (a n+2-2 a n+ 1 +a n )+2( a n+1-2a n +a n- 1) =0,- -所以 (a n+2-2a n+1 +a n ) =- (a n+1-2a n +a n-1 )=(a n -2 a n-1+a n-2 )= =·(a 3-2a 2+a 1 ).(14 分 )--因为1 2 2+a 3 0,所以an+ 2 2 n+1n0,a - a = - a+a =故数列 { a } 是等差数列 .(16 分 )n江苏省苏北四市 2018 届高三第一次模拟考试数学附加题参考答案及评分标准21 . A. 连接 AD. 因为 AB 为圆的直径 ,所以 AD ⊥BD , 又 EF ⊥AB ,则 A ,D ,E ,F 四点共圆 ,所以· ·(5 分)BD BE=BA BF.又△∽△,ABCAEF所以 = ,即 AB ·AF=AE ·AC ,所以· · · ··( ) 2. (10 分 )BE BD-AE AC=BA BF-AB AF=AB BF-AF=ABB. 因为 M=BA= =-(5 分 )- ,-所以 M - 1=.(10 分)- -C. 把直线方程 l :化成普通方程为 x+y= 2.(3 分)-2ρcos θ-2 ρsin θ=0 2 2-2 y=0,将圆 C :ρ+2 化成普通方程为 x +2x+y即( x+1) 2+( y-1) 2=2.(6 分)圆心 C 到直线 l 的距离为 d==,所以直线 l 与圆 C 相切 . (10 分 )D.因为 [(1 +a)+(1+b)+(1+c )+(1 +d)]·≥=(a+b+c+d )2=1,(5 分)又(1 +a)+(1 +b) +(1 +c)+(1 +d)=5,所以+++≥ .(10 分) 22 . (1)因为 AB=1,AA1=2,则 F(0,0,0), A,C -,B,E,所以=(-1,0,0),= -. (2分)记直线 AC 和 BE 所成的角为α,则 cos cos<,>|α =|=-=, -所以直线 AC 和 BE 所成角的余弦值为.(4 分) (2)设平面 BFC1的法向量为 m=(x1,y1, z1),因为=,=-,则-取 x1=4,得 m=(4,0,1) .(6 分)设平面BCC 1 的法向量为(2, 2, 2 ),n= x y z因为=,=(0,0,2),则取 x2=,得n=(,-1,0) .(8 分) -所以 cos <m, n>=-=.根据图形可知二面角 F -BC 1-C 为锐二面角,所以二面角-1-的余弦值为.(10 分)F BC C23 . (1) 因为抛物线 C 的方程为 y2 =4x,所以 F 的坐标为(1,0),设 M(m, n),因为圆 M 与 x 轴、直线 l 都相切,l 平行于 x 轴,所以圆M 的半径为|n|,点(2,2),P n n则直线 PF 的方程为= --,即 2 n(x-1) -y(n2-1) =0,(2 分)所以---=|n|,又,≠0,-m n所以22121,即n2-m+10,|m-n - |=n +=所以 E 的方程为 y2=x- 1( y≠0).(4 分) (2) 设Q(t2+1, t), A(0,y1 ),B(0,y2),由(1) 知, 点Q处的切线l1的斜率存在 ,由对称性不妨设t>0,由 y'=,所以k AQ=-=-- ,,k BQ==-2--所以1= -, 2233,(6 分)y y =t +t所以 AB=-=2t3+ t+ (t>0) .(8 分)令 f(t)=2t3+ t+ ,t>0,则 f' (t)=6 t2 + -=-,由 f' (t)>0,得 t>-;由 f' (t)<0,得0<t<所以 f(t)在区间-,-上单调递减 ,在-上单调递增 ,所以当-时 , ()取得极小值也是最小值,即AB 取得最小值 ,t= f t此时 s=t2 +1=.(10 分)。
2018届高三苏北四市第一次期末调研考试数学

连云港市2017-2018学年度高三第一次质量检测数学I 参考答案与评分标准一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置........ 1.{1,0,1} 2.1 3.(0,1] 4.13 5.750 67.598.54 9.4 1011.11 12.1] 13.[2,2] 14.277二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答..........,解答时应写出文字说明、证明过程或计算步骤.15.(1)在ABC △中,由3cos 5A ,得A为锐角,所以4sin 5A ,所以sin 4tan cos 3A A A ,………………………………………………………………2分所以tan()tan tan tan[()]1tan()tan B A AB B A A B A A. ………………………………4分1433314133…………………………………………………………6分 (2)在三角形ABC 中,由tan 3B ,所以sin B B, ………………………………………………8分由sin sin()sin cos cos sin C A B A B A B ,…………………………10分由正弦定理sin sin b c B C,得13sin sin c B b C ,………………………12分 所以ABC △的面积114sin 151378225S bc A . …………………………14分16.(1)证明:取AB 的中点P ,连结1,.PM PB因为,M P 分别是,AB AC 的中点,所以//,PM BC 且1.2PM BC在直三棱柱111ABC A B C 中,11//BC B C ,11BC B C , 又因为N 是11B C 的中点,所以1//,PM B N 且1PM B N . …………………………………………2分 所以四边形1PMNB 是平行四边形,所以1//MN PB , ………………………………………………………………4分而MN 平面11ABB A ,1PB 平面11ABB A ,所以//MN 平面11ABB A . ……………………………………………………6分 (2)证明:因为三棱柱111ABC A B C 为直三棱柱,所以1BB 面111A B C , 又因为1BB 面11ABB A ,所以面11ABB A 面111A B C , …………………8分 又因为90ABC,所以1111B C B A ,面11ABB A 面11111=A B C B A ,11111B C A B C 平面, 所以11B C 面11ABB A , ………………………10分 又因为1A B 面11ABB A , 所以111B C A B ,即11NB A B ,连结1AB ,因为在平行四边形11ABB A 中,1=AB AA , 所以11AB A B ,又因为111=NB AB B ,且1AB ,1NB 面1AB N ,所以1A B 面1AB N ,……………………………………………………………………12分 而AN 面1AB N ,所以1A B AN .……………………………………………………………………………14分 17.(1)设AO 交BC 于点D ,过O 作OE AB ,垂足为E ,在AOE 中,10cos AE ,220cos AB AE , …………………………………………………………2分在ABD 中,sin 20cos sin BD AB ,…………………………………………………………4分所以1220sin cos 20cos 2S2400sin cos ,(0)2……………………6分(2)要使侧面积最大,由(1)得:23400sin cos 400(sin sin )S …………8分设3(),(01)f x x x x 则2()13f x x ,由2()130f x x得:x当x 时,()0f x,当x 时,()0f x 所以()f x在区间上单调递增,在区间上单调递减, 所以()f x在x 时取得极大值,也是最大值;所以当sin 时,侧面积S 取得最大值,…………………………11分此时等腰三角形的腰长20cos AB(第16题)1答:侧面积S 取得最大值时,等腰三角形的腰AB.…………14分 18.(1)设椭圆方程为22221(0)x y a b a b ,由题意知:22121914c a a b ……………2分解之得:2a b ,所以椭圆方程为:22143x y ……………………………4分(2)若AF FC ,由椭圆对称性,知3(1,)2 A ,所以3(1,)2B ,此时直线BF 方程为3430x y , ……………………………………………6分由223430,1,43x y x y,得276130x x ,解得137x (1x 舍去),…………8分故1(1)713317BF FD .…………………………………………………………………10分(3)设00,)A x y (,则00(,)B x y ,直线AF 的方程为00(1)1y y x x ,代入椭圆方程22143x y,得 2220000(156)815240x x y x x , 因为0x x 是该方程的一个解,所以C 点的横坐标08552C x x x ,…………………12分又(,)c C C x y 在直线00(1)1y y x x 上,所以00003(1)152C c y y y x x x , 同理,D 点坐标为0085(52x x ,0352y x , ……………………………………………14分所以000002100000335552528585335252y y y x x k k x x x x x, 即存在53m ,使得2153k k . ………………………………………………………16分19.(1)函数()h x 的定义域为(0,)当1a 时,2()()()ln 2h x f x g x x x x ,所以1(21)(1)()21x x h x x x x………………………………………………2分 所以当102x 时,()0h x ,当12x 时,()0h x ,所以函数()h x 在区间1(0,2单调递减,在区间1(,)2单调递增,所以当12x 时,函数()h x 取得极小值为11+ln 24,无极大值;…………………4分(2)设函数()f x 上点11(,())x f x 与函数()g x 上点22(,())x g x 处切线相同,则121212()()()()f x g x f x g x x x所以211212121(ln )12x ax x a x a x x x……………………………………6分 所以12122ax x ,代入21211221(ln )x x x ax x a x 得:222221ln 20(*)424a a x a x x ………………………………………………8分 设221()ln 2424a a F x x a x x ,则23231121()222a x ax F x x x x x 不妨设2000210(0)x ax x 则当00x x 时,()0F x ,当0x x 时,()0F x 所以()F x 在区间0(0,)x 上单调递减,在区间0(,)x 上单调递增,……………10分 代入20000121=2x a x x x 可得:2min 000001()()2ln 2F x F x x x x x设21()2ln 2G x x x x x ,则211()220G x x x x对0x 恒成立,所以()G x 在区间(0,) 上单调递增,又(1)=0G所以当01x ≤时()0G x ≤,即当001x ≤时0()0F x ≤, ……………12分又当2a x e时222421()ln 2424a a a a a F x e a e e2211()04a a e≥ ……………………………………14分 因此当001x ≤时,函数()F x 必有零点;即当001x ≤时,必存在2x 使得(*)成立; 即存在12,x x 使得函数()f x 上点11(,())x f x 与函数()g x 上点22(,())x g x 处切线相同.又由12y x x 得:2120y x所以12(0,1)y x x在单调递减,因此20000121=2[1+)x a x x x ,所以实数a 的取值范围是[1,) .…………………………………………………16分 20.(1)证明:若=0,4 ,则当14n n S a (2n ≥),所以1114()n n n n n a S S a a , 即1122(2)n n n n a a a a ,所以12n n b b , ……………………………………………………………2分 又由12a ,1214a a a ,得2136a a ,21220a a ,即0n b ,所以12n n bb ,故数列{}n b 是等比数列.……………………………………………………………4分 (2)若{}n a 是等比数列,设其公比为q (0q ),当2n 时,2212S a a ,即12212a a a a ,得12q q , ① 当3n 时,3323S a a ,即123323a a a a a ,得 2213q q q q , ② 当4n 时,4434S a a ,即1234434a a a a a a ,得 233214+q q q q q , ③ ② ① q ,得21q ,③ ② q ,得31q , 解得1,1 q .代入①式,得0 .…………………………………………………………………8分 此时n n S na (2n ≥),所以12n a a ,{}n a 是公比为1的等比数列,故10 ,. ……………………………………………………………………10分 (3)证明:若23a ,由12212a a a a ,得562 , 又32,解得112,.…………………………………………………12分 由12a ,23a ,12 ,1 ,代入1n n n S na a 得34a ,所以1a ,2a ,3a 成等差数列,由12n n n n S a a ,得:1112n n n n S a a ,两式相减得:111122n n n n n n na a a a a 即11(1)(2)20n n n n a n a a 所以21(1)20n n n na n a a相减得:2112(1)(2)220n n n n n na n a n a a a 所以2111(2)2(2)0n n n n n n n a a a a a a所以221111-222(2)(2)(2)(1)n n n n n n n n n a a a a a a a a a n n n1321(2)(2)(1)2n a a a n n , ……………………………………14分因为12320a a a ,所以2120n n n a a a ,即数列{}n a 是等差数列.………………………………………………………………16分。
最新-江苏省苏北四市(徐、连、宿、淮)2018届高三数学
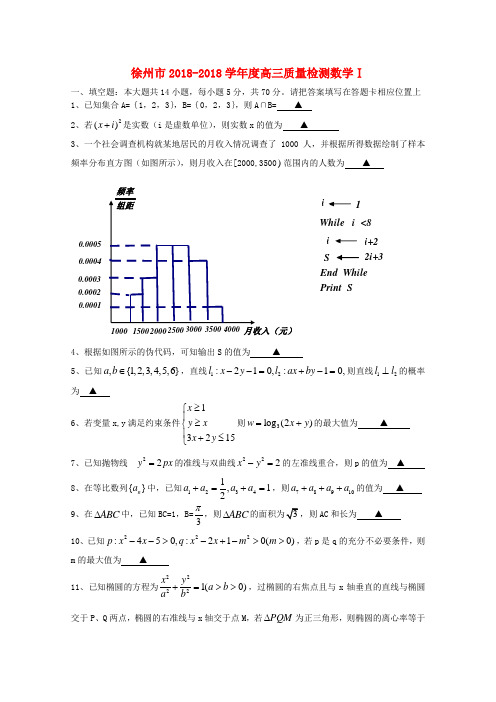
徐州市2018-2018学年度高三质量检测数学Ⅰ一、填空题:本大题共14小题,每小题5分,共70分。
请把答案填写在答题卡相应位置上 1、已知集合A={1,2,3},B={0,2,3},则A ∩B= ▲ 2、若2()x i +是实数(i 是虚数单位),则实数x 的值为 ▲3、一个社会调查机构就某地居民的月收入情况调查了1000人,并根据所得数据绘制了样本频率分布直方图(如图所示),则月收入在[2000,3500)范围内的人数为 ▲4、根据如图所示的伪代码,可知输出S 的值为 ▲5、已知,{1,2,3,4,5,6}a b ∈,直线12:210,:10,l x y l ax by --=+-=则直线12l l ⊥的概率为 ▲6、若变量x,y 满足约束条件13215x y x x y ≥⎧⎪≥⎨⎪+≤⎩则3log (2)w x y =+的最大值为 ▲7、已知抛物线22y px =的准线与双曲线222x y -=的左准线重合,则p 的值为 ▲8、在等比数列{}n a 中,已知12341,12a a a a +=+=,则78910a a a a +++的值为 ▲ 9、在ABC ∆中,已知BC=1,B=3π,则ABC ∆AC 和长为 ▲ 10、已知222:450,:210(0)p x x q x x m m -->-+->>,若p 是q 的充分不必要条件,则m 的最大值为 ▲11、已知椭圆的方程为22221(0)x y a b a b+=>>,过椭圆的右焦点且与x 轴垂直的直线与椭圆交于P 、Q 两点,椭圆的右准线与x 轴交于点M ,若P Q M ∆为正三角形,则椭圆的离心率等于月收入(元)40003500300025002000150010000.00050.00040.00030.00020.0001频率组距Print SEnd While 2i+3Si+2i<8While i 1i▲12、函数()cos()(0)f x a ax a θ=+>图象上两相邻的最低点与最高点之间的最小值是 ▲ 13、定义在R 上的()f x ,满足22()()2[()],,,f m n f m f n m n R +=+∈且(1)0f ≠,则(2012)f 的值 为 ▲14、已知函数111,[0,)22()12,[,2)2x x x f x x -⎧+∈⎪⎪=⎨⎪∈⎪⎩若存在12,x x ,当1202x x ≤<<时,12()()f x f x =,则12()x f x 的取值范围是 ▲二、解答题:本大题共6小题,共90分。
2018年江苏省高考数学一模试卷(解析卷)
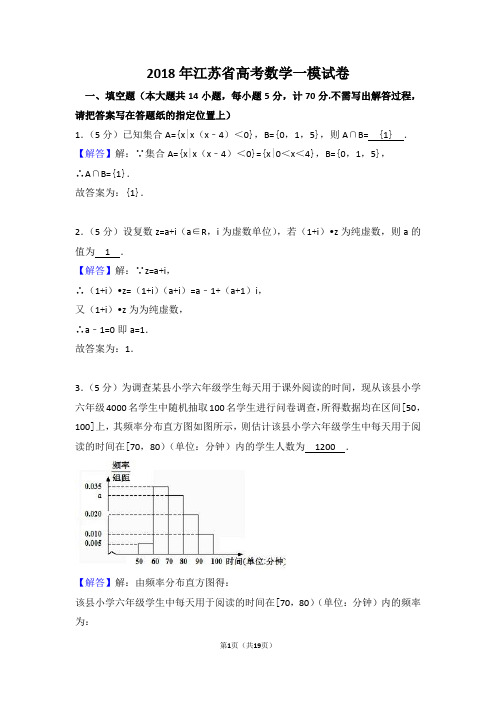
2018年江苏省高考数学一模试卷一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.(5分)已知集合A={x|x(x﹣4)<0},B={0,1,5},则A∩B={1} .【解答】解:∵集合A={x|x(x﹣4)<0}={x|0<x<4},B={0,1,5},∴A∩B={1}.故答案为:{1}.2.(5分)设复数z=a+i(a∈R,i为虚数单位),若(1+i)•z为纯虚数,则a的值为1.【解答】解:∵z=a+i,∴(1+i)•z=(1+i)(a+i)=a﹣1+(a+1)i,又(1+i)•z为为纯虚数,∴a﹣1=0即a=1.故答案为:1.3.(5分)为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为1200.【解答】解:由频率分布直方图得:该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的频率为:1﹣(0.005+0.035+0.020+0.010)×10=0.3,∴估计该县小学六年级4000名学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为:4000×0.3=1200.故答案为:1200.4.(5分)执行如图所示的伪代码,若x=0,则输出的y的值为1.【解答】解:根据题意知,执行程序后,输出函数y=,当x=0时,y=e0=1.故答案为:1.5.(5分)口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为.【解答】解:口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,从袋中一次随机摸出2个球,基本事件总数n==6,摸出的2个球的编号之和大于4包含的基本事件有:(1,4),(2,3),(2,4),(3,4),共4个,∴摸出的2个球的编号之和大于4的概率为p=.故答案为:.6.(5分)若抛物线y2=2px的焦点与双曲线的右焦点重合,则实数p 的值为6.【解答】解:∵双曲线的方程,∴a2=4,b2=5,可得c==3,因此双曲线的右焦点为F(3,0),∵抛物线y2=2px(p>0)的焦点与双曲线的右焦点重合,∴=3,解之得p=6.故答案为:6.7.(5分)设函数y=e x﹣a的值域为A,若A⊆[0,+∞),则实数a的取值范围是(﹣∞,2] .【解答】解:函数y=e x﹣a的值域为A∵e x=2,∴值域为A=[2﹣a,+∞).又∵A⊆[0,+∞),∴2﹣a≥0,即a≤2.故答案为:(﹣∞,2].8.(5分)已知锐角α,β满足(tanα﹣1)(tanβ﹣1)=2,则α+β的值为.【解答】解:∵(tanα﹣1)(tanβ﹣1)=2,可得:tanα+tanβ+1=tanαtanβ,∴tan(α+β)=═﹣1,∵锐角α,β,可得:α+β∈(0,π),∴α+β=.故答案为:.9.(5分)若函数y=sinωx在区间[0,2π]上单调递增,则实数ω的取值范围是(0,] .【解答】解:由函数y=sinωx,图象过原点,若ω<0,图象在x轴下方单调递减,∴ω>0,因为y=Sinωx在[0,2π]单调递增,说明其至少在[0,2π]单调递增,则其周期至少8π,∴,即.故答案为:(0,]10.(5分)设S n为等差数列{a n}的前n项和,若{a n}的前2017项中的奇数项和为2018,则S2017的值为4034.【解答】解:因为S n为等差数列{a n}的前n项和,且{a n}的前2017项中的奇数项和为2018,=a1+a3+a5+…+a2017=1009×(a1+a2017)×=2018,得a1+a2017═4.所以S奇则S2017=(a1+a2017)=2017×2=4034故答案为:4034.11.(5分)设函数f(x)是偶函数,当x≥0时,f(x)=,若函数y=f(x)﹣m 有四个不同的零点,则实数m的取值范围是[1,).【解答】解:由0≤x≤3可得f(x)∈[0,],x>3时,f(x)∈(0,1).画出函数y=f(x)与y=m的图象,如图所示,∵函数y=f(x)﹣m有四个不同的零点,∴函数y=f(x)与y=m的图象有4个交点,由图象可得m的取值范围为[1,),故答案为:[1,).12.(5分)在平面直角坐标系xOy中,若直线y=k(x﹣3)上存在一点P,圆x2+(y﹣1)2=1上存在一点Q,满足=3,则实数k的最小值为﹣.【解答】解:【解法一】设P(x1,y1),Q(x2,y2);则y1=k(x1﹣3)①,+(y2﹣1)2=1②;由=3,得,即,代入②得+=9;此方程表示的圆心(0,3)到直线kx﹣y﹣3k=0的距离为d≤r;即≤3,解得﹣≤k≤0.∴实数k的最小值为﹣.【解法二】设P(x,y),Q(x0,y0);则+(y0﹣1)2=1①;由=3,得,即,代入①化简得x2+(y﹣3)2=9;∴点P的轨迹是圆心为(0,3),半径为3的圆的方程,又点P在直线kx﹣y﹣3k=0上,如图所示;则直线与该圆有公共点,即圆心到直线的距离为d≤r;∴≤3,解得﹣≤k≤0;∴实数k的最小值为﹣.故答案为:﹣.13.(5分)如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若A,B,C,D四点均位于图中的“晶格点”处,且A,B的位置所图所示,则的最大值为24.【解答】解:建立如图的直角坐标系,则A(,),B(0,0),那么容易得到C(0,5)时,D的位置可以有三个位置,其中D1(﹣,),D2(﹣,0),D3(﹣,),此时=(﹣,﹣),=(﹣,﹣),=(﹣,﹣5),=(﹣,﹣),则•=21,•=24,•=22.5,则的最大值为24,故答案为:24.14.(5分)若不等式ksin2B+sinAsinC>19sinBsinC对任意△ABC都成立,则实数k的最小值为100.【解答】解:∵ksin2B+sinAsinC>19sinBsinC,由正弦定理可得:kb2+ac>19bc,∴k>,又∵c﹣b<a<b+c,∴﹣b﹣c<﹣a<b﹣c,∴<19+()=20﹣()2=100﹣(﹣10)2,当=10时,20﹣()2取得最大值20×10﹣102=100.∴k≥100,即实数k的最小值为100.故答案为:100二、解答题(共6小题,满分90分)15.(14分)如图所示,在直三棱柱ABC﹣A1B1C1中,CA=CB,点M,N分别是AB,A1B1的中点.(1)求证:BN∥平面A1MC;(2)若A1M⊥AB1,求证:AB1⊥A1C.【解答】证明:(1)因为ABC﹣A1B1C1是直三棱柱,所以AB∥A1B1,且AB=A1B1,又点M,N分别是AB、A1B1的中点,所以MB=A1N,且MB∥A1N.所以四边形A1NBM是平行四边形,从而A1M∥BN.又BN⊄平面A1MC,A1M⊂平面A1MC,所以BN∥平面A1MC;(2)因为ABC﹣A1B1C1是直三棱柱,所以AA1⊥底面ABC,而AA1⊂侧面ABB1A1,所以侧面ABB1A1⊥底面ABC.又CA=CB,且M是AB的中点,所以CM⊥AB.则由侧面ABB1A1⊥底面ABC,侧面ABB1A1∩底面ABC=AB,CM⊥AB,且CM⊂底面ABC,得CM⊥侧面ABB1A1.又AB1⊂侧面ABB1A1,所以AB1⊥CM.又AB1⊥A1M,A1M、MC平面A1MC,且A1M∩MC=M,所以AB1⊥平面A1MC.又A1C⊂平面A1MC,所以AB⊥A1C.16.(14分)在△ABC中,角A,B,C的对边分别为a,b,c 已知c=.(1)若C=2B,求cosB的值;(2)若=,求cos(B)的值.【解答】解:(1)因为c=,则由正弦定理,得sinC=sinB.…(2分)又C=2B,所以sin2B=sinB,即2sinBcosB=sinB.…(4分)又B是△ABC的内角,所以sinB>0,故cosB=.…(6分)(2)因为=,所以cbcosA=bacosC,则由余弦定理,得b2+c2﹣a2=b2+a2﹣c2,得a=c.…(10分)从而cosB==,…(12分)又0<B<π,所以sinB==.从而cos(B+)=cosBcos﹣sinBsin=.…(14分)17.(14分)有一矩形硬纸板材料(厚度忽略不计),一边AB长为6分米,另一边足够长.现从中截取矩形ABCD(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF是以O为圆心、∠EOF=120°的扇形,且弧,分别与边BC,AD相切于点M,N.(1)当BE长为1分米时,求折卷成的包装盒的容积;(2)当BE的长是多少分米时,折卷成的包装盒的容积最大?【解答】解:(1)在图甲中,连接MO交EF于点T.设OE=OF=OM=R,在Rt△OET中,因为∠EOT=∠EOF=60°,所以OT=,则MT=0M﹣OT=.从而BE=MT=,即R=2BE=2.故所得柱体的底面积S=S扇形OEF ﹣S△OEF=πR2﹣R2sin120°=﹣,又所得柱体的高EG=4,所以V=S×EG=﹣4.答:当BE长为1(分米)时,折卷成的包装盒的容积为﹣4立方分米.(2)设BE=x,则R=2x,所以所得柱体的底面积S=S扇形OEF﹣S△OEF=πR2﹣R2sin120°=(﹣)x2,又所得柱体的高EG=6﹣2x,所以V=S×EG=(﹣2)(﹣x3+3x2),其中0<x<3.令f(x)=﹣x3+3x2,0<x<3,则由f′(x)=﹣3x2+6x=﹣3x(x﹣2)=0,解得x=2.列表如下:所以当x=2时,f(x)取得最大值.答:当BE的长为2分米时,折卷成的包装盒的容积最大.18.(16分)如图,在平面直角坐标系xOy中,椭圆C:(a>b>0)的下顶点为B,点M,N是椭圆上异于点B的动点,直线BM,BN分别与x轴交于点P,Q,且点Q是线段OP的中点.当点N运动到点()处时,点Q 的坐标为().(1)求椭圆C的标准方程;(2)设直线MN交y轴于点D,当点M,N均在y轴右侧,且=2时,求直线BM的方程.【解答】解:(1)由N(),点Q的坐标为(),得直线NQ的方程为y=x﹣,令x=0,得点B的坐标为(0,﹣).所以椭圆的方程为+=1.将点N的坐标(,)代入,得+=1,解得a2=4.所以椭圆C的标准方程为+=1.(2):设直线BM的斜率为k(k>0),则直线BM的方程为y=x﹣.在y=kx﹣中,令y=0,得x P=,而点Q是线段OP的中点,所以x Q=.所以直线BN的斜率k BN=k BQ==2k.联立,消去y,得(3+4k2)x2﹣8kx=0,解得x M=.用2k代k,得x N=.又=2,所以x N=2(x M﹣x N),得2x M=3x N,故2×==3×,又k>0,解得k=.所以直线BM的方程为y=x﹣19.(16分)设数列{a n}满足a=a n+1a n﹣1+λ(a2﹣a1)2,其中n≥2,且n∈N,λ为常数.(1)若{a n}是等差数列,且公差d≠0,求λ的值;(2)若a1=1,a2=2,a3=4,且存在r∈[3,7],使得m•a n≥n﹣r对任意的n∈N*都成立,求m的最小值;=a n对任意(3)若λ≠0,且数列{a n}不是常数列,如果存在正整数T,使得a n+T的n∈N*均成立.求所有满足条件的数列{a n}中T的最小值.【解答】解:(1)由题意,可得a=(a n+d)(a n﹣d)+λd2,化简得(λ﹣1)d2=0,又d≠0,所以λ=1.(2)将a1=1,a2=2,a3=4,代入条件,可得4=1×4+λ,解得λ=0,所以a=a na n﹣1,所以数列{a n}是首项为1,公比q=2的等比数列,+1所以a n=2n﹣1.欲存在r∈[3,7],使得m•2n﹣1≥n﹣r,即r≥n﹣m•2n﹣1对任意n∈N*都成立,则7≥n﹣m•2n﹣1,所以m≥对任意n∈N*都成立.令b n=,则b n+1﹣b n=﹣=,<b n;当n=8时,b9=b8;当n<8时,b n+1>b n.所以当n>8时,b n+1所以b n的最大值为b9=b8=,所以m的最小值为;(3)因为数列{a n}不是常数列,所以T≥2,=a n恒成立,从而a3=a1,a4=a2,①若T=2,则a n+2所以,所以λ(a2﹣a1)2=0,又λ≠0,所以a2=a1,可得{a n}是常数列,矛盾.所以T=2不合题意.②若T=3,取a n=(*),满足a n+3=a n恒成立.由a22=a1a3+λ(a2﹣a1)2,得λ=7.则条件式变为a n2=a n+1a n﹣1+7.由22=1×(﹣3)+7,知a3k﹣12=a3k﹣2a3k+λ(a2﹣a1)2;由(﹣3)2=2×1+7,知a3k2=a3k﹣1a3k+1+λ(a2﹣a1)2;由12=2×(﹣3)+7,知a3k+12=a3k a3k+2+λ(a2﹣a1)2;所以,数列(*)适合题意.所以T的最小值为3.20.(16分)设函数f(x)=lnx,g(x)=ax+(a,b,c∈R).(1)当c=0时,若函数f(x)与g(x)的图象在x=1处有相同的切线,求a,b 的值;(2)当b=3﹣a时,若对任意x0∈(1,+∞)和任意a∈(0,3),总存在不相等的正实数x1,x2,使得g(x1)=g(x2)=f(x0),求c的最小值;(3)当a=1时,设函数y=f(x)与y=g(x)的图象交于A(x1,y1),B(x2,y2)(x1<x2)两点.求证:x1x2﹣x2<b<x1x2﹣x1.【解答】解:(1)由f(x)=lnx,得f(1)=0,又f′(x)=,所以f′(1)=1,当c=0时,g(x)=ax+,所以g′(x)=a﹣,所以g′(1)=a﹣b,因为函数f(x)与g(x)的图象在x=1处有相同的切线,所以,即,解得a=,b=﹣;(2)当x0>1时,则f(x0)>0,又b=3﹣a,设t=f(x0),则题意可转化为方程ax+﹣c=t(t>0)在(0,+∞)上有相异两实根x1,x2.即关于x的方程ax2﹣(c+t)x+(3﹣a)=0(t>0)在(0,+∞)上有相异两实根x1,x2.所以,得,所以c>2﹣t对t∈(0,+∞),a∈(0,3)恒成立.因为0<a<3,所以2≤2•=3(当且仅当a=时取等号),又﹣t<0,所以2﹣t的取值范围是(﹣∞,3),所以c≥3.故c的最小值为3.(3)当a=1时,因为函数f(x)与g(x)的图象交于A,B两点,所以,两式相减,得b=x1x2(1﹣),要证明x1x2﹣x2<b<x1x2﹣x1,即证x1x2﹣x2<x1x2(1﹣)<x1x2﹣x1,即证<<,即证<ln<,即证1﹣<ln<﹣1,令=t,则t>1,此时即证1﹣<lnt<t﹣1.令φ(t)=lnt+﹣1,所以φ′(t)=﹣=>0,所以当t>1时,函数φ(t)单调递增.又φ(1)=0,所以φ(t)=lnt+﹣1>0,即1﹣<lnt成立;再令m(t)=lnt﹣t+1,所以m′(t)=﹣1=<0,所以当t>1时,函数m(t)单调递减,又m(1)=0,所以m(t)=lnt﹣t+1<0,即lnt<t﹣1也成立.综上所述,实数x1,x2满足x1x2﹣x2<b<x1x2﹣x1.[选做题](在21.22.23.24四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内)[选修4-1:几何证明选讲]图21.(10分)如图,已知AB为⊙O的直径,直线DE与⊙O相切于点E,AD垂直DE于点D.若DE=4,求切点E到直径AB的距离EF.【解答】解:如图,连接AE,OE,因为直线DE与⊙O相切于点E,所以DE⊥OE,又因为AD⊥DE于D,所以AD∥OE,所以∠DAE=∠OEA,①在⊙O中,OE=OA,所以∠OEA=∠OAE,②…(5分)由①②得∠DAE=∠OAE,即∠DAE=∠FAE,又∠ADE=∠AFE,AE=AE,所以△ADE≌△AFE,所以DE=FE,又DE=4,所以FE=4,即E到直径AB的距离为4.…(10分)[选修4-2:矩阵与变换]22.(10分)已知矩阵M=,求圆x2+y2=1在矩阵M的变换下所得的曲线方程.【解答】解:设P(x0,y0)是圆x2+y2=1上任意一点,则=1,设点P(x0,y0)在矩阵M对应的变换下所得的点为Q(x,y),则=,即,解得,…(5分)代入=1,得=1,∴圆x2+y2=1在矩阵M的变换下所得的曲线方程为=1.…(10分)[选修4-4:坐标系与参数方程]23.在极坐标系中,直线ρcos(θ+)=1与曲线ρ=r(r>0)相切,求r的值.【解答】解:直线ρcos(θ+)=1,转化为:,曲线ρ=r(r>0)转化为:x2+y2=r2,由于直线和圆相切,则:圆心到直线的距离d=.所以r=1.[选修4-5:不等式选讲]24.已知实数x,y满足x2+3y2=1,求当x+y取最大值时x的值.【解答】解:由柯西不等式,得[x2+()2][12+()2]≥(x•1+)2,即≥(x+y)2.而x2+3y2=1,所以(x+y)2,所以﹣,…(5分)由,得,所以当且仅当x=,y=时,(x+y)max=.所以当x+y取最大值时x值为.…(10分)25.(10分)如图,四棱锥P﹣ABCD的底面ABCD是菱形,AC与BD交于点O,OP⊥底面ABCD,点M为PC中点,AC=4,BD=2,OP=4.(1)求直线AP与BM所成角的余弦值;(2)求平面ABM与平面PAC所成锐二面角的余弦值.【解答】解:(1)因为ABCD是菱形,所以AC⊥BD.又OP⊥底面ABCD,以O为原点,直线OA,OB,OP分别为x轴,y轴,z轴,建立如图所示空间直角坐标系.则A(2,0,0),B(0,1,0),P(0,0,4),C(﹣2,0,0),M(﹣1,0,2).=(﹣2,0,4),=(01,﹣1,2),cos<,>===.故直线AP与BM所成角的余弦值为.…(5分)(2)=(﹣2,1,0),=(﹣1,﹣1,2).设平面ABM的一个法向量为=(x,y,z),则,令x=2,得=(2,4,3).又平面PAC的一个法向量为=(0,1,0),∴cos<>===.故平面ABM与平面PAC所成锐二面角的余弦值为.…(10分)26.(10分)已知n∈N*,nf(n)=C n0C n1+2C n1C n2+…+nC n n﹣1C n n.(1)求f(1),f(2),f(3)的值;(2)试猜想f(n)的表达式(用一个组合数表示),并证明你的猜想.【解答】解:(1)由条件,nf(n)=C C C C①,在①中令n=1,得f(1)=1.在①中令n=2,得2f(2)=6,得f(2)=3.在①中令n=3,得3f(3)=30,故f(3)=10.(2)猜想f(n)=.要证猜想成立,只要证等式n=•+2•+…+n•成立.由(1+x)n=+x+x2+…+x n①,两边同时对x求导数,可得n(1+x)n﹣1=+2x+3x2+n x n﹣1②,把等式①和②相乘,可得n(1+x)2n﹣1=(+x+x2+…+x n)•(+2x+3x2+n x n﹣1)③.等式左边x n的系数为n,等式右边x n的系数为•+•2+•3+…+n•n=•+2•+3•+…+n•=C C C C,根据等式③恒成立,可得n=C C C C.故f(n)=成立.。
2018江苏苏锡常镇四市高三调研(一)数学试题与答案

2017-2018学年度苏锡常镇四市高三教学情况调研(一)数学Ⅰ试题一、填空题:本大题共14个小题,每小题5分,共70分.请把答案填写在答题..卡相应位置上....... 1.已知集合{1,1}A =-,{3,0,1}B =-,则集合AB = .2.已知复数z 满足34z i i ⋅=-(i 为虚数单位),则z = .3.双曲线22143x y -=的渐近线方程为 . 4.某中学共有1800人,其中高二年级的人数为600.现用分层抽样的方法在全校抽取n 人,其中高二年级被抽取的人数为21,则n = .5.将一颗质地均匀的正四面体骰子(每个面上分别写有数字1,2,3,4)先后抛掷2次,观察其朝下一面的数字,则两次数字之和等于6的概率为 .6.如图是一个算法的流程图,则输出S 的值是 .7.若正四棱锥的底面边长为2cm ,侧面积为28cm ,则它的体积为 3cm . 8.设n S 是等差数列{}n a 的前n 项和,若242a a +=,241S S +=,则10a = .9.已知0a >,0b >,且23a b+=,则ab 的最小值是 . 10.设三角形ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知tan 3tan A c bB b-=,则cos A = .11.已知函数,1()4,1x a e x f x x x x ⎧-<⎪=⎨+≥⎪⎩(e 是自然对数的底).若函数()y f x =的最小值是4,则实数a 的取值范围为 .12.在ABC ∆中,点P 是边AB 的中点,已知3CP =4CA =,23ACB π∠=,则CP CA ⋅= .13.已知直线l :20x y -+=与x 轴交于点A ,点P 在直线l 上,圆C :22(2)2x y -+=上有且仅有一个点B 满足AB BP ⊥,则点P 的横坐标的取值集合为 .14.若二次函数2()f x ax bx c =++(0)a >在区间[1,2]上有两个不同的零点,则(1)f a的取值范围为 .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答应写出文字说明、证明过程或演算步骤.15.已知向量(2sin ,1)a α=,(1,sin())4b πα=+.(1)若角α的终边过点(3,4),求a b ⋅的值; (2)若//a b ,求锐角α的大小.16.如图,正三棱柱111ABC A BC -,其底面边长为2.已知点M ,N 分别是棱11AC ,AC 的中点,点D是棱1CC 上靠近C 的三等分点.求证:(1)1//B M 平面1A BN ; (2)AD ⊥平面1A BN .17.已知椭圆C :22221x y a b +=(0)a b >>经过点1)2,(1,)2,点A 是椭圆的下顶点.(1)求椭圆C 的标准方程;(2)过点A 且互相垂直的两直线1l ,2l 与直线y x =分别相交于E ,F 两点,已知OE OF =,求直线1l 的斜率.18.如图,某景区内有一半圆形花圃,其直径AB 为6,O 是圆心,且OC AB ⊥.在OC 上有一座观赏亭Q ,其中23AQC π∠=.计划在BC 上再建一座观赏亭P ,记(0)2POB πθθ∠=<<.(1)当3πθ=时,求OPQ ∠的大小;(2)当OPQ ∠越大,游客在观赏亭P 处的观赏效果越佳,求游客在观赏亭P 处的观赏效果最佳时,角θ的正弦值.19.已知函数32()f x x ax bx c =+++,()ln g x x =.(1)若0a =,2b =-,且()()f x g x ≥恒成立,求实数c 的取值范围; (2)若3b =-,且函数()y f x =在区间(1,1)-上是单调递减函数. ①求实数a 的值;②当2c =时,求函数(),()()()(),()()f x f xg xh x g x f x g x ≥⎧=⎨<⎩的值域.20.已知n S 是数列{}n a 的前n 项和,13a =,且123n n S a +=-*()n N ∈. (1)求数列{}n a 的通项公式;(2)对于正整数i ,j ,()k i j k <<,已知j a λ,6i a ,k a μ成等差数列,求正整数λ,μ的值;(3)设数列{}n b 前n 项和是n T ,且满足:对任意的正整数n ,都有等式12132n n n a b a b a b --++113n n a b ++⋅⋅⋅+=33n --成立.求满足等式13n n T a =的所有正整数n . 2017-2018学年度苏锡常镇四市高三教学情况调研(一)数学Ⅱ(附加题)21.【选做题】在A ,B ,C ,D 四小题中只能选做两题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.A. 选修4-1:几何证明选讲如图,AB 是圆O 的直径,D 为圆O 上一点,过点D 作圆O 的切线交AB 的延长线于点C ,且满足DA DC =.(1)求证:2AB BC =; (2)若2AB =,求线段CD 的长. B. 选修4-2:矩阵与变换 已知矩阵4001A ⎡⎤=⎢⎥⎣⎦,1205B ⎡⎤=⎢⎥⎣⎦,列向量a X b ⎡⎤=⎢⎥⎣⎦. (1)求矩阵AB ;(2)若1151B A X --⎡⎤=⎢⎥⎣⎦,求a ,b 的值. C. 选修4-4:坐标系与参数方程 在极坐标系中,已知圆C经过点)4P π,圆心为直线sin()3πρθ-=点,求圆C 的极坐标方程. D. 选修4-5:不等式选讲已知x ,y 都是正数,且1xy =,求证:22(1)(1)9x y y x ++++≥.【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.22.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,PD 垂直于底面ABCD ,2PD AD AB ==,点Q 为线段PA (不含端点)上一点.(1)当Q 是线段PA 的中点时,求CQ 与平面PBD 所成角的正弦值; (2)已知二面角Q BD P --的正弦值为23,求PQPA的值. 23.在含有n 个元素的集合{1,2,,}n A n =⋅⋅⋅中,若这n 个元素的一个排列(1a ,2a ,…,n a )满足(1,2,,)i a i i n ≠=⋅⋅⋅,则称这个排列为集合n A 的一个错位排列(例如:对于集合3{1,2,3}A =,排列(2,3,1)是3A 的一个错位排列;排列(1,3,2)不是3A 的一个错位排列).记集合n A 的所有错位排列的个数为n D . (1)直接写出1D ,2D ,3D ,4D 的值;(2)当3n ≥时,试用2n D -,1n D -表示n D ,并说明理由; (3)试用数学归纳法证明:*2()n D n N ∈为奇数.2017-2018学年度苏锡常镇四市高三教学情况调研(一)数学Ⅰ试题参考答案一、填空题1. {1}2. 53. y x =4. 635. 3166. 258 9. 10. 1311. 4a e ≥+ 12. 6 13. 1,53⎧⎫⎨⎬⎩⎭14. [0,1)二、解答题15.解:(1)由题意4sin 5α=,3cos 5α=,所以sin()4a b a πα⋅=++sin cos 4παα=+cos sin 4πα+45=+35+=(2)因为//a b ,sin()14a πα+=,α(s i nc o s c o s s i n )144ππαα+=,所以2sin sin cos 1ααα+=,则2sin cos 1sin ααα=-2cos α=,对锐角α有cos 0α≠,所以tan 1α=,所以锐角4πα=.16.证明:(1)连结MN ,正三棱柱111ABC A B C -中,11//AA CC 且11AA CC =,则四边形11AAC C 是平行四边形,因为点M 、N 分别是棱11AC ,AC 的中点,所以1//MN AA 且1MN AA =,又正三棱柱111ABC A B C -中11//AA BB 且11AA BB =,所以1//MN BB 且1MN BB =,所以四边形1MNBB 是平行四边形,所以1//B M BN ,又1B M ⊄平面1A BN ,BN ⊂平面1A BN ,所以1//B M 平面1A BN ;(2)正三棱柱111ABC A B C -中,1AA ⊥平面ABC ,BN ⊂平面ABC ,所以1BN AA ⊥,正ABC ∆中,N 是AB 的中点,所以BN AC ⊥,又1AA 、AC ⊂平面11AAC C ,1AA AC A =,所以BN ⊥平面11AAC C ,又AD ⊂平面11AAC C ,所以AD BN ⊥,由题意,1AA =,2AC =,1AN =,CD =,所以1AA AN AC CD == 又12A AN ACD π∠=∠=,所以1A AN ∆与ACD ∆相似,则1AA N CAD ∠=∠,所以1ANA CAD ∠+∠112ANA AA N π=∠+∠=,则1AD A N ⊥,又1BN A N N =,BN ,1A N ⊂平面1A BN ,所以AD ⊥平面1A BN .17.解:(1)由题意得222231141314a b a b ⎧+=⎪⎪⎨⎪+=⎪⎩,解得2211411a b ⎧=⎪⎪⎨⎪=⎪⎩,所以椭圆C 的标准方程为2214x y +=; (2)由题意知(0,1)A -,直线1l ,2l 的斜率存在且不为零,设直线1l :11y k x =-,与直线y x =联立方程有11y k x y x=-⎧⎨=⎩,得1111(,)11E k k --,设直线2l :111y x k =--,同理1111(,)1111F k k ----, 因为OE OF =,所以1111||||111k k =---,①1111111k k =---,1110k k +=无实数解;②1111111k k =---,1112k k -=,211210k k --=,解得11k = 综上可得,直线1l的斜率为118.解:(1)设OPQ α∠=,由题,Rt OAQ ∆中,3OA =,AQO AQC π∠=-∠233πππ=-=,所以OQ =,在OPQ ∆中,3OP =,2POQ πθ∠=-236πππ=-=,由正弦定理得sin sin OQ OP OPQ OQP=∠∠,3sin()6ππα=--sin()6παπα=--5sin()6πα=-,5sincos 6παα=5cos sin 6πα-1cos 2αα=cos αα=, 因为α为锐角,所以cos 0α≠,所以tan α=,得6πα=;(2)设OPQ α∠=,在OPQ ∆中,3OP =,2POQ πθ∠=-236πππ=-=,由正弦定理得sin sin OQ OPOPQ OQP=∠∠3sin(())2ππαθ=---,所以sin(())2παπαθ=---sin(())2παθ=--cos()αθ=-cos cos sin sin αθαθ=+,从而sin )sin θαcos cos αθ=sin 0θ≠,cos 0α≠, 所以tanα=,记()f θ=,'()f θ=(0,)2πθ∈;令'()0f θ=,sin θ=0(0,)2πθ∈使得0sin θ=,当0(0,)θθ∈时'()0f θ>,()f θ单调增,当0(,)2πθθ∈时'()0f θ<,()f θ单调减,所以当0θθ=时,()f θ最大,即tan OPQ ∠最大,又OPQ ∠为锐角,从而OPQ ∠最大,此时sin θ=答:观赏效果达到最佳时,θ19.解:(1)函数()y g x =的定义域为(0,)+∞.当0a =,2b =-,3()2f x x x c =-+,∵()()f x g x ≥恒成立,∴32ln x x c x -+≥恒成立,即3ln 2c x x x ≥-+.令3()ln 2x x x x ϕ=-+,则21'()32x x x ϕ=-+3123x x x +-=2(1)(133)x x x x-++=,令'()0x ϕ≥,得1x ≤,∴()x ϕ在(0,1]上单调递增, 令'()0x ϕ≤,得1x ≥,∴()x ϕ在[1,)+∞上单调递减, ∴当1x =时,max [()](1)1x ϕϕ==. ∴1c ≥.(2)①当3b =-时,32()3f x x ax x c =+-+,2'()323f x x ax =+-. 由题意,2'()3230f x x ax =+-≤对(1,1)x ∈-恒成立, ∴'(1)3230'(1)3230f a f a =+-≤⎧⎨-=--≤⎩,∴0a =,即实数a 的值为0.②函数()y h x =的定义域为(0,)+∞.当0a =,3b =-,2c =时,3()32f x x x =-+.2'()33f x x =-,令2'()330f x x =-=,得1x =.∴当(0,1)x ∈时,()0f x >,当1x =时,()0f x =,当(1,)x ∈+∞时,()0f x >. 对于()ln g x x =,当(0,1)x ∈时,()0g x <,当1x =时,()0g x =,当(1,)x ∈+∞时,()0g x >.∴当(0,1)x ∈时,()()0h x f x =>,当1x =时,()0h x =,当(1,)x ∈+∞时,()0h x >. 故函数()y h x =的值域为[0,)+∞.20.解:(1)由123n n S a +=-*()n N ∈得1223n n S a ++=-,两式作差得1212n n n a a a +++=-,即213n n a a ++=*()n N ∈.13a =,21239a S =+=,所以13n n a a +=*()n N ∈,0n a ≠,则13n na a +=*()n N ∈,所以数列{}n a 是首项为3公比为3的等比数列, 所以3n n a =*()n N ∈;(2)由题意26j k i a a a λϕ+=⋅,即33263jkiλμ+=⋅⋅, 所以3312j ik i λμ--+=,其中1j i -≥,2k i -≥,所以333j i λλ-≥≥,399k i μμ-≥≥,123312j i k i λμ--=+≥,所以1j i -=,2k i -=,1λμ==;(3)由12132n n n a b a b a b --++113n n a b ++⋅⋅⋅+=33n --得,11231n n n a b a b a b +-++211n n a b a b ++⋅⋅⋅++233(1)3n n +=-+-,111213(n n n a b a b a b +-++121)n n a b a b -+⋅⋅⋅++233(1)3n n +=-+-,1113(333)n n a b n +++--233(1)3n n +=-+-,所以21333(1)n n b n ++=-+133(333)n n +----,即1363n b n +=+,所以121n b n +=+*()n N ∈,又因为111133133a b +=-⋅-=,得11b =,所以21n b n =-*()n N ∈, 从而135(21)n T n =+++⋅⋅⋅+-21212n n n +-==*()n N ∈,2*()3n n n T n n N a =∈, 当1n =时1113T a =;当2n =时2249T a =;当3n =时3313T a =; 下面证明:对任意正整数3n >都有13n n T a <, 11n n n n T T a a ++-121(1)3n n +⎛⎫=+ ⎪⎝⎭121133n n n +⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭1221((1)3)3n n n +⎛⎫+-= ⎪⎝⎭2(221)n n -++,当3n ≥时,22221(1)n n n -++=-(2)0n n +-<,即110n n n nT T a a ++-<, 所以当3n ≥时,n nT a 递减,所以对任意正整数3n >都有3313n n T T a a <=; 综上可得,满足等式13n n T a =的正整数n 的值为1和3. 2017-2018学年度苏锡常镇四市高三教学情况调研(一)数学Ⅱ(附加题)参考答案21.【选做题】A. 选修4-1:几何证明选讲证明:(1)连接OD ,BD .因为AB 是圆O 的直径,所以90ADB ∠=,2AB OB =. 因为CD 是圆O 的切线,所以90CDO ∠=,又因为DA DC =,所以A C ∠=∠,于是ADB CDO ∆≅∆,得到AB CO =,所以AO BC =,从而2AB BC =.(2)解:由2AB =及2AB BC =得到1CB =,3CA =.由切割线定理,2133CD CB CA =⋅=⨯=,所以CD =.B. 选修4-2:矩阵与变换解:(1)401248010505AB ⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦; (2)由1151B A X --⎡⎤=⎢⎥⎣⎦,解得51X AB ⎡⎤=⎢⎥⎣⎦485280515⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,又因为a X b ⎡⎤=⎢⎥⎣⎦,所以28a =,5b =.C. 选修4-4:坐标系与参数方程解:在sin()3πρθ-=0θ=,得2ρ=,所以圆C 的圆心的极坐标为(2,0).因为圆C 的半径PC 2==,于是圆C 过极点,所以圆的极坐标方程为4cos ρθ=.D. 选修4-5:不等式选讲证明:因为x ,y 都是正数,所以210x y ++≥>,210y x ++≥>,22(1)(1)9x y y x xy ++++≥,又因为1xy =,所以22(1)(1)9x y y x ++++≥.【必做题】22.解:(1)以D 为原点,DA ,DC ,DP 为坐标轴,建立如图所示空间直角坐标系;设AB t =,则(0,0,0)D ,(2,0,0)A t ,(2,,0)B t t ,(0,,0)C t ,(0,0,2)P t ,(,0,)Q t t ; 所以(,,)CQ t t t =-,(2,,0)DB t t =,(0,0,2)DP t =,设平面PBD 的法向量1(,,)n x y z =,则1100DB n DP n ⎧⋅=⎪⎨⋅=⎪⎩,即2020tx ty tz +=⎧⎨=⎩,解得200x y z +=⎧⎨=⎩,所以平面PBD 的一个法向量1(1,2,0)n =-, 111cos ,n CQn CQ n CQ⋅<>===, 则CQ 与平面PBD 所成角的正弦值为5. (2)由(1)知平面PBD 的一个法向量为1(1,2,0)n =-,设(01)PQ PA λλ=<<,则PQ PA λ=,DQ DP PQ =+(0,0,2)(2,0,2)t t t λ=+-(2,0,2(1))t t λλ=-,(2,,0)DB t t =,设平面QBD 的法向量2(,,)n x y z =,则2200DQ n DB n ⎧⋅=⎪⎨⋅=⎪⎩,即22(1)020t x t z tx ty λλ+-=⎧⎨+=⎩,解得(1)020x z x y λλ+-=⎧⎨+=⎩,所以平面QBD 的一个法向量2(1,22,)n λλλ=---,12cos ,n n =<>1212n n n n ⋅==,所以2255(1)96105λλλ-=-+,即2(2)()03λλ--=, 因为01λ<<,所以23λ=,则23PQ PA =.23. 解:(1)10D =,21D =,32D =,49D =,(2)12(1)()n n n D n D D --=-+,理由如下:对n A 的元素的一个错位排列(1a ,2a ,…,n a ),若1(1)a k k =≠,分以下两类: 若1k a =,这种排列是2n -个元素的错位排列,共有2n D -个;若1k a ≠,这种错位排列就是将1,2,…,1k -,1k +,…,n 排列到第2到第n 个位置上,1不在第k 个位置,其他元素也不在原先的位置,这种排列相当于1n -个元素的错位排列,共有1n D -个;根据k 的不同的取值,由加法原理得到12(1)()n n n D n D D --=-+;(3)根据(2)的递推关系及(1)的结论,n D 均为自然数;当3n ≥,且n 为奇数时,1n -为偶数,从而12(1)()n n n D n D D --=-+为偶数, 又10D =也是偶数,故对任意正奇数n ,有n D 均为偶数.下面用数学归纳法证明2n D (其中*n N ∈)为奇数.当1n =时,21D =为奇数;假设当n k =时,结论成立,即2k D 是奇数,则当1n k =+时,2(1)212(21)()k k k D k D D ++=++,注意到21k D +为偶数,又2k D 是奇数,所以212k k D D ++为奇数,又21k +为奇数,所以2(1)212(21)()k k k D k D D ++=++,即结论对1n k =+也成立; 根据前面所述,对任意*n N ∈,都有2n D 为奇数.。
苏北四市高三一检数学II试题(定稿)答案1234 (4)

22 y 1连云港市 2017-2018 学年度高三第一次质量检测数学Ⅱ(附加题)参考答案与评分标准21.A .证明:连接 AD ,因为 AB 为圆的直径,所以 AD BD ,又 EF AB ,则 A , D , E , F 四点共圆, 所以 B D B E BA B F . …………………………………………………………5 分又△ ABC ∽△ AEF ,所以 AB AC ,即 AB AF AE AC ,AE AF ∴ BE B D AE AC BA B F AB AF AB (BF AF ) AB 2 . …………10 分B .因为M B A 4 1 1 04 1 ,………………………………………5 分2 3 01 2 3 3 1 所以 M110 10 .………………………………………………………10 分 1 2 5 5C .把直线方程l : x 1 2t化为普通方程为x y 2 . ……………………………3 分 将圆C :2 2 cos 2sin 0 化为普通方程为 x 2 2x y 2 2 y 0 ,即(x 1)2( y 1) 22 . ………………………………………………………………6 分圆心C 到直线l 的距离 d2 ,所以直线l 与圆C 相切.…………………………………………………………………10 分a 2b 2c 2d 2D .证明:因为[(1 a ) (1 b ) (1 c ) (1 d )]( )1 a 1 b 1 c 1 d≥( 1 a1 a 1 b 1 b 1 c 1 c 1 d )21 d( a b c d ) 2 1 , …………………………………………5 分又(1 a ) (1 b ) (1 c ) (1 d ) 5 ,a 2b 2c 2d 2 1所以 .…………………………………………10 分1 a 1 b 1 c 1 d 532(1)2 (3)2 12 23334 3 (1) 0 10( 3)2 (1)2 02 42 0212222.(1)因为AB 1, AA 2 ,则F (0, 0, 0), A(1, 0, 0), C(1, 0,0), B(0,1,11 2 2 2, 0), E( , 0,1)2 所以AC (1,0,0) ,BE ( ,2 2记直线AC 和BE 所成角为,,1) ,………………………………………2 分11则cos| cos AC, B E || |2,4所以直线AC 和BE 所成角的余弦值为2.………………………………………4 分4(2)设平面BFC1的法向量为m (x1, y1, z1) ,因为1FB (0,2m3, 0) ,FC1(2, 0, 2) ,FB2y11 ,取x1 4 得:m (4, 0,1)……………………………6 分m F C x 2z 01 2 1 1设平面BCC1的一个法向量为n (x2, y2, z2) ,因为1CB ( , , 0) ,CC1(0,0, 2) ,2 2n1CB2x2 2y2,取x 得:n ( 3, 1, 0)………………………8 分n CC 2z 01 2cos m, n2 5117根据图形可知二面角F BC1C 为锐二面角,所以二面角F B C1C 的余弦值为2 51;……………………………………10 分1733则则2n (m 1) n (n 2 1)(2n )2 (n 2 1)22 x 1 2 t 2 1 1t 2 1 1 5 73 24 5 7324 5 7324 23.(1)因为抛物线C 的方程为 y 2 4x ,所以 F 的坐标为(1, 0) ,设 M (m , n ) ,因为圆 M 与 x 轴、直线l 都相切, l 平行于 x 轴, 所以圆 M 的半径为 n ,点 P (n 2 , 2n ) ,则直线 PF 的方程为 y x 1,即2n (x 1) y (n 21) 0 ,………………………2 分2n n 2 1所以 n ,又m , n 0 ,所以 2m n21n 21,即n 2m 1 0 ,所以 E 的方程为 y 2 =x 1 ( y 0) ………………………………………………4 分(2)设Q (t 21,t ) , A (0, y ) , B (0, y ) ,12由(1)知,点Q 处的切线l 1 的斜率存在,由对称性不妨设t 0 ,由 y 1 ,所以k t y 1 1 t 21 , k BQ t y 22 , t 2 1 所以 y 1t 1 , y 2 2t 22t 3 3t , ……………………………………………………6 分 所以 AB | 2t 3 3t t 1 | 2t 3 5 t 1(t 0) .……………………………………8 分2 2t 令 f (t ) 2t3 5 t 1, t 0 ,22t2 2t 则 f (t ) 6t 251 12t 4 5t2 1, 2 2t 22t 2由 f (t ) 0 得t,由 f (t ) 0 得0 t ,所以 f (t ) 在区间(0,5 2473) 单调递减,在( 5 2473, ) 单调递增,所以当t时, f (t ) 取得极小值也是最小值,即 AB 取得最小值此时 s t21 19 2473 .……………………………………………………………10 分AQ。
2018江苏苏锡常镇四市高三调研(一)数学试题答案

2021-2021学年度苏锡常镇四市高三教学情况调研〔一〕数学I试题一、填空题:本大题共14个小题,每题5分,共70分.请把答案填写在做题. 卡相应位置上.1.集合A ={-1,1}, B={Z0,1},那么集合AP|B=.2.复数z满足z j =3 -4i 〔i为虚数单位〕,那么z =.2 2X V3 .双曲线一=1的渐近线方程为4 34.某中学共有1800人,其中高二年级的人数为600.现用分层抽样的方法在全校抽取n人, 其中高二年级被抽取的人数为21 ,那么n =.5.将一颗质地均匀的正四面体骰子〔每个面上分别写有数字1, 2, 3, 4〕先后抛掷2次,观察其朝下一面的数字,那么两次数字之和等于6的概率为.6.如图是一个算法的流程图,那么输出S的值是.2 37.假设正四棱锥的底面边长为2cm,侧面积为8cm ,那么它的体积为cm .8.设S n是等差数列{4}的前n项和,假设az+a4=2, 5+S4 =1 ,那么劣.=.2 39.a >0 , b>0,且一+—= JOb ,那么ab的最小值是 .a btan A 3c-b10.设三角形ABC的内角A, B, C的对边分别为a, b, c,■tanA = V c—b ,那么tanB bcos A = ________a -e x ,x :: 111 .函数f(x)=«4 (e 是自然对数的底).假设函数y = f (x)的最小值是4, x , x ,1x那么实数a 的取值范围为 ___________ .12 .在AABC 中,点P 是边AB 的中点, CP|=J3, CA1 = 4, ZACB=2-,那么 CP CA =.2213 .直线l : x —y+2=0与x 轴交于点 A,点P 在直线l 上,圆C : (x-2) +y =2 上有且仅有一个点 B 满足AB_LBP,那么点P 的横坐标的取值集合为 .14 .假设二次函数f (x) =ax 2 +bx+c (a >0)在区间[1,2]上有两个不同的零点, 那么49的取 a 值范围为.二、解做题:本大题共6小题,共计90分.请在做题卡指定区域 内作答,解答 应写出文字说明、证实过程或演算步骤.(1)假设角口的终边过点(3,4),求a b 的值;⑵假设a//b,求锐角u 的大小.16.如图,正三棱柱 ABC -A 1B 1C 1的高为而,其底面边长为2.点M , N 分别是棱AG , AC 的中点,点D 是^^CC I 上靠近C 的三等分点(2) AD _L 平面 ABN .15.向量b=(1,sin(: -)).42 217.椭圆C: '+%=1 (a Ab A0)经过点(J3,1),.火),点A是椭圆的下顶点. a2 b2- 2 2(1)求椭圆C的标准方程;(2)过点A且互相垂直的两直线11, 12与直线y = x分别相交于E, F两点,OE =OF ,求直线l i的斜率.18.如图,某景区内有一半圆形花圃,其直径AB为6, O是圆心,且OC_LAB.在OC上2二_有一座欣赏学Q,其中ZAQC = —.方案在BC上再建一座欣赏亭P,记.POB - 乂0「二:二n, ,一一..(1)当日=一时,求/OPQ的大小;3(2)当NOPQ越大,游客在欣赏亭P处的欣赏效果越佳,求游客在欣赏亭P处的欣赏效果最正确时,角8的正弦值.19.函数f (x) =x3+ax2+bx+c , g(x)=lnx.(1)假设a=0, b = -2,且f (x)之g(x)恒成立,求实数c的取值范围;(2)假设b = -3,且函数y = f(x)在区间(一1,1)上是单调递减函数.①求实数a的值;f (x) f (x) _ g(x)②当c =2时,求函数h(x) = < (人()g()的值域. g(x), f (x):二g(x)20.S n是数列{a n}的前n项和,a1 =3,且2S n =a n由—3(n= N ).(1)求数列{a n}的通项公式;(2)对于正整数i , j , k(i < j <k),九aj , 6ai , ^a k成等差数列,求正整数% , 口的值;〔3〕设数列{b n }前n 项和是T n ,且满足:对任意的正整数 n ,都有等式一n 1 一 一 Tn 1a 〔b n +a 2b n°+a 3b nN +…3门〞=34n —3成立.求满足等式一=—的所有正整数n .a n 32021-2021学年度苏锡常镇四市高三教学情况调研〔一〕数学n 〔附加题〕21.【选做题】在A, B, C, D 四小题中只能选做两题,每题 10分,共计20 分.请在做题卡指定区域内作答,解答时应写出文字说明、证实过程或演算步骤. A.选彳4-1 :几何证实选讲如图,AB 是圆O 的直径,D 为圆O 上一点,过点D 作圆O 的切线交AB 的延长线于点 C , 且满足DA = DC .〔2〕假设AB =2,求线段CD 的长. B.选彳4-2 :矩阵与变换…4 0 1 矩阵A=, B = 〕1。
苏北四市2018届高三上 期末模拟考试数学试卷 (含答案)

2 , x 2, x 0,1 13.已知定义在 R 上的函数 f x 满足: f x 且f x 2 f x , 2 , 2 x , x 1,0 2x 5 ,则方程 f x g x 在区间 5,1 上的所有实根之和为 ▲ . g x x2 14.已知 m, n 为正整数,实数 x, y 满足 x y 4 x m y n ,若 x y 的最大值为
C B.选修 4—2 矩阵与变换
·
O
P
已知矩阵 M =
2 3
1 4
(1) 求矩阵 M 的逆矩阵; (2) 求矩阵 M 的特征值及特征向量;
C.选修 4—4
参数方程与极坐标
在极坐标系中, A 为曲线
2 2 cos 3 0 上的动点, B 为直线 cos sin 7 0
第 5 页 (共 18 页)
19. (本小题满分 16 分) 已知数列 (1)求数列 满足 a1 a(a 0, a N * ) , a1 a2 an pan1 0 ( p 0, p 1, n N ) .
*
的通项公式 an ;
(2) 若对每一个正整数 k ,若将 ak 1 , ak 2 , ak 3 按从小到大的顺序排列后,此三项均能构成 等差数列, 且公差为 d k . ①求 p 的值及对应的数列 ②记 S k 为数列 .
π 6
π 3
π 6
π π ( x )] 2 6
π π π 2sin( x ) cos( x ) sin(2 x ) , ………………………………………4 分 6 6 3
所以函数 f ( x) 的最小正周期为 (2)由(Ⅰ)得, f ( 由已知, sin C
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
苏北四市2018届高三第一次调研测试数学试题2018.1参考公式:1.柱体的体积公式:V Sh =,其中S 是柱体的底面面积,h 是高.2.圆锥的侧面积公式:12S cl =,其中c 是圆锥底面的周长,l 是母线长.一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置........ 1.已知集合2{0}A x x x =-=,{1,0}B =-,则A B =U ▲ . 2.已知复数2i 2iz +=-(i 为虚数单位),则z 的模为 ▲ .3.函数y =的定义域为 ▲ .4.如图是一个算法的伪代码,运行后输出b 的值为 ▲ .5.某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1 000名学生的成绩,并根据这1 000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[250,400)内的学生共有 ▲ 人.6.在平面直角坐标系xOy 中,已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线方程为20x y -=,则该双曲线的离心率为 ▲ .7.连续2次抛掷一颗质地均匀的骰子(六个面上分别标有数字1,2,3,4,5,6的正方体),观察向上的点数,则事件“点数之积是3的倍数”的概率为 ▲ .8.已知正四棱柱的底面边长为3cm ,侧面的对角线长是,则这个正四棱柱的体积是 ▲ 3cm .9.若函数()sin()(0,0)f x A x A ωϕω=+>>的图象与直线y m =的三个相邻交点的横坐标分别是6π,3π,23π,则实数ω的值为 ▲ .10.在平面直角坐标系xOy 中,曲线:C xy =P 到直线:0l x +=的距离的最小值为 ▲ .11.已知等差数列{}na 满足a 13579=10,a 8222=36,则a 11的值为 ▲ .12.在平面直角坐标系xOy 中,若圆1C :222(1)(0)xy r r +-=>上存在点P ,且点P 关于直线0x y -=的对称点Q 在圆2C :22(2)(1)1x y -+-=上,则r 的取值范围是 ▲ .13.已知函数2211()(1)1x x f x x x ⎧-+ ⎪=⎨- > ⎪⎩,≤,,,函数()()()g x f x f x =+-,则不等式()2g x ≤的解集为 ▲ .14.如图,在ABC △中,已知32120AB AC BAC == ∠=︒,,,D 为边BC 的中点.若CE AD ⊥,垂足为E ,则·的值为 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答..........,解答时应写出文字说明、证明过程或计算步骤. 15.(本小题满分14分)在△中,角所对的边分别为,且3cos 5A =,1tan()3B A -=.⑴求tan B 的值; ⑵若13c =,求△的面积.16.(本小题满分14分)如图,在直三棱柱111ABC A B C -中,90ABC ∠=o ,1=AB AA ,M ,N 分别是AC ,11B C 的中点.求证:⑴//MN 平面11ABB A ;⑵1AN A B ⊥.(第14A DC E17.(本小题满分14分)某艺术品公司欲生产一款迎新春工艺礼品,该礼品是由玻璃球面和该球的内接圆锥组成,圆锥的侧面用于艺术装饰,如图1.为了便于设计,可将该礼品看成是由圆O 及其内接等腰三角形绕底边上的高所在直线旋转180°而成,如图2.已知圆O 的半径为10 ,设∠θ,π02θ<<,圆锥的侧面积为S2.⑴求S关于θ的函数关系式;⑵为了达到最佳观赏效果,要求圆锥的侧面积S 最大.求S 取得最大值时腰的长度.18.(本小题满分16分)如图,在平面直角坐标系中,已知椭圆22221(0)x y a b a b +=>>的离心率为12,(第16且过点3 1 2(,)为椭圆的右焦点,为椭圆上关于原点对称的两点,连接,AF BF分别交椭圆于,C D两点.⑴求椭圆的标准方程;⑵若AF FC=,求BFFD的值;⑶设直线,的斜率分别为k12,是否存在实数m,使得k21,若存在,求出m的值;若不存在,请说明理由.19.(本小题满分16分)已知函数2()1()ln()f x x axg x x a a=++ =-∈R,.⑴当1a=时,求函数()()()h x f x g x=-的极值;⑵若存在与函数()f x,()g x的图象都相切的直线,求实数a的取值范围.(第1820.(本小题满分16分)已知数列{}n a ,其前n 项和为n S ,满足12a =,1n n n S na a λμ-=+,其中2n …,n *∈N ,λ,μ∈R .⑴若0λ=,4μ=,12n n n b a a +=-(n *∈N ),求证:数列{}n b 是等比数列; ⑵若数列{}n a 是等比数列,求λ,μ的值;⑶若23a =,且32λμ+=,求证:数列{}n a 是等差数列.数学Ⅱ(附加题)21.【选做题】本题包括A、B、C、D四小题,请选定其中两小题...........,并在相应的答题区域内作答.........,若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A.[选修4-1:几何证明选讲](本小题满分10分)如图,AB是圆O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.求证:2=⋅-⋅AB BE BD AE ACB .[选修4-2:矩阵与变换](本小题满分10分)已知矩阵1001⎡⎤=⎢⎥-⎣⎦A ,4123⎡⎤=⎢⎥⎣⎦B ,若矩阵=M BA ,求矩阵M 的逆矩阵1-M .C .[选修4-4:坐标系与参数方程](本小题满分10分)以坐标原点为极点,x 轴的正半轴为极轴,且在两种坐标系中取相同的长度单位,建立极坐标系,判断直线12:12x tl y t =+⎧⎨=-⎩(t 为参数)与圆2:2cos 2sin 0C ρρθρθ+-=的位置关系.D .[选修4-5:不等式选讲](本小题满分10分)已知,,,a b c d 都是正实数,且1a b c d +++=,求证: 2222111115a b c d a b c d +++++++….【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.22.(本小题满分10分)在正三棱柱111ABC A B C -中,已知1AB =,12AA =,E ,F ,G 分别是1AA ,AC 和11A C 的中点.以{,,}FA FB FG u u u r u u u r u u u r为正交基底,建立如图所示的空间直角坐标系F xyz -.⑴求异面直线AC 与BE 所成角的余弦值; ⑵求二面角1F BC C --的余弦值.23.(本小题满分10分)在平面直角坐标系中,已知平行于x 轴的动直线l 交抛物线2:4C y x 于点P ,点F 为C 的焦点.圆心不在y 轴上的圆M 与直线l ,PF ,x 轴都相切,设M 的轨迹为曲线E . ⑴求曲线E 的方程;⑵若直线1l 与曲线E 相切于点(,)Q s t ,过Q 且垂直于1l 的直线为2l ,直线1l ,2l 分别与y 轴相交于点A ,B .当线段AB 的长度最小时,求s 的值.数学参考答案与评分标准一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置........ 1.{1,0,1}- 2.1 3.(0,1] 4.13 5.750 67.598.549.4 10..11 12.1]- 13.[2,2]- 14.277-二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答..........,解答时应写出文字说明、证明过程或计算步骤. 15.(1)在ABC △中,由3cos 5A =,得A为锐角,所以4sin 5A =, 所以sin 4tan cos 3A A A ==,………………………………………………………………2分所以tan()tan tan tan[()]1tan()tan B A AB B A A B A A-+=-+=--⋅. (4)分1433314133+==-⨯ …………………………………………………………6分(2)在三角形ABC 中,由tan 3B =,所以sin B B =, ………………………………………………8分由sin sin()sin cos cos sin 50C A B A B A B =+=+=,…………………………10分由正弦定理sin sin b c B C =,得13sin sin c B b C ==,………………………12分所以ABC △的面积114sin 151378225S bc A ==⨯⨯⨯=. (14)分16.(1)证明:取AB 的中点P ,连结1,.PM PB因为,M P 分别是,AB AC 的中点, 所以//,PM BC 且1.2PM BC =在直三棱柱111ABC A B C -中,11//BC B C ,11BC B C =, 又因为N 是11B C 的中点, 所以1//,PM B N 且1PM B N =. (2)分所以四边形1PMNB 是平行四边形,所以1//MN PB , ………………………………………………………………4分而MN ⊄平面11ABB A ,1PB ⊂平面11ABB A , 所以//MN 平面11ABB A . (6)分(2)证明:因为三棱柱111ABC A B C -为直三棱柱,所以1BB ⊥面111A B C ,又因为1BB ⊂面11ABB A ,所以面11ABB A ⊥面111A B C , …………………8分 又因为90ABC ∠=o ,所以1111B C B A ⊥, 面11ABB A I 面11111=A B C B A ,11111B C A B C ⊂平面,所以11B C ⊥面11ABB A , ………………………10分 又因为1A B ⊂面11ABB A , 所以111B C A B ⊥,即11NB A B ⊥,连结1AB ,因为在平行四边形11ABB A 中,1=AB AA , 所以11AB A B ⊥, 又因为111=NB AB B I,且1AB ,1NB ⊂面1AB N ,所以1A B ⊥面1AB N ,……………………………………………………………………12分而AN ⊂面1AB N , 所以1A B AN ⊥.……………………………………………………………………………14分 17.(1)设AO 交BC 于点D ,过O 作OE AB ⊥,垂足为E ,在AOE ∆中,10cos AE θ=,220cos AB AE θ==,…………………………………………………………2分 在ABD ∆中,sin 20cos sin BD AB θθθ=⋅=⋅,…………………………………………………………4分 所以1220sin cos 20cos 2S θθθ=⋅π⋅⋅2400sin cos θθ=π,(0)2πθ<< ……………………6分(2)要使侧面积最大,由(1)得:23400sin cos 400(sin sin )S πθθπθθ==- (8)分设3(),(01)f x x x x =-<< 则2()13f x x '=-,由2()130f x x '=-=得:x =当x ∈时,()0f x '>,当x ∈时,()0f x '< 所以()f x在区间上单调递增,在区间上单调递减, 所以()f x在x 时取得极大值,也是最大值;所以当sin θ=时,侧面积S取得最大值, …………………………11分此时等腰三角形的腰长20cos AB θ====答:侧面积S取得最大值时,等腰三角形的腰AB的长度为.…………14分18.(1)设椭圆方程为22221(0)x y a b a b +=>>,由题意知:22121914c a a b ⎧=⎪⎪⎨⎪+=⎪⎩ (2)分解之得:2a b =⎧⎪⎨=⎪⎩,所以椭圆方程为:22143x y += ……………………………4分(2)若AF FC =,由椭圆对称性,知3(1,)2A ,所以3(1,)2B --,此时直线BF方程为3430x y --=, ……………………………………………6分由223430,1,43x y x y --=⎧⎪⎨+=⎪⎩,得276130x x --=,解得137x =(1x =-舍去),…………8分故1(1)713317BF FD --==-.…………………………………………………………………10分(3)设00,)A x y (,则00(,)B x y --,直线AF 的方程为00(1)1y y x x =--,代入椭圆方程22143x y +=,得 2220000(156)815240x x y x x ---+=,因为x x =是该方程的一个解,所以C点的横坐标8552C x x x -=-,…………………12分又(,)c C C x y 在直线00(1)1y y x x =--上,所以00003(1)152C c y y y x x x -=-=--,同理,D点坐标为085(52x x ++,3)52y x +, ……………………………………………14分所以000002100000335552528585335252y y y x x k k x x x x x --+-===+--+-, 即存在53m =,使得2153k k =. ………………………………………………………16分19.(1)函数()h x 的定义域为(0,)+∞当1a =时,2()()()ln 2h x f x g x x x x =-=+-+,所以1(21)(1)()21x x h x x x x-+'=+-=………………………………………………2分所以当102x <<时,()0h x '<,当12x >时,()0h x '>,所以函数()h x 在区间1(0,)2单调递减,在区间1(,)2+∞单调递增,所以当12x =时,函数()h x 取得极小值为11+ln 24,无极大值;…………………4分(2)设函数()f x 上点11(,())x f x 与函数()g x 上点22(,())x g x 处切线相同, 则121212()()()()f x g x f x g x x x -''==-所以211212121(ln )12x ax x a x a x x x ++--+==- ……………………………………6分 所以12122ax x =-,代入21211221(ln )x x x ax x a x -=++--得: 222221ln 20(*)424a a x a x x -++--= ………………………………………………8分设221()ln 2424a a F x x a x x =-++--,则23231121()222a x ax F x x x x x+-'=-++= 不妨设2000210(0)x ax x +-=>则当00x x <<时,()0F x '<,当0x x >时,()0F x '> 所以()F x 在区间0(0,)x 上单调递减,在区间0(,)x +∞上单调递增,……………10分代入20000121=2x a x x x -=-可得:2min 000001()()2ln 2F x F x x x x x ==+-+- 设21()2ln 2G x x x x x =+-+-,则211()220G x x x x'=+++>对0x >恒成立,所以()G x 在区间(0,)+∞上单调递增,又(1)=0G所以当01x <≤时()0G x ≤,即当001x <≤时0()0F x ≤, ……………12分 又当2a x e+=时222421()ln 2424a a a a a F x e a e e +++=-++--2211()04a a e+=-≥ ……………………………………14分因此当001x <≤时,函数()F x 必有零点;即当001x <≤时,必存在2x 使得(*)成立;即存在12,x x 使得函数()f x 上点11(,())x f x 与函数()g x 上点22(,())x g x 处切线相同.又由12y x x=-得:2120y x'=--<所以12(0,1)y x x=-在单调递减,因此20000121=2[1+)x a x x x -=-∈-∞, 所以实数a 的取值范围是[1,)-+∞.…………………………………………………16分 20.(1)证明:若=0,4 =λμ,则当14n n S a -=(2n ≥), 所以1114()n n n n n a S S a a ++-=-=-, 即1122(2)n n n n a a a a +--=-,所以12n n b b -=,……………………………………………………………2分 又由12a =,1214a a a +=,得2136a a ==,21220a a -=≠,即0n b ≠, 所以12nn b b -=,故数列{}n b 是等比数列.……………………………………………………………4分(2)若{}n a 是等比数列,设其公比为q (0q ≠ ), 当2n =时,2212S a a =+λμ,即12212a a a a +=+λμ,得12q q +=+λμ,①当3n =时,3323S a a =+λμ,即123323a a a a a ++=+λμ,得2213q q q q ++=+λμ,②当4n =时,4434S a a =+λμ,即1234434a a a a a a +++=+λμ,得 233214+q q q q q ++=+λμ,③②①q ,得21q =λ , ③②q ,得31q =λ ,解得1,1 q ==λ.代入①式,得0=μ.…………………………………………………………………8分 此时n n S na =(2n ≥),所以12n a a ==,{}n a 是公比为1的等比数列, 故10 ==,λμ. ……………………………………………………………………10分(3)证明:若23a =,由12212a a a a +=+λμ,得562=+λμ,又32+=λμ,解得112==,λμ. (12)分由12a =,23a =,12λ=,1μ=,代入1n n n S na a λμ-=+得34a =, 所以1a ,2a ,3a 成等差数列,由12n n n n S a a -=+,得1112n n n n S a a +++=+,两式相减得:111122n n n n n n n a a a a a ++-+=-+-即11(1)(2)20n n n n a n a a +-----= 所以21(1)20n n n na n a a ++---=相减得:2112(1)(2)220n n n n n na n a n a a a ++---+--+= 所以2111(2)2(2)0n n n n n n n a a a a a a +++--++-+=所以221111-222(2)(2)(2)(1)n n n n n n n n n a a a a a a a a a n n n +++---+=--+=-+- 1321(2)(2)(1)2n a a a n n --==-+-L L L , ……………………………………14分因为12320a a a -+=,所以2120n n n a a a ++-+=,即数列{}n a 是等差数列.………………………………………………………………16分数学Ⅱ(附加题)参考答案与评分标准21.A .证明:连接AD ,因为AB 为圆的直径,所以AD BD ⊥,又EF AB ⊥,则,,,A D E F 四点共圆,所以BD BE BA BF ⋅=⋅. …………………………………………………………5分又△ABC ∽△AEF ,所以AB AC AEAF=,即AB AF AE AC ⋅=⋅,∴2()BE BD AE AC BA BF AB AF AB BF AF AB ⋅-⋅=⋅-⋅=⋅-=. …………10分B .因为411041230123M BA -⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦, ………………………………………5分所以13110101255M -⎡⎤-⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦. (10)分 C.把直线方程12:12x tl y t=+⎧⎨=-⎩化为普通方程为2x y +=. (3)分将圆:C 22cos 2sin 0ρρθρθ+-=化为普通方程为22220x x y y ++-=, 即22(1)(1)2x y ++-=. ………………………………………………………………6分圆心C 到直线l的距离d ==所以直线l与圆C相切.…………………………………………………………………10分D .证明:因为2222[(1)(1)(1)(1)]()1111a b c d a b c d a b c d++++++++++++++2≥ 2()1a b c d =+++=, …………………………………………5分又(1)(1)(1)(1)5a b c d +++++++=, 所以2222111115a b c d a b c d +++≥++++.…………………………………………10分22.(1)因为11,2AB AA==,则111(0,0,0),(,0,0),(,0,0),(,0,1)222F A C B E -,所以(1,0,0)=-u u u rAC,1(,2=u u u rBE , ………………………………………2分记直线AC 和BE 所成角为α,则11cos |cos ,||4α-⨯=<>==u u u r u u u rAC BE ,所以直线AC和BE所成角的余弦值为. ………………………………………4分 (2)设平面1BFC 的法向量为111(,,)x y z =m ,因为2FB =u u u r ,11(,0,2)2FC =-u u u u r ,则111101202FB y FC x z ⎧⋅==⎪⎪⎨⎪⋅=-+=⎪⎩u u u r u u u u r m m ,取14x =得:(4,0,1)=m ……………………………6分设平面1BCC 的一个法向量为222(,,)x y z =n ,因为1(22CB =u u u r,1(0,0,2)CC =u u u u r ,则221210220CB x y CC z ⎧⋅=+=⎪⎨⎪⋅==⎩u u u r u u u u r n n,取2x =1,0)=-n ………………………8分cos ,∴<>==m n 根据图形可知二面角1F BCC --为锐二面角,所以二面角1F BCC --的余弦值为……………………………………10分23.(1)因为抛物线C 的方程为24y x =,所以F 的坐标为(1,0),设(,)M m n ,因为圆M 与x 轴、直线l 都相切,l 平行于x 轴, 所以圆M 的半径为n ,点P 2(,2)n n , 则直线PF 的方程为2121y x n n -=-,即22(1)(1)0n x y n ---=,………………………2分n=,又,0m n ≠,所以22211m n n --=+,即210n m -+=, 所以E 的方程为2=1y x -(0)y ≠ (4)分(2)设2(1,)+Q t t , 1(0,)A y ,2(0,)B y ,由(1)知,点Q 处的切线1l 的斜率存在,由对称性不妨设0>t ,由'=y ,所以121AQ t y k t -==+,221BQ t y k t -==-+所以1122=-t y t,3223=+y t t , (6)分所以33151|23|2(0)2222t AB t t t t t tt=+-+=++>.……………………………………8分令351()222f t t t t=++,0t >,则42222511251()6222t t f t t t t +-'=+-=,由()0f t'<得0t<<f t'>得t>()0所以()+∞单调递增,f t在区间单调递减,在)所以当t=()f t取得极小值也是最小值,即AB取得最小值此时21s t=+=.……………………………………………………………10分。
