土木工程毕业设计 第六章 竖向荷载(恒载+活载)作用下框架内力计算
4-竖向荷载作用下框架内力计算

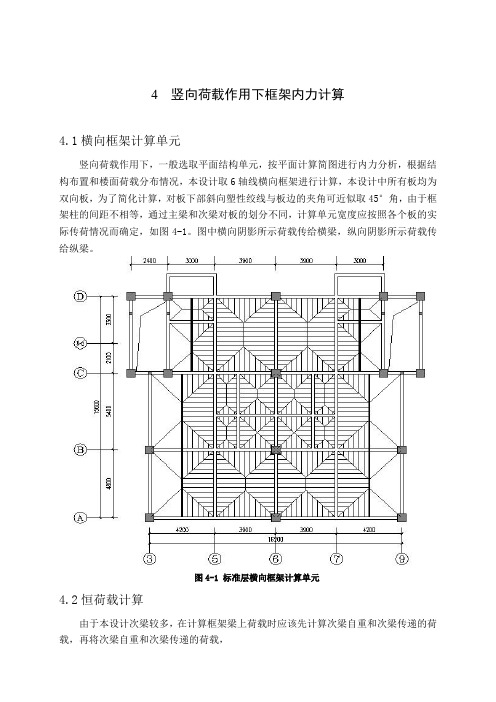
4 竖向荷载作用下框架内力计算4.1横向框架计算单元竖向荷载作用下,一般选取平面结构单元,按平面计算简图进行内力分析,根据结构布置和楼面荷载分布情况,本设计取6轴线横向框架进行计算,本设计中所有板均为双向板,为了简化计算,对板下部斜向塑性绞线与板边的夹角可近似取45°角,由于框架柱的间距不相等,通过主梁和次梁对板的划分不同,计算单元宽度应按照各个板的实际传荷情况而确定,如图4-1。
图中横向阴影所示荷载传给横梁,纵向阴影所示荷载传给纵梁。
图4-1 标准层横向框架计算单元4.2恒荷载计算由于本设计次梁较多,在计算框架梁上荷载时应该先计算次梁自重和次梁传递的荷载,再将次梁自重和次梁传递的荷载,次梁传给主梁的荷载可近似地看成一个集中力,因此在框架节点处还应作用有集中力矩。
4.2.1 标准层次梁恒荷载计算1、5或7轴线次梁上线荷载1)AB 跨的次梁上的荷载分布如图4-2所示。
图4-1 AB 跨的次梁上的荷载分布次梁自重:m kN m m m kN q /13.350.025.0/253=⨯⨯=次;根据《实用建筑结构静力计算手册》(第二版),对于双向板楼面荷载传递按45°塑性绞线方向分为三角形荷载和梯形荷载,三角形荷载和梯形荷载均折算成等效均布面荷载。
三角形荷载:q 85,梯形荷载:()q αα⋅+-3221,其中,0l a α=。
对于BC 跨中有三角形荷载和梯形荷载同时在同一跨中出现,按理应该按照结构力学的方法进行求解,但为了简化计算,本设计中的三角形荷载和梯形荷载按上述方法计算,且按上述方法计算的荷载也能满足工程精度要求。
44.04800/21001==mm mm α;()()223231211/18.3/54.444.044.02121m kN m kN q ααq =⨯+⨯-=⋅+-='; m kN m m kN l q q /68.61.2/18.32011=⨯=⋅'=; m kN m kN m kN q q q AB /49.162/68.6/13.31=⨯+=+=次;2)BC 跨的次梁上的荷载分布如图4-2所示。
土木工程毕业设计最终模板(计算书)

前 言本毕业设计说明书是本科高等学校土木工程专业本科生毕业设计的说明书,本说明书全部内容共分十四章,这十四章里包含了荷载汇集、水平作用下框架内力分析、竖向作用下框架内力分析、以及框架中各个结构构件的设计等,这些内容容纳了本科生毕业设计要求的全部内容,其中的计算方法都来自于本科四年所学知识,可以说是大学四年所学知识的一个很好的复习总结 同时也是培养能力的过程。
本毕业设计说明书根据任务书要求以及最新相关规范编写,内容全面、明确,既给出了各类问题解决方法的指导思想,又给出了具体的解决方案,并且明确地给出了各类公式及符号的意义和必要的说明。
本说明书概念清晰、语言流畅,每章都有大量的计算表格,并且对重点说明部分配置图解。
应该说本说明书很好地完成了本次毕业设计的任务要求、达到了本次毕业设计的预定目标。
第一章方案论述建筑方案论述设计依据依据土木工程专业 届毕业设计任务书。
遵照国家规定的现行相关设计规范。
设计内容、建筑面积、标高( )本次设计的题目为“彩虹中学教学楼”。
该工程位于沈阳市,为永久性建筑,建筑设计使用年限 年,防火等级二级。
( )本建筑结构为五层,层高均为 。
建筑面积: ,占地面积: 。
( )室内外高差 ,室外地面标高为 。
房间构成和布置( )房间构成本工程为一所中学教学楼,根据教学楼的功能要求,此次设计该教学楼共包括 个普通教室, 个 人合班教室, 个教师办公室,计算机室,语音室,物理实验室、电话总机室各 个, 个会议室,资料室,教师休息室,学生会办公室等配套房间若干个,以及配套的卫生间若干个。
( )房间布局充分考虑教学楼各种房间在功能和面积等方面的不同,尽量做到功能分区清晰,各功能分区之间联系紧密,以及结构布置合理等,在设计中主要注意了以下几点:①教室(包括普通教室和合班教室)布置在教学楼的阳面。
②语音教室以及录音室等需要安静环境的教室布置在教学楼相对较为偏僻的地方。
③充分考虑实验室办公室,实验准备室和实验室的紧密联系,各类实验室都设置了配套的教师办公室,实验准备室以及实验储藏室。
4-竖向荷载作用下框架内力计算
4 竖向荷载作用下框架内力计算4.1横向框架计算单元竖向荷载作用下,一般选取平面结构单元,按平面计算简图进行内力分析,根据结构布置和楼面荷载分布情况,本设计取6轴线横向框架进行计算,本设计中所有板均为双向板,为了简化计算,对板下部斜向塑性绞线与板边的夹角可近似取45°角,由于框架柱的间距不相等,通过主梁和次梁对板的划分不同,计算单元宽度应按照各个板的实际传荷情况而确定,如图4-1。
图中横向阴影所示荷载传给横梁,纵向阴影所示荷载传给纵梁。
图4-1 标准层横向框架计算单元4.2恒荷载计算由于本设计次梁较多,在计算框架梁上荷载时应该先计算次梁自重和次梁传递的荷载,再将次梁自重和次梁传递的荷载,次梁传给主梁的荷载可近似地看成一个集中力,因此在框架节点处还应作用有集中力矩。
4.2.1 标准层次梁恒荷载计算1、5或7轴线次梁上线荷载1)AB 跨的次梁上的荷载分布如图4-2所示。
图4-1 AB 跨的次梁上的荷载分布次梁自重:m kN m m m kN q /13.350.025.0/253=⨯⨯=次;根据《实用建筑结构静力计算手册》(第二版),对于双向板楼面荷载传递按45°塑性绞线方向分为三角形荷载和梯形荷载,三角形荷载和梯形荷载均折算成等效均布面荷载。
三角形荷载:q 85,梯形荷载:()q αα⋅+-3221,其中,0l a α=。
对于BC 跨中有三角形荷载和梯形荷载同时在同一跨中出现,按理应该按照结构力学的方法进行求解,但为了简化计算,本设计中的三角形荷载和梯形荷载按上述方法计算,且按上述方法计算的荷载也能满足工程精度要求。
44.04800/21001==mm mm α;()()223231211/18.3/54.444.044.02121m kN m kN q ααq =⨯+⨯-=⋅+-='; m kN m m kN l q q /68.61.2/18.32011=⨯=⋅'=; m kN m kN m kN q q q AB /49.162/68.6/13.31=⨯+=+=次;2)BC 跨的次梁上的荷载分布如图4-2所示。
土木工程毕业设计 第六章 竖向荷载(恒载 活载)作用下框架内力计算讲解
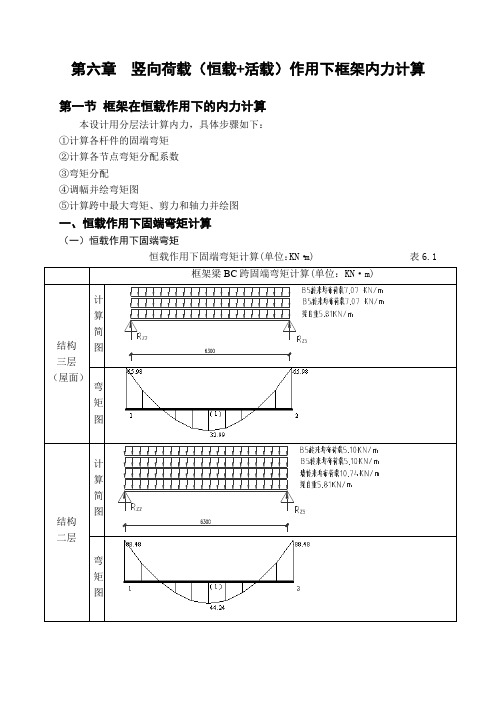
第六章竖向荷载(恒载+活载)作用下框架内力计算第一节框架在恒载作用下的内力计算本设计用分层法计算内力,具体步骤如下:①计算各杆件的固端弯矩②计算各节点弯矩分配系数③弯矩分配④调幅并绘弯矩图⑤计算跨中最大弯矩、剪力和轴力并绘图一、恒载作用下固端弯矩计算(一)恒载作用下固端弯矩恒载作用下固端弯矩计算(单位:KN·m) 表6.1弯矩图恒载作用下梁固端弯矩计算统计表6.2(二)计算各节点弯矩分配系数用分层法计算竖向荷载,假定结构无侧移,计算时采用力矩分配法,其计算要点是:①计算各层梁上竖向荷载值和梁的固端弯矩。
②将框架分层,各层梁跨度及柱高与原结构相同,柱端假定为固端。
③计算梁、柱线刚度。
对于柱,假定分层后中间各层柱柱端固定与实际不符,因而,除底层外,上层柱各层线刚度均乘以0.9修正。
有现浇楼面的梁,宜考虑楼板的作用。
每侧可取板厚的6倍作为楼板的有效作用宽度。
设计中,可近似按下式计算梁的截面惯性矩:一边有楼板:I=1.5Ir两边有楼板:I=2.0Ir④计算和确定梁、柱弯矩分配系数和传递系数。
按修正后的刚度计算各结点周围杆件的杆端分配系数。
所有上层柱的传递系数取1/3,底层柱的传递系数取1/2。
⑤按力矩分配法计算单层梁、柱弯矩。
⑥将分层计算得到的、但属于同一层柱的柱端弯矩叠加得到柱的弯矩。
(1)计算梁、柱相对线刚度图6.1 修正后梁柱相对线刚度(2)计算弯矩分配系数结构三层=5.37÷(5.37+1.18)=0.820①梁μB3C3μ=5.37÷(5.37+3.52+1.18)=0.533C3B3=3.52÷(5.37+3.52+1.18)=0.350μC3D3=3.52÷(3.52+1.18)=0.749μD3C3=1.18÷(5.37+1.18)=0.180②柱μB3B2=1.18÷(5.37+3.52+1.18)=0.117μC3C2=1.18÷(3.52+1.18)=0.251μD3D2结构二层①梁μ=5.37÷(1.18+1.18+5.37)=0.695B2C2=5.37÷(1.18+1.18+5.37+3.52)=0.477μC2B2μ=3.52÷(1.18+1.18+5.37+3.52)=0.313 C2D2=3.52÷(1.18+1.18+3.52)=0.5986 μD2C2=1.18÷(1.18+1.18+5.37)=0.1525②柱μB2B3μ=1.18÷(1.18+1.18+5.37)=0.1525B2B1=1.18÷(1.18+1.18+5.37+3.52)=0.105 μC2C3μ=1.18÷(1.18+1.18+5.37+3.52)=0.105 C2C1=1.18÷(1.18+1.18+3.52)=0.2007 μD2D3μ=1.18÷(1.18+1.18+3.52)=0.2007D2D1结构一层=5.37÷(1.18+1+5.37)=0.711①梁μB1C1=5.37÷(1.18+1+5.37+3.52)=0.485 μC1B1=3.52÷(1.18+1+5.37+3.52)=0.318 μC1D1=3.52÷(1.18+1+3.52)=0.618μD1C1=1.18÷(1.18+1+5.37)=0.156②柱μB1B2=1÷(1.18+1+5.37)=0.133μB1B0=1.18÷(1.18+1+5.37+3.52)=0.107μC1C2=1÷(1.18+1+5.37+3.52)=0.090μC1C0μ=1.18÷(1.18+1+3.52)=0.207D1D2μ=1÷(1.18+1+3.52)=0.175D1D0(三)分层法算恒载作用下弯矩恒载作用下结构三层弯矩分配表6.3B C D上柱偏心弯矩分配系数0固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配14.650 -13.883 226.915 20.861 -251.346 84.509 -112.810 二次分配14.512 -14.512 228.818 21.278 -250.096 105.707 -105.707恒载作用下结构二层弯矩分配表6.40.768 12.717 -28.301↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配 6.931 4.431 -4.607 308.811 46.295 47.232 -385.113 169.804 -113.072 -92.837二次分配 5.901 3.401 -9.302 300.595 44.486 45.423 -390.504 191.416 -105.826 -85.591恒载作用下结构一层弯矩分配表6.52.127 9.081 -7.935↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次二次7.030 5.338 -12.368 267.469 35.352 22.097 -324.919 357.349 -46.247 -15.172 -295.930图6.2 弯矩再分配后恒载作用下弯矩图(KN·m)(四)框架梁弯矩塑性调幅为了减少钢筋混凝土框架梁支座处的配筋数量,在竖向荷载作用下可以考虑竖向内力重分布,主要是降低支座负弯矩,以减小支座处的配筋,跨中则应相应增大弯矩。
4_竖向荷载作用下框架内力计算

4_竖向荷载作用下框架内力计算在结构设计过程中,框架结构是一种常见的结构形式。
在实际工程中,框架结构会受到各种荷载的作用。
竖向荷载是一种重要的荷载形式,常见的竖向荷载包括自重、活荷载和附加荷载等。
在框架结构内力计算中,需要首先确定结构的几何特征,包括框架的截面形状、材料参数和受力情况等。
然后根据几何特征和力学原理,分析结构的受力平衡和变形情况,最终得到内力的计算结果。
下面将以一个简单的框架结构为例,介绍竖向荷载作用下框架内力计算的基本步骤。
1.框架结构的受力分析首先,需要绘制框架的受力图。
在竖向荷载作用下,框架的受力主要包括竖向荷载的作用力、支座反力和框架内部的轴力、剪力和弯矩等。
通过受力分析,可以将框架结构简化为若干个矩形梁和柱,以便进行进一步的计算。
2.框架结构的力学模型化将框架结构进行力学模型化,即将结构划分为若干个杆件和节点,并确定节点的受力情况。
杆件的长度、截面形状和材料参数等需要根据实际情况进行设定,以便计算杆件的受力。
3.杆件的受力计算根据竖向荷载作用下杆件的受力平衡和变形情况,可以得到杆件的轴力、剪力和弯矩等。
对于轴力,可以利用静力平衡原理进行计算。
对于剪力和弯矩,可以根据杆件的受力分布和形状进行计算,常用的方法包括截面法和弯矩传递法等。
4.框架结构的内力计算根据杆件的受力计算结果,可以得到框架结构内各个节点的内力情况。
根据节点的受力平衡条件,可以计算出节点上的轴力、剪力和弯矩等。
此外,还需要考虑支座反力的作用,以及与其他荷载(如横向荷载)的叠加效应。
5.内力的承载能力和设计校核根据内力计算结果,可以对框架结构的承载能力进行评估和校核。
根据设计规范和材料参数,结合强度和稳定性要求,进行构件的截面尺寸校核。
如果结构的承载能力满足要求,则结构设计合理;否则,需要进行后续的调整和优化。
总的来说,竖向荷载作用下框架内力计算是结构设计中的重要环节。
通过合理的受力分析和计算,能够得到准确的内力计算结果,从而为结构设计和施工提供科学的依据。
土木工程毕业设计 第六章 竖向荷载作用下框架内力计算

第六章竖向荷载(恒载+活载)作用下框架内力计算第一节框架在恒载作用下的内力计算本设计用分层法计算内力,具体步骤如下:①计算各杆件的固端弯矩②计算各节点弯矩分配系数③弯矩分配④调幅并绘弯矩图⑤计算跨中最大弯矩、剪力和轴力并绘图一、恒载作用下固端弯矩计算(一)恒载作用下固端弯矩恒载作用下固端弯矩计算(单位:KN·m) 表恒载作用下梁固端弯矩计算统计表(二)计算各节点弯矩分配系数用分层法计算竖向荷载,假定结构无侧移,计算时采用力矩分配法,其计算要点是:①计算各层梁上竖向荷载值和梁的固端弯矩。
②将框架分层,各层梁跨度及柱高与原结构相同,柱端假定为固端。
③计算梁、柱线刚度。
对于柱,假定分层后中间各层柱柱端固定与实际不符,因而,除底层外,上层柱各层线刚度均乘以修正。
有现浇楼面的梁,宜考虑楼板的作用。
每侧可取板厚的6倍作为楼板的有效作用宽度。
设计中,可近似按下式计算梁的截面惯性矩:一边有楼板:I=两边有楼板:I=④计算和确定梁、柱弯矩分配系数和传递系数。
按修正后的刚度计算各结点周围杆件的杆端分配系数。
所有上层柱的传递系数取1/3,底层柱的传递系数取1/2。
⑤按力矩分配法计算单层梁、柱弯矩。
⑥将分层计算得到的、但属于同一层柱的柱端弯矩叠加得到柱的弯矩。
(1)计算梁、柱相对线刚度图修正后梁柱相对线刚度(2)计算弯矩分配系数结构三层=÷+=①梁μB3C3μ=÷++=C3B3=÷++=μC3D3μ=÷+=D3C3=÷+=②柱μB3B2μ=÷++=C3C2μ=÷+=D3D2结构二层=÷++=①梁μB2C2μ=÷+++=C2B2=÷+++=μC2D2μ=÷++=D2C2②柱μ=÷++=B2B3=÷++=μB2B1=÷+++=μC2C3=÷+++=μC2C1=÷++=μD2D3μ=÷++=D2D1结构一层=÷+1+=①梁μB1C1=÷+1++=μC1B1=÷+1++=μC1D1=÷+1+=μD1C1=÷+1+=②柱μB1B2=1÷+1+=μB1B0=÷+1++=μC1C2=1÷+1++=μC1C0μ=÷+1+=D1D2μ=1÷+1+=D1D0(三)分层法算恒载作用下弯矩恒载作用下结构三层弯矩分配表B C D上柱偏心弯矩分配系数0固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配二次分配恒载作用下结构二层弯矩分配表↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配二次分配恒载作用下结构一层弯矩分配表↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次二次图弯矩再分配后恒载作用下弯矩图(KN·m)(四)框架梁弯矩塑性调幅为了减少钢筋混凝土框架梁支座处的配筋数量,在竖向荷载作用下可以考虑竖向内力重分布,主要是降低支座负弯矩,以减小支座处的配筋,跨中则应相应增大弯矩。
第六章-框架在竖向荷载作用下的内力分析
第六章框架在竖向荷载作用下的内力分析(采用弯矩二次分配法)6.1 计算方法和荷载传递路线1. 计算方法框架结构在竖向荷载作用下的内力计算采用力矩分配法,因为框架结构对称,荷载对称;又属于奇数跨,故在对称轴上梁的截面只有竖向位移(沿对称轴方向)没有转角。
对称截面可取为滑动端。
弯矩二次分配法是一种近似计算方法,即将各节点的不平衡弯矩同时作分配和传递,并以两次分配为限。
(取一榀横向框架)2. 荷载传递路线2700对于边跨板,为7.2 m×4.5m,由于7.2/4.5<3.0 所以按双向板计算对于中跨板,为 4.5m×2. 7m,由于 4.5/2.7 〈3.0 所以按双向板计算6.2 竖向荷载计算5.2.1 A-B(C-D) 轴间框架梁板传至梁上的三角形或梯形荷载等效为均布荷载。
1. 屋面板传载恒载: 5.0 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=18.85kN/m活载:0.5 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=1.89kN/m2. 楼面板传荷载恒载: 3.99 ×4.5/2 ×(1-2 × 0.31 2+0.31 3) ×2=15.08kN/m活载: 2.0 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=7.56kN/m3. 梁自重: 5.46 kN/mA-B(C-D) 轴间框架梁均布荷载为:屋面梁:恒载=梁自重+板传荷载=5.46 kN/m+18.85 kN/m=24.31 kN/m 活载=板传荷载=1.89 kN/m楼面梁:恒载=梁自重+板传荷载=5.46 kN/m+15.08 kN/m=20.54 kN/m 活载=板传荷载=7.56 kN/m5.2.2 B-C 轴间框架梁1. 屋面板传载恒载: 5.0 ×2.4/2 ×5/8 ×2=8.44kN/m活载:0.5 ×2.7/2 ×5/8 ×2=0.84kN/m2. 楼面板传荷载恒载: 3.99 ×2.7/2 ×5/8 ×2=6.73kN/m活载: 2.0 ×2.7/2 ×5/8 ×2=4.22kN/m3. 梁自重: 3.9kN/mB-C 轴间框架梁均布荷载为:屋面梁:恒载=梁自重+板传荷载=3.9 kN/m+8.44kN/m=12.34kN/m 活载=板传荷载=0.84kN/m楼面梁:恒载=梁自重+板传荷载=3.9 kN/m+6.73kN/m=10.63kN/m 活载=板传荷载=4.22kN/m6.3 框架计算简图g=24.31KN/m g=12.34KN/m g=24.31KN/m(q=1.89KN/m)2700框架计算简图6.4. 梁固端弯矩梁端弯矩以绕杆端顺时针为正,反之为负。
土木工程毕业设计ZH03横向框架内力计算d.竖向活载内力计算
四、竖向活载作用下的横向框架(KJ-6)内力计算(一)、竖向活载计算1、屋面框架梁线载标准值屋面活载为0.7KN/m2屋面板传给边跨梁的线载为:0.7×1/2×(5+1)×2/5=0.84KN/m 屋面板传给中跨梁的线载为:0.7×1/2×1×2/2=0.35KN/m2、楼面框架梁线载标准值本例楼面、楼梯活载取2.0KN/m2。
楼面板传给边跨梁的线载为:2×1/2×(5+1)×2/5=2.4KN/m楼面板传给中跨梁的线载为:2×1/2×1×2/2=1KN/m3、屋面框架节点集中荷载标准值A柱(D柱)集中力:0.7×1/2×4×2/2=1.4KNB柱(C柱)集中力: 1.4+0.7×1/2×(4+2)×1=3.5KN4、楼面框架节点集中荷载标准值A柱(D柱)集中力:2×1/2×4×2/2=4KNB柱(C柱)集中力:4+2×1/2×(4+2)×1=10KN5、竖向活载作用下的结构计算简图(二)、竖向荷载作用下横向框架(KJ-6)内力计算 1、求各梁端的固端弯矩第五层 M AB = -M BA = M CD = -M DC =-121ql 2= -121×0.84×52= -1.75KNm M BC = -M CB =-121ql 2= -121×0.35×22= -0.12KNm 第一~四层 M AB = -M BA = M CD = -M DC = -121ql 2= -121×2.4×52= -5KNm M BC = -M CB =-121ql 2= -121×1×22 =-0.33KNm 2、计算各梁和柱的分配系数各梁柱的线刚度及相对线刚度如下图所示:梁柱的分配系数如下表所示:注:在计算分配系数时,除底层柱外的其余各层柱,其线刚度均应乘以折减系数0.9。
竖向荷载作用下框架结构的内力计算
竖向荷载作用下框架结构的内力计算6.1计算单元的选择确定取③轴线横向框架进行计算,如下图所示:图6.1框架计算简图计算单元宽度为6.4 m,由于房间内布置有次梁,故直接传给该框架的楼面荷载如图中的水平阴影所示。
计算单元范围内的其余楼面荷载则通过次梁和纵向框架梁以集中力的形式传给横向框架,作用于各节点上。
由于纵向框架梁的中心线与柱的中心线不重合,所以在框架节点上还作用有集中力矩。
6.2荷载计算6.2.1恒载作用下柱的内力计算:恒荷载作用下各层框架梁上的荷载分布如下图所示:2图6.2恒荷载作用下各层框架梁上的荷载分布图(1)、对于顶层屋面,q1、q1'代表横梁自重,为均布荷载形式。
q1=0.3×0.75×25=5.625kN/mq1'=0.3×0.75×25=5.625kN/mq2为屋面板传给横梁的梯形荷载。
q2=5.29×3.2=16.928kN/mP1、P2分别由边纵梁、中纵梁直接传给柱的恒载,它包括主梁自重、次梁自重、楼板重等重力荷载,计算如下:P1=6.4*0.3*0.75*25+8.5/2*0.25*0.6*25+5.29*3.2*1.6+(5.3+8.5)*1.6*5.29/4=108.223KN P2=6.4*0.3*0.75*25+6.4/2*0.25*0.6*25+5.29*3.2*1.6 +(3.2+6.4)*1.6*5.29/4=95.398KN P3=6.4*0.3*0.75*25+(8.5+6.4)*0.5*0.25*0.6*25+5.29*3.2*1.6*2++(3.2+6.4)*1.6*5.29/4= 190.64KN集中力矩M1=P1e1=108.223×(0.6 -0.3)/2=16.23kN·mM2=P2e2=147.23×(0.6 -0.3)/2=14.31kN·m(2)、对于3层,包括梁自重和其上横墙自重,为均布荷载,其它荷载的计算方法同第顶层。
土木工程毕业设计(优秀毕业设计)
摘要本设计主要进行了结构方案中横向框架20轴框架的抗震设计。
在确定框架布局之后,先进行了层间荷载代表值的计算,接着利用顶点位移法求出自震周期,进而按底部剪力法计算水平地震荷载作用下大小,进而求出在水平荷载作用下的结构内力(弯矩、剪力、轴力)。
接着计算竖向荷载(恒载及活荷载)作用下的结构内力,。
是找出最不利的一组或几组内力组合。
选取最安全的结果计算配筋并绘图。
此外还进行了结构方案中的室内楼梯的设计。
完成了平台板,梯段板,平台梁等构件的内力和配筋计算及施工图绘制。
整个结构设计分为三个阶段,结构方案阶段,结构计算阶段和施工图设计阶段。
关键词:框架结构设计抗震设计AbstractThe purpose of the design is to do the anti-seismic design in the longitudinal frames of axis 20. When the directions of the frames is determined, firstly the weight of each floor is calculated .Then the vibrate cycle is calculated by utilizing the peak-displacement method, then making the amount of the horizontal seismic force can be got by way of the bottom-shear force method. The seismic force can be assigned according to the shearing stiffness of the fra mes of the different axis. Then the internal force (bending moment, shearing force and axial force ) in the structure under the horizontal loads can be easily calculated. After the determination of the internal force under the dead and live loads, the combination of internal force can be made by using the Excel software, whose purpose is to find one or several sets of the most adverse internal force of the wall limbs and the coterminous girders, which will be the basis of protracting the reinforcing drawings of the components. The design of the stairs is also be approached by calculating the internal force and reinforcing such components as landing slab, step board and landing girder whose shop drawings are completed in the end. The structural design stage can be roughly divided into three stages, the structure of the programme stage, structural calculations of stage design and construction plans.Keywords : frames, structural design, anti-seismic design目录摘要 (I)Abstract (II)第1章绪论 (1)1.1 题目背景 (1)1.2 工程概况 (1)1.3设计内容与方法 (1)1.3.1建筑设计 (1)1.3.2结构设计 (1)第2章工程概况和建筑设计 (3)2.2建筑设计................................................. 错误!未定义书签。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章竖向荷载(恒载+活载)作用下框架内力计算第一节框架在恒载作用下的内力计算本设计用分层法计算内力,具体步骤如下:①计算各杆件的固端弯矩②计算各节点弯矩分配系数③弯矩分配④调幅并绘弯矩图⑤计算跨中最大弯矩、剪力和轴力并绘图一、恒载作用下固端弯矩计算(一)恒载作用下固端弯矩恒载作用下固端弯矩计算(单位:KN·m) 表6.1框架梁BC跨固端弯矩计算(单位:KN·m)结构三层(屋面)计算简图弯矩图结构二层计算简图弯矩图结构一层计算简图弯矩图楼层框架梁CD跨固端弯矩计算(单位:KN·m)结构三层(屋面)计算简图弯矩图节点3弯矩为125.68KN·m3单元最大负弯矩为131.01KN·m结构二层计算简图弯矩图结构一层计算简图弯矩图楼层框架梁D-1/D悬挑梁固端弯矩计算(单位:KN·m)结构一层计算简图弯矩图恒载作用下梁固端弯矩计算统计表6.2 结构层MBC(KN·m)MCB(KN·m)MCD(KN·m)MDC(KN·m)MD-1/D(KN·m)三层-65.98 65.98 -276.11 212.13 0二层-88.48 88.48 -429.29 315.57 0一层-88.48 88.48 -429.29 315.57 -295.93(二)计算各节点弯矩分配系数用分层法计算竖向荷载,假定结构无侧移,计算时采用力矩分配法,其计算要点是:①计算各层梁上竖向荷载值和梁的固端弯矩。
②将框架分层,各层梁跨度及柱高与原结构相同,柱端假定为固端。
③计算梁、柱线刚度。
对于柱,假定分层后中间各层柱柱端固定与实际不符,因而,除底层外,上层柱各层线刚度均乘以0.9修正。
有现浇楼面的梁,宜考虑楼板的作用。
每侧可取板厚的6倍作为楼板的有效作用宽度。
设计中,可近似按下式计算梁的截面惯性矩:一边有楼板:I=1.5Ir两边有楼板:I=2.0Ir④计算和确定梁、柱弯矩分配系数和传递系数。
按修正后的刚度计算各结点周围杆件的杆端分配系数。
所有上层柱的传递系数取1/3,底层柱的传递系数取1/2。
⑤按力矩分配法计算单层梁、柱弯矩。
⑥将分层计算得到的、但属于同一层柱的柱端弯矩叠加得到柱的弯矩。
(1)计算梁、柱相对线刚度图6.1 修正后梁柱相对线刚度(2)计算弯矩分配系数结构三层=5.37÷(5.37+1.18)=0.820①梁μB3C3μ=5.37÷(5.37+3.52+1.18)=0.533C3B3=3.52÷(5.37+3.52+1.18)=0.350μC3D3=3.52÷(3.52+1.18)=0.749μD3C3=1.18÷(5.37+1.18)=0.180②柱μB3B2=1.18÷(5.37+3.52+1.18)=0.117μC3C2=1.18÷(3.52+1.18)=0.251μD3D2结构二层①梁μ=5.37÷(1.18+1.18+5.37)=0.695B2C2=5.37÷(1.18+1.18+5.37+3.52)=0.477μC2B2μ=3.52÷(1.18+1.18+5.37+3.52)=0.313 C2D2=3.52÷(1.18+1.18+3.52)=0.5986 μD2C2=1.18÷(1.18+1.18+5.37)=0.1525②柱μB2B3μ=1.18÷(1.18+1.18+5.37)=0.1525B2B1=1.18÷(1.18+1.18+5.37+3.52)=0.105 μC2C3μ=1.18÷(1.18+1.18+5.37+3.52)=0.105 C2C1=1.18÷(1.18+1.18+3.52)=0.2007 μD2D3μ=1.18÷(1.18+1.18+3.52)=0.2007D2D1结构一层=5.37÷(1.18+1+5.37)=0.711①梁μB1C1=5.37÷(1.18+1+5.37+3.52)=0.485 μC1B1=3.52÷(1.18+1+5.37+3.52)=0.318 μC1D1=3.52÷(1.18+1+3.52)=0.618μD1C1=1.18÷(1.18+1+5.37)=0.156②柱μB1B2=1÷(1.18+1+5.37)=0.133μB1B0=1.18÷(1.18+1+5.37+3.52)=0.107μC1C2=1÷(1.18+1+5.37+3.52)=0.090μC1C0μ=1.18÷(1.18+1+3.52)=0.207D1D2μ=1÷(1.18+1+3.52)=0.175D1D0(三)分层法算恒载作用下弯矩恒载作用下结构三层弯矩分配表6.3B C D上柱偏心弯矩分配系数0固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配14.650 -13.883 226.915 20.861 -251.346 84.509 -112.810 二次分配14.512 -14.512 228.818 21.278 -250.096 105.707 -105.707恒载作用下结构二层弯矩分配表6.40.768 12.717 -28.301↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配 6.931 4.431 -4.607 308.811 46.295 47.232 -385.113 169.804 -113.072 -92.837二次分配 5.901 3.401 -9.302 300.595 44.486 45.423 -390.504 191.416 -105.826 -85.591恒载作用下结构一层弯矩分配表6.52.127 9.081 -7.935↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次二次7.030 5.338 -12.368 267.469 35.352 22.097 -324.919 357.349 -46.247 -15.172 -295.930图6.2 弯矩再分配后恒载作用下弯矩图(KN·m)(四)框架梁弯矩塑性调幅为了减少钢筋混凝土框架梁支座处的配筋数量,在竖向荷载作用下可以考虑竖向内力重分布,主要是降低支座负弯矩,以减小支座处的配筋,跨中则应相应增大弯矩。
《高层建筑混凝土结构技术规程》(JGJ3-2010)5.2.3条:在竖向荷载作用下,可考虑框架梁端塑性变形内力重分布对梁端负弯矩乘以调幅系数进行调幅,并应符合下列规定:①装配整体式框架梁端负弯矩调幅系数可取为0.7~0.8,现浇框架梁端负弯矩调幅系数可取为0.8~0.9;②框架梁端负弯矩调幅后,梁跨中弯矩应按平衡条件相应增大;③应先对竖向荷载作用下框架梁的弯矩进行调幅,再与水平作用产生的框架梁弯矩进行组合;④截面设计时,框架梁跨中截面正弯矩设计值不应小于竖向荷载作用下按简支梁计算的跨中弯矩设计值的50%。
本设计取梁端支座负弯矩调幅系数可取为0.85。
='(计算过程从略).0M85M图6.3 调幅后恒载作用下弯矩图(KN·m)(五)恒载作用下梁跨内最大弯矩、梁端剪力和柱轴力计算1.恒载作用下梁跨内最大弯矩计算本设计计算梁跨内最大弯矩时,采用按简支计算时的梁跨内最大弯矩与计算得的调幅后的梁端弯矩进行叠加得到。
计算过程计算如下:简支条件下恒载作用下固端弯矩计算表6.6 楼层框架梁BC跨固端弯矩计算(单位:KN·m)结构三层(屋面)计算简图弯矩图调幅后弯矩图结构二层计算简图弯矩图调幅后弯矩图结构一层计算简图弯矩图调幅后弯矩图楼层框架梁CD跨固端弯矩计算(单位:KN·m)结构一层计算简图弯矩图节点3弯矩大小为381.80KN·m,单元(3)跨内最大弯矩为382.73 KN·m 调幅后弯矩图结构二层计算简图弯矩图调幅后弯矩图结构一层计算简图弯矩图调幅后弯矩图楼层框架梁D-1/D悬挑梁固端弯矩计算(单位:KN·m)结构一层计算简图弯矩图调幅后弯矩图2.跨中最大弯矩(1)对于BC跨结构三层(屋面层)在简支条件下叠加调幅后弯矩剪力图如下剪力为0处距离B点距离:ml70.1)81.507.707.7(93.33=++÷=剪力为0处弯矩:mKNM•-=+⨯++⨯+⨯-=52.16335.1270.1)81.507.707.7(2170.193.332结构二层剪力为0处距离B点距离:ml68.1)81.574.1001.501.5(96.44=+++÷=剪力为0处弯矩:mKN M•-=+⨯++⨯⨯+⨯-=26.24907.768.1)81.574.10210.5(2168.194.442结构一层剪力为0处距离B 点距离:m l 71.1)81.574.1001.501.5(37.45=+++÷= 剪力为0处弯矩:m KN M •-=+⨯++⨯⨯+⨯-=96.27513.1071.1)81.574.10210.5(2171.137.452 (2)对于CD 跨 结构三层(屋面层)在简支条件下叠加调幅后弯矩剪力图如下剪力为0处距离C 点距离:m l 04.43)81.5207.7()96.9907.73212381.537.159(=++⨯÷-⨯⨯⨯-⨯-=剪力为0处距离D 点距离:m l 56.504.46.9=-= 剪力为0处弯矩:m KN M •-=+⨯+⨯⨯+⨯-=39.218851.8956.5)81.5207.7(2156.590.1102结构二层剪力为0处距离C 点距离:m l 53.33)74.1081.5210.5()18910.53212381.587.235(=+++⨯÷-⨯⨯⨯-⨯-=剪力为0处距离D 点距离:m l 07.653.36.9=-= 剪力为0处弯矩:m KN M •-=+⨯++⨯⨯+⨯-=32.330704.16207.6)74.1081.5210.5(2107.641.1622 结构一层在节点3处,剪力有突变,由182.64突变为KN V 36.618910.53212381.537.215-=-⨯⨯⨯-⨯-=故剪力为0处距离C 点距离:m l 3= 剪力为0处距离D 点距离:m l .636.9=-= 剪力为0处弯矩:m KN M •-=+⨯++⨯⨯+⨯-=21.312747.3036)74.1081.5210.5(21691.1822 本设计取调幅后的梁跨内弯矩最大值和简支时梁跨内弯矩最大值的50%中的较大者,比较如下表:梁跨内弯矩最大值取值 表7.7 楼层 BC 跨CD 跨m ax Mm axM20maxM 取值 m ax M0m axM20maxM 取值 三层 16.52 98.98 49.49 49.49 218.39 382.73 191.365 218.39 二层 24.26 132.71 66.355 66.355 330.32 605.63 302.815 330.32 一层27.96132.7166.35566.355312.21605.63302.815312.21m ax m ax M 依据上表绘制恒载作用下B ~D 轴×○3轴框架弯矩图如下图6.4 恒载作用下B~D轴×○3轴框架弯矩图(KN·m)3.恒载作用下梁、柱端剪力计算梁端剪力计算计算方法为取隔离体进行计算,具体计算如下:屋顶层BC跨M对B取矩=0BV C×6.3+12.335=194.495+(7.07×2+5.81)×6.3×3.15,故V C=91.76KN M对C取矩∑=0CV B×6.3+194.495=12.335+(7.07×2+5.81)×6.3×3.15,故V B=33.93KN对C取矩∑=0CMV D×9.6+212.582=89.851+5.81×9.6×4.8+7.07×3×1.5+14.14×6.6×6.3+99.96×3,故V D=110.90KN对D取矩∑=0DMV C×9.6+89.851=212.582+5.81×9.6×4.8+7.07×3×8.1+14.14×6.6×3.3+99.96×6.6, 故V C=159.37KN其他剪力计算类似,因此计算过程省略,以下汇总剪力:梁截面剪力(单位:KN.m) 表6.8VB3=VB2=(-14.512-5.901)÷4.2=-4.86KN综上,其他柱计算类似。
