用EXCEL求解最短路径问题
巧用Excel规划求解最短路径

= m i n { d i s t [ j ] , d i s t [ i ] + ma t r i x [ i ] [ j l } ) ; 直到
U= V, 停 止。
/ ¥ D U k s t r a 算法代 码c 语 言实现 : /
据” 选项卡中出现 “ 分 析” 选项组 , 菜 单
从i 到k 的最短路径。 例如, 对于源顶点
V0 , 首先 选 择其 直 接相 邻的顶 点中长
{
蕊衅= M A x ; / / 若_ 不与v O 直
度最 短 的顶 点v i , 那 么通 过 已知 可得
接相邻, 则权值置为无穷大
| 1 4 l l
f 2 0
行 . m a t r i x [ v O I i 0 & 披j ! = v O )
{
蕊噼_ g .  ̄t r Rv O l i ] ; p ( i } = = v O ; / / a p e r 记录最
为了求出最短路径, D i j k s t r a 就提
出了以最 短 路 径 长度 递 增 , 逐 次生 成
f o r t f = l ; i < g 冲
展 帙
/ / 循环扩
抵达地
出发 地 A学校 B学校 C学校 D学校 E学校 F学校 G学校 H学校 I学 校
{
i r r 0 mi n =I N T MAX ;
_
A学校 B学校
C学校 D学校 E学校
从V 0 到V j 顶点的最短距离d i s t [ j ] = mi n { d i s t [ j 】 , d i s t [ i ] + m a t r i x [ i [ j ] } 。 根据这种 思路, 假设存在G = < V, E >, 源顶点为 V 0 , u = { V 0 } , d i s t [ i 】 { 己 录V O 到i 的最短距 离, p a t h [ i ] i  ̄ 录从V 0 到i 路径上的i 前面
EXCEL规划求解功能操作说明

E X C E L规划求解功能操作说明集团标准化办公室:[VV986T-J682P28-JP266L8-68PNN]Excel规划求解功能操作说明以Microsoft Excel2003为例,说明使用Excel的求解线性规划问题功能的使用方法。
一、加载规划求解功能1.点击【工具】按钮,在下拉菜单中选择【加载宏】功能。
2.在弹出的【可加载宏】选项卡中勾选【规划求解】,点击确定按钮。
此时,【工具】下拉菜单中增加规划求解功能,表示加载成功。
二、构造表格Excel表格并填入各项数据以教材18页【例题2-8】为例,构造表格如下:标题栏约束条件区目标函数区计算结果显示区1.录入约束条件系数约束条件(1)为5x 1+x 2-x 3+x 4=3,则在约束系数的第一行的x 1,x 2,x 3,x 4,x 5,限制条件,常数b 列下分别录入5,1,-1,1,0,=,3如下图所示。
约束系数区的第二行录入约束条件(2)的系数、限制符号及常数b ,即-10,6,2,0,1,=,2;约束系数区的第三行录入约束条件(3)(x1≥0)的系数、限制符号及常数b,即1,0,0,0,0,≥,0;约束系数区的第四行录入约束条件(4)(x2≥0)的系数、限制符号及常数b,即0,1,0,0,0,≥,0;约束系数区的第五行录入约束条件(5)(x3≥0)的系数、限制符号及常数b,即0,0,1,0,0,≥,0;约束系数区的第六行录入约束条件(6)(x4≥0)的系数、限制符号及常数b,即0,0,0,1,0,≥,0;约束系数区的第七行录入约束条件(7)(x5≥0)的系数、限制符号及常数b,即0,0,0,0,1,≥,0。
如下图所示。
2.录入目标函数系数目标函数为maxZ=4x1-2x2-x3,则在目标函数的x1,x2,x3,x4,x5列下分别录入4,-2,-1,0,0,如下图所示。
3. 录入约束条件的计算公式双击约束条件(1)行的“总和”单元格,录入以下内容:“=B3*B12+C3*C12+D3*D12+E3*E12+F3*F12”说明:录入的内容即是约束条件(1)的计算公式,其中“B3*B12”代表5x1; “C3*C12”代表1x2;“D3*D12”代表-1x3;“E3*E12”代表1x4;“F3*F12”代表0x5。
运筹学最短路问题excel求解

Microsoft Excel 11.0 运算结果报告工作表 [20103848李园园.xls]Sheet1报告的建立: 2003-1-19 6:23:54目标单元格 (最小值)单元格名字初值终值$E$13V7010可变单元格单元格名字初值终值$D$2V2 路径00$D$3V5 路径01$D$4V7 路径00$D$5V5 路径00$D$6V2 路径00$D$7V6 路径00$D$8V3 路径00$D$9V8 路径00$D$10V6 路径01$D$11V8 路径01$D$12V5 路径00$D$13V7 路径00约束单元格名字单元格值公式状态型数值$G$2V1 网络流1$G$2>=$H$2到达限制值0 $G$3V2 网络流0$G$3=$H$3未到限制值0 $G$4V3 网络流0$G$4=$H$4未到限制值0 $G$5V4 网络流0$G$5=$H$5未到限制值0 $G$6V5 网络流0$G$6=$H$6未到限制值0 $G$7V6 网络流0$G$7=$H$7未到限制值0 $G$8V7 网络流0$G$8=$H$8未到限制值0 $D$2V2 路径0$D$2=二进制到达限制值0 $D$3V5 路径1$D$3=二进制到达限制值0 $D$4V7 路径0$D$4=二进制到达限制值0 $D$5V5 路径0$D$5=二进制到达限制值0 $D$6V2 路径0$D$6=二进制到达限制值0 $D$7V6 路径0$D$7=二进制到达限制值0 $D$8V3 路径0$D$8=二进制到达限制值0 $D$9V8 路径0$D$9=二进制到达限制值0 $D$10V6 路径1$D$10=二进制到达限制值0 $D$11V8 路径1$D$11=二进制到达限制值0 $D$12V5 路径0$D$12=二进制到达限制值0 $D$13V7 路径0$D$13=二进制到达限制值0。
excel最短路问题求解模型
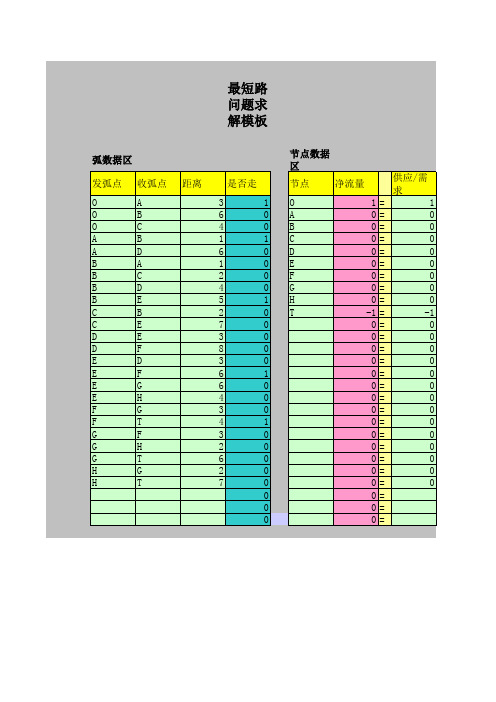
最短路问题求解模板需要对发弧点、收 弧点、距离、节点(节点名称字符随便,但 必须与发弧点和收弧点一致)和供应/需求 栏数据的录入,这里要求供应/需求栏数据 发点为‘1’,收点为“-1”,其余为‘0’。 录完数据,点“工具”→“规划求 解”→“求解”后,在“是否走”栏显示最 优解、“净流量”栏显示相应的约束条件实 际值,最优值显示在N6单元格。 注:使用本模板时,模板中的浅灰色区 域是录入数据的区域;黄色区域是标示区, 尽量不要修改;深浅灰色区域是系统显示最 优解数据的区域,也尽量不要修改;红色区 域中都录有公式,禁止往这些单元格中录入 数据。
最短路问题求解模板
弧数据区 发弧点 O O O A A B B B B C C D D E E E E F F G G G H H 收弧点 A B C B D A C D E B E E F D F G H G T F H T G T 距离 3 6 4 1 6 1 2 4 5 2 7 3 8 3 6 6 4 3 4 3 2 6 2 7 是否走 1 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 节点数据区 节点 净流量 O 1 A 0 B 0 C 0 D 0 E 0 F 0 G 0 H 0 T -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 = = = = = = = = = = = = = = = = = = = = = = = = = = = 供应/需求 1 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Excel中的逻辑函数和条件求最小值的应用方法

Excel中的逻辑函数和条件求最小值的应用方法随着电子表格软件Excel的广泛应用,逻辑函数和条件求最小值的应用方法也变得越来越重要。
在许多工作场景中,我们需要根据一定的条件来确定一组数据中的最小值。
Excel提供了多种逻辑函数和条件求最小值的方法,下面将介绍一些常用的应用方法。
1. IF函数IF函数是Excel中最常用的逻辑函数之一。
它的基本语法为:```IF(逻辑表达式, 值为真时的结果, 值为假时的结果)```逻辑表达式可以是任何返回TRUE或FALSE的表达式,值为真时的结果和值为假时的结果可以是一个具体的数值、文本或者其他函数。
要使用IF函数求最小值,我们可以将逻辑表达式设置为判断条件,值为真时的结果设置为要比较的数值,值为假时的结果设置为一个较大的数值。
例如,假设有一组数据在A1到A10的单元格中,我们想要找到其中最小的正数,并将结果显示在B1单元格中,可以使用如下公式:```=MIN(IF(A1:A10>0, A1:A10, 9999))```注意,这是一个数组公式,需要按下Ctrl+Shift+Enter来确认。
2. MIN函数和条件筛选MIN函数是Excel中用于求最小值的函数。
它的基本语法为:```MIN(数值1, 数值2, ...)```我们可以直接在MIN函数中输入需要比较的数值,也可以通过条件筛选来选择需要比较的数值范围。
例如,假设有一组数据在A1到A10的单元格中,我们想要找到其中大于0的最小值,并将结果显示在B1单元格中,可以使用如下公式:```=MIN(IF(A1:A10>0, A1:A10))```同样,这也是一个数组公式,需要按下Ctrl+Shift+Enter来确认。
3. SMALL函数和条件筛选SMALL函数也是Excel中用于求最小值的函数,但它可以求解一组数据中的第k个最小值。
它的基本语法为:```SMALL(数值数组, k)```其中,数值数组是需要比较的一组数据,k表示要求解的第几个最小值。
【必须收藏】只用60秒就能解决的Excel线性规划,你却熬了整个通宵...

【必须收藏】只用60秒就能解决的Excel线性规划,你却熬
了整个通宵...
箭头处“蓝色字”,
每天学一个表格技能!
领导给小王同志12个金额,让他凑数据,凑成26005元和33459元。
左拼右凑这个金额,凑了一个通宵,还没凑对,十分着急,同事3分钟就给解决了
❶在Excel中调出线性规划我们在Excel选项里面,找到加载项然后勾选规划求解加载项,点击确定
❷我们在C1单元格输入公式:=SUMPRODUCT(A2:A13*B2:B13)
❸前面加载了加载项之后,在数据选项卡下,就有了规划求解进行相关设置后,运行得到最终的结果,操作动图如下所示:
其中的设置是,设置目标是C1单元格,目标值是26005,可变的单元格区域是B2:B13,遵守约束是B2:B13是二进制
最终B2:B13单元格中的数据为1的这些值累加起来,正好就能得到我们需要的26005了
剩下的数据正好就是33459元了。
模糊凑数据
如果给定的一个金额是系统也不可能准确的凑出来,Excel一直在计算的过程中的时候,可以随时按ESC退出
或者我们改变公式,使得进行模糊的凑数据接近这个值,我们现在要把这些数据最接近30000
我们可以在C1输入公式:=ABS(SUMPRODUCT(A2:A13,B2:B13)-30000)
然后在线性规划中的设置是:C1是最小值
然后运行,这个时候,会一直在那里转,这个时候,我们需要按ESC,然后
保留求解
得到了一组结果。
这个例子还是找到了正好等于30000的数据。
如果不等于的话,那么会得出一个最接近的结果。
当然,平时不用这个功能的时候,需要把这个功能给关闭了,否则每次打开Excel的速度会变慢一点。
巧用Excel规划求解最短路径
巧用Excel规划求解最短路径作者:周忠林许大宏来源:《中国信息技术教育》2013年第11期● Excel规划求解的功能概述Excel具有规划求解的基本功能,包括线性规划和非线性规划。
对于常规的线性规划问题,Excel就可以给出求解结果。
借助规划求解,可求得工作表上某个单元格中公式的最优值。
规划求解将对直接或间接与目标单元格中公式相关联的一组单元格中的数值进行调整,最终在目标单元格公式中求得期望的结果。
● 加载规划求解功能在Excel2003版本中,通过点击菜单“工具→宏→加载宏”,加载规划求解加载项,便可加载该宏。
在Excel2007版本中,通过点击Office按钮,点击“Excel选项→加载项→转到Excel 加载项”,然后加载规划求解加载项,便可以加载规划求解的宏。
在Excel2010版本中,通过点击“文件”选项卡打开“Excel选项”对话框,单击左侧“加载项”标签,在右侧单击“转到”按钮,打开“加载宏”对话框,勾选“规划求解加载项”复选框,单击“确定”按钮,即可在工具栏的“数据”选项卡中出现“分析”选项组,菜单上面就有了“规划求解”按钮。
● 案例王老师从学校A到学校I参加会议,途中需要经过一些学校,学校之间的距离和线路已在图1中标明,请帮王老师规划一下,在不影响去学校I最短距离的情况下,顺便探访其他学校,请将路线描述出来。
1.Dijkstra算法描述及C语言函数实现为了求出最短路径,Dijkstra就提出了以最短路径长度递增,逐次生成最短路径的算法。
即如果存在一条从i到j的最短路径(Vi...Vk,Vj),Vk是Vj前面的一个顶点,那么(Vi...Vk)也必定是从i到k的最短路径。
例如,对于源顶点V0,首先选择其直接相邻的顶点中长度最短的顶点Vi,那么通过已知可得从V0到Vj顶点的最短距离dist[j]=min{dist[j],dist[i]+matrix[i][j]}。
根据这种思路,假设存在G=,源顶点为V0,U={V0},dist[i]记录V0到i 的最短距离,path[i]记录从V0到i路径上的i前面的一个顶点。
excel 函数 最优路径 计算
Excel函数在实际工作中扮演着重要的角色,它们能够帮助用户完成多种复杂的计算任务。
其中,最优路径计算是Excel函数中的一个重要应用场景,它可以帮助用户在给定的一组数据中找到最优的路径,并计算出最短路径或最优解。
本文将详细介绍Excel函数在最优路径计算中的应用,希望能够为读者提供有益的信息。
一、最优路径计算的应用场景最优路径计算通常用于解决一些实际问题,比如物流配送、旅行路线规划等。
在这些场景下,用户需要根据一定的条件和约束条件,找到一条最短路径或最优路径。
最优路径计算能够帮助用户在海量数据中快速找到最佳解决方案,提高工作效率。
二、Excel函数在最优路径计算中的应用在Excel中,用户可以借助一些常用的函数来进行最优路径计算,比如VLOOKUP、INDEX、MATCH等。
这些函数能够帮助用户快速查找和匹配数据,从而实现最优路径的计算和规划。
1. VLOOKUP函数VLOOKUP函数是Excel中常用的查找函数,它可以根据指定的数值在数据表中进行垂直查找,并返回相关的数值。
在最优路径计算中,用户可以借助VLOOKUP函数快速查找并获取相关的路径信息,从而对数据进行分析和规划。
2. INDEX函数INDEX函数可以根据指定的行号和列号返回数据区域中的数值。
在最优路径计算中,用户可以利用INDEX函数来获取指定路径中的相关数据,从而进行路径的比较和分析。
3. MATCH函数MATCH函数可以在数据区域中查找指定的数值,并返回它在数据区域中的位置。
在最优路径计算中,用户可以借助MATCH函数对路径进行匹配和比较,从而找到最短路径或最优解。
三、最优路径计算的实际案例为了更好地说明最优路径计算在Excel中的应用,我们举一个实际案例来进行分析。
假设某公司有多个仓库和多个客户,需要在给定的条件下规划最佳的配送路径。
在这种情况下,可以使用Excel函数进行最优路径的计算和规划。
1. 用户可以将仓库和客户的位置信息录入Excel表格中,包括经纬度等相关信息。
solve函数
solve函数
Solve函数是Excel中一项有用的功能,它可以帮助我们解决复杂的数学问题。
它使用简单的方法解决复杂的数学模型,比如线性规划,非线性规划,网络流,最短路径和最优化等问题。
Solve函数属于Excel优化工具箱,支持Microsoft Office Excel 2003和更高版本。
使用此函数,您可以在Excel中结合函数,公式和约束条件来解决数学模型。
使用Solve函数,可以在Excel中创建有效的模型,以及指定结果和变量。
例如,您可以指定最大值作为结果,并使用变量来表示不同的输入值。
然后,您可以使用Solve函数解决该模型,获得最佳的输入值。
Solve函数的另一个优点是它可以支持Excel中的其他函数,例如MAX,MIN和SUM等。
使用这些函数,您可以创建复杂的数学模型,并使用Solve函数来解决它们。
总而言之,Solve函数是Excel中一个有用的功能,它可以帮助我们解决复杂的数学问题,并支持Excel中的其他函数。
使用它,您可以在Excel中构建复杂的数学模型,并解决它们以获得最佳结果。
如何在Excel中使用函数计算最大值和最小值
如何在Excel中使用函数计算最大值和最小值在Excel中,函数是帮助我们进行各种数学和逻辑运算的强大工具。
其中,计算最大值和最小值是常见的需求之一。
本文将介绍如何在Excel中使用函数来计算最大值和最小值。
一、使用MAX函数计算最大值MAX函数是Excel中常用的函数之一,它可以计算一组数值中的最大值。
以下是使用MAX函数计算最大值的步骤:1. 打开Excel,并创建一个新的工作表。
2. 在工作表中选择一个单元格作为计算结果的位置。
3. 输入以下公式:=MAX(数值1, 数值2, ...)其中,数值1、数值2等为你需要比较的数值。
4. 按下回车键,即可得到计算结果,该结果为所选数值中的最大值。
举例来说,假设你有一列成绩数据,要计算其中的最高分。
你可以在一个单元格中输入以下公式:=MAX(A1:A10)其中,A1到A10为你所需计算的成绩数据范围。
二、使用MIN函数计算最小值MIN函数与MAX函数类似,它可以帮助我们计算一组数值中的最小值。
以下是使用MIN函数计算最小值的步骤:1. 打开Excel,并创建一个新的工作表。
2. 在工作表中选择一个单元格作为计算结果的位置。
3. 输入以下公式:=MIN(数值1, 数值2, ...)其中,数值1、数值2等为你需要比较的数值。
4. 按下回车键,即可得到计算结果,该结果为所选数值中的最小值。
举例来说,假设你有一列成绩数据,要计算其中的最低分。
你可以在一个单元格中输入以下公式:=MIN(A1:A10)其中,A1到A10为你所需计算的成绩数据范围。
三、使用IF函数结合MAX和MIN计算条件最值除了使用MAX和MIN函数来计算一组数值的最大值和最小值外,我们还可以结合IF函数使用,实现更灵活的条件最值计算。
IF函数是一个逻辑函数,它可以根据指定的条件返回不同的结果。
以下是使用IF函数结合MAX和MIN计算条件最值的步骤:1. 打开Excel,并创建一个新的工作表。
