高等数学作业下-5 (答案)
高等数学(下)课后习题答案

高等数学(下)习题七1. 在空间直角坐标系中,定出下列各点的位置:A(1,2,3); B(-2,3,4); C(2,-3,-4);D(3,4,0); E(0,4,3); F(3,0,0).解:点A在第Ⅰ卦限;点B在第Ⅱ卦限;点C在第Ⅷ卦限;点D在xOy面上;点E在yOz面上;点F在x轴上.2. xOy坐标面上的点的坐标有什么特点?yOz面上的呢?zOx面上的呢?答: 在xOy面上的点,z=0;在yOz面上的点,x=0;在zOx面上的点,y=0.3. x轴上的点的坐标有什么特点?y轴上的点呢?z轴上的点呢?答:x轴上的点,y=z=0;y轴上的点,x=z=0;z轴上的点,x=y=0.4. 求下列各对点之间的距离:(1)(0,0,0),(2,3,4);(2)(0,0,0),(2,-3,-4);(3)(-2,3,-4),(1,0,3);(4)(4,-2,3),(-2,1,3).解:(1)s=(2) s==(3) s=(4) s==.5. 求点(4,-3,5)到坐标原点和各坐标轴间的距离.解:点(4,-3,5)到x轴,y轴,z轴的垂足分别为(4,0,0),(0,-3,0),(0,0,5).s==故s==xs==ys==.5z6. 在z轴上,求与两点A(-4,1,7)和B(3,5,-2)等距离的点.解:设此点为M(0,0,z),则222222-++-=++--(4)1(7)35(2)z z解得149z=即所求点为M(0,0,149).7. 试证:以三点A(4,1,9),B(10,-1,6),C(2,4,3)为顶点的三角形是等腰直角三角形.证明:因为|AB|=|AC|=7.且有|AC|2+|AB|2=49+49=98=|BC|2.故△ABC为等腰直角三角形.8. 验证:()()++=++a b c a b c.证明:利用三角形法则得证.见图7-1图7-19. 设2,3.u v=-+=-+-a b c a b c 试用a, b, c表示23.u v-解:232(2)3(3)2243935117u v-=-+--+-=-++-+=-+a b c a b ca b c a b ca b c10. 把△ABC的BC边分成五等份,设分点依次为D1,D2,D3,D4,再把各分点与A 连接,试以AB=c,BC=a表示向量1D A,2D A,3D A和4D A.解:1115D A BA BD=-=--c a2225D A BA BD=-=--c a3335D A BA BD=-=--c a444.5D A BA BD=-=--c a11. 设向量OM的模是4,它与投影轴的夹角是60°,求这向量在该轴上的投影.解:设M的投影为M',则1Pr j cos604 2.2uOM OM=︒=⨯=12. 一向量的终点为点B(2,-1,7),它在三坐标轴上的投影依次是4,-4和7,求这向量的起点A的坐标.解:设此向量的起点A的坐标A(x, y, z),则{4,4,7}{2,1,7}AB x y z =-=----解得x =-2, y =3, z =0故A 的坐标为A (-2, 3, 0).13. 一向量的起点是P 1(4,0,5),终点是P 2(7,1,3),试求:(1) 12PP 在各坐标轴上的投影; (2) 12PP 的模;(3) 12PP 的方向余弦; (4) 12PP 方向的单位向量.解:(1)12Pr j 3,x x a PP ==12Pr j 1,y y a PP == 12Pr j 2.z z a PP ==-(2) 12(7PP == (3) 12cos 14xa PP α== 12cos 14ya PP β==12cos 14za PP γ==(4) 12012{14PPPP ===-e j . 14. 三个力F 1=(1,2,3), F 2=(-2,3,-4), F 3=(3,-4,5)同时作用于一点. 求合力R 的大小和方向余弦.解:R =(1-2+3,2+3-4,3-4+5)=(2,1,4)||==Rcos coscos αβγ=== 15. 求出向量a = i +j +k , b =2i -3j +5k 和c =-2i -j +2k 的模,并分别用单位向量,,a b c e e e 来表达向量a , b , c .解:||==a||==b||3==c, , 3. a b c ==a b c e16. 设m =3i +5j +8k , n =2i -4j -7k , p =5i +j -4k ,求向量a =4m +3n -p 在x 轴上的投影及在y 轴上的分向量.解:a =4(3i +5j +8k )+3(2i -4j -7k )-(5i +j -4k )=13i +7j +15k在x 轴上的投影a x =13,在y 轴上分向量为7j .17. 向量r 与三坐标轴交成相等的锐角,求这向量的单位向量e r .解:因αβγ==,故23cos 1 α=,cos αα==则{cos ,cos ,cos })r αβγ===++e i j k . 18. 已知两点M 1(2,5,-3),M 2(3,-2,5),点M 在线段M 1M 2上,且123M M MM =,求向径OM 的坐标.解:设向径OM ={x , y , z }12{2,5,3}{3,2,5}M M x y z MM x y z =--+=----因为,123M M MM = 所以,11423(3)153(2) 433(5)3x x x y y y z z z ⎧=⎪-=-⎧⎪⎪⎪-=--⇒=-⎨⎨⎪⎪+=-⎩=⎪⎪⎩故OM ={111,,344-}. 19. 已知点P 到点A (0,0,12)的距离是7,OP 的方向余弦是236,,777,求点P 的坐标. 解:设P 的坐标为(x , y , z ),2222||(12)49PA x y z =++-=得2229524x y z z ++=-+126570cos 6, 749z z γ==⇒==又122190cos 2, 749x x α==⇒==123285cos 3, 749y y β==⇒== 故点P 的坐标为P (2,3,6)或P (190285570,,494949). 20. 已知a , b 的夹角2π3ϕ=,且3,4a b ==,计算: (1) a ·b ; (2) (3a -2b )·(a + 2b ). 解:(1)a ·b =2π1cos ||||cos3434632ϕ⋅⋅=⨯⨯=-⨯⨯=-a b (2) (32)(2)3624-⋅+=⋅+⋅-⋅-⋅a b a b a a a b b a b b2223||44||334(6)41661.=+⋅-=⨯+⨯--⨯=-a a b b21. 已知a =(4,-2, 4), b =(6,-3, 2),计算:(1)a ·b ; (2) (2a -3b )·(a + b ); (3)2||-a b解:(1)46(2)(3)4238⋅=⨯+-⨯-+⨯=a b(2) (23)()2233-⋅+=⋅+⋅-⋅-⋅a b a b a a a b a b b b 222222222||3||2[4(2)4]383[6(3)2]23638349113=-⋅-=⨯+-+--+-+=⨯--⨯=-a a b b(3) 222||()()2||2||-=-⋅-=⋅-⋅+⋅=-⋅+a b a b a b a a a b b b a a b b 36238499=-⨯+=22. 已知四点A (1,-2,3),B (4,-4,-3),C (2,4,3),D (8,6,6),求向量AB 在向量CD 上的投影.解:AB ={3,-2,-6},CD ={6,2,3}Pr j CD AB CD AB CD ⋅=4.7==- 23. 设重量为100kg 的物体从点M 1(3, 1, 8)沿直线移动到点M 2(1,4,2),计算重力所作的功(长度单位为m ).解:取重力方向为z 轴负方向,依题意有f ={0,0, -100×9.8}s = 12M M ={-2, 3,-6}故W = f ·s ={0,0,-980}·{-2,3,-6}=5880 (J)24. 若向量a +3b 垂直于向量7a -5b ,向量a -4b 垂直于向量7a -2b ,求a 和b 的夹角. 解: (a +3b )·(7a -5b )=227||1615||0+⋅-=a a b b ①(a -4b )·(7a -2b ) = 227||308||0-⋅+=a a b b ② 由①及②可得:222221()1||||2||||4⋅⋅⋅==⇒=a b a b a b a b a b 又21||02⋅=>a b b ,所以1cos ||||2θ⋅==a b a b , 故1πarccos 23θ==. 25. 一动点与M 0(1,1,1)连成的向量与向量n =(2,3,-4)垂直,求动点的轨迹方程. 解:设动点为M (x , y , z )0{1,1,1}M M x y z =---因0M M n ⊥,故00M M n ⋅=.即2(x -1)+3(y-1)-4(z-1)=0整理得:2x +3y-4z-1=0即为动点M 的轨迹方程.26. 设a =(-2,7,6),b =(4, -3, -8),证明:以a 与b 为邻边的平行四边形的两条对角线互相垂直.证明:以a ,b 为邻边的平行四边形的两条对角线分别为a +b ,a -b ,且a +b ={2,4, -2}a-b ={-6,10,14}又(a +b )·(a-b )= 2×(-6)+4×10+(-2)×14=0故(a +b )⊥(a-b ).27. 已知a =3i +2j -k , b =i -j +2k ,求:(1) a ×b ;(2) 2a ×7b ;(3) 7b ×2a ; (4) a ×a .解:(1) 211332375122111--⨯=++=----a b i j k i j k(2) 2714()429870⨯=⨯=--a b a b i j k(3) 7214()14()429870⨯=⨯=-⨯=-++b a b a a b i j k(4) 0⨯=a a .28. 已知向量a 和b 互相垂直,且||3, ||4==a b .计算:(1) |(a +b )×(a -b )|;(2) |(3a +b )×(a -2b )|.(1)|()()|||2()|+⨯-=⨯-⨯+⨯-⨯=-⨯a b a b a a a b b a b b a bπ2||||sin 242=⋅⋅=a b (2) |(3)(2)||362||7()|+⨯-=⨯-⨯+⨯-⨯=⨯a b a b a a a b b a b b b aπ734sin 842=⨯⨯⨯= 29. 求垂直于向量3i-4j-k 和2i-j +k 的单位向量,并求上述两向量夹角的正弦. 解:411334555111221----⨯=++=--+--a b i j k i j k与⨯a b平行的单位向量)||⨯==--+⨯a b e i j k a b||sin ||||θ⨯===⨯a b a b . 30. 一平行四边形以向量a =(2,1,-1)和b =(1,-2,1)为邻边,求其对角线夹角的正弦. 解:两对角线向量为13=+=-l a b i j ,232=-=+-l a b i j k因为12|||2610|⨯=++l l i j k12||||==l l 所以1212||sin 1||||θ⨯===l l l l . 即为所求对角线间夹角的正弦.31. 已知三点A (2,-1,5), B (0,3,-2), C (-2,3,1),点M ,N ,P 分别是AB ,BC ,CA 的中点,证明:1()4MN MP AC BC ⨯=⨯. 证明:中点M ,N ,P 的坐标分别为31(1,1,), (1,3,), (0,1,3)22M N P -- {2,2,2}MN =--3{1,0,}2MP =- {4,4,4}AC =--{2,0,3}BC =- 22222235233100122MN MP ----⨯=++=++--i j k i j k 44444412208033220AC BC ---⨯=++=++--i j k i j k 故 1()4MN MP AC BC ⨯=⨯. 32. 求同时垂直于向量a =(2,3,4)和横轴的单位向量.解:设横轴向量为b =(x ,0,0)则同时垂直于a ,b 的向量为3442230000x x ⨯=++a b i j k =4x j -3x k故同时垂直于a ,b 的单位向量为1(43)||5⨯=±=±-⨯a b e j k a b . 33. 四面体的顶点在(1,1,1),(1,2,3),(1,1,2)和(3,-1,2)求四面体的表面积. 解:设四顶点依次取为A , B , C , D .{0,1,2}, {2,2,1}AB AD ==-则由A ,B ,D 三点所确定三角形的面积为111|||542|222S AB AD =⨯=+-=i j k .同理可求其他三个三角形的面积依次为12故四面体的表面积122S =+. 34. 已知三点A (2,4,1), B (3,7,5), C (4,10,9),证:此三点共线.证明:{1,3,4}AB =,{2,6,8}AC =显然2AC AB =则22()0AB AC AB AB AB AB ⨯=⨯=⨯=故A ,B ,C 三点共线.35. 求过点(4,1,-2)且与平面3x -2y +6z =11平行的平面方程.解:所求平面与平面3x -2y +6z =11平行故n ={3,-2,6},又过点(4,1,-2)故所求平面方程为:3(x -4)-2(y -1)+6(z +2)=0即3x -2y +6z +2=0.36. 求过点M 0(1,7,-3),且与连接坐标原点到点M 0的线段OM 0垂直的平面方程. 解:所求平面的法向量可取为0{1,7,3}OM ==-n故平面方程为:x -1+7(y -7)-3(z +3)=0即x +7y -3z -59=037. 设平面过点(1,2,-1),而在x 轴和z 轴上的截距都等于在y 轴上的截距的两倍,求此平面方程.解:设平面在y 轴上的截距为b 则平面方程可定为122x y z b b b++= 又(1,2,-1)在平面上,则有121122b b b-++= 得b =2. 故所求平面方程为1424x y z ++= 38. 求过(1,1,-1),(-2,-2,2)和(1,-1,2)三点的平面方程.解:由平面的三点式方程知1112121213131310x x y y z z x x y y z z x x y y z z ------=--- 代入三已知点,有1112121*********x y z --+----+=---+ 化简得x -3y -2z =0即为所求平面方程.39. 指出下列各平面的特殊位置,并画出其图形:(1) y =0; (2) 3x -1=0;(3) 2x -3y -6=0; (4) x –y =0;(5) 2x -3y +4z =0.解:(1) y =0表示xOz 坐标面(如图7-2)(2) 3x -1=0表示垂直于x 轴的平面.(如图7-3)图7-2 图7-3(3) 2x-3y-6=0表示平行于z轴且在x轴及y轴上的截距分别为x=3和y =-2的平面.(如图7-4)(4) x–y=0表示过z轴的平面(如图7-5)(5) 2x-3y+4z=0表示过原点的平面(如图7-6).图7-4 图7-5 图7-6 40. 通过两点(1,1,1,)和(2,2,2)作垂直于平面x+y-z=0的平面. 解:设平面方程为Ax+By+Cz+D=0则其法向量为n={A,B,C}已知平面法向量为n1={1,1,-1}过已知两点的向量l={1,1,1}由题知n·n1=0, n·l=0即0,.A B CC A BA B C+-=⎧⇒==-⎨++=⎩所求平面方程变为Ax-Ay+D=0又点(1,1,1)在平面上,所以有D=0故平面方程为x-y=0.41. 决定参数k的值,使平面x+ky-2z=9适合下列条件:(1)经过点(5,-4,6);(2)与平面2x-3y+z=0成π4的角. 解:(1)因平面过点(5,-4,6)故有 5-4k-2×6=9得k=-4.(2)两平面的法向量分别为n1={1,k,-2} n2={2,-3,1}且122123π2cos cos||||42514kkθ⋅-====+⋅n nn n解得2k =±42. 确定下列方程中的l 和m :(1) 平面2x +ly +3z -5=0和平面mx -6y -z +2=0平行; (2) 平面3x -5y +lz -3=0和平面x +3y +2z +5=0垂直. 解:(1)n 1={2,l ,3}, n 2={m ,-6,-1}12232,18613l m l m ⇒==⇒=-=--n n (2) n 1={3, -5, l }, n 2={1,3,2}12315320 6.l l ⊥⇒⨯-⨯+⨯=⇒=n n43. 通过点(1,-1,1)作垂直于两平面x -y +z -1=0和2x +y +z +1=0的平面.解:设所求平面方程为Ax +By +Cz +D =0 其法向量n ={A ,B ,C }n 1={1,-1,1}, n 2={2,1,1}12203203A C A B C A B C CB ⎧=-⎪⊥⇒-+=⎪⇒⎨⊥⇒++=⎪=⎪⎩n n n n 又(1,-1,1)在所求平面上,故A -B +C +D =0,得D =0故所求平面方程为2033CCx y Cz -++= 即2x -y -3z =044. 求平行于平面3x -y +7z =5,且垂直于向量i -j +2k 的单位向量. 解:n 1={3,-1,7}, n 2={1,-1,2}.12,⊥⊥n n n n故1217733152122111--=⨯=++=+---n n n i j k i j k则2).n =+-e i j k 45. 求通过下列两已知点的直线方程: (1) (1,-2,1), (3,1,-1); (2) (3,-1,0),(1,0,-3). 解:(1)两点所确立的一个向量为s ={3-1,1+2,-1-1}={2,3,-2}故直线的标准方程为:121232x y z -+-==- 或 311232x y z --+==- (2)直线方向向量可取为s ={1-3,0+1,-3-0}={-2,1,-3}故直线的标准方程为:31213x y z -+==-- 或 13213x y z -+==-- 46. 求直线234035210x y z x y z +--=⎧⎨-++=⎩的标准式方程和参数方程.解:所给直线的方向向量为12311223719522335--=⨯=++=----s n n i j k i j k另取x 0=0代入直线一般方程可解得y 0=7,z 0=17于是直线过点(0,7,17),因此直线的标准方程为:7171719x y z --==-- 且直线的参数方程为:771719x t y t z t =⎧⎪=-⎨⎪=-⎩47. 求下列直线与平面的交点:(1)11126x y z-+==-, 2x +3y +z -1=0; (2) 213232x y z +--==, x +2y -2z +6=0. 解:(1)直线参数方程为1126x ty t z t =+⎧⎪=--⎨⎪=⎩代入平面方程得t =1 故交点为(2,-3,6).(2) 直线参数方程为221332x t y t z t =-+⎧⎪=+⎨⎪=+⎩代入平面方程解得t =0. 故交点为(-2,1,3). 48. 求下列直线的夹角:(1)533903210x y z x y z -+-=⎧⎨-+-=⎩ 和 2223038180x y z x y z +-+=⎧⎨++-=⎩;(2)2314123x y z ---==- 和 38121y z x --⎧=⎪--⎨⎪=⎩解:(1)两直线的方向向量分别为:s 1={5, -3,3}×{3, -2,1}=533321ij k--={3,4, -1}s 2={2,2, -1}×{3,8,1}=221381i j k-={10, -5,10}由s 1·s 2=3×10+4×(-5)+( -1) ×10=0知s 1⊥s 2 从而两直线垂直,夹角为π2. (2) 直线2314123x y z ---==-的方向向量为s 1={4, -12,3},直线38121y z x --⎧=⎪--⎨⎪=⎩的方程可变为22010y z x -+=⎧⎨-=⎩,可求得其方向向量s 2={0,2, -1}×{1,0,0}={0, -1, -2},于是1212cos 0.2064785θθ⋅==≈⋅'≈︒s s s s 49. 求满足下列各组条件的直线方程:(1)经过点(2,-3,4),且与平面3x -y +2z -4=0垂直; (2)过点(0,2,4),且与两平面x +2z =1和y -3z =2平行; (3)过点(-1,2,1),且与直线31213x y z --==-平行. 解:(1)可取直线的方向向量为s ={3,-1,2}故过点(2,-3,4)的直线方程为234312x y z -+-==- (2)所求直线平行两已知平面,且两平面的法向量n 1与n 2不平行,故所求直线平行于两平面的交线,于是直线方向向量12102{2,3,1}013=⨯==--i j ks n n故过点(0,2,4)的直线方程为24231x y z --==- (3)所求直线与已知直线平行,故其方向向量可取为 s ={2,-1,3}故过点(-1,2,1)的直线方程为121213x y z +--==-. 50. 试定出下列各题中直线与平面间的位置关系:(1)34273x y z++==--和4x -2y -2z =3; (2)327x y z ==-和3x -2y +7z =8;(3)223314x y z -+-==-和x +y +z =3. 解:平行而不包含. 因为直线的方向向量为s ={-2,-7,3}平面的法向量n ={4,-2,-2},所以(2)4(7)(2)3(2)0⋅=-⨯+-⨯-+⨯-=s n于是直线与平面平行.又因为直线上的点M 0(-3,-4,0)代入平面方程有4(3)2(4)2043⨯--⨯--⨯=-≠.故直线不在平面上.(2) 因直线方向向量s 等于平面的法向量,故直线垂直于平面.(3) 直线在平面上,因为3111(4)10⨯+⨯+-⨯=,而直线上的点(2,-2,3)在平面上. 51. 求过点(1,-2,1),且垂直于直线23030x y z x y z -+-=⎧⎨+-+=⎩ 的平面方程.解:直线的方向向量为12123111-=++-i j ki j k , 取平面法向量为{1,2,3},故所求平面方程为1(1)2(2)3(1)0x y z ⨯-+++-=即x +2y +3z =0.52. 求过点(1,-2,3)和两平面2x -3y +z =3, x +3y +2z +1=0的交线的平面方程. 解:设过两平面的交线的平面束方程为233(321)0x y z x y z λ-+-++++= 其中λ为待定常数,又因为所求平面过点(1,-2,3) 故213(2)33(13(2)231)0λ⨯-⨯-+-++⨯-+⨯+= 解得λ=-4.故所求平面方程为2x +15y +7z +7=053. 求点(-1,2,0)在平面x +2y -z +1=0上的投影.解:过点(-1,2,0)作垂直于已知平面的直线,则该直线的方向向量即为已知平面的法向量,即s =n ={1,2,-1}所以垂线的参数方程为122x t y t z t =-+⎧⎪=+⎨⎪=-⎩将其代入平面方程可得(-1+t )+2(2+2t )-(-t )+1=0 得23t =-于是所求点(-1,2,0)到平面的投影就是此平面与垂线的交点522(,,)333- 54. 求点(1,2,1)到平面x +2y +2z -10=0距离.解:过点(1,2,1)作垂直于已知平面的直线,直线的方向向量为s =n ={1,2,2}所以垂线的参数方程为12212x t y t z t =+⎧⎪=+⎨⎪=+⎩将其代入平面方程得13t =. 故垂足为485(,,)333,且与点(1,2,1)的距离为1d == 即为点到平面的距离. 55. 求点(3,-1,2)到直线10240x y z x y z +-+=⎧⎨-+-=⎩的距离.解:过点(3,-1,2)作垂直于已知直线的平面,平面的法向量可取为直线的方向向量即11133211==-=---ij kn s j k 故过已知点的平面方程为y +z =1.联立方程组102401x y z x y z y z +-+=⎧⎪-+-=⎨⎪+=⎩解得131,,.22x y z ==-= 即13(1,,)22-为平面与直线的垂足于是点到直线的距离为2d ==56. 建立以点(1,3,-2)为中心,且通过坐标原点的球面方程. 解:球的半径为22213(2)14.R =++-=设(x ,y ,z )为球面上任一点,则(x -1)2+(y -3)2+(z +2)2=14即x 2+y 2+z 2-2x -6y +4z =0为所求球面方程.57. 一动点离点(2,0,-3)的距离与离点(4,-6,6)的距离之比为3,求此动点的轨迹方程.解:设该动点为M (x ,y ,z ),由题意知222222(2)(0)(3) 3.(4)(6)(6)x y z x y z -+-++=-+++-化简得:8x 2+8y 2+8z 2-68x +108y -114z +779=0 即为动点的轨迹方程.58. 指出下列方程所表示的是什么曲面,并画出其图形:(1)22()()22a a x y -+=; (2)22149x y -+=; (3)22194x z +=; (4)20y z -=; (5)220x y -=; (6)220x y +=. 解:(1)母线平行于z 轴的抛物柱面,如图7-7. (2)母线平行于z 轴的双曲柱面,如图7-8.图7-7 图7-8 (3)母线平行于y 轴的椭圆柱面,如图7-9. (4)母线平行于x 轴的抛物柱面,如图7-10.图7-9 图7-10(5)母线平行于z 轴的两平面,如图7-11. (6)z 轴,如图7-12.图7-11 图7-12 59. 指出下列方程表示怎样的曲面,并作出图形:(1)222149y z x ++=; (2)22369436x y z +-=; (3)222149y z x --=; (4)2221149y z x +-=; (5)22220x y z -+=; (6)22209z x y +-=. 解:(1)半轴分别为1,2,3的椭球面,如图7-13. (2) 顶点在(0,0,-9)的椭圆抛物面,如图7-14.图7-13 图7-14(3) 以x 轴为中心轴的双叶双曲面,如图7-15. (4) 单叶双曲面,如图7-16.图7-15 图7-16(5) 顶点在坐标原点的椭圆锥面,其中心轴是y 轴,如图7-17. (6) 顶点在坐标原点的圆锥面,其中心轴是z 轴,如图7-18.图7-17 图7-1860. 作出下列曲面所围成的立体的图形: (1) x 2+y 2+z 2=a 2与z =0,z =2a(a >0); (2) x +y +z =4,x =0,x =1,y =0,y =2及z =0; (3) z =4-x 2, x =0, y =0, z =0及2x +y =4; (4) z =6-(x 2+y 2),x =0, y =0, z =0及x +y =1. 解:(1)(2)(3)(4)分别如图7-19,7-20,7-21,7-22所示.图7-19 图7-20图7-21 图7-22 61. 求下列曲面和直线的交点:(1) 222181369x y z ++=与342364x y z --+==-; (2) 22211694x y z +-=与2434x y z +==-. 解:(1)直线的参数方程为334624x t y t z t =+⎧⎪=-⎨⎪=-+⎩代入曲面方程解得t =0,t =1. 得交点坐标为(3,4,-2),(6,-2,2). (2) 直线的参数方程为4324x t y tz t =⎧⎪=-⎨⎪=-+⎩代入曲面方程可解得t =1, 得交点坐标为(4,-3,2).62. 设有一圆,它的中心在z 轴上,半径为3,且位于距离xOy 平面5个单位的平面上,试建立这个圆的方程.解:设(x ,y ,z )为圆上任一点,依题意有2295x y z ⎧+=⎨=±⎩ 即为所求圆的方程.63. 建立曲线x 2+y 2=z , z =x +1在xOy 平面上的投影方程. 解:以曲线为准线,母线平行于z 轴的柱面方程为x 2+y 2=x +1即2215()24x y -+=. 故曲线在xOy 平面上的投影方程为2215()240x y z ⎧-+=⎪⎨⎪=⎩64. 求曲线x 2+y 2+z 2=a 2, x 2+y 2=z 2在xOy 面上的投影曲线.解:以曲线为准线,母线平行于z 轴的柱面方程为2222a x y +=故曲线在xOy 面上的投影曲线方程为22220a x y z ⎧+=⎪⎨⎪=⎩65. 试考察曲面22219254x y z -+=在下列各平面上的截痕的形状,并写出其方程. (1) 平面x =2; (2) 平面y =0; (3) 平面y =5; (4) 平面z =2.解:(1)截线方程为2212x ⎧=⎪⎪⎨⎪⎪=⎩ 其形状为x =2平面上的双曲线.(2)截线方程为221940x z y ⎧+=⎪⎨⎪=⎩为xOz 面上的一个椭圆.(3)截线方程为2215y ⎧==⎩为平面y =5上的一个椭圆.(4) 截线方程为2209252x y z ⎧-=⎪⎨⎪=⎩为平面z =2上的两条直线.66. 求单叶双曲面22211645x y z +-=与平面x -2z +3=0的交线在xOy 平面,yOz 平面及xOz 平面上的投影曲线. 解:以32x z +=代入曲面方程得 x 2+20y 2-24x -116=0.故交线在xOy 平面上的投影为2220241160x y x z ⎧+--=⎨=⎩ 以x =2z -3代入曲面方程,得 20y 2+4z 2-60z -35=0.故交线在yOz 平面上的投影为2220460350y z z x ⎧+--=⎨=⎩ 交线在xOz 平面上的投影为230,0.x z y -+=⎧⎨=⎩习题八1. 判断下列平面点集哪些是开集、闭集、区域、有界集、无界集?并分别指出它们的聚点集和边界:(1) {(x ,y )|x ≠0};(2) {(x ,y )|1≤x 2+y 2<4};(3) {(x ,y )|y <x 2};(4) {(x ,y )|(x -1)2+y 2≤1}∪{(x ,y )|(x +1)2+y 2≤1}.解:(1)开集、无界集,聚点集:R 2,边界:{(x ,y )|x =0}. (2)既非开集又非闭集,有界集,聚点集:{(x ,y )|1≤x 2+y 2≤4},边界:{(x ,y )|x 2+y 2=1}∪{(x ,y )| x 2+y 2=4}. (3)开集、区域、无界集,聚点集:{(x ,y )|y ≤x 2},边界:{(x ,y )| y =x 2}.(4)闭集、有界集,聚点集即是其本身,边界:{(x ,y )|(x -1)2+y 2=1}∪{(x ,y )|(x +1)2+y 2=1}. 2. 已知f (x ,y )=x 2+y 2-xy tanxy,试求(,)f tx ty . 解:222(,)()()tan(,).tx f tx ty tx ty tx ty t f x y ty=+-⋅= 3. 已知(,,)w u vf u v w u w+=+,试求(,,).f x y x y xy +-解:f (x +y , x -y , xy ) =(x +y )xy+(xy )x +y +x -y=(x +y )xy +(xy )2x.4. 求下列各函数的定义域:2(1)ln(21);z y x =-+(2)z=+(3)z =(4)u =+(5)z =(6)ln()z y x =-+(7)u =解:2(1){(,)|210}.D x y y x =-+>(2){(,)|0,0}.D x y x y x y =+>->22222(3){(,)|40,10,0}.D x y x y x y x y =-≥-->+≠(4){(,,)|0,0,0}.D x y z x y z =>>> 2(5){(,)|0,0,}.D x y x y x y =≥≥≥ 22(6){(,)|0,0,1}.D x y y x x x y =->≥+< 22222(7){(,,)|0,0}.D x y z x y x y z =+≠+-≥5. 求下列各极限:10y x y →→22001(2)lim;x y x y →→+00x y →→0x y →→00sin (5)lim ;x y xyx →→222222001cos()(6)lim .()e x y x y x y x y +→→-++ 解:(1)原式0ln 2.=(2)原式=+∞. (3)原式=001.4x y →→=-(4)原式=002.x y →→=(5)原式=00sin lim100.x y xyy xy →→⋅=⨯=(6)原式=22222222222()00001()2lim lim 0.()e 2ex y x y x x y y x y x y x y ++→→→→++==+6. 判断下列函数在原点O (0,0)处是否连续:33222222sin(),0,(1)0,0;x y x y z x y x y ⎧++≠⎪=+⎨⎪+=⎩33333333sin(),0,(2)0,0;x y x y z x y x y ⎧++≠⎪=+⎨⎪+=⎩(3) 222222222,0,(2)()0,0;x y x y z x y x y x y ⎧+≠⎪=+-⎨⎪+=⎩解:(1)由于3333333322223333sin()sin()sin()0()x y x y x y x y y x x y x y x y x y++++≤=≤+⋅++++ 又00lim()0x y y x →→+=,且3333000sin()sin lim lim 1x u y x y ux y u →→→+==+, 故0lim 0(0,0)x y z z →→==.故函数在O (0,0)处连续. (2)000sin lim lim1(0,0)0x u y uz z u→→→==≠=故O (0,0)是z 的间断点.(3)若P (x ,y ) 沿直线y =x 趋于(0,0)点,则2222000lim lim 10x x y x x x z x x →→=→⋅==⋅+, 若点P (x ,y ) 沿直线y =-x 趋于(0,0)点,则22222220000()lim lim lim 0()44x x x y x x x x z x x x x →→→=-→-===⋅-++ 故00lim x y z →→不存在.故函数z 在O (0,0)处不连续.7. 指出下列函数在向外间断:(1) f (x ,y )=233x y x y -+;(2) f (x ,y )=2222y xy x +-;(3) f (x ,y )=ln(1-x 2-y 2);(4)f (x ,y )=222e ,0,0,0.x y x y yy -⎧⎪≠⎨⎪=⎩解:(1)因为当y =-x 时,函数无定义,所以函数在直线y =-x 上的所有点处间断,而在其余点处均连续.(2)因为当y 2=2x 时,函数无定义,所以函数在抛物线y 2=2x 上的所有点处间断.而在其余各点处均连续.(3)因为当x 2+y 2=1时,函数无定义,所以函数在圆周x 2+y 2=1上所有点处间断.而在其余各点处均连续.(4)因为点P (x ,y )沿直线y =x 趋于O (0,0)时.1200lim (,)lime x x y x xf x y x-→→=→==∞. 故(0,0)是函数的间断点,而在其余各点处均连续. 8. 求下列函数的偏导数:(1)z =x 2y +2xy;(2)s =22u v uv+;(3)z =x(4)z =lntan x y; (5)z =(1+xy )y; (6)u =z xy;(7)u =arctan(x -y )z; (8)y zu x =.解:(1)223122,.z z x xy x x y y y∂∂=+=-∂∂ (2)u v s v u =+2211,.s v s u u v u v v u∂∂=-=-+∂∂(3)2222212ln(),2z x x x x y x x y ∂==++∂+222.z xy x y y x y ∂==∂+ (4)21122sec csc ,tan z x x x x y y y yy∂=⋅⋅=∂ 222122sec ()csc .tan z x x x x x y y y y yy∂=⋅⋅-=-∂ (5)两边取对数得ln ln(1)z y xy =+故[]221(1)(1)(1).ln(1)1y y y x z y xy xy y xy y xy x xy-∂'=+⋅=+⋅=++∂+[]ln(1)(1)(1)ln(1)1ln(1)(1).1y y y y x z xy yxy xy y xy xy y xy xy xy xy ∂⎡⎤'++=+⋅=++⎢⎥+∂⎣⎦⎡⎤++=+⎢⎥+⎣⎦(6)1ln ln xy xy xy u u uz z y z z x xy z x y z-∂∂∂=⋅⋅=⋅⋅=⋅∂∂∂ (7)11221()().1[()]1()z z z z u z x y z x y x x y x y --∂-=⋅-=∂+-+- 112222()(1)().1[()]1()()ln()()ln().1[()]1()z z z z z zz z u z x y z x y y x y x y u x y x y x y x y z x y x y --∂-⋅--==-∂+-+-∂----==∂+-+-(8)1.yzu y x x z-∂=∂ 2211ln ln .ln ln .y yzzyy z zu x x x x y z zu y y x x x x z z z ∂=⋅=∂∂⎛⎫=⋅=-- ⎪∂⎝⎭9.已知22x y u x y=+,求证:3u u x y u x y ∂∂+=∂∂. 证明: 222223222()2()()u xy x y x y x y xy x x y x y ∂+-+==∂++. 由对称性知 22322()u x y yx y x y ∂+=∂+. 于是 2223()3()u u x y x y x y u x y x y ∂∂++==∂∂+. 10.设11ex y z ⎛⎫+- ⎪⎝⎭=,求证:222z z xy z x y∂∂+=∂∂. 证明: 11112211e e x y x y z x xx ⎛⎫⎛⎫++-- ⎪ ⎪⎝⎭⎝⎭∂⎡⎤⎛⎫=-=- ⎪⎢⎥∂⎝⎭⎣⎦, 由z 关于x ,y 的对称性得1121ex y z y y⎛⎫+- ⎪⎝⎭∂=∂ 故 11111122222211e e 2e 2.x y x y x y z z x y x y z x y x y⎛⎫⎛⎫⎛⎫+++--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∂∂+⋅=⋅+⋅==∂∂11.设f (x ,y )=x +(yf x (x ,1) .解:1(,)1(x f x y y y =+- 则(,1)101x f x =+=.12.求曲线2244x y z y ⎧+=⎪⎨⎪=⎩在点(2,4,5)处的切线与正向x 轴所成的倾角.解:(2,4,5)1,1,2z z x x x ∂∂==∂∂ 设切线与正向x 轴的倾角为α, 则tan α=1. 故α=π4. 13.求下列函数的二阶偏导数: (1)z =x 4+ y 4-4x 2y 2; (2)z=arctan y x; (3)z =y x ;(4)z =2ex y+.解:(1)2322224812816z z z x xy x y xy x x x y∂∂∂=-=-=-∂∂∂∂ ,, 由x ,y 的对称性知22222128.16.z z y x xy y y x∂∂=-=-∂∂∂ (2)222211zy y xx y x y x ∂⎛⎫=⋅=-- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭,2222222222222222222222222222222222222222()022,()()11,12,()()2,()()2.()()z x y y x xyx x y x y z x y x x y y x z xyy x y z x y y y y x x y x y x y z x y x x y x y x x y x y ∂+⋅-⋅=-=∂++∂=⋅=∂+⎛⎫+ ⎪⎝⎭∂=-∂+∂+-⋅-=-=∂∂++∂+-⋅-=-=∂∂++ (3)222ln ,ln ,xx z z y y y y x x∂∂==∂∂ 21222112111,(1),1ln (1ln ),ln (1ln ).x x x x x x x x z z xy x x y y y z y xy y y x y x y y zy x y y y x y y x-------∂∂==-∂∂∂=⋅+=+∂∂∂=+⋅⋅=+∂∂ (4)22e 2,e ,x y x y z zx x y++∂∂=⋅=∂∂ 222222222e 22e 22e (21),e ,2e ,2e .x y x y x y x y x y x y z x x x xz z z x x y x y y x++++++∂=⋅⋅+⋅=+∂∂∂∂===∂∂∂∂∂14.设f (x ,y ,z )=xy 2+yz 2+zx 2,求(0,0,1),(0,1,0),(2,0,1).xx yz zzx f f f -解:2(,,)2x f x y z y zx =+22(,,)2,(0,0,1)2,(,,)2(,,)2,(0,1,0)0,(,,)2(,,)2(,,)0,(2,0,1)0.xx xx y yz yz z zz zzx zzx f x y z z f f x y z xy z f x y z z f f x y z yz x f x y z yf x y z f ===+=-==+===15.设z =x ln(xy ),求32z x y ∂∂∂及32zx y ∂∂∂.解:ln()1ln(),z yx xy xy x xy∂=⋅+=+∂ 232223221,0,11,.z y zx xy x x y z x z x y xy y x y y∂∂===∂∂∂∂∂===-∂∂∂∂16.求下列函数的全微分: (1)22ex y z +=;(2)z =(3)zy u x =; (4)yzu x =.解:(1)∵2222e 2,e 2x y x y z zx y x y++∂∂=⋅=⋅∂∂ ∴222222d 2e d 2e d 2e (d d )x y xy xy z x x y y x x y y +++=+=+(2)∵22223/21()z xy y x y x x y ∂⎛⎫-=⋅=- ⎪+∂+⎝⎭2223/2()z x yx y ∂==∂+ ∴223/2d (d d ).()xz y x x y x y =--+(3)∵11,ln z z z y y z u u y x x x zy x y--∂∂==⋅⋅∂∂ 2ln ln y z ux x y y z∂=⋅⋅⋅∂ ∴211d d ln d ln ln d .z z zy y z y z u y x x x x zy y x x y y z --=+⋅+⋅⋅⋅(4)∵1yz u y x x z-∂=∂ 1ln yz u x x y z∂=⋅⋅∂ln yz u y x x z z 2∂⎛⎫=⋅⋅- ⎪∂⎝⎭∴121d d ln d ln d .y y yz z z y y u x x x x y x x z z z z -⎛⎫=+⋅⋅+⋅⋅- ⎪⎝⎭17. 求下列函数在给定点和自变量增量的条件下的全增量和全微分: (1)222,2,1,0.2,0.1;z x xy y x y x y =-+==-∆=∆=- (2)e ,1,1,0.15,0.1.xy z x y x y ===∆=∆=解:(1)22()()()2()9.688 1.68z x x x x y y y y z ∆=+∆-+∆+∆++∆-=-=d (2)(4) 1.6z x y x x y y =-∆+-+∆=(2)()()0.265ee e(e 1)0.30e.x x y y xy z +∆+∆∆=-=-=d e e e ()0.25e xy xy xy z y x x y y x x y =∆+∆=∆+∆=18.利用全微分代替全增量,近似计算: (1) (1.02)3·(0.97)2;(3)(1.97)1.05.解:(1)设f (x ,y )=x 3·y 2,则223(,)3,(,)2,x y f x y x y f x y x y ==故d f (x ,y )=3x 2y 2d x +2x 3y d y =xy (3xy d x +2x 2d y ) 取x =1,y =1,d x =0.02,d y =-0.03,则(1.02)3·(0.97)2=f (1.02,0.97)≈f (1,1)+d f (1,1)d 0.02d 0.03x y ==-=13×12+1×1[3×1×1×0.02+2×12×(-0.03)]=1.(2)设f (x ,y,则(,)(,)x y f x y f x y ===故d (,)d d )f x y x x y y =+取4,3,d 0.05,d 0.07x y x y ====-,则d0.05d0.07(4.05,2.93)(4,3)d(4,3)0.053(0.07)]15(0.01)54.998xyf f f==-=≈+=⨯+⨯-=+⨯-=(3)设f(x,y)=x y,则d f(x,y)=yx y-1d x+x y ln x d y,取x=2,y=1,d x=-0.03,d y=0.05,则1.05d0.03d0.05(1.97)(1.97,1.05)(2,1)d(2,1)20.0393 2.0393.xyf f f=-==≈+=+=19.矩型一边长a=10cm,另一边长b=24cm,当a边增加4mm,而b边缩小1mm时,求对角线长的变化.解:设矩形对角线长为l,则d d).l l x x y y==+当x=10,y=24,d x=0.4,d y=-0.1时,d0.4240.1)0.062l=⨯-⨯=(cm)故矩形的对角线长约增加0.062cm.20. 1mol理想气体在温度0℃和1个大气压的标准状态下,体积是22.4L,从这标准状态下将温度升高3℃,压强升高0.015个大气压,问体积大约改变多少?解:由PV=RT得V=RTP,且在标准状态下,R=8.20568×10-2,ΔV≈d v=-2d dRT Rp TP P+=d dV RP TP P-+222.48.20568100.01530.0911-⨯=-⨯+⨯≈-故体积改变量大约为0.09.21. 测得一物体的体积V=4.45cm3,其绝对误差限是0.01cm3,质量m=30.80g,其绝对误差限是0.01g,求由公式mvρ=算出密度ρ的绝对误差与相对误差.解:当V=4.45,m=30.80,d v=0.01,d m=0.01时,22130.801d d d0.010.014.45 4.450.01330.0133mv mv vρ==-+-⨯+⨯≈=-当v=4.45, m=30.80时30.806.92134.45ρ=≈d 0.00192160.19216%ρρ≈=.22. 求下列复合函数的偏导数或全导数:(1)22,cos ,sin ,z x y xy x u v y u v =-==求z u ∂∂,z v∂∂; (2) z =arc tanx y ,x =u +v ,y =u -v ,求z u ∂∂,z v∂∂; (3) ln(e e )xyu =+,y =x 3,求d d ux; (4) u =x 2+y 2+z 2,x =e cos tt ,y =e sin tt ,z =e t,求d d ut. 解:(1)222(2)cos (2)sin 3sin cos (cos sin )z z x z y xy y v x xy v u x u y u u v v v v ∂∂∂∂∂=⋅+⋅=-⋅+-∂∂∂∂∂=-223333(2)sin (2)cos 2sin cos (sin cos )(sin cos ).z z x z yxy y u v x xy u v v x v y v u v v v v u v v ∂∂∂∂∂=⋅+⋅=--⋅+-⋅∂∂∂∂∂=-+++ (2)222222211111x z z x z y y x v y u x u y uyx yu v x x y y ∂∂∂∂∂--⎛⎫-=⋅+⋅=⋅+⋅== ⎪∂∂∂∂∂++⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭2222222111(1)11.x z z x z y y v x v y vyx x y y y x ux y u v -∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅⋅- ⎪∂∂∂∂∂⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭+==++ (3)33222d d d 11e 3e e 3e e e 3.d d d e e e e e e e ex y x x x y x y x y x yx x u u x u y x x x x x x y x ∂∂++=⋅+⋅=⋅+⋅⋅==∂∂++++ (4)d d d d d d d d u u x u y u z t x t y t z t∂∂∂=⋅+⋅+⋅∂∂∂ 22(e cos e sin )2(e sin e cos )2e 4e t t t t t t x t t y t t z =-+++⋅=.23. 设f 具有一阶连续偏导数,试求下列函数的一阶偏导数: (1)22(,e );xyu f x y =-(2),;x y u f y z ⎛⎫= ⎪⎝⎭(3)().,,u f x xy xyz = 解:(1)12122e 2e .xy xy uf x f y xf y f x∂''''=⋅+⋅⋅=+∂ 1212(2)e 2e .xy xy uf y f x yf x f y∂''''=⋅-+⋅⋅=-+∂ (2)1111u f f x y y∂''=⋅=∂ 121222222211..x u x f f f f y y z y z u y y f f z z z ∂⎛⎫''''-=⋅+⋅=-+ ⎪∂⎝⎭∂⎛⎫''=⋅=-- ⎪∂⎝⎭(3)1231231,uf f y f yz f yf yzf x∂''''''=⋅+⋅+⋅=++∂ 12323330,.uf f x f xz xf xzf yuf xy xyf z∂'''''=⋅+⋅+⋅=+∂∂''=⋅=∂24.设(),,()yz xy xF u u F u x=+=为可导函数,证明: .z z xy z xy x y∂∂+=+∂∂ 证明:2()()()()z y y y xF u F u F u y F u x x x ∂⎛⎫''=+⋅+=+-- ⎪∂⎝⎭1()().z x xF u x F u y x∂''=+⋅=+∂ 故[]()()()()()()().z z F u y xy x y x F u F u y x y x xF u xy yF u xy yF u xy xF u xyz xy '∂∂⎡⎤'+=+++-⎢⎥∂∂⎣⎦''=+-++=++=+ 25. 设22()yz f x y =-,其中f (u )为可导函数,验证:211z z zx x y y y∂∂+=∂∂. 证明:∵2222z yf x xyf x f f ''∂⋅=-=-∂, 222(2)2z f y f y f y f y f f ''∂-⋅⋅-+==∂, ∴22222112211z z yf f y f y zx x y y f yf yf f y y ''∂∂++=-+==⋅=∂∂⋅ 26. 22()z f x y =+,其中f 具有二阶导数,求22222,,.z z zx x y y ∂∂∂∂∂∂∂ 解:2,2,z zxf yf x y∂∂''==∂∂ 222222224,224,z f x xf f x f xzxf y xyf x y∂''''''=+⋅=+∂∂''''=⋅=∂∂由对称性知,22224.z f y f y∂'''=+∂27. 设f 是c 2类函数,求下列函数的二阶偏导数: (1),;x x z f y ⎛⎫= ⎪⎝⎭(2)()22;,z f xy x y =(3)().sin ,cos ,e x y z f x y += 解:(1)1212111,z f f f f x y y∂''''=⋅+⋅=+∂ 2212211121112222221222122222222222222222223211121,1111,,2z f f f f f f f y x y y y yx x z x f f f f f f y y y x y y y y yx z x f f y y y z x x f f y y y ∂⎛⎫''''''''''''''+⋅=+⋅+=+⋅+ ⎪∂⎝⎭∂⎛⎫⎛⎫⎛⎫''''''''''--+=⋅-+⋅=-- ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭⎝⎭∂⎛⎫''-==- ⎪∂⎝⎭∂''=-∂22222342.x x x f f y yy ⎛⎫''''-⋅=+ ⎪⎝⎭,。
福州大学高等数学(下)试题及答案

福州大学高等数学(下)试题及答案一、单项选择题1.设),(y x f 在点),(b a 处的偏导数存在,则xb x a f b x a f x ),(),(lim 0--+→= 。
A 、 0; B 、),2(b a f x ; C 、),(b a f x ; D 、),(2b a f x 。
2.设曲面),(y x f z =与平面0y y =的交线在点)),(,,(000y x f y x o 处的切线与x 轴正向所成的角为6π,则 。
A 、236cos ),(00==πy x f x ; B 、21)62cos(),(00=-=ππy x f y ; C 、336),(00==πtg y x f x ; D 、3)62(),(00=-=ππtg y x f y 。
3.0lim =∞→n n u是级数∑∞=0n n u 发散的 。
A 、 必要条件; B 、充分条件; C 、充要条件; D 、既非充分又非必要。
4.在区域D :220x R y -≤≤上的σd xy D ⎰⎰2值为 。
A 、2R π; B 、24R π; C 、332R π; D 、0。
5.下列函数中,哪个是微分方程02=-xdx dy 的解 。
A 、x y 2=;B 、2x y =;C 、x y 2-=;D 、2x y -=。
二、是非判断题(15分) 1.⎰+-L y x ydx xdy 22=0,其中L 为圆周122=+y x 按逆时针转一周( ) 2.如果x∂∂ϕ,y ∂∂ϕ均存在,则),(y x ϕϕ=沿任何方向的方向导数均存在( ) 3.以),(y x f 为面密度的平面薄片D 的质量可表为σd y x f D ⎰⎰),(。
( ) 4.)(x f 在],0(π上连续且符合狄利克雷条件,则它的余弦级数处处收敛,且],0[π上收敛于)(x f 。
( )1. 微分方程的通解包含了所有的解。
( )三、计算题(16分)1. 设),(22xye y xf -=μ,其中f 具有一阶连续偏导数,求x ∂∂μ,y x ∂∂∂μ2。
高等数学(黄立宏)(第三版)习题五课后答案
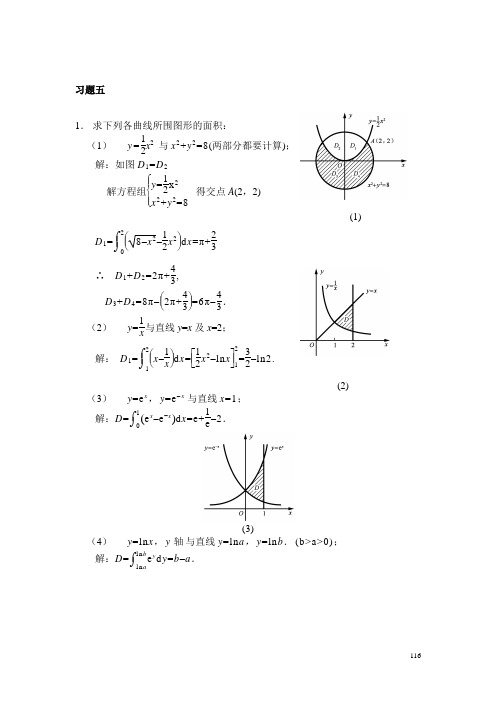
1.求下列各曲线所围图形的面积:
(1)与x2+y2=8(两部分都要计算);
解:如图D1=D2
解方程组得交点A(2,2)
(1)
∴,
.
(2)与直线y=x及x=2;
(16)
对于任意的y∈[0,h],过点(0,y)且垂直于y轴的平面截该立体为一椭圆,且该椭圆的半轴为:,同理可得该椭圆的另一半轴为:.
故该椭圆面积为
从而立体的体积为
.
5.计算底面是半径为R的圆,而垂直于底面一固定直径的所有截面都是等边三角形的立体体积.见图17.
(17)
解:以底面上的固定直径所在直线为x轴,过该直径的中点且垂直于x轴的直线为y轴,建立平面直角坐标系,则底面圆周的方程为:x2+y2=R2.
过区间[R,R]上任意一点x,且垂直于x轴的平面截立体的截面为一等边三角形,若设与x对应的圆周上的点为(x,y),则该等边三角形的边长为2y,故其面积等于
从而该立体的体积为
.
6. 求下列旋转体的体积:
(1)由y=x2与y2=x3围成的平面图形绕x轴旋转;
解:求两曲线交点得(0,0),(1,1)
.(14)
(9)极坐标曲线ρ=asin3φ;
解:
.
(9)
(10)ρ=2acosφ;
解:
.
(10)
2.求下列各曲线所围成图形的公共部分的面积:
(1)r=a(1+cosθ)及r=2acosθ;
解:由图11知,两曲线围成图形的公共部分为半径为a的圆,故D=πa2.
(11)
高等数学下册作业本答案

0
,q =
-1
.
3.微分方程 y′′ − 2 y′ + y =0 满足条件 y = 4, y′ = −2 的特解为 y= (4 − 6x)ex . =x 0=x 0
4.微分方程 y′′ − 2 y′ + 5y = 0= 的通解为 y ex (C1 cos 2x + C2 sin 2x) .
= 5.以 y ex (C1 sin x + C2 cos x) 为通解的二阶常系数线性微分方程为 y′′ − 2 y′ + 2 y = 0 .
0
0
y = f (x) ,即 y′′ − y = 0 ,对应的特征方程为 r 2 −1 = 0 ,特征根 r1 = 1, r2 = −1,所以通解
为 y = C1ex + C2e−x ,又 f (0) = 0 , f ′(0) = 0 ,代入得 C1 = 0, C2 = 0 ,故 f (x) = 0 .
第六章 微分方程
第一节 微分方程的基本概念
一、单项选择题
1. 下列各式中是常微分方程的为
B.
A. y2 + y =3 B. y′′ + y2 = y′ C. xy′ + y =(xy)′
D. x + z′x + z′y =y
2. 函数 y= C − x ( C 为任意常数)是微分方程 xy′′ − y′ = 1的 C .
y = C1ex + C2e4x ,由于 λ = 1 是特征方程的一个根,可设 y*(x) = axex 为原方程的一个特
解,代入得
a
=
−2 3
,所以
y*(x)
=
− 2 ex 3
,所以通解为
西工大2021年4月机考《高等数学(下)》作业参考答案非免费

西工大2021年4月机考《高等数学(下)》作业试卷总分:100 得分:100答案网叫福到(这四个字的拼音)一、单选题(共50 道试题,共100 分)1.设为连续函数,二次积分交换积分次序后等于().A.<img >B.<img >C.<img ">D.<img s">正确答案:B2.().A.<img s>B.<img sr">C.<img s>D.<img sr"正确答案:3.级数当()时绝对收敛.A.<img s>B.<img s">C.<img s>D.<img 1">正确答案:4.设区域是由及围的,则二重积分=().A.<img s>B.<img s>C.<img s">D.<img s">正确答案:5.设,则().A.<img s">B.0C.1D.2正确答案:6.级数的部分和数列的极限存在是级数收敛的().A.充分条件B.必要条件C.充分必要条件D.无关条件正确答案:7.设为连续函数,二次积分交换积分次序后等于().A.<img s>B.<img s>C.<img s">D.<img s>正确答案:8.若级数收敛,则下列级数不收敛的是().A.<img s>B.<img s>C.<img s">D.<img s正确答案:9.方程表示的曲面为().A.球面B.圆锥面C.椭圆抛物面D.柱面正确答案:10.设函数,则().A.<img s>B.<img s>C.<img s>D.<img s>正确答案:11.设是半径为A. 圆心在原点的上半圆周, 方向为逆时针方向,则().A.<img s">B.<img s">C.<img s1">正确答案:12.设D.是由直线及围成的平面区域,则().A.<img s>B.<img s>C.<img s>D.<img s>正确答案:13.设函数f(x, y)=x+y, 则点(0,0)是f(x, y)的().A.极值点B.连续点C.间断点D.驻点正确答案:14.已知为函数的极值,则A.1,1,-13B.-1,-1,3C.-1,-1,-3D.1,1,-3正确答案:15.().A.1B.<img s>C.<img sr">D.2正确答案:16.微分方程满足初始条件的特解为().A.<img s>B.<img ">C.<img s>D.<img ">正确答案:17.微分方程的通解为().B.y =C.eC.y = eC.D.y = C.e正确答案:18.微分方程的阶是().A.4B.3C.2D.1正确答案:19.设曲线L为圆周,则曲线积分().A.<img s>B.<img s>C.<img sr>D.<img s>正确答案:20.设向量,且与垂直,则().A.4B.6C.8D.10正确答案:21.设区域D.由确定,则().A.<img s1">B.<img s">C.<img s5">D.<img s1">正确答案:22.设是平面上以,和为顶点的三角形区域,是在第二象限的部分,则().A.<img s">B.<img sr">C.<img s>D.<img ">正确答案:A.<img s>B.<img s">C.<img s">D.<img s>正确答案:24.曲线A.<img s>B.<img s>C.<img s>D.<img s">正确答案:25.幂级数的收敛区间为().A.<img s">B.<img s">C.<img s"27D.<img s">正确答案:26.设,则().A.<img ">B.<img s">C.<img s>D.<img s">正确答案:27.设平面过点且与平面平行,则平面的方程为().A.<img s">B.<img s">C.<img >D.<img >正确答案:28.().A.<img s>B.<img s>C.<img s1">D.<img ">29.设区域,则二重积分=().A.<img s>B.<img srC.<img sD.<img s"正确答案:30.().A.0B.<img sC.<img s">D.1正确答案:31.设区域D.由确定,则().A.<img "B.0C.5D.18正确答案:32.设函数,则偏导数().A.<img s">B.<img s>C.<img s>D.<img s>正确答案:33.().A.<img s">B.<img s>C.<img s">D.<img s">正确答案:34.设为连续函数,二次积分交换积分次序后等于().B.<img s">C.<img s">D.<img s">正确答案:35.级数当().时绝对收敛.A.<img >B.<img s>C.<img s1">D.<img s>正确答案:36.设方程确定了隐函数,则().A.3B.2C.0D.1正确答案:37.为().A.<img 1">B.<img s1">C.<img s31" height="21">D.<img s>正确答案:38.二元函数在点处().A.连续,偏导数存在B.连续,偏导数不存在C.不连续,偏导数存在D.不连续,偏导数不存在正确答案:39.设L为任意一条分段光滑的闭曲线,则().A.<img sr>B.0C.2D.3正确答案:40.设方程确定了隐函数,则=().A.<img s1">B.<img s1">C.<img s>D.<img s">正确答案:41. 曲线A.<img s1">B.<img s">C.<img s">D.<img sr正确答案:42.幂级数的收敛区间为().A.<img s>B.<img s">C.<img s>D.<img s">正确答案:43.二重积分().A.<img s">B.<img s>C.<img s">D.<img >正确答案:44.微分方程的通解为().A.y = eC.B.y =C.eC.y = eC.D.y = C.正确答案:45.().A.<img s">B.<img 1">C.<img s">D.<img s>正确答案:46.设,则().A.<img >B.0C.1D.2正确答案:47.级数的部分和数列的极限存在是级数收敛的().A.充分条件B.必要条件C.充分必要条件D.无关条件正确答案:48.().A.<img s>B.<img s">C.<img s>D.<img sr>正确答案:49.设函数f(x, y)=x+y, 则点(0,0)是f(x, y)的().A.极值点B.连续点C.间断点D.驻点正确答案:50.().A.<img s">B.<img s">C.<img sr">D.<img s">正确答案:二、多选题(共0 道试题,共0 分)以下内容仅供学习参考,可不予理会11.微分方程的阶是().A.6B.3C.2D.1正确答案:12.设区域D.由确定,则().A.4B.5C.7D.8正确答案:13.级数的部分和数列的极限存在是级数收敛的().A.充分条件B.必要条件C.充分必要条件D.无关条件正确答案:。
高等数学练习册(1-5章)带答案

高等数学习题册(上册)目录习题1-1 函数 (1)习题1-2 常用的经济函数 (5)习题2-1 极限 (9)习题2-2 无穷小与无穷大,极限运算法则 (13)习题2-3 极限存在准则,两个重要极限及无穷小的比较 (17)习题2-4 函数的连续性 (21)习题2-5 闭区间上连续函数的性质 (25)第二章综合题 (29)第二章自测题 (36)习题3-1 导数概念 (40)习题3-2 求导法则与基本初等函数求导公式(一) (44)习题3-2 求导法则与基本初等函数求导公式(二) (48)习题3-3 高阶导数 (52)习题3-4 隐函数及由参数方程所确定的函数的导数 (56)习题3-5 函数的微分 (60)习题3-6 边际与弹性 (64)第三章综合题 (68)第三章自测题 (74)习题4-1 中值定理 (78)习题4-2 洛必达法则 (82)习题4-3 导数的应用(一) (86)习题4-3 导数的应用(二) (90)习题4-4 函数的最大值和最小值及其在经济中的应用 (94)习题4-5 泰勒公式 (98)第四章综合题 (100)第四章自测题 (104)习题5-1 不定积分的概念、性质 (108)习题5-2 换元积分法(一) (112)习题5-2 换元积分法(二) (116)习题5-3 分部积分法 (120)习题5-4 有理函数的积分 (122)第五章综合题 (124)第五章自测题 (128)微积分(上)模拟试卷一 (134)微积分(上)模拟试卷二 (138)参考答案 (142)习题1-1 函数1. 填空题:(1)()x y 32log log =的定义域 。
(2)523arcsin3xx y -+-=的定义域 。
(3)xxy +-=11的反函数 。
(4)已知31122++=⎪⎭⎫ ⎝⎛+xx x x f ,则=)(x f 。
2. 设⎪⎪⎩⎪⎪⎨⎧≥<=3x , 0 3 , sin )(ππϕx x x ,求()2,6-⎪⎭⎫⎝⎛ϕπϕ,并作出函数()x ϕη=的图形。
成考-高等数学作业(1、2、3、5)

】设在有定义,则下列函数中必为奇函数的是().A.B.C.(是常数)D.答案:D】设,则().A.B.C.D.答案:B】函数在内().ABCD答案:B】下列各组函数中,表示相同函数的是().A.B.C.D.答案:B】设,,则().A.B.C.D.答案:A】下列各对函数中,表示相同函数的是().A.,B.,C.,D.,答案:C】设,若曲线与关于直线对称,则表达式为().A.B.C.D.答案:B】函数在定义域内是().A.偶函数B.奇函数C.有界函数D.周期函数答案:A】设,则().A.B.C.D.【98433】函数的图形与的图形关于直线对称,则_____.答案:】下列各项函数中,互为反函数的是().A.与B.与C.与D.与答案:D】函数在定义域内是().A.偶函数B.奇函数C.有界函数D.周期函数答案:A】下列各对函数中,表示相同函数的是().A.,B.,C.,D.,答案:C】函数的定义域为().A.B.C.D.答案:C】下列各组函数中表示相同函数的是().A.与B.与C.与D.与】下列各对函数中,表示相同函数的是().A.,B.,C.,D.,答案:C【102089】函数的单调减区间为_____.答案:】函数的反函数是().A.B.C.D.答案:A】设在有定义,则下列函数中为奇函数的是().A.B.C.D.答案:D】下列各组函数中,表示相同函数的是().A.B.C.D.答案:B】设在有定义,则下列函数中为奇函数的是().A.B.C.D.答案:D】设,则().A.B.C.D.答案:C】下列函数中,函数图形关于原点对称的是().A.B.C.D.答案:B】下列各组函数中表示相同函数的是().A.与B.与C.与D.与答案:B】下列各对函数中,表示相同函数的是().A.,B.,C.,D.,单项】函数在内().A.单调增加B.单调减少C.不增不减D.有增有减答案:B】下列各项函数中,互为反函数的是().A.与B.与C.与D.与答案:D】设在有定义,则下列函数中为奇函数的是().A.B.C.D.答案:D】函数的定义域是().A.B.C.D.答案:D】函数的定义域是().A.B.C.D.】函数在内().A.单调增加B.单调减少C.不增不减D.有增有减答案:B】下列各项函数中,互为反函数的是().A.与B.与C.与D.与答案:D】设在有定义,则下列函数中为奇函数的是().A.B.C.D.答案:D】函数的定义域是().A.B.C.D.答案:D】函数的定义域是().A.B.C.D .答案:D】函数的定义域是().A.B.C.D.答案:D】下列各组函数中表示相同函数的是().A.与B.与C.与D.与答案:B】设,则().A.B.C.D.答案:C】函数在定义域内是().A.单调函数B.周期函数C.无界函数D.有界函数答案:D】下列各项函数中,互为反函数的是().A.与B .与C.与D.与答案:D】函数在内是().A.单调有界函数B.单调无界函数C.有界奇函数D.有界偶函数答案:D】设,,则().A.B.C.D.答案:A】下列各组函数中,表示相同函数的是().A.B.C.D.答案:B】下列各项函数中,互为反函数的是().A.与B.与C.与D.与答案:D单项选择题【44006】设在有定义,则下列函数中为奇函数的是().A.B.C.D.答案:D】函数在内是().A.单调有界函数B.单调无界函数C.有界奇函数D.有界偶函数答案:D】设,,则().A.B.C.D.答案:A】下列各组函数中,表示相同函数的是().A.B.C.D.答案:B】下列各项函数中,互为反函数的是().A.与B.与C.与D.与答案: D】 设在有定义,则下列函数中为奇函数的是( ).A .B .C .D .单项选择题【102072】 下列函数中,函数图形关于原点对称的是( ).A .B .C .D .答案: B】函数的反函数是().A.B.C.D.答案:A】函数的定义域为().A.B.C.D.答案:C【102089】函数的单调减区间为_____.答案:单项选择题【102060】设,则( ).A .B .C .D .答案: B单项选择题【99268】若,则当时,是( ).A .B . 振荡变量C . 无穷大量D . 无穷小量答案:D【98471】_____.答案:【98443】_____.答案:】当时,若有极限,无极限,则当时,().A.无极限B.有极限C.可能有,也可能没有极限D.若有极限,极限必为零答案:C【98468】_____.答案:】当时,与等价的无穷小量是().A.B.C.D.答案:C】().A.B.C.D.答案:D】当时,是().A.无穷大量B.无穷小量C.无界变量D.无法判定答案:B】若,则值为().A.B.C.D.答案:B【44014】存在是存在的().A.充分条件B.必要条件C.充分必要条件D.无关条件答案:D【98453】_____.答案:【98443】_____.答案:】若在时,与都是无穷小量,且,则在时,下列各式不一定是无穷小量的是().A.B.C.D.答案:D【98469】若函数在处连续,则_____.答案:【98442】若,则_____.答案:单项选择题若时,为无穷小量,则应满足的条件是().A.B.C.D.答案:C【102120】求极限.答案:解:=】().A.0B.1C.D.答案:C】当时下列变量中不是无穷小量的是().A.B.C.D.答案:D【102092】若,则_____.答案:单项选择题【44018】若时,为无穷小量,则应满足的条件是().A.B.C.D.答案:C【102120】求极限.答案:解:=】().A.0B.1C.D.答案:C】当时下列变量中不是无穷小量的是().A.B.C.D.答案:D【102092】若,则_____.答案:】下列变量中,当时,不是无穷小量的是().A.B.C.D.答案:C】若时,为无穷小量,则应满足的条件是().A.B.C.D.答案:C】当时,下列变量不是无穷小量的是().A.B.C.D.答案:C】设在连续,下列为偶函数的是().A.B.C.D.答案:B】当时,是().A.无穷大量B.无穷小量C.常量D.无界变量】下列变量中,当时,不是无穷小量的是().A.B.C.D.】若时,为无穷小量,则应满足的条件是().A.B.C.D.答案:C】当时,下列变量不是无穷小量的是().A.B.C.D.答案:C】设在连续,下列为偶函数的是().A.B.C.D.答案:B】当时,是().A.无穷大量B.无穷小量C.常量D.无界变量】当时,下列变量中是无穷小量的是().A.B.C.D.】当时,与等价的无穷小量是().A.B.C.D.答案:C【102090】_____.答案:【81962】设,求值,使在连续.答案:解:==依题意应满足,所以】下列命题中正确的是().A.函数在点无定义,则在点无极限B.函数在点不连续,则在点不可导C.函数在点不可导,则在点不连续D.函数在点不可导,则在点不取极值【102120】求极限.答案:解:=】当时,下列变量不是无穷小量的是().A.B.C.D.答案:C【98471】_____.答案:】若时,为无穷小量,则应满足的条件是().A.B.C.D.答案:C】当时,若有极限,无极限,则当时,().A.无极限B.有极限C.可能有,也可能没有极限D.若有极限,极限必为零答案:C单项选择题【65100】当时,下列变量中是无穷小量的是().A.B.C.D.答案:C单项选择题【65064】下列命题中正确的是().A.函数在点无定义,则在点无极限B.函数在点不连续,则在点不可导C.函数在点不可导,则在点不连续D.函数在点不可导,则在点不取极值答案:B【102090】_____.答案:【81962】设,求值,使在连续.答案:解:==依题意应满足,所以】当时,与等价的无穷小量是().A.B.C.D.】设可导,则必有().A.B.C.D.答案:D【102123】求曲线上处的切线方程.答案:将代入方程,得,故所求为:,即】设在可导,且,则().A.B.C.D.不存在答案:A】设,则().A.B.C.D.答案:C【102102】求曲线的平行于轴的切线方程.答案:解:,由题设,应有又当故所求为:,即】设可导,则必有().A.B.C.D.答案:D【102123】求曲线上处的切线方程.答案:将代入方程,得,故所求为:,即】设在可导,且,则().A.B.C.D.不存在答案:A】设,则().A.B.C.D.答案:C【102102】求曲线的平行于轴的切线方程.答案:解:,由题设,应有又当故所求为:,即单】设在处可导,且,则等于().A.B.C.D.答案:A】().A.B.C.D.答案:C】设可导,则必有().A.B.C.D.答案:D【98458】设,则_____.答案:【65143】设,求.答案:解:【65143】设,求.答案:解:】设,则().A.B.C.D.答案:D】设在点处可导,则().A.与都有关B.仅与有关与无关C.仅与有关与无关D.与都无关答案:C【81965】设曲线上任意一点处的切线斜率为该点纵坐标与横坐标之差,且曲线过坐标原点,求此曲线方程.答案:解:依题意,有,即,且===通解为=将代入通解,得故所求为】().A.B.C.D.【102093】设,则_____.答案:】设在可导,且,则().A.B.C.D.不存在答案:A【81965】设曲线上任意一点处的切线斜率为该点纵坐标与横坐标之差,且曲线过坐标原点,求此曲线方程.答案:解:依题意,有,即,且。
西交20春《高等数学(下)》在线作业参考答案

试卷总分:100得分:100
一、单选题(共25道试题,共50分)
1.y=1/(a^2+x^2)在区间[-a,a]上应用罗尔定理,结论中的点ξ=( ).
A.0
B.2
C.3/2
D.3
答案:B
2.f(x)=1/x+[e^(1/2-x)]/(x-1)的间断点的个数是( )
答案:正确
39.对于二元函数z=f(x,y),点P(x,y)趋于点Q(a,b)的过程中,对应的函数值f(x,y)无限接近于一个确定的常数A,就说A是函数f(x,y)当(x,y)趋于(a,b)时的极限
答案:正确
4.平面上一点与其法向量的向量积等于0是这一平面的点法式方程
答案:错误
42.{图}
答案:正确
43.两个曲面方程组成的方程组是其交线的一般方程
答案:正确
44.罗尔中值定理中的条件是充分的,但非必要条件.
答案:正确
45.{图}
答案:正确
46.函数在某点的各个偏导数连续,则函数在该点可微
答案:正确
47.{图}
答案:错误
48.两直线的方向向量的夹角称为两直线的夹角
答案:正确
A.A
B.B
C.C
D.D
答案:C
19.{图}
A.A
B.B
C.C
D.D
答案:D
20.当x→0时,函数(x2-1)/(x-1)的极限( )
A.等于2
B.等于0
C.为∞
D.不存在但不为∞
答案:D
21.{图}
A.A
B.B
C.C
D.D
答案:D
22.{图}
A.A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一章 习题答案1. 1常数项级数的概念及基本性质1.解:(1) +⋅+⋅+⋅+⋅+⋅651541431321211 (2) -+-+-514131211(3)+++++54325!54!43!32!21!1 (4)+⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅⋅⋅⋅+⋅⋅⋅⋅+⋅⋅+10864297531864275316425314231212. 解:(1)121-=n u n (2)12+-=n n u n (3))2(6422n x u nn ⋅⋅=(4)12)1(11+-=++n au n n n3. 解:(1)0131limlim ≠==∞→∞→nn n n u ,∴级数发散(不满足级数收敛的必要条件)。
(2)原级数可写为)4131211(31 ++++。
∵括号内级数为调和级数发散,∴原级数发散。
(3)原级数为公比等于23的几何级数,∵123>,∴原级数发散。
(4)原级数为发散的调和级数 +++++514131211去掉前三项,∴原级数发散。
(5)原级数为公比等于98-的几何级数,198<-,∴原级数收敛。
(6)∵级数+++32212121收敛(公比121<的几何级数),级数 +++32313131收敛(公比131<的几何级数),∴原级数收敛(收敛级数可以逐项相加减)。
4. 解:(1)a a a a a a a a a a S n n n n -=-++-+-+-=+-+12121257353)()()()( ,a a a S n n n n -=-=+∞→∞→1)(lim lim 12,∴此级数收敛。
(2)])2)(1(1)1(1[21)2)(1(1++-+=++=n n n n n n n u n+⋅-⋅+⋅-⋅+⋅-⋅=∴)541431(21)431321(21)321211(21n S])2)(1(1)1(1[21++-++n n n n =])2)(1(121[21++-n n ,41])2)(1(121[21lim =++-=∞→n n S n n ,∴此级数收敛。
(3))121121(21)12)(12(1+--=+-=n n n n u n)1211(21)121121(21)7151(21)5131(21)311(21+-=+--++-+-+-=∴n n n S n , 21)1211(21limlim =+-=∞→∞→n S n n n ,∴此级数收敛。
1. 2正项级数及其判敛法1.解:(1)nn u n 21121>-=,而级数∑∑∞=∞==1112121n n nn发散,∴原级数发散。
(2)21)1(1nn n u n <+=,而级数∑∞=121n n收敛(12>=P 的P 级数),∴原级数收敛。
(3)nnn n nn u n +=+++>++=112111122,而级数 +++=+∑∞=413121111n n发散(调和级数去掉第一项),∴原级数发散。
(4))0(sin ≥≤ααα ,nnn u 22sinππ≤=∴,而级数∑∑∞=∞==11212n nn nππ收敛(公比为121<的几何级数),∴原级数收敛。
(5))1(211>≤=n nu nnn ,而级数∑∞=121n n收敛,∴原级数收敛。
(6)4145125122+=+++>+++=n n n n n n n u n ,而级数 +++=+∑∞=716151411n n 发散(调和级数去掉前四项),∴原级数发散。
(7)111tanlim22=∞→nn n ,而级数∑∞=121n n收敛,∴原级数收敛。
(8)1ln )11ln(lim 1)11ln(lim==+=+∞→∞→e nnnnn n ,而级数∑∞=11n n发散,∴原级数发散。
2.解:(1)121)2(23lim222)3(limlim,2211<=++=+⋅+=+=∞→+∞→+∞→n n n n u u n u n nn n nn n nn ,∴原级数收敛。
(2)1313)1(lim33)1(limlim,32221212<=+=⋅+==∞→+∞→+∞→nn nn u u n u n n n n nn n nn ,∴原级数收敛。
(3)enn n n nn n u u nn u n n nn nnn n n nn n nnn 2])11[(lim 2)1(2lim !2)1()!1(2limlim,!21111=+=+=⋅++==-∞→∞→++∞→+∞→1<,∴原级数收敛。
(4)12122lim22lim 2tan2tan )1(limlim,2tan 21121211<===+==++→∞++→∞++→∞+→∞+n n n n n n n n n nn n n n n n u u n u πππππ,∴原级数收敛。
(5))13(52)34(51)14)(34(51)23)(13(52limlim1-⋅-⋅⋅+-⋅+-⋅=∞→+∞→n n n n n n u u n nn n 1423lim ++=∞→n n n 143<=,∴原级数收敛。
(6)14)1()22)(12(lim)!2()!(])!1[()!22(limlim2221>=+++=⋅++=∞→∞→+∞→n n n n n n n u u n n nn n ,∴原级数发散。
3.解:(1)12112lim)12(limlim <=+=+=∞→∞→∞→n n n n u n nnn nn n ,∴原级数收敛。
(2)191)31()13(lim lim212<==-=-∞→∞→nn n nn n n nu ,∴原级数收敛。
4.解:(1)143)43()43)(1(lim lim11<=+=+∞→+∞→n n n nn n n n u u ,∴原级数收敛。
(2))(11b a n bna u n +≥+=,而∑∑∞=∞=+=+1111)(1n n nba b a n 发散,∴原级数发散。
(3)02112limlim ≠=--=∞→∞→n nn u n n n ,∴原级数发散。
(4)nnnnn nnn n nn nn nn nu 121211])11[()11()1(2+=+=+=+,1lim 1=∞→n n n ,1])11[(lim 0122==+∞→e nn nn ,01lim ≠=∴∞→n n u , ∴原级数发散。
(5)25235323232)2)(1(32nnnn n n n u n +=+<+++=,∑∑∞=∞=1251232,2n n nn收敛,∑∞=+∴1532n nn 收敛,∴原级数收敛。
(6)∞====∞→∞→∞→∞→nn n n n nnn n n nn n n u 2lim )2(lim 2sinlim lim ,∴原级数发散。
(7)2311)11ln(,1)11ln(n n n nnu nnn =<+=∴<+,而∑∞=1231n n收敛,∴原级数收敛。
(8)12122lim lim1)1(<===-----∞→∞→nn n nn n nu ,∴原级数收敛。
(9))]12)(12(531[!999)!1000(,)]12(531[!999)!999(1+-⋅⋅+=-⋅⋅+=+n n n u n n u n n121121000limlim1<=++=∞→+∞→n n u u n nn n ,∴原级数收敛。
1. 3任意项级数1. 证明:1)!12)(12(1)!12)(12(1+=++>--=n n u n n n n u ,0)!12)(12(1limlim =--=∞→∞→n n u n n n 。
据莱布尼兹定理,所给交错级数收敛,且若取!551!33113⋅+⋅-=≈S S ,则误差满足0001.0352801!7713<=⋅<r 。
2. 证明:设)1(1)(≥+=x x x x f ,则0)1(21)(2/<+-=x x x x f (当1>x 时),于是)(x f在1≥x 上单调减。
故)1()(+≥n f n f ,即1+≥n n u u ,又1limlim +=∞→∞→n n u n n n nnn 11lim1+=∞→0=,据莱布尼兹定理,所给交错级数收敛。
3. 解:(1)该级数为交错级数。
1111+=+>=n n u n nu ,又01limlim ==∞→∞→nu n n n,据莱布尼兹定理该级数收敛。
再考察正项级数∑∑∞=∞==121111n n nn发散,∴原级数为条件收敛。
(2)先考察正项级数 +-++++222)12(151311n 。
221)12(1nn u n ≤-=,而∑∞=121n n收敛,∴级数∑∞=-12)12(1n n 收敛。
∴原级数收敛且为绝对收敛。
(3)1)2ln(1)1ln(1+=+>+=n n u n n u ,且0)1l n (1lim=+∞→n n ,∴由莱布尼兹定理知原级数收敛。
又∑∑∞=∞=++=+-111)1ln(1)1ln()1(n n n n n ,且11)1l n(1+>+n n ,而级数∑∞=+111n n 发散,∴∑∞=++-11)1ln()1(n n n 发散,∴原级数为条件收敛。
(4)在∑∑∞=-∞=--=-1111133)1(n n n n n nn 中,13-=n n n u ,13133)1(limlim11<=⋅⋅+=-∞→+∞→nn u u nn n nn n ,∴∑∞=---1113)1(n n n n 收敛。
∴原级数收敛且为绝对收敛。
(5)先考察正项级数1sin111+∑∞=+n n n ππ。
1111sin1++≤+n n n πππ,而级数∑∞=+111n n π为收敛的几何级数,∴该正项级数收敛。
∴原级数收敛且为绝对收敛。
(6)该级数为交错级数。
nn u n ln 1-=,n n n n ln )1ln(1->+-+ ,)1ln(11ln 1+-+>-∴n n nn ,即1+>n n u u ,又0ln 11limln 1limlim =-=-=∞→∞→∞→nn nnn u n n n n ,∴由莱布尼兹定理知∑∞=--1ln )1(n nnn 收敛。
再考察正项级数∑∞=-1ln 1n nn ,nnn 1ln 1≥-,而∑∞=11n n发散,∴级数∑∞=-1ln 1n nn 发散。
∴原级数为条件收敛。
3.1函数项级数的一般概念1.解:(1)xnxn x u x u n n n n 11lim)()(lim1=+=∞→+∞→ ,故当11<x,即当1>x 时,级数绝对收敛;当1<x 时,级数发散;而当1=x 时,由于一般项不趋于零,故级数发散。
