2013年高考题讲解
2013年高考试题答案和解析

2013年普通高等学校招生全国统一考试语文本试题卷共8页,六大题23小题。
全卷满分150分。
考试用时150分钟。
注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用统一提供的2B铅笔将答题卡上试卷类型A后的方框涂黑。
2.选择题的作答:每小题选出答案后,用统一提供的2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试题卷、草稿纸上无效。
3.非选择题的作答:用统一提供的签字笔直接答在答题卡上对应的答题区域内。
答在试题卷、草稿纸上无效。
4.考生必须保持答题卡的整洁。
考试结束后,请将本试题卷和答题卡一并上交。
一、语文基础知识(共15分,共5小题,每小题3分)1.下列各组词语中,加点字的注音全都正确的一组是A.踹(chuài)水竞(jìnɡ)赛蘸(zhàn)酒擂(léi)鼓助威B.跋涉(shè)陡(dǒu)峭攀登(dēnɡ)餐霜饮雪(xiě)C.善(shàn)良谦逊(sùn)璞(pú)玉不事雕琢(zhuó)D.荆棘(jí)飘泊(bó)青苔(tāi)红漆(qī)雕花2.下列各组词语中,没有错别字的一组是A.彷徨愁怨寂寥静默凄婉惆伥B.顾盼精捍步履稳健风神潇洒C.睿智禀赋崇高品质趋善避恶D.辩难商榷典藉满架旁稽博采3.依次填入下列横线处的词语,最恰当的一组是①宋人画雪常不用铅粉,把背景用墨衬黑,一层层,留出山头的白,树梢的白,甚至花蕾上的白,虚实映衬,意境悠远。
②因为睡不着,打开窗帘,遥望夜空,满天,斜月晶莹,薄雾似轻纱漫卷,。
我思念那个小山村,那个让我魂牵梦绕的地方!A.而是点染星汉如梦如幻B.总是浸染星云如诗如画C.却是绘染星光诗意盎然D.只是渲染星斗诗意朦胧4.下列各项中,没有语病的一项是A.《美丽中国》以歌舞为主,融入京剧演唱、茶艺表演、少林武术等元素,加上奇幻的灯光,震撼的音响,一幅美丽中国的大写意,声光舞影流溢着浓郁的中国情。
2013年高考试题及解析:文科数学(新课标Ⅰ卷)

绝密★启封并使用完毕前2013年普通高等学校招生全国统一考试文科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷3至4页。
全卷满分150分。
考试时间120分钟。
注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至3页,第Ⅱ卷3至5页。
2. 答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置。
3. 全部答案在答题卡上完成,答在本试题上无效。
4. 考试结束,将本试题和答题卡一并交回。
第Ⅰ卷一、 选择题共12小题。
每小题5分,共60分。
在每个小题给出的四个选项中,只有一项是符合题目要求的一项。
(1)已知集合A={1,2,3,4},B={x |x =n 2,n ∈A },则A ∩B= ( ) (A ){0} (B ){-1,,0} (C ){0,1} (D ){-1,,0,1} 【答案】A 【解析】【难度】容易【点评】本题考查集合之间的运算关系,即包含关系.在高一数学强化提高班上学期课程讲座1,第一章《集合》中有详细讲解,其中第02节中有完全相同类型题目的计算.在高考精品班数学(文)强化提高班中有对集合相关知识的总结讲解. (2)1+2i(1-i)2= ( ) (A )-1-12i(B )-1+12i(C )1+12i(D )1-12i【答案】B 【解析】【难度】容易【点评】本题考查复数的计算。
在高二数学(文)强化提高班下学期,第四章《复数》中有详细讲解,其中第02节中有完全相同类型题目的计算。
在高考精品班数学(文)强化提高班中有对复数相关知识的总结讲解。
(3)从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是( )(A )12(B )13(C )14(D )16【答案】B【难度】容易【点评】本题考查几何概率的计算方法。
在高二数学(文)强化提高班,第三章《概率》有详细讲解,在高考精品班数学(文)强化提高班中有对概率相关知识的总结讲解。
2013年全国高考理综试题及答案详解
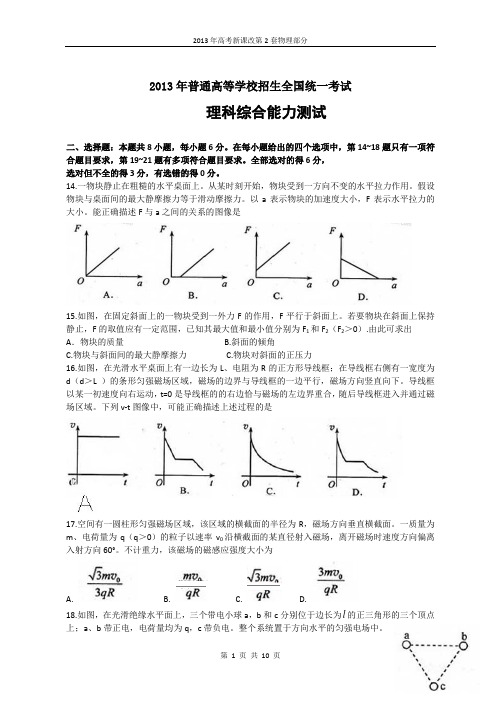
2013年普通高等学校招生全国统一考试理科综合能力测试二、选择题:本题共8小题,每小题6分。
在每小题给出的四个选项中,第14~18题只有一项符合题目要求,第19~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14.一物块静止在粗糙的水平桌面上。
从某时刻开始,物块受到一方向不变的水平拉力作用。
假设物块与桌面间的最大静摩擦力等于滑动摩擦力。
以a表示物块的加速度大小,F表示水平拉力的大小。
能正确描述F与a之间的关系的图像是15.如图,在固定斜面上的一物块受到一外力F的作用,F平行于斜面上。
若要物块在斜面上保持静止,F的取值应有一定范围,已知其最大值和最小值分别为F1和F2(F2>0).由此可求出A.物块的质量 B.斜面的倾角C.物块与斜面间的最大静摩擦力 C.物块对斜面的正压力16.如图,在光滑水平桌面上有一边长为L、电阻为R的正方形导线框;在导线框右侧有一宽度为d(d>L )的条形匀强磁场区域,磁场的边界与导线框的一边平行,磁场方向竖直向下。
导线框以某一初速度向右运动,t=0是导线框的的右边恰与磁场的左边界重合,随后导线框进入并通过磁场区域。
下列v-t图像中,可能正确描述上述过程的是17.空间有一圆柱形匀强磁场区域,该区域的横截面的半径为R,磁场方向垂直横截面。
一质量为m、电荷量为q(q>0)的粒子以速率v0沿横截面的某直径射入磁场,离开磁场时速度方向偏离入射方向60°。
不计重力,该磁场的磁感应强度大小为A. B. C. D.18.如图,在光滑绝缘水平面上,三个带电小球a,b和c分别位于边长为l的正三角形的三个顶点上;a、b带正电,电荷量均为q,c带负电。
整个系统置于方向水平的匀强电场中。
已知静电力常量为k。
若三个小球均处于静止状态,则匀强电场场强的大小为A. B. C. D.2l19.在物理学发展过程中,观测、实验、假说和逻辑推理等方法都起到了重要作用。
2013年高考试题及解析:语文(北京卷)

2013年普通高等学校招生全国统一考试语文(北京卷)本试卷共8页,150分。
考试时长150分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回。
一、本大题共5小题。
每小题3分,共15分。
1.下列词语,字形与加点字的注音全部正确的一项是()A.养殖业与日剧增便笺(jiān)独辟蹊(xī)径B.醉醺醺席不暇暖泥淖(nào)向隅(yú)而泣C.滥摊子自由竞争卷帙(dié)运筹帷幄(wò)D.颤巍巍信笔涂鸭蠹(dù)虫湮(yīn)没无闻【参考答案】B【答案解析】本题综合考查字音、字形的识记与辨析,与日俱增、卷帙(zhì)、信笔涂鸦、湮(yān)没无闻【试题点评】本题在高考强化提高班讲座2第2讲《字音的识记与辨析》第3讲《字形的识记与辨析》中有详细讲解,所考词语视频中已全部复习讲解。
在高考强化提高班讲座1、寒假特训班、百日冲刺班中也均有涉及。
2.下列语句中,没有语病的一项是()A.近几年,食品药品在安全方面出现的问题被媒体曝光,不同职能部门各管一段的监管模式也因此受到了社会的质疑。
B.第九届中国国际园林博览会在北京永定河西岸盛大开幕,对于513公顷的园博园,为了方便游客,专门开设了电瓶车专线。
C.据世界黄金协会分析,2013年春节前后中国黄金需求高涨的原因,主要由于消费者对中国经济前景充满信心所致。
D.日前,交通管理部门就媒体对酒驾事故的连续报道做出了积极回应,表示要进一步加大对交通违法行为的查处。
【参考答案】A【答案解析】本题考查病句的辨析及修改, B缺少主语,C重复,D搭配不当,加大……力度【试题点评】本题在高考强化提高班讲座2第6讲、第7讲、第8讲《病句的辨析与修改》中对以上几种病句类型有详细重点讲解,在高考强化提高班讲座1、寒假特训班、百日冲刺班中均有涉及。
3.依次填入句中横线处的词语,正确的一项是()①文学艺术创造来源于生活,作家塑造的人物形象,往往是以现实生活中的真实人物为创作而形成的。
2013年高考数学全国卷1(完整版试题+答案+解析)

2013年普通高等学校招生全国统一考试(全国卷)理科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共6页.考试时间120分钟.满分150分.答题前,考生务必用0.5毫米的黑色签字笔将自己的姓名、座号、考号填写在第Ⅰ卷答题卡和第Ⅱ卷答题纸规定的位置. 参考公式:样本数据n x x x ,,21的标准差nx x x x x x s n 22221)()()(-++-+-=其中x 为样本平均数球的面积公式24R S π=第Ⅰ卷(选择题 共60分)注意事项:1.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上. 2.第Ⅰ卷只有选择题一道大题.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.复数ii++121(i 是虚数单位)的虚部是 A .23 B .21C .3D .1 2.已知R 是实数集,{}11,12+-==⎭⎬⎫⎩⎨⎧<=x y y N x xM ,则=M C N R A .)2,1(B .[]2,0C .∅D .[]2,13.现有10个数,其平均数是4,且这10个数的平方和是200,那么这个数组的标准差是 A .1 B .2 C .3 D .44.设n S 为等比数列{}n a 的前n 项和,0852=-a a ,则=24S S A .5 B .8 C .8- D .15 5.已知函数)62sin()(π-=x x f ,若存在),0(π∈a ,使得)()(a x f a x f -=+恒成立,则a的值是A .6π B .3π C .4π D .2π 6.已知m 、n 表示直线,γβα,,表示平面,给出下列四个命题,其中真命题为 (1)βααβα⊥⊥⊂=则,,,m n n m (2)m n n m ⊥==⊥则,,,γβγαβα (3),,βα⊥⊥m m 则α∥β (4)βαβα⊥⊥⊥⊥则,,,n m n mA .(1)、(2)B .(3)、(4)C .(2)、(3)D .(2)、(4)7.已知平面上不共线的四点C B A O ,,,,若||,23BC AB OC OB OA -=等于A .1B .2C .3D .4 8.已知三角形ABC ∆的三边长成公差为2的等差数列,且最大角的正弦值为23,则这个三角形的周长是A .18B .21C .24D .15 9.函数xx x f 1lg )(-=的零点所在的区间是 A .(]1,0 B .(]10,1 C .(]100,10 D .),100(+∞ 10.过直线y x =上一点P 引圆22670x y x +-+=的切线,则切线长的最小值为A .22 B . 223 C .210 D .211.已知函数b ax x x f 2)(2-+=.若b a ,都是区间[]4,0内的数,则使0)1(>f 成立的概率是A .43 B .41 C .83D .8512.已知双曲线的标准方程为116922=-y x ,F 为其右焦点,21,A A 是实轴的两端点,设P 为双曲线上不同于21,A A 的任意一点,直线P A P A 21,与直线a x =分别交于两点N M ,,若0=⋅FN FM ,则a 的值为A .916 B .59 C .925 D .516题图第13第Ⅱ卷(非选择题 共90分)注意事项:1. 请用0.5毫米的黑色签字笔将每题的答案填写在第Ⅱ卷答题纸的指定位置.书写的答案如需改动,要先划掉原来的答案,然后再写上新答案.2. 不在指定答题位置答题或超出答题区域书写的答案无效.在试题卷上答题无效. 3. 第Ⅱ卷共包括填空题和解答题两道大题. 二、填空题:本大题共4小题,每小题4分,共16分. 13.如图所示的程序框图输出的结果为__________.14. 若一个底面是正三角形的三棱柱的正视图如下图所示,其在一个球面上,则该球的表面积为__________.15.地震的震级R 与地震释放的能量E 的关系为)4.11(lg 32-=E R .2011年3月11日,日本东海岸发生了9.0级特大地震,2008年中国汶川的地震级别为8.0级,那么2011年地震的能量是2008年地震能量的 倍. 16.给出下列命题: ①已知,,a b m都是正数,且bab a >++11,则a b <; ②已知()f x '是()f x 的导函数,若,()0x R f x '∀∈≥,则(1)(2)f f <一定成立; ③命题“x R∃∈,使得2210x x -+<”的否定是真命题; ④“1,1≤≤y x 且”是“2≤+y x ”的充要条件.其中正确命题的序号是 .(把你认为正确命题的序号都填上)第14题图三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知向量),2cos 2sin 3()2cos ,1(y xx b x a +==→→与共线,且有函数)(x f y =.(Ⅰ)若1)(=x f ,求)232cos(x -π的值;(Ⅱ)在ABC ∆中,角C B A ,,,的对边分别是c b a ,,,且满足b c C a 2cos 2=+,求函数)(B f 的取值范围.18.(本小题满分12分)已知等差数列{}n a 的前n 项和为n S ,公差,50,053=+≠S S d 且1341,,a a a 成等比数列. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设⎭⎬⎫⎩⎨⎧n n a b 是首项为1,公比为3的等比数列,求数列{}n b 的前n 项和n T .已知四棱锥BCDE A -,其中1====BE AC BC AB ,2=CD ,ABC CD 面⊥,BE∥CD ,F 为AD 的中点. (Ⅰ)求证:EF ∥面ABC ; (Ⅱ)求证:面ACD ADE 面⊥; (III )求四棱锥BCDE A -的体积.20.(本小题满分12分)在某种产品表面进行腐蚀性检验,得到腐蚀深度y 与腐蚀时间x 之间对应的一组数据:现确定的研究方案是:先从这6组数据中选取2组,用剩下的4组数据求线性回归方程,再对被选取的2组数据进行检验.(Ⅰ)求选取的2组数据恰好不相邻的概率;(Ⅱ)若选取的是第2组和第5组数据,根据其它4组数据,求得y 关于x 的线性回归方程26139134ˆ+=x y,规定由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2微米,则认为得到的线性回归方程是可靠的,判断该线性回归方程是否可靠.AB CDEF已知函数1)(2++=x bax x f 在点))1(,1(--f 的切线方程为03=++y x . (Ⅰ)求函数()f x 的解析式;(Ⅱ)设x x g ln )(=,求证:)()(x f x g ≥在),1[+∞∈x 上恒成立.22.(本小题满分14分)实轴长为34的椭圆的中心在原点,其焦点1,2,F F 在x 轴上.抛物线的顶点在原点O ,对称轴为y 轴,两曲线在第一象限内相交于点A ,且12AF AF ⊥,△12AF F 的面积为3. (Ⅰ)求椭圆和抛物线的标准方程;(Ⅱ)过点A 作直线l 分别与抛物线和椭圆交于C B ,,若AB AC 2=,求直线l 的斜率k .参考答案及评分标准一.选择题(本大题共12小题,每小题5分,共60分.)B D B A D B B D BC C B二.填空题(本大题共4小题,每小题4分,共16分.)13.2 14.π31915. 2310 16. ①③三.解答题17.(本小题满分12分) 解:(Ⅰ)∵→a 与→b 共线∴yxx x 2cos 2cos2sin 31=+21)6sin()cos 1(21sin 232cos 2cos 2sin 32++=++=+=πx x x x x x y …………3分∴121)6sin()(=++=πx x f ,即21)6sin(=+πx …………………………………………4分211)6(sin 21)3(cos 2)3(2cos )232cos(22-=-+=--=-=-ππππx x x x…………………………………………6分 (Ⅱ)已知b c C a 2cos 2=+由正弦定理得:CA C A C C A C ABC C A sin cos 2cos sin 2sin cos sin 2)sin(2sin 2sin cos sin 2+=++==+∴21cos =A ,∴在ABC ∆中 ∠3π=A …………………………………………8分 21)6sin()(++=πB B f∵∠3π=A ∴320π<<B ,6566πππ<+<B …………………………………………10分∴1)6sin(21≤+<πB ,23)(1≤<B f ∴函数)(B f 的取值范围为]23,1( …………………………………………12分18.(本小题满分12分) 解:(Ⅰ)依题意得⎪⎩⎪⎨⎧+=+=⨯++⨯+)12()3(5025452233112111d a a d a d a d a …………………………………………2分 解得⎩⎨⎧==231d a , …………………………………………4分 1212)1(23)1(1+=+=-+=-+=∴n a n n d n a a n n 即,.……………………………6分(Ⅱ)13-=n nna b ,113)12(3--⋅+=⋅=n n n n n a b …………………………………………7分 123)12(37353-⋅+++⋅+⋅+=n n n T n n n n n T 3)12(3)12(3735333132⋅++⋅-++⋅+⋅+⋅=- ……………………9分n n n n T 3)12(3232323212+-⋅++⋅+⋅+=--nnn n n 323)12(31)31(3231⋅-=+---⋅+=- ∴nn n T 3⋅= …………………………………………12分19.(本小题满分12分)解:(Ⅰ)取AC 中点G,连结FG 、BG , ∵F,G 分别是AD,AC 的中点∴FG ∥CD,且FG=21DC=1 .∵BE ∥CD ∴FG 与BE 平行且相等∴EF ∥BG . ……………………………2分ABC BG ABC EF 面面⊂⊄,∴EF ∥面ABC ……………………………4分 (Ⅱ)∵△ABC 为等边三角形 ∴BG ⊥AC 又∵DC ⊥面ABC,BG ⊂面ABC ∴DC ⊥BGABCDEF G∴BG 垂直于面ADC 的两条相交直线AC,DC ,∴BG ⊥面ADC . …………………………………………6分 ∵EF ∥BG ∴E F ⊥面ADC∵EF ⊂面ADE ,∴面ADE ⊥面ADC . …………………………………………8分 (Ⅲ)连结EC,该四棱锥分为两个三棱锥E -ABC 和E -ADC .43631232313114331=+=⨯⨯+⨯⨯=+=---ACD E ABC E BCDE A V V V .………………………12分另法:取BC 的中点为O ,连结AO ,则BC AO ⊥,又⊥CD 平面ABC ,∴C CD BC AO CD =⊥ , , ∴⊥AO 平面BCDE ,∴AO 为BCDE A V -的高,43232331,2321)21(,23=⨯⨯=∴=⨯+==-BCDE A BCDE V S AO . 20.(本小题满分12分)解:(Ⅰ)设6组数据的编号分别为1,2,3,4,5,6.设抽到不相邻的两组数据为事件A ,从6组数据中选取2组数据共有15种情况:(1,2)(1,3)(1,4)(1,5)(1,6)(2,3)(2,4)(2,5)(2,6)(3,4)(3,5)(3,6)(4,5)(4,6)(5,6),其中事件A 包含的基本事件有10种. …………………………………………3分所以321510)(==A P .所以选取的2组数据恰好不相邻的概率是32. ………………………6分(Ⅱ) 当10=x 时,;2|1026219|,262192613910134ˆ<-=+⨯=y……………………………………9分 当30=x 时,;2|1626379|,263792613930134ˆ<-=+⨯=y所以,该研究所得到的回归方程是可靠的. …………………………………………12分 21.(本小题满分12分)解:(Ⅰ)将1-=x 代入切线方程得2-=y ∴211)1(-=+-=-ab f ,化简得4-=-a b . …………………………………………2分 222)1(2)()1()(x xb ax x a x f +⋅+-+='12424)(22)1(-===-+=-'bb a b a f . …………………………………………4分解得:2,2-==b a∴122)(2+-=x x x f . …………………………………………6分 (Ⅱ)由已知得122ln 2+-≥x x x 在),1[+∞上恒成立化简得22ln )1(2-≥+x x x即022ln ln 2≥+-+x x x x 在),1[+∞上恒成立 . …………………………………………8分 设22ln ln )(2+-+=x x x x x h ,21ln 2)(-++='xx x x x h ∵1≥x ∴21,0ln 2≥+≥xx x x ,即0)(≥'x h . …………………………………………10分 ∴)(x h 在),1[+∞上单调递增,0)1()(=≥h x h∴)()(x f x g ≥在),1[+∞∈x 上恒成立 . …………………………………………12分22.(本小题满分14分)解(1)设椭圆方程为22221(0)x y a b a b+=>>,12,AF m AF n ==由题意知⎪⎪⎩⎪⎪⎨⎧==+=+6344222mn n m c n m …………………………………………2分解得92=c ,∴39122=-=b .∴椭圆的方程为131222=+y x …………………………………………4分 ∵3=⨯c y A ,∴1=A y ,代入椭圆的方程得22=A x ,将点A 坐标代入得抛物线方程为y x 82=. …………………………………………6分(2)设直线l 的方程为)22(1-=-x k y ,),(),,(2211y x C y x B2013年高考数学全国卷1(完整版试题+答案+解析)- 11 - / 11 由AB AC 2= 得)22(22212-=-x x , 化简得22221=-x x …………………………………………8分 联立直线与抛物线的方程⎪⎩⎪⎨⎧=-=-yx x k y 8)22(12, 得0821682=-+-k kx x ∴k x 8221=+① …………………………………………10分 联立直线与椭圆的方程⎪⎩⎪⎨⎧=+-=-124)22(122y x x k y 得0821632)2168()41(2222=--+-++k k x k k x k ∴22241821622kk k x +-=+② …………………………………………12分 ∴2222418216)228(222221=++---=-kk k k x x 整理得:0)4121)(2416(2=+--k k k ∴42=k ,所以直线l 的斜率为42 . …………………………………………14分。
2013年高考试题解析

22.已知函数 f ( x) 2 x ,无穷数列 an 满足 an+1=f(an),n∈N
*
(1)若 a1=0,求 a2,a3,a4; (2)若 a1>0,且 a1,a2,a3 成等比数列,求 a1 的值. (3)是否存在 a1,使得 a1,a2,„,an„成等差数列?若存在,求 出所有这样的 a1;若不存在,说明理由.
1, 2, 3且 i≠j, i,j,k,l∈
小值是
【解析】 根据对称性, 当向量 (ai a j )与(c k cl )互为相反向量,且它们 的模最大时
, (ai a j )( c k cl )最小。这时 ai AC , a j AD , c k CA, cl CB, (ai a j )( c k cl ) | ai a j ) | 2 5 .
u 2 2(u 2 4) 0 8 u 2 u [2 2,2 2 ],所以x y的最大值为 ,2 2
21. 已知函数 f ( x) 2 sin(x) ,其中常数ω >0.
(1)令ω =1,判断函数 F ( x) f ( x) f x 的奇偶性,并说明理由; 2
综上,a 2
x2 ny 2 x2 y2 x2 y2 18.【解析】 椭圆方程为: 1 lim 1 n 1 4 4n 1 4 4 4 4 n
x2 y2 1 联立 4 x 2 (u x) 2 4 2 x 2 2ux u 2 4 0 4u 2 8(u 2 4) 0 4 u x y
2
) 2 sin x 2 sin( x
2
)
2013高考全面解析

2013高考试卷第一时间全面解析语文基础:成语题虚晃一枪,新题型横空出世《考试说明》在语基部分最大的变动是成语题的重新出现,因此包括我在内的很多老师都觉得成语题是今年必考选项,然则结果却出乎很多人的意料——不但成语题没了,连文学常识都没有了。
本次五道题目为:字音字形、病句、近义词辨析、语义衔接以及……另一个全新题型。
这个新题型的出现可说是毫无征兆,其题干为“下列句中加点词的运用不同于其他三句的一项是?”,加点字均为单字动词,考点在于修辞手法。
这个考点本身并不难,然则考生们在临场乍然遇到难免出现心态波动。
其实语文考试就是如此,知识掌握也需要临场应用。
这个虚晃一枪出现的新题型,不知道是否会固定在今后的考试中。
此外,字音字形题中A选项出现了两个错别字,打破了以往“一个字错一个音错”的规律,这一点在今年一二模中已有征兆。
文言阅读:传记文重回视野,主观题概括大意文言选篇部分,并没有出现今年一模二模时文章体裁“百花齐放”的特色,回归相当传统的《宋史·曹彬传》,虽然本文以前曾经在广东省其他试卷中出现过,不过并不完全一致。
文言部分最受关注的是之前提过的“主观翻译题”,《考试说明》在此给出两种题型:一为逐字精译,一为概括大意,其中后者更像是“半道阅读延伸题”。
今年高考真题中命题人选择了相对较为简单的后者,对考生逐字翻译文言文的能力并未强调。
毕竟今年公布《考试说明》时间已经是1月,立即对应届生提升考试要求较为仓促。
但明年的考生务必在意,你们面对的可能就是较难的“逐字精译”了。
诗歌鉴赏:李太白古风再现,鲁仲连典故放水诗歌鉴赏是李白《古风·齐有倜傥生》,在选篇上重复了10年北京卷《古风五十九首》的文篇出处,而题目的难度甚至还颇有不如。
10年真题选择了一个“非典型”的怀才不遇愤懑消沉的李白,而今年则干脆在第二题主观题中安排了“结合诗中的鲁仲连典故分析李白的人生理想”这样直白的主旨分析题。
本诗是典型的咏古人明志,李白的人生理想高中生人尽皆知,鲁仲连的典故在注解中已经说明,这道题简直堪称零难度。
2013年高考全国Ⅰ理科数学试题及答案(word解析版)

2013年普通高等学校招生全国统一考试(全国Ⅰ)数学(理科)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)【2013年全国Ⅰ,理1,5分】已知集合{}{2|20,|A x x x B x x =->=<,则( ) (A )A B =∅ (B )A B =R (C )B A ⊆ (D )A B ⊆ 【答案】B【解析】∵2()0x x ->,∴0x <或2x >.由图象可以看出A B =R ,故选B . (2)【2013年全国Ⅰ,理2,5分】若复数z 满足(34i)|43i |z -=+,则z 的虚部为( )(A )4- (B )45- (C )4 (D )45【答案】D【解析】∵(34i)|43i |z -=+,∴55(34i)34i 34i (34i)(34i)55z +===+--+.故z 的虚部为45,故选D . (3)【2013年全国Ⅰ,理3,5分】为了解某地区的中小学生视力情况,拟从该地区的中小学生中抽取部分学生进行调查,事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异,而男女生视力情况差异不大,在下面的抽样方法中,最合理的抽样方法是( )(A )简单随机抽样 (B )按性别分层抽样 (C )按学段分层抽样 (D )系统抽样 【答案】C【解析】因为学段层次差异较大,所以在不同学段中抽取宜用分层抽样,故选C .(4)【2013年全国Ⅰ,理4,5分】已知双曲线C :()2222=10,0x y a b a b->>C 的渐近线方程为( )(A )14y x =± (B )13y x =± (C )12y x =± (D )y x =±【答案】C【解析】∵c e a ==,∴22222254c a b e a a +===.∴224a b =,1=2b a ±. ∴渐近线方程为12b y x x a =±±,故选C .(5)【2013年全国Ⅰ,理5,5分】执行下面的程序框图,如果输入的[]1,3t ∈-,则输出的s 属于( ) (A )[3,4]- (B )[5,2]- (C )[4,3]- (D )[2,5]- 【答案】D【解析】若[)1,1t ∈-,则执行3s t =,故[)3,3s ∈-.若[]1,3t ∈,则执行24s t t =-,其对称轴为2t =.故当2t =时,s 取得最大值4.当1t =或3时,s 取得最小值3,则[]3,4s ∈. 综上可知,输出的[]3,4s ∈-,故选D .(6)【2013年全国Ⅰ,理6,5分】如图,有一个水平放置的透明无盖的正方体容器,容器高8cm , 将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm ,如果不计容器的厚 度,则球的体积为( )(A )35003cm π (B )38663cm π (C )313723cm π(D )320483cm π【答案】B【解析】设球半径为R ,由题可知R ,2R -,正方体棱长一半可构成直角三角形,即OBA ∆为直角三角形,如图,2BC =,4BA =,2OB R =-,OA R =,由()22224R R =-+,得5R =,所以球的体积为34500533ππ=(cm 3),故选B .(7)【2013年全国Ⅰ,理7,5分】设等差数列{}n a 的前n 项和为11,2,0,3n m m m S S S S -+=-==,则m =( )(A )3(B )4 (C )5 (D )6【答案】C 【解析】∵12m S -=-,0m S =,13m S +=,∴()1022m m m a S S -=-=--=,11303m m m a S S ++=-=-=.∴1321m m d a a +=-=-=.∵()11102m m m S ma -=+⨯=,∴112m a -=-. 又∵1113m a a m +=+⨯=,∴132m m --+=.∴5m =,故选C . (8)【2013年全国Ⅰ,理8,5分】某几何体的三视图如图所示,则该几何体的体积为( ) (A )168π+ (B )88π+ (C )1616π+ (D )816π+ 【答案】A【解析】由三视图可知该几何体为半圆柱上放一个长方体,由图中数据可知圆柱底面半径2r =,长为4,在长方体中,长为4,宽为2,高为2,所以几何体的体积为24422816r ππ⨯⨯+⨯⨯=+,故选A .(9)【2013年全国Ⅰ,理9,5分】设m 为正整数,()2m x y +展开式的二项式系数的最大值为a , ()21m x y ++展开式的二项式系数的最大值为b ,若137a b =,则m =( )(A )5 (B )6 (C )7 (D )8 【答案】B【解析】由题意可知,2m m a C =,21mm b C +=,又∵137a b =,∴2!21!13=7!!!1!m m m m m m ()(+)⋅⋅(+),即132171m m +=+.解得6m =,故选B .(10)【2013年全国Ⅰ,理10,5分】已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为(3,0)F ,过点F 的直线交椭圆于,A B 两点.若AB 的中点坐标为(1,1)-,则E 的方程为( ) (A )2214536x y +=(B )2213627x y += (C )2212718x y += (D )221189x y +=【答案】D【解析】设11()A x y ,,22()B x y ,,∵A ,B 在椭圆上,∴2211222222221,1,x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩①②,①-②,得 1212121222=0x x x x y y y y a b (+)(-)(+)(-)+,即2121221212=y y y y b a x x x x (+)(-)-(+)(-), ∵AB 的中点为()1,1-,∴122y y +=-,122x x +=,而1212011=312AB y y k x x --(-)==--, ∴221=2b a .又∵229a b -=,∴218a =,29b =.∴椭圆E 的方程为22=1189x y +,故选D . (11)【2013年全国Ⅰ,理11,5分】已知函数()()220ln 10x x x f x x x ⎧-+≤⎪=⎨+>⎪⎩,若()f x a x ≥|,则a 的取值范围是( ) (A )(],0-∞ (B )(],1-∞ (C )[2,1]- (D )[2,0]-【答案】D【解析】由()y f x =的图象知:①当0x >时,y ax =只有0a ≤时,才能满足()f x ax ≥,可排除B ,C .②当0x ≤时,()2222y f x x x x x ==-+=-.故由()f x ax ≥得 22x x ax -≥.当0x =时,不等式为00≥成立.当0x <时,不等式等价于2x a -≤.∵22x -<-,∴2a ≥-.综上可知:[]2,0a ∈-,故选D .(12)【2013年全国Ⅰ,理12,5分】设n n n A B C ∆的三边长分别为n a ,n b ,n c ,n n n A B C ∆的面积为n S ,1,2,3.n =⋯,若11b c >,1112b c a +=,1n n a a +=,12n n n c a b ++=,12n nn b a c ++=,则( )(A ){}n S 为递减数列 (B ){}n S 为递增数列(C ){}21n S -为递增数列,{}2n S 为递减数列 (D ){}21n S -为递减数列,{}2n S 为递增数列 【答案】B第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答.第(22)题~第(24)题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分(13)【2013年全国Ⅰ,理13,5分】已知两个单位向量a ,b 的夹角为60°,()1t t =+-c a b .若·0=b c ,则t = . 【答案】2【解析】∵()1t t =+-c a b ,∴()2··1t t =+-bc ab b .又∵1==a b ,且a 与b 夹角为60°,⊥b c , ∴()0 601t cos t =︒+-a b ,1012t t =+-.∴2t =.(14)【2013年全国Ⅰ,理14,5分】若数列{}n a 的前n 项和2133n n S a =+,则{}n a 的通项公式是n a = .【答案】()12n --【解析】∵2133n n S a =+,① ∴当2n ≥时,112133n n S a --=+.② ①-②,得12233n n n a a a -=-,即12n n aa -=-.∵1112133a S a ==+,∴11a =.∴{}n a 是以1为首项,-2为公比的等比数列,()12n n a -=-.(15)【2013年全国Ⅰ,理15,5分】设当x θ=时,函数()2f x sinx cosx =-取得最大值,则cos θ= .【答案】 【解析】()s 2x f x sinx cosx x ⎫⎪==⎭-,令cos α=,sin α=,则()()f x x α=+,当22()x k k ππα=+-∈Z 时,()sin x α+有最大值1,()f x,即22()k k πθπα=+-∈Z ,所以cos θ=πcos =cos 2π+cos sin 22k πθααα⎛⎫⎛⎫-=-=== ⎪ ⎪⎝⎭⎝⎭(16)【2013年全国Ⅰ,理16,5分】若函数()()()221f x x x ax b =-++的图像关于直线2x =-对称,则()f x 的最大值为 .【答案】16【解析】∵函数()f x 的图像关于直线2x =-对称,∴()f x 满足()()04f f =-,()()13f f -=-,即151640893b a b a b =-(-+)⎧⎨=-(-+)⎩,得815a b =⎧⎨=⎩∴()432814815f x x x x x =---++.由()324242880f x x x x '=---+=,得12x =-22x =-,32x =-.易知,()f x在(,2-∞-上为增函数,在()22--上为减函数,在(2,2--上为增函数,在()2-+-∞上为减函数.∴(((((222122821588806416f ⎡⎤⎡⎤-=---+-+=---=-=⎢⎥⎢⎥⎣⎦⎣⎦.()()()()()22212282153416915f ⎡⎤⎡-=---+⨯⎤==-⎣⎦⎣⎦-+--+(((((222122821588806416f ⎡⎤⎡⎤-=---++-++=-++=-=⎢⎥⎢⎥⎣⎦⎣⎦.故f (x )的最大值为16.三、解答题:解答应写出文字说明,证明过程或演算步骤.(17)【2013年全国Ⅰ,理17,12分】如图,在ABC ∆中,90ABC ∠=︒,AB =,1BC =,P为ABC ∆内一点,90BPC ∠=︒.(1)若12PB =,求PA ;(2)若150APB ∠=︒,求tan PBA ∠.解:(1)由已知得60PBC ∠=︒,30PBA ∴∠=︒.在PBA ∆中,由余弦定理得211732cos 30424PA =+-︒=.故PA =(2)设PBA α∠=,由已知得sin PB α=.在PBA ∆sin sin(30)αα=︒-,4sin αα=.所以tan α,即tan PBA ∠= (18)【2013年全国Ⅰ,理18,12分】如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,160BAA ∠=︒. (1)证明:1AB A C ⊥;(2)若平面ABC ⊥平面11AA B B ,AB CB =,求直线1A C 与平面11BB C C 所成角的正弦值.解:(1)取AB 的中点O ,连结OC ,1OA ,1A B .因为CA CB =,所以OC AB ⊥.由于1AB AA =,160BAA ∠=︒,故1AA B ∆为等边三角形,所以1OA AB ⊥.因为1OC OA O = ,所以AB ⊥平面1OA C . 又1A C 平面1OA C ,故1AB A C ⊥.(2)由(1)知OC AB ⊥,1OA AB ⊥.又平面ABC ⊥平面11AA B B ,交线为AB ,所以OC ⊥平面11AA B B ,故OA ,1OA ,OC 两两相互垂直.以O 为坐标原点,OA 的方向为x 轴的正方向,OA为单位长,建立如图所示的空间直角坐标系O xyz -.由题设知()1,0,0A,1()0A ,(0,0C ,()1,0,0B -.则(1,03BC =,11()BB AA =-=,(10,A C = .设()n x y z =,,是平面11BB C C 的法向量,则100BC BB ⎧⋅=⎪⎨⋅=⎪⎩n n即0x x ⎧=⎪⎨-=⎪⎩可取1)n =-.故111cos ,n AC n AC n AC ⋅==⋅ .所以1A C 与平面11BB C C. (19)【2013年全国Ⅰ,理19,12分】一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n .如果n =3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n =4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.假设这批产品的优质品率为50%,即取出的每件产品是优质品的概率都为12,且各件产品是否为优质品相互独立.(1)求这批产品通过检验的概率;(2)已知每件产品的检验费用为100元,且抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X (单位:元),求X 的分布列及数学期望.解:(1)设第一次取出的4件产品中恰有3件优质品为事件1A ,第一次取出的4件产品全是优质品为事件2A ,第二次取出的4件产品都是优质品为事件1B ,第二次取出的1件产品是优质品为事件2B ,这批产品通过检验为事件A ,依题意有()()1122A A B A B = ,且11A B 与22A B 互斥,所以 ()()()()()()()112211122241113||161616264P A P A B P A B P A P B A P A P B A ==⨯++⨯==+.(2)X 可能的取值为400,500,800,并且()41114001161616P X ==--=,()500116P X ==,()80140P X ==. 所以X 的分布列为()111400+500+800506.2516164E X =⨯⨯⨯=. (20)【2013年全国Ⅰ,理20,12分】已知圆()2211M x y ++=:,圆()2219N x y -+=:,动圆P 与圆M 外切并且与圆N 内切,圆心P 的轨迹为曲线C .(1)求C 的方程;(2)l 是与圆P ,圆M 都相切的一条直线,l 与曲线C 交于A ,B 两点,当圆P 的半径最长时,求AB . 解:由已知得圆M 的圆心为()1,0M -,半径11r =;圆N 的圆心为()1,0N ,半径23r =.设圆P 的圆心为(),P xy ,半径为R .(1)因为圆P 与圆M 外切并且与圆N 内切,所以()()12124PM PN R r r R r r +=++-=+=.由椭圆的定义可知,曲线C 是以M ,N 为左、右焦点,长半轴长为2(左顶点除外),其方程为()22=1243x y x +≠-.(2)对于曲线C 上任意一点()P x y ,,由于222PM PN R -=-≤,所以2R ≤,当且仅当圆P 的圆心为()2,0时,2R =.所以当圆P 的半径最长时,其方程为()2224x y -+=.若l 的倾斜角为90︒,则l 与y 轴重 合,可得AB =l 的倾斜角不为90︒,由1r R ≠知l 不平行于x 轴,设l 与x 轴的交点为Q ,则1||||QP R QM r =,可求得()4,0Q -,所以可设()4l y k x =+:.由l 与圆M ,解得k =. 当k =时,将y =+22=13x y +,并整理得27880x x +-=,解得1,2x =. 2118|7AB x x =-=.当k =时,由图形对称性可知187AB =.综上,AB =187AB =. (21)【2013年全国Ⅰ,理21,12分】设函数()2f x x ax b =++,()()x g x e cx d =+.若曲线()y f x =和曲线()y g x =都过点()0,2P ,且在点P 处有相同的切线42y x =+.(1)求a ,b ,c ,d 的值;(2)若2x ≥-时,()()f x kg x ≤,求k 的取值范围.解:(1)由已知得()02f =,()02g =,()04f '=,()04g '=.而()2f x x a '=+,()()x g x e cx d c '=++, 故2b =,2d =,4a =,4d c +=.从而4a =,2b =,2c =,2d =. (2)由(1)知,()242f x x x =++,()()21x g x e x =+.设函数()()()()22142x F x kg x f x ke x x x =-=+---,()()()()2224221x x F x ke x x x ke '=+--=+-.()00F ≥ ,即1k ≥.令()0F x '=得1ln x k =-,22x =-. ①若21k e ≤<,则120x -<≤.从而当12()x x ∈-,时,()0F x '<;当1()x x ∈+∞,时,()0F x '>. 即()F x 在1(2)x -,单调递减,在1()x +∞,单调递增.故()F x 在[)2-+∞,的最小值为()1F x . 而()()11111224220F x x x x x =+---=-+≥.故当2x ≥-时,()0F x ≥,即()()f x kg x ≤恒成立. ②若2k e =,则()()()2222x F x e x e e -'=+-.∴当2x >-时,()0F x '>,即()F x 在()2-+∞,单调递增. 而()20F -=,故当2x ≥-时,()0F x ≥,即()()f x kg x ≤恒成立. ③若2k e >,则()()22222220F k eek e ---=-+=--<.从而当2x ≥-时,()()f x kg x ≤不可能恒成立.综上,k 的取值范围是2[1]e ,. 请考生在(22)、(23)、(24)三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做第一个题目计分,做答时,请用2B 铅笔在答题卡上将所选题号后的方框涂黑.(22)【2013年全国Ⅰ,理22,10分】(选修4-1:几何证明选讲)如图,直线AB为圆的切线,切点为B ,点C 在圆上,ABC ∠的角平分线BE 交圆于点E ,DB 垂直BE 交圆 于点D . (1)证明:DB DC =;(2)设圆的半径为1,BC =CE 交AB 于点F ,求BCF ∆外接圆的半径. 解:(1)连结DE ,交BC 于点G .由弦切角定理得,ABE BCE ∠=∠.而ABE CBE ∠=∠,故CBE BCE ∠=∠,BE CE =.又因为DB BE ⊥,所以DE 为直径,90DCE ∠=︒,DB DC =.(2)由(1)知,CDE BDE ∠=∠,DB DC =,故DG 是BC的中垂线,所以BG =设DE 的中点为O ,连结BO ,则60BOG ∠=︒.从而30ABE BCE CBE ∠=∠=∠=︒,所以CF BF ⊥,故Rt BCF ∆.(23)【2013年全国Ⅰ,理23,10分】(选修4-4:坐标系与参数方程)已知曲线1C 的参数方程为45cos 55sin x ty t=+⎧⎨=+⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2sin ρθ=. (1)把1C 的参数方程化为极坐标方程;(2)求1C 与2C 交点的极坐标(0ρ≥,02θπ≤<).解:(1)将45cos 55sin x t y t =+⎧⎨=+⎩消去参数t ,化为普通方程()()224525x y -+-=,即221810160C x y x y +--+=:.将cos sin x y ρθρθ=⎧⎨=⎩代入22810160x y x y +--+=得28cos 10sin 160ρρθρθ--+=. 所以1C 的极坐标方程为28cos 10sin 160ρρθρθ--+=.(2)2C 的普通方程为2220x y y +-=.由222281016020x y x y x y y ⎧+--+=⎨+-=⎩,解得11x y =⎧⎨=⎩或02x y =⎧⎨=⎩, 所以1C 与2C交点的极坐标分别为π4⎫⎪⎭,π2,2⎛⎫ ⎪⎝⎭.(24)【2013年全国Ⅰ,理24,10分】(选修4-5:不等式选讲)已知函数()212f x x x a =-++,()3g x x =+.(1)当2a =-时,求不等式()()f x g x <的解集;(2)设1a >-,且当1,22a x ⎡⎫∈-⎪⎢⎣⎭时,()()f x g x ≤,求a 的取值范围.解:(1)当2a =-时,()()f x g x <化为212230x x x -+---<.设函数21223y x x x =-+---,则y =15,212,1236,1x x y x x x x ⎧-<⎪⎪⎪=--≤≤⎨⎪->⎪⎪⎩,其图像如图所示.从图像可知,当且仅当()0,2x ∈时,0y <.所以原不等式的解集是{}2|0x x <<.(2)当1,22x a ⎡⎫-⎪⎢⎣⎭∈时,()1f x a =+.不等式()()f x g x ≤化为13a x +≤+.所以2x a ≥-,对1,22x a ⎡⎫-⎪⎢⎣⎭∈都成立.故22a a -≥-,即43a ≤.从而a 的取值范围是41,3⎛⎤- ⎥⎝⎦.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014届高考一轮复习 专题一、直线运动1,(2013全国新课标理综1第19题)如图,直线a 和曲线b 分别是在平直公路上形式的汽车a 和b 的位置一时间(x-t )图线,由图可知A.在时刻t 1,a 车追上b 车B.在时刻t 2,a 、b 两车运动方向相反C.在t 1到t 2这段时间内,b 车的速率先减少后增加D.在t 1到t 2这段时间内,b 车的速率一直不a 车大【命题意图】本题考查位移图象、追及问题等基础知识点,意在考查考生应用相关知识定量分析物理问题,解决问题的能力。
答案:BC解析:在时刻t 1,b 车追上a 车,选项A 错误。
根据位移图象的斜率表示速度可知,在时刻t 2,a 、b 两车运动方向相反,选项B 正确。
在t 1到t 2这段时间内,b 车的速率先减少后增加,选项C 正确D 错误。
2. (2013全国新课标理综1第14题)右图是伽利略1604年做斜面实验时的一页手稿照片,照片左上角的三列数据如下表。
表中第二列是时间,第三列是物体沿斜面运动的距离,第一列是伽利略在分析实验数据时添加的。
根据表中的数据,伽利略可以得出的结论是A.物体具有惯性B.斜面倾角一定时,加速度与质量无关C.物体运动的距离与时间的平方成正比D.物体运动的加速度与重力加速度成正比【命题意图】本题考查伽利略斜面实验等相关知识点,意在考查考生应用相关知识定量分析物理问题,解决问题的能力。
答案:C解析:根据表中的数据,第一列与第三列数据存在比例关系,第一列数据是第二列数据的二次方,伽利略可以得出的结论是:物体运动的距离与时间的平方成正比,选项C 正确。
3.(2013高考广东理综第13题)某航母跑道长为200m ,飞机在航母上滑行的最大加速度为6m/s 2,起飞需要的最低速度为50m/s.那么,飞机在滑行前,需要借助弹射系统获得的最小初速度为 A .5m/s B .10m/s C .15m/s D.20m/s考点:匀变速直线运动规律公式的应用答案:B解析:由as v v t 2202=-得:0v =ax v t 22-=10m/s 。
选项B 正确。
4.(2013全国高考大纲版理综第19题)将甲乙两小球先后以同样的速度在距地面不同高度处竖直向上抛出,抛出时间相隔2 s ,它们运动的图像分别如直线甲乙所示。
则( ) A .t =2 s 时,两球的高度相差一定为40 m B .t =4 s 时,两球相对于各自的抛出点的位移相等 C .两球从抛出至落到地面所用的时间间隔相等 D .甲球从抛出至到达最高点的时间间隔与乙球相等 答案:BD解析:由于甲乙两小球先后以同样的速度在距地面不同高度处竖直向上抛出,t =2 s 时,两球的高度相差不一定为40 m ,两球从抛出至落到地面所用的时间间隔不相等,选项AC 错误。
根据速度图象与横轴所夹面积表示位移可知,t =4 s 时,两球相对于各自的抛出点的位移相等,选项B 正确。
由于甲乙两小球先后以同样的速度竖直向上抛出,甲球从抛出至到达最高点的时间间隔与乙球相等,选项D 正确。
5.(2013高考四川理综第6题)甲、乙两物体在t=0时刻经过同一位置沿x 轴运动,其v-t 图像如图所示。
则A .甲、乙在t=0s 到t=1s 之间沿同一方向运动B .乙在t=0到t=7s 之间的位移为零C .甲在t=0到t=4s 之间做往复运动D .甲、乙在t=6s 时的加速度方向相同 答案.BD解析:乙在t=0s 到t=0.5s 之间沿沿x 轴负方向运动,在t=0.5s 到t=1s 之间沿x 轴正方向运动,而甲在t=0s 到t=1s 之间沿x 轴正方向运动,选项A 错误。
根据速度图象与横轴所夹面积表示位移可知,乙在t=0到t=7s 之间的位移为零,选项B 正确。
甲在t=0到t=4s 之间一直沿x 轴正方向运动,选项C 错误。
甲、乙在t=6s 时的加速度均为负值,方向相同,选项D 正确。
6.(15分)(2013全国高考大纲版理综第24题)一客运列车匀速行驶,其车轮在轨道间的接缝处会产生周期性的撞击。
坐在该客车中的某旅客测得从第1次到第16次撞击声之间的时间间隔为10.0 s 。
在相邻的平行车道上有一列货车,当该旅客经过货车车尾时,火车恰好从静止开始以恒定加速度沿客车行进方向运动。
该旅客在此后的20.0 s 内,看到恰好有30节货车车厢被他连续超过。
已知每根轨道的长度为25.0 m ,每节货车车厢的长度为16.0 m ,货车车厢间距忽略不计。
求 (1)客车运行的速度大小; (2)货车运行加速度的大小。
.(15分)解:(1)设连续两次撞击轨道的时间间隔为Δt ,每根轨道的长度为l ,则客车的速度为 lt=∆v (3分) 其中l =25.0 m ,10.0161s t -∆=解得 37.5 m/s =v (2分)(2)设从货车开始运动后t =20.0 s 内客车行驶的距离为s 1,货车行驶的距离为s 2,货车的加速度为a ,30节货车车厢的总长度为 L =30×16.0 m 由运动学公式有 1s t =v (3分) 2212s at =(3分) 由题意,有 12L s s =- (2分) 联立解得 a =1.35 m/s 2(2分)7.(2013高考四川理综第9题)9.近来,我国多个城市开始重点治理“中国式过马路”行为。
每年全国由于行人不遵守交通规则而引发的交通事故上万起,死亡上千人。
只有科学设置交通管制,人人遵守交通规则,才有保证行人的生命安全。
如右图所示,停车线AB 与前方斑马线边界CD 间的距离为23m 。
质量8t 、车长7m 的卡车以54km/h 的速度向北匀速行驶,当车前端刚驶过停车线AB ,该车前方的机动车交通信号灯由绿灯变黄灯。
(1)若此时前方C 处人行横道路边等待的行人就抢先过马路,卡车司机发现行人,立即制动,卡车受到的阻力为3×104N 。
求卡车的制动距离?(2)若人人遵守交通规则,该车将不受影响地驶过前方斑马线边界CD 。
为确保行人安全,D 处人行横道信号灯应该在南北向机动车信号灯变黄灯后至少多久变为绿灯? 7.解:(1)据题意 由 v 2-v 02=2ax , 得: x=a v v 222- ,①汽车刹车时,阻力产生的加速度为a由 牛顿第二定律 得a=F/m, ② 代入数据得制动距离 x=30 m ③(2)据题意汽车不受影响的行驶距离应该是x1=30m ④故黄灯的持续时间为t 则x1=v0t, ⑤代入数据得时间为t=2 s . ⑥7.(2012山东卷).(13分)(1)某同学利用图甲所示德实验装置,探究物块在水平桌面上的运动规律。
物块在重物的牵引下开始运动,重物落地后,物块再运动一段距离停在桌面上(尚未到达滑轮处)。
从纸带上便于测量的点开始,每5个点取1个计数点,相邻计数点间的距离如图议所示。
打点计时器电源的频率为50Hz。
○1通过分析纸带数据,可判断物块在相邻计数点和之间某时刻开始减速。
○2计数点5对应的速度大小为 m/s,计数点6对应的速度大小为 m/s。
(保留三位有效数字)。
○3物块减速运动过程中加速度的大小为a= m/s2,若用ag来计算物块与桌面间的动摩擦因数(g为重力加速度),则计算结果比动摩擦因数的真实值(填“偏大”或“偏小”)。
(1)○16;7【或7;6】○21.00;1.20○32.00;偏大解析:①由于计数点前后的间隔距离都小于它们的间隔距离,说明计数点6之前物块在加速,计数点7之后物块在减速,则开始减速的时刻在6和7之间。
答案6;7【或7;6】。
②计数点5对应的速度等于4和6间的平均速度00.12.010)01.1100.9(25=⨯+=-vm/s,同理80.02.010)01.700.9(24=⨯+=-vm/s,又2645vvv+=可解得计数点6对应的速度大小为1.20 m/s。
③在减速阶段00.2=∆x cm,则加速度为00.21.01000.2222=⨯=∆=-Txam/s2。
在减速阶段产生加速度的力是滑动摩擦力和纸带受到的阻力,所以计算结果比动摩擦因数的真实值“偏大”。
专题二、相互作用1. (2013全国新课标理综II第15题)如图,在固定斜面上的一物块受到一外力F的作用,F平行于斜面向上。
若要物块在斜面上保持静止,F的取值应有一定的范围,已知其最大值和最小值分别为F1和F2(F2>0)。
由此可求出A.物块的质量B.斜面的倾角C.物块与斜面间的最大静摩擦力D.物块对斜面的压力1.C【命题意图】本题考查受力分析、力的分解、摩擦力、平衡条件及其相关知识,意在考查考生分析解决问题的能力。
【解题思路】设斜面倾角为θ,斜面对物块的最大静摩擦力为f。
平行于斜面的外力F取最大值F1时,最大静摩擦力f方向沿斜面向下,由平衡条件可得:F1=f+mgsinθ;平行于斜面的外力F取最小值F2时,最大静摩擦力f方向沿斜面向上,由平衡条件可得:f+F2= mgsinθ;联立解得物块与斜面的最大静摩擦力f=( F2-F1)/2.选项C正确。
不能得出物块质量m,不能得出斜面倾角θ,不能得出物块对斜面压力,选项ABD错误。
【技巧点拨】分析此题,只需根据题述,利用最大静摩擦力平行斜面向上、平行斜面向下两种情况,应用平衡条件列出两个方程得出,不需要具体解出块与斜面的最大静摩擦力表达式。
2.(2013高考重庆理综第1题)如图所示,某人静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角θ。
若此人所受重力为G,则椅子各个部分对他作用力的合力大小为A.G B.G sinθC.G cosθD.G tanθ答案:A解析:人静躺在椅子上,受力平衡,由平衡条件可知椅子各个部分对他作用力的合力大小为G,,选项A正确。
3.(2013高考上海物理第8题)如图,质量m A>m B的两物体A、B叠放在一起,靠着竖直墙面。
让它们由静止释放,在沿粗糙墙面下落过程中,物体B的受力示意图是答案:A解析:两物体A、B叠放在一起,在沿粗糙墙面下落过程中,由于物块与竖直墙面之间没有压力,没有摩擦力,二者一起做自由落体运动,AB之间没有弹力作用,物体B的受力示意图是图A。
4.(2013高考上海物理第18题)两个共点力F l、F2大小不同,它们的合力大小为F,则(A)F1、F2同时增大一倍,F也增大一倍(B)F1、F2同时增加10N,F也增加10N(C)F1增加10N,F2减少10N,F一定不变(D)若F1、F2中的一个增大,F不一定增大答案:AD解析:F1、F2同时增大一倍,F也增大一倍,选项A正确。
F1、F2同时增加10N,F不一定增加10N,选项B错误;F1增加10N,F2减少10N,F可能变化,选项C错误。
若F1、F2中的一个增大,F不一定增大,选项D正确。
