陕西省2010—2017年中考数学第24、25、16题——压轴题陕西行2018年11月
陕西省中考数学试题:重难点突出

陕西省中考数学试题:重难点突出【重点题型分析】今年考题代数部分重点知识仍然以函数为主线,而几何部分主要围绕着全等以及位似变换,如下就几个重要题型进行简单的分析:1、第10题:作为选择题的压轴题,今年仍然选择了考查二次函数的平移,此类问题是第10题的常考考点,此题难度不大,能做对的学生比较多。
2、第16题:同样作为填空题的压轴,此题年年都是学生们的痛点,得分率不高,但今年梯形退出阵营后,改为利用相似解决的轴对称问题,较往年的梯形辅助线问题难度有所降低,但仍需要细心作答。
总体看来,往年的梯形问题,我们有梯形的辅助线模型,而今年的相似问题,可以利用十大相似模型仍能轻松解决。
3、第24题:今年考题总体难度的加大,第24题是功不可没的,此题虽然延续了二次函数与几何的综合题型,但考察到了等腰三角形、矩形多个几何图形的同时,还涉及到中心对称以及最值问题,考点众多,综合性较强,难度略为偏难,但对于基础扎实,思维灵活的学生来说,此题应不会有太大的困难。
4、第25题:每年的压轴题总是大家热议的话题,今年压轴题与我校模考班压轴题及其相似,均涉及到了有关三角形的内接正方形的问题。
前两问难度不太大,第一问利用位似变换画等边三角形的内接正方形,第二问求给定边长的等边三角形内接正方形的周长,正好可以利用我校模考班最后一题的解题方法,利用相似比与高之比相等解出;第三问需要利用函数思想去解决面积的最值问题,虽然考法比较常规,但由于需要拉开学生差距,故难度属于全卷最难。
此题计算量是比较大的。
从宏观上看,今年考题总体上较稳定,考点分布均匀,体现了陕西省中考试题的特点,但各题难度的调整及总体难度的变化仍然是值得大家关注的重点。
试题分析:周苗,西安新东方优能初中理科教研组长,中考骨干教师,负责初中理科项目教学产品研发。
长期从事中考数学教学工作,有多年的教学经验和严谨的数学逻辑思维,对新课标和中考数学有深入的研究,对中考考点有其独到见解。
陕西中考数学十年压轴题汇总
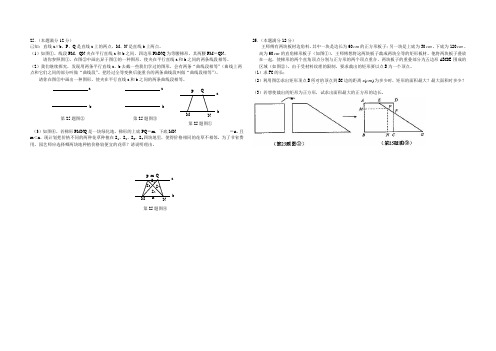
25.(本题满分12分)已知:直线a ∥b ,P 、Q 是直线a 上的两点,M 、N 是直线b 上两点。
(1)如图①,线段PM 、QN 夹在平行直线a 和b 之间,四边形PMNQ 为等腰梯形,其两腰PM =QN 。
请你参照图①,在图②中画出异于图①的一种图形,使夹在平行直线a 和b 之间的两条线段相等。
(2)我们继续探究,发现用两条平行直线a 、b 去截一些我们学过的图形,会有两条“曲线段相等”(曲线上两点和它们之间的部分叫做“曲线段”。
把经过全等变换后能重合的两条曲线段叫做“曲线段相等”)。
请你在图③中画出一种图形,使夹在平行直线a 和b 之间的两条曲线段相等。
(3)如图④,若梯形PMNQ 是一块绿化地,梯形的上底PQ =m ,下底MN =n ,且m <n 。
现计划把价格不同的两种花草种植在S 1、S 2、S 3、S 4四块地里,使得价格相同的花草不相邻。
为了节省费用,园艺师应选择哪两块地种植价格较便宜的花草?请说明理由。
25.(本题满分12分)王师傅有两块板材边角料,其中一块是边长为60cm 的正方形板子;另一块是上底为30cm ,下底为120cm ,高为60cm 的直角梯形板子(如图①),王师傅想将这两块板子裁成两块全等的矩形板材。
他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCDE 围成的区域(如图②),由于受材料纹理的限制,要求裁出的矩形要以点B 为一个顶点。
(1)求FC 的长;(2)利用图②求出矩形顶点B 所对的顶点.....到BC 边的距离)(cm x 为多少时,矩形的面积最大?最大面积时多少? (3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长。
P Q M Na b 第25题图① a b 第25题图② ab第25题图③P Q M Na b 第25题图④ S 1S 2S 3 S 4 n m25.(本题满分12分)如图,O 的半径均为R .(1)请在图①中画出弦AB CD ,,使图①为轴对称图形而不是..中心对称图形;请在图②中画出弦AB CD ,,使图②仍为中心对称图形; (2)如图③,在O 中,(02)AB CD m m R ==<<,且AB 与CD 交于点E ,夹角为锐角α.求四边形ACBD 面积(用含m α,的式子表示); (3)若线段AB CD ,是O的两条弦,且AB CD ==,你认为在以点A B C D ,,,为顶点的四边形中,是否存在面积最大的四边形?请利用图④说明理由.25、(本题满分12分)某县社会主义新农村建设办公室,为了解决该县甲、乙两村和一所中学长期存在的饮水困难问题,想在这三个地方的其中一处建一所供水站,由供水站直接铺设管道到另外两处。
2017陕西中考数学压轴题归类1

存在的饮水困难问题,想在这三个地方的其中一处建一所供水站,由供水站直接 铺设管道到另外两处。
如图,甲、乙两村坐落在夹角为 30°的两条公路的 AB 段和 CD 段(村子和 公路的宽均不计),点 M 表示这所中学。点 B 在点 M 的北偏西 30°的 3km 处, 点 A 在点 M 的正西方向,点 D 在点 M 的南偏西 60°的 2 3 km 处。
类型一:线段最值问题
题一: 最短和最长距离问题 知识点源于“两点之间线段最短 ”,更方便的理解“三角形任意两边之和大
于第三边,两边之差小于第三边 ”;历史名题“将军饮马”问题。经过了不断 的演变,以其极其丰富的表情展现于考生面前! 1、两点在河的两侧 (1)河的宽度忽略不计 (2)河的宽度不能够忽略
3
6.小明在学习轴对称的时候,老师留了这样一道思考题:如图,已知在直线 l 的同侧有 A、B 两点,请你在直线 l 上确定一点 P,使得 PA+PB 的值最小.小明 通过独立思考,很快得出了解决这个问题的正确方法,他的作法是这样的: ①作点 A 关于直线 l 的对称点 A′. ②连接 A′B,交直线 l 于点 P.则点 P 为所求.请你参考小明的作法解决下列 问题: (1)如图 1,在△ABC 中,点 D、E 分别是 AB、AC 边的中点,BC=6,BC 边上的 高为 4,请你在 BC 边上确定一点 P,使得△PDE 的周长最小. ①在图 1 中作出点 P.(三角板、刻度尺作图,保留作图痕迹,不写作法) ②请直接写出△PDE 周长的最小值______. (2)如图 2 在矩形 ABCD 中,AB=4,BC=6,G 为边 AD 的中点,若 E、F 为边 AB 上的两个动点,点 E 在点 F 左侧,且 EF=1,当四边形 CGEF 的周长最小时,请 你在图 2 中确定点 E、F 的位置.(三角板、刻度尺作图,保留作图痕迹,不写 作法),并直接写出四边形 CGEF 周长的最小值______.
2010陕西中考数学试题及答案

2010陕西中考数学试题及答案2010年陕西省中考数学试题一、选择题(每题3分,共30分)1. 下列哪个数是正整数?A. -3B. 2C. 0D. -12. 如果a和b是相反数,那么a+b的值是多少?A. 0B. 1C. 2D. -13. 一个直角三角形的两条直角边分别为3和4,斜边的长度是多少?A. 5B. 6C. 7D. 84. 下列哪个是二次根式?A. √3B. √(-1)C. √(2/3)D. √(-2)5. 一个数的平方根是4,这个数是多少?A. 16B. -16C. 8D. -86. 圆的周长是2πr,其中π是圆周率,r是半径,如果周长是12.56,那么半径r是多少?A. 2B. 4C. 6D. 87. 一个数的立方根是2,这个数是多少?A. 8B. 6C. 4D. 28. 一个等腰三角形的底边长度是10,两腰的长度是x,如果周长是30,那么x是多少?A. 10B. 5C. 15D. 209. 一个数的绝对值是5,这个数可能是多少?A. 5B. -5C. 5或-5D. 010. 一个数的倒数是1/2,这个数是多少?A. 2B. 1C. 1/2D. -1/2二、填空题(每题2分,共20分)11. 如果一个数的平方是25,那么这个数是________。
12. 一个数的立方是-8,那么这个数是________。
13. 一个数的绝对值是它本身,这个数是________。
14. 如果一个三角形的内角和是180°,那么一个四边形的内角和是________。
15. 如果一个数的平方根是2或-2,那么这个数是________。
16. 一个数的倒数是2,那么这个数是________。
17. 如果一个数的立方根是-3,那么这个数是________。
18. 一个数的平方是它本身,这个数可能是________。
19. 如果一个数的绝对值是3,那么这个数可能是________。
20. 如果一个三角形的周长是24,且三边长度的比是3:4:5,那么最短边的长度是________。
陕西中考数学十年压轴题汇总

25.(本题满分12分)已知:直线a ∥b ,P 、Q 是直线a 上的两点,M 、N 是直线b 上两点。
(1)如图①,线段PM 、QN 夹在平行直线a 和b 之间,四边形PMNQ 为等腰梯形,其两腰PM =QN 。
请你参照图①,在图②中画出异于图①的一种图形,使夹在平行直线a 和b 之间的两条线段相等。
(2)我们继续探究,发现用两条平行直线a 、b 去截一些我们学过的图形,会有两条“曲线段相等”(曲线上两点和它们之间的部分叫做“曲线段”。
把经过全等变换后能重合的两条曲线段叫做“曲线段相等”)。
请你在图③中画出一种图形,使夹在平行直线a 和b 之间的两条曲线段相等。
(3)如图④,若梯形PMNQ 是一块绿化地,梯形的上底PQ =m ,下底MN =n ,且m <n 。
现计划把价格不同的两种花草种植在S 1、S 2、S 3、S 4四块地里,使得价格相同的花草不相邻。
为了节省费用,园艺师应选择哪两块地种植价格较便宜的花草?请说明理由。
25.(本题满分12分)王师傅有两块板材边角料,其中一块是边长为60cm 的正方形板子;另一块是上底为30cm ,下底为120cm ,高为60cm 的直角梯形板子(如图①),王师傅想将这两块板子裁成两块全等的矩形板材。
他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCDE 围成的区域(如图②),由于受材料纹理的限制,要求裁出的矩形要以点B 为一个顶点。
(1)求FC 的长;(2)利用图②求出矩形顶点B 所对的顶点.....到BC 边的距离)(cm x 为多少时,矩形的面积最大?最大面积时多少?(3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长。
25.(本题满分12分)如图,O e的半径均为R .(1)请在图①中画出弦AB CD ,,使图①为轴对称图形而不是..中心对称图形;请在图②中画出弦AB CD ,,使图②仍为中心对称图形; (2)如图③,在O e中,(02)AB CD m m R ==<<,且AB 与CD交于点E ,夹角为锐角α.求四边形ACBD 面积(用含m α,的式子表示); (3)若线段AB CD ,是O e的两条弦,且AB CD ==,你认为在以点A B C D ,,,为顶点的四边形中,是否存在面积最大的四边形?请利用图④说明理由.的饮水困难问题,想在这三个地方的其中一处建一所供水站,由供水站直接铺设管道到另外两处。
陕西中考数学十年压轴题汇总

25.(本题满分12分)已知:直线a ∥b ,P 、Q 是直线a 上的两点,M 、N 是直线b 上两点。
(1)如图①,线段PM 、QN 夹在平行直线a 和b 之间,四边形PMNQ 为等腰梯形,其两腰PM =QN 。
请你参照图①,在图②中画出异于图①的一种图形,使夹在平行直线a 和b 之间的两条线段相等。
(2)我们继续探究,发现用两条平行直线a 、b 去截一些我们学过的图形,会有两条“曲线段相等”(曲线上两点和它们之间的部分叫做“曲线段”。
把经过全等变换后能重合的两条曲线段叫做“曲线段相等”)。
请你在图③中画出一种图形,使夹在平行直线a 和b 之间的两条曲线段相等。
(3)如图④,若梯形PMNQ 是一块绿化地,梯形的上底PQ =m ,下底MN =n ,且m <n 。
现计划把价格不同的两种花草种植在S 1、S 2、S 3、S 4四块地里,使得价格相同的花草不相邻。
为了节省费用,园艺师应选择哪两块地种植价格较便宜的花草?请说明理由。
25.(本题满分12分)王师傅有两块板材边角料,其中一块是边长为60cm 的正方形板子;另一块是上底为30cm ,下底为120cm ,高为60cm 的直角梯形板子(如图①),王师傅想将这两块板子裁成两块全等的矩形板材。
他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCDE 围成的区域(如图②),由于受材料纹理的限制,要求裁出的矩形要以点B 为一个顶点。
(1)求FC 的长;(2)利用图②求出矩形顶点B 所对的顶点.....到BC 边的距离)(cm x 为多少时,矩形的面积最大?最大面积时多少?(3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长。
25.(本题满分12分)如图,O 的半径均为R .(1)请在图①中画出弦AB CD ,,使图①为轴对称图形而不是..中心对称图形;请在图②中画出弦AB CD ,,使图②仍为中心对称图形; (2)如图③,在O 中,(02A B C D m m R ==<<,且AB 与CD交于点E ,夹角为锐角α.求四边形ACBD 面积(用含m α,的式子表示); (3)若线段AB CD ,是O的两条弦,且AB CD ==,你认为在以点A B C D ,,,为顶点的四边形中,是否存在面积最大的四边形?请利用图④说明理由.的饮水困难问题,想在这三个地方的其中一处建一所供水站,由供水站直接铺设管道到另外两处。
陕西中考数学十年压轴题汇总
25.(本题满分12分)已知:直线a ∥b ,P 、Q 是直线a 上的两点,M 、N 是直线b 上两点。
(1)如图①,线段PM 、QN 夹在平行直线a 和b 之间,四边形PMNQ 为等腰梯形,其两腰PM =QN 。
请你参照图①,在图②中画出异于图①的一种图形,使夹在平行直线a 和b 之间的两条线段相等。
(2)我们继续探究,发现用两条平行直线a 、b 去截一些我们学过的图形,会有两条“曲线段相等”(曲线上两点和它们之间的部分叫做“曲线段”。
把经过全等变换后能重合的两条曲线段叫做“曲线段相等”)。
请你在图③中画出一种图形,使夹在平行直线和b 之间的两条曲线段相等。
(3)如PMNQ 是梯形的上底PQ =m 底MN =n ,且m <n 。
现计划把价格不同的两种花草种植在S 1、S 2、S 3、S 4四块地里,使得价格相同的花草不相邻。
为了节省费用,园艺师应选择哪两块地种植价格较便宜的花草?请说明理由。
25.(本题满分12分)王师傅有两块板材边角料,其中一块是边长为60cm 的正方形板子;另一块是上底为30cm ,下底为120cm ,高为60cm 的直角梯形板子(如图①),王师傅想将这两块板子裁成两块全等的矩形板材。
他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCDE 围成的区域(如图②),由于受材料纹理的限制,要求裁出的矩形要以点B 为一个顶点。
(1)求FC 的长;(2)利用图②求出矩形顶点B 所对的顶点.....到BC 边的距离)(cm x 为多少时,矩形的面积最大?最大面积时多少?(3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长。
25.(本题满分12分) 如图,O e的半径均为R .(1)请在图①中画出弦AB CD ,,使图①为轴对称图形而不是..中心对称图形;请在图②中画出弦AB CD ,,使图②仍为中心对称图形;(2)如图③,在O e 中,(02)AB CD m m R ==<<,且AB 与CD 交于点E ,夹角为锐角α.求四边形ACBD 面积(用含m α,的式子表示);(3)若线段AB CD ,是O e 的两条弦,且AB CD ==,你认为在以点A B C D ,,,为顶点的四边形中,是否存在面积最大的四边形?请利用图④说明理由. 一所中学长期存在的饮水困难问题,想在这三个地方的其中一处建一所供水站,由供水站直接铺设管道到另外两处。
2010-2017陕西省历年中考真题(真题+真题答案解析)
2010陕西省初中毕业学业考试真题(数学)第 Ⅰ 卷(选择题)一、 选择题1 . 13-= ( )A. 3 B-3 C 13 D-132.如图,点O 在直线AB 上且AB ⊥OD 若∠COA=36°则∠DOB 的大小为( ) A 3 6° B 54° C 64° D 72°3.计算(-2a ²)·3a 的结果是 ( ) A -6a ² B-6a ³ C12a ³ D6a ³4.如图是由正方体和圆锥组成的几何体,他的俯视图是 ( )A B C D5.一个正比例函数的图像过点(2,-3),它的表达式为 ( ) A 32y x =-B 23y x =C 32y x =D 23y x =-6.中国2010年上海世博会充分体现“城市,让生活更美好”的主题。
据统计5月1日至5月7日入园数(单位:万人)分别为20.3;21.5;13.2;14.6;10.9;11.3; 13.9;这组数据中的中位数和平均数分别为( )A 14.6 ,15.1B 14.65 ,15.0C 13.9 , 15.1 D13.9 , 15.0 1102x -≥ 7.不等式组 3x+2>-1 的解集是 ( )A -1< x≤2B -2≤x<1C x<-1或x≥2D 2≤x<-18.若一个菱形的边长为2,则这个菱形两条对角线的平方和为()A 16B 8C 4D 19.如图,点A、B、P在⊙O上的动点,要是△ABM为等腰三角形,则所有符合条件的点M有()A 1个B 2个C 3个D 4个10.将抛物线C:y=x²+3x-10,将抛物线C平移到Cˋ。
若两条抛物线C,Cˋ关于直线x=1对称,则下列平移方法中正确的是()A将抛物线C向右平移52个单位 B将抛物线C向右平移3个单位C将抛物线C向右平移5个单位 D将抛物线C向右平移6个单位第Ⅱ卷(非选择题)二、填空题11、在1,-2,-30,π五个数中最小的数是12、方程x²-4x的解是 ________13、如图在△ABC中D是AB边上一点,连接CD,要使△ADC与△ABC相似,应添加的条件是___________14、如图是一条水铺设的直径为2米的通水管道横截面,其水面宽1.6米,则这条管道中此时最深为_______米15、已知A(x1,y2),B(x2,y2)都在6yx图像上。
陕西中考数学十年压轴题汇总
25.(本题满分12分)已知:直线a∥b,P、Q是直线a上的两点,M、N是直线b上两点。
(1)如图①,线段PM、QN夹在平行直线a和b之间,四边形PMNQ为等腰梯形,其两腰PM=QN。
请你参照图①,在图②中画出异于图①的一种图形,使夹在平行直线a 和b之间的两条线段相等。
(2)我们继续探究,发现用两条平行直线a、b去截一些我们学过的图形,会有两条“曲线段相等”(曲线上两点和它们之间的部分叫做“曲线段”。
把经过全等变换后能重合的两条曲线段叫做“曲线段相等”)。
请你在图③中画出一种图形,使夹在平行直线a和b之间的两条曲线段相等。
(3)如图④,若梯形PMNQ是一块绿化地,梯形的上底PQ=m,下底MN=n,且m<n。
现计划把价格不同的两种花草种植在S1、S2、S3、S4四块地里,使得价格相同的花草不相邻。
为了节省费用,园艺师应选择哪两块地种植价格较便宜的花草?请说明理由。
25.(本题满分12分)王师傅有两块板材边角料,其中一块是边长为60cm的正方形板子;另一块是上底为30cm,下底为120cm,高为60cm的直角梯形板子(如图①),王师傅想将这两块板子裁成两块全等的矩形板材。
他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCDE围成的区域(如图②),由于受材料纹理的限制,要求P QM Nab第25题图ab 第25题图ab第25题图P QM Nab第25题图S1S2S3 S4nm裁出的矩形要以点B 为一个顶点。
(1)求FC 的长;(2)利用图②求出矩形顶点B 所对的...顶点..到BC 边的距离)(cm x 为多少时,矩形的面积最大?最大面积时多少? (3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长。
25.(本题满分12分) 如图,O e 的半径均为R .(1)请在图①中画出弦AB CD ,,使图①为轴对称图形而不是..中心对称图形;请在图②中画出弦AB CD ,,使图②仍为中心对称图形;(2)如图③,在O e 中,(02)AB CD m m R ==<<,且AB 与CD 交于点E ,夹角为锐角α.求四边形ACBD 面积(用含m α,的式子表示); (3)若线段AB CD ,是O e 的两条弦,且AB CD ==,你认为在以点A B C D ,,,为顶点的四边形中,是否存在面积最大的四边形?请利用图④说明理由.12为了解决该县甲、乙两村和一所中学长期存在的饮水困难问题,想在这三个地方的其中一处建一所供水站,由供水站直接铺设管道到另外两处。
陕西中考数学十年压轴题汇总
25.(本题满分12分)已知:直线a∥b,P、Q是直线a上的两点,M、N是直线b上两点。
(1)如图①,线段PM、QN夹在平行直线a 和b之间,四边形PMNQ为等腰梯形,其两腰PM=QN。
请你参照图①,在图②中画出异于图①的一种图形,使夹在平行直线a和b之间的两条线段相等。
(2)我们继续探究,发现用两条平行直线a、b去截一些我们学过的图形,会有两条“曲线段相等”(曲线上两点和它们之间的部分叫做“曲线段”。
把经过全等变换后能重合的两条曲线段叫做“曲线段相等”)。
请你在图③中画出一种图形,使夹在平行直线a和b之间的两条曲线段相等。
(3)如图④,若梯形PMNQ是一块绿化地,梯形的上底PQ =m,下底MN=n,且m<n。
现计划把价格不同的两种花草种植在S1、S2、S3、S4四块地里,使得价格相同的花草不相邻。
为了节省费用,园艺师应选择哪两块地种植价格较便宜的花草请说明理由。
25.(本题满分12分)王师傅有两块板材边角料,其中一块是边长为60cm的正方形板子;另一块是上底为30cm,下底为120cm,高为60cm的直角梯形板子(如图①),王师傅想将这两块板子裁成两块全等的矩形板材。
他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCDE围成的区域(如图②),由于受材料纹理的限制,要求裁出的矩形要以点B为一个顶点。
(1)求FC的长;(2)利用图②求出矩形顶点B所.对的..距离顶点..到BC边的时,)(cmx为多少矩形的面积最大最大面积时多少(3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长。
P QM Nab第25题图ab 第25题图ab第25题图P QM Nab第25题图S1S2S3 S4nm25.(本题满分12分) 如图,O e 的半径均为R .(1)请在图①中画出弦AB CD ,,使图①为轴对称图形而不是..中心对称图形;请在图②中画出弦AB CD ,,使图②仍为中心对称图形;(2)如图③,在O e 中,(02)AB CD m m R ==<<,且AB 与CD 交于点E ,夹角为锐角α.求四边形ACBD 面积(用含m α,的式子表示);(3)若线段AB CD ,是O e的两条弦,且AB CD ==,你认为在以点A B C D,,,为顶点的四边形中,是否存在面积最大的四边形请利用图④说明理由.12解决该县甲、乙两村和一所中学长期存在的饮水困难问题,想在这三个地方的其中一处建一所供水站,由供水站直接铺设管道到另外两处。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
以抛物线为背景的压轴题陕西省中考数学第24题(2010年--2018年)例 2018年陕西省中考第24题已知抛物线L:y=x2+x-6与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.(1)求A、B、C三点的坐标,并求△ABC的面积;(2)将抛物线L向左或向右平移,得到抛物线L′,且L′与x轴相交于A′、B′两点(点A′在点B′的左侧),并与y轴相交于点C′,要使△A′B′C′和△ABC的面积相等,求所有满足条件的抛物线的函数表达式.(原题无图)例 2017年陕西省中考第24题在同一直角坐标系中,抛物线C1:y=ax2-2x-3与抛物线C2:y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧.(原题无图)(1)求抛物线C1、C2的函数表达式;(2)求A、B两点的坐标;(3)在抛物线C1上是否存在一点P,在抛物线C2上是否存在一点Q,使得以AB为边,且以A、B、P、Q为顶点的四边形是平行四边形?若存在,求出P、Q两点的坐标;若不存在,请说明理由.如图1,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+5经过点M(1, 3)和点N(3, 5).(1)试判断该抛物线与x轴的交点情况;(2)平移这条抛物线,使平移后的抛物线经过点A(-2, 0),且与y轴交于点B,同时满足以A、O、B为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.图1在平面直角坐标系中,抛物线y=x2+5x+4的顶点为M,与x轴交于A、B两点,与y 轴交于点C.(原题无图)(1)求点A、B、C的坐标;(2)求抛物线y=x2+5x+4关于坐标原点O对称的抛物线的函数表达式;(3)设(2)中所求抛物线的顶点为M′,与x轴交于A′、B′两点,与y轴交于点C′,在以A、B、C、M、A′、B′、C′、M′这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积.如图1,已知抛物线C:y=-x2+bx+c经过A(-3,0)和B(0, 3)两点.将这条抛物线的顶点记为M,它的对称轴与x轴的交点记为N.(1)求抛物线C的表达式;(2)求点M的坐标;(3)将抛物线C平移到抛物线C′,抛物线C′的顶点记为M′,它的对称轴与x轴的交点记为N′.如果以点M、N、M′、N′为顶点的四边形是面积为16的平行四边形,那么应将抛物线C怎样平移?为什么?在平面直角坐标系中,一个二次函数的图像经过A(1,0)、B(3,0)两点.(原题无图)(1)写出这个二次函数图像的对称轴;(2)设这个二次函数图像的顶点为D,与y轴交于点C,它的对称轴与x轴交于点E,连结AC、DE和DB.当△AOC与△DEB相似时,求这个二次函数的解析式.如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为“抛物线三角形”.(1)“抛物线三角形”一定是_______三角形;(2)若抛物线y=-x2+bx (b>0)的“抛物线三角形”是等腰直角三角形,求b的值;(3)如图1,△OAB是抛物线y=-x2+b′x (b′>0)的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,请说明理由.如图1,二次函数22133y x x =-的图像经过△AOB 的三个顶点,其中A (-1,m ),B (n ,n ). (1)求点A 、B 的坐标;(2)在坐标平面内找点C ,使以A 、O 、B 、C 为顶点的四边形是平行四边形. ①这样的点C 有几个? ②能否将抛物线22133y x x =-平移后经过A 、C 两点?若能,求出平移后经过A 、C 两点的一条抛物线的解析式;若不能,说明理由.图1如图1,在平面直角坐标系中,抛物线经过点A(-1,0)、B(3,0)、C(0,-1)三点.(1)求该抛物线的解析式;(2)点Q在y轴上,点P在抛物线上,要使以点Q、P、A、B为顶点的四边形是平行四边形,求所有满足条件的点P的坐标.以计算说理为主的压轴题陕西省中考数学第25题(2010年--2018年)例 2018年陕西省中考第25题问题提出(1)如图1,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为______.问题探究(2)如图2,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.问题解决(3)如图3所示,AB、AC、弧BC是某新区的三条规划路,其中AB=6km,AC=3km,∠BAC=60°,弧BC所对的圆心角为60°.新区管委会想在弧BC路边建物资总站P,在AB、AC路边分别建物资分站E、F,也就是,分别在弧BC、线段AB和AC上选取点P、E、F.由于总站工作人员每天都要将物资在各物资站间按P→E→F→P的路径进行运输,因此要在各物资站之间规划道路PE、EF和FP.为了快捷、环保和节约成本,要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).图1 图2 图3例 2017年陕西省中考第25题问题提出(1)如图1,△ABC是等边三角形,AB=12,若点O是△ABC的内心,则OA的长为________.问题探究(2)如图2,在矩形ABCD中,AB=12,AD=18.如果点P是AD边上一点,且AP=3,那么BC边上是否存在一点Q,使得线段PQ将矩形ABCD的面积平分?若存在,求出PQ的长;若不存在,请说明理由.问题解决(3)某城市街角有一草坪,草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成,如图3所示.管理员王师傅在M处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头时,既要确保草坪的每个角落都能浇上水,又能节约用水.于是,他让喷灌龙头的转角正好等于∠AMB(即每次喷灌龙头由MA转到MB,然后再转回,这样往复喷灌),同时,再合理设计好喷灌龙头的射程就可以了.如图3,已测出AB=24m,MB=10m,△AMB的面积为96m2;过弦AB的中点D作DE⊥AB交»AB于点E,又测得DE=8m.请你根据以上提供的信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米).图1 图2 图3例 2016年陕西中考第25题问题提出 (1)如图1,已知△ABC ,请画出△ABC 关于直线AC 对称的三角形. 问题探究 (2)如图2,在矩形ABCD 中,AB =4,AD =6,AE =4,AF =2.是否在边BC 、CD 上分别存在点G 、H ,使得四边形EFGH 的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.问题解决 (3)如图3,有一块矩形板材ABCD ,AB =3米,AD =6米,现想从此板材中截出一个面积尽可能大的四边形EFGH 部件,使∠EFG =90°,EF =FG∠EHG =45°.经研究,只有当点E 、F 、G 分别在边AD 、AB 、BC 上时,且AF <BF ,并满足点H 在矩形ABCD 内部或边上时,才有可能截出符合要求的部件.试问能否截得符合要求的面积尽可能大的四边形EFGH 部件?若能,求出截得的四边形EFGH 部件的面积;若不能,请说明理由.挑战压轴题公众号如图,在每一个四边形ABCD中,均有AD//BC,CD⊥BC,∠ABC=60°,AD=8,BC =12.(1)如图1,点M是四边形ABCD的边AD上一点,则△BMC的面积为______;(2)如图2,点N是四边形ABCD的边AD上任意一点,请你求出△BNC周长的最小值;(3)在四边形ABCD的边AD上,是否存在一点P,使得cos∠BPC的值最小?若存在,求出此时cos∠BPC的值;若不存在,请说明理由.问题探究 (1)如图1,在矩形ABCD 中,AB =3,BC =4.如果BC 边上存在点P ,使△APD 为等腰三角形,那么请画出满足条件的一个..等腰△APD ,并求出此时BP 的长; (2)如图2,在△ABC 中,∠ABC =60°,BC =12,AD 是BC 边上的高,E 、F 分别为边AB 、AC 的中点.当AD =6时,BC 边上存在一点Q ,使∠EQF =90°,求此时BQ 的长;问题解决 (3)有一山庄,它的平面图为如图3的五边形ABCDE ,山庄保卫人员想在线段CD 上选一点M 安监控装置,用来监视边AB .现只要使∠AMB 大约为60°,就可以让监控装置的效果达到最佳.已知∠A =∠E =∠D =90°,AB =270m ,AE =400m ,ED =285m ,CD =340m .问在线段CD 上是否存在点M ,使∠AMB =60°?若存在,请求出符合条件的DM 的长;若不存在,请说明理由.问题探究(1)请在图1中做出两条直线,使它们将圆面四等分;(2)如图2,M是正方形ABCD内一定点,请在图2中作出两条直线(要求其中一条直线必须过点M),使它们将正方形ABCD的面积四等分,并说明理由.问题解决(3)如图3,在四边形ABCD中,AB//CD,AB+CD=BC,点P是AD的中点.如果AB=a,CD=b,且b>a,那么在边BC上是否存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分?若存在,求出BQ的长;若不存在,请说明理由.正三角形ABC的边长为3(1)如图1,正方形EFPN的顶点E、F在边AB上,顶点N在边AC上.在正三角形ABC及其内部,以A为位似中心,作正方形EFPN的位似正方形E′F′P′N′,且使正方形E′F′P′N′的面积最大(不要求写作法);(2)求(1)中作出正方形E′F′P′N′的边长;(3)如图2,在正三角形ABC中放入正方形DEMN和正方形EFPH,使得DE、EF在边AB上,P、N分别在边CB、CA上,求这两个正方形面积和的最大值和最小值,并说明理由.如图1,在矩形ABCD中,将矩形折叠,使点B落在边AD(含端点)上,落点记为E,这时折痕与边BC或边CD(含端点)交于点F.然后再展开铺平,则以B、E、F为顶点的△BEF称为矩形ABCD的“折痕三角形”.(1)由“折痕三角形”的定义可知,矩形ABCD的任意一个“折痕△BEF”一定是一个___________三角形;(2)如图2,在矩形ABCD中,AB=2,BC=4.当它的“折痕△BEF”的顶点E位于边AD的中点时,画出这个“折痕△BEF”,并求出点F的坐标;(3)如图3,在矩形ABCD中,AB=2,BC=4.该矩形是否存在面积最大的“折痕△BEF”?若存在,说明理由,并求出此时点E的坐标;若不存在,为什么?问题探究(1)请你在图1中作一条直线,使它将矩形ABCD分成面积相等的两部分;(2)如图2,点M是矩形ABCD内一定点.请你在图2中过点M作一条直线,使它将矩形ABCD分成面积相等的两部分;问题解决如图3,在平面直角坐标系中,直角梯形OBCD是某市将要筹建的高新技术开发区用地示意图,其中DC//OB,OB=6,BC=4,CD=4.开发区综合服务委员会(其占地面积不计)设在点P(4,2)处.为了方便驻区单位,准备过点P修一条笔直的道路(路的宽度不计),并且使这条路所在的直线l将直角梯形OBCD分成面积相等的两部分.你认为直线l是否存在?若存在,求出直线的表达式;若不存在,请说明理由.图形运动中的最值问题陕西省中考数学第14题2015年以前,陕西省中考选择题填空题共16道题目;2015年开始,改为14道.选择题填空题的最后一道题目,属于选拔性的题目,需要挑战.知识回顾我们学过的最值:(1)两点之间,_________最短.由此得到:三角形的两边之和大于___________,两边之差小于___________.(2)直线外一点与直线上所有点的连线中,_________最短.由此得到:直角三角形的直角边小于__________.(3)________是圆中最长的弦.(4※)抛物线的开口向上时,抛物线的顶点是最_____点,顶点的纵坐标是函数的最____值;抛物线的开口向上时,抛物线的顶点是最_____点,顶点的纵坐标是函数的最____值.难点疏导(1)最小值中的最小值;(2)最小值中的最大值.课前热身1.如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C,点P是抛物线对称轴上的一个动点,如果△P AC的周长最小,求点P的坐标.2.如图,抛物线248293y x x =-++与y 轴交于点A ,顶点为B .点P 是x 轴上的一个动点,求线段P A 与PB 中较长的线段减去较短的线段的差的最小值与最大值,并求出相应的点P 的坐标.3.(1)梯子的长为2米,梯子沿墙下滑的过程中,梯子与地面、墙面围成的直角三角形的面积的最大值是多少?(2)斜边长为4的直角三角形的面积的最大值为________.4.(1)已知⊙的半径为2,圆周角∠ACB =30°,怎样找弦AB ?AC 的最大值是多少? (2)已知⊙的半径为2,圆周角∠ACB =45°,怎样找弦AB ?AC 的最大值是多少?真题讲解5.(09陕西16)如图,在锐角△ABC中,AB=,∠BAC=45°,∠BAC的平分线交BC于D,M、N分别是AD和AB上的动点,则BM+MN的最小值是_______.6.(13陕西16)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点G、H分别是AC、BC的中点,直线EF与⊙O交于E、F两点.若⊙O的半径为7,则GE+FH的最大值为_______.7.(14陕西16)如图,⊙O的半径是2.直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧.若∠AMB=45°,则四边形MANB面积的最大值是_______.8.(15陕西14)如图,AB是⊙O的弦,AB=6,点C是⊙O上的一个动点,且∠ACB =45°.若M、N分别是AB、BC的中点,那么MN长的最大值是__________.9.(16陕西14)如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为________.10.(11陕西16)如图,在梯形ABCD中,AD//BC,对角线AC⊥BD.若AD=3,BC =7,则梯形ABCD面积的最大值为_______.11.(18陕西14)如图1,点O 是平行四边形ABCD 的对称中心,AD >AB ,E 、F 是AB 边上的点,且EF =12AB ,G 、H 是BC 边上的点,且GH =13BC .若S 1、S 2分别表示△EOF 和△GOH 的面积,则S 1与S 2之间的等量关系是____________.图1他山之石12.(12台州10)如图,菱形ABCD 中,AB =2,∠A =120°,点P 、Q 、K 分别为线段BC 、CD 、BD 上的任意一点,则PK +QK 的最小值为_________.13.(16安徽10)如图,Rt △ABC 中,AB ⊥BC ,AB =6,BC =4.P 是△ABC 内部的一个动点,且满足∠P AB =∠PBC ,则线段CP 长的最小值为( ).A .32 B .2 C D . 14.(16娄底10)如图,已知Rt △ABC 中,∠ABC =90°,点D 沿BC 自B 向C 运动(点D 与点B 、C 不重合),作BE ⊥AD 于E ,作CF ⊥AD 于F ,则BE +CF 的值( ).A .不变B .增大C .减小D .先变大再变小第11题图 第12题图 第13题图15.(16苏州09)如图,矩形OABC 在平面直角坐标系中的位置如图所示,点B 的坐标为(3, 4),D 是OA 的中点,点E 在AB 上,当△CDE 的周长最小时,点E 的坐标为( ).A .3,1()B .43,3() C .53,3() D .3,2()16.(16台州10)如图,在△ABC 中,AB =10,AC =8,BC =6,以边AB 的中点O 为圆心,作半圆与AC 相切,点P 、Q 分别是边BC 和半圆上的动点,联结PQ ,则PQ 长的最大值与最小值的和是( ).A .6B .1C .9D .32317.(16无锡17)如图,已知平行四边形OABC 的顶点A 、C 分别在直线x =1和x =4上,O 是坐标原点,则对角线OB 长的最小值为________.第14题图 第15题图 第16题图。
