第五章 动态数列
第5章 动态数列 (《经济统计学》PPT课件)

an a1 a2 a3 an
a0 a0 a1 a2
an1
2、两个相邻时期的定基发展速
度之比,等于它们的环比发展速度,
即
an an1 an
a0
a0
an1
在实际工作中,还常要计算一 种年距发展速度指标
年距发展速度
报告期发展水平 上年同期发展水平
(二)增长速度
增长速度是表明社会经济 现象增长程度的相对指标
第二节 动态数列水平分析指标
一、发展水平和平均发展水平 (一)发展水平
在动态数列中,各项具体的指标数 值叫做发展水平或动态数列水平。
有最初水平、最末水平、中间各 项水平、基期水平和报告期水平之分。
(二)平均发展水平
将不同时期的发展水平加以 平均而得到的平均数叫平均发展 水平,在统计上又称为序时平均 数或动态平均数。
= 累计增长量 动态数列项数-1
1996-2000 年我国水泥产量 年 份 1996 1997 水泥产量 49119 51174 增长 逐期 - 2055 量 累计 - 2055
1998 53600 2426 4481
单位:万吨
1999 57300
2000 59700
3700 2400
8181 10581
f1
a2
2
a3
f2
n1
an1 an 2
f n 1
fi
i1
其中:
a 序时平均数; a 各时点值;
f 各时点间隔的距离。
某农场某年生猪存栏数
日期
1月 1日
3月 1日
生猪存 1420 1400
栏数
8月 1日
1200
10 月 1日
1250
统计原理课件 第五章动态数列分析

②相邻两期累计增长量之差等于相应时期的逐期增 长量,即:
(ai a1 ) (ai1 a1 ) ai ai1
5.2.2 增长水平与平均增长水平
③年距增长量 在实际统计分析中,为了消除季节变动的
5.1.1 动态数列的概念
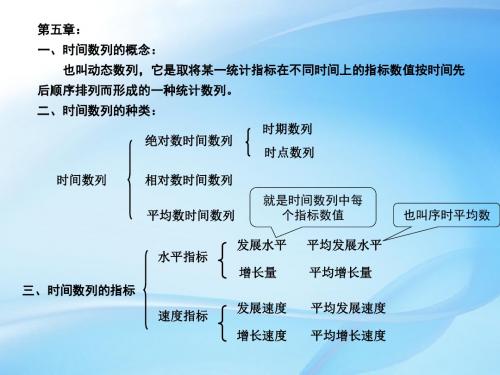
动态数列也称时间序列或时间数列,它是将 社会经济现象在不同时间上的指标数值,按其发 生的时间先后顺序排列而成的统计数列。
时间数列由两个基本要素组成: 一是被研究现象所属的时间; 二是反映该现象的统计指标数值。
5.1.1 动态数列的概念
动态数列的作用: ⑴ 可以描述总体现象的发展状态和结果。 ⑵ 可以研究总体现象变化的方向、速度和幅度。 ⑶ 可以揭示总体现象发展变化的规律性,从而对未
5.3 .1 发展速度与增长速度
⑴环比发展速度 环比发展速度也称逐期发展速度,是报告
期水平与前一期水平之比。用符号表示为 :
a1 , a2 , a3 ,..., an
a0 a1 a2
an1
5.3 .1 发展速度与增长速度
⑵定基发展速度
定基发展速度是报告期水平与某一固定基 期水平(通常为最初水平或特定时期水平)之 比,表明现象在较长时期内总的发展速度, 也称为总速度。用符号表示为 :
平均增长量
逐期增长量之和 逐期增长量个数
累计增长量 时间序列项数 1
5.3 .1 发展速度与增长速度
⒈ 发展速度 发展速度是两个不同时期的发展水平之比。
它表明现象发展的程度和方向,通常用百分 数或倍数表示,其计算公式为:
发展速度
报告期水平 基期水平
100 %
由于计算时采用的基期的不同,发展速度 又环比发展速度和定基发展速度之分。
第5章 统计学动态数列

动态数列(17) 第五章 动态数列(17)
三、动态数列速度指标
2.增长速度 2.增长速度 定基增长速度=定基发展速度(1)定基增长速度=定基发展速度-1 定基增长速度=环比发展速度(2)定基增长速度=环比发展速度-1 年距增长速度=年距增长量÷去年同期发展水平 年距增长速度=年距增长量÷ 年距发展速度=年距发展速度-1 3.平均发展速度 各期环比发展速度的平均值, 平均发展速度: 3.平均发展速度:各期环比发展速度的平均值,说明 现象在一较长时期内逐期平均发展变化的程度。 现象在一较长时期内逐期平均发展变化的程度。
动态数列(7) 第五章 动态数列(7)
二、动态数列水平指标
3.平均增长量 3.平均增长量 =逐期增长量之和 ÷ 逐期增长量个数 累计增长量÷ 时间数列项数=累计增长量÷(时间数列项数-1) 4、增长百分之一的绝对值 增长百分之一的绝对值 增长百分之一的绝对值=逐期增长量÷ 增长百00
a1 + a 2 + a 3 + L + a n a= = n
∑a
n
a 1 f 1 + a 2 f 2 + a 3 f 3 + L + a nfn a= = f 1 + f 2 + f 3 + L + fn
∑ af ∑f
动态数列(9) 第五章 动态数列(9)
二、动态数列水平指标
4.平均发展水平 4.平均发展水平 绝对数时间数列: 绝对数时间数列: 某商场1月营业员人数资料如下: 某商场1月营业员人数资料如下:
动态数列(15) 第五章 动态数列(15)
三、动态数列水平指标
4.平均发展水平 4.平均发展水平 平均数时间数列 (1)一般平均数时间数列的序时平均数 (1)一般平均数时间数列的序时平均数 方法: 方法:将子项数列与母项数列各求序时平均数再 对比计算。 对比计算。 (2)序时平均数时间数列的序时平均数 (2)序时平均数时间数列的序时平均数 采用简单算术平均数和加权算术平均数计算。 采用简单算术平均数和加权算术平均数计算。
第五章 动态数列分析.

ay n
593.1 6
98.85
yc a bt 98.85 2.66t
2012年粮食产量:98.85 2.669 122.79万吨
最小平方法案例2(简化公式)答案
b
ty t2
53.3 10
5.33
a y 507.6 101.52
n
5
yc a bt 101.52 5.33t
单位:万吨
年份 t
粮食产量 y
t2
ty
yc
2005 1
85.6
2006 2
91.0
1
85.6
85.6
4
182.0
90.9
2007 3 2008 4 2009 5
96.1 101.2 107.0
9
288.3
96.2
16
404.8
101.5
25
535.0
106.8
2010 6
112.2
36
673.2
112.1
2
4 1
473人
间断时点数列案例2
某工厂成品仓库中某产品在2010库存
量如下:
单位:台
日期 1.1 3.1 7.1 8.1 10.1 12.31 库存量 38 42 24 11 60 0
间断时点数列案例2答案
a
a1 a2 2
f1
a2
2
a3
f2
an1 2
an
f n1
合计 21
593.1
91
2168.9
593.1
最小平方法案例1(一般公式)答 案
b
第五章 动态序列分析

(a1 a0 ) (a2 a1 ) (an an1 ) an a0
14
2.平均增长量
逐期增长量之和 平均增长量 逐期增长量个数
计算方法
累计增长量 平均增长量 n 1
15
第三节 动态数列的速度指标
1.发展速度
报告期水平 发展速度 基期水平
根据采用基期的不同
课堂练习
11
某企业1号—30号每天的职工人数资料:
日 期
1日—8日 a1 102
9日—15日 a2 105
16日—30日 a3 108
职工人数(人)
则:1号至30号平均每天的职工人数为:
af a f
102 8 105 7 108 15 106 (人) 30
12
二、增长水平指标 1.增长量 两个时期发展水平相减的差额,用以反映现象在这段 时期内发展水平的变化。可分为:
逐期增长量 报告期前一期水平
环比增长速度
环比发展速度-1(100%)
定基增长速度
累计增长量 固定基期水平
定基发展速度-1(100%)
20
3.平均发展速度
因为,平均发展速度是对各期的环比发展速度 求平均数,对不同时期的环比速度求平均需采 用几何平均法。公式为:
平均发展速度
x n x1 x2 x3 xn
04
05
7 9 600 620 49 81 4200 4890
ty 4890 b 14 . 8 t 330
2
y 4830 a 483 n 10
yc 483 14.8t
预测2006年的销售量,t = 11, 则预测值为:
41
yc 483 14.8 11 645.(万吨) 8
第5章动态数列分析法
1.发展水平 发展水平就是时间数列中每个指标数值,它反映现象在不同时期或时点上所达到 的规模总量或总体水平,是计算其他动态分析指标的基础。发展水平可表现为绝对 数,如工资总额、工业产值、年末职工人数;也可表现为相对数或平均数,如人口 出生率、工人劳动生产率。 在时间数列中,由于发展水平所处的位置不同,有最初水平、中间水平和最末水 平之分。通常用符号a表示发展水平。在时间数列a0,a1,a2,…,an-1,an中,a0 最初水平,an为最末水平,其余a1,a2,a3,…,an-1为中间水平。在对时间的发 展水平作动态对比时,作为对比基础时期的发展水平称为基期,作为研究时期的指 标水平称为报告期水平或计算期水平。 2.平均发展水平 平均发展水平是将不同时期的发展水平加以平均而得到的平均数,在统计上又称 序时平均数或动态平均数,它表明现象在一段时间内发展过程达到的一般水平。 序时平均数与一般平均数(静态平均数)既有共同之处,也有区别。共同之处是 二者是将现象的个别数量差异抽象化了,概括出了现象在数量上达到的一般水平。 两者区别在于:第一,序时平均数是根据时间数列计算的,而一般平均数是根据变 量数列计算的;第二,序时平均数所平均的,是被研究现象本身的数量在不同时间 上的差异,一般平均数所平均的,是总体各单位某一数量标志值的差异;第三,序 时平均数是从动态上表明被研究现象本身在一段时期内的平均发展水平,而一般平 均数是从静态上说总体各单位某个数量标志值的平均水平。序时平均数在动态分析 中被广泛地运用。
b
分母数列的序时平均数;
增长量
= 报告期水平an - 基期水平a0 逐期增长量 增长量 累积增长量
a1 a0 , a2 a1 ,, an an1 a1 a0 , a2 a0 ,, an a0
统计学 第五章 动态数列
例
某商业企业2010年第二季度某商品库存 资料如下,求第二季度的月平均库存额
时间 3月末 4月末 5月末 6月末
库存量(百件)
66
72
64
68
解:第二季度的月平均库存额为:
66 68 72 64 2 2 67.67百件 a 4 1
※间隔不相等 时,采用加权序时平均法
一季 度初 二季 度初
af 解:a f
780 9 784 6 786 7 783 9 783(人) 9679
②由间断时点数列计算
一季 度初 二季 度初 三季 度初
不是逐日记录,而 是每隔一段时间登 记一次,表现为期 初或期末值
四季 度初 次年一 季度初
※间隔相等 时,采用首末折半法
时期数列
时期数列特点:
数列中各个指标数值是可加的; 数列中每个指标数值的大小随 着时期的长短而变动; 数列中每个指标数值通常通过连 续不断的登记而取得。
时点数列
在绝对数动态数列中,如果 各项指标都是反映某种现象在某 一时点上(瞬间)所处的数量水 平,这种绝对数动态数列就称为 时点数列。 如 表 4-1 中 所 列 的 我 国 20022008年全国人口年末数。
增速 3.8 9.2 14.2 13.5 12.6 10.5 9.6 8.8 7.8 7.1 8.0
例
某市职工2006-2010年年平均工资 单位:元
年份 年平均工资
2006 10663
2007 11425
2008 12059
2009 14147
2010 15420
三、动态数列的编制原则
时期长短应该统一 总体范围应该一致
⑵ a、b均为时点数列时
第五章 动态数列
上一页 下一页 返回
1.时期数列 时期数列是指由时期指标构成的数列,即数列中每一指标值都是反映
某现象在一段时间内发展变化的总量。如表5-2所示的某工厂年“总产值 ”资料。
通过对表5-2的观察可知,时期数列具有以下特点。 (1)时期数列中各个指标数值具有可加性。相加后的结果表示该现象更长 时期的指标数值。 (2)时期数列中各个指标数值的大小与所包括的时期长短有直接关系。通 常是时期越长,其指标数值就越大;反之,其指标数值越小。 (3)时期数列的指标数值需采用连续统计的方式取得。
1.时期数列计算序时平均数。时期数列的各项指标数值具有可加性,故时 期数列计算序时平均数的方法就类似于一般平均数中“算术平均数”的计
算方法,即将数列中各个不同时间上的指标数值相加后除以项数即可。其
计算公式如下
a a1 a2 an1 an a
n
n
式中,n为项数,a为发展水平。
上一页 下一页 返回
f
45768
928 30.9( 3 万元) 30
上一页 下一页 返回
例5-4 某企业2007年的库存量资料见表5-7,计算该企业的年平均库存量。 根据表5-7资料计算的该企业的年平均库存量为:
a
1 2
a1
a2
an1
1 2
an
28 36 52 18 8
2
2
31(件)
n 1
5 1
②间隔不等的时点数列,则应以间隔数为权数进行加权平均计算序时平均
上一页 下一页 返回
由于动态数列有三种,因此,计算序时平均数时就需要针对不同的动
态数列,采用不同的计算方法。其中,总量指标动态数列计算序时平均数
统计学基础-第五章------动态数列分析
统计学基础第五章动态数列分析【教学目的】1.区分不同种类的动态数列2.熟练掌握计算平均发展水平的各种方法3.掌握发展速度、增长速度的种类,运用它们之间的数量关系进行动态指标的相互推算4.理解趋势的意义,运用长期趋势测定方法对长期趋势进行测定5.计算季节比率,并且深刻理解季节比率的经济含义【教学重点】1.总量指标动态数列的种类和特点2.动态比较指标和动态平均指标的计算【教学难点】1.绝对数时间数列中的时点数列平均指标的计算2.相对数、平均数时间数列动态平均指标的计算【教学时数】教学学时为12课时【教学内容参考】第一节动态数列的意义和种类一、动态数列的概念将某一个统计指标在不同时间上的各个数值,按时间先后顺序排列,就形成了一个动态数列,也叫做时间数列。
动态数列一般由两个基本要素构成:一是被研究现象所属的时间;二是反映该现象的统计指标数值。
通过编制和分析动态数列,首先可以从现象的量变过程中反映其发展变化的方向、程度和趋势,研究其质量变化的规律性。
其次,通过对动态数列资料的研究,可以对某些社会经济现象进行预测。
第三,利用动态数列,可以在不同地区或国家之间进行比照分析。
编制和分析动态数列具有非常重要的作用,这种方法已成为对社会经济现象进行统计分析的一种重要方法。
【案例】下面图表列举了我国2004~2007年假设干经济指标的动态数列。
表5-1 我国2004-2007年假设干经济指标二、动态数列的种类按照构成动态数列的基本要素———统计指标的表现形式不同,动态数列可分为绝对数动态数列、相对数动态数列和平均数动态数列三种类型。
其中绝对数动态数列是基本的数列,相对数和平均数动态数列是派生数列。
(一)绝对数动态数列在这种动态数列中,统计指标值表现为总量指标。
根据指标值的时间特点,又可分为时期数列和时点数列。
国内生产总值就是时期数列,年底人口数就是时点数列。
时期数列中,每一指标值反映在一段时期内发展的结果,即“过程总量”。
统计学原理 第5章 动态数列
例题2 某企业2002年第三季度各月末商品库存额资料如
下表所示:试计算其平均商品库存额。 表5--8
日期 月末库存额 单位 万元 6月末 7月末 8月末 100 86 104 9月末 114
该企业第三季度平均商品库存额为:
an a1 a2 an 1 2 a 2 n 1 50 86 104 57 4 1 99(万元)
an a a1 a2 c ,c1 , c2 , , cn b b1 b2 bn
2.不同时期或时点上的相对指标或平均指标不具有可加性
3.不能直接计算它们的平均发展水平 4.计算原则:
C=a/b
------公式(6)
20
例1.某企业2001年各季度的销售额和销售利润率资料如下 表:试计算年平均利润率 表 5--10
4.是根据动态数列计算的平均数
5.不同种类的动态数列计算平均发展水平的方法有所不同。 除了静态平均数使用的所有方法外,还有其独有的方 法—高次方程法。
10
(一)绝对数动态数列的平均发展水平
1.时期数列平均发展水平(
a
)的计算:设
计
a1 , a2 , , an ,
表5--3
年份 1995
为一动态数列,用简单算术平均法
2.时点数列平均发展水平的计算 时点数列分为: (1)连续间隔相等的时点数列
(2)连续间隔不等的时点数列
(3)间断间隔相等的时点数列 (4)间断间隔不等的时点数列
12
四种时点数列的平均发展水平的计算
1、某企业2004年8月份每天的人口数如下:表5-4
8.1 129
时点连续 间隔相等 按日统计 逐日登记
ai ai 1 2 fi a fi 15.2 14.2 14.2 17.6 17.6 16.3 16.3 15.8 2 4 3 3 2 2 2 2 2 433 16.(万元) 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
总发展 速度 环比发展速度 yi y i-1 yn y0 (i 1, 2, ,n)
【例】
根据第四次、第五次人口普查资料,我 国大陆人口1990年普查时有113368万人, 2000年普查时为126583万人,则此两次人口 普查之间我国人口平均发展速度为:
四、增长1%的绝对值
指每增长1%所包含的绝对 增长量,是一个由相对数和绝 对数结合运用的指标。
逐期增长量 增长1%的绝对值 环比增长速度 100 前一期水平 100
【例】
已知某集团公司2006年利税总额比 2005年增长1000万元,环比增长速 度为20%,求该公司2006年利税总 额比2005年增长1%的绝对值。
(i 1, 2, ,n)
当i=n时
定基增 长速 度 yn y0 y0 yn -1 y0 yi -1 y i-1
定基发展速度 -1
环 比 发 展 速 度 -1 (环比增长速度 1) -1 y i - y i-1 ( 1) -1 y i-1 ( ( (
三、平均发展速度和 平均增长速度
平均发展速度:是指各个时期环比发 展速度的平均数,说明现象在一定时 期内逐期发展变化的一般水平。 平均增长速度:是现象在一段时间内 增减变化的平均程度。 平均增长速度=平均发展速度-1 平均发展速度总是正值,而平均增长 速度可为正值也可为负值
总发展速度
② 相邻的两个定基发展速度之商,等于 相应时期的环比发展速度。即:
y i y i 1 yi (i 1,2,3, ,n) y0 y0 y i 1
二、增长速度
增长量 增长速度 基期发展水平 报告期发展水平 基期发展水平 基期发展水平 发展速度 1
1.定基增长速度
1、选取合适的趋势方程: 直接观察法,也称散点图法。它以 时间t为横轴,以时间序列指标 值(或其对应数值)为纵轴,绘 出散点图,根据散点的分布来选 择趋势方程。
增Hale Waihona Puke 特征法① 若时间序列中的逐期增长量大致相 等,配合直线方程。yc=a+bt
② 若二级增长量大致相等,则配合抛 物线方程。yc=a+bt+ct2 ③ 若各期环比发展速度相等时,则配 合指数曲线。yc=abt
书上P121页例5-11 已知某企业2002-2010年的销售额资 料如下表所示。
年份 2002 2003 2004 2005 2006 2007 2008 2009 2010 合计
序号t 1 2 3 4 5 6 7 8 9 45
销售额y t 2 300 324 347 372 396 420 446 469 495 3569
2.直线趋势测定的方法
yc=a+bt 其中:
yc——时间序列的长期趋势 t——时间序列的时间序号 a——t=0时,yc的值, (截距) b——(斜率)t 每变动一个单位时, yc平 均增减的数量。b>0时,直线呈上升 趋势,b<0时,直线呈下降趋势。
(1)最小平方法
基本原理:要求配合的长期趋势直线的理 论值与原数列的实际值之间的离差平方和 为最小。即:∑(y-yc)2=最小值 ∑(y-a-bt)2=最小值 令G(a,b)=∑(y-a-bt)2,要使G(a,b)有最小 值,则需G对a、b的偏导数为零。
xn
y n 1 0 126583 101.1087% y0 113368
x -1=11.087‰ 平均增长速度为:
【例】
若要求在2010年底,把我国大陆人口 数控制在14亿以内,以2000年底全国人口 数为基数,10年内我国大陆人口增长率应 控制在什么水平上?
xn
y n 1 0 140000 101.0125% y0 126583
ty 1 4 9 16 25 36 49 64 81 285 300 648 1041 1488 1980 2520 3122 3752 4455 19306
趋势值yc 299.16 323.51 347.86 372.21 396.56 420.91 445.26 469.61 493.96 —
解:设直线方程为: yc=a+bt
累计增长量 定基增 长速 度 某一固定基期水平 报告期水平 -某一固定基期水平 某一固定基期水平 yi y 0 y0 定基发展速度 1 (i 1,2,3, ,n)
2.环比增长速度
逐期增长量 环比增 长速 度 前一期发展水平 报告期水平 -前一期水平 前一期水平 yi y i-1 y i-1 环比发展速度 1 (i 1,2,3, ,n)
某企业1996-2000年产量增长速度
年份 环比增长速度(%) 1996 20 1997 ( 2) 25 50 1998 25 1999 15 2000 ( 5) 7.8
20 定基增长速度(%) ( 1)
( 3) 115.6 (4) 132.5 87.5
1996年定基增长速度=20% 解: 1+50% 1997年环比增长速度= 1 25% 1+20% 1998年定基增长速度 =( ( 1 25%) ( 1 25%) 1 20%) 1 87.5% 1999年定基增长速度 = 1+87.5% 1 15% 1 115.6% 2000年环比增长速度 = 1+132.5% 1 115.6% 1 7.8%
2.季节变动(S)
指由于自然季节因素(气候条件)或人 文习惯因素(节假日)的影响,动态数 列随季节变动更替而呈现的周期性变动。 季节变动一般以年为周期。也有以一周 或一日为周期的。周期不到一年的规律 性变动称准季节变动,分析方法与季节 变动相同,纳入季节变动范畴。
3.循环变动(C)
指周期在一年以上,现象近 乎规律性的上升与下降交替 出现的循环往复变动。
平均增长速度为:10.125‰
【 例 】某地区GDP “九五” 前三年平均发展速度 为112%,后两年平均发展速度为109%,求该地 区“九五”期间GDP平均发展速度和平均增长速度
解:
平均发展速度 = (112%) ( 109%) 110.79%
5 3 2
平均增长速度 =平均发展速度-1=110.79%-1=10.79%
2.定基发展速度
yi 报告期发展水平 定基发展速度 某一固定基期发展水平 y 0
动态数列中,各期定基发展速度分别为:
yn y1 y 2 y3 , , , , y0 y0 y0 y0
环比发展速度与定基发展速度的关系: ① 各环比发展速度的连乘积等于相应的 定基发展速度。即: yi yi Π (i 1,2,3, ,n) y i 1 y 0
(一)数学模型法(模型拟合法) 它根据时间序列的数据特征, 用数学方法建立一个合适的趋势 方程(即配合一条适当的趋势线) 来描述时间序列的趋势变动,推 算各时期的趋势值,分析和预测 长期趋势。
数学模型法的主要步骤:
第一步,选取合适的数学模型; 第二步,估计模型参数。 第三步,计算趋势变动预测值。
【解】
逐期增长量 增长1%的绝对值 环比增长速度 100 1000 50(万元) 20
第四节 动态数列的趋势分析
一.动态数列的影响因素 二.长期趋势的分析
一、动态数列的影响因素
1.长期趋势(T) 指现象在一段较长的时间内, 由于普遍的、持续的、决定的基本 因素的影响作用,而使发展水平沿 着一个方向,表现为持续向上、向 下或稳定的趋势变动。
Σy na bΣt 3569 9a 45b 2 Σty aΣt bΣt 19306 45a 285b nΣty ΣtΣy b 2 2 nΣt (Σt) 把上表数值代入得 a y bt
如产品的生命周期、经济危机 周期等。
4.随机变动(I)
又称不规则变动。指动态数列由 于偶然性因素的影响而表现出的不规 则的波动。包括由突发的自然灾害、 意外事故或重大政治事件所引起的剧 烈变动,也包括大量无可名状的随机 因素干扰造成的起伏波动。
二、长期趋势的分析
长期趋势的测定方法: (一) 数学模型法 (二) 时距扩大法 (三) 序时平均法 (四) 移动平均法
第五章
动态数列
任课教师:郭卫萍
第三节
动态数列速度分析指标
一.发展速度 二.增长速度 三.平均发展速度和平均增长速度 四.增长1%的绝对值
一、发展速度
发展速度=报告期水平/基期水平
报告期发展水平 yi 1.环比发展速度 前一期发展水平 yi1
动态数列中,各期环比发展速度分别为:
y1 y 2 y 3 yn , , , , y 0 y1 y 2 y n 1
使方程式: y na bt 2 ty a t b t
变为 y na 2 ty b t
则参数a,b的计算公式简化为:
ty b 2 t a y y n
注:
原点改变前后的趋势值应该是相等的。 1)n为奇数时,a 值不等,b值相等。 2)n为偶数时,a 值不等,b值为原点 改变前的1/2。
yn 定基发展速度 由此可得: y0 y n - y n -1 y n -1 ( 1) * ( ) y n -1 y0
则: 所以
y n y n -1 y n - y n -1 1 y0 y0 y n -1 y n y n-1 y n - y n -1 -1 y0 y0 y n -1
nty ty b nt 2 ( t ) 2 a y b t
最小平方法的简捷计算
取时期 t 的中点为原点,使t=0 1)当n为奇数时,取数列中间的一项为原点0 大于中间项的 t 分别为1,2,3,…, 小于中间项的 t 分别为-1,-2,-3,… 2)当n为偶数时,取数列中间两项的中点为 原点0, 大于中间项的 t 分别为1,3,5,…, 小于中间项的 t 分别为-1,-3,-5,…。
