工字钢强度验算
工字钢截面验算计算程序

抗震设防烈度 (度) 6 截面高度 h (mm) 900 上翼缘宽度 b1 (mm) 300 上翼缘厚度 t1 (mm) 16 上翼缘厚度取值满足 计算长度 l0x (mm) 16050 注:本工字钢截面沿y轴对称 钢材屈服强度值 fy (N/mm2) 腹板厚度 tw (mm) 下翼缘宽度 b2 (mm) 下翼缘厚度 t2 (mm) 下翼缘厚度取值满足 计算长度 l0y (mm) 构件用途 受压翼缘为上翼缘 345 10 300 16 16050 梁
工字钢截面验算
一、GB50017-2003第4.3.2条 腹板计算高度 h0 (mm) h0/tw 验算 b/t ≤ 80(235/fy)
0.5
868 86.800 不满足
腹板厚度 tw (mm) 80(235/fy)0.5
10 66.026
二、GB50017-2003第4.3.8条 受压翼缘自由外伸宽度 b (mm) b/t 验算 b/t ≤ 13(235/fy)0.5 三、JGJ99-98第6.1.6条 受压翼缘自由外伸宽度 b (mm) b/t 验算 b/t 四、JGJ99-98第7.1.2条 受压翼缘自由外伸宽度 b (mm) b/t 验算 b/t ≤ 9(235/fy)0.5
145 9.063 满足
受压翼缘厚度 t (mm) 13(235/fy)0.5
16 10.729
Байду номын сангаас
145 9.063 满足
受压翼缘厚度 t (mm) 11(235/fy)0.5
16 9.079
145 9.063 不满足
受压翼缘厚度 t (mm) 9(235/fy)0.5
16 7.428
工字钢、圆管及贝雷梁强度及挠度验算

工字钢强度及挠度验算 一、有关工字钢计算公式 1、一孔梁计算
2、两孔梁计算
注:1.在均布荷载作用下:M =表中系数×ql 2
;V =表中系数×ql ;EI
w 100ql 表中系数4⨯= 3、三孔梁计算
注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI
w 100ql 表中系数4
⨯=
二、工字钢强度及挠度验算 1、工字钢截面特性参数 W x —截面抵抗矩(cm3) I x —截面惯性矩(cm4) 2、强度验算
σ=M/W (N/mm2)
计算结果与f=215 N/mm2 (钢材强度设计值)比较
3、挠度验算
F max=挠度公式计算
与L/400比较
钢材的弹性模量E=206×103
圆管稳定性验算
1、查圆管截面特性表
查的圆管的回转半径ix及截面面积A
2、确定圆管长度L
3、计算圆管长细比λ=L/ix
4、查《钢结构设计规范》表C—2,确定圆管折减系数ψ
5、钢材容许应力[σ]=180MPa(轴向力)
6、圆管稳定条件
σ=F/A<ψ[σ]
贝雷梁受力计算1、321贝雷梁特性
321贝雷梁弹性模量E=2.1×105 MPa
单排单层(不加强)A=5.1×103
mm
2
,
单排单层(加强)A=10.2×103 mm
2
[σ]=210MPa
挠度计算式为
计算值要小于L/400。
工字钢抗弯强度计算方法

工字钢抗弯强度计算方法一、梁的静力计算概况1、单跨梁形式:简支梁2、荷载受力形式:简支梁中间受集中载荷3、计算模型基本参数:长 L =6 M4、集中力:标准值Pk=Pg+Pq =40+40=80 KN设计值Pd=Pg*γG+Pq*γQ =40*+40*=104 KN二、选择受荷截面1、截面类型:工字钢:I40c2、截面特性: Ix= 23850cm4 Wx= 1190cm3 Sx=G= m翼缘厚度 tf= 腹板厚度 tw=三、相关参数1、材质:Q2352、x轴塑性发展系数γx:3、梁的挠度控制[v]:L/250四、内力计算结果1、支座反力 RA = RB =52 KN2、支座反力 RB = Pd / 2 =52 KN3、最大弯矩 Mmax = Pd * L / 4 =156五、强度及刚度验算结果1、弯曲正应力σmax = Mmax / (γx * Wx)= N/mm22、A处剪应力τA = RA * Sx / (Ix * t w)= N/mm23、B处剪应力τB = RB * Sx / (Ix * tw)= N/mm24、最大挠度 fmax = Pk * L ^ 3 / 48 * 1 / ( E * I )= mm5、相对挠度 v = fmax / L =1/弯曲正应力σmax= N/mm2 < 抗弯设计值 f : 205 N/mm2 ok!支座最大剪应力τmax= N/mm2 < 抗剪设计值 fv : 125 N/mm2 ok!跨中挠度相对值 v=L/ < 挠度控制值[v]:L/ 250 ok! 验算通过Re: 如何计算角钢的受力---[图,请教]1、? ? ? ? 设每个支点承载力为p=1875N,根据图所示,支点反力R=2p2、? ? ? ? 第一受力点弯矩M1=2p×=,第二受力点弯矩M2=2p×(+)-p×==如弯矩图所示3、? ? ? ? 查东北大学机械设计手册第一册3-157页的50×5的角钢抗弯W==×10-6m34、? ? ? ? 计算弯曲应力σ=M2/w=×10-6=491×106N/m2=491MPa5、? ? ? ? 角钢材料一般为Q235,其屈服应力为235MPa,故判断491>235,角钢将失效Q235钢抗弯强度设计值 = = =mm2 < f=205N/mm2 符合要求。
工字钢焊接强度验算(精编文档).doc

【最新整理,下载后即可编辑】工字钢对接工艺强度验算书焊缝质量等级应符合现行国家标准《钢结构工程施工质量验收规范》GB 50205的规定,规范将对接焊缝质量分为一级、二级和三级,考虑到实际施工中对接焊缝很难达到一级、二级的质量要求,因此,本次验算是针对焊缝质量等级为三级来进行强度验算。
对于采用自动焊、半自动焊和E43型焊条的手工焊,构件钢材为Q235钢的对接焊缝,其焊缝的抗压强度设计值2/215mm N f w c =和抗剪强度设计值2/125mm N f w v =均与母材的强度设计值相同,而三级的抗拉对接焊缝强度设计值为2/185mm N f w t =,Q235钢的抗拉强度设计值为2/215mm N f =,因此,需验算工字钢在采用对接焊缝以及周边焊共同作用时,焊缝的抗拉强度能否达到母材的抗拉强度设计值即可。
一、I22b 工字钢加强钢板选取计算1、I22b 工字钢截面达到设计强度的弯矩计算I x =3570cm 4 W x =325cm 3 I x / S x =18.7cmt w =12.3mm d=9.5mm设计强度)(/2151032523max mm N M W M x =⨯=M max =215N/mm 2×325×103mm 3=69.875KN.mI x ——x 轴的截面惯性矩W x ——x 轴的截面模量t w ——工字钢翼缘板厚度d ——工字钢腹板厚度M max ——使截面达到材料设计强度的计算截面弯矩2、三级焊缝达到设计强度的弯矩计算三级的抗拉对接焊缝强度设计值为2/185mm N f w t =2/185mm N W M ==σ M=185N/mm 2×325×103mm 3=60.125KN.m3、加强钢板截面尺寸计算焊缝对截面抵抗的削弱在腹板处和翼缘板处,由于施工中对翼缘板处平整的要求,一般不在翼缘板处加强,因此在腹板两边添加加强钢板来弥补焊缝对截面的削弱。
工字钢抗弯强度计算方法

工字钢抗弯强度计算方法一、梁的静力计算概况1、单跨梁形式:简支梁2、荷载受力形式:简支梁中间受集中载荷3、计算模型基本参数:长L =6 M4、集中力:标准值Pk=Pg+Pq =40+40=80 KN设计值Pd=Pg*γG+Pq*γQ =40*1.2+40*1.4=104 KN二、选择受荷截面1、截面类型:工字钢:I40c2、截面特性:Ix= 23850cm4 Wx= 1190cm3 Sx= 711.2cm3G= 80.1kg/m翼缘厚度tf= 16.5mm 腹板厚度tw= 14.5mm三、相关参数1、材质:Q2352、x轴塑性发展系数γx:1.053、梁的挠度控制[v]:L/250四、内力计算结果1、支座反力RA = RB =52 KN2、支座反力RB = Pd / 2 =52 KN3、最大弯矩Mmax = Pd * L / 4 =156 KN.M五、强度及刚度验算结果1、弯曲正应力σmax = Mmax / (γx * Wx)=124.85 N/mm22、A处剪应力τ A = RA * Sx / (Ix * tw)=10.69 N/mm23、B处剪应力τ B = RB * Sx / (Ix * tw)=10.69 N/mm24、最大挠度fmax = Pk * L ^ 3 / 48 * 1 / ( E * I )=7.33 mm5、相对挠度v = fmax / L =1/ 818.8弯曲正应力σmax= 124.85 N/mm2 <抗弯设计值 f : 205 N/mm2 ok!支座最大剪应力τmax= 10.69 N/mm2 <抗剪设计值fv : 125 N/mm2 ok!跨中挠度相对值v=L/ 818.8 <挠度控制值[v]:L/ 250 ok! 验算通过Re: 如何计算角钢的受力?---[图,请教]1、设每个支点承载力为p=1875N,根据图所示,支点反力R=2p2、第一受力点弯矩M1=2p×0.215m=0.43p,第二受力点弯矩M2=2p×(0.215+0.39)-p×0.39=0.82p=1537.5Nm如弯矩图所示3、查东北大学机械设计手册第一册3-157页的50×5的角钢抗弯W=3.13cm3=3.13×10-6m34、计算弯曲应力σ=M2/w=1537.5/3.13×10-6=491×106N/m2=491MPa5、角钢材料一般为Q235,其屈服应力为235MPa,故判断491>235,角钢将失效。
工字钢抗弯强度计算方法

工字钢抗弯强度计算方法【1】一、梁的静力计算概况1、单跨梁形式:简支梁2、荷载受力形式:简支梁中间受集中载荷3、计算模型基本参数:长 L =6 M4、集中力:标准值Pk=Pg+Pq =40+40=80 KN设计值Pd=Pg*γG+Pq*γQ =40*1.2+40*1.4=104 KN二、选择受荷截面1、截面类型:工字钢:I40c2、截面特性: Ix= 23850cm4 Wx= 1190cm3 Sx= 711.2cm3G= 80.1kg/m翼缘厚度 tf= 16.5mm 腹板厚度 tw= 14.5mm三、相关参数1、材质:Q2352、x轴塑性发展系数γx:1.053、梁的挠度控制[v]:L/250四、内力计算结果1、支座反力 RA = RB =52 KN2、支座反力 RB = Pd / 2 =52 KN3、最大弯矩 Mmax = Pd * L / 4 =156 KN.M五、强度及刚度验算结果1、弯曲正应力σmax = Mmax / (γx * Wx)=124.85 N/mm22、A处剪应力τA = RA * Sx / (Ix * tw)=10.69 N/mm23、B处剪应力τB = RB * Sx / (Ix * tw)=10.69 N/mm24、最大挠度 fmax = Pk * L ^ 3 / 48 * 1 / ( E * I )=7.33 mm5、相对挠度 v = fmax / L =1/ 818.8弯曲正应力σmax= 124.85 N/mm2 < 抗弯设计值 f : 205 N/mm2 ok!支座最大剪应力τmax= 10.69 N/mm2 < 抗剪设计值 fv : 125 N/mm2 ok!跨中挠度相对值 v=L/ 818.8 < 挠度控制值[v]:L/ 250 ok! 验算通过Re: 如何计算角钢的受力?---[图,请教]1、设每个支点承载力为p=1875N,根据图所示,支点反力R=2p2、第一受力点弯矩M1=2p×0.215m=0.43p,第二受力点弯矩M2=2p×(0.215+0.39)-p×0.39=0.82p=1537.5Nm如弯矩图所示3、查东北大学机械设计手册第一册3-157页的50×5的角钢抗弯W=3.13cm3=3.13×10-6m34、计算弯曲应力σ=M2/w=1537.5/3.13×10-6=491×106N/m2=491MPa5、角钢材料一般为Q235,其屈服应力为235MPa,故判断491>235,角钢将失效Q235钢抗弯强度设计值 = = =94.09N/mm2 < f=205N/mm2 符合要求2022年3月23日;第1页共1页。
工字钢两端固支梁集中载荷强度验算
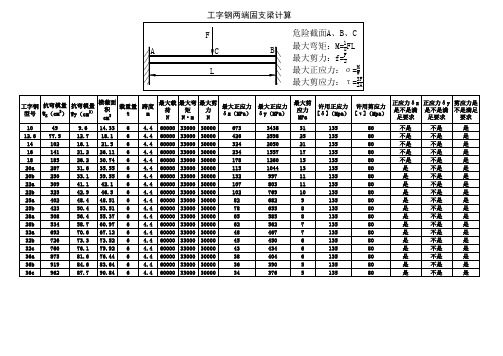
最大正应力 δ y(MPa) 3438 2598 2050 1557 1260 1044 997 803 769 682 655 585 562 467 450 434 404 390 376
横截面 最大载 最大弯 最大剪 载重量 跨度 最大正应力 积 荷 矩 力 t m δ x(MPa) N N·m N cm 2 14.33 18.1 21.5 26.11 30.74 35.55 39.55 42.1 46.5 48.51 53.51 55.37 60.97 67.12 73.52 79.92 76.44 83.64 90.84 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 4.4 4.4 4.4 4.4 4.4 4.4 4.4 4.4 4.4 4.4 4.4 4.4 4.4 4.4 4.4 4.4 4.4 4.4 4.4 60000 60000 60000 60000 60000 60000 60000 60000 60000 60000 60000 60000 60000 60000 60000 60000 60000 60000 60000 33000 33000 33000 33000 33000 33000 33000 33000 33000 33000 33000 33000 33000 33000 33000 33000 33000 33000 33000 30000 30000 30000 30000 30000 30000 30000 30000 30000 30000 30000 30000 30000 30000 30000 30000 30000 30000 30000 673 426 324 234 178 115 132 107 102 82 78 65 62 48 45 43 38 36 34
16#工字钢做立柱强度稳定性计算书

钢结构强度稳定性计算书
地下车库工字钢回顶方案:
最大跨度8.1×8.1,井子梁,间距2.7×2.7。
主梁尺寸:450×800,次梁尺寸:300×700,楼板厚度250
设计顶板荷载:5kN/㎡,消防车道荷载35kN/㎡
单跨梁及楼板自重:72T,车满载自重暂估算为:50T,合计荷载122T
每夸下顶12根工字钢,加上原砼框柱,则每根工字钢受载为:7.625T(75kN)计算依据:
1、《钢结构设计标准》GB50017-2017
一、构件受力类别:
轴心受压构件。
二、强度验算:
1、轴心受压构件的强度,可按下式计算:
σ = N/A n≤ f
式中N──轴心压力,取 N= 100 kN;A n──净截面面积,取A n= 1944 mm2;
轴心受压构件的强度σ= N / A n = 100×103 / 1944 = 51.44 N/mm2;
f──钢材的抗压强度设计值,取 f= 215 N/mm2;
由于轴心受压构件强度σ= 51.44 N/mm2≤承载力设计值f=215
N/mm2,故满足要求!
2、轴心受压构件的稳定性按下式计算:
≤ f
N/φA
n
式中 N──轴心压力,取 N= 100 kN;l──构件的计算长度,取 l=3200 mm;
i──构件的回转半径,取 i=18.9 mm;
λ──构件的长细比, λ= μl/i= 0.5×3200/18.9 = 84.6562;
[λ]──构件的允许长细比,取 [λ]=150 ;
构件的长细比λ= 84.656 >[λ] = 150,故满足要求;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)求a、b两点的正应力
5830 cm4
ya
18 2
3
6cm;
yb
3cm.
a
M c ya z
3103 0.06 5830108 3.09MPa;
b
M c yb z
3103 0.03 5830108
1.54MPa;
(4)求C截面最大拉应力+max和最大压应力
(2)确定中性轴位置 和截面惯性矩:
查型钢表
IZ=1660cm4
(3)求D截面a、b两点的正应力:
ya
yb
180 2
10.7
79.3mm;
a
M D ya z
30103 79.3103 1660108
143.3MPa;
b 143.3MPa;
返回 下一张 上一张 小结
Sz *—所求剪应力作用点处的横线以
下(或以上)的截面积A*对中性轴的面积矩。
矩形截面:
y1bdy
b (h2 24
y2 );
Iz
bh3 12
,
τ沿截面高度按 抛物线规律变化。
Q 2Iz
( h2 4
y2)
6Q bh3
(h2 4
第二节 梁横截面上的剪应力
一、矩形截面梁:
矩形截面梁任意截面上剪力Q 都与对称轴重合。对狭长横截面上 剪应力的分布规律可作两个假设:
(1)横截面上各点均与该面上Q 同向且平行;
(2)剪应力沿截面宽度均匀分布。
从梁微段中取窄条cdmn分析:
N1
A* 1dA
M Iz
Sz; N2
M
dM Iz
y 2 );
y
h ,
2
0; y
0, max
6Qh 2 4bh3
3 2
Q; bh
max
3 2
Q A
3;
2
( 平均剪应力)
由剪切虎克定律τ=Gγ,知剪应变 沿截面高度也按抛物线规律变化,引起 截面翘曲。但变形很小,可忽略不计。
返回 下一张 上一张 小结
二、其它形状截面的剪应力:
My
zdA
0
E
zydA
0; —中性轴是截面的形心主轴。
Mz
ydA
M
E
y2dA
M
My
1 M ; —纯弯曲梁的 Ez 变形计算公式
z —纯弯曲梁横截面上任一点正应力计算公式
式中: Iz—截面对其中性轴的惯性矩; M—截面上的弯矩; y—所求正应力点到中性轴的距离。
凸边伸长, 凹边缩短; ③横截面相对于纵向伸长区域缩
短,纵向缩短区域伸长。 假设:①平面假设—变形前 后横
截面保持平面不变;
②单向受力假设—纵向纤维之间互不挤压仅伸长或缩短。
中性层—长度不变的纤维层; 中性轴—中性层与横截面的交线。
返回 下一张 上一张 小结
二、正应力公式的推导: (一)变形几何关系:
1. 工字形截面梁: 工字形截面是由上、下翼缘及中间腹板组成的。
1)腹板上的剪应力:腹板为狭长矩形,承担截面绝大部分剪应力。 故中性轴处有最大剪应力
工字钢强度验算
第七章 梁的强度和刚度计算
梁的一般情况是横截面上同时 存在剪力和弯矩两种内力,称作剪 力(横力)弯曲。与此相应的截面 上任一点处有剪应力τ和正应力σ。 且剪应力τ只与剪力Q有关,正应力 σ只与弯矩M有关。
横截面上只有弯矩而没有剪力 的弯曲称作纯弯曲。
如图简支梁,AC、DB段为横 力弯曲;CD段为纯弯曲。
取梁微段dx考虑变形 几何关系,得应变规律:
S yd y ; dx d
当M>0时:y>0,ε>0,为受拉区;y<0,ε<0,为受压区。
(二)物理关系:
由假设2及虎克定律,梁横 截面上的正应力变化规律为:
E E y
此式表明:梁横截面上任一点的正应力,与该点距中性轴
(一般l/h>5为细长梁,其计算误差满足工程精度要求δ<5%。)
例7-1 图示悬臂梁。试求C截面上a、b两点的正应力和该截面最大拉、压应力。
解:(1)计算C截面的弯矩M
M c 2P 21.5 3KN m
(2)确定中性轴位置,并计算惯性矩
z
bh3 12
12 183 12
(z轴)的距离y成正比,而与该点距y轴的距离z无关。正应
力沿截面高度呈直线规律分布。中性层处y=0,σ=0;上下边
缘处有ymax,故有σmax。
返回 下一张 上一张 小结
(三)静力学关系:
纯弯曲梁上各点只有正应力,微面积dA上法
向合力dN=σdA。截面上各微内力形成沿X轴的空
间平行N 力 系d。可简0 化成E 三 y个d内力0 分—量中:性N轴xZ、必M通y、过M形z。心。
本章研究梁的应力和变形计算, 解决梁的强度和刚度计算问题。
返回 下一张 上一张 小结
第一节 梁横截面上的正应力
为推导梁横截面上的正应力,考虑纯弯曲情况。
用三关系法:实验观察→平面假设; 几何关系→变形规律, 物理关系→应力规律, 静力学关系→应力公式。
一、实验观察与分析:
①横线仍为直线,但倾斜角度d; ②纵线由直变弯,仍与横线正交,
为避免符号错误,计算中各量以绝对值代入,σ符号依点 所处区域直接判断。(根据弯矩方向,中性轴将截面分为受 拉区和受压区;M>0,上压下拉;M<0,上拉下压。)
返回 下一张 上一张 小结
正应力公式的使用范围:①纯弯曲梁;②弹性范围(σ≤σp); ③平面弯曲(截面有对称轴,形状不限);④细长梁的横力弯曲。
Sz;
dT 'bdx;
x 0, N1 N2 dT 0;
' dMSz , dM Q, ' ;
dxI zb dx
QS z ;
I zb
返回 下一张 上一张 小结
矩形截面剪应力计算公式:
QS
* z
式中:Q—横截面上的剪力;
Izb
Iz—横截面对其中性轴的惯性矩; b—所求剪应力作用点处的截面宽度;
max
ymax
h 2
18 2
9cm;
max
M c ymax z
3103 9102 5830108
4.63MPa
m
ax;
(在截面上下边缘。)
返回 下一张 上一张
小结
例7-2 18号工字钢制成的简支梁如图所示。试求D截面上a、b两 点处的正应力。
解:(1)求D截面的弯矩: MD=30kN.m
