轴抗弯强度计算公式12则
轴的强度和刚度计算

轴的强度和刚度计算一、轴的强度计算轴的强度是指在受到外界载荷作用下,轴能够抵抗破坏的能力。
轴的强度计算通常分为以下几个步骤:1.确定轴的应力状态首先需要确定轴在受载过程中的应力状态。
一般情况下,轴受力状态可以分为以下几种情况:拉伸、压缩、弯曲、剪切和扭转。
根据轴的几何形状、受载方式和材料性质,可以确定轴的应力状态。
2.计算轴的受力根据轴所受到的外界载荷,可以计算轴的受力。
在拉伸和压缩情况下,轴的受力可以通过受力公式F=σA来计算,其中F是轴所受到的载荷,σ是轴的应力,A是轴的截面积。
在弯曲情况下,轴的受力可以通过受力公式M=σS来计算,其中M是轴的弯矩,S是轴的截面模数。
在剪切和扭转情况下,轴的受力可以通过受力公式τ=T/(2A)来计算,其中τ是轴所受的剪应力,T是轴的剪矩,A是轴的等效截面面积。
3.计算轴的抗力轴的抗力是指轴抵抗外界载荷作用下破坏的能力。
轴的抗力通常由材料的强度指标来表示,如抗拉强度、抗压强度、抗弯强度、抗剪强度和抗扭强度等。
根据轴的应力状态和材料的强度指标,可以计算轴的抗力。
4.比较轴的受力和抗力最后,需要比较轴的受力和抗力。
如果轴的受力小于轴的抗力,则表明轴具有足够的强度;如果轴的受力大于轴的抗力,则表明轴的强度不足,需要采取相应的加强措施。
二、轴的刚度计算轴的刚度是指轴在受力过程中不发生明显变形的能力。
轴的刚度计算通常分为以下几个步骤:1.确定轴的变形状态首先需要确定轴在受载过程中的变形状态。
轴的变形状态可以分为弹性变形和塑性变形两种情况。
在弹性变形情况下,轴在受载后可以恢复到原始形状;在塑性变形情况下,轴在受载后无法恢复到原始形状。
2.计算轴的变形根据轴所受到的外界载荷和轴的受力分布情况,可以计算轴的变形。
在拉伸和压缩情况下,轴的变形可以通过变形公式δ=FL/(EA)来计算,其中δ是轴的变形,F是轴所受到的载荷,L是轴的长度,E是轴材料的弹性模量,A是轴的截面积。
在弯曲情况下,轴的变形可以通过变形公式δ=ML/(EI)来计算,其中δ是轴的变形,M是轴的弯矩,L是轴的长度,E是轴材料的弹性模量,I是轴的截面二阶矩。
抗弯截面系数及惯性矩公式大全

汇报人:XX
01
03
05
02
04
公式:W=bh^2/6
意义:表示矩形截 面对其弯曲中性轴 的惯性矩
影响因素:b(宽 度)、h(高度)
应用:用于计算梁 的抗弯承载能力
公式:W=bh^2/6
适用范围:工字形截面梁
影响因素:截面高度、宽度和 腹板厚度
风险。
添加标题
增强结构的承载能 力:抗弯截面系数 和惯性矩的大小直 接决定了结构的承 载能力。通过优化 设计,可以提高结 构的承载能力,从 而满足各种不同的
工程需求。
添加标题ห้องสมุดไป่ตู้
提高结构的经济 性:通过合理的 抗弯截面系数和 惯性矩设计,可 以有效地降低材 料的消耗量,减 少成本,提高结
构的经济性。
添加标题
抗弯截面系数与惯性矩是两个不同的概念,但它们之间存在密切的关系。
抗弯截面系数主要描述截面对弯曲的抵抗能力,而惯性矩则表示截面的惯性大小。
在弯曲截面系数中,惯性矩越大,抗弯截面系数越小,反之亦然。
了解抗弯截面系数与惯性矩的关系有助于更好地理解结构在受力时的行为和性能。
抗弯截面系数与材料的弹性模量有关,弹性模量越大,抗弯截面系数越小。 抗弯截面系数与材料的泊松比有关,泊松比越大,抗弯截面系数越小。 抗弯截面系数与材料的密度有关,密度越大,抗弯截面系数越小。 抗弯截面系数与材料的硬化指数有关,硬化指数越大,抗弯截面系数越小。
抗弯截面系数与惯性矩的关系 材料属性对惯性矩的影响 不同材料的惯性矩比较 惯性矩与材料强度的关联
计算梁的承载能力 确定梁的截面尺寸和形状
分析梁的稳定性
优化结构设计以降低成本和 提高性能
轴的强度校核方法

第二章 轴的强度校核方法常用的轴的强度校核计算方法进行轴的强度校核计算时,应根据轴的具体受载及应力情况,采取相应的计算方法,并恰当地选取其许用应力。
对于传动轴应按扭转强度条件计算。
对于心轴应按弯曲强度条件计算。
对于转轴应按弯扭合成强度条件计算。
2.2.1按扭转强度条件计算:这种方法是根据轴所受的扭矩来计算轴的强度,对于轴上还作用较小的弯矩时,通常采用降低许用扭转切应力的办法予以考虑。
通常在做轴的结构设计时,常采用这种方法估算轴径。
实心轴的扭转强度条件为:由上式可得轴的直径为为扭转切应力,MPa 式中:T 为轴多受的扭矩,N ·mmT W 为轴的抗扭截面系数,3mmn 为轴的转速,r/minP 为轴传递的功率,KWd 为计算截面处轴的直径,mm为许用扭转切应力,Mpa ,][r τ值按轴的不同材料选取,常用轴的材料及][r τ值见下表:T τnP A d 0≥[]TT T d n P W T ττ≤2.09550000≈3=[]T τ空心轴扭转强度条件为:dd 1=β其中β即空心轴的内径1d 与外径d 之比,通常取β=这样求出的直径只能作为承受扭矩作用的轴段的最小直径。
例如,在设计一级圆柱齿轮减速器时,假设高速轴输入功率P1=,输入转速n1=960r/min ,则可根据上式进行最小直径估算,若最小直径轴段开有键槽,还要考虑键槽对轴的强度影响。
根据工作条件,选择45#钢,正火,硬度HB170-217,作为轴的材料,A0值查表取A0=112,则mm n P A d 36.15960475.2112110min =⨯== 因为高速轴最小直径处安装联轴器,并通过联轴器与电动机相连接,设有一个键槽,则:mm d d 43.16%)71(36.15%)71(min 'min =+⨯=+= 另外,实际中,由于减速器输入轴通过联轴器与电动机轴相联结,则外伸段轴径与电动机轴径不能相差太大,否则难以选择合适的联轴器,取电动机轴d d 8.0'min =,查表,取mm d 38=电动机轴,则:mm d d 4.3038*8.08.0'min ===电动机轴 综合考虑,可取mm d 32'min =通过上面的例子,可以看出,在实际运用中,需要考虑多方面实际因素选择轴的直径大小。
抗弯强度的计算公式

抗弯强度的计算公式抗弯强度(Bending Strength)是指材料在受弯作用下发生破坏之前能承受的最大应力值,也是衡量材料抵抗弯曲变形和断裂的能力的重要参数之一、在工程设计和材料选择中,抗弯强度常常是一个关键的考虑因素。
弹性理论是计算抗弯强度的常用方法之一,它可以应用于弹性材料,如金属、混凝土等。
在弹性理论中,抗弯强度的计算公式可以通过应用梁理论中的弯曲应力公式得到。
假设梁的跨度为L,弯曲力矩为M。
根据梁理论,梁的弯曲应力σ可以表示为:σ=M/(W*y)其中,W是梁的截面模量(Section Modulus),y是梁截面上任意一点到中性轴的距离。
对于矩形截面梁,截面模量可以由下式计算:W=(b*h^2)/6其中,b是梁的宽度,h是梁的高度。
对于圆形截面梁,截面模量可以由下式计算:W=(π*d^3)/32其中,d是梁的直径。
这些公式可以用于计算梁的抗弯强度。
但需要注意的是,这些公式是在假设材料的应力应变关系服从线弹性的条件下得到的,对于非线性材料(如混凝土)或者具有大变形的材料,这些公式可能不适用。
除了基于弹性理论的计算方法外,还可以根据材料的破裂力学性质来计算抗弯强度。
破裂力学是研究材料在破裂前后力学性质变化的科学,通过分析材料的断裂行为和裂纹扩展来计算材料的抗弯强度。
破裂力学计算抗弯强度的方法有许多,常见的方法包括线弹性断裂力学(Linear Elastic Fracture Mechanics,LEFM)和非线性断裂力学(Nonlinear Fracture Mechanics,NLFM)等。
这些方法是基于裂纹尖端处的应力场和应变场的计算,通过计算裂纹尖端处的应力强度因子(Stress Intensity Factor,SIF)来确定材料的抗弯强度。
总之,计算抗弯强度的公式主要有两类:基于材料的弹性理论和基于材料的破裂力学。
这些公式可以帮助工程师和设计师选择合适的材料和设计结构,以满足抗弯强度的要求。
轴的强度计算
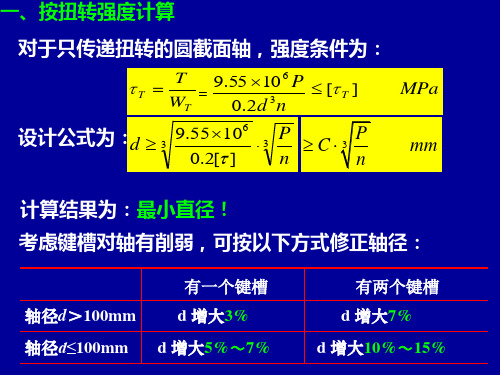
对于只传递扭转的圆截9.55 10 6 P 0.2d 3n
[ T ]
设计公式为:d 3 9.55106 3 P C 3 P
0.2[ ] n
n
MPa
mm
计算结果为:最小直径! 考虑键槽对轴有削弱,可按以下方式修正轴径:
轴径d>100mm 轴径d≤100mm
有一个键槽 d 增大3% d 增大5%~7%
有两个键槽 d 增大7% d 增大10%~15%
二、按弯扭合成强度计算
一般转轴强度用这 种方法计算,其步 骤如下:
减速器中齿轮轴的受力为典型的弯扭合成。
A
B CD
潘存云教授研制
L1
L2
L3
在完成单级减速器草图设计后,外载荷与支撑 反力的位置即可确定,从而可进行受力分析。
T A
1)轴的弯矩和扭矩分析 水平面受力及弯矩图→
铅垂面受力及弯矩图→ 水平铅垂弯矩合成图→
L1
L2
Fr
L3
Ft
Fa
F’NV1B
C
D
潘存云教授研制
FNV1 FNH1
ω
FNV2 FNH2
FNH1
F’NV1 FNV1
MH
FNH2
MH
Fr
Ma=Fa Fa
r
MV1
FNV2
MV2 M1 M2
扭矩图→
T
2)轴的强度校核
300
140
80
1000
330
150
90
铸钢
400
500
100
50
30
120
70
40
轴的设计实例
a
举例:计算某减速器输出轴危 d
轴抗弯强度计算公式12则

轴抗弯强度计算公式12 则抗弯强度计算公式(一)工字钢抗弯强度计算方法一、梁的静力计算概况1、单跨梁形式: 简支梁2、荷载受力形式: 简支梁中间受集中载荷3、计算模型基本参数: 长L =6 M4、集中力: 标准值Pk=Pg+Pq =40+40=80 KN设计值Pd=Pg*丫G+Pq*丫Q =40*1.2+40*1.4=104 KN工字钢抗弯强度计算方法二、选择受荷截面11 、截面类型: 工字钢:I40c2、截面特性: Ix= 23850cm4 Wx= 1190cm3 Sx= 711.2cm3G= 80.1kg/m翼缘厚度tf= 16.5mm 腹板厚度tw= 14.5mm 工字钢抗弯强度计算方法三、相关参数1 、材质:Q2352、x轴塑性发展系数丫x:1.053、梁的挠度控制〔v〕:L/250 工字钢抗弯强度计算方法四、内力计算结果1、支座反力RA = RB =52 KN2、支座反力RB = Pd / 2 =52 KN3、最大弯矩Mmax = Pd * L / 4 =156 KN.M 工字钢抗弯强度计算方法五、强度及刚度验算结果21、弯曲正应力Z max = Mmax / ( 丫x * Wx),124.85 N/mm22、A处剪应力n A = RA * Sx / (Ix * tw),10.69 N/mm23、B处剪应力n B = RB * Sx / (lx * tw),10.69 N/ 毫米为单位,直接把数值代入上述公式,得出即为每米方管的重量,以克为单位。
如30x30x2.5 毫米的方管,按上述公式即可算出其每米重量为:4x2.5x(30-2.5)x7.85=275x7.85=2158.75 克,即约2.16 公斤矩管抗弯强度计算公式1 、先计算截面模量WX=(a四次方-b四次方)/6a2、再根据所选材料的强度,计算所能承受的弯矩3、与梁上载荷所形成的弯矩比对,看看是否在安全范围内参见《机械设计手册》机械工业出版社2007年12月版第一卷第1-59 页玻璃的抗弯强度计算公式锦泰特种玻璃生产的玻璃的抗弯强度一般在60~220Mpa之间,玻璃样品的形式和表面状态对测试的结果影响较大,3通常采用万能压力测试仪测试。
混凝土弯曲强度计算公式

混凝土弯曲强度计算公式
1. 杨氏模量公式
杨氏模量是衡量混凝土弯曲强度的重要参数之一。
在弯曲计算中,可以使用以下公式计算混凝土的杨氏模量:
E = 0.043 * sqrt(f'c)
其中,E为混凝土的杨氏模量(单位为GPa),f'c为混凝土的抗压强度(单位为MPa)。
2. 抗弯承载力公式
混凝土在受弯载荷作用下的抗弯承载力可以使用以下公式进行计算:
M = f'b * W * d^2 / 6
其中,M为混凝土的抗弯弯矩(单位为kNm),f'b为混凝土
的轴心抗压强度(单位为MPa),W为截面的宽度(单位为mm),d为截面的有效高度(单位为mm)。
3. 弯曲应力公式
在已知抗弯弯矩和截面属性的情况下,可以使用以下公式计算
混凝土的弯曲应力:
f' = 6 * M / (b * d^2)
其中,f'为混凝土的弯曲应力(单位为MPa),M为混凝土的
抗弯弯矩(单位为kNm),b为截面的宽度(单位为mm),d为
截面的有效高度(单位为mm)。
请注意,以上公式仅为常用的混凝土弯曲强度计算公式之一,
实际计算应结合具体工程情况和规范要求进行。
主轴强度刚度等计算公式汇总及实例

320185280177a b c 17078248500.921.121.122.9574.993.9926.51.35140269.39538.7814.801.0202.731.960.910.60.680.214.3253.664.31OK 12022C截面弯矩 M C =3.99×106Nmm解得:圆柱滚子轴承支反力:FA=22.96KN 调心滚子轴承支反力:Fc=75.0KN 转子部分的磁极重约为0.92KN 轴伸处飞轮重约为1.12KN额定转矩(扭矩)T N =1100Nm=1.1×106N㎜外1)调心滚子轴承支承中点C截面一、选材 某种型号电机1.轴的结构设计和受力分析轴的结构尺寸参见WYJ133-20-3受力分析:轴伸端上轴的最大载荷为50KN 弯曲疲劳极限τ-1≮185MPb 许用静应力[σ+]≮280MPa许用疲劳应力[σ-1]=177~213MPa 二、轴的强度计算40Cr HB284~322抗拉强度σb ≮700MP b 抗扭断面系数 W P =πd 3/16=538.78㎝3弯曲应力幅σa =M C /W=14.81MP a 切应力幅τm =τa =T N /(2W P )=1.02MP a 对称循环弯曲应力的平均应力 σm =0屈服点σb ≮500MP b 弯曲疲劳极限σ-1≮320MPb 2.轴的C截面强度校算 (截面直径)抗弯断面系数 W =πd 3/32=269.39㎝3E截面弯矩M E =1.35×106N㎜2)轴伸端支承中点E截面弯矩, (E至受力点距离)S σ=σ-1/[K σσa /(βεσ)+ψσσm ]=4.32只考虑扭矩作用时的安全系数正应力有效应力集中系数K σ=2.73切应力有效应力集中系数K τ=1.96表面质量系数β=0.91尺寸系数εσ=0.6,3.轴的E截面强度校算 (截面直径,键槽宽,高, )S τ=τ-1/[K ττa /(βετ)+ψττm ]=53.70ετ=0.68C截面安全系数 S=S σS τ/√S σ2+S τ2=4.31 >[S]=1.3~2.5即C截面是足够安全的平均应力折算系数ψτ=0.21只考虑弯矩作用时的安全系数168.74338.398.531.6302.731.960.910.60.70.217.5034.637.33OK8.1d1140l1101d2120l269.54.74E-07OKd1d2d3d4d5d6d76074120120152140140l1l2l3l4l5l6l715.51943432326.551.5M0M1M2M3M4M5M60 3.567.9217.7928.0633.6839.87M 0'M 1'M 2'M 3'M 4'M 5'M 6'08.4318.7742.1722.5712.082.挠度计算各轴段的直径和长度: ㎜各轴段弯矩: ×105N㎜在B处加单位力不从1N时引起轴上各段的弯矩:N㎜在D处加单位力不从1N时引起轴上各段的弯矩:N㎜>[S]=1.3~2.5即E截面是足够安全的三、轴的钢度计算1.扭转变形材料的切变模量 G=8.1×108MPa 轴受转矩作用的长度和外直径: ㎜扭转角: T×10+6 ,G×10+8,抗弯断面系数 W =πd 3/32-bt(d-t)2/d=151.2㎝3抗扭断面系数 W P =πd 3/16-bt(d-t)2/d=320.9㎝3弯曲应力幅σa =M E /W=8.931MPa 只考虑扭矩作用时的安全系数S τ=τ-1/[K ττa /(βετ)+ψττm ]=53.70E截面安全系数 S=S σS τ/√S σ2+S τ2=4.31S σ=σ-1/[K σσa /(βεσ)+ψσσm ]=4.32切应力幅τm =τa =T N /(2W P )=1.71MPa 对称循环弯曲应力的平均应力 σm =0正应力有效应力集中系数K σ=2.73切应力有效应力集中系数K τ=1.96表面质量系数β=0.91尺寸系数εσ=0.6,ετ=0.7平均应力折算系数ψτ=0.21只考虑弯矩作用时的安全系数[]6/0.25/~1/m m m φ<=M 00'M 01'M 02'M 03'M 04'M 05'M 06'07.1115.8335.5655.2965.8478'1+M '2'2+M '14. 2M 1+M 28.4335.6479.71106.9057.2124.165. 2M '2+M '116.8745.98103.1187.3046.7312.087. Ii*105 6.3614.72101.79101.79262.03188.578. (l i /I i )105 2.44E-05 1.29E-05 4.22E-06 4.22E-068.78E-07 1.41E-069.M 1×(4.)(8.)0.00E+00 1.64E+02 2.67E+028.03E+02 1.41E+02 1.14E+0210.M 2×(5.)(8.) 1.46E+02 4.70E+027.75E+02 1.03E+03 1.38E+02 6.77E+0111.=9.+10. 1.46E+026.34E+02 1.04E+03 1.84E+032.79E+021.82E+0212.=Σ11 4.12E+0313.y=Σ11/6E0.0032703750.034结论OK4. 2M '01+M '027.1130.0567.22126.41176.42209.685. 2M '02+M '0114.2238.7786.95146.14186.97221.847. Ii*105 6.3614.72101.79101.79262.03188.578. (l i /I i )105 2.44E-05 1.29E-05 4.22E-06 4.22E-068.78E-07 1.41E-069.M 1×(4.)(8.)0.00E+001.38E+022.25E+029.50E+024.34E+029.92E+0210.M 2×(5.)(8.) 1.23E+02 3.96E+02 6.53E+02 1.73E+03 5.53E+02 1.24E+0311.=9.+10. 1.23E+02 5.34E+028.78E+02 2.68E+039.87E+02 2.24E+0312.=Σ11 1.01E+0413.y=Σ11/6E 0.0080154660.034结论OKM 10'M 11'M 12'M 13'M 14'M 15'M 16'材料的弹性模量 E=2.1×105MPa 截面的惯性矩 I=πd 4/64,单位㎜4 D处挠度3.轴上调心滚子轴承支承中点C截面的偏转角计算在C截面处加单位力矩1N㎜时引起轴上各段的弯矩: N㎜4. 2M'11+M'120.090.390.86 1.62 2.26 2.695. 2M'12+M'110.180.50 1.11 1.87 2.40 2.847. Ii*105 6.3614.72101.79101.79262.03188.578. (l i/I i)105 2.44E-05 1.29E-05 4.22E-06 4.22E-068.78E-07 1.41E-069.M1×(4.)(8.)0.00E+00 1.77E+00 2.88E+00 1.22E+01 5.57E+00 1.27E+0110.M2×(5.)(8.) 1.58E+00 5.08E+008.38E+00 2.22E+017.09E+00 1.59E+0111.=9.+10. 1.58E+00 6.85E+00 1.13E+01 3.44E+01 1.27E+01 2.87E+0112.=Σ119.54E+0113.θC=Σ11/6E7.57078E-05rad0.05结论OK四、轴的临界转速(本电机转速低,可以不验算临界转速)五、键的强度计算假设压力在键的接触长度内均匀分布,则根据挤压强度或耐磨性的条件性计算,求得联接所能传递的转矩静联接 键盘秘能伟递的力矩 T= 1/2 h'l'd〔σp〕MpaWYJ133WYJ103键规格22×1432×18h'67l'3948d120120〔σp〕8080T11232001612800T N11000002200000OK NO转子中点至左端面77.58d8120l826.5M7M813.550B 3A0D610.5441180.4558821AM07'M08'0.45882426.5021000018857410 8.433824182.5053.00131.0026.50188.57101.792.73E-06 2.60E-061.99E+03 1.87E+024.85E+020.00E+002.47E+03 1.87E+021。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
轴抗弯强度计算公式12则抗弯强度计算公式(一)工字钢抗弯强度计算方法一、梁的静力计算概况1、单跨梁形式: 简支梁2、荷载受力形式: 简支梁中间受集中载荷3、计算模型基本参数:长 L =6 M4、集中力:标准值Pk=Pg+Pq =40+40=80 KN设计值Pd=Pg*γG+Pq*γQ =40*1.2+40*1.4=104 KN工字钢抗弯强度计算方法二、选择受荷截面11、截面类型: 工字钢:I40c2、截面特性: Ix= 23850cm4 Wx= 1190cm3 Sx= 711.2cm3 G= 80.1kg/m翼缘厚度 tf= 16.5mm 腹板厚度 tw= 14.5mm工字钢抗弯强度计算方法三、相关参数1、材质:Q2352、x轴塑性发展系数γx:1.053、梁的挠度控制〔v〕:L/250工字钢抗弯强度计算方法四、内力计算结果1、支座反力 RA = RB =52 KN2、支座反力 RB = Pd / 2 =52 KN3、最大弯矩 Mmax = Pd * L / 4 =156 KN.M工字钢抗弯强度计算方法五、强度及刚度验算结果21、弯曲正应力ζmax = Mmax / (γx * Wx),124.85 N/mm22、A处剪应力ηA = RA * Sx / (Ix * tw),10.69 N/mm23、B处剪应力ηB = RB * Sx / (Ix * tw),10.69 N/毫米为单位,直接把数值代入上述公式,得出即为每米方管的重量,以克为单位。
如30x30x2.5毫米的方管,按上述公式即可算出其每米重量为:4x2.5x(30-2.5)x7.85=275x7.85=2158.75克,即约2.16公斤矩管抗弯强度计算公式1、先计算截面模量WX=(a四次方-b四次方)/6a2、再根据所选材料的强度,计算所能承受的弯矩3、与梁上载荷所形成的弯矩比对,看看是否在安全范围内参见《机械设计手册》机械工业出版社2007年12月版第一卷第1-59页玻璃的抗弯强度计算公式锦泰特种玻璃生产的玻璃的抗弯强度一般在60~220Mpa之间,玻璃样品的形式和表面状态对测试的结果影响较大,3通常采用万能压力测试仪测试。
样品可采用玻璃棒货玻璃片。
抗弯强度的计算公式如下:P=8F1L/D3——棒材P=3F1L/AB2——片材式中P——抗弯强度,Mpa;F1——极限荷载力,N;L——支点间的距离,m;D——棒材的直径,m;A——片材的宽度,m;B——片材的厚度,m.钢管的抗弯强度计算公式最大弯曲正应力的计算公式是:ζ=M/(γx*Wnx)。
其中:M是钢管承受的最大弯矩; γx——截面的塑性发展系数;对于钢管截面,取为1.15, Wnx——钢管净截面模量,也称为净截面抵抗矩。
如果截面没有削弱,可以通过钢结构设计手册中的型钢表格查到,如果截面有削弱,可以根据材料力学的公式根据截面尺寸通过计算公式计算得到钢带的抗弯截面系数抗弯截面系数跟截面形状有关,查表可得。
以下为在网上4搜到的:抗弯截面系数在构件的工程力学中的抗弯强度的计算中,梁的最大正应力点计算公式为: ,max=l,lmax/,y其中,,y称为抗弯截面系数,当抗弯截面系数越大时,截面的抗弯强度就越大。
截面高度:截面顶端到底端的垂直距离。
其中D1、D2、D3分别是圆形、正方形、三角形的截面高度。
分析: 当圆形、正方形和三角形的周长均为L,它们的截面高度的值不难分别求得: D1,L/nD2,L/4D3,?(L/3)2+(L/6)2,L/?12?L/3.46可见,三种形状的截面高度关系为:D1>D3>D2 根据抗弯截面系数的计算公式: 当圆形截面的截面高度为D1时,其抗弯截面系数,y1=πD13/32?L3/315.5 当正方形截面的截面高度为D2时,其抗弯截面系数,y2=D23/6?L3/384 显然,,y1>,y2 既在本试验的条件下,圆形截面的抗弯截面系数大于正方形截面的抗弯截面系数,也就是圆形截面的抗弯强度大于正方形截面的抗弯强度。
关于三角形截面的抗弯截面系数的公式计算,一般工程力5学书籍中很少讨论,其原因在于在相同面积下,三角形的面积矩小则抗弯强度小,且在工程实践中很少使用。
综上所述,当周长相同时,截面形状分别为圆形、正方形和三角形的构件,圆形截面构件的抗弯强度最大。
三点.四点抗弯强度.模量计算公式(二)三点.四点抗弯强度.模量计算公式板材 I=a*h /12棒材 I=d *3.1416/64弹性比率 s=Fmax/?L (Fmax-最大力,?L位移变化量)三点弯曲弹性模量C3P=L /(48*I)*s四点抗弯弹性模量C4P=L1*(3L) -4*L1 /48*I*s板材 W=a*h /6棒材 W=d *3.1416/326三点弯曲强度,已知力值F(机器测得)S3P=F*L/4W四点弯曲强度,已知力值FS4P=F*L1/2Wa-宽度,h-厚度,d-直径,L-跨距,s弹性比率,力值F(机器测得),L1-力臂,C3P-三点弯曲弹性模量,c4p-四点抗弯弹性模量,S3P-三点弯曲强度,S4P-四点弯曲强度轴心抗压强度计算公(三)混凝土立方体抗压强度换算轴心抗压强度计算公式混凝土轴心抗压强度Fck可以更好地反映混凝土的实际抗压能力,因此一般用混凝土轴心抗压强度来作为抗压强度标准值,而不是立方体抗压Fcu.k……Fck=0.88* a1* a2* Fcu.k当混凝土强度等级小于等于C50时,a1=0.76 a2=0.1所已混凝土轴心抗压强度标准值=0.76*0.88*混凝土立方体抗压强度标准值。
混凝土强度等级由立方体抗压强度标准值确定,立方体抗压强度标准值是混凝土各种力学指标的基本代表值。
7棱柱强度(轴心抗压强度)与立方强度之比值αc1 对普通混凝土为 0.76 ,对高强混凝土则大于 0.76 。
规范对 C50 及以下取αc1,0.76 ,对 C80 取αc1,0.82 ,中间按线性规律变化。
规范对 C40 以上混凝土考虑脆性折减系数αc2,对 C40 取αc2,1.0 ,对C80 取αc1 ,0.87 ,中间按线性规律变化。
考虑到结构中混凝土强度与试件混凝土强度之间的差异,根据以往的经验,并结合试验数据分析,以及参考其他国家的有关规定,对试件混凝土强度修正系数取为 0.88 。
规范的轴心抗压强度标准值与设计值分别按下式计算:fck=0.88αc1αc2fcu,kfc=fck/γc=fck/1.4以上详见《混凝土结构设计规范》GB50010-2002 条文说明工字钢抗弯强度计算(四)工字钢抗弯强度计算钢铁知识/jimmy8一、梁的静力计算概况1、单跨梁形式: 简支梁2、荷载受力形式: 简支梁中间受集中载荷3、计算模型基本参数:长 L =6 M4、集中力:标准值Pk=Pg+Pq =40+40=80 KN设计值Pd=Pg*γG+Pq*γQ =40*1.2+40*1.4=104 KN二、选择受荷截面1、截面类型: 工字钢:I40c2、截面特性: Ix= 23850cm4 Wx= 1190cm3 Sx=711.2cm3G= 80.1kg/m翼缘厚度 tf= 16.5mm 腹板厚度 tw= 14.5mm三、相关参数1、材质:Q2352、x 轴塑性发展系数γx :1.053、梁的挠度控制 ,v ,:L/250四、内力计算结果1、支座反力 RA = RB =52 KN2、支座反力 RB = Pd / 2 =52 KN3、最大弯矩 Mmax = Pd * L / 4 =156 KN.M五、强度及刚度验算结果91、弯曲正应力ζmax = Mmax / (γx * Wx),124.85 N/mm22、A 处剪应力ηA = RA * Sx / (Ix * tw),10.69 N/mm支梁2、荷载受力形式: 简支梁中间受集中载荷3、计算模型基本参数:长 L =6 M4、集中力:标准值Pk=Pg+Pq =40+40=80 KN设计值Pd=Pg*γG+Pq*γQ =40*1.2+40*1.4=104 KN二、选择受荷截面1、截面类型: 工字钢:I40c2、截面特性: Ix= 23850cm4 Wx= 1190cm3 Sx=711.2cm3G= 80.1kg/m翼缘厚度 tf= 16.5mm 腹板厚度 tw= 14.5mm三、相关参数1、材质:Q2352、x轴塑性发展系数γx:1.053、梁的挠度控制 ,v,:L/250四、内力计算结果1、支座反力 RA = RB =52 KN2、支座反力 RB = Pd / 2 =52 KN3、最大弯矩 Mmax = Pd * L / 4 =156 KN.M10五、强度及刚度验算结果1、弯曲正应力ζmax = Mmax / (γx * Wx),124.85 N/mm 钢铁知识/jimmy一、梁的静力计算概况1、单跨梁形式: 简支梁2、荷载受力形式: 简支梁中间受集中载荷3、计算模型基本参数:长 L =6 M4、集中力:标准值Pk=Pg+Pq =40+40=80 KN设计值Pd=Pg*γG+Pq*γQ =40*1.2+40*1.4=104 KN二、选择受荷截面1、截面类型: 工字钢:I40c2、截面特性: Ix= 23850cm4 Wx= 1190cm3 Sx=711.2cm3G= 80.1kg/m翼缘厚度 tf= 16.5mm 腹板厚度 tw= 14.5mm三、相关参数1、材质:Q2352、x轴塑性发展系数γx:1.053、梁的挠度控制 ,v,:L/250四、内力计算结果1、支座反力 RA = RB =52 KN112、支座反力 RB = Pd / 2 =52 KN3、最大弯矩 Mmax = Pd * L / 4 =156 KN.M五、强度及刚度验算结果1 124.85 N/mm2支撑梁的抗弯强度计算(七)简支梁抗弯强度计算问题:我要做一台简单的油压机。
跨度1200mm。
压力100吨,现打算用两根32a的工字钢并排做顶梁(即横梁)。
油缸装在两根工字钢中间。
请各位大师傅帮忙计算,抗弯强度够不够,如果不够,是否可以在上下贴钢板加强。
计算一:把双工字钢横梁看作是在中间承受集中载荷的简支梁。
每半边梁承受载荷P=100 t /2=50 t 。
中间截面上弯矩为Mmaxm=PL/4=50000 kg *120 cm /4=1500000 kg•cm 。
32A 工字钢抗弯截面系数W=692cm 。
最大应力:ζmax=Mmax/W=1500000kg•cm/692cm =2167.6312kg/cm =212.51MPa 。
普通碳素钢Q235的屈服点为240 MPa 。
安全系数仅为 240/212.51=1.13 。
实际梁并非简支,结构装配也还须钻孔等,因而抗弯强度近于临界,应适当加强。
