压杆的临界应力
材料力学10压杆稳定_1欧拉公式
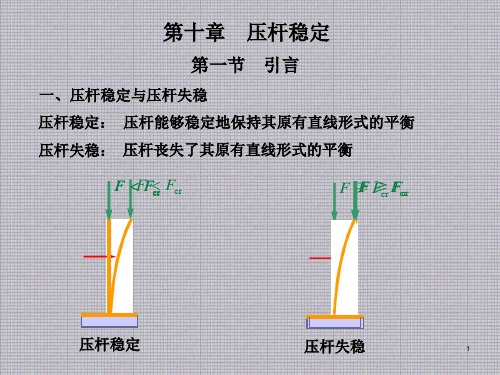
◆ 本例中,三杆截面面积基本相等,但由于其形状不同, Imin 不
同,致使临界力相差很大。最合理的截面形状为圆环形。
14
[例3] 图示各杆均为圆形截面细长压杆。已知各杆的材料及直径相 等。问哪个杆先失稳? 解:由于各杆的材料及 截面均相同,故只需比
1.3 a F F F
较其相当长度 l 即可
a
杆A: 2 l 2a
F
F
2 1
0.7
压杆两端固定可轴向移动:
0.5
6
上述弹性压杆临界力的计算公式称为欧拉公式
Fc r
π 2 EI
l
2
说明: 1)欧拉公式的适用范围:线弹性( ≤ p)
2)在压杆沿各个方向约束性质相同的情况下(即各个方向上 的 相等),I 应取最小值 3) l 称为压杆的相当长度
2
2000年10月25日上午10 时,南 京电视台演播中心由于脚手架 失稳使屋顶模板倒塌,导致死 6 人,伤 34 人。
3
2010年1月3日,通往昆明新机场的一座在建桥梁施工时因 支撑结构中的压杆失稳而坍塌,共导致 40 余人死伤。
4
二、压杆的临界力 使压杆由稳定向失稳转化的轴向压力的界限值称为压杆的临界力, 记作 Fcr 。即当 F < Fcr : 压杆稳定 F ≥ Fcr : 压杆失稳 亦可将压杆的临界力 Fcr 理解为使压杆失稳的最小轴向压力
hb3 1 Iy 90 403 48 108 m 4 12 12
根据欧拉公式,此压杆的临界力
Fcr
π 2 EI y l
2
23.8 kN
11
[例2] 一端固定,一端自由的中心细长压杆。已知杆长 l = 1m , 材 料的弹性模量 E = 200 GPa。当分别采用图示三种截面时,试计算 其临界力。
压杆的临界应力

a
1和b
是与材料有关的常数,可从有关的手册中查到。
1
2、scr=sS时,不存在失稳问题,应考虑强度问题强度破
坏,采用强度公式:
scr s s
三、临界应力总图
例1ቤተ መጻሕፍቲ ባይዱ三根材料、长度均相同、两端均为球铰支座的细 长杆结构,各自的截面形状如图,求三根杆的临界应力 之比以及临界力之比。
解:
s cr a :s cr b :s cr c
②柔度(细长比): l L
i
2.欧拉公式应用范围:
①线弹性状态下的大柔度杆:slj≤sp,即
p 2E l2
≤s
p
说明: 在推导欧拉公式时,使用了挠曲线的近似微分方程,
在推导该方程时, 应用了胡克定律。因此,欧拉公式也 只有在满足胡克定律时才能适用。
∴
l≥
p 2E sp
lp
3.注意 对于A3钢,E=200GPa,sp=200MPa:
A
E BC
[FNC ] 245kN
F2
[Nc ] 1.36
180kN
a
a
F D a
10-5 提高压杆稳定性的措施
一、从材料方面考虑 1.细长压杆:提高弹性模量E
2.中粗压杆和粗短压杆:提高屈服强度ss
二、从柔度方面考虑 1.采用合理的截面形状: (1)各方向约束相同时:
1)各方向惯性矩I相等—采用正方形、圆形截面; 2)增大惯性矩I—采用空心截面; (2)压杆两方向约束不同时:使两方向柔度接近相等, 可采用两个主惯性矩不同的截面,如矩形、工字形等。
p2E
l
2 1
p2E : l22
p2E
:
l
4PB应力计算公式

4PB应力计算公式
临界应力的计算公式就是欧拉公式:r+ v- e= 2。
具体情况介绍:
1、压杆处于临界平衡状态时(fp=fpcr ),其横截面上的正应力称为临界应力。
材料在力的作用下将发生变形。
通常把满足虎克定律规定的区域称弹性变形区。
把不满足虎克定律和过程不可逆的区域称塑性变形区。
由弹性变形区进入塑性变形区称之为屈服。
其转折点称为屈服点。
该点处的应力称为屈服应力或临界应力。
2、确定压杆的临界力是计算稳定问题的关键,临界力既不是外力,也不是内力。
它是压杆在一定条件下所具有的反映它承载能力的一个标志。
不同的压杆具有不同的临界力,它的大小与压杆的长度、截的形状和尺寸、两端的支承情况以及材料的性质有关。
细长杆(λ≥λ1)的临界力计算式——欧拉公式
长度系数μ:两端固定μ=0.5
一端固定,另一端铰支:μ=0.7
两铰支:μ=1
一端固定,另一端自由:μ=2
3、临界力计算的一般步骤:
①确定长度系数μ。
若压杆两端的支承情况在四周相同,则μ值相同。
若压杆的支承在两个形心主惯性平面内的约束条件不同,则应分别选用相应的长度系数μ(μx或μy)的值。
②计算柔度l。
根据压杆的实际尺寸,及两端的约束情况,分别计算出在两个形心主惯性平面内的柔度,从而得到lmax。
③确定临界力的计算式。
根据最大的柔度λmax,确定压杆的类型及临界力的计算公式。
细长压杆的临界力公式—欧拉公式.

细长压杆的临界⼒公式—欧拉公式.10.2 细长压杆的临界⼒公式—欧拉公式⼀、两端铰⽀压杆的临界⼒图9—4为两端受压杆件,⼈们经过对不同长度(l ),不同截⾯(I ),不同材料(E )的压杆在内⼒不超过材料的⽐例极限时发⽣失稳的临界⼒P cr 研究得知: 22lPcr EI=π(9—1)式中:π—圆周率;E —材料的弹性摸量;l —杆件长度;I —杆件截⾯对⾏⼼主轴的惯性矩。
图9-4当杆端在各⽅向的约束情况相同时,压杆总是在抗弯刚度最⼩的纵向平⾯内失稳,所以(9-1)式中的惯性矩应取截⾯最⼩的形⼼惯性矩I min 。
瑞⼠科学家欧拉(L.Eular )早在18世纪,就对理想细长压杆在弹性范围的稳定性进⾏了研究。
从理论上证明了上述(9-1)式是正确的,因此(9-1)式⼜称为计算临界⼒的欧拉公式。
⼆、杆端⽀承对临界⼒的影响图9-5(a)(b)(c)(d)⼯程上常见的杆端⽀承形式主要有四种,如图9-5所⽰,欧拉进⼀步研究得出各种⽀承情况下的临界⼒。
如⼀端固定,⼀端⾃由的杆件,这种⽀承形式下压杆的临界⼒,只要在(9-1)式中以2l 代替l 即可。
()222l P cr EI=π(a )同理,可得两端固定⽀承的临界⼒为()225.0l P cr EI=π(b )⼀端固定,⼀端铰⽀压杆的临界⼒为 ()227.0l P cr EIπ(c )式(a ),(b),(c)和(9-1)可归纳为统⼀的表达式()22l P cr µπEI = (9-2)式中l µ称为压杆计算长度,µ称为长度系数,⼏种不同杆端⽀承的各µ值列于表9—1中,µ反映了杆端⽀承情况对临界⼒的影响。
表9-1 各种杆端⽀承压杆的长度系数图例9.1 图⽰轴⼼受压杆,截⾯⾯积为10mm ?20mm 。
已知其为细长杆,弹性模量E=200GPa ,试计算其临界⼒。
2m20图9-6单位:mm解:由杆件的约束形式可知:7.0=µ4333min1067.112102012mm hb I I y ?=?===临界⼒:223320010 1.67101076.2 1.076()(0.7 2.510)cr EI P N kN l ππµ====?? 三、临界应⼒和柔度在临界⼒的作⽤下,细长压杆横截⾯上的平均应⼒叫做压杆的临界应⼒,⽤cr σ表⽰。
工程力学28-压杆的临界应力

——重点
(1) P cr S时: cr 临界a应力总b图
cr
a b
s
a s b
s
s p称为中柔度杆,用经验公式求其临界应力。
(2) S 时: cr S
S 称为小柔度杆,其临界应力为屈服极限。
目录
4
总结:
•压杆柔度
l μ的四种取值情况
i
i
I A
•临界柔度
P
2E P
9-
与长度、截面性质、约束条件有关
目录
4
2
2.欧拉公式的适用范围 着眼点——临界应力在线弹性内(小于比例极限)
cr
2E 2
P
2E P
P
P 时称为大柔度杆(或长细杆),用欧拉公式求临界力;
P 时称为中、小柔度杆,不能用欧拉公式求临界力。
3 目录
3.经验公式、临界应力总图
直线型经验公式
32. 压杆的临界应力
1.临界应力和柔度
(1)临界应力:压杆处于临界状态时横截面上的平均应力
Fcr cr A (2)细长压杆的临界应力:
cr
Fcr A
2EI (E 2
即: cr
(3)柔度:
l i
2E 2
i I — 惯性半径
A
— —杆的柔度(或长细比)
P 比例极限
•临界应力
s
a s b
s 屈服极限
P
(大柔度杆) cr
2E 2
欧拉公式
S P (中柔度杆)cr a b直线公式
s (小柔度杆) cr s 强度问题
材料力学压杆稳定第3节 欧拉公式及经验公式

S
P
2、抛物线型经验公式
在工程实际中,对于中、小柔度压杆的临界应力计 算,也有建议采用抛物线型经验公式的,此公式为
cr a1 b12
式中 a1 、b1 与是与材料
有关的常数,其单位是
MPa。与前式中的 a 、
b 值是不同。
根据欧拉公式与抛物线 经验公式,得低合金结
构钢等压杆的 cr总图。
定计算中的一个重要综合参数。
• 如果压杆在不同的纵向平面内具有不同的柔度值, 由于压杆失稳首先发生在柔度最大的纵向平面内。 因此,压杆的临界应力应按柔度的最大值计算。
二、欧拉公式的适用范围
欧拉公式是在材料符合胡克定律条件下,即在线弹
性范围内,推导出来的。因此只有当cr p 时欧拉
公式才适用,即
临界应力形式 的欧拉公式
临界应力形式 的欧拉公式
cr
2E 2
式中柔度 是一个无量纲的量,它综合反映了压杆
的长度 l 、杆端的约束以及截面尺寸对临界应力 cr
的影响。对于一定材料的压杆,其临界应力仅与柔
度 有关, 值越大,则压杆越细长,临界应力 cr 值也越小,压杆越容易失稳。所以柔度 是压杆稳
cr
2E 2
p
或
P
E
P
大柔度杆或细长杆:对于结构钢的 p 2108 Pa、 E 21011Pa,则由上式可算得欧拉公式的适用
范围为 100;同理对于铸铁,欧拉公式的适用 范围为 80 。这类杆称为大柔度杆或细长杆。
三、经验公式
若压杆的柔度 P,则这种压杆的临界力不能再
cr a1 b12
cr
2E 2
压杆临界力的计算公式

压杆临界力的计算公式1.欧拉公式:欧拉公式是压杆稳定性分析中最常用的一种方法。
根据欧拉公式,压杆的临界力可以通过以下公式计算:Pcr = ((π^2)EI) / ((KL)^2)其中,Pcr表示压杆的临界力,E表示材料的弹性模量,I表示压杆的截面面积惯性矩,K表示杆的端部支座的系数,L表示杆的长度。
欧拉公式适用于较细长的压杆,在其它条件相同的情况下,杆的截面越大,临界力就越大;杆的长度越长,临界力就越小。
同时,欧拉公式适用于直线变形的杆,不能用于弯曲变形。
2.莱昂哈德公式:莱昂哈德公式是考虑了杆的端部支座的影响,在欧拉公式的基础上进行修正的公式。
该公式计算压杆的临界力如下:Pcr = ((KLEI) / (r + ((2L)/π)) ^ 2)其中,Pcr表示压杆的临界力,E表示材料的弹性模量,I表示压杆的截面面积惯性矩,K表示杆的端部支座的系数,L表示杆的长度,r表示杆的端部支座的半径。
3. Adomian分解法:Adomian分解法是一种近似求解非线性微分方程的方法,在压杆临界力的计算中也有应用。
该方法通过将非线性方程分解为无穷级数的形式,然后将其逐级近似求解。
Adomian分解法的具体步骤如下:-(1)将压杆的平衡方程进行分解:Mx''(x)+f(x)=0,其中,M表示压杆的弯矩,f(x)表示外力。
-(2)将平衡方程表示为无穷级数的形式:x''(x)=∑An(x)。
-(3)通过逐级近似求解无穷级数,得到压杆临界力。
Adomian分解法的优点是可以处理非线性问题,但是在具体应用中需要取不同级数的项进行求解,并选择适当的近似方法。
4.极限平衡法:极限平衡法是一种通过平衡条件来确定压杆临界力的方法,它适用于复杂的压杆分析问题。
该方法的基本思想是,在压杆失稳之前,杆的初始形状必须满足平衡条件。
具体步骤如下:-(1)假设杆的初始形状(如弯曲、扭转等)。
-(2)根据平衡条件计算外力和内力。
怎样推导压杆的临界力和临界应力公式

怎样推导压杆的临界力和临界应力公式压杆(也称为压杆杆件或柱件)是一种承受压力的结构元素,常见于建筑、机械以及其他工程领域。
为了确定压杆在受力时的安全性,需要推导出压杆的临界力和临界应力公式。
首先,需要理解压杆在受力时的基本概念。
假设有一根长度为L、截面积为A的无限细长压杆,其两端受到等大反向的压力P。
压杆在受到压力时会发生弯曲,压杆的形状会发生改变。
当压力达到一定临界值时,压杆将完全失去稳定,从而发生屈曲(即压杆产生弯曲形变)。
临界力和临界应力是指当压力达到一定临界值时,压杆发生屈曲的压力和应力。
推导过程如下:1. 经典欧拉公式(Euler公式)欧拉公式是分析以柱轴为边界的理想无限长压杆屈曲的基本公式。
该公式基于以下假设:-压杆是均质、各向同性的杆件;-杆件的材料性质可用弹性线性理论描述;-压杆长度远大于其最小截面尺寸,即L>>d(d为压杆的最小截面尺寸)。
欧拉公式表达式如下:Pcr = (π²EI) / L²其中,Pcr为压杆的临界力,E为杨氏模量,I为压杆截面的惯性矩,L为压杆长度。
2. 完整欧拉公式(Timoshenko-Bazant公式)欧拉公式只适用于边界条件为完全铰接(即不受弯曲力矩)的压杆。
然而,在实际情况中,压杆的边界条件一般为受到端部弯曲力矩的约束。
在这种情况下,完整欧拉公式(Timoshenko-Bazant公式)需要被使用。
完整欧拉公式修正了边界条件的影响,并考虑到了剪切变形和截面的非对称性。
完整欧拉公式的表达式如下:Pcr = (π²EI) / [L²(1 + αL / r)^²]其中,α为修正系数,考虑了压杆的边界条件,r为截面回转半径。
3.临界应力临界应力的定义是在压杆屈曲时,杆件中最大的应力值。
根据杆件截面受到均匀分布的压力P,应力σ可以表示为:σ=P/A将欧拉公式(或完整欧拉公式)中的临界力Pcr代入上述表达式可得到临界应力的表达式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 C 30o
F 500
BD
l 11730 108
i
16AA3钢,λp=来自00,λ>λp,用欧拉公式
Fcr
2E 2
A
121 .54
10 3
N
121 .54kN
三、根据稳定条件求许可荷载
由:
Fcr FN max
[nst ]
FN max
Fcr [nst ]
121 .54 3
40.5KN
a(MPa) 304 461 578 9807 332.2 373 28.7
b(MPa) 1.12 2.568 3.744 5.296 1.454 2.15 0.19
②抛物线公式: s cr a1 b12
a
1和b
是与材料有关的常数,可从有关的手册中查到。
1
2、scr=sS时,不存在失稳问题,应考虑强度问题强度破
目录
压杆稳定 \提高压杆稳定性的措施
2.减少压杆支承长度:
(1)直接减少压杆长度;
(2)增加中间支承;
A
BC
2、求杆许可荷载:
a
a
(1)以BE杆为标准:
[FNB
]
[s
]A
160106
3.14 4
0.052
314kN
F D a
F1
FNB
0.283
1110kN
2)按压杆FC计算: [FNC ] [s w ]A
l
i
1 2 0.1
80
4
0.26
[s w ] 0.26[s y ]
A
E BC
[FNC ] 245kN
2E 2
小柔度杆
中柔度杆
O
s
a ss
b
p
大柔度杆
2E sp
l
i
例1:三根材料、长度均相同、两端均为球铰支座的细 长杆结构,各自的截面形状如图,求三根杆的临界应力 之比以及临界力之比。
解:
s cr a :s cr b :s cr c
2E
2 1
2E : 22
2E
:
2 3
i12 :i2 2 :i32
从而求得:
F
3 8
FN max
3 8
40.5
15.2KN
例4:图示结构,CF为铸铁圆杆,直径
d1=10cm,[s]=120MPa , E=120GPa。 BE为A3钢圆杆, 直径d2=5cm,
[s]=160MPa, E=200GPa, 如横梁视为刚
性,a=2m,求许可荷载F。
A
解:1、结构为一次超静定求杆内力
①直线公式:
s cr a b
1)∵scr<ss,∴ s s a b
,得到:0
a
ss
b
2) p≥≥0—中粗杆(中柔度杆);
3)对于A3钢:
0
a ss
b
304 240 60 1.12
4)对于式中的系数a,b,下表给出了一些常用材料的数值。
表 10-2 直线公式的系数 a 和 b
材料 A3 钢 优质碳钢 硅钢 铬钼钢 铸铁 强铝 松木
I1 : I2 : I3 A1 A2 A3
d4
64
d4
: 64
d 4
2
:
64
d2
4
d 2
2
4
d2 d2
d2
2
4
44
4
1:1:5
Fcra:Fcrb:Fcrc s cra A1:s crb A2:s crc A3
1:2:20
例2:图示圆截面压杆d=40mm,σs=235MPa。求可以用经验 公式σcr=304-1.12λ (MPa)计算临界应力时的最小杆长。
坏,采用强度公式:
scr s s
三、临界应力总图
1. 细长杆 ( p ), 用欧拉公式
2. 中长杆 ( s p ), 用经验公式 3. 粗短杆 ( s ), 用强度条件
s cr
2E
s
cr
2
s cr
a
b
s s
cr
s
s s s cr s s
sp
s cr a b
s cr
F
解: s
a ss
b
304 235 61.6
1.12
由
l
i
s
得:
l
0.04
l
s
i
61.6
4 0.7
0.88 m
目录
§10-4 压杆的稳定性计算
一、稳定性条件:
Fm a x
Fcr [nst ]
式中 Fmax
Fcr
[nst ]
------压杆所受最大工作载荷 ------压杆的临界压力 ------压杆的规定稳定安全系数
F2
[Nc ] 1.36
180kN
a
a
F D a
10-5 提高压杆稳定性的措施
一、从材料方面考虑 1.细长压杆:提高弹性模量E
2.中粗压杆和粗短压杆:提高屈服强度ss
二、从柔度方面考虑 1.采用合理的截面形状:
(1)各方向约束相同时: 1)各方向惯性矩I相等—采用正方形、圆形截面; 2)增大惯性矩I—采用空心截面; (2)压杆两方向约束不同时:使两方向柔度接近相等, 可采用两个主惯性矩不同的截面,如矩形、工字形等。
稳定性条件也可以表示成:
nst
Fcr Fm ax
[nst ]
式中 nst 为压杆实际的工作稳定安全系数。
例3 :托架,AB杆是圆管,外径D=50mm,内径d=40mm,两端为
球铰,材料为A3钢,E=206GPa,p=100。若规定[nst]=3,试确 定许可荷载F。
解:一、分析受力 取CBD横梁研究
MA 0:
2FNB 4FNC 6F 0
E F
D BC
a
a
a
F
FNB
F
变形条件:BE
1 2
BC
A BC
D
FNc
由:
N 代入 EA
FNB 2
1
FNC 2
200109 3.14 0.052 2 120109 3.14 0.12
4
4
FNC 4.8FNB
E
代入第一式后求解得:
FNB 0.283 F , FNC 1.36 F
2.欧拉公式应用范围:
①线弹性状态下的大柔度杆:slj≤sp,即
2E 2
≤s
p
说明: 在推导欧拉公式时,使用了挠曲线的近似微分方程,
在推导该方程时, 应用了胡克定律。因此,欧拉公式也 只有在满足胡克定律时才能适用。
∴
≥
2E sp
p
3.注意 对于A3钢,E=200GPa,sp=200MPa:
p
2 200109
200106 100
用柔度表示的临界压力:
Fcr
2E 2
•
A
≥p——细长杆(大柔度杆),
当压杆的长细比λ<λp时,欧拉公式已不适用。在工程
上,一般采用经验公式。在我国的设计手册和规范中给
出的是直线公式和抛物线公式。
二、中柔度杆临界应力的经验公式
1.ss>scr>sp时采用经验公式:
mc 0 NAB sin300 1500Q2000 0
1500 C 30o
F 500
BD
F
3 8
N AB
二、计算并求临界荷载
A C
F
B
NAB
i
I A
(D4 d 4)
64
(D2 d 2)
D2 d 2 16mm 4
4
1500
1500 lAB cos300 1730mm
