光电子学与光子学的原理及应用S.O.Kasa课后答案详解
SM Ch1
The beam width at a distance of 10 m is 2w = 2wo[1 + (z/zo)2]1/2 = (0.810-3 m){1 + [(10 m)/(0.79 m)]2}1/2 = 0.01016 m or 10.16 mm. 1.5 Gaussian beam in a cavity with spherical mirrors Consider an optical cavity formed by two aligned spherical mirrors facing each other as shown in Figure 1.54. Such an optical cavity is called a spherical mirror resonator, and is most commonly used in gas lasers. Sometimes, one of the reflectors is a plane mirror. The two spherical mirrors and the space between them form an optical resonator because only certain light waves with certain frequencies can exist in this optical cavity. The radiation inside a spherical mirror cavity is a Gaussian beam. The actual or particular Gaussian beam that fits into the cavity is that beam whose wavefronts at the mirrors match the curvature of the mirrors. Consider the symmetric resonator shown in Figure 1.54 in which the mirrors have the same radius of curvature R. When a wave starts at A, its wavefront is the same as the curvature of A. In the middle of the cavity it has the minimum width and at B the wave again has the same curvature as B. Such a wave in the cavity can replicate itself (and hence exist in the cavity) as it travels between the mirrors provided that it has right beam characteristics, that is the right curvature at the mirrors. The radius of curvature R of a Gaussian beam wavefront at a distance z along its axis is given by R(z) = z[1 + (zo/z)2] ; zo = wo2/ is the Rayleigh range Consider a confocal symmetric optical cavity in which the mirrors are separated by L = R. (a) Show that the cavity length L is 2zo, that is, it is the same as the Rayleigh range, which is the reason the latter is called the confocal length. (b) Show that the waist of the beam 2wo is fully determined only by the radius of curvature R of the mirrors, and given by 2wo = (2R/)1/2 (c) If the cavity length L = R = 50 cm, and = 633 nm, what is the waist of the beam at the center and also at the mirrors?
光电子技术课后答案
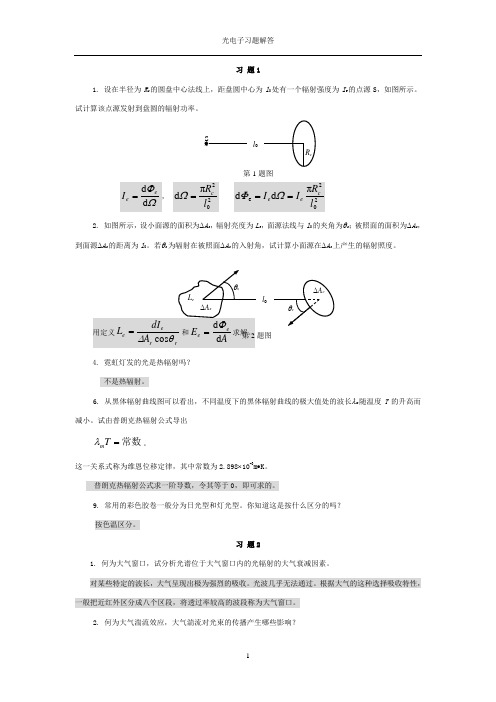
习 题11. 设在半径为R c 的圆盘中心法线上，距盘圆中心为l 0处有一个辐射强度为I e 的点源S ，如图所示。
试计算该点源发射到盘圆的辐射功率。
ΩΦd d e e I =， 202πd l R c =Ω 202e πd d l R I I c e e ==ΩΦ2. 如图所示，设小面源的面积为∆A s ，辐射亮度为L e ，面源法线与l 0的夹角为θs ；被照面的面积为∆A c ，到面源∆A s 的距离为l 0。
若θc 为辐射在被照面∆A c 的入射角，试计算小面源在∆A c 上产生的辐射照度。
用定义r r ee A dI L θ∆cos =和A E e e d d Φ=求解。
4. 霓虹灯发的光是热辐射吗？不是热辐射。
6. 从黑体辐射曲线图可以看出，不同温度下的黑体辐射曲线的极大值处的波长λm 随温度T 的升高而减小。
试由普朗克热辐射公式导出常数=T m λ。
这一关系式称为维恩位移定律，其中常数为2.898⨯10-3m ∙K 。
普朗克热辐射公式求一阶导数，令其等于0，即可求的。
9. 常用的彩色胶卷一般分为日光型和灯光型。
你知道这是按什么区分的吗？按色温区分。
习 题21. 何为大气窗口，试分析光谱位于大气窗口内的光辐射的大气衰减因素。
对某些特定的波长，大气呈现出极为强烈的吸收。
光波几乎无法通过。
根据大气的这种选择吸收特性，一般把近红外区分成八个区段，将透过率较高的波段称为大气窗口。
2. 何为大气湍流效应，大气湍流对光束的传播产生哪些影响？ l 0 SR c 第1题图L e∆A s ∆A c l 0 θs θc第2题图是一种无规则的漩涡流动，流体质点的运动轨迹十分复杂，既有横向运动，又有纵向运动，空间每一点的运动速度围绕某一平均值随机起伏。
这种湍流状态将使激光辐射在传播过程中随机地改变其光波参量，使光束质量受到严重影响，出现所谓光束截面内的强度闪烁、光束的弯曲和漂移（亦称方向抖动）、光束弥散畸变以及空间相干性退化等现象，统称为大气湍流效应。
光电子学与光子学讲义-作业答案(第1、2章)13版.doc
第一章1.10 Refractive index(a) Consider light of free-space wavelength 1300 nm traveling in pure silica medium. Calculate the phase velocity and group velocity of light in this medium. Is the group velocity ever greater than the phase velocity?(b) What is the Brewster angle(the polarization angle qp) and the critical angle(qc) for total internal reflection when the light wave traveling in this silica medium is incident on a silica/air interface. What happens at the polarization angle?(c) What is the reflection coefficient and reflectance at normal incidence when the light beam traveling in the silica medium is incident on a silica/air interface?(d) What is the reflection coefficient and reflectance at normal incidence when a light beam traveling in air is incident on an air/silica interface? How do these compare with part (c) and what is your conclusion?1.18 Reflection at glass-glass and air-glass interfaceA ray of light that is traveling in a glass medium of refractive index n1=1.460 becomes incident on a less dense glassmedium of refractive index n2=1.430. Suppose that the free space wavelength of the light ray is 850 nm.(a) What should the minimum incidence angle for TIR be?(b) What is the phase change in the reflected wave when the angle of incidence qi =85 ° and when qi =90° ?(c) What is the penetration depth of the evanescent wave into medium 2 when qi =85 ° and when qi =90° ?(d) What is the reflection coefficient and reflection at normal incidence (qi =0 ° )when thelight beam traveling in the glass medium (n=1.460) is incident on a glass-air interface?(e) What is the reflection coefficient and reflectance at normal incidence when a light beam traveling in air is incident on an air/-glass interface (n=1.460)? How do these compare with part (d) and what is your conclusion?1.20 TIR and polarization at water-air interface(1) Given that the refractive index of water is about 1.33, what is the polarization angle for light traveling in air and reflected from the surface of the water?(2) consider a diver in sea pointing a flashlight towards the surface of the water. What is the critical angle for the light beam to be reflected from the water surface?1.22 phase changes on TIRConsider a lightwave of wavelength 870nm traveling in a semiconductor medium (GaAs) of refractive index 3.6. It is incident on a different semiconductor medium (AIGaAs) of°. Will this result in total internal refractive index 3.4, and the angle of incidence is 80reflection? Calculate the phase change in the parallel and perpendicular components of the reflected electric field?1.25 Goos-Haenchen phase shiftAray of light that is traveling in a glass medium(1) of refractive index n1 =1.460 becomes incident on a less dense glass medium(2) of refractive index n2=1.430. Suppose that the free space wavelength of the light ray is 850nm.the angle of incidence(9=85 . Estimate the lateral Goos-Haenchen shift in the reflected wave for the perpendicular field component. Recalculate the Goos-Haenchen shift in the secondmedium has n2=1 (air). What is your conclusion?Assume that the virtual reflection occurs from a virtual plane in medium B at a distance d that is roughly the same as the penetration depth.Note that d actually depends on the polarization ,the direction of the field,but we will ignore this dependence.第二章作业习题：2.7Dielectric slab waveguide Consider a dielectric slab waveguide that has a thin GaAs layer of thickness 0.25 /w between two AIGaAs layers. The refractive index of GaAs is3.6 and that of the AIGaAs layers is 3.40. What is the cut-off wavelength beyond which only a single mode can propagate in the waveguide, assuming that the refractive index does not vary greatly with thewavelength? If a radiation of wavelength 860 nm (corresponding to bandgap radiation) is propagating in the GaAs layer, what is the penetration of the evanescent wave into the AIGaAs layer? What is the mode field width (MFW) of this radiation? Point out the effect of change of radiation wavelength (为on the MFW.2.9 Dielectric slab waveguide Consider a planar dielectric waveguide with a core thickness 10/m,ni=1.4446, n2=1.4440. Calculate the V -number, the mode angle 劣for m=0 (use a graphical solution, if necessary), penetration depth, and mode field distance (MFW=2 c(^2 9, for light wavelengths of 1.0 /xn and 5 /jn. What is your conclusion? Compare your MFW calculationwith 2»o =2a (V +1 )/V .The model angle 3is given as &=88.85?for ^=1 /m and ^=88.72 ?for ^=1.5 仰for the fundamental mode m=0.2.10 A multimode fibe r Consider a multimode fiber with a core diameter of 60 /m, core refractive index of 1.47, and a cladding refractive index of 1.45 both at 870 nm. Consider operating this fiber at ^=870nm.(e) Calculate the numerical aperture.(f) Find out the normalized core-cladding index difference.(g) Calculate the V-number for the fiber and estimate the number of guided modes.(h) Calculate the wavelength beyond which the fiber becomes single-mode.(i) Calculate the modal dispersion △ T and hence the bit rate x distance product.2.12 Single mode fiber Consider a fiber with a S1O2-13.5% GeOz core of diameter of 6 Wi and refractive index of 1.47 and a cladding refractive index of 1.46 both refractive indices at 1300 nm where the fiber is to be operated using a laser source with a half maximum width (FWHM) of 2 nm.. (j) Calculate the V -number for the fiver.(k) what is the maximum allowed diameter of the core that maintains oprations in single-mode?(l) Calculate the wavelength below which the fiber becomes multimode.(m) C alculate the numerical aperture.(n) Calculate the maximum acceptance angle.(o) Obtain the material dispersion and wavelength dispersion and hence estimate the bit rate x distance product ( B x L) of the fiber.。
光电子课后习题答案讲解
第一章1. 光电子器件按功能分为哪几类？每类大致包括哪些器件？光电子器件按功能分为光源器件、光传输器件、光控制器件、光探测器件、光存储器件、光显示器件。
光源器件分为相干光源和非相干光源。
相干光源主要包括激光器和非线性光学器件等。
非相干光源包括照明光源、显示光源和信息处理用光源等。
光传输器件分为光学元件(如棱镜、透镜、光栅、分束器等等)、光波导和光纤等。
光控制器件包括调制器、偏转器、光开关、光双稳器件、光路由器等。
光探测器件分为光电导型探测器、光伏型探测器、热伏型探测器等。
光存储器件分为光盘(包括CD、VCD、DVD、LD等)、光驱、光盘塔等。
光显示器件包括CRT、液晶显示器、等离子显示器、LED显示。
2．谈谈你对光电子技术的理解。
光电子技术主要研究物质中的电子相互作用及能量相互转换的相关技术，以光源激光化，传输波导（光纤）化，手段电子化，现代电子学中的理论模式和电子学处理方法光学化为特征，是一门新兴的综合性交叉学科。
⒌据你了解，继阴极射线管显示（CRT）之后，哪几类光电显示器件代表的技术有可能发展成为未来显示技术的主体？等离子体显示（PDP），液晶显示（LCD），场致发射显示（EL），LED显示。
第二章：光学基础知识与光场传播规律⒈ 填空题⑴ 光的基本属性是光具有波粒二象性，光粒子性的典型现象有光的吸收、发射以及光电效应等；光波动性的典型体现有光的干涉、衍射、偏振等。
⑵ 两束光相干的条件是频率相同、振动方向相同、相位差恒定；最典型的干涉装置有杨氏双缝干涉、迈克耳孙干涉仪；两束光相长干涉的条件是(0,1,2,)m m δλ==±±，δ为光程差。
⑶两列同频平面简谐波振幅分别为01E 、02E ，位相差为φ，则其干涉光强为22010201022cos E E E E φ++，两列波干涉相长的条件为2(0,1,2,)m m φπ==±±⑷波长λ的光经过孔径D 的小孔在焦距f 处的衍射爱里斑半径为1.22f D λ。
激光原理及应用(第二版)课后习题答案(全)
思考练习题4
2．He-Ne激光器辐射632.8nm光波，其方形镜对称共焦腔，腔长L＝
0.2m。腔内同时存在，，横模。若在腔内接近镜面处加小孔光阑选取
横模，试问：
(1)如只使模振荡，光阑孔径应多大？ (2)如同时使，模振荡而抑制振荡，光阑孔径应多大？ 答：(1)TEM00模在镜面处的光斑半径为 所以光阑孔径应该为0.2mm (2)TEM11模在镜面处的光斑半径为 所以光阑孔径为0.35mm
思考练习题1
1． 试计算连续功率均为1W的两光源，分别发射＝0.5000m， =3000MHz的光，每秒从上能级跃迁到下能级的粒子数各为多 少？
答：粒子数分别为：
11．静止氖原子的3S22P4谱线的中心波长为0.6328m，设氖原子分别以
0.1c,0.5c的速度向着接收器运动，问接收到的频率各为多少？ 答： 同理可求：；
答：（a）；
（b）
4.
稳定谐振腔的两块反射镜，其曲率半径分别为R1＝40cm，2＝
100cm，求腔长L的取值范围。
答：
10. 实验测得He-Ne激光器以波长＝0.6328工作时的小讯号增益系数 为G0＝310－4/d(cm-1)，d为腔内毛细管内径(cm)。以非均匀增宽 计算腔内光强I＝50W／cm2的增益系数G(设饱和光强Is＝30W／ cm2时，d＝1mm)，并问这时为保持振荡稳定，两反射镜的反射
3．一高斯光束束腰半径＝0.2mm，＝0.6328，今用一焦距f为3cm的短 焦距透镜聚焦，已知腰粗离透镜的距离为60cm，在几何光学近似下求 聚焦后光束腰粗。 答：
5．用如图（4－33）所示的倒置望远镜系统改善由对称共焦腔输出的光
光电子学与光子学的原理及应用s.o.kasa chapter4课后答案
(le3vpe1)lsarnedsuthlteinrgemfraoimninvgareioleucstrdoinffse(r2enp5t)vwaliutheisnoqfumanl atunmd mmsetchhaat nciacnalarsusilgesn.edNtoot
e all
sixth excited transitions to
spins parallel has a lower energy than that with opposite electron spins as indicated in Figure 4Q1. These
two He states can excite Ne atoms to either the 2p54s1 or 2p55s1. There is then a population inversion between these levels and the 2p53p1 and between 2p55s1 and 2p54p1 which leads to the above lasing
electron these
energy levels are allowed as photon emission requires quantum number selection rules to be obeyed.
a Table 4Q1, shows some typical commercial He-Ne laser characteristics (within 30-50%) for various wavelengths. Calculate the overall efficiencies of these lasers.
光电子学与光子学的原理及应用第二章-课后答案
光电子学与光子学的原理及应用第二章-课后答案1. 选择题1.1 题目一答案：C解析：光电效应是指物质受到光的照射后，吸收光能，将光能转化为电能的一种现象。
光电效应首先是由爱因斯坦在1905年提出的，他在描述光电效应时，引入了光子概念，假设光是由一组个别粒子组成的（即光量子），这些粒子就是后来被称为光子的电磁辐射量子。
1.2 题目二答案：A解析：光电倍增管是指通过光电效应，在光电面上光电发射物质外壳的钨丝和灯管之间加一个高达2000-3000伏的电压使其产生光电流，再对光电流进行电子倍增，最后输出检测的一种光电探测器。
光电倍增管的结构与普通的电子管相似，但是在各个电极和玻璃壳之间加入了紧密和高度真空的保护，同时在阳极和阳极网之间还添加了一个用直流电压加电的光电体。
当阳极对外加正电压使阳极电流开始增大时，就成为光电倍增管。
1.3 题目三答案：D解析：光电二极管是一种能够将光信号转化为电信号的器件。
光电二极管的基本原理是利用半导体材料的PN结在光照射下产生光电效应，使得PN结两端产生电荷，从而产生电压信号。
光电二极管的结构和普通二极管类似，主要由P型和N型的半导体材料组成，当光照射到光电二极管上时，光子能量被半导体材料所吸收，产生的热力激发电子，从而引起半导体PN结的载流子的复合和流动，产生感光电流。
光电二极管应用广泛，如光通信、光电测量、光谱分析等领域。
1.4 题目四答案：B解析：光导纤维是一种能够传输光信号的特殊纤维材料。
光导纤维的核心部分是由高折射率的材料构成，而外部由低折射率的材料构成。
当光线传输到光导纤维中时，会发生全反射现象，使得光线能够沿着光导纤维进行传输，最终到达目标地点。
光导纤维具有传输距离远、损耗小、带宽大、抗电磁干扰等优点，在通信、医疗、传感等领域得到广泛应用。
2. 填空题2.1 题目一答案：钠解析：钠具有低电离电势，激发电子的能量比较低，是光电电子极容易脱离的材料之一。
2.2 题目二答案：光电效应解析：光电效应是指物质受到光的照射后，吸收光能，将光能转化为电能的一种现象。
光电子学与光子学讲义-作业答案（第1、2章）13版.doc
光电⼦学与光⼦学讲义-作业答案（第1、2章）13版.doc 第⼀章1.10 Refractive index(a) Consider light of free-space wavelength 1300 nm traveling in pure silica medium. Calculate the phase velocity and group velocity of light in this medium. Is the group velocity ever greater than the phase velocity?(b) What is the Brewster angle(the polarization angle qp) and the critical angle(qc) for total internal reflection when the light wave traveling in this silica medium is incident on a silica/air interface. What happens at the polarization angle?(c) What is the reflection coefficient and reflectance at normal incidence when the light beam traveling in the silica medium is incident on a silica/air interface?(d) What is the reflection coefficient and reflectance at normal incidence when a light beam traveling in air is incident on an air/silica interface? How do these compare with part (c) and what is your conclusion?1.18 Reflection at glass-glass and air-glass interfaceA ray of light that is traveling in a glass medium of refractive index n1=1.460 becomes incident on a less dense glassmedium of refractive index n2=1.430. Suppose that the free space wavelength of the light ray is 850 nm.(a) What should the minimum incidence angle for TIR be?(b) What is the phase change in the reflected wave when the angle of incidence qi =85 ° and when qi =90° ?(c) What is the penetration depth of the evanescent wave into medium 2 when qi =85 ° and when qi =90° ?(d) What is the reflection coefficient and reflection at normal incidence (qi =0 ° )when thelight beam traveling in the glass medium (n=1.460) is incident on a glass-air interface?(e) What is the reflection coefficient and reflectance at normal incidence when a light beam traveling in air is incident on an air/-glass interface (n=1.460)? How do these compare with part (d) and what is your conclusion?1.20 TIR and polarization at water-air interface(1) Given that the refractive index of water is about 1.33, what is the polarization angle for light traveling in air and reflected from the surface of the water?(2) consider a diver in sea pointing a flashlight towards the surface of the water. What is the critical angle for the light beam to be reflected from the water surface?1.22 phase changes on TIRConsider a lightwave of wavelength 870nm traveling in a semiconductor medium (GaAs) of refractive index 3.6. It is incident on a different semiconductor medium (AIGaAs) of°. Will this result in total internal refractive index 3.4, and the angle of incidence is 80reflection? Calculate the phase change in the parallel and perpendicular components of the reflected electric field?1.25 Goos-Haenchen phase shiftAray of light that is traveling in a glass medium(1) of refractive index n1 =1.460 becomes incident on a less dense glass medium(2) of refractive index n2=1.430. Suppose that the free space wavelength of the light ray is 850nm.the angle of incidence(9=85 . Estimate the lateral Goos-Haenchen shift in the reflected wave for the perpendicular field component. Recalculate the Goos-Haenchen shift in the secondmedium has n2=1 (air). What is your conclusion?Assume that the virtual reflection occurs from a virtual plane in medium B at a distance d that is roughly the same as the penetration depth.Note that d actually depends on the polarization ,the direction of the field,but we will ignore this dependence.第⼆章作业习题：2.7Dielectric slab waveguide Consider a dielectric slab waveguide that has a thin GaAs layer of thickness 0.25 /w between two AIGaAs layers. The refractive index of GaAs is3.6 and that of the AIGaAs layers is 3.40. What is the cut-off wavelength beyond which only a single mode can propagate in the waveguide, assuming that the refractive index does not vary greatly with thewavelength? If a radiation of wavelength 860 nm (corresponding to bandgap radiation) is propagating in the GaAs layer, what is the penetration of the evanescent wave into the AIGaAs layer? What is the mode field width (MFW) of this radiation? Point out the effect of change of radiation wavelength (为on the MFW.2.9 Dielectric slab waveguide Consider a planar dielectric waveguide with a core thickness 10/m,ni=1.4446, n2=1.4440. Calculate the V -number, the mode angle 劣for m=0 (use a graphical solution, if necessary), penetration depth, and mode field distance (MFW=2 c(^2 9, for light wavelengths of 1.0 /xn and 5 /jn. What is your conclusion? Compare your MFW calculationwith 2?o =2a (V +1 )/V .The model angle 3is given as &=88.85?for ^=1 /m and ^=88.72 ?for ^=1.5 仰for the fundamental mode m=0.2.10 A multimode fibe r Consider a multimode fiber with a core diameter of 60 /m, core refractive index of 1.47, and a cladding refractive index of 1.45 both at 870 nm. Consider operating this fiber at ^=870nm.(e) Calculate the numerical aperture.(f) Find out the normalized core-cladding index difference.(g) Calculate the V-number for the fiber and estimate the number of guided modes.(h) Calculate the wavelength beyond which the fiber becomes single-mode.(i) Calculate the modal dispersion △ T and hence the bit rate x distance product.2.12 Single mode fiber Consider a fiber with a S1O2-13.5% GeOz core of diameter of 6 Wi and refractive index of 1.47 and a cladding refractive index of 1.46 both refractive indices at 1300 nm where the fiber is to be operated using a laser source with a half maximum width (FWHM) of 2 nm.. (j) Calculate the V -number for the fiver.(k) what is the maximum allowed diameter of the core that maintains oprations in single-mode?(l) Calculate the wavelength below which the fiber becomes multimode.(m) C alculate the numerical aperture.(n) Calculate the maximum acceptance angle.(o) Obtain the material dispersion and wavelength dispersion and hence estimate the bit rate x distance product ( B x L) of the fiber.。
《激光原理及应用》习题参考答案仅供大家学习参考用
《激光原理及应用》习题参考答案思考练习题11.解答：设每秒从上能级跃迁到下能级的粒子数为n 。
单个光子的能量：λνε/hc h == 连续功率：εn p =则，ε/p n =a. 对发射m μλ5000.0=的光： )(10514.2100.31063.6105000.01188346个⨯=⨯⨯⨯⨯⨯==--hc p n λ b. 对发射MHz 3000＝ν的光)(10028.51030001063.6123634个⨯=⨯⨯⨯==-νh p n 2.解答：νh E E =-12……………………………………………………………………..(a)TE E en nκ1212--=……………………………………………………………………….(b)λν/c =…………………………………………………………………………….(c) （1）由（a ），（b ）式可得：112==-T h e n n κν（2）由（a ），（b ）,(c)式可得： )(1026.6ln312K n n hcT ⨯=-=κλ3.解答：（1） 由玻耳兹曼定律可得TE E e g n g n κ121122//--=，且214g g =，202110=+n n 代入上式可得：≈2n 30（个）（2）)(10028.5)(1091228W E E n p -⨯=-= 4.解答：(1) 由教材（1-43）式可得317336343/10860.3/)106000.0(1063.68200018q m s J m s J h q ⋅⋅=⋅⋅⋅⋅⋅⋅=⋅=---πλπρν自激 （2）9344363107.5921063.68100.5)106328.0(8q ⋅=⋅⋅⋅⋅⋅==---ππρλνh q 自激5.解答：（1）红宝石半径cm r 4.0=，长cm L 8=，铬离子浓度318102-⋅=cm ρ，发射波长m 6106943.0-⋅=λ，巨脉冲宽度ns T 10=∆则输出最大能量)(304.2)(106943.0100.31063.684.0102)(68342182J J hcL r E =⋅⋅⋅⋅⋅⋅⋅⋅⋅==--πλπρ 脉冲的平均功率： )(10304.2)(1010304.2/89W W T E p ⋅=⋅=∆=- （2）自发辐射功率)(10304.2)(10106943.0)84.0102(100.31063.6)(22621883422W W L r hc hcN Q ⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅==---πλτπρλτ＝自6.解答：由λν/c =，λλνd cd 2=及λρνρλd d v =可得1185-==kThcehcd d λνλλπλνρρ7.解答： 由0)(=ννρd d 可得： 31=-kTh kTh m m mee kTh υυυ；令x kTh m=υ，则)1(3-=x x e xe ；解得：82.2=x 因此：1182.2--=kh T m ν 同样可求得：96.4=kThcm λ 故c m m 568.0=λν8解答：)]4(2[)(11)](4[114)(04042)(4202000πτνππτπτπτνννπττννπτνπτνννπτ--==+=-+=∞-∞∞-=-∞⎰⎰⎰arctg A x arctg A dxx A d A d f xN 令又04πτν数量级在810，所以2~)4(0ππτν--arctg ,代入上式得：τ/1=A9解答：由教材的（1-26）式可得：t A e n t n 21202)(-=，令en t n 1)(202=，则 21211,1A A ==ττ 10解答：相对论四维波矢量为：),(cik k ωμ = 对沿x 方向的特殊洛伦兹变换,有).(,,),(1'3'32'221'1k k k k k c k k υωγωωυγ-===-= (1)其中2211c υγ-=假设波矢量k 与x 轴的夹角为θ，'k 与x 轴的夹角为'θ，有'''11cos ,cos θωθωck ck == (2)代入（1）式可得)cos 1('θνωγωc-= (3)若'∑为光源的静止参考系，则0'ωω=。
激光原理及应用课后答案
11．试计算连续功率均为1W 的两光源，分别发射λ＝0.5000m，ν3000MHz 的光，每秒从上能级跃迁到下能级的粒子数各为多少？q 1 0.5 ×10 6答：粒子数分别为：n1 34 8 2.5138 ×1018 hν c 6.63 ×10 ×3 ×10 6.63 ×10 34 ×λq 1 n2 34 9 5.0277 ×10 23 hν 6.63 ×10 ×3 ×10 m co2．热平衡时，原子能级E 2 的数密度为n2，下能级E1 的数密度为n1 ，设g 1 g 2 ，求：1当原子跃迁时相应频率为ν＝3000MHz，T＝300K 时n2/n1 为若干。
2若原子跃迁时发光波长λ＝1，n2/n1 ＝0.1 时，则温度T 为多高？网E E ）hν答：（1）nm / gm e m n kT 则有：n2 e kT exp w. 6.63 ×10 34 × 3 ×10 9 1.38 ×10 23 ×300 ≈1 案nn / gn n1 答hνn2 6.63 ×10 34 ×3 ×108 （2）e kT exp 23 6 0.1 T 6.26 ×10 3 K da n1 1.38 ×10 ×1 ×10 ×T 后课3．已知氢原子第一激发态E2 与基态E 1之间能量差为1.64×l0 －18J，设火焰T＝2700K中含有1020 个氢原子。
设原子按玻尔兹曼分布，且4g1 ＝g2 。
求：1能级E 2 上的原子数n2 为kh多少？2设火焰中每秒发射的光子数为l0 8 n2，求光的功率为多少瓦？hνn2 g1 n 1.64 ×10 18答：（1）e kT 2 4 ×exp 23 3.11 ×10 19 n1 g 2 n1 1.38 ×10 ×2700 w. 且n1 n 2 10 20 可求出n 2 ≈31ww （2）功率＝108 ×31 × 1.64 ×10 18 5.084 ×10 9 W4．1普通光源发射λ＝0.6000m 波长时，如受激辐射与自发辐射光功率体密度之比q激 1 ，求此时单色能量密度ρν为若干？ 2 在He —Ne 激光器中若q自2000 q激ρν 5.0 ×10 4 J s / m3 ，λ为0.6328m，设＝1，求为若干？q自答：（1）1q激c3 λ3 1 0.6 ×10 6 3 ＝ρνρνρρν 3.857 ×10 17 J s / m3q自8πhν 3 8πh 2000 8π×6.63 ×10 34 νq激c3 λ3 0.6328 ×10 6 3 （2）＝3 ρνρν34 ×5 ×10 4 7.6 ×10 9 q自8πhν8πh 8π×6.63 ×105．在红宝石Q 调制激光器中，有可能将全部Cr3＋铬离子激发到激光上能级并产生巨脉冲。
光子学与光电子学 原荣邱琪 习题题解
《光子学与光电子学》习题及题解原荣 邱琪 编著第1章 概述和理论基础1-10 计算每个脉冲包含的光载波数考虑工作在1 550 nm 波长的10 Gb/s RZ 数字系统，计算每个脉冲有多少个光载波振荡？ 解：已知λ = 1.550 μm ，所以光频是Hz 101.93514×==λc f ，光波的周期是1T f ==5.168×10−15 s 。
已知数字速率是10 Gb/s RZ 码，所以脉冲宽度是T = 1/(10×109) = 10−10 s ，所以在该脉冲宽度内的光周期数是19349015.168/101510ele =×==−−T T N1-11 计算LD 光的相干长度和相干时间单纵模LD 的发射波长是1550 nm ，频谱宽度是0.02 nm ，计算它发射光的相干时间和相干长度。
解：由题可知，λ = 1550×10−9 m ，Δλ = 0.02 × 10−9 m ，从式（3.1.18）可知()()Hz 102.5100155/1031020.0/929892×=××××=Δ=Δ−−λλc v于是，相干时间是 019104)102.5/(1/1−×=×=Δ≈Δv t s 或者 0.4 ns相干长度是12.010*******c =×××=Δ=−t c l m 或者 12 cm与LED 相比（见例1.3.4），LD 的相干长度是LED 的6.3×103倍。
第2章 光波在光纤波导中的传输2-14 平面电介质波导中的模数平面电介质波导宽为100 μm ，，490.11=n 084.12=n ，使用式（2.2.6）估算波长为1.55 μm 的自由空间光入射进该波导时，它能够支持的模数。
并把你的估算与下面的取整公式进行比较1π2Int +⎟⎠⎞⎜⎝⎛=V M 解：全反射的相位变化不能够大于π，所以φ /π 小于1。
光电子学与光子学讲义-作业答案(第1、2章)13版
第一章1.10 Refractive index(a) Consider light of free-space wavelength 1300 nm traveling in pure silica medium. Calculate the phase velocity and group velocity of light in this medium. Is the group velocity ever greater than the phase velocity?(b) What is the Brewster angle(the polarization angle qp) and the critical angle(qc) for total internal reflection when the light wave traveling in this silica medium is incident on a silica/air interface. What happens at the polarization angle?(c) What is the reflection coefficient and reflectance at normal incidence when the light beam traveling in the silica medium is incident on a silica/air interface?(d) What is the reflection coefficient and reflectance at normal incidence when a light beam traveling in air is incident on an air/silica interface? How do these compare with part (c) and what is your conclusion?1.18 Reflection at glass-glass and air-glass interfaceA ray of light that is traveling in a glass medium of refractive index n1=1.460 becomes incident on a less dense glass medium of refractive index n2=1.430. Suppose that the free space wavelength of the light ray is 850 nm.(a) What should the minimum incidence angle for TIR be?(b) What is the phase change in the reflected wave when the angle of incidence qi =85°and when qi =90°?(c) What is the penetration depth of the evanescent wave into medium 2 when qi =85°and when qi =90°?(d) What is the reflection coefficient and reflection at normal incidence (qi =0 °)when the light beam traveling in the glass medium (n=1.460) is incident on a glass-air interface? (e) What is the reflection coefficient and reflectance at normal incidence when a light beam traveling in air is incident on an air/-glass interface (n=1.460)? How do these compare with part (d) and what is your conclusion?1.20 TIR and polarization at water-air interface(1) Given that the refractive index of water is about 1.33, what is the polarization angle for light traveling in air and reflected from the surface of the water?(2) consider a diver in sea pointing a flashlight towards the surface of the water. What is the critical angle for the light beam to be reflected from the water surface?1.22 phase changes on TIRConsider a lightwave of wavelength 870nm traveling in a semiconductor medium (GaAs) of refractive index 3.6. It is incident on a different semiconductor medium (AlGaAs) of refractive index 3.4, and the angle of incidence is 80o. Will this result in total internal reflection? Calculate the phase change in the parallel and perpendicular components of the reflected electric field?1.25 Goos-Haenchen phase shiftAray of light that is traveling in a glass medium(1) of refractive index n1=1.460 becomesincident on a less dense glass medium(2) of refractive index n2=1.430. Suppose that the free space wavelength of the light ray is 850nm.the angle of incidence θi =85°. Estimate the lateral Goos-Haenchen shift in the reflected wave for the perpendicular field component. Recalculate the Goos-Haenchen shift in the second medium has n2=1 (air). What is your conclusion?Assume that the virtual reflection occurs from a virtual plane in medium B at a distance d that is roughly the same as the penetration depth.Note that d actually depends on the polarization ,the direction of the field,but we will ignore this dependence.第二章 作业习题：θ2.7 Dielectric slab waveguide Consider a dielectric slab waveguide that has a thin GaAs layer of thickness 0.25μm between two AlGaAs layers. The refractive index of GaAs is3.6 and that of the AlGaAs layers is 3.40. What is the cut-off wavelength beyond which only a single mode can propagate in the waveguide, assuming that the refractive index does not vary greatly with the wavelength? If a radiation of wavelength 860 nm (corresponding to bandgap radiation) is propagating in the GaAs layer, what is the penetration of the evanescent wave into the AlGaAs layer? What is the mode field width (MFW) of this radiation? Point out the effect of change of radiation wavelength (λ) on the MFW.2.9 Dielectric slab waveguide Consider a planar dielectric waveguide with a core thickness 10μm , n 1=1.4446, n 2=1.4440. Calculate the V -number, the mode angle θm for m=0 (use a graphical solution, if necessary), penetration depth, and mode field distance (MFW=2α+2δ), for light wavelengths of 1.0μm and 5μm . What is your conclusion? Compare your MFW calculation with ()0221/a V V ω=+.The model angle θ0is given as θ0=88.85ᵒ for λ=1μm and θ0=88.72ᵒ for λ=1.5μm for the fundamental mode m=0.2.10 A multimode fibe r Consider a multimode fiber with a core diameter of 60μm , core refractive index of 1.47, and a cladding refractive index of 1.45 both at 870 nm. Consider operating this fiber at λ=870n m .(a) Calculate the numerical aperture.(b) Find out the normalized core-cladding index difference.(c) Calculate the V-number for the fiber and estimate the number of guided modes.(d) Calculate the wavelength beyond which the fiber becomes single-mode.(e) Calculate the modal dispersion τ∆and hence the bit rate ⨯distance product .2.12 Single mode fiber Consider a fiber with a 2SiO -13.5%2GeO core of diameter of 6m μ and refractive index of 1.47 and a cladding refractive index of 1.46 both refractive indices at 1300 nm where the fiber is to be operated using a laser source with a half maximum width (FWHM) of 2 nm..(a) Calculate the V -number for the fiver.(b)what is the maximum allowed diameter of the core that maintains oprations in single-mode?(c) Calculate the wavelength below which the fiber becomes multimode.(d) Calculate the numerical aperture.(e) Calculate the maximum acceptance angle.(f)Obtain the material dispersion and wavelength dispersion and hence estimate the bit rate⨯) of the fiber.⨯distance product (B L。
光电子学与光子学的原理及应用s.o.kasa 课后答案
1.4 Antireflection coating
For light traveling in medium 1 incident on the 1-2 interface at normal incidence,
For SiO2 For TiO2
d = λ = 900 × 10−9 m = 0.15 µm
4 n2
4(1.5)
d = λ = 900 × 10−9 m = 0.10 µm
4n2
4(2.3)
1.8 Thin film coating and multiple reflections:
Assume that n1 < n2 < n3 and that the thickness of the coating is d. For simplicity, we will assume normal incidence. The phase change in traversing the coating thickness d is φ = (2π/λ)n2d where λ is the free space wavelength. The wave has to be multiplied by exp(−jφ) to account for this phase difference.
The phase change for wave B going through the coating of thickness d is 2k2d where k2 = n2ko and ko = wavevector in free space = 2π/λ. This should be 180° or π. Thus we need 2n2(2π/λ)d = π or
光电子技术,习题解答
1. 什么是光电子技术？当前光电子技术备受重视的原因是什么？答：光电子技术是研究从红外波、可见光、X射线直至γ射线波段范围内的光波。
电子技术，是研究运用光子和电子的特性，通过一定媒介实现信息与能量转换、传递、处理及应用的科学。
因为光电子技术的飞速发展，使得光电子技术逐渐成为高新科学技术领域内的先导和核心，在科学技术，国防建设，工农业生产、交通、邮电、天文、地质、医疗、卫生等国民经济的各个领域内都获得了愈来愈重要的应用，特别是正逐渐进入人们的家庭，因此光电子技术备受重视。
2. 什么叫光的空间相干性？时间相干性？光的相干性能好差程度分别用什么衡量？它们的意义是什么？答：空间相干性是指在同一时刻垂直于光传播方向上的两个不同空间点上的光波场之间的相干性，空间相干性是用相干面积Ac来衡量，Ac愈大，则光的空间相干性愈好。
时间相干性是指同一空间点上，两个不同时刻的光波场之间的相干性，用相干时间t c=L c／c来衡量，t c愈大，光的时间相干性愈好。
3. 世界上第一台激光器是由谁发明的？它是什么激光器？它主要输出波长为多少？答：1960年5月16日、美国梅曼博士、红宝石激光器、6943Å。
4. 自发辐射与受激辐射的根本差别是什么？为什么说激励光子和受激光子属同一光子态？答：差别在有没有受到外界电磁辐射的作用；因为有相同的频率、相位、波矢和偏振状态。
5. 为什么说三能级系统实现能态集居数分布反转要比四能级系统困难？答：因为三能级系统的上能级为E2，下能级为E1，在E2上停留的时间很短，而四能级系统在E3上呆的时间较长，容易实现粒子数反转。
6. 激光器的基本组成有哪几部分？它们的基本作用是什么？答：组成部分：工作物质、泵浦系统、谐振腔工作物质提供能级系统、泵浦源为泵浦抽运让粒子从下能级到上能级条件、谐振腔起正反馈作用7. 工作物质能实现能态集居数分布反转的条件是什么？为什么？对产生激光来说，是必要条件还是充分条件，为什么？答：工作物质要具有丰富的泵浦吸收带，寿命较长的亚稳态，要求泵浦光足够强；必要条件，因为它还以kkk谐振腔内以提供正反馈。
光电子技术基础课后答案
光电⼦技术基础课后答案《光电⼦技术》参考答案第三章1.⼀纵向运⽤的 KD*P 电光调制器，长为 2cm ，折射率 n =2.5，⼯作频率为 1000kHz 。
试求此时光在晶体中的渡越时间及引起的相位延迟。
解：渡越时间为：L nL2.5 2 10c 2 m 1.671010sdc / n 310 m /s8在本题中光在晶体中的渡越引起的相位延迟量为：210 6Hz 1.6710101.051031m d对相位的影响在千分之⼀级别。
3.为了降低电光调制器的半波电压,采⽤ 4块 z 切割的 KD* P 晶体连接(光路串联,电路并联)成纵向串联式结构。
试问:(1)为了使 4块晶体的电光效应逐块叠加,各晶体 x 和 y 轴取向应如何?(2)若0.628m ,n 01.51,6323.6 10m /V ,计算其半波电压,并与单块晶体调制器⽐较之.。
12 答：⑴⽤与 x 轴或 y 轴成 45夹⾓（为 45°-z 切割）晶体，横向电光调制，沿 z 轴⽅向加电场，通光⽅向垂直于 z 轴，形成(光路串联,电路并联)的纵向串联式结构。
为消除双折射效应，采⽤“组合调制器”的结构予以补偿，将两块尺⼨、性能完全相同的晶体的光轴互成 90串联排列，即⼀块晶体的 y'和 z 轴分别与另⼀块晶体的 z 和 y'平⾏，形成⼀组调制器。
4块 z 切割的 KD P 晶体连接成*⼆组纵向串联式调制器。
（P96） (2)于是，通过四块晶体之后的总相位差为2 L Ld2n 3 or 63V 4 n 3 o r V 63 d相应的半波电压是1 d 1 r 63 L 4 1.51 0.628 10 6 m d 1V dLV0.77310 4 4 n o 33 23.6 10 12m /V L 4 0.19310 4 V dL 该半波电压是单块横向晶体调制器半波电压的四分之⼀倍，是单块纵向晶体调制器半波电压的 1/(2 L/d)倍。
光电子技术答案解析
光电子技术练习及思考题解答（收集整理版）配套光电子技术（第3版）安毓英刘继芳李庆辉冯喆珺编著电子工业出版社由于水平有限，练习及思考题解答难免有错误之处，敬请指正。
欢迎大家交流学习习 题11. 设在半径为R c 的圆盘中心法线上，距盘圆中心为l 0处有一个辐射强度为I e 的点源S ，如图所示。
试计算该点源发射到盘圆的辐射功率。
解：ΩΦd d e e I =， 202πd l R c =Ω202e πd d l R I I c e e ==ΩΦ2. 如图所示，设小面源的面积为∆A s ，辐射亮度为L e ，面源法线与l 0的夹角为θs ；被照面的面积为∆A c ，到面源∆A s 的距离为l 0。
若θc 为辐射在被照面∆A c 的入射角，试计算小面源在∆A c 上产生的辐射照度。
解：用定义rr ee A dI L θ∆cos =和A E e e d d Φ=求解。
3.假设有一个按郎伯余弦定律发射辐射的大扩展源（如红外装置面对的天空背景），其各处的辐亮度e L 均相同。
试计算该扩展源在面积为d A 的探测器表面上产生的辐照度。
解：辐射亮度定义为面辐射源在某一给定方向上的辐射通量，因为余弦辐射体的辐射亮度为eoe eo dI L L dS== 得到余弦辐射体的面元dS 向半空间的辐射通量为 0e e e d L dS L dS ππΦ==又因为在辐射接收面上的辐射照度e E 定义为照射在面元上的辐射通量e d Φ与该面元的面积dA 之比，即ee d E dAΦ=第1题图第2题图所以该扩展源在面积为d A 的探测器表面上产生的辐照度为e e dL dSE A π=单位是2/W m4. 霓虹灯发的光是热辐射吗？ 解： 不是热辐射。
5刚粉刷完的房间从房外远处看，它的窗口总显得特别黑暗，这是为什么？解：因为刚粉刷完的房间需要吸收光线，故从房外远处看它的窗口总显得特别黑暗 6. 从黑体辐射曲线图可以看出，不同温度下的黑体辐射曲线的极大值处的波长λm 随温度T 的升高而减小。
光电子学与光子学的原理及应用S.O.Kasa chapter6课后答案.pdf
6.3 Solar cell driving a loada A Si solar cell of area 4 cm 2 is connected to drive a load R as in Figure 6.8 (a). It has the I-Vcharacteristics in Figure 6.8 (b) under an illumination of 600 W m -2. Suppose that the load is 20 Ω and it is used under a light intensity of 1 kW m -2. What are the current and voltage in the circuit? What is the power delivered to the load? What is the efficiency of the solar cell in this circuit?b What should the load be to obtain maximum power transfer from the solar cell to the load at 1 kW m -2 illumination. What is this load at 600 W m -2?c Consider using a number of such a solar cells to drive a calculator that needs a minimum of 3V and draws 3.0 mA at 3 - 4V. It is to be used indoors at a light intensity of about 400 W m -2. How many solar cells would you need and how would you connect them? At what light intensity would the calculator stop working?Solutiona The solar cell is used under an illumination of 1 kW m -2. The short circuit current has to be scale up by 1000/600 = 1.67. Figure 6Q3-2 shows the solar cell characteristics scaled by a factor 1.67 along the current axis. The load line for R = 20 W and its intersection with the solar cell I-V characteristics at P which is the operating point P . Thus,I¢ ≈ 22.5 mA and V¢ ≈ 0.45 VThe power delivered to the load isP out = I¢V¢ = (22.5×10-3)(0.45V) = 0.0101W, or 10.1 mW.This is not the maximum power available from the solar cell. The input sun-light power is P in = (Light Intensity)(Surface Area)= (1000 W m -2)(4 cm 2 ´ 10-4 m 2/cm 2) = 0.4 WThe efficiency is η=100P out P in =1000.0100.4=2.500 which is poor.b Point M on Figure 6Q3-2 is probably close to the maximum efficiency point, I¢ ≈ 23.5 mA and V¢ ≈ 0.44 V. The load should be R = 18.7 W, close to the 20 W load. At 600 W m -2 illumination, the load has to be about 30 W as in Figure 6.8 (b). Thus, the maximum efficiency requires the load R to be decreased as the light intensity is increased. The fill factor isFF =I m V m I sc V oc =(23.5 mA)(0.44 V)(27 mA)(0.50 V)≈ 0.78 c The solar cell is used under an illumination of 400 W m -2. The short circuit current has to be scale up by 400/600 = 0.67. Figure 6Q3-2 shows the solar cell characteristics scaled by a factor 0.67 along the current axis. Suppose we have N identical cells in series, and the voltage across the calculator is V calculator . The current taken by the calculator is 3 mA in the voltage range 3 to 4 V and the calculator stops working when V calculator < 3 V. The cells are in series so each has the same current and equal to 3 mA, marked as I¢ in Figure 6Q-2. The voltage across one cell will be V¢ = V calculator /N . which is marked in Figure 6Q3-2. V¢ = 0.46 V. Minimum number of solar cells in series = N = 3 / 0.46 = 6.5 or 7 cells , since you must choose the nearest higher integer.If we want the calculator continue to work under low intensity levels, then we can connect more cells in series until we reach about 4 V; N = 4 V / 0.46 V = 8.7 or 9 cells in series.The easiest estimate for the minimum required light intensity is the following: The calculator will stop working when the light intensity cannot provide energy for the solar cell to deliver the 3 mA calculator current. The short circuit current at 400 W m -2 is 11 mA in Figure 6Q3-2. ThusMinimum light intensity = 3 mA 11 mA 400 W m −2=109 W m -2 Figure 6Q3-1Figure 6Q3-26.4 Open circuit voltage A solar cell under an illumination of 100 W m -2 has a short circuit current I s c of 50 mA and an open circuit output voltage V oc , of 0.55V. What are the short circuit current and open circuit voltages when the light intensity is halved?SolutionThe short circuit current is the photocurrent so that atI sc 2=I sc 1I 2I 1 =50 mA ()50 W m −2100 W m −2 = 25 mAAssuming n = 1, the new open circuit voltage is V oc 2=V oc 1+nk B T e ln I 2I 1 =0.55+10.0259()ln 0.5()= 0.508 VAssuming n = 2, the new open circuit voltage isVI (mA)R = 20 ž-2.V -2.V oc2=Voc1+nkBTelnI2I1=0.55+20.0259()ln0.5()= 0.467 V6.7 Series connected solar cells Consider two odd solar cells. Cell 1 has I o1 = 25´10-6 mA, n1 = 1.5, R s1 = 10 W and cell 2 has I o2 = 1´10-7 mA, n2 = 1, R s2 = 50 W. The illumination is such that I ph1 = 10 mA and I ph2 = 15 ma. Plot the individual I-V characteristics and the I-V characteristics of the two cells in series. Find the maximum power that can be delivered by each cell and two cells in series. Find the corresponding voltages and currents at the maximum power point. What is your conclusions?SolutionThe equivalent circuit is shown in Figure 6Q7-1. The current through both the devices has to be the same. Thus, for cell 1I=−Iph1+Io1expVd1n1VT−1=−Iph1+Io1expV1−IRs1n1VT−1∴V1−IRs1n1VT=lnI+Iph1Io1−1∴V1=n1VTlnI+Iph1Io1−1+IRs1For cell 2I=−Iph1+Io2expVd2n2VT−1=−Iph2+Io2expV2−IRs2n2VT−1∴V2=n2VTlnI+Iph2Io2+1+IRs2But V = V1 + V2∴V=n1VTlnI+Iph1Io1+1+IRs1+n2VTlnI+Iph2Io2+1+IRs2I phTwo different solar cells in series I ph2We can now substitute I o 1 = 25´10-6 mA, n 1 = 1.5, R s 1 = 10 W, I o 2 = 1´10-7 mA, n 2 = 1, R s 2 = 50 W and then plot V vs. I (rather I vs. V since we can calculate V from I ) for each cell and the two cells in series as in Figure 6Q7-2. Notice that the short circuit is determined by the smallest I sc cell. The total open circuit voltage is the sum of the two.Figure 6Q7-26.9 Solar cell efficiency The fill factor FF of a solar cell is given by the empirical expression FF ≈v oc−ln(v oc +0.72)v oc +2 where v oc = V oc /(nk B T/e ) is the normalized open circuit voltage (normalized with respect to the thermaltemperature k B T/e ). The maximum power output from a solar cell isP =FF I sc V oc Taking V oc = 0.58 V and I sc = I ph = 35 mA cm -2, calculate the power available per unit area ofsolar cell at room temperature 20 °C, at -40 °C and at 40 °CSolutionThe open circuit voltage depends on the temperature whereas I sc has very little temperature dependence. Use ′ V oc =V oc ′ T T +E g e 1−′ T T (1)to calculate the V oc at different temperature given V oc at one temperature. Then calculate v oc using v oc = V oc /(nk B T/e ) (2) then FF using FF ≈v oc−ln(v oc +0.72)v oc +2 (3)and then P using P =FF I sc V oc (4) Cell 1VoltageCurrent (mA)Cell 2Cell 1 in series with 2as summarized in Table 6Q9-1.Table 6Q9-1 n = 1I sc mA/cm 2 V oc ; Eq. (1) v oc ; Eq. (2) FF; Eq. (3) P mW cm -2; Eq. (4) 20 °C 35 0.580 V 22.97 0.793 16.03 -40 °C 35 0.686 V 34.19 0.847 20.34 40 °C 35 0.545 20.19 0.773 14.73 n = 2I sc mA/cm 2 V oc ; Eq. (1) v oc ; Eq. (2) FF; Eq. (3) P mW cm -2; Eq. (4) 20 °C 35 0.580 V 11.49 0.666 13.52 -40 °C 35 0.686 V 17.10 0.744 17.90 40 °C 35 0.545 10.09 0.638 12.15Conclusions: n = 2 case has a lower FF and also lower power delivery.NOTE: The temperature dependence of the open circuit voltage V oc was derived in the text as′ V oc =V oc ′ T T +E g e 1−′ T T This expression is valid whether n is 1 or 2. Recall that n = 1 represents diffusion in the neutral regionsand n = 2 is recombination in the space charge layer. In the n = 1 case I o µ n i 2 and in the n = 2 case I o µ n i , thus in generalI o µ n i 2/n Consider the open circuit voltage, V oc =nk B T e ln K I I o or eV oc nk BT =ln K I I o At two different temperatures T 1 and T 2 but at the same illumination level, by subtraction,eV oc 2nk B T 2−eV oc 1nk B T 1=ln I o 1I o 2 ≈ln n i 12/n n i 22/n where the subscripts 1 and 2 refer to the temperatures T 1 or T 2 respectively.We can substitute n i 2/n = (N c N v )1/2exp(-E g /nk B T ) and neglect the temperature dependences of N c and N v compared with the exponential part to obtain,eV oc 2nk B T 2−eV oc 1nk B T 1=E g nk B 1T 2−1T 1Rearranging for V oc 2 in terms of other parameters we find,V oc 2=V oc 1T 2T 1 +E g e 1−T 2T 1。
光电子学教程_课后作业答案
=
1.33 1013 Js / m 3
03电子科学与技术Company Logo
好好学习，天天上上
V K ( ) 3．解：光视效能： e
K V ( ) ，光视效率： Km
v 100 Km=683Lm/w，则 e 0.293W m1 Km K ( ) 683 0.50
则辐射能量 e e t 0.293 60 0.510 8.96W
03电子科学与技术Company Logo
好好学习，天天上上
4. 解：线性函数表示总辐射功率为I 0 的光谱中，其中落在频率
~ d
内的辐射功率与总功率之比随频率的分布情况 。
根据P49(3-1-13)，相干体积的物理意义：在单位面积光源辐射 出的单位频率宽度的光波，在其传播方向上发生相干现象的任 一体积范围为相对应的相干面积与光速的乘积。
v1 v0 vz c v0
返回目录
03电子科学与技术Company Logo
第三章激光振荡与工作特性
1.要使氦-氖激光器的相干长度达到1Km,它的单 色性Δλ/λ0应为多少？ 解：根据P48式(3-1-2)：
2 lc lc
632.8nm 632.8 10 6.328 10 12 10
好好学习，天天上上
3 108 13 3 10 HZ 7. 解： 1 10 106 1 c
3 108 14 2 6 10 HZ 6 2 0.5 10 c
dn21 (t ) I (t ) h dt
03电子科学与技术Company Logo
好好学习，天天上上
6。实现光放大的必要条件是什么，负温度状 态的概念是什么？