2020-2021学年最新冀教版九年级数学上册《过三点的圆》同步测试题及答案解析-精编试题
冀教版九上数学同步测试 28.2过三点的圆(带解析)

课堂检测1.下列说法正确的是( )A.三点确定一个圆B.任意的一个三角形一定有一个外接圆C.三角形的外心是它的三个角的角平分线的交点D.任意一个圆有且只有一个内接三角形解析:不在同一条直线上的三个点确定一个圆,所以A错;任意三角形的三个顶点不在同一条直线上,所以一定有一个外接圆,所以B正确;三角形的外心是三边垂直平分线的交点,所以C错;任意一个圆有无数个内接三角形,所以D错.故选B.2.如图所示,点A,B,C在同一条直线上,点D在直线AB外,过这4个点中的任意3个点,能画圆的个数是( )A.1B.2C.3D.4解析:根据题意得出:点D,A,B;点D,A,C;点D,B,C可以确定一个圆.故过这四点中的任意3个点,能画圆的个数是3.故选C.3.已知△ABC的一边长为10,另两边长分别是方程x2-14x+48=0的两个根,若用一圆形纸片将此三角形完全覆盖,则该圆形纸片的最小半径是.解析:解方程x2-14x+48=0,得x1=8,x2=6,即△ABC的三条边长为10,8,6.∵102=82+62,∴△ABC是直角三角形,圆形纸片将此三角形完全覆盖的最小圆为三角形的外接圆,那么圆形纸片的最小直径为直角三角形的斜边,即为10,那么半径为5.故填5.4.已知Rt△ABC的两直角边为a和b,且a,b是方程x2-3x+1=0的两根,求Rt △ABC的外接圆面积.解:∵两直角边a,b分别是一元二次方程x2-3x+1=0的两根,∴a+b=3,a·b=1,∴c2=a2+b2=(a+b)2-2a·b=7,∵圆的半径r=c=,∴Rt△ABC的外接圆的面积为πr2=π×π.课后检测1.对于三角形的外心,下列说法错误的是( )A.它到三角形三个顶点的距离相等B.它是三角形外接圆的圆心C.它是三角形三条边垂直平分线的交点D.它一定在三角形的外部2.下列说法正确的是( )A.过一点A的圆的圆心可以是平面上任意点B.过两点A,B的圆的圆心在一条直线上C.过三点A,B,C的圆的圆心有且只有一点D.过四点A,B,C,D的圆不存在3.如图所示,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )A.点PB.点QC.点RD.点M4.A,B,C为平面上的三点,AB=2,BC=3,AC=5,则( )A.可以画一个圆,使A,B,C都在圆周上B.可以画一个圆,使A,B在圆周上,C在圆内C.可以画一个圆,使A,C在圆周上,B在圆外D.可以画一个圆,使A,C在圆周上,B在圆内5.锐角三角形的外心在;直角三角形的外心在 ;钝角三角形的外心在 .6.若AB=4 cm,则过点A,B且半径为3 cm的圆有个.7.在Rt△ABC中,∠C=90°,BC=5,AC=12,则△ABC的外接圆半径为 .8.如图所示,△ABC,△ABD,△ABE都是以AB为斜边的直角三角形.求证点A,B,C,D,E在同一个圆上.9.如图所示,已知☉O是△ABC的外接圆,若AB=AC=5,BC=6,则☉O的半径为( )A.4B.3.25C.3.125D.2.2510.“不在同一直线上的三点确定一个圆”.请你判断平面直角坐标系内的三个点A(2,3),B(-3,-7),C(5,11)是否可以确定一个圆.11.已知,如图(1)所示,△ABC中,BA=BC,D是平面内不与A,B,C重合的任意一点,∠ABC=∠DBE,BD=BE.(1)求证△ABD≌△CBE;(2)如图(2)所示,当点D是△ABC的外接圆圆心时,请判断四边形BDCE的形状,并证明你的结论.答案与解析1.D(解析:三角形的外心是三角形外接圆的圆心,所以B正确;三角形的外心是三角形三边垂直平分线的交点,到三角形的三个顶点的距离相等,所以A,C正确;锐角三角形的外心在三角形的内部,直角三角形的外心在斜边的中点处,钝角三角形的外心在三角形的外部,所以D错误.故选D.)2.B(解析:过一点A的圆的圆心不能为点A,所以A错误;过两点A,B的圆的圆心在线段AB的垂直平分线上,所以B正确;过不在同一条直线上的三点确定一个圆,圆心有且只有一个,所以C错误;矩形ABCD的四个顶点在一个圆上,所以D错误.故选B.)3.B(解析:作弦AB和BC的垂直平分线,交点即为圆心.故选B.)4.D(解析:根据题意可得,A,B,C三点在同一条直线上,三点顺序依次为A,B,C或C,B,A,所以不可以画一个圆,使A,B,C都在圆周上,所以A错误;可以画过A,B两点的圆,此时点C在圆外,所以B错误;可以画过A,C两点的圆,此时点B在圆内,所以C错误,D正确.故选D.)5.三角形内部斜边的中点三角形外部(解析:三角形外心是三条边垂直平分线的中点,画三边垂直平分线确定交点的位置可得.)6.2(解析:过点A,B的圆的圆心在线段AB的垂直平分线上,线段AB的中点到两端点的距离是2 cm,所以半径为2 cm的圆有一个,半径小于2 cm的圆不存在,半径为3 cm的圆有两个.故填2.)7.6.5(解析:根据勾股定理可得斜边AB==13,又直角三角形的外心在斜边的中点,所以外接圆的半径为AB=6.5.故填6.5.)8.证明:取AB的中点为O,连接OD,OC,OE.∵△ABC,△ABD,△ABE都是以AB为斜边的直角三角形,∴OC=OD=OE=AB,即OC=OD=OE=OA=OB,∴点A,B,C,D,E在同一个圆上.9.C(解析:过A作AD⊥BC于D,连接BO,△ABC中,AB=AC,AD⊥BC,则AD必过圆心O,Rt△ABD中,AB=5,BD=3,∴AD=4,设☉O的半径为x,Rt△OBD中,OB=x,OD=4-x,根据勾股定理,得OB2=OD2+BD2,即x2=(4-x)2+32,解得x==3.125.故选C.)10.解:设经过A,B两点的直线解析式为y=kx+b,由A(2,3),B(-3,-7),得, --,解得,-.∴经过A,B两点的直线解析式为y=2x-1;当x=5时,y=2x-1=2×5-1=9≠11,所以点C(5,11)不在直线AB上,即A,B,C三点不在同一直线上,所以A,B,C三点可以确定一个圆.11.(1)证明:∵∠ABC=∠DBE,∴∠ABC+∠CBD=∠DBE+∠CBD,∴∠ABD=∠CBE,在△ABD与△CBE中,∵BA=BC,∠ABD=∠CBE,BD=BE,∴△ABD≌△CBE. (2)解:四边形BDCE是菱形.证明如下:同(1)可证△ABD≌△CBE,∴CE=AD,∵点D是△ABC外接圆圆心,∴DA=DB=DC,又∵BD=BE,∴BD=BE=CE=CD,∴四边形BDCE是菱形.。
冀教版初中数学九年级上册《28.2 过三点的圆》同步练习卷

冀教新版九年级上学期《28.2 过三点的圆》同步练习卷一.选择题(共23小题)1.如图,点A、B、C在同一条直线上,点D在直线AB外,过这四个点中的任意3个,能画的圆有()A.1 个B.2个C.3个D.4 个2.在平面直角坐标系中,点A的坐标是(﹣1,0),点B的坐标是(3,0),在y轴的正半轴上取一点C,使A、B、C三点确定一个圆,且使AB为圆的直径,则点C的坐标是()A.(0,)B.(,0)C.(0,2)D.(2,0)3.下列说法正确的是()A.长度相等的两条弧是等弧B.三点确定一个圆C.同一条弦所对的两条弧一定是等弧D.半圆是弧4.下列说法正确的是()A.三点确定一个圆B.长度相等的两条弧是等弧C.经过圆内一点有且仅有一条直径D.半圆是弧5.如图的矩形ABCD中,E为的中点,有一圆过C、D、E三点,且此圆分别与、相交于P、Q两点.甲、乙两人想找到此圆的圆心O,其作法如下:(甲)作∠DEC的角平分线L,作的中垂线,交L于O点,则O即为所求;(乙)连接、,两线段交于一点O,则O即为所求对于甲、乙两人的作法,下列判断何者正确?()A.两人皆正确B.两人皆错误C.甲正确,乙错误D.甲错误,乙正确6.确定一个圆的条件是()A.已知圆心B.已知半径C.过三个已知点D.过一个三角形的三个顶点7.下列说法中,正确的是()A.三点确定一个圆B.三角形有且只有一个外接圆C.四边形都有一个外接圆D.圆有且只有一个内接三角形8.小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是()A.第一块B.第二块C.第三块D.第四块9.△ABC的三边长分别为6、8、10,则其外接圆的半径是()A.3B.4C.5D.1010.如图,△ABC内接于圆O,连接OA、OB,∠C=40°,则∠AOB的度数是()A.80°B.50°C.45°D.40°11.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为()A.1B.C.D.212.三角形两边的长分别是8和6,第三边的长是方程x2﹣12x+20=0的一个实数根,则三角形的外接圆半径是()A.4B.5C.6D.813.如图,△ABC内接于⊙O,连接BO并延长,交⊙O于点D,已知BO=1,∠A=60°,则BC的长为()A.B.C.2D.314.如图,△ABC内接于⊙O,AD是△ABC边BC上的高,D为垂足.若BD=1,AD=3,BC=7,则⊙O的半径是()A.B.C.D.15.三角形的外接圆的圆心为()A.三条高的交点B.三条边的垂直平分线的交点C.三条角平分线的交点D.三条中线的交点16.已知⊙O的半径为5,锐角△ABC内接于⊙O,AB=8,BD⊥AC于D,若CD=4,则BD的长为()A.4B.5C.D.17.如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b﹣;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是()A.2B.3C.4D.518.如图,一副直角三角板满足∠ACB=∠EDF=90°,AC=BC,AB=DF,∠EFD=30°,将三角板DEF的直角顶点D放置于三角板ABC的斜边AB上,再将三角板DEF绕点D 旋转,并使边DE与边AC交于点M,边DF与边BC于点N.当∠EDF在△ABC内绕顶点D旋转时有以下结论:①点C,M,D,N四点共圆;②连接CD,若AD=DB,则△ADM∽△CDN;③若AD=DB,则DN•CM=BN•DM;④若AD=DB,则CM+CN=AD;⑤若DB=2AD,AB=6,则2≤S△DMN≤4.其中正确结论的个数是()A.2B.3C.4D.519.如图,在四边形ABCD中,AC、BD为对角线,点M、E、N、F分别为AD、AB、BC、CD边的中点,下列说法:①当AC=BD时,M、E、N、F四点共圆.②当AC⊥BD时,M、E、N、F四点共圆.③当AC=BD且AC⊥BD时,M、E、N、F四点共圆.其中正确的是()A.①②B.①③C.②③D.①②③20.锐角△ABC的三条高AD、BE、CF交于H,在A、B、C、D、E、F、H七个点中.能组成四点共圆的组数是()A.4组B.5组C.6组D.7组21.如图,已知(1)已知△ABC的两条中线BD、CE交于点M,A、D、M、E四点共圆,BC=8,则AM的长为()A.2B.C.D.322.如图,在△ABC中,∠B=75°,∠C=45°,BC=6﹣2,点P是BC上一动点,PE⊥AB于E,PD⊥AC于D.无论P的位置如何变化,线段DE的最小值为()A.3﹣3B.C.4﹣6D.223.在圆内接四边形ABCD中,∠BAD、∠ADC的角平分线交于点E,过E作直线MN平行于BC,与AB、CD交于M、N,则总有MN=()A.BM+DN B.AM+CN C.BM+CN D.AM+DN二.填空题(共22小题)24.已知直线l:y=x﹣4,点A(1,0),点B(0,2),设点P为直线l上一动点,当点P 的坐标为时,过P、A、B不能作出一个圆.25.如图,点A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为.26.要确定一个圆,需要两个基本条件,一个是,另一个是,其中,确定圆的位置,确定圆的大小.27.若A(1,2),B(3,﹣3),C(x,y)三点可以确定一个圆,则x、y需要满足的条件是.28.三点确定一个圆.(判断对错)29.当点A(1,2),B(3,﹣3),C(m,n)三点可以确定一个圆时,m,n需要满足的条件.30.平面直角坐标系内的三个点A(1,0)、B(0,﹣3)、C(2,﹣3)确定一个圆(填“能”或“不能”).31.如图,平面直角坐标系中,已知A,B两点的坐标分别为(2,0)(0,2),点P是△AOB外接圆上的一点,且∠BOP=45°,则点P的坐标为.32.如图,点O为△ABC的外接圆圆心,点E为圆上一点,BC、OE互相平分,CF⊥AE 于F,连接DF.若OE=2,DF=1,则△ABC的周长为.33.已知△ABC内接于半径为5厘米的⊙O,若∠A=60°,边BC的长为厘米.34.如图.在△ABC中,∠A=60°,BC=5cm.能够将△ABC完全覆盖的最小圆形纸片的直径是cm.35.如图,AD为△ABC的外接圆⊙O的直径,若∠BAD=50°,则∠ACB=°.36.已知△ABC的边BC=2cm,且△ABC内接于半径为2cm的⊙O,则∠A=度.37.如图,点O为等边△ABC内一点,OA=2,OC=,连接BO并延长交AC于点D,且∠DOC=30°,过点B作BF⊥BD交CO延长线于点F,连接AF,过点D作DE ⊥AF于点E,则DE=.38.如图,AB∥CD,∠CBE=∠CAD=90°.AC=AD=6,DE=4,则BD长为.39.如图,ABCD、CEFG是正方形,E在CD上,且BE平分∠DBC,O是BD中点,直线BE、DG交于H.BD,AH交于M,连接OH,则OH=,BM=.40.在四边形ABCD中,∠DAC=98°,∠DBC=82°,∠BCD=70°,BC=AD,则∠ACD =.41.已知二次函数y1=a1(x﹣1)2﹣2012,其图象顶点为M,且与x轴交于A(x1,0),B (x2,0)两点,又知二次函数y2=a2(x﹣1)2+1的顶点为N,若A,B,M,N四点共圆,则x1x2﹣x1﹣x2=.42.已知△ABC中,∠BAC≠90°,AD⊥BC,BE⊥AC,且AD、BE交于点H,连接CH,则∠ACH+∠BAE=.43.已知:AB=2,AC平分∠DAB,∠DAB+∠DCB=180°,∠DCB=120°,当∠ABD=∠CBF时,则AC=.44.正方形ABCD的中心为O,面积为1989cm2.P为正方形内一点,且∠OPB=45°,P A:PB=5:14.则PB=.45.如图,▱ABCD的边长为2,对角线AC、BD交于点O,E为DC上一点,∠DAE=30°,过D作DF⊥AE于F点,连接OF.则线段OF的长度为.三.解答题(共5小题)46.如图所示,BD,CE是△ABC的高,求证:E,B,C,D四点在同一个圆上.47.平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.(1)在图中清晰标出点P的位置;(2)点P的坐标是.48.如图,△ABC内接于⊙O,若⊙O的半径为6,∠B=60°,求AC的长.49.[发现]如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)[思考]如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?我们知道,如果点D不在经过A,B,C三点的圆上,那么点D要么在圆O外,要么在圆O内,以下该同学的想法说明了点D不在圆O外.(如图③,过A,B,C三点作圆,圆心为O,假设点D在圆O外,设AD交圆O于点E,连接BE,则∠AEB=∠ACB,又由∠AEB是△BDE的一个外角,得∠AEB>∠ADB,因此∠ACB>∠ADB,就与条件∠ACB=∠ADB矛盾,所以点D不在圆O外)请结合图④证明点D也不在⊙O内.[结论]综上可得结论:如图②,如果∠ACB=∠ADB=a(点C,D在AB的同侧),那么点D在经过A,B,C三点的圆上,即:点A、B、C、D四点共圆.[应用]利用上述结论解决问题:如图⑤,已知△ABC中,∠C=90°,将△ACB绕点A顺时针旋转一个角度得△ADE,连接BE、CD,延长CD交BE于点F,(1)求证:点B、C、A、F四点共圆;(2)求证:BF=EF.50.如图1,等腰△ABC中,AB=AC,点D在AC的垂直平分线上,射线BD与BC所夹锐角为30°,连接AD.(1)求证:AB=AD;(2)如图2,AD交BC于点E,将∠CBD沿BD翻折交CD的延长线于点F,直接写出DF 与DE的数量关系;(3)如图3,在(2)的条件下,延长AB,CD交于点H,若∠H=30°,HB=b,△ABE 的面积为a,求AB的长(用含a,b的式子表示).冀教新版九年级上学期《28.2 过三点的圆》2018年同步练习卷参考答案与试题解析一.选择题(共23小题)1.如图,点A、B、C在同一条直线上,点D在直线AB外,过这四个点中的任意3个,能画的圆有()A.1 个B.2个C.3个D.4 个【分析】根据不在同一直线上的三点确定一个圆解答.【解答】解:∵点A、B、C在同一条直线上,∴经过点A、B、D,或点A、C、D,或点B、C、D分别能画一个圆,故选:C.【点评】本题考查的是确定圆的条件,掌握不在同一直线上的三点确定一个圆是解题的关键.2.在平面直角坐标系中,点A的坐标是(﹣1,0),点B的坐标是(3,0),在y轴的正半轴上取一点C,使A、B、C三点确定一个圆,且使AB为圆的直径,则点C的坐标是()A.(0,)B.(,0)C.(0,2)D.(2,0)【分析】直接根据相交弦定理得出OC2=OA•OB,即可求出OC的长,即可得出C点坐标.【解答】解:如图,连结AC,CB.依相交弦定理的推论可得:OC2=OA•OB,即OC2=1×3=3,解得:OC=或﹣(负数舍去),故C点的坐标为(0,).故选:A.【点评】本题考查了确定圆的条件,坐标与图形性质,注意辅助线的作法.3.下列说法正确的是()A.长度相等的两条弧是等弧B.三点确定一个圆C.同一条弦所对的两条弧一定是等弧D.半圆是弧【分析】根据等弧的定义对A、C进行判断;根据确定圆的条件对B进行判断;根据弧的定义对D进行判断.【解答】解:A、长度相等的两条弧不一定是等弧,所以A选项错误;B、不共线的三点确定一个圆,所以B选项错误;C、同一条弦所对的两条弧不一定是等弧,所以C选项错误;D、半圆是弧,所以D选项正确.故选:D.【点评】本题考查了确定圆的条件:不在同一直线上的三点确定一个圆.也考查了圆的有关概念.4.下列说法正确的是()A.三点确定一个圆B.长度相等的两条弧是等弧C.经过圆内一点有且仅有一条直径D.半圆是弧【分析】利用确定圆的条件及圆的有关定义分别判断后即可确定正确的选项.【解答】解:A、不在同一直线上的三点确定一个圆,故错误;B、能够完全重合的两条弧是等弧,故错误;C、经过圆内除圆心外的一点有且只有一条直线,故错误;D、半圆是弧,正确,故选:D.【点评】本题考查了确定圆的条件及圆的认识,解题的关键是能够了解圆的有关定义,难度不大.5.如图的矩形ABCD中,E为的中点,有一圆过C、D、E三点,且此圆分别与、相交于P、Q两点.甲、乙两人想找到此圆的圆心O,其作法如下:(甲)作∠DEC的角平分线L,作的中垂线,交L于O点,则O即为所求;(乙)连接、,两线段交于一点O,则O即为所求对于甲、乙两人的作法,下列判断何者正确?()A.两人皆正确B.两人皆错误C.甲正确,乙错误D.甲错误,乙正确【分析】根据线段垂直平分线的性质判断甲,根据90°的圆周角所对的弦是直径判断乙.【解答】解:甲,∵=,∴△DEC为等腰三角形,∴L为之中垂线,∴O为两中垂线之交点,即O为△CDE的外心,∴O为此圆圆心.乙,∵∠ADC=90°,∠DCB=90°,∴、为此圆直径,∴与的交点O为此圆圆心,因此甲、乙两人皆正确.故选:A.【点评】本题考查的是确定圆的条件,掌握线段垂直平分线的性质、圆周角定理是解题的关键.6.确定一个圆的条件是()A.已知圆心B.已知半径C.过三个已知点D.过一个三角形的三个顶点【分析】已知圆心和半径所作的圆就是唯一的.【解答】解:确定一个圆的条件是圆心和半径,过一个三角形的三个顶点即可确定一个圆,故选:D.【点评】此题主要考查了确定圆的条件,根据不在一条直线上的三点确定一个圆得出是解题关键.7.下列说法中,正确的是()A.三点确定一个圆B.三角形有且只有一个外接圆C.四边形都有一个外接圆D.圆有且只有一个内接三角形【分析】根据确定圆的条件逐一判断后即可得到答案.【解答】解:A、不在同一直线上的三点确定一个圆,故原命题错误;B、三角形有且只有一个外切圆,原命题正确;C、并不是所有的四边形都有一个外接圆,原命题错误;D、圆有无数个内接三角形.故选:B.【点评】本题考查了确定圆的条件,不在同一直线上的三点确定一个圆.8.小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是()A.第一块B.第二块C.第三块D.第四块【分析】要确定圆的大小需知道其半径.根据垂径定理知第①块可确定半径的大小.【解答】解:第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.故选:A.【点评】本题考查了确定圆的条件,解题的关键是熟练掌握:圆上任意两弦的垂直平分线的交点即为该圆的圆心.9.△ABC的三边长分别为6、8、10,则其外接圆的半径是()A.3B.4C.5D.10【分析】先利用勾股定理的逆定理得到△ABC为直角三角形,利用斜边为外接圆的直径计算△ABC的外接圆的半径.【解答】解:∵62+82=102,∴△ABC为直角三角形,∴△ABC的外接圆的半径==5.故选:C.【点评】本题考查了三角形的外接圆与外心:经过三角形的三个顶点的圆,叫做三角形的外接圆;三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.10.如图,△ABC内接于圆O,连接OA、OB,∠C=40°,则∠AOB的度数是()A.80°B.50°C.45°D.40°【分析】依据圆周角定理求解即可.【解答】解:∵∠C=∠AOB,∴∠AOB=2∠C.又∵∠C=40°,∴∠AOB=2×40°=80°.故选:A.【点评】本题主要考查的是圆周角定理的应用,熟练掌握圆周角定理是解题的关键.11.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为()A.1B.C.D.2【分析】连接OC、OB、OD,根据圆周角定理求出∠BOC=60°,得到△OCB是等边三角形,求出OC=OB=BC=,根据旋转的性质得到∠COD=90°,根据勾股定理计算即可.【解答】解:连接OC、OB、OD,由圆周角定理得,∠BOC=2∠A=60°,∴△OCB是等边三角形,∴OC=OB=BC=,由旋转的性质可知,∠COD=90°,∴CD==2,故选:D.【点评】本题考查的是三角形的外接圆与外心的概念和性质,掌握圆周角定理、勾股定理、等边三角形的判定定理是解题的关键.12.三角形两边的长分别是8和6,第三边的长是方程x2﹣12x+20=0的一个实数根,则三角形的外接圆半径是()A.4B.5C.6D.8【分析】先解方程,根据三角形的三边关系可知x=10:三边分别为6、8、10,是直角三角形,所以其斜边就是外接圆的直径;【解答】解:x2﹣12x+20=0,(x﹣2)(x﹣10)=0,∴x=10或2,当x=2时,2+6=8,不符合题意,∴x=10,当第三边为10时,因为62+82=102,此三角形是直角三角形,如图1,此三角形的外接圆的直径为最大边10,则此三角形的外接圆半径为5,故选:B.【点评】本题考查了三角形的外接圆与外心、利用因式分解法解一元二次方程,明确三边垂直平分线的交点即是三角形外接圆的圆心,熟记特殊三角形的外接圆与外心:直角三角形的斜边是外接圆的直径,其斜边的中点即是外接圆的圆心.13.如图,△ABC内接于⊙O,连接BO并延长,交⊙O于点D,已知BO=1,∠A=60°,则BC的长为()A.B.C.2D.3【分析】连接CD,根据圆周角定理得到∠D=∠A=60°,根据正弦的概念计算即可.【解答】解:连接CD,∵BO=1,∴BD=2,由圆周角定理得,∠D=∠A=60°,∵BD是⊙O的直径,∴∠BCD=90°,∴BC=BD×sin∠BDC=,故选:B.【点评】本题考查的是三角形的外接圆与外心,掌握圆周角定理、解直角三角形的一般步骤是解题的关键.14.如图,△ABC内接于⊙O,AD是△ABC边BC上的高,D为垂足.若BD=1,AD=3,BC=7,则⊙O的半径是()A.B.C.D.【分析】过点A作直径AH,连接CH,根据勾股定理分别求出AB、AC,证明△ABD∽△AHC,根据相似三角形的性质列出比例式,计算即可.【解答】解:过点A作直径AH,连接CH,∵BD=1,BC=7,∴CD=6.∵AD⊥BC,∴AB==,AC==3,∵AH为⊙O的直径,∴∠ACH=90°,∴∠ADB=∠ACH,由圆周角定理得,∠B=∠H,∴△ABD∽△AHC,∴=,即=,解得,AH=5,∴⊙O的半径=,故选:C.【点评】本题考查的是三角形的外接圆与外心,掌握相似三角形的判定和性质、圆周角定理是解题的关键.15.三角形的外接圆的圆心为()A.三条高的交点B.三条边的垂直平分线的交点C.三条角平分线的交点D.三条中线的交点【分析】根据三角形外心的性质进行判断.【解答】解:A、三角形三条高的交点是三角形的垂心,故A错误;B、由于三角形的外心是三角形三条边的垂直平分线的交点,故B正确;C、三角形三条角平分线的交点是三角形的内心,故C错误;D、三角形三边中线的交点是三角形的重心,故D错误;故选:B.【点评】此题主要考查了三角形外心的性质.注意三角形重心、垂心、内心、外心的区别.16.已知⊙O的半径为5,锐角△ABC内接于⊙O,AB=8,BD⊥AC于D,若CD=4,则BD的长为()A.4B.5C.D.【分析】延长BO交⊙O于H,连接AH,根据勾股定理求出AH,证明△HAB∽△CDB,根据相似三角形的性质列式计算即可.【解答】解:延长BO交⊙O于H,连接AH,∵BH是⊙O的直径,∴∠HAB=90°,∴AH==6,∵∠HAB=∠CDB=90°,∠H=∠C,∴△HAB∽△CDB,∴=,即=,解得,BD=,故选:D.【点评】本题考查的是三角形的外接圆与外心、相似三角形的判定和性质,掌握圆周角定理、勾股定理是解题的关键.17.如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b﹣;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是()A.2B.3C.4D.5【分析】①根据正方形的性质得到∠BAD=∠ADC=∠B=90°,根据旋转的性质得到∠NAD=∠BAM,∠AND=∠AMB,根据余角的性质得到∠DAM+∠NAD=∠NAD+∠AND =∠AND+∠NAD=90°,等量代换得到∠DAM=∠AND,故①正确;②根据正方形的性质得到PC∥EF,根据相似三角形的性质得到CP=b﹣;故②正确;③根据旋转的性质得到GN=ME,等量代换得到AB=ME=NG,根据全等三角形的判定定理得到△ABM≌△NGF;故③正确;④由旋转的性质得到AM=AN,NF=MF,根据全等三角形的性质得到AM=NF,推出四边形AMFN是矩形,根据余角的想知道的∠NAM=90°,推出四边形AMFN是正方形,于是得到S四边形AMFN=AM2=a2+b2;故④正确;⑤根据正方形的性质得到∠AMP=90°,∠ADP=90°,得到∠ABP+∠ADP=180°,于是推出A,M,P,D四点共圆,故⑤正确.【解答】解:①∵四边形ABCD是正方形,∴∠BAD=∠ADC=∠B=90°,∴∠BAM+∠DAM=90°,∵将△ABM绕点A旋转至△ADN,∴∠NAD=∠BAM,∠AND=∠AMB,∴∠DAM+∠NAD=∠NAD+∠AND=∠AND+∠NAD=90°,∴∠DAM=∠AND,故①正确;②∵四边形CEFG是正方形,∴PC∥EF,∴△MPC∽△EMF,∴,∵大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),BM=b,∴EF=b,CM=a﹣b,ME=(a﹣b)+b=a,∴,∴CP=b﹣;故②正确;③∵将△MEF绕点F旋转至△NGF,∴GN=ME,∵AB=a,ME=a,∴AB=ME=NG,在△ABM与△NGF中,,∴△ABM≌△NGF;故③正确;④∵将△ABM绕点A旋转至△ADN,∴AM=AN,∵将△MEF绕点F旋转至△NGF,∴NF=MF,∵△ABM≌△NGF,∴AM=NF,∴四边形AMFN是矩形,∵∠BAM=∠NAD,∴∠BAM+DAM=∠NAD+∠DAN=90°,∴∠NAM=90°,∴四边形AMFN是正方形,∵在Rt△ABM中,a2+b2=AM2,∴S四边形AMFN=AM2=a2+b2;故④正确;⑤∵四边形AMFN是正方形,∴∠AMP=90°,∵∠ADP=90°,∴∠AMP+∠ADP=180°,∴A,M,P,D四点共圆,故⑤正确.故选:D.【点评】本题考查了四点共圆,全等三角形的判定和性质,相似三角形的判定和性质,正方形的性质旋转的性质,勾股定理,正确的理解题意是解题的关键.18.如图,一副直角三角板满足∠ACB=∠EDF=90°,AC=BC,AB=DF,∠EFD=30°,将三角板DEF的直角顶点D放置于三角板ABC的斜边AB上,再将三角板DEF绕点D 旋转,并使边DE与边AC交于点M,边DF与边BC于点N.当∠EDF在△ABC内绕顶点D旋转时有以下结论:①点C,M,D,N四点共圆;②连接CD,若AD=DB,则△ADM∽△CDN;③若AD=DB,则DN•CM=BN•DM;④若AD=DB,则CM+CN=AD;⑤若DB=2AD,AB=6,则2≤S△DMN≤4.其中正确结论的个数是()A.2B.3C.4D.5【分析】①正确,如图1中,只要证明∠MCN+∠MDN=180°.②正确,可以证明△ADM与△DCN全等.③正确,如图3中,只要证明△ADM≌△CDN,推出AM=CN,DM=DN,因为AC=BC,推出CM=BN,即可证明.④正确,如图4中,作DH⊥AC于H,DG⊥BC于G.只要证明四边形CHDG是正方形,△DHM≌△DGN,推出MH=NG,推出CM+CN=CH+MH+CG﹣NG=2CH,又因为AD =CD=CH,由此即可证明.⑤正确,如图5中,由△DHM∽△DGN,推出==,设DM=x,则DG=2x,推出S△DMN=•2x•x=x2,当DM⊥AC时,DM的值最小,此时DM=DH=,△DMN 的面积最小值为2,当DM⊥AB时,DM的值最大,此时DM=AD=2,△DMN的面积的最大值为4,由此即可判断.【解答】解:①正确.理由如下:如图1中,∵∠ACB=90°,∠EDF=90°,∴∠MCN+∠MDN=180°,∴点C,M,D,N四点共圆.②正确.理由如下:如图2中,连接CD.∵AC=BC.AD=DB.∴CD⊥AB,CD=AD=DB,∴∠ADC=∠MDN=90°,∴∠ADM=∠CDN,在△ADM和△CDN中,,∴△ADM≌△CDN.故②正确.③正确.理由如下:如图3中∵CA=CB,∠ACB=90°,AD=DB,∴CD=AD=DB,CD⊥AB,∠A=∠ACD=∠DCN=45°,∴∠ADC=∠EDF=90°,∴∠ADM=∠CDN,在△ADM和△CDN中,,∴△ADM≌△CDN,∴AM=CN,DM=DN,∵AC=BC,∴CM=BN,∴DN•CM=BN•DM④正确.理由如下:如图4中,作DH⊥AC于H,DG⊥BC于G.∵∠ACD=∠BCD=45°,∴DH=DG,∵∠DHC=∠HCG=∠CGD=90°,∴四边形CHDG是矩形,∵DH=DG,∴四边形CHDG是正方形,∴∠HDG=∠MDN=90°,CH=CG,∴∠MDH=∠GDN,在△DHM和△DGN中,,∴△DHM≌△DGN,∴MH=NG∴CM+CN=CH+MH+CG﹣NG=2CH,∵AD=CD=CH,∴CM+CN=AD.⑤正确.理由如下:如图5中,作DH⊥AC于H,DG⊥BC于G.∵AB=6,BD=2AD,∴AD=2,BD=4,∴AH=DH=,DG=GB=2,∵∠DHC=∠HCG=∠CGD=90°,∴四边形CHDG是矩形,∴∠HDG=∠MDN,∴∠MDH=∠NDG,∵∠DHM=∠DGN=90°,∴△DHM∽△DGN,∴==,设DM=x,则DG=2x,∴S△DMN=•2x•x=x2,当DM⊥AC时,DM的值最小,此时DM=DH=,△DMN的面积最小值为2,当DM⊥AB时,DM的值最大,此时DM=AD=2,△DMN的面积的最大值为4,∴2≤S△DMN≤4.故选:D.【点评】本题考查四点共圆、旋转变换、全等三角形的判定和性质、相似三角形的判定和性质,最值问题等知识,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.19.如图,在四边形ABCD中,AC、BD为对角线,点M、E、N、F分别为AD、AB、BC、CD边的中点,下列说法:①当AC=BD时,M、E、N、F四点共圆.②当AC⊥BD时,M、E、N、F四点共圆.③当AC=BD且AC⊥BD时,M、E、N、F四点共圆.其中正确的是()A.①②B.①③C.②③D.①②③【分析】连接EM、MF、FN、NE,连接EF、MN,交于点O,利用三角形中位线定理可证到四边形ENFM是平行四边形;然后根据条件判定四边形ENFM的形状,就可知道M、E、N、F四点是否共圆.【解答】解:连接EM、MF、FN、NE,连接EF、MN,交于点O,如图所示.∵点M、E、N、F分别为AD、AB、BC、CD边的中点,∴EM∥BD∥NF,EN∥AC∥MF,EM=NF=BD,EN=MF=AC.∴四边形ENFM是平行四边形.①当AC=BD时,则有EM=EN,所以平行四边形ENFM是菱形.而菱形的四个顶点不一定共圆,故①不一定正确.②当AC⊥BD时,由EM∥BD,EN∥AC可得:EM⊥EN,即∠MEN=90°.所以平行四边形ENFM是矩形.则有OE=ON=OF=OM.所以M、E、N、F四点共圆,故②正确.③当AC=BD且AC⊥BD时,同理可得:四边形ENFM是正方形.则有OE=ON=OF=OM.所以M、E、N、F四点共圆,故③正确.故选:C.【点评】本题考查了四点共圆、三角形的中位线定理、平行四边形的判定与性质、矩形的判定与性质、菱形的判定与性质、正方形的判定与性质等知识.在解决问题的过程中,可能会把AC、BD误认为是平行四边形ENFM的对角线,从而由AC=BD得到该四边形是矩形这样一个错误结论,需加以注意.20.锐角△ABC的三条高AD、BE、CF交于H,在A、B、C、D、E、F、H七个点中.能组成四点共圆的组数是()A.4组B.5组C.6组D.7组【分析】根据两个直角三角形公共斜边时,四个顶点共圆,完整选择.【解答】解:如图,以AH为斜边的两个直角三角形,四个顶点共圆(A、F、H、E),以BH为斜边的两个直角三角形,四个顶点共圆(B、F、H、D),以CH为斜边的两个直角三角形,四个顶点共圆(C、D、H、E),以AB为斜边的两个直角三角形,四个顶点共圆(A、E、D、B),以BC为斜边的两个直角三角形,四个顶点共圆(B、F、E、C),以AC为斜边的两个直角三角形,四个顶点共圆(A、F、D、C),共6组.故选:C.【点评】本题考查了四点共圆的判断方法.关键是明确有公共斜边的两个直角三角形的四个顶点共圆.21.如图,已知(1)已知△ABC的两条中线BD、CE交于点M,A、D、M、E四点共圆,BC=8,则AM的长为()A.2B.C.D.3【分析】延长AM交BC于F,连接ED,根据三角形中位线定理得出ED∥BC,即可求得∠DBC=∠MDE,根据四点共圆,可得∠MDE=∠BAF,由题意可得M是三角形的重心,则F是BC的中点,AM=2FM,证得△ABF∽△MBF,可得=,得出AF•FM=BF2=16,根据条件化成AM2=16,即可求得结论.【解答】解:延长AM交BC于F,连接ED,∵BD、CE是△ABC的两条中线,∴ED∥BC,∴∠DBC=∠MDE,∵A、D、M、E四点共圆,∴∠MDE=∠BAF,∵△ABC的两条中线BD、CE交于点M,∴BF=FC=BC=4,∴M为三角形的重心,∴AM=2FM,∵∠BAF=∠MBF,∠AFB=∠BFM,∴△ABF∽△MBF,∴=,∴AF•FM=BF2=16,(AM+AM)•AM=16,∴AM2=16,∴AM=.故选:C.【点评】本题考查了三角形的重心,圆周角定理,三角形相似的判定和性质,三角形中位线定理等,作出辅助线,构建相似三角形是解题的关键.22.如图,在△ABC中,∠B=75°,∠C=45°,BC=6﹣2,点P是BC上一动点,PE⊥AB于E,PD⊥AC于D.无论P的位置如何变化,线段DE的最小值为()A.3﹣3B.C.4﹣6D.2【分析】下面介绍两种解法:解法一:当AP⊥BC时,线段DE的值最小,利用四点共圆的判定可得:A、E、P、D四点共圆,且直径为AP,得出∠AED=∠C=45°,有一公共角,根据两角对应相等两三角形相似得△AED∽△ACB,则,设AD=2x,表示出AE和AC的长,求出AE与AC的比,代入比例式中,可求出DE的值.解法二:先通过四点共圆同理得到:△EFD为顶角为120°的等腰三角形,所以当AP⊥BC 时,线段DE的值最小,再作辅助线,求AP的长,从而得EF的长,由等腰三角形三线合一及勾股定理得DE的值.【解答】解:解法一:当AP⊥BC时,线段DE的值最小,如图1,∵PE⊥AB,PD⊥AC,∴∠AEP=∠ADP=90°,∴∠AEP+∠ADP=180°,∴A、E、P、D四点共圆,且直径为AP,在Rt△PDC中,∠C=45°,∴△PDC是等腰直角三角形,∠APD=45°,∴△APD也是等腰直角三角形,∴∠P AD=45°,∴∠PED=∠P AD=45°,∴∠AED=45°,∴∠AED=∠C=45°,∵∠EAD=∠CAB,∴△AED∽△ACB,∴,设AD=2x,则PD=DC=2x,AP=2x,如图2,取AP的中点O,连接EO,则AO=OE=OP=x,∵∠EAP=∠BAC﹣∠P AD=60°﹣45°=15°,∴∠EOP=2∠EAO=30°,过E作EM⊥AP于M,则EM=x,cos30°=,∴OM=x•=x,∴AM=x+x=x,由勾股定理得:AE=,=,=(+1)x,∴=,∴ED=.则线段DE的最小值为;解法二:如图3,取AP的中点F,连接EF、DF,有EF=DF=AP,∠EFD=120°,∴△EFD为顶角为120°的等腰三角形,∴当AP⊥BC时,线段DE的值最小,如图4,作AB的中垂线,交AP于一点O,交AB于G,连接OB,设OA=OB=2x,∵∠BOP=2∠BAO=30°,∴BP=x,OP=x,∴AP=PC=(2+)x,∵BC=6﹣2,∴x+2x+x=6﹣2,x=4﹣2,∴AP=(2+)x=(2+)(4﹣2)=2,∴EF=FD=1,如图5,过F作FH⊥ED于H,∴EH=DH,∵∠FED=30°,∴FH=,∴EH=DH=,∴DE=;故选:B.【点评】本题考查了四点共圆的问题,四点共圆的判定方法有:①将四点连成一个四边形,若对角互补,那么这四点共圆.②连接对角线,若这个四边形的一边同侧的两个顶角相等,那么这四点共圆;通过四点共圆可以利用同弧所对的圆周角得出角相等,从而证得三角形相似,得比例式,使问题得以解决.23.在圆内接四边形ABCD中,∠BAD、∠ADC的角平分线交于点E,过E作直线MN平行于BC,与AB、CD交于M、N,则总有MN=()A.BM+DN B.AM+CN C.BM+CN D.AM+DN【分析】在NM上截取NF=ND,连结DF,AF,由A,B,C,D四点共圆,得出∠MND+∠MAD=180°,由MN∥BC,得出∠AMN+∠ADN=180°,可得到A,D,N,M四点共圆,再由AE,DE分别平分∠BAD,∠CDA,A,F,E,D四点共圆,由∠MAF=180°﹣∠DAF﹣∠MND=180°﹣∠DEN﹣∠MND=∠EDN=∠ADE=∠AFM,可得出MA =MF,即得出MN=MF+NF=MA+ND.【解答】解:如图,在NM上截取NF=ND,连结DF,AF∴∠NFD=∠NDF,∵A,B,C,D四点共圆,∴∠ADC+∠B=180°,∵MN∥BC,∴∠AMN=∠B,∴∠AMN+∠ADN=180°,∴A,D,N,M四点共圆,∴∠MND+∠MAD=180°,∵AE,DE分别平分∠BAD,∠CDA,∴∠END+2∠DFN=∠END+2∠DAE=180°,∴∠DFN=∠DAE,∴A,F,E,D四点共圆,∴∠DEN=∠DAF,∠AFM=∠ADE,。
过三点的圆冀教版九年级数学(上册)-【完整版】

过三点的 圆-冀教 版九年 级数学 上册- 精品课 件ppt( 实用版)
③等边三角形外接圆的半径等于 边长的 3
3
A
在等边△ABC中,设边长为a,
O
N
两边的中垂线交于点O,则OB 为外接圆半径
B
M
∟
C
由BM 1 BC 1 a, 22
2.如图,点A、B、C在同一条直线上,点D在直线AB外,
过这四点中的任意三个点,能画圆的个数是(3个).
●
●
● ●
想一想
三角形的三个顶点一定在同一个圆上吗?
三角形的三个顶点不在同一直线上,因此它 们在同一个圆上.
知识点二:
①经过三角形三个顶点的圆,叫做三角形的外接圆.
C
②外接圆的圆心叫做三角形的外心.
正方形,其中E点在△ABC的外部,判断下列叙述是否
正确. A E
×②O是△ADB的外心×,O不
D 是△ADC的外心;
O B
分析:
C
过三点的 圆-冀教 版九年 级数学 上册- 精品课 件ppt( 实用版)
过三点的 圆-冀教 版九年 级数学 上册- 精品课 件ppt( 实用版)
例2.如图,小明家的房前有一块矩形的空地.空地上 有三棵树A、B、C,小明想建一个圆形花坛,使三棵 树都在花坛的边上.
②作线段BC的垂直平分线MN;
③以EF和MN的交点O为圆心,以 A
OA为半径作圆.
⊙O即为△ABC的外接圆.
B
.O C
试一试
分别画下面三角形的外接圆,并说明外心的位置与三角形的 形状之间具有怎样的关系.(用尺规在课本151页练习第2题中画出)
冀教版九年级数学上册《28.2过三点的圆》同步测试题带答案

冀教版九年级数学上册《28.2过三点的圆》同步测试题带答案学校:___________班级:___________姓名:___________考号:___________一、选择题1.下列命题中,真命题的个数是()①经过三点一定可以作圆;②任意一个圆只有一个内接三角形;③任意一个三角形一定有一个外接圆,并且只有一个外接圆;④三角形的外心到三角形的三边距离相等.A.4个B.3个C.2个D.1个2.如图,直角坐标系中A(0,4),B(4,4),C(6,2),经过A,B,C三点的圆,圆心为M,则点M的坐标为()A.(1,−1)B.(1,0)C.(2,0)D.(2,1)3.三角形的外心具有的性质是()A.到三边的距离相等B.到三个顶点的距离相等C.外心在三角形外D.外心在三角形内4.如图是一块被打碎的圆形玻璃,若想要去店里配到一块与原来大小一样的圆形玻璃,应该带去店里的碎片是()A.①B.②C.③D.④5.已知M(1,2),N(3,−3),P(x,y)三点可以确定一个圆,则以下P点坐标不满足要求的是()A.(3,5)B.(−3,5)C.(−1,7)D.(1,−3)6.设Rt△ABC的两条直角边长分别为6,8,则此直角三角形外接圆半径为()A.5B.10C.2√7D.5或2√77.校园内有一块三角形的花坛,现要在花坛内建一景观喷泉,要使喷泉到花坛三个顶点的距离相等,喷泉的位置应选在这个三角形花坛的()A.外心B.垂心C.重心D.内心8.如图所示,点A,B,C均在6×6的正方形网格格点上,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为()A.4B.5C.6D.79.已知Rt△ABC中∠A=90°,AB=6,AC=8,则△ABC外接圆的半径为()A.3B.4C.5D.不确定10.如图,△ABC外接圆的圆心坐标是()A.(5,2)B.(2,3)C.(1,4)D.(0,0)二、填空题11.已知平面直角坐标系中的三个点分别为A(1,−1)、B(−2,5)、C(4,−6),则A、B、C这三个点确定一个圆(填“可以”或“不可以”).12.如图,在△ABC中,BC=3cm,△BAC=60°,那么△ABC能被半径至少为cm的圆形纸片所覆盖.13.如图所示的网格中,每个小正方形的边长均为1,点A、B、C均在小正方形的顶点上,点C同⌢上,若点P是BC⌢的一个动点,则△ABP面积的最大值是.时也在AB三、解答题14.如图,学校某处空地上有A、B、C三棵树,现准备建一个圆形景观鱼池,要求A、B、C三棵树恰在圆周上,请你帮助设计鱼池,在图中作出它的鱼池轮廓,保留作图痕迹并将圆心标记为点O.15.如图,在△ABC中BC=16,AB=AC=10.(1)尺规作图:作△ABC的外接圆(保留作图痕迹)(2)求(1)中所作外接圆的半径R.16.如图,在平面直角坐标系中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).(1)若△ABC的外接圆的圆心为M,则圆心M的坐标为______,⊙M的半径为______;(2)△ABC的外接圆与x轴的另一个交点坐标是______;⌢的长是______.(3)⊙M中AC17.如图,正方形网格中每个小正方形的边长为1,点A,B,C,D都在小正方形的顶点上.(1)判断△ABC的形状,并说明理由.(2)若△ABC的外接圆为△O,判断点D与△O的位置关系,并说明理由.参考答案1.D2.C3.B4.B5.C6.A7.A8.B9.C10.A11.可以12.√3.13.8√5−814.解:如图所示.连接AB,BC,分别作AB,BC的垂直平分线,交于点O,以OA的长度为半径,O 为圆心作圆,则⊙O即为所求15.(1)解:如图所示:∴⊙O即为所求;(2)解:如图所示:∵OA⊥BC于D,且OB=OA,BC=16,AB=10∴BD=12BC=8在Rt△ABD中∠ADB=90°,则AD=√AB2−BD2=√102−82=6在Rt△BOD中∠DOB=90°,则OB2=OD2+BD2设OB=R,则OD=R−6,即R2=(R−6)2+64,解得R=253∴(1)中所作外接圆的半径R=253.16.(1)(5,5);√29(2)(7,0)(3)√29π217.(1)解:△ABC是等腰直角三角形,理由如下:由图可知:AB=AC,△BAC=90°∴△ABC是等腰直角三角形;(2)解:点D在△O上,理由如下:△ABC的外接圆如图∵OD=OA∴点D在△O上.则点D与△O的位置关系是:点D在△O上.。
2020-2021学年最新冀教版九年级数学上册《圆》达标检测卷及答案解析-精编试题
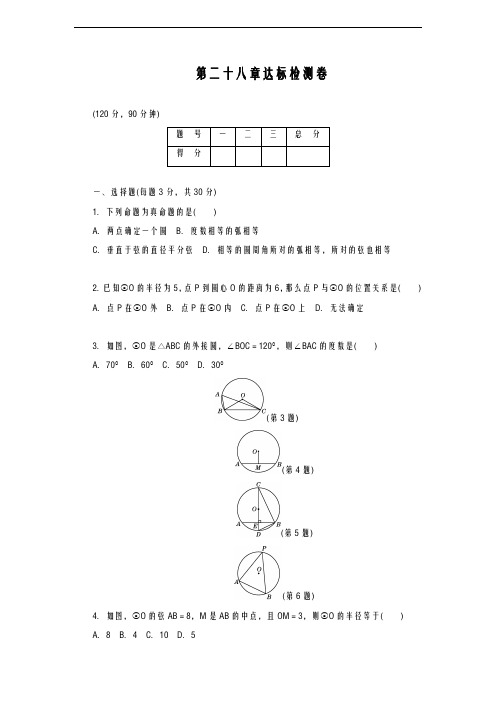
第二十八章达标检测卷(120分,90分钟)题号一二三总分得分一、选择题(每题3分,共30分)1.下列命题为真命题的是( )A.两点确定一个圆B.度数相等的弧相等C.垂直于弦的直径平分弦D.相等的圆周角所对的弧相等,所对的弦也相等2.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是( ) A.点P在⊙O外B.点P在⊙O内C.点P在⊙O上D.无法确定3.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是( )A.70°B.60°C.50°D.30°(第3题)(第4题)(第5题)(第6题)4.如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( ) A.8 B.4 C.10 D.55.(中考·兰州)如图,CD 是⊙O 的直径,弦AB ⊥CD 于E ,连接BC ,BD.下列结论中不一定正确的是( )A .AE =BE B.AD ︵=BD ︵C .OE =DED .∠DBC =90°6.如图,A ,B ,P 是半径为2的⊙O 上的三点,∠APB =45°,则弦AB 的长为( ) A .2 B .4 C. 2 D .2 27.如图,在△ABC 中,∠ACB =90°,∠ABC =30°,AB =2.将△ABC 绕直角顶点C 逆时针旋转60°得△A ′B ′C ,则点B 转过的路径长为( )A.π3 B.3π3 C.2π3D .π (第7题)(第8题)(第9题)(第10题)8.如图,如果从半径为9 cm 的圆形纸片剪去13圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为( )A .6 cmB .3 5 cmC .8 cmD .5 3 cm9.如图,将半径为2 cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( ) A.2 cm B. 3 cm C.2 3 cm D.2 5 cm10.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE =6,∠BAC+∠EAD=180°,则弦BC的弦心距等于( )A.412B.342C.4 D.3二、填空题(每题3分,共30分)11.如图,点A,B,C在⊙O上,∠AOC=60°,则∠ABC的度数是________.12.如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段OM的长的取值范围是________.13.如图,AD为⊙O的直径,AD=6 cm,∠DAC=∠ABC,则AC=________.(第11题)(第12题)(第13题)(第14题)(第16题)14.如图,在四边形ABCD中,若AB=AC=AD,则下列等式不一定成立的是________.①∠1=2∠4 ②∠2=2∠7 ③∠3+∠4=∠5 ④∠6=∠1+∠815.直角三角形的两边长分别为16和12,则此三角形的外接圆半径是________.16.如图,在⊙O 的内接五边形ABCDE 中,∠CAD =35°,则∠B +∠E =________°. 17.如图,水平放置的圆柱形油槽的截面直径是52 cm ,装入油后,油深CD 为16 cm ,那么油面宽度AB =________cm.(第17题)(第18题)(第20题)18.如图,半径为5的⊙P 与y 轴交于点M(0,-4),N(0,-10),函数y =kx (x<0)的图像过点P ,则k =________.19.已知在半径为4的⊙O 中,弦AB =43,点P 在⊙O 上,则∠APB =________. 20.如图,在扇形AOB 中,∠AOB =90°,点C 为OA 的中点,CE ⊥OA 交AB ︵于点E ,以点O 为圆心,OC 的长为半径作CD ︵交OB 于点D.若OA =2,则阴影部分的面积为________.三、解答题(21、22题每题8分,23、24题每题10分,其余每题12分,共60分) 21.如图,AB 是⊙O 的一条弦,OD ⊥AB ,垂足为点C ,交⊙O 于点D ,点E 在⊙O 上. (1)若∠AOD =52°,求∠DEB 的度数; (2)若OC =3,OA =5,求AB 的长.(第21题)22.“不在同一条直线上的三个点确定一个圆”.请你判断平面直角坐标系内的三个点A(2,3),B(-3,-7),C(5,11)是否可以确定一个圆.23.如图,△ABC 的三个顶点都在⊙O 上,AP ⊥BC 于P ,AM 为⊙O 的直径.求证:∠BAM =∠CAP.(第23题)24.如图,在△ABC 中,AB =AC =45,cosC =55.(1)动手操作:利用尺规作以AC 为直径的⊙O ,并标出⊙O 与AB 的交点D ,与BC 的交点E(保留作图痕迹,不写作法);(2)综合应用:在你所作的图中, ①求证:DE ︵=CE ︵; ②求点D 到BC 的距离.(第24题)25.如图,一拱形公路桥,圆弧形桥拱的水面跨度AB =80米,桥拱到水面的最大高度为20米.(1)求桥拱的半径.(2)现有一艘宽60米,顶部截面为长方形且高出水面9米的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.(第25题)26.如图,在Rt △ABC 中,∠ACB =90°,半径长为1的圆A 与边AB 相交于点D ,与边AC 相交于点E ,连接DE 并延长,与线段BC 的延长线交于点P ,连接AP.(1)当∠B =30°时,若△AEP 与△BDP 相似,求CE 的长; (2)若CE =2,BD =BC ,求∠BPD 的正切值;(3)若tan ∠BPD =13,设CE =x ,△ABC 的周长为y ,求y 关于x 的函数表达式.(第26题)答案一、1.C 2.A 3.B 4.D 5.C 6.D 7.B8.B 点拨:∵留下的扇形的弧长为23×2π×9=12π(cm).∴围成圆锥的底面圆半径r=12π2π=6(cm).又∵圆锥母线长l =9 cm ,∴圆锥的高h =l 2-r 2=92-62=35(cm). 9.C10.D 点拨:∵∠BAC +∠EAD =180°,(第10题)∴可将△ABC 旋转,让AC 和AD 重合,则AB 和AE 在一条直线上,如图所示. ∵BE 为直径, ∴∠BDE =90°.作AF ⊥DE ,垂足为F ,AG ⊥BD ,垂足为G ,则四边形AFDG 为矩形, ∴AG =DF =12DE =3.∴弦BC 的弦心距等于3. 二、11.150° 12.4≤OM ≤5 13.3 2 cm 14.④ 15.8或1016.215 点拨:∵A ,B ,C ,D 四点共圆,∴∠B +∠ADC =180°.又∵A ,C ,D ,E 四点共圆,∴∠E +∠ACD =180°.∴∠ACD +∠ADC +∠B +∠E =360°.∵∠ACD +∠ADC =180°-35°=145°,∴∠B +∠E =360°-145°=215°.17.48 18.28(第19题)19.60°或120° 点拨:如图,当点P(P 1)在弦AB 所对的优弧上时,过点O 作OC ⊥AB 于点C ,连接OA ,OB.在等腰三角形OAB 中易得AC =2 3.在Rt △OAC 中,OC =OA 2-AC 2=2=12OA ,所以∠OAC =30°,所以弦AB 所对的圆心角∠AOB =120°,所以∠AP 1B =60°.同理当点P(P 2)在弦AB 所对的劣弧上时,∠AP 2B =120°.20.32+π12 点拨:连接OE.∵点C 是OA 的中点,∴OC =12OA =1,∵OE =OA =2,∴OC =12OE =1.∵CE ⊥OA ,∴∠OEC =30°,∴∠COE =60°.在Rt △OCE 中,CE =OE 2-OC 2=3,∴S △OCE =12OC ·CE =32.∵∠AOB =90°,∴∠BOE =∠AOB -∠COE =30°,∴S 扇形OBE =30π×22360=π3.又S 扇形OCD =90π×12360=π4.因此S 阴影=S 扇形OBE +S △OCE -S 扇形OCD =π3+32-π4=π12+32. 三、21.解:(1)∵OD ⊥AB ,∴AD ︵=DB ︵. ∴∠DEB =12∠AOD =26°.(2)在Rt △AOC 中,OC =3,OA =5,由勾股定理得AC =4.∴AB =2AC =8. 22.解:设经过A ,B 两点的直线的解析式为y =kx +b. ∵A(2,3),B(-3,-7),∴⎩⎨⎧2k +b =3,-3k +b =-7.解得⎩⎨⎧k =2,b =-1.∴经过A ,B 两点的直线的解析式为y =2x -1. 当x =5时,y =2×5-1=9≠11, ∴点C(5,11)不在直线AB 上, 即A ,B ,C 三点不在同一条直线上.∴平面直角坐标系内的三个点A(2,3),B(-3,-7),C(5,11)可以确定一个圆.(第23题)23.证明:如图,连接BM.∵AP ⊥BC 于P ,∴∠CAP =90°-∠C. ∵AM 为⊙O 的直径, ∴∠ABM =90°,∴∠BAM =90°-∠M ,又∵∠M =∠C ,∴∠BAM =∠CAP. 24.(1)解:如图(1)所示.(2)①证明:如图(2),连接AE. ∵AC 为直径,∴∠AEC =90°. 又AB =AC ,∴∠BAE =∠CAE , ∴DE ︵=CE ︵.(第24题)②解:如图(2),连接CD ,过点D 作DF ⊥BC 于点F. ∵AB =AC =45,cos ∠ACB =55, ∴EC =AC ·cos ∠ACB =4. ∵AB =AC ,AE ⊥BC , ∴BC =2CE =8, ∴AE =AC 2-CE 2=(45)2-42=8.∵AC 为直径,∴∠ADC =90°, ∴S △ABC =12AB ·CD.又∠AEC =90°, ∴S △ABC =12AE ·BC ,∴12AB ·CD =12AE ·BC. 可得CD =1655,∴AD =AC 2-CD 2=1255,∴BD =AB -AD =855.∵S △DBC =12BD ·CD ,S △DBC =12DF ·BC ,∴BD ·CD =DF ·BC ,可得DF =165, ∴点D 到BC 的距离为165.25.解:(1)如图,点E 是桥拱所在圆的圆心.过点E 作EF ⊥AB 于点F ,延长EF 交⊙E 于点C ,连接AE , 则CF =20米.由垂径定理知,F 是AB 的中点,∴AF =FB =12AB =40米.设圆的半径是r 米,由勾股定理,得AE 2=AF 2+EF 2=AF 2+(CE-CF)2,即r 2=402+(r -20)2.解得r =50. ∴桥拱的半径为50米.(第25题)(2)这艘轮船能顺利通过.理由如下:宽60米的轮船可通过拱桥的最大高度为图中MN 所示.连接EM ,设EC 与MN 的交点为D , MD =30米.∵DE ⊥MN ,∴DE =EM 2-DM 2=502-302=40(米). ∵EF =EC -CF =50-20=30(米), ∴DF =DE -EF =40-30=10(米). ∵10米>9米,∴这艘轮船能顺利通过. 26.解:(1)∵∠B =30°,∠ACB =90°, ∴∠BAC =60°.又AD =AE ,∴∠AED =60°=∠PEC , ∴∠EPC =30°=∠B , ∴△BPD 为等腰三角形.又∵△AEP 与△BDP 相似,∴∠B =∠BPD =∠EAP =∠APE =30°,∴EP =AE =1,∴CE =12PE =12×1=12.(第26题)(2)过A 作AF ⊥DE 交BC 于F ,过F 作FM ⊥AB 于M(如图所示).易知∠FAC =∠BPD ,∵AF ⊥DE ,AD =AE ,∴∠FAC =∠FAM ,∵FM ⊥AB ,FC ⊥AC ,∴FM =FC ,∴Rt △AFM ≌Rt △AFC ,∴AC =AM.在Rt △ABC 中,设BC =m ,则AB =m +1,AC =CE +AE =2+1=3,由AC 2+BC 2=AB 2,解得m =4.∴AB =5.又AM =3,∴BM =2.又tanB =AC BC =34,tanB =MF BM =MF 2, ∴MF 2=34,∴MF =FC =32, ∴tan ∠FAC =FC AC =323=12, 即tan ∠BPD =12. (3)∵CE =x ,AE =1,∴AC =x +1.易知,∠FAC =∠FAB =∠BPD ,又tan ∠BPD =13,∴tan ∠CAF =13=CF AC =CF x +1, ∴CF =13(x +1)=FM , ∵∠B =∠B ,∠FMB =∠ACB =90°,∴△BFM ∽△BAC ,∴MF AC =BM BC =13(x +1)x +1=13, ∴BM =13BC ,设BM =a ,则BC =3a ,在Rt △BMF 中,由BM 2+MF 2=BF 2,有a 2+19(x +1)2=⎣⎢⎡⎦⎥⎤3a -13(x +1)2, 即a 2+19(x +1)2=9a 2-2a(x +1)+19(x +1)2,∴a =14(x +1),∴BC =3a =34(x +1). ∴AB =AM +BM =x +1+14(x +1)=54(x +1), ∴y =AB +AC +BC =54(x +1)+(x +1)+34(x +1)=3(x +1),即y =3x +3,其中x >0.。
九年级数学上册 第28章 圆 28.2 过三点的圆作业 (新版)冀教版

28.2 过三点的圆一、选择题1.三角形的外心具有的性质是( )A.到三边的距离相等B.到三个顶点的距离相等C.外心在三角形外D.外心在三角形内2.若△ABC的外接圆的圆心在△ABC的内部,则△ABC是( )A.锐角三角形 B.直角三角形C.钝角三角形 D.无法确定3.如图38-K-1,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )A.△ABE B.△ACF C.△ABD D.△ADE图38-K-1 图38-K-24.如图38-K-2,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )A.点P B.点Q C.点R D.点M5.小明不慎把家里的圆形镜子打碎了,其中四块碎片如图38-K-3所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )图38-K-3A.第①块 B.第②块 C.第③块 D.第④块二、填空题6.若AB=4 cm,则过点A,B且半径为3 cm的圆有____个.图38-K-47.新定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.根据准外心的定义,探究如下问题:如图38-K-4,在Rt△ABC中,∠C=90°,AB=10,AC=6.如果准外心P在BC边上,那么PC的长为________.三、解答题8.在△ABC中,AB=AC=10,BC=12,求△ABC的外接圆的直径.9.如图38-K-5,网格的小正方形的边长均为1,小正方形的顶点叫做格点.△ABC的三个顶点都在格点上.(1)在图上标出△ABC的外接圆的圆心O.(2)△ABC的外接圆的面积是________.图38-K-51.B2.A [解析] △ABC的外接圆的圆心在△ABC的内部,则△ABC是锐角三角形.故选A.3.B [解析] 由图可知,只有△ACF的三个顶点不都在⊙O的圆周上,故外心不是点O 的三角形是△ACF.故选B.4.B [解析] 作弦AB和BC的垂直平分线,交点Q即为圆心.故选B.5.A [解析] 第①块中有一段完整的弧,可在这段弧上任做两条弦,再作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.故选A.6.两[解析] 这样的圆能画两个.如图,作AB的垂直平分线l,再以点A为圆心,3 cm为半径作弧交l于点O1和O2,然后分别以O1和O2为圆心,3 cm为半径作圆,则⊙O1和⊙O2为所求圆.故答案为两.7.74或4 [解析] 在Rt△ABC中,∵C=90°,AB=10,AC=6,∴BC=AB2-AC2=102-62=8.若PB =PA ,连接PA , 设PC =x ,则PA =PB =8-x , 在Rt △PAC 中, ∵PA 2=PC 2+AC 2, ∴(8-x)2=x 2+62, ∴x =74,即PC =74;若PB =PC ,则PC =4;若PA =PC ,由图知,在Rt △PAC 中,不存在这种情况. 故PC 的长为74或4.8.[解析] 首先作出△ABC 的外心P ,连接点B 与外心P ,利用勾股定理求半径. 解:如图,作AD⊥BC 于点D ,与AC 的垂直平分线相交于点P ,则点P 即为△ABC 的外心,连接PB.∵AB =AC =10, ∴BD =DC =12BC =6.在Rt △ABD 中, AD =AB 2-BD 2=8.设△ABC 外接圆的半径为r ,则AP =BP =r ,PD =8-r. 在Rt △BPD 中,BP 2=BD 2+PD 2, 即r 2=62+(8-r)2. 解得r =254.∴△ABC 的外接圆的直径为252. 9.解:(1)△ABC 的外接圆的圆心O ,如图所示.(2)∵AO=32+12=10, ∴外接圆的面积是10π. 故答案为10π.。
2020-2021冀教版数学九年级上册 28.2 过三点的圆

拓展训练2020年冀教版数学九年级上册28.2 过三点的圆基础闯关全练1.如图所示,A、B、C为市内的三个住宅小区,环保公司要建一垃圾回收站,为方便起见,回收站要建在离三个小区都相等的某处,如果你是工程师,你将如何选址?(尺规作图,保留痕迹,不写作法)2.如图,一只花猫发现一只老鼠溜进了一个内部连通的鼠洞,鼠洞只有三个出口A,B,C,要想同时顾及这三个出口以防老鼠出洞,这只花猫最好蹲守在( )A.△ABC的三边高线的交点P处B.△ABC的三条角平分线的交点P处C.△ABC的三边中线的交点P处D.△ABC的三边中垂线的交点P处3.已知一个三角形的三边长分别为13 cm,12 cm,5cm,则此三角形的外接圆半径为___ cm. 能力提升全练1.已知一个三角形的三边长分别是6,8,10,则这个三角形的外接圆的直径是( ) A.5 B.10 C.6 D.82.当点A(1,2),B(3,-3),C(m,n)三点可以确定一个圆时,m,n需要满足的条件是_______.三年模拟全练选择题(2019河北衡水武邑中学月考,4.★☆☆)给出下列说法:①经过三点一定可以作圆;②任意一个三角形一定有一个外接圆,并且只有一个外接圆;③任意一个圆一定有一个内接三角形,并且只有一个内接三角形;④三角形的外心到三角形三个顶点的距离相等。
其中正确的有()A.4个B.3个C.2个D.1五年中考全练一、选择题1.(2017湖南永州中考.7.★☆☆)小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )A.AB,AC边上的中线的交点B.AB,AC边上的垂直平分线的交点C.AB,AC边上的高所在直线的交点D.∠BAC与∠ABC的平分线的交点2.(2015河北中考,6.★☆☆)如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是()A.△ABEB.△ACFC.△ABDD.△ADE二、填空题3.(2017江苏泰州中考,15,★★☆)如图,在平面直角坐标系xOy中,点A、B、P的坐标分别为(1,0),(2,5),(4,2).若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为____________.核心素养全练(2017宁夏中考)如图,点A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为______________.28.2 过三点的圆基础闯关全练1.解析在G处建垃圾回收站.2.D三角形三边垂直平分线的交点到三角形三个顶点的距离相等,故选D.3.答案 6.5解析∵5²+12²= 13².∴此三角形是直角三角形,斜边长为13 cm,∵直角三角形的斜边为它的外接圆的直径,∴这个三角形的外接圆的半径是6.5 cm.故答案为6.5.能力提升全练1.B.∵6²+8²=10²,∴此三角形为直角三角形,斜边长为10,∴直角三角形的外心在其斜边上,且为斜边的中点,∴这个三角形的外接圆的直径=斜边长=10.故选B.2.答案5m+2n≠9解析设直线AB的解析式为y=kx+b(k≠0),∵A(1,2),B(3,-3),∴解得,∴直线AB的解析式为,∵点A(1,2),B(3,-3),C(m,n)三点可以确定一个圆,∴点C不在直线AB上,∴5m+2n≠9.故答案为5m+2n≠9.三年模拟全练选择题C①不在同一条直线上的三个点才能确定一个圆,故此项中的说法错误;②根据不在同一条直线上的三个点确定一个圆,故此项中的说法正确;③连接圆上任意三点构成的三角形都是圆的内接三角形,所以每一个圆都可以有无数个内接三角形,故此项中的说法错误;④三角形的外心是三角形三条边垂直平分线的交点,所以三角形的外心到三角形三个顶点的距离相等,故此项中的说法正确.故选C.五年中考全练一、选择题1.B本题实际上是确定三角形外接圆的圆心,三角形外接圆的圆心是三角形三边垂直平分线的交点,故选B.2.B外心即为三角形外接圆的圆心,∵△ACF的顶点F不在圆O上,∴圆O不是△ACF的外接圆,∴点O不是△ACF的外心,故选B.二、填空题3.答案(7,4)或(6,5)或(1,4)解析∵点A、B、P的坐标分别为(1,0),(2,5),(4,2),∴.∵点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,∴,则点C的坐标为(7,4)或(6,5)或(1,4).故答案为(7,4)或(6,5)或(1,4).核心素养全练答案5解析如图,连接AB,BC,分别作AB、BC的中垂线,两直线的交点为O,以O为圆心、OA长为半径作圆,则⊙O即为过A,B,C三点的外接圆,由图可知,⊙O还经过点D、E、F、G、H这5个格点,故答案为5.。
冀教新版九年级数学(上)《28.2 过三点的圆》同步练习卷

小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )
A.第①块
B.第②块
C.第③块
D.第④块
12.(4 分)如图所示,A、B、C 分别表示三个村庄,AB=1000 米,BC=600 米,AC=800
米,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三
个村庄到活动中心的距离相等,则活动中心 P 的位置应在( )
第2页(共4页)
15.(12 分)小明家的房前有一块矩形的空地,空地上有三棵树 A、B、C,小明想建一个圆 形花坛,使三棵树都在花坛的边上. (1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹); (2)若△ABC 中 AB=8 米,AC=6 米,∠BAC=90°,试求小明家圆形花坛的面积.
圆的圆心是( )
A.点 P
B.点 Q
C.点 R
D.点 M
6.(4 分)对于三角形的外心,下列说法错误的是( )
A.它到三角形三个顶点的距离相等
B.它到三角形三个顶点的连线平分三内角
C.它到任一顶点的距离等于这三角形的外接圆的半径
D.以它为圆心,它到三角形一顶点的距离为半径作圆,必通过另外两个顶点
7.(4 分)下列说法中,正确的是( )
16.(10 分)已知直线 l:y=x+4 和点 A(0,4),B(﹣4,0),设点 C 为直线 l 上一点,判 断 A,B,C 是否在同一个圆上.
17.(12 分)将图中的破轮子复原,已知弧上三点 A,B,C. (1)画出该轮的圆心; (2)若△ABC 是等腰三角形,底边 BC=16cm,腰 AB=10cm,求圆片的半径 R.
; 15.
;
16.
; 17.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
28.2过三点的圆
1.经过一点的圆有_______个,经过两点的圆有_______ 个。
2.若平面上A、B、C三点所满足的条件是__________。
3.直角三角形的两直角边分别为3cm ,4cm 则这个三角形的外接圆半径是________。
4.下列关于外心的说法正确的是()
A.外心是三个角的平分线的交点
B.外心是三条高的交点
C.外心是三条中线的交点
D.外心是三边的垂直平分线的交点
5.下列条件中不能确定一个圆的是()
A.圆心和半径
B.直径
C.三角形的三个顶点
D.平面上的三个已知点
6.三角形的外心具有的性质是()
A.到三边的距离相等
B.到三个顶点的距离相等
C.外心在三角形外
D.外心在三角形内
7.等腰三角形底边上的中线所在的直线与一腰的垂直平分线的交点是()
A.重心
B.垂心
C.外心
D.无法确定
8.已知直线l :y=x-2和点A (0,-2 )和点B(2,0),设点P 为l 上一点,试判断过P、A、B三点能否作一个圆。
9.若等腰直角三角形的直角边长为2cm ,则它的外接圆面积为_________.
10.图27-3-1为一残破古物,请做出它的圆心
11.如图27-3-2,已知一条直线l和直线l外两定点A、B,且AB在l两旁,则经过A、B 两点且圆心在l上面的圆有()
A.0个
B.1个
C.无数个
D.0个或1个或无数个
12.如图27-3-3,A,B,C表示三个工厂,要建一个供水站,使它到这三个工厂的距离相等,求作供水站的位置。
13.经过平面上的任意四点是否一定能作图,如果能,四点应满足什么条件?
14.某校计划在校园内修建一座周长为12cm的花坛,同学们设计出证三角形、正方形和圆共三种图案,通过计算求出使花坛面积最大的图案是哪一种图形。
15.如图27-3-4,有一个圆形的盖水桶的铁片,部分边沿由于水生锈残缺了一些,很不美观,为了废物利用,将铁片剪去一些使其成为圆形的,应找到圆心,并找到合理的半径,在铁片上画出圆,沿圆剪下即可,问应怎么样找到圆心和半径?
16.对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都大于这个圆的半径,则称图形A被这个圆所覆盖。
对于平面图形A母如果存在两个或两个以上的圆,使图形A上的任意一点到其中某个圆的圆心距离都不大于这个圆的半径,则称图形A被这些圆所覆盖。
例如:图27-3-5中的三角形被一个圆所覆盖,图27-3-6中的四边形被两个圆覆盖。
回答下列问题:
(1)边长为1cm的正方形被一个半径为r的圆所覆盖,r 的最小值是________cm 。
(2)边长为1cm的等边三角形被一个半径为r的圆所覆盖,r 的最小值是______cm。
(3)边长为2cm,宽为1cm的距离被两个半径都为r的圆所覆盖,r 的最小值是______cm,这两个圆的圆心距是________cm.
17.边长为2的等边ABC ∆内接于O ,则圆心O 到ABC ∆一边的距离为________。
18.如果三角形三条边长分别为5,12,13 ,那么这个三角形外接圆半径的长为_____。
19.如图27-3-7,O 是ABC ∆的外接圆,BAC=30∠,BC=2 cm ,则OBC ∆的面
积是_______2cm .
20.已知等腰三角形ABC 的底边BC 的长为10cm ,顶角为120,求它的外接圆直径。
21.一阵阵“加油”、“加油”的喊声把握引向游泳池边,这里甲、乙、丙、丁四个班级的代表队正在进行班际接力比赛,我来到水花飞溅的池边,遇到了李明、赵刚、王磊等几个同学,我请他们对比赛的结果进行猜测:
李明说:“我看甲班只能取得第三名,丙班才是冠军。
” 赵刚说:“丙班只能得个第二名吧,至于第三名,我看是乙班。
”
王磊很干脆,他说:“丁班第二,甲班第一。
”比赛结束了,我又找到了这几个同学,他们发现,三个人的猜测只对一半,你能推测出比赛的结果吗?
参考答案:
1.无数,无数
2.三点不共线
3.2.5cm
4.D
5.D
6.B
7.C
8.解:当x =0 时,y=0-2=-2,∴点A 在直线l 上,同理点B 也在直线l 上,即P 、A 、B 在同一直线上,∴过P 、A 、B 三点不能作一个圆。
9.2
2cm π 10.略 11.D
12.点拨:连结AB 、AC ,作线段AB 、AC 的垂直平分线,垂直平分线的交点即为供水站的位置。
13.不一定能作圆,如果能,其中以四点为顶点的四边形各边的垂直平分线应交于同一
点。
14.解:若设计为正三角形,则边长长为123=4(m),÷面积为
2134(4)43(m )2⨯⨯⨯=,若设计为正方形,则边长为123=4(m),÷,面积为2239(m )=,若设计为圆型,则半径为
126
(m)2ππ
=,面积为2263636
()(m ),439,ππππ
⋅=∴<<
∴使花坛面积最大的是圆。
15.作法:(1)在没有残缺的边上任取三点A 、B 、C ;(2)连结AC 、AB 分别作AC 、AB 的垂直平分线1l 和2l ,两条直线交于点O ;(3)以点O 为圆心,以O 点到残缺处的最短长度为半径作圆;(4)沿着做出的
O 剪下即可。
16.(1) r 的最小值应是边长为1cm 的正方形外接圆的半径之长,即2
r=
(cm)2
,如图(1),(2)r 的最小值应是边长为1cm 的等边三角形外接圆的半径之长,即3
r=
(cm)3
,如图(2),(3)min 2
r =
(cm)2
,圆心距12O O =1cm ,如图(3)。
3
3 20.解:如图,连结OA 、OB ,
AB AC
=1
AB AC,OA BC,BAO=BAC 60
2
∴=∴⊥∴∠∠=。
OA OB,OAB =∴∆为等边三角形,OA=AB=10 cm ∴∴外接圆直径为20cm..
21.李明的前半句话错,一、二、三名分别由丙、丁、乙三个班获得,甲班获得第四名。
