理论力学(机械工业出版社)第十章动量定理习题解答
理论力学课后答案10

课
答
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
案
网
w.
kh
da
w.
co
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
10.9 质量为 m1 和 m2 的两重物,分别挂在两条绳子上,绳又分别绕在半径为 r1 和 r2 并装在同一轴的鼓轮上,已知鼓轮对转轴 O 的转动惯量为 J ,系统在重力作用 下发生运动,求鼓轮的角加速度。
kh
da
1 (a): mr 2 2 1 (b): m(r 2 2e 2 ) 2
w.
co
解:
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
10.2 如图所示,质量为 m 的偏心轮在水平地面上作平面运动。轮子轴心为 A , 质心为 C , AC e ,轮子半径为 R ,对轴心 A 的转动惯量为 J A ; C 、 A 、 B 三 点在同一铅直线上。 (1)当轮子只滚不滑时,若 v A 已知,求轮子的动量和对地面上 B 点的动量矩。 (2)当轮子又滚又滑时,若 v A 、 已知,求轮子的动量和对地面上 B 点的动量矩。
魏 魏
泳 泳
涛 涛 涛
m
系统对 z 轴动量矩守恒。设圆盘角速度为 。则圆盘和人对轴 z 的动量矩分 别为 1 hz1 MR 2 2 ds hz 2 rm(r ) mr 2 mrat dt 初始时刻动量矩为零: hz1 hz 2 0 2mrat MR 2 2mr 2 2mra MR 2 2mr 2
魏 魏 魏
后
泳 泳 泳
理论力学 第十章 动量定理

——质点动量守恒定律
22
第十章 动量定理
二、质点系的动量定理
对质点系内任一质点i
:
d dt
(mivi )
=
Fi
=
F (e) i
+
F (i) i
∑ ∑ ∑ 对整个质点系:
d dt
(mivi
)
=
F (e) i
+
F (i) i
∑ Q Fi(i) = 0
∑ ∑ d dt
(mivi
)
=
d dt
(mivi
)
=
dp dt
∑ d p =
dt
F (e) i
——质点系的动量定理
即:质点系的动量对时间的一阶导数等于作用于质点系 所有外力的矢量和(外力系的主矢)。
23
第十章 动量定理
∑ 结论:只有外力才能改变质点系的动 d p =
量,内力不能改变整个质点系的动量。 d t
F (e) i
微分形式
∑ ∑ d p =
Oω
vC
vC
ω
C
C
C
(a)
(b)
(c)
解:(a) 长为 l、质量m的均质细杆,角速度为ω 。
则其动量为
p=
mvC
= m⋅ l ω
2
=
ml ω
2
方向与质心速度方向相同。
12
第十章 动量定理
Oω
vC
vC
C
C
vC = 0
ω
C
(a)
(b)
(c)
(b) 质量为m的均质滚轮,质心的速度为vC 。
p = mvC
2. 与质点动力学基本方程的比较
《理论力学》第十章--动量矩定理试题及答案
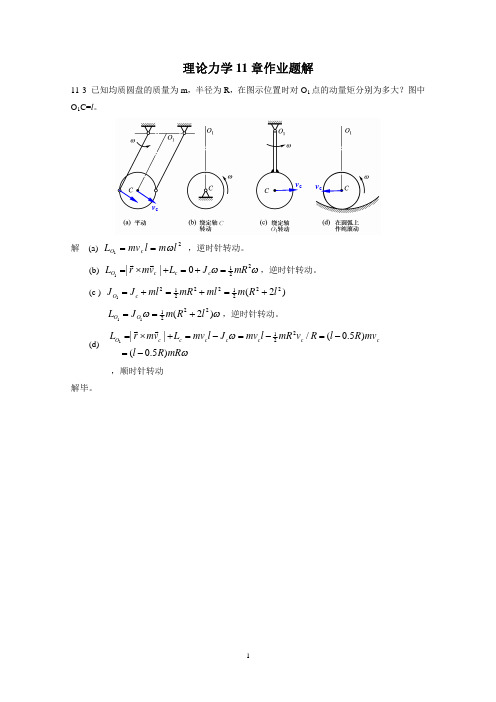
理论力学11章作业题解11-3 已知均质圆盘的质量为m ,半径为R ,在图示位置时对O 1点的动量矩分别为多大?图中O 1C=l 。
解 (a) 21l m l mv L c O w == ,逆时针转动。
(b) w w 2210||1mR J L v m r L c c c O =+=+´=rr ,逆时针转动。
(c ) )2(2221222121l R m ml mR ml J J c O +=+=+=w w )2(222111l R m J L O O +==,逆时针转动。
(d)ww mR R l mv R l R v mR l mv J l mv L v m r L c c c c c c c O )5.0()5.0(/||2211-=-=-=-=+´= r r,顺时针转动解毕。
v cv cv c11-5 均质杆AB 长l 、重为G 1,B 端刚连一重G 2的小球,弹簧系数为k ,使杆在水平位置保持平衡。
设给小球B 一微小初位移0d 后无初速度释放,试求AB 杆的运动规律。
解 以平衡位置(水平)为0=j ,顺时针转为正。
平衡时弹簧受力为:)5.0(312G G F s +=弹簧初始变形量:k G G k F s st /)5.0(3/12+==d在j 角时弹簧的拉力为(小位移):3/)5.0(3)3/(12l k G G l k F st s j j d ++=+=¢系统对A 点的动量矩:j j j&&&221233l gG G l l g G J L A A +=×+= 对点的动量矩定理)(/å=Ei A A F M dt dL r :j j 93/5.033221221kl l F lG lG l g G G s -=¢-+=+&& 0)3(321=++j jG G gk &&,令)3(3212G G gkp +=则有02=+j jp &&,其解为: )cos()sin(pt B pt A +=j由初始条件0| ,/|000====t t l jd j &得l B A / ,00d ==。
理论力学

1、运动分析。----说明机构中主要构件的运动形式。 2、作速度分析,需要画出相关速度,求一点速度或图形角
速度。(若要分析加速度,一般需要求图形的角速度)
画速度 (1)沿点的运动轨迹切线,与相关的角速度方向协调。
(2)要符合速度投影定理。
3、作加速度分析,需要画出相关加速度,求一点加速度 或图形角加速度。 画加速度
例8-10
如图所示,在椭圆规的机构中,曲柄OD以匀角速度ω绕O 轴转动。
OD=AD=BD=l。求:当 60 时,尺AB的角加速度和点A的加速度。
B ABC AB D
O O
O
A A
vD
O
aA
n a BA
a A B
aD
v A
aD
n a AD y’ a AD
n a AD l 2
n x’ a A cos aD cos 2 a AD
y’ n a A 0 aD sin aAD cos a AD sin
x’
若OD变速转动,有什么变化?
a A l
2
a 0 AD AD
a AD 0 AD
解:
(1)动点:OA上的A点
动系:摇杆O1B
(2)运动分析: 绝对运动: 圆周运动。 相对运动: 直线运动。 牵连运动: 摇杆转动。
(3)速度分析与计算
v a r
ve
O ω
va
B vr
A ω1
vr va cos
ve va sin
r 2 O1 1 2 2 O1 A l r ve
理论力学课后的习题及答案解析...doc
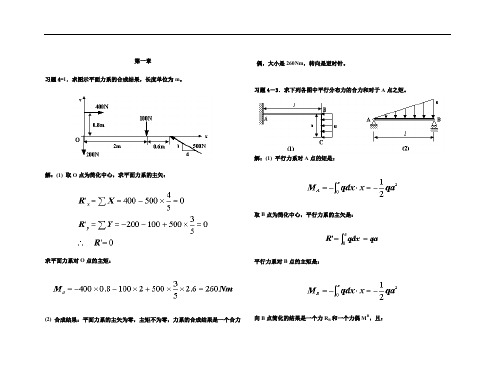
第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力R B和一个力偶M B,且:如图所示;将R B向下平移一段距离d,使满足:最后简化为一个力R,大小等于R B。
其几何意义是:R的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力R A和一个力偶M A,且:如图所示;将R A向右平移一段距离d,使满足:最后简化为一个力R,大小等于R A。
其几何意义是:R的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
习题4-8.图示钻井架,G=177kN,铅垂荷载P=1350kN,风荷载q=1.5kN/m,水平力F=50kN;求支座A的约束反力和撑杆CD所受的力。
《理论力学》第10章 质心运动定理

第10章 质心运动定理
26
3、求质心加速度
aC
aB
aCt B
aCnB
4、质心运动定理求约束力,受力分析
ma Cx FixE FA sin450 maCy FiyE FB mg FA cos 450
O
450
1m
A
C
vB
aB
450
B
FA
A
mg
x
FB
C
450
B
★理论力学电子教案
0
px const
★理论力学电子教案
第10章 质心运动定理
18
例题 图示机构,均质杆OA长l,质量为m1,滑块A的质量为m2, 滑道CD的质量为m3。OA杆在一力偶(图中未画出)作用下作 匀角度ω转动。试求O处的水平约束反力(机构位于铅直平面
内,各处摩擦不计)。 C
A
O
E
D
★理论力学电子教案
第10章 质心运动定理
第10章 质心运动定理
27
ma A
第10章 质心运动定理
14
M
C aC mg
FN
F
★理论力学电子教案
第10章 质心运动定理
§2 质点系动量、冲量
质点动量: 质点系动量:
p mv
P mivi mvC
问:刚体系动量?
元冲量:
dI F dt
冲量:
t2 t2
I dI F dt
t1
t1
15
p mv
★理论力学电子教案
第10章 质心运动定理
1
第十章 质心运动定理&动量定理
★理论力学电子教案
第10章 质心运动定理
理论力学课后习题答案 第10章 动能定理及其应用 )

(a)A(a)O第10章 动能定理及其应用10-1 计算图示各系统的动能:1.质量为m ,半径为r 的均质圆盘在其自身平面内作平面运动。
在图示位置时,若已知圆盘上A 、B 两点的速度方向如图示,B 点的速度为v B ,θ = 45º(图a )。
2.图示质量为m 1的均质杆OA ,一端铰接在质量为m 2的均质圆盘中心,另一端放在水平面上,圆盘在地面上作纯滚动,圆心速度为v(图b )。
3.质量为m 的均质细圆环半径为R ,其上固结一个质量也为m 的质点A 。
细圆环在水平面上作纯滚动,图示瞬时角速度为ω(图c )。
解:1.222222163)2(2121)2(212121BB BC C C mv r v mr v m J mv T =⋅+=+=ω 2.222122222214321)(21212121v m v m r v r m v m v m T +=⋅++=3.22222222)2(212121ωωωωmR R m mR mR T =++=10-2 图示滑块A 重力为1W ,可在滑道内滑动,与滑块A 用铰链连接的是重力为2W 、长为l 的匀质杆AB 。
现已知道滑块沿滑道的速度为1v ,杆AB 的角速度为1ω。
当杆与铅垂线的夹角为ϕ时,试求系统的动能。
解:图(a )B A T T T +=)2121(21222211ωC C J v g W v g W ++=21221121212211122]cos 22)2[(22ωϕωω⋅⋅+⋅++++=l gW l l v l v l g W v g W]cos 31)[(2111221222121ϕωωv l W l W v W W g +++=10-3 重力为P F 、半径为r 的齿轮II 与半径为r R 3=的固定内齿轮I 相啮合。
齿轮II 通过匀质的曲柄OC 带动而运动。
曲柄的重力为Q F ,角速度为ω,齿轮可视为匀质圆盘。
试求行星齿轮机构的动能。
华中科技大学理论力学习题答案

量为P3 ; 轮A上作用常力矩M1 。
求 物体C上升的加速度。
解:
取轮A为研究对象12
P1 g
r12
1
M1
Tr1
(1)
取轮B连同物体C为研究对象
d dt
(
1 2
P2 g
r2 2
2
P3 g
v r2
)T
'r2
P3
r2
(2)
补充运动学条件 r22 v, r22 a r11
化简(2)
得:P2
2 2g
F
左边可写成
r
d
(mv dt
)
d dt
(r
mv
)
dr dt
mv
而dr dt
mv
v
mv
0
,
r F mO (F ) ,
故:
d dt
(r
mv
)r
F
,
ddt[mO (mv )]mO (F )
质点对任一固定点的动量矩对时间的导数,等于作用在质 点上的力对同一点之矩。这就是质点对固定点的动量矩定理。
5
将上式在通过固定点O的三个直角坐标轴上投影,得
,得
19
(2)由质心运动定理
FN (m m1 m2 )g (m m1 m2 )aCy
aCy
yC
mi yi mi
m1a1 m2a2 m m1 m2
(m1r1 m2r2 )
m m1 m2
FN (m m1 m2 )g (m1r1 m2r2 )
(3) 研究 m1
222111rvmrvmjloo????120cynammmgmmmf2121??????212211212211mmmrmrmmmmamammymyaiiiccy????????????????????111111rmamfgmt???111?rgmft??221121rmrmgmmmfn???????2由质心运动定理3研究1m?222222rmamgmft???222?rgmft??2m4研究21一动力学方程对于一个定轴转动刚体代入质点系动量矩定理有?zzjl?ezzmjdtd??22ezzezzmdtdjmj?????或刚体定轴转动微分方程解决两类问题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习 题10-1 计算图10-7所示各种情况下系统的动量。
(1) 如图10-7a 所示,质量为m 的匀质圆盘沿水平面滚动,圆心O 的速度为0v ;(2) 如图10-7b 所示,非匀质圆盘以角速度ω绕O 轴转动,圆盘质量为m ,质心为C ,偏心距OC=a ;(3) 如图10-7c 所示,胶带轮传动,大轮以角速度ω转动。
设胶带及两胶带轮为匀质的;(4) 如图10-7d 所示,质量为m 的匀质杆,长度为l ,绕铰O 以角速度ω转动。
图10-7(a) 0v p m =; (b) ωma p =(方向与C 点速度方向相同);(c) 0=p ;(d) 2ωml p = (方向与C点速度方向相同)。
10-2 如图10-8所示,椭圆规尺AB 的质量为2m 1,曲柄OC 的质量为m 1,而滑块A 和B 的质量均为m 2。
已知:OC =AC =CB = l ;曲柄和尺的质心分别在其中点上;曲柄绕O 轴转动的角速度ω为常量。
当开始时,曲柄水平向右,试求此时质点系的动量。
图10-8方法一CAB COC B B A A m m m m v v v v p +++=2CC B A m m m m v v v v 112222+++=C B A m m v v v 1225)(++=因)c o s s i n (j i v ϕϕω+-=l Cj v ϕωcos 2l A = i v ϕωs i n 2l B -=故)cos sin (25)sin 2cos 2(12j i i j p ϕϕωϕωϕω+-+-=l m l l m)cos sin (24521j i ϕϕω+-+=l m m (与v C 方向相同)方法二规尺AB 、滑块A 和B 质心C 处,质量为2(m 1+m 2) 因此系统质心在OC 上,离O 轴距离mlm m ml m m l m 245)(2221211+=++⨯=ξ质心速度ωξωξl m m m m 24521+===v p (方向垂直于OC )10-3 跳伞者质量为60kg ,自停留在高空中的直升飞机中跳出,落下100m 后,将降落伞打开。
设开伞前的空气阻力略去不计,伞重不计。
开伞后阻力不变,经5s 后跳伞者的速度减为4.3m/s 。
试求阻力的大小。
gh v 21=222122t ghv t v v a -=-=22)2(t gh v m ma F mg -==-)2(22t gh v g m F --=N7.1067)9944.78.9(60)51008.923.48.9(60=+=⨯⨯--=10-4 图10-9所示浮动起重机举起质量为m 1=2000kg 的重物。
设起重机质量为m 2=20000kg ,杆长OA =8m ;开始时与铅直位置成60°角。
水的阻力与杆重均略去不计。
当起重杆OA 转到与铅直位置成30°角时,试求起重机的位移。
图10-9设起重机向左移动s ,则重物向右移动)30sin 60(sin s OA -︒-︒质心运动守恒x C =常量0])30sin 60(sin [21=--︒-︒s m s OA m 211)30sin 60(sin m m OA m s +︒-︒=m2662.0220002/)13(82000=-⨯⨯=10-5 如图10-10所示,两小车A 和B 的质量分别为600kg 和800kg ,在水平轨道上分别以匀速v A =1m/s ,v B =0.4m/s 运动。
一质量为40kg 的重物C 以俯角30°,速度v C =2m/s 落入A 车内,A 车与B 车相碰后紧接在一起运动。
试求两车共同的速度。
摩擦忽略不计。
图10-10动量守恒︒++=30cos 1C C B B A A x v m v m v m p v m m m p C B A x )(2++=v m m m v m v m v m C B A C C B B A A )(30cos ++=︒++CB AC C B B A A m m m v m v m v m v ++︒++=30cosm/s6870.0144034092040800600232404.08001600=+=++⨯⨯+⨯+⨯=10-6 平台车质量m 1=500kg ,可沿水平轨道运动。
平台车上站有一人,质量m 2=70kg ,车与人以共同速度v 0向右方运动。
如人相对平台车以速度v r =2m/s 向左方跳出,不计平台车水平方向的阻力及摩擦,试问平台车增加的速度为多少? 动量守恒0211)(v m m p x +=)()(r 02012v v v m v v m p x -+++=∆∆021r 0201)()()(v m m v v v m v v m +=-+++∆∆m/s2456.05701407050027021r 2==+⨯=+=m m v m v ∆10-7 如图10-11所示,质量为m 1的平台AB 放于水平面上,平台与水平面间的动滑动摩擦因数为 。
质量为m 2的小车D ,由绞车拖动,相对于平台的运动规律为s=0.5bt 2,其中b 为常数。
不计绞车的质量,试求平台的加速度。
图10-11设平台向左运动的速度为v ,则小车D 向右运动的速度为v r - v)(r 21v v m v m p x -+-= gm m F F ex )(21N +==∑μμ由动量定理eixx F tp ∑=d d得gm m a a m a m )()(21r 21+=-+-μ212122121r 2)()(m m gm m b m m m gm m a m a ++-=++-=μμ10-8 图10-12所示机构中,鼓轮A 质量为m 1。
转轴O 为其质心。
重物B 的质量为m 2,重物C 的质量为m 3。
斜面光滑,倾角为θ。
已知重物B 的加速度为a ,试求轴承O 处的约束反力。
图10-12由质心运动定理e yCy e x Cx Fma F ma ∑=∑=得θθsin cos N 3F F a rR m Ox -=θθθθθsin cos cos sin cos 3N 3mg a rR m F a rR m F Ox +=+=θθcos )(sin N 32123F g m m m F a m a rR m Oy +++-=- θθcos )(sin N 32123F g m m m a m a rR m F Oy -+++-=θθ232123cos )(sin mg g m m m a m a rR m -+++-=10-9 如图10-13所示,质量为m 的滑块A ,可以在水平光滑槽中运动,具有刚性系数为k 的弹簧一端与滑块相连,另一端固定。
杆长度为l ,质量可忽略不计,A 端与滑块铰接,B 端装有质量为m 1的小球,在铅垂面内绕A 点转动。
设在力偶M 作用下转动角速度w 为常数。
试求滑块A 的运动微分方程。
图10-131111sin )sin (m m t l m x m m t l x m mx x C ++=+++=ωω质心运动定理e x C F xm m ∑=+ )(1 kx t l m x m m -=-+ωωsin )(211t l m kx xm m ωωsin )(211=++tm m l m x m m k xωωsin 1211+=++10-10 如图10-14所示,均质杆OA 长2l ,质量为m ,绕着通过O 端的水平轴在铅直面内转动,转到与水平线成f 角时,角速度与角加速度分别为w 及a 。
试求此时O 端的反力。
图10-14由质心运动定理e yCy e x Cx Fma F ma ∑=∑=得OxC C F a a m =--)sin cos (τnϕϕ)sin cos ()sin cos (2τnϕαϕωϕϕ+-=+-=ml a a m F C C OxmgF a a m Oy C C -=-)cos sin (τn ϕϕmgml mg a a m F C C Oy +-=+-=)cos sin ()cos sin (2τnϕαϕωϕϕ10-11 在图10-15所示曲柄滑杆机构中,曲柄以等角速度 绕O 轴转动,开始时,曲柄OA 水平向右。
已知曲柄质量为m 1,滑块A 的质量为m 2,滑杆的质量为m 3,曲柄的质心在OA 的中点,OA = l ;滑杆的质心在C 点,而2/l BC=。
试求:(1)机构质心的运动方程;(2)作用在O 点的最大水平力。
图10-15ml t l m t l m t l m x C )2cos (cos cos 2321+++=ωωω)(2c o s )22()(23213213213m m m tl m m m m m m lm +++++++=ωmtl m t l m y C ωωs i n s i n 221+=)(2s i n )2(32121m m m t l m m +++=ω质心运动定理ex C F xm ∑=OxF tl m m m =++-2cos )22(2321ωω 2cos )22(2321tl m m m F Ox ωω++-=2)22(2321max ωl m m m F Ox ++=10-12 如图10-16所示,均质杆AB 长l ,直立在光滑的水平面上,试求它从铅直位置无速地倒下时,端点A 相对图示坐标系的轨迹.图10-16任意位置时0=∑exF ,初始速度为零,故质心运动守恒0=C x ,质心沿铅垂方向向下运动θco s2l x A =θs i n l y A =故1)()2(22=+ly lx A A2224ly x A A =+10-13 图10-17所示水平面上放一均质三棱柱A ,在其斜面上又放一均质三棱柱B ,两三棱柱的横截面均为直角三角形。
三棱柱A 的质量m A 为三棱柱B 质量m B 的三倍,其尺寸如图示,若各处摩擦不计,初始时系统静止。
试求当三棱柱B 沿三棱柱A 滑下接触到水平面时,三棱柱A 移动的距离。
图10-17任意位置时0=∑e xF,初始系统静止,故质心运动守恒x C =常量3231b m a m x B A C ⨯+⨯=设三棱柱A 向左移动s ,则三棱柱B 向右移动s b a --)32()3(2s b a b m s a m x B A C --+⨯+-⨯=12C C x x =0)(=--+-s b a m s m B A4)(b a m m b a m s BA B -=+-=10-14 试求题10-13中三棱柱A 运动的加速度及地面的支持力。
任意位置时0=∑exF ,0=Cx a设三棱柱A 向左运动的加速度为a A ,三棱柱B 沿斜面运动的相对加速度为a r0)c o s (r =-+-A B A A a a m a m θ θcos )(r B AB A m a m m a +=三棱柱Bθθsin )cos (r g m a a m B A B =-θθθsin ]cos cos )([g m a m a m m m B A B AB A B =-+θθθsin cos cos )(2g m a m m m B A B B A =-+gm m g m a B A B A θθθθθθ22sin 3cos sin sin cos sin +=+=ga θθ2r sin 3sin 4+=系统eyCy F ma ∑=gm m F a m B A B )()sin (N r +-=-θθθθ22r N sin 3sin 4)(sin )(+-+=-+=gm g m m a m g m m F B B A B B A)sin 3(sin 4422θθ+-=gm g m B Bgm B θ2sin 312+=。
