实用文档之全等三角形题型归纳(经典完整)
(完整版)全等三角形的判定常考典型例题及练习

(完整版)全等三角形的判定常考典型例题及练习-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN全等三角形的判定一、知识点复习 ①“边角边”定理:两边和它们的夹角对应相等的两个三角形全等。
(SAS )图形分析:书写格式: 在△ABC 和△DEF 中⎪⎩⎪⎨⎧=∠=∠=EFBC E B DEAB∴△ABC ≌△DEF (SAS )②“角边角”定理:两角和它们的夹边对应相等的两个三角形全等。
(ASA)图形分析:书写格式: 在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧∠=∠=∠=∠FC EF BC EB∴△ABC ≌△DEF(ASA)③“角角边”定理:两个角和其中一个角的对边对应相等的两个三角形全等。
(AAS )图形分析:书写格式:在△ABC 和△DEF 中⎪⎩⎪⎨⎧=∠=∠∠=∠EFBC F C EB∴△ABC ≌△DEF(AAS)④“边边边”定理:三边对应相等的两个三角形全等。
(SSS )图形分析:书写格式: 在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧===EF BC DF AC DE AB∴△ABC ≌△DEF(AAS)⑤“斜边、直角边”定理:斜边和一条直角边对应相等的两个直角三角形全等。
(HL )图形分析:书写格式:在△ABC 和△DEF 中 ⎩⎨⎧==DF AC DE AB ∴△ABC ≌△DEF (HL )一个三角形共有三条边与三个角,你是否想到这样一问题了:除了上述四种识别法,还有其他的三角形全等识别法吗比如说“SSA ”、“AAA ”能成为判定两个三角形全等的条件吗两个三角形中对应相等的元素 两个三角形是否全等反例 SSA⨯AAA⨯二、常考典型例题分析第一部分:基础巩固1.下列条件,不能使两个三角形全等的是( )A.两边一角对应相等 B.两角一边对应相等 C.直角边和一个锐角对应相等 D.三边对应相等2.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD()A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD3.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是()A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙4.如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是()A.AB=DE B.DF∥AC C.∠E=∠ABC D.AB∥DE5.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是()A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD6.如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线OC,作法用得的三角形全等的判定方法是()A.SAS B.SSS C.ASA D.HL第二部分:考点讲解考点1:利用“SAS ”判定两个三角形全等1.如图,A 、D 、F 、B 在同一直线上,AD=BF ,AE=BC ,且AE ∥BC .求证:△AEF ≌△BCD .2.如图,AB=AC ,AD=AE ,∠BAC=∠DAE .求证:△ABD ≌△ACE .考点2:利用“SAS ”的判定方法解与全等三角形性质有关的综合问题3.已知:如图,A 、F 、C 、D 四点在一直线上,AF=CD ,AB ∥DE ,且AB=DE ,求证:FEC CBF ∠=∠考点3:利用“SAS ”判定三角形全等解决实际问题 4.有一座小山,现要在小山A 、B 的两端开一条隧道,施工队要知道A 、B 两端的距离,于是先在平地上取一个可以直接到达A 和B 的点C ,连接AC 并延长到D ,使CD=CA ,连接BC 并延长到E ,使CE=CB ,连接DE ,那么量出DE 的长,就是A 、B 的距离,你能说说其中的道理吗?考点4:利用“ASA”判定两个三角形全等5.如图,已知AB=AD,∠B=∠D,∠1=∠2,求证:△AEC≌△ADE.6.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.求证:△AEC≌△BED;考点6:利用“ASA”与全等三角形的性质解决问题:7.如图,已知EC=AC,∠BCE=∠DCA,∠A=∠E;求证:BC=DC考点7:利用“SSS”证明两个三角形全等8.如图,A、D、B、E四点顺次在同一条直线上,AC=DF,BC=EF,AD=BE,求证:△ABC≌△EDF.考点8:利用全等三角形证明线段(或角)相等9.如图,AE=DF,AC=DB,CE=BF.求证:∠A=∠D.考点9:利用“AAS”证明两个三角形全等10.如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,求证:△ABD≌△ACE.考点10:利用“AAS”与全等三角形的性质求证边相等11.(2017秋?娄星区期末)已知:如图所示,△ABC中,∠ABC=45°,高AE与高BD交于点M,BE=4,EM=3.(1)求证:BM=AC;(2)求△ABC的面积.考点11:利用“HL”证明两三角形全等12.如图,在△ABC中,D是BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF。
(完整word版)全等三角形经典题型50题(含),文档
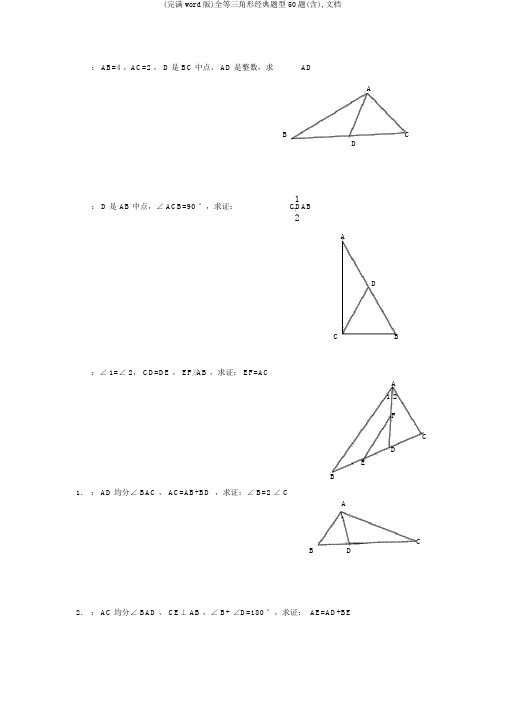
: AB=4 ,AC=2 , D 是 BC 中点, AD 是整数,求ADAB CD: D 是 AB 中点,∠ ACB=90 °,求证:1CDAB2ADC B:∠ 1=∠ 2, CD=DE , EF//AB ,求证: EF=ACA1 2FCDEB1. : AD 均分∠ BAC , AC=AB+BD ,求证:∠ B=2 ∠ CACB D2. : AC 均分∠ BAD , CE⊥ AB ,∠ B+ ∠D=180 °,求证: AE=AD+BE6. 如图,四边形ABCD 中, AB ∥ DC, BE 、 CE 分别均分∠ ABC 、∠ BCD ,且点 E 在 AD上。
求证: BC=AB+DC 。
.7.: AB//ED ,∠ EAB= ∠ BDE , AF=CD , EF=BC ,求证:∠ F= ∠CE DCFA B8 : AB=CD ,∠ A= ∠ D,求证:∠ B=∠ CA DB C9.∠ ABC=3 ∠C,∠ 1=∠ 2, BE ⊥AE ,求证: AC-AB=2BEDF A CE B 10.如图,在△ABC 中, BD =DC ,∠ 1=∠ 2,求证: AD⊥BC .12.如图①, E、F 分别为线段AC 上的两个动点,且 DE⊥AC 于 E,BF⊥ AC 于 F,假设 AB=CD ,AF=CE ,BD 交 AC 于点 M.(1〕求证: MB=MD , ME =MF(2〕当 E、F 两点搬动到如图②的地址时,其余条件不变,上述结论能否成立?假设成立请恩赐证明;假设不成立请说明原由.13.:如图,DC∥ AB,且 DC =AE, E 为 AB 的中点,〔 1〕求证:△ AED≌△ EBC.〔 2〕观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.〔直接写出结果,不要求证明〕:AE ODB C24.〔 7 分〕如图,△ ABC 中,∠ BAC=90 度, AB=AC, BD 是∠ ABC 的均分线, BD 的延长线垂直于过 C 点的直线于 E,直线 CE 交 BA 的延长线于 F.求证: BD=2CE.F证明:延长 BA 、CE,两线订交于点 F ∵ BE⊥ CE ∴∠ BEF= ∠ BEC=90°A在△BEF 和△BEC 中∠ FBE= ∠CBE,BE=BE, ∠ BEF=∠ BEC∴△ BEF ≌△ BEC(ASA)∴ EF=EC∴ CF=2CE E∵∠ ABD+ ∠ ADB=90° ,∠ ACF+ ∠ CDE=90°又∵∠ ADB= ∠CDE D∴∠ ABD= ∠ ACF 在△ ABD 和△ACF 中∠ ABD= ∠ ACF, AB=AC,∠ BAD= ∠ CAF=90° ∴△ ABD ≌△ ACF(ASA)∴BD=CF ∴ BD=2CEB C25、〔 10 分〕如图: DF=CE, AD=BC,∠ D=∠ C。
全等三角形知识总结及典型例题

全等三角形知识总结及典型例题知识点 1:全等三角形的定义和表示方法(1)定义:能够完整重合的两个三角形叫做全等三角形。
重合的极点叫做对应极点,重合的边叫做对应边,重合的角叫做对应角(2)“全等”用“≌”表示,读作“全等于”,记两个三角形全等时,往常把表示对应极点的字母写在对应的地点上。
例 1.如下图,图中两个三角形能完整重合,以下写法正确的选项是()A.△ ABE≌△ AFB B.△ ABE≌△ ABF C.△ ABE≌△ FBA D.△ ABE≌△ FAB 知识点 2:全等三角形的性质FB AE性质:全等三角形中,对应边相等,对应角相等。
【注意:全等三角形的对应线段(对应边上的中线,对应边上的高,对应角的均分线)相等;全等三角形的周长相等,面积相等。
】例 2. 如图,△ ABD≌△ ACE,点 B 和点 C 是对应极点, AB=8,AD=6,BD=7,则 BE的长是()A.1 B .2C.4 D .6C D例 3. 如图,△ ABD≌△ EBC, AB=3cm, BC=.(1)求 DE的长;(2)判断AC与BD的地点关系,并说明原因.A BEDEAB C(1)“边边边” ( SSS):三边对应相等的两个三角形全等。
(2)“边角边” ( SAS):两边和它们的夹角对应相等的两个三角形全等。
(3)“角边角” ( ASA):两角和它们的夹边对应相等的两个三角形全等。
(4)“角角边” ( AAS):两个角和此中一个角的对边对应相等的两个三角形全等。
(5)“斜边,直角边” ( HL):斜边和一条直角边对应相等的两个直角三角形全等。
【注意:① 三角形全等证明时要注意应用“公共边” 、“公共角” 、“对顶角” 等。
②证明线段或角相等往常变换证明线段或角所在的三角形全等。
③在判断两个三角形全等时,起码有一边对应相等。
④有两边和一角对应相等,角一定是这两边的夹角。
⑤“HL”只合适于 Rt ⊿ 。
⑥利用全等三角形能够测出不可以(或不易)直接丈量长度的线段长,比如,河宽,或利用全等丈量小口瓶的内径等。
全等三角形经典题型

全等三角形经典题型全等三角形是几何学中的一个重要概念,它指的是具有相同形状和大小的两个三角形。
在解决全等三角形的经典题型时,我们通常会利用全等三角形的性质和一些几何定理来推导和证明。
以下是一些经典的全等三角形题型以及解题思路:1. SSS(边-边-边)判定法,当两个三角形的三条边分别相等时,可以判定两个三角形全等。
例如,已知三角形ABC和三角形DEF,且AB=DE,BC=EF,AC=DF,那么可以得出三角形ABC全等于三角形DEF。
2. SAS(边-角-边)判定法,当两个三角形的两边和夹角分别相等时,可以判定两个三角形全等。
例如,已知三角形ABC和三角形DEF,且AB=DE,BC=EF,∠BAC=∠EDF,那么可以得出三角形ABC 全等于三角形DEF。
3. ASA(角-边-角)判定法,当两个三角形的两角和一边分别相等时,可以判定两个三角形全等。
例如,已知三角形ABC和三角形DEF,且∠BAC=∠EDF,∠ABC=∠DEF,AC=DF,那么可以得出三角形ABC全等于三角形DEF。
4. RHS(直角边-斜边-直角边)判定法,当两个直角三角形的一个直角边和斜边分别相等时,可以判定两个三角形全等。
例如,已知直角三角形ABC和直角三角形DEF,且∠BAC=∠EDF,AC=DF,AB=DE,那么可以得出三角形ABC全等于三角形DEF。
5. AAS(角-角-边)判定法,当两个三角形的两角和一边的对应边分别相等时,可以判定两个三角形全等。
例如,已知三角形ABC和三角形DEF,且∠BAC=∠EDF,∠ABC=∠DEF,AB=DE,那么可以得出三角形ABC全等于三角形DEF。
在解决全等三角形题型时,我们要注意使用合适的判定法,并根据题目给出的已知条件进行推导和证明。
同时,还要注意运用其他几何定理和性质,如平行线的性质、垂直线的性质、等腰三角形的性质等,来辅助解题。
以上是关于全等三角形经典题型的回答,希望对你有所帮助。
全等三角形重点题型(供参考)

全等三角形知识点总结知识点总结一、全等图形、全等三角形:1.全等图形:能够完全 ______ 的两个图形就是全等图形。
2.________________________________ 全等图形的性质:全等多边形的、分别相等。
3.全等三角形:三角形是特殊的多边形,因此,全等三角形的对应边、对应角分别相等。
同样,如果两个三角形的边、角分別对应相等,那么这两个三角形全等。
说明:全等三角形对应边上的高,中线相等,对应角的平分线相等:全等三角形的周长,而积也都相等。
这里要注意:(1)周长相等的两个三角形,不一定全等;(2)而积相等的两个三角形,也不一定全等。
二、全等三角形的判定:1.一般三角形全等的判定(1) __________________________________________________ 三边对应相等的两个三角形全等(“边边边”或“______________________________________ ”)。
(2) ______________________________________________________________ 两边和它们的夹角对应相等的两个三角形全等(“边角边”或“__________________________ ”)。
(3) ____________________________________________________________________ 两个角和它们的夹边分别对应相等的两个三角形全等("角边角”或“”)。
(4) ____________________________________________________________________ 有两角和其中一角的对边对应相等的两个三角形全等(“角角边”或“” )02.直角三角形全等的判定利用一般三角形全等的判定都能证明直角三角形全等.斜边和一条直角边对应相等的两个直角三角形全等("斜边、直角边”或“_____________________________________________________________________________ ”).注意:两边一对角(SSA)和三角(AAA)对应相等的两个三角形不一定全等。
全等三角形总结经典题型

全等三角形【知识要点】 济宁学院附属中学中李涛 1.全等图形定义:两个能够重合的图形称为全等图形.2.全等图形的性质:对应边相等,对应角相等(1)两个全等三角形,重合的顶点叫做对应点,重合的边叫做对应边,重合的角叫做对应角. (2)全等用符号“≌”连接时,把表示对应顶点的字母写在对应的位置上. 3.全等三角形的判定(一):三边对应相等的两个三角形全等,简与成“边边边”或“SSS ”.在ABC ∆和DEF ∆中⎪⎩⎪⎨⎧===DF AC EF BC DEAB ABC ∆∴≌DEF ∆(SSS)全等三角形的判定(二):两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS ”,几何表示在ABC ∆和DEF ∆中, ABC EF BC E B DE AB ∆∴⎪⎩⎪⎨⎧=∠=∠=全等三角形的判定(三):ASA 公理:有两角和它们的夹边对应相等的两个三角形全等. 在ABC ∆与DEF ∆中EB DE AB D A ∠=∠=∠=∠∴)(ASA DEF ABC∆≅∆全等三角形的判定(四):ASA 公理推论(AAS 公理):有两角和其中一角的对边对应相等的两个三角形全等.如图,在ABC∆与DEF ∆中∴)(ASA DEF ABC ∆≅∆方法技巧:三角形全等的证明及其运用关键点在于“把相等的边(角)放入正确的三角形中”,去说明“相等的边(角)所在的三角形全等”,利用三角形全等来说明两个角相等(两条边相等)是初中里面一个非常常见而又重要的方法。
CFA DABCE DFB例1.如图,ABE ∆≌DCF ∆,点A 和点D 、点E 和点F 分别是对应点,则AB= ,=∠A ,AE= ,CE= ,AB// ,若BC AE ⊥,则DF 与BC 的关系是 . 例2.如图,在,90︒=∠∆C ABC 中D 、E 分别为AC 、AB 上的点,且BE=BC ,DE=DC ,求证:(1)AB DE ⊥; (2)BD 平分ABC ∠例3. 如图,21,∠=∠∠=∠D A ,AC ,BD 相交于O , 求证:①AB=CD ②OA=OD例4. 已知,如图BC=BE ,21,∠=∠∠=∠E C ,求证:AC=DE例5.已知:如图,已知AB=AC ,AD=AE ,求证:BE=CD.若BF=CF ,求证:BDF ∆≌CEF ∆ADA全等三角形练习1.下面给出四个结论:①若两个图形是全等图形,则它们形状一定相同;②若两个图形的形状相同,则它们一定是全等图形;③若两个图形的面积相等,则它们一定是全等图形;④若两个图形是全等图形,则它们的大小一定相同,其中正确的是( ) A 、①④ B 、①② C 、②③ D 、③④ 2.如图,ABC∆≌BAD∆,A 和 B 以及C 和D 分别是对应点,如果︒=∠︒=∠35,60ABD C ,则BAD ∠的度数为( )A 、︒85B 、︒35C 、︒60D 、︒80 3.在△ABC 和△C B A '''中,若AB=B A '',AC=C A '',还要加一个角的条件,使△ABC ≌△C B A ''',那么你加的条件是( ) A .∠A=∠A ' B.∠B=∠B ' C.∠C=∠C ' D.∠A=∠B ' 4.下列条件不可推得ABC ∆和'''C B A ∆全等的条件是( )A. AB=A 'B ','A A ∠=∠,'C C ∠=∠ B. AB= A 'B ',AC=A 'C ',BC='B C 'C. AB= A 'B ',AC=A 'C ','B B ∠=∠ D. AB= A 'B ','A A ∠=∠,'B B ∠=∠ 5.如图,ABC ∆≌AED ∆,若=∠︒=∠︒=∠︒=∠BAC C EAB B 则,45,30,40 ,=∠D,6.已知AB=AC ,EB=EC ,有 对全等三角形,请写出全等三角形7.已知,如图,CD AF D A =∠=∠∠=∠,21,,求证:①AB=DE ②EF//BC ,8.如图,AB//CD ,AD//BC ,求证:AB=CD9. 如图,已知AB ⊥AC ,AD ⊥AE ,AB=AC ,AD=AE , 求证:(1)BE=DC ,(2)BE ⊥DC.D第5题图DDABQCPE第6题。
(完整版)全等三角形知识总结和经典例题

全等三角形复习[ 知识要点 ]一、全等三角形1.判定和性质一般三角形直角三角形边角边( SAS)、角边角( ASA)具备一般三角形的判定方法判定斜边和一条直角边对应相等( HL )角角边( AAS)、边边边( SSS)对应边相等,对应角相等性质对应中线相等,对应高相等,对应角平分线相等注:①判定两个三角形全等必须有一组边对应相等;② 全等三角形面积相等.2.证题的思路:找夹角( SAS)已知两边找直角( HL )找第三边( SSS)若边为角的对边,则找任意角( AAS)找已知角的另一边(SAS)已知一边一角边为角的邻边找已知边的对角(AAS)找夹已知边的另一角(ASA)找两角的夹边(ASA)已知两角找任意一边(AAS)性质1、全等三角形的对应角相等、对应边相等。
2、全等三角形的对应边上的高对应相等。
3、全等三角形的对应角平分线相等。
4、全等三角形的对应中线相等。
5、全等三角形面积相等。
6、全等三角形周长相等。
( 以上可以简称 : 全等三角形的对应元素相等)7、三边对应相等的两个三角形全等。
(SSS)8、两边和它们的夹角对应相等的两个三角形全等。
(SAS)9、两角和它们的夹边对应相等的两个三角形全等。
(ASA)10、两个角和其中一个角的对边对应相等的两个三角形全等。
(AAS)11、斜边和一条直角边对应相等的两个直角三角形全等。
(HL)运用1、性质中三角形全等是条件,结论是对应角、对应边相等。
而全等的判定却刚好相反。
2、利用性质和判定,学会准确地找出两个全等三角形中的对应边与对应角是关键。
在写两个三角形全等时,一定把对应的顶点,角、边的顺序写一致,为找对应边,角提供方便。
3,当图中出现两个以上等边三角形时,应首先考虑用 SAS找全等三角形。
4、用在实际中,一般我们用全等三角形测等距离。
以及等角,用于工业和军事。
有一定帮助。
5、角平分线的性质及判定性质:角平分线上的点到这个角的两边的距离相等判定:到一个角的两边距离相等的点在这个角平分线上做题技巧一般来说考试中线段和角相等需要证明全等。
(完整word版)人教版八年级上全等三角形经典例题整理

全等三角形的典型习题一、全等在特殊图形中的运用1、如图,等边△ABC 中,D 、E 分别是AB 、CA 上的动点,AD =CE ,试求∠DFB 的度数.2、如下图所示,等边△ABC 中,D 、E 、F 是AB 、BC 、CA 上动点,AD =BE =CF ,试判断△DEF 的形状.3、如下图所示,△ABC 和△ADE 都是等边三角形,且点B 、A 、D 在同一直线上,AC 、BE 相交于点G ,AE 、CD 相交于点F ,试说明△AGF 是等边三角形.Ex 、如图,四边形ABCD 与BEFG 都是正方形,AG 、CE 相交于点O ,AG 、BC 相交于点M ,BG 、CE 相交于点N ,请你猜测AG 与CE 的关系(数量关系和位置关系)并说明理由.4、△ABC 是等腰直角三角形,AB =AC ,∠BAC =90°,∠B =∠C =45°,D 是底边BC 的中点,DE ⊥DF ,试说明BE 、CF 、EF 为边长的三角形是直角三角形。
AB AAm二.证明全等常用方法(截长法或补短法)5、如图所示,在△ABC 中,∠ABC =2∠C ,∠BAC 的平分线交BC 于点D .请你试说明AB +BD =AC .Ex1,∠C +∠D =180°,∠1=∠2,∠3=∠4.试用截长法说明AD +BC =AB .Ex2、五边形ABCDE 中,AB =AE,∠BAC +∠DAE =∠CAD,∠ABC +∠AED =180°,连结AC ,AD .请你用补短法说明BC +DE =CD .(也可用截长法,自己考虑)6、如图,正方形ABCD 中,E 是AB 上的点,F 是BC 上的点,且∠EDF =45°.请你试用补短法说明AE +CF =EF .Ex1.、如图所示,在△ABC 中,边BC 在直线m 上,△ABC 外的四边形ACDE 和四边形ABFG 均为正方形,DN ⊥m 于N ,FM ⊥m 于M .请你说明BC =FM +DN 的理由.(分别用截长法和补短法) (连结GE ,你能说明S △ABC =S △AGE 吗?)BB C F C A B三.全等在探究题中的运用7、数学课上,张老师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF ∠=o,且EF 交正方形外角DCG ∠的平行线CF 于点F ,求证:AE =EF .经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证AME ECF △≌△,所以AE EF =.(1) 请你写出△ABC ≌△ECF 的理由; 在此基础上,同学们作了进一步的研究:(2)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE =EF ”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由; (3)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE =EF ”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.8、已知,△ABC 中,∠BAC = 90°,AB = AC ,过A 任作一直线l ,作BD ⊥l 于D ,CE ⊥l 于E ,观察三条线段BD ,CE ,DE 之间的数量关系.⑴如图1,当l 经过BC 中点时,DE = ,此时BD CE.⑵如图2,当l 不与线段BC 相交时,BD ,CE ,DE 三者的数量关系为 ,并证明你的结论. ⑶如图3,当l 与线段BC 相交,交点靠近B 点时,BD ,CE ,DE 三者的数量关系为 . 证明你的结论,并画图直接写出交点靠近C 点时,BD ,CE ,DE 三者的数量关系为 .图1 图2 图3 A D FGB图1A D F GB图2A D FC GB图3 A l B CA B C DE lA B C lE D四.动点问题中的全等、9、如图,已知ABC △中,20AB AC ==厘米,BC=16厘米,点D 为AB 的中点.(1)如果点P 在线段BC 上以6厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A点运动.①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由; ②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动 速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多 长时间点P 与点Q 第一次在ABC △的哪条边上相遇?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实用文档之"一,证明边或角相等"
方法:证明两条线段相等或角相等,如果这两条线段或角在两个三角形内,就证明这两个三角形全等;如果这两条线段或角在同一个三角形内,就证明这个三角形是等腰三角形;如果看图时两条线段既不在同一个三角形内,也不在两个全等三角形内,那么就利用辅助线进行等量代换,同样如果角不在同一个三角形内,也不在两个全等三角形内,也是用等量代换(方法是:(1)同角(等角)的余角相等(2)同角(等角)的补角相等,此类型问题一般不单独作一大题,往往是通过得出角相等后用来证明三角形全等,而且一般是在双垂直的图形中)
1.已知,如图,AB⊥AC,AB=AC,AD⊥AE,AD=AE。
求证:BE=CD。
2.如图,在四边形ABCD中,E是AC上的一点,∠1=∠2,∠3=∠4,求证:
∠5=∠6.
3.已知:如图△ABC中,AB=AC,BD⊥AC,CE⊥AB,BD、CE交于H。
求证:HB=HC。
2、如图, 已知:AB⊥BC于B , EF⊥AC于G , DF⊥BC于D , BC=DF.求
证:AC=EF.
A
E
D
C
B
6
5
4
3
2
1
E
D
C
B
A
E
D
C
B
A
二.证明线段和差问题 (形如:AB+BC=CD,AB=AD - CD)
证明两条线段和等于另一条线段,常常使用截长补短法。
①截长法即为在这三条最长的线段截取一段使它等于较短线段中的一条,然后证明剩下的一段等于另一条较短的线段。
②补短法即为在较短的一条线段上延长一段,使它们等于最长的线段,然后证明延长的这一线段等于另一条较短的线段。
证明两条线段差等于另一条线段,只需把差化成和来解决即可。
1.如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA
的平分线相交于E ,CE 的连线
交AP 于D .求证:AD +BC =AB .
2、如图,已知:△ABC 中,∠BAC =90, AB =AC ,AE 是过A 一直线,且点B 、C 在AE 的异侧,BD ⊥AE 于D ,CE ⊥AE 于E . 求证:BD =DE +CE ;
P E D C
B
A
F
G
E D C
B
A
3、如图,AB ∥CD ,DE 平分∠ADC ,AE 平分∠BAD ,求证:AB=AD - CD
三.证明线段的
2倍或2
1关系 ( AB CE =2, MN BN =
1
2
) 1. 利用含30
角的直角三角形的性质证明
例1. 已知,如图1,∆ABC 是等边三角形,在AC 、BC 上分别取点D 、E ,且AD =CE ,连结AE 、BD 交于点N ,过B 作BM AE ⊥,垂足为M ,求证:
MN BN =
1
2
(提示:先证∠=BNE 60)
2. 利用等线段代换(充分利用中点)
例1.如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,
BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F . 求证:BD =2CE .
F
E D
C
B
A
3.转化为线段和问题,利用截长补短法
例5. 已知:如图5,四边形ABCD 中,∠=D 90
,对角线AC 平分∠BAD ,
AC BC =,求证:AD AB =
12
四.证明二倍角关系
利用三角形外角和定理和等量代换
如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B
D C
B
A。
