《相交线与平行线》的单元测试题(含答案)(可编辑修改word版)
相交线与平行线单元测试题总集完整含答案
B E DA CF87654321DCBA第五章 相交线与平行线测试题一、选择题(每题3分,共30分)1、如图1，直线a ，b 相交于点O ，若∠1等于40°，则∠2等于（ ）A ．50°B ．60°C ．140°D ．160°图1 图2 图3 2、如图2，已知AB ∥CD ，∠A ＝70°，则∠1的度数是（ ）A ．70°B ．100°C ．110°D ．130°3、已知：如图3，AB CD ⊥，垂足为O ，EF 为过点O 的一条直线，则1∠ 与2∠的关系一定成立的是（ ）A ．相等B ．互余C ．互补D ．互为对顶角4、如图4，AB DE ∥，65E ∠=，则B C ∠+∠=（ ）A ．135B ．115C ．36D ．65图4 图5 图65、如图5，小明从A 处出发沿北偏东60°方向行走至B 处，又沿北偏西20方向行走至C 处，此时需把方向调整到与出发时一致，则方向的调整应是（ ）A ．右转80°B ．左转80°C ．右转100°D ．左转100° 6、如图6，如果AB ∥CD ，那么下面说法错误的是（ ）A ．∠3=∠7；B ．∠2=∠6C 、∠3+∠4+∠5+∠6=1800D 、∠4=∠87、如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30，那么这两个角是（ ）A ． 42138、；B ． 都是10；C ． 42138、或4210、；D ． 以上都不对8、下列语句：①三条直线只有两个交点，则其中两条直线互相平行；②如果两条平行线被第三条截，同旁内角相等，那么这两条平行线都与第三条直线垂直；③过一点有且只有一条直线与已知直线平行，其中（ ）A ．①、②是正确的命题；B ．②、③是正确命题；C ．①、③是正确命题 ；D ．以上结论皆错DB A C1ab1 2OABCD EF 2 1Oa b M P N 1 2 3A B C a b1 23 B E9、下列语句错误的是（ ）A ．连接两点的线段的长度叫做两点间的距离；B ．两条直线平行，同旁内角互补C ．若两个角有公共顶点且有一条公共边，和等于平角，则这两个角为邻补角D ．平移变换中，各组对应点连成两线段平行且相等10、如图7，a b ∥，M N ，分别在a b ，上，P 为两平行线间一点，那么123∠+∠+∠=（ ）A ．180B ．270C ．360D ．540二、填空题(每题3分,共18分)11、如图8，直线a b ∥，直线c 与a b ，相交．若170∠=，则2_____∠=．图7 图8 图9 图1012、如图9，已知170,270,360,∠=︒∠=︒∠=︒则4∠=______︒．13、如图10，已知AB ∥CD ，BE 平分∠ABC ，∠CDE ＝150°，则∠C ＝______14、如图11，已知a b ∥，170∠=，240∠=，则3∠ 图11 1315、如图12的一个条件 ．16、如图13，已知AB CD //，∠α=____________ 三、解答题（共52分）17、推理填空：(每空1分,共12分)如图： ① 若∠1=∠2，则 ∥ （ ） 若∠DAB+∠ABC=1800，则∥ （）②当 ∥ 时，∠ C+∠ABC=1800 （ ） 当 ∥ 时，∠3=∠C （ ）18、如图，∠1＝30°，AB ⊥CD ，垂足为O ，EF 经过点O .求∠2、∠3的度数. (8分)12 bac b ac d1 2 3 4 A BCDE 321DCBAABCDO123EF19、已知：如图AB ∥CD ，EF 交AB 于G ，交CD 于F ，FH 平分∠EFD ，交AB 于H ，∠AGE=500，求：∠BHF 的度数．(8分)20、(10分（1）如图a ，图中共有＿＿＿对对顶角；（2）如图b ，图中共有＿＿＿对对顶角； （3）如图c ，图中共有＿＿＿对对顶角.（4）研究（1）～（3）小题中直线条数与对顶角的对数之间的关系，若有n 条直线相交于一点，则可形成多少对对顶角？（5）若有2008条直线相交于一点，则可形成 多少对对顶角？21、(6分)如图，AD 是∠EAC 的平分线，AD ∥BC ，∠B ＝30º，求∠EAD ，∠DAC ，∠C 的度数。
相交线与平行线单元测试题(含答案)
相交线与平行线一、选择题（本大题共8小题，每小题只有一个正确选项，每小题3分，共24分）1．在下面各图中，∠1与∠2是对顶角的是（）A．B．C．D．2．如图，直线a、b相交于点O，若∠1＝30°，则∠2等于（）A．60°B．30°C．140°D．150°3．如图，直线a，b相交于点O，若∠1＝40°，则∠2＝（）A．40°B．50°C．60°D．140°4．如图，点P在直线l外，点A，B在直线l上，PA＝3，PB＝7，点P到直线l的距离可能是（）A．2 B．4 C．7 D．85．如图，直线a∥b，∠1＝50°，则∠2的度数为（）A．40°B．50°C．55°D．60°6．如图，工人师傅用角尺画出工件边缘AB的垂线a和b，得到a∥b．理由是（）A．连接直线外一点与直线上各点的所有线段中，垂线段最短B．在同一平面内，垂直于同一条直线的两条直线互相平行C．在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线D．经过直线外一点，有且只有一条直线与这条直线平行7．如图，已知ON丄a，OM丄a，所以OM与ON重合的理由是（）A．两点确定一条直线B．经过一点有且只有一条线段垂直于己知直线C．过一点只能作一条垂线D．垂线段最短8．如图，直线AB∥CD，∠A＝70°，∠E＝30°，则∠C等于（）A．30°B．40°C．60°D．70°二、填空题（本大题共6小题，每小题3分，共18分）9．如图所示，在铁路旁边有一李庄，现要建一火车站，为了使李庄人乘火车最方便（即距离最近），请你在铁路旁选一点来建火车站（位置已选好），说明理由：．10．如图，已知O是直线AB上一点，∠1＝30°，OD平分∠BOC，则∠2＝．11．如图，直线AB、CD相交于点O，EO⊥AB，∠AOC＝25°。
(完整版)新人教版七年级下《相交线与平行线》单元测试题及答案
订交线与平行线单元测试题班级姓名一、选择题（选择填空 2 分一题）1、假如一个角的补角是150°，那么这个角的度数是（）A.30 °B. 60°C.90°D.120 °2、如图，已知直线a、 b 被直线 c 所截， a∥ b，∠ 1＝ 130°，则∠2＝（）A. 130 °B. 50°C.40°D.60°3、以下说法错误的选项是( )Ａ . 内错角相等，两直线平行．Ｂ.两直线平行，同旁内角互补．C. 相等的角是对顶角．D.等角的补角相等．4、以下图中∠ 1 和∠ 2 是同位角的是（）A. ⑴、⑵、⑶，B.⑵、⑶、⑷，C.⑶、⑷、⑸，D.⑴、⑵、⑸5、已知 :如图,∠1＝∠2,则有()A.AB∥ CDB.AE∥DFC. AB∥ CD且AE∥ DFD.以上都不对6、如图 , 直线 AB与 CD交于点 O,OE⊥ AB于 O,图∠ 1 与∠ 2 的关系是 ( )A. 对顶角B.互余C.互补D相等7、如图， DH∥ EG∥ BC，且 DC∥ EF，那么图中和∠ 1 相等的角的个数是（）A.2，B.4，C.5，D.68、如图， AB//CD， BC//DE，则∠ B+∠ D的值为（）A.90 °B.150°C.180°D.以上都不对9、如图，直线AB与 CD订交于点 O， OB均分∠ DOE.若∠ DOE＝ 60 o，则∠ AOE的度数是（） A.90° B.150° C.180° D.不可以确立10、一束光芒垂直照耀在水平川面，在地面上放一个平面镜，欲使这束光芒经过平面镜反射后成水平光芒，则平面镜与地面所成锐角的度数为（）A.45 oB.60 oC.75 oD.80 o11、以下图形中，由 AB ∥ CD ，能获得 12 的是（）A1 B A1BA 1 2BA B12C 2DCDCDD CA ．B ．2C ．D ．12、如图 , 已知∠ 1=∠ 2，∠ 3=80O ，则∠ 4=（）OB. 70 OOD. 50 OA.80 C. 6013、如图，已知 AC ∥ ED ，∠ C =26°，∠ CBE =37°，则∠ BED 的度数是 ( ) A ． 63°B ． 83°C ． 73°D ． 53°21 AB34DCE15 题14 题13 题14、如图，在所表记的角中，同位角是（ ）．A ． 1和2 B ．1和3C ． 1和4 D ． 2 和 3ACD 55°15、如图， Rt △ ABC中，ACB90°DE ∥AB，若，DE 过点 C ，且，则∠ B 的度数（ ）A ．35° B ．45 C ．55° D ．65° AEF16、如图，把矩形 ABCD 沿 EF 对折后使两部分重合， 若 1 50°=（），则 A ． 110°B． 115°C． 120°D． 130°A EDBF 1C二、填空1、黎老师家在小星家的北偏东 68 度，则小星家在黎老师家的南偏西 度 。
八年级第五章相交线与平行线单元测试卷练习(Word版 含答案)
八年级第五章相交线与平行线单元测试卷练习（Word 版 含答案）一、选择题1．如图，∠1＝20º，AO ⊥CO ，点B 、O 、D 在同一条直线上，则∠2的度数为（ ）A ．70ºB ．20ºC ．110ºD ．160º2．下列结论中：①同一平面内，两条不相交的直线被第三条直线所截，形成的同旁内角互补；②在同一平面内，若,//a b b c ⊥，则a c ⊥； ③直线外一点到直线的垂线段叫点到直线的距离；④同一平面内，过一点有且只有一条直线与已知直线平行，正确的个数有（ ）A ．1个B ．2个C ．3个D ．4个3．如图，AD ∥CE ，∠ABC ＝95°，则∠2﹣∠1的度数是（ ）A ．105°B ．95°C ．85°D ．75° 4．如图，在四边形ABCD 中，要得到AB CD ∥，只需要添加一个条件，这个条件可以是（ ）A ．13∠=∠B ．24∠∠=C ．BD ∠=∠ D ．12180B ∠+∠+∠=︒5．如图，将矩形ABCD 沿GH 折叠，点C 落在点Q 处，点D 落在AB 边上的点E 处，若∠AGE=32°，则∠GHC 等于（ ）A ．112°B ．110°C ．108°D ．106°6．如图，有一块含有30°角的直角三角形板的两个顶点放在直尺的对边上．如果∠2=44°，那么∠1的度数是（ ）A ．14°B ．15°C ．16°D ．17°7．如图所示，若AB ∥EF ，用含α、β、γ的式子表示x ，应为（ ）A ．αβγ++B ．βγα+-C ．180αγβ︒--+D ．180αβγ︒++- 8．如图，AB ∥CD ，BF ,DF 分别平分∠ABE 和∠CDE ，BF ∥DE ，∠F 与∠ABE 互补，则∠F 的度数为A ．30°B ．35°C ．36°D ．45°9．如图，直线AB 、CD 相交于点E ，DF ∥AB ．若∠AEC=100°，则∠D 等于（ ）A ．70°B ．80°C ．90°D ．100° 10．如图，直线a ∥b ，AC ⊥AB 于A ，AC 交直线b 于点C ，∠1=50°，则∠2的度数是（ ）A ．50°B ．40°C ．25°D ．20°11．下列命题中，其逆命题为真命题的是（ ）A ．若a ＝b ，则a 2＝b 2B ．同位角相等C ．两边和一角对应相等的两个三角形全等D ．等腰三角形两底角不相等12．如图所示，已知 AB ∥CD ，下列结论正确的是（ ）A ．∠1=∠2B ．∠2=∠3C ．∠1=∠4D ．∠3=∠4二、填空题13．如图，AB //CD BED 110BF ，，∠=平分ABE DF ∠，平分CDE ∠，则BFD ∠= ______ ．14．如图，△ABC 的角平分线CD 、BE 相交于F ，∠A ＝90°，EG ∥BC ，且CG ⊥EG 于G ，下列结论：①∠CEG ＝2∠DCB ；②∠DFB ＝12∠CGE ；③∠ADC ＝∠GCD ；④CA 平分∠BCG ．其中正确的结论是_______．15．如图，一条公路修到湖边时，需拐弯绕湖而过，在A ，B ，C 三处经过三次拐弯，此时道路恰好和第一次拐弯之前的道路平行(即AE ∥CD )，若∠A =120°，∠B =150°,则∠C 的度数是________16．如图，直线a ∥b ∥c ，直角∠BAC 的顶点A 在直线b 上，两边分别与直线a ，c 相交于点B ，C ，则∠1＋∠2的度数是___________．17．如图，已知AB ，CD ，EF 互相平行，且∠ABE ＝70°，∠ECD ＝150°，则∠BEC ＝________°.18．如图，已知AB ∥DE ，∠ABC ＝76°，∠CDE ＝150°，则∠BCD 的度数为__°．19．如图，//AB CD ，GF 与AB 相交于点H ，与CD 于F ，FE 平分HFD ∠，若50EHF ∠=︒，则HFE ∠的度数为______．20．将一张长方形纸片折叠成如图所示的形状，则∠ABC=_________．三、解答题21．（感知）如图①，AB ∥CD ，点E 在直线AB 与CD 之间，连结AE 、BE ，试说明∠BAE+∠DCE=∠AEC ；（探究）当点E 在如图②的位置时，其他条件不变，试说明∠AEC+∠BAE+∠DCE=360°； （应用）点E 、F 、G 在直线AB 与CD 之间，连结AE 、EF 、FG 和CG ，其他条件不变，如图③，若∠EFG=36°，则∠BAE+∠AEF+∠FGC+∠DCG=______°.22．（1）问题发现如图①，直线AB ∥CD ，E 是AB 与AD 之间的一点，连接BE ，CE ，可以发现∠B +∠C ＝∠BEC ．请把下面的证明过程补充完整：证明：过点E 作EF ∥AB ，∵AB ∥DC （已知），EF ∥AB （辅助线的作法），∴EF ∥DC （ ）∴∠C ＝∠CEF ．（ ）∵EF ∥AB ，∴∠B ＝∠BEF （同理），∴∠B +∠C ＝ （等量代换）即∠B +∠C ＝∠BEC ．（2）拓展探究如果点E 运动到图②所示的位置，其他条件不变，求证：∠B +∠C ＝360°﹣∠BEC ． （3）解决问题如图③，AB ∥DC ，∠C ＝120°，∠AEC ＝80°，则∠A ＝ ．（之间写出结论，不用写计算过程）23．已知，90AOB ︒∠=，点C 在射线OA 上，//CD OE ．（1）如图 1，若120OCD ︒∠=，求∠BOE 的度数；（2）把“90AOB ︒∠=°”改为“120AOB ︒∠=”，射线OE 沿射线OB 平移，得到O E '，其它条件不变（如 图 2 所示），探究,OCD BO E '∠∠ 的数量关系；（3）在（2）的条件下，作PO OB '⊥，垂足为O ' ，与OCD ∠ 的角平分线CP 交于点P ，若BO E α'∠= ， 用含 α 的式子表示CPO '∠（直接写出答案）．24．课题学习：平行线的“等角转化”功能．阅读理解：如图1，已知点A 是BC 外一点，连接AB ，AC ，求BAC B C ∠+∠+∠的度数．（1）阅读并补充下面推理过程．解：过点A 作ED BC ∥B EAB ∴∠=∠，C ∠=__________．__________180=︒180B BAC C ∴∠+∠+∠=︒解题反思：从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将BAC ∠，B ，C ∠“凑”在一起，得出角之间的关系，使问题得以解决．方法运用：（2）如图2，已知AB ED ，试说明：180D BCD B ∠+∠-∠=︒（提示：过点C 做CF AB ∥）．深化拓展：（3）已知AB CD ∥，点C 在点D 的右侧，70ADC ∠=︒．BE 平分ABC ∠，DE 平分ADC ∠，BE ，DE 所在的直线交于点E ，点E 在AB 与CD 两条平行线之间． ①如图3，点B 在点A 的左侧，若60ABC ∠=︒，则BED ∠的度数为________． ②如图4，点B 在点A 的右侧，且<AB CD ，AD BC <．若ABC n ∠=︒，则BED ∠的度数为________．（用含n 的代数式表示）25．[感知发现]：如图，是一个“猪手”图，AB ∥CD ，点E 在两平行线之间，连接BE ，DE ，我们发现：∠E=∠B+∠D证明如下：过E 点作EF ∥AB ．∴∠B=∠1(两直线平行，内错角相等．） 又AB ∥CD(已知）∴CD ∥EF(如果两条直线都与第三条直线平行，那么这两条直线也互相平行．） ∴∠2=∠D(两直线平行，内错角相等．）∴∠1+∠2=∠B+∠D(等式的性质1．）即：∠E=∠B+∠D[类比探究]：如图是一个“子弹头”图，AB ∥CD ，点E 在两平行线之间，连接BE ，DE ．试探究∠E+∠B+∠D=360°．写出证明过程．[创新应用]：(1)．如图一，是两块三角板按如图所示的方式摆放，使直角顶点重合，斜边平行，请直接写出∠1的度数．(2)．如图二，将一个长方形ABCD 按如图的虚线剪下，使∠1=120o ，∠FEQ=90°． 请直接写出∠2的度数．26．（1）如图1，已知直线//m n ，在直线n 上取A B 、两点，C P 、为直线m 上的两点，无论点C P 、移动到任何位置都有：ABC S ____________ABP S △（填“>”、“<”或“=”）（2）如图2，在一块梯形田地上分别要种植大豆（空白部分）和芝麻（阴影部分），若想把种植大豆的两块地改为一块地，且使分别种植两种植物的面积不变，请问应该怎么改进呢？写出设计方案，并在图中画出相应图形并简述理由．（3）如图3，王爷爷和李爷爷两家田地形成了四边形DEFG ，中间有条分界小路（图中折线ABC ），左边区域为王爷爷的，右边区域为李爷爷的。
第五章相交线与平行线单元试卷练习(Word版 含答案)
第五章相交线与平行线单元试卷练习（Word 版 含答案）一、选择题1．如图，O 是直线AB 上一点，OE 平分∠BOD ，OF ⊥OE ，∠D ＝110°，添加一个条件，仍不能判定AB ∥CD ，添加的条件可能是（ ）A ．∠BOE ＝55°B ．∠DOF ＝35°C ．∠BOE +∠AOF ＝90°D ．∠AOF ＝35° 2．如图，将矩形ABCD 沿GH 折叠，点C 落在点Q 处，点D 落在AB 边上的点E 处，若∠AGE=32°，则∠GHC 等于（ ）A ．112°B ．110°C ．108°D ．106°3．如图，给出下列条件：①∠3=∠4；②∠1=∠2；③∠5=∠B ；④AD ∥BE ，且∠D =∠B ．其中能说明AB ∥DC 的条件有（ ）A ．4个B ．3个C ．2个D ．1个4．如图，已知直线a ∥b ，∠1=100°，则∠2等于（ ）A ．80°B ．60°C ．100°D ．70°5．如图，//,AD BC D ABC ∠=∠,点E 是边DC 上一点，连接AE 交BC 的延长线于点H ，点F 是边AB 上一点，使得FBE FEB ∠=∠，作FEH ∠的角平分线EG 交BH 于点G ，若100DEH ︒∠=，则BEG ∠的度数是（ ）A ．30︒B ．40︒C ．50︒D ．60︒6．下列说法中,错误的有( )①若a 与c 相交,b 与c 相交,则a 与b 相交;②若a∥b,b∥c,那么a∥c;③过直线外一点有且只有一条直线与已知直线平行;④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.A ．3个B ．2个C ．1个D ．0个7．如图，25AOB ︒∠=，90AOC ︒∠=，点B ，O ，D 在同一直线上，则COD ∠的度数为（ ）A ．65B ．25C ．115D ．1558．下列命题：①两边及其中一边的对角对应相等的两个三角形全等；②两角及其中一角的对边对应相等的两个三角形全等；③有两条边和第三条边上的高对应相等的两个三角形全等；④面积相等的两个三角形肯定全等；⑤有两条直角边对应相等的两个直角三角形全等．其中正确的个数是（ ）A ．1个B ．2个C ．3个D ．4个9．如图，1∠与2∠是同位角的共有（ ）个A ．1个B ．2个C ．3个D ．4个10．交换下列命题的题设和结论，得到的新命题是假命题的是( )A ．两直线平行，同位角相等B ．相等的角是对顶角C ．所有的直角都是相等的D ．若a=b ，则a ﹣3=b ﹣3 11．能说明命题“若a ＞b ，则3a ＞2b “为假命题的反例为（ ）A ．a ＝3，b ＝2B ．a ＝﹣2，b ＝﹣3C ．a ＝2，b ＝3D ．a ＝﹣3，b ＝﹣2 12．下列选项中，不是运用“垂线段最短”这一性质的是（ ）A ．立定跳远时测量落点后端到起跳线的距离B ．从一个村庄向一条河引一条最短的水渠C ．把弯曲的公路改成直道可以缩短路程D ．直角三角形中任意一条直角边的长度都比斜边短 二、填空题13．如图，已知AB ∥CD ，点E ，F 分别在直线AB ，CD 上点P 在AB ，CD 之间且在EF 的左侧．若将射线EA 沿EP 折叠，射线FC 沿FP 折叠，折叠后的两条射线互相垂直，则∠EPF 的度数为 _____．14．若平面上4条直线两两相交且无三线共点，则共有同旁内角________对．15．如图，直线MN∥PQ，点A 在直线MN 与PQ 之间，点B 在直线MN 上，连结AB ．∠ABM 的平分线BC 交PQ 于点C ，连结AC ，过点A 作AD⊥PQ 交PQ 于点D ，作AF⊥AB 交PQ 于点F ，AE 平分∠DAF 交PQ 于点E ，若∠CAE=45°，∠ACB=∠DAE，则∠ACD 的度数是_____．16．α∠与β∠的两边互相垂直，且o 50α∠=，则β∠的度数为_________.17．如图，将一张长方形纸片ABCD 沿EF 折叠，使顶点C ，D 分别落在点C′、D′处，C′E 交AF 于点G ，若∠CEF=64°，则∠GFD′=_____________.18．如图，AD ∥BC ，∠D=100°，CA 平分∠BCD ，则∠DAC=________度．19．如图，CB∥OA，∠B＝∠A＝100°，E、F在CB上，且满足∠FOC＝∠AOC，OE平分∠BOF，若平行移动AC，当∠OCA的度数为_____时，可以使∠OEB＝∠OCA．20．如图，∠AOB＝60°，在∠AOB的内部有一点P，以P为顶点，作∠CPD，使∠CPD的两边与∠AOB的两边分别平行，∠CPD的度数为_______度．三、解答题21．阅读下面材料：彤彤遇到这样一个问题：已知：如图甲，AB//CD，E为AB，CD之间一点，连接BE，DE，得到∠BED．求证：∠BED＝∠B+∠D．彤彤是这样做的：过点E作EF//AB，则有∠BEF＝∠B．∵AB//CD，∴EF//CD．∴∠FED＝∠D．∴∠BEF+∠FED＝∠B+∠D．即∠BED＝∠B+∠D．请你参考彤彤思考问题的方法，解决问题：如图乙．已知：直线a//b，点A，B在直线a上，点C，D在直线b上，连接AD，BC，BE平分∠ABC，DE平分∠ADC，且BE，DE所在的直线交于点E．（1）如图1，当点B在点A的左侧时，若∠ABC＝60°，∠ADC＝70°，求∠BED的度数；（2）如图2，当点B在点A的右侧时，设∠ABC＝α，∠ADC＝β，直接写出∠BED的度数（用含有α，β的式子表示）．22．如图1，AB ∥CD ，点E 在AB 上，点G 在CD 上，点 F 在直线 AB ，CD 之间，连接EF ，FG ，EF 垂直于 FG ，∠FGD =125°．(1)求出∠BEF 的度数；(2)如图 2，延长FE 到H ，点M 在FH 的上方，连接MH ，Q 为直线 AB 上一点，且在直线 MH 的右侧， 连接 MQ ，若∠EHM=∠M +90°，求∠MQA 的度数；(3)如图 3，S 为 NB 上一点，T 为 GD 上一点，作直线 ST ，延长 GF 交 AB 于点 N ，P 为直线 ST 上一动点，请直接写出∠PGN ，∠SNP 和∠GPN 的数量关系 ．（题中所有角都是大于 0°小于 180°的角）23．已知，90AOB ︒∠=，点C 在射线OA 上，//CD OE ．（1）如图 1，若120OCD ︒∠=，求∠BOE 的度数；（2）把“90AOB ︒∠=°”改为“120AOB ︒∠=”，射线OE 沿射线OB 平移，得到O E '，其它条件不变（如 图 2 所示），探究,OCD BO E '∠∠ 的数量关系；（3）在（2）的条件下，作PO OB '⊥，垂足为O ' ，与OCD ∠ 的角平分线CP 交于点P ，若BO E α'∠= ， 用含 α 的式子表示CPO '∠（直接写出答案）．24．如图1，AB//CD ，在AB 、CD 内有一条折线EPF ．（1）求证：AEP CFP EPF ∠∠∠+=．（2）如图2，已知BEP ∠的平分线与DFP ∠的平分线相交于点Q ，试探索EPF ∠与EQF ∠之间的关系；（3）如图3，已知BEQ ∠=1BEP 3∠，1DFQ DFP 3∠∠=，则P ∠与Q ∠有什么关系，请说明理由．25．如图1，//PQ MN ，点A ，B 分别在MN ，QP 上，2BAM BAN ∠=∠射线AM 绕A 点顺时针旋转至AN 便立即逆时针回转，射线BP 绕B 点顺时针旋转至BQ 便立即逆时针回转．射线AM 转动的速度是每秒2度，射线BQ 转动的速度是每秒1度．（1）直接写出QBA ∠的大小为_______；（2）射线AM 、BP 转动后对应的射线分别为AE 、BF ，射线BF 交直线MN 于点F ，若射线BP 比射线AM 先转动30秒，设射线AM 转动的时间为t ()0180t <<秒，求t 为多少时，直线//BF 直线AE ？（3）如图2，若射线BP 、AM 同时转动m ()090m <<秒，转动的两条射线交于点C ，作120ACD ∠=︒，点D 在BP 上，请探究BAC ∠与BCD ∠的数量关系．26．问题情境（1）如图①，已知360B E D ∠+∠+∠=︒，试探究直线AB 与CD 有怎样的位置关系？并说明理由．小明给出下面正确的解法：直线AB 与CD 的位置关系是//AB CD ．理由如下：过点E 作//EF AB （如图②所示）所以180B BEF ∠+∠=︒（依据1）因为360B BED D ∠+∠+∠=︒（已知）所以360B BEF FED D ∠+∠+∠+∠=︒所以180FED D ∠+∠=︒所以//EF CD （依据2）因为//EF AB所以//AB CD （依据3）交流反思上述解答过程中的“依据1”，“依据2”，“依据3”分别指什么？“依据1”：________________________________；“依据2”：________________________________；“依据3”：________________________________．类比探究（2）如图，当B 、E ∠、F ∠、D ∠满足条件________时，有//AB CD ． 拓展延伸（3）如图，当B 、E ∠、F ∠、D ∠满足条件_________时，有//AB CD ．27．在△ABC 中，∠BAC ＝90°，点D 是BC 上一点，将△ABD 沿AD 翻折后得到△AED ，边AE 交BC 于点F ．(1)如图①，当AE ⊥BC 时，写出图中所有与∠B 相等的角： ；所有与∠C 相等的角： ．(2)若∠C －∠B ＝50°，∠BAD ＝x °(0＜x ≤45) ．① 求∠B 的度数；②是否存在这样的x 的值，使得△DEF 中有两个角相等．若存在，并求x 的值；若不存在，请说明理由．28．在平面直角坐标系中，如图1，将线段AB 平移至线段CD ，连接AC 、BD ．（1）已知A（﹣3，0）、B（﹣2，﹣2），点C在y轴的正半轴上，点D在第一象限内，且三角形ACO的面积是6，求点C、D的坐标；（2）如图2，在平面直角坐标系中，已知一定点M（1，0），两个动点E（a，2a+1）、F （b，﹣2b+3）．①请你探索是否存在以两个动点E、F为端点的线段EF平行于线段OM且等于线段OM，若存在，求出点E、F两点的坐标；若不存在，请说明理由；②当点E、F重合时，将该重合点记为点P，另当过点E、F的直线平行于x轴时，是否存在△PEF的面积为2？若存在，求出点E、F两点的坐标；若不存在，请说明理由．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】根据平行线的判定定理判断即可．【详解】解：∵OE平分∠BOD，∠BOE=55°，∴∠BOD=2∠BOE=110°，∵∠D=110°，∴∠BOD=∠D，∴CD∥AB，故A不符合题意；∵OF⊥OE，∴∠FOE=90°，∠DOF=35°，∴∠DOE=55°，∵OE平分∠BOD，∴∠DOB=2∠DOE=110°，∵∠D=110°，∴∠DOB=∠D，∴AB∥CD，故B不符合题意；∵∠BOE+∠AOF=90°，∴∠EOF=90°，但不能判断AB ∥CD ，故C 符合题意；∵OF ⊥OE ，∴∠FOE=90°，∠AOF=35°，∴∠BOE=55°，∵OE 平分∠BOD ，∴∠DOB=2∠BOE=110°，∵∠D=110°，∴∠DOB=∠D ，∴AB ∥CD ，故D 不符合题意；故选：C ．【点睛】本题考查了角平分线的性质和平行线的判定定理，熟练掌握平行线的判定定理即可得到结论．2．D解析：D【解析】分析：由折叠可得：∠DGH=12∠DGE=74°，再根据AD ∥BC ，即可得到∠GHC=180°﹣∠DGH=106°．详解：∵∠AGE=32°，∴∠DGE=148°，由折叠可得：∠DGH=12∠DGE=74°． ∵AD ∥BC ，∴∠GHC=180°﹣∠DGH=106°．故选D ．点睛：本题主要考查了平行线的性质，解题时注意：两直线平行，同旁内角互补． 3．B解析：B【详解】解：34∠∠=//AB CD ∴,①正确；12∠=∠//AD BC ∴,②不正确；5B ∠=∠//AB CD ∴,③正确；//AD BE5D ∴∠=∠B D ∠=∠5∴∠=∠B∴,④正确；//AB CD综上所述，①、③、④正确，故选B．4．A解析：A【解析】试题分析：根据对顶角相等可得∠3=∠1=100°，再根据两直线平行，同旁内角互补可得∠2=180°﹣∠3=180°﹣100°=80°．故答案选A．考点：平行线的性质.5．B解析：B【分析】AD∥BC，∠D=∠ABC，则AB∥CD，则∠AEF=180°-∠AED-∠BEG=180°-2β，在△AEF中，100°+2α+180°-2β=180°，故β-α=40°，即可求解．【详解】解：设FBE=∠FEB=α，则∠AFE=2α，∠FEH的角平分线为EG，设∠GEH=∠GEF=β，∵AD∥BC，∴∠ABC+∠BAD=180°，而∠D=∠ABC，∴∠D+∠BAD=180°，∴AB∥CD，∠DEH=100°，则∠CEH=∠FAE=80°，∠AEF=180°-∠FEG-∠BEG=180°-2β，在△AEF中，在△AEF中，80°+2α+180-2β=180°故β-α=40°，而∠BEG=∠FEG-∠FEB=β-α=40°，故选：B．【点睛】此题考查平行线的性质，解题关键是落脚于△AEF内角和为180°，即100°+2α+180°-2β=180°，题目难度较大．6．B解析：B【解析】①若a与b相交，b与c相交，则a与c相交或平行，故本小题错误；②若a∥b，b∥c，则a∥c；根据平行公理的推论：如果两条直线都和第三条直线平行，那么两条直线也互相平行，上面说法正确；③过直线外一点有且只有一条直线与已知直线平行，故正确；④在平面内，两条直线的位置关系有平行和相交两种，故不正确.因此只有②③正确.故选：B.7．C解析：C【分析】先求出∠BOC，再由邻补角关系求出∠COD的度数．【详解】∵∠AOB=25°，∠AOC=90°，∴∠BOC=90°-25°=65°，∴∠COD=180°-65°=115°．故选：C．【点睛】本题考查了余角、邻补角的定义和角的计算；弄清各个角之间的关系是解题的关键．8．B解析：B【分析】根据全等三角形的判断定理逐项判断即可．【详解】解：①两边及其夹角对应相等的两个三角形全等，故该项错误；②两角及其中一角的对边对应相等的两个三角形全等，符合AAS定理，故该项正确；③有两条边和第三条边上的高对应相等的两个三角形不一定全等，有可能是锐角三角形，也有可能是钝角三角形，故该项错误；④面积相等的两个三角形不一定全等，因为形状可能不相同，故该项错误；⑤有两条直角边对应相等的两个直角三角形全等，符合ASA定理，故该项正确．故选：B．【点睛】此题主要考查对全等三角形的判定定理的掌握，正确理解判定定理是解题关键．9．B解析：B【分析】根据同位角的概念对每个图形一一判断，选出正确答案即可．【详解】图1：1∠与2∠是同位角；图2：1∠与2∠不是同位角；图3：1∠与2∠不是同位角；图4：1∠与2∠是同位角；只有图1、图4中1∠与2∠是同位角．故选：B ．【点睛】本题主要考查同位角的概念，熟记同位角的概念是解题关键．10．C解析：C【分析】写出原命题的逆命题，根据相关的性质、定义判断即可．【详解】解：交换命题A 的题设和结论，得到的新命题是同位角相等，两直线平行是真命题； 交换命题B 的题设和结论，得到的新命题是对顶角相等是真命题；交换命题C 的题设和结论，得到的新命题是所有的相等的角都是直角是假命题； 交换命题D 的题设和结论，得到的新命题是若a-3=b-3，则a=b 是真命题，故选C ．【点睛】本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．11．B解析：B【分析】本题每一项代入题干命题中，不满足题意即为反例．【详解】解：当a ＝﹣2，b ＝﹣3时，﹣2＞﹣3，而3×（﹣2）＝2×（﹣3），即a ＞b 时，3a ＝2b ，∴命题“若a ＞b ，则3a ＞2b ”为假命题，故选：B ．【点睛】本题考查的是假命题的证明，任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．12．C解析：C【分析】垂线段最短，指的是从直线外一点到这条直线所作的垂线段最短．它是相对于这点与直线上其他各点的连线而言．据此逐个分析即可.【详解】解：A．立定跳远时测量落点后端到起跳线的距离，运用“垂线段最短”这一性质；B．从一个村庄向一条河引一条最短的水渠，运用“垂线段最短”这一性质；C．把弯曲的公路改成直道可以缩短路程，运用“两点之间，线段最短”这一性质；D．直角三角形中任意一条直角边的长度都比斜边短，运用“垂线段最短”这一性质；故选：C．【点睛】本题主要考查了垂线段最短，实际问题中涉及线路最短问题时，其理论依据应从“两点之间，线段最短”和“垂线段最短”这两个中去选择．二、填空题13．45°或135°【分析】根据题意画出图形，然后利用平行线的性质得出∠EMF与∠AEM和∠CFM的关系，然后可得答案．【详解】解：如图1，过作，，，，，，，同理可得，由折叠可解析：45°或135°【分析】根据题意画出图形，然后利用平行线的性质得出∠EMF与∠AEM和∠CFM的关系，然后可得答案．【详解】解：如图1，过M 作//MN AB ，//AB CD ，////AB CD NM ∴，AEM EMN ∴∠=∠，NMF MFC ∠=∠，90EMF ∠=︒，90AEM CFM ∴∠+∠=︒，同理可得P AEP CFP ∠=∠+∠， 由折叠可得：12AEP PEM AEM ∠=∠=∠，12PFC PFM CFM ∠=∠=∠， 1()452P AEM CFM ∴∠=∠+∠=︒， 如图2，过M 作//MN AB ，//AB CD ， ////AB CD NM ∴，180AEM EMN ∴∠+∠=︒，180NMF MFC ∠+∠=︒，360AEM EMF CFM ∴∠+∠+∠=︒，90EMF ∠=︒，36090270AEM CFM ∴∠+∠=︒-︒=︒，由折叠可得：12AEP PEM AEM ∠=∠=∠，12PFC PFM CFM ∠=∠=∠， 12701352P ∴∠=︒⨯=︒， 综上所述：EPF ∠的度数为45︒或135︒，故答案为：45°或135°．【点睛】本题主要考查了平行线的性质，关键是正确画出图形，分两种情况分别计算出∠EPF的度数．14．24【解析】【分析】根据三线八角的特点，对四条直线产生的6个交点，两两一组进行分类求解即可.【详解】解：如图所示观测点A和点B，同旁内角有2对；A和C有2对；A和D，没有同旁内角；A和解析：24【解析】【分析】根据三线八角的特点，对四条直线产生的6个交点，两两一组进行分类求解即可.【详解】解：如图所示观测点A和点B，同旁内角有2对；A和C有2对；A和D，没有同旁内角；A和E有2对；A和F有2对.B和C有2对；B和D有2对；B和E有2对；B和F没有同旁内角.C和D有2对，C和E没有同旁内角，C和F有2对.D和E有2对；D和F有2对.E和F有2对.共有2×12=24对.故答案是：24.【点睛】本题主要考察三线八角中的同旁内角，正确理解同旁内角和准确的分类是解题的关键. 15．27°．【解析】【分析】延长FA与直线MN交于点K，通过角度的不断转换解得∠BCA=45°.【详解】解：延长FA与直线MN交于点K，由图可知∠ACD=90°-∠CAD=90°-(45°解析：27°．【解析】【分析】延长FA与直线MN交于点K，通过角度的不断转换解得∠BCA=45°.【详解】解：延长FA与直线MN交于点K，由图可知∠ACD=90°-∠CAD=90°-(45°+∠EAD)=45°-∠FAD=45°-(90°-∠AFD)=∠AFD，因为MN∥PQ，所以∠AFD=∠BKA=90°-∠KBA=90°-(180°-∠ABM)=∠ABM-90°，所以∠ACD=∠AFD=(∠ABM-90°)=∠BCD-45°，即∠BCD-∠ACD=∠BCA=45°，所以∠ACD=90°-(45°+∠EAD)=45°-∠EAD=45°-∠BCA=45°-18°=27°.故∠ACD的度数是：27°.【点睛】本题利用平行线、垂直、角平分线综合考查了角度的求解.16．130°或50°【解析】【分析】作图分析，若两个角的边互相垂直，那么这两个角必相等或互补，可据此解答．【详解】如图∵β的两边与α的两边分别垂直，∴α+β=180°故β=130°，在上述情解析：130°或50°【解析】【分析】作图分析，若两个角的边互相垂直，那么这两个角必相等或互补，可据此解答．【详解】如图∵β的两边与α的两边分别垂直，∴α+β=180°故β=130°，在上述情况下，若反向延长∠β的一边，那么∠β的补角的两边也与∠α的两边互相垂直，故此时∠β=50；综上可知：∠β=50°或130°，故正确答案为：【点睛】本题考核知识点：四边形内角和. 解题关键点：根据题意画出图形，分析边垂直的2种可能情况.17．520【解析】因为AD∥BC，所以∠CEF=∠AFE=64°，∠DFE=180°-∠CEF=180°-64°=116°，由折叠得∠EFD=∠EFD′，所以∠EFD′=116°，所以∠GFD′=∠解析：520【解析】因为AD∥BC，所以∠CEF=∠AFE=64°，∠DFE=180°-∠CEF=180°-64°=116°，由折叠得∠EFD=∠EFD′，所以∠EFD′=116°，所以∠GFD′=∠EFD′-∠AFE=116°-64°=52°，故答案为52°.18．40°【分析】本题主要利用两直线平行，同旁内角互补、两直线平行，内错角相等以及角平分线的定义进行做题．【详解】∵AD∥BC，∴∠BCD=180°-∠D=80°，又∵CA平分∠BCD，∴解析：40°【分析】本题主要利用两直线平行，同旁内角互补、两直线平行，内错角相等以及角平分线的定义进行做题．【详解】∵AD∥BC，∴∠BCD=180°-∠D=80°，又∵CA平分∠BCD，∴∠ACB=12∠BCD=40°，∴∠DAC=∠ACB=40°．【点睛】本题重点考查了平行线的性质及角平分线的定义，是一道较为简单的题目．19．60°【分析】设∠OCA=a,∠AOC=x,利用三角形外角，内角和定理，平行线定理即可解答. 【详解】解：设∠OCA=a,∠AOC=x,已知CB∥OA，∠B=∠A=100°，即a+x=80解析：60°【分析】设∠OCA=a,∠AOC=x,利用三角形外角，内角和定理，平行线定理即可解答.【详解】解：设∠OCA=a,∠AOC=x,已知CB∥OA，∠B=∠A=100°，即a+x=80°，又因为∠OEB=∠EOC+∠ECO=40°+x.当∠OEB=∠OCA，a=80°-x,40°+x=a,解得∠OCA=60°.【点睛】本题考查角度变换和平行线定理的综合运用，熟悉掌握是解题关键.20．60或120【分析】根据题意分两种情况，如图所示（见解析），再分别根据平行线的性质即可得．【详解】由题意，分以下两种情况：（1）如图1，，（两直线平行，同位角相等），（两直线平行，内错解析：60或120【分析】根据题意分两种情况，如图所示（见解析），再分别根据平行线的性质即可得．【详解】由题意，分以下两种情况：PC OB PD OA，（1）如图1，//,//60AOBPDB∴=∠=∠︒（两直线平行，同位角相等），60PDBCPD∴=∠=∠︒（两直线平行，内错角相等）；（2）如图2，//,//PC OB PD OA，60AOBPDB∴=∠=∠︒（两直线平行，同位角相等），180120C P BP DD∠=︒-∴∠=︒（两直线平行，同旁内角互补）；综上，CPD∠的度数为60︒或120︒，故答案为：60或120．【点睛】本题考查了平行线的性质，依据题意，正确分两种情况讨论是解题关键．三、解答题21．（1）65°；（2）11 18022αβ︒-+【分析】（1）如图1，过点E作EF∥AB，当点B在点A的左侧时，根据∠ABC=60°，∠ADC=70°，参考彤彤思考问题的方法即可求∠BED的度数；（2）如图2，过点E作EF∥AB，当点B在点A的右侧时，∠ABC=α，∠ADC=β，参考彤彤思考问题的方法即可求出∠BED的度数．【详解】（1）如图1，过点E作EF∥AB，有∠BEF=∠EBA．∵AB∥CD，∴EF∥CD．∴∠FED=∠EDC．∴∠BEF+∠FED=∠EBA+∠EDC．即∠BED=∠EBA+∠EDC，∵BE平分∠ABC，DE平分∠ADC，∴∠EBA=12∠ABC=30°，∠EDC=12∠ADC=35°，∴∠BED=∠EBA+∠EDC=65°．答：∠BED的度数为65°；（2）如图2，过点E 作EF ∥AB ，有∠BEF +∠EBA =180°．∴∠BEF =180°﹣∠EBA ，∵AB ∥CD ，∴EF ∥CD ，∴∠FED =∠EDC ．∴∠BEF +∠FED =180°﹣∠EBA +∠EDC ．即∠BED =180°﹣∠EBA +∠EDC ，∵BE 平分∠ABC ，DE 平分∠ADC ，∴∠EBA =12∠ABC =12α，∠EDC =12∠ADC =12β， ∴∠BED =180°﹣∠EBA +∠EDC =180°﹣12α +12β． 答：∠BED 的度数为180°﹣12α +12β． 【点睛】 本题考查了平行线的判定与性质以及角平分线的定义，解决本题的关键是熟练掌握平行线的判定与性质．22．（1）145︒；（2）55︒;（3）2125PGN SNP NPG ∠+∠-︒=∠【分析】（1）过点F 作//FN AB ，根据AB ∥CD ，EF 垂直于FG ，∠FGD =125°可计算NFG ∠，EFN ∠，从而求算BEF ∠；（2）作//FN AB ,//HK AB 交MQ 于点K ，由（1）知55,=35NFG EFN ∠=︒∠︒，从而求算35AEF EHL ∠=∠=︒，再根据90EHM M ∠=∠+︒，设M x ∠=︒，利用外角求出MHL ∠，从而求算MQA ∠;（3）作//PI AB 交NG 于I ，连接NP ，GP ，FP ，设SNP x ∠=︒ ，则NPI x ∠=︒ 设IPG y ∠=︒ ，则PGT y ∠=︒，从而表示PGN ∠，进而寻找数量关系．【详解】（1）过点F 作//FN AB ，如图：∵AB ∥CD ，EF 垂直于FG ，∠FGD =125°∴55,905535NFG EFN ∠=︒∠=︒-︒=︒∴180145BEF EFN ∠=︒-∠=︒（2）作//FN AB ,//HK AB 交MQ 于点K ，如图：由（1）知：55,905535NFG EFN ∠=︒∠=︒-︒=︒∴35AEF EHL ∠=∠=︒又∵90EHM M ∠=∠+︒，设M x ∠=︒∴90EHM x ∠=︒+︒∴903555MHL x x ∠=︒+︒-︒=︒+︒∴5555MKH MQA MHL M x x ∠=∠=∠-∠=︒+︒-︒=︒（3）作//PI AB 交NG 于I ，连接NP ，GP ，FP ，如图：设SNP x ∠=︒ ，则NPI x ∠=︒设IPG y ∠=︒ ，则PGT y ∠=︒又∵125FGD ∠=︒∴125PGN y ∠=︒-︒∴2125PGN SNP NPG ∠+∠-︒=∠【点睛】本题考查平行线的性质综合，转化相关的角度是解题关键．23．(1) 150°；(2) ∠OCD+∠BO'E=240°；(3) 30°+12α．【分析】（1）先求出到∠AOE 的度数，再根据直角、周角的定义即可求解；（2）过O 点作OF//CD ，根据平行线的判定和性质可得∠OCD 、∠BO'E 的数量关系； （3）根据四边形内角和为360°，再结合（2）的结论以及角平分线的定义即可解答．【详解】解：（1）∵CD//OE ，∴∠AOE=∠OCD=120°，∴∠BOE=360°-90°-120°=150°；（2）如图2，过O 点作OF//CD ，∴CD//OE ，∴OF ∥OE ，∴∠AOF=180°-∠OCD ，∠BOF=∠EO'O=180°-∠BO'E ，∴∠AOB=∠AOF+∠BOF=180°-∠OCD+180°-∠BO'E=360°-（∠OCD+∠BO'E ）=120°， ∴∠OCD+∠BO'E=240°；（3）∵CP 是∠OCD 的平分线，∴∠OCP=12∠OCD ， ∴∠CPO'=360°-90°-120°-∠OCP=150°-12∠OCD =150°-12（240°-∠BO'E ） =30°+12α【点睛】本题考查了平行线的判定和性质、周角的定义、角平分线的定义，确定∠OCD、∠B0'E的数量关系是解答本题的关键．24．（1）见解析；（2）∠EPF+2∠EQF＝360°；（3）∠P+3∠Q＝360°．【分析】（1）首先过点P作PG∥AB，然后根据AB∥CD，PG∥CD，可得∠AEP＝∠1，∠CFP＝∠2，据此判断出∠AEP+∠CFP＝∠EPF即可．（2）首先由（1），可得∠EPF＝∠AEP+CFP，∠EQF＝∠BEQ+∠DFQ；然后根据∠BEP的平分线与∠DFP的平分线相交于点Q，推得∠EQF＝1(360)2EPF⨯︒-∠，即可判断出∠EPF+2∠EQF＝360°．（3）首先由（1），可得∠P＝∠AEP+CFP，∠Q＝∠BEQ+∠DFQ；然后根据∠BEQ＝1 3∠BEP，∠DFQ＝13∠DFP，推得∠Q＝13×（360°﹣∠P），即可判断出∠P+3∠Q＝360°．【详解】（1）证明：如图1，过点P作PG∥AB，∵AB∥CD，∴PG∥CD，∴∠AEP＝∠1，∠CFP＝∠2，又∵∠1+∠2＝∠EPF，∴∠AEP+∠CFP＝∠EPF．（2）如图2，，由（1），可得∠EPF＝∠AEP+CFP，∠EQF＝∠BEQ+∠DFQ，∵∠BEP的平分线与∠DFP的平分线相交于点Q，∴∠EQF＝∠BEQ+∠DFQ＝12（∠BEP+∠DFP）＝1[360()] 2AEP CFP︒-∠+∠＝1(360)2EPF⨯︒-∠，∴∠EPF+2∠EQF＝360°．（3）如图3，，由（1），可得∠P＝∠AEP+CFP，∠Q＝∠BEQ+∠DFQ，∵∠BEQ＝13∠BEP，∠DFQ＝13∠DFP，∴∠Q＝∠BEQ+∠DFQ＝13（∠BEP+∠DFP）＝13[360°﹣（∠AEP+∠CFP）]＝13×（360°﹣∠P），∴∠P+3∠Q＝360°．【点睛】此题主要考查了平行线的性质的应用，要熟练掌握，解答此题的关键是要明确：（1）定理1：两条平行线被第三条直线所截，同位角相等．简单说成：两直线平行，同位角相等．（2）定理2：两条平行线被地三条直线所截，同旁内角互补．简单说成：两直线平行，同旁内角互补．（3）定理3：两条平行线被第三条直线所截，内错角相等．简单说成：两直线平行，内错角相等．25．（1）60°；（2）当30t =秒或110秒时//BF 直线AE ；（3）BAC ∠和BCD ∠关系不会变化，2BAC BCD ∠=∠．【分析】(1)根据2BAM BAN ∠=∠得到60BAN ∠=︒，再根据直线平行的性质即可得到答案；(2)设灯转动t 秒，直线//BF 直线AE ，分情况讨论重合前平行、重合后平行即可得到答案；(3)根据补角的性质表示出BAC ∠，再根据三角形内角和即可表示出BCD ∠，即可得到答案；【详解】解：（1）∵2BAM BAN ∠=∠180BAM BAN ∠+∠=︒，∴60BAN ∠=︒，∴QBA ∠60BAN =∠=︒（两直线平行，内错角相等）故结果为：60︒；（2）设灯转动t 秒，直线//BF 直线AE ，①当090t <<时，如图，//PQ MN ，PBF BFA ∴∠=∠，//AE BF ，EAM BFA ∴∠=∠，EAM PBF ∴∠=∠，21(30)t t ∴=⋅+，解得30t =；②当90180t <<时，如图，//PQ MN ，180PBF BFA ∴∠+∠=︒，//AE BF ，EAN BFA ∴∠=∠180PBF EAN ∴∠+∠=︒，1(30)(2180)180t t ∴⋅++-=，解得110t =，综上所述，当30t =秒或110秒时//BF 直线AE ；（3）BAC ∠和BCD ∠关系不会变化，理由：设射线AM 转动时间为m 秒，作//CH PQ ，//PQ MN ，////CH PQ MN ∴，2180QBC ∴∠+∠=︒，1180MAC ∠+∠=︒，21360QBC MAC ∴∠+∠+∠+∠=︒，180QBC m ∠=︒-，2MAC m ∠=，()123601802180BCA m m m ∴∠=∠+∠=---=︒︒-︒，而120ACD ∠=︒，()12012018060BCD BCA m m ︒︒∴∠=-∠=--=-︒︒，1802CAN m ∠=︒-，()18022120BAC QBA m m ︒︒∴∠=∠--=-，:2:1BAC BCD ∴∠∠=，即2BAC BCD ∠=∠，BAC ∴∠和BCD ∠关系不变．【点睛】本题主要考查了补角、角的运算、直线平行的性质和判定以及三角形的内角和定理，结合图形添加辅助线、分类讨论是解题的关键．26．（1）两直线平行，同旁内角互补；同旁内角互补，两直线平行；如果两条直线都与第三条直线平行，那么这两条直线也互相平行；（2）∠B ＋∠E ＋∠F ＋∠D ＝540°；（3）∠B ＋∠E ＋∠D －∠F ＝180°．【分析】（1）根据平行线的性质和判定，平行公理的推论回答即可；（2）过点E 、F 分别作GE ∥HF ∥CD ，根据两直线平行，同旁内角互补及已知条件求得同旁内角∠ABE ＋∠BEG ＝180°，得到AB ∥GE ，再根据平行线的传递性来证得AB ∥CD ； （3）过点E 、F 分别作ME ∥FN ∥CD ，根据两直线平行，内错角相等及已知条件求得同旁内角∠B ＋∠BEM ＝180°，得到AB ∥ME ，再根据平行线的传递性来证得AB ∥CD ．【详解】解：（1）由题意可知：“依据1”：两直线平行，同旁内角互补；“依据2”： 同旁内角互补，两直线平行；“依据3”： 如果两条直线都与第三条直线平行，那么这两条直线也互相平行；（2）当∠B 、∠E 、∠F 、∠D 满足条件∠B ＋∠E ＋∠F ＋∠D ＝540°时，有AB ∥CD ． 理由：如图，过点E 、F 分别作GE ∥HF ∥CD ，则∠GEF ＋∠EFH ＝180°，∠HFD ＋∠CDF ＝180°，∴∠GEF ＋∠EFD ＋∠FDC ＝360°；又∵∠B ＋∠BEF ＋∠EFD ＋∠D ＝540°，∴∠ABE ＋∠BEG ＝180°，∴AB ∥GE ，∴AB ∥CD ；（3）当∠B 、∠E 、∠F 、∠D 满足条件∠B ＋∠E ＋∠D －∠F ＝180°时，有AB ∥CD ． 如图，过点E 、F 分别作ME ∥FN ∥CD ，则∠MEF ＝EFN ，∠D ＝∠DFN ，∵∠B ＋∠BEF ＋∠D －∠EFD ＝180°，∴∠B ＋∠BEM ＋∠MEF ＋∠D －∠EFN －∠DFN ＝180°，∴∠B ＋∠BEM ＝180°，∴AB ∥ME ，∴AB ∥CD ．【点睛】本题考查平行线的判定和性质的综合应用，作出合适的辅助线，灵活运用平行线的性质定理和判定定理是解题的关键．27．(1)∠E 、∠CAF ；∠CDE 、∠BAF ； (2)①20°；②30【分析】（1）由翻折的性质和平行线的性质即可得与∠B 相等的角；由等角代换即可得与∠C 相等的角；（2）①由三角形内角和定理可得90B C ∠+∠=︒，再由50C B ∠∠︒-=根据角的和差计算即可得∠C 的度数，进而得∠B 的度数．②根据翻折的性质和三角形外角及三角形内角和定理，用含x 的代数式表示出∠FDE 、∠DFE 的度数，分三种情况讨论求出符合题意的x 值即可．【详解】（1）由翻折的性质可得：∠E ＝∠B ，∵∠BAC ＝90°，AE ⊥BC ，∴∠DFE ＝90°，∴180°－∠BAC ＝180°－∠DFE ＝90°，即：∠B ＋∠C ＝∠E ＋∠FDE ＝90°，∴∠C ＝∠FDE ，∴AC ∥DE ，∴∠CAF ＝∠E ，∴∠CAF ＝∠E ＝∠B故与∠B 相等的角有∠CAF 和∠E ；∵∠BAC ＝90°，AE ⊥BC ，∴∠BAF ＋∠CAF ＝90°, ∠CFA ＝180°－（∠CAF ＋∠C ）＝90°∴∠BAF ＋∠CAF ＝∠CAF ＋∠C ＝90°∴∠BAF ＝∠C又AC ∥DE ，∴∠C ＝∠CDE ，∴故与∠C 相等的角有∠CDE 、∠BAF ；（2）①∵90BAC ∠=︒∴90B C ∠+∠=︒又∵50C B ∠∠︒-=，∴∠C ＝70°，∠B ＝20°;②∵∠BAD ＝x °, ∠B ＝20°则160ADB x ∠︒︒=-,20ADF x ∠︒︒=+,由翻折可知：∵160ADE ADB x ∠∠︒︒==-, 20E B ∠∠︒==,∴1402FDE x ∠︒︒=-, 202DFE x ∠︒︒=+,当∠FDE ＝∠DFE 时，1402202x x ︒︒︒︒-=+, 解得：30x ︒︒=；当∠FDE ＝∠E 时，140220x ︒︒︒-=，解得：60x ︒︒=（因为0＜x ≤45，故舍去）； 当∠DFE ＝∠E 时，20220x ︒︒︒+=，解得：0x ︒＝（因为0＜x ≤45，故舍去）； 综上所述，存在这样的x 的值，使得△DEF 中有两个角相等．且30x =．【点睛】本题考查图形的翻折、三角形内角和定理、平行线的判定及其性质、三角形外角的性质、等角代换，解题的关键是熟知图形翻折的性质及综合运用所学知识．28．（1）C 的坐标为（0，4），点D 的坐标为（1，2）；（2）①点E 的坐标为（1，3），F 的坐标为（0，3）或点E 的坐标为（0，1），F 的坐标为（1，1）；②存在△PEF 的面积为2，点E 、F 两点的坐标为E （﹣，0）、F （，0），或E （，4）、F （﹣，4）．【解析】【分析】（1）由点A和点C在y轴上确定出向右平移3个单位，再根据△ACD的面积求出向上平移的单位，然后写出点C、D的坐标即可．（2）①根据线段EF平行于线段OM且等于线段OM，得出2a+1＝﹣2b+3，|a﹣b|＝1，解答即可；②首先根据题意求出点P的坐标为（，2），设点E在F的左边，由EF∥x轴得出a+b＝1，求出△PEF的面积＝（b﹣a）×|2a+1﹣2|＝2，得出（b﹣a）|2a﹣1|＝4，当EF在点P 的上方时，（b﹣a）（2a﹣1）＝4，与a+b＝1联立得：，此方程组无解；当EF在点P的下方时，（b﹣a）（1﹣2a）＝4，与a+b＝1联立得：，解得：，或；分别代入点E（a，2a+1）、F（b，﹣2b+3）即可．【详解】解：（1）∵A（﹣3，0），点C在y轴的正半轴上，∴向右平移3个单位，设向上平移x个单位，∵S△ACO＝OA×OC＝6，∴×3x＝6，解得：x＝4，∴点C的坐标为（0，4），﹣2+3＝1，﹣2+4＝2，故点D的坐标为（1，2）．（2）①存在；理由如下：∵线段EF平行于线段OM且等于线段OM，∴2a+1＝﹣2b+3，|a﹣b|＝1，解得：a＝1，b＝0或a＝0，b＝1，即点E的坐标为（1，3），F的坐标为（0，3）或点E的坐标为（0，1），F的坐标为（1，1）；②存在，理由如下：如图2所示：当点E、F重合时，，解得：，∴2a+1＝2，∴点P的坐标为（，2），设点E在F的左边，∵EF∥x轴，∴2a+1＝﹣2b+3，∴a+b＝1，∵△PEF的面积＝（b﹣a）×|2a+1﹣2|＝2，即（b﹣a）|2a﹣1|＝4，当EF在点P的上方时，（b﹣a）（2a﹣1）＝4，与a+b＝1联立得：，此方程组无解；当EF在点P的下方时，（b﹣a）（1﹣2a）＝4，与a+＝1联立得：，解得：，或；分别代入点E（a，2a+1）、F（b，﹣2b+3）得：E（﹣，0）、F（，0），或E（，4）、F（﹣，4）；综上所述，存在△PEF的面积为2，点E、F两点的坐标为E（﹣，0）、F（，0），或E （，4）、F（﹣，4）．【点睛】本题是三角形综合题目，考查了平移的性质、三角形面积公式、坐标与图形性质、方程组的解法、平行线的性质等知识；本题综合性强，根据题意得出方程组是解题的关键．。
(完整版)《相交线与平行线》单元测试卷含答案
第4章相交线与平行线单元测试卷一、选择题(每题2分,共20分)1.如图,直线a,b被直线c所截,∠1与∠2的位置关系是()A.同位角B.内错角C.同旁内角D.对顶角2.如图,AB∥CD,AD平分∠BAC,若∠BAD=65°,那么∠ACD的度数为()A.40°B.35°C.50°D.45°1 2 33.如图,AB∥EC,下列说法不正确的是()A. ∠B=∠ECDB. ∠A=∠ECDC. ∠B+∠ECB=180°D. ∠A+∠B+∠ACB=180°4.如图,在俄罗斯方块游戏中,出现一小方块拼图向下运动,通过平移运动拼成一个完整的图案,最终所有图案消失,则对小方块进行的操作为()A.向右平移1格再向下B.向右平移3格再向下C.向右平移2格再向下D.以上答案均可5.如图所示,3块相同的三角尺拼成一个图形,图中有很多对平行线,其中不能由下面的根据得出两直线平行的是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.平行于同一直线的两直线平行D.垂直于同一直线的两直线平行6.如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是()A.40°B.70°C.80°D.140°7.同一平面内的四条互不重合的直线满足a⊥b,b⊥c,c⊥d,则下列各选项中关系能成立的是()A.a∥dB.a⊥cC.a⊥dD.b⊥d8.如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=()A.120 °B.130°C.140°D.150°9.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为()A.30°B.60°C.80°D.120°10.如图,把一块含有45°角的直角三角尺的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是()6 8 9 10二、填空题(每题3分,共21分)11.如图所示,某地一条小河的两岸都是直的,小明和小亮分别在河的两岸,他们拉紧了一根细绳,当测出∠1和∠2满足关系________时,河岸的两边才是平行的.12.同一个平面内的三条直线两两相交,最多有a个交点,最少有b个交点,则a+b=________.13.在测量跳远成绩时,从落地点到起跳线所拉的皮尺应当与起跳线________.14.如图,在三角形ABC中,BC=5 cm,将三角形ABC沿BC方向平移至三角形A'B'C'的位置时,B'C=3 cm,则三角形ABC平移的距离为cm.11 14 1515.如图是我们常用的折叠式小刀,刀柄外形是一个长方形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图所示的∠1与∠2,则∠1与∠2的度数和是度.16.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=°.17.如图所示,第1个图案是由黑白两种颜色的六边形地面砖组成的,第2个,第3个图案可以看成是第1个图案经过平移而得,那么第2015个图案中有白色六边形地面砖块.三、解答题(22~24题每题9分,其余每题8分,共59分)18.如图,在一条公路l的两侧有A,B两个村庄.(1)现在镇政府为民服务,沿公路开通公共汽车,同时修建A,B两个村庄到公路的道路,要使两个村庄村民乘车最为方便,请你设计道路路线,在图中画出(标明①),并标出公共汽车停靠点的位置,说出你这样设计的理由;(2)为方便两村物流互通,A,B两村计划合资修建一条由A村到达B村的道路,要使两个村庄物流、通行最为方便,请你设计道路路线,在图中画出(标明②),说出你这样设计的理由.19.如图所示,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,求∠D的度数.20.如图,CD⊥AB,EF⊥AB,∠E=∠EMC,说明:CD是∠ACB的平分线.21.如图,已知点A,O,B在同一直线上,OC是从点O出发的任意一条射线,OD是∠AOC的平分线,OE是∠COB的平分线,试确定OD和OE的位置关系,并说明理由.22.如图,∠E=∠3,∠1=∠2,试说明:∠4+∠BAP =180°.23.如图所示,潜望镜中的两个镜子是互相平行放置的,光线经过镜子反射时,入射光线与平面镜的夹角等于反射光线与平面镜的夹角(∠1=∠2,∠3=∠4).请说明为什么进入潜望镜的光线和离开潜望镜的光线是平行的.24.如图,直线AC∥BD,连接AB,直线AC,BD及线段AB把平面分成①②③④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(1)当动点P落在第①部分时,如图①,试说明:∠APB=∠PAC+∠PBD;(2)当动点P落在第②部分时,如图②,∠APB=∠PAC+∠PBD是否成立?若不成立,请说明理由.参考答案一、1.【答案】B 2.【答案】C3.【答案】B解：根据两直线平行,同位角相等,得出A正确;根据两直线平行,同旁内角互补,得出C正确;根据两直线平行,内错角相等,得出∠A=∠ACE,而∠ACE+∠B+∠ACB=180°,则∠A+∠B+∠ACB=180°.得出D正确.故选B.4.【答案】C5.【答案】C6.【答案】B7.【答案】C8.【答案】C9.【答案】A10.【答案】B二、11.【答案】∠1=∠212.【答案】4解：a=3,b=1.13.【答案】垂直14.【答案】215.【答案】9016.【答案】14017.【答案】8062三、18.解:(1)画图如图,P,Q即为公共汽车停靠点的位置垂线段最短;(2)画图如图,两点之间,线段最短.19.解:因为AB∥CD,所以∠ECD=∠A=37°,又因为DE⊥AE,所以∠CED=90°,所以∠D=180°-90°-37°=53°.20.解:因为CD⊥AB,EF⊥AB,所以CD∥EF(垂直于同一直线的两直线平行).相等),又因为∠E=∠EMC,所以∠BCD=∠ACD(等量代换).所以CD是∠ACB的平分线(角平分线定义).21.解:OD和OE互相垂直,即OD⊥OE.理由如下:因为点A,O,B在同一直线上,所以∠AOB=180°.又因为OD是∠AOC的平分线,OE是∠COB的平分线,所以∠DOC=∠AOC,∠COE=∠COB.所以∠DOE=∠DOC+∠COE=(∠AOC+∠COB)=∠AOB=×180°=90°,所以OD⊥OE.22.解:因为∠ENM=∠3(对顶角相等),∠E=∠3(已知),所以∠ENM=∠E(等量代换),所以AE∥HM(内错角相等,两直线平行).所以∠EAM=∠AMH(两直线平行,内错角相等).又因为∠1=∠2,所以∠EAM+∠1=∠AMH+∠2(等式性质),即∠BAM=∠AMC.所以AB∥CD(内错角相等,两直线平行).所以∠AMD+∠BAP=180°(两直线平行,同旁内角互补).因为∠4=∠AMD(对顶角相等),所以∠4+∠BAP=180°(等量代换).23.解:根据题意,作出如图所示的几何图形,已知:AB∥CD,∠1=∠2,∠3=∠4.试说明:EF∥GH.说明过程:因为AB∥CD(已知),所以∠2=∠3(两直线平行,内错角相等).又因为∠1=∠2,∠3=∠4,所以∠1=∠2=∠3=∠4.因为∠5=180°-(∠1+∠2),∠6=180°-(∠3+∠4),所以∠5=∠6,所以EF∥GH(内错角相等,两直线平行).即进入潜望镜的光线和离开潜望镜的光线是平行的.24.解:(1)如图①:过点P作MP∥AC,则MP∥BD,因为MP∥AC,所以∠APM=∠PAC,因为MP∥BD,所以∠BPM=∠PBD,所以∠APM+∠BPM =∠PAC+∠PBD,①②(2)不成立.理由如下:如图②,过点P作MP∥AC,则MP∥BD, 因为MP∥AC,所以∠APM=∠PAC,因为MP∥BD,所以∠BPM=∠PBD,所以∠APM+∠BPM =∠PAC+∠PBD,即:360°-∠APB=∠PAC+∠PBD.所以∠APB=∠PAC+∠PBD不成立.。
《相交线与平行线》单元测试题及答案
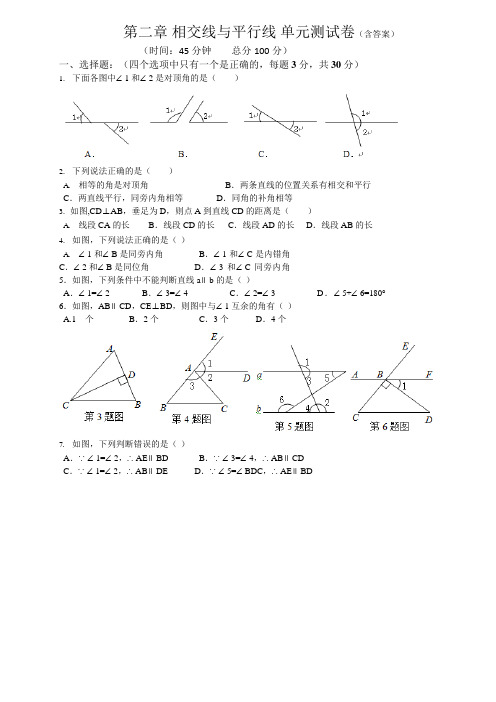
第二章相交线与平行线单元测试卷（含答案）（时间：45 分钟总分 100 分）一、选择题：（四个选项中只有一个是正确的，每题3 分，共30 分）1.下面各图中∠1 和∠2 是对顶角的是（）2.下列说法正确的是（）A.相等的角是对顶角B．两条直线的位置关系有相交和平行C．两直线平行，同旁内角相等D．同角的补角相等3.如图,CD⊥AB，垂足为D，则点A 到直线CD 的距离是（）A.线段CA 的长B．线段CD 的长C．线段AD 的长D．线段AB 的长4.如图，下列说法正确的是（）A.∠1 和∠B 是同旁内角B．∠1 和∠C 是内错角C．∠2 和∠B 是同位角D．∠3 和∠C 同旁内角5．如图，下列条件中不能判断直线a∥b 的是（）A．∠1=∠2 B．∠3=∠4 C．∠2=∠3 D．∠5+∠6=180°6．如图，AB∥CD，CE⊥BD，则图中与∠1 互余的角有（）A.1个B．2 个C．3 个D．4 个7.如图，下列判断错误的是（）A．∵∠1=∠2，∴AE∥BD B．∵∠3=∠4，∴AB∥CDC．∵∠1=∠2，∴AB∥DE D．∵∠5=∠BDC，∴AE∥BD8.如图，AB∥CD∥EF，BC∥DE，则∠B 与∠E 的关系是（）A．相等B．互余C．互补D．不能确定9．如图，AB∥CD，∠1=58°，FG 平分∠EFD，则∠FGB 的度数等于（）A．122°B．151°C．116°D．97°10．如图，直线a∥b，直角三角形ABC 的顶点B 在直线a 上，∠C=90°，∠β=55°，则∠α的度数为（）A．15°B．25°C．35°D．55°二．填空题：（将答案填在题目的横线上，每空3 分，共18 分）11．如图，∠1=∠2，∠4=58°，则∠3= 度；12.如图，AB∥CD，EF⊥CD 于点F，射线FN 交AB 于点M，∠NMB=57°，则∠EFN=；13.若一个角的余角是它的3 倍，则这个角的度数为；14．如图，已知AB∥DE，∠ABC=80°，∠CDE=140°，则∠BCD= ；15.如图，把矩形（长方形）ABCD 沿EF 对折，若∠1=40°，则∠AEF= ；16.老师在黑板上随便画了两条直线AB，CD 相交于点0，还作了∠BOC 的平分线OE 和CD 的垂线OF（如图），若∠DOE 被OB 分成2：3 两部分，则∠AOF 等于度；三、解答题：（写出必要的说明过程、解答步骤，共52 分）17.尺规作图：已知∠ABC，求作一个角等于∠ABC；（保留作图痕迹）（6 分）18.已知：如图，BE∥DF，∠B=∠D；试说明AD∥BC；（8 分）19.如图，直线EF，CD 相交于点O，OA⊥OB，且OC 平分∠AOF；若∠AOE=40°，求∠BOD 的度数；（9 分）20.推理填空：（9 分）如图，已知DG⊥BC，BC⊥AC，EF⊥AB，∠1=∠2，试判断CD 与AB 的位置关系；解：∵DG⊥BC，BC⊥AC（已知）∴∠DGB=∠=90°（）∴DG∥，∴∠2=∠，∵∠1=∠2（已知）∴∠1=∠（）∴EF∥，∴∠AEF=∠（）∵EF⊥AB，∴∠AEF=90°∴∠ADC=90°即：CD⊥AB．21.如图，BE 平分∠ABD，DE 平分∠BDC，DG 平分∠CDF，且∠1+∠2=90°，试说明BE∥DG；（9 分）22.已知一个角的两边与另一个角的两边分别平行，请结合图①②探索这两个角之间的关系；(11 分)(1)如图①，AB∥CD，BE∥DF，则∠1 与∠2 的关系是；(2)如图②，AB∥CD，BE∥DF，则∠1 与∠2 的关系是；并说明理由；(3)由此得出结论，如果两个角的两边分别平行，那么这两个角；(4)若两个角的两边分别平行，且一个角比另一个角的3 倍少60°，则这两个角分别为多少度？参考答案：1~10 CDCDB ACBBA 11．58；12．33°；13．22.5°；14．40°；15．110°；16．45°或90度；717.略；（参考课本P56 步骤5 的图）18.方法一：（利用同旁内角互补，两直线平行）∵BE∥DF（已知），∴∠B+∠BCD=180°（两直线平行，同旁内角互补）∵∠B=∠D（已知）∴∠D+∠BCD=180°(等量代换)∴AD∥BC (同旁内角互补,两直线平行)方法二：（利用三角形内角和等于180°）(略)19.∵OA⊥OB（已知）∴∠AOB=90°(垂直的定义)∵∠AOE=40°（已知）∴∠BOE=∠AOB-∠AOE=90°-40°=50°∵OC 平分∠AOF(已知)∴∠AOC = 1 ∠AOF =1 (∠EOF -∠AOE) =1 (1800- 400 ) = 7002 2 2∴∠BOD = ∠COD -∠AOC -∠AOB = 1800- 700- 900= 200∴∠BOD=20°20.按顺序分别填：BCA，垂直的定义，AC，ACD，ACD，等量代换，CD，ADC，两直线平行，同位角相等；21.方法一：通过证明∠E=∠EDG 得到；∵∠1+∠2=90°（已知）∴△BDE 中，∠E=180°-(∠1+∠2)=90°∵DE 平分∠BDC，DG 平分∠CDF(已知)∴∠EDG=∠EDC+∠CDG= 1 ∠BDC+ 1 ∠CDF =1 ∠BDF =1 ⨯1800= 9002 2 2 2∴∠E=∠EDG(等量代换)∴BE∥DG （内错角相等，两直线平行）方法二：通过证明∠1=∠3 得到；（略）22．（1）相等；（2）互补；∵AB∥CD（已知）∴∠1=∠3（两直线平行，内错角相等）∵BE∥DF（已知）∴∠2+∠3=180°（两直线平行，同旁内角互补）∴∠1+∠2=180°（等量代换）（3）相等或互补；（4）30°，30°；或60°，120°；解：设一个角为x，则另一个角为3x-60°，①由x=3x-60°得：x=30°，3x-60°=30°②由x+3x-60°=180°得：x=60°，3x-60°=120°∴这两个角分别30°，30°或60°，120°；。
七年级数学下册《相交线与平行线》单元测试卷(附答案)
七年级数学下册《相交线与平行线》单元测试卷(附答案)一、选择题(每题3分，共30分)1．如图1，A、B两个村庄在一条河l（不计河的宽度）的两侧，现要建一座码头，使它到A、B两个村庄的距离之和最小．如图2，连接AB，与l交于点C，则C点即为所求的码头的位置，这样做的理由是（）A．垂线段最短B．两点确定一条直线C．两点之间，线段最短D．平行于同一条直线的两条直线平行2．如图，将一个含有30°角的直角三角尺放置在两条平行线a，b上．若∠1＝135°，则∠2的度数为（）A．95°B．110°C．105°D．115°3．如图，将△ABC沿BC方向平移1个单位得△DEF，若△ABC的周长等于10，则四边形ABFD 的周长为（）A．12 B．10 C．9 D．84．下面四个图案中，能由如图经过平移得到的是（）A．B． C． D．5．如图，将△ABC沿BC方向平移2cm得到△DEF，若△ABC的周长为16cm，则四边形ABFD的周长为（）A．16cm B．18cm C．20cm D．22cm6．如图，如果把△ABC的顶点A先向下平移3格，再向左平移1格到达A′点，连接A′B，则线段A′B与线段AC的关系是（）A．垂直B．相等C．平分D．平分且垂直7.如图，下列说法错误的是（）A.∠A与∠3是同位角B.∠4与∠B是同旁内角C.∠A与∠C是内错角D.∠1与∠2是同旁内角8．平面内两两相交的3条直线，其交点个数最少为m个，最多为n个，则m+n等于（）A．4 B．5 C．6 D．以上都不对9．甲、乙、丙3人从图书馆各借了一本书（如下表所示），他们相约在每个星期天相互交换读完的书，经过数次交换后，他们都读完了这3本书．已知甲读的第三本书是乙读的第二本书，则丙读的第二本书是（）甲乙丙书A书B书C A．书A B．书B C．书C D．无法确定10．下列各项正确的是（）A．直线外一点到已知直线的垂线段叫做这点到直线的距离B．过一点有且只有一条直线与已知直线垂直C．同一平面内，两条直线的位置关系只有相交和平行两种D．有公共顶点且相等的两个角是对顶角二、填空题(每题3分，共24分)11．如图，已知∠1+∠2＝180°，则图中与∠1相等的角共有_____个．12．如图，在图中标注的∠1、∠3、∠4、∠5中，当∠2 =∠_______时，AE∥BF．13．如图，已知a∥b，∠1=45°，则∠2=_________．14．“互补的两个角一定是同旁内角”是命题（填“真”或“假”）．15．如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠2＝24°，则∠1的度数为．16．一平面内，三条直线两两相交，最多有3个交点；4条直线两两相交，最多有6个交点；5条直线两两相交，最多有10个交点；8条直线两两相交，最多有个交点．17．如图所示，l1∥l2，点A，E，D在直线l1上，点B，C在直线l2上，满足BD平分∠ABC，BD⊥CD，CE平分∠DCB，若∠BAD＝128°，那么∠AEC＝．18．如图，将一张长方形纸片ABCD沿EF折叠，使顶点C，D分别落在点C′，D′处，C′E 交AF于点G，若∠CEF＝70°，则∠GFD′＝°．三.解答题(19题6分，20、21、22、23、24题分别8分，共46分)19．如图，直线AB与CD相交于点O，OE平分∠BOC，∠AOD＝110°，求∠AOE的度数.20．已知，如图a∥b，c∥d，∠1=73°，求∠2和∠3的度数．21.（8分）如图,已知AB∥CD,试再添加一个条件,使∠1=∠2成立.(1)写出两个不同的条件;(2)从(1)中选择一个来证明.22.（8分）如图，已知∠1+∠2＝180°，∠3＝∠B．（1）试判断DE与BC的位置关系，并说明理由．（2）若DE平分∠ADC，∠2＝3∠B，求∠1的度数．23．完成下列画图(1)如图，将△ABC向右平移4个单位，再向上平移2个单位长度，得到△A′B′C′，线段AB 与A′B′位置及数量关系是．(2)如图，一辆汽车在笔直的公路AB上由A向B行驶，M、是位于公路AB一侧的村庄．设汽车行驶到点P时，离村庄M的距离最小，请在图中公路AB上画出点P的位置，并说明数学原理．24．在ABC 中，D 是BC 边上一点，且CDA CAB ∠=∠，MN 是经过点D 的一条直线.（1）若直线MN AC ⊥，垂足为点E . ①依题意补全图1.②若70,CAB ︒∠=20DAB ︒∠=，则CAD ∠=________，CDE ∠=________. （2）如图2，若直线MN 交AC 边于点F ，且CDF CAD ∠=∠，求证：FD AB ∥.参考答案一、选择题: 题号 1 2 3 4 5 6 7 8 9 10 答案 CCABCDAAAC二、填空题:11．312．413．45°. 解析：∵a∥b，∠1=45°，∴∠2=∠1=45°．14．解：如图，∠1＝∠2＝90°，∵∠1+∠2＝180°，∴∠1与∠2互补，但它们是一对内错角，不是同旁内角，∴“互补的两个角一定是同旁内角”是假命题，故答案为：假．15．解：如图，延长AB交CF于E，∵∠ACB＝90°，∠A＝30°，∴∠ABC＝60°，∵GH∥EF，∴∠AEC＝∠2＝24°，∴∠1＝∠ABC﹣∠AEC＝36°．故答案为：36°．16．解：∵由已知总结出在同一平面内，n条直线两两相交，则最多有个交点，∴8条直线两两相交，交点的个数最多为＝28．故答案为：28．17．【分析】根据平行线的性质和角平分线的性质，可以得到∠AEC的度数，本题得以解决．【解答】解：∵l1∥l2，∴∠BAD+∠ABC＝180°，∵∠BAD＝128°，∴∠ABC＝52°，∵BD平分∠ABC，∴∠DBC＝26°，∵BD⊥CD，∴∠BDC＝90°，∴∠BCD＝64°，∵CE平分∠DCB，∴∠ECB＝32°，∵l1∥l2，∴∠AEC+∠ECB＝180°，∴∠AEC＝148°，故答案为：148°．【点评】本题考查平行线的性质、角平分线的性质、垂线，解答本题的关键是明确题意，利用数形结合的思想解答．18．【分析】由AD∥BC可得∠AFE＝∠CEF，∠CEF+∠DFE＝180°，由翻折可得∠D'FE＝∠DFE，进而求解．【解答】解：∵AD∥BC，∴∠AFE＝∠CEF＝70°，∵∠CEF+∠DFE＝180°，∴∠DFE＝180°﹣∠CEF＝110°，由翻折可得∠D'FE＝∠DFE＝110°，∴∠GFD'＝∠D'FE﹣∠AFE＝110°﹣70°＝40°，故答案为：40．【点评】本题考查角的相关计算，解题关键是掌握平行线的性质．三.解答题(19题6分，20、21、22、23、24题分别8分，共46分)19．【答案】解：∵∠AOD=110°，∴∠COB=110°，∠AOC=70°，∵OE平分∠BOC，∴∠COE=55°，∴∠AOE=70°+55°=125°.故答案为：∠AOE=125°.20．【答案】解：∵a∥b，∴∠1=∠2=73°，∵c∥d，∴∠3=180°-73°=107°．21.解:此题答案不唯一,合理即可.(1)添加∠FCB=∠CBE或CF∥BE.(2)已知AB∥CD,CF∥BE.求证:∠1=∠2.证明:∵AB∥CD,∴∠DCB=∠ABC.∵CF∥BE,∴∠FCB=∠CBE,∴∠DCB-∠FCB=∠ABC-∠CBE,即∠1=∠2.22.解：（1）DE∥BC，理由如下：∵∠1+∠4＝180°，∠1+∠2＝180°，∴∠2＝∠4，∴AB∥EF，∴∠3＝∠5，∵∠3＝∠B，∴∠5＝∠B，∴DE∥BC，（2）∵DE平分∠ADC，∴∠5＝∠6，∵DE∥BC，∴∠5＝∠B，∵∠2＝3∠B ，∴∠2+∠5+∠6＝3∠B +∠B +∠B ＝180°， ∴∠B ＝36°， ∴∠2＝108°， ∵∠1+∠2＝180°， ∴∠1＝72°．23.(1)解：如图，△A ′B ′C ′即为所求作；线段AB 与A ′B ′位置及数量关系分别是平行且相等， 故答案为：平行且相等． (2)解：如图，点P 即为所求．数学原理是：连接直线外一点与直线上各点的所有线段中，垂线段最短， 24.（1）①如图所示.②70,CAB ︒∠=20DAB ︒∠=，50CAD ︒∴∠=.70CDA CAB ︒∠=∠=，18060C CAD CDA ︒︒∴∠=-∠-∠=.DE AC ⊥，第 11 页 共 11 页 9030CDE C ︒︒∴∠=-∠=. 故答案为50,︒30︒.（2）CDA CAB ∠=∠， 且,CDA CDF ADF ∠=∠+∠CAB CAD BAD ∠=∠+∠， CDF ADF CAD BAD ∴∠+∠=∠+∠. ,CDF CAD ∠=∠,ADF BAD ∴∠=∠FD AB ∴∥.。
相交线与平行线单元测试题含答案
相交线与平行线单元测试题含答案相交线与平行线单元测试题一、选择题1、下列说法正确的是（） A. 相交的两条直线一定有一个交点 B. 同位角相等 C. 两直线平行，对角线一定相等 D. 相等的两个角一定是对顶角2、以下不能说明直线AB与CD平行的是（） A. AB//CD，A与B在同一方向，C与D在同一方向 B. $\angle 3 = \angle 4$ C. $\angle A = \angle C$ D. $\angle A + \angle B = 180^{\circ}$，$\angleC + \angleD = 180^{\circ}$3、下列说法正确的是（） A. 过一点有且只有一条直线与已知直线平行 B. 两直线平行，同位角相等 C. 内错角相等，两直线平行 D. 如果两条直线都与第三条直线平行，那么这两条直线也互相平行4、下列说法正确的是（） A. 两条直线被第三条直线所截，同位角相等 B. 相等的两个角是对顶角 C. 两直线平行，同旁内角互补 D. 互补的两个角不一定是邻补角5、下列说法正确的是（） A. 同位角相等 B. 互补的角是邻补角 C. 两直线平行，同旁内角相等 D. 两直线平行，内错角相等二、填空题1、同一平面内，如果两条直线都与第三条直线平行，那么这两条直线互相________，简述为________.2、两直线平行，同位角________；两直线平行，内错角________；两直线平行，同旁内角________．3、两条直线的位置关系有________、________．4、若三条直线两两相交，则共有________个交点．5、在同一平面内，若两直线都垂直于第三条直线，那么这两条直线________．6、如图所示，若$\angle A + \angle B = 180^{\circ}$，$\angle A = \angle D$，则$\angle B =$________．7、如图所示，若$\angle A = \angle B$，则$\angle C =$________．8、如图所示，若$\angle A + \angle B = 90^{\circ}$，$\angle B + \angle C = 90^{\circ}$，则$\angle A =$________．9、若一个角的两边分别和另一个角的两边分别平行，则这两个角的关系是________．10、如图所示，若AB//CD，则$\angle A + \angle B + \angle C=$________．三、解答题1、已知两条平行线被第三条直线所截，则形成的同位角的数量是多少？这些同位角还具有什么性质？2、利用所给图形探究规律。
第五章相交线与平行线单元试卷试卷(word版含答案)
第五章相交线与平行线单元试卷试卷（word 版含答案）一、选择题1．下列命题是真命题的是（ ）A ．直角三角形中两个锐角互补B ．相等的角是对顶角C ．同旁内角互补，两直线平行D ．若a b =，则a b = 2．如图，给出下列条件：①∠3=∠4；②∠1=∠2；③∠5=∠B ；④AD ∥BE ，且∠D =∠B ．其中能说明AB ∥DC 的条件有（ ）A ．4个B ．3个C ．2个D ．1个 3．如图，直线l 1，l 2，l 3交于一点，直线l 4∥l 1，若∠1=124°，∠2=88°，则∠3的度数为（ ）A ．26°B ．36°C ．46°D ．56° 4．如果A ∠与B 的两边分别平行，A ∠比B 的3倍少36，则A ∠的度数是( )A ．18B ．126C ．18或126D ．以上都不对 5．①如图1,AB∥CD,则∠A +∠E +∠C=180°；②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E－∠1=180° ； ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )A ．、1个B ．2个C ．3个D ．4个 6．下列命题中，假命题的个数为（ ） （1）“是任意实数，”是必然事件； （2）抛物线的对称轴是直线；（3）若某运动员投篮2次，投中1次，则该运动员投1次篮，投中的概率为；（4）某件事情发生的概率是1，则它一定发生；（5）某彩票的中奖率为10%，则买100张彩票一定有1张会中奖；（6）函数与轴必有两个交点．A ．2B ．3C ．4D ．57．已知两个角的两边两两互相平行，则这两个角的关系是( )A ．相等B ．互补C ．相等或互补D ．相等且互补8．已知∠A 的两边与∠B 的两边互相平行，且∠A=20°，则∠B 的度数为（ ）. A ．20° B ．80° C ．160° D ．20°或160°9．如图，直线l 1∥l 2∥l 3，等腰Rt △ABC 的三个顶点A ，B ，C 分别在l 1，l 2，l 3上，∠ ACB=90°，AC 交l 2于点D ，已知l 1与l 2的距离为1，l 2与l 3的距离为3，则AB:BD 的值为（ ）A ．425B ．345C ．528D ．322010．下列命题中，是真命题的是（ ） A ．对顶角相等 B ．两直线被第三条直线所截，截得的内错角相等 C ．等腰直角三角形都全等 D ．如果a b >，那么22a b > 11．在同一平面内，有3条直线a ，b ，c ，其中直线a 与直线b 相交，直线a 与直线c 平行，那么b 与c 的位置关系是（ ）A ．平行B ．相交C ．平行或相交D ．不能确定12．如图，直线//a b ，直线AB AC ⊥，若150∠=，则2∠=（ ）A ．50B ．45C ．40D ．30二、填空题13．如图，直线a ∥b ，且∠1＝28°，∠2＝50°，则∠ABC ＝_______．14．若∠A 与∠B 的两边分别平行，且∠A 比∠B 的3倍少40°，则∠B ＝_____度．15．如图，请你添加一个条件．．．．使得AD ∥BC ，所添的条件是__________．16．如图，点О为直线AB 上一点，,,135OC OD OE AB ⊥⊥∠=︒．（1）EOD ∠= °，2∠= °；（2）1∠的余角是_ ，EOD ∠的补角是__ ．17．如图，已知AB ∥DE ，∠ABC ＝76°，∠CDE ＝150°，则∠BCD 的度数为__°．18．如图，AB ∥CD ，∠1=64°，FG 平分∠EFD ，则∠EGF=__________________°．19．如图，//AB CD ，BD 平分ABC ∠，:4:1C DBA ∠∠=，则CDB ∠=______．20．在数学拓展课程《玩转学具》课堂中，老师把我们常用的一副三角板带进了课堂．（1）嘉嘉将一副三角板按如图1所示的方式放置，使点A 落在DE 上，且//BC DE ，则ACE ∠的度数为__________．（2）如图2，淇淇将等腰直角三角板放在一组平行的直线与之间，并使直角顶点A 在直线a 上，顶点C 在直线b 上，现测得130∠=，则2∠的度数为__________．三、解答题21．(1)如图1，已知任意ABC ∆，过点C 作//DE AB ，求证：180A B ACB ∠+∠+∠=︒；(2)如图2，求证：∠AGF=∠AEF+∠F ；(3)如图3，//,119,AB CD CDE GF ∠=︒交DEB ∠的角平分线EF 于点,150F AGF ∠=︒，求F ∠的度数．22．如图1所示，AB ∥CD ，E 为直线CD 下方一点，BF 平分∠ABE ．（1）求证：∠ABE +∠C ﹣∠E ＝180°．（2）如图2，EG 平分∠BEC ，过点B 作BH ∥GE ，求∠FBH 与∠C 之间的数量关系． （3）如图3，CN 平分∠ECD ，若BF 的反向延长线和CN 的反向延长线交于点M ，且∠E +∠M ＝130°，请直接写出∠E 的度数．23．如图，已知C 为两条相互平行的直线AB ，ED 之间一点，ABC ∠和CDE ∠的角平分线相交于F ，180FDC ABC ∠+∠=︒．（1）求证：//AD BC ；（2）连结CF ，当//CF AB ，且32CFB DCF ∠=∠时，求BCD ∠的度数；（3）若DCF CFB ∠=∠时，将线段BC 沿直线AB 方向平移，记平移后的线段为PQ （B ，C 分别对应P ，Q ，当20PQD QDC ∠-∠=︒时，请直接写出DQP ∠的度数______．24．如图，已知直线12//l l ，直线3l 交1l 于C 点，交2l 于D 点，P 是线段CD 上的一个动点，（1）若P 点在线段CD （C 、D 两点除外）上运动，问PAC ∠，APB ∠，PBD ∠之间的关系是什么？这种关系是否变化？（2）若P 点在线段CD 之外时，PAC ∠，APB ∠，PBD ∠之间的关系怎样？说明理由25．在△ABC 中，∠BAC ＝90°，点D 是BC 上一点，将△ABD 沿AD 翻折后得到△AED ，边AE 交BC 于点F ．(1)如图①，当AE⊥BC时，写出图中所有与∠B相等的角：；所有与∠C相等的角：．(2)若∠C－∠B＝50°，∠BAD＝x°(0＜x≤45) ．①求∠B的度数；②是否存在这样的x的值，使得△DEF中有两个角相等．若存在，并求x的值；若不存在，请说明理由．∥，且直线AB、CD与AD、BC分别交于A、D和26．如图`，已知：直线AD BCB、C两点，点P在直线AB上．∠、(1)如图1,当点P在A、B两点之间时(点P不与点A、B重合)，探究ADP、DPC ∠之间的关系，并说明理由.BCP∠、(2)若点P不在A、B两点之间，在备用图中画出图形，直接写出ADP、DPC∠之间的关系，不需说理．BCP27． [问题解决]：如图1，已知AB∥CD，E是直线AB，CD内部一点，连接BE，DE，若∠ABE=40°，∠CDE=60°，求∠BED的度数．嘉琪想到了如图2所示的方法，但是没有解答完，下面是嘉淇未完成的解答过程：解：过点E作EF∥AB，∴∠ABE=∠BEF=40°∵AB∥CD，∴EF∥CD，…请你补充完成嘉淇的解答过程：[问题迁移]：请你参考嘉琪的解题思路，完成下面的问题：如图3，AB∥CD，射线OM与直线AB，CD分别交于点A，C，射线ON与直线AB，CD分别交于点B，D，点P在射线ON上运动，设∠BAP=α，∠DCP=β．（1）当点P 在B ，D 两点之间运动时(P 不与B ，D 重合)，求α，β和∠APC 之间满足的数量关系．（2）当点P 在B ，D 两点外侧运动时(P 不与点O 重合)，直接写出α，β和∠APC 之间满足的数量关系．28．将一副三角板中的两个直角顶点C 叠放在一起（如图①），其中30A ∠=︒，60B ∠=︒，45D E ∠=∠=︒.（1）猜想BCD ∠与ACE ∠的数量关系，并说明理由；（2）若3BCD ACE ∠=∠，求BCD ∠的度数；（3）若按住三角板ABC 不动，绕顶点C 转动三角DCE ，试探究BCD ∠等于多少度时//CE AB ，并简要说明理由.【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】分别利用直角三角形的性质、对顶角和平行线的判定方法以及绝对值的性质分析得出答案．【详解】解：A 、直角三角形中两个锐角互余，故此选项错误；B 、相等的角不一定是对顶角，故此选项错误；C 、同旁内角互补，两直线平行，正确；D 、若|a|=|b|，则a=±b ，故此选项错误；故选C ．【点睛】此题主要考查了命题与定理，正确把握相关性质是解题关键．2．B解析：B【详解】解：34∠∠=//AB CD ∴,①正确；12∠=∠//AD BC ∴,②不正确；5B ∠=∠//AB CD ∴,③正确；//AD BE5D ∴∠=∠B D ∠=∠5B ∴∠=∠//AB CD ∴,④正确；综上所述，①、③、④正确，故选B ．3．B解析：B【解析】试题分析：如图，首先根据平行线的性质（两直线平行，同旁内角互补），可求∠4=56°，然后借助平角的定义求得∠3=180°-∠2-∠4=36°.故选B考点：平行线的性质4．C解析：C【分析】由∠A与∠B的两边分别平行，即可得∠A与∠B相等或互补，然后分两种情况，分别从∠A与∠B相等或互补去分析，即可求得∠A的度数．【详解】解：∵∠A与∠B的两边分别平行，∴∠A与∠B相等或互补．分两种情况：①如图1，当∠A+∠B=180°时，∠A=3∠B-36°，解得：∠A=126°；②如图2，当∠A=∠B，∠A=3∠B-36°，解得：∠A=18°．所以∠A=18°或126°．故选：C．【点睛】此题考查的是平行线的性质，如果两角的两边分别平行，则这两个角相等或互补．此题还考查了方程组的解法．解题要注意列出准确的方程组．5．C解析：C【详解】①如图1，过点E作EF∥AB，因为AB∥CD，所以AB∥EF∥CD，所以∠A+∠AEF=180°，∠C+∠CEF=180°，所以∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°，则①错误；②如图2，过点E作EF∥AB，因为AB∥CD，所以AB∥EF∥CD，所以∠A=∠AEF，∠C=∠CEF，所以∠A+∠C=∠AEC+∠AEF=∠AEC，则②正确；③如图3，过点E作EF∥AB，因为AB∥CD，所以AB∥EF∥CD，所以∠A+∠AEF=180°，∠1=∠CEF，所以∠A+∠AEC-∠1=∠A+∠AEC-∠CEF=∠A+∠AEF=180°，则③正确；④如图4，过点P作PF∥AB，因为AB∥CD，所以AB∥PF∥CD，所以∠A=∠APF，∠C=∠CPF，所以∠A=∠CPF+∠APC=∠C+∠APC，则④正确；故选C.6．C解析：C【解析】试题解析：（1）“a是任意实数，|a|-5＞0”是不确定事件，是假命题；（2）抛物线y=（2x+1）2的对称轴是直线x=-，是假命题；（3）若某运动员投篮2次，投中1次，则该运动员投1次篮，投中的概率为，是假命题；（4）某件事情发生的概率是1，则它一定发生，是真命题；（5）某彩票的中奖率为10%，则买100张彩票中奖的可能性很大，但不是一定中奖，是假命题；（6）函数y=-9（x+2014）2+与x轴必有两个交点，是真命题，则假命题的个数是4；故选C．考点：命题与定理．7．C解析：C【解析】分类讨论：两个角的两边方向是否相同.若相同，则相等；否则互补.故选C. 8．D解析：D【解析】试题分析：如图，∵∠A=20°，∠A的两边分别和∠B的两边平行，∴∠B和∠A可能相等也可能互补，即∠B的度数是20°或160°，9．A解析：A 【解析】解：如图，作3BF l ⊥， 3AE l ⊥，∵090ACB ∠=，∴090BCF ACE ∠+∠=，∵090BCF CFB ∠+∠=，∴ACE CBF ∠=∠，在ACE ∆和CBF ∆中，{BFC CEACBF ACE BC AC∠=∠∠=∠=∴ACE CBF ∆≅∆，∴3,4CE BF CF AE ====，∵1l 与2l 的距离为1， 2l 与3l 的距离为3，∴1,7AG BG EF CF CE ===+=， ∴2252AB BG AG +=∵23//l l ， ∴14DG AG CE AE ==， ∴1344DG CE ==， ∴325744BD BG DG =-=-=， ∴52424AB BD == 故选A ．【点睛】本题考查了全等三角形的性质和判定，平行线分线段成比例定理等，构造全等三角形是解决本题的关键．10．A【分析】分别利用对顶角的性质、平行线的性质及不等式的性质分别判断后即可确定正确的选项．【详解】解：A.对顶角相等，正确，是真命题；B.两直线被第三条直线所截，内错角相等，错误，是假命题；C.等腰直角三角形不一定都全等，是假命题；D.如果0＞a ＞b ，那么a 2＜b 2，是假命题．【点睛】本题考查了命题与定理的知识，解题的关键是了解对顶角的性质、平行线的性质及不等式的性质，难度不大．11．B解析：B【分析】根据a ∥c ，a 与b 相交，可知c 与b 相交，如果c 与b 不相交，则c 与b 平行，故b 与a 平行，与题目中的b 与a 相交矛盾，从而可以解答本题．【详解】解：假设b ∥c ，∵a ∥c ，∴a ∥b ，而已知a 与b 相交于点O ，故假设b ∥c 不成立，故b 与c 相交，故选：B ．【点睛】本题考查平行线的性质，解答本题的关键是明确题意，利用平行线的性质解答．12．C解析：C【分析】根据垂直的定义和余角的定义列式计算得到3∠，根据两直线平行，同位角相等可得23∠∠=．【详解】如图，直线AB AC ⊥，1390︒∴∠+∠=．150︒∠=，390140︒︒∴∠=-∠=，直线//a b ，2340︒∴∠=∠=，故选C ．【点睛】本题考查了平行线的性质，垂直的定义，熟记性质并准确识图是解题的关键．二、填空题13．78°【解析】解：过点B 作BE∥a，∵a∥b，∴a∥b∥BE，∴∠1=∠3=28°，∠2=∠4=50°，∴∠ABC=∠3+∠4=78°．故答案为：78°．点睛：此题考查了平行线的性质：两直线解析：78°【解析】解：过点B 作BE ∥a ，∵a ∥b ，∴a ∥b ∥BE ，∴∠1=∠3=28°，∠2=∠4=50°，∴∠ABC =∠3+∠4=78°．故答案为：78°．点睛：此题考查了平行线的性质：两直线平行，内错角相等．解此题的关键是辅助线的作法．14．55或20【分析】根据平行线性质得出∠A+∠B＝180°①，∠A＝∠B②，求出∠A＝3∠B﹣40°③，把③分别代入①②求出即可．【详解】解：∵∠A 与∠B 的两边分别平行，∴∠A+∠B＝180解析：55或20【分析】根据平行线性质得出∠A+∠B ＝180°①，∠A ＝∠B②，求出∠A ＝3∠B ﹣40°③，把③分别代入①②求出即可．【详解】解：∵∠A 与∠B 的两边分别平行，∴∠A+∠B ＝180°①，∠A ＝∠B②，∵∠A 比∠B 的3倍少40°，∴∠A ＝3∠B ﹣40°③，把③代入①得：3∠B ﹣40°+∠B ＝180°，∠B ＝55°，把③代入②得：3∠B ﹣40°＝∠B ，∠B ＝20°，故答案为：55或20．【点睛】本题考查平行线的性质，解题的关键是掌握由∠A 和∠B 的两边分别平行，即可得∠A ＝∠B 或∠A ＋∠B ＝180° ，注意分类讨论思想的应用．15．∠EAD＝∠B 或∠DAC＝∠C【解析】当∠EAD＝∠B 时，根据“同位角相等，两直线平行”可得AD//BC ；当∠DAC＝∠C 时，根据“内错角相等，两直线平行”可得AD//BC ；当∠DAB+∠B解析：∠EAD ＝∠B 或∠DAC ＝∠C【解析】当∠EAD ＝∠B 时，根据“同位角相等，两直线平行”可得AD//BC ；当∠DAC ＝∠C 时，根据“内错角相等，两直线平行”可得AD//BC ；当∠DAB+∠B=180°时，根据“同旁内角互补，两直线平行”可得AD//BC ，故答案是：∠EAD ＝∠B 或∠DAC ＝∠C 或∠DAB+∠B=180°（答案不唯一）.16．（1）35，55；（2）与，【分析】（1）由，可得，，所以，，，所以，已知的度数，即可得出与的度数；（2）由（1）可得的余角是与，要求的补角，即要求的补角，的补角是．【详解】（1），，，解析：（1）35，55；（2）COE ∠与2∠，COB ∠【分析】（1）由OC OD ⊥，OE AB ⊥可得=90COD ∠︒，=90AOE ∠︒，所以1290∠+∠=︒，190COE ∠+∠=︒，90EOD COE ∠+∠=︒，所以1=EOD ∠∠，已知1∠的度数，即可得出2∠与EOD ∠的度数；（2）由（1）可得1∠的余角是COE ∠与2∠，要求EOD ∠的补角，即要求1∠的补角，1∠的补角是COB ∠．【详解】（1）OC OD ⊥，OE AB ⊥，∴=90COD ∠︒，=90AOE ∠︒，∴1290∠+∠=︒，190COE ∠+∠=︒，90EOD COE ∠+∠=︒，∴1=EOD ∠∠，135∠=︒，∴255∠=︒，35=EOD ∠︒；（2）由（1）可得1∠的余角是COE ∠与2∠，1180COB =∠∠+︒，∴1∠的补角是COB ∠，∴EOD ∠的补角是COB ∠．故答案为：（1）35，55；（2）COE ∠与2∠，COB ∠．【点睛】 本题主要考查余角、补角以及垂直的定义，熟记补角、余角以及垂直的定义是解题关键． 17．46【分析】过点C 作CF∥AB，根据平行线的传递性得到CF∥DE，根据平行线的性质得到∠ABC＝∠BCF，∠CDE+∠DCF＝180°，根据已知条件等量代换得到∠BCF＝76°，由等式性质得到∠解析：46【分析】过点C 作CF ∥AB ，根据平行线的传递性得到CF ∥DE ，根据平行线的性质得到∠ABC ＝∠BCF ，∠CDE +∠DCF ＝180°，根据已知条件等量代换得到∠BCF ＝76°，由等式性质得到∠DCF ＝30°，于是得到结论．【详解】解：过点C 作CF ∥AB ，∵AB ∥DE ，∴AB ∥DE ∥CF ，∴∠ABC ＝∠BCF ，∠CDE +∠DCF ＝180°，∵∠ABC ＝76°，∠CDE ＝150°，∴∠BCF ＝76°，∠DCF ＝30°，∴∠BCD ＝46°，故答案为：46．【点睛】本题主要考查平行线的性质，关键是根据平行线的性质得到角之间的等量关系．18．【分析】根据两直线平行，同位角相等求出∠EFD，再根据角平分线的定义求出∠GFD，然后根据两直线平行，内错角相等解答．【详解】解：∵AB∥CD，∠1=64°，∴∠EFD=∠1=64°，∵解析：【分析】根据两直线平行，同位角相等求出∠EFD，再根据角平分线的定义求出∠GFD，然后根据两直线平行，内错角相等解答．【详解】解：∵AB∥CD，∠1=64°，∴∠EFD=∠1=64°，∵FG平分∠EFD，∴∠GFD=12∠EFD=12×64°=32°，∵AB∥CD，∴∠EGF=∠GFD=32°．故答案为：32．考点：平行线的性质．19．30°【分析】先由AB//CD得到∠CDB=∠ABD，∠C+∠ABC=180︒,设出∠ABD=x°，依据“平分，”列出方程，求出∠ABD即可解决问题．【详解】∵AB//CD∴∠ABD=x°解析：30°【分析】先由AB//CD得到∠CDB=∠ABD，∠C+∠ABC=180︒,设出∠ABD=x°，依据“BD平分ABC ∠，:4:1C DBA ∠∠=”列出方程，求出∠ABD 即可解决问题．【详解】∵AB//CD∴∠ABD=x°，∠ABD ，∠C+∠ABC=180︒,BD 平分ABC ∠，∴∠ABD=∠CBD∵:4:1C DBA ∠∠=，∴4C DBA ∠=∠设∠ABD=x°，则∠CBD=x°，∠C=4x°，∴2x°+4x°=180°,解得，x=30∴∠ABD=30°，∴∠CDB=30°，故答案为：30°．【点睛】此题主要考查了平行线的性质以及角平分线的定义，求出∠ABD=30°是解此题的关键． 20．15° 15°【分析】（1）根据平行线的性质得出∠D+∠BCD=180°，从而得到∠BCD，再利用角的和差得到∠ACE；（2）根据平行线的性质得出∠2+∠BAC+∠ACB+∠1=解析：15° 15°【分析】（1）根据平行线的性质得出∠D+∠BCD=180°，从而得到∠BCD ，再利用角的和差得到∠ACE ；（2）根据平行线的性质得出∠2+∠BAC+∠ACB+∠1=180°，再由等腰直角三角形的性质得到∠BAC=90°，∠ACB=45°，结合∠1的度数可得结果．【详解】解：（1）由三角板的性质可知：∠D=60°，∠ACB=45°，∠DCE=90°，∵BC ∥DE ，∴∠D+∠BCD=180°，∴∠BCD=120°，∴∠BCE=∠BCD-∠DCE=30°，∴∠ACE=∠ACB-∠BCE=15°，故答案为：15°；（2）∵a ∥b ，∴∠2+∠BAC+∠ACB+∠1=180°，∵△ABC 为等腰直角三角形，∴∠BAC=90°，∠ACB=45°，∴∠1+∠2=180°-∠BAC-∠ACB=45°，∵∠1=30°，∴∠2=15°，故答案为：15°．【点睛】本题考查了三角板的性质，平行线的性质，解题时注意：两直线平行，同旁内角互补．三、解答题21．（1）见详解；（2）见详解；（3）29.5°．【分析】（1）根据平行线的性即可A ACD ∠=∠，B BCE ∠=∠，再根据平角的定义进行等量代换即可证明；（2）因为根据平角的定义和三角形的内角和定理即可得到结论；（3）根据平行线的性质得到119DEB ∠=︒，61AED ∠=︒，由角平分线的性质得到59.5DEF ∠=︒，根据三角形的外角的性质即可得到结论．【详解】（1）如图1所示，在ABC ∆中，//DE AB ，A ACD ∴∠=∠，B BCE ∠=∠．180ACD BCA BCE ∠+∠+∠=︒，180A B ACB ∴∠+∠+∠=︒．即三角形的内角和为180︒；（2）180AGF FGE ∠+∠=︒，由（1）知，180GEF F FGE ∠+∠+∠=︒，AGF AEF F ∴∠=∠+∠；（3）//AB CD ，119CDE ∠=︒，119DEB CDE ∴∠=∠=︒，18061AED CDE ∠=︒-∠=︒，∵EF 平分DEB ∠，59.5DEF ∴∠=︒，120.5AEF AED FED ∴∠=∠+∠=︒，150AGF ∠=︒，AGF AEF F ∠=∠+∠，150120.529.5F ∴∠=︒-︒=︒．【点睛】本题考查了平行线的性质，三角形的内角和定理的证明与应用，三角形外角定理证明与应用，熟练掌握平行线的性质定理是解题的关键，此类题目每一步都为后续解题提供了解题条件或方法．22．（1）见解析；（2）2∠FBH +∠C ＝180°；（3）80°【分析】（1）过点E 作//EK AB ，由平行线的性质得出,180ABE BEK CEK C ∠=∠∠+∠=︒，进而得出答案；（2）设,ABF EBF BEG CEG αβ∠=∠=∠=∠=，由平行线的性质得出,HBE BEG FBH FBE HBE βαβ∠=∠=∠=∠-∠=-，由（1）知180ABE C BEC ∠+∠-∠=︒，即可得出答案；（3）设,ABF EBF x ECN DCN y ∠=∠=∠=∠=，由（1）知2()180E x y ∠=+-︒，过M 作////PQ AB CD ，由平行线的性质得出,PMF ABF x QMN DCN y ∠=∠=∠=∠=，求出130E FMN x y ∠+∠=+=︒，即可得出答案．【详解】（1）如图1，过点E 作//EK AB∴ABE BEK ∠=∠∵//AB CD∴//EK CD∴180CEK C ∠+∠=︒∴180ABE C E BEC CEK C BEC CEK C ∠+∠-∠=∠+∠+∠-∠=∠+∠=︒； （2）∵BF 、EG 分别平分ABE ∠、BEC ∠∴,ABF EBF BEG CEG ∠=∠∠=∠设,ABF EBF BEG CEG αβ∠=∠=∠=∠=∵//BH EG∴HBE BEG β∠=∠=∴FBH FBE HBE αβ∠=∠-∠=-由（1）知，180ABE C BEC ∠+∠-∠=︒即222()180C C αβαβ+∠-=-+∠=︒∴2180FBH C ∠+∠=︒；（3）∵CN 、BF 分别平分ECD ∠、ABE ∠∴,ABF EBF ECN DCN ∠=∠∠=∠设,ABF EBF x ECN DCN y ∠=∠=∠=∠=由（1）知：180ABE C E ∠+∠-∠=︒即2()180E x y ∠=+-︒如图3，过M 作////PQ AB CD则,PMF ABF x QMN DCN y ∠=∠=∠=∠=∴180180()FMN PMF QMN x y ∠=︒-∠-∠=︒-+130E FMN ∠+∠=︒∴2()180180()130x y x y +-︒+︒-+=︒130x y ∴+=︒∴2()180213018080E x y ∠=+-︒=⨯︒-︒=︒．【点睛】本题考查了角平分线的定义、平行线的性质、角的和差等知识点，较难的是题（3），通过作辅助线，构造平行线是解题关键．23．（1）证明见解析；（2）∠BCD＝108°；（3）70°【分析】（1）根据两直线平行，内错角相等得出∠EDF＝∠DAB，由角平线的定义得出∠EDF＝∠FDC，最后根据同旁内角互补，两直线平行进行求证；（2）设∠DCF＝x，则∠CFB＝1.5x，由两直线平行，内错角相等得出∠ABF＝1.5x，由角平分线的定义得出∠ABC＝3x，最后利用两直线平行，同旁内角互补得出关于x的方程，求解即可；（3）画出图形，根据两直线平行，同旁内角互补得出∠CDF＝∠CBF，由角平分线的定义与已知条件可求出∠ABC与∠FDC，由平移的性质与平行公理的推论得出AD∥PQ，最后根据两直线平行，同旁内角互补列式求解．【详解】解：（1）证明：∵AB∥DE，∴∠EDF＝∠DAB，∵DF平分∠EDC，∴∠EDF＝∠FDC，∴∠FDC＝∠DAB，∵∠FDC+∠ABC＝180°，∴∠DAB+∠ABC＝180°，∴AD∥BC；（2）∵32CFB DCF∠=∠，设∠DCF＝x，则∠CFB＝1.5x，∵CF∥AB，∴∠ABF＝∠CFB＝1.5x，∵BE平分∠ABC，∴∠ABC＝2∠ABF＝3x，∵AD∥BC，∴∠FDC+∠BCD＝180°，∵∠FDC+∠ABC＝180°，∴∠BCD＝∠ABC＝3x，∴∠BCF＝2x，∵CF∥AB，∴∠ABC+∠BCF＝180°，∴3x+2x＝180°，∴x＝36°，∴∠BCD＝3×36°＝108°；（3）如图，∵∠DCF＝∠CFB，∴BF∥CD，∴∠CDF +∠BFD＝180°，∵AD∥BC，∴∠CBF +∠BFD＝180°，∴∠CDF＝∠CBF，∵AD，BE分别平分∠ABC，∠CDE，∴∠ABC＝2∠CBF，∠CDE＝2∠FDC，∴∠ABC＝∠CDE＝2∠FDC，∵∠FDC+∠ABC＝180°，∴∠ABC＝120°，∠FDC＝60°，∵线段BC沿直线AB方向平移得到线段PQ，∴BC∥PQ，∵AD∥BC，∴AD∥PQ，∵∠PQD﹣∠QDC＝20°，∴∠QDC＝∠PQD﹣20°，∴∠FDC+∠QDC +∠PQD＝60°+∠PQD﹣20°+∠PQD＝180°，∴∠PQD＝70°，即∠DQP＝70°．故答案为：70°．【点睛】本题考查平行线的判定与性质，平行公理的推论，角平分线的定义，平移的性质，熟练运用平行线的判定与性质是解题的关键．24．（1）∠APB=∠PAC +∠PBD，不会变化；（2）∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB，理由见解析．【分析】（1）当P点在C、D之间运动时，首先过点P作PE∥l1，由l1∥l2，可得PE∥l2∥l1，根据两直线平行，内错角相等，即可求得：∠APB=∠PAC+∠PBD，即∠APB、∠PAC、∠PBD之间的关系不发生变化；（2）当点P在C、D两点的外侧运动时，由直线l1∥l2，根据两直线平行，同位角相等以及三角形外角的性质，即可求得∠PAC，∠APB，∠PBD之间的关系．【详解】（1）如图①，当P点在C、D之间运动时，∠APB=∠PAC+∠PBD．理由如下：过点P作PE∥l1，∵l1∥l2，∴PE∥l2∥l1，∴∠PAC=∠1，∠PBD=∠2，∴∠APB=∠1+∠2=∠PAC+∠PBD，即∠APB、∠PAC、∠PBD之间的关系不发生变化；（2）如图②，当点P在C、D两点的外侧运动，且在l1上方时，∠PBD=∠PAC+∠APB．理由如下：∵l1∥l2，∴∠PEC=∠PBD，∵∠PEC=∠PAC+∠APB，∴∠PBD=∠PAC+∠APB．当点P在C、D两点的外侧运动，且在l2下方时，∠PAC=∠PBD+∠APB．如图③，理由如下：∵l 1∥l 2，∴∠PED=∠PAC ，∵∠PED=∠PBD+∠APB ，∴∠PAC=∠PBD+∠APB ．【点睛】本题主要考查平行线的性质与三角形外角的性质．解题的关键是掌握：两直线平行，内错角相等与两直线平行，同位角相等，注意辅助线的作法．25．(1)∠E 、∠CAF ；∠CDE 、∠BAF ； (2)①20°；②30【分析】（1）由翻折的性质和平行线的性质即可得与∠B 相等的角；由等角代换即可得与∠C 相等的角；（2）①由三角形内角和定理可得90B C ∠+∠=︒，再由50C B ∠∠︒-=根据角的和差计算即可得∠C 的度数，进而得∠B 的度数．②根据翻折的性质和三角形外角及三角形内角和定理，用含x 的代数式表示出∠FDE 、∠DFE 的度数，分三种情况讨论求出符合题意的x 值即可．【详解】（1）由翻折的性质可得：∠E ＝∠B ，∵∠BAC ＝90°，AE ⊥BC ，∴∠DFE ＝90°，∴180°－∠BAC ＝180°－∠DFE ＝90°，即：∠B ＋∠C ＝∠E ＋∠FDE ＝90°，∴∠C ＝∠FDE ，∴AC ∥DE ，∴∠CAF ＝∠E ，∴∠CAF ＝∠E ＝∠B故与∠B 相等的角有∠CAF 和∠E ；∵∠BAC ＝90°，AE ⊥BC ，∴∠BAF ＋∠CAF ＝90°, ∠CFA ＝180°－（∠CAF ＋∠C ）＝90°∴∠BAF ＋∠CAF ＝∠CAF ＋∠C ＝90°∴∠BAF ＝∠C又AC ∥DE ，∴∠C ＝∠CDE ，∴故与∠C 相等的角有∠CDE 、∠BAF ；（2）①∵90BAC ∠=︒∴90B C ∠+∠=︒又∵50C B ∠∠︒-=，∴∠C ＝70°，∠B ＝20°;②∵∠BAD ＝x °, ∠B ＝20°则160ADB x ∠︒︒=-,20ADF x ∠︒︒=+,由翻折可知：∵160ADE ADB x ∠∠︒︒==-, 20E B ∠∠︒==,∴1402FDE x ∠︒︒=-, 202DFE x ∠︒︒=+,当∠FDE ＝∠DFE 时，1402202x x ︒︒︒︒-=+, 解得：30x ︒︒=；当∠FDE ＝∠E 时，140220x ︒︒︒-=，解得：60x ︒︒=（因为0＜x ≤45，故舍去）； 当∠DFE ＝∠E 时，20220x ︒︒︒+=，解得：0x ︒＝（因为0＜x ≤45，故舍去）； 综上所述，存在这样的x 的值，使得△DEF 中有两个角相等．且30x =．【点睛】本题考查图形的翻折、三角形内角和定理、平行线的判定及其性质、三角形外角的性质、等角代换，解题的关键是熟知图形翻折的性质及综合运用所学知识．26．（1）∠ADP+∠BCP=∠DPC ，理由见解析；（2）∠ADP=∠DPC+∠BCP ，理由见解析【分析】（1）过P 作直线PQ ∥AD ，交CD 于点Q ，根据平行线的性质进行推理；（2）过P 作直线PQ ∥AD ，交CD 于点Q ，根据平行线的性质进行推理；【详解】解：（1）过P 作直线PQ ∥AD ，交CD 于点Q ，∵AD ∥BC ，∴PQ ∥AD ∥BC ，∴∠ADP=∠DPQ ，∠BCP=∠CPQ ，∴∠ADP+∠BCP=∠DPC ；（2）∠ADP=∠DPC+∠BCP .过P 作直线PQ ∥AD ，交CD 于点Q ，∵AD ∥BC ，∴PQ ∥AD ∥BC ，∴∠ADP=∠DPQ=∠DPC+∠CPQ，∠BCP=∠CPQ，∴∠ADP=∠DPC+∠BCP.【点睛】本题考查了平行线的性质，利用平行线的性质得出角的和差关系是解题的关键. 27．[问题解决]见解析；[问题迁移]（1）∠APC=α+β；（2）当点P在BN上时，∠APC=β-α；当点P在OD上时，∠APC=α-β．【分析】问题解决：过点E作EF∥AB，依据平行线的性质，即可得到∠BED的度数；问题迁移：（1）过P作PQ∥AB，依据平行线的性质，即可得出α，β和∠APC之间满足的数量关系．（2）分两种情况讨论：过P作PQ∥AB，易得当点P在BN上时，∠APC=β-α；当点P在OD上时，∠APC=α-β．【详解】问题解决：如图2，过点E作EF∥AB，∴∠ABE=∠BEF=40°∵AB∥CD，∴EF∥CD，∴∠B=∠BEF，∠D=∠DEF，∴∠BED=∠B+∠D=40°+60°=100°；问题迁移：（1）如图3，过P作PQ∥AB，∵AB ∥CD ，∴PQ ∥CD ，∴∠BAP=∠APQ ，∠DCP=∠CPQ ，∴∠APC=∠BAP+∠DCP ，即∠APC=α+β；（2）如图4，当点P 在BN 上时，∠APC=β-α；如图5，当点P 在OD 上时，∠APC=α-β．【点睛】本题主要考查了平行线的性质与判定的运用，解决问题的关键是掌握：两直线平行，内错角相等，并利用角的和差关系进行推算．28．（1）180BCD ACE ∠+∠=︒，理由详见解析；（2）135°；（3）BCD ∠等于150︒或30时，//CE AB .【分析】（1）依据∠BCD=∠ACB+∠ACD=90°+∠ACD ，即可得到∠BCD+∠ACE 的度数；（2）设∠ACE=α，则∠BCD=3α，依据∠BCD+∠ACE=180°，即可得到∠BCD 的度数； （3）分两种情况讨论，依据平行线的性质，即可得到当∠BCD 等于150°或30°时，CE//4B.【详解】解：（1）180BCD ACE ∠+∠=︒，理由如下：90BCD ACB ACD ACD ∠=∠+∠=︒+∠，∴90BCD ACE ACD ACE ∠+∠=︒+∠+∠9090180=︒+︒=︒；（2）如图①，设ACE α∠=，则3BCD α∠=，由（1）可得180BCD ACE ∠+∠=︒，∴3180αα+=︒，∴45α=，∴3135BCD α∠==︒；（3）分两种情况：①如图1所示，当//AB CE 时，180120BCE B ∠=︒-∠=︒， 又90DCE ∠=︒，∴36012090150BCD ∠=︒-︒-︒=︒；②如图2所示，当//AB CE 时，60BCE B ∠=∠=︒， 又90DCE ∠=︒，∴906030BCD ∠=︒-︒=︒.综上所述，BCD ∠等于150︒或30时，//CE AB .【点睛】本题考查了平行线的判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行.熟练掌握定理并且能够准确识图是解题的关键.。
相交线与平行线测试题及答案doc
相交线与平行线测试题及答案doc一、选择题（每题5分，共20分）1. 在同一平面内，两条直线的位置关系有几种？A. 一种B. 两种C. 三种D. 四种答案：B2. 下列说法中，正确的是：A. 同一平面内，两条直线不相交，则它们一定平行B. 同一平面内，两条直线相交，则它们一定垂直C. 同一平面内，两条直线平行，则它们永不相交D. 同一平面内，两条直线相交，则它们一定平行答案：C3. 如果两条直线都与第三条直线平行，那么这两条直线的关系是：A. 相交B. 平行C. 垂直D. 无法确定答案：B4. 两条直线相交，交点处的夹角为90°，那么这两条直线的关系是：A. 相交B. 平行C. 垂直D. 重合答案：C二、填空题（每题5分，共20分）1. 如果两条直线都与第三条直线相交，且交角相等，则这两条直线____。
答案：平行2. 在同一平面内，两条直线不相交，则它们是____。
答案：平行3. 垂直于同一直线的两条直线一定是____。
答案：平行4. 两条平行线被第三条直线所截，同位角相等，内错角互补，同旁内角和为____。
答案：180°三、解答题（每题10分，共20分）1. 已知直线AB与直线CD相交于点O，且∠AOB=∠COD=90°，求证：AB∥CD。
证明：因为∠AOB=∠COD=90°，所以AB⊥OB，CD⊥OD。
根据垂直于同一条直线的两条直线平行，所以AB∥CD。
2. 已知直线l1与直线l2相交于点P，且l1∥l3，l2∥l4，求证：l3与l4相交。
证明：因为l1∥l3，l2∥l4，所以∠l1P=∠l3P，∠l2P=∠l4P。
根据同位角相等，两直线平行，所以l3∥l1，l4∥l2。
又因为l1与l2相交，所以l3与l4相交。
四、计算题（每题10分，共40分）1. 在同一平面内，直线m与直线n相交，交点为O。
已知∠1=45°，求∠2的度数。
答案：∠2=180°-45°=135°2. 已知直线a与直线b平行，直线c与直线a相交于点A，且∠BAC=60°，求∠ABC的度数。
相交线与平行线 单元测试题(含答案)
相交线与平行线 单元测试题一、选择题（每小题3分，共30分）1. 如图，直线AB 、CD 相交于O 点，若︒=∠301，则∠2、∠3的度数分别为（ ）第3题图A. 120°、60°B. 130°、50°C. 140°、40°D. 150°、30°2. 已知同一平面内的直线l 1、l 2、l 3，如果l 1⊥l 2，l 2∥l 3，那么l 1与l 3的位置关系是( ).A.平行B.相交C.垂直D.以上均不对3.如图，AB ∥CD ，若∠1=45°，则∠2的度数是（ ） A. 45° B. 90° C. 30° D. 135°4. 下列说法中，正确的是 （ ）A ．同一平面内，两条直线的位置关系只有相交、平行两种；B ．同一平面内，不相交的两条线段互相平行；C ．不相交的两条直线是平行线；D ．同一平面内，不相交的两条射线互相平行．5.如图，AOC ∠和BOD ∠都是直角，且︒=∠30DOC ，则=∠AOB ( ). A ．︒30 B ．︒60C ．︒120D ．︒1506. 以下判定中，正确的个数有（ ） （1）若a ∥b ，b ∥c ，则a ∥c （2）若a ⊥b ，b ⊥c ，则a ⊥cA B CD12 123A BCD O 第1题图AODCBDC B A 1（3）若同旁内角相等，则两直线平行（4）若同位角相等，则两直线平行 A ．1个 B ．2个 C ．3个 D ．4个7.将含300角的三角板ABC 如图放置，使其三个顶点分别落在三条平行直线上，其中∠ACB=900，当∠1=600时，图中等于300的角的个数是（ ）A.6个B.5个C.4个D.3个 8. 如图，若∠1=70°，∠2=110°，∠3=70°，则有（ ） Ａ．a ∥b Ｂ．c ∥dＣ．a ⊥d Ｄ．任两条都无法判定是否平行bcda3217题图 8题图 9题图9. 如图，直线AB ∥CD ，∠A ＝70︒，∠C ＝40︒，则∠E 等于（ ） A ．30° Ｂ．40° C ．60° Ｄ．70°10. Rt ABC △中， 90ACB ∠=°，DE 过点C ，且DE AB ∥，若 55ACD ∠=°，则∠B 的度数是（ ）A ．35°B ．45°C ．55°D ．65° 二、填空题（每小题3分，共30分）1. 如图，AB ∥CD ，则与∠1相等的角(∠1除外)共有 个．2.如图，直线l 1与l 2相交于点O ，1OM l ⊥，若44α∠=︒，则β∠等于 ．A B CD EACBDEFEDCB A12N MG F EDC BA GF EDCB A 12第2题图 第3题图3.如图，l ∥m ，矩形ABCD 的顶点B 在直线m 上，则∠α= 度.4. 如图，如果DE ∥AB ，那么∠A + =180°，或∠B + =180°，根据是 ；如果∠CED =∠FDE ，那么 ∥ ．根据是内错角相等，两直线平行．F E DCBA第4题图 第5题图 第6题图 第7题图 5. 如图，已知AB ∥CD ，∠1=65°，∠2=45°，则∠ADC =________． 6．如图，若AB ∥EF ，BC ∥DE ，则∠B +∠E =________．7.如图，BC ⊥AE ，垂足为C ，过C 作CD ∥AB ．若∠ECD =48°，则∠BAC 的度数是 ．8．如图，已知直线AB ，CD 被直线EF 所截，若∠1=∠2，•则∠AEF+∠CFE =________．第8题图 第9题图 第10题图9.如图，已知AB ∥CD ，直线EF 分别交AB ，CD 于E ，F ，EG •平分∠BEF ，若∠1=72°，则∠2=_______．10. 如图所示，把一张长方形纸片ABCD 沿EF 折叠，若∠EFG =50°，则∠DEG 的度数为 .三、解答题55DαAC BlmO l 2l 1βα1. 读句画图：如图，直线CD 与直线AB 相交于C ，根据下列语句画图： （1）过点P 作PQ ∥CD ，交AB 于点Q ； （2）过点P 作PR ⊥CD ，垂足为R ．2.已知以下基本事实：①对顶角相等；②一条直线截两条平行直线所得的同位角相等；③两条直线被第三条直线所截，若同位角相等，则这两条直线平行； (1)在利用以上基本事实作为依据来证明命题“两直线平行，内错角相等”时，必须要用的基本事实有 (填入序号即可)；(2)根据在(1)中的选择，结合所给图形，请你证明命题“两直线平行，内错角相等”． 已知：如图，_____________________． 求证：_____ ______．cb a123.如图，AB 与CD 相交于点O ，OE ⊥CD ，∠BOE =54°，求∠AOC 的度数．4. 如图，在网格图中，平移三角形ABC 使点A 平移到点D ．FE21DCBA（1）画出平移后的三角形DEF ；（2）三角形DEF 与三角形ABC 有什么关系？5.如图，已知B 、E 分别是AC 、DF 上的点，∠1=∠2，∠C =∠D ． (1)∠ABD 与∠C 相等吗?为什么? (2)∠A 与∠F 相等吗?请说明理由．6. 如图，MN 、EF 是两面互相平行的镜面，根据镜面反射规律，若一束光线AB 照射到镜面MN 上，反射光线为BC ，则一定有∠1=∠2．试根据这一规律：（1）利用直尺和量角器作出光线BC 经镜面EF 反射后的反射光线CD ； （2）试判断AB 与CD 的位置关系，并说明理由．7.有一天李小虎同学用《几何画板》画图，他先画了两条平行线线AB 、CD ，然后在平行线间画了一点E ，连结BE 、CE 后（如图①），它用鼠标左键点住点E ，拖动后，分别得到如图②、③、④等图形，这时它突然一想，∠B 、∠D 与∠BED 之间的度数有没有某种联系呢？接着小虎同学通过利用《几何画板》的“度量角度”和“计算”的功能，找到了这三个角之间的关系。
第五章相交线与平行线单元试卷试卷(word版含答案)
第五章相交线与平行线单元试卷试卷（word 版含答案）一、选择题1．如图，A 、P 是直线m 上的任意两个点，B 、C 是直线n 上的两个定点，且直线m ∥n ．则下列说法正确的是（ ）A ．AC=BPB ．△ABC 的周长等于△BCP 的周长 C ．△ABC 的面积等于△ABP 的面积D ．△ABC 的面积等于△PBC 的面积 2．如图，AB CD ∥，154FGB ∠︒＝，FG 平分EFD ∠，则AEF ∠的度数等于（ ）．A ．26°B ．52°C ．54°D ．77° 3．如图，AB ∥CD ，BF ,DF 分别平分∠ABE 和∠CDE ，BF ∥DE ，∠F 与∠ABE 互补，则∠F 的度数为A ．30°B ．35°C ．36°D ．45°4．两条平行线被第三条直线所截，则下列说法错误的是（ ）A ．一对邻补角的平分线互相垂直B ．一对同位角的平分线互相平行C ．一对内错角的平分线互相平行D ．一对同旁内角的平分线互相平行5．已知：点A ，B ，C 在同一条直线上，点M 、N 分别是AB 、BC 的中点，如果AB =10cm ，AC =8cm ，那么线段MN 的长度为（ ）A ．6cmB ．9cmC ．3cm 或6cmD ．1cm 或9cm6．如图，若180A ABC ∠+∠=︒，则下列结论正确的是（ ）A ．12∠=∠B ．24∠∠=C ．13∠=∠D ．23∠∠=7．在同一平面内，有3条直线a ，b ，c ，其中直线a 与直线b 相交，直线a 与直线c 平行，那么b 与c 的位置关系是（ ）A ．平行B ．相交C ．平行或相交D ．不能确定8．光线在不同介质中的传播速度不同，因此当光线从空气射向水中时，会发生折射．如图，在空气中平行的两条入射光线，在水中的两条折射光线也是平行的．若水面和杯底互相平行，且∠1＝122°，则∠2＝（ ）A ．61°B ．58°C ．48°D ．41° 9．在下列命题中，为真命题的是（ ） A ．相等的角是对顶角B ．平行于同一条直线的两条直线互相平行C ．同旁内角互补D ．垂直于同一条直线的两条直线互相垂直10．下列选项中，不是运用“垂线段最短”这一性质的是（ ）A ．立定跳远时测量落点后端到起跳线的距离B ．从一个村庄向一条河引一条最短的水渠C ．把弯曲的公路改成直道可以缩短路程D ．直角三角形中任意一条直角边的长度都比斜边短11．如图，直线l 与直线AB 、CD 分别相交于点E 、点F ，EG 平分BEF ∠交直线CD 与点G ，若168BEF ∠=∠=︒，则EGF ∠的度数为（ ）．A ．34°B ．36°C ．38°D ．68°12．下列说法中不正确的个数为（ ）．①在同一平面内，两条直线的位置关系只有两种：相交和垂直．②有且只有一条直线垂直于已知直线．③如果两条直线都与第三条直线平行，那么这两条直线也互相平行．④从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离．⑤过一点，有且只有一条直线与已知直线平行．A ．2个B ．3个C ．4个D ．5个二、填空题13．如图， 已知//AB CF ，//CF DE ， 90BCD ∠=︒，则D B ∠-∠=_________14．某段铁路两旁安置了两座可旋转探照灯，主道路是平行，即PQ ∥MN ． 如图所示，灯A 射线从AM 开始顺时针旋转至AN 便立即回转，灯B 射线从BP 开始顺时针旋转至BQ 便立即回转，两灯不停交叉照射巡视．若灯A 转动的速度是每秒2度，灯B 转动的速度是每秒1度． 若灯B 射线先转动30秒，灯A 射线才开始转动，在灯B 射线到达BQ 之前，A 灯转动_________秒，两灯的光束互相平行．15．平面内不过同一点的n 条直线两两相交，它们交点个数记作n a ，并且规定10a =，则2a =__________，1n n a a --=____________．16．如图，有两个正方形夹在AB 与CD 中，且AB//CD,若∠FEC=10°，两个正方形临边夹角为150°，则∠1的度数为________度(正方形的每个内角为90°)17．如图，Rt △AOB 和Rt △COD 中，∠AOB ＝∠COD ＝90°，∠B ＝40°，∠C ＝60°，点D 在边OA 上，将图中的△COD 绕点O 按每秒10°的速度沿顺时针方向旋转一周，在旋转的过程中，在第________秒时，边CD 恰好与边AB 平行．18．如图，直线a ∥b ∥c ，直角∠BAC 的顶点A 在直线b 上，两边分别与直线a ，c 相交于点B ，C ，则∠1＋∠2的度数是___________．19．如图，已知AB 、CD 相交于点O,OE ⊥AB 于O ，∠EOC=28°，则∠AOD=_____度；20．如图，直角△ABC 中，AC=3，BC=4，AB=5，则内部五个小直角三角形的周长为_____．三、解答题21．如图，AD 平分∠BAC 交BC 于点D ，点F 在BA 的延长线上，点E 在线段CD 上，EF 与AC 相交于点G ，∠BDA+∠CEG=180°．（1）AD 与EF 平行吗？请说明理由；（2）若点H 在FE 的延长线上，且∠EDH=∠C ，则∠F 与∠H 相等吗，请说明理由．22．已知：直线//AB CD ，点E ，F 分别在直线AB ，CD 上，点M 为两平行线内部一点． （1）如图1，∠AEM ，∠M ，∠CFM 的数量关系为________；(直接写出答案)（2）如图2，∠MEB 和∠MFD 的角平分线交于点N ，若∠EMF 等于130°，求∠ENF 的度数；（3）如图3，点G 为直线CD 上一点，延长GM 交直线AB 于点Q ，点P 为MG 上一点，射线PF 、EH 相交于点H ，满足13PFG MFG ∠=∠，13BEH BEM ∠=∠，设∠EMF =α，求∠H 的度数(用含α的代数式表示)．23．如图1，//,AB CD 直线MN 分别交AB CD 、于点,E F BEF ∠、与EFD ∠的角平分线交于点P EP ，与CD 交于点G GH EG ⊥,交MN 于H ．（1）求证：// ;PF GH （2）如图2，连接PH K ,为GH 上一动点，PHK HPK PO ∠=∠,平分EPK ∠交MN 于,Q 则HPQ ∠的大小是否发生变化？若不变，求出其值；若改变，请说明理由．24．如图，已知C 为两条相互平行的直线AB ，ED 之间一点，ABC ∠和CDE ∠的角平分线相交于F ，180FDC ABC ∠+∠=︒．（1）求证：//AD BC ；（2）连结CF ，当//CF AB ，且32CFB DCF ∠=∠时，求BCD ∠的度数；（3）若DCF CFB ∠=∠时，将线段BC 沿直线AB 方向平移，记平移后的线段为PQ （B ，C 分别对应P ，Q ，当20PQD QDC ∠-∠=︒时，请直接写出DQP ∠的度数______．25．如图1．已知直线AB ED ．点C 为AB ，ED 内部的一个动点，连接CB ，CD ，作ABC ∠的平分线交直线ED 于点E ，作CDE ∠的平分线交直线BA 于点A ，BE 和DA 交于点F ．（1）若180FDC ABC ∠+∠=︒，猜想AD 和BC 的位置关系，并证明；（2）如图2，在（1）的基础上连接CF ，则在点C 的运动过程中，当满足CF AB ∥且32CFB DCF ∠=∠时，求BCD ∠的度数． 26．AB ∥CD ，点P 为直线AB ，CD 所确定的平面内的一点．（1）如图1，写出∠APC 、∠A 、∠C 之间的数量关系，并证明；（2）如图2，写出∠APC 、∠A 、∠C 之间的数量关系，并证明；（3）如图3，点E 在射线BA 上，过点E 作EF ∥PC ，作∠PEG ＝∠PEF ，点G 在直线CD 上，作∠BEG 的平分线EH 交PC 于点H ，若∠APC ＝30°，∠PAB ＝140°，求∠PEH 的度数．27．（问题提出）（1）如图①，已知 AB ∥CD ，求证 ：∠1+∠MEN+∠2=360°（推广应用）（2）如图②，已知 AB ∥ CD ，求∠1+∠2+∠3+∠4+∠5 +∠6的度数为___________． 如图③，已知 AB ∥CD ，求∠1+∠2+∠3+∠4+∠5 +∠6+…+∠n 的度数为_________．∥，且直线AB、CD与AD、BC分别交于A、D和28．如图`，已知：直线AD BCB、C两点，点P在直线AB上．∠、(1)如图1,当点P在A、B两点之间时(点P不与点A、B重合)，探究ADP、DPC ∠之间的关系，并说明理由.BCP∠、(2)若点P不在A、B两点之间，在备用图中画出图形，直接写出ADP、DPC∠之间的关系，不需说理．BCP【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】根据平行线之间的距离及三角形的面积即可得出答案．【详解】解：∵A、P是直线m上的任意两个点，B、C是直线n上的两个定点，且直线m∥n，根据平行线之间的距离相等可得：△ABC与△PBC是同底等高的三角形，故△ABC的面积等于△PBC的面积．故选D．【点睛】本题考查平行线之间的距离；三角形的面积．2．B解析：B【分析】根据平行线的性质可得26GFD ︒∠= ,再根据角平分线的性质可得52ECD ︒∠=,因此可计算的AEF ∠的度数.【详解】解：∵AB CD ∥，∴180FGB GFD ∠+∠=︒，∴18026GFD FGB ∠=︒-∠=︒，∵FG 平分EFD ∠，∴252EFD GFD ∠=∠=︒，∵AB CD ∥，∴52AEF EFD ∠=∠=︒．故选B ．【点睛】本题主要考查平行线的性质和角平分线的性质.平行线的性质 1.两直线平行，同位角相等；2.两直线平行，内错角相等；3.两直线平行，同旁内角互补. 角平分线的性质: 角平分线可以得到两个相等的角.3．C解析：C【解析】【分析】延长BG 交CD 于G,然后运用平行的性质和角平分线的定义，进行解答即可.【详解】解：如图延长BG 交CD 于G∵BF ∥ED∴∠F=∠EDF又∵DF 平分∠CDE，∴∠CDE=2∠F，∵BF∥ED∴∠CGF=∠EDF=2∠F，∵AB∥CD∴∠ABF=∠CGF=2∠F，∵BF平分∠ABE∴∠ABE=2∠ABF=4∠F，又∵∠F 与∠ABE 互补∴∠F +∠ABE =180°即5∠F=180°，解得∠F=36°故答案选C.【点睛】本题考查了平行的性质和角平分线的定义，做出辅助线是解答本题的关键.4．D解析：D【解析】试题分析：A、两条平行线被第三条直线所截，一对邻补角的平分线互相垂直，故本选项正确；B、两条平行线被第三条直线所截，同位角的平分线互相平行，故本选项正确；C、两条平行线被第三条直线所截，内错角的平分线互相平行，故本选项正确；D、两条平行线被第三条直线所截，同旁内角的平分线互相垂直，故本选项错误；故选：D．5．D解析：D【解析】试题分析：有两种情况：①点C在AB上，②点C在AB的延长线上，这两种情况根据线段的中点的性质，可得BM、BN的长，再利用线段的和、差即可得出答案．解：（1）点C在线段AB上，如：点M是线段AB的中点，点N是线段BC的中点，MB=12AB=5，BN=12CB=4，MN=BM-BN=5-4=1cm；（2）点C在线段AB的延长线上，如：点M是线段AB的中点，点N是线段BC的中点，MB=12AB=5，BN=12CB=4，MN =MB +BN =5+4=9cm ，故选D ．点睛：本题考查了两点间的距离. 解题的关键在于要利用分类讨论思想结合线段中点的性质、线段的和差进行解答．6．C解析：C【分析】由∠A+∠ABC=180°可得到AD ∥BC ，再根据平行线的性质判断即可得答案．【详解】∵180A ABC ∠+∠=︒，∴//AD BC （同旁内角互补，两直线平行），∴13∠=∠（两直线平行，内错角相等）．故选：C ．【点睛】本题考查的是平行线的判定与性质，同旁内角互补，两直线平行；两直线平行内错角相等；熟知平行线的判定定理是解答此题的关键．7．B解析：B【分析】根据a ∥c ，a 与b 相交，可知c 与b 相交，如果c 与b 不相交，则c 与b 平行，故b 与a 平行，与题目中的b 与a 相交矛盾，从而可以解答本题．【详解】解：假设b ∥c ，∵a ∥c ，∴a ∥b ，而已知a 与b 相交于点O ，故假设b ∥c 不成立，故b 与c 相交，故选：B ．【点睛】本题考查平行线的性质，解答本题的关键是明确题意，利用平行线的性质解答．8．B解析：B【分析】由水面和杯底互相平行，利用“两直线平行，同旁内角互补”可求出∠3的度数，由水中的两条折射光线平行，利用“两直线平行，同位角相等”可得出∠2的度数．【详解】如图，∵水面和杯底互相平行，∴∠1+∠3＝180°，∴∠3＝180°﹣∠1＝180°﹣122°＝58°．∵水中的两条折射光线平行，∴∠2＝∠3＝58°．故选：B．【点睛】本题考查了平行线的性质，牢记“两直线平行，同旁内角互补”和“两直线平行，同位角相等”是解题的关键．9．B解析：B【分析】分别利用对顶角的性质以及平行线的性质和推论进而判断得出即可．【详解】解：A、相等的角不一定是对顶角，故此选项错误；B、平行于同一条直线的两条直线互相平行，正确；C、两直线平行，同旁内角互补，故此选项错误；D、垂直于同一条直线的两条直线互相平行，故此选项错误．故选B．【点睛】此题主要考查了命题与定理，熟练掌握平行线的性质与判定是解题关键．10．C解析：C【分析】垂线段最短，指的是从直线外一点到这条直线所作的垂线段最短．它是相对于这点与直线上其他各点的连线而言．据此逐个分析即可.【详解】解：A．立定跳远时测量落点后端到起跳线的距离，运用“垂线段最短”这一性质；B．从一个村庄向一条河引一条最短的水渠，运用“垂线段最短”这一性质；C．把弯曲的公路改成直道可以缩短路程，运用“两点之间，线段最短”这一性质；D．直角三角形中任意一条直角边的长度都比斜边短，运用“垂线段最短”这一性质；故选：C．【点睛】本题主要考查了垂线段最短，实际问题中涉及线路最短问题时，其理论依据应从“两点之间，线段最短”和“垂线段最短”这两个中去选择．11．A解析：A【分析】由角平分线的性质可得∠GEB=12∠BEF=34°，由同位角相等，两直线平行可得CD∥AB，即可求解．【详解】∵EG平分∠BEF，∴∠GEB=12∠BEF=34°，∵∠1=∠BEF=68°，∴CD∥AB，∴∠EGF=∠GEB=34°，故选：A．【点睛】本题考查了平行线的判定和性质,角平分线的定义，灵活运用这些性质进行推理是本题的关键．12．C解析：C【分析】根据在同一平面内，根据两条直线的位置关系、垂直的性质、平行线平行公理及推论、点到直线的距离等逐一进行判断即可．【详解】∵在同一平面内，两条直线的位置关系只有两种：相交和平行，故①不正确；∵过直线外一点有且只有一条直线垂直于已知直线．故②不正确；如果两条直线都与第三条直线平行，那么这两条直线也互相平行．故③正确；从直线外一点到这条直线的垂线段的长度，叫做这点到这条直线的距离．故④不正确；过直线外一点，有且只有一条直线与已知直线平行．故⑤不正确；∴不正确的有①②④⑤四个．故选：C．【点睛】本题考查了直线的知识；解题的关键是熟练掌握直线相交、直线垂直、直线平行以及垂线的性质，从而完成求解．二、填空题13．90°【分析】根据AB∥CF，可得出∠B和∠B CF的关系，根据CF∥DE，可得出∠FED和∠D的关系，合并即可得出∠D―∠B的大小【详解】∵AB∥CF，∴∠B=∠BCF∵CF∥DE∴∠解析：90°【分析】根据AB∥CF，可得出∠B和∠BCF的关系，根据CF∥DE，可得出∠FED和∠D的关系，合并即可得出∠D―∠B的大小【详解】∵AB∥CF，∴∠B=∠BCF∵CF∥DE∴∠FCD+∠D=180°∴∠FCD+∠D－∠B=180°－∠BCF，化简得：∠D－∠B=180°－(∠BCF+∠FCD)∵∠BCD=90°，∴∠BCF+∠FCD=90°∴∠D―∠B=90°故答案为：90°【点睛】本题考查平行线的性质，解题关键是将∠BCD分为∠BCF和∠FCD，然后利用平行线的性质进行角度转换．14．30或110【分析】分两种情况讨论：两束光平行；两束光重合之后（在灯B射线到达BQ之前）平行，然后利用平行线的性质求解即可．【详解】解：设灯转动t秒，两灯的光束互相平行，即AC∥BD，①当解析：30或110【分析】分两种情况讨论：两束光平行；两束光重合之后（在灯B射线到达BQ之前）平行，然后利用平行线的性质求解即可．【详解】解：设灯转动t秒，两灯的光束互相平行，即AC∥BD，①当0＜t≤90时，如图1所示：∵PQ∥MN，则∠PBD＝∠BDA，∵AC∥BD，则∠CAM＝∠BDA，∴∠PBD＝∠CAM有题意可知：2t＝30＋t解得：t＝30，②当90＜t＜150时，如图2所示：∵PQ∥MN，则∠PBD＋∠BDA＝180°，∵AC∥BD，则∠CAN＝∠BDA，∴∠PBD＋∠CAN＝180°，∴30＋t＋（2t－180）＝180解得：t＝110综上所述，当t＝30秒或t＝110秒时，两灯的光束互相平行．故答案为：30或110【点睛】本题主要考查补角、角的运算、平行线的性质的应用，解题的关键是熟练掌握平行线的性质，注意分两种情况谈论．15．【分析】条直线相交只有一个交点，条直线相交，交点数是，条直线相交，交点数是，即，可写出，的解.【详解】解：求平面内不过同一点的条直线两两相交的交点个数，可由简入繁，当2条直线相交时，交点解析：1n -【分析】2条直线相交只有一个交点，3条直线相交，交点数是12+，n 条直线相交，交点数是123(1)n ++++-，即1123(1)(1)2n a n n n =++++-=-，可写出2a ， 1n n a a --的解.【详解】解：求平面内不过同一点的n 条直线两两相交的交点个数，可由简入繁，当2条直线相交时，交点数只有一个；当3条直线相交时，交点数为两条时的数量+第3条直线与前两条的交点2个，即交点数是12+；同理，可以推导当n 条直线相交时，交点数是123(1)n ++++-，即1123(1)(1)2n a n n n =++++-=-， 212(21)12a ∴=⨯⨯-=， 111(1)(1)(2)122n n a a n n n n n -∴-=----=-， 本题的答案为：1，1n -.【点睛】本题考查了平面内直线两两相交交点数的计算，涉及到一种很重要的数学方法数学归纳法的初步应用接触，此方法在推导证明中比较常用.16．【解析】【详解】作IF ∥AB,GK ∥AB,JH ∥AB因为AB ∥CD所以，AB ∥CD ∥ IF ∥GK ∥JH所以，∠IFG=∠FEC=10°所以，∠GFI=90°-∠IFG=80°所以，∠解析：【解析】【详解】作IF ∥AB,GK ∥AB,JH ∥AB因为AB ∥CD所以，AB ∥CD ∥ IF ∥GK ∥JH所以，∠IFG=∠FEC=10°所以，∠GFI=90°-∠IFG=80°所以，∠KGF=∠GFI=80°所以，∠HGK=150°-∠KGF=70°所以，∠JHG=∠HGK=70°同理，∠2=90°-∠JHG=20°所以，∠1=90°-∠2=70°故答案为70【点睛】本题考查了平行线的性质，正确作出辅助线是关键，注意掌握平行线的性质：两直线平行，内错角相等．17．10或28【解析】【分析】作出图形，分①两三角形在点O的同侧时，设CD与OB相交于点E，根据两直线平行，同位角相等可得∠CEO=∠B，根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠解析：10或28【解析】【分析】作出图形，分①两三角形在点O的同侧时，设CD与OB相交于点E，根据两直线平行，同位角相等可得∠CEO=∠B，根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠DOE，然后求出旋转角∠AOD，再根据每秒旋转10°列式计算即可得解；②两三角形在点O的异侧时，延长BO与CD相交于点E，根据两直线平行，内错角相等可得∠CEO=∠B，再根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠DOE，然后求出旋转角度数，再根据每秒旋转10°列式计算即可得解．【详解】解：①两三角形在点O的同侧时，如图1，设CD与OB相交于点E，∵AB∥CD，∴∠CEO=∠B=40°，∵∠C=60°，∠COD=90°，∴∠D=90°-60°=30°，∴∠DOE=∠CEO-∠D=40°-30°=10°，∴旋转角∠AOD=∠AOB+∠DOE=90°+10°=100°，∵每秒旋转10°，∴时间为100°÷10°=10秒；②两三角形在点O的异侧时，如图2，延长BO与CD相交于点E，∵AB∥CD，∴∠CEO=∠B=40°，∵∠C=60°，∠COD=90°，∴∠D=90°-60°=30°，∴∠DOE=∠CEO-∠D=40°-30°=10°，∴旋转角为270°+10°=280°，∵每秒旋转10°，∴时间为280°÷10°=28秒；综上所述，在第10或28秒时，边CD恰好与边AB平行．故答案为10或28．【点睛】本题考查了平行线的判定，平行线的性质，旋转变换的性质，难点在于分情况讨论，作出图形更形象直观．18．270°【分析】根据题目条件可知∠1+∠3=∠2+∠4=180°，再结合∠BAC是直角即可得出结果．【详解】解：如图所示，∵a∥b，∴∠1+∠3=180°，则∠3=180°-∠1，∵解析：270°【分析】根据题目条件可知∠1+∠3=∠2+∠4=180°，再结合∠BAC 是直角即可得出结果．【详解】解：如图所示，∵a ∥b ，∴∠1+∠3=180°，则∠3=180°-∠1，∵b ∥c∴∠2+∠4=180°，则∠4=180°-∠2，∵∠BAC 是直角，∴∠3+∠4=180°-∠1+180°-∠2，∴90°=360°-（∠1+∠2），∴∠1+∠2=270°．故答案为：270°【点睛】本题主要考查的是平行线的性质，掌握平行线的性质是解题的关键．19．62【详解】∵，，∴∠BOC=90°-28°=62°∵∠BOC=∠AOD∴∠AOD=62°.解析：62【详解】∵OE AB ⊥，28EOC ∠=，∴∠BOC=90°-28°=62°∵∠BOC=∠AOD∴∠AOD=62°.20．12【解析】分析：由图形可知，内部小三角形直角边是大三角形直角边平移得到的，故内部五个小直角三角形的周长为大直角三角形的周长．详解：由图形可以看出：内部小三角形直角边是大三角形直角边平移得到的 解析：12【解析】分析：由图形可知，内部小三角形直角边是大三角形直角边平移得到的，故内部五个小直角三角形的周长为大直角三角形的周长．详解：由图形可以看出：内部小三角形直角边是大三角形直角边平移得到的， 故内部五个小直角三角形的周长为AC+BC+AB=12．故答案为12．点睛：本题主要考查了平移的性质，需要注意的是：平移前后图形的大小、形状都不改变．三、解答题21．见解析【解析】分析：（1）求出∠ADE +∠FEB =180°，根据平行线的判定推出即可；（2）根据角平分线定义得出∠BAD =∠CAD ，推出HD ∥AC ，根据平行线的性质得出∠H =∠CGH ，∠CAD =∠CGH ，推出∠BAD =∠F 即可．详解：（1）AD ∥EF ．理由如下：∵∠BDA +∠CEG =180°，∠ADB +∠ADE =180°，∠FEB +∠CEF =180°∴∠ADE +∠FEB =180°，∴AD ∥EF ；（2）∠F =∠H ，理由是：∵AD 平分∠BAC ，∴∠BAD =∠CAD ．∵∠EDH =∠C ，∴HD ∥AC ，∴∠H =∠CGH ．∵AD ∥EF ，∴∠CAD =∠CGH ，∴∠BAD =∠F ，∴∠H =∠F ．点睛：本题考查了平行线的性质和判定的应用，主要考查学生的推理能力，题目是一道比较好的题目，难度适中．22．（1）M AEM CFM ∠=∠+∠；（2）115ENF ∠=︒；（3）1603H α∠=︒-． 【分析】（1）过点M 作//ML AB ，利用平行线的性质可得1AEM ∠=∠，2CFM ∠=∠，由12EMF ∠=∠+∠，经过等量代换可得结论；（2）过M 作//ME AB ，利用平行线的性质以及角平分线的定义计算即可．（3）如图②中设BEH x ∠=，PFG y ∠=，则3BEM x ∠=，3MFG y ∠=，设EH 交CD 于K ．证明H x y ∠=-，求出x y -即可解决问题．【详解】（1）如图1，过点M 作//ML AB ，//AB CD ，////ML AB CD ∴，1AEM ∴∠=∠，2CFM ∠=∠，12EMF ∠=∠+∠，M AEM CFM ∴∠=∠+∠；（2）过M 作//ME AB ，//AB CD ，//ME CD ∴，24180BEM DFM ∴∠+∠=∠+∠=︒，1802BEM ∴∠=︒-∠，1804DFM ∠=︒-∠， EN ，FN 分别平分MEB ∠和DFM ∠， 112BEM ∴∠=∠，132DFM ∠=∠， 111113(1802)(1804)180(24)1801301152222∴∠+∠=︒-∠+︒-∠=︒-∠+∠=︒-⨯︒=︒， 36013360115130115ENF EMF ∴∠=︒-∠-∠-∠=︒-︒-︒=︒；（3）如图②中设BEH x ∠=，PFG y ∠=，则3BEM x ∠=，3MFG y ∠=，设EH 交CD 于K ．//AB CD ，BEH DKH x ∴∠=∠=，PFG HFK y ∠=∠=，DKH H HFK ∠=∠+∠，H x y ∴∠=-，EMF MGF α∠=∠=，180BQG MGF ∠+∠=︒，180BQG α∴∠=︒-，QMF QMF EMF MGF MFG ∠=∠+∠=∠+∠，3QME MFG y ∴∠=∠=，BEM QME MQE ∠=∠+∠，33180x y α∴-=︒-，1603x y α∴-=︒-， 1603H α∴∠=︒-． 【点睛】本题考查平行线的性质和判定，三角形的外角的性质，三角形的内角和定理等知识，作出平行线，利用参数解决问题是解题的关键．23．（1）详见解析；（2）HPQ ∠的大小不发生变化，一直是45︒．【分析】（1）利用平行线的性质推知180BEF EFD ∠+∠=︒；然后根据角平分线的性质、三角形内角和定理证得90EPF ∠=︒，即EG PF ⊥，故结合已知条件GH EG ⊥，易证//PF GH ；（2）利用三角形外角定理、三角形内角和定理求得49039022∠=︒-∠=︒-∠；然后由邻补角的定义、角平分线的定义推知14522QPK EPK ∠=∠=︒+∠；最后根据图形中的角与角间的和差关系求得HPQ ∠的大小不变，是定值45︒．【详解】解：（1）证明：如图1，//AB CD ，180BEF EFD ∴∠+∠=︒．又BEF ∠与EFD ∠的角平分线交于点P ，1()902FEP EFP BEF EFD ∴∠+∠=∠+∠=︒， 90EPF ∴∠=︒，即EG PF ⊥．GH EG ⊥，//PF GH ∴；（2）HPQ ∠的大小不发生变化，理由如下：如图2，12∠=∠， 322∠=∠∴． 又GH EG ⊥，49039022∠=︒-∠=︒-∠∴．18049022EPK ∠=︒-∠=︒+∠∴．PQ ∵平分EPK ∠，14522QPK EPK ∴∠=∠=︒+∠． ∴245HPQ QPK ∠=∠-∠=︒，∴HPQ ∠的大小不发生变化，一直是45︒．【点睛】本题主要考查平行线的性质和判定，掌握平行线的性质和判定是解题的关键，即①两直线平行⇔同位角相等，②两直线平行⇔内错角相等，③两直线平行⇔同旁内角互补，④//a b ，////b c a c ⇒．24．（1）证明见解析；（2）∠BCD ＝108°；（3）70°【分析】（1）根据两直线平行，内错角相等得出∠EDF ＝∠DAB ，由角平线的定义得出∠EDF ＝∠FDC ，最后根据同旁内角互补，两直线平行进行求证；（2）设∠DCF ＝x ，则∠CFB ＝1.5x ，由两直线平行，内错角相等得出∠ABF ＝1.5x ，由角平分线的定义得出∠ABC ＝3x ，最后利用两直线平行，同旁内角互补得出关于x 的方程，求解即可；（3）画出图形，根据两直线平行，同旁内角互补得出∠CDF ＝∠CBF ，由角平分线的定义与已知条件可求出∠ABC 与∠FDC ，由平移的性质与平行公理的推论得出AD ∥PQ ，最后根据两直线平行，同旁内角互补列式求解．【详解】解：（1）证明：∵AB ∥DE ，∴∠EDF ＝∠DAB ，∵DF 平分∠EDC ，∴∠EDF ＝∠FDC ，∴∠FDC ＝∠DAB ，∵∠FDC+∠ABC＝180°，∴∠DAB+∠ABC＝180°，∴AD∥BC；（2）∵32CFB DCF∠=∠，设∠DCF＝x，则∠CFB＝1.5x，∵CF∥AB，∴∠ABF＝∠CFB＝1.5x，∵BE平分∠ABC，∴∠ABC＝2∠ABF＝3x，∵AD∥BC，∴∠FDC+∠BCD＝180°，∵∠FDC+∠ABC＝180°，∴∠BCD＝∠ABC＝3x，∴∠BCF＝2x，∵CF∥AB，∴∠ABC+∠BCF＝180°，∴3x+2x＝180°，∴x＝36°，∴∠BCD＝3×36°＝108°；（3）如图，∵∠DCF＝∠CFB，∴BF∥CD，∴∠CDF +∠BFD＝180°，∵AD∥BC，∴∠CBF +∠BFD＝180°，∴∠CDF＝∠CBF，∵AD，BE分别平分∠ABC，∠CDE，∴∠ABC＝2∠CBF，∠CDE＝2∠FDC，∴∠ABC＝∠CDE＝2∠FDC，∵∠FDC+∠ABC＝180°，∴∠ABC＝120°，∠FDC＝60°，∵线段BC沿直线AB方向平移得到线段PQ，∴BC∥PQ，∵AD∥BC，∴AD∥PQ，∵∠PQD﹣∠QDC＝20°，∴∠QDC＝∠PQD﹣20°，∴∠FDC+∠QDC +∠PQD＝60°+∠PQD﹣20°+∠PQD＝180°，∴∠PQD＝70°，即∠DQP＝70°．故答案为：70°．【点睛】本题考查平行线的判定与性质，平行公理的推论，角平分线的定义，平移的性质，熟练运用平行线的判定与性质是解题的关键．25．（1）AD BC ∥，见解析；（2）108°【分析】（1）//AD BC ，根据角平分线的性质可知EDF FDC ∠=∠，又因为//AB ED ，因此EDF DAB ∠=∠，推出FDC DAB ∠=∠，再结合已知条件即可得出结论；（2）设DCF x ，则32CFB x ∠=，根据平行线的的性质有32ABF CFB x ∠=∠=，再根据角平分线性质可得23ABC ABF x ∠=∠=，又因为//AD BC ，推出3BCD ABC x ∠=∠=，2BCF x ∠=，由//CF AB 得180ABC BCF ∠+∠=︒，从而可解得x 的值，即可得出答案．【详解】解：（1）//AD BC ．证明如下：∵//AB ED ，∴EDF DAB ∠=∠，∵DF 平分EDC ∠，∴EDF FDC ∠=∠，∴FDC DAB ∠=∠，∵180FDC ABC ∠+∠=︒，∴180DAB ABC ∠+∠=︒，∴//AD BC ．（2）∵32CFB DCF ∠=∠， ∴设DCF x ，则32CFB x ∠=， ∵//CF AB ， ∴32ABF CFB x ∠=∠=， ∵BE 平分ABC ∠，∴23ABC ABF x ∠=∠=，由（1）得//AD BC ，∴180FDC BCD ∠+∠=︒，∵180FDC ABC ∠+∠=︒，∴3BCD ABC x ∠=∠=，∴2BCF x ∠=，∵//CF AB ，∴180ABC BCF ∠+∠=︒，即32180x x +=︒，解得36x =︒，∴3108BCD x ∠==︒．【点睛】本题考查的主要知识点是平行线的判定及性质以及角平分线的性质，根据图形找准角与角之间的关系 是解此题的关键．26．（1）∠A +∠C +∠APC ＝360°，证明详见解析；（2）∠APC ＝∠A −∠C ，证明详见解析；（3）55°．【分析】（1）首先过点P 作PQ ∥AB ，结合题意得出AB ∥PQ ∥CD ，然后由“两直线平行，同旁内角互补”进一步分析即可证得∠A+∠C+∠APC ＝360°；（2）作PQ ∥AB ，结合题意得出AB ∥PQ ∥CD ，根据“两直线平行，内错角相等”进一步分析即可证得∠APC ＝∠A −∠C ；（3）由（2）知，∠APC ＝∠PAB −∠PCD ，先利用平行线性质得出∠BEF ＝∠PQB ＝110°，然后进一步得出∠PEG ＝12∠FEG ，∠GEH ＝12∠BEG ，最后根据∠PEH ＝∠PEG −∠GEH 即可得出答案．【详解】（1）∠A+∠C+∠APC ＝360°，证明如下：如图1所示，过点P 作PQ ∥AB ，∴∠A+∠APQ ＝180°，又∵AB ∥CD ，∴PQ ∥CD ，∴∠C+∠CPQ ＝180°，∴∠A+∠APQ+∠C+∠CPQ ＝360°，即∠A+∠C+∠APC ＝360°；（2）∠APC ＝∠A −∠C ，证明如下：如图2所示，过点P 作PQ ∥AB ，∴∠A ＝∠APQ ，∵AB ∥CD ，∴PQ ∥CD ，∴∠C ＝∠CPQ ，∵∠APC ＝∠APQ −∠CPQ ，∴∠APC ＝∠A −∠C ；（3）由（2）知，∠APC ＝∠PAB −∠PCD ，∵∠APC ＝30°，∠PAB ＝140°，∴∠PCD ＝110°，∵AB ∥CD ，∴∠PQB ＝∠PCD ＝110°，∵EF ∥PC ，∴∠BEF ＝∠PQB ＝110°，∵∠PEG ＝∠PEF ，∴∠PEG ＝12∠FEG ， ∵EH 平分∠BEG ， ∴∠GEH ＝12∠BEG ， ∴∠PEH ＝∠PEG −∠GEH ＝12∠FEG −12∠BEG ＝12∠BEF ＝55°．【点睛】本题主要考查了利用平行线性质与角平分线性质求角度的综合运用，熟练掌握相关概念是解题关键.27．（1）见解析，（2）900,180(1).n ︒︒-【分析】（1）过点E 作EF ∥CD ，根据平行线的判定得出EF ∥AB ，根据平行线的性质得出即可；（2）如图②过E 作EQ ∥CD ，过F 作FW ∥CD ，过G 作GR ∥CD ，过H 作HY ∥CD ，根据平行线的判定得出EQ ∥FW ∥GR ∥HY ∥AB ∥CD ，根据平行线的性质得出即可；如图③，利用（1）（2）②发现规律，直接得到答案．【详解】证明：（1）证明：过点E 作EF ∥CD ，∵AB ∥CD ， ∴EF ∥AB ，∴∠1+∠MEF=180°，同理∠2+∠NEF=180°，∴∠1+∠2+∠MEN =360°；（2）如图②过E 作EQ ∥CD ，过F 作FW ∥CD ，过G 作GR ∥CD ，过H 作HY ∥CD ，∵CD ∥AB ， ∴EQ ∥FW ∥GR ∥HY ∥AB ∥CD ，∴∠1+∠MEQ=180°，∠QEF+∠EFW=180°，∠WFG+∠FGR=180°，∠RGH+∠GHY=180°，∠YHN+∠6=180°，∴∠1+∠2+∠3+∠4+∠5+∠6=5×180°=900°，如图③，由∠1+∠2+∠MEN 3601802=︒=︒⨯，∠1+∠2+∠3+∠4+∠5+∠69001805=︒=︒⨯，可得：∠1+∠2+∠3+∠4+∠5+∠6+…+∠n 180(1)n =︒-，故答案为：900°，180(1)n ︒-；【点睛】本题考查了平行线的性质和判定，能灵活运用平行线的性质进行推理是解此题的关键．28．（1）∠ADP+∠BCP=∠DPC ，理由见解析；（2）∠ADP=∠DPC+∠BCP ，理由见解析【分析】（1）过P 作直线PQ ∥AD ，交CD 于点Q ，根据平行线的性质进行推理；（2）过P 作直线PQ ∥AD ，交CD 于点Q ，根据平行线的性质进行推理；【详解】解：（1）过P作直线PQ∥AD，交CD于点Q，∵AD∥BC，∴PQ∥AD∥BC，∴∠ADP=∠DPQ，∠BCP=∠CPQ，∴∠ADP+∠BCP=∠DPC；（2）∠ADP=∠DPC+∠BCP.过P作直线PQ∥AD，交CD于点Q，∵AD∥BC，∴PQ∥AD∥BC，∴∠ADP=∠DPQ=∠DPC+∠CPQ，∠BCP=∠CPQ，∴∠ADP=∠DPC+∠BCP.【点睛】本题考查了平行线的性质，利用平行线的性质得出角的和差关系是解题的关键.。
相交线与平行线单元练习(含答案)
第五章相交线与平行线一、选择题1.a、b、c是同一平面内的任意三条直线，其交点有()A． 1或2个B． 1或2或3个C． 0或1或3个D． 0或1或2或3个【答案】D【解析】由题意画出图形，如图所示：2.如图，在高为3米，水平距离为4米楼梯的表面铺地毯，地毯的长度至少需多少米()A． 4B． 5C． 6D． 72.【答案】D【解析】地毯长度至少需3＋4＝7米．故选D.3.下列语句中，是对顶角的语句为()A．有公共顶点并且相等的两个角B．两条直线相交，有公共顶点的两个角C．顶点相对的两个角D．两条直线相交，有公共顶点没有公共边的两个角【答案】D【解析】A.有公共顶点并且两边分别都在同一条直线上的两个角是对顶角，故本选项错误；B．两条直线相交所成的角是对顶角或邻补角，故本选项错误；C．顶点相对的两个角的两边不一定在同一条直线上，不一定是对顶角，故本选项错误；D．两条直线相交，有公共顶点没有公共边的两个角的两边在同一条直线上，是对顶角，故本选项正确；故选D.4.如图，能判定EC∥AB的条件是()A．∠B＝∠ACBB．∠B＝∠ACEC．∠A＝∠ACED．∠A＝∠ECD【答案】C【解析】根据∠B＝∠ACB，不能得到EC∥AB，故A错误；根据∠B＝∠ACE，不能得到EC∥AB，故B错误；根据∠A＝∠ACE，能判定EC∥AB，故C正确；根据∠A＝∠ECD不能得到EC∥AB，故D错误；故选C.5.有下列说法：①△ABC在平移的过程中，对应线段一定相等．②△ABC在平移的过程中，对应线段一定平行．③△ABC在平移的过程中，周长不变．④△ABC在平移的过程中，面积不变．其中正确的有()A．①②③B．①②④C．①③④D．②③④【答案】C【解析】①∵平移不改变图形的大小，∴△ABC在平移过程中，对应线段一定相等，故正确；②∵经过平移，对应线段所在的直线共线或平行，∴对应线段一定平行错误；③∵平移不改变图形的形状和大小，∴△ABC在平移过程中，周长不变，故正确；④∵平移不改变图形的大小和形状，∴△ABC在平移过程中，面积不变，正确；∴①、③、④都符合平移的基本性质，都正确．故选C.6.如图，已知AB∥CD∥EF，FC平分∠AFE，∠C＝25°，则∠A的度数是()A． 25°B． 35°C． 45°D． 50°【答案】D【解析】∵CD∥EF，∠C＝∠CFE＝25°，∵FC平分∠AFE，∴∠AFE＝2∠CFE＝50°，又∵AB∥EF，∴∠A＝∠AFE＝50°，故选D.7.如图，木工师傅在一块木板上画两条平行线，方法是：用角尺画木板边缘的两条垂线，这样画的理由有下列4种说法：其中正确的是()①同位角相等，两直线平行；②内错角相等，两直线平行；③同旁内角互补，两直线平行；④平面内垂直于同一直线的两条直线平行．A．①②③B．①②④C．①③④D．①③答案】C【解析】由图可知，用角尺画木板边缘的两条垂线，这样画的理由：①同位角相等，两直线平行；③同旁内角互补，两直线平行；④平面内垂直于同一直线的两条直线平行．故选C.8.两条直线相交所构成的四个角中：①有三个角都相等；②有一对对顶角互补；③有一个角是直角；④有一对邻补角相等．其中能判定这两条直线垂直的有()A． 1个B． 2个C． 3个D． 4个【答案】D【解析】①有三个角都相等，能判定互相垂直；②有一对对顶角互补，可计算出夹角是90°，可以判定垂直；③有一个角是直角，可以判定垂直；④有一对邻补角相等，可以判定垂直．故选D.二、填空题9.已知，如图，AD∥BE，∠1＝20°，∠DCE＝45°，则∠2的度数为______．【答案】25°【解析】∵AD∥BE，∠DCE＝45°，∴∠DCE＝∠ADC＝45°.∵∠1＝20°，∴∠2＝∠ADC－∠1＝45°－20°＝25°.故答案为25°10.如图，已知点A、B、C、F在同一条直线上，AD∥EF，∠D＝40°，∠F＝30°，那么∠ACD的度数是________．【答案】110°【解析】∵AD∥EF，∴∠A＝∠F＝30°，∵∠D＝40°，∴∠ACD＝180°－30°－40°＝110°.故答案为110°.11.如图∠1＝(3x－40)°，∠2＝(220－3x)°，那么AB与CD的位置关系是________．【答案】平行【解析】因为∠2＝(220－3x)°，所以∠3＝180°－∠2＝(3x－40)°，可得：∠1＝∠3，所以AB与CD平行，故答案为平行．12.把下列命题改写成“如果…那么…“的形式：(1)互补的两个角不可能都是锐角：________________________________________.(2)垂直于同一条直线的两条直线平行：________________________________________.(3)对顶角相等：____________________________________________________.【答案】如果两个角互补，那么这两个角不可能都是锐角如果两直线都垂直于第三条直线，那么这两直线平行如果两个角为对顶角，那么这两个角相等【解析】(1)如果两个角互补，那么这两个角不可能都是锐角；(2)如果两直线都垂直于第三条直线，那么这两直线平行；(3)如果两个角为对顶角，那么这两个角相等．故答案为：如果两个角互补，那么这两个角不可能都是锐角；如果两直线都垂直于第三条直线，那么这两直线平行；如果两个角为对顶角，那么这两个角相等．13.如图，与∠2互为同旁内角的是________；与∠3互为同位角的是________；∠6与∠9是______，它们是直线________与______被直线______所截得的；∠3与∠5是直线______与直线______被直线______所截得的；与∠1是同位角的有______，在标有数字的九个角中，大小一定相等的角有__________________．【答案】∠1和∠3∠4和∠5内错角AC DE BE AC BC BE∠7和∠8∠2＝∠6，∠5＝∠7【解析】由图可得，∠1，∠3与∠2互为同旁内角；∠4，∠5与∠3互为同位角；∠6与∠9是内错角，它们是直线AC与DE被直线BE所截得的；∠3与∠5是直线AC与直线BC被直线BE所截得的同位角；∠7，∠8与∠1是同位角；根据对顶角相等可得，在标有数字的九个角中，大小一定相等的角有∠2＝∠6，∠5＝∠7.故答案为：∠1，∠3；∠4，∠5；内错角，AC，DE，BE；AC，BC，BE；∠7，∠8；∠2＝∠6，∠5＝∠7.14.如图，请你添加一个条件________，使AB∥CD.【答案】∠1＝∠5【解析】添加∠1＝∠5.∵∠1＝∠5，∴AB∥CD.故答案为∠1＝∠5.15.如图，直线a∥b，∠2＝∠3，若∠1＝45°，则∠4＝______.【答案】45°【解析】延长DC交a于E，如图，∵∠2＝∠3，∴AB∥DE，∴∠4＝∠5，∵a∥b，∴∠1＝∠5＝45°，∴∠4＝∠5＝45°.故答案为45°.16.如图，∠1和∠3是直线______、______被直线______所截得到的______角；∠3和∠2是直线______、______被直线______所截得到的______角．【答案】a b c同旁内a c b内错【解析】如题图，∠1和∠3是直线a、b被直线c所截得到的同旁内角；∠3和∠2是直线a、c被直线b所截得到的内错角．故答案为：a，b，c，同旁内；a，c，b，内错角．17.如图，已知直线AB与CD交于点O，ON平分∠DOB，若∠BOC＝110°，则∠DON为________度．【答案】35【解析】∵∠BOC＝110°，∴∠BOD＝70°，∵ON为∠BOD平分线，∴∠DON＝35°.故答案为35.18.如图，一张三角形纸片ABC，∠B＝45°，现将纸片的一角向内折叠，折痕ED∥BC，则∠AEB的度数为________．【答案】90°【解析】∵ED∥BC，∴∠FED＝∠B＝45°，由折叠可得∠AEF＝2∠FED＝90°，∴∠AEB＝180°－90°＝90°，故答案为90°.三、解答题19.已知：如图，∠C＝∠1，∠2和∠D互余，BE⊥FD于点G.求证：AB∥CD.【答案】证明∵BE⊥FD，∴∠EGD＝90°，∴∠1＋∠D＝90°，又∠2和∠D互余，即∠2＋∠D＝90°，∴∠1＝∠2，又已知∠C＝∠1，∴∠C＝∠2，∴AB∥CD.【解析】首先由BE⊥FD，得∠1和∠D互余，再由已知，∠C＝∠1，∠2和∠D互余，所以得∠C ＝∠2，从而证得AB∥CD.20.(1)图①是将线段AB向右平移1个单位长度，图②是将线段AB折一下再向右平移1个单位长度，请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形．(2)若长方形的长为a，宽为b，请分别写出三个图形中除去阴影部分后剩余部分的面积．(3)如图④，在宽为10 m，长为40 m的长方形菜地上有一条弯曲的小路，小路宽为1 m，求这块菜地的面积．20.【答案】(1)如图：(2)三个图形中除去阴影部分后剩余部分的面积：①ab－b；②ab－b；③ab－b；(3)40×10－10×1＝390(m2)．答：这块菜地的面积是390m2.【解析】(1)根据两个折点，可得小路是三个平行四边形；(2)根据路的形状是矩形，可得路的面积，根据面积的和差，可得答案；(3)根据等底等高的面积相等，可得路的面积，根据面积的和差，可得答案．21.直线a∥b，b∥c，直线d与a相交于点A.(1)判断a与c的位置关系，并说明理由；(2)判断c与d的位置关系，并说明理由．【答案】(1)a与c的位置关系是平行，理由是：∵直线a∥b，b∥c，∴a∥c；(2)c与d的位置关系是相交，理由是：∵c∥a，直线d与a相交于点A，∴c与d的位置关系是相交．【解析】(1)根据平行公理得出即可；(2)根据c∥a和直线d与a相交推出即可．22.如图，直线AB、CD相交于点O，OE平分∠BOD.(1)若∠AOC＝68°，∠DOF＝90°，求∠EOF的度数；(2)若OF平分∠COE，∠BOF＝15°，若设∠AOE＝x°，求∠AOC的度数．【答案】(1)∵∠AOC＝68°，∴∠BOD＝68°，∵OE平分∠BOD，∴∠BOE＝∠DOE＝34°，∵∠DOF＝90°，∴∠EOF＝∠DOF－∠DOE＝90°－34°＝56°；(2)∵OE平分∠BOD，∴∠BOE＝∠DOE，∵∠BOE＋∠AOE＝180°，∠COE＋∠DOE＝180°，∴∠COE＝∠AOE＝x，∵OF平分∠COE，∴∠FOE＝x.∴∠BOE＝∠FOE－∠BOF＝x－15°.又∵∠BOE＋∠AOE＝180°，∴x－15°＋x＝180°，解得x＝130°，∴∠AOC＝2∠BOE＝2×＝100°.【解析】(1)根据角平分线的定义结合∠AOC＝68°即可求出∠BOE＝∠DOE＝34°，再由∠EOF与∠DOE互余即可求出∠EOF的度数；(2)由角平分线的定义可得出∠BOE＝∠DOE，根据∠BOE＋∠AOE＝180°、∠COE＋∠DOE＝180°即可找出∠AOE＝∠COE＝x，再根据角平分线的定义可知∠FOE＝x.23.如图，给出下列论断：①∠1＝∠E；②∠4＝∠B；③∠2＋∠B＝180°；④∠3＋∠E＝180°；⑤∠A＋∠E＝180°；⑥AB∥CD；⑦AB∥EF；⑧CD∥EF.请你从中选出一个论断作为题设，一个论断作为结论，组成一个真命题，至少写出三个．(格式：如果…，那么…)23.【答案】如果①∠1＝∠E；那么⑧CD∥EF；如果②∠4＝∠B；那么⑥AB∥CD；如果③∠2＋∠B＝180°；那么⑥AB∥CD.【解析】根据平行线的性质与判定，结合所给条件即可作出答案．24.如图，在Rt△ABC中，∠C＝90°，AC＝4 cm，BC＝3 cm，将△ABC沿AB方向向右平移得到△DEF，若AE＝8 cm，DB＝2 cm.(1)求△ABC向右平移的距离AD的长；(2)求四边形AEFC的周长．【答案】(1)∵△ABC沿AB方向向右平移得到△DEF，∴AD＝BE＝CF，BC＝EF＝3 cm，∵AE＝8 cm，DB＝2 cm，∴AD＝BE＝CF＝＝3 cm；(2)四边形AEFC的周长＝AE＋EF＋CF＋AC＝8＋3＋3＋4＝18 cm.【解析】(1)根据平移的性质可得AD＝BE＝CF，BC＝EF＝3 cm，然后根据AE、BD的长度求解即可；(2)根据平移的性质可得EF＝BC，CF＝AD，然后根据四边形的周长的定义列式计算即可得解．。
第五章《相交线与平行线》单元测试卷(含答案)
第五章 相交线与平行线单元测试班级： 姓名： 考生得分：一、选择题（每小题3分，共30分） 1.已知∠α=35°，则∠α的补角的度数是( ) A.55° B.65° C.145° D.165° 2.将图中所示的图案平移后得到的图案是( )A. B. C. D.3．如图，AB ∥CD ,FE ⊥DB ,垂足为E ，∠1＝50°，则∠2的度数 是（ ）A.60°B.50°C.40°D.30°4．如图，a ∥b ，∠1=∠2，∠3=40°，则∠4等于（ ） A.40° B.50° C.60° D.70° 5．如图所示，已知AB ∥CD ，∠C ＝70°，∠F ＝30°，则∠A 的度数为（ ） A ．30° B ．35° C ．40° D ．45°6．如图，AB ∥CD ，AC ⊥BC ，图中与∠CAB 互余的角有（ ） A ．1个 B ．2个 C ．3个 D ．4个7．如图，点E 在CD 的延长线上，下列条件中不能判定AB ∥CD 的是（ ） A ．∠1=∠2 B ．∠3=∠4 C ．∠5=∠B D ．∠B +∠BDC =180°8．如图，DH ∥EG ∥BC ，DC ∥EF ，那么与∠DCB 相等的角的个数为（ ） A ．2个 B ．3个 C ．4个 D ．5个 9. 下列条件中能得到平行线的是（ ）①邻补角的角平分线；②平行线内错角的角平分线；③平行线同旁内角的角平分线． A ．①② B ．②③ C ．② D ．③10. 两平行直线被第三条直线所截，同位角的平分线（ ） A ．互相重合 B ．互相平行 C ．互相垂直 D ．相交二、填空题（每小题3分，满分24分） 11.图中是对顶角量角器，用它测量角的原理是 .12．如图，l ∥m ，∠1＝120°，∠A ＝55°，则∠ACB 的大小是 . 13．如图，计划把河水引到水池A 中，先作AB ⊥CD ，垂足为B ，然后沿AB 开渠， 能使所开的渠道最短，这样设计的依据是 ．14．如图，直线AB ，CD ，EF 相交于点O ，且AB ⊥CD ，∠1与∠2的关系是 ．15．如图,在△ABC 中，∠A =90°，点D 在AC 边上，DE ∥BC ，若∠1=155°，则∠B 的度数为 ．16．如图，AB ∥CD ，直线EF 分别交AB 、CD 于E 、F ，EG 平分∠BEF ，若∠1=72°，则∠2= ．1718第2题图第6题图 第7题图 第8题图第11题图第13题图 第14题图 第15题图 第16题图 第17题图第18题图第3题图三、解答题（共46分）19．（7分）读句画图：如图，直线CD与直线AB相交于C，根据下列语句画图：（1）过点P作PQ∥CD，交AB于点Q；（2）过点P作PR⊥CD，垂足为R；（3）若∠DCB=120°，猜想∠PQC是多少度？并说明理由．20．（7分）如图，方格中有一条美丽可爱的小金鱼．（1）若方格的边长为1，则小鱼的面积为；（2）画出小鱼向左平移3格后的图形．（不要求写作图步骤和过程）21．（8分）已知：如图，∠BAP+∠APD =180°，∠1 =∠2.求证：∠E =∠F．22．（8分）已知：如图，∠1 =∠2，∠3 =∠4，∠5 =∠6.求证：ED∥FB．23．（8分）如图，CD平分∠ACB，DE∥BC，∠AED=80°，求∠EDC的度数．24．（9分）如图，已知AB∥CD，∠B=65°，CM平分∠BCE，∠MCN=90°，求∠DCN的度数．25．（10分）如图，直线EF，CD相交于点0，OA⊥OB，且OC平分∠AOF，（1）若∠AOE=40°，求∠BOD的度数；（2）若∠AOE=α，求∠BOD的度数；（用含α的代数式表示）（3）从（1）（2）的结果中能看出∠AOE和∠BOD有何关系？第19题图第五章相交线与平行线检测题参考答案1.C 解析：∵∠α=35°，∴∠α的补角的度数为180°35°=145°,故选C.2. C 解析：根据平移的性质可知C正确.3. C 解析：因为FE⊥DB，所以∠FED=90°，由∠1=50°可得∠FDE=90°-50°=40°.因为AB∥CD，由两直线平行，同位角相等，可得∠2=∠FDE=40°.4. D 解析：因为a∥b，所以∠2=∠4.又∠2=∠1，所以∠1=∠4.因为∠3=40°，所以∠1=∠4==70°.5. C 解析：由AB∥CD可得，∠FEB＝∠C＝70°，∵∠F＝30°，又∵∠FEB＝∠F+∠A，∴∠A＝∠FEB∠F＝70°30°＝40°.故选项C是正确的.6. C 解析：∵AB∥CD，∴∠ABC=∠BCD.设∠ABC的对顶角为∠1，则∠ABC=∠1.又∵AC⊥BC，∴∠ACB=90°，∴∠CAB+∠ABC=∠CAB+∠BCD=∠CAB+∠1=90°，因此与∠CAB互余的角为∠ABC，∠BCD，∠1．故选C．7. A 解析：选项B中，∵∠3=∠4，∴AB∥CD（内错角相等，两直线平行），故正确；选项C中，∵∠5=∠B，∴AB∥CD（内错角相等，两直线平行），故正确；选项D中，∵∠B+∠BDC=180°，∴AB∥CD（同旁内角互补，两直线平行），故正确；而选项A中，∠1与∠2是直线AC、BD被直线AD所截形成的内错角，∵∠1=∠2，∴AC∥BD，故A错误．选A．8. D 解析：如题图所示，∵DC∥EF，∴∠DCB=∠EFB.∵DH∥EG∥BC，∴∠GEF=∠EFB，∠DCB=∠HDC，∠DCB=∠CMG=∠DME，故与∠DCB相等的角共有5个．故选D．9. C 解析：结合已知条件，利用平行线的判定定理依次推理判断．10. B 解析：∵两条平行直线被第三条直线所截，同位角相等，∴它们角的平分线形成的同位角相等，∴同位角相等的平分线平行．故选B．11.对顶角相等解析：根据图形可知量角器测量角的原理是：对顶角相等.12. 65°解析：∵l∥m，∴∠ABC=180°-∠1=180°-120°=60°.在△ABC中，∠ACB=180°-∠ABC-∠A=180°-60°-55°=65°.13. 垂线段定理：直线外一点与直线上所有点的连线中，垂线段最短解析：根据垂线段定理，直线外一点与直线上所有点的连线中，垂线段最短，∴沿AB开渠，能使所开的渠道最短．14. ∠1+∠2=90°解析：∵直线AB、EF相交于O点，∴∠1=∠DOF.又∵AB⊥CD，∴∠2+∠DOF=90°，∴∠1+∠2=90°．15. 65°解析：∵∠1=155°，∴∠EDC=180°-155°=25°.∵DE∥BC，∴∠C=∠EDC=25°.∵在△ABC中，∠A=90°，∠C=25°，∴∠B=180°-90°-25°=65°．故答案为65°．16. 54°解析：∵AB∥CD，∴∠BEF=180°∠1=180°72°=108°，∠2=∠BEG.又∵EG平分∠BEF，∴∠BEG=∠BEF=×108°=54°，故∠2=∠BEG=54°．17. 78°解析：延长BC与直线a相交于点D，∵a∥b，∴∠ADC=∠DBE=50°. ∴∠ACB=∠ADC +28°=50°+28°=78°.故应填78°.18. 120 解析：∵AB∥CD，∴∠1=∠3，而∠1=60°，∴∠3=60°.又∵∠2+∠3=180°，∴∠2=180°-60°=120°．故答案为120．19．解：（1）（2）如图所示.第19题答图（3）∠PQC=60°.理由：∵PQ∥CD,∴∠DCB+∠PQC=180°.∵∠DCB=120°,∴∠PQC=180°120°=60°．20. 解：（1）小鱼的面积为7×621×5×621×2×521×4×221××121×21×11=16.（2）将每个关键点向左平移3个单位，连接即可．第20题答图21.证明：∵ ∠BAP +∠APD = 180°，∴ AB ∥CD .∴ ∠BAP =∠APC . 又∵ ∠1 =∠2,∴ ∠BAP −∠1 =∠APC −∠2.即∠EAP =∠APF .∴ AE ∥FP .∴ ∠E =∠F .22．证明：∵ ∠3 =∠4,∴ AC ∥BD .∴ ∠6+∠2+∠3 = 180°. ∵ ∠6 =∠5，∠2 =∠1,∴ ∠5+∠1+∠3 = 180°. ∴ ED ∥FB .23. 解：∵ DE ∥BC ，∠AED =80°，∴ ∠EDC =∠BCD ，∠ACB=∠AED=80°.∵ CD 平分∠ACB ，∴ ∠BCD = 21∠ACB =40°，∴ ∠EDC =∠BCD =40°．24. 解：∵ AB ∥CD ，∴ ∠B +∠BCE =180°（两直线平行，同旁内角互补）.∵ ∠B =65°，∴ ∠BCE =115°.∵ CM 平分∠BCE ，∴ ∠ECM =21∠BCE =57.5°. ∵ ∠ECM +∠MCN +∠NCD =180°，∠MCN =90°，∴ ∠NCD =180°-∠ECM -∠MCN =180°-57.5°-90°=32.5°．25、解：（1）∵∠AOE +∠AOF =180°（互为补角），∠AOE =40°，∴∠AOF =140°； 又∵OC 平分∠AOF ，∴∠FOC =∠AOF =70°，∴∠EOD =∠FOC =70°（对顶角相等）；而∠BOE =∠AOB ﹣∠AOE =50°，∴∠BOD =∠EOD ﹣∠BOE =20°； (2)(3)略。
八年级上册第五章相交线与平行线单元测试卷测试卷 (word版,含解析)
八年级上册第五章相交线与平行线单元测试卷测试卷 （word 版，含解析）一、选择题1．给出下列4个命题：①同旁内角互补；②相等的角是对顶角；③等角的补角相等；④两直线平行，同位角相等．其中，假命题的个数为（ ）A ．1B ．2C ．3D ．42．如图，AB ∥CD ∥EF ，AF ∥CG ，则图中与∠A （不包括∠A ）相等的角有（ ）A ．5个B ．4个C ．3个D ．2个3．如图，直线12//,,140l l αβ∠=∠∠=︒，则2∠等于（ ）A ．140︒B ．130︒C ．120︒D ．110︒4．如图，要得到AB ∥CD ，只需要添加一个条件，这个条件不可以．．．是（ ）A ．∠1＝∠3B ．∠B ＋∠BCD ＝180°C ．∠2＝∠4D ．∠D ＋∠BAD ＝180°5．如图，已知直线AB 、CD 被直线AC 所截，AB ∥CD ，E 是平面内任意一点（点E 不在直线AB 、CD 、AC 上），设∠BAE=α，∠DCE=β．下列各式：①α+β，②α﹣β，③β﹣α，④360°﹣α﹣β，∠AEC 的度数可能是（ ）A ．①②③B ．①②④C ．①③④D ．①②③④6．如图，直线AB 、CD 相交于点E ，DF ∥AB ．若∠AEC=100°，则∠D 等于（ ）A ．70°B ．80°C ．90°D ．100°7．如图，////OP QR ST 下列各式中正确的是（ ）A ．123180∠+∠+∠=B ．12390∠+∠-∠=C ．12390∠-∠+∠=D ．231180∠+∠-∠= 8．如图，在△ABC 中，AB=AC ，CD∥AB，点E 在BC 的延长线上.若∠A=30°，则∠DCE 的大小为（ ）A ．30°B ．52.5°C ．75°D ．85°9．如图，BD 是△ABC 的角平分线，DE ∥BC ，DE 交AB 于E ，若AB ＝BC ，则下列结论中错误的是（ ）A ．BD ⊥ACB ．∠A ＝∠EDAC ．2AD ＝BC D ．BE ＝ED10．已知：点A ，B ，C 在同一条直线上，点M 、N 分别是AB 、BC 的中点，如果AB =10cm ，AC =8cm ，那么线段MN 的长度为（ ）A ．6cmB ．9cmC ．3cm 或6cmD ．1cm 或9cm11．下列命题中，属于假命题的是（ ）A ．如果三角形三个内角的度数比是1:2:3，那么这个三角形是直角三角形B ．内错角不一定相等C ．平行于同一直线的两条直线平行D ．若数a 使得a a >-，则a 一定小于012．如图，△ABC 经平移得到△EFB ，则下列说法正确的有 （ ）①线段AC 的对应线段是线段EB ；②点C 的对应点是点B ；③AC ∥EB ；④平移的距离等于线段BF 的长度．A ．1B ．2C ．3D ．4二、填空题13．如图，有两个正方形夹在AB 与CD 中，且AB//CD,若∠FEC=10°，两个正方形临边夹角为150°，则∠1的度数为________度(正方形的每个内角为90°)14．如图，BC AE ⊥，垂足为C ，过C 作CD AB ．若48ECD ∠=︒，则B ∠=__________．15．探究题：(1)如图1，两条水平的直线被一条竖直的直线所截，同位角有____对，内错角有_____对，同旁内角有_____对；(2)如图2，三条水平的直线被一条竖直的直线所截，同位角有____对，内错角有___对，同旁内角有___对；(3)根据以上探究的结果，n(n 为大于1的整数)条水平直线被一条竖直直线所截，同位角有______对，内错角有_______对，同旁内角有______对．(用含n 的式子表示)16．如图，已知EF ∥GH ，A 、D 为GH 上的两点，M 、B 为EF 上的两点，延长AM 于点C ，AB 平分∠DAC ，直线DB 平分∠FBC ，若∠ACB=100°，则∠DBA 的度数为________．17．如图，AB ∥CD ，点P 为CD 上一点，∠EBA 、∠EPC 的角平分线于点F ，已知∠F ＝40°，则∠E ＝_____度．18．如图，把直角梯形ABCD 沿AD 方向平移到梯形EFGH ，28HG cm =，5MG cm =，4MC cm =，则阴影部分的面积是___19．如图,点A 、B 为定点,直线l ∥AB,P 是直线l 上一动点，对于下列各值:①线段AB 的长；②△PAB 的周长；③△PAB 的面积；④∠APB 的度数，其中不会随点P 的移动而变化的是(填写所有正确结论的序号)______________.20．如图，直线AB ，CD 相交于点O ，OA 平分∠EOC ，∠EOD=120°，则∠BOD=__________°．三、解答题21．问题情境：如图1，AB ∥CD ，∠PAB=130°，∠PCD=120°．求∠APC 度数．小明的思路是：如图2，过P 作PE ∥AB ，通过平行线性质，可得∠APC=50°+60°=110°． 问题迁移：(1)如图3，AD ∥BC ，点P 在射线OM 上运动，当点P 在A 、B 两点之间运动时，∠ADP=∠α，∠BCP=∠β．∠CPD 、∠α、∠β之间有何数量关系？请说明理由；(2)在(1)的条件下，如果点P 在A 、B 两点外侧运动时(点P 与点A 、B 、O 三点不重合)，请你直接写出∠CPD 、∠α、∠β间的数量关系．22．问题情境：如图1，AB CD ，130PAB ∠=，120PCD ∠=．求 APC ∠ 度数． 小明的思路是：如图2，过 P 作 PE AB ，通过平行线性质，可得5060110APC ∠=+=．问题迁移：（1）如图3，AD BC ，点 P 在射线 OM 上运动，当点 P 在 A 、 B 两点之间运动时，ADP α∠=∠，BCP β∠=∠．CPD ∠ 、 α∠ 、 β∠ 之间有何数量关系?请说明理由；（2）在（1）的条件下，如果点 P 在 A 、 B 两点外侧运动时（点 P 与点 A 、 B 、 O 三点不重合），请你直接写出 CPD ∠ 、 α∠ 、 β∠ 间的数量关系．23．如图1所示，AB ∥CD ，E 为直线CD 下方一点，BF 平分∠ABE ．（1）求证：∠ABE +∠C ﹣∠E ＝180°．（2）如图2，EG 平分∠BEC ，过点B 作BH ∥GE ，求∠FBH 与∠C 之间的数量关系． （3）如图3，CN 平分∠ECD ，若BF 的反向延长线和CN 的反向延长线交于点M ，且∠E +∠M ＝130°，请直接写出∠E 的度数．24．如图，已知C 为两条相互平行的直线AB ，ED 之间一点，ABC ∠和CDE ∠的角平分线相交于F ，180FDC ABC ∠+∠=︒．（1）求证：//AD BC ；（2）连结CF ，当//CF AB ，且32CFB DCF ∠=∠时，求BCD ∠的度数；（3）若DCF CFB ∠=∠时，将线段BC 沿直线AB 方向平移，记平移后的线段为PQ （B ，C 分别对应P ，Q ，当20PQD QDC ∠-∠=︒时，请直接写出DQP ∠的度数______．25．如图，AB ∥CD ．（1）如图1，∠A 、∠E 、∠C 的数量关系为 ．（2）如图2，若∠A ＝50°，∠F ＝115°，求∠C ﹣∠E 的度数；（3）如图3，∠E ＝90°，AG ，FG 分别平分∠BAE ，∠CFE ，若GD ∥FC ，试探究∠AGF 与∠GDC 的数量关系，并说明理由．26．如图1，直线AB 与直线OC 交于点O ，()090BOC αα∠=︒<<．小明将一个含30的直角三角板PQD 如图1所示放置，使顶点P 落在直线AB 上，过点Q 作直线MN AB 交直线OC 于点H (点H 在Q 左侧)．（1）若PD OC ∥，45NQD ∠=︒，则α=__________︒．（2）若PQH ∠的角平分线交直线AB 于点E ，如图2．①当QE OC ∥，60α=︒时，求证：OC PD ． ②小明将三角板保持PD OC ∥并向左平移，运动过程中，PEQ ∠=__________．(用α表示)． 27． [问题解决]：如图1，已知AB ∥CD ，E 是直线AB ，CD 内部一点，连接BE ，DE ，若∠ABE=40°，∠CDE=60°，求∠BED 的度数．嘉琪想到了如图2所示的方法，但是没有解答完，下面是嘉淇未完成的解答过程： 解：过点E 作EF ∥AB ，∴∠ABE=∠BEF=40°∵AB ∥CD ，∴EF ∥CD ，…请你补充完成嘉淇的解答过程：[问题迁移]：请你参考嘉琪的解题思路，完成下面的问题：如图3，AB ∥CD ，射线OM 与直线AB ，CD 分别交于点A ，C ，射线ON 与直线AB ，CD 分别交于点B ，D ，点P 在射线ON 上运动，设∠BAP=α，∠DCP=β．（1）当点P在B，D两点之间运动时(P不与B，D重合)，求α，β和∠APC之间满足的数量关系．（2）当点P在B，D两点外侧运动时(P不与点O重合)，直接写出α，β和∠APC之间满足的数量关系．28．阅读材料（1），并利用（1）的结论解决问题（2）和问题（3）．（1）如图1，AB∥CD，E为形内一点，连结BE、DE得到∠BED，求证：∠E＝∠B+∠D悦悦是这样做的：过点E作EF∥AB．则有∠BEF＝∠B．∵AB∥CD，∴EF∥CD．∴∠FED＝∠D．∴∠BEF+∠FED＝∠B+∠D．即∠BED＝∠B+∠D．（2）如图2，画出∠BEF和∠EFD的平分线，两线交于点G，猜想∠G的度数，并证明你的猜想．（3）如图3，EG1和EG2为∠BEF内满足∠1＝∠2的两条线，分别与∠EFD的平分线交于点G1和G2，求证：∠FG1E+∠G2＝180°．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【分析】根据平行线的判定方法对①进行判断；据对顶角的定义对②进行判断；根据平行线的性质对④进行判断；根据补角的定义对③进行判断．【详解】两直线平行，同旁内角互补，所以①错误;相等的角不一定是对顶角，所以②错误；等角的补角相等，所以③正确；两条平行直线被第三条直线所截，同位角相等，所以④正确；；故选B.【点睛】本题主要考查了平行线的性质及判定，对顶角的性质等，熟练掌握各性质定理是解答此题的关键．2．B解析：B【分析】由平行线的性质，可知与∠A相等的角有∠ADC、∠AFE、∠EGC、∠GCD．【详解】∵AB∥CD，∴∠A=∠ADC；∵AB∥EF，∴∠A=∠AFE；∵AF∥CG，∴∠EGC=∠AFE=∠A；∵CD∥EF，∴∠EGC=∠DCG=∠A；所以与∠A相等的角有∠ADC、∠AFE、∠EGC、∠GCD四个，故选B．3．A解析：A【分析】作出如下图所示的辅助线，然后再利用平行线的性质即可求解．【详解】解：如图所示，作直线m∥n∥l1∥l2，此时有∠3=∠1=40°，∠6=180°-∠2，∠4=∠5，又∠α=∠3+∠4，∠β=∠5+∠6=∠5+(180°-∠2)，且∠α=∠β，∴∠3+∠4=∠5+(180°-∠2)，由于∠4=∠5，∴∠3=180°-∠2，代入数据：40°=180°-∠2，∴∠2=140°，故选：A．【点睛】本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．熟记性质并作辅助线是解题的关键．4．A解析：A【分析】根据B、D中条件结合“同旁内角互补，两直线平行”可以得出AB∥CD，根据C中条件结合“内错角相等，两直线平行”可得出AB∥CD，而根据A中条件结合“内错角相等，两直线平行”可得出AD∥BC．由此即可得出结论．【详解】解：A．∵∠1=∠3，∴AD∥BC（内错角相等，两直线平行）；B．∵∠B+∠BCD=180°，∴AB∥CD（同旁内角互补，两直线平行）；C．∠2=∠4，∴AB∥CD（内错角相等，两直线平行）；D．∠D+∠BAD=180°，∴AB∥CD（同旁内角互补，两直线平行）．故选A．【点睛】本题考查了平行线的判定，解题的关键是根据四个选项给定的条件结合平行线的性质找出平行的直线．本题属于基础题，难度不大，解决该题型题目时，根据相等或互补的角找出平行的两直线是关键．5．D解析：D【分析】根据E点有4中情况，分四种情况讨论分别画出图形，根据平行线的性质与三角形外角定理求解.【详解】E点有4中情况，分四种情况讨论如下：由AB∥CD，可得∠AOC=∠DCE1=β∵∠AOC=∠BAE1+∠AE1C，∴∠AE1C=β-α过点E2作AB的平行线，由AB∥CD，可得∠1=∠BAE2=α,∠2=∠DCE2=β∴∠AE2C=α+β由AB∥CD，可得∠BOE3=∠DCE3=β∵∠BAE3=∠BOE3+∠AE3C，∴∠AE3C=α-β由AB∥CD，可得∠BAE4+∠AE4C+∠DCE4=360°，∴∠AE4C=360°-α-β∴∠AEC的度数可能是①α+β，②α﹣β，③β-α，④360°﹣α﹣β，故选D.【点睛】此题主要考查平行线的性质与外角定理，解题的关键是根据题意分情况讨论. 6．B解析：B【解析】因为AB∥DF，所以∠D+∠DEB=180°，因为∠DEB与∠AEC是对顶角，所以∠DEB=100°，所以∠D=180°﹣∠DEB=80°．故选B．7．D解析：D【解析】试题分析：延长TS，∵OP∥QR∥ST，∴∠2=∠4，∵∠3与∠ESR互补，∴∠ESR=180°﹣∠3，∵∠4是△FSR的外角，∴∠ESR+∠1=∠4，即180°﹣∠3+∠1=∠2，∴∠2+∠3﹣∠1=180°．故选D．考点：平行线的性质．8．C【解析】试题分析：根据等腰三角形的性质：等边对等角，可得∠B=∠ACB，然后根据三角形的内角和可求得∠B=75°，然后根据平行线的性质可得∠B=∠DCE=75°.故选：C.点睛：此题主要考查了等腰三角形的性质，解题关键是利用等腰三角形的性质求得两底角的值，然后根据平行线的性质可求解问题.9．C解析：C【解析】试题分析：BD是△ABC的角平分线， AB＝BC，则BD是AC边上的高及中线，所以∠ABD＝∠DBC ,BD⊥AC，2AD=AC, ∠A＝∠BCA；因为DE∥BC，所以∠EDA＝∠BCA,∠EDB＝∠DBC，所以∠A＝∠EDA, ∠ABD＝∠EDB，所以BE＝ED。
相交线与平行线单元测试卷(含答案)
第五章《相交线与平行线》测试卷姓名 ＿＿__＿_＿ 成绩 _______一、选择题(每小题4分,共 40 分)1、如图所示,∠１与∠2就是对顶角得就是( )A B C D 121212122、如图,在正方体中与AB 垂直得边有( )条.A 。
１B 。
2 Ｃ、3 D 。
43、如图AB ∥CD,∠A ＢE ＝120°,∠E ＣＤ＝25°,则∠E ＝( )A.７5° Ｂ、80° C 。
85° D.95°4、如图所示,直线a 、ｂ被直线ｃ所截,现给出下列四种条件:①∠2＝∠6 ②∠２=∠８ ③∠1＋∠4＝18０° ④∠３=∠８,其中能判断就是a ∥b 得条件得序号就是( )A 、①② Ｂ、①③ C 、①④ Ｄ、③④5、某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯得角度可能就是( )A 、第一次左拐３0°,第二次右拐30°B 、第一次右拐50°,第二次左拐1３0°C 、第一次右拐50°,第二次右拐130°D 、第一次向左拐5０°,第二次向左拐13０°6、下列哪个图形就是由左图平移得到得( )7、如图,在一个有４×４个小正方形组成得正方形网格中,阴影部分面积与正方形ABCD 面积得比就是( )A 、3:4B 、5:8C 、9:１6 Ｄ、１:２8、下列现象属于平移得就是( )① 打气筒活塞得轮复运动,② 电梯得上下运动,③ 钟摆得摆动,④ 转动得门,⑤ 汽车在一条笔直得马路上行走A 、③ Ｂ、②③ Ｃ、①②④ D 、①②⑤９、下列说法正确得就是( )A 、有且只有一条直线与已知直线平行B 、垂直于同一条直线得两条直线互相垂直C 、从直线外一点到这条直线得垂线段,叫做这点到这条直线得距离。
D、在平面内过一点有且只有一条直线与已知直线垂直。
《相交线与平行线》单元测试卷含答案
第4章相交线与平行线单元测试卷一、选择题(每题２分,共2０分)1、如图,直线a,b被直线c所截,∠1与∠2得位置关系就是()Ａ、同位角ﻩB、内错角ﻩＣ、同旁内角D。
对顶角2、如图,ＡＢ∥ＣD,ＡD平分∠BAC,若∠BAD=6５°,那么∠ACＤ得度数为() Ａ.40°B、35°ﻩＣ。
5０°ﻩD。
4５°12 33.如图,AＢ∥EC,下列说法不正确得就是()A。
∠B=∠ECＤ B.∠Ａ＝∠ＥＣDC、∠Ｂ+∠ECB=1８0°ﻩ D. ∠A+∠B+∠ＡCB=180°4。
如图,在俄罗斯方块游戏中,出现一小方块拼图向下运动,通过平移运动拼成一个完整得图案,最终所有图案消失,则对小方块进行得操作为( )Ａ.向右平移1格再向下ﻩＢ、向右平移3格再向下C。
向右平移２格再向下ﻩD。
以上答案均可5。
如图所示,3块相同得三角尺拼成一个图形,图中有很多对平行线,其中不能由下面得根据得出两直线平行得就是()A、同位角相等,两直线平行ﻩB。
内错角相等,两直线平行C.平行于同一直线得两直线平行ﻩD、垂直于同一直线得两直线平行6。
如图,直线AB∥ＣD,AＥ平分∠CAB,AＥ与CD相交于点E,∠ＡCD=４0°,则∠ＢＡE得度数就是( )Ａ、４0°B。
７0°C。
80°D、1４0°7。
同一平面内得四条互不重合得直线满足a⊥ｂ,ｂ⊥c,c⊥d,则下列各选项中关系能成立得就是( )A。
ａ∥d B。
ａ⊥ｃﻩC、a⊥d D.b⊥d8。
如图,AB∥ＥF,CＤ⊥EF,∠BAC=５0°,则∠ACD=()A.12０°B。
130°ﻩＣ.14０° D.１50°９。
如图,AD就是∠EＡC得平分线,ＡＤ∥BC,∠B=30°,则∠C为( )Ａ。
30°B。
6０°ﻩ C.８0°ﻩＤ、1２0°１0、如图,把一块含有45°角得直角三角尺得两个顶点放在直尺得对边上。
(完整版)《相交线与平行线》单元测试卷含答案
第4章相交线与平行线单元测试卷一、选择题(每题2分,共20分)1。
如图，直线a,b被直线c所截，∠1与∠2的位置关系是（)A.同位角B.内错角C.同旁内角D。
对顶角2.如图,AB∥CD，AD平分∠BAC，若∠BAD=65°，那么∠ACD的度数为( )A.40°B.35° C。
50°D。
45°31 2 3。
如图,AB∥EC，下列说法不正确的是（)A. ∠B=∠ECDB. ∠A=∠ECDC。
∠B+∠ECB=180° D. ∠A+∠B+∠ACB=180°4.如图，在俄罗斯方块游戏中,出现一小方块拼图向下运动，通过平移运动拼成一个完整的图案,最终所有图案消失，则对小方块进行的操作为( ）A。
向右平移1格再向下 B。
向右平移3格再向下C.向右平移2格再向下D.以上答案均可5。
如图所示,3块相同的三角尺拼成一个图形，图中有很多对平行线,其中不能由下面的根据得出两直线平行的是（)A.同位角相等，两直线平行B.内错角相等，两直线平行C.平行于同一直线的两直线平行D。
垂直于同一直线的两直线平行6。
如图，直线AB∥CD，AE平分∠CAB，AE与CD相交于点E，∠ACD=40°,则∠BAE的度数是( ）A.40°B.70°C.80° D。
140°7。
同一平面内的四条互不重合的直线满足a⊥b,b⊥c，c⊥d，则下列各选项中关系能成立的是( )A。
a∥d B。
a⊥c C。
a⊥d D。
b⊥d8。
如图,AB∥EF，CD⊥EF，∠BAC=50°，则∠ACD=( )A.120 ° B。
130° C.140° D。
150°9。
如图，AD是∠EAC的平分线,AD∥BC,∠B=30°，则∠C为( )A。
30° B.60° C。
80° D。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
FDO 1M2N一、填空题相交线与平行线 单元测试1. a 、b 、c 是直线，且 a ∥b ，b ⊥c ，则 a 与 c 的位置关系是．2. 如图 5-1，MN ⊥AB ，垂足为 M 点，MN 交 CD 于 N ，过 M 点作 MG ⊥CD ，垂足为 G ，EF 过点 N 点，且 EF ∥AB ，交 MG 于 H 点，其中线段 GM 的长度是 到 的距离， 线段 MN的长度是到 的距离，又是 的距离，点 N 到直线 MG 的距离是．AC E图 5-1FDC图 5-23. 如图 5-2，AD ∥BC ，EF ∥BC ，BD 平分∠ABC ，图中与∠ADO 相等的角有个，分别是．4. 因为 AB ∥CD ，EF ∥AB ，根据，所以 ．5. 命题“等角的补角相等”的题设，结论是．6. 如图 5-3，给出下列论断：①AD ∥BC ：②AB ∥CD ；③∠A =∠C ．以上其中两个作为题设，另一个作为结论，用“如果……，那么……”形式，写出一个你认为正确的命题是 ．aABb C ECcl图 5-3图 5-4图 5-52 17. 如图 5-4，直线 AB 、CD 、EF 相交于同一点 O ，而且∠B O C= ∠AOC ，∠DOF = ∠AOD ，那么∠FOC =33_度．8．如图 5-5，直线 a 、b 被 c 所截，a ⊥l 于 M ，b ⊥l 于 N ，∠1=66°，则∠2=．9. 如图 5-6，∠ACB =90°，CD ⊥AB ，则图中与∠A 互余的角有个，它们分别是．∠A =∠，根据是 ．10. 如图 5-7，一棵小树生长时与地面所成的角为 80°，它的根深入泥土，如果根和小树在同一条直线上，那么∠2 等于°．11． 如 图 5-8， 量 得 ∠ 1=80° ， ∠ 2=80° ， 由 此 可 以 判 定 ∥， 它 的 根 据是．BMG NH图1图3CA180°EADBG 1 3 C F 42 H 2B 图 5-6图 5-7D图 5-8量得∠3=100°，∠4=100°，由此可以判定∥ ，它的根据是 ．12. 猜谜语：（打本章两个几何名称）剩下十分钱： ；斗牛．13. a 、b 、c 是直线，且 a ∥b ， b ∥c ， 则 ac ; a 、b 、c 是直线，且 a ⊥b ， b ⊥c ， 则 ac ;14.如图 5-9，直线 AD 、BC 交于 O 点， ∠AOB + ∠COD = 110︒ ，则∠COD 的度数为．CEADAOBCFDD图 5-9图 5-10 图 5-1115． 如图 5-10，直线 AB 与 CD 交于 O 点， ∠3 - ∠1 = 80︒，则∠2 =．16. 如图 5-11，直线 AB 、EF 相交于 O 点， CD ⊥AB 于 O 点， ∠EOD = 128︒19' ，则∠BOF , ∠AOF 的度数分别为 ．二、选择题17. 若 a ⊥b ，c ⊥d 则 a 与 c 的关系是（ ）A ．平行B ．垂直C ．相交D ．以上都不对18．如图 5-12，∠ADE 和∠CED 是（ ）A ．同位角B ．内错角C ．同旁内角D ． 互 为 补 角19．如图 5-13， l 1 / /l 2 ，∠1 = 105 ，∠2 = 140 ，则∠= （） A ． 55B ． 60C ． 65D ． 70B OCA42O31BCBD21O Cl 1El 2BC图 5-12图 5-13图 5-1420. 如图 5-14，能与∠构成同旁内角的角有（ ）A ． 5 个B ．4 个C ． 3 个D ． 2 个21．如图 5-15，已知 AB / /CD ， ∠等于（ ）A ． 75B ． 80C ． 85D ． 95A B 120°α25° CDBMCA N P D图 5-15图 5-1622． 如图 5-16， AB / /CD ，MP / / AB ，MN 平分 ∠AMD ，∠A = 40 ，∠D = 30 ， 则 ∠NMP 等于（ ）A ． 10B ． 15C ． 5D ． 7.523．如果两个角的两边分别平行，而其中一个角比另一个角的 4 倍少30 ，那么这两个角是（）A ． 42 、138B ． 都是10C ． 42 、138 或42 、10D ． 以上都不对24．如图 5-17，a ∥b ，∠1 与∠2 互余，∠3=1150，则∠4 等于（）A ．115０B ． 155０C ． 135０D ．125０cda 21 43bAADB图 5-17图 5-18图 5-1925．如图 5-18，∠1=15０ ， ∠AOC =90０，点 B 、O 、D 在同一直线上，则∠2 的度数为（）A ．75０B ．15０C ．105０D ． 165０A D1 α2α26.如图5-19，能表示点到直线（或线段）距离的线段有（）A．2 条B．3 条C．4 条D．5 条27．下列语句错误的是（）A．连接两点的线段的长度叫做两点间的距离B．两条直线平行，同旁内角互补C．若两个角有公共顶点且有一条公共边，和等于平角，则这两个角为邻补角D．平移变换中，各组对应点连成两线段平行且相等28.如图5-20，如果AB∥CD，那么图中相等的内错角是（）A．∠1 与∠5，∠2 与∠6；B．∠3 与∠7，∠4 与∠8；C．∠5 与∠1，∠4 与∠8；D．∠2 与∠6，∠7 与∠3图5-2029.下列语句：①三条直线只有两个交点，则其中两条直线互相平行；②如果两条平行线被第三条截，同旁内角相等，那么这两条平行线都与第三条直线垂直；③过一点有且只有一条直线与已知直线平行，其中（）A．①、②是正确的命题B．②、③是正确命题C．①、③是正确命题D．以上结论皆错30.下列与垂直相交的洗法：①平面内，垂直于同一条直线的两条直线互相平行；②一条直线如果它与两条平行线中的一条垂直，那么它与另一条也垂直;③平行内，一条直线不可能与两条相交直线都垂直，其中说法错误个数有（）A．3 个B．2 个C．1 个D．0 个三、解答题31.如图5-21，过P 点，画出OA、OB 的垂线．2.图5-2132.如图5-22，过P 点，画出AB、CD 的垂线．3. BA P A BC D图5-22图5-2333.如图5-23，是一条河，C 河边AB 外一点：（1）过点C 要修一条与河平行的绿化带，请作出正确的示意图．（2）现欲用水管从河边AB，将水引到C 处，请在图上测量并计算出水管至少要多少?（本图比例尺为1：2000）FC E AF D2AB134. 如图 5-24，AB ⊥BD ，CD ⊥MN ，垂足分别是 B 、D 点，∠FDC =∠EBA ．（1） 判断 CD 与 AB 的位置关系; （2） BE 与 DE 平行吗?为什么?35．如图 5-25，∠1+∠2=180°，∠DAE =∠BCF ，DA 平分∠BDF ．（1） AE 与 FC 会平行吗?说明理由． （2） AD 与 BC 的位置关系如何?为什么? （3） BC 平分∠DBE 吗?为什么．MBN图 5-24C图 5-2536．如图 5-26，已知：CE =DF ，AC =BD ， ∠ 1= ∠ 2．求证： ∠ A = ∠ B ．EFA37. 如图 5-27，已知：AB //CD ，AB =CD ，求证：AC 与 BD 互相平分． 1 2CD B图 5-26ADOB C图 5-2638. 如图 5-27，已知：E 、F 分别是 AB 和 CD 上的点，DE 、AF 分别交 BC 于 G 、H ， ∠ A = ∠ D ， ∠ 1= ∠ 2，求证： ∠ B = ∠ C ．ED E F图5-2739.如图5-28，已知：在∆ABC 中，∠C = 90︒，AC=BC，BD 平分∠CBA，DE⊥AB 于E，求证：AD+DE=BE．CA B图5-2840.如图5-29，已知：AB//CD，求证：∠B+ ∠D+ ∠BED= 360︒（至少用三种方法）图5-29⎩ ⎩参考答案一、填空题 1. 互相垂直 2. 点 M ，直线 CD 点 M ，直线 EF 平行线 AB 、EF 间 线段 GN 的长度 3．4 个 ∠EOB 、 ∠DOF 、 ∠ABD 、 ∠CBD 4．两条直线都与第三条直线平行，这两条直线也互相平行 CD ∥EF 5．两个角是相等两角的补角 这两个角相等6．如果一个四边形的两组对边平行，那么它的对角相等;或若一个四边形的一组对边平行，一组对角相等， 那么它的另一组对边也互相平行7．156 8．114°9．两;∠ACD 和∠B;∠BCD;同角的余角相等 10．10°11. AB ∥CD;同位角相等，两直线平行;EF ∥GH;内错角相等，两直线平行 12. 余角;对顶角 13．∥;∥14． 55︒ （点拨： ∠AOB = ∠COD ∴ ∠AOB = ∠COD = 55︒ ）⎧∠3 + ∠1 = 180︒ 15． 50︒ （点拨： ⎨∠3 - ∠1 = 80︒ ⎧∠1 = 50︒，∴ ⎨∠3 = 130︒ ，又 ∠1 = ∠2 ∴∠2 = 50︒ ）16． 38︒19' ；141︒41'（点拨： ∠AOD = 90︒∴ ∠AOE = ∠EOD - ∠AOD = 128︒19' - 90︒ = 38︒19'，∴∠BOF = ∠AOE = 38︒19' ，又 ∠BOF + ∠AOF = 180︒ ， ∴∠AOF = 180︒ - 38︒19' = 141︒41' ）二、选择题 17．C 18．B 19．C 20．A 21．C 22．C 23．D 24．B 25．C 26．D 27．C 28．D 29．A 30．D三、解答题 31．如图 5-12. A答图5-132．如图5-233．略．34．（1）CD∥AB因为CD⊥MN，AB⊥MN，所以CDN=∠ABM=90°所以CD∥AB（2）平行因为∠CDN=∠ABN=90°，∠FDC=EBA所以∠FDN=∠EBN所以FD∥EB35．（1）平行因为∠1+∠2=180°，∠2+∠CDB=180°（邻补角定义）所以∠1=∠CDB所以AE∥FC（同位角相等两直线平行）（2）平行，因为AE∥CF，所以∠C=∠CBE（两直线平行，内错角相等）又∠A=∠C 所以∠A=∠CBE所以AF∥BC（两直线平行，内错角相等）（3）平分因为DA 平分∠BDF，所以∠FDA=∠ADB因为AE∥CF，AD∥BC所以∠FDA=∠A=∠CBE，∠ADB=∠CBD所以∠EBC=∠CBD36.证明：O P B1. APO B3. BA PC答图5-2⎨∠1 = ∠2（已知）∴ ∠ECB = ∠FDA （等角的补角相等） AC = BD （已知） ∴ AC + CD = BD + CD 即AD = BC在∆ADF 和∆BCE 中，⎧DF = CE （已知） ⎪∠FDA = ∠ECB （已证） ⎪⎩AD = BC （已证） ∴ ∆ADF ≅ ∆BCE （SAS ）∴ ∠A = ∠B （全等三角形的对应角相等） 37. 证明： AB / /CD （已知）∴ ∠BAO = ∠DCO ，∠ABO = ∠CDO （两直线平行，内错角相等） 在∆ABO 和∆CDO 中⎧∠BAO = ∠DCO （已证） ⎪⎨ AB = CD （已知）⎪⎩∠ABO = ∠CDO （已证） ∴ ∆ABO ≅ ∆CDO （ASA ）∴ AO = CO ，BO = DO （全等三角形对应边相等）即 AC 与 BD 互相平分． 38． 证明： ∠1 = ∠2（已知）∠1 = ∠AHB （对顶角相等） ∴ ∠2 = ∠AHB （等量代换）∴ AF / / ED （同位角相等，两直线平行） ∴ ∠D = ∠AFC （两直线平行，同位角相等） 又 ∠A = ∠D （已知） ∴ ∠A = ∠AFC （等量代换）∴ AB / /CD （内错角相等，两直线平行） ∴ ∠B = ∠C （两直线平行，内错角相等） 39. 证明： BD 平分∠CBA （已知）∴ ∠EBD = ∠CBD （角平分线的定义） DE ⊥AB （已知）∴ ∠DEB = 90︒ （垂直的定义） ∠C = 90︒ （已知） ∴ ∠DEB = ∠C （等量代换） 在∆DEB 和∆DCB 中⎨ ⎧∠DEB = ∠C （已证） ⎪∠EBD = ∠CBD （已证） ⎪⎩DB = DB （公共边） ∴ ∆DEB ≅ ∆DCB （AAS ）∴ DE = DC ，BE = BC （全等三角形的对应边相等） AD + DC = AC = BC （已知） ∴ AD + DE = BE （等量代换） 40. 证明：（1）连结 BD ，如图 5-3AB / /CD （已知）∴ ∠ABD + ∠CDB = 180︒ （两直线平行，同旁内角互补） ∠1 + ∠2 + ∠BED = 180︒ （三角形内角和为180︒ ） ∴ ∠ABD + ∠1 + ∠CDB + ∠2 + ∠BED = 360︒ 即∠ABE + ∠CDE + ∠BED = 360︒（2） 延长 DE 交 AB 延长线于 F ，如图 5-4AB / /CD （已知）∴ ∠F + ∠D = 180︒ （两直线平行，同旁内角互补） ∠ABE = ∠FEB + ∠F ，∠BED = ∠FBE + ∠F （三角形一个外角等于和它不相邻的两个内角的和） ∴ ∠ABE + ∠CDE + ∠BED= ∠FEB + ∠F + ∠CDE + ∠FBE + ∠F= 180︒+180︒= 360︒ （3） 过点 E 作 EF//AB ，如图 5-5AB / /CD∴AB / / EF / /CD（如果两条直线都和第三条直线平行，那么这两条直线也互相平行）∴∠B +∠BEF = 180︒∠D +∠DEF = 180︒（两直线平行，同旁内角互补）∴∠B +∠BEF +∠D +∠DEF = 180︒+180︒= 360︒∴∠B +∠D +∠BED = 360︒- 11 -。