中考数学真题一次函数图像与性质

合集下载

中考数学专题复习之一次函数的图像及性质测试卷

中考数学专题复习之一次函数的图像及性质测试卷一．选择题1．若y ＝x +2﹣3b 是正比例函数，则b 的值是（）A ．0B ．﹣C ．D ．﹣2．函数y ＝（k ﹣1）x ，y 随x 增大而减小，则k 的范围是（）A ．k ＜0B ．k ＞1C ．k ≤1D ．k ＜13．已知点M （﹣2，m ）和点N （3，n ）是直线y ＝2x +1上的两个点，那么有（）A ．m ＝nB ．m ＞nC ．m ＜nD ．不能确定mn 的大小关系4．一次函数y ＝8x 的图象经过的象限是（）A ．一、三B ．二、四C ．一、三、四D ．二、三、四5．若点(1,2)M 关于y 轴的对称点在正比例函数(32)y k x =+的图象上，则k 的值为( )A ．13B ．13-C ．43-D ．06． 1(A x ，1)y 和2(B x ，2)y 是一次函数2(1)2y k x =++图象上的两点，且12x x <，则1y 与2y 的大小关系是( )A ．12y y =B ．12y y <C ．12y y >D ．不确定7．下列图形中，表示一次函数y ＝mx +n 与正比例函数y ＝﹣mnx （m ，n 为常数，且mn ≠0）的图象不正确的是（）A ．B ．C ．D ．8．下列关于一次函数y ＝﹣2x +2的图象的说法中，错误的是（）A．函数图象经过第一、二、四象限B．函数图象与x轴的交点坐标为（2，0）C．当x＞0时，y＜2D．y的值随着x值的增大而减小9．如图，一次函数y＝k1x+b1的图象l1与一次函数y＝k2x+b2的图象l2相交于点P，则不等式组的解集为（）A．x＞﹣2B．﹣2＜x＜1.5C．x＞﹣1D．x＞210．如图，直线y＝﹣x+5交坐标轴于点A、B，与坐标原点构成的△AOB向x轴正方向平移4个单位长度得△A′O′B′，边O′B′与直线AB交于点E，则图中阴影部分面积为（）A．B．15C．10D．14二．填空题11．在平面直角坐标系中，已知一次函数y＝﹣2x+1的图象经过P1（x1，y1）、P2（x2，y2）两点，若x1＞x2，则y1y2（填“＞”或“＜”）．12．当m＝时，函数y＝（2m﹣1）x2m﹣2是正比例函数．13．一次函数y＝mx+|m﹣1|的图象经过（0，3），且y随x增大而减小，则m＝．14．定义：点P与图形W上各点连接的所有线段中，若线段P A最短，则线段P A的长度称为点P到图形W的距离，记为d（P，图形W）．例如，在图1中，原点O（0，0）与直线l：x＝3的各点连接的所有线段中，线段OA最短，长度为3，则d（O，直线x＝3）＝3．特别地，点P在图形W上，则点P到图形的距离为0，即d（P，图形W）＝0．①在平面直角坐标系中，原点O（0，0）与直线l：y＝x的距离d（O，y＝x）＝；②如图2，点P的坐标为（0，m）且d（p，y＝2x﹣2）＝，则m＝．15．如图，直线l1⊥x轴于点（1，0），直线l2⊥x轴于点（2，0），直线l3⊥x轴于点（3，0），…直线l n⊥x轴于点（n，0）．函数y＝x的图象与直线l1，l2，l3，……l n分别交于点A1，A2，A3，……A n；函数y＝3x的图象与直线l1，l2，l3，……l n分别交于点B1，B2，B3，……B n，如果△OA1B1的面积记的作S1，四边形A1A2B2B1的面积记作S2，四边形A2A3B3B2的面积记作S3，…四边形A n﹣1A n B n B n﹣1的面积记作S n，那么S2020＝．16．如图，在平面直角坐标系中，点C的坐标是（0，4），作点C关于直线AB：y＝x+1的对称点D，则点D的坐标是．三．解答题17．已知函数y＝（m+2）x|m|﹣1+n+4．（1）当m，n为何值时，此函数是正比例函数？（2）当m，n为何值时，此函数是一次函数？18．如图，已知直线y＝x+5与x轴交于点A，直线y＝kx+b与x轴交于点B（1，0），且与直线y＝x+5交于第二象限点C（m，n）．（1）若△ABC的面积为12，求点C的坐标及关于x的不等式的x+5＞kx+b解集；（2）求k的取值范围．19．如图，一次函数y＝﹣x+5的图象l1分别与x轴，y轴交于A、B两点，正比例函数的图象l2与l1交于点C（m，）．（1）求m的值及l2的解析式；（2）求得S△AOC﹣S△BOC的值为；（3）一次函数y＝kx+1的图象为l3且l1，l2，l3可以围成三角形，直接写出k的取值范围．20．如图，在平面直角坐标系中，直线y＝2x+3与y轴交于点A，直线y＝kx﹣1与y轴交于点B，与直线y＝2x+3交于点C（﹣1，n）．（1）求n、k的值；（2）求△ABC的面积．21．如图，已知一次函数y＝﹣x+6的图象与x轴、y轴分别交于点A和点B，与直线y ＝x相交于点C．过点B作x轴的平行线l，点P是直线l上的一个动点．①点C坐标是；②若点E是直线y＝x上的一个动点，且处于直线AB下方，当△APE是以∠EAP为直角的等腰直角三角形时，点E的坐标是．22．如图，正比例函数y＝x与一次函数y＝ax+7的图象相交于点P（4，n），过点A（t，0）作x轴的垂线l，且0＜t＜4，交一次函数的图象于点B，交正比例函数的图象于点C，连接OB．（1）求a值；（2）设△OBP的面积为s，求s与t之间的函数关系式；（3）当t＝2时，在正比例函数y＝x与一次函数y＝ax+7的图象上分别有一动点M、N，是否存在点M、N，使△CMN是等腰直角三角形，且∠CNM＝90°，若存在，请直接写出点M、N的坐标；若不存在，请说明理由．23．如图1，在平面直角坐标系中，直线y＝﹣x+2与坐标轴交于A，B两点，以AB为斜边在第一象限内作等腰直角三角形ABC．点C为直角顶点，连接OC．（1）A点坐标为，B点坐标为．（2）请你过点C作CE⊥y轴于E点，试探究并证明OB+OA与CE的数量关系．（3）如图2，将线段AB绕点B沿顺时针方向旋转至BD，且OD⊥AD，延长DO交直线y＝x+5于点P，求点P的坐标．。

2020年中考数学二轮专题——一次函数的图象与性质(含详细解答)

2020年中考数学二轮专题——一次函数的图象与性质一、基础过关1. (2019益阳)下列函数中，y 总随x 的增大而减小的是( ) A. y ＝4x B. y ＝－4x C. y ＝x －4 D. y ＝x 22. (2019扬州)若点P 在一次函数y ＝－x ＋4的图象上，则点P 一定不在．．( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限3. 一次函数y ＝－2x ＋4图象与y 轴的交点坐标是( ) A ．(0，4) B ．(4，0) C ．(2，0) D ．(0，2)4. (2019荆门)如果函数y ＝kx ＋b (k ，b 是常数)的图象不经过第二象限，那么k ，b 应满足的条件是( ) A. k ≥0且b ≤0 B. k >0且b ≤0 C. k ≥0且b <0 D. k >0且b <05. (2019陕西)在平面直角坐标系中，将函数y ＝3x 的图象向上平移6个单位长度，则平移后的图象与x 轴交点的坐标为( )A. (2，0)B. (－2，0)C. (6，0)D. (－6，0)6. (2019辽阳)若ab <0且a >b ，则函数y ＝ax ＋b 的图象可能是( )7. (2019绍兴)若三点(1，4)，(2，7)，(a ，10)在同一直线上，则a 的值等于( ) A. －1B. 0C. 3D. 48. 如图，一次函数y ＝ax ＋b 和y ＝－13x 的图象交于点P ，则根据图象可得，关于x ，y 的二元一次方程组⎩⎪⎨⎪⎧－ax ＋y ＝b x ＋3y ＝0的解是( ) A. ⎩⎪⎨⎪⎧x ＝3y ＝－1B. ⎩⎪⎨⎪⎧x ＝－3y ＝－1C. ⎩⎪⎨⎪⎧x ＝－3y ＝1D. ⎩⎪⎨⎪⎧x ＝－1y ＝3第8题图9. 如图，一次函数y 1＝mx －3与y 2＝－x －1图象的交点A 的纵坐标为2，则m 的值是( ) A. 53B. －53C. 1D. －1第9题图10. 已知点(－2，y 1)，(1，0)，(3，y 2)都在一次函数y ＝kx －2的图象上，则y 1，y 2，0的大小关系为( ) A. 0<y 1<y 2 B. y 1<0<y 2 C. y 1<y 2<0D. y 2<0<y 111. (2019临沂)下列关于一次函数y ＝kx ＋b (k ＜0，b ＞0)的说法，错误的是( ) A. 图象经过第一、二、四象限 B. y 随x 的增大而减小 C. 图象与y 轴交于点(0，b ) D. 当x ＞－bk时，y ＞012. 一次函数y ＝(k －2)x ＋2k ＋4的图象如图所示，则点(3－k ，6＋k )所在的象限是( ) A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限第12题图13. (2019邵阳)一次函数y 1＝k 1x ＋b 1的图象l 1如图所示，将直线l 1向下平移若干个单位后得直线l 2，l 2的函数表达式为y 2＝k 2x ＋b 2.下列说法中错误的是( )A. k 1＝k 2B. b 1<b 2C. b 1>b 2D. 当x ＝5时，y 1>y 2第13题图14. (2019潍坊)当直线y＝(2－2k)x＋k－3经过第二、三、四象限时，则k的取值范围是________．15. 已知一次函数y＝kx＋2k＋3(k≠0)，不论k为何值，该函数的图象都经过点A，则点A的坐标为______．16. (2019烟台)如图，直线y＝x＋2与直线y＝ax＋c相交于点P(m，3)，则关于x的不等式x＋2≤ax＋c 的解为________．第16题图17. (2019 乐山)如图，已知过点B(1，0)的直线l1与直线l2：y＝2x＋4相交于点P(－1，a)．(1)求直线l1的解析式；(2)求四边形P AOC的面积．第17题图二、能力提升1. (2019锦江区一诊)若关于x的一元二次方程mx2－2x－1＝0无实数根，则一次函数y＝mx＋m的图象不经过()A. 第一象限B. 第二象限C. 第三象限D. 第四象限2. (2019杭州)已知一次函数y1＝ax＋b和y2＝bx＋a(a≠b)，函数y1和y2的图象可能是()3. (2019桂林)如图，四边形ABCD 的顶点坐标分别为A (－4，0)，B (－2，－1)，C (3，0)，D (0，3)，当过点B 的直线l 将四边形ABCD 分成面积相等的两部分时，直线l 所表示的函数表达式为( )第3题图A. y ＝1110x ＋65B. y ＝23x ＋13C. y ＝x ＋1D. y ＝54x ＋324. 如图，将直线y ＝－x 沿y 轴向下平移后的直线恰好经过点A (2，－4)，且与y 轴交于点B ，在x 轴上存在一点P ，使得P A ＋PB 的值最小，则点P 的坐标为__________．第4题图三、满分冲关1. (2019攀枝花)在平面直角坐标系xOy 中，已知A (0，2)，动点P 在y ＝33x 的图象上运动(不与O 重合)，连接AP .过点P 作PQ ⊥AP ，交x 轴于点Q ，连接AQ .(1)求线段AP 长度的取值范围；(2)试问：点P 运动过程中，∠QAP 是否为定值？如果是，求出该值；如果不是，请说明理由； (3)当△OPQ 为等腰三角形时，求点Q 的坐标．第1题图2. (2019遂宁模拟)为落实“绿水青山就是金山银山”的发展理念，某县政府部门决定，招标一工程队负责完成一座水库的土方施工任务．该工程队有A，B两种型号的挖掘机，已知1台A型和2台B型挖掘机同时施工1小时共挖土70立方米，2台A型和3台B型挖掘机同时施工1小时共挖土120立方米．每台A型挖掘机一个小时的施工费用是350元，每台B型挖掘机一个小时的施工费用是200元．(1)分别求每台A型，B型挖掘机一小时各挖土多少立方米？(2)若A型和B型挖掘机共10台同时施工4小时，至少完成1080立方米的挖土量，且总费用不超过13400元．问施工时有哪几种调配方案？且指出哪种调配方案的施工费用最低，最低费用为多少元？3. (2019雅安模拟)某学校为改善办学条件，计划采购A、B两种型号的空调，已知采购3台A型空调和2台B型空调，需花费39000元；4台A型空调比5台B型空调的费用多6000元．(1)求采购A型空调和B型空调每台各花费多少元；(2)若学校计划采购A、B两种型号空调共30台，且A型空调的台数不少于B型空调的一半，两种型号空调的采购总费用不超过217000元，该校共有哪几种采购方案？(3)在(2)的条件下，采用哪一种采购方案可使总费用最低，最低费用是多少元？参考答案一、基础过关1. B【解析】对于函数y＝4x和y＝x－4，y总随x的增大而增大，不符合题意，A、C均错误；对于函数y＝－4x，∵k＝－4<0，∴y总随x的增大而减小，B正确；对于函数y＝x2，当x>0时，y随x的增大而增大，当x<0时，y随x的增大而减小，D错误．2. C【解析】∵－1<0，4>0，∴一次函数不经过第三象限，∴点P一定不在第三象限．3. A【解析】令x＝0，得y＝－2×0＋4＝4，则函数与y轴的交点坐标是(0，4)．4. A【解析】∵y＝kx＋b(k，b是常数)的图象不经过第二象限，当k＝0，b≤0时成立；当k＞0，b≤0时成立．综上所述，k ≥0，b ≤0.5. B 【解析】∵函数y ＝3x 向上平移6个单位后可得函数y ＝3x ＋6，∴将y ＝0代入y ＝3x ＋6，可得3x ＋6＝0，解得x ＝－2，∴平移后的图象与x 轴交点的坐标为(－2，0)．6. D 【解析】∵ab ＜0，∴a ，b 异号，∵a ＞b ，∴a ＞0＞b ，∴函数y ＝ax ＋b 的图象经过第一、三、四象限．7. C 【解析】∵点(1，4)，(2，7)，(a ，10)在同一直线上，∴设这条直线的解析式为y ＝kx ＋b ，将点(1，4)，(2，7)代入解析式得⎩⎪⎨⎪⎧k ＋b ＝42k ＋b ＝7，解得⎩⎪⎨⎪⎧k ＝3b ＝1.∴这条直线的解析式为y ＝3x ＋1，将(a ，10)代入得3a＋1＝10，解得a ＝3.8. C 【解析】当y ＝1时，－13x ＝1，解得x ＝－3，则点P 的坐标为(－3，1)，∴关于x ，y 的二元一次方程组⎩⎪⎨⎪⎧－ax ＋y ＝b x ＋3y ＝0的解为⎩⎪⎨⎪⎧x ＝－3y ＝1.9. B 【解析】∵当y 2＝2时，－x －1＝2，解得x ＝－3，∴A (－3，2)．将A (－3，2)代入y 1＝mx －3中，得2＝－3m －3，解得m ＝－53.10. B 【解析】∵点(1，0)在一次函数y ＝kx －2的图象上，∴k －2＝0，∴k ＝2>0，∴y 随x 的增大而增大，∵－2<1<3，∴y 1<0<y 2.11. D 【解析】∵k ＜0，b ＞0，根据一次函数图象性质可得y 随x 的增大而减小，图象过第一、二、四象限，当x ＝0时，y ＝b ，∴函数与y 轴交于点(0，b )，则A 、B 、C 选项正确；当y ＝0时，x ＝－bk ，与x轴交于点(－b k ，0)，根据函数图象可得，当x ＞－bk时，y ＜0，D 项错误．12. A 【解析】由题意得，⎩⎪⎨⎪⎧k －2<02k ＋4>0，解得－2<k <2，∴3－k ＞0，6＋k ＞0，∴点(3－k ，6＋k )所在的象限为第一象限．13. B 【解析】∵一次函数y 1＝k 1x ＋b 1的图象l 1向下平移若干个单位得到l 2的表达式y 2＝k 2x ＋b 2，∴k 1＝k 2，b 1＞b 2，当x ＝5时可以看出y 1＞y 2，∴B 选项错误．14. 1＜k ＜3 【解析】∵直线y ＝(2－2k )x ＋k －3经过第二、三、四象限，∴⎩⎪⎨⎪⎧2－2k ＜0k －3＜0，解得1＜k ＜3.15. (－2，3) 【解析】∵y ＝kx ＋2k ＋3＝k (x ＋2)＋3，当x ＝－2时，y ＝3，∴不论k 为何值，该函数的图象都经过点A (－2，3)．16. x ≤1 【解析】将点P (m ，3)代入y ＝x ＋2，得3＝m ＋2，∴m ＝1.∴点P 坐标为(1，3)．由题图可知，x ＋2≤ax ＋c 的解即为直线y ＝ax ＋c 的图象在直线y ＝x ＋2的上方时x 的取值范围，且包含交点的横坐标，∴x ＋2≤ax ＋c 的解为x ≤1.17. 解：(1)∵点P (－1，a )在直线l 2：y ＝2x ＋4上， ∴2×(－1)＋4＝a ，即a ＝2，则点P 的坐标为(－1，2)．设直线l 1的解析式为y ＝kx ＋b (k ≠0)， ∴将点B (1，0)，P (－1，2)代入得，⎩⎪⎨⎪⎧k ＋b ＝0－k ＋b ＝2，解得⎩⎪⎨⎪⎧k ＝－1b ＝1.∴直线l 1的解析式为y ＝－x ＋1； (2)∵直线l 1与y 轴相交于点C ， ∴C 点的坐标为(0，1)，又∵直线l 2与x 轴相交于点A ， ∴A 点的坐标为(－2，0)，则AB ＝3，∴S 四边形P AOC ＝S △P AB －S △BOC ＝12×3×2－12×1×1＝52.二、能力提升1. A 【解析】∵关于x 的一元二次方程mx 2－2x －1＝0无实数根，∴m ≠0且(－2)2－4m ×(－1)＜0，∴m ＜－1，∴一次函数y ＝mx ＋m 的图象经过第二、三、四象限，不经过第一象限．2. A 【解析】令ax ＋b ＝bx ＋a ，即(a －b )x ＝a －b ，∵a ≠b ，∴解得x ＝1，即这两个一次函数图象交点的横坐标为1，4个选项都满足. A 选项中，两函数图象都经过第一、二、三象限，若当x <1时，位于上方的图象是y 1，由y 1的图象可知a >0，b ＞0，由y 2的图象可知a >0，b ＞0，两结论不矛盾，故A 正确；B 选项中，如果经过第一、二、三象限的图象是y 1，由y 1的图象可知a >0，b ＞0，由y 2的图象可知a >0，b <0，两结论相矛盾，故B 错误；C 选项中，两函数图象都经过第一、二、四象限，若当x <1时，位于上方的图象是y 1，由y 1的图象可知，a ＜0，b ＞0，由y 2的图象可知，a >0，b ＜0，两结论相矛盾，故C 错误；D 选项中，如果经过第二、三、四象限的图象是y 1，由y 1的图象可知a ＜0，b ＜0，由y 2的图象可知a <0，b >0，两结论相矛盾，故D 错误．3. D 【解析】S 四边形ABCD ＝S △ACD ＋S △ACB ＝12×7×3＋12×7×1＝14，12S 四边形ABCD ＝7.当直线l 过点D 时，设BD 所在直线的解析式为y ＝mx ＋n ，将点B (－2，－1)，D (0，3)代入易得y ＝2x ＋3，∴BD 所在直线与x 轴交于点(－32，0)，∴S △ABD ＝12(－32＋4)×(3＋1)＝5，∴直线l 与直线CD 相交．如解图所示，过点B 作直线交CD 于点E ，交AC 于点F .设直线l 所表示的函数表达式为y ＝kx ＋b ，将点B (－2，－1)代入y ＝kx ＋b ，得－2k ＋b ＝－1，b ＝2k －1，∴y ＝kx ＋2k －1.由题意易得直线CD 的解析式为y ＝－x ＋3，联立⎩⎪⎨⎪⎧y ＝kx ＋2k －1y ＝－x ＋3，解得⎩⎪⎨⎪⎧x＝4－2kk ＋1y ＝5k －1k ＋1，∴E (4－2k k ＋1，5k －1k ＋1)．令y ＝kx ＋2k －1＝0，得x ＝1－2k k ，∴直线l 与x 轴的交点坐标为F (1－2kk ，0)．S △BCE ＝S △BCF ＋S △CEF ＝12×1×(2k －1k ＋3)＋12×(2k －1k ＋3)×5k －1k ＋1＝7，解得k ＝54，∴直线l 的表达式为y＝54x ＋32.第3题解图4. (23，0) 【解析】如解图，作点B 关于x 轴的对称点B ′，连接AB ′，交x 轴于点P ，则点P 即为所求，设直线y ＝－x 沿y 轴向下平移后的直线的解析式为y ＝－x ＋a ，把A (2，－4)代入可得a ＝－2，∴平移后的直线的解析式为y ＝－x －2，令x ＝0，则y ＝－2，即B (0，－2)，∴B ′(0，2)，设直线AB ′的解析式为y ＝kx＋b ，把A (2，－4)，B ′(0，2)代入可得⎩⎪⎨⎪⎧－4＝2k ＋b 2＝b ，解得⎩⎪⎨⎪⎧k ＝－3b ＝2，∴直线AB ′的解析式为y ＝－3x ＋2，令y＝0，则x ＝23，∴P (23，0)．第4题解图三、满分冲关1. 解：(1)如解图①，过点A 作AH ⊥OP 于点H ，则AP ≥AH ， ∵点P 在y ＝33x 的图象上， ∴∠HOQ ＝30°，∠HOA ＝60°. ∵A (0，2)，∴AH ＝AO ·sin60°＝3， ∴AP ≥3；第1题解图①(2)是．理由如下：①如解图②，当点P在第三象限时，由∠QP A＝∠QOA＝90°，可得Q、P、O、A四点共圆，∴∠QAP＝∠POQ＝30°；第1题解图②②如解图③，当点P在第一象限的线段OH上时，由∠QP A＝∠QOA＝90°，可得Q、P、O、A四点共圆，∴∠P AQ＋∠POQ＝180°，又∵∠POQ＝150°，∴∠QAP＝180°－∠POQ＝30°；第1题解图③③如解图④，当点P在第一象限的线段OH的延长线上时，由∠QP A＝∠QOA＝90°，可得∠APQ＋∠AOQ＝180°，∴Q、P、O、A四点共圆，∴∠P AQ＝∠POQ＝30°；第1题解图④(3)设P (m ，33m )， ∵A (0，2)，∴OP 2＝4m 23，AP 2＝4m 23－43m 3＋4.在Rt △APQ 中，∵∠QAP ＝30°， ∴PQ 2＝(AP ·tan30°)2＝4m 29－43m 9＋43，AQ 2＝(AP cos30°)2＝16m 29－163m 9＋163， ∵在Rt △AOQ中，OQ 2＝AQ 2－OA 2＝16m 29－1639m ＋43＝169(m －32)2， ∴Q (4m －233，0)．①当OP ＝OQ 时，则43m 2＝169m 2－163m 9＋43，解得m ＝23±3，∴Q 1(23＋4，0)，Q 2(23－4，0)； ②当OP ＝PQ 时，则43m 2＝49m 2－43m 9＋43，解得m ＝32或m ＝－3，当m ＝32时，点Q 与点O 重合，舍去， ∴m ＝－3， ∴Q 3(－23，0)；③如解图④，当QO ＝QP 时，则169m 2－163m 9＋43＝49m 2－43m 9＋43，解得m ＝3或m ＝0，当m ＝0时，点P 与点O 重合，舍去， ∴m ＝ 3. ∴Q 4(233，0)．综上所述，当△OPQ 为等腰三角形时，点Q 的坐标为(23＋4，0)或(23－4，0)或(－23，0)或(233，0)．2. 解：(1)设每台A 型挖掘机一小时挖土x 立方米，每台B 型挖掘机一小时挖土y 立方米，根据题意，得⎩⎪⎨⎪⎧x ＋2y ＝702x ＋3y ＝120，解得⎩⎪⎨⎪⎧x ＝30y ＝20. 答：每台A 型挖掘机一小时挖土30立方米，每台B 型挖掘机一小时挖土20立方米；(2)设m 台A 型挖掘机参与施工，施工总费用为W 元，则有(10－m )台B 型挖掘机参与施工，根据题意得⎩⎪⎨⎪⎧30×4m ＋20×4（10－m ）≥1080350×4m ＋200×4（10－m ）≤13400，解得7≤m ≤9，∴共有三种调配方案：①调配7台A 型、3台B 型挖掘机施工；②调配8台A 型挖掘机、2台B 型挖掘机施工；③调配9台A 型挖掘机、1台B 型挖掘机施工；依题意，得：W ＝350×4m ＋200×4(10－m )＝600m ＋8000，∵600＞0，∴W 随m 的增大而增大，∴当m ＝7时，即选择方案①时，W 取得最小值，最小值为12200元．即调配7台A 型挖掘机，3台B 型挖掘机的施工费用最低，最低费用为12200元．3. 解：(1)设A 型空调和B 型空调每台各需x 元、y 元，由题意得，⎩⎪⎨⎪⎧3x ＋2y ＝390004x －5y ＝6000，解得⎩⎪⎨⎪⎧x ＝9000y ＝6000，答：采购A 型空调每台需花费9000元，采购B 型空调每台需花费6000元；(2)设购买A 型空调a 台，则购买B 型空调(30－a )台，由题意得，⎩⎪⎨⎪⎧a ≥12（30－a ）9000a ＋6000（30－a ）≤217000，解得10≤a ≤1213， ∵a 为整数，∴a ＝10、11、12，共有三种采购方案，方案一：采购A 型空调10台，B 型空调20台，方案二：采购A 型空调11台，B 型空调19台，方案三：采购A 型空调12台，B 型空调18台；(3)设总费用为W 元，W＝9000a＋6000(30－a)＝3000a＋180000，∴当a＝10时，W取得最小值，此时W＝210000，答：采购A型空调10台，B型空调20台可使总费用最低，最低费用是210000元．。

2024年中考数学专题复习：一次函数的图像与性质-试卷

2024年中考数学专题复习：一次函数的图像与性质一、选择题（本大题共10道小题）1. (2023•沈阳)一次函数y ＝-3x+1的图象不经过( )A.第一象限B.第二象限C.第三象限D.第四象限2. (2023八上·太原期中)课堂上,同学们研究正比例函数y=-x 的图象时,得到如下四个结论,其中错误的是( )A.当x=0时,y=0,所以函数y=-x 的图象经过原点B.点P(t,-t)一定在函数y=-x 的图象上C.当x>0时,y<0,当x<0时,y>0,所以函数y=-x 的图象经过二、四象限D.将函数的图象向左平移2个单位,即可得到函数y=-x+2的图象3. (2023·太原模拟)已知y 是x 的正比例函数,当x ＝3时,y ＝－6,则y 与x 的函数关系式为( )A.y ＝2xB.y ＝－2xC.y ＝12 xD.y ＝－12x 4. (2023•柳州)若一次函数y ＝kx+b 的图象如图所示,则下列说法正确的是( )A.k ＞0B.b ＝2C.y 随x 的增大而增大D.x ＝3时,y ＝0 5. (2023·贵州毕节·二模)已知正比例函数y=kx(k ≠0)的图象过点(2,3),把正比例函数y=kx(k ≠0)的图象平移,使它过点(1,-1),则平移后的函数图象大致是( )A. B. C.D. 6. (2023秋•会宁县)已知关于x 的一次函数y ＝(k 2+1)x-2图象经过点A(3,m)、B(-1,n),则m,n 的大小关系为( )A.m ≥nB.m ＞nC.m ≤nD.m ＜n7. (2023·随州模拟)如图,在平面直角坐标系中,动点A,B 分别在x 轴上和函数y ＝x 的图象上,AB ＝4,CB ⊥AB,BC ＝2,则OC 的最大值为( )A.222B.224C.2 5D.2528. (2023·鄂州中考)数形结合是解决数学问题常用的思想方法.如图,直线y ＝2x －1与直线y ＝kx ＋b(k ≠0)相交于点P(2,3).根据图象可知,关于x 的不等式2x －1＞kx ＋b 的解集是( )A.x ＜2B.x ＜3C.x ＞2D.x ＞39. (2023•贵阳)小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线y ＝k n x+b n (n ＝1,2,3,4,5,6,7),其中k 1＝k 2,b 3＝b 4＝b 5,则他探究这7条直线的交点个数最多是( )A.17个B.18个C.19个D.21个10. (2023·湖南永州·中考真题)已知点P(x 0,y 0)和直线y=kx+b,求点P 到直线y=kx+b 的距离d 可用公式0021kx y b d k -+=+计算.根据以上材料解决下面问题:如图,⊙C 的圆心C 的坐标为(1,1),半径为1,直线l 的表达式为y=-2x+6,P 是直线l 上的动点,Q 是⊙C 上的动点,则PQ 的最小值是( )A.355B.3515-C.6515-D.2二、填空题（本大题共8道小题）11. (2023•毕节市)将直线y ＝-3x 向下平移2个单位长度,平移后直线的解析式为 .12. (2023·四川成都市)在正比例函数y=kx 中,y 的值随着x 值的增大而增大,则点P(3,k)在第_____象限.13. (2023·贵州黔西·二模)如图,平面直角坐标系中,经过点B(-4,0)的直线y ＝kx+b 与直线y ＝mx+2相交于点3(,1)2A --,则关于x 的方程mx+2＝kx+b 的解为________.14. (2023秋•宁化县)若函数y ＝4x ﹣1与y ＝﹣x+a 的图象交于x 轴上一点,则a 的值为( )A.4B.﹣4C.D.±415. (2023黔西南州)如图,正比例函数的图象与一次函数y ＝－x ＋1的图象相交于点P,点P 到x 轴的距离是2,则这个正比例函数的解析式是 .16. (2023·湖南湘西·中考真题)在平面直角坐标系中,O 为原点,点A(6,0),点B 在y 轴的正半轴上,∠ABO=30o .矩形CODE 的顶点D,E,C 分别在OA,AB,OB 上,OD=2.将矩形CODE 沿x 轴向右平移,当矩形CODE 与△ABO 重叠部分的面积为63时,则矩形CODE 向右平移的距离为___________.17. (2023•毕节市)如图,在平面直角坐标系中,点N 1(1,1)在直线l:y ＝x 上,过点N 1作N 1M 1⊥l,交x 轴于点M 1;过点M 1作M 1N 2⊥x 轴,交直线于N 2;过点N 2作N 2M 2⊥l,交x 轴于点M 2;过点M 2作M 2N 3⊥x 轴,交直线l 于点N 3;…,按此作法进行下去,则点M 2023的坐标为 .18. (2023•泰安)如图,点B 1在直线l:y ＝21x 上,点B 1的横坐标为2,过点B 1作B 1A 1⊥l,交x 轴于点A 1,以A 1B 1为边,向右作正方形A 1B 1B 2C 1,延长B 2C 1交x 轴于点A 2;以A 2B 2为边,向右作正方形A 2B 2B 3C 2,延长B 3C 2交x 轴于点A 3;以A 3B 3为边,向右作正方形A 3B 3B 4C 3,延长B 4C 3交x 轴于点A 4;…;照这个规律进行下去,则第n 个正方形A n B n B n+1∁n 的边长为 (结果用含正整数n 的代数式表示).三、解答题（本大题共6道小题）19. (2023秋•安徽月考)已知经过点A(4,-1)的直线y ＝kx+b 与直线y ＝-x 相交于点B(2,a),求两直线与x 轴所围成的三角形的面积.20. (2023春•西丰县)如图,一次函数y＝kx+b的图象经过A(2,4),B(﹣2,﹣2)两点,与y轴交于点C.(1)求k,b的值,并写出一次函数的解析式;(2)求点C的坐标.21. (2023秋•兰州)如图,直线l1:y＝-x+4分别与x轴,y轴交于点D,点A,直线l2:y x+1与x轴交于点C,两直线l1,l2相交于点B,连AC.(1)求点B的坐标和直线AC的解析式;(2)求△ABC的面积.22. (2023•滨州)如图,在平面直角坐标系中,直线y x﹣1与直线y＝﹣2x+2相交于点P,并分别与x轴相交于点A、B.(1)求交点P的坐标;(2)求△PAB的面积;(3)请把图象中直线y＝﹣2x+2在直线y x﹣1上方的部分描黑加粗,并写出此时自变量x的取值范围.23. (2023·河北中考真题)表格中的两组对应值满足一次函数y=kx+b,现画出了它的图象为直线l ,如图.而某同学为观察k,b 对图象的影响,将上面函数中的k 与b 交换位置后得另一个一次函数,设其图象为直线l '.(1)求直线l 的解析式; (2)请在图上画出．．直线l '(不要求列表计算),并求直线l '被直线l 和y 轴所截线段的长; (3)设直线y=a 与直线l ,l '及y 轴有三个不同的交点,且其中两点关于第三点对称,直接．．写出a 的值.24. (2023•黑龙江)如图,矩形ABOC 在平面直角坐标系中,点A 在第二象限内,点C 在y 轴正半轴上,OA 2-9x+20＝0的两个根.解答下列问题:(1)求点A 的坐标;(2)若直线MN 分别与x 轴,AB,AO,y 轴交于点D,M,F,N,E,S △AMN ＝2,tan ∠AMN ＝1,求直线MN 的解析式;(3)在(2)的条件下,点P 在第二象限内,使以E,F,P,Q 为顶点的四边形是正方形？若存在;若不存在,请说明理由.。

中考数学考点10一次函数图像与性质总复习(原卷版)

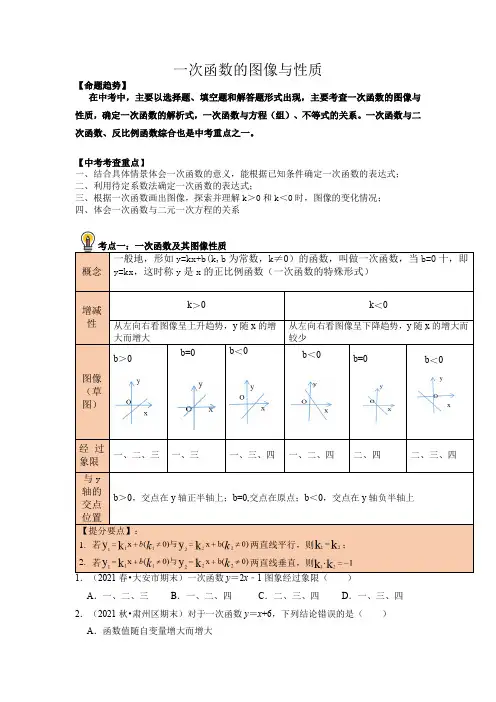
一次函数的图像与性质【命题趋势】在中考中，主要以选择题、填空题和解答题形式出现，主要考查一次函数的图像与性质，确定一次函数的解析式，一次函数与方程（组）、不等式的关系。

一次函数与二次函数、反比例函数综合也是中考重点之一。

【中考考查重点】一、结合具体情景体会一次函数的意义，能根据已知条件确定一次函数的表达式；二、利用待定系数法确定一次函数的表达式；三、根据一次函数画出图像，探索并理解k＞0和k＜0时，图像的变化情况；四、体会一次函数与二元一次方程的关系考点一：一次函数及其图像性质概念一般地，形如y=kx+b(k,b为常数，k≠0）的函数，叫做一次函数，当b=0十，即y=kx，这时称y是x的正比例函数（一次函数的特殊形式）增减性k＞0k＜0从左向右看图像呈上升趋势，y随x的增大而增大从左向右看图像呈下降趋势，y随x的增大而较少图像（草图）b＞0b=0b＜0b＜0b=0 b＜0经过象限一、二、三一、三一、三、四一、二、四二、四二、三、四与y轴的交点位置b＞0，交点在y轴正半轴上；b=0,交点在原点；b＜0，交点在y轴负半轴上【提分要点】：1.若两直线平行，则；2.若两直线垂直，则1．（2021春•大安市期末）一次函数y＝2x﹣1图象经过象限（）A．一、二、三B．一、二、四C．二、三、四D．一、三、四2．（2021秋•肃州区期末）对于一次函数y＝x+6，下列结论错误的是（）A．函数值随自变量增大而增大B．函数图象与x轴正方向成45°角C．函数图象不经过第四象限D．函数图象与x轴交点坐标是（0，6）3．（2021秋•东港市期中）点A（﹣1，y1）和点B（﹣4，y2）都在直线y＝﹣2x上，则y1与y2的大小关系为（）A．y1＞y2B．y1＜y2C．y1＝y2D．y1≥y2 4．（2021秋•三水区期末）若一次函数y＝kx+b的图象经过第一、二、四象限，则一次函数y＝bx+k的图象大致是（）A．B．C．D．考点二：一次函数解析式的确定方法待定系数法步骤1.设：一般式y=kx+b（k≠0）（题干中未给解析式需设）2.代：找出一次函数图像上的两个点，并且将点坐标代入函数解析式，得到二元一次方程组；3.求：解方程（组）求出k、b的值；4.写：将k、b的值代入，直接写出一次函数解析式5．（2021秋•尤溪县期中）已知一次函数y＝x+b过点（﹣1，﹣2），那么这个函数的表达式为（）A．y＝x﹣1B．y＝x+1C．y＝x﹣2D．y＝x+2 6．（2021春•海珠区期末）已知一次函数y＝mx﹣4m，当1≤x≤3时，2≤y≤6，则m 的值为（）A．3B．2C．﹣2D．2或﹣2 7．（2021秋•萧山区月考）已知y与x﹣2成正比例，且当x＝1时，y＝1，则y与x之间的函数关系式为．8．（2021春•古丈县期末）某个一次函数的图象与直线y＝x+6平行，并且经过点（﹣2，﹣4），则这个一次函数的解析式为（）A．y＝﹣x﹣5B．y＝x+3C．y＝x﹣3D．y＝﹣2x﹣8考点三：一次函数图像的平移平移前平移方式（m＞0）平移后简记y=kx+b 向左平移m个单位长度y=k（x+m）+bx左加右减向右平移m个单位长度y=k（x-m）+b向上平移m个单位长度y=kx+b+m等号右端整体上加下减向下平移m个单位长度y=kx+b-m9．（2021秋•金安区校级期中）将直线y＝2x向右平移1个单位，再向上平移1个单位后，所得直线的表达式为（）A．y＝2x﹣1B．y＝2x C．y＝2x+4D．y＝2x﹣2 10．（2021春•米易县期末）一次函数y＝2x﹣4的图象由正比例函数y＝2x的图象（）A．向左平移4个单位长度得到B．向右平移4个单位长度得到C．向上平移4个单位长度得到D．向下平移4个单位长度得到11．（2021秋•长丰县月考）已知点A（2，4）沿水平方向向左平移3个单位长度得到点A'，若点A'在直线y＝x+b上，则b的值为（）A．1B．3C．5D．﹣1考点四：一次函数与方程（组）、不等式与一元一次方程的关系方程ax+b=0（a≠0）的解是一次函数y=ax+b(a≠0）的函数值为0时自变量的取值，还是直线y=ax+b(a≠0）与x 轴交点的横坐标与二元一次方程组的关系方程组的解时直线的交点坐标与一元一次不等式的关系1.从“数”来看（1）kx+b＞0的解集是y=kx+b中，y＞0时x的取值范围（2）kx+b＞＜0的解集是y=kx+b中，y＜0时x的取值范围2.从“形”上看（1）kx+b＞0的解集是y=kx+b函数图像位于x上方部分对应的点的横坐标（2）kx+b＜0的解集是y=kx+b函数图像位于x下方部分对应的点的横坐标12．（2021秋•乐平市期中）一次函数y＝kx+b的图象如图所示，则关于x的方程kx+b ＝0的解为（）A．x＝0B．x＝3C．x＝﹣2D．x＝﹣3 13．（2021秋•安徽期中）已知一次函数y＝ax﹣1与y＝mx+4的图象交于点A（3，1），则关于x的方程ax﹣1＝mx+4的解是（）A．x＝﹣1B．x＝1C．x＝3D．x＝414．（2021春•沧县期末）如图，直线y＝x+5和直线y＝ax+b相交于点P（20，25），根据图象可知，方程x+5＝ax+b的解是（）A．x＝20B．x＝5C．x＝25D．x＝15 15．（2020秋•建湖县期末）如图，一次函数y＝kx+b（k≠0）的图象经过点A（﹣1，﹣2）和点B（﹣2，0），一次函数y＝2x的图象过点A，则不等式2x＜kx+b≤0的解集为（）A．x≤﹣2B．﹣2≤x＜﹣1C．﹣2＜x≤﹣1D．﹣1＜x≤0 16．（2021秋•兴宁区校级月考）如图，直线y＝kx+b交x轴于点A（﹣2，0），直线y ＝mx+n交x轴于点B（5，0），这两条直线相交于点C（2，c），则关于x的不等式组的解集为（）A．x＜5B．1＜x＜5C．﹣2＜x＜5D．x＜﹣217．（2020秋•西林县期末）如图所示是函数y＝kx+b与y＝mx+n的图象，则方程组的解是（）A．B．C．D．1．（2021春•扎兰屯市期末）将直线y＝﹣2x﹣2向右平移1个单位长度，可得直线的表达式为（）A．y＝2x B．y＝﹣2x﹣4C．y＝﹣2x D．y＝﹣2x+4 2．（2021春•玉田县期末）下列有关一次函数y＝﹣6x﹣5的说法中，正确的是（）A．y的值随着x值的增大而增大B．函数图象与y轴的交点坐标为（0，5）C．当x＞0时，y＞﹣5D．函数图象经过第二、三、四象限3．（2021春•红寺堡区期末）点P1（x1，y1），点P2（x2，y2）是一次函数y＝﹣4x+3图象上的两个点，且x1＜x2，则y1与y2的大小关系是（）A．y1＞y2B．y1＞y2＞0C．y1＜y2D．y1＝y2 4．（2021秋•运城期中）在平面直角坐标系中，一次函数y＝kx+3（k≠0）的图象经过点A（2，﹣1），则这个一次函数的表达式是（）A．y＝﹣2x+3B．y＝x+3C．y＝2x+3D．y＝x+35．（2021秋•南海区期中）如图，一次函数y＝kx+b的图象经过点（2，0）、（0，1），则下列结论正确的是（）A．k＝1B．关于x的方程kx+b＝0的解是x＝2C．b＝2D．关于x的方程kx+b＝0的解是x＝16．（2021秋•滕州市期中）直线y＝ax+b（a≠0）过点A（0，2），B（1，0），则关于x的方程ax+b＝0的解为（）A．x＝0B．x＝2C．x＝1D．x＝3 7．（2021秋•龙凤区期末）一次函数y＝mx﹣n（m，n为常数）的图象如图所示，则不等式mx﹣n≥0的解集是（）A．x≥2B．x≤2C．x≥3D．x≤3 8．（2020秋•开化县期末）如图，直线y＝2x+n与y＝mx+3m（m≠0）的交点的横坐标为﹣1，则关于x的不等式2x+n＜mx+3m＜0的整数解为（）A．﹣1B．﹣2C．﹣3D．﹣3.59．（2021春•单县期末）已知方程组的解为，则直线y＝﹣x+2与直线y＝2x﹣7的交点在平面直角坐标系中位于（）A．第一象限B．第二象限C．第三象限D．第四象限10．（2021春•武陵区期末）对于实数a，b，我们定义符号max{a，b}的意义为：当a ≥b时，max{a，b}＝a；当a＜b时，max{a，b}＝b；如：max{4，﹣2}＝4，max{3，3}＝3，若关于x的函数为y＝max（2x﹣1，﹣x+2}，则该函数的最小值是（）A．2B．1C．0D．﹣1 11．（2020秋•成安县期末）如图，若直线y＝kx+b与x轴交于点A（﹣4，0），与y 轴正半轴交于B，且△OAB的面积为4，则该直线的解析式为（）A．B．y＝2x+2C．y＝4x+4D．12．（2021春•饶平县校级期末）已知2y﹣3与3x+1成正比例，则y与x的函数解析式可能是（）A．y＝3x+1B．C．D．y＝3x+2 13．（2021秋•榆林期末）已知直线l1交x轴于点（﹣3，0），交y轴于点（0，6），直线l2与直线l1关于x轴对称，将直线l1向下平移8个单位得到直线l3，则直线l2与直线l3的交点坐标为（）A．（﹣1，﹣4）B．（﹣2，﹣4）C．（﹣2，﹣1）D．（﹣1，﹣1）1．（2021•长沙）下列函数图象中，表示直线y＝2x+1的是（）A．B．C．D．2．（2021•嘉峪关）将直线y＝5x向下平移2个单位长度，所得直线的表达式为（）A．y＝5x﹣2B．y＝5x+2C．y＝5（x+2）D．y＝5（x﹣2）3．（2021•陕西）在平面直角坐标系中，将直线y＝﹣2x向上平移3个单位，平移后的直线经过点（﹣1，m），则m的值为（）A．﹣1B．1C．﹣5D．5 4．（2021•抚顺）如图，直线y＝2x与y＝kx+b相交于点P（m，2），则关于x的方程kx+b＝2的解是（）A．x＝B．x＝1C．x＝2D．x＝4 5．（2020•牡丹江）两个一次函数y＝ax+b和y＝bx+a，它们在同一个直角坐标系的图象可能是（）A．B．C．D．6．（2021•乐山）如图，已知直线l1：y＝﹣2x+4与坐标轴分别交于A、B两点，那么过原点O且将△AOB的面积平分的直线l2的解析式为（）A．y＝x B．y＝x C．y＝x D．y＝2x 7．（2021•娄底）如图，直线y＝x+b和y＝kx+4与x轴分别相交于点A（﹣4，0），点B（2，0），则解集为（）A．﹣4＜x＜2B．x＜﹣4C．x＞2D．x＜﹣4或x＞2 8．（2019•苏州）若一次函数y＝kx+b（k，b为常数，且k≠0）的图象经过点A（0，﹣1），B（1，1），则不等式kx+b＞1的解集为（）A．x＜0B．x＞0C．x＜1D．x＞19．（2021•德阳）关于x，y的方程组的解为，若点P（a，b）总在直线y＝x上方，那么k的取值范围是（）A．k＞1B．k＞﹣1C．k＜1D．k＜﹣1 10．（2021•呼和浩特）在平面直角坐标系中，点A（3，0），B（0，4）．以AB为一边在第一象限作正方形ABCD，则对角线BD所在直线的解析式为（）A．y＝﹣x+4B．y＝﹣x+4C．y＝﹣x+4D．y＝4 11．（2019•江西）如图，在平面直角坐标系中，点A，B的坐标分别为（﹣，0），（，1），连接AB，以AB为边向上作等边三角形ABC．（1）求点C的坐标；（2）求线段BC所在直线的解析式．1．（2021•庐阳区校级一模）一次函数y＝﹣2x﹣3的图象和性质．叙述正确的是（）A．y随x的增大而增大B．与y轴交于点（0，﹣2）C．函数图象不经过第一象限D．与x轴交于点（﹣3，0）2．（2021•陕西模拟）平面直角坐标系中，直线y＝﹣2x+m沿x轴向右平移4个单位后恰好经过（1，2），则m＝（）A．﹣1B．2C．﹣4D．﹣3 3．（2021•商河县校级模拟）若一次函数y＝kx+b的图象经过一、二、四象限，则一次函数y＝﹣bx+k的图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限4．（2021•萧山区一模）已知y﹣3与x+5成正比例，且当x＝﹣2时，y＜0，则y关于x的函数图象经过（）A．第一、二、三象限B．第一、二、四象限C．第一、三、四象限D．第二、三、四象限5．（2021•陕西模拟）一次函数y＝kx+b的图象经过点A（2，3），每当x增加1个单位时，y增加3个单位，则此函数表达式是（）A．y＝x+3B．y＝2x﹣3C．y＝3x﹣3D．y＝4x﹣4 6．（2021•蕉岭县模拟）在平面直角坐标系中，一次函数y＝mx+b（m，b均为常数）与正比例函数y＝nx（n为常数）的图象如图所示，则关于x的方程mx＝nx﹣b的解为（）A．x＝3B．x＝﹣3C．x＝1D．x＝﹣17．（2021•奉化区校级模拟）八个边长为1的正方形如图摆放在平面直角坐标系中，经过原点的一条直线l将这八个正方形分成面积相等的两部分，则该直线l的解析式为（）A．y＝﹣x B．y＝﹣x C．y＝﹣x D．y＝﹣x8．（2021•遵义一模）如图，直线y＝kx+b（k＜0）与直线y＝x都经过点A（3，2），当kx+b＞x时，x的取值范围是（）A．x＜2B．x＞2C．x＜3D．x＞3 9．（2021•饶平县校级模拟）如图，函数y＝ax+b和y＝﹣x的图象交于点P，则根据图象可得，关于x，y的二元一次方程组中的解是（）A．B．C．D．10．（2021•杭州模拟）已知直线l：y＝kx+b经过点A（﹣1，a）和点B（1，a﹣4），若将直线l向上平移2个单位后经过原点，则直线的表达式为（）A．y＝2x+2B．y＝2x﹣2C．y＝﹣2x+2D．y＝﹣2x﹣2 11．（2021•南山区校级二模）我国古代很早就对二元一次方程组进行了研究，古著《九章算术》记载用算筹表示二元一次方程组，发展到现代就是用矩阵式＝来表示二元一次方程组，而该方程组的解就是对应两直线（不平行）a1x+b1y＝c1与a2x+b2y＝c2的交点坐标P（x，y）据此，则矩阵式＝所对应两直线交点坐标是．12．（2021•杭州模拟）已知直线y＝kx+b经过点A（5，0），B（1，4）．（1）求直线AB的解析式；（2）若直线y＝2x﹣4与直线AB相交于点C，求点C的坐标；（3）根据图象，写出关于x的不等式2x﹣4＞kx+b的解集．。

中考数学总复习《一次函数图像与坐标轴的问题》专题测试卷带答案

中考数学总复习《一次函数图像与坐标轴的问题》专题测试卷带答案班级：___________姓名：___________考号：___________一、单选题(共12题；共24分)1．一次函数y＝x﹣3的图象与y轴的交点坐标是（）A．（0，﹣3）B．（0，3）C．（3，0）D．（﹣3，0）2．如图，直线y=−x+4与坐标轴交于A、B两点，点C为坐标平面内一点BC=1，点M为线段AC的中点，连接OM，则线段OM的最小值是（）A．2√2+12B．2√2−12C．1D．2√23．如图在平面直角坐标系中，直线l1对应的函数表达式为y=2x，直线l2与x，y轴分别交于A、B，且l1∥ l2，OA=2，则线段OB的长为（）A．3B．4C．2√2D．2√34．背面图案、形状大小都相同的四张卡片的正面分别记录着有关函数y=2x−4的四个结论，现将卡片背面朝上，随机抽取一张，抽到卡片上的结论正确的概率是（）A．14B．12C．34D．15．已知一次函数的图象与y=2x+3平行，且过点(4，2)，则该一次函数与坐标轴围成图形的面积为（）A．6B．9C．12D．186．如图，已知直线y=−13x+√10与与双曲线y=kx(x>0)交于A、B两点，连接OA，若OA⊥AB，则k的值为()A．B．C．D．7．对于一次函数y=−x−2，下列说法错误的是（）A．图象不经过第一象限B．图象与y轴的交点坐标为(0，−2)C．图象可由直线y=−x向下平移2个单位长度得到D．若点(−1，y1)，(4，y2)在一次函数y=−x−2的图象上，则y1<y28．若一次函数y＝ax+b的图象如图所示，则方程ax+b＝0的解为（）A．x＝3B．x＝0C．x＝﹣2D．x＝﹣39．我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：y=kx+4 √3与x轴、y轴分别交于A，B，∥OAB=30°，点P在x轴上，∥P与l相切，当P在线段OA上运动时，使得∥P成为整圆的点P个数是（）A．6B．8C．10D．1210．一次函数y＝ax＋b交x轴于点(－5，0)，则关于x的方程ax＋b＝0的解是() A．x＝5B．x＝－5C．x＝0D．无法求解11．下列四个选项中，不符合直线y＝x﹣2的性质特征的选项是（）A．经过第一、三、四象限B．y随x的增大而增大C．与x轴交于（﹣2，0）D．与y轴交于（0，-2）12．下列图形中，阴影部分的面积为2的有（）个A．4个B．3个C．2个D．1个二、填空题(共6题；共7分)13．在直角坐标系xOy中，若直线y=x+4a-12与y轴的交点在x轴上方，则a的取值范围．14．函数y=m2x2+(2m+1)x+1与x轴有交点，则m的取值范围．15．如图，一次函数y＝x＋2的图像与坐标轴分别交于A，B两点，点P，C分别是线段AB，OB 上的点，且∥OPC＝45°，PC＝PO，则点P的坐标为．16．如果一次函数y=kx+4与两坐标轴围成的三角形面积为4，则k=．17．如图，在平面直角坐标系xOy中，直线y=−34x+3与x轴交于点A，与y轴交于点B，将∥AOB沿过点A的直线折叠，使点B落在x轴负半轴上，记作点C，折痕与y轴交点交于点D，则点C的坐标为，点D的坐标为．18．如图示直线y=√3x+√3与x轴、y轴分别交于点A、B，当直线绕着点A按顺时针方向旋转到与x轴首次重合时，点B运动到点B1，线段BB1长度为.三、综合题(共6题；共54分)19．如图，直线y=2x+1与x轴交于点A，与y轴交于点B．（1）求A、B两点的坐标；（2）过B点作直线BP与x轴交于点P，且使OP=2OA，求直线BP的函数关系式．20．如图，在直角坐标系中放入一个矩形纸片ABCO，将纸片翻折后，点B恰好落在x轴上，记为B′折痕为CE．直线CE的关系式是y=−12x+8，与x轴相交于点F，且AE=3．（1）OC=，OF=；（2）求点B′的坐标；（3）求矩形ABCO的面积．21．已知一次函数y=kx+b的图象经过点(0，1)和(1，-2)。

中考数学-一次函数正比例函数的图像及性质(含答案)专题练习

中考数学-一次函数正比例函数的图像及性质（含答案）专题练习一、单选题1.已知正比例函数y=kx（k≠0），点（2，-3）在函数上，则y随x的增大而（）A. 增大B. 减小C. 不变D. 不能确定2.已知函数y=x+k+1是正比例函数，则k的值为（）A.1B.﹣1C.0D.±13.正比例函数y=（2k+1）x，若y随x增大而减小，则k的取值范围是（）A. k＞﹣B. k＜﹣C. k=D. k=04.若正比例函数y=kx的图象经过点A（k，9），且经过第一、三象限，则k的值是（）A. ﹣9B. ﹣3C. 3D. ﹣3或35.若正比例函数y＝(1－2m)x的图象经过点A(x1，y1)和点B(x2，y2)，当x1< x2时，y1>y2，则m的取值范围是（）A. m<0B. m>0C.D.6.在下列四组点中，可以在同一个正比例函数图象上的一组点是（）A. （2，﹣3），（﹣4，6）B. （﹣2，3），（4，6）C. （﹣2，﹣3），（4，﹣6）D. （2，3），（﹣4，6）7.正比例函数y=kx（k≠0）的图像在第二、四象限，则一次函数y=x+k的图像大致是（）A. B. C. D.8.下列点不在正比例函数y=﹣2x的图象上的是（）A. （5，﹣10）B. （0，0）C. （2，﹣1）D. （1，﹣2）9.正比例函数y=（2k+1）x，若y随x增大而减小，则k的取值范围是（）A. k＞﹣B. k＜﹣C. k=D. k=010.关于函数y=﹣x，下列结论正确的是（）A. 函数图象必过点（﹣2，﹣1）B. 函数图象经过第1、3象限C. y随x的增大而减小D. y随x的增大而增大11.下列式子中，表示y是x的正比例函数的是（）A.y=x﹣1B.y=2xC.y=2x2D.y2=2x12.下列变量之间关系中，一个变量是另一个变量的正比例函数的是（）A. 正方形的面积S随着边长x的变化而变化B. 正方形的周长C随着边长x的变化而变化C. 水箱有水10L，以0.5L/min的流量往外放水，水箱中的剩水量V（L）随着放水时间t（min）的变化而变化D. 面积为20的三角形的一边a随着这边上的高h的变化而变化13.P1（x1，y1），P2（x2，y2）是正比例函数图象上的两点，下列判断中，正确的是A. y1＞y2B. y1＜y2C. 当x1＜x2时，y1＜y2D. 当x1＜x2时，y1＞y214.下列四个点中，在正比例函数的图象上的点是（）A. （2，5）B. （5，2）C. （2，—5）D. （5，—2）15.若正比例函数的图象经过点（2，﹣3），则这个图象必经过点（）A. （﹣3，﹣2）B. （2，3）C. （3，﹣2）D. （﹣2，3）16.下列关系中，是正比例关系的是（）A. 当路程s一定时，速度v与时间tB. 圆的面积S与圆的半径RC. 正方体的体积V与棱长aD. 正方形的周长C与它的一边长a17.下列问题中，两个变量成正比例关系的是（）A. 等腰三角形的面积一定，它的底边和底边上的高B. 等边三角形的面积与它的边长C. 长方形的长确定，它的周长与宽D. 长方形的长确定，它的面积与宽18.下列各点中，在正比例函数y＝－2x图象上的是（）A. （－2，－1）B. （1，2）C. （2，－1）D. （1，－2）19.一次函数y=4x，y=﹣7x，y=的共同特点是（）A. 图象位于同样的象限B. y随x增大而减小C. y随x增大而增大D. 图象都过原点二、填空题20.已知正比例函数y=kx（k是常数，k≠0），y随x的增大而减小，写出一个符合条件的k的值为________．21.写出一个正比例函数，使其图象经过第二、四象限：________．22.若函数y=（2m+6）x+（1﹣m）是正比例函数，则m的值是________．23.写一个图象经过第二、四象限的正比例函数：________24.将正比例函数y＝2x的图象向上平移3个单位，所得的直线不经过第________象限．答案解析部分一、单选题1.已知正比例函数y=kx（k≠0），点（2，-3）在函数上，则y随x的增大而（）A. 增大B. 减小C. 不变D. 不能确定【答案】B【考点】正比例函数的图象和性质【解析】【解答】∵点（2，-3）在正比例函数y=kx（k≠0）上，∴函数图象经过二四象限，∴y随着x的增大而减小，故选B【分析】首先根据函数的图象经过的点的坐标确定函数的图象经过的象限，然后确定其增减性即可2.已知函数y=x+k+1是正比例函数，则k的值为（）A.1B.﹣1C.0D.±1【答案】B【考点】正比例函数的图象和性质【解析】【解答】解：由题意，得k+1=0，解得k=﹣1，故选：B．【分析】根据正比例函数的定义，可得答案．3.正比例函数y=（2k+1）x，若y随x增大而减小，则k的取值范围是（）A. k＞﹣B. k＜﹣C. k=D. k=0 【答案】B【考点】正比例函数的图象和性质【解析】【解答】解：∵正比例函数y=（2k+1）x中，y的值随自变量x的值增大而减小，∴2k+1＜0，解得，k＜﹣；故选B．【分析】根据正比例函数图象与系数的关系列出关于k的不等式2k+1＜0，然后解不等式即可．4.若正比例函数y=kx的图象经过点A（k，9），且经过第一、三象限，则k的值是（）A. ﹣9B. ﹣3C. 3D. ﹣3或3 【答案】C【考点】正比例函数的图象和性质【解析】【解答】解：∵正比例函数y=kx（k≠0）的图象经过第一、三象限∴k＞0，把（k，9）代入y=kx得k2=9，解得k1=﹣3，k2=3，∴k=3，故选C．【分析】根据正比例函数的性质得k＞0，再把（k，9）代入y=kx得到关于k的一元二次方程，解此方程确定满足条件的k的值．5.若正比例函数y＝(1－2m)x的图象经过点A(x1，y1)和点B(x2，y2)，当x1< x2时，y1>y2，则m的取值范围是（）A. m<0B. m>0C.D.【答案】D【考点】正比例函数的图象和性质【解析】【分析】由题目所给信息“当x1＜x2时，y1＞y2”可以知道，y随x的增大而减小，则由一次函数性质可以知道应有：1-2m＜0，进而可得出m的取值范围．【解答】由题目分析可知：在正比例函数y=（1-2m)x中，y随x的增大而减小由一次函数性质可知应有：1-2m＜0，即-2m＜-1，解得：m＞．【点评】此题主要考查了一次函数的图象性质，只有掌握它的性质才能灵活运用．6.在下列四组点中，可以在同一个正比例函数图象上的一组点是（）A. （2，﹣3），（﹣4，6）B. （﹣2，3），（4，6）C. （﹣2，﹣3），（4，﹣6）D. （2，3），（﹣4，6）【答案】A【考点】正比例函数的图象和性质【解析】【分析】根据正比例函数关系式y=kx，可得k=，再依次分析各选项即可判断。

专题12 一次函数的图象和性质(原卷版)2021年中考数学二轮复习之难点突破热点解题方法

专题12 一次函数的图象和性质一、单选题1．如图，点C 、B 分别在两条直线y ＝﹣3x 和y ＝kx 上，点A 、D 是x 轴上两点，若四边形ABCD 是正方形，则k 的值为（）A ．3B ．2C ．23D ．32二、解答题 2．如图，在平面直角坐标系中，点O 为坐标原点，直线AB 与x 轴、y 轴分别交于B 、A 两点，OA OB =，AOB 的面积是8．（1）求点A 坐标；（2）点P 是第二象限直线AB 上一动点，连接OP ，把线段OP 绕点O 逆时针旋转90°得到线段OC ，设点P 的横坐标为t ，点C 的横坐标为m ，求出m 与t 的关系式，（不要求写出t 的取值范围）；（3）在（2）的条件下，且2t =-时，过点P 作PH x ⊥轴于H ，在PH 上取点K ，连接BK ，过点H 作HI BK ⊥于I ，延长HI 交PB 于点J ，连接KJ ，若PKJ HKB ∠=∠，求K 点坐标． 3．如图1，在平面直角坐标系中，直线1:3l y kx =+与直线2:6l y x =--交于点A ，已知点A 的横坐标为185-，直线1l 与x 轴交于点B ，与y 轴交于点C ，直线2l 与x 轴交于点F ，与y 轴交于点D ．（1）求直线1l 的解析式；（2）将直线2l 向上平移92个单位得到直线3l ，直线3l 与y 轴交于点E ，过点E 作y 轴的垂线4l ，若点M 为垂线4l 上的一个动点，点N 为2l 上的一个动点，求DM MN +的最小值；（3）已知点P Q 、分别是直线12l l 、上的两个动点，连接EP EQ PQ 、、，是否存在点P Q 、，使得EPQ △是以点Q 为直角顶点的等腰直角三角形，若存在，求点Q 的坐标若不存在，说明理由．4．如图，已知一次函数y ＝3x +3与y 轴交于点A ，与x 轴交于点B ，直线AC 与x 正半轴交于点C ，且AC ＝BC ．（1）求直线AC 的解析式；（2）点D 为线段AC 上一点，点E 为线段CD 的中点，过点E 作x 轴的平行线交直线AB 于点F ，连接DF 交x 轴于点G ，求证：AD ＝BG ；（3）在（2）的条件下，线段EF 、DG 分别与y 轴交于点M 、N ，若∠AFD ＝2∠BAO ，求线段MN 的长．5．如图1，在△ABC 中，BC=5，tan ∠ABC=2，tan ∠ACB=12，以边BC 所在直线为x 轴，建立直角坐标系，使得y 轴经过点A ，过点C 作AB 的平行线，交y 轴于点D ．（1）求直线CD 的解析式；（2）如图2，点P 是直线CD 上一个动点，①连接AP 、BP ，直线AP 把四边形ABPC 的面积分成2：3的两部分，求点P 的坐标；②当∠PBC=2∠BAO 时，直接写出此时点P 的坐标．6．如图，直线y ＝43x+4与x 轴、y 轴分别交于点A 和点B ．（1）求A ，B 两点的坐标；（2）过B 点作直线与x 轴交于点P ，若△ABP 的面积为8，试求点P 的坐标．（3）点M 是OB 上的一点，若将△ABM 沿AM 折叠，点B 恰好落在x 轴上的点B 1处，求出点M 的坐标．（4）点C 在y 轴上，连接AC ，若△ABC 是以AB 为腰的等腰三角形，请直接写出点C 的坐标．7．如图1，一次函数22y x =-+的图象与y 轴交于点A ，与x 轴交于点B ，过点B 作线段BC AB ⊥且BC AB =，直线AC 交x 轴于点D ．（1）点A 的坐标为______，点B 的坐标为______；（2）直接写出点C 的坐标______，并求出直线AC 的函数关系式；（3）若点P 是图1中直线AC 上的一点，连接OP ，得到图2．当点P 在第二象限，且到x 轴，y 轴的距离相等时，求出AOP 的面积；（4）若点Q 是图1中坐标平面内不同于点B 、点C 的一点，当以点C ，D ，Q 为顶点的三角形与BCD △全等时，直接写出点Q 的坐标．8．如图，直线6y kx =+与x 轴、y 轴分别相交于点E 、F ，点E 的坐标为()8,0-，点A 的坐标为()6,0-，点(),P x y 是第二象限内的直线上的一个动点．（1）求k 的值．（2）在点P 的运动过程中，写出OPA 的面积S 与x 的函数表达式，并写出自变量x 的取值范围．（3）已知()0,2Q -，当点P 运动到什么位置时，直线PQ 将四边形EPOQ 分成两部分，面积比为1:2，请直接写出P 点坐标．9．如图，在平面直角坐标系中，(,0)A m 、(0,)B n ，m 、n 满足2()|4|0m n m -+-=．点D 是x 轴正半轴上一动点．（1）OB 的长度为__________；（2）若点P 是线段AB 上一动点，且PO PD =，DE AB ⊥于E ．①如图，当点D 在线段OA 上时，PE 与AB 的数量关系为__________；②如图，当点D 在线段OA 的延长线上时，①中结论是否还成立？若成立，请证明；若不成立，说明理由；（3）如图，当点D 在线段OA 的延长线上时，连接BD ，以BD 为腰在其右侧作等腰Rt BDF ，90BDF ∠=，连接FA 并延长交y 轴于G 点，请问线段BG 的长度是否发生改变？若改变，请求出它的变化范围；若不变，求出它的长度．10．如图，已知直线113y x =+与x 轴交于点A ，与y 轴交于点B ，将△AOB 绕点O 顺时针旋转90︒后得到COD △．（1）点C 的坐标为_________，线段AD =_________；（2）点M 在CD 上，且CM OM =，抛物线2y x bx c =++经过点C M ，，求抛物线的解析式；（3）如果点E 在y 轴上，且位于点C 的下方，点F 在直线AC 上，那么在（2）中的抛物线上是否存在点P ，使得以C E F P ，，，为顶点的四边形是菱形？若存在，请求出该菱形的周长l ；若不存在，请说明理由．11．如图所示，在平面直角坐标系中，点A 坐标为（2， 0），点B 坐标为（3， 1），将直线AB 沿x 轴向左平移经过点C （1，1）．（1）求平移后直线L 的解析式；（2）若点P 从点C 出发，沿（1）中的直线L 以每秒1个单位长度的速度向直线L 与x 轴的交点运动，点Q 从原点O 出发沿x 轴以每秒2个单位长度的速度向点A 运动，两点中有任意一点到达终点运动即停止，设运动时间为t ．是否存在t ，使得△OPQ 为等腰三角形?若存在，直接写出此时t 的值：若不存在，请说明理由，12．如图1，在平面直角坐标系xOy 中，矩形ABCD 的边8AB =，20BC =，若不改变矩形ABCD 的形状和大小．（1）当矩形顶点C 在x 轴的正半轴上左右移动时，矩形的另一个顶点B 始终在y 轴的正半轴上随之上下移动．当30OCB ∠=︒时，求点A 的坐标．（2）如图2、3，长方形ABCD 中，BC 在x 轴上，且O 与B 重合．将矩形折叠，折痕GF 的一个端点F在边AD 上，另一个端点G 在边BC 上，且()100G ，，顶点B 的对应点为E ，连接BF ． ①如图2，当顶点B 的对应点E 落在边AD 上时，求折痕FG 的长．②如图3，当顶点B 的对应点E 落在长方形内部，E 的纵坐标为6，求AF 的长．13．如图，矩形AOBC 的两条边OA ，OB 的长是方程318800x x -+=的两根，其中OA OB <，沿直线AD 将矩形折叠，使点C 与y 轴上的点E 重合，（1）求A ，B 两点的坐标；（2）求直线AD 的解析式；（3）若点P 在y 轴上，平面内是否存在点Q ，使以A ，D ，P ，Q 为顶点的四边形为矩形？若存在，请直接写出点Q 的坐标；若不存在，请说明理由．14．如图，在平面直角坐标系中，已知矩形AOBC 的顶点C 的坐标是，动点P 从点A 出发，沿线段AO 向终点O 运动，同时动点Q 从点B 出发，沿线段BC 向终点C 运动．点P Q 、的运动速度均为每秒1个单位，运动时间为(06)t t <<秒，过点P 作PE AO ⊥交AB 于点E ．（1）求直线AB 的解析式；（2）设PEQ 的面积为S ，求当03t <<时，S 与t 时间的函数关系；（3）在动点P Q 、运动的过程中，点H 是矩形AOBC 内（包括边界）一点，且以B Q E H 、、、为顶点的四边形是菱形，直接写出t 值和与其对应的点H 的坐标．15．综合与探究：如图，在平面直角坐标系中，直线33:42l y x =+与x 轴交于点A ，与直线BC 交于点()2,B m ，直线BC与x 轴交于点()3,0C ．（1）求直线BC 的函数表达式；（2）在线段BC 上找一点D ，使得ABO ∆与ABD ∆的面积相等，求出点D 的坐标；（3）y 轴上有一动点P ，直线BC 上有一动点M ，若APM ∆是以线段AM 为斜边的等腰直角三角形，求出点M 的坐标．16．如图，在平面直角坐标系中，直线24y x =+与x 轴交于点A ，与y 轴交于点B ，过点B 的直线交x 轴于C ，且ABC ∆面积为10．（1）求点C 的坐标及直线BC 的解析式．（2）如图1设点F 为线段AB 中点，点G 为y 轴上一动点，连接FG ，以FG 为边向FG 右侧作以G 为直角顶点的等腰Rt FGQ ∆，在G 点运动过程中，当点Q 落在直线BC 上时，求点G 的坐标．（3）如图2，若M 为线段BC 上一点，且满足AMB AOB S S ∆∆=，点E 为直线AM 上一动点，在x 轴上是否存在点D ，使以点D ，E ，B ，C 为顶点的四边形为平行四边形？若存在，请直接写出点D 的坐标；若不存在，请说明理由．17．如图，在平面直角坐标系中，点O 是坐标原点，四边形ABCO 是菱形，点A 的坐标为()3,4-，点C 在x 轴的正半轴上，直线AC 交y 轴于点M ，AB 边交y 轴于点H ，连接BM ．（1）菱形ABCO 的边长是_______；（2）求直线AC 的解析式；（3）动点P 从点A 出发，沿折线ABC 方向以2个单位/秒的速度向终点C 匀速运动，设PMB △的面积为()0S S ≠，点P 的运动时间为t 秒，当点P 在AB 边上运动时，求S 与t 之间的函数关系式．18．综合与探究如图，在平面直角坐标系中，点A 、B 分别在x 轴y 轴的正半轴上，线段OA 的长是不等式()5432x x -<+的最大整数解，线段OB 的长是一元二次方程2230x x --=的一个根，将Rt ABO ∆沿BE 折叠，使AB 边落在OB 边所在的y 轴上，点A 与点D 重合．（1）求OA 、OB 的长；（2）求直线BE 的解析式；（3）在平面内是否存在点M ，使B 、O 、E 、M 为顶点的四边形为平行四边形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．。

初中数学一次函数的图象和性质

一次函数的图象和性质一、知识要点：1、一次函数：若两个变量x,y存在关系为y=kx+b (k≠0, k,b为常数)的形式，则称y是x的函数。

注意：（1）k≠0,否则自变量x的最高次项的系数不为1；（2）当b=0时，y=kx，y叫x的正比例函数。

2、图象：一次函数的图象是一条直线（1）两个常有的特殊点：与y轴交于（0，b）；与x轴交于（- ，0）。

（2）正比例函数y=kx(k≠0)的图象是经过（0，0）和（1，k）的一条直线；一次函数y=kx+b(k≠0)的图象是经过（- ，0）和（0，b）的一条直线。

（3）由图象可以知道，直线y=kx+b与直线y=kx平行，例如直线：y=2x+3与直线y=2x-5都与直线y=2x平行。

3、一次函数图象的性质：（1）图象在平面直角坐标系中的位置:（2）增减性：k>0时，y随x增大而增大；k<0时，y随x增大而减小。

4、求一次函数解析式的方法求函数解析式的方法主要有三种：一是由已知函数推导，如例题1；二是由实际问题列出两个未知数的方程，再转化为函数解析式，如例题4的第一问。

三是用待定系数法求函数解析式，如例2的第二小题、例7。

其步骤是：①根据题给条件写出含有待定系数的解析式；②将x、y的几对值或图象上几个点的坐标代入上述的解析式中，得到以待定系数为未知数的方程或方程组；③解方程，得到待定系数的具体数值；④将求出的待定系数代入要求的函数解析式中。

二、例题举例：例1、已知变量y与y1的关系为y=2y1,变量y1与x的关系为y1=3x+2，求变量y与x的函数关系。

分析：已知两组函数关系，其中共同的变量是y1,所以通过y1可以找到y与x 的关系。

解：∵y=2y1y1=3x+2,∴y=2(3x+2)=6x+4,即变量y与x的关系为：y=6x+4。

例2、解答下列题目（1）（甘肃省中考题）已知直线与y轴交于点A，那么点A的坐标是（）。

（A）（0，–3）（B）（C）（D）（0，3）（2）(杭州市中考题)已知正比例函数，当x=–3时，y=6．那么该正比例函数应为（）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

三、解答题 1．（2010浙江绍兴）在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形, 叫做此一次函数的坐标三角形.例如，图中的一次函数的图象与 x ,y 轴分别交于点A ,B ,则△OAB 为此函数的坐标三角形.（1）求函数y ＝43-x ＋3的坐标三角形的三条边长；（2）若函数y ＝43-x ＋b （b 为常数）的坐标三角形周长为16, 求此三角形面积.【答案】解：(1) ∵ 直线y ＝43-x ＋3与x 轴的交点坐标为（4,0），与y 轴交点坐标为（0,3）， ∴函数y ＝43-x ＋3的坐标三角形的三条边长分别为3,4,5.(2) 直线y ＝43-x ＋b 与x 轴的交点坐标为（b 34,0），与y 轴交点坐标为（0,b ），当b >0时,163534=++b b b ，得b =4，此时,坐标三角形面积为332；当b <0时，163534=---b b b ，得b =－4，此时,坐标三角形面积为332.综上,当函数y ＝43-x ＋b 的坐标三角形周长为16时,面积为332．2．（2010江西）已知直线经过点（1，2）和点（3，0），求这条直线的解读式.【答案】解：设这直线的解读式是(0)y kx b k =+≠，将这两点的坐标（１，２）和（３，０）代入，得2,30,k b k b +=⎧⎨+=⎩，解得1,3,k b =-⎧⎨=⎩所以，这条直线的解读式为3y x =-+．3．（2010北京）如图，直线y =2x +3与x 轴相交于点A ，与y 轴相交于点B .⑴ 求A ，B 两点的坐标；⑵ 过B 点作直线BP 与x 轴相交于P ，且使OP =2OA ，求ΔABP 的面积.Ay OB x第21题图【答案】解(1)令y=0，得x=32-∴A点坐标为(32-，0).令x=0，得y=3∴B点坐标为(0，3).(2)设P点坐标为(x，0)，依题意，得x=±3. ∴P点坐标为P1(3，0)或P2(－3，0).∴S△ABP1=13(3)322⨯+⨯=274S△ABP2=13(3)322⨯-⨯=94.∴△ABP的面积为274或94.4．（2010湖北随州）某同学从家里出发，骑自行车上学时，速度v（M/秒）与时间t（秒）的关系如图a，A（10，5），B（130，5），C（135，0）.（1）求该同学骑自行车上学途中的速度v与时间t的函数关系式；（2）计算该同学从家到学校的路程（提示：在OA和BC段的运动过程中的平均速度分别等于它们中点时刻的速度，路程＝平均速度×时间）；（3）如图b，直线x＝t（0≤t≤135），与图a的图象相交于P、Q，用字母S表示图中阴影部分面积，试求S与t的函数关系式；（4）由（2）（3），直接猜出在t时刻，该同学离开家所超过的路程与此时S的数量关系.图a图b【答案】（1）1(010)25(10130)135(130135) v t tv tv t t⎧=≤<⎪⎪=≤<⎨⎪=-≤≤⎪⎩（2）2.5×10+5×120+2×5＝635（M ）（3）221(010)4525(10130)1(130135)2S t t S t t S t t ⎧=≤<⎪⎪=-≤<⎨⎪⎪=-≤≤⎩ +135t-8475 (4) 相等的关系5．（2010陕西西安）某蒜薹（t ái ）生产基地喜获丰收，收获蒜薹200吨，经市场调查，可采用批发、零售、冷库储藏后销售三种方式，并且按这三种方式销售，计划每吨平均的售价及成本如下表：销售方式批发零售储藏后销售售价（元/吨） 3 000 4 500 5 500 成本（元/吨）7001 0001 200若经过一段时间，蒜薹按计划全部售出获得的总利润为y （元），蒜薹零售x （吨），且零售量是批发量的.31（1）求y 与x 之间的函数关系式；（2）由于受条件限制，经冷库储藏售出的蒜薹最多80吨，求该生产基地按计划全部售完蒜薹获得的最大利润。

【答案】解：（1）由题意，得批发蒜薹3x 吨，储藏后销售)4200(x -吨，则)12005500()4200()10004500()7003000(3-⋅-+-⋅+-⋅=x x x y.8600006800+-=x（2）由题意，得.30,.804200≥≤-x x 得解之..06800,8600006800的值增大而减小的值随x y x y ∴<-+-=∴当.656000860000306800,30=+⨯-==最大值时y x∴该生产基地按计划全部售完蒜薹获得的最大利润为656 000元。

6．（2010陕西西安）问题探究（1）请你在图①中作一条．．直线，使它将矩形ABCD 分成面积相等的两部分；（2）如图②，点M 是矩形ABCD 内一定点，请你在图②中过点M 作一条直线，使它将矩形ABCD 分成面积相等的两部分。

问题解决（3）如图③，在平面直角坐标系中，直角梯形OBCD 是某市将要筹建的高新技术开发区用地示意图，其中CD//OB ，OB=6，BC=4，CD=4。

开发区综合服务经管委员会（其占地面积不计）设在点P （4，2）处，为了方便驻区单位，准备过点P 修一条笔直的道路（路的宽度不计），并且使这条路所在的直线l 将直角梯形OBCD 分成面积相等的两部分，你认为直线l 是否存在？若存在，求出直线l 的表达式；若不存在，请说明理由。

【答案】解：（1）如图①，作直线DB ，直线DB 即为所求。

（所求直线不唯一，只要过矩形对称中心的直线均可）（2）如图②，连接AC 、DB 交于点P ，则点P 为矩形ABCD 的对称中心，作直线MP ，直线MP 即为所求（3）如图③，存在符合条件的直线l ，过点D 作DA ⊥OB 于点A ，则点P （4，2）为矩形ABCD 的对称中心 ∴过点P 的直线只要平分DOA ∆的面积即可。

易知，在OD 边上必存在点H ，使得直线PH 将DOA ∆面积平分，从而，直线PH 平分梯形OBCD 的面积。

即直线PH 为所求直线.l设直线PH 的表达式为,b kx y +=且点)2,4(P.42,42k b b k -=+=∴即∵直线OD 的表达式为.2x y =⎩⎨⎧=-+=∴.2,42x y k kx y 解之，得⎪⎪⎩⎪⎪⎨⎧--=--=.284,242k k y k k x ∴点H 的坐标为).284,242(kk k k ---- ∴PH 与线段AD 的交点F 的坐标为),22,2(k -.11.4220<<-∴<-<∴k k∴.422121)2422()224(21⨯⨯⨯=---⋅+-=∆k k k S DHF 解之，得)2313.(2313舍去不合题意，k k --=-=.1328-=∴b∴直线l 的表达式为.13282313-+-=x y 7．（2010江西省南昌）已知直线经过点（1,2）和点（3,0），求这条直线的解读式. 【答案】解：设这条直线的解读式为b kx y +=，把两点的坐标（1，2），（3，0）代入，得⎩⎨⎧=+=+.03,2b k b k 解得⎩⎨⎧=-=.3,1b k所以，这条直线的解读式为3+-=x y .8．（2010湖北襄樊）为了扶持农民发展农业生产，国家对购买农机的农户给予农机售价13%的政府补贴．某市农机公司筹集到资金130万元，用于一次性购进A 、B 两种型号的收割机共30台．根据市场需求，这些收割机可以全部销售，全部销售后利润不少于15万元．其中，收割机的进价和售价见下表：A 型收割机B 型收割机进价（万元/台） 5.3 3.6 售价（万元/台）64设公司计划购进A 型收割机x 台，收割机全部销售后公司获得的利润为y 万元．（1）试写出y 与x 的函数关系式；（2）市农机公司有哪几种购进收割机的方案可供选择？（3）选择哪种购进收割机的方案，农机公司获利最大？最大利润是多少？此种情况下，购买这30台收割机的所有农户获得的政府补贴总额W 为多少万元？【答案】解：（1）y =(6－5.3)x +(4－3.6)(30－x )=0.3x +12．（2）依题意，有 5.3(30) 3.6130,0.31215.x x x +-⨯⎧⎨+⎩≤≥即1612,1710.x x ⎧⎪⎨⎪⎩≤≥ ∴10≤x ≤121617．∵x 为整数，∴x =10，11，12．即农机公司有三种购进收割机的方案可供选择：方案1：购A 型收割机10台，购B 型收割机20台；方案2：购A 型收割机11台，购B 型收割机19台；方案3：购A 型收割机12台，购B 型收割机18台．（3）∵0.3＞0，∴一次函数y 随x 的增大而增大．即当x =12时，y 有最大值，y 最大=0.3×12+12=15.6（万元）．此时，W=6×13%×12+4×13%×18=18.72（万元）． 9．（2010 江苏镇江）运算求解在直角坐标系xOy 中，直线l 过（1，3）和（3，1）两点，且与x 轴，y 轴分别交于A ，B 两点.（1）求直线l 的函数关系式；（2）求△AOB 的面积.【答案】（1）设直线l 的函数关系式为)0(≠+=k b kx y ， ① （1分）把（3，1），（1，3）代入①得⎩⎨⎧=+=+,3,13b k b k （2分）解方程组得⎩⎨⎧=-=.4,1b k （3分）∴直线l 的函数关系式为.4+-=x y ② （4分）（2）在②中，令)0,4(,4,0),4,0(,4,0A x y B y x ∴==∴==得令得（5分）.8442121=⨯⨯=⋅=∴∆BO AO S AOB （6分）10．（2010 贵州贵阳）如图7，直线与x 轴、y 轴分别交于A 、B 两点. （1）将直线AB 绕原点O 沿逆时针方向旋转90°得到直线11B A . 请在《答题卡》所给的图中画出直线11B A ，此时直线AB 与11B A 的位置关系为（填“平行”或“垂直”）（6分）（2）设（1）中的直线AB 的函数表达式为111b x k y +=，直线11B A 的函数表达式为222b x k y +=，则k 1·k 2=.（4分）【答案】（1）如图所示，………………………………3分垂直………………………………………6分（2）－1………………………………………10分11．（2010宁夏回族自治区）如图，已知：一次函数：4y x =-+的图像与反比例函数：2y x=(0)x >的图像分别交于A 、B 两点，点M 是一次函数图像在第一象限部分上的任意一点，过M 分别向x 轴、y 轴作垂线，垂足分别为M 1、M 2，设矩形MM 1OM 2的面积为S 1；点N 为反比例函数图像上任意一点，过N 分别向x 轴、y 轴作垂线，垂足分别为N 1、N 2，设矩形NN 1ON 2的面积为S 2；（1）若设点M 的坐标为(x ，y )，请写出S 1关于x 的函数表达式，并求x 取何值时，S 1的最大值；（2）观察图形，通过确定x 的取值，试比较S 1、S 2的大小．【答案】(1)x x x x S 4)4(21+-=+-= ------------------2分=4)2(2+--x当2=x 时，41=最大值S -------------------------4分（2）∵2S 2=由21S S =可得：24x 2=+-x0242=--x x（图7）A 1B1∴22±=x ----------------------------------5分通过观察图像可得：当22±=x 时，21S S =当22220+>-<<x x 或时，21S S < 当2222+<<-x 时，21S S > -----------------------------------------8分12．（2010 湖北咸宁）在一条直线上依次有A 、B 、C 三个港口，甲、乙两船同时分别从A 、B 港口出发，沿直线匀速驶向C 港，最终达到C 港．设甲、乙两船行驶x （h ）后，与．B ．港的．．距离．．分别为1y 、2y （km ），1y 、2y 与x 的函数关系如图所示．（1）填空：A 、C 两港口间的距离为km ，=a ；（2）求图中点P 的坐标，并解释该点坐标所表示的实际意义；（3）若两船的距离不超过10 km 时能够相互望见，求甲、乙两船可以相互望见时x 的取值范围．【答案】解：（1）120，2a =；……2分（2）由点（3，90）求得，230y x =．当x ＞0.5时，由点（0.5，0），（2，90）求得，16030y x =-．……3分当12y y =时，603030x x -=，解得，1x =．此时1230y y ==．所以点P 的坐标为（1，30）．……5分该点坐标的意义为：两船出发1 h 后，甲船追上乙船，此时两船离B 港的距离为30 km ．…6分求点P 的坐标的另一种方法：由图可得，甲的速度为30600.5=（km/h ），乙的速度为90303=（km/h ）．则甲追上乙所用的时间为3016030=-（h ）．此时乙船行驶的路程为30130⨯=（km ）．所以点P 的坐标为（1，30）．（3）①当x ≤0.5时，由点（0，30），（0.5，0）求得，16030y x =-+．依题意，(6030)30x x -++≤10．解得，x ≥23．不合题意．……7分②当0.5＜x ≤1时，依题意，30(6030)x x --≤10．解得，x ≥23．所以23≤x ≤1．……8分③当x ＞1时，依题意，(6030)30x x --≤10．O y/km 9030 a0.53P（第23题）甲乙x/h解得，x ≤43．所以1＜x ≤43．……9分综上所述，当23≤x ≤43时，甲、乙两船可以相互望见．……10分13．（2010青海西宁）如图12，直线y=kx-1与x 轴、y 轴分别交与B 、C 两点，tan∠OCB=21. （1）求B 点的坐标和k 的值；（2）若点A （x ，y ）是第一象限内的直线y=kx-1上的一个动点.当点A 运动过程中，试写出△AOB 的面积S 与x 的函数关系式；（3）探索：①当点A 运动到什么位置时，△AOB 的面积是41； ②在①成立的情况下，x 轴上是否存在一点P ，使△POA 是等腰三角形.若存在，请写出满足条件的所有P 点的坐标；若不存在，请说明理由.图12【答案】解：（1）∵y= kx-1与y 轴相交于点C ，∴OC=1∵tan ∠OCB=OC OB =21∴OB=21∴B 点坐标为：⎪⎭⎫ ⎝⎛021，把B 点坐标为：⎪⎭⎫ ⎝⎛021，代入y= kx-1得 k=2 （2）∵S = y 21⨯⨯OB ∵y=kx-1 ∴S =()1-x 22121⨯ ∴S =4121-x（3）①当S =41时，4121-x =41∴x=1，y=2x-1=1∴A 点坐标为（1，1）时，△AOB 的面积为41 ②存在.满足条件的所有P 点坐标为： P 1(1,0), P 2(2,0), P 3(2,0), P 4(2-,0). ……………………………12分14．（2010新疆乌鲁木齐）如图6，在平面直角坐标系中，直线434:+-=x y l 分别交x 轴、y 轴于点A 、B ，将△AOB 绕点O 顺时针旋转90°后得到△A ′OB ′（1）求直线A ′B ′的解读式；（2）若直线A ′B ′与直线l 相交于点，求△ABC 的面积。