陕西近10年中考数学真题及副题整理专题
陕西中考数学十年压轴题汇总

25.(本题满分12分)已知:直线a ∥b ,P 、Q 是直线a 上的两点,M 、N 是直线b 上两点。
(1)如图①,线段PM 、QN 夹在平行直线a 和b 之间,四边形PMNQ 为等腰梯形,其两腰PM =QN 。
请你参照图①,在图②中画出异于图①的一种图形,使夹在平行直线a 和b 之间的两条线段相等。
(2)我们继续探究,发现用两条平行直线a 、b 去截一些我们学过的图形,会有两条“曲线段相等”(曲线上两点和它们之间的部分叫做“曲线段”。
把经过全等变换后能重合的两条曲线段叫做“曲线段相等”)。
请你在图③中画出一种图形,使夹在平行直线a 和b 之间的两条曲线段相等。
(3)如图④,若梯形PMNQ 是一块绿化地,梯形的上底PQ =m ,下底MN =n ,且m <n 。
现计划把价格不同的两种花草种植在S 1、S 2、S 3、S 4四块地里,使得价格相同的花草不相邻。
为了节省费用,园艺师应选择哪两块地种植价格较便宜的花草?请说明理由。
25.(本题满分12分)王师傅有两块板材边角料,其中一块是边长为60cm 的正方形板子;另一块是上底为30cm ,下底为120cm ,高为60cm 的直角梯形板子(如图①),王师傅想将这两块板子裁成两块全等的矩形板材。
他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCDE 围成的区域(如图②),由于受材料纹理的限制,要求裁出的矩形要以点B 为一个顶点。
(1)求FC 的长;(2)利用图②求出矩形顶点B 所对的顶点.....到BC 边的距离)(cm x 为多少时,矩形的面积最大?最大面积时多少?(3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长。
25.(本题满分12分) 如图,O e的半径均为R .(1)请在图①中画出弦AB CD ,,使图①为轴对称图形而不是..中心对称图形;请在图②中画出弦AB CD ,,使图②仍为中心对称图形; (2)如图③,在O e中,(02)AB CD m m R ==<<,且AB 与CD 交于点E ,夹角为锐角α.求四边形ACBD 面积(用含m α,的式子表示); (3)若线段AB CD ,是O e的两条弦,且AB CD ==,你认为在以点A B C D ,,,为顶点的四边形中,是否存在面积最大的四边形?请利用图④说明理由.存在的饮水困难问题,想在这三个地方的其中一处建一所供水站,由供水站直接铺设管道到另外两处。
2013~2019陕西中考数学真题及其2019副题

1 14. 如图,点 O 是▱ABCD 的对称中心,AD>AB,E、F 是 AB 边上的点,且 EF= AB;G、H 是 BC 边上的
2
1
点,且
GH= BC.若 3
S1,S2
分别表示△EOF
和△GOH
的面积,则
S1
与
S2
之间的等量关系是________.
三、解答题(共 11 小题,计 78 分.解答应写出过程)
16.(本题满分 5 分)
解方程:
5x x2
8 9
1
3 x
x 3
17.(本题满分 5 分) 如图,已知∠AOB,点 M 在边 OA 上.请用尺规作图法,求作⊙M,使⊙M 与 OB 相切.(保留作图痕迹,不写做法)
3
18.(本题满分 5 分) 如图,在△ABC 中,D 是 BC 的中点,过点 D 做 DE//AB,并与 AC 交于点
2019 陕西中考数学试卷及解析
解:设古树AB高度为x
过C作AB的垂线CH,垂足为H,则BH=CD=0.5米
∵∠ACH=45°
∴CH=AH=AB-HB=x-0.5
CH=BD=x-0.5
在 EFG和 ABG中
由题意得:∠EGF=∠AGB
EF⊥AB AB⊥FB
∴ EFG∽ ABG
EF FG 1.6
BD,则∠DBC 的大小为( )
A. 15° B. 35° C. 25° D. 45°
10. 对于抛物线 y=ax2+(2a-1)x+a-3,当 x=1 时,y>0,则这条抛物线的顶点一定在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
第二部分(非选择题 共 90 分)
陕西近10年中考数学真题及副题选择题

陕西近7年中考数学真题及副题选择题一、选择题(共14小题,每小题3分,计30分.每小题只有一个选项是符合题意的) 1. 计算:(-3)0=( )(2019)A. 1B.0 C 3 D.131、下列四个实数中,最大的是( ) (2019副) A. 2 B.3 C. 0 D. ﹣11. -78的相反数是()(2018)A .-87 B. 87 C .-78 D. 781. -711的倒数是( )(2018副)A.711 B. -711 C. 117 D. -1171、 计算:(-12)2-1=( )(2017)A. -54B. -14C. -34 D. 01. 计算: 3-2=( )(2017副)A. -19B. 19C. -6D. -161. 计算:(-12)×2=( )(2016)A. -1B. 1C. 4D. -41.计算:(-3)×(-13)=( )(2016副)A.-1B.1C.-9D.9 1. 计算:(-23)0=( )(2015)A. 1B. -32C. 0D. 231.下列四个实数中,最大的是( )(2015副)A.0B.3C.2D.-1 1. 计算:(-3)2=( )(2014副)A. -6B. 6C. -9D. 91. 4的算术平方根是( )(2014)A. -2B. 2C. -12D. 121.-23的倒数是( )(2013副)A.-32B.32C.-23D.231.下列四个数中最小的数是( )(2013) A.-2 B.0 C.13D.52. 如图,是由两个正方体组成的几何体,则该几何体的俯视图为( )(2019)2.下列图形中,经过折叠可以得到四棱柱的是 ( )(2018副)2. 如图,是一个几何体的表面展开图,则该几何体是( )2018)A. 正方体B. 长方体C. 三棱柱D. 四棱锥2.如图的几何体是由一平面将一圆柱体截去一部分后所得,则该几何体的俯视图是()(2017副)2. 如图所示的几何体是由一个长方体和一个圆柱体组成的,则它的主视图是( )(2017)2.如图,下面的几何体由两个大小相同的正方体和一个圆柱体组成,则它的左视图是()(2016副)2. 如图,下面的几何体由三个大小相同的小立方块组成,则它的左视图是()(2016)2、如图是一枚古钱币的示意图,它的左视图是()(2015副)2. 如图是一个螺母的示意图,它的俯视图是()(2015)2、如图,下面几何体是由一个圆柱被经过上下底面圆心的平面截得的,则它的左视图是()(2014副)2、下图是一个正方体被截去一个直三棱柱得到的几何体,则该几何体的左视图是() (2014)2、如图,将直角三角形绕其一条直角边所在直线l旋转一周,得到的几何体是()(2013副)2、如图,下面的几何体是由一个圆柱和一个长方体组成的,则它的俯视图是()(2013)3.如图,OC是∠AOB的平分线,l OB,若∠1=52º,则∠2的度数为()(2019)A.52ºB.54ºC.64ºD.69º3. 如图,直线a∥b,在Rt△ABC中,∠C=90°,AC⊥b,垂足为A,则图中与∠1互余的角有()(2018副)A.2个B.3个C.4个D.5个3. 如图,若l1∥l2,l3∥l4,则图中与∠1互补的角有()(2018)A. 1个B. 2个C. 3个D. 4个3 如图,直线a∥b,点A在直线b上,∠BAC=108°,∠BAC的两边与直线a分别交于B、C两点.若∠1=42°,则∠2的大小为()(2017副)A. 30°B. 38°C. 52°D. 72°3. 如图,直线a∥b,Rt△ABC的直角顶点B落在直线a上.若∠1=25°,则∠2的大小为()(2017)A. 55°B. 75°C. 65°D. 85°3..如图,AB∥CD.若∠1=40°,∠2=65°,则∠CAD=()(2016副)A.50°B.65°C.75°D.85°3.如图,AB∥CD,AE平分∠CAB交CD于点E.若∠C=50°,则∠AED=()(2016)A. 65°B. 115°C. 125°D. 130°3、如图,AB∥CD,直线EF交直线AB、CD于点E、F,FH平分∠CFE.若∠EFD=70°,则∠EHF的度数为()(2015副)A.35°B.55°C.65°D.70°3、. 如图,AB∥CD,直线EF分别交直线AB、CD于点E、F.若∠1=46°30′,则∠2的度数为()(2015)A. 43°30′B. 53°30′C. 133°30′D. 153°30′3. 如图,∠B=40°,∠ACD=108°.若B、C、D三点在一条直线上,则∠A的大小是()(2014副)(第4题图)A. 148°B. 78°C. 68°D. 50°3. 小军旅行箱的密码是一个六位数,由于他忘记了密码的末位数字,则小军能一次打开该旅行箱的概率是()(2014)A. 110 B.19 C.16 D.153、.如图,AB∥CD,AE平分∠CAB交CD于点E.若∠C=50°,则∠AED的大小为()(2013副)(第4题图)A.55°B.105°C.65°D.115°3.如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D的大小为()(2013)A.65°B.55°C.45°D.35°。
陕西省中考数学历年(2016-2022年)真题分类汇编习题集(真题解析版)

一、单选题陕西省中考数学历年(2016-2022 年)真题分类汇编专题 1 实数【知识点】相反数及有理数的相反数【解析】【解答】解:-37 的相反数是37.1.计算:(﹣1)×2=()2A.﹣1 B.1 C.4 D.﹣4【答案】A【知识点】有理数的乘法【解析】【解答】解:原式=﹣1,故选 A【分析】原式利用乘法法则计算即可得到结果.此题考查了有理数的乘法,熟练掌握运算法则是解本题的关键.故答案为:B.【分析】根据只有符号不同的两个数互为相反数进行解答.5.计算:3 × (−2) = ()A.1 B.-1 C.6 D.-6 【答案】D【知识点】有理数的乘法【解析】【解答】解: 3 × (−2) = −6 ;故答案为:D.2.计算:(﹣A.﹣5 4【答案】C 1)2﹣1=()2B.﹣14C.﹣34D.0【分析】根据有理数的乘法法则“两数相乘,同号得正,异号得负,并把绝对值相乘”可求解.6.2019 年,我国国内生产总值约为990870 亿元,将数字990870 用科学记数法表示为()A.9.9087×105 B.9.9087×104C.99.087×104 D.99.087×103【知识点】有理数的加减乘除混合运算【解析】【解答】原式= 1﹣1=﹣3,4 4故答案为:C【分析】根据有理数的乘方和减法法则即可得出答案.7【答案】A【知识点】科学记数法—表示绝对值较大的数【解析】【解答】解:990870=9.9087×105.故答案为:A.【分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,确定n 的值时,要看把原数变成 a3.-的倒数是()11时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.A.711【答案】D【知识点】有理数的倒数B.-711C.117D.-1177.如图,是A 市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是()A.4℃B.8℃C.12℃D.16℃【答案】C【解析】【解答】∵(−7 ) × (−11=1,【知识点】函数的图象;有理数的减法∴-71111 7)的倒数是-11,7【解析】【解答】解:从折线统计图中可以看出,这一天中最高气温8℃,最低气温是﹣4℃,这一天中最高气温与最低气温的差为12℃,故答案为:D.【分析】根据乘积为1 的两个数,叫做互为倒数,即可得出答案。
陕西省中历年中考数学试卷(10)

陕西省初中毕业学业考试(全卷共120分,考试时间120分钟)第Ⅰ卷(选择题共30分)一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)1.计算:023⎛⎫-⎪⎝⎭=()A.1B.32- C.0 D.322.如图是一个螺母的示意图,它的俯视图是第2题图A B C D3.下列计算正确的是()A.a2·a3=a6B.(-2ab)2=4a2b2C.(a2)3=a5D.3a3b2÷a2b2=3ab4.如图,AB∥CD,直线EF分别交直线AB,CD于点E,F.若∠1=46°30′,则∠2的度数为()A.43°30′B.53°30′C.133°30′D.153°30′第4题图5.设正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则m=()A.2B.-2C.4D.-46.如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有()A.2个B.3个C.4个D.5个第6题图7.不等式组11322(3)0xx x⎧+≥-⎪⎨⎪-->⎩的最大整数解为()A.8B.6C.5D.48.在平面直角坐标系中,将直线l1:y=-2x-2平移后,得到直线l2:y=-2x+4,则下列平移作法正确的是()A.将l1向右平移3个单位长度B.将l1向右平移6个单位长度C.将l1向上平移2个单位长度D.将l1向上平移4个单位长度9.在平行四边形ABCD中,AB=10,BC=14,E,F分别为边BC,AD上的点,若四边形AECF为正方形,则AE的长为()A.7B.4或10C.5或9D.6或810.下列关于二次函数y=ax2-2ax+1(a>1)的图象与x轴交点的判断,正确的是()A.没有交点B.只有一个交点,且它位于y轴右侧C.有两个交点,且它们均位于y轴左侧D.有两个交点,且它们均位于y轴右侧第Ⅱ卷(非选择题共90分)二、填空题(共4小题,每小题3分,计12分)11.将实数5,π,0,-6由小到大用“<”号连起来,可表示为_____________________.12.(节选)正八边形一个内角的度数为_______________.13.如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=4x的图象交于A,B两点,则四边形MAOB的面积为____________.第13题图14.如图,AB是⊙O的弦,AB=6,点C是⊙O上的一个动点,且∠ACB=45°.若点M,N分别是AB,BC的中点,则MN长的最大值是__________.第14题图三、解答题(共11小题,计78分.解答应写出过程)15.(本题满分5313(6)|22|2-⎛⎫+-+ ⎪⎝⎭.16.(本题满分5分)解分式方程:13332=--+-x x x .17.(本题满分5分)如图,已知△ABC ,请用尺规过点A 作一条直线,使其将△ABC 分成面积相等的两部分(保留作图痕迹,不写作法).第17题图18.(本题满分5分)某校为了了解本校九年级女生体育测试项目“仰卧起坐”的训练情况,让体育老师随机抽查了该年级若干名女生,并严格地对她们进行了1分钟“仰卧起坐”测试,同时统计了每个人做的个数(假设这个个数为x ),现在我们将这些同学的测试结果分为四个等级:优秀(x ≥44)、良好(36≤x ≤43)、及格(25≤x ≤35)和不及格(x ≤24),并将统计结果绘制成如下两幅不完整的统计图. 根据以上信息,解答下列问题:(1)补全上面的条形统计图和扇形统计图;(2)被测试女生1分钟“仰卧起坐”个数的中位数落在___________等级;(3)若该年级有650名女生,请你估计该年级女生中1分钟“仰卧起坐”个数达到优秀的人数.第18题图19.(本题满分7分)如图,在△ABC 中,AB =AC ,作AD ⊥AB 交BC 的延长线于点D ,作AE ∥BD ,CE ⊥AC ,且AE ,CE 相交于点E ,求证:AD =CE .第19题图20.(本题满分7分)晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ 移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长(结果精确到0.01米).第20题图21.(本题满分7分)胡老师计划组织朋友暑假去革命圣地延安两日游,经了解,现有甲、乙两家旅行社比较合适,报价均为每人640元,且提供的服务完全相同,针对组团两日游的游客,甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按七五折收费,假设组团参加甲、乙两家旅行社两日游的人数均为x人.(1)请分别写出甲、乙两家旅行社收取组团两日游的总费用y(元)与x(人)之间的函数关系式;(2)若胡老师组团参加两日游的人数共有32人,请你通过计算,在甲、乙两家旅行社中,帮助胡老师选择收取总费用较少的一家.22.(本题满分7分)某中学要在全校学生中举办“中国梦·我的梦”主题演讲比赛,要求每班选一名代表参赛.九年级(1)班经过投票初选,小亮和小丽票数并列班级第一,现在他们都想代表本班参赛.经班长与他们协商决定,用他们学过的掷骰子游戏来确定谁去参赛(胜者参赛).规则如下:两人同时随机各掷一枚完全相同且质地均匀的骰子一次,向上一面的点数都是奇数,则小亮胜;向上一面的点数都是偶数,则小丽胜;否则,视为平局,若为平局,继续上述游戏,直至分出胜负为止.如果小亮和小丽按上述规则各掷一次骰子,那么请你解答下列问题:(1)小亮掷得向上一面的点数为奇数的概率是多少?(2)该游戏是否公平?请用列表或树状图等方法说明理由(骰子:六个面上分别刻有1,2,3,4,5,6个小圆点的小正方体).23.(本题满分8分)如图,AB是⊙O的直径,AC是⊙O的弦,过点B作⊙O的切线DE,与AC的延长线交于点D,作AE⊥AC交DE于点E.(1)求证:∠BAD=∠E;(2)若⊙O的半径为5,AC=8,求BE的长.第23题图24.(本题满分10分)在平面直角坐标系中,抛物线y=x2+5x+4的顶点为M,与x轴交于A,B两点,与y轴交于C点.(1)求点A,B,C的坐标;(2)求抛物线y=x2+5x+4关于坐标原点O对称的抛物线的函数表达式;(3)设(2)中所求抛物线的顶点为M′,与x轴交于A′,B′两点,与y轴交于C′点,在以A,B,C,M,A′,B′,C′,M′这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积.25.(本题满分12分)如图,在每一个四边形ABCD中,均有AD∥BC,CD⊥BC,∠ABC=60°,AD=8,BC=12.(1)如图①,点M是四边形ABCD边AD上的一点,则△BMC的面积为________;(2)如图②,点N是四边形ABCD边AD上的任意一点,请你求出△BNC周长的最小值;(3)如图③,在四边形ABCD的边AD上,是否存在一点P,使得cos∠BPC的值最小?若存在,求出此时cos∠BPC的值;若不存在,请说明理由.第25题图参考答案1.A2.B 【解析】从上往下看外面是一个正六边形,里面是一个没有圆心的圆.故选B.3.B 【解析】A.a 2·a 3=a 5,故错误;B.正确;C.(a 2)3=a 6,故错误;D.3a 3b 2÷a 2b 2=3a ,故错误.故选B.4.C 【解析】∵AB ∥CD ,∠1=46°30′,∴∠EFD =∠1=46°30′,∴∠2=180°-46°30′=133°30′.故选C.5.B 【解析】把A (m ,4)代入y =mx 中,可得m =±2,∵y 的值随x 值的增大而减小,∴m =-2.故选B.6.D 【解析】∵AB =AC ,∴△ABC 是等腰三角形;∵AB =AC ,∠A =36°,∴∠ABC =∠C =21(180°-36°)=72°,又∵BD 是△ABC 的角平分线,∴∠ABD =∠DBC =21∠ABC =36°,∴∠A =∠ABD =36°,∴BD =AD ,∴△ABD 是等腰三角形;在△BCD 中,∵∠BDC =180°-∠DBC -∠C=180°-36°-72°=72°,∴∠C =∠BDC =72°,∴BD =BC ,∴△BCD 是等腰三角形;∵BE =BC ,∴BD =BE ,∴△BDE 是等腰三角形;∴∠BED =21(180°-36°)=72°,∴∠AED =180°-∠BED =108°,∵∠A =36°,∴∠ADE =∠180°-∠AED -∠A =180°-108°-36°=36°,∴∠A =∠ADE ,∴DE =AE ,∴△ADE 是等腰三角形.∴图中的等腰三角形有5个.故选D. 7.C 【解析】⎪⎩⎪⎨⎧>---≥+②①0)3(23121x x x ,∵解不等式①得x≥-8,解不等式②得x <6,∴原不等式组的解集为-8≤x <6,∴不等式组的最大整数解为5,故选C.8.A 【解析】∵将直线l 1:y=-2x -2平移后,得到直线l 2:y=-2x+4,∴-2(x+a )-2=-2x+4或-2x -2+b=-2x+4,解得a=-3或b=6,故将直线l 1向右平移3个单位长度或向上平移6个单位长度得到直线l 2.故选A.9.D 【解析】如答图,设AE 的长为x ,根据正方形的性质可得BE =14-x ,在Rt △ABE 中,根据勾股定理可得x 2+(14-x )2=102,解得x 1=6,x 2=8,故AE 的长为6或8.故选D.第9题答图10.D 【解析】当y =0时,ax 2-2ax +1=0,∵a >1,∴Δ=(-2a )2-4a =4a (a -1)>0,ax 2-2ax +1=0有两个不相等的根,函数与x 轴有两个交点,x =aa a a 2)1(42-->0.即它们均位于y 轴右侧.故选D.11.-6<0<5<π 【解析】5≈2.236,π≈3.14,∵-6<0<2.236<3.14,∴-6<0<5<π.12.135° 【解析】正八边形的内角和为(8-2)×180°=1080°,每一个内角的度数为81×1080°=135°. 13.10 【解析】如答图,设点A 的坐标为(a ,b ),点B 的坐标为(c ,d ).∵反比例函数y =x4的图象过A ,B 两点,∴ab =4,cd =4,∴S △AOC =21|ab |=2,S △BOD =21|cd |=2.∵点M (-3,2),∴S 矩形MCOD =3×2=6,∴四边形MAOB 的面积=S △AOC +S △BOD +S 矩形MCOD =2+2+6=10.第13题答图14.32 【解析】∵点M ,N 分别是AB ,BC 的中点,∴MN =21AC ,∴当AC 取得最大值时,MN 就取得最大值,即当AC 是直径时,取得最大值.如答图,连接AO ,并延长AO 交⊙O 于点D.∵∠ACB =∠D =45°,AB =6,∴BD =AB =6,∴AD =22BD AB +=62,∴MN =21AD =32.第14题答图15.解:原式=2263+⨯-+8 =-32+22+8 =8-2.16.解:去分母得(x -2)(x -3)-3(x +3)=(x +3)(x -3)即x 2-5x +6-3x -9=x 2-9, 合并同类项得-8x =-6, 系数化为1,得x =43,经检验,x =43是原分式方程的解.17.解:如答图,直线AD 即为所求.第17题答图18.解:(1)总人数为5÷10%=50(人),则良好的人数为50-13-12-5=20(人),及格人数所占的百分比为1-10%-26%-40%=24%.补全统计图如答图所示:第18题答图(2)良好.由(1)知共抽查了50,50÷2=25,25+1=26, ∴中位数落在良好等级. (3)650×26%=169(人)答:该年级女生中1分钟“仰卧起坐”个数达到优秀的人数是169. 19.证明:∵AE ∥BD ,∴∠EAC =∠ACB ,又∵AB =AC , ∴∠B =∠ACB ,∴∠B =∠EAC , 在△ABD 和△CAE 中, ⎪⎩⎪⎨⎧∠=∠=∠=∠ACE BAD CAAB EAC B ’ ∴△ABD ≌△CAE (ASA ),∴AD =CE .20.解:由题意得∠CAD =∠MND =90°,∠CDA =∠MDN , ∴△CAD ∽△MND,∴NDAD MNCA =,∴8.0)15(8.016.1⨯+⨯=MN , ∴MN =9.6(米),又∵∠EBF =∠MNF =90°,∠EFB =∠MFN , ∴△EFB ∽△MFN ,∴NFBF MNEB =,∴8.0)92(8.026.9⨯+⨯=EB , ∴EB ≈1.75(米),∴小军身高约1.75米.21.解:(1)甲旅行社的总费用:y 甲=640×0.85x =544x , 乙旅行社的总费用:当0≤x ≤20时,y 乙=640×0.9x =576x ; 当x >20时,y 乙=640×0.9×20+640×0.75(x -20)=480x +1920;(2)当x =32时,y 甲=544×32=17408,y 乙=480×32+1920=17280,∴y 甲>y 乙. 答:胡老师选择乙旅行社总费用较少.22.解:(1)∵掷骰子共有6种等可能结果,向上一面的点数为奇数的有3种情况, ∴小亮掷得向上一面的点数为奇数的概率P =63=21.(2)列表如下:由上表可知,一共有36种等可能的结果,其中小亮、小丽获胜各有9种结果.∴P (小亮胜)=936=14,P (小丽胜)=369=41,∵P (小亮胜)=P (小丽胜),∴游戏是公平的. 23.(1)证明:∵⊙O 与DE 相切于点B ,AB 是⊙O 的直径, ∴∠ABE =90°,∴∠BAE +∠E =90°,∵∠DAE =90°,AC 是⊙O 的弦,DE 是⊙O 的切线, ∴∠BAD +∠BAE =90°,∴∠BAD =∠E .第23题答图(2)解:如答图,连接BC , ∵AB 是⊙O 的直径,∴∠ACB =90°. ∵AC =8,AB =2×5=10, ∴BC =22AC AB -=6.∵∠BCA =∠ABE =90°,∠BAD =∠E , ∴△ABC ∽△EAB , ∴AB BC EB AC =,∴1068=EB ,解得BE =340.24.解:(1)令y=0,得x 2+5x +4=0,∴x 1=-4,x 2=-1,令x =0,得y =4,∴A (-4,0),B (-1,0),C (0,4).(2)∵A ,B ,C 关于坐标原点O 对称后的点分别为A ′(4,0),B ′(1,0),C ′(0,-4),∴所求抛物线的函数表达式为y =ax 2+bx -4,将A ′(4,0),B ′(1,0)代入上式,得⎩⎨⎧=-+=-+0404416b a b a , 解得⎩⎨⎧=-=51b a , ∴所求抛物线的函数表达式为y=-x 2+5x -4.(3)如答图,取四点A ,M ,A ′,M ′,连接AM ,MA ′,A ′M ′,M ′A ,MM ′,由中心对称性可知,MM ′过点O ,OA =OA ′,OM =OM ′,∴四边形AMA ′M ′为平行四边形,又知AA ′与MM ′不垂直,∴平行四边形AMA ′M ′不是菱形.过点M 作MD ⊥x 轴于点D ,∵y=x 2+5x+4=49252-⎪⎭⎫ ⎝⎛+x , ∴M (25-,49-), 又∵A (-4,0),A ′(4,0),∴AA ′=8,MD =49. ∴S 平行四边形AMA ′M ′=2S △AMA ′=2×21×AA ′×MD =2×21×8×49=18.第24题答图25.解:(1)如答图①,过点A 作AE ⊥BC 于点E ,∴四边形AECD 为矩形,∴EC =AD =8,BE=BC -EC =12-8=4,在Rt △AB E 中,∠ABE =60°,BE =4,∴AB =2BE =8,AE=2248-=43,则S △BMC =21BC ·AE =21×12×43=243. (2)如答图②,作点C 关于直线AD 的对称点C ′,连接C ′N ,C ′D ,C ′B 交AD 于点N ′,连接CN ′,则BN +NC =BN +NC ′≥BC ′=BN ′+CN ′,∴△BNC 的周长的最小值为△BN ′C 的周长=BN ′+CN ′+BC=BC ′+BC .∵AD ∥BC ,CD ⊥BC ,∠ABC =60°,∴过点A 作AE ⊥BC 于点E ,则CE =AD =8,∴BE =4,AE =BE ·tan60°=43,∴CC ′=2CD =2AE =83. ∵BC =12,∴BC ′=22C C BC '+=421,∴△BNC 的周长的最小值为421+12.第25题答图(3)如答图③所示,存在点P ,使得cos ∠BPC 的值最小.作BC 的中垂线PQ 交BC 于点Q ,交AD 于点P ,连接BP ,CP ,作△BPC 的外接圆O ,⊙O 与直线PQ 交于点N ,则PB=PC ,圆心O 在PN 上,∵AD ∥BC ,∴⊙O 与AD 相切于点P .∵PQ =DC =43>6,∴PQ >BQ ,∴∠BPC <90°,圆心O 在弦BC 的上方,在AD 上任取一点P ′,连接P ′B ,P ′C ,P ′B 交⊙O 于点M ,连接MC ,∴∠BPC =∠BMC ≥∠BP ′C ,∴∠BPC 最大,cos ∠BPC 的值最小.连接OB ,则∠BON =2∠BPN =∠BPC ,∵OB =OP =43-OQ ,在Rt △BOQ 中,根据勾股定理得OQ 2+62=(43-OQ )2,解得OQ =23,∴OB =237, ∴cos ∠BPC =cos ∠BOQ =17OQ OB =, 则此时cos ∠BPC 的值为71.。
陕西省中考数学历年(2016-2022年)真题分类汇编专题 代数式

陕西省中考数学历年(2016-2022年)真题分类汇编专题代数式一、单选题(共8题;共16分)1.(2分)计算:2x⋅(−3x2y3)=()A.6x3y3B.−6x2y3C.−6x3y3D.18x3y3【答案】C【解析】【解答】解:2x⋅(−3x2y3)=2×(−3)×x⋅x2×y3=−6x3y3.故答案为:C.【分析】单项式乘单项式,积的系数等于原来两个单项式的系数的积,它的各个变数字母的幂指数,等于在原来两个单项式中相应的变数字母的幂指数的和,对于只在某一个单项式中含有的字母,则连同指数作为积的一个因式,据此计算.2.(2分)计算:(﹣23x2y)3=()A.﹣2x6y3B.827x6y3C.﹣827x6y3D.﹣827x5y4【答案】C【解析】【解答】解:(﹣23x2y)3=(−23)3⋅(x2)3⋅y3=−827x6y3.故答案为:C.【分析】先根据积的乘方运算法则计算,再根据幂的乘方运算法则进行计算即可,积的乘方,等于每个因式乘方的积.3.(2分)计算:(−3)0=()A.1B.0C.3D.−13【答案】A【解析】【解答】解:(−3)0=1。
故答案为:A。
【分析】任何一个不为0的数的0次幂都等于1。
4.(2分)下列计算正确的是()A.x2+3x2=4x4B.x2y•2x3=2x4yC.(6x2y2)÷(3x)=2x2D.(﹣3x)2=9x2【答案】D【解析】【解答】解:A、原式=4x2,错误;B、原式=2x5y,错误;C、原式=2xy2,错误;D、原式=9x2,正确,故选D【分析】A、原式合并得到结果,即可作出判断;B、原式利用单项式乘以单项式法则计算得到结果,即可作出判断;C、原式利用单项式除以单项式法则计算得到结果,即可作出判断;D、原式利用积的乘方运算法则计算得到结果,即可作出判断.此题考查了整式的除法,合并同类项,幂的乘方与积的乘方,以及单项式乘单项式,熟练掌握运算法则是解本题的关键.5.(2分)计算:(a3b)−2=()A.1a6b2B.a6b2C.1a5b2D.−2a3b【答案】A【解析】【解答】解:(a3b)−2=1a6b2,故答案为:A.【分析】根据负整数指数幂的意义“任何一个不为0的数的负整数指数幂等于这个数的正整数指数幂的倒数.”和积的乘方法则“积的乘方等于把积中每一个因式分别乘方再把所得的幂相乘”可求解.6.(2分)下列计算正确的是()A.2a2⋅3a2=6a2B.(−3a2b)2=6a4b2C.(a−b)2=a2−b2D.−a2+2a2=a2【答案】D【解析】【解答】解:A. 2a2⋅3a2=6a4,故A不符合题意;B. (−3a2b)2=9a4b2,故B不符合题意;C. (a−b)2=a2−2ab+b2,故C不符合题意;D. −a2+2a2=a2,故D符合题意。
陕西近10年中考数学真题及副题整理专题

陕西近10年中考数学真题及副题整理专题陕西近7年中考数学真题及副题选择题⼀、选择题(共14⼩题,每⼩题3分,计30分.每⼩题只有⼀个选项是符合题意的) 1. 计算:(-3)0=()(2019)A. 1B.0 C 3 D.13-1、下列四个实数中,最⼤的是()(2019副) A. 2 B.3 C. 0 D. ﹣11. -78的相反数是()(2018)A .-87 B. 87 C .-78 D. 781. -711的倒数是( )(2018副)A.711 B. -711 C. 117 D. -1171、计算:(-12)2-1=( )(2017)A. -54B. -14C. -34 D. 01. 计算: 3-2=()(2017副)A. -19B. 19C. -6D. -161. 计算:(-1A. -1B. 1C. 4D. -41.计算:(-3)×(-13)=()(2016副)A.-1B.1C.-9D.9 1. 计算:(-23)0=( )(2015)A. 1B. -32C. 0D. 231.下列四个实数中,最⼤的是()(2015副) A.0 B.3 C.2 D.-1 1. 计算:(-3)2=()(2014副)A. -6B. 6C. -9D. 9 1. 4的算术平⽅根是( )(2014)A. -2B. 2C. -12D. 121.-23的倒数是()(2013副)A.-32B.32C.-233-D.52. 如图,是由两个正⽅体组成的⼏何体,则该⼏何体的俯视图为()(2019)2.下列图形中,经过折叠可以得到四棱柱的是 ( )(2018副)2. 如图,是⼀个⼏何体的表⾯展开图,则该⼏何体是( )2018)A. 正⽅体B. 长⽅体C. 三棱柱D. 四棱锥2.如图的⼏何体是由⼀平⾯将⼀圆柱体截去⼀部分后所得,则该⼏何体的俯视图是()(2017副)2. 如图所⽰的⼏何体是由⼀个长⽅体和⼀个圆柱体组成的,则它的主视图是( )(2017)2.如图,下⾯的⼏何体由两个⼤⼩相同的正⽅体和⼀个圆柱体组成,则它的左视图是()(2016副)2. 如图,下⾯的⼏何体由三个⼤⼩相同的⼩⽴⽅块组成,则它的左视图是( )(2016)2、如图是⼀枚古钱币的⽰意图,它的左视图是()(2015副)2. 如图是⼀个螺母的⽰意图,它的俯视图是()(2015)2、如图,下⾯⼏何体是由⼀个圆柱被经过上下底⾯圆⼼的平⾯截得的,则它的左视图是()(2014副)2、下图是⼀个正⽅体被截去⼀个直三棱柱得到的⼏何体,则该⼏何体的左视图是() (2014)2、如图,将直⾓三⾓形绕其⼀条直⾓边所在直线l旋转⼀周,得到的⼏何体是()(2013副)2、如图,下⾯的⼏何体是由⼀个圆柱和⼀个长⽅体组成的,则它的俯视图是()(2013)3.如图,OC是∠AOB的平分线,l P OB,若∠1=52o,则∠2的度数为()(2019)A.52oB.54oC.64oD.69o3. 如图,直线a∥b,在Rt△ABC中,∠C=90°,AC⊥b,垂⾜为A,则图中与∠1互余的⾓有()(2018副)A.2个B.3个C.4个D.5个3. 如图,若l1∥l2,l3∥l4,则图中与∠1互补的⾓有()(2018)A. 1个B. 2个C. 3个D. 4个()(2017副)A. 30°B. 38°C. 52°D. 72°3. 如图,直线a∥b,Rt△ABC的直⾓顶点B落在直线a上.若∠1=25°,则∠2的⼤⼩为()(2017)A. 55°B. 75°C. 65°D. 85°3..如图,AB∥CD.若∠1=40°,∠2=65°,则∠CAD=()(2016副)A.50°B.65°C.75°D.85°3.如图,AB∥CD,AE平分∠CAB交CD于点E.若∠C=50°,则∠AED=()(2016)A. 65°B. 115°C. 125°D. 130°3、如图,AB∥CD,直线EF交直线AB、CD于点E、F,FH 平分∠CFE.若∠EFD=70°,则∠EHF的度数为()(2015副)A.35°B.55°C.65°D.70°3、. 如图,AB∥CD,直线EF分别交直线AB、CD于点E、F.若∠1=46°30′,则∠2的度数为()(2015)A. 43°30′D. 153°30′3. 如图,∠B=40°,∠ACD=108°.若B、C、D三点在⼀条直线上,则∠A的⼤⼩是()(2014副)(第4题图)A. 148°B. 78°C. 68°D. 50°3. ⼩军旅⾏箱的密码是⼀个六位数,由于他忘记了密码的末位数字,则⼩军能⼀次打开该旅⾏箱的概率是()(2014)A. 110 B.19 C.16 D.153、.如图,AB∥CD,AE平分∠CAB交CD于点E.若∠C=50°,则∠AED的⼤⼩为()(2013副)(第4题图)A.55°B.105°C.65°D.115°3.如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D的⼤⼩为()(2013)A.65°B.55°C.45°D.35°4.若正⽐例函数y=-2x的图象经过点(a-1,4),则a的值为()A.-1B.0C.1D.24. 若正⽐例函数y=kx的图象经过第⼆、四象限,且过点A(2m,12B.-2 C.-1 D.14. 如图,在矩形AOBC中,A(-2,0),B(0,1).若正⽐例函数y =kx的图象经过点C,则k的值为()A. -12 B.12 C. -2 D. 24. 若正⽐例函数y=kx(k≠0)的图象经过点(2,1-k),则k的值为A. 1B. -13 C. -1 D.134. 若⼀个正⽐例函数的图象经过A(3,-6),B(m,-4)两点,则m的值为()A. 2B. 8C. -2D. -84.设点A(-3,a),B(b,12)在同⼀个正⽐例函数的图象上,则ab的值为()A.-23 B.-32 C.-6 D.322x图象上的任意⼀点,则下列等式⼀定成⽴的是()A. 2a+3b=0B. 2a-3b=0C.3a-2b=0D. 3a+2b=04..对于正⽐例函数y=-3x,当⾃变量x的值增加1时,函数y的值增加()A.-3B.3C.-13 D.135. 设正⽐例函数y=mx的图象经过点A(m,4),且y的值随x值的增⼤⽽减⼩,则m=()A. 2B. -2C. 4D. -43. 若正⽐例函数y=2x的图象经过点A(m,3m+1),则m的值为()A. 1B. -1C.25 D. -254.若点A(-2,m)在正⽐例函数y=-12x的图象上,则m的值是14 B. -14 C. 1 D. -14..若⼀个正⽐例函数的图象经过点(-3,2),则这个图象⼀定也经过点()A.(2,-3)B.(32,-1) C.(-1,1) D.(2,-2)4.如果⼀个正⽐例函数的图象经过不同..象限的两点A(2,m),B(n,3),那么⼀定有()A.m>0,n>0B.m>0,n<0C.m<0,n>0D.m<0,n<05.下列计算正确的是()A.222236a a a=g B.2242(36a b a b-=)C.222--a b a b=() D.222-2A.a2+a3=a5B.2x2·(-13xy)=-23x3yC.(a-b)(-a-b)=a2-b2D.(-2x2y)3=-6x6y35. 下列计算正确的是()A. a2·a2=2a4B. (-a2)3=-a6C. 3a2-6a2=3a2D. (a-2)2=a2-45. 化简:a+1-a2a+1,结果正确的是A. 2a+1B. 1C.1a+1D.2a+1a+15. 化简:yxyyxx+A. 1B.2222yxyx-+C.yxyx+-D. x2+y23.计算:(-2x2y)3=A.-8x6y3B.8x6y3C.-6x6y3D.6x5y35. 下列计算正确的是()A. x2+3x2=4x4B. x2y·2x3=2x6yC. (6x3y2)÷(3x)=2x2D. (-3x)2=9x25.下列计算正确的是()A.a2+a3=a5D.6a2b÷(-2ab)=-3a5. 下列计算正确的是()A. a2·a3=a6B. (-2ab)2=4a2b2C. (a2)3=a5D. 3a3b2÷a2b2=3ab5. ⼀天上午,张⼤伯家销售了10箱西红柿,销售的情况如下表:箱数 1 2 3 4各箱的售价80 87 85 86则这10箱西红柿售价的中位数和众数分别是()A. 85和86B. 85.5和86C. 86和86D. 86.5和865. 某区10名学⽣参加市级汉字听写⼤赛,他们得分情况如下表:⼈数342 1分数80859095那么这10名学⽣所得分数的平均数和众数分别是() A. 85和82.5 B. 85.5和85 C. 85和85 D. 85.5和805.若a≠0,则下列运算正确的是()A.a3-a2=aB.a3·a2=a6C.a3+a2=a5D.a3÷a2=a5.我省某市五⽉份第⼆周连续七天的空⽓质量指数分别为:111,96,47,68,70,77,105,则这七天空⽓质量指数的平均数是()A.71.8 B.77 C.82 D.95.76.如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂⾜为E.若DE=1,则BC的长为( )A.2+2B.2+3C.2+3D.36. 如图,在Rt△ABC中,∠ACB=90°,∠A=65°,CD⊥AB,垂⾜为D,E是BC的中点,连接ED,则∠DEC的度数是A.25°B.30°C.40°D.50°6. 如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂⾜为D,∠ABC的平分线交AD于点E,则AE的长为()A.43 2 B. 2 2 C.83 2 D. 3 26. 如图,在△ABC中,∠A=60°,∠B=45°.若边AC的垂直平分线DE交边AB于点D,交边AC于点E,连接CD,则∠DCB=A. 15°B. 20°C. 25°D. 30°6. 如图,将两个⼤⼩、形状完全相同的△ABC和△A′B′C′拼在⼀起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为()A. 3 3B. 6C. 3 2D. 216.如图,在△ABC中,∠BAC=90°,AB=20,AC=15,△ABC的⾼AD与⾓平分线CF交于点E,则AFDE的值为()A.35 B.34C.12 D.236. 如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC 的中位线,延长DE交△ABC的外⾓∠ACM的平分线于点F,则线段DF的长为()A. 7B. 8C. 9D. 106.如图,点P是△ABC内⼀点,且P A=PB=PC,则点P是()A.△ABC三条中线的交点B.△ABC三条⾼线的交点C.△ABC三条⾓平分线的交点D.△ABC三边垂直平分线的交点6. 如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的⾓平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三⾓形共有()A. 2个B. 3个C. 4个D. 5个6. 不等式组≤-+13252xx>的最⼩整数解是()A. -3B. -2C. 0D. 16. 把不等式组x+2>13-x≥0的解集表⽰在数轴上,正确的是()7.在平⾯直⾓坐标系中,将函数 y =3x 的图象向上平移 6个单位长度,则平移后的图象与x 轴交点的坐标为 ( ) A.(2,0) B.(-2,0) C.(6,0) D.(-6,0) 7.将直线y=32x -1沿x 轴向左平移4个单位,则平移后的直线与y 轴交点的坐标是A .(0,5)B .(0,3)C .(0,-5)D .(0,-7)7. 若直线l 1经过点(0,4),l 2经过点(3,2),且l 1与l 2关于x 轴对称,则l 1与l 2的交点坐标为( ) A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)7. 设⼀次函数y =kx +b (k ≠0)的图象经过点(1,-3),且y 的值随x 的值增⼤⽽增⼤,则该⼀次函数的图象⼀定不...经过A. 第⼀象限B. 第⼆象限C. 第三象限D. 第四象限7. 如图,已知直线l 1:y =-2x +4与直线l 2:y =kx +b (k ≠0)在第⼀象限交于点M .若直线l 2与x 轴的交点为A (-2,0),则k 的取值范围是( )A. -2B. -2C. 0D. 07.已知两个⼀次函数y =3x +b 1和y =-3x +b 2. 若b 1<b 2<0,则它们图象的交点在()A.第⼀象限B.第⼆象限C.第三象限D.第四象限 7. 已知⼀次函数y =kx +5和y =k′x +7.假设k >0且k ′<0,则这两个⼀次函数图象的交点在( )A. 第⼀象限B. 第⼆象限C. 第三象限D. 第四象限已知⼀次函数y =kx +b 的图象经过点(1,2),且y 的值随x 值的增⼤⽽减⼩,则下列判断正确的是() A.k>0,b >0 B.k >0,b <0C.k <0,b >0D.k <0,b <07. 在平⾯直⾓坐标系中,将直线l 1:y =-2x -2平移后,得到直线l 2:y =-2x +4,则下列平移作法正确的是( ) A. 将l 1向右平移3个单位长度 B. 将l 1向右平移6个单位长度 C. 将l 1向上平移2个单位长度 D. 将l 1向上平移4个单位长度7. ⽤配⽅法解⼀元⼆次⽅程2x 2-3x =1,下列配⽅正确的是( A. (x -34)2=1716 B. (x -12)2=1716C. (x -32)2=1516D. (x -316)2=1387. 若x =-2是关于x 的⼀元⼆次⽅程x 2-52ax +a 2=0的⼀个根,则a 的值为( )A. 1或4B. -1或-4C. -1或4D. 1或-48.如果点A (m ,n )、B (m +1,n +2)均在⼀次函数y =kx.+b (k ≠0)的图象上,那么k 的值为()A.2B.1C.-1D.-2 7.根据下表中⼀次函数的⾃变量x 与函数y 的对应值,可得p 的值为()A.1B.-1C.3D.-38.如图,在矩形 ABCD 中,AB =3,BC =6.若点 E ?F 分别在 AB ?CD 上,且 BE = 2AE ,DF =2FC ,G ?H 分别是 AC 的三等分点,则四边形 EHFG 的⾯积为() A.1 B.32 C.2 D.48. 如图,在菱形ABCD 中,AC =2,BD =4,点E 、F 、G 、H 分别在AB 、BC 、CD 和DA 上,且EF ∥AC .若四边形EFGH 是正⽅形,则EF 的长为 A. 23 B .1 C. 43D .28. 如图,在菱形ABCD 中,点E 、F 、G 、H 分别是边AB 、BC 、CD 和DA 的中点,连接EF 、FG 、GH 和HE .若EH =2EF ,则下列结论正确的是( )A. AB =2EFB. AB =2EFC. AB =3EFD. AB =5EF8. 如图,在正⽅形ABCD 中,AB =2.若以CD 边为底边向其形外作等腰直⾓△DCE ,连接BE ,则BE 的长为 A. 5 B. 2 2 C.10 D. 2 38. 如图,在矩形ABCD 中,AB =2,BC =3.若点E 是边CD 的中点,连接AE ,过点B 作BF ⊥AE 交AE 于点F ,则BF 的长为( ) A.3102 B. 3105 C. 105 D. 3558..如图,△ABC 和△DBC 均为等腰三⾓形,∠A =60°,∠D =90°,AB =12.若点E 、F 、G 、H 分别为边AB 、AC 、CD 、BD 的中点,则四边形EFGH 的⾯积为()A.9(3+1)B.12(3+1)C.18(3+1)D.36(3+1)8.在?ABCD中,AB=10,BC=14,E、F分别为边BC、AD 上的点.若四边形AECF为正⽅形,则AE的长为()A. 7B. 4或10C. 5或9D. 6或88.如图,在矩形ABCD中,AB=3,BC=4.若过点C作CE⊥BD,垂⾜为E,则BE的长为()(第9题图)A. 2B. 3C. 95 D.1658. 如图,在菱形ABCD中,AB=5,对⾓线AC=6.若过点A 作AE⊥BC,垂⾜为E,则AE的长为()第9题图A. 4B. 125 C.245 D. 58.如图,在矩形ABCD中,AB=3.4,BC=5,以BC为直径作半圆O,点P是半圆O上的⼀点.若PB=4,则点P到AD 的距离为()A.45 B.1 C.65 D.858.如图,在矩形ABCD中,AD=2AB,点M,N分别在边AD、BC 上,连接BM、DN,若四边形MBND是菱形,则AMMD等于()A.38B.23C.35D.459.如图,AB是⊙O的直径,EF?EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF.若∠AOF=40°,则∠F的度数是()A.25oB.35oC.40oD.55o9. 如图,四边形ABCD是⊙O的内接四边形,AD=BC.若∠BAC =45°,∠B=75°,则下列等式成⽴的是A.AB=2CD B.AB=3CD C.AB=32CD D.AB=2CD9. 如图,△ABC是⊙O的内接三⾓形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的⼤⼩为()A. 15°B. 35°C. 25°D. 45°9. 如图,矩形ABCD内接于⊙O,点P是AD︵上⼀点,连接PB、PC.若AD=2AB,则sin∠BPC的值为A.55 B.255 C.32 D.35109. 如图,△ABC是⊙O的内接三⾓形,∠C=30°,⊙O的半径为5.若点P是⊙O上的⼀点,在△ABP中,PB=AB,则P A的长为()A. 5B.532 C. 5 2 D. 5 39.如图,在⊙O中,弦AB垂直平分半径OC,垂⾜为D.若点P是⊙O上异于点A、B的任意⼀点,则∠APB=()A.30°或60°B.60°或150°C.30°或150°D.60°或120°9. 如图,⊙O的半径为4,△ABC是⊙O的内接三⾓形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为()A. 3 3B. 4 3C. 5 3D. 6 311.已知实数1-2,0,16,3,π,25,34,其中为⽆理数的是_________.11.-27的⽴⽅根是__________.11. ⽐较⼤⼩:3________10(填“>”、“<”或“=”)11. 如图,数轴上的A 、B 两点所表⽰的数分别为a 、b ,则a +b ________0(填“>”,“=”或“<”).11. 在实数-5,-3,0,π,6中,最⼤的⼀个数是________.11.不等式-2x +1>-5的最⼤整数解是________. 11. 不等式-12x +3<0的解集是________.11.-8的⽴⽅根是______.11. 因式分解:m (x -y )+n (x -y )=________.11.在5,-1,227,π这四个数中,⽆理数有________个.11.计算:(-2)3+(3-1)0= .12.若正六边形的边长为3,则其较长的⼀条对⾓线长为__________.12.如图,在正六边形ABCDEF 中,连接DA 、DF ,则DFDA 的值为__________ .12. 如图,在正五边形ABCDE 中,AC 与BE 相交于点F ,则∠AFE 的度数为________.12. 请从以下两个⼩题中任选⼀个....作答,若多选,则按第⼀题计分.A. 如图,⽹格上的⼩正⽅形边长均为1,△ABC 和△DEF 的顶点都在格点上.若△DEF 是由△ABC 向右平移a 个单位,再向下平移b 个单位得到的,则ba的值为________.12. (节选)如图,在△ABC 中,BD 和CE 是△ABC 的两条⾓平分线.若∠A =52°,则∠1+∠2的度数为________.12. 如图,五边形ABCDE 的对⾓线共有________条. 12. (节选)⼀个正多边形的⼀个外⾓为45°,则这个正多边形的边数是________.12.请从以下两个⼩题中任选⼀个....作答,若多选,则按第⼀题计分. A.⼀个n 边形的内⾓和为900°,则n =______.B.如图,⼀⼭坡的坡长AB =400⽶,铅直⾼度BC =150⽶,则坡⾓∠A 的⼤⼩为______.(⽤科学计算器计算,结果精确到1°)12. (节选)正⼋边形⼀个内⾓的度数为________. 12. 正五边形⼀个内⾓的度数是________.13.如图,D 是矩形 AOBC 的对称中⼼,A (0,4),B (6,0).若⼀个反⽐例函数的图象经过点 D ,交 AC 于点 M ,则点 M 的坐标为_________.13.若⼀个反⽐例函数的图象与直线y =-2x +6的⼀个交点为A (m ,-4),则这个反⽐例函数的表达式是__________.13. 若⼀个反⽐例函数的图象经过点A (m ,m )和B (2m ,-1),则这个反⽐例函数的表达式为________.13. 已知A ,B 两点分别在反⽐例函数y =3mx (m ≠0)和y =2m -5x (m ≠52)的图象上.若点A 与点B 关于x 轴对称,则m 的值为________.13.如图,在x 轴上⽅,平⾏于x 轴的直线与反⽐例函数y =xk 1和y =xk 2的图象分别交于A 、B 两点,连接OA 、OB .若△AOB 的⾯积为6,则k 1-k 2=________.13. 已知⼀次函数y =2x +4的图象分别交x 轴、y 轴于A 、B 两点.若这个⼀次函数的图象与⼀个反⽐例函数的图象在第⼀象限交于点C ,且AB =2BC ,则这个反⽐例函数的表达式为________13.在平⾯直⾓坐标系中,反⽐例函数y =xk的图象位于第⼆、四象限,且经过点(1,k 2-2),则k 的值为______.13. 如图,在平⾯直⾓坐标系中,过点M (-3,2)分别作x 轴、y 轴的垂线与反⽐例函数y =4x 的图象交于A 、B 两点,则四边形MAOB 的⾯积为________.15.计算:-231-2-27+1-3-2?()16.化简:22-2822-4-2a a a a a a a++÷+().15.计算:(-12)-1+|2-5|+2×(-8) .16. 解⽅程:3233--=+-x xx x .15. (本题满分5分)计算:(-3)×(-6)+|2-1|+(5-2π)0.16. (本题满分5分)化简:(a +1a -1-aa +1)÷3a +1a 2+a .15. 计算:18-(π-5)0+|22-3|.16. 解分式⽅程:2x -1x +2=2-3x -2.15. (本题满分5分)计算:(-2)×6+|3-2|-(12)-1.16. (本题满分5分)解⽅程:3233+--+x x x =1.15.)计算: (-3)2+|2-5|-20.16.化简:(937222--+a a a —34++a a )÷33-+a a .15. (本题满分5分)计算:12-|1-3|+(7+π)0.16. (本题满分5分)化简:(x -5+91)3162--÷+x x x15.计算: 8×3-2×|-5|+(-13)-2.16.(本题满分5分)解分式⽅程: 23+x +2=22-x x .15. (本题满分5分)计算:3×(-6)+|-22|+(12)-3.16. (本题满分5分)解分式⽅程:x -2x +3-3x -3=1.17.(本题满分 5分)如图,在△ABC 中,AB =AC ,AD 是 BC 边上的⾼,请⽤尺规作图法,求作△ABC 的外接圆.(保留作图痕迹,不写作法) 17. (本题满分5分)如图,已知:在正⽅形ABCD 中,M 是BC 边上⼀定点,连接AM .请⽤尺规作图法,在AM 上求作⼀点P ,使△DP A ∽△ABM .(不写作法,保留作图痕迹)17. (本题满分5分)如图,在△ABC中,AD是BC边上的⾼.请⽤尺规作图法在⾼AD上求作⼀点P,使得点P到AB的距离等于PD的长.(保留作图痕迹,不写作法)17. (本题满分5分)如图,在钝⾓△ABC中,过钝⾓顶点B作BD⊥BC交AC于点D.请⽤尺规作图法在BC边上求作⼀点P,使得点P到AC的距离等于BP的长.(保留作图痕迹,不写作法)第17题图17.(本题满分5分)如图,已知锐⾓△ABC,点D是AB边上的⼀定点,请⽤尺规在AC边上求作⼀点E,使△ADE与△ABC相似.(作出符合题意的⼀个点即可,保留作图痕迹,不写作法.)(第17题图)17. (本题满分5分)如图,已知△ABC,∠BAC=90°,请⽤尺规过点A作⼀条直线,使其将△ABC分成两个相似的三⾓形.(保留作图痕迹,不写作法)第17题图17.(本题满分5分)如图,请⽤尺规在△ABC的边BC上找⼀点D,使得点D到边AB、AC的距离相等.(保留作图痕迹,不写作法)17. (本题满分5分)如图,已知△ABC,请⽤尺规过点A作⼀条直线,使其将△ABC分成⾯积相等的两部分.(保留作图痕迹,不写作法)18.(本题满分5分)如图,点A?E?F?B在直线l上,AE=BF,AC∥BD,且AC=B D.求证:CF=DE .第18题图18. (本题满分5分)如图,在△ABC中,AB=AC,O是边BC的中点,延长BA到点D,使AD=AB,延长CA到点E,使AE=AC,连接OD,OE,求证:∠BOE=∠COD .18. (本题满分5分)如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交于点G、H,若AB=CD.求证:AG=DH.18. (本题满分5分)如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交于点G、H,若AB=CD.求证:AG=DH.18. (本题满分7分)如图,在正⽅形ABCD中,E、F分别为边AD和CD上的点,且AE=CF,连接AF、CE交于点G. 求证:AG =CG .18. (本题满分7分)如图,在?ABCD中,延长BA到点E,延长DC到点F,使AE=CF,连接EF交AD边于点G,交BC边于点H.求证:DG=BH . 18.(本题满分7分)如图,在菱形ABCD中,点E是边AD上⼀点,延长AB⾄点F,使BF=AE,连接BE、CF.求证:BE=CF .18. (本题满分7分)如图,在?ABCD中,连接BD,在BD的延长线上取⼀点E,在DB的延长线上取⼀点F,使BF=DE,连接AF、CE.求证:AF∥CE .18.(本题满分7分)如图,在△ABC中,AB=AC. D是边BC延长线上的⼀点,连接AD,过点A、D分别作AE∥BD、DE∥AB,AE、DE交于点E,连接CE.求证:AD=CE.18. (本题满分7分)如图,在△ABC中,AB=AC.作AD⊥AB交BC的延长线于点D,作AE∥BD、CE⊥AC,且AE、CE相交于点E.求证:AD=CE.第19题图。
2010-2017陕西省历年中考真题(真题+真题答案解析)
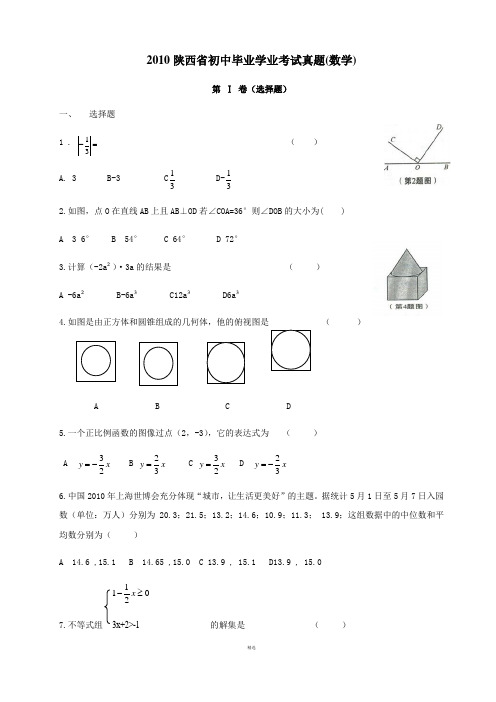
2010陕西省初中毕业学业考试真题(数学)第 Ⅰ 卷(选择题)一、 选择题1 . 13-= ( )A. 3 B-3 C 13 D-132.如图,点O 在直线AB 上且AB ⊥OD 若∠COA=36°则∠DOB 的大小为( ) A 3 6° B 54° C 64° D 72°3.计算(-2a ²)·3a 的结果是 ( ) A -6a ² B-6a ³ C12a ³ D6a ³4.如图是由正方体和圆锥组成的几何体,他的俯视图是 ( )A B C D5.一个正比例函数的图像过点(2,-3),它的表达式为 ( ) A 32y x =-B 23y x =C 32y x =D 23y x =-6.中国2010年上海世博会充分体现“城市,让生活更美好”的主题。
据统计5月1日至5月7日入园数(单位:万人)分别为20.3;21.5;13.2;14.6;10.9;11.3; 13.9;这组数据中的中位数和平均数分别为( )A 14.6 ,15.1B 14.65 ,15.0C 13.9 , 15.1 D13.9 , 15.0 1102x -≥ 7.不等式组 3x+2>-1 的解集是 ( )A -1< x≤2B -2≤x<1C x<-1或x≥2D 2≤x<-18.若一个菱形的边长为2,则这个菱形两条对角线的平方和为()A 16B 8C 4D 19.如图,点A、B、P在⊙O上的动点,要是△ABM为等腰三角形,则所有符合条件的点M有()A 1个B 2个C 3个D 4个10.将抛物线C:y=x²+3x-10,将抛物线C平移到Cˋ。
若两条抛物线C,Cˋ关于直线x=1对称,则下列平移方法中正确的是()A将抛物线C向右平移52个单位 B将抛物线C向右平移3个单位C将抛物线C向右平移5个单位 D将抛物线C向右平移6个单位第Ⅱ卷(非选择题)二、填空题11、在1,-2,-30,π五个数中最小的数是12、方程x²-4x的解是 ________13、如图在△ABC中D是AB边上一点,连接CD,要使△ADC与△ABC相似,应添加的条件是___________14、如图是一条水铺设的直径为2米的通水管道横截面,其水面宽1.6米,则这条管道中此时最深为_______米15、已知A(x1,y2),B(x2,y2)都在6yx图像上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
陕西近7年中考数学真题及副题选择题一、选择题(共14小题,每小题3分,计30分.每小题只有一个选项是符合题意的) 1. 计算:(-3)0=( )(2019)A. 1B.0 C 3 D.13-1、下列四个实数中,最大的是( ) (2019副) A. 2 B.3 C. 0 D. ﹣11. -78的相反数是()(2018)A .-87 B. 87 C .-78 D. 781. -711的倒数是( )(2018副)A.711 B. -711 C. 117 D. -1171、 计算:(-12)2-1=( )(2017)A. -54B. -14C. -34 D. 01. 计算: 3-2=( )(2017副)A. -19B. 19C. -6D. -161. 计算:(-12)×2=( )(2016)A. -1B. 1C. 4D. -41.计算:(-3)×(-13)=( )(2016副)A.-1B.1C.-9D.9 1. 计算:(-23)0=( )(2015)A. 1B. -32C. 0D. 231.下列四个实数中,最大的是( )(2015副) A.0 B.3 C.2 D.-1 1. 计算:(-3)2=( )(2014副)A. -6B. 6C. -9D. 9 1. 4的算术平方根是( )(2014)A. -2B. 2C. -12D. 121.-23的倒数是( )(2013副)A.-32B.32C.-23D.231.下列四个数中最小的数是( )(2013) A.-2 B.0 C.13-D.52. 如图,是由两个正方体组成的几何体,则该几何体的俯视图为( )(2019)2.下列图形中,经过折叠可以得到四棱柱的是 ( )(2018副)2. 如图,是一个几何体的表面展开图,则该几何体是( )2018)A. 正方体B. 长方体C. 三棱柱D. 四棱锥2.如图的几何体是由一平面将一圆柱体截去一部分后所得,则该几何体的俯视图是()(2017副)2. 如图所示的几何体是由一个长方体和一个圆柱体组成的,则它的主视图是( )(2017)2.如图,下面的几何体由两个大小相同的正方体和一个圆柱体组成,则它的左视图是( )(2016副)2. 如图,下面的几何体由三个大小相同的小立方块组成,则它的左视图是( )(2016)2、如图是一枚古钱币的示意图,它的左视图是( )(2015副)2. 如图是一个螺母的示意图,它的俯视图是()(2015)2、如图,下面几何体是由一个圆柱被经过上下底面圆心的平面截得的,则它的左视图是()(2014副)2、下图是一个正方体被截去一个直三棱柱得到的几何体,则该几何体的左视图是() (2014)2、如图,将直角三角形绕其一条直角边所在直线l旋转一周,得到的几何体是()(2013副)2、如图,下面的几何体是由一个圆柱和一个长方体组成的,则它的俯视图是()(2013)3.如图,OC是∠AOB的平分线,l P OB,若∠1=52º,则∠2的度数为()(2019)A.52ºB.54ºC.64ºD.69º3. 如图,直线a∥b,在Rt△ABC中,∠C=90°,AC⊥b,垂足为A,则图中与∠1互余的角有()(2018副)A.2个B.3个C.4个D.5个3. 如图,若l1∥l2,l3∥l4,则图中与∠1互补的角有()(2018)A. 1个B. 2个C. 3个D. 4个3 如图,直线a∥b,点A在直线b上,∠BAC=108°,∠BAC的两边与直线a分别交于B、C两点.若∠1=42°,则∠2的大小为()(2017副)A. 30°B. 38°C. 52°D. 72°3. 如图,直线a∥b,Rt△ABC的直角顶点B落在直线a上.若∠1=25°,则∠2的大小为()(2017)A. 55°B. 75°C. 65°D. 85°3..如图,AB∥CD.若∠1=40°,∠2=65°,则∠CAD=()(2016副)A.50°B.65°C.75°D.85°3.如图,AB∥CD,AE平分∠CAB交CD于点E.若∠C=50°,则∠AED=()(2016)A. 65°B. 115°C. 125°D. 130°3、如图,AB∥CD,直线EF交直线AB、CD于点E、F,FH平分∠CFE.若∠EFD=70°,则∠EHF的度数为()(2015副)A.35°B.55°C.65°D.70°3、. 如图,AB∥CD,直线EF分别交直线AB、CD于点E、F.若∠1=46°30′,则∠2的度数为()(2015)A. 43°30′B. 53°30′C. 133°30′D. 153°30′3. 如图,∠B=40°,∠ACD=108°.若B、C、D三点在一条直线上,则∠A的大小是()(2014副)(第4题图)A. 148°B. 78°C. 68°D. 50°3. 小军旅行箱的密码是一个六位数,由于他忘记了密码的末位数字,则小军能一次打开该旅行箱的概率是()(2014)A. 110 B.19 C.16 D.153、.如图,AB∥CD,AE平分∠CAB交CD于点E.若∠C=50°,则∠AED的大小为()(2013副)(第4题图)A.55°B.105°C.65°D.115°3.如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D的大小为()(2013)A.65°B.55°C.45°D.35°4.若正比例函数y=-2x的图象经过点(a-1,4),则a的值为()A.-1B.0C.1D.24. 若正比例函数y=kx的图象经过第二、四象限,且过点A(2m,1)和B(2,m),则k的值为A.-12B.-2 C.-1 D.14. 如图,在矩形AOBC中,A(-2,0),B(0,1).若正比例函数y=kx的图象经过点C,则k的值为()A. -12 B.12 C. -2 D. 24. 若正比例函数y=kx(k≠0)的图象经过点(2,1-k),则k的值为A. 1B. -13 C. -1 D.134. 若一个正比例函数的图象经过A(3,-6),B(m,-4)两点,则m的值为()A. 2B. 8C. -2D. -84.设点A(-3,a),B(b,12)在同一个正比例函数的图象上,则ab的值为()A.-23 B.-32 C.-6 D.324. 设点A(a,b)是正比例函数y=-32x图象上的任意一点,则下列等式一定成立的是()A. 2a+3b=0B. 2a-3b=0C.3a-2b=0D. 3a+2b=04..对于正比例函数y=-3x,当自变量x的值增加1时,函数y的值增加()A.-3B.3C.-13 D.135. 设正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则m=()A. 2B. -2C. 4D. -43. 若正比例函数y=2x的图象经过点A(m,3m+1),则m的值为()A. 1B. -1C.25 D. -254.若点A(-2,m)在正比例函数y=-12x的图象上,则m的值是()A.14 B. -14 C. 1 D. -14..若一个正比例函数的图象经过点(-3,2),则这个图象一定也经过点()A.(2,-3)B.(32,-1) C.(-1,1) D.(2,-2)4.如果一个正比例函数的图象经过不同..象限的两点A(2,m),B(n,3),那么一定有()A.m>0,n>0B.m>0,n<0C.m<0,n>0D.m<0,n<05.下列计算正确的是()A.222236a a a=g B.2242(36a b a b-=)C.222--a b a b=() D.222-2a a a+=5. 下列计算正确的是A.a2+a3=a5B.2x2·(-13xy)=-23x3yC.(a-b)(-a-b)=a2-b2D.(-2x2y)3=-6x6y35. 下列计算正确的是()A. a2·a2=2a4B. (-a2)3=-a6C. 3a2-6a2=3a2D. (a-2)2=a2-45. 化简:a+1-a2a+1,结果正确的是A. 2a+1B. 1C.1a+1D.2a+1a+15. 化简:yxyyxx+--,结果正确的是()A. 1B.2222yxyx-+C.yxyx+-D. x2+y23.计算:(-2x2y)3=A.-8x6y3B.8x6y3C.-6x6y3D.6x5y35. 下列计算正确的是()A. x2+3x2=4x4B. x2y·2x3=2x6yC. (6x3y2)÷(3x)=2x2D. (-3x)2=9x25.下列计算正确的是()A.a2+a3=a5B.(-2a)3=-6a3C.(a+1)2=a2+1D.6a2b÷(-2ab)=-3a5. 下列计算正确的是()A. a2·a3=a6B. (-2ab)2=4a2b2C. (a2)3=a5D. 3a3b2÷a2b2=3ab5. 一天上午,张大伯家销售了10箱西红柿,销售的情况如下表:箱数 1 2 3 4各箱的售价80 87 85 86则这10箱西红柿售价的中位数和众数分别是()A. 85和86B. 85.5和86C. 86和86D. 86.5和865. 某区10名学生参加市级汉字听写大赛,他们得分情况如下表:人数342 1分数80859095那么这10名学生所得分数的平均数和众数分别是() A. 85和82.5 B. 85.5和85 C. 85和85 D. 85.5和805.若a≠0,则下列运算正确的是()A.a3-a2=aB.a3·a2=a6C.a3+a2=a5D.a3÷a2=a5.我省某市五月份第二周连续七天的空气质量指数分别为:111,96,47,68,70,77,105,则这七天空气质量指数的平均数是()A.71.8 B.77 C.82 D.95.76.如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若DE=1,则BC的长为( )A.2+2B.2+3C.2+3D.36. 如图,在Rt△ABC中,∠ACB=90°,∠A=65°,CD⊥AB,垂足为D,E是BC的中点,连接ED,则∠DEC的度数是A.25°B.30°C.40°D.50°6. 如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为()A.43 2 B. 2 2 C.83 2 D. 3 26. 如图,在△ABC中,∠A=60°,∠B=45°.若边AC的垂直平分线DE交边AB于点D,交边AC于点E,连接CD,则∠DCB=A. 15°B. 20°C. 25°D. 30°6. 如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为()A. 3 3B. 6C. 3 2D. 216.如图,在△ABC中,∠BAC=90°,AB=20,AC=15,△ABC的高AD与角平分线CF交于点E,则AFDE的值为()A.35 B.34C.12 D.236. 如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为()A. 7B. 8C. 9D. 106.如图,点P是△ABC内一点,且P A=PB=PC,则点P是()A.△ABC三条中线的交点B.△ABC三条高线的交点C.△ABC三条角平分线的交点D.△ABC三边垂直平分线的交点6. 如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有()A. 2个B. 3个C. 4个D. 5个6. 不等式组⎪⎩⎪⎨⎧≤-+13252xx>的最小整数解是()A. -3B. -2C. 0D. 16. 把不等式组⎩⎪⎨⎪⎧x+2>13-x≥0的解集表示在数轴上,正确的是()7.在平面直角坐标系中,将函数 y =3x 的图象向上平移 6个单位长度,则平移后的图象与x 轴交点的坐标为 ( ) A.(2,0) B.(-2,0) C.(6,0) D.(-6,0) 7.将直线y=32x -1沿x 轴向左平移4个单位,则平移后的直线与y 轴交点的坐标是A .(0,5)B .(0,3)C .(0,-5)D .(0,-7)7. 若直线l 1经过点(0,4),l 2经过点(3,2),且l 1与l 2关于x 轴对称,则l 1与l 2的交点坐标为( ) A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)7. 设一次函数y =kx +b (k ≠0)的图象经过点(1,-3),且y 的值随x 的值增大而增大,则该一次函数的图象一定不...经过 A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限7. 如图,已知直线l 1:y =-2x +4与直线l 2:y =kx +b (k ≠0)在第一象限交于点M .若直线l 2与x 轴的交点为A (-2,0),则k 的取值范围是( )A. -2<k <2B. -2<k <0C. 0<k <4D. 0<k <27.已知两个一次函数y =3x +b 1和y =-3x +b 2. 若b 1<b 2<0,则它们图象的交点在( )A.第一象限B.第二象限C.第三象限D.第四象限 7. 已知一次函数y =kx +5和y =k′x +7.假设k >0且k ′<0,则这两个一次函数图象的交点在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限 已知一次函数y =kx +b 的图象经过点(1,2),且y 的值随x 值的增大而减小,则下列判断正确的是( ) A.k >0,b >0 B.k >0,b <0C.k <0,b >0D.k <0,b <07. 在平面直角坐标系中,将直线l 1:y =-2x -2平移后,得到直线l 2:y =-2x +4,则下列平移作法正确的是( ) A. 将l 1向右平移3个单位长度 B. 将l 1向右平移6个单位长度 C. 将l 1向上平移2个单位长度 D. 将l 1向上平移4个单位长度7. 用配方法解一元二次方程2x 2-3x =1,下列配方正确的是( A. (x -34)2=1716 B. (x -12)2=1716C. (x -32)2=1516D. (x -316)2=1387. 若x =-2是关于x 的一元二次方程x 2-52ax +a 2=0的一个根,则a 的值为( )A. 1或4B. -1或-4C. -1或4D. 1或-48.如果点A (m ,n )、B (m +1,n +2)均在一次函数y =kx.+b (k ≠0)的图象上,那么k 的值为( )A.2B.1C.-1D.-2 7.根据下表中一次函数的自变量x 与函数y 的对应值,可得p 的值为( )A.1B.-1C.3D.-38.如图,在矩形 ABCD 中,AB =3,BC =6.若点 E 、F 分别在 AB 、CD 上,且 BE = 2AE ,DF =2FC ,G 、H 分别是 AC 的三等分点,则四边形 EHFG 的面积为 ( ) A.1 B.32 C.2 D.48. 如图,在菱形ABCD 中,AC =2,BD =4,点E 、F 、G 、H 分别在AB 、BC 、CD 和DA 上,且EF ∥AC .若四边形EFGH 是正方形,则EF 的长为 A. 23 B .1 C. 43D .28. 如图,在菱形ABCD 中,点E 、F 、G 、H 分别是边AB 、BC 、CD 和DA 的中点,连接EF 、FG 、GH 和HE .若EH =2EF ,则下列结论正确的是( )A. AB =2EFB. AB =2EFC. AB =3EFD. AB =5EF8. 如图,在正方形ABCD 中,AB =2.若以CD 边为底边向其形外作等腰直角△DCE ,连接BE ,则BE 的长为 A. 5 B. 2 2 C. 10 D. 2 38. 如图,在矩形ABCD 中,AB =2,BC =3.若点E 是边CD 的中点,连接AE ,过点B 作BF ⊥AE 交AE 于点F ,则BF 的长为( ) A.3102 B. 3105 C. 105 D. 3558..如图,△ABC 和△DBC 均为等腰三角形,∠A =60°,∠D =90°,AB =12.若点E 、F 、G 、H 分别为边AB 、AC 、CD 、BD 的中点,则四边形EFGH 的面积为( )A.9(3+1)B.12(3+1)C.18(3+1)D.36(3+1)8.在▱ABCD中,AB=10,BC=14,E、F分别为边BC、AD 上的点.若四边形AECF为正方形,则AE的长为()A. 7B. 4或10C. 5或9D. 6或88.如图,在矩形ABCD中,AB=3,BC=4.若过点C作CE⊥BD,垂足为E,则BE的长为()(第9题图)A. 2B. 3C. 95 D.1658. 如图,在菱形ABCD中,AB=5,对角线AC=6.若过点A 作AE⊥BC,垂足为E,则AE的长为()第9题图A. 4B. 125 C.245 D. 58.如图,在矩形ABCD中,AB=3.4,BC=5,以BC为直径作半圆O,点P是半圆O上的一点.若PB=4,则点P到AD 的距离为()A.45 B.1 C.65 D.858.如图,在矩形ABCD中,AD=2AB,点M,N分别在边AD、BC上,连接BM、DN,若四边形MBND是菱形,则AMMD等于()A.38B.23C.35D.459.如图,AB是⊙O的直径,EF、EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF.若∠AOF=40°,则∠F的度数是()A.25ºB.35ºC.40ºD.55º9. 如图,四边形ABCD是⊙O的内接四边形,AD=BC.若∠BAC=45°,∠B=75°,则下列等式成立的是A.AB=2CD B.AB=3CD C.AB=32CD D.AB=2CD9. 如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为()A. 15°B. 35°C. 25°D. 45°9. 如图,矩形ABCD内接于⊙O,点P是AD︵上一点,连接PB、PC.若AD=2AB,则sin∠BPC的值为A.55 B.255 C.32 D.35109. 如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5.若点P是⊙O上的一点,在△ABP中,PB=AB,则P A的长为()A. 5B.532 C. 5 2 D. 5 39.如图,在⊙O中,弦AB垂直平分半径OC,垂足为D.若点P是⊙O上异于点A、B的任意一点,则∠APB=()A.30°或60°B.60°或150°C.30°或150°D.60°或120°9. 如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为()A. 3 3B. 4 3C. 5 3D. 6 311.已知实数1-2,0,16,3,π,25,34,其中为无理数的是_________.11.-27的立方根是__________.11. 比较大小:3________10(填“>”、“<”或“=”)11. 如图,数轴上的A 、B 两点所表示的数分别为a 、b ,则a +b ________0(填“>”,“=”或“<”).11. 在实数-5,-3,0,π,6中,最大的一个数是________.11.不等式-2x +1>-5的最大整数解是________. 11. 不等式-12x +3<0的解集是________.11.-8的立方根是______.11. 因式分解:m (x -y )+n (x -y )=________.11.在5,-1,227,π这四个数中,无理数有________个.11.计算:(-2)3+(3-1)0= .12.若正六边形的边长为3,则其较长的一条对角线长为__________.12.如图,在正六边形ABCDEF 中,连接DA 、DF ,则DFDA 的值为__________ .12. 如图,在正五边形ABCDE 中,AC 与BE 相交于点F ,则∠AFE 的度数为________.12. 请从以下两个小题中任选一个....作答,若多选,则按第一题计分.A. 如图,网格上的小正方形边长均为1,△ABC 和△DEF 的顶点都在格点上.若△DEF 是由△ABC 向右平移a 个单位,再向下平移b 个单位得到的,则ba的值为________.12. (节选)如图,在△ABC 中,BD 和CE 是△ABC 的两条角平分线.若∠A =52°,则∠1+∠2的度数为________.12. 如图,五边形ABCDE 的对角线共有________条. 12. (节选)一个正多边形的一个外角为45°,则这个正多边形的边数是________.12.请从以下两个小题中任选一个....作答,若多选,则按第一题计分. A.一个n 边形的内角和为900°,则n =______.B.如图,一山坡的坡长AB =400米,铅直高度BC =150米,则坡角∠A 的大小为______.(用科学计算器计算,结果精确到1°)12. (节选)正八边形一个内角的度数为________. 12. 正五边形一个内角的度数是________.13.如图,D 是矩形 AOBC 的对称中心,A (0,4),B (6,0).若一个反比例函数的图象经过点 D ,交 AC 于点 M ,则点 M 的坐标为_________.13.若一个反比例函数的图象与直线y =-2x +6的一个交点为A (m ,-4),则这个反比例函数的表达式是__________. 13. 若一个反比例函数的图象经过点A (m ,m )和B (2m ,-1),则这个反比例函数的表达式为________.13. 已知A ,B 两点分别在反比例函数y =3mx (m ≠0)和y =2m -5x (m ≠52)的图象上.若点A 与点B 关于x 轴对称,则m 的值为________.13.如图,在x 轴上方,平行于x 轴的直线与反比例函数y =xk 1和y =xk 2的图象分别交于A 、B 两点,连接OA 、OB .若△AOB 的面积为6,则k 1-k 2=________.13. 已知一次函数y =2x +4的图象分别交x 轴、y 轴于A 、B 两点.若这个一次函数的图象与一个反比例函数的图象在第一象限交于点C ,且AB =2BC ,则这个反比例函数的表达式为________13.在平面直角坐标系中,反比例函数y =xk的图象位于第二、四象限,且经过点(1,k 2-2),则k 的值为______.13. 如图,在平面直角坐标系中,过点M (-3,2)分别作x 轴、y 轴的垂线与反比例函数y =4x 的图象交于A 、B 两点,则四边形MAOB 的面积为________.15.计算:-231-2-27+1-3-2⨯()16.化简:22-2822-4-2a a a a a a a++÷+().15.计算:(-12)-1+|2-5|+2×(-8) .16. 解方程:3233--=+-x xx x .15. (本题满分5分)计算:(-3)×(-6)+|2-1|+(5-2π)0.16. (本题满分5分)化简:(a +1a -1-aa +1)÷3a +1a 2+a .15. 计算:18-(π-5)0+|22-3|.16. 解分式方程:2x -1x +2=2-3x -2.15. (本题满分5分)计算:(-2)×6+|3-2|-(12)-1.16. (本题满分5分)解方程:3233+--+x x x =1.15.)计算: (-3)2+|2-5|-20.16.化简:(937222--+a a a —34++a a )÷33-+a a .15. (本题满分5分)计算:12-|1-3|+(7+π)0.16. (本题满分5分)化简:(x -5+91)3162--÷+x x x15.计算: 8×3-2×|-5|+(-13)-2.16.(本题满分5分)解分式方程: 23+x +2=22-x x .15. (本题满分5分)计算:3×(-6)+|-22|+(12)-3.16. (本题满分5分)解分式方程:x -2x +3-3x -3=1.17.(本题满分 5分)如图,在△ABC 中,AB =AC ,AD 是 BC 边上的高,请用尺规作图法,求作△ABC 的外接圆.(保留作图痕迹,不写作法)17. (本题满分5分)如图,已知:在正方形ABCD 中,M 是BC 边上一定点,连接AM .请用尺规作图法,在AM 上求作一点P ,使△DP A ∽△ABM .(不写作法,保留作图痕迹)17. (本题满分5分)如图,在△ABC中,AD是BC边上的高.请用尺规作图法在高AD上求作一点P,使得点P到AB的距离等于PD的长.(保留作图痕迹,不写作法)17. (本题满分5分)如图,在钝角△ABC中,过钝角顶点B作BD⊥BC交AC于点D.请用尺规作图法在BC边上求作一点P,使得点P到AC的距离等于BP的长.(保留作图痕迹,不写作法)第17题图17.(本题满分5分)如图,已知锐角△ABC,点D是AB边上的一定点,请用尺规在AC边上求作一点E,使△ADE与△ABC相似.(作出符合题意的一个点即可,保留作图痕迹,不写作法.)(第17题图)17. (本题满分5分)如图,已知△ABC,∠BAC=90°,请用尺规过点A作一条直线,使其将△ABC分成两个相似的三角形.(保留作图痕迹,不写作法)第17题图17.(本题满分5分)如图,请用尺规在△ABC的边BC上找一点D,使得点D到边AB、AC的距离相等.(保留作图痕迹,不写作法)17. (本题满分5分)如图,已知△ABC,请用尺规过点A作一条直线,使其将△ABC分成面积相等的两部分.(保留作图痕迹,不写作法)18.(本题满分5分)如图,点A、E、F、B在直线l上,AE=BF,AC∥BD,且AC=B D.求证:CF=DE .第18题图18. (本题满分5分)如图,在△ABC中,AB=AC,O是边BC的中点,延长BA到点D,使AD=AB,延长CA到点E,使AE=AC,连接OD,OE,求证:∠BOE=∠COD .18. (本题满分5分)如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交于点G、H,若AB=CD.求证:AG=DH.18. (本题满分5分)如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交于点G、H,若AB=CD.求证:AG=DH.18. (本题满分7分)如图,在正方形ABCD中,E、F分别为边AD和CD上的点,且AE=CF,连接AF、CE交于点G. 求证:AG=CG .18. (本题满分7分)如图,在▱ABCD中,延长BA到点E,延长DC到点F,使AE=CF,连接EF交AD边于点G,交BC边于点H.求证:DG=BH . 18.(本题满分7分)如图,在菱形ABCD中,点E是边AD上一点,延长AB至点F,使BF=AE,连接BE、CF.求证:BE=CF .18. (本题满分7分)如图,在▱ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE.求证:AF∥CE .18.(本题满分7分)如图,在△ABC中,AB=AC. D是边BC延长线上的一点,连接AD,过点A、D分别作AE∥BD、DE∥AB,AE、DE交于点E,连接CE.求证:AD=CE.18. (本题满分7分)如图,在△ABC中,AB=AC.作AD⊥AB交BC的延长线于点D,作AE∥BD、CE⊥AC,且AE、CE相交于点E.求证:AD=CE.第19题图。
