博弈论作业
博弈论作业——精选推荐

博弈论作业1.海盗分金中如果假设需要同意的人超过半数提议才能通过,则理性结局又会是什么?如果200个人参加(只要半数即可通过)又将如何?500人呢?解:半数即可通过——倒推分析结果如下(1000,0)(999,0,1)(999,0,1,0)(998,0,1,0,1)下一步的分钱方案中,只需要把上一步得钱非0的强盗的得钱数改为0,而其它强盗则反之。
进而有非0和0的间隔分布,除了提出方案的强盗外,其它得钱非0的强盗得到1块钱。
因此有200个强盗分1000个金币的情形为 ( X, 0, 1, …, 0 )可得X=901因此有500个强盗分1000个金币的情形为 ( X, 0, 1, …, 0 )可得X=751超过半数才可通过——倒推结果如下(0,1000)(999,1,0)(997,0,2,1)(997,0,1,0,2)因此,5个强盗分1000个金币的情形为(997,0,1,0,2)2.在无限期的鲁宾斯坦模型中,假设分割只能是0.01的整数倍,即X只能为0,0.01;0.02;…….0.99或1,求δ=0.5和δ非常接近于1时的子博弈完美均衡(假设两个人的折现因子相同)两个人要分一块冰淇淋,甲将分得冰淇淋的x份额(x ≥ 0),乙将得到1-x的份额(1-x ≥ 0)。
两人进行轮流出价。
首先,甲提出一个划分方法(x,1-x),乙可以接受或拒绝这个提议,如果他接受了,则博弈结束,他们按照这种划分去切割冰淇淋;如果乙拒绝这个提议,那么他会提出一个划分方法(y,1-y),甲可以接受或者拒绝,博弈过程将这个方式持续进行下去,直到他们达成一个协议。
每当协议的达成拖延时,他们的得益会有一个折扣(贴现),两人的贴现因子由iδ (0<iδ<1)表示。
这种折扣代表了讨价还价的成本。
其它条件相同,对参与者而言,达成一个协议所需的时间越长,冰淇淋就会越小。
两人贴现相同,如果假定1δ=2δ=δ的话,上述讨价还价博弈的唯一的均衡结果将会是(1 / (1 + δ), δ / (1 + δ))。
大学博弈论试题及答案

大学博弈论试题及答案一、选择题(每题2分,共20分)1. 在博弈论中,非合作博弈是指:A. 参与者之间可以达成协议B. 参与者之间不能达成协议C. 参与者之间必须达成协议D. 参与者之间只能通过合作达到目标答案:B2. 纳什均衡是博弈论中的一个概念,它描述了一种情况,即:A. 所有参与者都处于最优策略B. 至少有一个参与者处于非最优策略C. 所有参与者都处于非最优策略D. 至少有一个参与者可以单方面改变策略以获得更好的结果答案:A3. 囚徒困境中,如果两个参与者都选择合作,那么:A. 他们都将获得最大收益B. 他们都将获得最小收益C. 他们都将获得中等收益D. 他们中的一个将获得最大收益,另一个获得最小收益答案:C4. 零和博弈是指:A. 一个参与者的收益等于另一个参与者的损失B. 参与者的总收益为零C. 参与者的总损失为零D. 参与者的总收益和总损失相等答案:B5. 在博弈论中,策略是指:A. 参与者的行动计划B. 参与者的收益C. 参与者的损失D. 参与者的支付结构答案:A6. 博弈论中的“混合策略”是指:A. 参与者随机选择策略B. 参与者总是选择相同的策略C. 参与者的策略是固定的D. 参与者的策略是预先确定的答案:A7. 博弈论中的“支配策略”是指:A. 无论对手选择什么策略,都是最优的策略B. 只有在特定情况下才是最优的策略C. 只有在对手选择特定策略时才是最优的策略D. 参与者总是选择的策略答案:A8. 博弈论中的“重复博弈”是指:A. 博弈只进行一次B. 博弈进行多次,但每次都是独立的C. 博弈进行多次,且参与者的记忆会影响后续决策D. 博弈进行多次,但参与者不能记住之前的决策答案:C9. 在博弈论中,如果一个策略在任何情况下都不是最优的,那么这个策略被称为:A. 支配策略B. 支配策略的反面C. 支配策略的替代D. 非支配策略答案:B10. 博弈论中的“共同知识”是指:A. 所有参与者都知道的信息B. 只有部分参与者知道的信息C. 参与者之间的秘密D. 参与者之间共享的信念答案:A二、填空题(每题2分,共20分)1. 在博弈论中,如果一个策略在任何情况下都不是最优的,那么这个策略被称为________。
博弈论作业

博弈论作业博弈论作业一、 下面的得益矩阵表示博弈方之间的一个静态博弈。
该博弈有没有纯策略纳什均衡?博弈的结果是什么?博弈方 2L C R博弈 T 方 M 1 B 答:此博弈有两个纳什均衡:1、ML 得益(3,4)2、TR 得益(4,2)二、 求出下图中得益矩阵所表示的博弈中的混合策略纳什均衡与得益。
博弈方 2L R博弈 T 方 B 1答:(一)求混合策略均衡1、博弈方1的概率P则对博弈方2而言,有1×P +2(1-P )=2×P +0(1-P )2-P =2PP =2/3当P ﹤2/3,2-P ﹥2P ,则q ﹡=1是最合适的策略,即选择L 。
当P =2/3,2-P =2P ,则q ﹡∈(0,1)是最适合反应。
当P ﹥2/3,2-P ﹤2P ,则q ﹡=0是最适合策略,即选择R 。
2、给定博弈方2的概率q则对博弈方1而言,有2×q +0(1-q )=1×q +3(1-q )2q =3-2qq =3/4当q ﹤3/4,2q ﹤3-2q ,则P ﹡=0是最合适的策略,即选择B 。
当q =3/4,2q =3-2q ,则P ﹡∈(0,1)是最适合反应。
当q ﹥3/4,2q ﹥3-2q ,则P ﹡=1是最适合策略,即选择T 。
所以:混合策略的均衡点为(2/3,3/4)。
(二)得益:∪1=2×P ×q +0×P ×(1-q)+1×(1-P)×q+3(1-P)(1-q)=2×2/3×3/4+1×1/3×3/4+3×1/3×1/4=3/2∪2=1×P ×q +2×P ×(1-q)+2×(1-P)×q+0(1-P)(1-q)=1×2/3×3/4+2×2/3×1/4+2×1/3×3/4=4/3三、 设一四阶段两博弈方之间的动态博弈如下图所示。
§博弈论作业题4道

企业战略决策和管理中的博弈作业:一、优利公司和埃克森公司是生产一种非常精密的摄象机的仅有的两家公司。
他们在商业杂志上投入或高或低的广告费。
他们的赢得矩阵如下所示:(单位:万美元)埃克森低高┏━━━━━━┳━━━━━┓低┃1200,1300┃1100,1200┃优利┣━━━━━━╋━━━━━┫高┃1300,1200┃1200,1100┃┗━━━━━━┻━━━━━┛1、优利公司在商业杂志上的广告支出是高还是低?答:在优利公司广告支出低的情况下:如果埃克森公司也支出低,优利公司可赢得1200万,如果埃克森公司支出高,优利公司则赢得1100万。
在优利公司广告支出高的情况下:如果埃克森公司支出低,优利公司可赢得1300万,如果埃克森公司支出高,优利公司则赢得1200万。
因此,优利公司为获得尽可能高的利润,只有选择广告支出高的策略。
2、埃克森公司的广告支出是高还是低?答:在埃克森公司广告支出低的情况下:优利公司支出低,埃克森公司可赢得1300万,如果优利公司支出高,埃克森公司则赢得1200万;在埃克森公司广告支出高时: 如果优利公司支出低,埃克森公司赢得1200万,如果优利公司支出高,埃克森公司仅赢得1100万。
因此,埃克森公司应选择低的广告支出策略。
3、每家公司是否都存在占优(最优)策略?答:埃克森公司与优利公司都存在各自的占优策略。
二、两家肥皂制造商:富特纳公司和梅森公司,在即将到来的广告战中或侧重于报纸,或侧重于杂志。
他们的赢得矩阵如下所示:(单位:万美元)梅森报纸杂志┏━━━━━┳━━━━━┓报纸┃800,900┃700,800┃富特纳┣━━━━━╋━━━━━┫杂志┃900,800┃800,700┃┗━━━━━┻━━━━━┛1、对每家公司来说是否存在占优策略?如果存在,各是什么?答:富特纳公司与梅森公司都存在占优策略。
富特纳公司广告投入侧重于杂志,梅森公司侧重于报纸。
2、每家公司的利润各是多少?答:富特纳公司与梅森公司在各自占优策略下的利润均为900万美元。
博弈论基础作业及答案

博弈论基础作业一、名词解释纳什均衡占优战略均衡纯战略混合战略子博弈精炼纳什均衡贝叶斯纳什均衡精炼贝叶斯纳什均衡共同知识见PPT二、问答题1.举出囚徒困境和智猪博弈的现实例子并进行分析。
囚徒困境的例子:军备竞赛;中小学生减负;几个大企业之间的争相杀价等等;以中小学生减负为例:在当前的高考制度下,给定其他学校对学生进行减负,一个学校最好不减负,因为这样做,可以带来比其他学校更高的升学率。
给定其他学校不减负,这个学校的最佳应对也是不减负。
否则自己的升学率就比其他学校低。
因此,不论其他学校如何选择,这个学校的最佳选择都是不减负。
每个学校都这样想,所以每个学校的最佳选择都是不减负,因此学生的负担越来越重。
请用同样的方法分析其他例子。
智猪博弈的例子:大企业开发新产品;小企业模仿;股市中,大户搜集分析信息,散户跟随大户的操作策略以股市为例:给定散户搜集资料进行分析,大户的最佳选择是跟随。
而给定散户跟随,大户的最佳选择是自己搜集资料进行分析。
但是不论大户是选择分析还是跟随,散户的最佳选择都是跟随。
因此如果大户和散户是聪明的,并且大户知道散户也是聪明的,那么大户就会预见到散户会跟随,而给定散户跟随,大户只有自己分析。
请用同样的方法分析其他例子。
2.请用博弈论来说明“破釜沉舟”和“穷寇勿追”的道理。
破釜沉舟是一个承诺行动。
目的是要断绝自己的退路,让自己无路可退,让自己决一死战变得可以置信。
也就是说与敌人对决时,只有决一死战,这样才可以取得胜利。
否则,如果不破釜沉舟,那么遇到困难时,就很有可能退却,也就无法取得胜利。
穷寇勿追就是要给对方一个退路,由于有退路,对方就不会殊死抵抗。
否则,对方退无可退,只有坚决抵抗一条路,因而必然决一死战。
自己也会付出更大的代价。
3.当求职者向企业声明自己能力强时,企业未必相信。
但如果求职者拿出自己的各种获奖证书时,却能在一定程度上传递自己能力强的信息。
这是为什么?由于口头声明几乎没有成本,因此即便是能力差的求职者也会向企业声明自己能力强。
博弈论智力题

A.逻辑推理2、请把一盒蛋糕切成8 份,分给8个人,但蛋糕盒里还必须留有一份。
3、小明一家过一座桥,过桥时是黑夜,所以必须有灯。
现在小明过桥要 1 秒,小明的弟弟要3 秒,小明的爸爸要6 秒,小明的妈妈要8 秒,小明的爷爷要12 秒。
每次此桥最多可过两人,而过桥的速度依过桥最慢者而定,而且灯在点燃后30 秒就会熄灭。
问:小明一家如何过桥?4、一群人开舞会,每人头上都戴着一顶帽子。
帽子只有黑白两种,黑的至少有一顶。
每个人都能看到其他人帽子的颜色,却看不到自己的。
主持人先让大家看看别人头上戴的是什么帽子,然后关灯,如果有人认为自己戴的是黑帽子,就打自己一个耳光。
第一次关灯,没有声音。
于是再开灯,大家再看一遍,关灯时仍然鸦雀无声。
一直到第三次关灯,才有劈劈啪啪打耳光的声音响起。
问有多少人戴着黑帽子?5、请估算一下CN TOWER电视塔的质量。
7、U2 合唱团在17分钟内得赶到演唱会场,途中必需跨过一座桥,四个人从桥的同一端出发,你得帮助他们到达另一端,天色很暗,而他们只有一只手电筒。
次同时最多可以有两人一起过桥,而过桥的时候必须持有手电筒,所以就得有人把手电筒带来带去,来回桥两端。
手电筒是不能用丢的方式来传递的。
四个人的步行速度各不同,若两人同行则以较慢者的速度为准。
Bono需花1分钟过桥,Edge需花2 分钟过桥,Adam 需花5 分钟过桥,Larry 需花10 分钟过桥。
他们要如何在17 分钟内过桥呢?11、有7克、2克砝码各一个,天平一只,如何只用这些物品三次将140克的盐分成50、90 克各一份?13、你有两个罐子,50个红色弹球,50 个蓝色弹球,随机选出一个罐子,随机选取出一个弹球放入罐子,怎么给红色弹球最大的选中机会?在你的计划中,得到红球的准确几率是多少?14、想象你在镜子前,请问,为什么镜子中的影像可以颠倒左右,却不能颠倒上下?16、如果你有无穷多的水,一个3 夸脱的和一个5 夸脱的提桶,你如何准确称出4 夸脱的水?21、假设一张圆盘像唱机上的唱盘那样转动。
博弈论作业——精选推荐
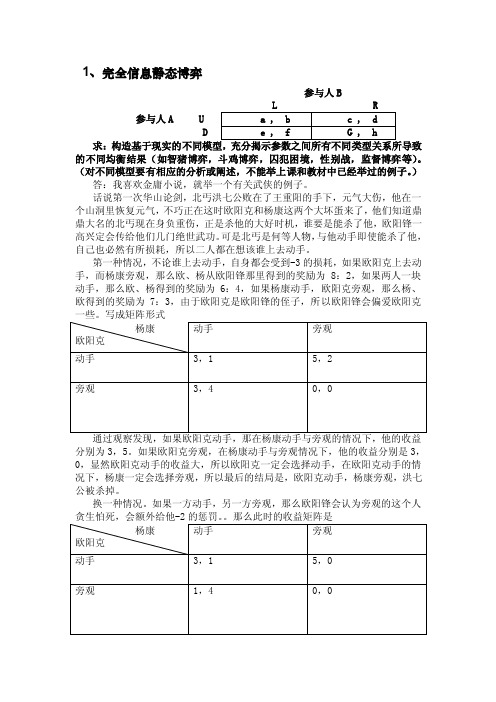
1、完全信息静态博弈参与人B参与人A UD求:的不同均衡结果(如智猪博弈,斗鸡博弈,囚犯困境,性别战,监督博弈等)。
(对不同模型要有相应的分析或阐述,不能举上课和教材中已经举过的例子。
)答:我喜欢金庸小说,就举一个有关武侠的例子。
话说第一次华山论剑,北丐洪七公败在了王重阳的手下,元气大伤,他在一个山洞里恢复元气,不巧正在这时欧阳克和杨康这两个大坏蛋来了,他们知道鼎鼎大名的北丐现在身负重伤,正是杀他的大好时机,谁要是能杀了他,欧阳锋一高兴定会传给他们几门绝世武功。
可是北丐是何等人物,与他动手即使能杀了他,自己也必然有所损耗,所以二人都在想该谁上去动手。
第一种情况,不论谁上去动手,自身都会受到-3的损耗,如果欧阳克上去动手,而杨康旁观,那么欧、杨从欧阳锋那里得到的奖励为8:2,如果两人一块动手,那么欧、杨得到的奖励为6:4,如果杨康动手,欧阳克旁观,那么杨、欧得到的奖励为7:3,由于欧阳克是欧阳锋的侄子,所以欧阳锋会偏爱欧阳克分别为3,5。
如果欧阳克旁观,在杨康动手与旁观情况下,他的收益分别是3,0,显然欧阳克动手的收益大,所以欧阳克一定会选择动手,在欧阳克动手的情况下,杨康一定会选择旁观,所以最后的结局是,欧阳克动手,杨康旁观,洪七公被杀掉。
换一种情况。
如果一方动手,另一方旁观,那么欧阳锋会认为旁观的这个人可见,如果欧阳克动手,那在杨康动手与旁观的情况下,他的收益分别为3,5。
如果欧阳克旁观,那在杨康动手与旁观的情况下,他的收益分别为1,0。
所以他一定会选择动手,对杨康来说,动手的收益分别为1,4,旁观的收益分别是0,0,所以他一定会选择动手,最终的结果一定是,欧、杨两人一起动手杀掉七公。
第三种情况。
由于洪七公是天下第一大帮丐帮帮主,杀掉他的人一定会得罪丐帮,得罪天下武林同道,以后难以立足江湖,自身会受到-3的损伤,此时的如果杨康选择旁观,那么它的收益分别为0,0。
所以杨康一定不会动手。
同样,欧阳克选择动手,收益分别是-1,1.如果选择旁观收益分别为1,0。
博弈论试题及答案

博弈论试题及答案【正文】博弈论试题及答案一、选择题1.博弈论是研究:A. 地理分布B. 人类视力C. 决策制定D. 古典文学答案:C2.下列哪个不是博弈论中常见的概念?A. 纳什均衡B. 优势策略C. 输家效应D. 零和博弈答案:C3.描述纳什均衡的最佳方式是:A. 所有参与者都达到最佳策略B. 至少有一个参与者达到最佳策略C. 所有参与者都达到次优策略D. 至少有一个参与者达到次优策略答案:A4.下列哪个案例体现了零和博弈的情况?A. 两国签订贸易协定B. 赌徒在赌博中争夺赌注C. 两家公司合作推出新产品D. 好友一起玩棋盘游戏答案:B5.下列哪个不是博弈论的应用之一?A. 经济决策B. 政治博弈C. 生物进化D. 音乐创作答案:D二、填空题1.博弈论最早由_____________等人于20世纪40年代提出。
答案:冯·诺依曼(John von Neumann)2.博弈论是研究参与者间的_____________和_____________的学科。
答案:互动行为;决策制定3.零和博弈是指参与者的利益总和恒为_____________。
答案:零4.博弈论中的最佳策略指的是在其他参与者采取某个策略时,使某一参与者的_____________最大化的策略。
答案:利益5.斯坦福大学的_____________教授以其对博弈论的突出贡献而获得2005年诺贝尔经济学奖。
答案:约翰·纳什(John Nash)三、简答题1.简要解释博弈论中的纳什均衡。
答:纳什均衡是博弈论中的一个重要概念,指的是在参与者选择自己最佳策略的情况下,不存在任何一个参与者可以通过单独改变自己的策略来获得更好收益的状态。
简言之,纳什均衡是一种理性选择下的稳定状态。
2.举例说明博弈论在实际生活中的应用。
答:博弈论在经济学、政治学、生物学等领域中都有广泛应用。
例如,在贸易谈判中,两个国家之间的博弈就是典型的博弈论应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程名称:信息经济学与博弈论课程编号:SX0071F23 课程类型:非学位课考核方式:考查学科专业:管理科学与工程年级:2014 级姓名:学号:10076140185河北工程大学2014 ~ 2015学年第2学期研究生课程论文报告基于GA一RL的进化博弈求解主从博弈结构的供应链协调问题摘要:供应链协调问题多数基于主从博弈结构建模,但如果研究对象是相对复杂的供应链结构,理论求解主从博弈问题就变得困难。
因此从求解一对一的供应链协调问题开始,针对主从博弈问题的特点,利用个体学习的进化博弈仿真手段,设计了经销商利用经验分布的预期随机需求的信念更新模式与最优反应的决策模式,为生产商分别设计了基于强化学习的信念更新模式与基于遗传算法搜索策略空间的决策模式,并将两者有机结合,取得了博弈问题的均衡解并且验证该解与理论求解结果一致,为进一步求解复杂问题提供了新的途径。
关键词:供应链协调;进化博弈论;强化学习(RL);遗传算法(GA)Coordinating supply chain of Stackelberg game model based on evolutionary game with GA一RL Abstract: Problems of coordinating supply chain are based on Stackelberg game model, but if research object is complex supply chain, it is difficult to find equilibrium of Stackelberg game ,so evolutionary Game theory was introduced. According to characteristics of leaders and followers in Stackelberg game model, learning Meehan is designed for each Player respectively. An algorithm of reinforcement learning combined with genetic searching is proposed for leaders, and a learning model of best一reply is designed for followers(retailers).Keywords: supply chain coordination; evolutionary game theory; reinforcement learning(RL);genetic algorithm(GA)1引言供应链协调问题是研究如何订立协调机制使分散控制的供应链中个体与整体之间的目标一致,解决供应链中企业个体自身的优化目标与供应链整体的最优解相冲突的状况。
目前关于不同协调机制研究可以分为以下几类,一类是根据数量给予价格折扣,如根据经销商的销售量给予目标折扣(Sale re-bate)的问题[1],根据订货量给予线性折扣(Quantity discount)的问题[2];第二类是根据订货周期给予价格折扣,依据订货周期(order frequency)实行价格折扣的分销系统协调机制[3],为了分散供应商的库存风险,提供给提前定货经销商价格折扣,建立单周期模型研究在需求的不确定有限情况下生产商制定合适的价格折扣激励经销商提早订货[4],在他的模型里生产商可以改变经销商竞争状态(领导/跟随);第三类是弹性的订货数量,如弹性订货经销商可以以全部价格退还商品,类似的回购契约[5]经销商可以一定的折扣价格退还未售出的商品。
但由于数学求解的困难,上述模型多数是针对两周期一对一的供应链问题,并且很多研究也只证明了哪种形式的协调机制可以协调供应链[6],但协调机制的参数如何制定却无法给出.而现实中的供应链往往是包括多个企业的链状和网状结构,解决这类问题应用数学建模与理论求解有相当的难度,因此本文尝试应用进化博弈的分析框架[7]。
本文在对目标数量折扣问题证明与求解的基础上,通过进化博弈的手段求解这类问题的均衡,为求解复杂的供应链协调问题提供一个新的途径。
而对于进化博弈领域,基本没有对效用函数结构复杂博弈问题的研究。
因此对于个体学习的进化博弈也是一种新的尝试。
2模型假定模型中包括一个生产商(上游企业)和一个经销商(下游企业),他们都是风险中性的,面对的是报童问题(连续随机需求的订货问题):经销商必须在随机需求发生之前订购一定数量的产品.因此模型可以理解为如下过程:生产商向经销商提出某种协调机制形式和参数;假设这种协调机制被经销商接受,于是经销商在此基础上提出一定数量的订货[8]。
模型参数设置如下:q=经销商的订货量,p=经销商制定的市场零售价格,D=市场需求,分布为F(),需求的期望值为μ, c r=经销商每件产品的边际成本, C s=生产商每件产品的生产成本, g r=经销商的边际缺货损失成本, g s=生产商缺货损失成本,v=期末未售出产品残值令c=c r+c s, g=g r+g s,T=调机制(生产商与经销商之间的转移支付) [9]。
定义期望销售量:S q=Emin q,D=q1−F q+yf y dy=q0q−F yqdy期望剩余库存:I q=E q−D=q−S q期望缺货量:L q=E D−q=μ−S q因此经销商期望利润为:Eπγq,T=pS q+vI q−g r L q−c r q−T=p−v+g r S q−c r−v q−g rμ−T假设供应商可以保证任何可能发生的订货,则生产商的期望利润为[10]:Eπs q,T=T−g s L q−C s q=g s S q−g sμ−C s q+T供应链的整体利润就是企业的利润之和,即:Eπq=Eπγq,T+EπS q,T=P−v+g S q−gμ−c−v q 上述模型相当于一种生产商作为领导者的主从博弈间题.博弈过程分成两个阶段,第一阶段生产商决定决策变量一协调机制T的参数;第二阶段经销商观测到生产商的决策后,确定决策变量一订货量q。
作者已根据主从博弈的理论求解方法一逆向归纳法,从理论上求解博弈问题的均衡解为:q 0, q 0,πγ qW −πγ q 0 ωq 03进化博弈仿真求解供应链协调问题供应链协调问题的过程可以描述为:首先,生产商选择自己的行动一某种协调机制形式和参数;然后,经销商在此基础上选择自己的行动一订货量:最后,经销商销售产品,在销售周期结束之后,实现了市场的需求,经销商与生产商分别获得相应的收益一个基本的进化博弈模型的分析框架为:决策者在博弈重复进行的过程中,只能观察到部分外界环境和对手的信息,决策者 根据一定的信念更新规则对未来的收益做出预期,然后根据预期采取某种决策规则进行决策[11]。
因此针对供应链协调问题设计进化博弈实验模型的结构为:生产商根据对收益或者经销商订货量的预期采取行动:对经销商来讲,生产商的行动已知,经销商面对的是未知的随机需求,因此在决策之前根据对需求做出一定预期,而采取相应的订货量;最后根据需求、经销商的订货量、生产商的协调机制分别产生的经销商与生产商的利润;生产商根据历史上经销商的订货量和自己获得的利润,更新对它们预期,经销商则根据历史的需求信息,更新对需求的预期,通过决策规则确定下一周期的行动,进入下一周期的博弈[12]。
3.1经销商学习机制预期需求方法经销商在每个周期的博弈中面对的只有未知的随机需求,这里以经验分布作为对需求分布的预期.这种预期方法本质上是决策者对某一需求量发生的概率的预期,这个概率是这个需求量在历史上出现的频率。
[13]因此,如果在周期艺发生需求为d,,那么更新需求d 发生的概率Pt(d:)的预期:P t d i =p t −1 d i × t −1 +1t , P t d i =p t −1 d i × t −1 t ,j ≠i决策规则经销商在知道生产商的行动之后,并对每一个需求量发生的概率预期为尸(司,采取最优反应的决策规则在离散的需求分布下,经销商在生产商给定一定的目标数量折扣T 万时,最优订货量Q 满足:P d Q d=0≥p +g −c p +g −v ≥ P d Q −1d=0经销商学习机制算法形式如下:l)在博弈的开始艺t=0时,初始化对于需求的预测p 0 d i =0;2)重复(a)按照最优反应决策准则确定行动q t =argmax πt q r |T,σ,P d(b)如果在时刻t 发生需求为d,。
那么更新对于需求发生概率的预期为p t d i =p t −1 d i × t −1 +1, p t d i =p t −1 d i × t −1 , j ≠i 3.2生产商学习机制在进化博弈的分析中,个体的学习机制以强化学习为主,但传统的强化学习通常采取贪婪策略,对于初始状态有很强的依赖性,导致搜索广度不足.因此,本文引入遗传算法作为决策规则,遗传算法中采取复制,变异与交叉的策略来搜索策略空间,其中复制保留下了优良解的特点,而变异和交叉策略恰恰保证了对策略空间的搜索广度[14]。
信念更新规则—强化学习每一轮博弈之后。
生产商根据自己的历史策略与利润,采取强化学习更新行动.定义生产商的每一个行动的倾向值函数。
每个阶段博弈之后,生产商根据历史行动与利润,更新每一个行动的预期收益函数,得到的实际收益为:time t a i=time t−1a i+`1 ,πt a i=πt−1a i×time t−1a i+πt a it i对其他行动a j,j≠itime t a j=time t−1a j, πt a j=πt−1a j决策规则—遗传搜索策略当采取传统的遗传算法,利用每一轮博弈中企业得到利润函数作为适应值,因为外部的需求是一个随机变量,企业每一周期的利润会随着需求而波动,因此这种适应值会受短期利润的干扰。
因此将强化学习中对利润的预期反(。
,),作为遗传算法的适应值,并借鉴遗传算法的种群复制、交叉、变异规则,产生新策略。
遗传算法需要选定一组行动作为种群,对种群中的每个行动都要计算适应值,对于博弈问题,需要对每个行动都进行一次博弈,这里有两种可行的处理方法:其一为设置对应种群个数的个体,在每一轮博弈中,每个个体与对手随机匹配,进行博弈得到利润,进而计算每个个体在这一轮博弈中行动的适应值;第二种方法是,在确定一个种群之后,重复进行博弈,每一轮博弈中,决策者轮流采取种群中的行动,进而得到利润计算适应值。
当一个种群中的所有行动都完成博弈,按照遗传算法的规则产生下一代群体,继续进行博弈.在本文的模型中,我们选择的是第二种处理方法,为了区别遗传算法的遗传代数与博弈的周期,用坛表示代数.产生下一代种群的遗传规则依次为:复制规则:按照轮盘赌规则将种群中个体复制到下一代种群中[15];被选择保留下来交叉规则:因为生产商的行动空间为目标订货量与折扣系数,交叉操作就是在复制后产生的种群中,以交叉概率p。
