中南大学 机械振动复习材料
1、机械振动基本知识——一轮复习
一、理想化模型:弹簧振子和单摆
机械振动
弹簧+物体
(1)不计阻力 (2)不计弹簧质量 (3)物体视为质点 (4)不超过弹簧形变
②振子位置在t轴上方,表示位移为正 振子位置在t轴下方,表示位移为负
③对x-t图象的理解 x-t图象上的 x 坐标表示振子相对平衡位 置的位移,也表示振子的位置坐标.x-t图 象反映了振子位移随时间变化的规律.
注意 x-t 图象不是振子的运动轨迹.
2.图象的应用
(1)可直接读出不同时刻t的位移x值.位于t轴上方的x值表示位移为正,位于t
轴下方的x值表示位移为负,如图甲所示.
甲
(2)可直接读出振子正(负)位移的最大值.
(3)判断任意时刻质点的振动方向.看下一相邻时刻质点的位置,如图乙中a点,
下一相邻时刻离平衡位置更远,故a点此刻向+x方向运动.
(4)速度的大小和方向:
乙
①根据图象上某点的切线的斜率判断:
图象上某点切线的斜率的大小表示速度大小,斜率的正负表示速度的方向.
及E-t图象 E
机械能
势能
0A O B
动能 t
往复性-重复性-周期性 全振动 振子的运动最显著的特点是什么?
(1)、一次全振动:
振子在AA/之间振动,O为平衡位置。如果从A点开始运动,经O点运动到A/点, 再经过O点回到A点,就说它完成了一次全振动,此后振子只是重复这种运动。
x ----振子离开平衡位置的位移,简称位移,
方向总是背离平衡位置.(由平衡位置指向振动物体所在位置)
机械振动2015试题及参考答案-1

中南大学考试试卷(A卷)2015 - 2016学年上学期时间110分钟《机械振动基础》课程 32 学时 2 学分考试形式:闭卷专业年级:机械13级总分100分,占总评成绩 70 %注:此页不作答题纸,请将答案写在答题纸上1、简述机械振动定义,以及产生的内在原因。
(10分)答:机械振动指机械或结构在它的静平衡位置附近的往复弹性运动。
(5分)产生机械振动的内在原因是系统本身具有在振动时储存动能和势能,而且释放动能和势能并能使动能和势能相互转换的能力。
(5分)2、简述随机振动问题的求解方法,随机过程基本的数字特征包括哪些?(10分)答:随机振动问题只能用概率统计方法来求解,只能知道系统激励和相应的统计值(5分)。
随机过程基本的数字特征包括:均值、方差、自相关函数、互相关函数。
(5分)3、阻尼对系统的自由振动有何影响?若仪器表头可等效为具有黏性阻尼的单自由度系统,欲使其在受扰动后尽快回零,最有效的办法是什么?(10分)答:阻尼消耗振动系统的能量,它使自由振动系统的振动幅值快速减小(5分)。
增加黏性阻尼量,可使指针快速回零位(5分)。
4、简述求解周期强迫振动和瞬态强迫振动问题的方法。
(10分)答:求解周期强迫振动时,可利用傅里叶级数将周期激励力转化为简谐激励力,然后利用简谐激励情况下的周期解叠加,可以得到周期强迫振动的解(5分)。
求解瞬态强迫振动的解时,利用脉冲激励后的自由振动函数,即单位脉冲响应函数,与瞬态激励外力进行卷积积分,可以求得瞬态激励响应(5分)。
周期强迫振动和瞬态强迫振动,也可以通过傅里叶积分变换、拉普拉斯积分变换来求解。
5、如图1所示,系统中质量m 位于硬质杆2L (杆质量忽略)的中心,阻尼器的阻尼系数为c ,弹簧弹性系数为k ,(1)建立此系统的运动微分方程; (5分) (2)求出临界阻尼系数表示式; (5分) (3)阻尼振动的固有频率表示式。
(5分)答:(1)可以用力矩平衡方法列写平衡方程,也可以用能量方法列写方程,广义坐标可以选质量块的垂直直线运动,也可以选择杆的摆角,以质量块直线运动坐标为例,动能212TE mx =&,势能21(2)2U k x =,能量耗散212D cx =&,由222,,T T ij ij ij i j i j i jE D Um c k x x x x x x ∂∂∂===∂∂∂∂∂∂,得到:40mx cx kx ++=&&&;(2)e c ==(3)d n ω==6、如图2所示系统,两个圆盘的直径均为r ,设I 12,k 12,k 3=3k , (1)选取适当的坐标,求出系统动能、势能函数; (5分) (2)求出系统的质量矩阵、刚度矩阵; (5分) (3)写出该系统自由振动时运动微分方程。
机械振动考试复习9页word文档

2.1 弹簧下悬挂一物体,弹簧静伸长为δ。
设将物体向下拉,使弹簧有静伸长3δ,然后无初速度地释放,求此后的运动方程。
解:设物体质量为m ,弹簧刚度为k ,则:mg k δ=,即:n ω==取系统静平衡位置为原点0x =,系统运动方程为: δ⎧+=⎪=⎨⎪=⎩00020mx kx x x (参考教材P14)解得:δω=()2cos n x t t 2.2 弹簧不受力时长度为65cm ,下端挂上1kg 物体后弹簧长85cm 。
设用手托住物体使弹簧回到原长后无初速度地释放,试求物体的运动方程、振幅、周期及弹簧力的最大值。
解:由题可知:弹簧的静伸长0.850.650.2()m =-=所以:7(/)0.2n rad s ω=== 取系统的平衡位置为原点,得到:系统的运动微分方程为:20n x x ω+=其中,初始条件:(0)0.2(0)0x x =-⎧⎨=⎩ (参考教材P14) 所以系统的响应为:()0.2cos ()n x t t m ω=-弹簧力为:()()cos ()k n mg F kx t x t t N ω===-因此:振幅为0.2m 、周期为2()7s π、弹簧力最大值为1N 。
2.3 重物1m 悬挂在刚度为k 的弹簧上并处于静平衡位置,另一重物2m 从高度为h 处自由落到1m 上而无弹跳,如图所示,求其后的运动。
解:取系统的上下运动x 为坐标,向上为正,静平衡位置为原点0x =,则当m 有x 位移时,系统有:由()0T d E U +=可知:12()0m m x kx ++=即:n ω=系统的初始条件为:⎧=⎪⎨=-⎪+⎩20012m gx x m (能量守恒得:221201()2m gh m m x =+) 因此系统的响应为:01()cos sin n n x t A t A t ωω=+ 其中:ω⎧==⎪⎨==-⎪⎩20001n m g A x x A即:ωω=-2()(cos )n n m g x t t t k 2.4 一质量为m 、转动惯量为I 的圆柱体作自由纯滚动,圆心受到一弹簧k 约束,如图所示,求系统的固有频率。
《机械振动》考试试题

2009--2011中南大学考试试卷一、填空题(本题15分,每空1分)1、按不同情况进行分类,振动系统大致可分成,线性振动和(非线性振动);(确定性振动)和随机振动;自由振动和(强迫振动);周期振动和(瞬态振动);(连续系统)和离散系统。
2、(惯性)元件、(弹性)元件、(阻尼)元件是离散振动系统的三个最基本元素。
3、系统固有频率主要与系统的(质量)和(刚度)有关,与系统受到的激励无关。
4、研究随机振动的方法是(概率统计),工程上常见的随机过程的数字特征有:(均值),(方差),(自相关函数)和(互相关函数)。
二、简答题(本题40分,每小题8分)1、简述机械振动的定义和系统发生振动的原因。
(10分)答:机械振动是指机械或结构在它的静平衡位置附近往复弹性运动。
振动系统发生振动的原因是由于外界对系统运动状态的影响,即外界对系统的激励或作用。
2、简述振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。
答:实际阻尼是度量系统消耗能量的能力的物理量,阻尼系数c是度量阻尼的量;临界阻尼是c2enm ω=;阻尼比是/eccξ=(8分)3、共振具体指的是振动系统在什么状态下振动?简述其能量集聚过程?答:共振是指振动系统在激励频率约等于系统的固有频率时的振动状态。
在此过程中,激励力与阻尼力平衡,弹性力与惯性力平衡。
即动能与势能相互转化,激励力提供阻尼消耗。
4、简述线性系统在振动过程中动能和势能之间的关系。
(8分)5、简述刚度矩阵[K]中元素k ij的意义。
答:如果系统的第j个自由度沿其坐标正方向有一个单位位移,其余各个自由度的位移保持为零,为保持系统这种变形状态需要在各个自由度施加外力,其中在第i个自由度上施加的外力就是kij(8分)三、计算题(45分)3.1、(10分)求如图1所示的扭转系统的固有频率。
图13.2、(15分)如图2所示系统,轮子可绕水平轴转动,对转轴的转动惯量为I,轮缘绕有软绳,下端挂有重量为P的物体,绳与轮缘之间无滑动。
中南大学机械振动2012试题及答案要点
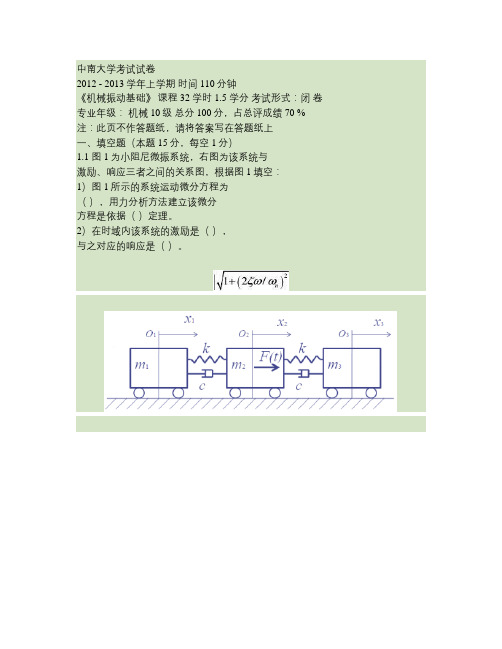
中南大学考试试卷2012 - 2013学年上学期时间110分钟《机械振动基础》课程 32 学时 1.5 学分考试形式:闭卷专业年级:机械10级总分100分,占总评成绩 70 % 注:此页不作答题纸,请将答案写在答题纸上一、填空题(本题15分,每空1分)1.1 图1为小阻尼微振系统,右图为该系统与激励、响应三者之间的关系图,根据图1填空:1)图1所示的系统运动微分方程为(),用力分析方法建立该微分方程是依据()定理。
2)在时域内该系统的激励是(),与之对应的响应是()。
3)如果F(t)=kA cosωt,则该系统稳态响应的频率为(),而系统的固有频率为()4)如果F(t) 为t=0时刻的单位脉冲力,则系统的响应h(t)称为()。
5)如果F(t)为非周期激励,可以采用()、()或()等方法求系统响应。
1.2 图2是多自由度线性振动系统,根据图2填空:1)该系统有()个自由度,如果已知[M],[K],[C],系统运动的矩阵微分方程通式是()。
2)如果F(t)作用在第二个自由度上,则微分方程中系统的激励向量是(),对应的响应向量是();3)如果系统的刚度矩阵为非对角矩阵,则微分方程存在()耦合,求解微分方程需要解耦。
二、简答题(本题40分,每小题8分)2.1(8分)在图1中,若F(t)是频率为ω的简谐激励,写出系统放大因子计算公式,分析抑制系统共振的方法;2.2 (8分)在图1中,如果已知x(t)=AH(ω)cosωt,分析系统(在垂直方向)作用在基础上的弹簧力FS(t),阻尼力Fd(t),分析二者的相位差,证明合力的峰值为kAH(ω2.3 (8分)当系统受非简谐周期激励作用时,简述系统响应的求解方法,分析该类激励引起系统共振的特点。
2.4 (8分)简述振型的物理含义,振型矩阵的构成方法,振型矩阵的作用。
2.5 (8分)简述随机振动与确定性振动求解方法的区别,随机过程有那些基本的数字特征,各态遍历随机过程的主要特点。
中南大学机械设计复习整理精华1

1.3
由此可见,对于M10—M64普通螺纹的钢制紧螺栓 联接,在拧紧时,虽然同时承受拉伸和扭转的联合 作用,但在计算时,可以只考虑拉伸强度计算,并 将预紧力增大30%来考虑扭转的影响。
特别注意,轴向载荷: F2≠ F0+F 加预紧力后→螺栓受拉伸长λb0 →被联接件受压缩短λm0 加载 F 后:
潘存云教授研制
潘存云教授研制
3º
梯 形 螺纹的基本尺寸:
锯齿形
30º
粗牙普通螺纹、细牙普通螺纹和梯形螺纹的基 本尺寸见后续各表(或查阅相关机械设计手册)。
中南大学专用 作者: 潘存云教授
注意:对于重要的联接,应尽可能采用>M12的螺栓。
二、
拧紧力矩
d
或预紧力(不受轴向载荷)
设轴向力为Fa
Faad 22 总力矩: T T11 T22 tg ( '')) f c Fa rf tg ( 2
轴线的垂线间的夹角。
nP πd2
轴向截面内螺纹牙型相邻两侧边的夹角。牙型侧边与螺纹
β
β
牙侧角 β
ψ
内外螺纹旋合后,接触面的径向高度。
S
(8)接触高度 h 中南大学专用
作者: 潘存云教授
π d2
螺纹的精度等级: A级 公差小,精度最高,用于配合精确,防振动等场合; B级 受载较大且经常拆卸,调整或承受变载荷的联接; C级 用于一般联接,最常用。 普通螺纹以大径d为公称直径,同一公称直径可 以有多种螺距,其中螺距最大的称为粗牙螺纹,其 余的统称为细牙螺纹。 粗牙螺纹应用最广 细牙螺纹的优点:升角小、小径大、自锁性好、强度高 缺点:不耐磨易滑扣。 应用:薄壁零件、受动载荷的联接和微调机构。
机械振动复习资料
机械振动全章复习资料一、简谐运动的基本概念1.定义物体在跟偏离平衡位置的位移大小成正比,并且总指向平衡位置的回复力的作用下的振动,叫简谐运动。
表达式为:F回= -kx(判断一个振动是否是简谐运动的方法)⑴振动的位移必须是指偏离平衡位置的位移(实质与位置对应)。
也就是说,在研究简谐运动时所说的位移的起点都必须在平衡位置处。
简谐运动的位移随时间变化的规律是正弦函数(判断一个振动是否是简谐运动的方法)。
⑵回复力是一种效果力。
是振动物体在沿振动方向上所受的合力。
⑶“平衡位置”不等于“平衡状态”。
平衡位置是指回复力为零的位置,物体在该位置所受的合外力不一定为零。
(如单摆摆到最低点时,沿振动方向的合力为零,但在指向悬点方向上的合力却不等于零,所以并不处于平衡状态)⑷F=-kx是判断一个振动是不是简谐运动的充分必要条件。
凡是简谐运动沿振动方向的合力必须满足该条件;反之,只要沿振动方向的合力满足该条件,那么该振动一定是简谐运动。
例1.简谐运动的判断方法。
两根质量均可不计的弹簧,劲度系数分别为K1、K2,它们与一个质量为m的小球组成的弹簧振子,如图1所示。
试证明弹簧振子做的运动是简谐运动。
证明:以平衡位置O为原点建立坐标轴,当振子离开平衡位置O时,因两弹簧发生形变而使振子受到指向平衡位置的合力。
设振子沿X正方向发生位移x,则物体受到的合力为F=F1+F2=-k1x-k2x=-(k1+k2)x=-kx.所以,弹簧振子做的运动是简谐运动。
要判定一个物体的运动是简谐运动,首先要判定这个物体的运动是机械振动,即看这个物体是不是做的往复运动;看这个物体在运动过程中有没有平衡位置;看当物体离开平衡位置时,会不会受到指向平衡位置的回复力作用,物体在运动中受到的阻力是不是足够小。
然后再找出平衡位置并以平衡位置为原点建立坐标系,再让物体沿着x轴的正方向偏离平衡位置,求出物体所受回复力的大小,若回复力为F=-kx,则该物体的运动是简谐运动。
机械振动一轮二轮复习
机械振动第1讲一、高考夺分要点:1、机械振动——物体(或物体一部分)在某一中心位置附近所做的往复运动 2.回复力:振动物体所受的总是指向平衡位置的合外力,使物体返回平衡位置的力 注意:①恢复力不一定是物体所受的合力,如单摆②回复力的意义是指向平衡位置方向上的合力③恢复力是根据效果命名的3.平衡位置:回复力为零的位置,并非合外力为零的位置。
例如单摆。
4.位移:是离开平衡位置的位移5.简谐运动——物体在跟偏离平衡位置的位移大小成正比,并且总指向平衡位置的回复力的作用下的振动,叫简谐运动。
表达式为:F = -kx6.振幅:振动物体离开平衡位置的最大距离,是标量,表示振动的强弱,无正负之分。
7.周期和频率:表示振动快慢的物理量。
完成一次全振动所用的时间叫周期,单位时间内完成全振动次数叫频率,大小由系统本身的性质决定,所以叫固有周期和频率。
任何简谐运动都有共同的周期公式:km T π2= 8.简谐振动的方程:)sin(ϕω+=t A x ,其中A 为振幅,ω为圆频率,ϕ为初相位。
二、考点精讲:1.(2009•天津)某质点做简谐运动,其位移随时间变化的关系式为t A x 4si n π=则质点( )A .第1s 末与第3s 末的位移相同B .第1s 末与第3s 末的速度相同C .3s 末至5s 末的位移方向都相同D .3s 末至5s 末的速度方向都相同 2.(2011•静安区二模)如图所示,一弹簧振子在B 、C 两点间做机械振动,B 、C 间距为12cm ,O 是平衡位置,振子每次从C 运动到B 的时间均为0.5s ,则下列说法中正确的是( )A .该弹簧振子的振幅为12cmB .该弹簧振子的周期为1sC .该弹簧振子的频率为2HzD .振子从O 点出发到再次回到O 点的过程就是一次全振动3.(2004•天津)公路上匀速行驶的货车受一扰动,车上货物随车厢底板上下振动但不脱离底板.一段时间内货物在竖直方向的振动可视为简谐运动,周期为T .取竖直向上为正方向,以某时刻作为计时起点,即t=0,其振动图象如图所示,则( )A.4Tt =时,货物对车厢底的压力最大 B.2Tt =时,货物对车厢底的压力最小C.43T t =时,货物对车厢底的压力最大D.43T t =时,货物对车厢底的压力最小三、随堂练习:1.(2014•东城区模拟)一弹簧振子的位移y 随时间t 变化的关系式为t y π5.2sin 1.0=,位移y 的单位为m ,时间t 的单位为s .则( ) A .弹簧振子的振幅为0.2m B .弹簧振子的周期为1.25sC .在t=0.2s 时,振子的速度为零D .在任意0.2s 时间内,振子的位移均为0.1m2.(2012•黄埔区模拟)某质点做简谐运动,下列说法中正确的是( ) A .质点通过平衡位置时,速度最大,加速度最大B .若位移为负值,则速度一定为正值,加速度也一定为正值C .质点每次通过平衡位置时,加速度不一定相同,速度也不一定相同D .质点每次通过同一位置时,其速度不一定相同,但加速度一定相同3.(2014•徐汇区二模)如图所示,弹簧振子以O 点为平衡位置,在A 、B 两点之间做简谐运动.以向左为正,振子的位移x 随时间t 的变化如图所示,则由图可知( )A .t=0.2s 时,振子在O 点右侧6cm 处B .t=1.4s 时,振子的速度方向向右C .t=0.4s 和t=1.2s 时,振子的加速度相同D .t=0.4s 到t=0.8s 的时间内,振子的速度逐渐增大四、课后练习:1.(2012•重庆)装有砂粒的试管竖直静浮于水面,如图所示.将试管竖直提起少许,然后由静止释放并开始计时,在一定时间内试管在竖直方向近似做简谐运动.若取竖直向上为正方向,则以下描述试管振动的图象中可能正确的是( )A. B.C. D.2.(2013•新课标Ⅱ)如图,一轻弹簧一端固定,另一端连接一物块构成弹簧振子,该物块是由a 、b 两个小物块粘在一起组成的.物块在光滑水平面上左右振动,振幅为A 0,周期为T 0.当物块向右通过平衡位置时,a 、b 之间的粘胶脱开;以后小物块a 振动的振幅和周期分别为A 和T ,则A A 0(填“>”、“<”或“=”),T T 0(填“>”、“<”或“=”).3.(2014•奉贤区二模)一弹簧振子做简谐运动的振动图象如图所示,则弹簧振子沿x 轴正方向的最大速度的位置是图中的( )A.aB.bC.cD.d4.(2012•普陀区一模)有一作简谐运动的弹簧振子,周期为2秒.如果从弹簧振子向右运动通过平衡位置时开始计时,则在t=3.4秒至t=3.5秒的过程中,摆球的( )A .速度向右在增大,加速度向右在减小B .速度向 左在增大,加速度向左也在增大C .速度向左在减小,加速度向右在增大D .速度向右在减小,加速度向左也在减小5.(2014•嘉定区二模)某质点作简谐振动时的位移x 随时间t 变化的规律如图所示,该质点在t 1与t 2时刻( )A .振幅不同B .加速度方向相同C .在t 1时刻速度较大D .在t 2时刻向x 正方向运动机械振动第1讲参考答案一、考点精讲:1.AD A 、由关系式可知,,将t=1s 和t=3s 代入关系式中求得两时刻位移相同.故A 正确.B 、画出对应的位移-时间图象,由图象可以看出,第1s 末和第3s 末的速度方向不同.故B 错误.C 、由图象可知,3s 末至5s 末的位移大小相同,方向相反.故C 错误.D 、由图象可知,3s 末至5s 末的而速度是大小相同,方向也相同.故D 正确.2.D A 、质点通过平衡位置时,速度最大,加速度为零,A 错误;B 、若位移为负值,质点远离平衡位置时速度方向为负值,B 错误;C 、质点每次通过平衡位置时,加速度为零,速度不一定相同,C 错误;D 、质点每次通过同一位置时,其速度不一定相同,但加速度一定相同,D 正确; 3.C A 、4Tt =在时刻,由图看出,货物的位移为正向最大,则货物的加速度为负向最大,即加速度向下最大,根据牛顿第二定律可知,货物受到的弹力最小,则货物对车厢底板的压力最小.故A 错误. B 、在2Tt =时刻,货物的位移为零,加速度为零,弹簧的弹力大小等于货物的重力,而在4Tt =时刻,货物的弹簧小于货物的重力,说明在2Tt =时刻,弹簧的弹力不是最小,则货物对车厢底板的压力不是最小.故B 错误.C 、D 在T t 43=时刻,由图看出,货物的位移为负向最大,则货物的加速度为正向最大,即加速度向上最大,根据牛顿第二定律可知,货物受到的弹力最大,则货物对车厢底板的压力最大.故C 正确,D 错误.二、随堂练习:1.C A 、质点做简谐运动,振动方程为t y π5.2sin 1.0=,可读出振幅A=0.1m ,故A 错误;B 、质点做简谐运动,振动方程为t y π5.2sin 1.0=,可读出角频率为2.5π,故周期s T 8.05.222===ππωπ,故B 错误;C 、在t=0.2s 时,振子的位移最大,故速度最小,为零,故C 正确;D 、根据周期性可知,质点在一个周期内通过的路程一定是4A ,但四分之一周期内通过的路程不一定是A ,D 错误; 2.C 根据简谐运动的表达式为x=Asin (ωt+φ),A 为振幅,等于8cm .故A 错误;简谐运动的表达式为x=Asin (ωt+φ),ω为圆频率,s T 4222===ππωπ,故B 错误;C 、由题目中的公式可得,当t=0时,x=0物体处于平衡位置;当t=1s 时,质点运动了1/4周期,到达最大位置,该过程中质点的位移增大,速度减小.故C 正确;D 、由题目中的公式可得,当t=2s 时,x=0物体处于平衡位置,在1~2s 内,质点从最大位移处向平衡位置运动,物体的速度增大,动能逐渐增大.故D 错误.3.D A 、t=0.2s 时,振子在O 点左侧;故A 错误;B 、1.4s 时,振子在O 点右方正向平衡位置移动,故速度方向向左;故B 错误;C 、0.4s 和1.2s 时振子分别到达正向和反向最大位置处,加速度大小相等,但方向相反;故C 错误;D 、0.4s 到0.8s 内振子在向平衡位置移动,故振子的速度在增大;故D 正确; 三、课后练习:1.D 根据题中规定的正方向,开始计时时刻位移为正的最大值,由于t A x 4si n π=,简谐运动的图象是正弦或余弦曲线,可知D 正确.2.<,< 当物块向右通过平衡位置时a 、b 之间的粘胶脱开,a 向右做减速运动,b 向右匀速运动,弹簧振子总的机械能将减小,振幅减小,即有A <A 0.根据弹簧振子简谐运动的周期公式kmT π2=,知,振子的质量减小,周期减小,则有T <T 0.故答案为:<,<3.D A 、C 、弹簧振子经过平衡位置时速度最大,此时振子的位移为0.故AC 错误.B 、D 、根据振动图象切线的斜率等于速度,可知b 对应的速度为负向最大,d 对应的速度为正向最大,故D 正确,B 错误.4.C 由题,弹簧振子的周期是2s ,一个周期分成四个41周期,从单摆向右运动通过平衡位置时开始计时,则在t=3.4秒至t=3.5秒的过程中,单摆是由平衡位置向左向最大位移处运动,所以速度向左在减小,加速度方向向右在增大.C 正确.5.D A 、振幅是振子能达到的最大位移,故振幅不变;故A 错误;B 、由图可知,两时刻时振子的位移大小相等,方向相反;故加速度方向相反;故B 错误;C 、由图可知,t 1时刻距平衡位置的距离大小t 2时刻距离平衡位置的距离,则可知t 2时刻的速度要大于t 1时刻的速度;故C 错误;D 、振动图象随时间延伸,由图可知,t 2时刻向x 轴正方向运动;故D 正确;。
机械振动复习与巩固
机械振动复习与巩固一、目标与策略明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数!学习目标:●通过观察和分析,理解简谐运动的特征。
能用公式和图像描述简谐运动的特征;●通过实验,探究单摆的周期与摆长的关系;●知道单摆周期与摆长、重力加速度的关系。
会用单摆测定重力加速度。
●通过实验,认识受迫振动的特点。
了解产生共振的条件以及在技术上的应用。
重点难点:●简谐运动的特点与图像。
学习策略:●简谐运动是一种新的运动形式。
要把握起受力特点和运动热点及其内在关系,并能运用能量的观点解决、分析问题。
二、学习与应用“凡事预则立,不预则废”。
科学地预习才能使我们上课听讲更有目的性和针对性。
我们要在预习的基础上,认真听讲,做到眼睛看、耳朵听、心里想、手上记。
知识回顾——复习学习新知识之前,看看你的知识贮备过关了吗?1、请尝试整理本章的知识脉络。
2、简述简谐运动图像的应用?知识要点——预习和课堂学习认真阅读、理解教材,尝试把下列知识要点内容补充完整,带着自己预习的疑惑认真听课学习。
请在虚线部分填写预习内容,在实线部分填写课堂学习内容。
课堂笔记或者其它补充填在右栏。
详细内容请学习网校资源ID:#65002#414653要点一、简谐运动1.定义表达式为:______F =,是判断一个振动是不是简谐运动的充分必要条件。
凡是简谐运动沿振动方向的合力必须满足该条件;反之,只要沿振动方向的合力满足该条件,那么该振动一定是简谐运动。
(1)简谐运动的位移必须是指偏离平衡位置的位移。
也就是说,在研究简谐运动时所说的位移的起点都必须在__________。
(2)回复力是一种效果力,是振动物体在沿振动方向上所受的合力。
(3)“平衡位置”不等于“平衡状态”。
平衡位置是指回复力为零的位置,物体在该位置所受的合外力不一定为零。
(如单摆摆到最低点时,沿振动方向的合力为零,但在指向悬点方向上的合力却不等于零,所以并不处于平衡状态。
)要点诠释:简谐运动的位移大小和方向都是相对平衡位置来说的,是从平衡位置指向所在位置的矢量。
机械振动复习文档
机械振动一、机械振动(1)定义:中心位置;往复运动(2)条件:回复力;阻力足够小。
(3)特点:中心位置;往复运动例1下列属于机械振动选择完整的是()①乒乓球在地面上的来回上下运动;②弹簧振子在竖直方向的上下运动;③秋千在空中来回的运动;④竖于水面上的圆柱形玻璃瓶上下振动A、①②B、②③C、③④D、②③④二、简谐运动1.定义:物体在跟偏离平衡位置的位移大小成正比,并且总指向平衡位置的回复力的作用下的振动,叫简谐运动。
表达式为:F= -kx(1)简谐运动的位移必须是指偏离平衡位置的位移。
也就是说,在研究简谐运动时所说的位移的起点都必须在平衡位置处。
(2)回复力是一种效果力。
是振动物体在沿振动方向上所受的合力。
(3)“平衡位置”不等于“平衡状态”。
平衡位置是指回复力为零的位置,物体在该位置所受的合外力不一定为零。
(如单摆摆到最低点时,沿振动方向的合力为零,但在指向悬点方向上的合力却不等于零,所以不处于平衡状态)(4)F = -kx 是判断一个振动是不是简谐运动的充分必要条件。
凡是简谐运动沿振动方向的合力必须满足该条件;反之,只要沿振动方向的合力满足该条件,那么该振动一定是简谐运动。
1.怎样判断某一振动是简谐运动:方法一:从动力学:证明物体在运动方向上所受合力F =-kx 。
方法二:从运动学特点:例1 证明竖直弹簧振子的振动是简谐运动.解析:如图9—1—1所示,设振子的平衡位置为O ,向下方向为正方向,此时弹簧的形变为x 0,根据胡克定律及平衡图9—1—1mg -kx 0=0当振子向下偏离平衡位置xF 回=mg-k (x +x 0)将①代入②得:F 回=-kx ,故重物的振动满足简谐运动的条件.说明:分析一个振动系统是否为简谐运动,关键是判断它的回复力是否满足:其大小随着位移的变化作正比变化,其方向总与位移方向相反.应理解F =-kx 式中的k 值是由振动系统本身条件所决定,不要将F =-kx 简单理解为胡克定律中的弹力,在这里就理解为产生简谐运动的回复力的定义和重力的合力.是否满足F =-kx . 例2 如图所示,m 和M 叠放在一起,弹簧的作用下相对静止一起运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
32 m k
( 2 ) k 1
0
1 2 2 2 m
k 1
0
1 0 32 m
k
固有频率:
即: (3 2 m )2 (2 2 m ) 2(3 2 m ) 0
k
k
k
12 (2
2) k m
<
22
3k m
<
32 (2
2) k m
0
m
0
2
0 ;
0 0 m3 0 0 1
k1 k2
K
k2
0
k2 k2 k3 k5 k6
k3
0 3 2 0
k3
k
2
10
2
k3 k4 0 2 3
得到系统的广义特征值问题方程:
(
K
2
M
)
u1 u2
0
u3
和频率方程:
3k 2m (2 ) 2k
0
2k 10k 22m
2k
0 2k 0 3k 2m
即: ( 2 ) (3k 2m)(2m2 4 16km 2 22k2 ) 0
解得: 2 (4 5) k 和 2 3 k
1)求系统的质量矩阵和刚度矩阵和频率方程; 2)求出固有频率; 3)求系统的振型,并做图。
(6 分) (7 分) (6 分)
解:1)以静平衡位置为原点,设 I1, I2 , I3 的位移1,2 ,3 为广义坐标,画出 I1, I2 , I3 隔离体,根据牛顿
第二定律得到运动微分方程:
m
0
0 m
{
x
}+
4k
0
0 9k
{
x
}=0
(4)求系统的固有频率(4 分)
4k-mω2 0
0
9k -mω2 = (4k-m2)(9k- m2)= 0
4k
2 1
=
m
9k
2 2
=
m
(5)求系统的振型、绘制振型图(4 分)
由 ([K ] r2[M ]){ur} 0 有:
P 的物体,绳与轮缘之间无滑动。在图示位置,由水平弹簧维持平衡。半径 R 与 a 均已知。
1)写出系统的动能函数和势能函数;(5 分)
2) 求系统的运动方程;(4 分)
2)求出系统的固有频率。(5 分)
解:取轮的转角 为坐标,顺时针为正,系统平衡时 0 ,则当轮子有 转角时,系统有:
ET
1 I2 1 P (R )2
x2 )2
1 2 k3(x2
x3 )2
1 2
k4x
2 3
1 2
(k5
k6
)x
2 2
U
1 2 (k1
k2 )x12
1 2 (k2
k3
k5
k6 )x22
1 2 (k3
k4 )x32
k2x1x2
k3x2x3
求偏导得到:
m1 0 0 1 0 0
M
0
m2
y A
2
1 2
m1 y12
1 2
m2 y22
(3)系统的势能:(2 分)
1
1
1
1
U=
2
k1y
2 1
+
2
k2y
2 2
+
2
k3(yA-y1)2+
2
k4(yB-y2)2
(4)求质量矩阵:(2 分)
m 11
2ET
y
2 A
M 4
I L2
m 22
2ET
y
2 B
M 4
2
2g
1(I P 2g
R 2)2
U 1 k(a)2 2
由d(E T
U
) 0 可知:(I P R 2)2 ka2 g
0
即:n
ka2 (rad/s),故 T 2 2
IP R2
n
g
IP R2 g
ka 2
(s)
3.3、 (19 分)图 2 所示为 3 自由度无阻尼振动系统,kt1 kt 2 kt3 kt 4 k ,I1 I2 / 5 I3 I 。
I11 I22
kt11 kt 2 (2
kt 2(1 2) 1) kt3(2
0
3
)
0
I33
kt 3 ( 3
2)
kt 43
0
I1 0 0 1 0 0
M
0
I2
0
I
0
4
0 ;
所以:
0 0 I3 0 0 1
(4k-m2)u11 =0
(4k-
2 r
m)u22=0
由此可知:u21 与 u11、u12 与 u22 毫不相关,即该系统是两个独立振动的单自由度系统。 令 u11= u22=1 即振型为: {u1}={1,0}T {u2}={0,1}T
固有频率为1 时振型图
固有频率为2 时振型图
五、如图 3 所示系统,试用能量法求出其质量矩阵、刚度矩阵。假设为均质杆。
kt1 kt2
K
kt 2
0
kt 2 kt 2 kt3
kt 3
0 2
kt 3
k
1
kt3 kt4 0
1 0 2 1 1 2 222
U 1 k(r)2 2
由d(E T U ) 0 可知:(I m r2) kr2 0
即:n kr2 /(I m r2) (rad/s)
3、求如图 3 所示的三自由度弹簧质量系统的固有频率和振型。(25 分)(设 m1 m3 m; m2 2m;
1
1
[K] =
2、一质量为 m 、转动惯量为 I 的圆柱体作自由纯滚动,圆心受到一弹簧 k 约束,如图 2 所示,求系
统的固有频率。(15 分)
解:取圆柱体的转角 为坐标,逆时针为正,静平衡位置时 0 ,则当 m 有 转角时,系统有:
ET
1 I2 1 m (r)2 1 (I m r2 )2
m
m
所以: 1
(4
5)
k m
2
3
k m
3
(4
5) k m
将频率代入广义特征值问题方程解得:
u11 : u21 : u31 1: 0.618 :1 ;
u12 : u22 : u32 1: 0 :1 ;
u13 : u23 : u33 0.618 :1: 0.618 ;
0
0
M I 4 L2 M I 4 L2
0 0
0
0
0 0
m1 0 0 m2
(5)求刚度矩阵:(2 分)
∂ 2U
y y k11=
= k3
∂∂
A
A
∂ 2U
y y k13=
∂∂
=- k3= k31
1
A
∂ 2U
y y ∂ k12=
∂
=0= k21
B
A
∂ 2U
y y k14=
∂∂
k1 k4 k; k2 k3 2k; k5 k6 3k; )
解:以静平衡位置为原点,设 m1, m2 , m3 的位移 x1, x2 , x3 为广义坐标,系统的动能和势能分别为
ET
1m 2
1x12
1m 2
2x22
1m 2
3x32
U
1 2
k1x12
1 2 k2(x1
三、计算题(45 分) 3.1、(14 分)如图所示中,两个摩擦轮可分别绕水平轴 O1,O2 转动,无相对滑动;摩擦轮的半径、
质量、转动惯量分别为 r1、m1、I1 和 r2、m2、I2。轮 2 的轮缘上连接一刚度为 k 的弹簧,轮 1 的轮缘上有软 绳悬挂质量为 m 的物体,求:
1)系统微振的固有频率;(10 分) 2)系统微振的周期;(4 分)。
Z1
Z x2=
x1
2
(2)系统的动能:(4 分)
Z2 Z2 Z1 Z1
Z Z Z Z x3=
x2=
×
x1=
x1
3
3
2
3
ZZ ZZ ET
=
1 2
I1
x12
+
1 2
I2
x 22
+
1 2
I3
x32
=
1 2
[
I1+
I2(
1
)2+ I3(
2
1
)2]
x12
3
(3)系统的势能:(4 分)
Z Z 1
1
1
1
Z Z U=
3
ZZ ZZ ZZ ZZ
2 n
=
[
k1+
k2(
