2015年希望杯第二试试题(初三年级)
希望杯数学邀请赛九年级二试模拟试题
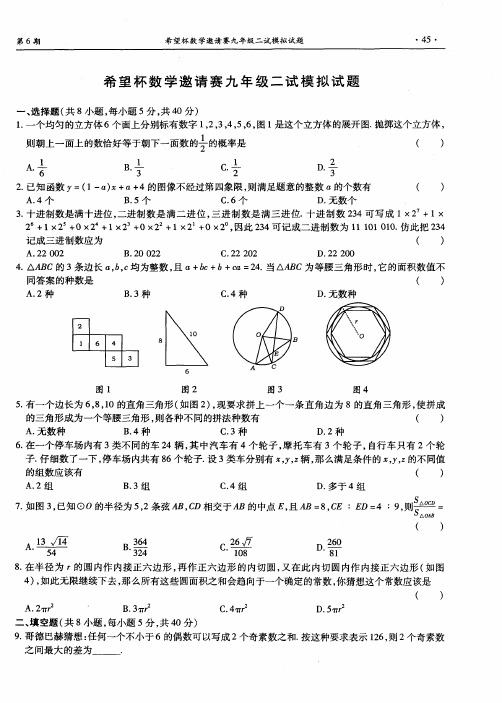
)
8 在半径 为 r . 的圆内作 内接正六边形 , 再作正六边形的 内切圆, 又在此 内切圆内作内接正六边形 ( 如图 4, ) 如此无限继续下去 , 那么所有这些圆面积之和会趋向于一个确定 的常数 , 你猜想这个常数应该是
(
A. r2 27r B
.
)
3 P =
C 4r2 ., r r
1. 123, ,95 0 将 , , … 4 ,O任意 分 成 1 O组 , 组 5个 数 , 组 中 有 1个 中位 数 , 这 1 中 位数 之 和 的最 大 每 每 则 O个 值是一 1. 个 长方 体 的长 、 、 1一 宽 高分 别 为 9c 6c 5c 先 从 这个 长方 体 上 尽 可 能 大地 切 下 一个 正 方 体 , 从 m, m, m. 再
一
、
1
则朝上一面上的数恰好等于朝下一面数的÷的概率是
' 1 1 , ,
(
)
A ÷ .
U
B÷ .
J
c÷ .
二
D ÷ .
J
2 已知 函数 Y 1 a x+ 4的图像不经过第 四象限 , . =( 一 ) 0+ 则满足题意的整数 口的个数有 ( ) A. 4个 B 5个 . C 6个 . D 无数 个 . 3 十进制 数 是 满 十进位 , 进制 数 是 满 二 进 位 , 进 制 数 是 满 三 进 位. 进 制 数 2 4可写 成 1× +1× . 二 三 十 3 2 2 + l ×2 +O ×2 + 1× 2 +O ×2 + l × 2 +O ×2 因此 2 4可 记 成 二进 制 数 为 1 11 . 。 3 1 0 0 仿此 把 2 4 0 3 记成三进制数应为 ( )
初中二年级历届“希望杯”二试解答题

初中二年1-17届“希望杯”二试解答题1.1、从自然数354 , , 3 , 2 , 1 中仸取178个数,试证:其中必有两个数,它们的差是177。
1.2、平面上有两个边长相等的正方形ABCD 和D C B A '''',且正方形D C B A ''''的顶点A '在正方形ABCD 的中心。
当正方形D C B A ''''绕A '转动时,两个正方形的重合部分的面积必然是一个定值。
这个结论对吗?证明你的判断。
1.3、用1,9,9,0四个数码组成的所有可能的四位数中,每一个这样的四位数与自然数n 之和被7除余数都不为1,将所有满足上述条件的自然数n 由小到大排成一列 <<<<4321n n n n ,试求:21n n ⋅之值。
2.1、已知两个正数的立方和是最小的质数,求证:这两个数之和不大于2。
2.2、一块四边形的地(如图2.2所示)(KG OH FK EO //,//)内有一段曲折的水渠,现在要把这段水渠EOHGKF 改成直的(即两边都是直线)。
但进水口EF 的宽度不能改变,新渠占地面积与原水渠面积相等,且要尽可能利用原水渠以节省工时,那么新渠的两条边应当怎么作?写出作法,幵加以证明。
A B 图2.23.1、若0 , , , >d c b a ,证明:在方程02212=+++cd x b a x , 02212=+++da x c b x ,02212=+++ab x d c x ,02212=+++bc x a d x 中,至少有两个方程有不相等的实数根。
3.2、(1)能否把1992 , , 3 , 2 , 1 这1992个数分成八组,使得第二组各数之和比第一组各数之和多10,第三组各数之和比第二组各数之和多10,…,最后第八组各数之和比第七组各数之和也多10?请加以说明。
2015年世界少年奥林匹克数学竞赛九年级海选赛试题含答案

九年级 第1页 九年级 第2页2015年世界少年奥林匹克数学竞赛九年级海选赛试题含答案绝密★启用前世界少年奥林匹克数学竞赛(中国区)选拔赛地方海选赛试题(2015年10月)选手须知:1、本卷共三部分,第一部分:填空题,共计50分;第二部分:计算题,共计12分;第三部分:解答题,共计58分。
2、答题前请将自己的姓名、学校、赛场、参赛证号码写在规定的位置。
3、比赛时不能使用计算工具。
4、比赛完毕时试卷和草稿纸将被收回。
九年级试题(A卷)(本试卷满分120分 ,考试时间90分钟 )一、填空题。
(每题5分,共计50分)1、两块三角形面板如图放置,等腰直角三角形板ABC 的斜边BC 与∠F=30°的直角三角板DEF 的直角边EF 重合,则∠a 的度数为 。
2、若a 、b 都为实数,且b = 20131-a + 2014a -1+ 2015 则a b= 。
3.设x 1,x 2是方程x 2 - x -2013 = 0 的两实数根,则x 13+2014x 22-2013= 。
4、已知三个实数x ,y ,z 中,x 与y 的平均数是127,y 与z 的和的31是78,x 与z 的和的41是52,则这三个数x ,y ,z 的平均数是 。
5、如图,矩形ABCD 中,已知AB=5,AD=12,P 是AD 上的动点,PE ⊥AC 与E ,PF ⊥BD 与F ,则PE+PF= 。
6、如图,在平面直角坐标系中,△ABC 是等腰直角三角形,∠ACB = Rt, CA ⊥x 轴,垂足为点A ,点B 在反比例函数y 1=x4(x>0)的图像上,反比例 函数y 2=x2(x>0)的图像经过点C ,交AB 于点D ,则点D 的坐标 。
7、若有理数x ,y ,z 满足2121=-+-+z y x (x+y+z )则(x-zy)2= 。
8、我国汉代数学家赵爽为了证明勾股定理,创制了一副"弦图",后人称其为"赵爽弦图"如图,也是由八个全等的直角三角形拼接而成,记图中正方形ABCD ,正方形EFGH,正方形MNKT 的面积,分别为S 1,S 2,S 3,若S 1+S 2+S 3 = 10 ,则S 2的值是 。
2015年全国初中数学联合竞赛(初三)试题及解答

第一试(A)
一、选择题(本题满分 42 分,每小题 7 分) 1. 设实数 a, b, c 满足: a b c 3, a2 b2 c2 4 ,则 A.0 【答】D. 【解析】 B.3 C.6
a 2 b2 b2 c 2 c 2 a 2 =( 2c 2a 2b
D.9
)
a 2 b2 b2 c 2 c 2 a 2 4 c 2 4 a 2 4 b2 (2 c) (2 a) (2 b) 9 . 2c 2a 2b 2c 2a 2b
2. 若抛物线 y x2 bx c 与 x 轴只有一个公共点, 且过 A(m, n) ,B(m 8, n) , 则 n ( A.8. 【答】 C 【解析】法一(LTX) : 依题意,设抛物线解析式为 y ( x h)2 , 因为它过 A(m, n) , B(m 8, n) , 所以 h m 4 ,故 n (m h)2 (4)2 16 ,选 C . 法二: 由题意, b 8 2m ,
2 2 2
)
A.3 【答】D.
B.6.
C .9
D.12
【解析】设 x y t ,则 x y t , 代入题设等式得 ( y t )2 ( y t ) y y 2 3 ,整理得 3 y 2 3ty t 2 3 0 . 由判别式 (3t )2 12(t 2 3) 3 得 2 3 t 2 3 ,故 ( x y)2 t 2 12 . 5.题目和解答与(A)卷第 4 题相同. 6.设 n 是小于 100 的正整数且使 2n2 3n 2 是 6 的倍数,则符合条件的所有正整数 n 的和 是( ) B.850 C.1536 D.1634
-年初一希望杯第二试试题及答案(word版)

2015 年初一希望杯第二试1、请你想好一个数。
将该数与2015之和乘以4,减去12,再将其差除以4,然后减去你想好的那个数,最后的结果等于()(A) 0 (B) 2008 (C) 2012 (D)20152、若a + 2015 = 0,则a − 2015的值是()(A) − 4030 (B) − 2015 (C) 0 (D)20153、如图1,MA//BN//CP,若BA =BC,∠MAC = 50°,∠NBC =150°,则∠ABC =()(A) 60°(B) 150°(C) 140°(D) 130°4、红光中学初一年级有3个班,已知一班、二班的平均人数与三班人数之和为45,二班、三班的平均人数与一班人数之和为48,一班、三班的平均人数与二班人数之和为47。
则三个班的总人数为()(A) 68 (B) 70 (C) 72 (D)745、As shown in the Fig.2,Points A,B and C on the number axis represent nonzero rational numbera ,b,and c respectively . If |a| + |a + b| + |b − c| = −c,then the point represent 0 is()(A) on the right side of A(B) on the left side of C(C) between B and C(D) between B and A(翻译)如图2,数轴上的点A,B,C代表非零数字a,b和c,如果|a| + |a +b| + |b − c| =−c,则代表0的点位于()(A) A点的右边(B) C点的左边(C) B , C之间(D) B , A之间6、如图3,正方形ABCD由四个相同的小长方形和一个小正方形EFGH组成。
历届(第1-23届)希望杯数学竞赛初一七年级真题及答案

“希望杯”全国数学竞赛(第1-23届)初一年级/七年级第一/二试题目录1.希望杯第一届(1990年)初中一年级第一试试题......................003-0052.希望杯第一届(1990年)初中一年级第二试试题......................010-0123.希望杯第二届(1991年)初中一年级第一试试题...... 0错误!未定义书签。
-0204.希望杯第二届(1991年)初中一年级第二试试题...... 0错误!未定义书签。
-0265.希望杯第三届(1992年)初中一年级第一试试题...... 0错误!未定义书签。
-0326.希望杯第三届(1992年)初中一年级第二试试题...... 0错误!未定义书签。
-0407.希望杯第四届(1993年)初中一年级第一试试题...... 0错误!未定义书签。
-0508.希望杯第四届(1993年)初中一年级第二试试题...... 0错误!未定义书签。
-0589.希望杯第五届(1994年)初中一年级第一试试题...... 0错误!未定义书签。
-06610.希望杯第五届(1994年)初中一年级第二试试题..... 0错误!未定义书签。
-07311.希望杯第六届(1995年)初中一年级第一试试题..... 0错误!未定义书签。
-080 12希望杯第六届(1995年)初中一年级第二试试题..... 0错误!未定义书签。
-08713.希望杯第七届(1996年)初中一年级第一试试题..... 0错误!未定义书签。
-09814.希望杯第七届(1996年)初中一年级第二试试题....... 错误!未定义书签。
-10515.希望杯第八届(1997年)初中一年级第一试试题....... 错误!未定义书签。
-11316.希望杯第八届(1997年)初中一年级第二试试题....... 错误!未定义书签。
-12017.希望杯第九届(1998年)初中一年级第一试试题....... 错误!未定义书签。
15年(二模)九年级数学试题
2014—2015学年度第二学期教学质量阶段性检测九年级数学试题(满分:120分时间:120分钟)友情提示:亲爱的同学,你好!今天是你展示才能的时候,只要你仔细审题、认真答题,你就会有出色的表现!第Ⅰ卷一、选择题:(本题满分24分,共有8道小题,每小题3分)请把唯一正确答案的字母标号涂在答题卡的相应位置1.12-的倒数是().A.2 B.12C.-2 D.12-2.下列图形中,中心对称图形有()个A .1 B. 2 C. 3 D.43.一种病毒的长度约为0.0000046mm,用科学记数法表示为().A.0.46×105-B.4.6 × 106-C. 46 ×106-D. 4.6×106 4.如图,AB是⊙O的直径,C、D是⊙O上的点,若∠ABC=64°,则∠BDC等于().A.26° B.64° C. 52° D. 128°D FECBA5.如图,在四边形ABCD中,∠A=90°,对角线BD平分∠ABC,若BC=5,AD=4,则△BCD 的面积为().A.6 B.10 C.12 D.20第4题OBDCAAB CD第5题图6.如图,在方格纸上△DEF 是由△ABC 绕定点P 顺时针旋转得到的。
如果用(2,1)表示方格纸上A 点的位置,(1,2)表示B 点的位置,那么点P 的位置为( )。
A .(5, 2) B .(2, 5) C .(2, 1) D .(1, 2)7.若反比例函数()0ky k x =≠的图象经过点A (-2, 1),则当x <-1时,函数值y 的取值范围是( ) .A .y >2 B. -2<y <0 C .y >-2 D .0<y <2 8.已知函数ax ax y +=2与函数y =xa,则它们在同一坐标系中的大致图象是( )第Ⅱ卷二、填空题:(本题满分18分,共有6道小题,每小题3分) 请把正确答案填写在答题卡的相应位置9.化简:01127(3.14)3π---+=() .10.某工厂生产某种产品,今年产量为200件,计划通过技术革新,使今后两年的产量都比前一年增长相同的百分数,这样三年的产量达到1400件,设这个百分数为x ,根据题意,可列方程为 __________________.11.在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:次数12 3 4 5 6 7 8 9 10 黑棋数 132342113根据以上数据,估算袋中的白棋子数量为 枚.12.如图,将边长为3cm 的正方形ABCD 沿 其对角线AC 剪开,再把△ABC 沿着AD 方向平移,得到△A 1B 1C 1,若两个三角形 重叠部分的面积是49cm 2,则△ABC 移动 的距离A A 1是 cm . 第12题图第8题1 3.如图所示的图案(阴影部分)是这样设计的:在△ABC 中,AB =AC =2cm ,∠ABC =30°,以A 为圆心,以AB 为半径作弧BEC ,以BC 为直径作半圆BFC ,则图案(阴影部分)的面积是 .(结果保留π)14.在直角坐标系中,正方形A 1B 1C 1O 1、A 2B 2C 2C 1、A 3B 3C 3C 2、…、A n B n C n C n -1按如图所示的方式放置,其中点A 1、A 2、A 3、…、A n 均在一次函数y kx b =+的图象上,点C 1、C 2、C 3、…、C n 均在x 轴上。
2015年中考二模名校考试数学试题及答案
2015年中考数学二模名校考试数学试题(卷)时间120分钟满分120分2015、2、28一、选择题(1-6小题,每小题2分7-16小题每小题3分,共42分)1.下列各数中,最小的数是()A.﹣2 B.﹣0.1 C.0D.|﹣1| 2.计算(﹣9)2﹣2×(﹣9)×1+12的值为()A.﹣98 B.﹣72 C.64 D.1003.下列式子正确的是()A.﹣(x﹣3)=﹣x﹣3 B. 5a﹣a=5C. 2﹣1=﹣2 D. 2<<34.如图,将一个正六边形分割成六个全等的等边三角形,其中有两个已涂灰,如果再随意涂灰一个空白三角形,则所有涂灰部分恰好成为一个轴对称图形的概率是()A.B.C.D.14题图 5题图 7题图5.如图,直线a、b及木条c在同一平面上,将木条c绕点O旋转到与直线a平行时,其最小旋转角为()A.100°B.90°C.80°D.70°6.下列一元二次方程中,无解的是()A. x2+4x+2=0 B.x2+4x+3=0 C.x2﹣4x+4=0 D.x2﹣4x+5=07.如图,Rt△ABC中,∠C=90°,∠B=45°,AD是∠CAB的平分线,DE⊥AB于E,AB=a,CD=m,则AC的长为()A. 2m B.a﹣m C.a D.a+m8.如图,在正方形网格中,△ABC的三个顶点及点D、E、F、G、H都在格点上,现以D、E、F、G、H中的三点为顶点画三角形,则下列与△ABC面积相等但不全等的三角形是()A.△EHD B.△EGF C.△EFH D.△HDF9.计算(﹣)÷的结果为()A.B.C.D.10.如图,平行四边形ABCD的顶点B,D都在反比例函数y=(x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形向左平移2个单位、再向下平移3个单位后点C的坐标为()A.(1,3)B.(4,3)C.(1,4)D.(2,4)8题图 10题图11.张昆早晨去学校共用时15分钟.他跑了一段,走了一段,他跑步的平均速度是250m/分钟,步行的平均速度是80m/分钟;他家离学校的距离是2900m,如果他跑步的时间为x分钟,则列出的方程是()A. 250x+80(﹣x)=2900 B.80x+250(15﹣x)=2900C. 80x+250(﹣x)=2900 D.250x+80(15﹣x)=290012.已知⊙O及⊙O外一点P,过点P作出⊙O的一条切线(只有圆规和三角板这两种工具).以下是甲、乙两同学的作业:甲:①连接OP,作OP的垂直平分线l,交OP于点A;②以点A为圆心、OA为半径画弧、交⊙O于点M;③作直线PM,则直线PM即为所求(如图1).乙:①让直角三角板的一条直角边始终经过点P;②调整直角三角板的位置,让它的另一条直角边过圆心O,直角顶点落在⊙O上,记这时直角顶点的位置为点M;③作直线PM ,则直线PM 即为所求(如图2). 对于两人的作业,下列说法正确的是( ) A .甲对,乙不对 B . 甲不对,乙对 C . 两人都对 D . 两人都不对13.如图,直线l 经过点P (1,2),与坐标轴交于A (a ,0),B (0,b )两点(其中a <b ,如果a+b=6,那么tan∠ABO 的值为( )A .B . 1C .D . 213题图 14题图 16题图 14.如图,在⊙O 中,AB 为直径,点C 为圆上一点,将劣弧沿弦AC 翻折交AB 于点D ,连接CD .如果∠BAC=20°,则∠BDC=( )A . 80°B . 70°C . 60°D . 50° 15.对于实数m ,n ,定义一种运算“※”:m※n=m 2﹣mn ﹣3.下列说法错误的是( ) A . 0※1=﹣3 B . 方程x※2=0的根为x 1=﹣1,x 2=3 C .不等式组无解D . 函数y=x※(﹣2)的顶点坐标是(1,﹣4)16.如图1,S 是矩形ABCD 的AD 边上的一点,点E 以每秒kcm 的速度沿折线BS ﹣SD ﹣DC 匀速运动,同时点F 从点C 出发,以每秒1cm 的速度沿边CB 匀速运动,并且点F 运动到点B 时点E 也运动到点C .动点E ,F 同时停止运动.设点E ,F 出发t 秒时,△EBF的面积为ycm 2.已知y 与t 的函数图象如图2所示.其中曲线OM ,NP 为两段抛物线,MN 为线段.则下列说法:①点E 运动到点S 时,用了2.5秒,运动到点D 时共用了4秒; ②矩形ABCD 的两邻边长为BC=6cm ,CD=4cm ; ③sin∠ABS=;④点E 的运动速度为每秒2cm .其中正确的是( )A .①②③B .①③④C .①②④D . ②③④二、填空题(每小题3分,共12分.)17.在△ABC中,若|sinA﹣|+(1﹣tanB)2=0,则∠C的度数为_________ °.18.如图,已知点A、B、C在⊙O上,CD⊥OB于D,AB=2OD,若∠C=40°,则∠B=_________ °.18题图 19题图 20题图19.如图,一条4m宽的道路将矩形花坛分为一个直角三角形和一个直角梯形,根据图中数据,可知这条道路的占地面积为_________ m2.20.如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第60个点的横坐标为_________ .三、解答题(共66分)21.(9分)已知关于x,y的二元一次方程x﹣y=3a和x+3y=4﹣a.(1)如果是方程x﹣y=3a的一个解,求a的值;(2)当a=1时,求两方程的公共解;(3)若是已知方程的公共解,当x0≤1时,求y的取值范围.22.(10分)某中学对校园卫生进行清理,某班有13名同学参加这次卫生大扫除,按要求他们需要完成总面积为80m2的三项清扫工作,三项工作的面积比例如图1,每人每分钟完成各项的工作量如图2.(1)从统计图中可知:擦玻璃、擦课桌椅、扫地拖地的面积分别是_________ m2,_________ m2,_________ m2;(2)如果x人每分钟擦玻璃面积ym2,那么y关于x的函数关系式是_________ ;(3)完成扫地拖地的任务后,把13人分成两组,一组去擦玻璃,一组去擦课桌椅,怎样分配才能同时完成任务?23.(10分)河北省赵县A、B两村盛产雪花梨,A村有雪花梨200吨,B村有雪花梨300吨,现将这些雪花梨运到C、D两个冷藏仓库,已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为40元/吨和45元/吨;从B村运往C、D两处的费用分别为25元/吨和32元/吨,设从A村运往C仓库的雪花梨为x吨,A、B两村往两仓库运雪花梨的运输费用分别为yA 元,yB元.C D 总计A x吨_________ 300吨B _________ _________ 400吨总计240吨260吨500吨(1)请填写下表,并求出yA ,yB与x之间的函数关系式:(2)当x为何值时,A村的运输费用比B村少?(3)请问怎样调运,才能使两村的运费之和最小?求出最小值.24.(11分)(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形,并证明:BE=CD;(尺规作图,不写作法,保留作图痕迹);(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?简单说明理由;(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.25.(12分)已知,抛物线y=ax2+x+c的顶点为M(﹣1,﹣2),它与x轴交于点B,C(点B在点C左侧).(1)求点B、点C的坐标;(2)将这个抛物线的图象沿x轴翻折,得到一个新抛物线,这个新抛物线与直线l:y=﹣4x+6交于点N.①求证:点N是这个新抛物线与直线l的唯一交点;②将新抛物线位于x轴上方的部分记为G,将图象G以每秒1个单位的速度向右平移,同时也将直线l以每秒1个单位的速度向上平移,记运动时间为t,请直接写出图象G 与直线l有公共点时运动时间t的范围.26.(3分)1)如图1、图2,点P是⊙O外一点,作直线OP,交⊙O于点M、N,则有结论:①点M是点P到⊙O的最近点;②点N是点P到⊙O的最远点.请你从①和②中选择一个进行证明.(注:图1和图2中的虚线为辅助线,可以直接利用)(2)如图,已知,点A、B分别是直角∠XOY的两边上的动点,并且线段AB=4,如果点T是线段AB的中点,则线段TO的长等于_________ ,所以,当点A和B在直角∠XOY 的两边上运动时,点O一定在以点_________ 为圆心,以线段_________ 为直径的圆上.(3)如图,△ABC的等边三角形,AB=4,直角∠XOY的两边OX,OY分别经过点A和点B (点O与点A、点B都不重合),连接OC,求OC的最大值与最小值.(4)如图,在直角坐标系xOy中,点A、B分别是x轴与y轴上的动点,并且线段AB 等于4为一定值.以AB为边作正方形ABCD,连接OC,则OC的最大值与最小值的乘积等于_________ .参考答案三、解答题(本大题共6个小题,共66分.解答应写出文字说明、证明过程或演算步骤)21.解:(1)将代入方程x﹣y=3a得:5+1=3a,∴a=2.(2)当a=1时,两方程为:由①得:x=3+y,代入②得:3+y+3y=3,∴y=0,∴x=3.所以方程组的公共解为:.(3)因为是已知方程的公共解,∴解得:,∵x≤1,∴2a+1≤1,∴a≤0,所以1﹣a≥1,≥1.∴y22.解:(1)擦玻璃的面积:80×20%=16(m2);擦课桌椅的面积:80×25%=20(m2);扫地拖地的面积:80×55%=44(m2);故答案为:16,22,44;(2)由题意可得,每人每分钟擦玻璃的面积为=,得y=x;故答案为:y=x;(3)设擦玻璃的人数为x人,则擦课桌的人数为(13﹣x)人,根据题意得:16÷x=20÷[0.5×(13﹣x)],即=,解得x=8,经检验x=8是原方程的解,则擦课桌椅的有:13﹣8=5(人),答:擦玻璃的8人,擦课桌椅的有5人.23.解:(1)填表如图所示,y=40x+45(200﹣x)=﹣5x+9000,Ay=25(240﹣x)+32(60+x)=7x+7920;B(2)∵A村的运输费用比B村少,∴﹣5x+9000<7x+7920,解得x>90,∵A村有雪花梨200吨,故200≥x>90吨时,A村的运输费用比B村少;(3)A、B两村的运输费用之和为:﹣5x+9000+7x+7920=2x+16920,∵2>0,∴运输费用随x的增大而增大,∵,∴x≤200,∴当x=0时,运输费用最小,为16920元.24.解:(1)完成图形,如图所示:证明:∵△ABD和△ACE都是等边三角形,∴AD=AB,AC=AE,∠BAD=∠CAE=60°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB,∵在△CAD和△EAB中,,∴△CAD≌△EAB(SAS),∴BE=CD;(2)BE=CD,理由同(1),∵四边形ABFD和ACGE均为正方形,∴AD=AB,AC=AE,∠BAD=∠CAE=90°,∴∠CAD=∠EAB,∵在△CAD和△EAB中,,∴△CAD≌△EAB(SAS),∴BE=CD;(3)由(1)、(2)的解题经验可知,过A作等腰直角三角形ABD,∠BAD=90°,则AD=AB=100米,∠ABD=45°,∴BD=100米,连接CD,则由(2)可得BE=CD,∵∠ABC=45°,∴∠DBC=90°,在Rt△DBC中,BC=100米,BD=100米,根据勾股定理得:CD==100米,则BE=CD=100米.25.解:(1)∵抛物线y=ax2+x+c的顶点为M(﹣1,﹣2),∴该抛物线的解析式为y=a(x+1)2﹣2.即:y=ax2+2ax+a﹣2.∴2a=1.解得 a=.故该抛物线的解析式是:y=x2+x﹣.当y=0时,x2+x﹣=0.解之得 x1=﹣3,x2=1.∴B(﹣3,0),C(1,0);(2)①证明:将抛物线y=x2+x﹣沿x轴翻折后的图象,即新图象,仍过点B、C,其顶点M′与点M关于x轴对称,则M′(﹣1,2).设新抛物线的解析式为:y=a′(x+1)2+2.∵y=a′(x+1)2+2过点C(1,0),∴a′(1+1)2+2=0,解得,a′=﹣.∴翻折后得到的新抛物线的解析式为:y=﹣x2﹣x+.当﹣4x+6=x2+x﹣时,有:x2﹣6x+9=0,解得,x1=x2=3,此时,y=﹣6.∴新抛物线y=﹣x2﹣x+与直线l有唯一的交点N(3,﹣6);②≤t≤6.附解答过程:∵点N是新抛物线y=﹣x2﹣x+与直线l有唯一的交点,∴直线l与新抛物线y=﹣x2﹣x+在x轴上方部分(即G)无交点,∴当直线l经过点C时产生第一个公共点,经过点B时是最后一个公共点,运动t秒时,点B的坐标为(﹣3+t,0),点C的坐标为(1+t,0),直线与x轴交点为(,0).∵当=﹣3+t时,t=6∴图象G与直线l有公共点时,≤t≤6.26.解:(1)①如图1,根据两点之间线段最短可得:PO≤PR+OR.∴PM+MO≤PR+OR.∵MO=RO,∴PM≤PR.∴点M是点P到⊙O的最近点.②如图2,根据两点之间线段最短可得:PS≤PO+OS.∵OS=ON,∴PS≤PO+ON,即PS≤PN.∴点N是点P到⊙O的最远点.(2)如图3,∵∠XOY=90°,点T是线段AB的中点,∴TO=AB=2.∴点O在以点T为圆心,以线段AB为直径的圆上.故答案为:2、T、AB.(3)取AB的中点T,连接TO、CT、OC,如图4.∵∠AOB=90°,点T是线段AB的中点,∴TO=AB=2.∵△ABC的等边三角形,点T是线段AB的中点,∴CT⊥AB,AT=BT=2.∴CT===2.根据两点之间线段最短可得:OC≤OT+CT,即OC≤2+2;CT≤OC+OT,即OC≥CT﹣OT,也即OC≥2﹣2.∴OC的最大值为2+2,OC的最小值为2﹣2.(4)取AB的中点T,连接TO、CO、CT,如图5.∵∠AOB=90°,点T是线段AB的中点,∴TO=AB=2.∵四边形ABCD是正方形,∴BC=AB=4,∠ABC=90°.∵点T是线段AB的中点,∴BT=AB=2.∴CT===2.根据两点之间线段最短可得:OC≤OT+CT,即OC≤2+2;CT≤OC+OT,即OC≥CT﹣OT,也即OC≥2﹣2.∴OC的最大值为2+2,OC的最小值为2﹣2.∵(2+2)(2﹣2)=20﹣4=16.∴OC的最大值与最小值的乘积等于16.故答案为:16.。
二十五届希望杯初三二试有答案
第二十五届 希望杯 全国数学邀请赛初三㊀第2试试题一㊁选择题(每小题4分,共40分.)1.I fb o t h a a n d c a r e r e a l n u m b e r s ,2a n d 3a r e t h e t w o s o l u t i o n s o f t h e e qu a t i o n a x 2-10x +c =0f o r x ,t h e n t h e v a l u e o f a +c i s ()(A )10.(B )12.(C )14.(D )16.图12.如图1,在әA B C 中,B C >C A >A B ,D ㊁E ㊁F 分别是A B ㊁B C ㊁C A 边上的点,D E ʊA C ,F D ʊC B ,若A D ʒD B =1ʒ2,则图中的相似三角形有()对.(A )3.(B )4.(C )5.(D )6.3.若a -b =4,a b +c 2+4=0,则a 的值是()(A )2.(B )3.(C )4.(D )5.4.将抛物线y =x 2先向左平移1个单位,再向下平移2个单位,则所得的抛物线的解析式是()(A )y =x 2-2x +1.(B )y =x 2+2x -1.(C )y =x 2+4x +3.(D )y =x 2-2x -1.5.若3x 2-x =1,则9x 4+12x 3-2x 2-7x +2014的值是()(A )2013.(B )2014.(C )2015.(D )2016.6.半径分别是1,2的☉O 1和☉O 2相外切,若半径是3的☉O 3和它们都相切,则满足条件的☉O 3的个数是()(A )6.(B )3.(C )4.(D )5.7.给如图2所示的无水游泳池注水,如果进水速度是均匀的,那么,泳池内水的高度h 随时间t 变化的图象可能是()图28.三角形内的一点和三角形三个顶点的连线将三角形分成三部分,若这三部分的面积比是1ʒ2ʒ3,则这样的点的个数是()(A )1.(B )3.(C )6.(D )9.9.G i v e n p o s i t i v e i n t e g e r m w h i c h i s n o l a r g e r t h a n 10,a n d m 2014+2014mc a nb ed i v i de db y5,t h e n t h en u m b e r o f s u c h m i s()图3(A )2.(B )3.(C )4.(D )5.10.如图3,在平面直角坐标系x O y 中,点A (2,0),M (0,33),N (5,23),N B ʅx 轴于点B ,P 为MN 上一动点,则P A +P B 的最小值为()(A )33.(B )23.(C )323.(D )343.二㊁填空题(每小题4分,共40分.)11.若y =a x 2+b x +c (a ʂ0)的图象如图4所示,则a b c 的值是(填: 正数 ㊁ 负数 或 0 ).12.若关于x 的方程x 2+p x +q =0有两个负根,则直线y =p x +q 不经过第象限.(填: 一 ㊁ 二 ㊁ 三 或 四 )13.已知{x +x y +y =6,x 2+y 2=12,则x 3+y 3的值是.14.在әA B C 中,A C =8,B C =6,øA C B =90ʎ,C D ʅA B 于点D ,若әA B C ㊁әA C D ㊁әB C D的内切圆的半径分别是r 1,r 2,r 3,则r 1+r 2+r 3的值是.15.若关于x 的方程x 2-(m +5)|x |+4=m 恰有3个实数解,则实数m =.16.在平面直角坐标系x O y 中,若直线x =-1,x =3,y =3,y =kx -2围成的四边形的面积是16,则k =.图4F i g .5图6图717.A ss h o w ni n F i g .5,t h e r ea r e3s q u a r e s i nt h er i g h tt r i a n gl e .T h es i d e so ft h et w o s m a l l e r s q u a r e s a r e a a n d4.T h e s i d eo f t h e s qu a r e i n t h em i d d l e i s x ,t h e n x =(i n t e r m s o f a ).18.如图6,在边长为2的正方形A B C D 内有等边三角形C D E ,A C 交D E 于点F ,则S әC F E =.19.如图7,将长为4,宽为2的长方形A B C D 绕顶点A 顺时针旋转90ʎ到达A B ᶄC ᶄD ᶄ,图中的两段弧线分别是顶点C ㊁D 经过的路径,则阴影部分的面积为.(π取3)20.长与宽的比是2ʒ1的长方形称为 特征长方形 .用宽分别为a 1,a 2,a 3,a 4,a 5(a 1<a 2<a 3<a 4<a 5)的5个 特征长方形 拼成的大长方形,记为(a 1,a 2,a 3,a 4,a 5),则大长方形(1,2,a 3,a 4,a 5)的面积最大是.三、解答题.21.(本题满分10分)如图8,在边长为1的正方形A B C D 中,以A 为圆心㊁A B 为半径的弧与以D C 为直径的半圆交于点E ,连结D E 并延长交B C 于F ,连结B E 并延长交D C 于G .(1)求D G ʒG C 的值;(2)求四边形E F C G 的面积.图8图9图1022.(本题满分15分)如图9,排球场总长18m ,设球网高为2m ,运动员站在离网3m 的线上(图中虚线所示)正对网前跳起将球水平击出.以击球点为原点,建立如图10的直角坐标系,球运动的轨迹方程是y =5x 2v2(x ,y 单位:m ),其中v 是球被击出时的速度(单位:m /s ).(1)设击球点在3m 线的正上方,高度为2.5m ,求使球既不触网也不出界的击球速度的范围;(2)若击球点在3m 线的正上方,当高度小于h (单位:m )时,无论水平击球的速度多大,球不是触网就是越界,求h .23.(本题满分15分)如图11,有一束光线,从中心为O 的圆环的A 点射入,在圆环内经过两次反射后从A 点射出;如图12,从A 点射入的光线经过三次反射后从A 点射出.图11图12图13图14(1)如图13,若从A 点射入的光线经过五次反射后从A 点射出,求从A 点射入的光线和圆环半径O A 的夹角α的度数;(2)如图14,若从A 点射入的光线和圆环半径O A 的夹角是50ʎ,则经过几次反射后光线从A 点射出?初三第2试答案21.(1)=2DG GC.(2)760CGEF S =.22.(1)击球速度的范围是v <<;(2)若击球点在3m 线的正上方3215m 处,则无论水平击球的速度多大,球不是触网就是越界.23.(1)60α=︒.(2)经过8次反射后,从A 点出来.。
2015年东城初三数学二模试题及答案
B
A
F E
C
D
19.若实数 a 满足 a 2a 1 0 ,计算 4(a 1)(a 1) 2a(a 2) 的值.
20. 已知关于 x 的方程 (k 1) x (k 1) x
2
1 0 有两个相等的实数根,求实数 k 的值. 4
21. A,B 两个火车站相距 360km.一列快车与一列普通列车分别从 A,B 两站同时出发相向而行,快车的 速度比普通列车的速度快 54km/h,当快车到达 B 站时,普通列车距离 A 站还有 135km.求快车和普通 列车的速度各是多少?
1 ,则 a 等于 3
A.1 B.2 C.3 D.4 7. 如图,将△ABC 沿 BC 方向向右平移 2cm 得到△DEF,若△ABC 的周长为 16cm,则四边形 ABFD 的周长 为
A. 16cm
B. 18cm
C. 20cm
D. 22cm
1
8. 如图, 在已知的△ABC 中, 按以下步骤作图: ①分别以 B, C 为圆心, 以大于
1 BC 2
C
M
的长为半径作弧,两弧相交于点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 A CD=AC,∠B=25° ,则∠ACB 的度数为 D N A. 90° B. 95° C. 100° D. 105° 9.如果三角形的一个角是另一个角的 3 倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能 作为一个智慧三角形三边长的一组是 A.1,2,3 B.1,1, C.1,1, D.1, , 2 10. 如图,矩形 ABCD 中,AB=3,BC=4,动点 P 从 A 点出发,按 A→B→C 的方向在 AB 和 BC 上移动,记 PA=x,点 D 到直线 PA 的距离为 y,则 y 关于 x 的函数图象大致是
