上教安徽省六安皋城中学秋学期八年级数学期中考试卷
安徽省六安市八年级上学期期中数学试卷

安徽省六安市八年级上学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分)下列图形中,既是轴对称图形又是中心对称图形的是()A . CB . LC . XD . Z2. (2分)下列各组数作为三条线段的长,使它们能构成三角形的一组是()A . 2,3,5B . 4,4,8C . 14,6,7D . 15,10,93. (2分)下列命题是真命题的是()A . 若x2=y2 ,则x=yB . 若|a|=|b|,则a=bC . 若xy=1,则x,y互为倒数D . 若a+b=0,则=-14. (2分)对于命题“a、b是有理数,若a>b,则a2>b2”,若结论保持不变,怎样改变条件,命题才是真命题,给出下列以下四种说法:①a、b是有理数,若a>b>0,则a2>b2;②a、b是有理数,若a>b,且a+b >0,则a2>b2;③a、b是有理数,若a<b<0,则a2>b2;④a、b是有理数,若a<b且a+b<0,则a2>b2.其中,真命题的个数是()A . 1个B . 2个C . 3个D . 4个5. (2分)已知,三角形三边长分别为4,4,4,则此三角形是()A . 等边三角形B . 等腰三角形C . 等腰直角三角形D . 直角三角形6. (2分) (2017八上·宁河月考) 已知等腰三角形的两边长分别为3和6,则它的周长等于()A . 12B . 12或15C . 15D . 15或187. (2分)小冬不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1,2,3,4的四块),你认为将其中的哪一块带去,能配一块与原来一样大小的三角形?应该带()A . 第1块B . 第2块C . 第3块D . 第4块8. (2分) (2015高二上·昌平期末) 等腰三角形的两边长分别为3、6,则该三角形的周长为()A . 12或15B . 9C . 12D . 159. (2分)满足下列哪种条件时,能判定△ABC与△DEF全等的是()A . ∠A=∠E,AB=EF,∠B=∠D;B . AB=DE,BC=EF,∠C=∠F;C . AB=DE,BC=EF,∠A=∠E;D . ∠A=∠D,AB=DE,∠B=∠E10. (2分)下列语句正确的是()A . 线段绕着它的中点旋转180°后与原线段重合,那么线段是中心对称图形B . 正三角形绕着它的三边中线的交点旋转120°后与原图形重合,那么正三角形是中心对称图形C . 正方形绕着它的对角线交点旋转90°后与原图形重合,则正方形是中心对称图形D . 正五角星绕着它的中心旋转72°后与原图形重合,则正五角星是中心对称图形二、填空题 (共10题;共13分)11. (1分) (2016八上·港南期中) 如图,在△ABC中,AB=1.8,BC=3.9,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为________.12. (1分)(2018·遵义模拟) 如图,在平面直角坐标系中,等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3 ,以OA3为直角边作第三个等腰直角三角形OA3A4 ,…,依此规律,得到等腰直角三角形OA2017A2018 ,则点A2017的坐标为________.13. (1分)如图,在Rt△ABC中,∠C=90°,∠A=40°,则∠B=________14. (2分)如图,△ABC中,AB=AC,DE是AB的垂直平分线,AB=8,BC=4,∠A=36°,则∠D BC=________,△BDC的周长C△BDC=________.15. (1分)不等式 3x-2≥4(x-1)的所有非负整数解的和为________.16. (1分)(2016·开江模拟) 命题“等腰三角形两底角的平分线相等”的逆命题________17. (1分)我国传统木质结构房屋,窗子常用各种图案装饰,如图是一常见的图案,这个图案有________条对称轴.18. (1分) (2020八上·广元期末) 如图,在中,,,BC边上的中线,线段AC为________.19. (3分)观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41,…请你写出有以上规律的第⑤组勾股数________,________,________.20. (1分) (2019八上·荔湾期末) △ABC 中,AB=AC ,AD⊥BC 于 D 点,DE⊥AB 于点 E ,BF⊥AC 于点 F , DE=3cm,则 BF=________cm.三、解答题 (共6题;共60分)21. (5分)解不等式:.22. (5分)(2017·泰兴模拟) 写出下列命题的已知、求证,并完成证明过程.命题:如果一个三角形的两条边相等,那么两条边所对的角也相等(简称:“等边对等角”.)已知:().求证:().证明:23. (5分) (2017八下·定州期中) 如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,求梯子顶端A下落了多少米?24. (10分)已知⊙O为△ABC的外接圆,圆心O在AB上.SA'>”不对,理由为:根据规则:每一题抢答对得10分,抢答错扣20分,抢答不到不得分也不扣分.(1)在图1中,用尺规作图作∠BAC的平分线AD交⊙O于D(保留作图痕迹,不写作法与证明);(2)如图2,设∠BAC的平分线AD交BC于E,⊙O半径为5,AC=4,连接OD交BC于F.①求证:OD⊥BC;②求EF 的长.25. (15分)(2019·内江) 与⊙ 相切于点,直线与⊙ 相离,于点,且,与⊙ 交于点,的延长线交直线于点.(1)求证:;(2)若⊙ 的半径为3,求线段的长;(3)若在⊙ 上存在点,使是以为底边的等腰三角形,求⊙ 的半径的取值范围.26. (20分)(2019·包头) 如图,在平面直角坐标系中,已知抛物线与轴交于),两点,与轴交于点,连接.(1)求该抛物线的解析式,并写出它的对称轴;(2)点为抛物线对称轴上一点,连接,若,求点的坐标;(3)已知,若是抛物线上一个动点(其中),连接,求面积的最大值及此时点的坐标.(4)若点为抛物线对称轴上一点,抛物线上是否存在点,使得以为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点的坐标;若不存在,请说明理由.四、附加题 (共3题;共11分)27. (1分) (2019八上·杭州期中) 下列命题中,逆命题是真命题的是 ________(只填写序号)。
安徽省六安市八年级上学期数学期中考试试卷

安徽省六安市八年级上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)(2012·海南) 一个三角形的两边长分别为3cm和7cm,则此三角形的第三边的长可能是()A . 3cmB . 4cmC . 7cmD . 11cm2. (2分) (2018八上·肇庆期中) 下面有4个汽车标志图案,其中是轴对称图形的是()A . ②③④B . ①②③C . ①②④D . ①③④3. (2分)若多边形的每一个内角都等于150° ,则从此多边形的一个顶点出发的对角钱有()A . 10条B . 9条C . 8条D . 7条4. (2分)如图,在△ABC中,AB=BC=10,AC=12,BO⊥AC,垂足为点O,过点A作射线AE∥BC,点P是边BC 上任意一点,连结PO并延长与射线AE相交于点Q,设B,P两点之间的距离为x,过点Q作直线BC的垂线,垂足为R. 下面五个结论,正确的有()个①△AOB≌△COB;②当0<x<10时,△AOQ≌△COP;③当x =5时,四边形ABPQ是平行四边形;④当x =0或x =10时,都有△PQR∽△CBO;⑤当时,△PQR与△CBO一定相似.C . 4D . 55. (2分) (2017八下·君山期末) 下列多边形中,具有稳定性的是()A . 正方形B . 矩形C . 梯形D . 三角形6. (2分)(2017·台州) 如图,已知△ABC,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是()A . AE=ECB . AE=BEC . ∠EBC=∠BACD . ∠EBC=∠ABE7. (2分)已知直角三角形纸片的两条直角边长分别为m和n(m<n),过锐角顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则()A . m2+2mn+n2=0B . m2﹣2mn+n2=0C . m2+2mn﹣n2=0D . m2﹣2mn﹣n2=08. (2分) (2018八上·台州期中) 已知点关于y轴的对称点的坐标是,则的值为()A . 10B . 259. (2分)如图,O是Rt△ABC的角平分线的交点,OD∥AC,AC=5,BC=12,OD等于()A . 2B . 3C . 4D . 110. (2分)(2018·广元) 一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向平行行驶,那么这两个拐弯的角度可能是()A . 先向左转130°,再向左转50°B . 先向左转50°,再向右转50°C . 先向左转50°,再向右转40°D . 先向左转50°,再向左转40°11. (2分)(2020·宁波模拟) 如图,点A在双曲线上,且OA=4,过A作AC⊥ 轴,垂足为C,OA 的垂直平分线交OC于B,则△ABC的周长为()A . 4B . 5C .D .12. (2分) (2017七下·晋中期末) 如图,是把一张长方形的纸片沿长边中点的连线对折两次后得到的图形,再沿虚线裁剪,展开后的图形是()A .B .C .D .二、填空题 (共6题;共8分)13. (1分) (2017七下·肇源期末) 已知任意三角形的内角和为180°,试利用多边形中过某一点的对角线条数,寻求多边形内角和的公式.根据上图所示,一个四边形可以分成2个三角形;于是四边形的内角和为360度;一个五边形可以分成3个三角形,于是五边形的内角和为540度,…,按此规律n边形的内角和为________度.14. (2分) (2016八上·鄱阳期中) 三角形ABC中,AD是中线,且AB=4,AC=6,求AD的取值范围是________.15. (1分) (2016八上·江阴期末) 如图所示,等边△ABC中,B点在坐标原点,C点坐标为(4,0),点A 关于x轴对称点A′的坐标为________.16. (2分) (2013八下·茂名竞赛) 在平面直角坐标系中,有两点,现另取一点,当 ________时,的值最小.17. (1分) (2017七下·扬州月考) 在△ABC中,∠C=90°,三角形的角平分线AD、BE相交于F,则∠EFD=________度.18. (1分) (2018八下·深圳月考) 如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、M在BC上,则∠EAN=________.三、解答题 (共8题;共44分)19. (5分) (2019八上·普兰店期末) 如图,点A、D、C、F在同一直线上,AB∥EE,AB=EF,AD=CF.求证:△ABC≌△FED20. (2分) (2016八上·重庆期中) a,b分别代表铁路和公路,点M,N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置,不写作法,保留痕迹.21. (5分)(2017·河北模拟) 如图,点A,C,D,B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.22. (5分)如图所示,AB⊥BC,DC⊥AC,垂足分别为B,C,过D点作BC的垂线交BC于F,交AC于E,AB=EC,试判断AC和ED的长度有什么关系并说明理由.23. (5分)如图:已知AB∥DC,AD∥BC,求证:∠B=∠D.24. (15分) (2016八下·鄄城期中) 如图,在平面直角坐标系中,点A的坐标为(﹣2,0),等边△AOC经过平移或轴对称或旋转都可以得到△OBD.(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是________个单位长度;△AOC与△BOD关于直线对称,则对称轴是________;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是________度.(2)连接AD,交OC于点E,求AD的长.25. (5分) (2016八上·中堂期中) 已知:如图,AB⊥BC,AD⊥DC,垂足分别为B,D,∠1=∠2.求证:AB=AD.26. (2分)(2017·石狮模拟) 如图,四边形ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.(1)作出满足题意的点F,简要说明你的作图过程;(2)依据你的作图,证明:DF=BE.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共6题;共8分)13-1、14-1、15-1、16-1、17-1、18-1、三、解答题 (共8题;共44分)19-1、20-1、21-1、22-1、23-1、24-1、24-2、25-1、26-1、26-2、。
安徽省六安市八年级上学期数学期中考试试卷

安徽省六安市八年级上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共8题;共8分)1. (1分)(2018·青岛模拟) 下列图形中,是轴对称图形,但不是中心对称图形的是()A .B .C .D .2. (1分) (2017八上·深圳期中) 以下列各组数中的三个数据为边长构建三角形,能组成直角三角形的一组是()A . 7,14,15B . 12,16,20C . 4,6,8D . ,,3. (1分)正方形ABCD中,点P是对角线AC上的任意一点(不包括端点),以P为圆心的圆与AB相切,则AD与⊙P的位置关系是()A . 相离B . 相切C . 相交D . 不确定4. (1分)如右图,数轴上点N表示的数可能是()A .B .C .D .5. (1分) (2019八上·海安月考) 如图,△ABC 中,点 D 在 BC 上,△ACD 和△ABD 面积相等,线段 AD 是三角形的()A . 高B . 角平分线C . 中线D . 无法确定6. (1分)有下列说法:①有理数和数轴上的点一一对应;②不带根号的数一定是有理数;③负数没有立方根;④是7的平方根;其中正确的说法有()A . 0个B . 1个C . 2个D . 3个7. (1分) (2019七上·泰安期中) 如图,在 . ,分别以点B和点C为圆心,大于的长为半径作弧,两弧相交于D、E两点,作直线交于点F,交于点G,连接,,,则的长为()A . 4B . 5C . 6D . 78. (1分)如图,矩形ABCD中,AB=3,BC=5.过对角线交点O作OE⊥AC交AD于E,则AE的长是()A . 1.6B . 2.5C . 3D . 3.4二、填空题 (共8题;共8分)9. (1分) (2019九上·秀洲期末) 在线段、等边三角形、平行四边形、圆中任意抽取两个图形,抽到的既是中心对称图形又是轴对称图形的概率是________.10. (1分)(2017·武汉模拟) 如图,AB=AC,FD⊥BC于D,DE⊥AB于E,若∠AFD=145°,则∠EDF=________度.11. (1分)将一根长为12cm的筷子置于底面直径为6cm,高为8cm的圆柱形水杯中,设筷子露在杯子外面的长为hcm,则h的取值范围是________.12. (1分) (2019八上·天台月考) 如图1,已知∠B=60°,∠C=75°,把△ABC沿DE折叠,使点A落在点A’处,∠1+∠2的度数是________.13. (1分) (2019八上·平川期中) 的算术平方根是________ ,的相反数是________,-的倒数是________.14. (1分) (2020八上·遂宁期末) 如图,△ACE≌△DBF,如果∠E=∠F,DA=12,CB=2,那么线段AB的长是________.15. (1分) (2017七下·金乡期末) 在△ABC中,∠A=30°,D是AC边上的点;先将△ABC沿着BD翻折,翻折后△ABD的边AB交AC于点E;又将△BCE沿着BE翻折,C点恰好落在BD上,此时∠BEC=78°,则原三角形的∠ABC=________度.16. (1分) (2016九上·萧山月考) 如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为________.三、解答题 (共9题;共19分)17. (2分) (2019七下·封开期中) 已知一个数x的两个平方根分别是3a+2和a+14,求a和x的值.18. (3分) (2020八上·嘉陵期末) 如图,在4×4的网格中,有格点三角形,试画出与它成轴对称的格点三角形。
六安市八年级上学期期中数学试卷

六安市八年级上学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题. (共10题;共20分)1. (2分)下列说法正确的是()A . 三角形的三条高都在三角形的内部B . 等边三角形一角的平分线是一条射线C . 三个角对应相等的三角形全等D . 两直角边对应相等的两个直角三角形全等2. (2分)如图,两棵大树间相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为lm/s,小华走的时间是()A . 13B . 8C . 6D . 53. (2分)(2017·株洲) 如图,点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,则关于四边形EFGH,下列说法正确的为()A . 一定不是平行四边形B . 一定不是中心对称图形C . 可能是轴对称图形D . 当AC=BD时它是矩形4. (2分)在平面直角坐标系中,已知点A(2,3),则点A关于x轴的对称点坐标为()A . (2,﹣3)B . (3,2)C . (﹣2,3)D . (﹣2,﹣3)5. (2分) (2015七下·南山期中) 计算(﹣0.25)2013×42013的结果是()A . ﹣1B . 1C . 0.25D . 440266. (2分) (2016九上·新疆期中) 已知实数x,y满足,则以x,y的值为两边长的等腰三角形的周长是()A . 20或16B . 20C . 16D . 以上答案均不对7. (2分) (2018八上·山东期中) 等腰三角形的底角为15°,腰长为2a,则腰上的高为()A .B . 2aC . 2a-1D . a8. (2分)一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是(用含a、b的式子表示)()A . (a+b)2B . (a﹣b)2C . 2abD . ab9. (2分)如图,是人字型金属屋架的示意图,该屋架由BC、AC、BA、AD四段金属材料焊接而成,其中A、B、C、D四点均为焊接点,且AB=AC,D为BC的中点,假设焊接所需的四段金属材料已截好,并已标出BC段的中点D,那么,如果焊接工身边只有可检验直角的角尺,而又为了准确快速地焊接,他应该首先选取的两段金属材料及焊接点是()A . AD和BC,点DB . AB和AC,点AC . AC和BC,点CD . AB和AD,点A10. (2分)给出两个命题:①三角形的一个外角大于任何一个内角;②各边对应成比例的两个矩形一定相似()A . ①真②真B . ①假②真C . ①真②假D . ①假②假二、填空题. (共10题;共10分)11. (1分)(2018·高邮模拟) 一个多边形的每个外角都等于60°,这个多边形的内角和为________.12. (1分) (2019八上·浦东期中) 在△ABC中,若其中一个内角等于另外两个内角的差,则必有一个内角等于________°.13. (1分) (2018八上·海淀期末) 如图,在平面直角坐标系xOy中,△DEF可以看作是△ABC经过若干次的图形变化(轴对称、平移)得到的,写出一种由△AB C得到△DEF的过程:________.14. (1分) (2017八上·汉滨期中) 如图,已知AD平分∠BAC,要使△ABD≌△ACD,根据“AAS”需要添加条件________.15. (1分)如图,在5×2方格纸中,有一个以格点为顶点的△ABC,请你找出方格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有________个.16. (1分) (2020八上·遂宁期末) 若,,则 ________.17. (1分)(2016·黔南) 如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线ED交AB于点E,交BC于点D,若CD=3,则BD的长为________.18. (1分) (2018八上·彝良期末) 如图1,AC是正五边形ABCDE的一条对角线,则 =________.19. (1分)若3x+2y=3,则8x×4y=________.20. (1分) (2018八上·青山期末) 如图中的四边形均为长方形,根据图形,写出一个正确的等式:________.三、解答题 (共9题;共69分)21. (9分) (2016八上·庆云期中) 如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).(1)在图中作出△ABC关于y轴对称的△A1B1C1.(2)写出A1,B1,C1的坐标(直接写出答案),A1________;B1________;C1________.(3)△A1B1C1的面积为________.22. (15分) (2016八上·长春期中) 计算:(1)a•a2+a5÷a2﹣3a3;(2)(2x2﹣1)(x﹣3)+2x(3x+ );(3) [(a+b)2﹣b(2a+b)﹣8a]÷2a.23. (5分)化简求值:(1)已知x=﹣2,y=﹣1,求5xy2﹣{2x2y﹣[3xy2﹣﹙4xy2﹣2x2y)]}的值,(2)关于x,y的多项式6mx2+4nxy+2x+2xy﹣x2+y+4不含二次项,求6m﹣2n+2的值.24. (5分)如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.25. (5分) (2016七上·萧山竞赛) 若,则单项式和是同类项吗?如果是,请把它们进行加法运算;如果不是同类项,请从下列代数式中找出同类项进行加法运算:,26. (5分)解下列不等式(组):(1);(2)﹣≤1.27. (10分)(2018·秀洲模拟) 已知:如图,Rt△ABC中,∠ACB=90°(1)用直尺和圆规作∠ABC的平分线,交AC于点O;(2)在(1)的条件下,若BC=3,AC=4,求点O到AB的距离。
安徽省六安市城南中学八级上学期期中考试数学试题

___________ 得分试卷分值:150分)(考试时间:120分钟分.)小题,每小题3分,共27一.选择题:(本大题共9 ).下列平面图形中,不是轴对称图形的是( 1B A D C°则此等腰三角形相交所成锐角为40AB=AC,AB的垂直平分线与直线AC2. △ABC 中,( )的顶角为150°° D. 50°或 A. 50° B. 60° C. 150)3.小明在镜子里看到自己的像在用右手拿着梳子向左梳头,那么他实际是(用左手向右梳头 A.用右手向左梳头 B.用左手向左梳头C.用右手向右梳头 D. a+b=( ) 轴对称,则-3)关于X P(a+b,2a-b)与点Q(-2,4.点12BA. C. -2 D. 2 33的是CDNABM≌△MBA=∠NDC,下列条件中不能判定△5.如图,已知MB=ND,∠)(MN N B.AM=CN ∠∠M=∥C.AB=CD D.AM ADCB则下列结论不一定于F?,,DF⊥AC的角平分线,过点D作DE⊥AB于E6. AD是△ABC )正确的是(ADF∠AE=AF D..∠ADE= A.DE=DF B.BD=CD C则其顶点的坐(-2,0),(6,0),在直角坐标系中,底边的两端点坐标是7. 等腰三角形ABC)(标,能确定的是横坐标或纵坐标横坐标及纵坐标 D.A.横坐标B.纵坐标C.)35°,两腰垂直平分线交于点P,则(等腰三角形的底角为8.P在三角形底边上在三角形内 B.点A.点P 的位置与三角形的边长有关D.点PC.点P在三角形外,那么,纸沿对角线折叠,设重叠部分为△EBD9.如图,把长方形纸片ABCD 一定相等ABE②折叠后∠和∠CBD EBD有下列说法:①△是等腰三角形,EB=EDEDC一定是全等三角形EBA③折叠后得到的图形是轴对称图形④△和△)其中正确的有(C E- 1 - / 9ADB.个个A.1 B.2个 C.3个 D.4分.)二.填空题:(本大题共9小题,每小题3分,共27已知:10.?y0,x?x2?1?2y?3?。
安徽省六安市八年级上学期数学期中试卷

安徽省六安市八年级上学期数学期中试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分) (2017九下·江阴期中) 下列各数中,属于无理数的是()A . ()0B .C .D .2. (2分)(2020·柳江模拟) 直线必过的点是()A .B .C .D .3. (2分) (2019七下·卧龙期末) 如图,在△ABC中,AB=10,AC=6,BC=8,将△ABC折叠,使点C落在AB 边上的点E处,AD是折痕,则△BDE的周长为()A . 6B . 8C . 12D . 144. (2分) (2016八上·端州期末) 在平面直角坐标系中,点(-3,5)关于x轴的对称点的坐标是()A . (3,5)B . (3,-5)C . (5,-3)D . (-3,-5)5. (2分) (2019八上·德阳月考) 如图,∠A+∠B+∠C+∠D+∠E+∠F的度数是()A . 360°B . 480°C . 540°D . 720°6. (2分)下列计算正确的是()A .B .C .D .7. (2分)(2019·广西模拟) 函数y= 中,自变量x的取值范围是()A . x>0B . x≥0C . x<0D . x≤08. (2分) (2020八上·蕉城月考) 如图数轴上的点O表示的数是0,点A表示的数是2,OB⊥OA,垂足为O,且OB=1,以A为圆心,AB长为半径画弧,交数轴于点C,则点C表示的数为()A . ﹣B . ﹣2+C . 2﹣D . ﹣2﹣9. (2分) (2020八下·江岸期中) 如图,有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,这根芦苇的长度为()尺A . 10B . 12C . 13D . 1410. (2分) (2019八下·蜀山期末) 若x- ,则x-y的值为()A . 2B . 1C . 0D . -111. (2分) (2020八上·陆川期末) 如图,在△ABD中,AD=AB,∠DAB=90⁰,在△ACE中,AC=AE,∠EAC=90⁰,CD,BE相交于点F,有下列四个结论:①DC=BE;②∠BDC=∠BEC;③DC⊥BE;④FA平分∠DFE.其中,正确的结论有()A . 4个B . 3个C . 2个D . 1个12. (2分)如图,已知点A(﹣1,0)和点B(1,2),在y轴上确定点P,使得△ABP为直角三角形,则满足条件的点P共有()A . 5个B . 4个C . 3个D . 2个二、填空题 (共4题;共5分)13. (1分) (2016八上·河源期末) 若a<0,则 =________.14. (1分) (2020八下·金山月考) 如果是一次函数,那么的值是________.15. (2分) (2020九上·米易期末) 已知实数a在数轴上的位置如图所示,则化简________.16. (1分) (2020八下·韶关期末) 正方形按如图放置,其中点在轴的正半轴上,点在直线上,则点的坐标为________ .三、解答题 (共7题;共66分)17. (5分)计算。
六安市八年级上学期期中数学试卷
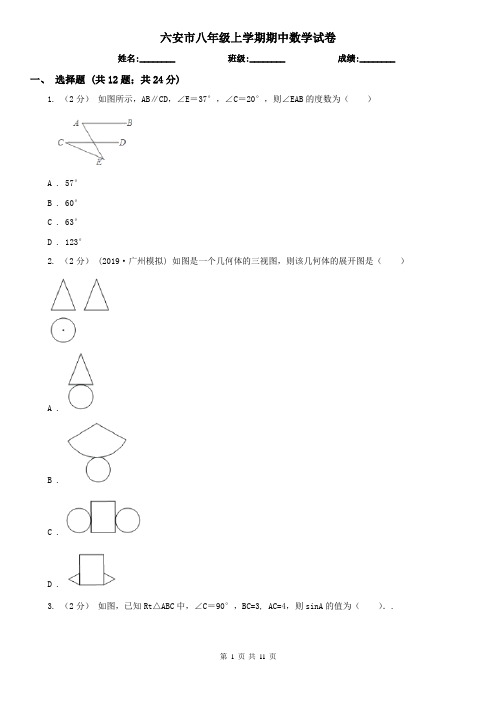
六安市八年级上学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)如图所示,AB∥CD,∠E=37°,∠C=20°,则∠EAB的度数为()A . 57°B . 60°C . 63°D . 123°2. (2分)(2019·广州模拟) 如图是一个几何体的三视图,则该几何体的展开图是()A .B .C .D .3. (2分)如图,已知Rt△ABC中,∠C=90°,BC=3, AC=4,则sinA的值为()..A .B .C .D .4. (2分) (2017八上·乌审旗期中) 下列图形中具有稳定性的是()A . 正三角形B . 正方形C . 正五边形D . 正六边形5. (2分)若△ABC中,∠A:∠B:∠C=1:2:3,则△ABC一定是()A . 锐角三角形B . 钝角三角形C . 直角三角形D . 任意三角形6. (2分) (2016八上·博白期中) 在R t△ABC中,∠C=90°,∠B=30°,斜边AB的长为2,则AC长为()A . 4B . 2C . 1D .7. (2分)下列说法正确的是()A . 形状相同的两个三角形全等B . 面积相等的两个三角形全等C . 完全重合的两个三角形全等D . 所有的等边三角形全等8. (2分) (2016八上·博白期中) 用直尺和圆规作已知角的平分线的示意图如右,则说明∠CAD=∠DAB的依据是()A . SSSB . SASC . ASAD . AAS9. (2分) (2016八上·博白期中) 根据下列已知条件,能唯一画出△ABC的是()A . AB=3,BC=4,AC=8B . ∠C=90°,AB=6C . ∠A=60°,∠B=45°,AB=4D . AB=3,BC=3,∠A=30°10. (2分) (2016八上·博白期中) 如图,在等腰三角形纸片ABC中,AB=AC,∠A=40°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE的度数是()A . 20°B . 30°C . 40°D . 70°11. (2分) (2016八上·博白期中) 如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC 与∠ACE的平分线相交于点D,则∠D的度数为()A . 15°B . 17.5°C . 20°D . 22.5°12. (2分) (2016八上·博白期中) 如图,等腰三角形ABC中,AB=AC,D、E都在BC上,要使△ABD≌△ACE,需要添加一个条件,某学习小组在讨论这个条件时给出了如下几种方案:①AD=AE;②BD=CE;③BE=CD;④∠BAD=∠CAE,其中可行的有()A . 1种B . 2种C . 3种D . 4种二、填空题 (共6题;共6分)13. (1分)在Rt△ABC中,∠C=90°,如果AB=6,cosA=,那么AC=________.14. (1分)(2017·新乡模拟) 如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD折叠,使得点B落在边AD 上,记为点G,BC的对应边GI与边CD交于点H,折痕为EF,则AE________时,△EGH为等腰三角形.15. (1分)(2019·濮阳模拟) 如图,在Rt△ABC中,AB=2,BC=1.将边BA绕点B顺时针旋转90°得线段BD,再将边CA绕点C顺时针旋转90°得线段CE,连接DE,则图中阴影部分的面积是________.16. (1分)(2020·温州模拟) 在▱ABCD中,E是AD上一点,且点E将AD分为2:3的两部分,连接BE、AC相交于F,则S△AEF:S△CBF是________.17. (1分) (2017九上·抚宁期末) 如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′=________.18. (1分)在矩形纸片ABCD中,AB=16,AD=12,点P在边AB上,若将△DAP沿DP折叠,使点A恰好落在矩形对角线上的点A′处,则AP的长为________.三、解答题 (共8题;共60分)19. (5分)已知:在△ABC中,AB=AC.(1)尺规作图:作AD⊥BC于点D.(不要求写作法,保留作图痕迹)(2)延长AD至E点,使得DE=AD.求证:四边形ABEC是菱形.20. (5分)如图,已知正方形ABCD的边长是2,∠EAF=m°,将∠EAF绕点A顺时针旋转,它的两边分别交BC、CD于点E、F,G是CB延长线上一点,且始终保持BG=DF.(1)求证:△ABG≌△ADF;(2)求证:AG⊥AF;(3)当EF=BE+DF时,①求m的值;②若F是CD的中点,求BE的长.21. (5分) (2016八上·博白期中) 如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN 上.(1)图中点B的对称点是________,点C的对称点是________;(2)写出图中相等的一对线段是________,相等的一对角是________;(3)写出图中全等的一对三角形是________.22. (5分) (2016八上·博白期中) 如图,在△ABC中,∠B=40°,∠C=70°,AD是△BAC的角平分线,求∠ADC的度数.23. (5分) (2016八上·博白期中) 已知:如图,CE⊥AB,BF⊥AC,CE与BF相交于D,且BD=CD.求证:D 在∠BAC的平分线上.24. (10分) (2016八上·博白期中) 如图,已知AB=CD,∠B=∠C,AC和BD相交于点O,E是AD的中点,连接OE.(1)求证:△AOB≌△DOC;(2)求∠AEO的度数.25. (10分) (2016八上·博白期中) 如图,在△ABC中,AB=AC,∠BAC=120°,AE=BE,D为EC中点.(1)求∠CAE的度数;(2)求证:△ADE是等边三角形.26. (15分) (2016八上·博白期中) 以点A为顶点作等腰Rt△ABC,等腰Rt△ADE,其中∠BAC=∠DAE=90°,如图1所示放置,使得一直角边重合,连接BD、CE.(1)试判断BD、CE的数量关系,并说明理由;(2)延长BD交CE于点F,试求∠BFC的度数;(3)把两个等腰直角三角形按如图2放置,(1)中的结论是否仍成立?请说明理由.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共6题;共6分)13-1、14-1、15-1、16-1、17-1、18-1、三、解答题 (共8题;共60分)19-1、20-1、21-1、21-2、21-3、22-1、23-1、24-1、24-2、25-1、25-2、26-1、26-2、26-3、第11 页共11 页。
2021-2022学年-有答案-安徽省六安市某校初二(上)期中考试数学试卷

2021-2022学年安徽省六安市某校初二(上)期中考试数学试卷一、选择题1. 下列坐标平面内的点,在第二象限的是()A.(1,2)B.(−1,−2)C.(−1,2)D.(1,−2)2. 以下列各组线段的长为边,能组成三角形的是( )A.1cm,2cm,3cmB.1cm,5cm,6cmC.1cm,3cm,3cmD.2cm,4cm,7cm3. 函数y=自变量的取值范围是()√x+3A.x≠−3B.x>−3C.x≥−3D.x≤−34. 把直线y=2x−3沿y轴向上平移2个单位后,得到的直线的函数表达式为()A.y=2x+2B.y=2x−5C.y=2x−1D.y=2x+15. 若点A(−1,a),B(−4,b)在一次函数y=−5x−3的图象上,则a与b的大小关系是()A.a<bB.a>bC.a=bD.无法确定6. 如图,已知正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y= x+k的图象大致是( )A. B.C. D.7. 以下命题中,是真命题的是( )A.若|a|=|b|,则a=bB.如果ab>0,那么a,b都是正数C.两条平行线被第三条直线所截,同旁内角互补D.互为补角的两个角的平分线互相垂直8. 如图,四个图形中,线段BE是△ABC的高的图是( )A. B.C. D.9. 如图,△ABC≅△DEF,BC=7,EC=4,则CF的长为( )A.2B.3C.5D.710. 如图①,在矩形ABCD中,动点P从点C出发,沿C−D−A−B方向运动至点B处停止,设点P运动的路程为x,△PBC的面积为y,如果y关于x的函数图象如图②所示,则矩形ABCD的周长为( )A.11B.14C.16D.24二、填空题如果点P在第二象限内,点P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为________.已知等腰三角形的两边长分别为3cm和6cm,则这个等腰三角形的周长为________.如图,把一副常用的三角板如图所示拼在一起,那么图中∠ABF=________度.在平面直角坐标系xOy中,一次函数图象经过点A (3,0),且与y轴交于点B,△OAB的面积为6,则点B的坐标为________.三、解答题已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度).(1)在图中画出平移后的△A1B1C1;直接写出A1坐标.A1________;(2)求出△ABC的面积.已知y是x的一次函数,且当x=1时,y=1;当x=2时,y=4.(1)求y与x之间的函数关系式;(2)该函数截距是________.已知△ABC的三边长分别为a,b,c.(1)若a,b,c满足(a−b)2+(b−c)2=0,试判断△ABC的形状;(2)若a=5,b=2,且c为整数,求△ABC的周长的最大值.已知:如图,AB=AC,AE=AF.求证:△ABE≅△ACF.已知直线y=kx+b经过点A(5, 0),B(1, 4).(1)求直线AB的解析式;(2)若直线y=2x−4与直线AB相交于点C,求点C的坐标;(3)根据图象,直接写出关于x的不等式2x−4>kx+b的解集.如图,AM为△ABC边BC的中线.(1)若AB=6,AC=4,则△AMB与△AMC周长之差为________;(2)若△AMB面积为6,且BM上高为3,求BC的长.如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.(1)求A,B两点的坐标;(2)过B点作直线BP与x轴正半轴相交于点P,且使AP=2OA,求△BOP的面积.为预防新冠肺炎,某公司需要购买甲、乙两种防护器材共150件,甲、乙两种防护器材每件的价格分别为600元和1000元.且要求乙种器材的件数不少于甲种器材件数的2倍.设购买甲种商品x件,购买两种商品共花费y元.(1)请求出y与x的函数关系式及x的取值范围;(2)试利用函数的性质说明,当购买多少件甲种器材时,所需要的费用最少,最少为多少元?在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“智慧三角形”.如三个内角分别为120∘,40∘,20∘的三角形是“智慧三角形”.如图,∠MON=60∘,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交射线OB于点C.(1)∠ABO的度数为________∘,△AOB________(填“是”或“不是”)智慧三角形;(2)若∠OAC=20∘,求证:△AOC为“智慧三角形”;(3)当△ABC为“智慧三角形”时,求∠OAC的度数.参考答案与试题解析2021-2022学年安徽省六安市某校初二(上)期中考试数学试卷一、选择题1.【答案】C【考点】点的坐标【解析】此题暂无解析【解答】解:第二象限的点横坐标为负,纵坐标为正,故点(−1,2)在第二象限.故选C.2.【答案】C【考点】三角形三边关系【解析】根据三角形的三边关系来判断即可.【解答】解:A,1+2=3,不能组成三角形;B,1+5=6,不能组成三角形;C,1+3>3,能组成三角形;D,2+4<7,不能组成三角形.故选C.3.【答案】B【考点】函数自变量的取值范围【解析】本题考查了函数式有意义的x的取值范围.一般地从两个角度考虑:分式的分母不为0;偶次根式被开方数大于或等于0;当一个式子中同时出现这两点时,应该是取让两个条件都满足的公共部分.【解答】解:根据题意得到:x+3>0,解得x>−3.故选B.4.【答案】C【考点】一次函数图象与几何变换【解析】根据平移法则上加下减可得出平移后的解析式.【解答】解:由题意得:平移后的解析式为:y=2x−3+2,即y=2x−1.故选C.5.【答案】A【考点】一次函数的性质【解析】根据一次函数的性质来解答即可.【解答】解:∵一次函数y=−5x−3中,k=−5<0,∴y随x的增大而减小.∵−1>−4,点A(−1,a),B(−4,b),∴a<b,故选A.6.【答案】A【考点】正比例函数的性质一次函数图象与系数的关系【解析】先根据正比例函数y=kx的函数值y随x的增大而增大判断出k的符号,再根据一次函数的性质即可得出结论.【解答】解:∵正比例函数y=kx的函数值y随x的增大而增大,∴k>0,∵b=k>0,∴一次函数y=x+k的图象经过一、二、三象限.故选A.7.【答案】C【考点】真命题,假命题平行线的性质邻补角绝对值【解析】根据绝对值的意义判定A,根据有理数的乘法判定B,根据平行线的性质判定C,根据邻补角的定义来判D.【解答】解:A,若|a|=|b|,则a=±b,故A错误;B,如果ab>0,那么a,b同号,但不一定都为正数,故B错误;C,两条平行线被第三条直线所截,同旁内角互补,故C正确;D,互为邻补角的两个角的平分线互相垂直,故D错误.故选C.8.【答案】D【考点】三角形的高【解析】根据高的画法知,过点B作AC边上的高,垂足为E,其中线段BE是△ABC的高.【解答】解:根据高的画法知,过点B作AC边上的高,垂足为E,其中线段BE是△ABC的高. 由图可得,线段BE是△ABC的高的图是D.故选D.9.【答案】B【考点】全等三角形的性质【解析】利用全等三角形的性质可得EF=BC=7,再解即可.【解答】解:∵△ABC≅△DEF,∴EF=BC=7.∵EC=4,∴CF=3.故选B.10.【答案】B【考点】一次函数的应用一次函数的图象【解析】根据三角形的面积公式和一次函数的图象来解答即可.【解答】解:由题意知:当点P在边CD上时,y随x的增大而增大;当点P在边AD上时,y不随x的变化而变化;当点P在边AB上时,y随x的增大而减小.结合一次函数的图象可知,CD=3,AD=4,∴矩形ABCD的周长为:2(AD+CD)=2×(3+4)=14.故选B.二、填空题【答案】(−3,4)【考点】点的坐标【解析】根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度解答.【解答】解:∵点P在第二象限内,点P到x轴的距离是4,到y轴的距离是3,∴点P的横坐标是−3,纵坐标是4,∴点P的坐标为(−3,4).故答案为:(−3,4).【答案】15cm【考点】三角形三边关系等腰三角形的性质【解析】根据等腰三角形的性质分类计算即可.【解答】解:若3cm是腰长,则三角形的三边分别为3cm,3cm,6cm,3+3=6,故不能组成三角形;若3cm是底边,则三角形的三边分别为3cm,6cm,6cm,能组成三角形,周长=3+6+6=15(cm).综上所述,这个等腰三角形的周长是15cm.故答案为:15cm.【答案】15【考点】三角形的外角性质【解析】根据常用的三角板的特点求出∠EAD和∠BFD的度数,根据三角形的外角的性质计算即可.【解答】解:由一副常用的三角板的特点可知,∠EAD=45∘,∠BFD=30∘,∴∠ABF=∠EAD−∠BFD=15∘.故答案为:15.【答案】(0, 4)或(0, −4)【考点】一次函数图象上点的坐标特点三角形的面积【解析】由点A的坐标可得出OA的长,利用三角形的面积公式可求出OB的长,进而可得出点B 的坐标.【解答】解:∵点A的坐标为(3, 0),∴OA=3.∵S△OAB=6,即12OA⋅OB=6,∴OB=4,∴点B的坐标为(0, 4)或(0, −4).故答案为:(0, 4)或(0, −4).三、解答题【答案】解:(1)如图所示:△A1B1C1,即为所求;由图知A1(4,−2).(2)△ABC的面积为:3×3−12×1×3−12×1×2−12×2×3=3.5.【考点】作图-平移变换点的坐标三角形的面积【解析】(1)直接利用平移的性质得出A,B,C平移后对应点位置.利用ΔABC所在矩形面积减去周围三角形面积即可得出答案.【解答】解:(1)如图所示:△A 1B 1C 1,即为所求;由图知A 1(4,−2).(2)△ABC 的面积为:3×3−12×1×3−12×1×2−12×2×3=3.5.【答案】解:(1)设一次函数解析式为y =kx +b(k ≠0),把x =1,y =1;x =2,y =4代入得{k +b =1,2k +b =4,解得{k =3,b =−2,则一次函数解析式为y =3x −2.−2【考点】待定系数法求一次函数解析式一次函数的图象【解析】设一次函数解析式为y =kx +b(k ≠0),把x 与y 的值代入求出k 与b 的值,即可确定出解析式;一次函数的截距就是当x =0时,y 的值.【解答】解:(1)设一次函数解析式为y =kx +b(k ≠0),把x =1,y =1;x =2,y =4代入得{k +b =1,2k +b =4,解得{k =3,b =−2,则一次函数解析式为y =3x −2.(2)一次函数中的截距就是b 的值,即当x =0,y =b =−2.故答案为:−2.【答案】解:(1)∵ (a −b)2+(b −c)2=0,∴ a −b =0,b −c =0,∴ a =b =c ,∴ △ABC 是等边三角形.(2)∵ a =5,b =2,且c 为整数,∴ 5−2<c <5+2,即3<c <7,∴ c =4,5,6,∴ 当c =6时,△ABC 周长的最大值=5+2+6=13.【考点】三角形三边关系非负数的性质:偶次方【解析】(1)直接根据非负数的性质即可得出结论;(2)根据三角形的三边关系可得出c 的取值范围,进而可得出结论.【解答】解:(1)∵ (a −b)2+(b −c)2=0,∴ a −b =0,b −c =0,∴ a =b =c ,∴ △ABC 是等边三角形.(2)∵ a =5,b =2,且c 为整数,∴ 5−2<c <5+2,即3<c <7,∴ c =4,5,6,∴ 当c =6时,△ABC 周长的最大值=5+2+6=13.【答案】证明:如图,∠A 是△ABE 和△ACF 的公共角,在△ABE 和△ACF 中,∵ {AB =AC(已知),∠A =∠A(公共角),AE =AF(已知),,∴ △ABE ≅△ACF(SAS) .【考点】全等三角形的判定【解析】根据三角形全等判定定理边角边(SAS)进行证明.【解答】证明:如图,∠A 是△ABE 和△ACF 的公共角,在△ABE 和△ACF 中,∵ {AB =AC(已知),∠A =∠A(公共角),AE =AF(已知),,∴ △ABE ≅△ACF(SAS) .【答案】解:(1)根据题意得{5k +b =0,k +b =4,解得{k =−1,b =5.则直线AB 的解析式是y =−x +5.(2)根据题意得{y =−x +5,y =2x −4,解得{x =3,y =2,则C 的坐标是(3, 2).(3)根据图象可得,当2x −4>kx +b 时,x 的值大于C 点时x 的取值,即x >3.【考点】待定系数法求一次函数解析式二元一次方程组的应用——几何问题一次函数与一元一次不等式【解析】(1)利用待定系数法即可求得函数的解析式;(2)解两个函数解析式组成方程组即可求解;(3)关于x 的不等式2x −4≤kx +b 的解集就是函数y =kx +b 的图象在上边的部分自变量的取值范围.【解答】解:(1)根据题意得{5k +b =0,k +b =4,解得{k =−1,b =5.则直线AB 的解析式是y =−x +5.(2)根据题意得{y =−x +5,y =2x −4,解得{x =3,y =2,则C 的坐标是(3, 2).(3)根据图象可得,当2x −4>kx +b 时,x 的值大于C 点时x 的取值,即x >3.【答案】2(2)由题意得:S △AMB =12×BM ×ℎ=12×BM ×3=6, 解得:BM =4,∴ BC =2BM =8.【考点】三角形的中线三角形的面积【解析】(1)根据中线得到BM =MC ,把两个三角形周长表示出来,即可得出答案;(2)根据三角形面积公式可求BC 的长.【解答】解:(1)∵ AM 是△ABC 边BC 的中线,∴ BM =MC ,△AMB 的周长=AB +AM +BM ,△AMC 的周长=AM +AC +MC ,∴ AB +AM +BM −(AM +AC +MC)=AB +AM +BM −AM −AC −MC=AB −AC =6−4=2.故答案为:2.(2)由题意得:S △AMB =12×BM ×ℎ=12×BM ×3=6,解得:BM =4,∴ BC =2BM =8.【答案】解:(1)当y =0时,2x +3=0,解得x =−32,则A 点坐标为(−32, 0); 当x =0时,y =2x +3=3,则B 点坐标为(0, 3).(2)当点P 在x 轴的正半轴上,∵ AP =2OA ,∴ OA =OP ,∴ P 点坐标为(32, 0),∴ △BOP 的面积=12⋅32⋅3=94. 【考点】一次函数图象上点的坐标特点三角形的面积【解析】(1)根据坐标轴上点的坐标特征求A 点和B 点坐标;(2)分类讨论:当点P 在x 轴的正半轴上,如图1,由AP =2OA 得到OA =OP =32,则P 点坐标为(32, 0),然后根据三角形面积公式计算;当点P 在x 轴的负半轴上,如图2,由AP =2OA 得到OP =3OA =92,则P 点坐标为(−92, 0),然后根据三角形面积公式计算.【解答】解:(1)当y =0时,2x +3=0,解得x =−32,则A 点坐标为(−32, 0);当x =0时,y =2x +3=3,则B 点坐标为(0, 3).(2)当点P 在x 轴的正半轴上,∵ AP =2OA ,∴ OA =OP ,∴ P 点坐标为(32, 0), ∴ △BOP 的面积=12⋅32⋅3=94.【答案】解:(1)设甲器材有x 件,则乙器材有(150−x)件,根据题意得{150−x ≥2x,x >0,解得0<x ≤50.则y 与x 的函数关系式是y =600x +1000(150−x)=−400x +150000(0<x ≤50).(2)∵ k =−400<0,∴ 一次函数y 随x 的增大而减少,∴ 当x =50时,y min =−400×50+150000=130000(元).则购买50件甲种器材时,所需费用最少,为130000元.【考点】一次函数的应用【解析】(1)设甲商品有x 件,则乙商品则有(150−x)件,根据甲、乙两种商品共150件和乙种商品的件数不少于甲种商品件数的2倍,列出不等式组,求出x 的取值范围,再根据甲、乙两种商品的价格列出一次函数关系式即可.(2)根据(1)得出一次函数y 随x 的增大而减少,即可得出当x =50时,所需要的费用最少.【解答】解:(1)设甲器材有x 件,则乙器材有(150−x)件,根据题意得{150−x ≥2x,x >0,解得0<x ≤50.则y 与x 的函数关系式是y =600x +1000(150−x)=−400x +150000(0<x ≤50).(2)∵ k =−400<0,∴ 一次函数y 随x 的增大而减少,∴ 当x =50时,y min =−400×50+150000=130000(元).则购买50件甲种器材时,所需费用最少,为130000元.【答案】30,是(2)证明:∵ ∠AOC =60∘,∠OAC =20∘,∴ ∠AOC =3∠OAC ,∴ △AOC 为“智慧三角形”.(3)∵ △ABC 为“智慧三角形”,①当点C 在线段OB 上时,∵ ∠ABO =30∘,∴∠BAC+∠BCA=150∘,∠ACB≥60∘,∠BAC≤90∘,Ⅰ、当∠ABC=3∠BAC时,∠BAC=10∘,∴∠OAC=80∘,Ⅱ、当∠ABC=3∠ACB时,∴∠ACB=10∘,∴此种情况不存在,Ⅲ、当∠BCA=3∠BAC时,∴∠BAC+3∠BAC=150∘,∴∠BAC=37.5∘,∴∠OAC=52.5∘,Ⅳ、当∠BCA=3∠ABC时,∴∠BCA=90∘,∴∠BAC=60∘,∴∠OAC=90∘−60∘=30∘,Ⅴ、当∠BAC=3∠ABC时,∴∠BAC=90∘,∴∠OAC=0∘,∵此时C与点O重合,Ⅵ、当∠BAC=3∠ACB时,∴3∠ACB+∠ACB=150∘,∴∠ACB=37.5∘,∴此种情况不存在,②当点C在线段OB的延长线上时,∵∠ACO<30∘,∴∠ABC=150∘,∴∠ACB+∠BAC=30∘,Ⅰ、当∠ACB=3∠BAC时,∴3∠BAC+∠BAC=30∘,∴∠BAC=7.5∘,∴∠OAC=90∘+∠BAC=97.5∘,Ⅱ、当∠BAC=3∠BCA时,∴3∠BCA+∠BCA=30∘,∴∠BCA=7.5∘,∴∠BAC=3∠BCA=22.5∘,∴∠OAC=90∘+22.5∘=112.5∘.当△ABC为“智慧三角形”时,∠OAC的度数为0∘或80∘或52.5∘或30∘或97.5∘或112.5∘.【考点】三角形内角和定理【解析】(1)根据垂直的定义、三角形内角和定理求出∠ABO的度数,根据“智慧三角形”的概念判断;(2)根据“智慧三角形”的概念证明即可;(3)分点C在线段OB和线段OB的延长线上两种情况,根据“智慧三角形”的定义计算.【解答】(1)解:∵AB⊥OM,∴∠OAB=90∘,∴∠ABO=90∘−∠MON=30∘.∵∠OAB=3∠ABO,∴△AOB是“智慧三角形”.故答案为:30;是.(2)证明:∵∠AOC=60∘,∠OAC=20∘,∴∠AOC=3∠OAC,∴△AOC为“智慧三角形”.(3)∵△ABC为“智慧三角形”,①当点C在线段OB上时,∵∠ABO=30∘,∴∠BAC+∠BCA=150∘,∠ACB≥60∘,∠BAC≤90∘,Ⅰ、当∠ABC=3∠BAC时,∠BAC=10∘,∴∠OAC=80∘,Ⅱ、当∠ABC=3∠ACB时,∴∠ACB=10∘,∴此种情况不存在,Ⅲ、当∠BCA=3∠BAC时,∴∠BAC+3∠BAC=150∘,∴∠BAC=37.5∘,∴∠OAC=52.5∘,Ⅳ、当∠BCA=3∠ABC时,∴∠BCA=90∘,∴∠BAC=60∘,∴∠OAC=90∘−60∘=30∘,Ⅴ、当∠BAC=3∠ABC时,∴∠BAC=90∘,∴∠OAC=0∘,∵此时C与点O重合,Ⅵ、当∠BAC=3∠ACB时,∴3∠ACB+∠ACB=150∘,∴∠ACB=37.5∘,∴此种情况不存在,②当点C在线段OB的延长线上时,∵∠ACO<30∘,∴∠ABC=150∘,∴∠ACB+∠BAC=30∘,Ⅰ、当∠ACB=3∠BAC时,∴3∠BAC+∠BAC=30∘,∴∠BAC=7.5∘,∴∠OAC=90∘+∠BAC=97.5∘,Ⅱ、当∠BAC=3∠BCA时,∴3∠BCA+∠BCA=30∘,∴∠BCA=7.5∘,∴∠BAC=3∠BCA=22.5∘,∴∠OAC=90∘+22.5∘=112.5∘.当△ABC为“智慧三角形”时,∠OAC的度数为0∘或80∘或52.5∘或30∘或97.5∘或112.5∘.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010~2011学年度第一学期期中考试
八年级数学试题
2010.11.11上午8:30~10:10 满分:120分 命题人:夏骏
一、选择题(每题4分,共40分)
、2010年3月是六安撤地建市十周年,原县级六安市分设为金安区、裕安区。
能够
】
、东经116° B
、北纬32° C 、
在合肥的西边 D 、北纬32°,东经116°
、在下图中,正确画出AC 边上高的是……………………………………………【 】
A 、
B 、
C 、
D 、
、如图,D3081次六安至汉口动车在金寨境内匀速通过一条隧道(隧道长大于火车长),
x 与火车在隧道内的长度y 之间的关系用图象描述大致是【 】 A 、 B 、 C 、 D 、
、一个三角形的两边长分别为3和7,且第三边长为整数,这样的三角形的周长最小值 】 A 、 14 B 、 15 C 、16 D 、 17
、一次函数)1()2(m x m y -++=,若y 随x 的增大而减小,且该函数的图象与x 轴交
m 的取值范围是………………………………………………【 】 A 、m>-2 B 、m<1 C 、-2<m<1 D 、m<-2
o
o
o
o
y
y
y
y
x
x
x
x
6、下列函数图象不可能是一次函数y=ax -(a -2)的图象是………………………【 】
A B C D
7、已知y 关于x 的函数图象如图所示,则当0y <时,自变量x 的取值范围是…【 】
A 、0x <
B 、11x -<<或2x >
C 、1x >-
D 、1x <-或12x <<
8、已知一个等腰三角形底边的长为5cm ,一腰上的中线把其周长分成的两部分的差为3 cm,
则腰长为………………………………………………………………………………【 】
A 、2 cm
B 、8 cm
C 、2 cm 或8 cm
D 、10 cm
9、用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图
象(如图所示),则所解的二元一次方程组是………………………………………【 】 A .203210x y x y +-=⎧⎨--=⎩,
B .2103210x y x y --=⎧⎨--=⎩,
C .2103250x y x y --=⎧⎨+-=⎩
,
D .20210x y x y +-=⎧⎨--=⎩
,
10、已知一次函数y =kx +b ,当0≤x ≤2时,对应的函数值y 的取值范围是
-2≤y ≤4,则kb 的值为…………………………………………………………………………………【 】
A 、12
B 、-6
C 、-6或-12
D 、 6或12
二、填空题(每题5分,共20分)
11、小明根据某个一次函数关系式填写了右表:
其中有一格不慎被墨汁遮住了,想想看,该空格 里原来填的数是________。
12、函数3
x y -=
的自变量x 的取值范围是____________. 13、已知直线7y ax =+与直线21y x =-+相交于x 轴上一点,则a = . 14、如图,直线1l :1y x =+与直线2l :y mx n =+相交于点
P (a ,2),则关于x 的不等式1x +≥mx n +的解集为 .
1 O y
1-
2
· P (1,1)
1 1
2 2
3 3
-1 -1
O
x y
y x
O P
2
a
1l
l
三、解答题(15题8分,16、17、18、19题各10分,20题12分,共60分)
15、如图△ABC中,∠BAC=80°,∠B=60°,AD⊥BC,垂足为D,AE平分∠DAC,求∠AEC 度数。
16、在如图所示的直角坐标系中,画图并解答下列问题:
(1)分别写出A、B两点的坐标;
(2)将△ABC先向上平移4个单位,再向左平移3个单位得到△A1B1C1;
(3)求出线段A1B1所在直线L的函数解析式,并写出在直线L上线段A1B1从B1到A1的自变量x的取值范围.
17、一根弹簧的的原长是10 cm,且每挂重1kg就伸长0.5 cm,它的挂重不超过10kg。
⑴、挂重后弹簧的长度y(cm)与挂重x(kg)之间的函数关系式;
⑵、写出自变量的取值范围;
⑶、挂重多少千克时,弹簧长度为12.5cm?
18、若y 与x+2成正比例,且x=5时,y=-21,求:
(1)y 与x 之间的函数关系式. (2)它的截距.
19、已知:如图,在△AOB 中, A (3,2),B (5,0),
E (4,m ),求(1)m 的值.(2)△AOE 的面积。
20、一手机经销商计划购进NOKIA 的5220型、5320型、5310型三款手机共60部,每
款手机至少要购进8部,且恰好用完购机款61000元.设购进5220型手机x 部,5320型手机y
(1)用含x ,y 的式子表示购进5310型手机的部数; (2)求出y 与x 之间的函数关系式;
(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机
过程中需另外支出各种费用共1500元.
①求出预估利润P (元)与x (部)的函数关系式; (注:预估利润P =预售总额-购机款-各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
A
B
E
O
x
y。
