数学模型期末考试试题及答案
2009数学建模试题与答案
华南农业大学期末考试试卷（A卷）2009学年第二学期考试科目：数学模型考试类型：（闭卷）考试时间：120分钟学号姓名年级专业1、（13分）设已知某正方形板材边长20cm，现将之加工出半径为1cm的圆盘，请对下面给出的两种排列方法，写出能加工出的尽可能多的圆盘数。
（1）排列1：圆盘中心按正方形排列（如右图）的尽可能多的圆盘数。
（4分）解：圆盘总数：202010022⨯=排列2：圆盘中心按六角形排列（如右图）的尽可能多的圆盘数。
（4分）解：行数：111+=圆盘总数：20111110522-⨯+=（2）设计出不同于(1)(2)的方案，且加工出的圆盘更多。
（5分）解：前三行正方形，后八行六角形，圆盘总数为106（此题考虑的是当两种方案当两种方案被提出的时候，但仍需改进的时候，应该考虑这两者的综合是否可行，如果可行，则给出方案。
）2、（10分）在举重比赛中，运动员在高度和体重方面差别很大，请就下面两种假设，建立一个举重能力和体重之间关系的模型：（1）假设肌肉的强度和其横截面的面积成比例。
5分（2）假定体重中有一部分是与成年人的尺寸无关，请给出一个改进模型。
5分解：设体重w（千克）与举重成绩y （千克）（1）由于肌肉强度(I)与其横截面积(S)成比例，所以y∝I∝S设h为个人身高，又横截面积正比于身高的平方，则S ∝ h2再体重正比于身高的三次方，则w ∝ h3（2）a, 则一个最粗略的模型为更好的模型：()y k w aγ=-3、 （10分）在超币购物时你压意到大包发商品比小包装面品便宜这种现象了吗？比如洁银牙膏50g 装的每支1.50元，120g 装的每支3.00元，二者单位重量的价格比是1.2:1，试用比例方法构造模型解释这个现象。
（1）请写出商品价恪c 与商品重量w 的关系，其中价格由生产成本、包装成本和其它成本等决定，这些成本中有的与重量w 成正比，有的与表面积成正比，还有与w 无关的因素。
（5分） （2）给出单位重量价格c与w 的关系，并解释。
数学建模基础问题与答案!(有答案).
‘牡丹江师范学院期末考试试题库科目：数学模型与数学实验年级：2006 学期：2008-2009-2 考核方式：开卷命题教师：数学模型与数学实验课程组一、解答题：（每小题30分）x=[0.1 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.2 0.21 0.23]';n=length(x)X=[ones(n,1) x];Y=[42 43.5 45 45.5 45 47.5 49 53 50 55 55 60]';[b,bint,r,rint,stats]=regress(Y,X);b,bint,stats% 预测y=b(1)+b(2)*x%E误差平方和E=sum((Y-y).^2)参考结果：回归直线：ˆ28.4928130.8348=+y x误差平方和：17.4096是否重点：重点难易程度：中知识点所在章节：第十六章第一节检查数据中有无异常点、由x的取值对y作出预测。
解：参考程序(t2.m)：x=[0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.2 0.21 0.23]';Y=[42.0 41.5 45.0 45.0 45 47.5 49.0 55.0 50.0 55.0 55.5 60.5]'; scatter(x,Y);n=length(x)X=[ones(n,1) x];b,bint,stats %残差图 rcoplot(r,rint) % 预测y=b(1)+b(2)*x%剔除异常点重新建模 X(8,:)=[]; Y(8)=[];[b,bint,r,rint,stats]=regress(Y,X); b,bint,stats,rcoplot(r,rint) 结果和图：b =27.0269 140.6194 bint =22.3226 31.7313 111.7842 169.4546 stats =0.9219 118.0670 0.0000结果分析：由20.9226,119.2528,P =0.0000R F ==知，2R 接近1，10.5(1,10)F F ->，0.05P <，故x 对y 的影响显著，回归模型可用。
数学建模期末考试A试的题目与答案
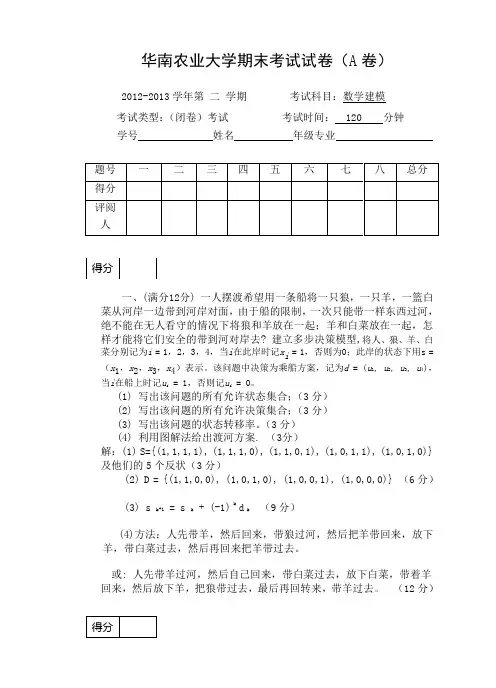
华南农业大学期末考试试卷（A 卷）2012-2013学年第 二 学期 考试科目：数学建模考试类型：（闭卷）考试 考试时间： 120 分钟学号 姓名 年级专业一、(满分12分) 一人摆渡希望用一条船将一只狼，一只羊，一篮白菜从河岸一边带到河岸对面，由于船的限制，一次只能带一样东西过河，绝不能在无人看守的情况下将狼和羊放在一起；羊和白菜放在一起，怎样才能将它们安全的带到河对岸去? 建立多步决策模型,将人、狼、羊、白菜分别记为i = 1，2，3，4，当i 在此岸时记x i = 1，否则为0；此岸的状态下用s =（x 1，x 2，x 3，x 4）表示。
该问题中决策为乘船方案，记为d = (u 1, u 2, u 3, u 4)，当i 在船上时记u i = 1，否则记u i = 0。
(1) 写出该问题的所有允许状态集合；（3分）(2) 写出该问题的所有允许决策集合；（3分）(3) 写出该问题的状态转移率。
（3分）(4) 利用图解法给出渡河方案. （3分）解：(1) S={(1,1,1,1), (1,1,1,0), (1,1,0,1), (1,0,1,1), (1,0,1,0)} 及他们的5个反状（3分）(2) D = {(1,1,0,0), (1,0,1,0), (1,0,0,1), (1,0,0,0)} （6分）(3) s k+1 = s k + (-1) k d k （9分）(4)方法：人先带羊，然后回来，带狼过河，然后把羊带回来，放下羊，带白菜过去，然后再回来把羊带过去。
或: 人先带羊过河，然后自己回来，带白菜过去，放下白菜，带着羊回来，然后放下羊，把狼带过去，最后再回转来，带羊过去。
（12分）1、 二、(满分12分) 在举重比赛中，运动员在高度和体重方面差别很大，请就下面两种假设，建立一个举重能力和体重之间关系的模型：（1） 假设肌肉的强度和其横截面的面积成比例。
6分（2） 假定体重中有一部分是与成年人的尺寸无关，请给出一个改进模型。
数学建模精讲_西南交通大学中国大学mooc课后章节答案期末考试题库2023年
数学建模精讲_西南交通大学中国大学mooc课后章节答案期末考试题库2023年1.Lingo软件是常用的优化问题的求解软件。
参考答案:正确2.0-1规划是整数规划。
参考答案:正确3.求解整数规划一定能得到最优解。
参考答案:错误4.整数规划是指规划问题中的全部变量限制为整数。
参考答案:错误5.所有决策变量均要求为整数的整数规划称为纯整数规划。
参考答案:正确6.整数规划与线性规划不同之处在于增加了整数约束。
参考答案:正确7.分枝定界法是整数规划的常见算法。
参考答案:正确8.原线性规划有最优解，当自变量限制为整数后，其整数规划也一定有最优解。
参考答案:错误9.整数规划最优解常可以按照实数最优解简单取整而获得。
参考答案:错误10.与线性规划连续的可行域不同，整数规划的可行域是离散的。
参考答案:正确11.整数规划由于限制变量是整数，增加了求解难度，但整数解是有限个，所以有时候可以采用枚举法。
参考答案:正确12.非线性规划已经有一般的适合所有问题的成熟的解法。
参考答案:错误13.非线性规划的局部最优解和全局最优解等价。
参考答案:错误14.多目标规划的目标函数多于1个。
参考答案:正确15.非线性规划是指规划模型的目标函数或者约束条件中至少有一个为非线性表达式。
参考答案:正确16.多目标规划的解法包括分枝定界法，单纯形法。
参考答案:错误17.根据地球上任意两点的经纬度就可以计算这两点间的距离。
参考答案:正确18.如果可能，把非线性规划转换为线性规划是非常好的一个思路，原因是线性规划有比较成熟的算法。
参考答案:正确19.Lingo软件求解非线性规划的结果都是全部最优解。
参考答案:错误20.求解多目标规划的线性加权和法，在确定权系数之前，一般要对目标函数值做统一量纲处理，其目的是避免出现大数吃小数、权系数失去其作用的问题。
参考答案:正确21.哥尼斯堡七桥问题由欧拉证明了是可以走通的。
参考答案:错误22.“健康中国2030”规划纲要其中一项主要指标是将我国人均预期寿命提升至79岁左右。
数学模型(专升本)期末考试答案
数学模型(专升本)期末考试答案1. (单选题) 说明某事物内部各组成部分所占比例应选____。
(本题2.0分)A、率B、构成比C、相对比D、标准差标准答案：B解析：得分： 22. (单选题) 两样本均数比较用t检验,其目的是检验( )(本题2.0分)A、两样本均数是否不同B、两总体均数是否不同C、两个总体均数是否相同D、两个样本均数是否相同标准答案：C解析：3. (单选题) 人该指标的数值,为推断这组人群该指标的总体均值μ与μ0之间的差别是否有显著性意义,若用t检验,则自由度应该是(本题2.0分)A、 5B、28C、29D、 4标准答案：C解析：4. (单选题) 正态分布曲线下,横轴上,从μ-1.96σ到μ+1.96σ的面积为(本题2.0分)A、95%B、49.5%C、99%D、97%标准答案：A解析：5. (单选题) 两样本均数间的差别的假设检验时,查t界值表的自由度为(本题2.0分)A、n-1B、(r-1)(c-1)C、n1+n2-2D、 1标准答案：C解析：6. (单选题) 最小二乘法是指各实测点到回归直线的( )(本题2.0分)A、垂直距离的平方和最小B、垂直距离最小C、纵向距离的平方和最小D、纵向距离最小标准答案：C解析：7. (单选题) 对含有两个随机变量的同一批资料,既作直线回归分析,又作直线相关分析。
令对相关系数检验的t值为tr,对回归系数检验的t值为tb,二者之间具有什么关系?( )(本题2.0分)A、tr>tbB、tr<tbC、tr= tbD、二者大小关系不能肯定标准答案：C解析：8. (单选题) 设配对资料的变量值为x1和x2,则配对资料的秩和检验( )(本题2.0分)A、分别按x1和x2从小到大编秩B、把x1和x2综合从小到大编秩C、把x1和x2综合按绝对值从小到大编秩D、把x1和x2的差数按绝对值从小到大编秩标准答案：D解析：9. (单选题) 四个样本率作比较,χ2>χ20.05,ν可认为( )(本题2.0分)A、各总体率不同或不全相同B、各总体率均不相同C、各样本率均不相同D、各样本率不同或不全相同标准答案：A解析：10. (单选题) 某学院抽样调查两个年级学生的乙型肝炎表面抗原,其中甲年级调查35人,阳性人数4人;乙年级调查40人,阳性人数8人。
数学建模期末答案
《数学建模》期末考试A卷姓名：专业：学号：学习中心：成绩：一、判断题（每题3分，共15分）1、模型具有可转移性。
------------------------------（√）2、一个原型，为了不同的目的可以有多种不同的模型。
------（√）3、一个理想的数学模型需满足模型的适用性和模型的可靠性。
---------------------------------------------（√）4、力学中把质量、长度、时间的量纲作为基本量纲。
-------（√）5、数学模型是原型的复制品。
-------------------- （×）二、不定项选择题（每题3分，共15分）1、下列说法正确的有AC 。
A、评价模型优劣的唯一标准是实践检验。
B、模型误差是可以避免的。
C、生态模型属于按模型的应用领域分的模型。
D、白箱模型意味着人们对原型的内在机理了解不清楚。
2、建模能力包括ABCD 。
A、理解实际问题的能力B、抽象分析问题的能力C、运用工具知识的能力D、试验调试的能力3、按照模型的应用领域分的模型有AE 。
A、传染病模型B、代数模型C、几何模型D、微分模型E、生态模型4、对黑箱系统一般采用的建模方法是 C 。
A、机理分析法B、几何法C、系统辩识法D、代数法5、一个理想的数学模型需满足AC 。
A、模型的适用性B、模型的可靠性C、模型的复杂性D、模型的美观性三、用框图说明数学建模的过程。
（10分）四、建模题（每题15分，共60分）1、四条腿长度相等的椅子放在起伏不平的地面上，4条腿能否同时着地？解：4条腿能同时着地（一）模型假设对椅子和地面都要作一些必要的假设：对于此题，如果不用任何假设很难证明，结果很可能是否定的。
因此对这个问题我们假设:(1)地面为连续曲面(2)长方形桌的四条腿长度相同(3)相对于地面的弯曲程度而言，方桌的腿是足够长的(4)方桌的腿只要有一点接触地面就算着地。
那么，总可以让桌子的三条腿是同时接触到地面。
福建师范大学2020年秋作业《数学建模》期末考试A卷答案
《数学建模》期末考试A卷姓名：专业：学号：学习中心：一、判断题（每题3分，共15分）1、模型具有可转移性。
------------------------------（对）2、一个原型，为了不同的目的可以有多种不同的模型。
----（对）3、一个理想的数学模型需满足模型的适用性和模型的可靠性。
-------------------------------------------（对）4、力学中把质量、长度、时间的量纲作为基本量纲。
------（对）5、数学模型是原型的复制品。
----------------- （错）二、不定项选择题（每题3分，共15分）1、下列说法正确的有AC 。
A、评价模型优劣的唯一标准是实践检验。
B、模型误差是可以避免的。
C、生态模型属于按模型的应用领域分的模型。
D、白箱模型意味着人们对原型的内在机理了解不清楚。
2、建模能力包括ABCD 。
A、理解实际问题的能力B、抽象分析问题的能力C、运用工具知识的能力D、试验调试的能力3、按照模型的应用领域分的模型有AE 。
A、传染病模型B、代数模型C、几何模型D、微分模型E、生态模型4、对黑箱系统一般采用的建模方法是 C 。
A、机理分析法B、几何法C、系统辩识法D、代数法5、一个理想的数学模型需满足AB 。
A、模型的适用性B、模型的可靠性C、模型的复杂性D、模型的美观性三、用框图说明数学建模的过程。
（10分）答：概括的说，数学模型就是一个迭代的过程，其一般建模步骤用框架图表示如下：四、建模题（每题15分，共60分）1、四条腿长度相等的椅子放在起伏不平的地面上，4条腿能否同时着地？解：4条腿能同时着地（一）模型假设对椅子和地面都要作一些必要的假设：对于此题，如果不用任何假设很难证明，结果很可能是否定的。
因此对这个问题我们假设:(1)地面为连续曲面(2)长方形桌的四条腿长度相同(3)相对于地面的弯曲程度而言，方桌的腿是足够长的(4)方桌的腿只要有一点接触地面就算着地。
2021数学建模期末试卷A及答案
2021数学建模期末试卷A及答案2021《数学建模》期末试卷A考试形式：开卷考试时间：120分钟姓名：学号：成绩： ___ 1．（10分）叙述数学建模的基本步骤，并简要说明每一步的基本要求。
2．（10分）试建立不允许缺货的生产销售存贮模型。
设生产速率为常数k，销售速率为常数r，r?k。
在每个生产周期T内，开始一段时间（0边生产边销售，后一段时间（T0?t?T?t?T0））只销售不生产，存贮量q(t)的变化如图所示。
设每次生产开工费为c1，每件产品单位时间的存贮费为c2，以总费用最小为准则确定最优周期T，并讨论r??k和r?k的情况。
3．（10分）设x(t)表示时刻t的人口，试解释阻滞增长（Logistic）模型x?dx?r(1?)x?xm?dt?x(0)?x0?中涉及的所有变量、参数，并用尽可能简洁的语言表述清楚该模型的建模思想。
4．（25分）已知8个城市v0，v1，…,v7之间有一个公路网（如图所示），每条公路为图中的边，边上的权数表示通过该公路所需的时间．（1）设你处在城市v0，那么从v0到其他各城市，应选择什么路径使所需的时间最短？（2）求出该图的一棵最小生成树。
5．（15分）求解如下非线性规划:Max z?x1?2x1?x2s.t. 0?x2?x1?2226．（20分）某种合金的主要成分使金属甲与金属乙.经试验与分析, 发现这两种金属成分所占的百分比之和x与合金的膨胀系数y之间有一定的相关关系.先测试了12次, 得数据如下表：表2 xi 37.0 37.5 38.0 38.5 39.0 39.5 40.0 yi xi yi 3.40 3.00 40.5 41.01.70 1.80 3.00 41.5 1.902.27 42.0 2.35 2.10 42.5 2.54 1.83 43.0 2.90 1.53试建立合金的膨胀系数y与两种金属成分所占的百分比之和x的模型。
7．（10分）有12个苹果，其中有一个与其它的11个不同，或者比它们轻，或者比它们重，试用没有砝码的天平称量三次，找出这个苹果，并说明它的轻重情况。
数学建模方法期末考试试卷
《数学建模方法》期末考试试卷一、某工厂要安排A 、B 、C 三种产品生产，生产这些产品均需要三种主要资源：技术服务、劳动力和行政管理。
每件产品所需资源数、资源限量以及每单位产品利润如下表。
试确定这三种产品的产量使总利润最大，建立线性规划问题的数学⎪⎩⎪⎨⎧≥≥≥≤++≤++++=0,0,06054390536..423max 321321321321x x x x x x x x x t s x x x S 三、上海红星建筑构配件厂是红星集团属下之制造建材设备的专业厂家。
其主要产品有４种，分别用代号Ａ、Ｂ、Ｃ、Ｄ表示，生产Ａ、Ｂ、Ｃ、Ｄ四种产品主要经过冲压、成形、装配和喷漆四个阶段。
根据工艺要求及成本核算，单位产品所需要现设置上述问题的决策变量如下：1234,,,x x x x 分别表示A 、B 、C 、D 型产品的日产量，则可建立线性规划模型如下：⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤+++≤+++≤+++≤++++++=0,,,300048462000552424005284480..81169max 432143214321432143214321x x x x x x x x x x x x x x x x x x x x t s x x x x z 利用LINGO8.0软件进行求解，得求解结果如下：Global optimal solution found at iteration: 4Objective value: 4450.000Variable Value Reduced CostX1 400.0000 0.000000X2 0.000000 0.5000000X3 70.00000 0.000000X4 10.00000 0.000000Row Slack or Surplus Dual Price1 4450.000 1.0000002 0.000000 2.5000003 610.0000 0.0000004 0.000000 0.50000005 0.000000 0.7500000（1）指出问题的最优解并给出原应用问题的答案；（2）写出线性规划问题的对偶线性规划问题，并指出对偶问题的最优解，解释对偶问题最优解的经济意义；（3）灵敏度分析结果如下：Ranges in which the basis is unchanged:Objective Coefficient RangesCurrent Allowable AllowableVariable Coefficient Increase DecreaseX1 9.000000 0.5000000 0.1666667X2 6.000000 0.5000000 INFINITYX3 11.00000 0.3333333 1.000000X4 8.000000 1.000000 1.000000Righthand Side RangesRow Current Allowable AllowableRHS Increase Decrease2 480.0000 20.00000 80.000003 2400.000 INFINITY 610.00004 2000.000 400.0000 20.000005 3000.000 40.00000 280.0000对灵敏度分析结果进行分析四、一个公司要分派4个推销员去4个地区推销某种产品，4个推销员在各个地区推销这种产品的预期利润（万元）如下表。
人教版八年级上册数学期末考试试卷含答案
人教版八年级上册数学期末考试试题一、单选题1．下列图形中有且只有一条对称轴的是（）A ．B ．C ．D ．2．如果分式62x -有意义，那么x 满足（）A ．2x =B ．2x ≠C ．0x =D ．0x ≠3．下列各式不能用平方差公式计算的是（）A ．（2a －3b ）（3a ＋2b ）B ．（4a 2－3bc ）（4a 2＋3bc ）C ．（3a ＋2b ）（2b －3a ）D ．（3m ＋5）（5－3m ）4．从正多边形的一个顶点可以引出5条对角线,则这个正多边形每个外角的度数为（）A ．135°B ．45°C ．60°D ．120°5．如图，在△ABC 中，F 是高AD 和BE 的交点，BC ＝6，CD ＝2，AD ＝BD ，则线段AF 的长度为（）A ．2B ．1C ．4D ．36．如图，OP 平分∠MON ，PA ⊥ON 于点A ，点Q 是射线OM 上的一个动点，若PA=2，则PQ 的最小值为（）A ．1B ．2C ．3D ．47．如图，在△ABC 中，D 是CA 延长线上一点，∠B=40°，∠BAD=76°，则∠C 的度数为（）A ．36︒B ．116︒C ．26︒D ．104︒8．已知：如图，在△ABC 中，边AB 的垂直平分线分别交BC 、AB 于点G 、D ，若△AGC 的周长为31cm ，AB=20cm ，则△ABC 的周长为（）A ．31cmB ．41cmC ．51cmD ．61cm二、填空题9．数据0.00000008m ，用科学记数法表示为______________m10．若代数式02(2)(2)m m -++-有意义，则m 的取值范围是___________.11．因式分解：22123xy -=__________．12．若23x =，25y =，则2x y +=_____．13．如图，在△ABC 中，点E 、F 分别是AB 、AC 边上的点，EF ∥BC ，点D 在BC 边上，连接DE 、DF 请你添加一个条件___________________，使△BED ≌△FDE14．等腰三角形一腰上的高与另一腰的夹角的度数为20°，则顶角的度数是__________．15．如图，在Rt △ABC 中，∠C=90°，∠B=30°，边AB 的垂直平分线DE 交AB 于点E ，交BC 于点D ，CD=3，则BC 的长为___________16．当x_________时，分式235x -有意义.17．甲、乙两个搬运工搬运某种货物．已知乙比甲每小时多搬运600kg ，甲搬运5000kg 所用的时间与乙搬运8000kg 所用的时间相等．设甲每小时搬运xkg 货物，则可列方程为___．18．如图，过边长为1的等边ABC ∆的边AB 上一点P ，作PE AC ⊥于E ，Q 为BC 延长线上一点，当PA CQ =时，连接PQ 交AC 边于D ，则DE 的长为______.三、解答题19．解方程：1x -53x +=020．先化简，再求值：()()2(23)22x y x y x y +-+-，其中13x =，12y =-．21．如图，在平面直角坐标系中（1）请在图中作出△ABC 关于直线m 的轴对称图形△A 1B 1C 1（2）坐标系中有一点M(-3，3)，点M 关于直线m 的对称点为点N ，点N 关于直线n 的对称点为点E ，写出点N 的坐标；点E 的坐标．22．已知：如图，点E 、A 、C 在同一直线上，AB ∥CD ，AB ＝CE ，AC ＝CD求证：∠B ＝∠E23．如图，BD是△ABC的角平分线,AE丄BD交BD的'延长线于点E,∠ABC=72°，∠C：∠ADB=2：3,求∠BAC和∠DAE的度数.24．如图，在△ABC中，已知AB=AC，AB的垂直平分线交AB于点N，交AC于点M，连接MB（1）若∠ABC=65°，则∠NMA的度数为（2）若AB=10cm，△MBC的周长是18cm①求BC的长度②若点P为直线MN上一点，则△PBC周长的最小值为cm25．问题：分解因式（a+b）2-2（a+b）+1答：将“a+b”看成整体，设M=a+b，原式=M2-2M+1=（M-1）2，将M还原，得原式=（a+b-1）2上述解题用到的是“整体思想”，这是数学解题中常用的一种思想方法．请你仿照上面的方法解答下列问题：（1）因式分解：（2a+b）2-9a2=（2）求证：（n+1）（n+2）（n 2+3n ）+1的值一定是某一个正整数的平方（n 为正整数）26．如图，△ABC 是等边三角形，D 是边AC 的中点，EC ⊥BC 与点C ，连接BD 、DE 、AE 且CE=BD ，求证：△ADE 为等边三角形27．水果店的老板用2400元购进一批仙桃，很快售完；老板又用3700元购进第二批仙桃，所购件数是第一批的32倍，但进价比第一批每件多了5元．（1）第一批仙桃每件进价是多少元？（2）老板以每件225元的价格销售第二批仙桃，售出80%后，为了尽快售完，剩下的决定打折促销．要使得第二批仙桃的销售利润不少于440元，剩余的仙桃每件售价至少打几折？（利润＝售价﹣进价）28．如图①，∠BAD=90°，AB=AD ，过点B 作BC ⊥AC 于点C ，过点D 作DE ⊥CA 的延长线点E ，由∠1+∠2=∠D+∠2=90°，得∠1=∠D ，又∠ACB=∠AED=90°，AB=AD ，得△ABC ≌△DAE 进而得到AC=DE ，BC=AE ，我们把这个数学模型称为“K 字”模型或“一线三等角”模型．请应用上述“一线三等角”模型，解决下列问题：（1）如图②，∠BAD=∠CAE=90°，AB=AD ，AC=AE ，连接BC 、DE ，且BC ⊥AH 于点H ，DE 与直线AH 交于点G ，求证：点G 是DE 的中点．（2）如图③，在平面直角坐标系中，点A 为平面内任意一点，点B 的坐标为（4，1），若△AOB 是以OB 为斜边的等腰直角三角形，请直接写出点A 的坐标．参考答案1．D【分析】根据轴对称图形的概念求解，如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．【详解】解：A．不是轴对称图形，故此选项不合题意；B．有4条对称轴，故此选项不合题意；C．有3条对称轴，故此选项不合题意；D．有1条对称轴，故此选项符合题意．故选：D．2．B【分析】根据分式有意义的条件：分母不为零，得到不等式解不等式即可.【详解】要使分式62x-有意义，则x-2≠0，得到2x≠，故选B3．A【分析】利用平方差公式的结构特征判断即可．【详解】解：A.(2a－3b)(3a＋2b)不符合平方差公式的特点，故不能用平方差公式计算；B.(4a2－3bc)(4a2＋3bc)=16a4-9b2c2，故能用平方差公式计算；C.(3a＋2b)(2b－3a)=4b2-9a2，故能用平方差公式计算；D.(3m＋5)(5－3m)=25-9m2，故能用平方差公式计算；故选：A．4．B【分析】先由n边形从一个顶点出发可引出（n-3）条对角线，可求出多边形的边数，再根据正多边形的每个外角相等且外角和为360°．【详解】解：∵经过多边形的一个顶点有5条对角线，∴这个多边形有5+3=8条边，∴此正多边形的每个外角度数为360°÷8=45°，故选B5．A【分析】先求BD，AD的长，再证△BFD≌△ADC，即可得到FD的长，即可求解.【详解】∵BC＝6，CD＝2，∴BD=BC-CD ＝6-2=4，∴AD ＝BD=4∵AD 和BE 是三角形的高∴∠ADB=∠ADC=∠BEC=90°∴∠DAC+∠C=90°，∠EBC+∠C=90°∴∠DAC=∠EBC在△BFD 和△ADC 中DAC EBC BD AD ADB ADC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BFD ≌△ADC （ASA ）∴FD=DC=2∴AF=AD-FD=2故选A6．B【分析】根据题意点Q 是射线OM 上的一个动点，要求PQ 的最小值，需要找出满足题意的点Q ，根据直线外一点与直线上各点连接的所有线段中，垂线段最短，所以我们过点P 作PQ 垂直OM ，此时的PQ 最短，然后根据角平分线上的点到角两边的距离相等可得PA=PQ ，利用已知的PA 的值即可求出PQ 的最小值．【详解】解：过点P 作PQ ⊥OM ，垂足为Q ，则PQ 为最短距离，∵OP 平分∠MON ，PA ⊥ON ，PQ ⊥OM ，∴PA=PQ=2，故选：B ．7．A【详解】解：∵∠BAD 是△ABC 的一个外角，∴∠BAD=∠B+∠C ，∴∠C=∠BAD-∠B=76°-40°=36°.故选A.8．C【分析】已知△AGC 的周长，因为GB 等于AG ，所以△ABC 的周长等于AC+CG+GB+AB ，即等于△AGC 的周长+AB.【详解】∵DG 是AB 边的垂直平分线，∴GA=GB ，△AGC 的周长=AG+AC+CG=AC+BC=31cm ，又AB=20cm ，∴△ABC 的周长=AC+BC+AB=51cm ，故选C.【点睛】本题考查线段的垂直平分线的性质.把求△ABC 的周长进行转化是解题的关键.9．8810-⨯【分析】将原数写成10n a ⨯的形式，a 是大于等于1小于10的数．【详解】解：80.00000008810-=⨯．故答案是：8810-⨯．【点睛】本题考查科学记数法，解题的关键是掌握科学记数法的表示方法．10．2m ≠±【分析】根据零指数幂的法则和负整数指数幂的法则可得关于m 的不等式组，解不等式组即可得出答案.【详解】解：根据题意，得：20m +≠且20m -≠，解得：2m ≠±.故答案为2m ≠±.【点睛】本题考查了零指数幂和负整数指数幂的知识，属于基础题型，熟知运用零指数幂和负整数指数幂的运算法则进行计算的前提条件是解此题的关键.11．3(2x+y)(2x-y)【分析】先提取公因式，然后根据平方差公式因式分解即可.【详解】解：原式=3（4x 2-y 2）=3（2x+y ）（2x-y ）.【点睛】因式分解是本题的考点，熟练掌握因式分解的方法是解题的关键，本题用到了提取公因式法和公式法.12．15【分析】由23x=，25y =，根据同底数幂的乘法可得222x y x y +=⋅，继而可求得答案．【详解】∵23x=，25y =，∴2223515x y x y +=⋅=⨯=，故答案为15.【点睛】本题考查了同底数幂的乘法，熟练掌握运算法则是解题的关键.本题中要注意掌握公式的逆运算．13．BD=FE （答案不唯一）；【分析】根据平行四边形的判定和性质、全等三角形的判定定理即可解答．【详解】当BD=FE 时，△BED ≌△FDE ，∵EF ∥BC ，当BD=FE 时，∴四边形BEFD 是平行四边形，∴∠B ＝∠DFE ，BE ＝FD∵BD ＝FE∴△BED ≌△FDE ，故答案为：BD ＝FE ．【点睛】本题考查了全等三角形的判定，利用了平行四边形的判定及其性质，全等三角形的判定，利用平行四边形的性质得出三角形全等的条件是解题关键．14．110°或70°【详解】解：分情况讨论：当等腰三角形的顶角是钝角时，腰上的高在外部．根据三角形的一个外角等于与它不相邻的两个内角的和，即可求得顶角是90°+20°=110°；当等腰三角形的顶角是锐角时，腰上的高在其内部，故顶角是90°﹣20°=70°．故答案为110°或70°．考点：1．等腰三角形的性质；2．分类讨论．15．9【详解】∵DE是AB的垂直平分线，∴AD=BD，∴∠DAE=∠B=30°，∴∠ADC＝∠DAE＋∠B=60°，∴∠CAD=30°，∴AD=2DC=6，即BD=6，∴BC=9．【点睛】本题主要考查的知识点有线段垂直平分线的性质、直角三角形30°角所对的直角边等于斜边的一半的性质，熟练运用各性质是解题的关键．16．5 3≠【分析】根据分母不等于0列式求解即可.【详解】由题意得3x-5≠0，x5 3≠.故答案为5 3≠.【点睛】本题考查了分式有意义的条件，熟知分母不为零时分式有意义是解答本题的关键.17．5000x＝8000600+x【分析】设甲每小时搬运x千克，则乙每小时搬运（x+600）千克，根据甲搬运5000kg所用时间与乙搬运8000kg所用时间相等建立方程求出其解就可以得出结论．【详解】解：设甲每小时搬运x千克，则乙每小时搬运（x+600）千克，由题意得：5000x＝8000600+x．故答案是：5000x ＝8000600+x ．【点睛】本题考查了由实际问题抽象出分式方程，根据题意找到等量关系是关键．18．12【分析】过P 作PF ∥BC 交AC 于F ，得出等边三角形APF ，推出AP=PF=QC ，根据等腰三角形性质求出EF=AE ，证△PFD ≌△QCD ，推出FD=CD ，推出DE=12AC 即可．【详解】解：过P 作PF ∥BC 交AC 于F，∵PF ∥BC ，△ABC 是等边三角形，∴∠PFD=∠QCD ，∠APF=∠B=60°，∠AFP=∠ACB=60°，∠A=60°，∴△APF 是等边三角形，∴AP=PF=AF ，∵PE ⊥AC ，∴AE=EF ，∵AP=PF ，AP=CQ ，∴PF=CQ ，在△PFD 和△QCD 中PFD QCDPDF CDQ PF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△PFD ≌△QCD ，∴FD=CD ，∵AE=EF ，∴EF+FD=AE+CD ，∴AE+CD=DE=12AC ，∵AC=1，∴DE=12；故答案为：12.【点睛】本题综合考查了全等三角形的性质和判定，等边三角形的性质和判定，等腰三角形的性质，平行线的性质等知识点的应用，能综合运用性质进行推理是解此题的关键，通过做此题培养了学生分析问题和解决问题的能力，题型较好，难度适中．19．x=34【分析】方程两边同乘以x(x+3)，得到整式方程，解整式方程，把得到的根代入最简公分母检验即可．【详解】解：x ＋3－5x=04x=3x=34检验：当x=34时，x （x+3）≠0，故x=34是原方程的根．【点睛】本题考查的是分式方程的解法，解分式方程的步骤：①去分母；②求出整式方程的解；③检验；④得出结论．20．21210xy y +，12【分析】先利用完全平方公式与平方差公式计算乘法，再合并同类项，最后代入计算即可．【详解】()()2(23)22x y x y x y +-+-()222241294x xy y x y =++--22222412941210x xy y x y xy y =++-+=+，当13x =，12y =-时，原式21111210322⎛⎫⎛⎫=⨯⨯-+⨯- ⎪ ⎪⎝⎭⎝⎭522=-+12=．【点睛】本题主要考查了整式的混合运算，涉及了完全平方公式，平方差公式，解题的关键是熟练掌握整式混合运算的运算顺序和运算法则．21．（1）见解析；（2）（1，3），（1，1）．【分析】（1）利用网格结构分别找出点A 、B 、C 关于直线m 的对称点，然后顺次连接即可．（2）利用网格结构找出点M 关于直线m 的对称点N ，再找出点N 关于直线n 的对称点E ，写出其坐标即可．【详解】（1）如图即为ABC 关于直线m 的轴对称图形111A B C △．（2）如图，即可知点M 关于直线m 的对称点N 的坐标是(1，3)；点N 关于直线n 的对称点E 的坐标是(1，1)．故答案为：(1，3)；(1，1)．【点睛】本题考查画轴对称图形和轴对称-坐标的变化．了解轴对称的性质是解答本题的关键．22．见解析【分析】根据平行线的性质可得∠BAC=∠ECD ，再由条件AB=CE ，AC=CD 可证出△BAC 和△ECD 全等，再根据全等三角形对应角相等即可求证结论．【详解】证明：∵AB ∥CD∴∠BAC=∠ECD∵在△ABC 和△CED 中，AB CE BAC ECD AC CD =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△CED （SAS ）∴∠B=∠E【点睛】本题考查了平行线的性质，全等三角形的判定和性质，解题的关键是证明△ABC ≌△CED ．23．∠BAC =36°，∠DAE=18°.【分析】先根据BD 是△ABC 的角平分线，∠ABC =72°求出∠EBC=36°，由∠C ：∠ADB =2：3可设∠C=2x ，则∠ADB=3x,根据在△BCD 中的外角定理列出方程即可求解x,再根据等腰三角形的及垂直的性质求解.【详解】∵BD 是△ABC 的角平分线，∠ABC =72°∴∠EBC=36°，∵∠C ：∠ADB =2：3可设∠C=2x ，则∠ADB=3x,在△BCD 中∠ADB=∠EBC+∠C即3x=36°+2x解得x=36°，∴∠C=72°，∠ADB=108°，故∠BAC=180°-∠C-∠ABC=36°，在△DAE 中，AE 丄BD∴∠DAE=∠ADB-90°=18°.【点睛】此题主要考查角度的求解，解题的关键是熟知三角形的外角定理.24．（1）40°；（2）①8cm ；②18【分析】（1）先根据等腰三角形的性质求出∠A=50°，根据垂直平分线的定义得到∠ANM ＝90°，然后根据直角三角形两锐角互余求解即可；（2）①根据垂直平分线的性质得AM=BM ，△MBC 的周长是18cm ，AC=AB=10cm ，即可求BC 的长度；②当点P 与点M 重合时，△PBC 周长的最小，即为△MBC 的周长．【详解】解：（1）∵AB=AC ，∴∠ABC=∠C∵∠ABC=65°，∴∠C=65°，∴∠A=50°，∵MN 是AB 的垂直平分线，∴∠ANM ＝90°，∴∠NMA=90°-50°=40°；（2）①∵MN 是线段AB 的垂直平分线，∴AM=MB ．∵△MBC 的周长是18cm ，AB=10cm ，∴BM+MC+BC=AM+MC+BC=AC+BC=AB+BC=18cm ，∴BC=18-AB=18-10=8cm ；②∵MN 是线段AB 的垂直平分线，∴点A 和点B 关于直线MN 对称，∴当点P 与点M 重合时，△PBC 周长的值最小，∴△PBC 的周长的最小值为18cm ．【点睛】本题考查了等腰三角形的性质，线段垂直平分线的性质，轴对称-最短路线问题，解决本题的关键是掌握线段垂直平分线的性质和等腰三角形的性质．25．（1）()()5+a b b a -；（2）见解析【分析】（1）根据平方差公式分解因式即可求解；（2）先根据多项式乘以多项式进行计算，再根据完全平方公式分解即可求解．【详解】解：（1）原式()()22=2+3a b a -()()=2+32+3a b a a b a +-()()=5+a b b a -证明（2）（n+1）（n+2）（n 2+3n ）+1=（n 2+3n+2）（n 2+3n ）+1=（n 2+3n ）2+2（n 2+3n ）+1=（n 2+3n+1）2故当n 为正整数时，（n+1）（n+2）（n 2+3n ）+1的值一定是某一个正整数的平方【点睛】本题考查因式分解，解题的关键是熟练掌握平方差公式、完全平方公式的应用．26．证明见解析【分析】利用△ABC 是等边三角形，D 为边AC 的中点，求得∠ADB=90°，再用SAS 证明△CBD ≌△ACE ，推出AE=CD=AD ，∠AEC=∠BDC=90°，根据直角三角形斜边上中线性质求出DE=AD ，即可证明．【详解】证明：∵△ABC 是等边三角形，D 是边AC 的中点，∴AD=DC ，BC=CA ，BD ⊥AC ，∴∠BDC=90°，即∠DBC+∠DCB=90°，∵EC ⊥BC ，∴∠BCE=90°，即∠ACE+∠BCD=90°，∴∠ACE=∠DBC ，在△CBD 和△ACE 中，BC CA DBC ACE BD CE =⎧⎪∠=∠⎨⎪=⎩∴△CBD ≅△ACE （SAS ）∴CD=AE ，∴∠AEC=∠CDB=90°∵D 为AC 的中点∴AD=DE ，AD=DC ，∴AD=AE=DE ，即△ADE 为等边三角形．【点睛】本题主要考查等边三角形的性质和判定，全等三角形的性质和判定，直角三角形斜边上的中线等．解答此题的关键是先证明△CBD ≌△ACE ，然后再利用三边相等证明此三角形是等边三角形．27．（1）进价为180元；（2）至少打6折．【分析】（1）根据题意，列出等式24003370025x x ⨯=+，解等式，再验证即可得到答案；（2）设剩余的仙桃每件售价打y 折，由题意得到不等式，再解不等式，即可得到答案.【详解】解：（1）设第一批仙桃每件进价x 元，则24003370025x x ⨯=+，解得180x =．经检验，180x =是原方程的根．答：第一批仙桃每件进价为180元；（2）设剩余的仙桃每件售价打y 折．则：3700370022580%225(180%)0.1370044018051805y ⨯⨯+⨯⨯-⨯-≥++，解得6y ≥．答：剩余的仙桃每件售价至少打6折．【点睛】本题考查分式方程的应用和一元一次不等式的应用，解题的关键是熟练掌握分式方程的应用和一元一次不等式的应用.28．（1）见解析；（2）A(32，52)或(52，-32)．【分析】（1）过点D 作DM ⊥AM 交AG 于点M ，过点E 作EN ⊥AG 于点N ．根据“K 字模型”即可证明AH=DM 和AH=EN ，即EN=DM ，再根据全等三角形的判定和性质即可证明DG=EG ，即点G 是DE 的中点．（2）分情况讨论①当A 点在OB 的上方时，作AC 垂直于y 轴，BE 垂直于x 轴，CA 和EB 的延长线交于点D ．根据“K 字模型”即可证明AC BD OC AD DE ===，，再利用B 点坐标即可求出A 点坐标．②当A 点在OB 的下方时，作AP 垂直于y 轴，BM 垂直于x 轴，PA 和BM 的延长线交于点Q ．同理即能求出A 点坐标．【详解】（1）如图，过点D 作DM ⊥AM 交AG 于点M ，过点E 作EN ⊥AG 于点N ，则∠DMA=90°，∠ENG=90°．∵∠BHA=90，∴∠2+∠B=90°．∵∠BAD=90°，∴∠1+∠2=90°．∴∠B=∠1．在△ABH 和△DAM 中1BHA AMD B AB DA ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABH ≅△DAM （AAS ），∴AH=DM ．同理△ACH ≅△EAN （AAS ），∴AH=EN ．∴EN=DM ．在△DMG 和△ENG 中MGD NGE DMG ENG DM EN ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△DMG ≅△ENG （AAS ）．∴DG=EG ．∴点G 是DE的中点．（2）根据题意可知有两种情况，A 点分别在OB 的上方和下方．①当A 点在OB 的上方时，如图，作AC 垂直于y 轴，BE 垂直于x 轴，CA 和EB 的延长线交于点D ．利用“K 字模型”可知ACO BDA ≅ ，∴AC BD OC AD DE ===，，设AC x =，则BD x =，∵1DE BD BE x =+=+，∴1OC AD DE x ===+，又∵4CD AD AC =+=，即14x x ++=，解得32x =，∴32AC =，35122DE =+=．即点A 坐标为(32，52)．②当A点在OB的下方时，如图，作AP垂直于y轴，BM垂直于x轴，PA和BM的延长线交于点Q．根据①同理可得：52AP=，32MQ=．即点A坐标为(52，32-)．。
数学建模考试
这一讲，我们按教学大纲与考核要求对所学知识进行全面复习和总结，并就考核要求进行必要的说明。
一、基本内容与基本要求我们按文字教材内容顺序总结如下。
第一讲数学建模与数学建模竞赛（一）知识点：1．数学建模的概念、特点和作用。
2．建模基本过程：问题分析、合理的简化假设、模型的建立、模型的求解、模型的分析（含检验、修改与推广应用）．3．常用建模方法：机理分析法和数据分析法，具体地有利用相关学科的有关定律建模、利用类比法、图示法建模、利用平衡原理建模、基于测试数据的经验公式建模。
4．某些简单例子：椅子放稳问题；相逢地点、时间问题（二）要求1．了解数学模型与数学建模的含义，理解数学模型的作用与特点。
2．掌握建模基本过程，会对实际问题进行问题分析，善于做出合理的简化假设。
3．熟练掌握建模常用方法，会使用相关定律、类比方法、平衡原理以及数据分析法对比较简单的实际问题进行建模与分析。
4．会用已有知识处理一些简单的实际问题。
第二讲初等模型（一）知识点雨中行走问题、动物的身长与体重、船艇会合问题、崖高估算、代表名额的分配与森林救火模型的建立过程和所使用的方法。
（二）要求进一步理解基本建模过程，掌握平衡原理法、类比法、图示法，理解问题分析、合理简化假设的内涵和数学模型的作用与特点。
第三讲微分方程模型（一）知识点人口增长模型（Malthus模型与Logistic模型）、药物在人体内的分布、单种群增长问题与多物种相互作用问题等数学模型的建立过程与所使用的方法（二）要求进一步理解建模基本方法与基本建模过程，重点掌握平衡原理在建模中的用法，理解人口增长模型、种群的相互关系模型的建立原理与结论，会建立较为简单的相关实际问题的数学模型，会用稳定性理论的结论解决模型求解、分析中遇到的问题。
第四讲线性代数与差分方程模型（一）知识点状态转移问题、减肥问题、差分形式的阻滞增长模型。
（二）要求掌握状态转移问题的思想方法及对人口及种群模型的应用与改进的建模原理、分析与求解方法，建立离散问题或连续问题的差分模型。
2023届石家庄市第四十中学数学高一上期末考试试题含解析
所以 ，所以 ，所以 是一条对称轴
故选C
2、C
【解析】如下图所示, 三条直线平行, 与 异面,而 与 异面, 与 相交,故选C.
3、D
【解析】根据角度制与弧度制的关系求解.
【详解】因为 ，
所以 .
故选：D.
4、D
【解析】先逐个求解所有5个三角形的面积，再根据要求计算概率.
【详解】如图所示， ， ， ， ， 的面积分别为 ， ，
【方法点睛】本题主要考查函数的奇偶性，属于中档题.已知函数的奇偶性求参数，主要方法有两个，一是利用：（1）奇函数由 恒成立求解，（2）偶函数由 恒成立求解；二是利用特殊值：奇函数一般由 求解，偶函数一般由 求解，用特殊法求解参数后，一定要注意验证奇偶性
三、解答题：本大题共5小题，共70分。解答时应写出文字说明、证明过程或演算步骤。
C. D.1和
7．设a，b，c均为正数，且 ， ， ，则a，b，c的大小关系是（）
A. B.
C. D.
8．我国东汉数学家赵爽在《周髀算经》中利用一副“弦图”给出了勾股定理的证明，后人称其为“赵爽弦图”，它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形，如图所示，在“赵爽弦图”中，若 ， ， ，则 （）
13．公元前6世纪，古希腊的毕达哥拉斯学派通过研究正五边形和正十边形的作图，发现了黄金分割值约为0.618，这一数值也可以表示为 .若 ，则 _________.
14．某时钟的秒针端点 到中心点 的距离为6cm，秒针均匀地绕点 旋转，当时间 时，点 与钟面上标12的点 重合，将 ， 两点的距离 表示成 的函数，则 _______，其中
15．在空间直角坐标系中，一点到三个坐标轴的距离都是1，则该点到原点的距离是________.
最新数学建模(数学模型)期末考试题(试卷)及答案详解(附答案)
数学建模（数学模型）期末考试卷及答案详解第一部分 基本理论和应用1、计算题(满分10分)设电路供电网内有10000盏灯，夜间每一盏灯开着的概率为0.7，假设各灯的开关是相互独立的，利用中心极限定理计算同时开着的灯数在6900与7100之间的概率.2、计算题（满分10分）设某种电子元件的使用寿命服从正态分布) ,(2σμN ，现随机抽取了10个元件进行检测， 得到样本均值(h)1500=x ，样本标准差(h)14=S . 求总体均值μ的置信概率为99％的置信区间3、计算题（满分10分）从正态总体)6 ,4.3(~2N X 中抽取容量为n 的样本，如果要求样本均值位于区间 (1.4，5.4) 内的概率不小于0.95，问样本容量n 至少应取多大？4、计算题（满分10分） 设总体X 的概率密度为：⎩⎨⎧<<+=其他，,0,10,)1();(x x x f θθθ )1(->θn X X X ,,,21 是来自总体X 的简单随机样本，求参数θ的矩估计量和极大似然估计量.5．（15分）设总体X 服从区间[0，θ]上的均匀分布，θ＞0未知，12,,,n X X X 是来自X的样本,（1）求θ的矩估计和极大似然估计；（2）上述两个估计量是否为无偏估计量，若不是请修正为无偏估计量；（3）试问（2）中的两个无偏估计量哪一个更有效？6. （15分）设),(~2σμN X ，n X X X ,,,21 是取自总体的简单随机样本，X 为样本均值，2nS 为样本二阶中心矩，2S 为样本方差，问下列统计量：（1）22σnnS ，（2）1/--n S X n μ，（3）212)(σμ∑=-ni iX各服从什么分布？7. （10分）一个小班有8位学生,其中有5人能正确回答老师的一个问题.老师随意地逐个请学生回答,直到得到正确的回答为止,求在得到正确的回答以前不能正确回答问题的学生个数的概率分布.8. （10分）设某人有100位朋友都会向他发送电子邮件,在一天中每位朋友向他发出电子邮件的概率都是0.04,问一天中他至少收到4位朋友的电子邮件的概率是多少?试用二项分布公式和泊松近似律分别计算.9. （10分）某商品的每包重量2~(200,)X N σ.若要求{195205}0.98P X <<≥,则需要把σ控制在什么范围内.10. （15分）设系统L 由两个相互独立的子系统12,L L 联接而成,联接的方式分别为串联,并联和备用(当系统1L 损坏时,系统2L 开始工作),如图7.1所示.1L 和2L 的寿命为X 和Y ,分别有密度(0,)()()x X p x e I x αα-+∞=和(0,)()()y Y p y e I y ββ-+∞=,其中0,0αβ>>且αβ≠.请就这三种联接方式分别写出系统L 的寿命Z 的密度.答案第一部分 基本理论和应用 1、计算题(满分10分)设电路供电网内有10000盏灯，夜间每一盏灯开着的概率为0.7，假设各灯的开关是相互独立的，利用中心极限定理计算同时开着的灯数在6900与7100之间的概率. 解：设同时开着的灯数为X ，(10000,0.7)Xb ……………2分(0,1)N （近似） ……………3分 {69007100}210.971P X ≤≤=Φ-= …………5分 2、计算题（满分10分）设某种电子元件的使用寿命服从正态分布) ,(2σμN ，现随机抽取了10个元件进行检测，得到样本均值(h)1500=x ，样本标准差(h)14=S . 求总体均值μ的置信概率为99％的置信区间. 解： T =(1)X t n - 0.005{(1)}0.99P T t n <-= ………4分0.0050.005{(1)(1)}0.99P X n X X n -<<+-= ………………4分 所求为（1485.61，1514.39） …………2分3、计算题（满分10分）从正态总体)6 ,4.3(~2N X 中抽取容量为n 的样本，如果要求样本均值位于区间 (1.4，5.4) 内的概率不小于0.95，问样本容量n 至少应取多大？ 解：(0,1)X N ………………3分{1.4 5.4}21P X P <<=<=Φ- ……………4分解210.95Φ-≥ 得34.6n ≥ n 至少取35 ……………3分4、计算题（满分10分） 设总体X 的概率密度为：⎩⎨⎧<<+=其他，,0,10,)1();(x x x f θθθ )1(->θn X X X ,,,21 是来自总体X 的简单随机样本，求参数θ的矩估计量和极大似然估计量.解： 1101()(2E X dx θθθθ++==+⎰+1)x ……………3分 解12X θθ+=+，得θ的矩估计量为211X X -- ……………2分 1()1()ni i L x θθθ=+∏n＝（） 1ln ln 1ln nii L n x θθ==+∑（）+ ……………2分令1ln ln 01ni i d L nx d θθ==+=+∑ 得θ的极大似然估计量为11ln nii nX=--∑ …………3分5．（15分）设总体X 服从区间[0，θ]上的均匀分布，θ＞0未知，12,,,n X X X 是来自X的样本,（1）求θ的矩估计和极大似然估计；（2）上述两个估计量是否为无偏估计量，若不是请修正为无偏估计量；（3）试问（2）中的两个无偏估计量哪一个更有效？ 解：（1）2EX θ=，令2X θ=，得θ的矩估计量1ˆ2X θ=； ……………5分 似然函数为：()12121,0,,,(,,,;)0n n n x x x L x x x θθθ⎧<<⎪=⎨⎪⎩，其它其为θ的单调递减函数，因此θ的极大似然估计为{}212()ˆmax ,,,n n X X X X θ==。
(完整版)数学建模期末考试题
班级：通工13**学号：0313****姓名：***成绩：西安邮电大学理学院2014年12月3日一、解释下列词语，并举例说明(每小题满分5分，共15分)1．模型答:为了一定的目的，人们对原型的一个抽象。
通过抽象和化简，使用数学语言，对实际问题的一个近似描述，以便于人们更深刻的认识所研究的对象。
举例：牛顿定律。
假设：(1)物体为质点，忽略物体的大小和形状。
(2)没有阻力、摩擦力及其他外力。
令x （t ）表示在t 时刻物体的位置，则F =ma =m d 2x dt 22．数学模型答:数学模型是架于数学与实际问题之间的桥梁，在数学发展的进程中无时无刻不留下数学模型的印记。
它包括三大特征：1.实践性：有实际背景，有针对性，接受实践的检验。
2.应用性：注意实际问题的要求。
强调模型的实用价值。
3.综合性：数学知识的综合，模型的综合。
举例：管道包扎问题：用带子包扎管道，使带子全部包住管道，且用料最省。
假设：(1)直圆管，粗细一致。
(2)带子无弹性等宽。
(3)带宽小于圆管截面周长。
(4)包扎时不剪断带子且不重叠。
设W 为带宽，C 为截面周长，L 为管长，M 为带长。
则M=+LC W C 2‒W 23．抽象模型答：通过人们对原型的反复认识，将获取的知识以经验的形式直接存储在大脑中的模型称之谓抽象模型。
举例：如汽车司机对方向盘的操作。
二、简答题（每小题满分8分，共24分）1．模型的分类答：（1） 按研究方法和对象的数学特征分：初等模型、几何模型、优化模型、微分方程模型、图论模型、逻辑模型、稳定性模型、扩展模型等。
（2） 按研究对象的实际领域（或所属学科）分：人口模型、交通模型、环境模型、生态模型、生理模型、城镇规划模型、水资源模型、污染模型、经济模型、社会模型等。
（3） 按是否考虑随机因素分:确定性模型、随机性模型。
（4） 按是否考虑模型的变化分：静态模型、动态模型。
（5） 按应用的离散方法或连续方法分：离散模型、连续模型。
【2017年整理】数学建模试题与答案
【2017年整理】数学建模试题与答案华南农业大学期末考试试卷(A卷)2009学年第二学期考试科目: 数学模型考试类型:(闭卷) 考试时间: 120分钟学号姓名年级专业题号 1 2 3 4 5 6 7 8 9 总分得分评阅人1、 (13分)设已知某正方形板材边长20cm，现将之加工出半径为1cm的得分圆盘，请对下面给出的两种排列方法，写出能加工出的尽可能多的圆盘数。
(1) 排列1:圆盘中心按正方形排列(如右图)的尽可能多的圆盘数。
(4分)2020，,100 解:圆盘总数: 22排列2:圆盘中心按六角形排列(如右图)的尽可能多的圆盘数。
(4分)202,，，解:行数: ，,111,,3，，2011,圆盘总数: 11105，，,22(2) 设计出不同于(1)(2)的方案，且加工出的圆盘更多。
(5分)解:前三行正方形，后八行六角形，圆盘总数为106得分 2、 (10分)在举重比赛中，运动员在高度和体重方面差别很大，请就下面两种假设，建立一个举重能力和体重之间关系的模型:(1) 假设肌肉的强度和其横截面的面积成比例。
5分(2) 假定体重中有一部分是与成年人的尺寸无关，请给出一个改进模型。
5分解:设体重w(千克)与举重成绩y (千克)(1) 由于肌肉强度(I)与其横截面积(S)成比例，所以 y I S2 设h为个人身高，又横截面积正比于身高的平方，则S , h32 再体重正比于身高的三次方，则w , h 3ykw, 故举重能力和体重之间关系的模型为:(2) 体重中与成年人尺寸无关的重量为a, 则一个最粗略的模型为 2 3ykwa,,(),更好的模型: ykwa,,()得分3、 (10分)在超币购物时你压意到大包发商品比小包装面品便宜这种现象1了吗,比如洁银牙膏50g装的每支1.50元，120g装的每支3.00元，二者单位重量的价格比是1.2:1，试用比例方法构造模型解释这个现象。
(1)请写出商品价恪c与商品重量w的关系，其中价格由生产成本、包装成本和其它成本等决定，这些成本中有的与重量w成正比，有的与表面积成正比，还有与w无关的因素。
2023届四川省绵阳市绵阳中学资阳育才学校数学高一上期末学业水平测试试题含解析
C. D.
10．如果 ，那么下列不等式中，一定成立的是（）
A. B.
C. D.
二、填空题：本大题共6小题，每小题5分，共30分。
11．已知 ， ，则 的值为
12．若坐标原点在圆 的外部，则实数m的取值范围是___
13．已知函数 ， ，则它的单调递增区间为______
14．已知函数 的图象过原点，且无限接近直线 ，但又不与该直线相交，则 ______
考点：几何体的体积
4、A
【解析】根据三角函数定义求解即可.
【详解】角 的终边经过点 ，即 ，则 .
故选：A.
5、A
【解析】对集合B中的 分类讨论分析，再根据集合间的关系判断即可
【详解】当 时， ，
当 时， ，
当 时， ，
所以 ，或 ，或
因为 ，
所以 .
故选：A
6、D
【解析】作出函数 的图像，结合图像即可得出结论.
故选：D.
二、填空题：本大题共6小题，每小题5分，共30分。
11、3
【解析】 ，故答案为3.
12、
【解析】方程 表示圆，得 ，根据点在圆外，得不等式 ，解不等式可得结果.
【详解】圆 的标准方程为 ，则 ，
若坐标原点在圆 的外部，则 ，解得 ，则实数m的取值范围是 ，
故答案为：
【点睛】本题考查圆的一般方程，考查点与圆的位置关系的应用，属于简单题.
【详解】由题意分析得：
取函数 与 中的较小的值，
则 ，如图所示（实线部分）：
由图可知：函数 的值域为： .
故选：D.
【点睛】本题主要考查了指数函数的性质和应用.考查了数形结合思想.属于较易题.
7、D
【解析】连DE，交AF于G，根据平面几何知识可得 ，于是
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
试卷学期《数学模型》期末考试A山东轻工业学院08/09学年II
页）本试卷共4<
题说明总号考次开试分考卷试，参加考试的同学可以携带任何资料，可以
使用计算器，但上述物品严禁相互借用。
16分，每小题8分）一、简答题<本题满分得分）式，写出与§2.2录像机计数器的用途中，仔细推算一下<11、在阅卷人<2）式的差别，并解释这个差别；中不允许缺货的存储模型中为什么没有考虑生产
费用，在什么条件下可2、试说明在§3.1 以不考虑它；8分）二、简答题<本题满分16分，每小题得分1阅卷人?s)(ti的变化情时、对于1§5.1传染病的SIR 模型，叙述当0?况并加以证明。
E 2、在§6.1捕鱼业的持续收获的效益模型中，若单位捕捞强度的费用为捕捞强度的减函数，)0?0,b?c?a?bE,(a即，请问如何达到最大经济效益？本题满分16分，每小题8分）三、
简答题<得分s程是法图解说明为什么方策、1在§9.3 随机存储略中，请用)S?(x)?cI(I的最小正根。
阅卷人0、请结合自身特点谈一下如何培养数学建模
的能力？2 分）四、<本题满分20得分219人，二年级有某中学有三个年级共1000名学生，一年级有人。
现要选20名校级优秀学生，请用下列办316人，三年级有465 阅卷人Q ;<2））按比例加惯例的方法法分配各年级的优秀学生名额：<1值法。
另外如果校级优秀学个，重新进行分配，并按照席位分配的理想生名额增加
到21化准则分析分配结果。
得分分）16五、<本题满分阅
卷人大学生毕业生小李为选择就业岗位建立了层次分析模型，影响就业的因素考虑了收入情况、发展空间、社会声誉三个方面，有三个层次结构图如图，已知准则层。
选可业就岗位供择对目标层的成对比较矩阵1 / 4
选择就业岗位
71/1/43511????????23111/2/AB??41，比较矩阵分别为成，方案层对准则层的对
????1????22171/51/1????117463????????3112/B?3B?1/41。
，JhYEQB29bj
????32????1/21/6111/71/3????请根据层次分析方法为小李确定最佳的工作岗位。
16分）六、<本题满分得分某保险公司欲开发一种人寿保险，投保人需要每年缴纳一定数的阅卷人<额保险费，如果投保人某年未按时缴纳保费则视为保险合同终止保险公司需要对投保人的健康、疾病、死亡和退保的情况作出评估，从而制退保）。
定合适的投保金额和理赔金额。
各种状态间相互转移的情况和概率如图。
试建立马氏链模型分析在投保人投保时分别为健康或疾病状态下，平均需要经过多少年投保人就会出现退保或死亡的情况，以及出现每种情况的概率各是多少？5Y944Acbad
退保死亡II 学期《数学模型》期末考试A试卷解答山东轻工业
学院08/09学年0.05
0.03 分）分，每小题8一、简答题<本题满分160.15 0.07
m(m?1)???2mr?vt2?）得4分1、答：由<1，。
20.1
健康疾病2???knk2?)t?2r?n?(knm?代入得。
，6分将
vv0.6
???2r?r2??r，则得<2因为）。
所以。
8分
crc，每天的平均费用是，则平均每天的生产费用为2、答：假设每件产品的生产费用为
33ccrT112??crC(T)?4分，。
1132T1)TdC()TdC(11)T(TC?下面求最小，发现使，所以111dTdT12c1??TT，与生产费用无关，所以不考虑。
81cr2分
二、简答题<本题满分16分，每小题8分）
1di??s?),(1s??i，1、答：由<14若）0?dtdi1s)(t??s,?0i时，4增
加; 。
分当0?dtdi1?i(ts),?0i时，达到最大值当；
m?dt2 / 4
1di?0,?i(t)s i?0当。
减少且由时，1.知8??dt分
E)?bEpEx?(a)ER?T?S?S?(a?bE分，则2、答：。
2，
pNE2E?)E?(bE)?(pN?xN(1??a))R(5将代入，得，。
0rr分
pNa?r??E?0?R分。
得。
8令
R pNrb?2 8分）<本题满分16分，每小题三、简答题xS?Su?)J(u且为最小值点。
从而有唯一驻点的增加单调递增，因此1、由于方程<4）左边随着Sx?)(xu)I(x)IJ(u)J(和也是下凸的，而且在的表达式的相似性知是下凸的。
而由处达最小值)(SI分。
4。
5Y944Acbad
s)}I(S(x)?cc?I(S)}?B?{xIIA?{x(x)?BA，此与记则集合，的分界点即为订货点00)S?I((x)?cI 分8 。
即方程的最小正根05Y944Acbad
察洞力和）培养想象、2答：<回答要点分8 。
力。
5Y944Acbad 分）本题满分20四、<46531621930.?9.32?2020?4.38?20?6?）、<1，解：20，因此比例加惯例个席位：1000100010002219?Q?，个、6、9先果为5、6、9个。
<2）三方分得4分2398.05，配结154?2316?Q?2377.525Y944Acbad
276?2465?Q?Q Q10、4、，6最大，按结值法分配果为2402.53310?9分。
8个。
465316219765.?96.636?21599?21?4.?21?）个席位：，<1，21因此比例加惯例分配1000100010002465?Q??Q Q <2）三方先分得4、6、10195.68，个，最大，按结果为值法分4、7、10个。
311110?16。
10、个。
配结果为5、6分5Y944Acbad
Q值法分配结果恰好也满足准则显然此例中比例加惯例的方法违背了席位分配的理想化准则1，而Q则准1和符合准则同因此值法分配结果是时2，分。
20 2.。
5Y944Acbad
分）16五、<本题满分解：用“和法”近似计算得：T A00180.?CI)023.,.120650(.,，矩阵对征大，最特根：量向权应的为，为3.0036970031.?CR0
3 / 4
T B CI?0.001)60,0.(0.08,0.32，，矩阵向对应的权量为：根为3.001982，最大特征10017.?0CR T B006.?00.0035CRCI?)24,0.090(0.67,.，，矩阵，最大特征根为对应的权向量为：3.007032T
B0080..0046CR?CI?0)110.,(0.700.19,，，最大特征根为3.00922矩阵，对应的权向量为：3。
12分
T).423664283708,00(.292628,0.组合权向量为因此最佳的岗位为岗位3。
16分5Y944Acbad
六、<本题满分16分）
0001????1000??解：由题意，转移概率矩阵为，从而知状态“退保”和“死亡”为两个吸??01.0.70.150.05??0.030.070.60.3??收状态，此为吸收链。
6分5Y944Acbad
22??1?1..3?00??4??1?)?Q?M?(I= 33??760..?0????24??11T56)5(,Me?y或6=年投保人就会出现退，因此在投保时健康或疾病状态下，平均需要经过33保或死亡的情况。
12分5Y944Acbad
0.720.28??F?MR=，因此在投保时健康状态下，被“退保”和“死亡”吸收的概率分别为??0.660.34??0.72和0.28；在投保时疾病状态下，被“退保”和“死亡”吸收的概率分别为0.66和0.34。
5Y944Acbad。
18分
申明：
所有资料为本人收集整理，仅限个人学习使用，勿做商业用途。
4 / 4。