等倾干涉与牛顿环干涉条纹级次顺序相反的剖析
光的干涉 知识点总结

第二章 光的干涉 知识点总结2.1。
1光的干涉现象两束(或多束)光在相遇的区域内产生相干叠加,各点的光强不同于各光波单独作用所产生的光强之和,形成稳定的明暗交替或彩色条纹的现象,称为光的干涉现象。
2。
1。
2干涉原理注:波的叠加原理和独立性原理成立于线性介质中,本书主要讨论的就是线性介质中的情况. (1)光波的独立传播原理当两列波或多列波在同一波场中传播时,每一列波的传播方式都不因其他波的存在而受到影响,每列波仍然保持原有的特性(频率、波长、振动方向、传播方向等) (2)光波的叠加原理在两列或多列波的交叠区域,波场中某点的振动等于各个波单独存在时在该点所产生振动之和。
波叠加例子用到的数学技巧: (1)(2)注:叠加结果为光波复振幅的矢量和,而非强度和。
分为相干叠加(叠加场的光强不等于参与叠加的波的强度和)和非相干叠加(叠加场的光强等于参与叠加的波的强度和)。
2.1。
3波叠加的相干条件干涉项:相干条件:(干涉项不为零) (为了获得稳定的叠加分布) (为了使干涉场强不随时间变化) 2。
1。
4 干涉场的衬比度1.两束平行光的干涉场(学会推导) (1)两束平行光的干涉场 干涉场强分布:21ωω=10200⋅≠E E 2010ϕϕ-=常数()()212121212()()()2=+⋅+=++⋅I r E E E E I r I r E E 12102012201021212010212{cos()()()cos()()()}⋅=⋅+⋅++-++-⋅+---E E E E k k r t k k r t ϕϕωωϕϕωω()()()*12121212,(,)(,)(,)(,)2cos =++=++∆I x y U x y U x y U x y U x y I I I I ϕ亮度最大值处:亮度最小值处:条纹间距公式空间频率:(2)定义衬比度以参与相干叠加的两个光场参数表示:衬比度的物理意义 1。
光强起伏2.相干度2。
等厚干涉与牛顿环

三、等厚干涉条纹
·
平行光照射到表面平整、厚度不均匀的薄膜上产生 的干涉条纹。
2nd cos r 2
薄膜厚度d 相同之处对应于同一级条纹, · 因此称为等厚干涉条纹。 光线垂直入射时:
k 2nd 2 2k 1 2
牛顿环:内疏外密
返回
退出
k
(6)将牛顿环置于 n 1 的液体中,条纹 如何变?
光程差
Δ 2nd
2
n玻璃 n 1 前提:
1 r 2dR ( Δ ) R n 2
1 1 r (k ) R n 2
r 1 kR n
明环半径
条纹变密
暗环半径
返回
退出
• 牛顿环的应用
解:
rk k R
rk 5 (k 5) R
O
R
r
联立求解:
k 4
R 6.79 m
返回
退出
例12-16 已知标准平凸透镜 R1=102.3 cm,入射光 =583.9 nm,测得第4条暗环(k=4)的半径 r4=2.25 cm,
求待测凹面镜的半径 R2。 解: 2 2
r r d d1 d 2 2 R1 2 R2 2d (2k 1)
h
b2
返回
退出
解: 观察到的干涉条纹弯向空气膜的左端, 可判断工件表面是下凹的,如图所示。
由图中相似直角三角形:
a h h b ( d k d k 1 ) / 2 a h b2
d k 1
b
a
h
dk B A h B 处有凹陷 h
返回
退出
光学中的光的干涉与牛顿环

光学中的光的干涉与牛顿环光是一种电磁波,是由电场和磁场相互作用形成的。
光学是研究光的传播、干涉、衍射、偏振等性质的学科,而光的干涉是光学中重要的现象之一。
干涉是指两个或多个波相遇时产生的干涉效应,具有波动性的光会在相遇的地方产生叠加效应,形成明暗交替的干涉条纹,这种现象被称为光的干涉。
光的干涉可以分为两类:干涉现象和干涉条纹。
干涉现象是指当两束或多束光波发生相遇时,根据不同的相位关系,会出现明暗相间的亮度变化。
干涉条纹则是指这些明暗相间的亮度变化在干涉平面上的分布形态。
其中,牛顿环是光的干涉现象中的一种。
牛顿环是由英国物理学家牛顿于18世纪初提出的,它是光源放在半透明膜上方的一个凸透镜和在薄透镜上形成的彩色圆环的干涉现象。
在牛顿环实验中,将一个光源放在平行平面透镜的上方,并且光源和透镜之间有一个半透明膜,当透镜上方有一个相当小的空气隙时,光波在透镜与薄膜之间反射、折射和干涉,从而形成一系列明亮的环形条纹。
牛顿环主要是由光的反射和折射造成的。
当光波从光源经过透镜折射到薄透镜上,会产生一些发散的光波和屈射的光波,这些光波在透镜与隙缝之间发生干涉,形成明暗相间的干涉条纹。
其中,圆环的半径决定了光波叠加后的相位差,从而决定了干涉条纹的明暗度。
在牛顿环实验中,随着半径的增大,明条纹和暗条纹的亮度逐渐减弱,但是干涉条纹的间距保持恒定。
这是由于明条纹和暗条纹的亮度与光的相位差有关,而相位差与半径的平方成正比。
所以增加半径的平方会使明暗条纹的亮度减弱,但是干涉的间距仍然保持不变。
牛顿环实验的结果显示出了光的波动性质,同时也验证了光的反射和折射现象。
通过测量牛顿环的半径和波长,还可以计算出光的折射率。
牛顿环实验不仅是光学研究中的重要基础实验,也为光的干涉现象的理解和应用提供了重要的指导。
总结起来,牛顿环实验证明了光的干涉现象和反射、折射现象之间的关系,深化了人们对光学性质的理解,对光学技术的发展和应用具有重要的意义。
光的干涉 知识点总结

鉴于 0,L0是决定光场纵向相干性的特征量,人们称 0为相干时间(coherent time) L0为相干长度(coherentlength) 光场中这类相干性称为时间相干性 (temporal coherence)
光场的空间相干性
光场的空间相干性是指在光源照明空间中横向任意两点位置处的光场U~1 和U~2 之间的相干
I 0(1
sin v v
cos k0L)
其中
v
k 2
L
则
(L) sin v
sin
k 2
L
k
第一次出现 此时 求得
0时的光程差称为最大光 程差LM k L / 2
LM =2 / k 2 /
准单色光持续发光时间有限,因而发射的波列长度是有限的,相邻波列之间相位关系是随机
的。
L0 c 0
(5)干涉条纹间距公式
由 I(x ,y )
I 0(1
cos(k
d D
x )),k
d D
x
2
d D
x
2j
得 x j
j
D d
条纹间距:
e
(j
1)
D d
j
D d
D d
(6) 干涉条纹的物理意义: 光程差
r2 r1 m
时
亮条纹;
r2
r1
(m
1 2
)
时
暗条纹;
物理意义:
1、干涉条纹代表着光程差的等值线。
分波前干涉(将波前先分割再叠加,叠加广场来自同波源具有相同初始位相) 分振幅干涉(将光的能量分为几部分,参与叠加的光波来自同一波列,保证相位差 稳定) 杨氏双孔干涉实验:两个球面波的干涉 (1) 杨氏双孔干涉实验装置及其历史意义
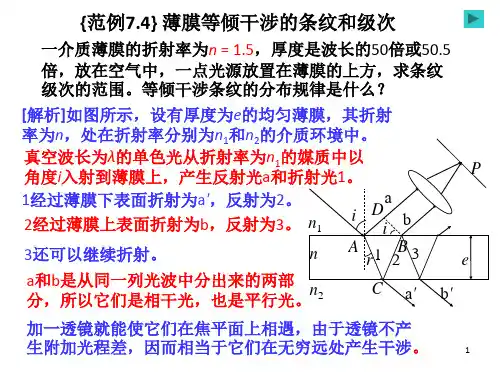
光学之薄膜等倾干涉的条纹和级次
射频技术在通信电子行业的应用通信电子行业是当今科技行业的热点之一,各种基于射频技术的设备和系统得到了广泛应用,包括无线电通信、广播电视、雷达、卫星通信和导航等领域。
其中,射频技术作为通信电子行业中不可或缺的一个部分,发挥着至关重要的作用。
本文将从射频技术的概念、应用、发展趋势等角度,对其在通信电子行业中的应用进行分析。
一、射频技术的概念射频技术(Radio Frequency Technology,简称RF技术)是利用无线电波在空间中传输信息的技术。
射频波的频率范围在3kHz~300GHz之间,可以被人类或动物的耳朵听到或者看到。
通俗地说,RF技术就是在无线电波的传输中,对电气信号进行调制、解调、信号处理和放大等技术处理的综合体。
同时,射频技术也是电子技术中一种高频技术,主要应用于通信、测量、探测、电子干扰等领域。
二、射频技术在通信电子行业中的应用1. 无线通信射频技术在无线通信技术中扮演着重要的角色。
从最早的移动电话到如今的智能手机,无线通信设备越来越小、功能越来越强大,而射频技术的发展也在不断地满足着这一需求。
射频技术在无线通信中的应用包含很多方面,例如:手机、蓝牙、WLAN、GPS、NF等都是射频技术在无线通信领域的代表应用。
2. 广播电视广播电视是人们最常使用的媒体,也是射频技术应用中一个重要领域。
射频技术在广播电视中的应用包括:调频广播、电视信号发送、卫星信号接收等。
其中,无线电视信号的传输,一般采用数字方式,即通过调制、多路化、遥测等技术,提高传输质量和效率。
3. 雷达雷达是一种电磁波传感器,主要用于检测、跟踪和识别远离发射源的物体。
射频技术在雷达中的应用,包括信号发射、接收、处理和放大等多个环节。
雷达技术的发展也成为了现代战争和民用领域中的关键技术之一。
4. 卫星通信卫星通信是一种可以覆盖全球范围的通信方式。
射频技术在卫星通信中的应用,主要是卫星的信号接收和转发。
将地面上发射的信号通过卫星传送到另一个地方,可以使通信质量得到明显提高。
3部分等厚干涉、牛顿环、迈克尔逊干涉仪(1)概述

2d
2
光程差的改变量: 2d
光所程以差移改过变 条纹,的条数纹目移为过一根,N
2d
解2:h 变化 /2,条纹集体移一个
间距。 N d 2d
/2
2021/4/23
DUT 常葆荣
d
24
例:如图所示,牛顿环装置的平凸透镜与平板玻璃有一小缝隙 e0, 现用波长为的单色光垂直照射。已知平凸透镜的曲率半径 为R,求反射光形成的牛顿环的各暗环半径 。
可调
2hn cos i2 = (2k 1) 暗
G2
M1
条纹特点
2
l1 望远镜
1、同心圆 2、内疏外密
3、中心级次是最高的
2021/4/23
DUT 常葆荣
13
k
M1
d = 2hncosi2 =
(2k 1) 2
平移M1 h 变化 条纹分布变化
M2
更高级次的环从
h k Max
中心“涌出”,所
解:设某暗环半径为r,则根据几何关系,可有:
R2 = r 2 + (R - h)2 近似有 h r 2 / (2R)
再根据干涉相消条件有
R
2(h e0 )
1
2
(2k
1)
2
由前两式可得 r R(k 2e0 ) 空气
e0
k为整数,且k>2e0/
2021/4/23
DUT 常葆荣
25
9、在空气中用白光垂直照射在厚度为d且均匀的肥皂膜上后反 射,在可见光谱中观察到1=630nm的干涉极大, 2=525nm的 干涉极小,且它们之间没有另外的级值情况, 求肥皂膜的厚度 h.(肥皂膜的折射率n=1.33)
解:等厚干涉,要考虑半波损失:
等倾干涉与等厚干涉的比较
目录本科生毕业论文诚信声明 (1)等厚干涉与等倾干涉的比较 (2)中文摘要 (2)英文摘要 (2)1. 引言 (2)2 等厚干涉和等倾干涉 (2)2.1等厚干涉 (2)2.2等倾干涉 (3)3.干涉条纹之比较 (4)3.1 牛顿环干涉条纹的半径和间距 (4)3.2等倾干涉条纹的半径和间距 (4)3.3 两种干涉条纹形状的比较 (5)4 .干涉条纹移动规律之比较 (5)参考文献 (5)致谢 (6)本科生毕业论文诚信声明本人郑重声明:所呈交的本科毕业论文,是本人在指导老师的指导下,独立进行研究工作所取得的成果,成果不存在知识产权争议,除文中已经注明引用的内容外,本论文不含任何其他个人或集体已经发表或撰写过的作品成果。
对本文的研究做出重要贡献的个人和集体均已在文中以明确方式明。
本人完全意识到本声明的法律结果由本人承担。
作者签名:二0一年月日等厚干涉与等倾干涉的比较刘xx,付文羽(陇东学院电气工程学院,甘肃庆阳 74500)摘要:对牛顿环等厚干涉和薄膜等倾干涉条纹形成原理, 干涉条纹的半径、间距、干涉级次等进行比较和分析, 揭示两种相似条纹的本质区别。
关键词:等厚干涉等倾干涉条纹半径条纹间距干涉级次Thickness Interference And Isoclinic InterferenceLIU xx, FU Wen-yu(Electrical Engineering College,Longdong University,Qingyang 74500,Gansu)Abstract:Of Newton ring thickness interference and film isoclinic interference fringe formation principle, the radius of the interference fringes,spacing,interference levels compare and analysis,reveals the essential difference between two similar stripe.Key Words: Isopach interference Isoclinic interference Stripe radiusFringe spacing Interference levels1 引言在光学教学中,关于等倾干涉和等厚干涉学生理解起来往往比较困难,有时显得似是而非,容易望文生义从字面上认为“等厚干涉”是指薄膜厚度是等厚的干涉这一错误结论,从而把等倾干涉和等厚干涉混淆起来,笔者通过几年的教学,总结出了等倾干涉和等厚干涉的异同点,以便学习。
§1.7 等厚干涉——牛顿环1解析
4. 波长对条纹的影响:增大λ,条纹间隔变大;
5.光源是白光:中心暗点,暗点附近少数几级彩环,内紫外红。 6.透射光与反射光的情况互补 7.膜厚变化时,条纹的移动:膜厚增加,中心点亮暗交替, 各圆
环向中心收缩、沉没,条纹的整体形状及疏密不变。
四. 应用:
依据公式 rj2 m rj2 mRλ
解:根据牛顿环的第 k级暗环的半径为 r 得到:rj2 jR和rj25 j 5R 两式联立,解得 rj25 rj2 5 R 求得透镜的曲率半径为 R rj25 rj2 4.00 10 5 5 0.400106 将R 10.0m代回联立方程中的任一 个,立即可求得 k 4
j 0, 1 , 2, 3
jR
(2 j 1) R 2
j
j 0, 1 , 2, 3
R ( j 1) 4j
(自己推导)
相邻两环的间隔(r 对j 求导): r rj 1 rj
条纹
思考
▲ 白光入射条纹情况如何? ▲ 透射光条纹情况如何? ▲ 平凸透镜向上移,条纹怎样移动?
①
再根据干涉减弱条件有
2d 2e0
2
(2 j 1)
2
j 0, 1 , 2, 3
②
把式①代入②可得
r R( j 2e0 ) (j为整数,且j > 2e0 )
哪里有天才,我 是把别人喝咖啡 的时间都用在工 作上的。
鲁迅
作业 :
1.15,1.16
r R ( R d ) 2R d
2 2 2
平晶 (2 j 1) 干涉相消(暗纹) 2d 2 (2) 暗环 2 j干涉相长(明纹)
两种圆环形干涉条纹的对比
两种圆环形干涉条纹的对比作者:胡晓颖荆丽丽葛俊峰来源:《科技风》2020年第01期摘;要:在物理学专业学生的光学课教学过程中,牛顿环与迈克尔逊干涉形成的干涉条纹都是明暗相间的同心圆环,由此,学生们在学习时对这两种干涉的原理和条纹特点常常混淆,本文对这两种干涉进行了介绍和对比,从而有利于同学们的学习。
关键词:牛顿环;迈克尔逊干涉;圆环条纹物理学的光学课教学过程中,牛顿环与迈克尔逊干涉是光的干涉这一章中的重点教学内容,这两种干涉形成的都是明暗相间的同心圆环,由此,同学们在学习时对两种条纹的成因和特点不易区分,本文对这两种干涉条纹特点进行比较,以供大家学习参考。
1;干涉的形成如图1所示,在折射率分别为n′和n″的介质中放入折射率为n的透明薄膜,在点S处放一个光源,并使其将波长为λ的真空光线0如图方式发射至薄膜上的A 点,使光線分为折射和反射两部分,而这两束光在下半部分B处反射后在C处折射至介质n′中,为图中光束2。
光束1和光束2是两束平行的光,他们经过透镜L后于P点汇聚。
又因为,光束1和光束2均由同一入射光而来,所以振动方向相同,频率一致,位相差在P点也是恒定的,由此两者产生干涉。
如果一束光在某一薄膜的上下表面经过折射和反射后仍然能再次相遇的干涉便被称为薄膜干涉。
在图1分振幅干涉所示的光束1和2均为入射光0的一部分,所以这种干涉又被称之为分振幅干涉。
图1;分振幅干涉光束1和光束2的光程差为:δ=2dn2-n′sin2i=;kλ;(k=1,2,…);明纹(2k+1)λ2;(k=0,1,…);暗纹(1)在上列式子中,k为条纹级数,分析干涉的成因,薄膜干涉可根据入射角i和薄膜厚度d是否改变分类:干涉时薄膜厚度不变,倾角i决定条纹的级次,倾角相同则干涉条纹的级次相同,称之为等倾干涉;干涉时入射角不变,薄膜厚度决定条纹的级次,相同厚度薄膜产生干涉条纹的级次相同,称之为等厚干涉。
2;牛顿环等厚干涉如图2牛顿环,如果使用平行的单色光对空气薄膜垂直照射,此时形成的条纹为等厚干涉条纹,该组条纹是以如图O为中心的同心圆环。
光的等厚干涉及其应用原理
光的等厚干涉及其应用原理光的等厚干涉是指在透明介质中,当光线通过介质表面时发生折射并产生反射波和透射波,在反射波和透射波交相干的情况下,由于光的波长和介质厚度之间的关系,发生干涉现象。
光的等厚干涉原理主要包括三个方面:相位差、干涉条件和光的干涉条纹。
相位差是光的等厚干涉的关键概念。
相位差是指两个光波在某一点上的相位差异。
在光的干涉中,当两个波的相位差为整数倍的2π时,两个波的振幅叠加增强,称为相干叠加;当两个波的相位差为半整数倍的2π时,两个波的振幅叠加减弱,称为相干抵消。
相干叠加和相干抵消决定了干涉现象的出现。
干涉条件是产生干涉现象的必要条件。
在光的等厚干涉中,必须满足一定条件才能产生明显的干涉现象。
首先,光源必须是频宽很窄的单色光源,这样才能保证光的波长相对稳定,以满足相邻波面上的相干叠加或抵消。
其次,光的传播路径必须有一定的差异,即光线经过的光程差必须明显,否则将无法显示出明显的干涉现象。
最后,光的传播路径必须在一定范围内保持平行,以满足光波之间的相干叠加。
光的干涉条纹是光的等厚干涉现象的显示形式。
当具备相干叠加和相干抵消条件时,光的等厚干涉会在空间中形成干涉条纹。
干涉条纹是由于光的相位差引起的亮度变化,通常呈现出交替的明暗条纹形式。
根据相位差的变化规律,干涉条纹可分为等距干涉和等倾干涉。
在等距干涉中,干涉条纹的间距恒定,条纹数目相等,例如牛顿环实验;在等倾干涉中,条纹的亮度变化相同,但间距随位置的移动而改变,例如天线环洞实验。
光的等厚干涉应用十分广泛,主要包括以下几个方面:1. 测量物体的厚度和形状:利用光的等厚干涉原理,可以测量物体的厚度和形状。
通过测量干涉条纹的宽度和间距,可以计算出透明物体的厚度,并进行形状分析。
例如,光学显微镜、干涉仪等设备都是利用光的等厚干涉原理进行物体测量的。
2. 光谱仪的构建和使用:光的等厚干涉也可用于构建光谱仪,并用于光谱分析。
光谱仪是利用光的等厚干涉原理,通过控制光的反射和透射波的光程差,使不同波长的光线产生相干叠加或相干抵消,进而实现对光谱的分离和测量。
