应用统计方法(大作业)
应用数理统计大作业

应用数理统计大作业In statistics, the central limit theorem plays a crucial role in understanding the distribution of sample means. By stating that, regardless of the shape of the underlying population distribution, the distribution of sample means approaches a normal distribution as the sample size increases, the central limit theorem provides a powerful tool for making inferences about population parameters based on sample data. 统计学中,中心极限定理在理解样本均值的分布方面扮演着关键角色。
通过表明,无论底层人群分布的形状如何,随着样本量的增加,样本均值的分布会逼近正态分布,中心极限定理为根据样本数据对人群参数进行推断提供了一个强大的工具。
Another important concept in statistical inference is confidence intervals, which provide a range within which the true population parameter is estimated to lie with a certain level of confidence. Confidence intervals are essential in interpreting the results of hypothesis tests, as they indicate the precision of the estimate and allow for an assessment of the uncertainty associated with the sample data. 统计推断中的另一个重要概念是置信区间,它提供了一个范围,真实人群参数被估计在其中的概率。
应用统计方法(大作业)
应用统计方法作业一、在某项实验中,测得变量y 与因素x 数据如表1所示。
试建立适当的y 与因素x 的回归方程(0.01α= )。
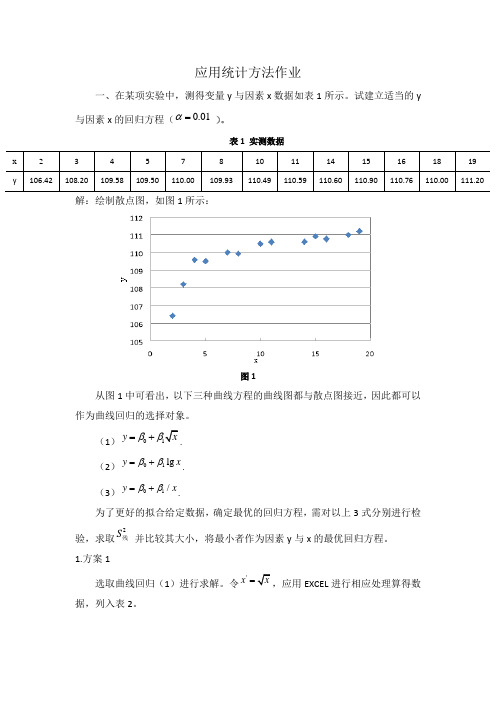
表1 实测数据x 2 3 4 5 7 8 10 11 14 15 16 18 19 y106.42108.20109.58109.50110.00109.93110.49110.59110.60110.90110.76110.00111.20解:绘制散点图,如图1所示:图1从图1中可看出,以下三种曲线方程的曲线图都与散点图接近,因此都可以作为曲线回归的选择对象。
(1)0y x ββ=+. (2)01lg y x ββ=+.(3)01/y xββ=+.为了更好的拟合给定数据,确定最优的回归方程,需对以上3式分别进行检验,求取2S 残并比较其大小,将最小者作为因素y 与x 的最优回归方程。
1.方案1选取曲线回归(1)进行求解。
令'x x =EXCEL 进行相应处理算得数据,列入表2。
表2 方案1数据处理计算由表2得:''13''2111.6670()i x x i l x x ==-=∑1321()21.2105yy i i l y y ==-=∑'13''1()()13.9389i i x y i l x x y y ==--=∑由此得: µ'''113.938911.667194701.x y x x l l β===¶µ'011.1947109.9362 3.0424=106.3014y x ββ=-=⨯- 故所求的回归方程为:$'106.3014 1.1947y x =+进行变量还原得回归方程:$106.3014y =+检验假设H 01:10β=.'21= 1.194713.938916.6528x y S l β=⨯=回2221.210516.6528 4.5577yy S l S =-=-=回残2216.652840.1915/11 4.5577/11S F S ===回残对给定的0.01α=,查F(1,11)表(附表5)得临界值9.65λ=。
应用统计学大作业-房价统计分析

2003年至2012年间重庆市主城区房价波动及其影响因素浅谈——应用统计学大作业学院:机械工程学院专业班级:工业工程2班学号:20102666姓名:梁佩馨辅导教师:邓蕾时间:2012年12月6日摘要本文通过在互联网搜索数据,查得2003年至2012年的重庆市主城区平均房价(元/平方米)的数据及其可能的影响因素。
主要考察的影响因素包括国民人均收入(城镇居民人均可支配收入,农村居民人均纯收入)及银行个人住房贷款利率(个人住房商业贷款利率,个人住房公积金贷款利率)。
利用Excel等工具对数据进行描述统计、相关分析、回归分析等处理,并利用处理结果预测、验证2012年上半年的重庆主城区平均房价,最后进行误差分析和纠错。
关键词:平均房价,回归分析,国民人均收入1、背景介绍自1999年以来,人们每天从报纸上看到的几乎都是房价上涨的消息。
房子是一个家庭相当重要的民生问题,是一个人经济上和心理上都需要的保证。
随着房价一天天势头凶猛地上涨,“买房”变成了横亘在众多人民群众心头的硬伤,高房价已经成为困扰我国民生发展的大问题。
抛开居高不下的房价为何发生和是否具有其合理性、是否违背市场规律不谈,作为普通民众,我们应该如何掌控纷杂的信息、做出正确的判断和如何分配财产、在正确的时间投资房产以获得最大利益是非常值得人深思的。
本文收集整理了2003年至2012年关于重庆主城房价及其波动的相关数据(其中包括:2003年至2011年的重庆市主城区平均房价、国民人均收入,2003年至2012年的银行个人住房贷款利率,2012年上半年城镇居民人均可支配收入,及2012年上半年各月的平均房价),以期能够利用课堂所学提供房价波动趋势、相关影响因素及粗略预测的方法,并服务于普通有相关需求的人群。
2、数据收集及整理2.1 数据收集2003年至2011年间重庆市主城区的房价数据和2012年上半年重庆主城区房价数据均采取网上获取第一手资料的方法查找,主要来源为新浪网和百度;2003年至2011年间的国民人均收入为第二手资料,来源于国家统计局数据库;2003年至2012年银行个人住房贷款利率为第二手资料,来源于百度、豆瓣网及新浪新闻。
应用统计学大作业

应用统计学大作业在当今数字化和信息化的时代,数据无处不在。
从社交媒体的互动到医疗保健的记录,从金融市场的交易到科学研究的成果,数据以惊人的速度积累和增长。
而应用统计学作为一门处理、分析和解释数据的学科,发挥着至关重要的作用。
它不仅帮助我们从海量的数据中提取有价值的信息,还为决策提供了坚实的依据。
应用统计学的应用领域广泛而多样。
在商业领域,企业利用统计学来分析市场趋势、消费者行为和销售数据,以制定营销策略、优化生产流程和预测需求。
例如,一家电商公司可以通过分析用户的浏览和购买历史,了解不同产品的受欢迎程度,从而调整商品推荐和库存管理。
在医学领域,统计学有助于评估新药物的疗效、研究疾病的发病机制和预测疾病的流行趋势。
研究人员通过对大量病例数据的分析,能够确定治疗方法的有效性和安全性,为医疗决策提供科学依据。
教育领域也是应用统计学的重要舞台。
学校可以通过分析学生的考试成绩、学习行为和家庭背景等数据,评估教学质量,发现学生的学习困难,制定个性化的教育方案。
在社会科学中,统计学被用于研究人口趋势、社会现象和民意调查,为政策制定提供参考。
要进行有效的数据分析,首先需要收集合适的数据。
数据的收集方法多种多样,包括问卷调查、实验观测、数据库查询等。
然而,无论采用哪种方法,都需要确保数据的准确性和代表性。
不准确或有偏差的数据可能导致错误的结论和决策。
在收集到数据后,接下来的关键步骤是数据的整理和预处理。
这包括检查数据的完整性、纠正错误、处理缺失值和异常值等。
例如,如果在一份调查问卷中发现大量缺失的回答,就需要考虑这些缺失值对分析结果的影响,并采取适当的方法进行处理,如删除含有缺失值的样本或通过其他变量进行推测填补。
数据分析的方法众多,常见的有描述性统计分析和推断性统计分析。
描述性统计分析主要用于概括和描述数据的特征,如均值、中位数、标准差、频率分布等。
通过这些统计量,我们可以对数据有一个初步的了解。
例如,通过计算学生考试成绩的平均分和标准差,可以了解学生整体的学习水平和成绩的离散程度。
统计学大作业

宁波大红鹰学院工商管理分院《应用统计学》实验(践)报告专业:工商管理专业班级:学生姓名:同组人员:无任课老师:黄涛2017年6月12日目录实验(一) SPSS安装 (2)实验(二)统计数据的搜集与整理 (6)实验(三)统计数据的图表描述 (9)实验四统计数据的度量 (16)实验五统计抽样与参数估计 (19)实验六相关与回归分析 (24)实验七统计数据的动态分析 (33)实验八统计指数分析 (35)实验(一) SPSS安装一、实验名称:SPSS安装二、实验目的:学会安装spss软件及有关操作三、实验步骤:SPSS的安装和启动在启动SPSS软件之前,需要先在计算机上进行安装。
其安装方法主要有两种:一是直接使用SPSS安装光盘进行安装;二是通过网络下载SPSS安装程序进行安装。
本小节使用第二种方法详细介绍SPSS的安装步骤(以IBM SPSS 19.0为例)。
1.打开计算机,找到已经下载到计算机上的SPSS安装程序。
如图一图一2.单击该图标,按照顺序下去,直到出现如下界面,单击“下一步”,则弹出对话框;个人用户选择第一个“单个用户许可证”,如果图二所示。
图二3.单击“下一步”,切换到用户协议对话框。
在该对话框中接受用户协议,然后单击“下一步”,如图三所示。
图三4.单击“下一步”,显示客户信息。
在该对话框中填写好用户姓名与单位,然后单击“下一步”,如图四所示。
图四5.单击“下一步”,语言选择。
选择“英语”,然后单击“下一步”,如图五所示。
图五6.在弹出的对话框中是选择文件安装位置,如图六所示。
在该对话框中单击“更改”,可调整软件的安装位置。
图七7.在选择文件安装对话框中单击“下一步”,在弹出的对话框中单击“安装”即可,如图七所示。
图七8.此时则弹出正在安装的界面,如图八所示。
图八9.在以上安装程序完后,则弹出授权许可证的对话框。
把框中的勾去掉,单击“确定”,如图九所示。
图九10.此时则弹出产品授权对话框,选择“启用以用于临时使用”按钮,单击“下一步”,如图十所示。
应用统计大作业 哈工大

《应用统计》大作业——2013年秋季学期题目:大学生手机话费消费调查院系:机电学院工业工程系班号: 1108401姓名:王震宇学号: 1100800609时间:10月6日第一节:引言在这个信息高速社会,手机在我们生活中扮演不可或缺的角色,时下大学生几乎人手一部手机。
在此,我们将对大学生在手机话费消费做一次详细调查。
以了解大学生每月手机话费消费情况和大学生手机话费消费观念。
第二节:调查方案一、调查目的:分析研究大学生的话费消费情况及影响大学生话费消费的各项因素,从而为大学生的话费消费提供相关建议。
二、调查对象哈尔滨工业大学在校大学生采用的随机抽取人员进行调查,由于此次调查的时间和经费有限,调查的人数为100人,男生为主。
三、调查的时间2013年9月26日——9月30日四、调查的内容此次调查采用问卷调查。
第三节:调查结果及分析一、大学生每月手机话费费用根据市场调查所得到的信息的统计,我们得到表一:每月手机话费频数百分比50元以内61 61%50—100元32 32%100—150元 5 5%150元以上 2 2%1020304050607050元以下50-100元100-150元150元以上对上述数据进行描述统计,可得关于大学生手机话费的各项指标如表二平均 49.00 中位数 40.98 众数 33.89 方差 1173.75 标准差34.26二、通信运营商的选择表三, 大学生通信运营商选择的频数分布表通信运营商 频数 百分比 移动 68 68% 联通 15 15% 电信 17 17% 其他0%众数为移动。
目前移动的动感地带仍然在学生群体中广泛使用,它的卖点主要是服务和价格。
移动联通电信其他扇面 5三、大学生选择此通信运营商的原因表四 大学生选择此通信运营商原因的频数分布表 选择此通信运营商的原因频数 百分比 套餐优惠 4141% 通话质量好 9 9% 随大流 39 39% 其他1111%1020304050套餐优惠通话质量好随大流其他条形图 3条形图 2条形图 1从表三和表四来看,哈工大学生绝大多数选择了移动,而他们选择该运营商的原因是随大流和套餐优惠,这也难怪,移动退出的套餐确实比较实惠,而且它有庞大的短号网,我相信这是最吸引人的地方。
天津大学应用统计学大作业

答案+我名字应用统计学要求:一、独立完成,下面已将五组题目列出,请按照学院平台指定..的做题组数作答,每人只答一组题目........,多答无效....,满分100分;平台查看做题组数操作:学生登录学院平台→系统登录→学生登录→课程考试→离线考核→离线考核课程查看→做题组数,显示的数字为此次离线考核所应做哪一组题的标识;例如:“做题组数”标为1,代表学生应作答“第一组”试题;二、答题步骤:1.使用A4纸打印学院指定答题纸(答题纸请详见附件);2.在答题纸上使用黑色水笔....按题目要求手写..作答;答题纸上全部信息要求手写,包括学号、姓名等基本信息和答题内容,请写明题型、题号;三、提交方式:请将作答完成后的整页答题纸以图片形式依次粘贴在一个.......Word....文档中...上传(只粘贴部分内容的图片不给分),图片请保持正向、清晰;1.上传文件命名为“中心-学号-姓名-科目.doc”2.文件容量大小:不得超过20MB。
提示:未按要求作答题目的作业及雷同作业,成绩以....................0.分记..!题目如下:第一组:一、计算题(每小题25分,共50分)1、某茶叶制造商声称其生产的一种包装茶叶平均每包重量不低于150克,已知茶叶包装重量服从正态分布,现从一批包装茶叶中随机抽取100包,检验结果如下:每包重量(克) 包数(包)f x xfx-(x-)2f148—149 10 148.5 1485 -1.8 32.4149—150 20 149.5 2990 -0.8 12.8150—151 50 150.5 7525 0.2 2.0 151—152 20 151.5 3030 1.2 28.8合计100 -- 15030 -- 76.0要求:(1)计算该样本每包重量的均值和标准差;(2)以99%的概率估计该批茶叶平均每包重量的置信区间(t0.005(99)≈2.626);(3)在ɑ=0.01的显著性水平上检验该制造商的说法是否可信(t0.01(99)≈2.364)(4)以95%的概率对这批包装茶叶达到包重150克的比例作出区间估计(Z0.025=1.96);(写出公式、计算过程,标准差及置信上、下保留3位小数)2、一种新型减肥方法自称其参加者在第一个星期平均能减去至少8磅体重.由40名使用了该种方法的个人组成一个随机样本,其减去的体重的样本均值为7磅,样本标准差为3.2磅.你对该减肥方法的结论是什么?(α=0.05,μα/2=1.96, μα=1.647)二、简答题(每小题25分,共50分)1、简述算术平均数、几何平均数、调和平均数的适用范围。
应用统计大作业
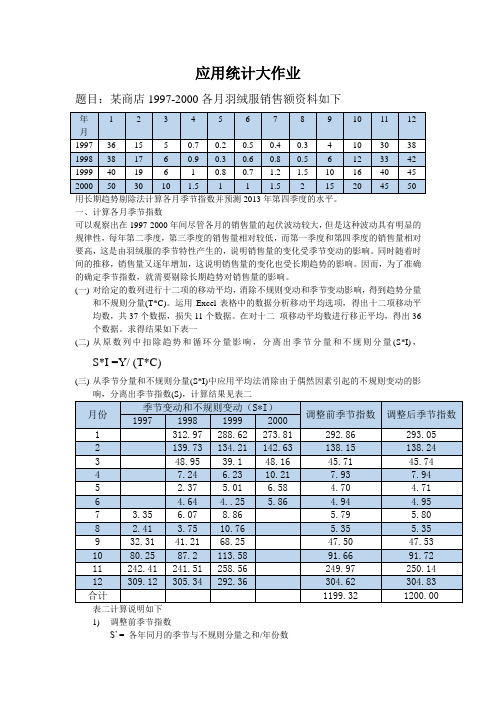
应用统计大作业题目:某商店1997-2000各月羽绒服销售额资料如下年月1 2 3 4 5 6 7 8 9 10 11 12 1997 36 15 5 0.7 0.2 0.5 0.4 0.3 4 10 30 38 1998 38 17 6 0.9 0.3 0.6 0.8 0.5 6 12 33 42 1999 40 19 6 1 0.8 0.7 1.2 1.5 10 16 40 45 2000 50 30 10 1.5 1 1 1.5 2 15 20 45 50 用长期趋势剔除法计算各月季节指数并预测2013年第四季度的水平。
一、计算各月季节指数可以观察出在1997-2000年间尽管各月的销售量的起伏波动较大,但是这种波动具有明显的规律性,每年第二季度,第三季度的销售量相对较低,而第一季度和第四季度的销售量相对要高,这是由羽绒服的季节特性产生的,说明销售量的变化受季节变动的影响。
同时随着时间的推移,销售量又逐年增加,这说明销售量的变化也受长期趋势的影响。
因而,为了准确的确定季节指数,就需要剔除长期趋势对销售量的影响。
(一)对给定的数列进行十二项的移动平均,消除不规则变动和季节变动影响,得到趋势分量和不规则分量(T*C)。
运用Excel表格中的数据分析移动平均选项,得出十二项移动平均数,共37个数据,损失11个数据。
在对十二项移动平均数进行移正平均,得出36个数据。
求得结果如下表一(二)从原数列中扣除趋势和循环分量影响,分离出季节分量和不规则分量(S*I),S*I =Y/ (T*C)(三)从季节分量和不规则分量(S*I)中应用平均法消除由于偶然因素引起的不规则变动的影响,分离出季节指数(S),计算结果见表二月份季节变动和不规则变动(S*I)调整前季节指数调整后季节指数1997 1998 1999 20001 312.97 288.62 273.81 292.86 293.052 139.73 134.21 142.63 138.15 138.243 48.95 39.1 48.16 45.71 45.744 7.24 6.23 10.21 7.93 7.945 2.37 5.01 6.58 4.70 4.716 4.64 4..25 5.86 4.94 4.957 3.35 6.07 8.86 5.79 5.808 2.41 3.75 10.76 5.35 5.359 32.31 41.21 68.25 47.50 47.5310 80.25 87.2 113.58 91.66 91.7211 242.41 241.51 258.56 249.97 250.1412 309.12 305.34 292.36 304.62 304.83 合计1199.32 1200.00 表二计算说明如下1)调整前季节指数S’ = 各年同月的季节与不规则分量之和/年份数即将季节分量和不规则分量经过简单平均消除不规则变动的影响后,分离出季节分量S’。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应用统计方法作业
一、在某项实验中,测得变量y 与因素x 数据如表1所示。
试建立适当的y 与因素x 的回归方程(0.01α= )。
表1 实测数据
x 2 3 4 5 7 8 10 11 14 15 16 18 19 y
解:绘制散点图,如图1所示:
图1
从图1中可看出,以下三种曲线方程的曲线图都与散点图接近,因此都可以作为曲线回归的选择对象。
(1)0y x ββ=+. (2)01lg y x ββ=+.
(3)
01/y x
ββ=+.
为了更好的拟合给定数据,确定最优的回归方程,需对以上3式分别进行检验,求取
2
S 残
并比较其大小,将最小者作为因素y 与x 的最优回归方程。
1.方案1
选取曲线回归(1)进行求解。
令'x x =EXCEL 进行相应处理算得数
据,列入表2。
表2 方案1数据处理计算
由表2得:
''13
''2111.6670()i x x i l x x ==-=∑
13
21
()21.2105yy i i l y y ==-=∑
'13
''1
()()13.9389i i x y i l x x y y ==--=∑
由此得:
'''
113.9389
11.66719470
1.x y x x l l β=
=
=
'01 1.1947109.9362 3.0424=106.3014y x ββ=-=⨯-
故所求的回归方程为:
'106.3014 1.1947y x =+
进行变量还原得回归方程:
106.3014y =+检验假设H 01:10β=.
'21= 1.194713.938916.6528x y S l β=⨯=回
2221.210516.6528 4.5577yy S l S =-=-=回残
2
216.652840.1915/11 4.5577/11
S F S ===回残
对给定的0.01α=,查F(1,11)表(附表5)得临界值9.65λ=。
由于F>λ,检验效果显著,所以拒绝H 01,即回归方程有意义。
2.方案2
曲线回归(2)的求取过程,如课本例3-7示。
最终求得的回归方程为:
'106.3147 3.9466y x =+
2 2.6022,78.6605S F ==残。
3.方案3
选取曲线回归(3)求解。
令'1
x x
=
,应用EXCEL 可算的数据,列入表3。
表3 方案3数据处理计算
由表3得
''13
''21()0.2137i x x i l x x ==-=∑
13
21
()21.2105yy i i l y y ==-=∑
'13
''1
()() 2.1011i i x y i l x x y y ==--=-∑
由此得:
'''
1 2.1011
9.83200.2137
x y x x l l β-=
=
=-
'01109.93629.0.18320=111.4877578y x ββ=-=⨯+
故所求的回归方程为:
'111.48779.8320y x =-
进行变量还原得回归方程:
1
111.48779.8320y x
=-
检验假设H 01:10β=.
'21=(9.8320)( 2.1011)20.6580x y S l β=-⨯-=回
2221.210520.65800.5525yy S l S =-=-=回残 2
220.6580411.2905/110.5525/11
S F S ===回残
对给定的0.01α=,查F(1,11)表(附表5)得临界值9.65λ=。
由于F>λ,检验效果显著,所以拒绝H 01,即回归方程有意义。
4.三种方案的综合对比
通过以上求解分析,可知式(1)、(2)和(3)作为回归方程表征y 与因素x 的关系均是有意义的。
三者统计的计算结果如表4示:
表4 三种方案综合对比
由表4,方案3的残差平方和是最小的,因而其回归方程是最优的,拟合效果是最好的,方案2次之,方案1最差。
