从勾股定理到图形面积关系拓展
勾股定理专题总结
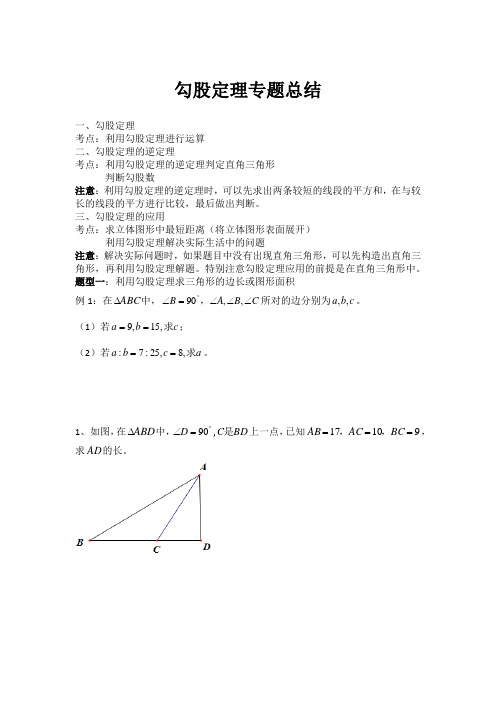
勾股定理专题总结一、勾股定理考点：利用勾股定理进行运算二、勾股定理的逆定理考点：利用勾股定理的逆定理判定直角三角形判断勾股数注意：利用勾股定理的逆定理时，可以先求出两条较短的线段的平方和，在与较长的线段的平方进行比较，最后做出判断。
三、勾股定理的应用考点：求立体图形中最短距离（将立体图形表面展开）利用勾股定理解决实际生活中的问题注意：解决实际问题时，如果题目中没有出现直角三角形，可以先构造出直角三角形，再利用勾股定理解题。
特别注意勾股定理应用的前提是在直角三角形中。
题型一：利用勾股定理求三角形的边长或图形面积例1：在ABC ∆中，C B A B ∠∠∠=∠︒,,90，所对的边分别为c b a ,,。
（1）若c b a 求,15,9==；（2）若a c b a 求,8,25:7:==。
1、如图，在ABD ∆中，︒=∠90D ,BD C 是上一点，已知91017===BC AC AB ，，，求AD 的长。
2、如图，275490====∠=∠︒AF AB BC FAC B ，，，，求正方形CDEF 的面积。
3、在ABC ∆中，BC cm AC cm AB ,20,13==边上的高为12cm ，则ABC ∆的面积为cm.题型二：利用勾股定理说明图形面积之间的关系例2：（1）如图1，分别以ABC Rt ∆三边为边向外作三个正方形，其面积分别用321S S S ，，表示，那么321S S S ，，之间有什么关系？（2）如图2，分别以ABC Rt ∆三边为边向外作三个半圆，其面积分别用321S S S ，，表示，那么321S S S ，，之间有什么关系？4、如图，如果正方形A 的面积是25，正方形C 的面积是169，则正方形B 的面积是。
5、如图是“赵爽弦图”，DAE CDF BCG ABH ∆∆∆∆和,,是四个全等的直角三角形，四边形EFGH ABCD 和都是正方形，如果210==EF AB ，,那么AH 等于。
初二数学(人教版)勾股定理应用(第二课时)—3学习任务单
《勾股定理应用（第二课时）》学习任务单【学习目标】本课应用勾股定理解决问题，体会数形结合、转化、分类讨论的思想方法，感受勾股定理的应用价值，提升数学推理的素养，提高分析问题、解决问题的能力。
共设计四道例题，由图形的几何特征，依据勾股定理发现数量关系（例1，例2，例3（1）），由数量关系发现构图的方法,拼接、画出几何图形(例3（2)，例4)。
【课前预习任务】复习勾股定理.【课上学习任务】1．例1从勾股定理几何原本中的表述起步，改变题目中的条件使图形从正方形到等边三角形到半圆，应用勾股定理，探讨图形发生变化,面积之间不变的数量关系.体验从几何图形特征到代数数量关系的转化，感受勾股定理的应用价值，提升逻辑推理素养。
2．例2的本质是把例1中一条直角边上的正方形经过全等变换改变图形位置得到的新图形，让学生从图形的几何特征，根据勾股定理探讨3个正方形面积间数量关系.使学生再次体验从几何图形特征到代数数量关系的转化，感受勾股定理的应用价值，提升逻辑推理素养。
3．例3(1)借助赵爽弦图，根据勾股定理,把图形面积转化为代数式的值；（2）问根据勾股定理，借助根号13的平方等于13恰好等于2与3的平方和这个数量关系，完成了从长方形到正方形的拼接.本题使学生体会从形到数，从数到形的转化,感受勾股定理的应用价值，提升逻辑推理素养。
4．由满足特殊的数量关系边长，根据勾股定理，找到画线段的方法,再通过按空间顺序有序展开线段的位置的分类讨论，最终应用勾股定理计算线段长度，确定图形。
让我们学生感受到数与形的交汇交融，再次感受勾股定理的应用价值.【课后作业】1。
如图,分别以在Rt∆ABC的三边AC ，BC , AB 为直径画半圆，求证：所得两个月形图案AFCD和月形图案BGCE的面积和等于Rt△ABC的面积。
122.有5个边长为1的正方形，排列形式如图，请把它们分割后拼接成一个大正方形。
3。
∆ABC 三边长分别为2216m n +，2294m n +，222m n +，其中 00,m n >>，且m n >， 请你画出∆ABC 并求出它的面积。
从勾股定理到图形面积关系的拓展定稿版
从勾股定理到图形面积关系的拓展HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】从勾股定理到图形面积的拓展教学目标：1.通过观察图形，探索图形间的关系，发展学生的拓展性思维．2.在将实际问题抽象成数学问题的过程中，提高分析问题、解决问题的能力及渗透数学建模的思想．3.在利用勾股定理解决实际问题的过程中，体验数学学习的实用性．感受数学学习的魅力教学重点：利用勾股定理，解决实际问题教学难点：通过体验图形的变式，学会分析问题解决问题的能力及数学建模思想。
教学过程：一、 向外拓展正方形如图，在Rt △ ABC ，∠C=090中，AB=c,AC=b,BC=a,分别以a,b,c 三边为边做正四边形，那么有132s s s =+证明：∵ 22b s =，23a s =，21c s = 根据勾股定理：222c b a =+∴ 132s s s =+拓展练习：1、如图，是一些由正方形和直角三角形拼合成的图形，其中最大的正方形的边长为7cm．你能求出正方形A、B、C、D的面积之和吗？请试一试．2、如图，在四边形ABCD中，∠DAB=∠BCD=90°，分别以四边形的四条边为边向外作四个正方形，若S1+S4=100，S3=36，则S2=（）3、如图,直线L上有三个正方形a,b,c,若a,c的面积分别为5和11.求正方形b的面积.4、如图,已知1号、4号两个正方形的面积和为7,2号,3号两个正方形的面积为4则A,B,C三个正方形的面积和为多少?二、向外拓展正三角形如图，在Rt △ ABC ，∠C=090中，AB=c,AC=b,BC=a,分别以a,b,c 三边为边做正三角形，那么有132s s s =+如图做三角形2s 的高h ，因为2s 是以b 为边的等边三角形，易得 h=b 23，2s =b b 2321••=243b 同理：2343a s =，2143c s =；)(432232b a s s +=+，根据勾股定理222c b a =+得23243c s s =+=1s 即：132s s s =+三、向外拓展正五边形如图以直角三角形的三边为边长做正五边形，求证：132s s s =+1s S2 3s证明：如图连接正五边形的中心O 与一边端点的连线构成一个等腰三角形，并做出等腰三角形底边上的高h,∵cot α=2c h , ∴αcot 2c h =, ∴ααcot 455cot 22121•=••=c c c S . 同理：αcot 4522•=b s ，αcot 4523•=a s ，∴)(cot 45cot 45cot 45222232a b a b s s +=•+•=+ααα 由勾股定理得：222c b a =+，∴1232cot 45s c s s =•=+α 即：132s s s =+依次类推：以直角三角形的三边为边长做正n 边形时. αcot 422•=b n s ，αcot 423•=a n s ，αcot 421•=c n S ，根据勾股定理：222cb a =+，1232cot 4sc n s s =•=+α 即：132s s s =+通过上面的证明我们就得到了“以任意直角三角形的三边为边长做边数相等的正多边形，以斜边边长为边的正多边形的面积等于以直角边边长为边的两正多边形的面积之和.”四、向外拓展半圆 同样我们还能得到以“任意直角三角形的三边为直径做半圆（或圆），以斜边边长为直径的半圆（或圆）的面积等于以直角边为直径的两个半圆（或圆）的面积之和”. 下面我们来看证明： 已知：如图，直角三角形的两直角边为a,b ，斜边为c,分别以a,b,c 为直径做半圆. 求证：132s s s =+证明：∵ 2218)2(21c c s ππ==，2228)2(21b b s ππ==， 2238)2(21a a s ππ== ∴ )(888222232a b a b s s +=+=+πππ，由勾股定理222c b a =+得：122222328)(888s c a b a b s s ==+=+=+ππππ，即：132s s s =+拓展练习：把大半圆向上翻折，得到如下图：SS欣赏勾股图教学总结：学生畅所欲言自己的切身感受与实际收获，从勾股定理到图形面积关系的拓展练习中感受学习数学的魅力，体会古代数学的文化成就．。
解题技巧专题：勾股定理与面积问题、方程思想压轴题七种模型全攻略(学生版)
解题技巧专题：勾股定理与面积问题、方程思想压轴题七种模型全攻略【考点导航】目录【典型例题】【类型一三角形中，利用面积求斜边上的高】【考点二结合乘法公式巧求面积或长度】【考点三巧妙割补求面积】【考点四“勾股树”及其拓展类型求面积】【考点五几何图形中的方程思想-折叠问题(利用等边建立方程)】【考点六几何图形中的方程思想-公边问题(利用公边建立方程)】【考点七实际问题中的方程思想】【典型例题】【类型一三角形中，利用面积求斜边上的高】1(2023春·新疆阿克苏·八年级校联考阶段练习)若一个直角三角形的两条直角边长分别是5cm 和12cm ，则斜边上的高为多少()A.8013B.13C.6D.6013【变式训练】1(2023春·内蒙古鄂尔多斯·八年级统考期末)如图，在2×2的方格中，小正方形的边长是1，点A 、B 、C 都在格点上，则AC 边上的高为()A.5B.322 C.355D.322(2023春·辽宁朝阳·八年级校考期中)如果一个等腰三角形的腰长为13，底边长为24，那么它底边上的高为()A.12B.24C.6D.53(2022·全国·八年级课时练习)如图，在网格中，每个小正方形的边长均为1．点A、B，C都在格点上，若BD是△ABC的高，则BD的长为．4(2023春·安徽合肥·八年级校考期末)如图所示，在边长为单位1的网格中，△ABC是格点图形，求△ABC中AB边上的高．5如图，在Rt△ABC中，∠C=90°，AC=8，在△ABE中，DE是AB边上的高，DE=12，S△ABE=60．(1)求BC的长．(2)求斜边AB边上的高．6(2023秋·全国·八年级专题练习)在△ABC中，∠C=90°，AC=3，CB=4，CD是斜边AB上高．(1)求△ABC的面积；(2)求斜边AB；(3)求高CD．【类型二结合乘法公式巧求面积或长度】1已知在Rt△ABC中，∠C=90°,∠A,∠B,∠C所对的边分别为a，b，c，若a+b=10cm,c=8cm，则Rt△ABC的面积为()A.9cm2B.18cm2C.24cm2D.36cm2【变式训练】1在△ABC中，AD是BC边上的高，AD=4,AB=410,AC=5，则△ABC的面积为()A.18B.24C.18或24D.18或302直角△ABC三边长分别是x，x+1和5，则△ABC的面积为．【类型三巧妙割补求面积】1(2023春·河南许昌·八年级校考期中)如图，在四边形ABCD中，已知∠B=90°，∠ACB=30°，AB=6，AD=13，CD=5．(1)求证：△ACD是直角三角形；(2)求四边形ABCD的面积．【变式训练】1(2023春·内蒙古呼伦贝尔·八年级校考期中)如图所示，是一块地的平面图，其中AD=4米，CD=3米，AB=13米，BC=12米，∠ADC=90°，求这块地的面积.2(2023春·安徽马鞍山·八年级校考期末)已知a，b，c是△ABC的三边，且a=23，b=36，c=66．(1)试判断△ABC的形状，并说明理由；(2)求△ABC的面积．3(2023春·山东菏泽·八年级校考阶段练习)四边形草地ABCD中，已知AB=3m，BC=4m，CD= 12m，DA=13m，且∠ABC为直角．(1)求这个四边形草地的面积；(2)如果清理草地杂草，每平方米需要人工费20元，清理完这块草地杂草需要多少钱？4(2022春·重庆綦江·八年级校考阶段练习)计算：如图，每个小正方形的边长都为1．(1)求线段CD与BC的长；(2)求四边形ABCD的面积；(3)求证：∠BCD=90°．【类型四“勾股树”及其拓展类型求面积】1(2023秋·重庆渝中·八年级重庆巴蜀中学校考期末)如图，所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、D的面积分别是6、10、4、6，则最大正方形E的面积是()A.20B.26C.30D.52【变式训练】1(2023·广西柳州·校考一模)如图，∠BDE=90°，正方形BEGC和正方形AFED的面积分别是289和225，则以BD为直径的半圆的面积是()A.16πB.8πC.4πD.2π2(2023春·全国·八年级专题练习)如图，以Rt△ABC的三边向外作正方形，其面积分别为S1,S2,S3且S1=4,S2=8，则S3=；以Rt△ABC的三边向外作等边三角形，其面积分别为S1,S2,S3，则S1,S2,S3三者之间的关系为．3(2023春·八年级课时练习)已知：在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别记作a、b、c．如图1，分别以△ABC的三条边为边长向外作正方形，其正方形的面积由小到大分别记作S1、S2、S3，则有S1+S2=S3，(1)如图2，分别以△ABC的三条边为直径向外作半圆，其半圆的面积由小到大分S1、S2、S3，请问S1+S2与S3有怎样的数量关系，并证明你的结论；(2)分别以直角三角形的三条边为直径作半圆，如图3所示，其面积由小到大分别记作S1、S2Sa，根据(2)中的探索，直接回答S1+S2与S3有怎样的数量关系；(3)若Rt△ABC中，AC=6，BC=8，求出图4中阴影部分的面积．4(2023春·江西南昌·八年级南昌市第三中学校考期中)勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理．在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”(如图1)，后人称之为“赵爽弦图”，流传至今．(1)①如图2，3，4，以直角三角形的三边为边或直径，分别向外部作正方形、半圆、等边三角形，面积分别为S1，S2，S3，利用勾股定理，判断这3个图形中面积关系满足S1+S2=S3的有个．②如图5，分别以直角三角形三边为直径作半圆，设图中两个月牙形图案(图中阴影部分)的面积分别为S1，S2，直角三角形面积为S3，也满足S1+S2=S3吗？若满足，请证明；若不满足，请求出S1，S2，S3的数量关系．(2)如果以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程就可以得到如图6所示的“勾股树”．在如图7所示的“勾股树”的某部分图形中，设大正方形M的边长为定值m，四个小正方形A，B，C，D的边长分别为a，b，c，d，则a2+b2+c2+d2=．【类型五几何图形中的方程思想-折叠问题(利用等边建立方程)】1(2023春·河南许昌·八年级统考期中)已知直角三角形纸片ABC的两直角边长分别为6，8，现将△ABC 按如图所示的方式折叠，使点A与点B重合，则CE的长是()A.54B.74C.154D.254【变式训练】1(2023春·湖北咸宁·八年级校考阶段练习)如图，有一块直角三角形纸片，∠C=90°，AC=4，BC= 3，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则BD的长为()A.34B.1.5 C.53D.32(2023春·山东菏泽·八年级统考期中)如图，Rt△ABC中，∠B=90°，AB=4，BC=6，将△ABC折叠，使点C与AB的中点D重合，折痕交AC于点M，交BC于点N，则线段CN的长为．3(2023·辽宁葫芦岛·统考二模)如图，在Rt△ABC中，∠C=90°,∠A=30°,BC=2，点D是AC的中点，点E是斜边AB上一动点，沿DE所在直线把△ADE翻折到△A DE的位置，A D交AB于点F．若△BA F为直角三角形，则AE的长为．4(2022秋·河北张家口·八年级统考期中)在△ABC中，∠C=90°，点D、E分别在AC、AB边上(不与端点重合)．将△ADE沿DE折叠，点A落在A 的位置．(1)如图①，当A 与点B重合且BC=3,AB=5．①直接写出AC的长；②求△BCD的面积．(2)当∠A=37°．①A 与点E在直线AC的异侧时．如图②，直接写出∠A EB-∠A DC的大小；②A 与点E在直线AC的同侧时，且△A DE的一边与BC平行，直接写出∠ADE的度数．【类型六几何图形中的方程思想-公边问题(利用公边建立方程)】1如图，在△ABC中，AB=10，BC=9，AC=17，则BC边上的高为．【变式训练】1已知：如图，在△ABC中，∠C=90°，AD是△ABC的角平分线，CD=3，BD=5，则AC=．2如图，在Rt△ABC和Rt△ADE中，∠B=∠D=90°，AC=AE，BC=DE，延长BC，DE交于点M．(1)求证：点A在∠M的平分线上；(2)若AC∥DM，AB=12，BM=18，求BC的长．【类型七实际问题中的方程思想】1(2022·全国·八年级)明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，踏板一尺离地，送行二步恰竿齐，五尺板高离地⋯⋯”翻译成现代文为：如图，秋千绳索OA悬挂于O点，静止时竖直下垂，A点为踏板位置，踏板离地高度为一尺(AC=1尺)．将它往前推进两步(EB⊥OC于点E，且EB=10尺)，踏板升高到点B位置，此时踏板离地五尺(BD=CE=5尺)，则秋千绳索(OA或OB)长尺．【变式训练】1(2022·全国·八年级课时练习)如图1、2(图2为图1的平面示意图)，推开双门，双门间隙CD的距离为2寸，点C和点D距离门槛AB都为1尺(1尺=10寸)，则AB的长是()A.50.5寸B.52寸C.101寸D.104寸2(2022·河南·金明中小学八年级期中)《九章算术》是我国古代数学名著，有题译文如下：今有门，不知其高宽；有竿，不知其长短．横放，竿比门宽长出4尺；竖放，竿比门高短2尺；斜放，门对角线长恰好是竿长的2倍．问门高、门宽各为多少？3(2022·重庆市求精中学校八年级期中)在一条东西走向的河的一侧有一村庄C，河边原有两个取水点A，B，其中AB=AC，由于某种原由C到A的路现在已经不通，某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上)，并新修一条路CH，测得CB=1.5千米，CH=1.2千米，HB=0.9千米．(1)问CH是否为从村庄C到河边的最近路？请通过计算加以说明．(2)求原来的路线AC的长．4(2022·浙江·浦江县实验中学八年级期中)图1是一张可以折叠的小床展开后支撑起来放在地面的示意图，此时点A、B、C在同一直线上，且∠ACD=90°，图2是小床支撑脚CD折叠的示意图，在折叠过程中，△ACD变形为四边形ABC'D'，最后折叠形成一条线段BD ．某家装厂设计的折叠床是AB=4cm，BC=8cm，(1)此时CD为 cm；(2)折叠时，当AB⊥BC′时，四边形ABC′D′的面积为cm2．。
勾股定理数形结合
勾股定理数形结合勾股定理是数学中非常重要的概念之一，指的是一个直角三角形的两条直角边平方和等于斜边平方，即a²+b²=c²。
这个简单的公式在很多领域都有广泛的应用，例如在建筑、物理、航空、地理、计算机等领域。
在数学中，勾股定理可以用来推导其它三角形的性质和关系，例如三角形面积公式，三角恒等式等。
同时，勾股定理也与许多数学图形和形式紧密相关，例如矩形、正方形、梯形、圆等。
矩形是一个具有四个直角的平面图形。
以矩形为例，可以利用勾股定理推导出其边长和对角线的关系：假设矩形的长为a，宽为b，则矩形的对角线的长度为c，根据勾股定理可以得到a²+b²=c²。
因此，可以得出矩形对角线的长度为sqrt(a²+b²)。
正方形是一个四边相等、四角相等的矩形。
因此，正方形的对角线长度可以利用勾股定理计算。
如果设正方形的边长为a，则正方形对角线长度为sqrt(2a²)。
可以看出，正方形的对角线长度是其边长的sqrt(2)倍。
梯形是一个上底和下底不相等的四边形。
如果将梯形划分成两个直角三角形，可以利用勾股定理求出梯形的高：假设梯形上底长度为a，下底长度为b，斜边长度为c，梯形高为h，则有a²-h²=d，b²-(c-h)²=d，其中d是梯形的高平方。
将这两个式子相加可以消去h²，得到(a²-b²+c²)/2 = h²，从而可以得到梯形的高，即h=sqrt{(a²-b²+c²)/2}。
圆和勾股定理总结勾股定理作为数学中的重要概念，可以与许多数形结合进行应用，例如矩形、正方形、梯形、圆等。
在应用勾股定理时，需要注意图形的性质和特点，根据不同的情况灵活运用公式，才能得出正确的结论。
勾股定理知识点总结
勾股定理知识点总结勾股定理是数学中一个著名的定理，也是初中数学学习的重点内容之一。
它描述了直角三角形中三条边的关系，并且可以应用于解决许多与三角形和几何有关的问题。
本文将对勾股定理的相关知识点进行总结和探讨。
一、勾股定理的表述和公式勾股定理的表述是：“直角三角形斜边上的正方形面积等于其他两边上的正方形面积之和。
”这就是我们通常所说的勾股定理。
勾股定理的公式可以表示为：a² + b² = c²其中，a、b代表直角三角形的两条直角边，c代表直角三角形的斜边。
二、勾股定理的证明勾股定理的证明有多种方法，在此我们以几何证明和代数证明为例进行说明。
几何证明：通过图形的构造和推理来证明勾股定理。
一种常见的几何证明方法是构造以a、b、c为边长的正方形，然后计算正方形的面积，从而证明等式成立。
代数证明：通过数学计算和变换来证明勾股定理。
一种常见的代数证明方法是将直角三角形的三条边的平方进行计算，然后将其相加和化简，最终得到等式成立的结果。
三、勾股定理的应用勾股定理不仅仅是一个数学定理，还有着广泛的应用。
1. 解决三角形的边长和角度问题：通过勾股定理，我们可以已知两条边长来求解第三条边长，或者已知两条边长和一个角度来求解其他角度。
2. 判断三角形的形状：我们可以利用勾股定理来判断一个三角形是直角三角形、锐角三角形还是钝角三角形，从而进一步研究和分析三角形的性质。
3. 解决几何问题：勾股定理还可以应用于解决一些几何问题，例如求解两条直线的交点坐标、求解平面图形的面积、判断是否存在重合图形等等。
四、勾股定理的推广除了直角三角形，勾股定理还可以推广到其他形状的图形。
1. 平方和定理：平方和定理是勾股定理的推广，它描述了非直角三角形中三条边平方的关系。
2. 多边形的对角线：在多边形中，通过某个顶点可以连接其他顶点，形成对角线。
对角线之间的关系也可以通过勾股定理进行研究和计算。
3. 空间中的勾股定理：在空间几何中，勾股定理可以推广到三维空间，描述直角棱柱、直角锥等图形的三条棱或边之间的关系。
中考数学专题复习拓展勾股定理与图形面积关系公开课精品课件
勾股定理的惊奇之处
勾股定理与图形面积关系
重温经典 勾股定理 不同版本教材中的证明方法
a2+b2=c2
c a
b
浙教版
苏教版
沪教版
人教版
简单问题 探寻奥秘
5 3
❶
4
5
=
3❸❷4源自❶=❷5
4
？
+❸
3
对比探索 领悟共性 猜想
a2 b2 c2 线段关系
s1+s2=s3 面积关系
A
S1 3S1aSS11
B
S2 SSS333 4b C
S3 5c
D
9 + 16 = 25
SSS222
实验
推理 共性
S1 1• a2
S1
3 a2 4
S1
8
a2
S2 1•b2
S2
3 b2 4
S2
8
b2
S3 1• c2
S3
3 c2 4
S3
8
c2
S1 Fa2 S2 Fb2 S3 Fc2
提炼总结 品味经典
S3 S1
S2
S3 S1
S2
S3 S1
S2
…… 形状相同，大小不同
在一个直角三角形中，在斜边上所画的任何图形的面积， 等于在两条直角边上所画的与其相似的图形的面积之和。
35 4
形状相同，大小不同
……
拓展延伸，精准深化
S3 S1
S2
S3 S1
S2
S1
S5
S4
S3
S2
S1 S3
S4 S2
S3 S1
S2
S1
S3
S2
勾股定理知识点总结
勾股定理知识点总结一、勾股定理的定义在直角三角形中，两直角边的平方和等于斜边的平方。
如果直角三角形的两条直角边长分别为 a 和 b，斜边长为 c，那么 a²＋ b²＝ c²。
这一定理是数学中非常重要的一个定理，它揭示了直角三角形三条边之间的数量关系。
二、勾股定理的证明勾股定理的证明方法有很多种，以下为大家介绍几种常见的证明方法。
1、赵爽弦图法赵爽弦图是由四个全等的直角三角形拼成一个大正方形，中间是一个小正方形。
大正方形的面积等于四个直角三角形的面积加上小正方形的面积。
设直角三角形的两条直角边分别为 a 和 b，斜边为 c。
大正方形的边长为 c，面积为 c²。
四个直角三角形的面积为 4×（1/2)ab ＝ 2ab，小正方形的边长为（b a)，面积为（b a)²＝ a² 2ab ＋ b²。
所以 c²＝ 2ab ＋ a² 2ab ＋ b²，即 c²＝ a²＋ b²，证明完毕。
2、毕达哥拉斯证明法以直角三角形的斜边为边长作一个正方形，再以两条直角边为边长分别作两个正方形。
通过计算三个正方形的面积，可以证明勾股定理。
设直角三角形的两条直角边分别为 a 和 b，斜边为 c。
斜边为边长的正方形面积为 c²，两条直角边为边长的正方形面积分别为 a²和 b²。
通过将直角边为边长的两个正方形进行分割和拼接，可以发现它们能够恰好填满斜边为边长的正方形，从而证明 a²＋ b²＝ c²。
三、勾股定理的应用1、已知直角三角形的两条边，求第三条边例如，已知一个直角三角形的两条直角边分别为 3 和 4，求斜边的长度。
根据勾股定理，斜边的长度 c ＝√（3²＋ 4²) ＝ 5 。
2、实际生活中的应用（1）建筑工程中，计算建筑物的高度、跨度等。
第18章 勾股定理-认识勾股定理拓展课件 2022--2023学年沪科版数学八年级下册
（2）仿照上面的方法，再结合上面你写出的勾股数，你能否只用绳子，设计一种不同于上面的方法得
到一个直角三角形（在图2中，只需画出示意图．）
分析：
3²+4²=5²
5
∠C是直角
4
10
8
3 C
6
O
图1
图2
例2：古埃及人用下面的方法得到直角三角形，把一根长绳打上等距离的13个结（12段），然后用桩钉钉
（填A或B）
A．勾股定理：直角三角形两直角边的平方和等于斜边的平方
B．勾股定理逆定理：如果三角形的三边长a、b、c满足：a2+b2＝c2，那么这个三角形是直角三角形
（2）仿照上面的方法，再结合上面你写出的勾股数，你能否只用绳子，设计一种不同于上面的方法得
到一个直角三角形（在图2中，只需画出示意图．）
+−
=
2
++
即2ab＝（a+b+c）（a+b-c）
化简得a2+b2＝c2．
B
E
F
C
例3：如图，将直角三角形分割成一个正方形和两对全等的直角三角形，直角三角形
A
ABC中，∠ACB＝90°，BC＝a，AC＝b，AB＝c，正方形IECF中，IE＝EC＝CF＝FI＝x
（1）小明发明了求正方形边长的方法：
+−
2
D
因为AB＝BD+AD，所以a-x+b-x＝c，解得x＝
I
（2）小亮也发现了另一种求正方形边长的方法：
利用S△ABC＝S△AIB+S△AIC+S△BIC可以得到x与a、b、c的关系，请根据小亮的思路完成他
浙教版数学八年级上册《阅读材料 从勾股定理到图形面积关系的拓展》教学设计1
浙教版数学八年级上册《阅读材料从勾股定理到图形面积关系的拓展》教学设计1一. 教材分析《阅读材料从勾股定理到图形面积关系的拓展》是浙教版数学八年级上册的一篇阅读材料。
本节课主要通过介绍勾股定理及其在几何图形面积计算中的应用，让学生了解勾股定理的来历，理解勾股定理的本质，掌握运用勾股定理解决一些简单几何图形面积问题的方法。
教材通过丰富的阅读材料，激发学生的学习兴趣，培养学生的阅读理解能力，提高学生运用数学知识解决实际问题的能力。
二. 学情分析学生在七年级时已经学习了勾股定理的定义和证明，对勾股定理有一定的了解。
但部分学生对勾股定理的理解停留在死记硬背上，缺乏深入理解和灵活运用。
此外，学生在之前的学习中已经接触过一些几何图形的面积计算，但对于如何运用勾股定理解决面积问题还不太清楚。
因此，在教学过程中，教师需要帮助学生深化对勾股定理的理解，引导学生将勾股定理与面积计算相结合，提高学生运用数学知识解决实际问题的能力。
三. 教学目标1.了解勾股定理的来历，理解勾股定理的本质。
2.掌握运用勾股定理解决一些简单几何图形面积问题的方法。
3.培养学生的阅读理解能力，提高学生运用数学知识解决实际问题的能力。
4.激发学生的学习兴趣，培养学生的探究精神。
四. 教学重难点1.重点：了解勾股定理的来历，理解勾股定理的本质；掌握运用勾股定理解决一些简单几何图形面积问题的方法。
2.难点：如何引导学生将勾股定理与面积计算相结合，提高学生运用数学知识解决实际问题的能力。
五. 教学方法1.讲授法：教师通过讲解勾股定理的来历、证明和应用，帮助学生了解和掌握勾股定理。
2.阅读理解法：学生通过阅读教材中的阅读材料，提高阅读理解能力，理解勾股定理在面积计算中的应用。
3.实践操作法：学生通过动手操作，解决实际问题，提高运用数学知识解决实际问题的能力。
4.讨论交流法：学生通过小组讨论，分享学习心得，互相学习，提高学习效果。
六. 教学准备1.教材：浙教版数学八年级上册。
《第一章 3 勾股定理的应用》作业设计方案-初中数学北师大版12八年级上册
《勾股定理的应用》作业设计方案（第一课时）一、作业目标通过本课时作业设计，使学生能够掌握勾股定理的基本概念和应用，培养运用数学知识解决实际问题的能力，加深对勾股定理的理解，并能在实际生活中发现和运用勾股定理。
二、作业内容1. 基础练习：（1）通过不同形式的习题，如填空题、选择题等，让学生熟练掌握勾股定理的公式及计算方法。
（2）设计一些简单的直角三角形问题，让学生运用勾股定理计算边长或角度。
2. 应用实践：（1）设计一些实际问题，如建筑、物理实验等场景中的直角三角形问题，让学生运用勾股定理解决。
（2）设计一些需要运用多个勾股定理解决的复杂问题，培养学生分析问题和解决问题的能力。
3. 拓展提高：（1）让学生尝试自己构造直角三角形，并运用勾股定理解决相关问题。
（2）设计一些需要运用多种数学知识和方法解决的综合性问题，提高学生的数学思维能力和应用能力。
三、作业要求1. 作业量适中，既要保证学生能够掌握知识，又要避免过多作业导致学生负担过重。
2. 题目设计要有层次性，既要包括基础练习，又要包括拓展提高，以满足不同层次学生的需求。
3. 题目要具有代表性，能够充分体现勾股定理的应用和重要性。
4. 作业要注明解题步骤和答案，方便学生自查和教师批改。
5. 要求学生认真完成作业，独立思考，不抄袭他人答案。
四、作业评价1. 教师批改作业时，要关注学生的解题思路和步骤，以及答案的正确性。
2. 对于基础练习部分，要关注学生的掌握情况，对于错误的地方要及时指出并帮助学生改正。
3. 对于应用实践和拓展提高部分，要关注学生的创新能力和解决问题的能力，给予适当的鼓励和指导。
4. 评价结果要及时反馈给学生，让学生了解自己的学习情况和进步。
五、作业反馈1. 教师根据学生的作业情况，及时调整教学计划和教学方法，帮助学生更好地掌握知识。
2. 对于共性问题，可以在课堂上进行讲解和讨论，帮助学生解决疑惑。
3. 对于个别学生的问题，可以通过个别辅导或线上解答等方式进行解决。
八年级上数学勾股定理：练习(拓展)
勾股定理练习1.如图，阴影部分是3个直角三角形，若最大正方形的边长为16，则正方形A，B，C，D的面积和是。
2.如图，Rt△ABC中，∠C=90°，AC=3，BC=4．分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN，四块阴影部分的面积分别为S1、S2、S3、S4．则S1-S2+S3+S4等于。
3.《九章算术》是中国古代的数学代表作，书中记载：今有开门去阃（读kun,门槛的意思）一尺，不合二寸，问门广几何？题目大意是：如图1、2（图2为图1的平面示意图），从点O处推开双门，双门间隙CD的长度为2寸，点C和点D到门槛AB的距离都为1尺（1尺=10寸），则AB的长是。
4.如图，在△ABC中，已知AB=AC=4，BC=6，P是BC边上的一动点（P不与点B、C重合），连接AP，∠B=∠APE，边PE与AC交于点D，当△APD为等腰三角形时，则PB 之长为。
5.在Rt△ABC中，直角边的长分别为a,b,斜边长c,且a+b=3√5，c=5，则ab的值为。
6.已知，CD是Rt△ABC中斜边AB上的高，若BC=6，AC=8，则AD= 。
7.已知一直角三角形的三边长都是正整数，斜边长13，周长为30，则该直角三角形的面积是。
8.已知一直角三角形的三边为a、b、c,其中斜边长c为13，并且周长为30，则这个直角三角形斜边上的高为。
9.如图，在矩形纸片ABCD中，AB=4，BC=8，将△ABC沿AC折叠，使点B落在点E处，CE交AD于点F．（1）求证：△AEF≌△CDF．（2）求FD的长．10.如图所示，在△ABC中，点D是BC上的一点，已知AC=CD=5，AD=6，BD=5，则△ABD3的面积是。
11．如图，在Rt△ABC中，∠ABC=90°，AB=20，BC=15，点D为AC边上的动点，点D 从点C出发，沿边CA往A运动，当运动点A时停止，若设点D运动的时间为t秒，点D运动的速度为每秒2个单位长度．（1）当t=2时，CD= ，AD= ；（请直接写出答案）（2）当t= 时，△CBD是直角三角形；（请直接写出答案）（3）求当t为何值时，△CBD是等腰三角形？并说明理由.12.在Rt△ACB中，∠ACB=90°，点D在边AB上，连接CD，将△ADC沿直线CD翻折，点A恰好落在BC边上的点E处，若AC=3，BE=1，则DE的长是。
浙教版数学八年级上册《阅读材料 从勾股定理到图形面积关系的拓展》教案1
浙教版数学八年级上册《阅读材料从勾股定理到图形面积关系的拓展》教案1一. 教材分析《阅读材料从勾股定理到图形面积关系的拓展》是浙教版数学八年级上册的一篇阅读材料。
本节课主要通过介绍勾股定理以及图形面积关系的拓展，让学生了解并掌握勾股定理在解决实际问题中的应用，以及图形面积计算方法的拓展。
教材通过阅读材料的形式，引导学生主动探究，提高学生的数学素养。
二. 学情分析学生在七年级时已经学习了勾股定理，对勾股定理有一定的认识和理解。
但如何在实际问题中应用勾股定理，以及图形面积关系的拓展，可能还不够熟练。
因此，在教学过程中，教师需要引导学生将已知的勾股定理与实际问题相结合，通过探究和解决实际问题，加深对勾股定理的理解和应用。
三. 教学目标1.了解勾股定理在解决实际问题中的应用。
2.掌握图形面积计算方法的拓展。
3.培养学生的数学思维能力和解决问题的能力。
四. 教学重难点1.重点：勾股定理在解决实际问题中的应用，图形面积计算方法的拓展。
2.难点：如何将勾股定理与实际问题相结合，运用图形面积计算方法解决实际问题。
五. 教学方法采用问题驱动法、案例分析法、小组合作法等教学方法。
通过设置问题情境，引导学生主动探究，以实际案例分析为基础，让学生在解决问题的过程中掌握勾股定理的应用和图形面积计算方法的拓展。
六. 教学准备1.准备相关的实际问题案例。
2.准备图形面积计算的相关材料。
3.准备教学PPT。
七. 教学过程1.导入（5分钟）通过一个实际问题情境，如测量一个直角三角形的斜边长度，引导学生回顾勾股定理。
让学生思考：勾股定理在解决这个问题中起到了什么作用？2.呈现（15分钟）呈现一系列与勾股定理相关的实际问题，让学生独立思考并尝试解决。
如：一个直角三角形的两条直角边长分别为3cm和4cm，求斜边长度。
引导学生运用勾股定理解决问题。
3.操练（20分钟）让学生分组合作，探讨并解决更多的实际问题。
如：一个长方形的长和宽分别为8cm和6cm，求长方形的对角线长度。
基于勾股定理探究图形面积之间的关系
基于勾股定理探究图形面积之间的关系作者：王玲来源：《新课程教学》2015年第02期【摘要】勾股定理是平面几何中一个基本而重要的定理，勾股定理对于解决一些与直角三角形相关的问题起到了不可低估的作用.本文结合实例阐述了勾股定理与其关联图形面积之间的关系以及运用勾股定理解决图形面积问题.【关键词】初中数学勾股定理图形面积勾股定理是平面几何中一个基本而重要的定理.它揭示了直角三角形三边之间的平方关系，即平面上的直角三角形的两条直角边的长度（古称勾长、股长）的平方和等于斜边长（古称弦长）的平方.勾股定理对于解决一些与直角三角形相关的问题起到了不可低估的作用.从一个直角三角形出发，分别以其三边为边长向外作正方形，斜边上正方形的面积等于两直角边上正方形面积之和，此称为勾股图（如图1）.在平常解题过程中，我们会经常遇到一些由勾股图延伸出来的图形，并且要求我们找出图形面积之间的关系.万变不离其宗，这些问题始终都与勾股定理有关.下面就运用勾股定理处理图形的面积问题举例说明.一、分类探究勾股定理与其关联图形面积之间的关系例1如图2，从一个直角三角形出发，分别以其三边为边长向外作正三角形，其面积分别为S1，S2，S3，则S1，S2，S3之间的关系是图2分析：这一问题是将勾股图中的正方形变化为正三角形加以考查，因此自然地联系到勾股定理的相关知识. 设直角三角形的两条直角边分别为a，b，斜边为c，则有a2+b2=c2.解：已知△ABC是直角三角形，由勾股定理得a2+b2=c2.因为分别以直角三角形的三边为边长向外作正三角形，所以S1=34a2， S2=34b2， S3=34c2.现已知a2+b2=c2，在这个等式左右两边同时乘34，得34a2+34b2=34c2，即S1+S2=S3.通过分析所得结论，不难发现：三个正三角形的面积关系与勾股图中三个正方形的面积关系相同，都是：S1+S2=S3. 上题是针对正三角形而加以讨论和分析的，而勾股图中研究的是正方形，正方形即正四边形，那么我们是否可以猜想：如果从一个直角三角形出发，分别以其三边为边长向外作正n边形，其面积分别为S1，S2，S3，那么就有S1+S2=S3呢？（如图3，图4）下面进行验证：易知，正n边形的面积公式是：S正n边形=14n·tan90°-180°n·l2（其中n表示边数， l表示边长）， 14n·tan90°-180°n是一常数，那么在等式a2+b2=c2的左右两边同时乘以14n·tan90°-180°n，等式仍然成立，即14n·tan90°-180°n·a2+14n·tan90°-180°n·b2=14n·tan90°-180°n·c2，得S1+S2=S3，因此我们的猜想是正确的.图5例2如图5，从一个直角三角形出发，分别以其三边为直径向外作半圆，其面积分别为S1， S2，S3，则S1，S2，S3之间的关系是分析：本题是将勾股图中的正方形变化为半圆，同样利用勾股定理相关知识进行解答.解：由勾股定理得a2+b2=c2，又S1=π8a2，S2=π8b2，S3=π8c2，在等式a2+b2=c2左右两边同时乘π8，得π8a2+π8b2=π8c2，即S1+S2=S3.由此，我们得出如下结论：从一个直角三角形出发，先以斜边为边向外作任一平面图形，再以两条直角边为边向外作与之相似的平面图形，那么较大的图形的面积就等于较小的两个图形的面积之和.像上面所提及的所有的正n边形、所有的半圆，还有我们初中阶段接触的所有的等腰直角三角形都是相似图形，（就向外作等腰直角三角形而言，要么三边都做直角边，要么三边都作斜边）遇到这些图形或问题时，直接利用这个结论即可. 若不能够直接得出其相似，则首先进行分析和判断.二、基于勾股定理解决图形面积问题例3如图6，已知△ABC的三边长分别为5，12，13，分别以三边为直径向上作三个半圆，求图中阴影部分的面积.图6分析：此题由例2变化而生成，不妨仍延续图5中的解法.解：由勾股定理的逆定理知△ABC为直角三角形，那么S阴影=S1+S2+SΔABC-S3=SΔABC=30.显然利用上述结论，处理这一问题要简捷许多.例4如图7，梯形ABCD中，AB∥DC，∠ADC+∠BCD=90°，且DC=2AB，分别以DA，AB，BC为边向梯形外作正方形，其面积分别为S1，S2，S3，则S1，S2，S3之间的关系是分析：图上有三个正方形，结合问题，仍然是找出这三个正方形面积之间的关系，但是仔细观察此图形，发现与勾股图有所不同的是将直角三角形变成了梯形.如图8，过点A作AE∥BC交CD于点E，得到平行四边形AECB和Rt△ADE，根据平行四边形的性质和勾股定理，不难证明三个正方形的边长分别等于对应所得直角三角形的三边解：如图8，过点A作AE∥BC交CD于点E，∵AB∥DC，∴四边形AECB是平行四边形，∴AB=EC， BC=AE，∠BCD=∠AED，∵∠ADC+∠BCD=90°， DC=2AB，∴AB=DE，∠ADC+∠AED=90°，∴∠DAE=90°那么AD2+AE2=DE2.∵S1=AD2， S2=AB2=DE2， S3=BC2=AE2，∴S2=S1+S3.本题的关键在于通过作辅助线把梯形的问题转换为平行四边形和直角三角形的问题，然后把三个正方形的边长整理到一个三角形中进行解题. 掌握了勾股定理与图形面积之间的关系，那么做此类题就游刃有余了.图9例4变式题如图9，梯形ABCD中，AB∥CD，∠ADC+∠BCD=90°，以AD，AB，BC为斜边向外作等腰直角三角形，其面积分别是S1，S2，S3 ，且S1 +S3 =4S2，则CD=（）.① 25AB ② 3AB ③ 35AB ④4AB分析：本题首先给出图形面积之间的关系，反过来推导边之间的关系，是针对例4一次很好的逆向思维的考查：当熟知本题基本探究思路后，解题会很顺畅，不难得出正确答案：选项②.图10例5如图10，△ABC中，∠ACB=90°，AC>BC，分别以△ABC的边AB，BC，CA 为一边向△ABC外作正方形ABDE，BCMN，CAFG，连接EF，GM，ND，设△AEF，△BND，△CGM的面积分别为S1，S2，S3，则下列结论正确的是（）.AS1=S2=S3BS1=S2CS1=S3分析：本题在勾股图的基础上进行延伸，灵活而巧妙地考查了解直角三角形及三角形的面积等一系列知识.基于勾股定理而与之相关联的图形面积问题是中考中常见的题型之一.解：过点E作EH⊥FA交FA的延长线于点H，∵∠CAB+∠BAH=90°，∠EAH+∠BAH=90°，∴∠CAB=∠EAH.又∠ACB=∠AHE=90°，AB=AE，∴△ACB≌△AHE（AAS），∴CB=EH.易知 S2=12·CM·CG=12·CB·AC= S△ACB，S1=12·FA·EH=12·AC·CB = S△ACB∴S1=S2. 同理，S3=S△ACB ，∴S1=S2=S3.总之，在运用勾股定理解决数学问题时，应该注意变通及创新，这样才能做到无论试题怎么改头换面，都能够根据所学的知识点顺利解答.参考文献[1]华建女.例解已知图形面积的一类几何问题[J].初中数学教与学，2011（01）.[2]刘清泉.构造“弦图”巧解题[J].中学数学，2013（02）.。
勾股定理中数形结合思想之应用
勾股定理中数形结合思想之应用摘要：深度学习勾股定理中数形结合思想的应用，进一步体会勾股定理的美妙之处，体会数形结合这种数学思想在勾股定理中的应用。
在数学学习过程中，要抓住问题的根本，深挖教材，数学考题万变不离其宗。
关键词：勾股定理数形结合思想面积我们在日常教学中时常也会出现类似情况：只知道有问题，却不能抓住问题的核心和根基。
初中要学勾股定理的变式及应用，好多学生对勾股定理简单的应用掌握得很好，比如在直角三角形中，知道两边求第三边，学生立刻会想到用勾股定理去解决问题，但是勾股定理的灵活变式题目，好多学生遇到这种灵活变式题目会感到束手无策，追根到底是对勾股定理中的数学思想方法没有彻底理解掌握。
山东教育出版社七年级上册数学第三章是勾股定理，勾股定理的内容相信对每个学习过初中数学的人来说都不陌生，美丽的勾股树带给人无穷的遐想，为深度学习勾股定理中数形结合思想的应用，进一步体会勾股定理的美妙之处，体会数形结合这种数学思想在勾股定理中的应用，我们先通过具体的例子来看一下，课本68页有这样的一个题目：原题：如图所有的四边形都是正方形，所有的三角形都是直角三角形，请在图中找出若干个图形，使得它们的面积之和恰好等于最大的正方形的面积。
本题能很好地考察学生对勾股定理中数形结合思想的应用：从a2+b2=c2数量关系转化到图形之间面积的关系。
解析：第一种：1号和2号正方形的面积之和等于最大的正方形的面积。
第二种：3号、4号和2号正方形的面积之和等于最大的正方形的面积。
第三种：5号、6号和1号正方形的面积之和等于最大的正方形的面积。
第四种：3号、4号、5号和6号正方形的面积之和等于最大的正方形的面积。
学生常见失误分析：学生考虑不全，不会勾股定理中数形结合思想的应用，从a2+b2=c2数量关系转化到图形之间面积的关系不熟练。
通过书本上的题目，我们能收获到勾股定理中数形结合思想的应用，从a2+b2=c2数量关系转化到图形之间面积的关系，我们再来看一下上述题目的变式题目1：已知：如上图正方形ABCD的面积是150，3号、4号、2号正方形面积之和是 150 ；若5号，6号正方形面积之和是70，则3号，4号正方形面积之和是 80 。
勾股定理面积与等边三角形
不难证明S1=S2+S3 .
C S2
S1 a b
B
c
A
S3
五变： 直角三角形ABC的面积为20cm2 ,在 AB的同侧分别以AB、BC、CA为直径做三 个半圆，求阴影部分的面积。
C
b
a
A
c
B
S阴=S较大半圆 +S小半圆 +S△ S大半圆
如图6，Rt△ABC中，AC=8，BC=6，∠C=90°，分别以 AB、BC、AC为直径作三个半圆，那么阴影部分的面 积为
面积.
A
⑴求它的高. ⑵求它的面积.
6 30° 6
33
B
D
C
6
1、如图，在△ABC中，AB=AC=17， BC=16，求△ABC的面积。
(2)求腰AC上的高。
A
17 15 17
88
B
D
C
16
2 、 如 图 6 ， 在 △ ABC 中 ， AD⊥BC ， AB=15，AD=12，AC=13，求△ABC的 周长和面积。
A
17 8 10
∟
B
C
∟
D
2
A
4
6
B4 C
如图，在等腰梯形ABCD中，AB=2,BC=4, ∠B= 450 求梯形的面积。
如图，在直角梯形ABCD中，AD=6,BC=11, AB=13,求梯形的周长。
已知：如图，四边形ABCD
中，∠B＝900，AB＝3，BC＝4，
CD＝12，AD＝13,求四边形
ABCD的面积?
解 在直角三角形ABC中
c2
S1
S2
1
a2
b2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
如图所示， sⅠ，sⅡ，sⅢ之间有什么数量关系？
sⅡ
sⅠ
sⅢ
s1s2 s3 sⅠ+ sⅡ=sⅢ
这节课你收获了……
a2+b2=c2
s1+s2=s3
如图，已知△ABC的三边长为别为5，12， 13，分别以三边为直径向上作三个半圆， 求图中阴影部分的面积。
四边形ABCD中AB∥CD，∠ADC＋∠BCD＝ 90°，以AD、AB、BC为斜边均向形外作等腰 直角三角形，其面积分别是S1、S2、S3 ，且S1 ＋S3＝4S2，则CD＝( ) A．2.5AB B．3AB C．3.5AB D．4AB
E
S1
F
A
D
C
B
G
S3
S2
M
如图，在△ABC中，∠ACB＝90º，AC＞BC，分别以AB、BC、CA来自一边向△ABC外作正方形ABDE、
BCMN、CAFG，连接EF、GM、ND，设△AEF、
△BND、△CGM的面积分别为S1、S2、S3，则下 列结论正确的是（ ）
A．S1＝S2＝S3 C．S1＝S3＜S2
B．S1＝S2＜S3 D．S2＝S3＜S1
已知：如图，以Rt△ABC的三边a、b、c为
边分别向外作等腰直角三角形．面积分别为S1、
S2、S3，若斜边c＝6，则S1+S2为
．
斜边或直角边
其实，在欧几 里得时代，人 们就已经知道 了勾股定理的 一些拓展。例 如，《原本》 第六卷曾介绍： “在一个直角 三
角形中，在斜边 上所画的任何图 形的面积，等于 在两条直角边上 所画的与其相似 的图形的面积之 和。”
AB=4，分别以AC、BC为直径作半圆，面积 分别记为S1、S2，则S1+S2的值等于 2π .
S1
A
C
S2
B
已知：如图，以Rt△ABC的三边a、b、c为
边分别向外作等腰直角三角形．面积分别为S1、
S2、S3，若斜边c＝6，则S1+S2为
．
S1+S2= 18
S1+S2= 9
s11 2a2,s21 2b2,s31 4c2
A、13 B、26 C、47
D、94
34
13
2、如图，阴影正方形部分的面积是 84 .
3、如图，直线l上有三个正
10 4
方形，面积分别为a,b,c,若
a=5,c=11，则b为（ C ）
A．5 B．6 C．16 D．55
如图，如果以直角三角形的三条边a，b，c为 边，向外分别作正三角形，那么是否存在 s1+s2=s3呢？
如图，如果以直角三角形的三条边a，b，c为 直径，向外分别作半圆，那么s1+s2=s3依然成 立吗？
s112π(a2)2
1πa2 8
同理 s2， 8 1b2,s38 1c2
s1 s28 1a 28 1b 28 1(a 2 b 2)
a2b2c2
s1s2
1c2
8
s3
如图，已知在Rt△ABC中， ∠ ACB=Rt∠，
在Rt△ABC中，分别以a,b,c为边向外作正方 形，如图所示，则s1,s2,s3有什么数量关系？
a2+b2=c2
s1+s2=s3
1．如图是一株美丽的勾股树，其中所有的四
边形都是正方形，所有的三角形都是直角三角
形．若正方形A、B、C、D的面积分别是9、
25、4、9，则最大正方形E的面积是 （ C ）