反三角函数知识点总结
反三角函数知识点总结
反三角函数知识点总结一、反正弦函数反正弦函数记作y = arcsin x，其中x ∈ [–1，1]，y ∈ [–π/2，π/2]。
1．定义域和值域反正弦函数的定义域是[-1,1]，值域是[-π/2,π/2]。
即反正弦函数的输入值在[-1,1]之间，输出值在[-π/2,π/2]之间。
2．性质（1）y = arcsin x ⇔ sin y = x；（2）反正弦函数是奇函数，即arcsin(-x) = -arcsin x；（3）反正弦函数在[-1,1]上是单调递增的；（4）反正弦函数的图像在[-1,1]上是关于直线x=y对称的；（5）反正弦函数是周期函数，其最小正周期是2π；（6）反正弦函数的导数是1 / √(1 - x²)，其中|x| < 1；（7）反正弦函数在x=0处的导数为1。
二、反余弦函数反余弦函数记作y = arccos x，其中x ∈ [–1，1]，y ∈ [0，π]。
1．定义域和值域反余弦函数的定义域是[-1,1]，值域是[0,π]。
即反余弦函数的输入值在[-1,1]之间，输出值在[0,π]之间。
2．性质（1）y = arccos x ⇔ cos y = x；（2）反余弦函数是偶函数，即arccos(-x) = arccos x；（3）反余弦函数在[-1,1]上是单调递减的；（4）反余弦函数的图像在[-1,1]上是关于直线x=y对称的；（5）反余弦函数是周期函数，其最小正周期是2π；（6）反余弦函数的导数是-1 / √(1 - x²)，其中|x| < 1；（7）反余弦函数在x=1处的导数为0。
三、反正切函数反正切函数记作y = arctan x，其中x ∈ R，y ∈ (-π/2，π/2)。
1．定义域和值域反正切函数的定义域是R，值域是(-π/2，π/2)。
即反正切函数的输入值是实数，输出值在(-π/2，π/2)之间。
2．性质（1）y = arctan x ⇔ tan y = x；（2）反正切函数是奇函数，即arctan(-x) = -arctan x；（3）反正切函数在整个定义域上是单调递增的；（4）反正切函数的图像在整个定义域上是关于直线x=y对称的；（5）反正切函数是周期函数，其最小正周期是π；（6）反正切函数的导数是1 / (1 + x²)；（7）反正切函数在x=0处的导数为1。
反三角函数知识点总结
反三角函数知识点总结反三角函数知识点总结反三角函数并不难，关键是要理解反三角函数的意义，这是其一，第二要充分掌握诱导公式，反三角其实是考察由三角函数值表示非特殊角，所以经常要用到π+arcsin,π-arcsin，2π+，2π-等，欢迎阅读反三角函数知识点总结，了解清楚，大家要准确表示反三角函数一定要学好诱导公式哦。
反三角函数主要是三个：y=arcsin(x)，定义域[-1,1] ，值域[-π/2,π/2]图象用红色线条;y=arccos(x)，定义域[-1,1] ，值域[0,π]，图象用蓝色线条;y=arctan(x)，定义域(-∞,+∞)，值域(-π/2,π/2)，图象用绿色线条;sin(arcsin x)=x,定义域[-1,1],值域 [-1,1] arcsin(-x)=-arcsinx其他公式arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)当x∈[—π/2，π/2]时，有arcsin(sinx)=x当x∈[0,π],arccos(cosx)=xx∈(—π/2，π/2),arctan(tanx)=xx∈(0，π),arccot(cotx)=xx〉0,arctanx=π/2-arctan1/x,arccotx类似若(arctanx+arctany)∈(—π/2，π/2),则arctanx+arctany=arctan(x+y/1-xy)。
高三数学教案_第六章_6-3反三角函数
反三角函数[知识点归纳]例4 求函数2()lg arccos 84x x f x ⎡⎤⎛⎫=+⎢⎥⎪⎝⎭⎣⎦的定义域与值域 解：2arccos 0.84x x ⎛⎫+> ⎪⎝⎭21 1.84x x∴-≤+<解上述不等式，得4 2.x -<<2()lg arccos 84x x f x ⎡⎤⎛⎫∴=+⎢⎥⎪⎝⎭⎣⎦的定义域为(4,2).- 22211111(21)(1)8488888x x x x x +=++-=+-≥-210arccos arccos .848x x ⎛⎫⎛⎫∴<+≤- ⎪ ⎪⎝⎭⎝⎭所以函数2()lg arccos 84x x f x ⎡⎤⎛⎫=+⎢⎥⎪⎝⎭⎣⎦的值域为1(,lg arccos ].8⎛⎫-∞- ⎪⎝⎭例6 已知arcsin arcsin(1).x x >- 求x 的取值范围解：因为反正弦函数是增函数，由反三角函数的定义域可得不等式组11,111,1,x x x x -≤≤⎧⎪-≤-≤⎨⎪>-⎩解不等式组，得1 1.2x <≤例7计算：cos 3π⎛⎫⎪⎝⎭解：设α=则tan α且0.2πα<<cos sin αα∴==则25cos 22cos 1,sin 27ααα=-=-=原式＝515cos 2cos sin 2sin33727214ππαα+-=-⋅-=-12．关于t 的方程2253172(23)0848t x t x x +++++=有两个不同的实数根，求函数sin y x =的反函数。
解：225317(23)420848x x x ⎛⎫∆=+-⨯⨯++>⎪⎝⎭即，2680x x -+<，解得2 4.x <<,22x πππ⎡⎤-∈-⎢⎥⎣⎦，sin()sin .x x y π-==sin (24)y x x ∴=<<的反函数为arcsin ,(sin 4,sin 2).y x x π=-∈13．设方程240x ++=的2个实根为1x 、2x ，若1arctan x α=，2arctan x β=，求αβ+的值。
三角函数和反三角函数图像性质、知识点总结(精编文档).doc
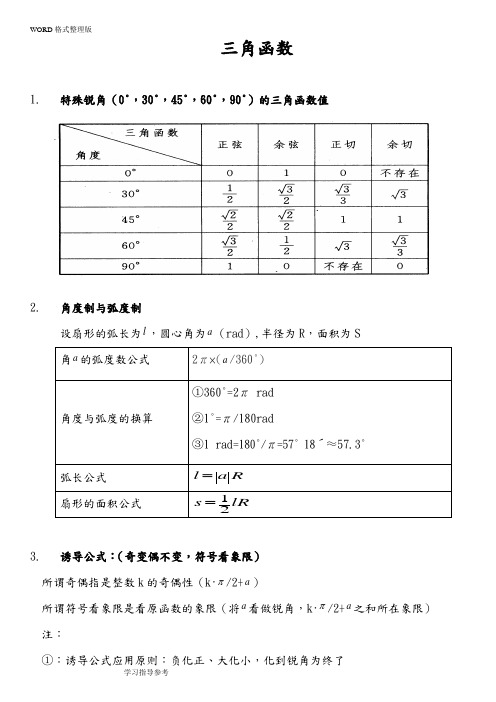
【最新整理，下载后即可编辑】三角函数1. 特殊锐角（0°，30°，45°，60°，90°）的三角函数值2. 角度制与弧度制设扇形的弧长为l ，圆心角为a （rad ）,半径为R ，面积为S角a 的弧度数公式2π×(a /360°)角度与弧度的换算①360°=2π rad ②1°=π/180rad③1 rad=180°/π=57° 18′≈57.3°弧长公式 l a R =扇形的面积公式 12s lR =3.诱导公式：（奇变偶不变，符号看象限） 所谓奇偶指是整数k 的奇偶性（k ·π/2+a ）所谓符号看象限是看原函数的象限（将a 看做锐角，k ·π/2+a 之和所在象限） 注：①：诱导公式应用原则：负化正、大化小，化到锐角为终了 4. 三角函数的图像和性质：（其中z k ∈） ①：三角函数 xy sin =x y cos = xy tan = cot y x=函 数 图 象定义域 R R 2x k ππ≠+x k π≠值域 [-1,1][-1,1]RR周期2π2πππ奇偶性 奇 偶奇非奇非偶单 调 性2,222k k ππππ⎡⎤-+↑⎢⎥⎣⎦2,222k k ππππ⎡⎤-+↑⎢⎥⎣⎦ []2,2k k πππ-↑ []2,2k k πππ+↓,22k k ππππ⎡⎤-+↑⎢⎥⎣⎦ [],k k πππ+↓对 称 性 :2x k ππ=+对称轴对称中心:(,0)k π :x k π=对称轴:对称中心(+,0)2k ππ:对称中心(,0)2k π零值点 πk x = 2ππ+=k xπk x =2ππ+=k x最 值 点2ππ+=k x ,1max=y2ππ-=k x ,1min -=yπk x 2=，1max =y ；2y k ππ=+，1min -=y)sin(ϕω+=x A y （1） 函数)sin(ϕω+=x A y 和)cos(ϕω+=x A y 的周期都是ωπ2=T（2） 函数)tan(ϕω+=x A y 和)cot(ϕω+=x A y 的周期都是ωπ=T5.三角函数尺度变换sin y x =经过变换变为sin y x ϖϕ=+A （）的步骤（先平移后伸缩）：1sin sin sin sin y x y x y x y x ϖϕϖϖϖϕϖϕ=−−−−−−−→=−−−−−→=+−−−−−−−→=+横坐标变为原来的倍向左或向右纵坐标不变平移个单位纵坐标变为原来的A 倍横坐标不变（）A （）6.三角函数的对称变换：① )()(x f y x f y -=→=) 将)(x f y =图像绕y 轴翻折180°（整体翻折） （对三角函数来说：图像关于x 轴对称）② )()(x f y x f y -=→=将)(x f y =图像绕x 轴翻折180°（整体翻折） （对三角函数来说：图像关于y 轴对称）③ )()(x f y x f y =→= 将)(x f y =图像在y 轴右侧保留，并把右侧图像绕y 轴翻折到左侧（偶函数局部翻折）④ )()(x f y x f y =→=保留)(x f y =在x 轴上方图像，x 轴下方图像绕x 轴翻折上去（局部翻动）7.反三角函数的图像与性质：性质图像定义域 ［-1，1］ ［-1，1］ (-∞，+∞) (-∞，+∞) 值域 ［-2π，2π］［0，π］(-2π，2π)(0，π)单调性 []1,1- 增函数 []1,1- 减函数 (),-∞+∞增函数 (),-∞+∞减函数 奇偶性arcsin()arcsin θθ-=-arccos()arccos θπθ-=-arctan()arctan θθ-=-arccot()arccot θπθ-=-周期性非周期函数非周期函数非周期函数非周期函数7.三角函数公式：（1）倒数关系： （2）平方关系：tan cot 1sin csc 1cos sec 1αααααα⋅=⋅=⋅= 222222sin cos 11tan sec 1cot csc αααααα+=+=+=（3）三角和与差公式：sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβαβαβαβαβαβαβ+=++=-++=- sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβαβαβαβαβαβαβ-=--=+--=+（4）二倍角公式：()22222sin 22sin cos cos 2cos sin 2cos 112sin 2tan tan 21tan ααααααααααα==-=-=-=-升幂公式22221cos 2sin 1cos 22sin 2(1cos 21cos 22cos cos 2αααααααα-⎫=⎪⎧-=⎪⎪⇒⎬⎨++=⎪⎩⎪=⎪⎭降幂公式） （5）三角函数的和差化积公式 （6）三角函数的积化和差公式sin sin 2sin cos22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅[][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+-- 六边形记忆法：图形结构“上弦中切下割，左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
三角函数及反三角函数图像性质、知识点总结
三角函数 1. 特殊锐角（0°，30°，45°，60°，90°）的三角函数值2.角度制与弧度制设扇形的弧长为l ，圆心角为a （rad ）,半径为R ，面积为S 角a 的弧度数公式 2π×(a /360°)角度与弧度的换算①360°=2π rad ②1°=π/180rad③1 rad=180°/π=57° 18′≈57.3°弧长公式 l a R =扇形的面积公式 12s lR =3.诱导公式：（奇变偶不变，符号看象限）所谓奇偶指是整数k 的奇偶性（k ·π/2+a ）所谓符号看象限是看原函数的象限（将a 看做锐角，k ·π/2+a 之和所在象限） 注：①：诱导公式应用原则：负化正、大化小，化到锐角为终了4. 三角函数的图像和性质：（其中z k ∈）①：三角函数x y sin = x y cos =x y tan = cot y x=函 数 图 象定义域 R R 2x k ππ≠+x k π≠值域 [-1,1][-1,1]RR周期 2π2πππ奇偶性 奇偶奇非奇非偶单 调 性 2,222k k ππππ⎡⎤-+↑⎢⎥⎣⎦2,222k k ππππ⎡⎤-+↑⎢⎥⎣⎦[]2,2k k πππ-↑ []2,2k k πππ+↓,22k k ππππ⎡⎤-+↑⎢⎥⎣⎦[],k k πππ+↓对 称 性 :2x k ππ=+对称轴对称中心:(,0)k π:x k π=对称轴:对称中心(+,0)2k ππ:对称中心(,0)2k π零值点 πk x =2ππ+=k xπk x =2ππ+=k x最 值 点2ππ+=k x ,1max=y2ππ-=k x ,1min-=yπk x 2=，1max =y ；2y k ππ=+，1min -=y②：函数)sin(ϕω+=x A y 的图像与性质：（1） 函数)sin(ϕω+=x A y 和)cos(ϕω+=x A y 的周期都是ωπ2=T（2） 函数)tan(ϕω+=x A y 和)cot(ϕω+=x A y 的周期都是ωπ=T5.三角函数尺度变换sin y x =经过变换变为sin y x ϖϕ=+A （）的步骤（先平移后伸缩）： 1sin sin sin sin y x y x y x y x ϖϕϖϖϖϕϖϕ=−−−−−−−→=−−−−−→=+−−−−−−−→=+横坐标变为原来的倍向左或向右纵坐标不变平移个单位纵坐标变为原来的A 倍横坐标不变（）A （）6.三角函数的对称变换：① )()(x f y x f y -=→=) 将)(x f y =图像绕y 轴翻折180°（整体翻折） （对三角函数来说：图像关于x 轴对称）② )()(x f y x f y -=→=将)(x f y =图像绕x 轴翻折180°（整体翻折） （对三角函数来说：图像关于y 轴对称）③ )()(x f y x f y =→= 将)(x f y =图像在y 轴右侧保留，并把右侧图像绕y 轴翻折到左侧（偶函数局部翻折）④ )()(x f y x f y =→=保留)(x f y =在x 轴上方图像，x 轴下方图像绕x 轴翻折上去（局部翻动）7.反三角函数的图像与性质：名称y=arsinx y=arccosx y=arctanx y=arccotx定义y=sinx((,))22xππ∈-的反函数，叫做反正弦函数y=cosx((0,))xπ∈的反函数，叫做反余弦函数y=tanx((,))22xππ∈-的反函数，叫做反正切函数y=cotx((0,))xπ∈的反函数，叫做反余切函数性质图像定义域［-1，1］［-1，1］(-∞，+∞)(-∞，+∞)值域［-2π，2π］［0，π］(-2π，2π) (0，π) 单调性[]1,1-增函数[]1,1-减函数(),-∞+∞增函数(),-∞+∞减函数奇偶性arcsin()arcsinθθ-=-arccos()arccosθπθ-=-arctan()arctanθθ-=-arccot()arccotθπθ-=-周期性非周期函数非周期函数非周期函数非周期函数7.三角函数公式：（1）倒数关系： （2）平方关系：tan cot 1sin csc 1cos sec 1αααααα⋅=⋅=⋅= 222222sin cos 11tan sec 1cot csc αααααα+=+=+=（3）三角和与差公式：sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβαβαβαβαβαβαβ+=++=-++=- sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβαβαβαβαβαβαβ-=--=+--=+（4）二倍角公式：()22222sin 22sin cos cos 2cos sin 2cos 112sin 2tan tan 21tan ααααααααααα==-=-=-=-升幂公式 22221cos 2sin 1cos 22sin 2(1cos 21cos 22cos cos 2αααααααα-⎫=⎪⎧-=⎪⎪⇒⎬⎨++=⎪⎩⎪=⎪⎭降幂公式） （5）三角函数的和差化积公式 （6）三角函数的积化和差公式sin sin 2sin cos22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅ [][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+-- 六边形记忆法：图形结构“上弦中切下割，左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
反三角函数知识点总结
《反三角函数知识点总结》一、引言三角函数是数学中一个重要的分支，在几何学、物理学、工程学等领域都有广泛的应用。
而反三角函数则是三角函数的反函数，它们为解决一些特定类型的问题提供了有力的工具。
本文将对反三角函数的知识点进行全面总结，帮助读者更好地理解和掌握这一重要概念。
二、反三角函数的定义1. 反正弦函数- 定义：对于任意实数\(x\)，如果\(\sin y = x\)，且\(-\frac{\pi}{2}\leq y\leq\frac{\pi}{2}\)，那么\(y=\arcsin x\)，反正弦函数\(\arcsin x\)的定义域是\([-1,1]\)，值域是\([-\frac{\pi}{2},\frac{\pi}{2}]\)。
- 图像：反正弦函数的图像是一段在\([-\frac{\pi}{2},\frac{\pi}{2}]\)区间内的曲线，关于原点对称。
2. 反余弦函数- 定义：对于任意实数\(x\)，如果\(\cos y = x\)，且\(0\leq y\leq\pi\)，那么\(y=\arccos x\)，反余弦函数\(\arccos x\)的定义域是\([-1,1]\)，值域是\([0,\pi]\)。
- 图像：反余弦函数的图像是一段在\([0,\pi]\)区间内的曲线，关于\(y\)轴对称。
3. 反正切函数- 定义：对于任意实数\(x\)，如果\(\tan y = x\)，且\(-\frac{\pi}{2}\lt y\lt\frac{\pi}{2}\)，那么\(y=\arctan x\)，反正切函数\(\arctan x\)的定义域是\(R\)，值域是\((-\frac{\pi}{2},\frac{\pi}{2})\)。
- 图像：反正切函数的图像是一条在\((-\frac{\pi}{2},\frac{\pi}{2})\)区间内的曲线，关于原点对称。
三、反三角函数的性质1. 定义域和值域- 反正弦函数、反余弦函数和反正切函数的定义域都是有一定限制的，分别是\([-1,1]\)、\([-1,1]\)和\(R\)。
反三角函数知识点
反三角函数知识点反三角函数是一类与三角函数相反的函数，它们在数学和工程领域有着广泛的应用。
反三角函数包括反正弦函数（arcsin）、反余弦函数（arccos）、反正切函数（arctan）等。
以下是反三角函数的知识点概述：1.反三角函数的定义：反三角函数是三角函数的反函数，定义为：反正弦函数（arcsin）：y = arcsin(x) 表示一个角度x（弧度制），其正弦值为y。
反余弦函数（arccos）：y = arccos(x) 表示一个角度x（弧度制），其余弦值为y。
反正切函数（arctan）：y = arctan(x) 表示一个角度x（弧度制），其正切值为y。
2.反三角函数的性质：（1）定义域和值域：反三角函数的定义域和值域是有限的，并且在实数范围内是连续的。
例如，arcsin函数的定义域是[-1, 1]，值域是[-π/2, π/2]。
（2）奇偶性：反三角函数中的反正弦函数和反余弦函数是奇函数，而反正切函数是偶函数。
（3）周期性：反三角函数不是周期函数，但它们可以在一定范围内表现出周期性。
例如，arctan函数在实数范围内是周期函数，其周期为π。
3.反三角函数的计算：（1）利用三角函数的性质计算：反三角函数可以通过三角函数的性质进行计算。
例如，利用三角恒等式和三角函数的单调性可以求解反三角函数的值。
（2）利用反三角函数的定义计算：反三角函数的定义可以用于求解反三角函数的值。
例如，对于arcsin(x)，可以通过解方程sin(y) = x来求解y的值。
4.反三角函数的应用：（1）在几何学中的应用：反三角函数可以用于解决一些几何问题，例如计算角度、距离等。
（2）在物理学中的应用：反三角函数可以用于解决一些物理问题，例如振动、波动等。
（3）在工程学中的应用：反三角函数可以用于解决一些工程问题，例如信号处理、图像处理等。
5.反三角函数的图像和性质：反三角函数的图像和性质可以通过图像法和公式法进行描述。
反三角函数知识点总结
千里之行，始于足下。
反三角函数知识点总结反三角函数是数学中的一个重要概念，用来求解三角函数的反函数。
在解决三角函数相关问题时，反三角函数能够帮助我们转化为求反三角函数的值，从而得到所需结果。
接下来，我将总结一下关于反三角函数的一些重要知识点。
一、反三角函数的定义1. 反正弦函数（arcsin）反正弦函数是指将给定值的正弦值（-1≤ sinx ≤ 1）作为自变量，输出对应的角度值（-π/2 ≤ x ≤π/2）的一个单值函数。
其函数表示为：y = arcsin(x)其中，x 的取值范围为 [-1, 1]，y 的取值范围为 [-π/2, π/2]。
2. 反余弦函数（arccos）反余弦函数是指将给定值的余弦值（-1≤ cosx ≤ 1）作为自变量，输出对应的角度值（0≤ x ≤π）的一个单值函数。
其函数表示为：y = arccos(x)其中，x 的取值范围为 [-1, 1]，y 的取值范围为 [0, π]。
3. 反正切函数（arctan）反正切函数是指将给定值的正切值作为自变量，输出对应的角度值（-π/2 < x < π/2）的一个单值函数。
其函数表示为：y = arctan(x)其中，x 的取值范围为 (-∞, +∞)，y 的取值范围为 (-π/2, π/2)。
二、反三角函数的性质1. 定义域和值域：反正弦函数的定义域为 [-1, 1]，值域为 [-π/2, π/2]；第1页/共3页锲而不舍，金石可镂。
反余弦函数的定义域为 [-1, 1]，值域为 [0, π]；反正切函数的定义域为 (-∞, +∞)，值域为 (-π/2, π/2)。
2. 关系：对于任意的实数 x，有 sin(arcsin(x)) = x，-1 ≤ x ≤ 1；对于任意的实数 x，有 cos(arccos(x)) = x，-1 ≤ x ≤ 1；对于任意的实数 x，有 tan(arctan(x)) = x。
3. 奇偶性：反正弦函数为奇函数，即 arcsin(-x) = -arcsin(x)；反余弦函数为偶函数，即 arccos(-x) = arccos(x)；反正切函数为奇函数，即 arctan(-x) = -arctan(x)。
高考数学必考知识点：反三角函数公式归纳
2019高考数学必考知识点：反三角函数公式归纳反三角函数主要是三个：y=arcsin（x），定义域[-1，1]，值域[-π/2，π/2]图象用红色线条；y=arccos（x），定义域[-1，1]，值域[0，π]，图象用蓝色线条；y=arctan（x），定义域（-∞，+∞），值域（-π/2，π/2），图象用绿色线条；sin（arcsinx）=x，定义域[-1，1]，值域[-1，1]arcsin（-x）=-arcsinx 其他公式：三角函数其他公式arcsin（-x）=-arcsinxarccos（-x）=π-arccosxarctan（-x）=-arctanxarccot（-x）=π-arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin（arcsinx）=x=cos（arccosx）=tan（arctanx）=cot（arccotx）当x∈[—π/2，π/2]时，有arcsin（sinx）=x当x∈[0，π]，arccos（cosx）=xx∈（—π/2，π/2），arctan（tanx）=xx∈（0，π），arccot（cotx）=x死记硬背是一种传统的教学方式，在我国有悠久的历史。
但随着素质教育的开展，死记硬背被作为一种僵化的、阻碍学生能力发展的教学方式，渐渐为人们所摒弃；而另一方面，老师们又为提高学生的语文素养煞费苦心。
其实，只要应用得当，“死记硬背”与提高学生素质并不矛盾。
相反，它恰是提高学生语文水平的重要前提和基础。
x〉0，arctanx=π/2-arctan1/x，arccotx类似我国古代的读书人，从上学之日起，就日诵不辍，一般在几年内就能识记几千个汉字，熟记几百篇文章，写出的诗文也是字斟句酌，琅琅上口，成为满腹经纶的文人。
为什么在现代化教学的今天，我们念了十几年书的高中毕业生甚至大学生，竟提起作文就头疼，写不出像样的文章呢?吕叔湘先生早在1978年就尖锐地提出:“中小学语文教学效果差，中学语文毕业生语文水平低，……十几年上课总时数是9160课时，语文是2749课时，恰好是30%，十年的时间，二千七百多课时，用来学本国语文，却是大多数不过关，岂非咄咄怪事!”寻根究底，其主要原因就是腹中无物。
反三角函数知识点总结
反三角函数知识点总结是高中数学中的重要内容之一，它与三角函数有着密切的联系。
在学习之前，我们首先需要明确三角函数的定义和性质。
三角函数是角度的函数，通常包括正弦函数、余弦函数和正切函数。
它们分别用sin、cos和tan表示。
假设角度为θ，则正弦函数的值为sinθ，余弦函数的值为cosθ，正切函数的值为tanθ。
三角函数的值可以用一个单位圆来表示，圆的半径为1，角度θ对应于圆上的一个点坐标。
是以三角函数为基础的，它们的定义和三角函数有所不同。
对于sin的反函数，我们称为反正弦函数，记为arcsin，即sinθ=x，那么θ=arcsin(x)。
同样的，cos的反函数为arccos，tan的反函数为arctan。
的意义在于，给定一个三角函数的值，我们可以通过求出对应的角度。
例如，假如我们需要求出sinθ=0.5的θ的值，我们可以用arcsin(0.5)，得到θ=30°。
除了正弦、余弦和正切函数的反函数，还有其他几个常用的，它们分别为正割函数、余割函数和余切函数的反函数，记为arcsec、arccsc和arccot。
在解三角方程、计算三角函数的角度等方面有着广泛的应用。
下面我们来具体了解一下的性质和一些常见的计算方法。
首先是反正弦函数的性质。
反正弦函数的定义域是[-1,1]，值域是[-π/2,π/2]，它是一个递增函数，对应的三角函数sinθ也是递增函数。
反正弦函数的图像是一条光滑的曲线，图像在x轴的两个端点(-1,-π/2)和(1,π/2)处有两个水平渐近线。
接下来是反余弦函数的性质。
反余弦函数的定义域是[-1,1]，值域是[0,π]，它是一个递减函数，对应的三角函数c osθ也是递减函数。
反余弦函数的图像是一条光滑的曲线，图像在x轴的两个端点(-1,π)和(1,0)处有两个垂直渐近线。
最后是反正切函数的性质。
反正切函数的定义域是实数集R，值域是(-π/2,π/2)，它是一个奇函数，对应的三角函数tanθ也是奇函数。
反三角函数知识点总结
千里之行，始于足下。
反三角函数学问点总结反三角函数是三角函数的逆运算，是一组函数，包括反正弦函数（arcsin 或sin^(-1)）、反余弦函数（arccos或cos^(-1)）、反正切函数（arctan或tan^(-1)）等。
1. 反正弦函数（arcsin）：- 定义域为[-1, 1]，值域为[-π/2, π/2]。
- 表示为y = arcsin(x)或y = sin^(-1)(x)。
- 用于求解一个角的正弦值等于给定的值x，即sin(y) = x。
- 反正弦函数的图像是一个关于直线y = x的对称图像。
2. 反余弦函数（arccos）：- 定义域为[-1, 1]，值域为[0, π]。
- 表示为y = arccos(x)或y = cos^(-1)(x)。
- 用于求解一个角的余弦值等于给定的值x，即cos(y) = x。
- 反余弦函数的图像是一个关于直线y = π/2的对称图像。
3. 反正切函数（arctan）：- 定义域为实数集，值域为[-π/2, π/2]。
- 表示为y = arctan(x)或y = tan^(-1)(x)。
- 用于求解一个角的正切值等于给定的值x，即tan(y) = x。
- 反正切函数的图像是一个关于原点对称的S型曲线。
反三角函数的性质：- 反三角函数是单调递增的。
- 反三角函数的导数可以通过三角函数的导数求得。
- 反三角函数具有周期性，周期为2π。
第1页/共2页锲而不舍，金石可镂。
- 反三角函数在定义域内的值域是唯一确定的。
- 反三角函数有多个解，可以通过在定义域内添加限制条件（如设定主值范围）来确定一个解。
- 反三角函数的值可以通过计算器或数表查找。
应用：- 反三角函数常用于解三角方程、解三角关系、求角度等问题。
- 反三角函数在计算机图形学、信号处理等领域有广泛的应用。
- 反三角函数在数学、物理、工程学等科学领域中常被使用。
在使用反三角函数时需要留意以下几点：- 反三角函数的定义域和值域。
三角函数和反三角函数图像性质、知识点总结
三角函数和反三角函数图像性质、知识点总结②：函数)sin(ϕω+=x A y 的图像与性质：（1） 函数)sin(ϕω+=x A y 和)cos(ϕω+=x A y 的周期都是ωπ2=T（2） 函数)tan(ϕω+=x A y 和)cot(ϕω+=x A y 的周期都是ωπ=T5.三角函数尺度变换sin y x =经过变换变为sin y x ϖϕ=+A （）的步骤（先平移后伸缩）： 1sin sin sin sin y x y x y x y x ϖϕϖϖϖϕϖϕ=−−−−−−−→=−−−−−→=+−−−−−−−→=+横坐标变为原来的倍向左或向右纵坐标不变平移个单位纵坐标变为原来的A 倍横坐标不变（）A （）6.三角函数的对称变换：① )()(x f y x f y -=→=) 将)(x f y =图像绕y 轴翻折180°（整体翻折） （对三角函数来说：图像关于x 轴对称）② )()(x f y x f y -=→=将)(x f y =图像绕x 轴翻折180°（整体翻折） （对三角函数来说：图像关于y 轴对称）③ )()(x f y x f y =→= 将)(x f y =图像在y 轴右侧保留，并把右侧图像绕y 轴翻折到左侧（偶函数局部翻折）④ )()(x f y x f y =→=保留)(x f y =在x 轴上方图像，x 轴下方图像绕x 轴翻折上去（局部翻动）7.反三角函数的图像与性质： ((,))22x ππ∈-的反函数，叫做反正弦函数((0,))x π∈ 的反函数，叫做反余弦函数((,))22x ππ∈-的反函数，叫做反正切函数的反函数，余切函数 图像域 ［-1，1］ ［-1，1］ (-∞，+∞) (-∞，+∞)值域 ［-2π，2π］［0，π］(-2π，2π)(0，π性[]1,1- 增函数 []1,1- 减函数 (),-∞+∞增函数 (),-∞+∞7.三角函数公式：（1）倒数关系： （2）平方关系：tan cot 1sin csc 1cos sec 1αααααα⋅=⋅=⋅= 222222sin cos 11tan sec 1cot csc αααααα+=+=+=（3）三角和与差公式：sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβαβαβαβαβαβαβ+=++=-++=- sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβαβαβαβαβαβαβ-=--=+--=+（4）二倍角公式：()22222sin 22sin cos cos 2cos sin 2cos 112sin 2tan tan 21tan ααααααααααα==-=-=-=-升幂公式 22221cos 2sin 1cos 22sin 2(1cos 21cos 22cos cos 2αααααααα-⎫=⎪⎧-=⎪⎪⇒⎬⎨++=⎪⎩⎪=⎪⎭降幂公式） （5）三角函数的和差化积公式 （6）三角函数的积化和差公式sin sin 2sincos 22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅[][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+--8.正、余弦定理： ①正弦定理： 在ABC ∆中有:2sin sin sin a b cR A B C===（R 为ABC ∆外接圆半径） 2sin 2sin 2sin a R A b R B c R C =⎧⎪=⎨⎪=⎩ ⇒ sin 2sin 2sin 2a A R b B R c C R ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩面积公式：111sin sin sin 222ABC S abs C ac B bc A ∆=== ②余弦定理： 在三角形ABC ∆中有:2222222222cos 2cos 2cos a b c bc A b a c ac B c a b ab C⎧=+-⎪=+-⎨⎪=+-⎩ ⇒ 222222222cos 2cos 2cos 2b c a A bc a c b B ac a b c C ab ⎧+-=⎪⎪+-⎪=⎨⎪⎪+-=⎪⎩。
02 三角 反三角函数
02 三角反三角函数02三角反三角函数02三角.反三角函数第二章三角、反三角函数1.理解任意角的概念、弧度的意义，能正确进行弧度和角度的互换。
2.掌控任一角的正弦、余弦、正弦的定义，介绍余切、余割、正割的定义，掌控同角三角函数的基本关系式，掌控正弦、余弦的诱导公式，认知周期函数与最轻正周期的意义。
3.掌握两角和与两角差的正弦、余弦、正切公式，掌握二倍角的正弦、余弦、正切公式。
4.能正确运用三角公式，进行简单三角函数式的化简，求值和恒等式的证明。
5.介绍正弦函数、余弦函数，正弦函数的图像和性质，可以用“五点法”画正弦函数，余弦函数和函数y=asin(wx+ϕ)的体图，认知a、w、ϕ的物理意义。
6.会由已知三角函数值求角，并会用符号arcsinx、arccosx、arctgx表示。
7.掌控正弦定理、余弦定理，并能够初步运用它们解斜三角形，能够利用计算器化解三角形的排序问题。
8.理解反三角函数的概念，能由反三角函数的图像得出反三角函数的性质，能运用反三角函数的定义、性质解决一些简单问题。
9.能熟练地写下最简单的三角方程的边值问题。
二、知识结构1.角的概念的推广：(1)定义：一条射线oa由原来的位置oa，绕着它的端点o按一定方向旋转到另一位置ob，就形成了角α。
其中射线oa叫角α的始边，射线ob叫角α的终边，o叫角α的顶点。
(2)正角、零角、负角：由始边的转动方向而的定。
(3)象限角：由角的终边所在位置确认。
第一象限角：2kπ＜α＜2kπ+,k∈z第二象限角：2kπ+＜α＜2kπ+π,k∈z第三象限角：2kπ+π＜α＜2kπ+第四象限角：2kπ+＜α＜2kπ+2π,k∈z(4)终边相同的角：通常地，所有与α角终边相同的角，联同α角在内(而且只有这样的角)，可以则表示为k²360°+α，k∈z。
(5)特殊角的集合：终边在坐标轴上的角的子集｛α｜α＝，k∈z｝终边在一、三象限角平分线上角的集合｛α｜α＝kπ+终边在二、四象限角平分线上角的集合｛α｜α＝kπ-终边在四个象限角平分线上角的集合｛α｜α＝kπ-π，k∈z｝，k∈z｝，k∈z｝2.弧度制：(1)定义：用“弧度”做单位来度量角的制度，叫做弧度制。
反三角函数知识点
反三角函数知识点在数学的广阔领域中，反三角函数是一个重要且有趣的概念。
它为我们解决各种与角度和数值之间的相互转换问题提供了有力的工具。
首先，让我们来理解一下什么是反三角函数。
简单来说，反三角函数是三角函数的反函数。
就像加法和减法、乘法和除法互为逆运算一样，三角函数和反三角函数也有着这样的逆运算关系。
常见的反三角函数有反正弦函数（arcsin）、反余弦函数（arccos）、反正切函数（arctan）等。
反正弦函数arcsin，它的定义域是-1, 1，值域是π/2, π/2。
这意味着，如果 sin A ＝ x，那么 A ＝ arcsin x。
例如，sin(π/6) ＝ 1/2，所以arcsin(1/2) ＝π/6 。
反余弦函数 arccos，定义域同样是-1, 1，但值域是0, π。
比如，cos(π/3) ＝ 1/2，那么 arccos(1/2) ＝π/3 。
反正切函数 arctan，它的定义域是 R（全体实数），值域是(π/2,π/2)。
例如，tan(π/4) ＝ 1，所以 arctan 1 ＝π/4 。
反三角函数有着一些重要的性质。
它们是单调函数。
反正弦函数和反正切函数在其定义域内单调递增，而反余弦函数在其定义域内单调递减。
反三角函数之间也存在一些关系。
比如，arcsin x ＋ arccos x ＝π/2 ，当 x 在-1, 1内。
在计算反三角函数的值时，我们可以利用三角函数的特殊值来帮助我们。
比如，我们知道sin(π/4) ＝√2/2 ，那么arcsin(√2/2) ＝π/4 。
反三角函数在解决几何问题中也经常出现。
比如，在一个直角三角形中，如果已知一条直角边和斜边的比值，我们可以通过反正弦或反余弦函数求出其中一个锐角的大小。
在实际应用中，反三角函数在物理学、工程学、计算机科学等领域都有广泛的应用。
比如在电路分析中，计算交流信号的相位差；在计算机图形学中，计算物体的旋转角度等。
要注意的是，在使用反三角函数时，一定要注意定义域和值域的限制，否则可能会得到错误的结果。
沪教高三数学第一轮复习：反三角函数及简单三角方程
sin x cos xsin x 6 cos x 0
sin x cos x或sin x 6 cos x tan x 1或tan x 6
所以，原方程的解集是：
x cos x t 则sin 2 x t 2 1 t 2 t 0
解： 设sin
t 0或t 1
2 tan x 1或sin( x ) 4 2
x x k 或x k arctan 6, k Z 4
所以，原方程的解集是：
k ,k Z x x k 或x k (1) 4 4 4
,k Z
0
k 1,
6
f ( x) 2 sin(x ) cos(x ) 2 3 cos2 ( x ) 3 。 例 7.已知 2 2 2
（3）在（2）成立的条件下，求满足 f ( x) 1, x , 的 x 的 集合。
图像
2
y arccos x
y
2
y arctan x
y
2
y
o
-1
-
1
x
1
o
2
o
x
-
1
x
2
定 义 域 值域
- 1,1
2 , 2
- 1,1
R
, 2 2
在 R 上单调递增
0,
在 1,1 上单调递减
解： 当
时, f ( x) 2 sin( 2 x ) 2 cos 2 x 6 2
反三角函数知识点总结归纳
反三角函数知识点总结归纳反三角函数并不难，关键是要理解反三角函数的意义，这是其一，第二要充分掌握诱导公式，反三角其实是考察由三角函数值表示非特殊角，所以经常要用到π+arcsin,π-arcsin，2π+，2π-等，欢迎阅读反三角函数知识点总结，了解清楚，大家要准确表示反三角函数一定要学好诱导公式哦。
反三角函数主要是三个：y=arcsin(x)，定义域[-1,1] ，值域[-π/2,π/2]图象用红色线条;y=arccos(x)，定义域[-1,1] ，值域[0,π]，图象用蓝色线条;y=arctan(x)，定义域(-∞,+∞)，值域(-π/2,π/2)，图象用绿色线条;sin(arcsin x)=x,定义域[-1,1],值域[-1,1] arcsin(-x)=-arcsinx其他公式arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)当x∈[—π/2，π/2]时，有arcsin(sinx)=x当x∈[0,π],arccos(cosx)=xx∈(—π/2，π/2),arctan(tanx)=xx∈(0，π),arccot(cotx)=xx〉0,arctanx=π/2-arctan1/x,arccotx类似若(arctanx+arctany)∈(—π/2，π/2),则arctanx+arctany=arctan(x+y/1-xy)搜集整理，仅供参考学习，请按需要编辑修改。
反三角函数知识点总结
三一文库（）/总结
〔反三角函数知识点总结〕
反三角函数并不难，关键是要理解反三角函数的意义，
这是其一，第二要充分掌握诱导公式，反三角其实是考察由
三角函数值表示非特殊角，所以经常要用到π+arsin,π
-arsin，2π+，2π-等，欢迎阅读反三角函数知识点总结，
了解清楚，大家要准确表示反三角函数一定要学好诱导公式
哦。
▲反三角函数主要是三个：
y=arsin(x)，定义域[-1,1] ，值域[-π/2,π/2]图象
用红色线条;
y=ars(x)，定义域[-1,1] ，值域[0,π]，图象用蓝色
线条;
y=aran(x)，定义域(-∞,+∞)，值域(-π/2,π/2)，图
象用绿色线条;
sin(arsin x)=x,定义域[-1,1],值域 [-1,1]
arsin(-x)=-arsinx
第1页共2页。
高三数学知识点之反三角函数的公式知识点总结
高三数学知识点之反三角函数的公式知识点总结
为高三同学总结归纳高三数学知识点之反三角函数的公式。
希望对高三考生在备考中有所帮助，欢迎大家阅读作为参考。
反三角函数主要是三个：
y=arcsin(_)，定义域[-1,1] ，值域[-/2]图象用红色线条;
y=arccos(_)，定义域[-1,1] ，值域[0,]，图象用蓝色线条;
y=arctan(_)，定义域(-,+)，值域(-/2)，图象用绿色线条;
sin(arcsin _)=_,定义域[-1,1],值域 [-1,1] arcsin(-_)=-arcsin_
其他公式:
三角函数其他公式
arcsin(-_)=-arcsin_
arccos(-_)=-arccos_
arctan(-_)=-arctan_
arccot(-_)=-arccot_
arcsin_+arccos_=/2=arctan_+arccot_
sin(arcsin_)=_=cos(arccos_)=tan(arctan_)=cot(arccot_)
当_[/2，/2]时，有arcsin(sin_)=_
当_[0,],arccos(cos_)=_
_(/2，/2),arctan(tan_)=_
_(0，),arccot(cot_)=_
_〉0,arctan_=/2-arctan1/_,arccot_类似
若(arctan_+arctany)(/2，/2),则arctan_+arctany=arctan(_+y/1-_y)
以上就是高三数学知识点之反三角函数的公式，希望能帮助到大家。