招商银行A股的β系数估计---基于EVIEWS的金融计量学
金融市场β系数分析

金融市场β系数分析β系数是金融市场中常用的一个统计量,用于衡量一个资产对市场指数的变动敏感程度。
本文将探讨β系数的定义、计算方法以及其在金融市场分析中的应用。
首先,β系数是通过计算资产的收益率与市场指数的收益率之间的协方差来衡量的。
β系数的定义为:β = Cov(Asset, Market) / Var(Market)其中,Cov(Asset, Market)表示资产收益率与市场指数收益率的协方差,Var(Market)表示市场指数收益率的方差。
β系数的值可以为正数、负数或零。
当β系数大于1时,表示资产的价格变动比市场指数的变动更剧烈,即具有比市场更高的波动率。
反之,当β系数小于1时,资产的价格变动比市场指数的变动更为平缓。
计算β系数的方法有多种,其中最常用的方法是通过回归分析来计算。
具体而言,可以将资产的收益率作为因变量,市场指数的收益率作为自变量,通过最小二乘法来拟合线性回归模型,从而得到β系数的估计值。
在金融市场分析中,β系数具有广泛的应用。
首先,β系数可以帮助投资者评估资产的风险特征。
当一个资产的β系数较高时,表明该资产的价格波动与市场的波动密切相关,投资者在选择资产时需要考虑市场的整体情况。
相反,当一个资产的β系数较低时,表明其价格变动与市场指数的变动关系较弱,投资者可以将资产作为分散风险的一种策略。
其次,β系数还可以用于资产组合的构建和管理。
通过计算资产的β系数,投资者可以确定不同资产在组合中的权重,从而实现风险与收益之间的平衡。
在构建资产组合时,通常选择具有低β系数的资产来降低整体风险,同时选择具有较高β系数的资产来提高组合的收益。
此外,β系数还可以用于金融市场的预测和投资策略。
通过观察β系数的变化,投资者可以判断市场的趋势和资产的估值水平。
当市场的β系数高企时,可能表明市场热度较高,投资者可能需要警惕市场的过热情况。
反之,当市场的β系数较低时,可能标志着市场的冷清,此时投资者可以积极寻找低估值的投资机会。
如何用EViews计量软件帮金融类论文建模分析

Eviews7.2 金融论文计量教学根据我以往写论文所用到的检验方法,特别总结出这篇《如何用EViews计量软件帮金融类论文建模分析》,其中有基本操作、单位根检验、VAR模型估计、格兰杰因果关系检验、脉冲响应分析以及方差分解。
希望能够帮助有这方面需求的同学们排难解疑。
关键词:单位根 VAR Granger 脉冲响应方差分解目录一、录入数据 (2)二、取对数 (7)三、单位根检验 (8)四、VAR模型 (13)五、格兰杰因果关系检验 (18)六、脉冲响应 (20)七、方差分解 (22)一、录入数据写金融类论文,常常会用到股市的日数据,而股市是一周5天制的时间序列数据,因此,一般按照(很多事实证明一般都是错的)下面这样创建文件,File—New--Workfile如图1-1图1-1然后录入数据:打开Quick—Empty Group,从Excel文档直接复制粘贴到下面数据录入窗口,如图1-2图1-2再然后,我们会发现,数据和样本区间不一致,如下图1-3:图1-3相信不少同学在这里就抓狂了,尼玛这EViews咋这么难啊!!!这是因为股市日数据属于不规则类型的时间序列数据即非规范日期数据,关于这类数据如何导入到EViews软件中的问题,相信很多写论文的同学们遇到过,下面将为同学们介绍正确的导入不规则时间序列数据的方法。
首先,创建一个新的Excel文档,把想录入的数据依列排好,注意A列就是数据的日期,后面才是选用的样本数据,而第一行是各数据的英文缩写。
如下图1-4所示:图1-4然后保存文档,例如:另存为:桌面/Book1.xlsx(注意关闭该Excel 文档,文档处于打开状态将影响下面的导入数据步骤)其次,打开EViews点击左上角的File—Open—Foreign Data asWorkfile,如下图1-5所示:图1-5选中桌面/Book1.xlsx,点击打开,就出现下图1-6的情况:图1-6接下来,直接点击完成,就出现下图1-7:图1-7然后,双击Range最后一步,在弹出的对话框中选择Dated-specificed by date series,这是eviews为我们提供的处理非规范日期数据的工具。
计量经济学EViews操作
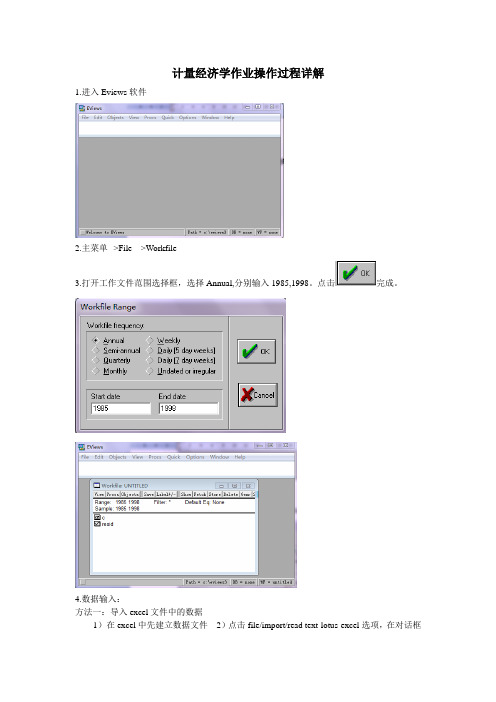
计量经济学作业操作过程详解1.进入Eviews软件2.主菜单-->File--->Workfile3.打开工作文件范围选择框,选择Annual,分别输入1985,1998。
点击完成。
4.数据输入:方法一:导入excel文件中的数据1)在excel中先建立数据文件2)点击file/import/read text-lotus-excel选项,在对话框中选择已建立的excel文件4)打开后,在新的对话框中输入想要分析的变量名称,然后点击OK即可。
此时工作文件中出现变量图标。
方法二:手工数据输入主菜单--->Quick----->Empty Group分别输入变量Y、GDP的数据。
点击obs后面的灰色格子中分别输入Y、GDP。
(方法一:一个一个输入方法二:在Excel中输入完再复制粘贴)5.主菜单---->Quick----->Estimate Equation打开估计模型对话框,输入Y C GDP ,(如上图所示,注意字母之间要有空格)点击OK键。
得出Eviews的估计结果:β(上面还要带个帽子,电脑打不出来),26.95415为1β。
其中12596.27为0第五步可以直接输入LS Y C GDP 等出结果6.一元线性回归模型的预测1)在工作文件主窗口点击procs/change workfile range(改变范围),弹出对话框,在对话框的end date栏中输入预测值的时间或序号,点击OK2)在工作文件窗口中双击解释变量文件,在变量窗口中点击edit+/-键,进入编辑模式,在变量窗口底端输入新序号的数值,再点击edit+/-键,关闭编辑模式3)再次进行估计,点击quick/estimate equation,在对话框中输入方程,注意样本范围应不包括新序号,点击OK得到估计结果4)点击结果窗口中的forecast键,产生对话框,在对话框中选择样本范围,点击OK可得预测曲线图。
财务计量经济学5 上市公司beta系数估计

财务计量经济学5:上市公司beta 系数估计 ——异方差、序列相关性和多重共线性检验与修正马科维茨的投资组合理论与夏普的资本资产定价模型(CAPM ),解决了市场处于均衡状态时风险资产收益率的决定问题,其中心思想是认为股票i 的预期收益率是由它所含的系统风险惟一确定的,其数学形式为,()[()]f m f i i E R r E R r β=+-()i E R 为股票i 的期望收益率;f r 为无风险收益率,投资者能以这个利率进行无风险的借贷;()m E R 是市场组合的期望收益率,通常用市场指数的收益率来代表。
2,(,)()m m i mi i mCOV R R VAR R σβσ==(,)m i COV R R 为股票i 收益率与市场组合收益率的协方差,而()m VAR R 是市场组合收益率的方差。
i β作为衡量股票i 的价格的变化率对市场指数变化率的敏感程度,用来表示该股票系统风险的大小。
单个资产的价格(或预期收益率)只与该资产的系统风险的大小有关。
若1i β>,则这只股票被称为进取性股票,因为该股票收益率的变化大于市场指数收益率的变化。
反之,这只股票被称为防守性股票。
CAPM 模型描述的是均衡状态下的证券或证券组合的期望收益率与由i β系数所测定的系统风险之间的线性关系。
但在实际计量中,我们需要建立下面两个模型,采用OLS ,来求得i β系数。
模型1:用股票i 的收益率it R 与市场组合收益率mt R ,建立回归模型:i i t it mt R R αβε=++模型2:用股票i 的超额收益率f it R r -与市场组合的超额收益率f mt R r -,建立回归模型,()f i i f t it mt R r R r αβε-=+-+模型1中i β的估计为,22,()()(,)()()m m m m it i mt i mi i mt m R R R R COV R R R R VAR R σβσ--===-∑∑其中模型1也称为单指数模型。
β系数计算过程范文

β系数计算过程范文β系数(Beta coefficient)是一种风险度量指标,用于衡量一项资产相对于整个市场的波动情况。
它是通过计算资产收益与市场收益之间的协方差来确定的。
β系数的计算过程涉及到以下几个步骤:1.收集数据:要计算β系数,首先需要收集资产的收益率数据和市场的收益率数据。
一般来说,收益率可以按日、按周、按月或按年进行计算。
可以通过金融数据提供商、交易所网站等渠道获取所需的数据。
2.计算资产的收益率:收益率是指资产的价格变动所导致的收益。
计算资产的收益率可以使用以下公式:收益率=(当前价格-上期价格)/上期价格例如,假设股票在两个期间内的价格分别为100和120,那么收益率可以计算为:收益率=(120-100)/100=20%将所有期间的收益率计算出来并记录下来。
3.计算市场的收益率:市场的收益率可以通过计算市场指数的收益率来代表。
市场指数在大多数情况下会反映整个市场的整体变化情况,如标普500指数、纳斯达克指数等。
计算市场的收益率的方法与计算资产的收益率相同。
4.计算协方差:协方差用于衡量两个变量之间的线性关系。
在计算β系数时,需要计算资产收益率和市场收益率之间的协方差。
协方差可以使用以下公式计算:协方差=SUM((资产收益率-资产平均收益率)*(市场收益率-市场平均收益率))/(n-1)其中,资产平均收益率为所有期间资产收益率之和除以期间数,市场平均收益率同理。
5.计算市场的方差:方差是衡量一个变量的离散程度的指标。
在计算β系数时,还需要计算市场收益率的方差。
方差=SUM((市场收益率-市场平均收益率)^2)/(n-1)6.计算β系数:根据协方差和市场方差的计算结果,可以计算β系数。
β系数可以使用以下公式计算:β=协方差/方差β系数表示资产收益率对市场收益率的敏感性。
如果β系数大于1,表明资产的波动性高于市场;如果β系数小于1,表明资产的波动性低于市场;如果β系数等于1,表明资产的波动性与市场相同。
国际金融中b值的计算方法

国际金融中b值的计算方法在国际金融中,b值通常是指贝塔系数(Beta coefficient),用来衡量一个资产或投资组合相对于整个市场的波动性,即该资产或投资组合与市场收益率的相关性。
贝塔系数是投资学中一个重要的指标,用于评估一个资产的系统性风险。
计算贝塔系数的方法有多种,其中最常用的是基于历史数据的计算方法。
以下是一种常见的计算贝塔系数的方法:步骤一:选择一个参考指标选择一个与所要计算的资产或投资组合有相关性的市场指数作为参考指标。
这个市场指数可以是整个股市的指数,例如标普500指数(S&P 500)或道琼斯工业平均指数(Dow Jones Industrial Average),也可以是其中一个特定行业的指数,例如金融指数或科技指数。
步骤二:收集相关数据收集所要计算的资产或投资组合的历史价格数据和参考指标的历史收益率数据。
这些数据可以从金融数据提供商、证券交易所或金融网站等渠道获取。
步骤三:计算资产或投资组合的收益率使用所收集到的历史价格数据计算资产或投资组合每期的收益率。
收益率可以通过计算价格变动的百分比来得到,即(当前价格-上一期价格)/上一期价格。
步骤四:计算市场指数的收益率使用所收集到的参考指标的历史数据计算每期的收益率。
同样,收益率可以通过计算指数的价格变动的百分比来得到。
步骤五:计算协方差和方差将资产或投资组合的收益率和参考指标的收益率按照时间配对,计算它们的协方差和方差。
协方差度量了资产或投资组合收益率与参考指标收益率的联动程度,方差度量了收益率的波动性。
步骤六:计算贝塔系数使用协方差和方差的值,通过下述公式计算贝塔系数:贝塔系数=协方差/方差计算得到的贝塔系数反映了资产或投资组合与市场指数的相关性程度。
如果贝塔系数为1,则表示该资产或投资组合与市场指数的波动性相等;如果贝塔系数大于1,则表示该资产或投资组合的波动性高于市场指数;如果贝塔系数小于1,则表示该资产或投资组合的波动性低于市场指数。
商业银行系统风险—β系数的测算

商业银行系统风险—β系数的测算
β系数是根据统计学方法来测算商业银行系统风险的一个重要工具。
β系数可以衡量商业银行系统风险在市场整体波动中所占的比例。
本文将介绍β系数的测算方法以及其在商业银行系统风险评估中的应用。
要计算β系数,首先需要选择一个指标作为市场整体风险的参考。
通常,我们可以选择股市指数作为市场整体风险的代表,如上证指数或深证成指。
然后,我们需要选择商业银行股票的价格作为被测量的对象,如招商银行或工商银行。
接下来,我们需要收集一段时间内的市场整体风险和商业银行股票价格的历史数据。
在收集到足够的历史数据后,我们可以用回归分析的方法来计算β系数。
回归分析可以帮助我们建立一个线性关系模型,用来衡量商业银行系统风险与市场整体风险的关系。
在使用回归分析时,我们将商业银行股票的收益率作为因变量,市场整体风险的收益率作为自变量。
根据回归分析的结果,我们可以得到一个β系数。
β系数的计算结果可以辅助我们评估商业银行系统风险。
β系数越高,表示商业银行系统风险受市场整体风险的影响越大,波动性也越大。
相反,β系数越低,表示商业银行系统风险相对较低,受市场整体风险的影响相对较小。
β系数的应用不仅限于风险评估,还可以用来进行风险管理。
商业银行可以利用β系数来确定投资组合的合理配置。
如果一个投资组合中存在高β系数的股票,那么该投资组合的风险也会相对较高。
商业银行可以通过将高β系数的股票与低β系数的股票进行组合来降低整体风险。
实验六β系数估计

实验六β系数估计一、实验预习部分(一)实验目的要求:运用贝塔系数的估计模型,独立设计案例,通过对案例的操作与分析,达到掌握贝塔系数估计方法的目的。
(二) 实验理论原理:(金融原理) β系数(Beta coefficient )1.概念:β系数是一种风险指数,用来衡量个别股票或股票基金相对于整个股市的价格波动情况。
β系数是一种评估证券系统性风险的工具,用以度量一种证券或一个投资证券组合相对总体市场的波动性。
其绝对值越大,显示其收益变化幅度相对于大盘的变化幅度越大;绝对值越小,显示其变化幅度相对于大盘越小。
如果是负值,则显示其变化的方向与大盘的变化方向相反;大盘涨的时候它跌,大盘跌的时候它涨。
2.经济含义:Beta 则体现了特定资产的价格对整体经济波动的敏感性,即,市场组合价值变动1个百分点,该资产的价值变动了几个百分点——或者用更通俗的说法:大盘上涨1个百分点,该股票的价格变动了几个百分点。
如果 β 为 1 ,则市场上涨 10 %,股票上涨 10 %;市场下滑 10 %,股票相应下滑 10 %。
如果 β 为 1.1, 市场上涨 10 %时,股票上涨 11%, ;市场下滑 10 %时,股票下滑 11% 。
如果 β 为 0.9, 市场上涨 10 %时,股票上涨 9% ;市场下滑 10 %时,股票下滑 9% 。
3.计算模型:(1)市场模型 E (Ri )=αi+βiRm2mim i σσβ=,其中()22m m m R R E -=σ ,()()m m i i im R R R R E --=σ(2)CAPM模型:资本资产定价模型,也称证券市场线模型,security market line):E(Ri)= Rf+βi (Rm-Rf)其中:E(Ri)= 资产i的期望收益率,Rf =无风险收益率,Rm = 市场平均收益率4.影响β系数的因素(1)证券对β系数的影响:市场平均收益率Rm通常采用证券市场的某一指数的收益率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题 目: 招商银行A 股的β系数估计 课程名称:《基于EVIEWS 的金融计量学》 学 院: 经济学院 专 业: 年 级: 学生姓名: 学 号: 指导教师:
2010 年 6 月 9 日
《基于EVIEWS 的金融计量学》课程论文
招商银行A股的β系数估计
摘要:本文章中,我利用我国上海证券交易所上证指数(代码:000001)和招商银行A 股(代码:600036)2002年4月到2012年5月的月收盘价数据,构建单指数模型对招商银行A股的β系数进行估计,运用eviews 软件建立、估计、检验线性回归模型。
关键词:Eviews软件β系数单指数模型t统计量DW统计量残差正态分布检验自相关的LM检验异方差的White检验
引言:
一、公司背景
招商银行是一家全国性商业银行,国内最大的零售银行。
在境内30多个大中城市、香港设有分行,网点总数400多家,在美国设立了代表处,并与世界70多个国家和地区的900多家银行建立了代理行关系。
公司在香港、上海两地上市,其发行的“一卡通”被誉为我国银行业在个人理财方面的一个创举,公司同时也是国内信用卡发卡最多的银行。
公司正加快实现战略转型,加大收入结构和客户结构的调整力度,大力发展零售银行业务、中间业务、信用卡业务和中小企业业务,不断提高非利息收入的占比,经营转型取得了良好的效果。
自成立以来,招商银行先后进行了三次增资扩股,并于2002年3月成功地发行了15亿A股,4月9日在上交所挂牌(股票代码:600036),是国内第一家采用国际会计标准上市的公司。
2006年9月又成功发行了22亿H股,9月22日在香港联交所挂牌交易(股票代码:3968),10月5日行使H股超额配售,共发行了24.2亿H股。
目前,招商银行总资产逾8000亿元,在英国《银行家》杂志“世界1000家大银行”的最新排名中,资产总额位居114位。
招商银行股份有限公司被巴菲特杂志、世界企业竞争力实验室、世界经济学人周刊联合评为2010年(第七届)中国上市公司100强,排名第40位。
二、研究目的
资本资产定价模型(CAPM)认为,总体风险等于系统风险加上非系统风险,而非系统风险可以通过一个充分分散化的投资组合消除,剩下的只有系统风险了,那么某个证券或者证券组合的预测收益就是由它所含有的系统性风险唯一确定,可表示为:
E(r i)=r f+[E(r m)-r f]βi (1)
其中:E(r i)表示证券i期望收益率;r f表示无风险收益率;E(r m)表示市场组合的期望收益率。
这里βi=cov(r i,r m)/var(r m)=σim/σ2m,称为β系数,表示证券i的风险相对于
市场的风险比率,反映证券i的收益率对市场收益率的敏感性,即该证券系统性风险的大小。
根据以上理论,本文就以该理论来对招商银行A股的β系数进行估计,看看招商银行A股和上证指数的收益是否具有相关性,检验招商银行A股的价格波动是否与市场一致。
三、初步分析
在大智慧上导出上证指数(代码:000001)和招商银行A股(代码:600036)2002年4月到2012年5月的月收盘价数据(总共122个月),创建eviews 工作文件夹,导入数据,对数据进行分析。
创建序列对象sh和zsyh,分别用来保存上证指数和招商银行A股的月收盘数据。
得到上证指数折线图:
图1----上证指数月收盘价数据折线图
招商银行A股月收盘价数据折线图:
图2----招商银行A股月收盘价数据折线图
由图1和图2可以看出,招商银行A股和上证指数走势基本一致。
为了利用单指数模型估计招商银行A股的β系数,还需要建立招商银行A股和上证指数的收益率序列,我们取百分比收益率。
由公式
rsh=(sh-sh(-1))/sh(-1) (2)
建立一个新序列rsh,为上证指数百分比收益率序列,其中,sh(-1)表示sh序列的滞后一期。
由公式:
r zsyh=(zsyh-zsyh(-1))/zsyh(-1) (3)
以类似方法建立招商银行A股百分比收益率序列rzsyh 。
为了确定招商银行A股和上证指数收益的相关关系,可以将rsh 和r zsyh序列以组织的形式进行观察,首先观察两者的二维散点图:
图3----rsh和rzsyh二维散点图
从图3可以看出,大多数点分布在一条直线(回归线)附近,可以初步认为rsh 和rzsyh 线性相关。
为了进一步观察rsh 和r zsyh序列的相关系数,得出rsh 和r zsyh序列的相关系数矩阵:
表1----rsh 和rzsyh序列的相关系数矩阵
如表1所示,可见,rsh 和rzsyh序列的相关系数为0.701。
建立单指数模型:
1、建立模型
为了估计招商银行A股的β系数,可以建立单指数模型,模型的形式为:
r it=a+br mt+u t(4)
在方程定义对话框中输入“rzsyh c rsh ”选择框选择LS估计法和样本区间“2002M04 2012M05”,得到如图所示结果:
图4----方程输出结果
由图4可看出,常数项的t统计量值为0.238,相伴概率为0.812,因为t统计量的相伴概率大于0.05,则在5%的显著水平上接受原假设,认为系数为零,对应的解释变量不应包括在模型中。
由于没有通过显著性检验,因此,应该从方程中剔除,重新定义方程为“rzsyh rsh”,得到回归结果如图所示:
图5----剔除常数项的方程输出结果
对应回归的表达式是:
RZSYH=0.959*RSH (5)
(10.81) R2= 0.491 DW=2.24
RSH的系数估计值为0.959,t统计量的相伴系数为0,通过显著性检验,也就是说招商银行A股的β系数的估计值为0.959,跟1很接近,说明招商银行A股的价格波动基本与市场一致,这与对图1和图2的观察结果一致。
R2=0.491,说明方程的拟合程度并不是很高,但是作为金融资产的收益率序列拟合,还是可以接受的。
其经济意义是,招商银行A股的系统风险占总风险的比例为49.1%,DW=2.24,说明基本没有一阶自相关。
还可以观察真实值、拟合值与残差图:
图6----真实值、拟合值与残差图
2、模型检验
1)、残差正态性检验
如图:
图7----残差正态性检验结果
如图7所示,可以看到残差序列的偏度为-0.252,峰度为4.753,JB统计量为16.777,JB统计量的相伴概率为0.000227,小于0.05,可以认为在5%的显著性水平上认为残差序列不服从正态分布。
2)、残差序列自相关的LM检验
图8----LM检验结果
由图8所示可以看出,LM统计量得相伴概率为0.168,大于0.05,可以认为在5%的显著性水平上,不存在一阶自相关。
这与DW检验结果一致。
3)、残差序列异方差性的White检验
由eviews软件得出下图:
图9----White检验结果
可见nR2的相伴概率为0.217,大于0.05,可以认为在5%的显著水平上,不存在异方差性。
结论:
本文利用单指数模型对招商银行A股的β系数进行估计,建立的一元线性回归方程总的效果不错:系数通过显著性检验,残差没有自相关和异方差。
但不足的是正态性检验没有通过,样本决定系数R2=0.491不是很高,但是作为金融资产的收益率序列拟合,还是可以接受的。
最后的到的招商银行A股的β系数估计值为0.959,跟1很接近,说明招商银行A股的价格波动基本与市场一致。
同时,方程的样本决定系数R2=0.491,说明招商银行A股的系统风险占总风险的比例为49.1%。
参考文献:
1.曲青青:《金融计量学实验》东北财经大学出版社2008
2.张晓峒:《计量经济学软件eviews使用指南》,天津,南开大学出版社2004
3.李子奈、潘文卿:《计量经济学》,高等教育出版社2010
4.汪昌云、戴稳胜、张成思:《基于EVIEWS的金融计量学》,中国人民大学出版社 2011。
