贝叶斯分类作业题
贝叶斯作业
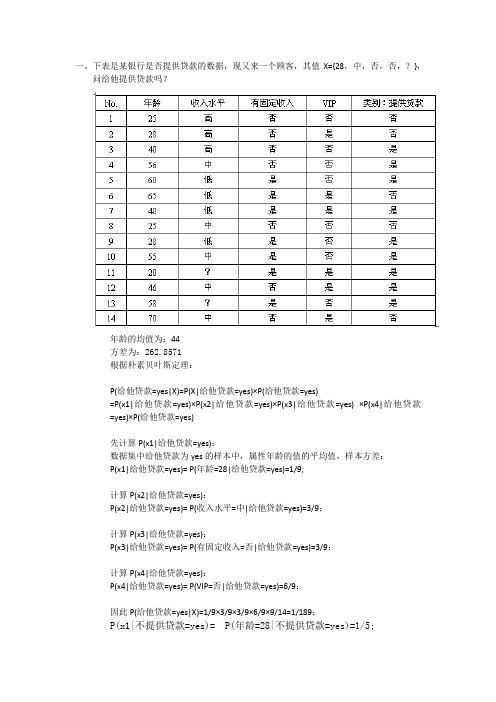
一、下表是某银行是否提供贷款的数据，现又来一个顾客，其值X={28，中，否，否，？}，问给他提供贷款吗？年龄的均值为：44方差为：262.8571根据朴素贝叶斯定理：P(给他贷款=yes|X)=P(X|给他贷款=yes)×P(给他贷款=yes)=P(x1|给他贷款=yes)×P(x2|给他贷款=yes)×P(x3|给他贷款=yes) ×P(x4|给他贷款=yes)×P(给他贷款=yes)先计算P(x1|给他贷款=yes)：数据集中给他贷款为yes的样本中，属性年龄的值的平均值，样本方差：P(x1|给他贷款=yes)= P(年龄=28|给他贷款=yes)=1/9;计算P(x2|给他贷款=yes)：P(x2|给他贷款=yes)= P(收入水平=中|给他贷款=yes)=3/9；计算P(x3|给他贷款=yes)：P(x3|给他贷款=yes)= P(有固定收入=否|给他贷款=yes)=3/9；计算P(x4|给他贷款=yes)：P(x4|给他贷款=yes)= P(VIP=否|给他贷款=yes)=6/9；因此P(给他贷款=yes|X)=1/9×3/9×3/9×6/9×9/14=1/189；P(x1|不提供贷款=yes)= P(年龄=28|不提供贷款=yes)=1/5;计算P(x2|不提供贷款=yes)：P(x2|不提供贷款=yes)= P(收入=中|不提供贷款=yes)=2/5；计算P(x3|不提供贷款=yes)：P(x3|不提供贷款=yes)= P(无固定收入|不提供贷款=yes)=4/5；计算P(x4|不提供贷款=yes)：P(x4|不提供贷款=yes)= P(不是VIP|不提供贷款=yes)=2/5；因此P(不提供贷款=yes|X)=5/14*1/5*2/5*4/5*2/5=8/875；1/189<8/875 所以，不提供贷款二、下表是某高尔夫球场记录天气数据以及是否打球的数据，现今天，其值X={sunny，hot，high，strong，？}，问会有人打球吗？P(x1|打球=yes)= P(outlook=sunny|打球=yes)=2/9计算P(x2|打球=yes)：P(x2|打球=yes)= P(Temperature=hot|打球=yes)=2/9；计算P(x3|打球=yes)：P(x3|打球=yes)= P(Humidity=high|打球=yes)=3/9=1/3；计算P(x4|打球=yes)：P(x4|打球=yes)= P(wind=strong|打球=yes)=3/9=1/3；因此P(打球=yes|X)=9/14*2/9*2/9*1/3*1/3=2/567；P(不打球)=5/14P(不打球=yes|X)=P(X|不打球=yes)×P(不打球=yes) =P(x1|不打球=yes)×P(x2|不打球=yes)×P(x3|不打球=yes) ×P(x4|不打球=yes)×P(不打球=yes)先计算P(x1|不打球=yes)：P(x1|不打球=yes)= P(outlook=sunny|不打球=yes)=3/5计算P(x2|不打球=yes)：P(x2|不打球=yes)= P(Temperature=hot|不打球=yes)=2/5；计算P(x3|不打球=yes)：P(x3|不打球=yes)= P(Humidity=high|不打球=yes)=4/5；计算P(x4|不打球=yes)：P(x4|不打球=yes)= P(wind=strong|不打球=yes)=3/5；因此P(不打球=yes|X)=5/14*3/5*2/5*4/5*3/5=36/875；2/567<36/875 所以，不打球三、某银行的办卡数据如下，用贝叶斯分类器判断（女性，31-45，不是学生，收入低，？）是否会办卡？P(x1|办卡=yes)= P(性别=女|办卡=yes)=5/7计算P(x2|办卡=yes)：P(x2|办卡=yes)= P(年龄=31-45|办卡=yes)=3/7；计算P(x3|办卡=yes)：P(x3|办卡=yes)= P(学生身份=否|办卡=yes)=5/7；计算P(x4|办卡=yes)：P(x4|办卡=yes)= P(收入=低|办卡=yes)=2/7；因此P(办卡=yes|X)=7/10*5/7*3/7*5/7*2/7=15/343；P(x1|不办卡=yes)= P(性别=女|不办卡=yes)=1/3计算P(x2|不办卡=yes)：P(x2|不办卡=yes)= P(年龄=31-45|不办卡=yes)=1/3；计算P(x3|不办卡=yes)：P(x3|不办卡=yes)= P(学生身份=否|不办卡=yes)=0/3；计算P(x4|不办卡=yes)：P(x4|不办卡=yes)= P(收入=低|不办卡=yes)=1/3；因此P(不办卡=yes|X)=0显然P(办卡=yes|X)>p(不办卡=yes|X)所以会办卡。
贝叶斯分类作业题
作业：在下列条件下，求待定样本x=(2,0)T的类别，画出分界线，编程上机。
1、二类协方差不等Matlab程序如下：>> x1=[mean([1,1,2]),mean([1,0,-1])]',x2=[mean([-1,-1,-2]),mean([1,0,-1])]'x1 =1.3333x2 =-1.3333>> m=cov([1,1;1,0;2,-1]),n=cov([-1,1;-1,0;-2,-1])m =0.3333 -0.5000-0.5000 1.0000n =0.3333 0.50000.5000 1.0000>> m1=inv(m),n1=inv(n)m1 =12.0000 6.00006.0000 4.0000n1 =12.0000 -6.0000-6.0000 4.0000>> p=log((det(m))/(det(n)))p =>> q=log(1)q =>> x=[2,0]'x =2>> g=0.5*(x-x1)'*m1*(x-x1)-0.5*(x-x2)'*n1*(x-x2)+0.5*p-qg =-64（说明：g<0,则判定x=[2,0]T属于ω1类）（化简矩阵多项式0.5*(x-x1)'*m1*(x-x1)-0.5*(x-x2)'*n1*(x-x2)+0.5*p-q，其中x1,x2已知，x 设为x=[ x1,x2]T,化简到(12x1-16+6x2）(x1-4/3)+(6x1-8+4x2)-(12x1+16-6x2)(x1+4/3)-(-6x1-8+4x2)x2，下面用matlab化简，程序如下）>> syms x2;>> syms x1;>>w=(12*x1-16+6*x2)*(x1-4/3)+(6*x1-8+4*x2)*x2-(12*x1+16-6*x2)*(x1+4/3)-(-6*x1-8+4*x2)*x 2,simplify(w)w =(12*x1-16+6*x2)*(x1-4/3)+(6*x1-8+4*x2)*x2-(12*x1+16-6*x2)*(x1+4/3)-(-6*x1-8+4*x2)*x2ans =-64*x1+24*x2*x1(说明：则-64×x1+24×x2×x1=0,即x1=0，或者x2=8/3,很显然分界线方程为x1=0，因为x2=8/3连ω1类与ω2都分不开)2、二类协方差相等Matlab程序如下：>> l=m+nl =0.6667 00 2.0000>> l1= inv(l)l1 =1.5000 00 0.5000>> g1=(x2-x1)'*m1*x+0.5*(x1'*l1*x1-x2'*l1*x2)-qg1 =-64.0000（说明：g1<0,则判定x=[2,0]T属于ω1类）>> (x2-x1)'*m1ans =-32.0000 -16.0000>> syms x11;>> syms x22;>> w1=-32*x11+(-16)*x22+0.5*(x1'*l1*x1-x2'*l1*x2)-q,simplify(w1)w1 =-32*x11-16*x22ans =-32*x11-16*x22（说明：分界线方程为-32×x1-16×x2=0,即2×x1+x2=0）以下是matlab 绘图程序：>> x1=[1;1;2]; x2=[1;0;-1];plot(x1,x2,'mx','markersize',15);axis([-5,5,-5,5]);grid on;hold on >> x1=[-1;-1;-2]; x2=[1;0;-1];plot(x1,x2,'m*','markersize',15);axis([-5,5,-5,5]);hold on >> x1=[2]; x2=[0];plot(x1,x2,'mp','markersize',15);axis([-5,5,-5,5]);hold on>> x2=-5:0.02:5;x1=0;plot(x1,x2,'b');axis([-5,5,-5,5]);>> x1=-5:0.02:5;x2=-2*x1;plot(x1,x2,'-.k');axis([-5,5,-5,5]);绘图如下：-5-4-3-2-112345（说明：×点为ω1类的样本点，*点位ω2类的样本点，五角星为待定样本，实直线为二类协方差不等时的分界线，点划线为二类协方差相等时的分界线。
贝叶斯定理例题解答
贝叶斯定理例题解答贝叶斯定理是概率论中的一个重要定理，它描述了在已知某些先验条件的情况下，通过新的证据来更新我们对事件发生概率的估计。
下面给出一个贝叶斯定理的例题及解答，以帮助读者更好地理解和运用该定理。
例题：一家医院进行了一项新药物的临床试验，试验结果显示该药物对治疗某种疾病的有效率为80%。
然而，对于使用该药物的患者中，有10%的人实际上并不需要该药物，但仍然会有治疗效果。
对于需要该药物的患者，有5%的人没有治疗效果。
现在，一个病人想接受该药物治疗，但你并不确定他是否真的需要该药物。
如果该病人最终被治愈了，求他真正需要该药物的概率是多少？解答：设A表示病人需要该药物的事件，B表示该病人被治愈的事件，则题目所给的信息可以转化为以下条件概率：P(B|A)=0.8 （病人需要该药物并且得到治愈的概率）P(B|A')=0.1 （病人不需要该药物但得到治愈的概率）P(B'|A)=0.2 （病人需要该药物但没有治愈的概率）P(B'|A')=0.9 （病人不需要该药物且没有治愈的概率）由题意可知，该病人被治愈了，因此我们需要求解的是在B发生的条件下，A发生的概率，即：P(A|B)=P(B|A)*P(A)/P(B)其中，P(B)可以利用全概率公式计算：P(B)=P(B|A)*P(A)+P(B|A')*P(A')根据题目所给的信息，可以得到：P(A)=1-0.1=0.9P(A')=0.1代入上式，可得：P(B)=0.8*0.9+0.1*0.1=0.73再代入P(B|A)和P(A)，可得：P(A|B)=0.8*0.9/0.73=0.9877因此，该病人真正需要该药物的概率为0.9877，即约为98.77%。
变态难的贝叶斯公式试题
变态难的贝叶斯公式试题
1.某地区肝癌的发病率为0.0004，先用甲胎蛋白法进行普查。
化验结果存在错误。
已知患有肝癌的人其化验结果99%呈阳性(有病)，而没有患肝癌的人其化验结果99.9%呈阴性(无病)。
现某人的检查结果呈阳性，问他真患肝癌的概率是多少？
2.一个用户所有邮件分为两类：A1代表垃圾邮件，A2代表非垃圾邮件。
根据经验，P(A1)=0.7，P(A2)=0.3。
令B表示邮件包含“免费”这一关键词，由历史邮件得知，P(B|A1)=0.9，P(B|A2)=0.01（注意：它们之和并不一定等于1）。
问若收到一封新邮件，包含了“免费”这一关键字，那么它是垃圾邮件的概率是多少？
3.设某工有两个车间生产同型号家用电器，第一车间的次品率为，第二车间的次品率为，两个车间的成品都混合堆放在一个仓库，假设第1、2车间生产的成品比例为2:3，今有一客户从成品仓库中随机提一台产品，求该产品合格的概率。
4.盒中有a个红球，b个黑球，今随机地从中取出一个，观察其颜色后放回，并加上同色球c个，再从盒中第二次抽取一球，求第二次抽出的是黑球的概率。
5.已知甲袋中有6个红球，4个白球。
乙袋中有8个红球，6个白球。
求下列事件的概率：
(1)随机取一只袋，再从该袋中随机取一球，该球是红球；
(2)合并两只袋，从中随机取一球，该球是红球。
贝叶斯分类器例题
贝叶斯分类器例题（原创实用版）目录1.贝叶斯分类器的基本概念2.贝叶斯分类器的例子3.贝叶斯分类器的应用领域正文贝叶斯分类器是一种基于贝叶斯定理和特征条件独立假设的分类方法。
它是由英国数学家贝叶斯提出的，其核心思想是：对于任意一个待分类的样本，我们通过计算各个类别的概率，选择概率最大的类别作为该样本的分类结果。
下面，我们通过一个例子来详细了解贝叶斯分类器的工作原理。
假设我们有一个电子邮件垃圾邮件分类任务，其中包含两个特征：是否包含“垃圾邮件词汇”（如“免费”、“优惠”等）和是否包含“正常邮件词汇”（如“会议”、“工作”等）。
我们已知，如果一封邮件是垃圾邮件，那么它包含“垃圾邮件词汇”的概率是 0.8，包含“正常邮件词汇”的概率是 0.4；如果一封邮件是正常邮件，那么它包含“垃圾邮件词汇”的概率是 0.2，包含“正常邮件词汇”的概率是 0.6。
假设我们已收集到了一定数量的邮件，其中一部分是垃圾邮件，一部分是正常邮件。
我们现在的任务是通过这些已知信息，训练一个贝叶斯分类器，使得它能够准确地对新的邮件进行分类。
在训练过程中，贝叶斯分类器会根据已知信息计算出各个类别的条件概率。
具体地，它会计算垃圾邮件在包含“垃圾邮件词汇”和“正常邮件词汇”的条件下出现的概率，以及正常邮件在包含“垃圾邮件词汇”和“正常邮件词汇”的条件下出现的概率。
然后，对于一个待分类的邮件，贝叶斯分类器会根据这两个条件概率计算出该邮件属于垃圾邮件和正常邮件的概率，并选择概率最大的类别作为该邮件的分类结果。
贝叶斯分类器在许多领域都有广泛的应用，如文本分类、图像识别、垃圾邮件过滤等。
它具有良好的分类性能，且具有较强的理论依据。
然而，贝叶斯分类器也存在一定的局限性，例如对先验概率的依赖性、计算复杂度较高等。
贝叶斯判别习题[整理]
![贝叶斯判别习题[整理]](https://img.taocdn.com/s3/m/2708355b842458fb770bf78a6529647d272834a0.png)
1.办公室新来了一个雇员小王，小王是好人还是坏人大家都在猜测。
按人们主观意识，一个人是好人或坏人的概率均为0.5。
坏人总是要做坏事，好人总是做好事，偶尔也会做一件坏事，一般好人做好事的概率为0.9，坏人做好事的概率为0.2，一天，小王做了一件好事，小王是好人的概率有多大，你现在把小王判为何种人。
解：A ：小王是个好人 a ：小王做好事B ：小王是个坏人B ：小王做坏事()(/)(/)()(/)()(/)P A P a A P A a P A P a A P B P a B =+0.5*0.90.820.5*0.90.5*0.2==+=0.18()(/)0.5*0.2(/)()(/)()(/)0.5*0.90.5*0.2P B P a B P B b P A P a A P B P a B ==++0.82>0.18 所以小王是个好人、2. 设 m = 1,k = 2 ，X 1 ~ N (0,1) ，X 2 ~ N (3,2 2 ) ，试就C(2 | 1) = 1，C(1 | 2) = 1，且不考虑先验概率的情况下判别样品2，1 属于哪个总体，并求出 R = (R1, R2 ) 。
解：2222121/821()()/}1,221(2)(20)}0.05421(2)(23)/4}0.1762i i i P x x i P P μσ--=--==--===--==由于<，所以2属于1(2)P 2(2)P 2π21/2121/221(1)(10)}0.24221(1)(13)/4}0.1202P P --=--===--==>，所以1属于1(1)P 2(1)P 1π由1()Px 22211}()(3)/4}22x P x x -==--即2=21exp{}2x -21exp{(69)}8x x --+2211ln 2(69)28x x x -=--+解得=1.42 =-3.14.所以R=([-3.41,1.42],(-,-3.41)1x 2x ∞U(1.42,+)).∞3.已知，的先验分布分别为=,=,C(2|1)=1，C(1|2)=1，1π2π1q 352q 25且11,01()2,120,x x f P x x x <≤⎧⎪==-<≤⎨⎪⎩他他22(1)/4,13()(5)/4,350,x x f P x x x -<≤⎧⎪==-<≤⎨⎪⎩他他使判别= ，=2所属总体。
贝叶斯分类器例题
贝叶斯分类器例题
1.朴素贝叶斯分类器：一个例子是识别垃圾邮件。
给定一封邮件，可以根据邮件中的关键词和主题来判断该邮件是否为垃圾邮件。
通过朴素贝叶斯分类器，可以将邮件分为垃圾邮件和非垃圾邮件两类。
2.贝叶斯网络分类器：另一个例子是疾病诊断。
给定一个病人的症状和病史，可以根据贝叶斯网络分类器来预测该病人可能患有哪种疾病。
通过计算每个疾病的概率，可以得出最可能的诊断结果。
3.信用卡欺诈识别：在这个例子中，我们使用贝叶斯分类器来识别信用卡欺诈行为。
给定一系列交易数据，包括交易金额、交易地点、交易时间等，我们需要判断这些交易是否为欺诈行为。
通过训练一个贝叶斯分类器，可以学习到正常交易和欺诈交易的特征，并利用这些特征来预测新的交易是否为欺诈行为。
4.情感分析：在这个例子中，我们使用贝叶斯分类器来进行情感分析。
给定一篇文章或一段评论，我们需要判断该文本的情感倾向是积极还是消极。
通过训练一个贝叶斯分类器，可以学习到积极和消极文本的特征，并利用这些特征来预测新的文本的情感倾向。
5.基因分类：在这个例子中，我们使用贝叶斯分类器来进行基因分类。
给定一个基因序列，我们需要将其分类为不同的基因家族或亚家族。
通过训练一个贝叶斯分类器，可以学习到不同基因家族或亚家族的特征，并利用这些特征来预测新的基因序列的家族或亚家族归属。
以上这些例题只是贝叶斯分类器的一些应用示例，实际上贝叶斯分类器的应用非常广泛，它可以应用于任何需要分类的领域，如金融、医疗、社交媒体等。
贝叶斯决策的例题练习
贝叶斯决策的例题练习公司内部档案编码：[OPPTR-OPPT28-OPPTL98-OPPNN08]一、贝叶斯决策(Bayes decision theory)【例】某企业设计出一种新产品，有两种方案可供选择：—是进行批量生产，二是出售专利。
这种新产品投放市场，估计有3种可能：畅销、中等、滞销，这3种情况发生的可能性依次估计为：，和。
方案在各种情况下的利润及期望利润如下表。
企业可以以1000元的成本委托专业市场调查机构调查该产品销售前景。
若实际市场状况为畅销，则调查结果为畅销、中等和滞销的概率分别为、和；若实际市场状况为中等，则调查结果为畅销、中等和滞销的概率分别为、和；若实际市场状况为滞销，则调查结果为畅销、中等和滞销的概率分别为、和。
问：企业是否委托专业市场调查机构进行调查解：1.验前分析：记方案d1为批量生产，方案d2为出售专利E(d1)=*80+*20+*(-5)=(万元)E(d2)=40*+7*+1*=(万元)记验前分析的最大期望收益为E1，则E1=max{E(d1),E(d2)}=(万元)因此验前分析后的决策为：批量生产E1不作市场调查的期望收益2.预验分析：（1）设调查机构调查的结果畅销、中等、滞销分别用H1、H2、H3表示由全概率公式P(H1)=*+*+*=P(H2)=*+*+*=P(H3)=*+*+*=（2）由贝叶斯公式有P(?1|H1)=*=P(?2|H1)=*=P(?3|H1)=*=P(?1|H2)=*=P(?2|H2)=*=P(?3|H2)=*=P(?1|H3)=*=P(?2|H3)=*=P(?3|H3)=*=（3）用后验分布代替先验分布，计算各方案的期望收益值a)当市场调查结果为畅销时E(d1|H1)=80* P(?1|H1)+20* P(?2|H1)+(-5)* P(?3|H1)=80*+20*+(-5)*=(万元)E(d2|H1)=40* P(?1|H1)+7* P(?2|H1)+1* P(?3|H1)=40*+7*+1*=(万元)因此，当市场调查畅销时，最优方案是d1，即批量生产b)当市场调查结果为中等时E(d1|H2)=80* P(?1|H2)+20* P(?2|H2)+(-5)* P(?3|H2)=(万元)E(d2|H2)=40* P(?1|H2)+7* P(?2|H2)+1* P(?3|H2)=40*+7*+1*=(万元)所以市场调查为中等时，最优方案是：d1，即批量生产c)当市场调查结果为滞销时E(d1|H3)=80* P(?1|H3)+20* P(?2|H3)+(-5)* P(?3|H3)=80*+20*+(-5)*=（万元）E(d2|H3)=40* P(?1|H3)+7* P(?2|H3)+1* P(?3|H3)=40*+7*+1*=（万元）因此市场调查为滞销时，最优方案是：d2，即出售专利（4）通过调查，该企业可获得的收益期望值为E2= E(d1|H1)* P(H1)+ E(d1|H2)* P(H2)+ E(d2|H3)* P(H3)=*+*+*=（万元）通过调查，该企业收益期望值能增加E2-E1=（万元）因此，在调查费用不超过万元的情况下，应进行市场调查3.验后分析（1）本题中调查费用1000<9600,所以应该进行市场调查（2）当市场调查结果为畅销时，选择方案1，即批量生产（3）当市场调查结果为中等时时，选择方案1，即批量生产（4）当市场调查结果为滞销时，选择方案2，即出售专利。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
作业：在下列条件下，求待定样本x=(2,0)T的类别，画出分界线，编程上机。
1、二类协方差不等
Matlab程序如下：
>> x1=[mean([1,1,2]),mean([1,0,-1])]',x2=[mean([-1,-1,-2]),mean([1,0,-1])]'
x1 =
1.3333
x2 =
-1.3333
>> m=cov([1,1;1,0;2,-1]),n=cov([-1,1;-1,0;-2,-1])
m =
0.3333 -0.5000
-0.5000 1.0000
n =
0.3333 0.5000
0.5000 1.0000
>> m1=inv(m),n1=inv(n)
m1 =
12.0000 6.0000
6.0000 4.0000
n1 =
12.0000 -6.0000
-6.0000 4.0000
>> p=log((det(m))/(det(n)))
p =
>> q=log(1)
q =
>> x=[2,0]'
x =
2
>> g=0.5*(x-x1)'*m1*(x-x1)-0.5*(x-x2)'*n1*(x-x2)+0.5*p-q
g =
-64
（说明：g<0,则判定x=[2,0]T属于ω1类）
（化简矩阵多项式0.5*(x-x1)'*m1*(x-x1)-0.5*(x-x2)'*n1*(x-x2)+0.5*p-q，其中x1,x2已知，x 设为x=[ x1,x2]T,化简到(12x1-16+6x2）(x1-4/3)+(6x1-8+4x2)
-(12x1+16-6x2)(x1+4/3)-(-6x1-8+4x2)x2，
下面用matlab化简，程序如下）
>> syms x2;
>> syms x1;
>>
w=(12*x1-16+6*x2)*(x1-4/3)+(6*x1-8+4*x2)*x2-(12*x1+16-6*x2)*(x1+4/3)-(-6*x1-8+4*x2)*x 2,simplify(w)
w =
(12*x1-16+6*x2)*(x1-4/3)+(6*x1-8+4*x2)*x2-(12*x1+16-6*x2)*(x1+4/3)-(-6*x1-8+4*x2)*x2
ans =
-64*x1+24*x2*x1
(说明：则-64×x1+24×x2×x1=0,即x1=0，或者x2=8/3,很显然分界线方程为x1=0，因为x2=8/3连ω1类与ω2都分不开)
2、二类协方差相等
Matlab程序如下：
>> l=m+n
l =
0.6667 0
0 2.0000
>> l1= inv(l)
l1 =
1.5000 0
0 0.5000
>> g1=(x2-x1)'*m1*x+0.5*(x1'*l1*x1-x2'*l1*x2)-q
g1 =
-64.0000
（说明：g1<0,则判定x=[2,0]T属于ω1类）
>> (x2-x1)'*m1
ans =
-32.0000 -16.0000
>> syms x11;
>> syms x22;
>> w1=-32*x11+(-16)*x22+0.5*(x1'*l1*x1-x2'*l1*x2)-q,simplify(w1)
w1 =
-32*x11-16*x22
ans =
-32*x11-16*x22
（说明：分界线方程为-32×x1-16×x2=0,即2×x1+x2=0）
以下是matlab 绘图程序：
>> x1=[1;1;2]; x2=[1;0;-1];plot(x1,x2,'mx','markersize',15);axis([-5,5,-5,5]);grid on;hold on >> x1=[-1;-1;-2]; x2=[1;0;-1];plot(x1,x2,'m*','markersize',15);axis([-5,5,-5,5]);hold on >> x1=[2]; x2=[0];plot(x1,x2,'mp','markersize',15);axis([-5,5,-5,5]);hold on
>> x2=-5:0.02:5;x1=0;plot(x1,x2,'b');axis([-5,5,-5,5]);
>> x1=-5:0.02:5;x2=-2*x1;plot(x1,x2,'-.k');axis([-5,5,-5,5]);
绘图如下：
-5-4
-3
-2
-1
1
2
3
4
5
（说明：×点为ω1类的样本点，*点位ω2类的样本点，五角星为待定样本，实直线为二类协方差不等时的分界线，点划线为二类协方差相等时的分界线。
）。