模式识别大作业
模式识别大作业
一、问题描述现有sonar 和wdbc 这两个样本数据集，取一半数据作为训练样本集，其余数据作为测试样本集，通过编程实现分别用C 均值算法对测试样本集中的数据进行分类，进行10次分类求正确率的平均值。
二、算法描述1.初始化：选择c 个代表点,...,,321c p p p p2.建立c 个空间聚类表：C K K K ...,213.按照最小距离法则逐个对样本X 进行分类：),(),,(min arg J i iK x add p x j ∂=4.计算J 及用各聚类列表计算聚类均值，并用来作为各聚类新的代表点（更新代表点）5.若J 不变或代表点未发生变化，则停止。
否则转2.),(1∑∑=∈=ci K x i i p x J δ6.计算正确率：将dtat(i,1)与trueflag(i,1)（i=1~n ）进行比较，统计正确分类的样本数，并计算正确率将上述过程循环10次，得到10次的正确率，并计算平均正确率ave算法流程图三、实验数据表1 实验数据四、实验结果表2 实验结果准确率（%）注：表中准确率是十次实验结果的平均值五、程序源码用C均值算法对sonar分类（对wdbc分类的代码与之类似）clc;clear;accuracy = 0;for i = 1:10data = xlsread('sonar.xls');data = data';%初始划分2个聚类rand(:,1:size(data,2)) = data(:,randperm(size(data,2))'); %使矩阵元素按列重排A(:,1) = rand(:,1);B(:,1) = rand(:,2); %选取代表点m = 1;n = 1;for i = 3:size(rand,2)temp1 = rand(:,i) - A(:,1);temp2 = rand(:,i) - B(:,1);temp1(61,:) = [];temp2(61,:) = []; %去掉标号后再计算距离if norm(temp1) < norm(temp2)m = m + 1; %A类中样本个数A(:,m) = rand(:,i);elsen = n + 1; %B类中样本个数B(:,n) = rand(:,i);endend%划分完成m1 = mean(A,2);m2 = mean(B,2);%计算JeJ = 0;for i = 1:mtemp = A(:,i) - m1;temp(61,:) = []; %去掉标号的均值J = J + norm(temp)^2;endfor i = 1:ntemp = B(:,i) - m2;temp(61,:) = [];J = J + norm(temp)^2;endtest = [A,B];N = 0; %Je不变的次数while N < m + nrarr = randperm(m + n); %产生1-208即所有样本序号的随机不重复序列向量y = test(:,rarr(1,1));if rarr(1,1) <= m %y属于A类时if m == 1continueelsetemp1 = y - m1;temp1(61,:) = [];temp2 = y - m2;temp2(61,:) = [];p1 = m / (m - 1) * norm(temp1);p2 = n / (n + 1) * norm(temp2);if p2 < p1test = [test,y];test(:,rarr(1,1)) = [];m = m - 1;n = n + 1;endendelse %y属于B类时if n == 1continueelsetemp1 = y - m1;temp1(61,:) = [];temp2 = y - m2;temp2(61,:) = [];p1 = m / (m + 1) * norm(temp1);p2 = n / (n - 1) * norm(temp2);if p1 < p2test = [y,test];test(:,rarr(1,1)) = [];m = m + 1;n = n - 1;endendendA(:,1:m) = test(:,1:m);B(:,1:n) = test(:,m + 1:m + n);m1 = mean(A,2);m2 = mean(B,2);%计算JetempJ = 0;for i = 1:mtemp = A(:,i) - m1;temp(61,:) = []; %去掉标号的均值tempJ = tempJ + norm(temp)^2;endfor i = 1:ntemp = B(:,i) - m2;temp(61,:) = [];tempJ = tempJ + norm(temp)^2;endif tempJ == JN = N + 1;elseJ = tempJ;endend %while循环结束%判断正确率correct = 0;false = 0;A(:,1:m) = test(:,1:m);B(:,1:n) = test(:,m + 1:m + n);c = mean(A,2);if abs(c(61,1) - 1) < abs(c(61,1) - 2) %聚类A中大多为1类元素for i = 1:mif A(61,i) == 1correct = correct + 1;elsefalse = false + 1;endendfor i = 1:nif B(61,i) == 2correct = correct + 1;elsefalse = false + 1;endendelse %聚类A中大多为2类元素for i = 1:mif A(61,i) == 2correct = correct + 1;elsefalse = false + 1;endendfor i = 1:nif B(61,i) == 1correct = correct + 1;elsefalse = false + 1;endendendaccuracy = accuracy + correct / (correct + false);endaver_accuracy = accuracy / 10fprintf('用C均值算法对sonar进行十次分类的结果的平均正确率为%.2d %%.\n',aver_accuracy*100)六．实验心得本算法确定的K 个划分到达平方误差最小。
模式识别大作业02125128(修改版)
模式识别大作业班级 021252 姓名 谭红光 学号 021251281.线性投影与Fisher 准则函数各类在d 维特征空间里的样本均值向量：∑∈=ik X x kii xn M 1，2,1=i (1)通过变换w 映射到一维特征空间后，各类的平均值为：∑∈=ik Y y kii yn m 1，2,1=i (2)映射后，各类样本“类内离散度”定义为：22()k ii k i y Y S y m ∈=-∑，2,1=i (3)显然，我们希望在映射之后，两类的平均值之间的距离越大越好，而各类的样本类内离散度越小越好。
因此，定义Fisher 准则函数：2122212||()F m m J w s s -=+ (4)使FJ 最大的解*w 就是最佳解向量，也就是Fisher 的线性判别式. 从)(w J F 的表达式可知，它并非w 的显函数，必须进一步变换。
已知：∑∈=ik Y y kii yn m 1，2,1=i , 依次代入上两式，有：i TX x ki Tk X x Ti i M w x n w x w n m ik ik ===∑∑∈∈)1(1，2,1=i (5) 所以：221221221||)(||||||||M M w M w M w m m T T T -=-=-w S w w M M M M w b T T T =--=))((2121 (6)其中：Tb M M M M S ))((2121--= (7)bS 是原d 维特征空间里的样本类内离散度矩阵，表示两类均值向量之间的离散度大小，因此，b S 越大越容易区分。
将(4.5-6)i Ti M w m =和(4.5-2)∑∈=ik X x kii xn M 1代入(4.5-4)2iS 式中：∑∈-=ik X x iT k T i M w x w S 22)(∑∈⋅--⋅=ik X x Tik i k T w M x M x w ))(( w S w i T= (8)其中：T iX x k i k i M x M x S ik ))((--=∑=，2,1=i (9)因此：w S w w S S w S S w T T =+=+)(212221 (10)显然：21S S S w += (11)w S 称为原d 维特征空间里，样本“类内离散度”矩阵。
模式识别大作业
模式识别专业：电子信息工程班级：电信****班学号：********** 姓名：艾依河里的鱼一、贝叶斯决策（一）贝叶斯决策理论 1.最小错误率贝叶斯决策器在模式识别领域，贝叶斯决策通常利用一些决策规则来判定样本的类别。
最常见的决策规则有最大后验概率决策和最小风险决策等。
设共有K 个类别，各类别用符号k c ()K k ,,2,1 =代表。
假设k c 类出现的先验概率()k P c以及类条件概率密度()|k P c x 是已知的，那么应该把x 划分到哪一类才合适呢？若采用最大后验概率决策规则，首先计算x 属于k c 类的后验概率()()()()()()()()1||||k k k k k Kk k k P c P c P c P c P c P P c P c ===∑x x x x x然后将x 判决为属于kc ~类，其中()1arg max |kk Kk P c ≤≤=x若采用最小风险决策，则首先计算将x 判决为k c 类所带来的风险(),k R c x ，再将x 判决为属于kc ~类，其中()min ,kkk R c =x可以证明在采用0-1损失函数的前提下，两种决策规则是等价的。
贝叶斯决策器在先验概率()k P c 以及类条件概率密度()|k P c x 已知的前提下，利用上述贝叶斯决策规则确定分类面。
贝叶斯决策器得到的分类面是最优的，它是最优分类器。
但贝叶斯决策器在确定分类面前需要预知()k P c 与()|k P c x ，这在实际运用中往往不可能，因为()|k P c x 一般是未知的。
因此贝叶斯决策器只是一个理论上的分类器，常用作衡量其它分类器性能的标尺。
最小风险贝叶斯决策可按下列步骤进行： (1)在已知)(i P ω，)(i X P ω，i=1,…，c 及给出待识别的X 的情况下，根据贝叶斯公式计算出后验概率：∑==cj iii i i P X P P X P X P 1)()()()()(ωωωωω j=1,…，x(2)利用计算出的后验概率及决策表，按下面的公式计算出采取i a ,i=1,…，a 的条件风险∑==cj j j i i X P a X a R 1)(),()(ωωλ,i=1,2,…,a(3)对(2)中得到的a 个条件风险值)(X a R i ,i=1,…，a 进行比较，找出使其条件风险最小的决策k a ，即()()1,min k i i aR a x R a x ==则k a 就是最小风险贝叶斯决策。
模式识别大作业
模式识别大作业引言：转眼之间，研一就结束了。
这学期的模式识别课也接近了尾声。
我本科是机械专业，编程和算法的理解能力比较薄弱。
所以虽然这学期老师上课上的很精彩，但是这学期的模式识别课上的感觉还是有点吃力。
不过这学期也加强了编程的练习。
这次的作业花了很久的时间，因为平时自己的方向是主要是图像降噪，自己在看这一块图像降噪论文的时候感觉和模式识别的方向结合的比较少。
我看了这方面的模式识别和图像降噪结合的论文，发现也比较少。
在思考的过程中，我想到了聚类的方法。
包括K均值和C均值等等。
因为之前学过K均值，于是就选择了K均值的聚类方法。
然后用到了均值滤波和自适应滤波进行处理。
正文：k-means聚类算法的工作过程说明如下：首先从n个数据对象任意选择 k 个对象作为初始聚类中心；而对于所剩下其它对象，则根据它们与这些聚类中心的相似度（距离），分别将它们分配给与其最相似的（聚类中心所代表的）聚类；然后再计算每个所获新聚类的聚类中心（该聚类中所有对象的均值）；不断重复这一过程直到标准测度函数开始收敛为止。
一般都采用均方差作为标准测度函数。
k-means 算法接受输入量k ；然后将n个数据对象划分为k个聚类以便使得所获得的聚类满足：同一聚类中的对象相似度较高；而不同聚类中的对象相似度较小。
聚类相似度是利用各聚类中对象的均值所获得一个“中心对象”（引力中心）来进行计算的。
k个聚类具有以下特点：各聚类本身尽可能的紧凑，而各聚类之间尽可能的分开。
均值滤波是常用的非线性滤波方法 ,也是图像处理技术中最常用的预处理技术。
它在平滑脉冲噪声方面非常有效,同时它可以保护图像尖锐的边缘。
均值滤波是典型的线性滤波算法，它是指在图像上对目标像素给一个模板，该模板包括了其周围的临近像素（以目标象素为中心的周围8个象素，构成一个滤波模板，即去掉目标象素本身）。
再用模板中的全体像素的平均值来代替原来像素值。
即对待处理的当前像素点（x，y），选择一个模板，该模板由其近邻的若干像素组成，求模板中所有像素的均值，再把该均值赋予当前像素点（x，y），作为处理后图像在该点上的灰度个g（x，y），即个g（x，y）=1/m ∑f（x，y）m为该模板中包含当前像素在内的像素总个数。
模式识别大作业
模式识别大作业(总21页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--作业1 用身高和/或体重数据进行性别分类（一）基本要求：用和的数据作为训练样本集，建立Bayes分类器，用测试样本数据对该分类器进行测试。
调整特征、分类器等方面的一些因素，考察它们对分类器性能的影响，从而加深对所学内容的理解和感性认识。
具体做法：1．应用单个特征进行实验：以（a）身高或者（b）体重数据作为特征，在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数，建立最小错误率Bayes分类器，写出得到的决策规则，将该分类器应用到测试样本，考察测试错误情况。
在分类器设计时可以考察采用不同先验概率（如对, 对, 对等）进行实验，考察对决策规则和错误率的影响。
图1-先验概率:分布曲线图2-先验概率:分布曲线图3--先验概率:分布曲线图4不同先验概率的曲线有图可以看出先验概率对决策规则和错误率有很大的影响。
程序：和2．应用两个特征进行实验：同时采用身高和体重数据作为特征，分别假设二者相关或不相关（在正态分布下一定独立），在正态分布假设下估计概率密度，建立最小错误率Bayes分类器，写出得到的决策规则，将该分类器应用到训练/测试样本，考察训练/测试错误情况。
比较相关假设和不相关假设下结果的差异。
在分类器设计时可以考察采用不同先验概率（如 vs. , vs. , vs. 等）进行实验，考察对决策和错误率的影响。
训练样本female来测试图1先验概率 vs. 图2先验概率 vs.图3先验概率 vs. 图4不同先验概率对测试样本1进行试验得图对测试样本2进行试验有图可以看出先验概率对决策规则和错误率有很大的影响。
程序和3．自行给出一个决策表，采用最小风险的Bayes决策重复上面的某个或全部实验。
W1W2W10W20close all;clear all;X=120::200; %设置采样范围及精度pw1=;pw2=; %设置先验概率sample1=textread('') %读入样本samplew1=zeros(1,length(sample1(:,1)));u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布figure(1);subplot(2,1,1);plot(X,y1);title('F身高类条件概率分布曲线');sample2=textread('') %读入样本samplew2=zeros(1,length(sample2(:,1)));u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布subplot(2,1,2);plot(X,y2);title('M身高类条件概率分布曲线');P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);figure(2);subplot(2,1,1);plot(X,P1);title('F身高后验概率分布曲线');subplot(2,1,2);plot(X,P2);title('M身高后验概率分布曲线');P11=pw1*y1;P22=pw2*y2;figure(3);subplot(3,1,1);plot(X,P11);subplot(3,1,2);plot(X,P22);subplot(3,1,3);plot(X,P11,X,P22);sample=textread('all ') %读入样本[result]=bayes(sample1(:,1),sample2(:,1),pw1,pw2);%bayes分类器function [result] =bayes(sample1(:,1),sample2(:,1),pw1,pw2); error1=0;error2=0;u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);for i = 1:50if P1(i)>P2(i)result(i)=0;pe(i)=P2(i);elseresult(i)=1;pe(i)=P1(i);endendfor i=1:50if result(k)==0error1=error1+1;else result(k)=1error2=error2+1;endendratio = error1+error2/length(sample); %识别率,百分比形式sprintf('正确识别率为%.2f%%.',ratio)作业2 用身高/体重数据进行性别分类（二）基本要求：试验直接设计线性分类器的方法，与基于概率密度估计的贝叶斯分离器进行比较。
模式识别大作业-许萌-1306020
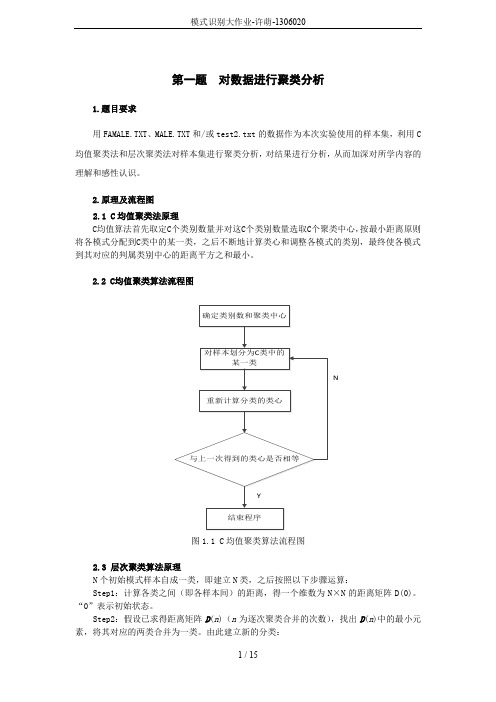
第一题对数据进行聚类分析1.题目要求用FAMALE.TXT、MALE.TXT和/或test2.txt的数据作为本次实验使用的样本集，利用C 均值聚类法和层次聚类法对样本集进行聚类分析，对结果进行分析，从而加深对所学内容的理解和感性认识。
2.原理及流程图2.1 C均值聚类法原理C均值算法首先取定C个类别数量并对这C个类别数量选取C个聚类中心，按最小距离原则将各模式分配到C类中的某一类，之后不断地计算类心和调整各模式的类别，最终使各模式到其对应的判属类别中心的距离平方之和最小。
2.2 C均值聚类算法流程图N图1.1 C均值聚类算法流程图2.3 层次聚类算法原理N个初始模式样本自成一类，即建立N类，之后按照以下步骤运算：Step1：计算各类之间（即各样本间）的距离，得一个维数为N×N的距离矩阵D(0)。
“0”表示初始状态。
Step2：假设已求得距离矩阵D(n)（n为逐次聚类合并的次数），找出D(n)中的最小元素，将其对应的两类合并为一类。
由此建立新的分类：Step3：计算合并后所得到的新类别之间的距离，得D (n +1)。
Step4：跳至第2步，重复计算及合并。
直到满足下列条件时即可停止计算：①取距离阈值T ，当D (n )的最小分量超过给定值 T 时，算法停止。
所得即为聚类结果。
②或不设阈值T ，一直到将全部样本聚成一类为止，输出聚类的分级树。
2.4层次聚类算法流程图N图1.2层次聚类算法流程图3 验结果分析对数据文件FAMALE.TXT 、MALE.TXT 进行C 均值聚类的聚类结果如下图所示：图1.3 C 均值聚类结果的二维平面显示将两种样本即进行聚类后的样本中心进行比较，如下表：从下表可以纵向比较可以看出，C 越大，即聚类数目越多，聚类之间差别越小，他们的聚类中心也越接近。
横向比较用FEMALE,MALE 中数据作为样本和用FEMALE,MALE ，test2中),1(),1(21++n G n G数据作为样本时，由于引入了新的样本，可以发现后者的聚类中心比前者都稍大。
模式识别大作业
作业1 用身高和/或体重数据进行性别分类（一）基本要求：用和的数据作为训练样本集，建立Bayes分类器，用测试样本数据对该分类器进行测试。
调整特征、分类器等方面的一些因素，考察它们对分类器性能的影响，从而加深对所学内容的理解和感性认识。
具体做法：1．应用单个特征进行实验：以（a）身高或者（b）体重数据作为特征，在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数，建立最小错误率Bayes分类器，写出得到的决策规则，将该分类器应用到测试样本，考察测试错误情况。
在分类器设计时可以考察采用不同先验概率（如对, 对, 对等）进行实验，考察对决策规则和错误率的影响。
图1-先验概率:分布曲线图2-先验概率:分布曲线图3--先验概率:分布曲线图4不同先验概率的曲线有图可以看出先验概率对决策规则和错误率有很大的影响。
程序：和2．应用两个特征进行实验：同时采用身高和体重数据作为特征，分别假设二者相关或不相关（在正态分布下一定独立），在正态分布假设下估计概率密度，建立最小错误率Bayes 分类器，写出得到的决策规则，将该分类器应用到训练/测试样本，考察训练/测试错误情况。
比较相关假设和不相关假设下结果的差异。
在分类器设计时可以考察采用不同先验概率（如vs. , vs. , vs. 等）进行实验，考察对决策和错误率的影响。
训练样本female来测试图1先验概率vs. 图2先验概率vs.图3先验概率vs. 图4不同先验概率对测试样本1进行试验得图对测试样本2进行试验有图可以看出先验概率对决策规则和错误率有很大的影响。
程序和3．自行给出一个决策表，采用最小风险的Bayes决策重复上面的某个或全部实验。
W1W2W10W20close all;clear all;X=120::200; %设置采样范围及精度pw1=;pw2=; %设置先验概率sample1=textread('') %读入样本samplew1=zeros(1,length(sample1(:,1)));u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布figure(1);subplot(2,1,1);plot(X,y1);title('F身高类条件概率分布曲线');sample2=textread('') %读入样本samplew2=zeros(1,length(sample2(:,1)));u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布subplot(2,1,2);plot(X,y2);title('M身高类条件概率分布曲线');P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);figure(2);subplot(2,1,1);plot(X,P1);title('F身高后验概率分布曲线');subplot(2,1,2);plot(X,P2);title('M身高后验概率分布曲线');P11=pw1*y1;P22=pw2*y2;figure(3);subplot(3,1,1);plot(X,P11);subplot(3,1,2);plot(X,P22);subplot(3,1,3);plot(X,P11,X,P22);sample=textread('all ') %读入样本[result]=bayes(sample1(:,1),sample2(:,1),pw1,pw2);%bayes分类器function [result] =bayes(sample1(:,1),sample2(:,1),pw1,pw2);error1=0;error2=0;u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);for i = 1:50if P1(i)>P2(i)result(i)=0;pe(i)=P2(i);elseresult(i)=1;pe(i)=P1(i);endendfor i=1:50if result(k)==0error1=error1+1;else result(k)=1error2=error2+1;endendratio = error1+error2/length(sample); %识别率,百分比形式sprintf('正确识别率为%.2f%%.',ratio)作业2 用身高/体重数据进行性别分类（二）基本要求：试验直接设计线性分类器的方法，与基于概率密度估计的贝叶斯分离器进行比较。
模式识别大作业
模式识别大作业对sonar数据进行分类，用Fisher线性判别法和最近邻算法对其进行分类，并用MATLAB写程序对其进行模拟。
Fisher线性判别法的源程序如下clear,close all%¶ÁÈ¡È«²¿Êý¾ÝRock=xlsread('C:\Users\Administrator\Documents\data\rock');Mine=xlsread('C:\Users\Administrator\Documents\data\mine');%²úÉúËæ»úÊýr1=randperm(97,48);r2=randperm(111,56);%È¡³öѵÁ·Ñù±¾for i=1:48vtrainrock(i,:)=Rock(r1(1,i),:);endtrainrock=vtrainrock';for i=1:56vtrainmine(i,:)=Mine(r2(1,i),:);endtrainmine=vtrainmine';%È¡³ö²âÊÔÑù±¾Rock(r1',:)=[];testrock=Rock';Mine(r2',:)=[];testmine=Mine';%¼ÆËã¾ùÖµÏòÁ¿mrock=mean(trainrock,2);mmine=mean(trainmine,2);%¼ÆËãÀàÄÚÀëÉ¢¶È¾ØÕófor j=1:48s1=(trainrock(:,j)-mrock);sr=s1*s1';srock=zeros(60);srock=sr+srock;endfor j=1:56s2=(trainmine(:,j)-mmine);sm=s2*s2';smine=zeros(60);smine=sm+smine;endSw=srock+smine;%¼ÆËãÀà¼äÀëÉ¢¶È¾ØÕóSb=(mrock-mmine)*(mrock-mmine)';%¼ÆËã×î¼ÑͶӰ·½ÏòW=inv(Sw)*(mrock-mmine);%¶ÔѵÁ·Ñù±¾½øÐÐͶӰintestrock=W'*testrock;intestmine=W'*testmine;%¼ÆËãÅбðãÐÖµµãintrainrock=W'*trainrock;intrainmine=W'*trainmine;w0=(mean(intrainrock,2)*48+mean(intrainmine,2)*56)/104;%·ÖÀಢ¼ÆËã׼ȷÂÊ%¶Ô´ý²âÑù±¾½øÐзÖÀàj1=1;k1=1;RocksortRock1=zeros(size(intestrock));%¼ì²âÑù±¾Rock±»ÕýÈ·µØ·ÖΪRockµÄÊýRocksortMine1=zeros(size(intestmine));%¼ì²âÑù±¾Rock±»´íÎóµØ·ÖΪMineµÄÊýRocksortRocknumber1=zeros(size(intestrock));%¼ì²âÑù±¾Rock±»ÕýÈ·µØ·ÖΪRockµÄÊýÔÚ¼ì²âÑù±¾ÀïµÄÐòºÅRocksortMinenumber1=zeros(size(intestmine));%¼ì²âÑù±¾Rock±»´íÎóµØ·ÖΪMineµÄÊýÔÚ¼ì²âÑù±¾ÀïµÄÐòºÅfor i=1:49if(intestrock(1,i)>w0)RocksortRock1(1,j1)=intestrock(1,i);RocksortRocknumber1(1,j1)=i;j1=j1+1;elseRocksortMine1(1,k1)=intestrock(1,i);RocksortMinenumber1(1,k1)=i;k1=k1+1;endendj2=1;k2=1;MinesortMine2=zeros(size(intestmine));%¼ì²âÑù±¾Mine±»ÕýÈ·µØ·ÖΪMineµÄÊýMinesortRock2=zeros(size(intestrock));%¼ì²âÑù±¾Mine±»´íÎóµØ·ÖΪRockµÄÊýMinesortMinenumber2=zeros(size(intestmine));%¼ì²âÑù±¾Mine±»ÕýÈ·µØ·ÖΪMineµÄÊýÔÚ¼ì²âÑù±¾ÀïµÄÐòºÅMinesortRocknumber2=zeros(size(intestrock));%¼ì²âÑù±¾Mine±»´íÎóµØ·ÖΪRockµÄÊýÔÚ¼ì²âÑù±¾ÀïµÄÐòºÅfor i=1:55if(intestmine(1,i)<=w0)MinesortMine2(1,j2)=intestmine(1,i);MinesortMinenumber2(1,j2)=i;j2=j2+1;elseMinesortRock2(1,k2)=intestmine(1,i);MinesortRocknumber2(1,k2)=i;k2=k2+1;endend%¼ÆËã·ÖÀà½á¹ûµÄÕýÈ·ÂÊright=(j1+j2-2)/(j1+j2+k1+k2-4);disp(right);最近邻算法的源程序如下clear,close all%¶ÁÈ¡È«²¿Êý¾ÝRock=xlsread('C:\Users\Administrator\Documents\data\rock'); Mine=xlsread('C:\Users\Administrator\Documents\data\mine'); %²úÉúËæ»úÊýr1=randperm(97,48);r2=randperm(111,56);%È¡³öѵÁ·Ñù±¾for i=1:48vtrainrock(i,:)=Rock(r1(1,i),:);endtrainrock=vtrainrock';for i=1:56vtrainmine(i,:)=Mine(r2(1,i),:);endtrainmine=vtrainmine';%È¡³ö²âÊÔÑù±¾Rock(r1',:)=[];testrock=Rock';Mine(r2',:)=[];testmine=Mine';%×î½üÁÚ·ÖÀàrocklast=zeros(size(Rock'));minelast=zeros(size(Mine'));rgr=0;rwm=0;mgm=0;mwr=0;for i=1:49for j=1:48Ar(j,1)=(testrock(:,i)-trainrock(:,j))'*(testrock(:,i)-trainrock(:,j)) ;endfor k=1:56Br(k,1)=(testrock(:,i)-trainmine(:,k))'*(testrock(:,i)-trainmine(:,k)) ;end%¶Ô´ý²âÑù±¾½øÐзÖÀàif(min(Ar)<=min(Br))rocklast(:,i)=testrock(:,i);rgr=rgr+1;Ar=zeros(48,1);Br=zeros(56,1);elseminelast(:,i)=testrock(:,i);rwm=rwm+1;Ar=zeros(48,1);Br=zeros(56,1);endendfor i=1:55for j=1:48Am(j,1)=(testmine(:,i)-trainrock(:,j))'*(testmine(:,i)-trainrock(:,j)) ;endfor k=1:56Bm(k,1)=(testmine(:,i)-trainmine(:,k))'*(testmine(:,i)-trainmine(:,k)) ;end%¶Ô´ý²âÑù±¾½øÐзÖÀàif(min(Am)<min(Bm))rocklast(:,i)=testmine(:,i);mwr=mwr+1;Am=zeros(48,1);Bm=zeros(56,1);elseminelast(:,i)=testmine(:,i);mgm=mgm+1;Am=zeros(48,1);Bm=zeros(56,1);endendright=(rgr+mgm)/(rgr+mgm+rwm+mwr);disp(right);以上为两种算法在MATLAB里的源代码。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
作业1 用身高和/或体重数据进行性别分类（一）基本要求：用FAMALE.TXT和MALE.TXT的数据作为训练样本集，建立Bayes分类器，用测试样本数据对该分类器进行测试。
调整特征、分类器等方面的一些因素，考察它们对分类器性能的影响，从而加深对所学内容的理解和感性认识。
具体做法：1．应用单个特征进行实验：以（a）身高或者（b）体重数据作为特征，在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数，建立最小错误率Bayes分类器，写出得到的决策规则，将该分类器应用到测试样本，考察测试错误情况。
在分类器设计时可以考察采用不同先验概率（如0.5对0.5, 0.75对0.25, 0.9对0.1等）进行实验，考察对决策规则和错误率的影响。
图1-先验概率0.5:0.5分布曲线图2-先验概率0.75:0.25分布曲线图3--先验概率0.9:0.1分布曲线图4不同先验概率的曲线有图可以看出先验概率对决策规则和错误率有很大的影响。
程序：bayesflq1.m和bayeszcx.m2．应用两个特征进行实验：同时采用身高和体重数据作为特征，分别假设二者相关或不相关（在正态分布下一定独立），在正态分布假设下估计概率密度，建立最小错误率Bayes 分类器，写出得到的决策规则，将该分类器应用到训练/测试样本，考察训练/测试错误情况。
比较相关假设和不相关假设下结果的差异。
在分类器设计时可以考察采用不同先验概率（如0.5 vs. 0.5, 0.75 vs. 0.25, 0.9 vs. 0.1等）进行实验，考察对决策和错误率的影响。
训练样本female来测试图1先验概率0.5 vs. 0.5 图2先验概率0.75 vs. 0.25图3先验概率0.9 vs. 0.1 图4不同先验概率对测试样本1进行试验得图对测试样本2进行试验有图可以看出先验概率对决策规则和错误率有很大的影响。
程序bayesflq2.m和bayeszcx2.m 3．自行给出一个决策表，采用最小风险的Bayes决策重复上面的某个或全部实验。
W1 W2W1 0 0.7W2 0.3 0close all;clear all;X=120:0.1:200; %设置采样范围及精度pw1=0.9;pw2=0.1; %设置先验概率sample1=textread('FEMALE.txt') %读入样本samplew1=zeros(1,length(sample1(:,1)));u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布figure(1);subplot(2,1,1);plot(X,y1);title('F身高类条件概率分布曲线');sample2=textread('MALE.txt') %读入样本samplew2=zeros(1,length(sample2(:,1)));u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布subplot(2,1,2);plot(X,y2);title('M身高类条件概率分布曲线');P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);figure(2);subplot(2,1,1);plot(X,P1);title('F身高后验概率分布曲线');subplot(2,1,2);plot(X,P2);title('M身高后验概率分布曲线');P11=pw1*y1;P22=pw2*y2;figure(3);subplot(3,1,1);plot(X,P11);subplot(3,1,2);plot(X,P22);subplot(3,1,3);plot(X,P11,X,P22);sample=textread('all sample.txt') %读入样本[result]=bayes(sample1(:,1),sample2(:,1),pw1,pw2);%bayes分类器function [result] =bayes(sample1(:,1),sample2(:,1),pw1,pw2);error1=0;error2=0;u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);for i = 1:50if P1(i)>P2(i)result(i)=0;pe(i)=P2(i);elseresult(i)=1;pe(i)=P1(i);endendfor i=1:50if result(k)==0error1=error1+1;else result(k)=1error2=error2+1;endendratio = error1+error2/length(sample); %识别率,百分比形式sprintf('正确识别率为%.2f%%.',ratio)作业2 用身高/体重数据进行性别分类（二）基本要求：试验直接设计线性分类器的方法，与基于概率密度估计的贝叶斯分离器进行比较。
具体做法：同时采用身高和体重数据作为特征，用Fisher线性判别方法求分类器，将该分类器应用到训练和测试样本，考察训练和测试错误情况。
将训练样本和求得的决策边界画到图上，同时把以往用Bayes方法求得的分类器也画到图上，比较结果的异同。
解答：Clcclear allsample1=textread('FEMALE.txt') %读入样本sample2=textread('MALE.txt') %读入样本[length1,width1]=size(sample1);[length2,width2]=size(sample2);One1 = ones(length1, 1);One2 = ones(length2, 1);plot(sample1(:,1), sample1(:,2), 'r*',sample2(:,1), sample2(:,2), 'bo')title('Famale和male身高体重聚类图'); Y1=sample1(:,1:2);Y2=sample2(:,1:2);m1 = mean(Y1);m2 = mean(Y2);S1 = (Y1 - One1 * m1)'*(Y1 - One1 * m1); S2 = (Y2 - One2 * m2)'*(Y2 - One2 * m2); sw = S1+S2;ww=inv(sw);w = inv(sw)*(m1 - m2)';Y = [Y1;Y2];z = Y*w;hold ont = z*w'/norm(w)^2;plot(t(:,1), t(:,2))for i = 1:length1+length2plot([Y(i,1) t(i,1)], [Y(i,2) t(i,2)], '-.')endaxis([120 200 40 100])title('fisher线性变换后');grid作业2图一作业2图二利用K-L 变换进行特征提取的实验一、基本要求用FAMALE.TXT 和MALE.TXT 的数据作为本次实验使用的样本集，利用K-L 变换对该样本集进行变换，与过去用Fisher 线性判别方法或其它方法得到的分类面进行比较，从而加深对所学内容的理解和感性认识。
二、具体做法1. 不考虑类别信息对整个样本集进行K-L 变换（即PCA ），并将计算出的新特征方向表示在二维平面上，考察投影到特征值最大的方向后男女样本的分布情况并用该主成分进行分类2. 利用类平均向量提取判别信息，选取最好的投影方向，考察投影后样本的分布情况并用该投影方向进行分类。
3. 将上述投影和分类情况与以前做的各种分类情况比较，考察各自的特点和相互关系。
三、实验原理K-L 变换是一种基于目标统计特性的最佳正交变换。
它具有一些优良的性质：即变换后产生的新的分量正交或者不相关；以部分新的分量表示原矢量均方误差最小；变换后的矢量更趋确定，能量更集中。
这一方法的目的是寻找任意统计分布的数据集合之主要分量的子集。
设n 维矢量12,,,Tn x x x ⎡⎤⎣⎦=x L ，其均值矢量E ⎡⎤⎣⎦=μx ，协方差阵()Tx E ⎡⎤⎣⎦=--C x u)(x u ，此协方差阵为对称正定阵，则经过正交分解克表示为x =TC U ΛU ,其中12,,,[]n diag λλλ=ΛL ，12,,,n u u u ⎡⎤⎣⎦=U L 为对应特征值的特征向量组成的变换阵，且满足1T -=U U 。
变换阵T U 为旋转矩阵，再此变换阵下x 变换为()T -=x u y U ,在新的正交基空间中，相应的协方差阵12[,,,]x n diag λλλ==x UC U C L 。
通过略去对应于若干较小特征值的特征向量来给y 降维然后进行处理。
通常情况下特征值幅度差别很大，忽略一些较小的值并不会引起大的误差。
1.不考虑类别信息对整个样本集进行K-L 变换（即PCA ）（1）读入female.txt 和male.txt 两组数据，组成一个样本集。
计算样本均值向量u E x ⎡⎤⎣⎦=和协方差()()T x u x u c E ⎡⎤--⎣⎦= （2）计算协方差阵C 的特征值Λ和特征向量U （3）选取特征值最大的特征向量作为投影方向 （4）选取阈值进行判断 2.利用类平均信息提取判别信息（1）读入female.txt 和male.txt 两组数据，分别计算样本均值向量i u E x ⎡⎤⎣⎦=和协方差()()Ti x u x u c E ⎡⎤--⎣⎦=，及总均值向量()122u u u += （2）计算类间离散度矩阵S b （()()()21Tb i i i i S p u u u u ω==--∑）与类内离散度矩阵S w（21w i i i S P ==∑∑）（3）用()T j b jj ju S u J X λ=比较分类性能，选择最佳投影方向（4）选取阈值进行判断 四、实验结果与分析1.不考虑类别信息对整个样本集进行K-L 变换（即PCA ） U=(0.6269,0.7791)T ,P 1=0.5, P 2=0.52.利用类平均信息提取判决信息 U=(0.5818,0.8133)T ,P 1=0.5, P 2=0.5%不考虑类别信息clc;clear all;[FH FW]=textread('C:\Users\rengang\Desktop\homework\FEMALE.txt','%f %f');[MH MW]=textread('C:\Users\rengang\Desktop\homework\MALE.txt','%f %f');FA=[FH FW];FA=FA';MA=[MH MW];MA=MA';for k=1:50NT(:,k)=FA(:,k);endfor k=51:100NT(:,k)=MA(:,k-50);endX=(sum(NT')/length(NT))';%这里NT'是一个100*2的矩阵，X为总样本均值。