西电随机大作业
西电2022年秋季《面向对象程序设计(c++)》大作业及答案

学习中心/函授站姓名学号西安电子科技大学网络与继续教育学院2022 学年下学期《面向对象程序设计(C++)》期末考试试题(综合大作业)考试说明:1、大作业试题公布时间:(1)毕业班:2022 年10 月21 日;(2)正常班:2022 年11 月18 日;2、考试必须独立完成,如发现抄袭、雷同均按零分计;3、答案须用《西安电子科技大学网络与继续教育学院2022 秋期末考试答题纸》(个人专属答题纸)手写完成,要求字迹工整、卷面干净、整齐;4、在线上传时间:(1)毕业班学生于2022 年10 月21 日至2022 年11 月1 日在线上传大作业答卷;(2)正常班学生于2022 年11 月18 日至2022 年12 月5 日在线上传大作业答卷;5、拍照要求完整、清晰,一张图片对应一张个人专属答题纸(A4 纸),正确上传。
一、简答题(10 分)1、运算符 new 和 delete 的功能分别是什么?(3 分)答案:运算符new的功能是创建动态对象;delete的功能是释放由new创建的动态对象。
2、若派生类以 private 方式从一个基类派生,派生类的对象可以访问基类中的哪些成员?派生类的成员函数可以访问基类中的哪些成员?(3 分)答案:若派生类以private方式从一个基类派生,派生类的对象不能访问基类中的任何成员(1分);派生类的成员函数可以访问基类中的public和protected成员(2分)。
3、构造函数的作用是什么?在创建派生类的对象时,应按照怎样的顺序调用构造函数?(4 分)答案:构造函数的作用是创建对象并对其进行必要的初始化。
(1分)构造函数调用顺序:基类构造函数、子对象类构造函数(如果有)、派生类构造函数。
(2分)二、填空题(每空 2 分,共 20 分)1、函数的返回值是通过函数体中的return语句带回的;若被调用函数被定义为 void 类型,则被调用函数不带回任何值。
2、表示逻辑关系“ a 大于等于8 或者 a 小于等于5”的C++表达式是。
2020秋西安电子科技大学《数字逻辑电路》大作业期末试题及答案
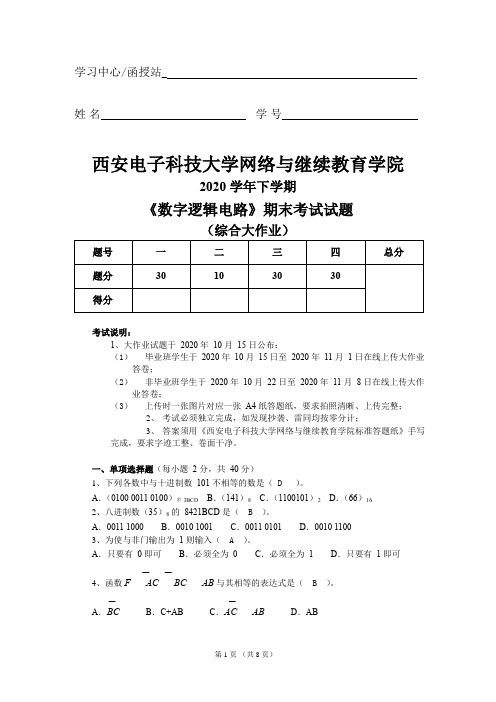
学习中心/函授站_姓名学号西安电子科技大学网络与继续教育学院2020 学年下学期《数字逻辑电路》期末考试试题(综合大作业)题号一二三四总分题分30 10 30 30得分考试说明:1、大作业试题于2020 年10 月15 日公布:(1)毕业班学生于2020 年10 月15 日至2020 年11 月1 日在线上传大作业答卷;(2)非毕业班学生于2020 年10 月22 日至2020 年11 月8 日在线上传大作业答卷;(3)上传时一张图片对应一张A4 纸答题纸,要求拍照清晰、上传完整;2、考试必须独立完成,如发现抄袭、雷同均按零分计;3、答案须用《西安电子科技大学网络与继续教育学院标准答题纸》手写完成,要求字迹工整、卷面干净。
一、单项选择题(每小题2 分,共40 分)1、下列各数中与十进制数101 不相等的数是( D )。
A.(0100 0011 0100)余3BCD B.(141)8C.(1100101)2D.(66)162、八进制数(35)8的8421BCD 是( B )。
A.0011 1000B.0010 1001C.0011 0101D.0010 11003、为使与非门输出为1 则输入( A )。
A.只要有0 即可B.必须全为0C.必须全为1D.只要有1 即可4、函数F AC BC AB与其相等的表达式是( B )。
A.BC B.C+AB C.AC AB D.AB5、使函数F AB AC BC 等于 0 的输入 ABC 的组合是( C )。
A .ABC=111 B .ABC=110 C .ABC=100 D .ABC=0116、四变量的最小项ABCD 的逻辑相邻项是( A )。
A .ABCDB .ABCDC .ABCD D .ABCD 7、函数 F ABC B .C (A D )BC 的对偶式是( C )。
A .G (A B C )(B C )(AD B C )B .G A BC (B C )ADB CC .G A B C (B C )(AD B C )D .G A BC (B C )AD B C8、FA B C ADE BDE ABC 的最简式为( A )。
概率论与数理统计西安电子科技大学大作业

学习中心/函授站姓名学号西安电子科技大学网络与继续教育学院2018学年上学期概率论与数理统计》期末考试试题(综合大作业)考试说明:1、大作业于2018年4月19日下发,2018年5月5日交回,此页须在答卷中保留;2、考试必须独立完成,如发现抄袭、雷同均按零分计;3、答案须手写完成,要求字迹工整、卷面干净。
—、选择每题3分,共30分)1・A B、C是随机事件,且A r>C ,则()oA C ■AUB B・ A C且B CcS B Cc AB D・ A2•设一盒子中有5件产品,其中3件正品,2件次品。
从盒子中任取2件, 则取出的2件产品中至少有1件次品的概率为()oA ?c R 510103•设F(x)是随机变量X 的分布函 数.则( AF ( x)—定连续■CF(x)是单调不增的4. 设连续型随机变量X 的概率密度为(x),且(x)(x), F(x)是X 的分布函 数,则对任何的实数a ,有()。
° 7 f 1105)oB 2(x)定右连续° _T (x)定左连续A・ F(a) i 0 (x)dx B・ F( a) o (x)dx7 20彳<・F( a) F(a) D. F(a) 2F(a) 1金各贝旳釵字崩圭分)oA・6B•(灼丫)的联合概率密7・8 D・98-设连续型随机变X的概率密度为则此人得f (X) 又EX 0.5,贝ljDX ()。
1 1A. B.a bx, 0 x 10,其他1C. D.4112C. DY 0 D・ DX DY 0 2 i "10•设Xi, Xz, z Xn为来自总体X的一个样本,且EX Z DX X Xi,riii 则下列估计量是的无偏估计的是()。
12A. (XiX)2n.i(:・1门1亿X)2n If、填空题(每题3分共30分)1 n 2B. (XiX) n li i 1 n 2D・(XiX)2 mi9•设随机变量X与丫满足D (X Y) D (X Y),贝lj ( ) oA. X与Y相互独立B. COV(X Z Y) 01.设 P(A) 0.5,P(B) 0.6,P(B A) 0.8,则 P(AU B)。
西电随机信号大作业

50
0 -50
0 w 正 弦 信 号 hilbert变 换 后 频 谱 图
50
1
Fxi(jw) Gxi(w)
60 40 20 0 -50 0 w -3 x 10 复 合 信 号 变 换 后 功 率 密 度 图 50
0.5
0 -50
0 w 复 合 信 号 hilbert变 换 后 频 谱 图
50
1
Fy3i(jw) Gy3i(w)
随机信号 大作业
班级:02xxxx 姓名:xx 学号:02xxxxx
第一章
1.23 上机题: 设有随机初相信号 X(t)=5cos (t+φ) , 其中相位φ是在区间 (0,2π) 上均匀分布的随机变量。试用 Matlab 编程产生其三个样本函数。 解:程序: clc clear m=unifrnd(0,2*pi,1,10); for k=1:3 t=1:0.1:10; X=5*cos(t+m(k)); plot(t,X); hold on end title('其三个样本函数'); xlabel('t');ylabel('X(t)'); grid on;axis tight;
Hilbert 变换后频谱图和功率密度图:
高 斯 白 噪 声 hilbert变 换 后 频 谱 图 100
Fyi(jw) Gyi(w)
高 斯 白 噪 声 hilbert变 换 后 功 率 密 度 图 60 40 20 0 -50 0 50 w 正 弦 信 号 hilbert变 换 后 功 率 密 度 图
y_output(p)=y_lim(q); break; end end end y_output_fft=fftshift(fft(y_output)); subplot(2,1,1); plot(,abs(y_output_fft),'r'); title('正弦信号加高斯白噪声经过平滑限幅器幅度谱'); ylabel('y_output_fft');xlabel('t/20pi'); nfft=200; fs=100; window=boxcar(length(y_output)); %矩形窗 [Pxx,f]=periodogram(y_output,window,nfft,fs); %直接法 subplot(2,1,2); plot(f,10*log10(Pxx)); title('正弦信号加高斯白噪声经过平滑限幅器功率谱'); ylabel('Gy');xlabel('t/20pi');
西安电子科技大学2021春 数字逻辑电路(大作业)题目
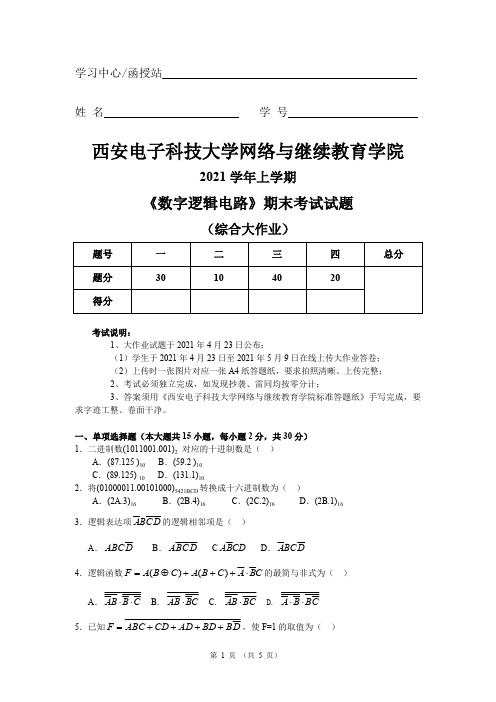
学习中心/函授站_姓 名学 号西安电子科技大学网络与继续教育学院2021学年上学期《数字逻辑电路》期末考试试题(综合大作业)题号 一 二 三 四 总分 题分 30104020得分考试说明:1、大作业试题于2021年4月23日公布:(1)学生于2021年4月23日至2021年5月9日在线上传大作业答卷; (2)上传时一张图片对应一张A4纸答题纸,要求拍照清晰、上传完整; 2、考试必须独立完成,如发现抄袭、雷同均按零分计;3、答案须用《西安电子科技大学网络与继续教育学院标准答题纸》手写完成,要求字迹工整、卷面干净。
一、单项选择题(本大题共15小题,每小题2分,共30分) 1.二进制数(1011001.001)2 对应的十进制数是( )A .(87.125 )10B .(59.2 )10C .(89.125) 10D .(131.1)102.将(01000011.00101000)5421BCD 转换成十六进制数为( )A .(2A.3)16B .(2B.4)16C .(2C.2)16D .(2B.1)16 3.逻辑表达项的逻辑相邻项是( ) D C B A A .B .CD .D ABC D C B A CD B A D A 4.逻辑函数的最简与非式为( ) C B A C B A C B A F ⋅+++⊕=)()( A . B . C . D. C B B A ⋅⋅C B AB ⋅BC B A ⋅C B B A ⋅⋅5.已知,使F=1的取值为( )B BD AD CD ABC F ++++=A .ABC=011B .BCD=111C .BC=11D .BD=006.逻辑函数对偶函数为( )D B C A BD F ⋅++=A . B .))()((D B C A D B F +++=))()((D B C A D B F +++=C .D .D B C A D B F +++=D B C A D B F +++=7.电路如图1.1所示,输出函数F 的表达式为( )A .B . BC C A F +=BC C A F ⋅=C .D .BC F ⋅=BC C A F +=8.函数的最简或非表达∑∑+=dF )14,10,8,3()12,6,5,4,2,1,0(式为( )A .B .C AD F ++=C A D F ++=C .D .F +++=F +++=9.在TTL 电路中,能实现“线与”逻辑的是( )A .OC 门B .异或门C .TS 门D .与或非门10.如果把JK 触发器的输入端J=K=1,该触发器就转换为( )A .DB .C .RSD .JK'T 11.8级触发器组成的计数器,其最大计数模是( )A. B.8 C. D . 1682=⨯6482=25628=12.下列逻辑部件属于时序逻辑电路的是( )A .数据分配器B.译码器C.移位寄存器D .数据比较器13.由555定时器构成的单稳态触发器,其暂态时间t w 为( )A .0.7RCB .RCC .1.1RCD .1.4RC14.n 位环形移位寄存器的无效状态数是( )A . B. C .n D.2nn n -2n n 22-15.下列说法中,哪一种是正确的( )A.单稳态电路可以作为方波产生器B.施密特电路可以定时F图1.1C.多谐振荡器可以将非矩形波矩形波D.施密特电路可以作为幅度鉴别器二、填空题(本大题共5小题,每小题2分,共10分) 16.十进制的4用余3BCD 码表示其代码是 。
西安电子科技大学2021学年上学期 大作业-人机工程学

学习中心/函授站_
姓名学号
西安电子科技大学网络与继续教育学院
2021 学年上学期
《人机工程学》期末考试试题
(综合大作业)
考试说明:
1、大作业试题于2021 年4 月23 日公布:
(1)学生于2021 年4 月23 日至2021 年5 月9 日在线上传大作业答卷;
(2)上传时一张图片对应一张A4 纸答题纸,要求拍照清晰、上传完整;
2、考试必须独立完成,如发现抄袭、雷同均按零分计;
3、答案须用《西安电子科技大学网络与继续教育学院标准答题纸》完成。
以下题目中任选一题:
1、市场上办公桌椅的人机学评析
2、照相机发展中的人机学因素
大作业的要求:
一、大作业是对特定事物的人机学分析,为此需进行相关文献资料的检索、查阅、研
读、评价、质疑,或对现有事物进行调研,锻炼调研能力。
需注意避免“资料式搬家”
现象。
二、大作业中应有学生独立完成的分析、评论、论点等实质内容,切忌内容空洞。
要
求结构清楚、层次分明、论述严谨、文字简练(若有调研,应附调研表;有测试的,应附实验记录原始件的示例等)。
具体格式要求如下:
1、题目之后与正文前要有摘要(150-200 字为宜),然后列出关键词(3-5 个)。
2、正文(主要部分,要有实质内容)。
3、参考文献。
4、字数要求5000-15000 之间。
三、以A4 规格纸张打印或誊写规范。
插图可用附页,也可插入到文稿中,要认真绘制,切
忌潦草。
要有简朴大方的封面设计,并装订好。
第 1 页(共1 页)。
西电最优化上机报告(大作业)

上机报告一.最速下降法算法简述:1.在本例中,先将最速下降方向变量赋一个值,使其二范数满足大于ε的迭代条件,进入循环。
2.将函数的一阶导数化简,存在一个矩阵,将其hesse矩阵存在另一个矩阵。
依照公式求出α,进而求出下一任迭代的矩阵初值。
循环内设置一个计数功能的变量,统计迭代次数。
3.求其方向导数的二范数,进行判别,若小于ε,则跳出循环,否则将继续迭代。
4.显示最优解,终止条件,最小函数值。
心得体会:最速下降法的精髓,无疑是求梯度,然后利用梯度和hesse矩阵综合计算,求解下一个当前最优解。
但是,要求函数是严格的凸函数,结合严格凸函数的大致图像,这就给初值的选取提供了一点参考。
例如在本例中,由于含有两个变量的二次方之和,结合大致图像,想当然的,初值的选取应当在原点附近;又因为变量的二次方之和后面,还减去了变量的一次形式和一次混合积,所以初值的选取应该再向第一象限倾斜。
综合以上考量,第一次选取(1,1)作为初值,判别精度方面,取到千分位,暂定为0.001。
运行以后,结果显示迭代了25次,最优解为(3.9995,1.9996),终止条件为5.4592e-04,目标函数为-8.0000。
这个结果已经相当接近笔算结果。
整体的运行也比较流畅,运算速度也比较快。
第二次取值,决定保留判别精度不变,将初值再适当向第一象限倾斜,取(2,2)作为初值,运行后,显示只迭代了11次!最优结果显示(3.9996,1.9997),终止条件为3.6204e-04,最优解-8.0000。
可见,最优结果更接近理想值,终止条件也变小了,最关键的是,迭代次数减少至第一次的一半以下!这说明以上初选取的方向是对的!第三次再进行初值细化,判别精度仍然不变,初值取(3,3)。
结果令人兴奋,只迭代了四次!最优解已经显示为(4.0000,2.0000),终止条件为2.4952e-04,目标函数-8.0000。
第四次,判别精度不变,取初值(4,4)。
西电算法设计大作业

算法设计大作业寻找多数元素班级:021151学号:02115037姓名:隋伟哲(1)问题提出:令A[1,2,…n]是一个整数序列,A中的整数a如果在A中出现的次数多余⎣n/2⎦,那么a称为多数元素。
例如在序列1,3,2,3,3,4,3中,3是多数元素,因为在7个元素中它出现了四次。
有几个方法可以解决这个问题。
蛮力方法是把每个元素和其他各个元素比较,并且对每个元素计数,如果某个元素的计数大于⎣n/2⎦,就可以断定它是多数元素,否则在序列中就没有多数元素。
但这样比较的次数是n(n-1)/2=Θ(错误!未找到引用源。
),这种方法的代价太昂贵了。
比较有效的算法是对这些元素进行排序,并且计算每个元素在序列中出现了多少次。
这在最坏情况下的代价是Θ(n 错误!未找到引用源。
).因为在最坏情况下,排序这一步需要Ω(n 错误!未找到引用源。
)。
另外一种方法是寻找中间元素,就是第⎡n/2⎤元素,因为多数元素在排序的序列中一定是中间元素。
可以扫描这个序列来测试中间元素是否是多数元素。
由于中间元素可以在Θ(n)时间内找到,这个方法要花费Θ(n)时间。
有一个漂亮的求解方法,它比较的次数要少得多,我们用归纳法导出这个算法,这个算法的实质是基于下面的观察结论。
观察结论:在原序列中去除两个不同的元素后,原序列的多数元素在新序列中还是多数元素。
这个结论支持下述寻找多数元素候选者的过程。
将计数器置1,并令c=A[1]。
从A[2]开始逐个扫描元素,如果被扫描的元素和c相等。
则计数器加1,否则计数器减1.如果所有的元素都扫描完并且计数器的值大于0,那么返回c作为多数元素的候选者。
如果在c和A[j](1<j<n)比较式计数器为0,那么对A[j+1,…n]上的过程调用candidate过程。
算法的伪代码描述如下。
(2)算法Input: An array A[1…n] of n elements;Output: The majority element if it exists; otherwise none;1. c←candidate(1);2. count←0;3. for j←1 to n4. if A[j]=c then count←count+1;5. end for;6. if count>⎣n/2⎦ then return c;7. else return none;candidate(m)1. j←m; c←A[m]; count←1;2. while j<n and count>03. j←j+1;4. if A[j]=c then count←count+1;5. else count←count-1;6. end while;7. if j=n then return c;8. else return candidate(j+1);(3)代码//Majority.cpp#include<iostream>using namespace std;int Candidate(int *A, int n, int m);int Majority(int *A, int n);int main(){int n;cout << "please input the number of the array: ";cin >> n;int *A;A = (int *) malloc(n*sizeof(int) );cout << "please input the array: ";for (int i = 0; i < n; i++)cin >> A[i];if (Majority(A, n) != 'N')cout << "the majority is: " << Majority(A, n);elsecout << "the majority element do not exist! ";free(A);cin.get();cin.get();return 0;}int Majority(int *A, int n){int c = Candidate(A, n, 0), count = 0;for (int j = 0; j < n; j++)if (A[j] == c)count += 1;if (count > n / 2)return c;else return'N';}int Candidate(int *A, int n, int m){int j = m, c = A[m], count = 1;while (j < n && count>0){j += 1;if (A[j] == c)count += 1;else count -= 1;}if (j == n)return c;else return Candidate(A, n, j + 1); }(4)运行结果(5)设计实例首先输入数据的个数n=7,然后依次读入n个数(1,3,2,3,3,4,3)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
随机大作业题目:高频窄带随机信号的统计特征分析
学院:电子工程
班级:1402071
姓名:张吉凯
学号:14020710021
摘要
随机信号是客观世界中普遍存在的一类信号,因此深入理解其统计特性并掌握相
应的处理与分析方法很重要。
因此本文主要分析了随机信号的基本概念,涉及平稳、
遍历随机信号的基本内容;平稳随机信号的谱分析;线性系统对随机信号的作用机理,涉及到一些随机信号特别是平稳随机信号的线性变换或线性滤波的基本问题;窄带随
机信号的表示及其统计特性。
为实现窄带信号的表示,对希尔伯特变换给出了较细致
的分析。
引言
在日常生活中,由于噪声和干扰的存在使得我们接受到的信号不再是确知信号,
而是一个随机过程,通常称之为随机信号。
随机信号又称随机过程,它是一连串随机
事件动态关系的定量描述。
随机信号论目前已经得到广泛的应用,在诸如天气预报、
统计物理、天体物理、运筹决策、经济数学、安全科学、人口理论、可靠性及计算机
科学等很多领域都要经常用到随机过程的理论来建立数学模型。
随机信号的分析越来
越重要了。
一、理论分析部分
1.平稳随机信号的定义,满足各态历经性的随机信号的定义和相关性质
狭义平稳概念:所谓平稳随机过程,是指它的任何n维分布函数或概率密度函数
与时间起点无关。
也就是说,如果对于任意的n和τ,随机过程ξ(t)的n维概率密度函数满足
则称ξ(t)是平稳随机过程。
该平稳称为严格平稳,狭义平稳或严平稳。
若一个随机过程的数学期望及方差与时间无关,而其相关函数仅与τ有关,则称这个随机过程为广义平稳随机过程。
对于一个平稳的随机过程,如果统计平均=时间平均,这个随机过程就叫做各态历经的平稳随机过程。
时间均值必定是与时间无关的常量,而时间自相关函数必定只是时刻间隔的单值
函数,可见遍历过程必定是平稳过程,但反之,并非所有的平稳过程都是遍历过程。
2. 平稳随机信号通过线性系统的分析方法:卷积积分法和频域分析法
具有叠加性和比例性的系统称为线性系统。
线性系统的常系数微分方程有时域分析法和频域分析法。
时域分析法常用的是卷积积分法,
()()()()()Y t X t h t X h t d τττ∞
-∞=⊗=-⎰
对于时不变系统,还可以采用频域分析法。
利用叠加原理,在频域叠加,即傅里叶变换;在复频域叠加,即拉普拉斯变换。
系统的传递函数为: ()()()XY Y G G H ωωω=
写成幅频响应和相频响应的形式:
2*()()()()()()Y X X G G H H G H ωωωωωω==
3. 高频窄带实随机信号的hilbert 变换和解析信号
将实信号()s t 表示成复信号~^
()()()s t s t j s t =+;其中()s t 为实随机信号,若其频谱满足 ~
2(),0()0,0S S ωωωω≥⎧=⎨<⎩ 具有上式所示单边谱特性的复信号,称为实信号的解析信号。
解析信号的虚部为实部的Hilbert 变换,变换公式如下:
^1()t s s d t ττπτ∞
-∞-⎰()=
4. 高频窄带实随机信号与其hilbert 变换的功率谱密度之间的关系
实随机信号与其Hilbert 变换的功率谱密度相等:
2^()()()()()Y X X G G G H G ωωωωω===
~=j X X x G ωωω ()-G ()sgn()
5.高频窄带实随机信号与其解析信号的功率谱密度之间的关系
解析信号功率谱密度在小于零时为零,在大于零时是实随机信号功率谱密度的四倍: ~~()2[()()]X X X X G G jG ωωω=+
2()[1sgn()]4()()X X G G U ωωωω=+=
6.解析随机信号与其复包络的功率谱密度之间的关系
解析信号可以用复指数表示为:~~
[()]00()()()j t t j t Y t A t e
A t e ωϕω+== 其中,~()()()j t A t A t e ϕ=为解析信号复包络。
复包络的功率谱密度是将解析信号功率谱左移,即变到基带,这表明解析信号是复包络的调幅信号:
~~0()()A Y
G G ωωω=+ 二、 实验仿真部分
1. 三种信号的产生
实随机信号:
Hilbert变换信号:
解析信号:
Hilbert变换信号的自相关函数:
实随机信号的功率谱密度:
Hilbert变换信号的功率谱密度:
解析信号的功率谱密度:
三、结果分析与心得体会部分
实随机信号的自相关函数满足在零时为最大值,Hilbert变换信号的自相关与它相似,解析信号自相关函数为复数,其模值有以较大峰值,其余值大小随机性很大,这与理论一致。
实随机信号的功率谱密度模值偶对称,Hilbert变换信号的功率谱密度与它相似,解析信号的功率谱密度是一个复信号,其功率谱密度在正半轴为实信号的四倍,而在负半轴为零,即解析信号的功率谱密度为单边谱,这得到验证。
要注意的一点是:
sa = hilbert(s) MATLAB函数得到的信号是合成的复信号即解析信号
sh = imag(sa) 虚部为书上定义的Hilbert变换信号
与书写习惯不一致。
通过这次大作业对三种信号有了更深的理解,对它们之间的关系更加清楚!
四、附程序段
clear
clc
%%三种信号产生部分
N = 500;
t = -N:N;
A = 0.2;
si = A*randn(1,2*N+1);
s = (1+si).*cos(0.2*t);%实随机信号
T = 128;
sa = hilbert(s);%MATLAB函数得到的信号是合成的复信号即解析信号
sh = imag(sa); %虚部为书上定义的Hilbert变换信号
%%自相关部分
%实随机信号自相关
for k=-T:T;
Rs(T+k+1)=1/(2*T+1)*sum(s(N+1-T:N+1+T).*s(N+1-T+k:N+1+T+k));
end
%Hilbert变换信号自相关
for k=-T:T;
Rsh(T+k+1)=1/(2*T+1)*sum(sh(N+1-T:N+1+T).*sh(N+1-T+k:N+1+T+k)); end
%解析信号自相关
for k=-T:T;
Rsa(T+k+1)=1/(2*T+1)*sum(sa(N+1-T:N+1+T).*conj(sa(N+1-T+k:N+1+T+k))); end
%%功率谱密度部分
Ps = fft(Rs);%实随机信号功率谱
Psh= fft(Rsh);%Hilbert信号功率谱
Psa= fft(Rsa);%解析信号功率谱
%%绘制图形部分
figure(1);plot(s);grid on;
title('实随机信号');
figure(2);plot(sh);grid on;
title('Hilbert变换信号');
figure(3);plot(abs(sa));grid on;
title('解析信号');
figure(4);plot(Rs);grid on;
title('实随机信号自相关函数');
figure(5);plot(Rsh);grid on;
title('Hilbert变换自相关函数');
figure(6);plot(abs(Rsa));grid on;
title('解析信号自相关函数');
figure(7);plot(abs(fftshift(Ps)));grid on; title('实随机信号功率谱密度');
figure(8);plot(abs(fftshift(Psh)));grid on; title('Hilbert变换信号功率谱密度'); figure(9);plot(abs(fftshift(Psa)));grid on; title('解析信号功率谱密度');。
