模式识别大作业02125128(修改版)
模式识别大作业

一、问题描述现有sonar 和wdbc 这两个样本数据集,取一半数据作为训练样本集,其余数据作为测试样本集,通过编程实现分别用C 均值算法对测试样本集中的数据进行分类,进行10次分类求正确率的平均值。
二、算法描述1.初始化:选择c 个代表点,...,,321c p p p p2.建立c 个空间聚类表:C K K K ...,213.按照最小距离法则逐个对样本X 进行分类:),(),,(min arg J i iK x add p x j ∂=4.计算J 及用各聚类列表计算聚类均值,并用来作为各聚类新的代表点(更新代表点)5.若J 不变或代表点未发生变化,则停止。
否则转2.),(1∑∑=∈=ci K x i i p x J δ6.计算正确率:将dtat(i,1)与trueflag(i,1)(i=1~n )进行比较,统计正确分类的样本数,并计算正确率将上述过程循环10次,得到10次的正确率,并计算平均正确率ave算法流程图三、实验数据表1 实验数据四、实验结果表2 实验结果准确率(%)注:表中准确率是十次实验结果的平均值五、程序源码用C均值算法对sonar分类(对wdbc分类的代码与之类似)clc;clear;accuracy = 0;for i = 1:10data = xlsread('sonar.xls');data = data';%初始划分2个聚类rand(:,1:size(data,2)) = data(:,randperm(size(data,2))'); %使矩阵元素按列重排A(:,1) = rand(:,1);B(:,1) = rand(:,2); %选取代表点m = 1;n = 1;for i = 3:size(rand,2)temp1 = rand(:,i) - A(:,1);temp2 = rand(:,i) - B(:,1);temp1(61,:) = [];temp2(61,:) = []; %去掉标号后再计算距离if norm(temp1) < norm(temp2)m = m + 1; %A类中样本个数A(:,m) = rand(:,i);elsen = n + 1; %B类中样本个数B(:,n) = rand(:,i);endend%划分完成m1 = mean(A,2);m2 = mean(B,2);%计算JeJ = 0;for i = 1:mtemp = A(:,i) - m1;temp(61,:) = []; %去掉标号的均值J = J + norm(temp)^2;endfor i = 1:ntemp = B(:,i) - m2;temp(61,:) = [];J = J + norm(temp)^2;endtest = [A,B];N = 0; %Je不变的次数while N < m + nrarr = randperm(m + n); %产生1-208即所有样本序号的随机不重复序列向量y = test(:,rarr(1,1));if rarr(1,1) <= m %y属于A类时if m == 1continueelsetemp1 = y - m1;temp1(61,:) = [];temp2 = y - m2;temp2(61,:) = [];p1 = m / (m - 1) * norm(temp1);p2 = n / (n + 1) * norm(temp2);if p2 < p1test = [test,y];test(:,rarr(1,1)) = [];m = m - 1;n = n + 1;endendelse %y属于B类时if n == 1continueelsetemp1 = y - m1;temp1(61,:) = [];temp2 = y - m2;temp2(61,:) = [];p1 = m / (m + 1) * norm(temp1);p2 = n / (n - 1) * norm(temp2);if p1 < p2test = [y,test];test(:,rarr(1,1)) = [];m = m + 1;n = n - 1;endendendA(:,1:m) = test(:,1:m);B(:,1:n) = test(:,m + 1:m + n);m1 = mean(A,2);m2 = mean(B,2);%计算JetempJ = 0;for i = 1:mtemp = A(:,i) - m1;temp(61,:) = []; %去掉标号的均值tempJ = tempJ + norm(temp)^2;endfor i = 1:ntemp = B(:,i) - m2;temp(61,:) = [];tempJ = tempJ + norm(temp)^2;endif tempJ == JN = N + 1;elseJ = tempJ;endend %while循环结束%判断正确率correct = 0;false = 0;A(:,1:m) = test(:,1:m);B(:,1:n) = test(:,m + 1:m + n);c = mean(A,2);if abs(c(61,1) - 1) < abs(c(61,1) - 2) %聚类A中大多为1类元素for i = 1:mif A(61,i) == 1correct = correct + 1;elsefalse = false + 1;endendfor i = 1:nif B(61,i) == 2correct = correct + 1;elsefalse = false + 1;endendelse %聚类A中大多为2类元素for i = 1:mif A(61,i) == 2correct = correct + 1;elsefalse = false + 1;endendfor i = 1:nif B(61,i) == 1correct = correct + 1;elsefalse = false + 1;endendendaccuracy = accuracy + correct / (correct + false);endaver_accuracy = accuracy / 10fprintf('用C均值算法对sonar进行十次分类的结果的平均正确率为%.2d %%.\n',aver_accuracy*100)六.实验心得本算法确定的K 个划分到达平方误差最小。
《模式识别》课程2019年度大作业

《模式识别》课程2019年度大作业注意事项:(请务必详细阅读所有注意事项)1.本作业发布时间2019.5.5,交作业时间:2018.5.30日第一节课下课后,第二节课上课前(即上午9点整)。
与平时作业不同,不允许迟交,迟交则成绩以0分计。
2.与平时作业不同,大作业只有研究生同学完成,保送本系的本科同学也需要完成,但其他本科生无需完成。
请在作业的开始部分写上姓名、学号,缺少该信息的,本次作业总分扣除10分。
如果是已经完成保送手续,先修研究生课程的本校本科生,请一定每次作业在姓名后加注“(本科保送)”,否则无法拿到学分。
3.与平时作业不同,作业评分以电子版为准。
需要提交代码,具体的提交要求请仔细阅读作业说明。
总体文件大小不超过5MB(可以提交压缩文件)。
上传地址为/。
初始用户名和密码为学号。
研究生学号以MP18开头的暂时无法登陆,可将电子版email给助教(wangguohua@, yik@),其余同学务必使用网站系统上传。
是否迟交以cslabcms系统的时间戳或电子邮件的时间戳为准。
大作业:1.仔细阅读以下网页的内容(/weixs/project/DDT/DDT.html),包括其中提供链接的英文论文,理解DDT方法的运行步骤。
2.自行实现DDT算法。
实现时可以参考上述网页提供的Matlab代码以加深对DDT方法的理解,但是不可以使用MatConvNet这一深度学习框架,除此以外的其余任意深度学习软件框架都可以使用。
3.如尚未有深度学习、CNN的编程经验,请搜索网络资源完成自学。
4.如有可供使用的GPU加速卡资源,可以自由使用。
如无这种资源,可在编程中指定使用CPU(即,不使用GPU)来完成计算。
DDT方法的计算量很小,使用CPU也可完成计算。
5.在上述网页提供下载的代码链接里有少量图片可供使用,利用这些图片完成DDT方法的学习,利用可视化技术(参考论文和代码)直观考察DDT方法的效果。
6.请提交完成上述任务的文档和代码,需提交的内容如下:a.说明文档:自行组织文档的格式,保证文档的内容能让助教清晰地理解你的代码运行环境、实现的主要思路、你通过实现并运行代码后对DDT方法的理解等。
大学模式识别考试题及答案详解()

一、填空与选择填空(本题答案写在此试卷上,30分)1、模式识别系统的基本构成单元包括:模式采集、特征提取与选择和模式分类。
2、统计模式识别中描述模式的方法一般使用特真矢量;句法模式识别中模式描述方法一般有串、树、网。
3、聚类分析算法属于(1);判别域代数界面方程法属于(3)。
(1)无监督分类 (2)有监督分类(3)统计模式识别方法(4)句法模式识别方法4、若描述模式的特征量为0-1二值特征量,则一般采用(4)进行相似性度量。
(1)距离测度(2)模糊测度(3)相似测度(4)匹配测度5、下列函数可以作为聚类分析中的准则函数的有(1)(3)(4)。
(1)(2) (3)(4)6、Fisher线性判别函数的求解过程是将N维特征矢量投影在(2)中进行。
(1)二维空间(2)一维空间(3)N-1维空间7、下列判别域界面方程法中只适用于线性可分情况的算法有(1);线性可分、不可分都适用的有(3)。
(1)感知器算法(2)H-K算法(3)积累位势函数法8、下列四元组中满足文法定义的有(1)(2)(4)。
(1)({A, B}, {0, 1}, {A?01, A? 0A1 , A? 1A0 , B?BA , B? 0}, A) (2)({A}, {0, 1}, {A?0, A? 0A}, A)(3)({S}, {a, b}, {S ? 00S, S ? 11S, S ? 00, S ? 11}, S)(4)({A}, {0, 1}, {A?01, A? 0A1, A? 1A0}, A)二、(15分)简答及证明题(1)影响聚类结果的主要因素有那些?(2)证明马氏距离是平移不变的、非奇异线性变换不变的。
答:(1)分类准则,模式相似性测度,特征量的选择,量纲。
(2)证明:(2分)(2分)(1分)设,有非奇异线性变换:(1分)(4分)三、(8分)说明线性判别函数的正负和数值大小在分类中的意义并证明之。
答:(1)(4分)的绝对值正比于到超平面的距离平面的方程可以写成式中。
模式识别大作业

模式识别大作业引言:转眼之间,研一就结束了。
这学期的模式识别课也接近了尾声。
我本科是机械专业,编程和算法的理解能力比较薄弱。
所以虽然这学期老师上课上的很精彩,但是这学期的模式识别课上的感觉还是有点吃力。
不过这学期也加强了编程的练习。
这次的作业花了很久的时间,因为平时自己的方向是主要是图像降噪,自己在看这一块图像降噪论文的时候感觉和模式识别的方向结合的比较少。
我看了这方面的模式识别和图像降噪结合的论文,发现也比较少。
在思考的过程中,我想到了聚类的方法。
包括K均值和C均值等等。
因为之前学过K均值,于是就选择了K均值的聚类方法。
然后用到了均值滤波和自适应滤波进行处理。
正文:k-means聚类算法的工作过程说明如下:首先从n个数据对象任意选择 k 个对象作为初始聚类中心;而对于所剩下其它对象,则根据它们与这些聚类中心的相似度(距离),分别将它们分配给与其最相似的(聚类中心所代表的)聚类;然后再计算每个所获新聚类的聚类中心(该聚类中所有对象的均值);不断重复这一过程直到标准测度函数开始收敛为止。
一般都采用均方差作为标准测度函数。
k-means 算法接受输入量k ;然后将n个数据对象划分为k个聚类以便使得所获得的聚类满足:同一聚类中的对象相似度较高;而不同聚类中的对象相似度较小。
聚类相似度是利用各聚类中对象的均值所获得一个“中心对象”(引力中心)来进行计算的。
k个聚类具有以下特点:各聚类本身尽可能的紧凑,而各聚类之间尽可能的分开。
均值滤波是常用的非线性滤波方法 ,也是图像处理技术中最常用的预处理技术。
它在平滑脉冲噪声方面非常有效,同时它可以保护图像尖锐的边缘。
均值滤波是典型的线性滤波算法,它是指在图像上对目标像素给一个模板,该模板包括了其周围的临近像素(以目标象素为中心的周围8个象素,构成一个滤波模板,即去掉目标象素本身)。
再用模板中的全体像素的平均值来代替原来像素值。
即对待处理的当前像素点(x,y),选择一个模板,该模板由其近邻的若干像素组成,求模板中所有像素的均值,再把该均值赋予当前像素点(x,y),作为处理后图像在该点上的灰度个g(x,y),即个g(x,y)=1/m ∑f(x,y)m为该模板中包含当前像素在内的像素总个数。
模式识别大作业1

模式识别大作业--fisher线性判别和近邻法学号:021151**姓名:**任课教师:张**I. Fisher线性判别A. fisher线性判别简述在应用统计方法解决模式识别的问题时,一再碰到的问题之一是维数问题.在低维空间里解析上或计算上行得通的方法,在高维里往往行不通.因此,降低维数就成为处理实际问题的关键.我们考虑把维空间的样本投影到一条直线上,形成一维空间,即把维数压缩到一维.这样,必须找一个最好的,易于区分的投影线.这个投影变换就是我们求解的解向量.B.fisher线性判别的降维和判别1.线性投影与Fisher准则函数各类在维特征空间里的样本均值向量:,(1)通过变换映射到一维特征空间后,各类的平均值为:,(2)映射后,各类样本“类内离散度”定义为:,(3)显然,我们希望在映射之后,两类的平均值之间的距离越大越好,而各类的样本类内离散度越小越好。
因此,定义Fisher准则函数:(4)使最大的解就是最佳解向量,也就是Fisher的线性判别式。
2.求解从的表达式可知,它并非的显函数,必须进一步变换。
已知:,, 依次代入上两式,有:,(5)所以:(6)其中:(7)是原维特征空间里的样本类内离散度矩阵,表示两类均值向量之间的离散度大小,因此,越大越容易区分。
将(4.5-6)和(4.5-2)代入(4.5-4)式中:(8)其中:,(9)因此:(10)显然:(11)称为原维特征空间里,样本“类内离散度”矩阵。
是样本“类内总离散度”矩阵。
为了便于分类,显然越小越好,也就是越小越好。
将上述的所有推导结果代入表达式:可以得到:其中,是一个比例因子,不影响的方向,可以删除,从而得到最后解:(12)就使取得最大值,可使样本由维空间向一维空间映射,其投影方向最好。
是一个Fisher线性判断式.这个向量指出了相对于Fisher准则函数最好的投影线方向。
C.算法流程图左图为算法的流程设计图。
II.近邻法A. 近邻法线简述K最近邻(k-Nearest Neighbor,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。
模式识别大作业
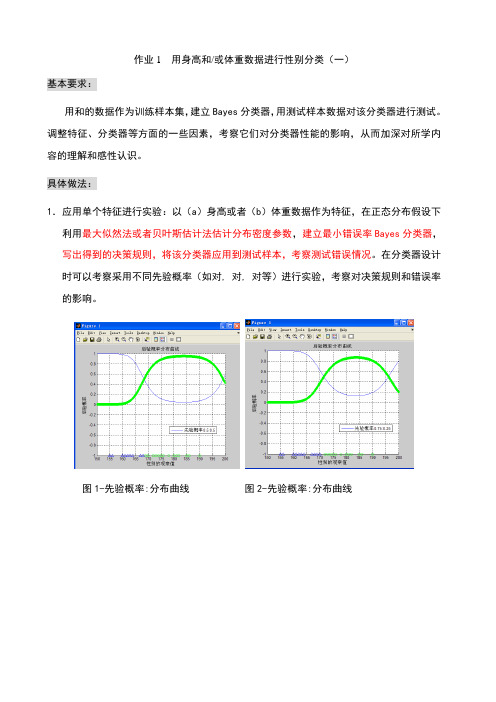
作业1 用身高和/或体重数据进行性别分类(一)基本要求:用和的数据作为训练样本集,建立Bayes分类器,用测试样本数据对该分类器进行测试。
调整特征、分类器等方面的一些因素,考察它们对分类器性能的影响,从而加深对所学内容的理解和感性认识。
具体做法:1.应用单个特征进行实验:以(a)身高或者(b)体重数据作为特征,在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到测试样本,考察测试错误情况。
在分类器设计时可以考察采用不同先验概率(如对, 对, 对等)进行实验,考察对决策规则和错误率的影响。
图1-先验概率:分布曲线图2-先验概率:分布曲线图3--先验概率:分布曲线图4不同先验概率的曲线有图可以看出先验概率对决策规则和错误率有很大的影响。
程序:和2.应用两个特征进行实验:同时采用身高和体重数据作为特征,分别假设二者相关或不相关(在正态分布下一定独立),在正态分布假设下估计概率密度,建立最小错误率Bayes 分类器,写出得到的决策规则,将该分类器应用到训练/测试样本,考察训练/测试错误情况。
比较相关假设和不相关假设下结果的差异。
在分类器设计时可以考察采用不同先验概率(如 vs. , vs. , vs. 等)进行实验,考察对决策和错误率的影响。
训练样本female来测试图1先验概率 vs. 图2先验概率 vs.图3先验概率 vs. 图4不同先验概率对测试样本1进行试验得图对测试样本2进行试验有图可以看出先验概率对决策规则和错误率有很大的影响。
程序和3.自行给出一个决策表,采用最小风险的Bayes决策重复上面的某个或全部实验。
设以ceshi1单个特征身高进行试验:决策表W1W2W10W20close all;clear all;X=120::200; %设置采样范围及精度pw1=;pw2=; %设置先验概率sample1=textread('') %读入样本samplew1=zeros(1,length(sample1(:,1)));u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布figure(1);subplot(2,1,1);plot(X,y1);title('F身高类条件概率分布曲线');sample2=textread('') %读入样本samplew2=zeros(1,length(sample2(:,1)));u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布subplot(2,1,2);plot(X,y2);title('M身高类条件概率分布曲线');P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);figure(2);subplot(2,1,1);plot(X,P1);title('F身高后验概率分布曲线');subplot(2,1,2);plot(X,P2);title('M身高后验概率分布曲线');P11=pw1*y1;P22=pw2*y2;figure(3);subplot(3,1,1);plot(X,P11);subplot(3,1,2);plot(X,P22);subplot(3,1,3);plot(X,P11,X,P22);sample=textread('all ') %读入样本[result]=bayes(sample1(:,1),sample2(:,1),pw1,pw2);%bayes分类器function [result] =bayes(sample1(:,1),sample2(:,1),pw1,pw2); error1=0;error2=0;u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);for i = 1:50if P1(i)>P2(i)result(i)=0;pe(i)=P2(i);elseresult(i)=1;pe(i)=P1(i);endendfor i=1:50if result(k)==0error1=error1+1;else result(k)=1error2=error2+1;endendratio = error1+error2/length(sample); %识别率,百分比形式sprintf('正确识别率为%.2f%%.',ratio)作业2 用身高/体重数据进行性别分类(二)基本要求:试验直接设计线性分类器的方法,与基于概率密度估计的贝叶斯分离器进行比较。
模式识别大作业(二)

模式识别大作业(二)————C-均值算法与模糊C 均值聚类的比较姓名:谭红光 学号:02125128 班级:021252一 原理:1.C 均值的原理:C 均值聚类算法是一种典型的无监督动态聚类算法。
该算法是在类别数目已知(=k )的条件下进行的,能够使聚类结果的距离平方和最小,即算法的基础是误差平方和准则。
其基本过程是建立初始的聚心和聚类,通过多次迭代,逐渐调整各类的聚心和各像元的类别,直至得到聚类准则约束下的最好结果为止。
本实验的具体过程如下:选择初始类别中心,假设有c 个类别,设置其中心分别为(1)(1)(1)12,,,c Z Z Z 在第k 步迭代中,对于任何一个像元x(是一个N 维向量,N 是高光谱图像的波段数目),按如下方法把它调整到。
各类别中的某一个类别中去。
令d(x ,y)为向量x ,y 之间的距离,若:()()(,)(,)k k i jd x Z d x Z <=, j = 1 2 … c (j i ≠) 则()k i x S∈,其中()k i S 是以()k iZ 为中心的类。
由上一步得到的()k iS(i =1 2…c )个类别新的中心(1)k i Z +()(1)1k i k ix S iZxN +∈=∑其中N i是类别()k iS 的数目。
(1)k i Z +是按照最小J 的原则,J 的表达式为:()(1)1(,)k i ck i i x S J d x Z +=∈=∑∑对所有的i =1 2…c 。
如果,(1)()k k i i Z Z +=,则迭代结束(在程序中,则按照每个类别的对应的那些像素不再变化,则停止迭代),否则转到第二步继续迭代。
2.模糊C 均值的原理在数字图像由于存在混合像素的原因,也就是说一个像素中不仅存在一类地物,因而采用硬分类方式往往不合适,而模糊C 均值就是引入模糊集对每个像素的划分概率不单单是用0或1这样的硬分类方式,而是0和1之间的范围内(包括0和1)。
模式识别大作业

模式识别大作业(总21页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--作业1 用身高和/或体重数据进行性别分类(一)基本要求:用和的数据作为训练样本集,建立Bayes分类器,用测试样本数据对该分类器进行测试。
调整特征、分类器等方面的一些因素,考察它们对分类器性能的影响,从而加深对所学内容的理解和感性认识。
具体做法:1.应用单个特征进行实验:以(a)身高或者(b)体重数据作为特征,在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到测试样本,考察测试错误情况。
在分类器设计时可以考察采用不同先验概率(如对, 对, 对等)进行实验,考察对决策规则和错误率的影响。
图1-先验概率:分布曲线图2-先验概率:分布曲线图3--先验概率:分布曲线图4不同先验概率的曲线有图可以看出先验概率对决策规则和错误率有很大的影响。
程序:和2.应用两个特征进行实验:同时采用身高和体重数据作为特征,分别假设二者相关或不相关(在正态分布下一定独立),在正态分布假设下估计概率密度,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到训练/测试样本,考察训练/测试错误情况。
比较相关假设和不相关假设下结果的差异。
在分类器设计时可以考察采用不同先验概率(如 vs. , vs. , vs. 等)进行实验,考察对决策和错误率的影响。
训练样本female来测试图1先验概率 vs. 图2先验概率 vs.图3先验概率 vs. 图4不同先验概率对测试样本1进行试验得图对测试样本2进行试验有图可以看出先验概率对决策规则和错误率有很大的影响。
程序和3.自行给出一个决策表,采用最小风险的Bayes决策重复上面的某个或全部实验。
W1W2W10W20close all;clear all;X=120::200; %设置采样范围及精度pw1=;pw2=; %设置先验概率sample1=textread('') %读入样本samplew1=zeros(1,length(sample1(:,1)));u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布figure(1);subplot(2,1,1);plot(X,y1);title('F身高类条件概率分布曲线');sample2=textread('') %读入样本samplew2=zeros(1,length(sample2(:,1)));u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布subplot(2,1,2);plot(X,y2);title('M身高类条件概率分布曲线');P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);figure(2);subplot(2,1,1);plot(X,P1);title('F身高后验概率分布曲线');subplot(2,1,2);plot(X,P2);title('M身高后验概率分布曲线');P11=pw1*y1;P22=pw2*y2;figure(3);subplot(3,1,1);plot(X,P11);subplot(3,1,2);plot(X,P22);subplot(3,1,3);plot(X,P11,X,P22);sample=textread('all ') %读入样本[result]=bayes(sample1(:,1),sample2(:,1),pw1,pw2);%bayes分类器function [result] =bayes(sample1(:,1),sample2(:,1),pw1,pw2); error1=0;error2=0;u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);for i = 1:50if P1(i)>P2(i)result(i)=0;pe(i)=P2(i);elseresult(i)=1;pe(i)=P1(i);endendfor i=1:50if result(k)==0error1=error1+1;else result(k)=1error2=error2+1;endendratio = error1+error2/length(sample); %识别率,百分比形式sprintf('正确识别率为%.2f%%.',ratio)作业2 用身高/体重数据进行性别分类(二)基本要求:试验直接设计线性分类器的方法,与基于概率密度估计的贝叶斯分离器进行比较。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模式识别大作业班级 021252 姓名 谭红光 学号 021251281.线性投影与Fisher 准则函数各类在d 维特征空间里的样本均值向量:∑∈=ik X x kii xn M 1,2,1=i (1)通过变换w 映射到一维特征空间后,各类的平均值为:∑∈=ik Y y kii yn m 1,2,1=i (2)映射后,各类样本“类内离散度”定义为:22()k ii k i y Y S y m ∈=-∑,2,1=i (3)显然,我们希望在映射之后,两类的平均值之间的距离越大越好,而各类的样本类内离散度越小越好。
因此,定义Fisher 准则函数:2122212||()F m m J w s s -=+ (4)使FJ 最大的解*w 就是最佳解向量,也就是Fisher 的线性判别式. 从)(w J F 的表达式可知,它并非w 的显函数,必须进一步变换。
已知:∑∈=ik Y y kii yn m 1,2,1=i , 依次代入上两式,有:i TX x ki Tk X x Ti i M w x n w x w n m ik ik ===∑∑∈∈)1(1,2,1=i (5) 所以:221221221||)(||||||||M M w M w M w m m T T T -=-=-w S w w M M M M w b T T T =--=))((2121 (6)其中:Tb M M M M S ))((2121--= (7)bS 是原d 维特征空间里的样本类内离散度矩阵,表示两类均值向量之间的离散度大小,因此,b S 越大越容易区分。
将(4.5-6)i Ti M w m =和(4.5-2)∑∈=ik X x kii xn M 1代入(4.5-4)2iS 式中:∑∈-=ik X x iT k T i M w x w S 22)(∑∈⋅--⋅=ik X x Tik i k T w M x M x w ))(( w S w i T= (8)其中:T iX x k i k i M x M x S ik ))((--=∑=,2,1=i (9)因此:w S w w S S w S S w T T =+=+)(212221 (10)显然:21S S S w += (11)w S 称为原d 维特征空间里,样本“类内离散度”矩阵。
w S 是样本“类内总离散度”矩阵。
为了便于分类,显然iS 越小越好,也就是wS 越小越好。
将上述的所有推导结果代入)(w J F 表达式:可以得到:)(211*M M S w w -=-λγ其中,λγ是一个比例因子,不影响*w 的方向,可以删除,从而得到最后解:)(211*M M S w w -=- (12)就使)(w J F 取得最大值,*w 可使样本由d 维空间向一维空间映射,其投影方向最好。
)(211*M M S w w -=-是一个Fisher 线性判断式.这个向量指出了相对于Fisher 准则函数最好的投影线方向。
2.近邻法线简述最近邻(Nearest Neighbor ,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。
该方法的思路是:如果一个样本在特征空间中的k 个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
KNN 算法中,所选择的邻居都是已经正确分类的对象。
该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
KNN 方法虽然从原理上也依赖于极限定理,但在类别决策时,只与极少量的相邻样本有关。
由于KNN 方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN 方法较其他方法更为适合。
将与测试样本最近邻样本的类别作为决策的结果。
对一个C 类别问题,每类有i N 个样本,1,2,i C =,则第i 类i ω的判别函数为:()min ||||,1,2,,k i i i kg x x x k N =-= (1)因此,最近邻决策规则: 若()min (),1,2,j i ig x g x i c == (2)3.设计思路根据公式用Matlab 计算出w0,然后对测试数据进行与w0的比较进行分类。
在用欧式距离进行分类。
流程图:算法的流程设计图。
2.程序代码:mine=xlsread('C:\Users\Administrator\Desktop\mine.xls'); %导入mine数据rock=xlsread('C:\Users\Administrator\Desktop\rock.xls'); %导入rock数据amine=randsample(111,55,'false'); %产生55个随机数作为mine行下标bmine=zeros(55,60);for i=1:55for j=1:60bmine(i,j)=mine(amine(i,1),j);mine(amine(i,1),j)=2;endend%选出mine训练样本dmine=zeros(56,60);r=1;for i=1:111if mine(i,1)==2i=i+1;else for j=1:60dmine(r,j)=mine(i,j);endr=r+1;endend%选出mine测试样本cmine=zeros(1,60);for i=1:60for j=1:55cmine(1,i)=cmine(1,i)+bmine(j,i);endendarock=randsample(97,48,'false');brock=zeros(48,60);for i=1:48for j=1:60brock(i,j)=rock(arock(i,1),j);rock(arock(i,1),j)=2;endend%选出rock的训练样本drock=zeros(49,60);p=1;for i=1:97if rock(i,1)==2i=i+1;else for j=1:60drock(p,j)=rock(i,j);endp=p+1;endend%选出rock的测试样本crock=zeros(1,60);for i=1:60for j=1:48crock(1,i)=crock(1,i)+brock(j,i);endend%fisher线性判别mm=cmine/55; %mine的类均值向量mr=crock/48; %rock的类均值向量mm=mm';mr=mr';s_mine=zeros(60,60);s_rock=zeros(60,60);for i=1:55s_mine=s_mine+(bmine(i,:)'-mm)*(bmine(i,:)'-mm)';end%mine的类内离散度矩阵for i=1:48s_rock=s_rock+(brock(i,:)'-mr)*(brock(i,:)'-mr)';end%rock的类内离散度矩阵sw=s_mine+s_rock;w1=inv(sw)*(mm-mr); %最佳投影方向w0=w1'*(mm+mr)/2; %阈值%画坐标轴x=-1:2;y=-1:2;hold on;plot(x,y);y=w0;plot(y,y,'xk'); %阈值的坐标text(0.6,0.5,'w');text(-0.4,0,'rock');text(0.4,0.2,'mine');title('fisher02125128');xlabel('mine');ylabel('rock');%测验分类器emine=0;erock=0;for i=1:56y=w1'*dmine(i,:)';if y>w0plot(y,y,'og'); %分对的mine样本的坐标else plot(y,y,'+m');emine=emine+1; %mine分错的个数endendfor i=1:49y=w1'*drock(i,:)';if y<w0plot(y,y,'oc'); %分对的rock样本的坐标else plot(y,y,'+r');erock=erock+1; %rock分错的个数endenddisp(w0);disp(erock/97);disp(emine/111);text(-0.2,0.63,['errmine:' num2str(emine*100/111) '%']); text(-0.2,-0.43,['errrock:' num2str(erock*100/97) '%']); %最近临法eemine=0;eerock=0;for i=1:56min1=inf;min2=inf;for j=1:55x=norm(dmine(i,1:60)-bmine(j,:));if(x<min1)min1=x;endendfor jj=1:48y=norm(dmine(i,1:60)-brock(jj,:));if(y<min2)min2=y;endendif(min1>min2)eemine=eemine+1;endendfor i=1:49min3=inf;min4=inf;for j=1:55xx=norm(drock(i,1:60)-bmine(j,:));if(xx<min3)min3=xx;endendfor jj=1:48yy=norm(drock(i,1:60)-brock(jj,:));if(yy<min4)min4=yy;endendif(min4>min3)eerock=eerock+1;endenddisp(eemine/111);disp(eerock/97);3.运行结果截图4.结果分析次数 1 2 3 4 5 6 7 8 9 10 平均值erock 0.1546 0.1753 0.1959 0.1856 0.0722 0.1753 0.1959 0.134 0.2165 0.1546 0.1672 emine 0.1351 0.1712 0.1081 0.1892 0.1532 0.0991 0.1261 0.2072 0.1532 0.1532 0.1496 eemine 0.0721 0.0901 0.0901 0.0811 0.0811 0.0721 0.0811 0.0631 0.0721 0.0901 0.0793 eerock 0.1753 0.1856 0.1753 0.0928 0.1649 0.1546 0.1341 0.1959 0.1856 0.1649 0.1629可以看出近邻法得到的识别率比fisher得到的识别率高,这也说明了近邻法比fisher更优。
