周期函数注意点以及常见抽象函数周期性的证明
(完整版)函数奇偶性、对称性、周期性知识点总结,推荐文档
抽象函数的对称性、奇偶性与周期性常用结论一.概念:抽象函数是指没有给出具体的函数解析式或图像,只给出一些函数符号及其满足的条件的函数,如函数的定义域,解析递推式,特定点的函数值,特定的运算性质等,它是高中函数部分的难点,也是大学高等数学函数部分的一个衔接点,由于抽象函数没有具体的解析表达式作为载体,因此理解研究起来比较困难，所以做抽象函数的题目需要有严谨的逻辑思维能力、丰富的想象力以及函数知识灵活运用的能力1、周期函数的定义：对于定义域内的每一个，都存在非零常数，使得()f x x T ()()f x T f x +=恒成立，则称函数具有周期性，叫做的一个周期，则（()f x T ()f x kT ）也是的周期，所有周期中的最小正数叫的最小正周期。
,0k Z k ∈≠()f x ()f x 分段函数的周期：设是周期函数，在任意一个周期内的图像为C:)(x f y =),(x f y =。
把个单位即按向量[]a b T b a x -=∈,,)()(a b K KT x x f y -==轴平移沿在其他周期的图像：)()0,(x f y kT a ==平移，即得。
[]b kT a kT x kT x f y ++∈-=,),(2、奇偶函数：设[][][]b a a b x b a x x f y ,,,),( --∈∈=或①若为奇函数；则称)(),()(x f y x f x f =-=-②若。
为偶函数则称)()()(x f y x f x f ==-分段函数的奇偶性3、函数的对称性：（1）中心对称即点对称：①点对称；关于点与),()2,2(),(b a y b x a B y x A --②对称；关于与点),(),(),(b a y b x a B y b x a A ++--③成中心对称；关于点与函数),()2(2)(b a x a f y b x f y -=-=④成中心对称；关于点与函数),()()(b a x a f y b x a f y b +=+-=-⑤成中心对称。
函数周期性公式大总结
竭诚为您提供优质文档/双击可除函数周期性公式大总结篇一：函数周期性结论总结函数周期性结论总结①f(x+a)=-f(x)T=2a②f(x+a)=±1T=2af(x)③f(x+a)=f(x+b)T=|a-b|证明：令x=x-b得f(x-b+a)=f(x-b+b)f(x-b+a)=f(x)根据公式f(x)=f(x+T)=f(x+nT)得T=-b+a即a-b④f(x)为偶函数，且关于直线x=a对称，T=2a证明：f(x+2a)=f(-x)=f(x)证明：因为偶函数,所以f(-x)=f(x)因为关于x=a对称所以f(a+x)=f(a-x)(对称性质）设x=x+a所以f(x+2a)=f(x)所以周期T=2a)⑤f(x)为奇函数，且关于直线x=a对称，T=4a证明：f(x+2a)=f(-x)=-f(x)根据①可知T=2·2a=4a证明：由于图像关于直线x=a对称、所以f(a+x)=f(a-x)令x=x+a得：f(x+2a)=f(-x)又f(x)=-f(-x)故f(x)=-f(x+2a)代换x=x+2a得：f(x+2a)=-f(x+4a)即得f(x)=f(x+4a)于是函数f(x)的周期为4a⑥f(x)=f(x+a)+f(x-a)有三层函数，用递推的方法来证明。
f(x+a)=f(x+2a)+f(x)f(x+2a)=-f(x-a)换元：令x-a=t那么x=a+tf(t+3a)=-f(t)根据①可知T=6a⑦f(x)关于直线x=a,直线x=b对称，T=2|a-b|证明：f(a+x)=f(a-x)f(b+x)=f(b-x)f(2b-x)=f(x)假设a＞b(当然假设a＜b也可以同理证明出)T=2(a-b)现在只需证明f(x+2a-2b)=f(x)即可⑧f(x)的图像关于(a,0)(b,0)对称，T=2a-2b(a＞b)f(x+2a-2b)=f[a+(x+a-2b)]关于直线x=a对称=f[a-(x+a-2b)]关于直线x=b对称=f(2b-x)=f(x) 证明：根据奇函数对称中心可知：f(a+x)=-f(a-x)f(2b-x)=-f(x)f(x+2a-2b)=f[a+(x+a-2b)]=-f[a-(x+a-2b)]=-f(2b-x)=f(x)篇二：函数周期公式主要知识：1．周期函数：对于f(x)定义域内的每一个x，都存在非零常数T，使得f(x?T)?f(x)恒成立，则称函数f(x)具有周期性，T叫做f(x)的一个周期，则kT（k?Z,k?0）也是f(x)的周期，所有周期中的最小正数叫f(x)的最小正周期．2．几种特殊的抽象函数：具有周期性的抽象函数：函数y?f?x?满足对定义域内任一实数x（其中a为常数），(1)f?x??f?x?a?，则y?f?x?是以T?a为周期的周期函数；(2)f?x?af?x?，则f?x?是以T?2a为周期的周期函数；(3)f?x?a1，则f?x?是以T?2a为周期的周期函数；fx(4)f?x?a??f?x?b?，则f?x?是以T?a?b为周期的周期函数；以上（1）-（4）比较常见，其余几种题目中出现频率不如前四种高，并且经常以数形结合的方式求解。
最全最详细抽象函数的对称性、奇偶性与周期性常用结论
分段函数的周期：设 y f (x) 是周期函数，在任意一个周期内的图像为 C: y f (x),
x a,b,T b a 。把 y f (x)沿x轴平移KT K(b a) 个单位即按向量
a (kT,0)平移，即得y f (x) 在其他周期的图像：
y f (x kT), x kT a, kT b。
y＝f(*＋a)为奇函数，则 f(－*＋a)＝－f(a＋*)
〔3〕y＝f(*＋a)为偶〔或奇〕函数，等价于单层函数 y＝f(*)关于直线*＝
a 轴对称〔或关于点〔a，0〕中心对称〕
.
>
.
3、复合函数的对称性 性质 3 复合函数 y＝f(a＋*)与 y＝f(b－*)关于直线*＝〔b－a〕/2 轴对称 性质 4、复合函数 y＝f(a＋*)与 y＝－f(b－*)关于点〔〔b－a〕/2，0〕中 心对称 推论 1、 复合函数 y＝f(a＋*)与 y＝f(a－*)关于 y 轴轴对称 推论 2、 复合函数 y＝f(a＋*)与 y＝－f(a－*)关于原点中心对称 4、函数的周期性 假设 a 是非零常数，假设对于函数 y＝f(*)定义域内的任一变量*点有以下 条件之一成立，则函数 y＝f(*)是周期函数，且 2|a|是它的一个周期。 ①f(*＋a)＝f(*－a) ②f(*＋a)＝－f(*) ③f(*＋a)＝1/f(*) ④f(*＋a)＝－1/f(*) 5、函数的对称性与周期性 性质 5 假设函数 y＝f(*)同时关于直线*＝a 与*＝b 轴对称，则函数 f(*)必 为周期函数，且 T＝2|a－b| 性质 6、假设函数 y＝f(*)同时关于点〔a，0〕与点〔b，0〕中心对称，则 函数 f(*)必为周期函数，且 T＝2|a－b| 性质 7、假设函数 y＝f(*)既关于点〔a，0〕中心对称，又关于直线*＝b 轴 对称，则函数 f(*)必为周期函数，且 T＝4|a－b|
高中数学知识点;抽像函数周期性公式(基础知识总结)
高中数学抽线函数周期性难题解题技巧（名师总结）今天跟同学们分享一个专题就是抽象函数怎么想周期，同学们抽象等式给到我们的时候有的时候，有得时候让我们找周期性、找对称中心、看奇偶函数等等一系列的问题，同学内题型还是比较困扰同学们的，今天就给同学分享一下抽象函数找周期性的问题！今天通过4个例题的讲解，同学们在遇到这类题型的时候，就知道是找抽象函数周期行的题型！函数周期性技巧原理讲解：首先这是定义是对每一位同学基本的要求，你必须要要掌握，同学们考试的时候给我们的周期式肯定不会这样简单，比如说f(x+8)=f(x)那么一目了然就知道周期式8，同学们这类题的考察本质是函数周期，那么它一定不会给那么简单地式子，而他会隐身给周期的解析式；接下来老师会分享四个抽象等式的式子，同学能够完全记住，在以后做题的时候才能节约时间；接下看一下不等式的两种出现方式；同学先讲两个f()型的题型，两个f()型我们要找到周期原本的定义，那怎么来找出周期的本质定义了，这里来看老师的具体讲解，怎样来理解；接下来；老师会由浅入深给同学讲一些难点，能够做到循序渐进；接下来要注意了，重点来了，这个式子两两个都是复杂，同学们分享到这里，同学以后做题的时候对函数周期的了解、掌握不仅仅局限于定义式，而是这四个你都要记住，这里重要说一个知识点：第二个式子与第三个式子其实是一个类型的，二式m为正、三式前面有负号，这里正负其实没有关系，只要是这种形式那么周期一定等于a的2倍:第四式是绝对值括号内部相减，绝对值括号内x+a-x-b,这个时候正x、负x约掉就是绝对值a减b或者b减a,接下来要解决这样的问题，就要掌握什么样的情况想周期、什么情况想奇偶性、什么情况想对称轴、什么情况想对称中心，要解决这些问题老师给同学们总结了一句话，这句话是非常重要的。
只要把这句话掌握清楚明白周期一眼就能看出来；此类抽象等式：当f()内x前系数相同时一定想周期！我们来看一下前面的不等式是不是这么一会事了，不要想要眨眼，是时候表演真正的技巧了：这里讲的是正常周期，正常周期是f()外侧的系数相同，等式中f()外面的系数的绝对值是相等的；今天没有分享内周期，所以不要抬杠！接着分享：上面讲的都是两个f()型，这道题函有三个f()型；这里体现了数学的逻辑性，是一环扣一环的，如果没有看懂，可以找老师要视频资料；好的这道就把周期给大家解决掉，我可以告诉大家，这道题的答案是1，同学可以自己算，我把最重要的东西给大家搞定就可以了，接着在看一题，今天分享抽象函数周期型那题尽分享完了，这篇文章有对应的视频资料，需要的可以联系老师！。
高中数学周期函数、公式总结、推导、证明过程
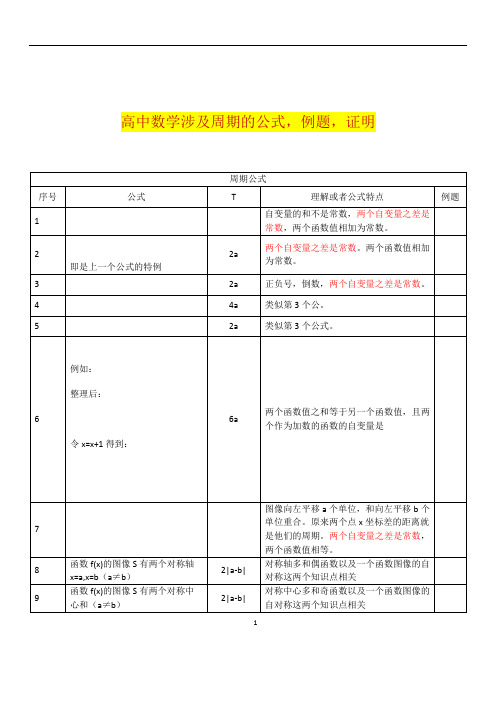
高中数学涉及周期的公式，例题，证明12以上基本是高中阶段遇到的各种周期公式及其变形的总结。
解周期问题，两种方法：1.列举多个数据，找寻规律和周期；2.通过抽象函数直接得到周期。
1. 已知f(X)是R 上不恒为零的偶函数，且对任意实数x 都有xf (x +1)=(x +1)f(x)，则f [f (52)]= 解：令x=0，f(0)=0; 令x =−12，f (−12)=0； 令x =12，f (32)=0； 令x =32，f (52)=0； ∴ f [f (52)]=f (0)=02. 定义在R 上的函数f(x)满足f (x )={log 2(1−x ),x ≤0f (x −1)−f (x −2),x >0，则f(2009)=解：整理f (x )=f (x −1)−f (x −2)， 得到f (x −1)=f (x )+f (x −2)令x=x+1得到，f (x )=f (x +1)+f (x −1)由公式6知道周期为6，即f (x +6)=f(x)，x>0 f(2009)=f (334×6+5)=f(5)。
由公式f (x )=f (x −1)−f (x −2)得f(5)=f(4)−f(3)=(f(3)−f(2))−f(3)=−f(2)=−(f(1)−f(0))=−((f(0)−f(−1))−f(0))=f(−1)=0，4f(x)f(y)=f(x+y)+f(x−y),x,y∈R，则f(2010)=3.已知函数f(x)满足f(1)=14思路：消元和赋值。
令x=x,y=1，则f(x)=f(x+1)+f(x−1)，根据公式6知道，f(x+6)=f(x)，∴f(2010)=f(335×6)=f(0)。
令y=0，则4f(x)f(0)=2f(x)，∵ x不恒为零，∴f(0)=12∴f(2010)=1。
2下面两页是周期函数公式的周期推导证明过程，并总结了推导周期过程的一般思路。
高中数学周期函数、公式总结、推导、证明过程.docx
高中数学涉及周期的公式,例题,证明以上基本是高中阶段遇到的各种周期公式及其变形的总结。
解周期问题,两种方法：1.列举多个数据,找寻规律和周期；2.通过抽象函数直接得到周期。
1.已知f(X)是R上不恒为零的偶函数,且对任意实数x都有xf(x+1)=(x+1)f(x),则f[f(52)]=解：令x=0 ,f(0)=0;令x=−12,f(−12)=0；令x=12,f(32)=0；令x=32,f(52)=0；∴ f[f(52)]=f(0)=02.定义在R上的函数f(x)满足f(x)={log2(1−x),x≤0f(x−1)−f(x−2),x>0,则f(2009)= 解：整理f(x)=f(x−1)−f(x−2),得到f(x−1)=f(x)+f(x−2)令x=x+1得到,f(x)=f(x+1)+f(x−1)由公式6知道周期为6 ,即f(x+6)=f(x),x>0f(2009)=f(334×6+5)=f(5)。
由公式f(x)=f(x−1)−f(x−2)得f(5)=f(4)−f(3)=(f(3)−f(2))−f(3)=−f(2)=−(f(1)−f(0))=−((f(0)−f(−1))−f(0))=f(−1)=0,4f(x)f(y)=f(x+y)+f(x−y),x,y∈R,则f(2010)=3.已知函数f(x)满足f(1)=14思路：消元和赋值。
令x=x,y=1 ,则f(x)=f(x+1)+f(x−1) ,根据公式6知道,f(x+6)=f(x) ,∴f(2010)=f(335×6)=f(0)。
令y=0 ,则4f(x)f(0)=2f(x) ,∵ x不恒为零,∴f(0)=12∴f(2010)=1。
2下面两页是周期函数公式的周期推导证明过程,并总结了推导周期过程的一般思路。
因为word 输入数学公式太过麻烦,所以手写了出来,以图片的形式奉上。
函数的周期性的知识点总结
函数的周期性的知识点总结一、周期函数的定义周期函数是指具有周期性的函数，即在一定的区间内，函数的数值在一定的时间间隔内重复出现。
更具体地说，对于函数f(x)来说，如果存在一个常数T>0，使得对任意的x，有f(x+T)=f(x)，那么函数f(x)就是周期函数，而这个常数T被称为函数的周期。
二、周期函数的性质1. 周期函数的性质：周期函数的周期T是一个正数，且函数的周期性对于所有的自变量都成立，即对于任意的x，有f(x+T)=f(x)成立。
2. 周期函数的图像性质：周期函数的图像通常具有重复出现的特点，这使得它在图像上形成规律的波形。
3. 周期函数的特殊性质：有些周期函数具有特殊的对称性，比如正弦函数、余弦函数等。
三、周期函数的分类1. 固定周期函数：在一个确定的周期内，函数的数值是固定的，比如正弦函数、余弦函数等。
2. 变周期函数：在一个周期内，函数的数值是变化的，比如三角函数的变型函数、指数函数、对数函数等。
四、周期的求法对于周期函数，我们通常需要求解它的周期T，有以下几种方法：1. 观察法：通过观察函数的图像特征，找到函数的周期性。
2. 公式法：对于一些已知的周期函数，可以直接利用其性质和公式来求解周期。
3. 方程求解法：将周期函数的周期T代入函数的周期性公式中，得到关于T的方程，然后求解方程得到周期T。
五、周期函数的图像特征1. 周期函数的波形特点：周期函数的图像通常呈现出规律性的波形，如正弦函数、余弦函数的波形特点。
2. 周期函数的振幅：周期函数的振幅代表了波形的最大振幅，它决定了函数波形的高低。
3. 周期函数的相位：周期函数的相位代表了波形的平移特征，它决定了函数波形的水平位置。
六、周期函数的应用周期函数在很多领域都有重要的应用，如物理、工程、经济等，常见的应用包括：1. 物理波动：周期函数常常用于描述物理中的波动现象，如声波、光波等。
2. 电路分析：在电路分析中，周期函数可用于描述电流、电压的周期性变化。
周期函数注意点以及常见抽象函数周期性的证明
周期函数一、周期函数的 定义1、 对于函数 f (x) ，假如存在一个非零常数，使适当x 取定义域内的每一个值 时，都有．．．．T．．．．f ( x T ) f ( x) ，那么函数 f (x) 就叫做周期函数，非零常数 T 叫做这个函数的周期。
注意：① 定义域：对于任何函数， 都需要明确其定义域， 对于周期函数来说， 其定义域必为起码一端无界 的会合。
原因：设周期为 T, 由周期函数的定义知 f(x+T)=f(x), 易得 f(x+nT)=f(x) ( 此中 n 是整数 ), 即 x+nT 也在定义域内 , 故周期函数定义域必是无界集。
例题： y sin x(0 x 10 ) 是周期函数吗？② 变的只好是 xT 的变化只好发生在 x 上。
比如 f ( x) sin(3 x 8) 是周期函数，则 f (x T ) sin[3( x T ) 8] ，不可以写成 f (x T ) sin(3x T 8)。
例题： sin x 2sin x，那么 2 是 sin ( x) 的周期吗？333③ 图像为周期颠簸的函数不必定是周期函数，要察看定义域。
比如： f ( x) x [ x] （ 3 x 3 ）（ [ x] 是取整函数， 表示不超出 x 的最大整数），该函数的图像以下所示，该图像重复出现，可是由于其定义域两 端都有界，因此其必不为周期函数。
二、 周期函数问题的有关题型及解答。
中心：全部周期函数的问题，中心在求出周期 T ，马上题目里各样 f ( x) 的等 式往 f ( x T) f ( x) 方向化简。
化简过程中需要注意的有关函数观点 ：化简过程中要注意 f (x) 自己的对称性和奇偶性。
三、抽象函数的周期总结1. f ( x)f (x T ) 型： f ( x) 的周期为 T 。
证明：对 x 取定义域内的每一个值时，都有 f ( x T)f ( x) ，则 f (x) 为周期函数， T 叫函数 f (x) 的周期。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
周期函数的定义
1、对于函数f(x)，如果存在一个非零常数.T ,使得当x 取定义域内的每一个值.时，都有
f(x T) f(x)，那么函数f(x)就叫做周期函数，非零常数 T 叫做这个函数的周期。
① 定义域：对于任何函数，都需要明确其定义域，对于周期函数来说，其 定义域必为至少一端无界的集合。
理由：设周期为T,由周期函数的定义知f(x+T)=f(x),易得f(x+nT)=f(x) (其中n 是整数),即x+nT 也在定义域内，故周期函数定义域必是无界集。
例题：y sin x(0 x 10 )是周期函数吗？
② 变的只能是x
T 的变化只能发生在 x 上。
例如f(x) sin(3x 8)是周期函数，则 f (x T) sin[3( x T) 8]，不能写成 f (x T) sin(3x T 8)。
③ 图像为周期波动的函数不一定是周期函数，要观察定义域。
例如：f (x) x [x] ( 3 x 3 ) ([x]是取整函数，表示不超过 x 的 最大整数)，该函数的图像如下所示，该图像重复出现，但是因为其定义域 两端都有界，所以其必不为周期函数。
周期函数问题的相关题型及解答。
核心：所有周期函数的问题，核心在求出周期 T ,即将题目里各种f(x)的等 式往f(x T) f (x)方向化简。
化简过程中需要注意的相关函数概念：化简过程中要注意f(x)本身的对称 性和奇偶性。
抽象函数的周期总结
周期函数
例题：sin - 2
3
sin -，那么2
3
是sin (为的周期吗?
3
1. f(x) f(x T)型：f(x)的周期为 T o 证明：对x 取定义域内的每一个值时，都有 f (x T) f (x)，贝y f (x)为周期函数，T 叫
函数f (x)的周期。
2. f (x a) f (x b)型：f(x)的周期为 |b a|。
证明：f (x a) f (x b) f (x) f (x b a)。
3. f (x a) f (x)型：f (x)的周期为 2a o
1
4. f (x a)
型：f (x)的周期为2a o
f(x)
1
—f(x)。
f(x)
1
5. f (x a) —型：f (x)的周期为 2a 。
f(x)
6. f (x a) 1一型 型：f (x)的周期为4a 。
1 f(x)
f(x)
证明：f (x 2a) f [(x a) a]
f (x a) [f(x)] f(x)
证明：f (x 2a) f [(x a) a]
1 f(x a)
证明：f (x 2a) f [(x a) a]
1 f (x a)
1 1 f(x)
f (x) o
证明：f (x 2a)
1
1 f (x a) 1 f (x) 1 1 f (x
a)
1 1 f(x)
1 f (x)
f(x)'
f (x 4a) f [(x 2a) 2a]
1 f(x 2a)
f (x) o
7. f (x a)
1 f (x) 1 f (x)
y f(x)的周期为T 2a
f [(x a) a]
1 1 f(x)
8、 f (x a)
y f (x)的周期为 T 3a
f (x) 1
证明：
f[(x f[(x
f(x a)
2a) 3a)
a]-
a]
f(x)
1
1
f(x) 1 f(x) f(x)
f(x a) 1
1 1
1
1 f(x) 1 1 f (x 2a)
f(x) 1 1 f(x)
9、f (x 2a) f (x a)
f(x)
y
f (x)的周期为T 6a
证明： f(x
2a) f(x a) f(x)
f(x
3a)
f(x
2a) f(x a)
f(x 3a) f (x)
f[(x 3a) 3a] (f(x))
f (x)
10.两线对称型： 函数 f (x)关于直线x
a 、x
b 对称，则 f (x)的周期为|2b
2a|。
证明：
f (x)
f (2a x),
f (2a x)
f (2b
x) f(x)
f(x 2b 2a)。
f (x) f (2b x)
8. 一线一点对称型
：函数f (x)关于直线x a 及点(b , 0)对称，贝U f (x)的周期为
f (x 4b 4a) f [(x 2b 2a) 2b 2a] f (x 2b 2a) [ f (x)] f (x)
证明：f(x 2a) f[(x a) a]
1 f(x a) 1 f(x a)
1 1 f(x)
1 f(x) 1 1 f(x) 1 f(x)
f(x)。
|4b 4a|。
证明：
f (x)
f (2a
x) f(2a x)
f(2b
f (2b x)
f(x)
x) f (x 2b 2a) f (x),所以
函数f(x)关于点(a , 0)、(b , 0)对称，则f(x)的周期为2b 2a|。
x) f (x)
f (2a x) f (2b x) f (x) f (x 2b 2a) 。
x) f (x)
9. 两点对称型：
证明：
f (2a
f (2b。