2020上海高三数学崇明一模

合集下载

2020年上海崇明县高考理科数学一模卷答案

上海市崇明县2020届高三一模数学试题（理科）参考答案一、填空题1、3+5i2、512π 3、+=0x y 4、[]-1,1 5、1- 6、10 7、30 8、4 9、89 10、-2a ≤ 11、12 12、( 13、1830 14、(-4,-2) 二、选择题15、C 16、C 17、C 18、A三、解答题19、1(x)=sin2x+cos2x f （）(2x+)4π=T π∴（2）因为32x+444πππ⎡⎤∈-⎢⎥⎣⎦，，所以sin (2x+)4π⎡⎤∈⎢⎥⎣⎦ ,所以(x)f ⎡∈-⎣ 函数的增区间为48ππ⎡⎤-⎢⎥⎣⎦，，减区间为84ππ⎡⎤⎢⎥⎣⎦， 20、（1）方法一、以A 为坐标原点，以AB 、AD 、AA 1分别为x 轴、y 轴、z 轴方向建立空间直角坐标系,设AB a =，则1,1,12a B E ⎛⎫=-- ⎪⎝⎭u u u r ，1(0,1,1)AD =u u u u r . 所以 , 11110,B E AD B E AD ⋅=⊥u u u r u u u u r 。

另解：11AA D D 为正方形，所以11A D AD ⊥，111111A D AD AD B CD CD AD ⊥⎫⇒⊥⎬⊥⎭面A 。

11111B E A B CD AD B E ⊆⇒⊥又面。

（2）因为()()12,0,11,1,0,AB AE ==u u u r u u u r ，所以取面AB 1E 的一个法向量为()1=1,-1,-2n u r ，同理可取面A 1B 1E 一个法向量为()2=0,1,1n u u r ，设二面角A-B 1E-A 1为α，则1212cos =2n n n n α⋅=⋅，=6πα所以即二面角A-B 1E-A 1的大小为6π. 22、解：（1）22(x)=x +-1f x ，令2(x)=0f，得x所以21(x)(,1)22f 在区间内的零点是x=。

（2）证明：因为 n 1()<02f ，n (1)>0f 。

上海市2020届高三数学各区(16区已全)一模考试汇编：解析几何(解析版)

2020年一模汇编——解析几何一、填空题【普陀1】若抛物线2y mx =的焦点坐标为1(,0)2，则实数m 为___________.【答案】2【解析】抛物线的性质：p=1，所以m=2【黄浦3】抛物线28x y =的焦点到准线的距离为___________. 【答案】4【解析】由题抛物线的焦点为(0,2)，准线为直线2x =-，易得焦点到准线的距离为4【青浦3】直线1:10l x -=和直线20l y -=的夹角大小是【答案】6π 【解析】设夹角为θ，则23213cos =⨯=θ，故夹角6πθ=【静安3】若直线1l 和直线2l 的倾斜角分别为32和152则1l 与2l 的夹角为_____.【答案】60【解析】1801523260-+=【静安4】若直线l 的一个法向量为(2,1)n =，则若直线l 的斜率k =_____. 【答案】2-【解析】(2,1)n =，则单位向量(1,2)d =-，221k ==-【宝山5】以抛物线x y 62-=的焦点为圆心，且与抛物线的准线相切的圆的方程是 .【答案】9)23(22=++y x【解析】焦点)0,23(-，半径3==p r 【松江5】已知椭圆22194x y +=的左、右焦点分别为1F 、2F ，若椭圆上的点P 满足122PF PF =，则1=PF【答案】4【解析】由椭圆定义得：1226PF PF a +==，又122PF PF =，联立得：1=PF 4【虹口6】抛物线26x y =的焦点到直线3410x y +-=的距离为_________. 【答案】1【解析】抛物线26x y =的焦点为)23,0(，焦点到直线3410x y +-=的距离33041215d ⨯+⨯-==【杨浦7】椭圆22194x y +=焦点为1F ，2F ，P 为椭圆上一点，若15PF =，则12cos F PF ∠= 【答案】35【解析】因为3a ==，2b ==，所以c ==，所以1(F，2F ，225651PF a =-=-=，所以22212513cos 2155F PF +-∠==⋅⋅【奉贤7】若双曲线的渐近线方程为3y x =±，它的焦距为则该双曲线的标准方程为____________.【答案】2219y x -=±【解析】根据双曲线的渐近线方程为3y x =±，可知3b a =或3ab=；由焦距为得出c =222c a b =+，求得,,a b c 的值【普陀8】设椭圆222:1(1)x y a aΓ+=＞，直线l 过Γ的左顶点A 交y 轴于点P ，交Γ于点Q ，若AOP △是等腰三角形（O 为坐标原点），且2PQ QA →→=，则Γ的长轴长等于_________.【答案】【解析】由题知(),0A a -、()0,P a ，设(),Q x x a +，有(),PQ x x =、(),QA a x x a =----，所以()2x a x =⋅--，解得23x a =-，将(),Q x x a +代入2221x y a +=得22211210x ax a a ⎛⎫+++-= ⎪⎝⎭，整理得Γ的长轴长2a = 【崇明8】若双曲线的一个顶点坐标为(3,0)，焦距为10，则它的标准方程是__________．【答案】116922=-y x 【解析】由题意得3=a ，5210=÷=c ，16222=-=a c b ，标准方程为116922=-y x【杨浦9】在直角坐标平面xOy 中，(2,0)A -，(0,1)B ，动点P 在圆22:+2C x y =上，则PA PB ⋅的取值范围为___________.【答案】(22+【解析】因为22+2x y =，设)P θθ，则(2,)PA θθ=--，(,1)PB θθ=-，22222cos 2sin PA PB θθθθ⋅=++，22)PA PB θθθϕ⋅=+=++，【崇明9】已知,a b R +∈，若直线230x y ++=与(1)2a x by -+=互相垂直，则ab 的最大值等于___________.【答案】81 【解析】两直线互相垂直得1121-=-⋅-ba ，b a 21-=，代入得b b ab )21(-=， 0,0a b >>，最小值为81【宝山9】已知直线l 过点)0,1(-且与直线02=-y x 垂直，则圆08422=+-+y x y x 与直线l 相交所得的弦长为___________.【答案】152【解析】直线方程为012=++y x ，圆心到直线的距离5=d ⇒222||d r AB -=【奉贤9】设平面直角坐标系中，O 为原点，N 为动点，6ON =，5ON OM =，过点M 作1MM x ⊥轴于1M ，过N 作1NN x ⊥轴于点1N ，M 与1M 不重合，N 与1N 不重合，设11OT M M N N =+，则点T 的轨迹方程是______________.【答案】22536x y +=05x x ⎛≠≠ ⎝⎭且【解析】设(),T x y ，点()11,N x y ，则()11,0N x ，又1111,OM y M y ⎫⎛⎫==⎪ ⎪⎭⎝⎭11,0M M ⎫=⎪⎭，()110,N N y =，于是1111,OT M M N N x y ⎫=+=⎪⎭，由此能求出曲线C的方程。

崇明区2020 学年度第一学期高三年级模拟质量调研数学学科试卷(解析版)

( ) 所以有
2n −
3r
2r = = 12
4
解得
n r
= =
6 4
，则 T5
=
C64
2a2
2 b12 = 60a4b12 ， m = 60
10.设 O 为坐标原点，直线 x
= a 与双曲线 C :
x2 a2
−
y2 b2
= 1(a
0,b 0) 的两条渐近线分别交
于 D、E 两点，若 ODE 的面积为1，则双曲线 C 的焦距的最小值为 .
（1）求函数 y = f (x) 的最小值正周期；
（2）在 ABC 中，角 A, B,C 的对边分别为 a,b,c 若锐角 A 满足 f (A) = 1− 3 ,C = ,c = 2,
2
6
求 ABC 的面积.
【解析】（1）∵ f (x) = 1 sin 2x − 3 cos 2x +1 = sin(2x − ) − 3 ,
2
2
32
∴ T = 2 = 2 = . || 2
（2）∵ f ( A) = 1− 3 , ∴ sin(2A − ) − 3 = 1− 3 , ∴ sin(2A − ) = 1 ,
2
32 2
32
∴解得 2A − = +2k 或 2A − = 5 +2k ,(k Z ),
36
36
∴ A= +k 或 A= 7 +k ,(k Z ), 又 A(0, ) ,
y = f ( f ( x)) = − f (− f ( x)) = − f ( f (−x)) 也是奇函数，正确；
对于（2）若函数 f ( x) 是周期函数，则. f ( x + T ) = f ( x) .

2020年上海市高三数学一模分类汇编：集合与命题

1（2020闵行一模）. 已知集合{3,1,0,1,2}A =--，{|||1}B x x =>，则AB = 1（2020青浦一模）. 已知集合{1,3,5,9}U =，{1,3,9}A =，{1,9}B =，则()U A B = 1（2020松江一模）. 已知集合{|10}A x x =-≥，{0,1,2}B =，则A B =1（2020崇明一模）. 已知集合{0,1,2,3}A =，{|02}B x x =<≤，则AB = 1（2020虹口一模）. 设全集U =R ，若21{|1}x A x x-=>，则U A = 1（2020徐汇一模）. 已知集合{|2}M x x =>，集合{|1}N x x =≤，则M N = 1（2020嘉金一模）. 已知集合{1,2,3,4,5}A =，{2,4,6,8}B =，则AB = 7（2020徐汇一模）. 已知x ∈R ，条件2:p x x <，条件1:q a x ≥（0a >），若p 是q 的充分不必要条件，则实数a 的取值范围是12（2020杨浦一模）. 向量集合{|(,),,}S a a x y x y ==∈R ，对于任意α、S β∈，以及任意(0,1)λ∈，都有(1)S λαλβ+-∈，则称S 为“C 类集”. 现有四个命题：① 若S 为“C 类集”，则集合{|,}M a a S μμ=∈∈R 也是“C 类集”；② 若S 、T 都是“C 类集”，则集合{|,}M a b a S b T =+∈∈也是“C 类集”； ③ 若1A 、2A 都是“C 类集”，则12A A 也是“C 类集”；④ 若1A 、2A 都是“C 类集”，且交集非空，则12A A 也是“C 类集”. 其中正确的命题有13（2020嘉金一模）. 已知x ∈R ，则“0x >”是“1x >”的（）A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既非充分也非必要条件13（2020虹口一模）. 设x ∈R ，则“|1|1x -<”是“24x <”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件13（2020普陀一模）.“{1,2}m ∈”是“ln 1m <”的成立的（）A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既非充分也非必要条件14（2020闵行一模）. 命题“若x a >，则10x x->”是真命题，实数a 的取值范围是（） A. (0,)+∞ B. (,1]-∞ C. [1,)+∞ D. (,0]-∞14（2020松江一模）. 设,x y ∈R ，则“2x y +>”是“x 、y 中至少有一个数大于1”的（）A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既非充分又非必要条件14（2020普陀一模）. 设集合{|||1}A x x a =-=，{1,3,}B b =-，若A B ⊆，则对应的实数对(,)a b 有（）A. 1对B. 2对C. 3对D. 4对16（2020松江一模）. 已知集合{1,2,3,,10}M =⋅⋅⋅，集合A M ⊆，定义()M A 为A 中元素的最小值，当A 取遍M 的所有非空子集时，对应的()M A 的和记为10S ，则10S =（）A. 45B. 1012C. 2036D. 9217。

2020年上海崇明县高考理科数学一模卷

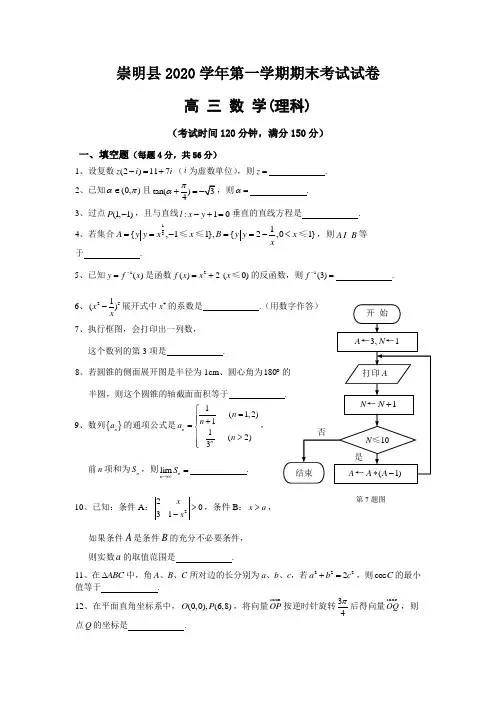
崇明县2020学年第一学期期末考试试卷高三数学(理科)（考试时间120分钟，满分150分）一、填空题（每题4分，共56分）1、设复数(2)117z i i -=+（i 为虚数单位），则z =.2、已知(0,)απ∈且tan()4πα+=，则α=.3、过点(1,1)P -，且与直线:10l x y -+=垂直的直线方程是.4、若集合131{,11},{2,01}A y y x x B y y x x==-==-<≤≤≤，则A B I 等于 .5、已知1()y f x -=是函数2()2f x x =+(0)x ≤的反函数，则1(3)f -=.6、251()x x -展开式中x 7这个数列的第389、数列{}n a 前n 项和为n S ，则n 10、已知：条件A ：22031xx >-，条件B ：x a >，如果条件A 是条件B 的充分不必要条件，则实数a 的取值范围是.11、在ABC ∆中，角A 、B 、C 所对边的长分别为a 、b 、c ，若2222a b c +=，则cos C 的最小值等于 .12、在平面直角坐标系中，(0,0),(6,8)O P ，将向量OP u u u r 按逆时针旋转34π后得向量OQ u u u r ，则点Q 的坐标是 .第7题图13、数列{}n a 满足1(1)21n n n a a n ++-=-，则{}n a 的前60项和等于.14、已知()(2)(3)f x m x m x m =-++,()22x g x =-，若同时满足条件：①对于任意x R ∈，()0f x <或()0g x <成立； ②存在(,4)x ∈-∞-，使得()()0f x g x ⋅<成立．则m 的取值范围是.二、选择题（每题5分，共20分）15、设函数()sin ,f x x =x R ∈，则下列结论错误的是………………………………………（） A ．()f x 的值域为[0,1] B ．()f x 是偶函数C ．()f x 不是周期函数D ．()f x 不是单调函数16、下面是关于复数21z i=-+的四个命题： ①2z =； ②22z i =； ③z 的共轭复数为1i +； ④z 的虚部为1-．其中正确的命题……………………………………………………………………………（）A ．②③B ．①②C ．②④D ．③④17、等轴双曲线C ：222x y a -=与抛物线216y x =的准线交于,A B 两点，AB =，则双曲线C 的实轴长等于……………………………………………………………………（）AB ．C ．4D ．818、某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课各1节，则在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为……………………（）A ．35B ．815C ．25D ．15三、解答题（本大题共74分，解答下列各题需要必要的步骤）19、（本题12分，第(1)小题6分，第(2)小题6分）已知函数2()=sin(2+)+sin(2)+2cos 133f x x x x ππ--, x R ∈.（1）求函数()f x 的最小正周期；（2）当[,]44x ππ∈-时，求函数()f x 的值域以及函数()f x 的单调区间．20、（本题14分，第(1)小题6分，第(2)小题8分）如图，在长方体1111ABCD A B C D -中, 11AA AD ==, E 为CD 中点．（1）求证：11B E AD ⊥；（2）若2AB =，求二面角11A B E A --的大小．21、（本题14分，第(1)小题6分，第(2)小题8分）已知数列{}n a ，记123()n A n a a a a =+++⋅⋅⋅⋅⋅⋅+, 2341()n B n a a a a +=+++⋅⋅⋅⋅⋅⋅+, 3452()n C n a a a a +=+++⋅⋅⋅⋅⋅⋅+, (1,2,3,......)n =，并且对于任意n N *∈，恒有0n a >成立．（1）若121,5a a ==，且对任意n N *∈，三个数(),(),()A n B n C n 组成等差数列，求数列{}n a 的通项公式；（2）证明：数列{}n a 是公比为q 的等比数列的充分必要条件是：对任意n N *∈，三个数(),(),()A n B n C n 组成公比为q 的等比数列．ABCE DA 1D 1B 1C 1。

2019-2020学年上海市崇明区高考数学一模试卷

上海市崇明区高考数学一模试卷一、填空题（本大题共有12题，满分54分，其中1-6题每题4分，7-12题每题5分）1．（4分）已知集合A={1，2，5}，B={2，a }，若A ∪B={1，2，3，5}，则a= ．2．（4分）抛物线y 2=4x 的焦点坐标为．3．（4分）不等式＜0的解是．4．（4分）若复数z 满足iz=1+i （i 为虚数单位），则z= ． 5．（4分）在代数式（x ﹣）7的展开式中，一次项的系数是．（用数字作答）6．（4分）若函数y=2sin （ωx ﹣）+1（ω＞0）的最小正周期是π，则ω= ．7．（5分）若函数f （x ）=x a 的反函数的图象经过点（，），则a= ． 8．（5分）将一个正方形绕着它的一边所在的直线旋转一周，所得几何体的体积为27πcm 3，则该几何体的侧面积为 cm 2．9．（5分）已知函数y=f （x ）是奇函数，当x ＜0 时，f （x ）=2x ﹣ax ，且f （2）=2，则a= ．10．（5分）若无穷等比数列{a n }的各项和为S n ，首项 a 1=1，公比为a ﹣，且S n =a ，则a= ．11．（5分）从5男3女共8名学生中选出队长1人，副队长1人，普通队员2人组成 4人志愿者服务队，要求服务队中至少有 1 名女生，共有种不同的选法．（用数字作答）12．（5分）在ABC 中，BC 边上的中垂线分别交BC ，AC 于点D ，E ．若•=6，||=2，则AC= ．二、选择题（本大题共有4题，满分20分） 13．（5分）展开式为ad ﹣bc 的行列式是（）祝您高考马到成功！A ．B ．C ．D ．14．（5分）设a ，b ∈R ，若a ＞b ，则（） A ．＜ B ．lga ＞lgb C ．sin a ＞sin b D ．2a ＞2b15．（5分）已知等差数列{a n }的公差为d ，前n 项和为S n ，则“d ＞0”是“S 4+S 6＞2S 5”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 16．（5分）直线x=2与双曲线﹣y 2=1的渐近线交于A ，B 两点，设P 为双曲线上任一点，若=a+b（a ，b ∈R ，O 为坐标原点），则下列不等式恒成立的是（） A ．a 2+b 2≥1 B ．|ab |≥1 C ．|a +b |≥1 D ．|a ﹣b |≥2三、解答题（本大题共有5题，满分76分）17．（14分）如图，长方体ABCD ﹣A 1B 1C 1D 1中，AB=BC=2，A 1C 与底面ABCD 所成的角为60°，（1）求四棱锥A 1﹣ABCD 的体积；（2）求异面直线A 1B 与 B 1D 1所成角的大小．18．（14分）已知f （x ）=2sinxcosx +2cos 2x ﹣1．（1）求f （x ）的最大值及该函数取得最大值时x 的值；（2）在△ABC 中，a ，b ，c 分别是角 A ，B ，C 所对的边，若a=，b=，且f （）=，求边c 的值．19．（14分）2016 年崇明区政府投资 8 千万元启动休闲体育新乡村旅游项目．规祝您高考马到成功！划从 2017 年起，在今后的若干年内，每年继续投资 2 千万元用于此项目.2016 年该项目的净收入为 5 百万元，并预测在相当长的年份里，每年的净收入均为上一年的基础上增长50%．记 2016 年为第 1 年，f （n ）为第 1 年至此后第 n （n ∈N*）年的累计利润（注：含第 n 年，累计利润=累计净收入﹣累计投入，单位：千万元），且当 f （n ）为正值时，认为该项目赢利．（1）试求 f （n ）的表达式；（2）根据预测，该项目将从哪一年开始并持续赢利？请说明理由． 20．（16分）在平面直角坐标系中，已知椭圆C ：+y 2=1 （a ＞0，a ≠1）的两个焦点分别是F 1，F 2，直线l ：y=kx +m （k ，m ∈R ）与椭圆交于A ，B 两点．（1）若M 为椭圆短轴上的一个顶点，且△MF 1F 2是直角三角形，求a 的值；（2）若k=1，且△OAB 是以O 为直角顶点的直角三角形，求a 与m 满足的关系；（3）若a=2，且k OA •k OB =﹣，求证：△OAB 的面积为定值．21．（18分）若存在常数k （k ＞0），使得对定义域D 内的任意x 1，x 2（x 1≠x 2），都有|f （x 1）﹣f （x 2）|≤k |x 1﹣x 2|成立，则称函数f （x ）在其定义域 D 上是“k ﹣利普希兹条件函数”．（1）若函数f （x ）=，（1≤x ≤4）是“k ﹣利普希兹条件函数”，求常数k 的最小值；（2）判断函数f （x ）=log 2x 是否是“2﹣利普希兹条件函数”，若是，请证明，若不是，请说明理由；（3）若y=f （x ）（x ∈R ）是周期为2的“1﹣利普希兹条件函数”，证明：对任意的实数x 1，x 2，都有 |f （x 1）﹣f （x 2）|≤1．祝您高考马到成功！上海市崇明区高考数学一模试卷参考答案与试题解析一、填空题（本大题共有12题，满分54分，其中1-6题每题4分，7-12题每题5分）1．（4分）已知集合A={1，2，5}，B={2，a }，若A ∪B={1，2，3，5}，则a= 3 ．【解答】解：∵集合A={1，2，5}，B={2，a }， A ∪B={1，2，3，5}， ∴a=3．故答案为：3．2．（4分）抛物线y 2=4x 的焦点坐标为（1，0）．【解答】解：∵抛物线y 2=4x 是焦点在x 轴正半轴的标准方程，p=2∴焦点坐标为：（1，0）故答案为：（1，0）3．（4分）不等式＜0的解是（﹣1，0）．【解答】解：不等式＜0，即 x （x +1）＜0，求得﹣1＜x ＜0，故答案为：（﹣1，0）．4．（4分）若复数z 满足iz=1+i （i 为虚数单位），则z= 1﹣i ．【解答】解：由iz=1+i ，得z==1﹣i故答案为：1﹣i ．5．（4分）在代数式（x ﹣）7的展开式中，一次项的系数是 21 ．（用数字作答）祝您高考马到成功！【解答】解：（x ﹣）7的展开式的通项为=，由7﹣3r=1，得r=2， ∴一次项的系数是．故答案为：21．6．（4分）若函数y=2sin （ωx ﹣）+1（ω＞0）的最小正周期是π，则ω= 2 ．【解答】解：根据正弦函数的图象与性质，知函数y=2sin （ωx ﹣）+1（ω＞0）的最小正周期是T==π，解得ω=2．故答案为：2．7．（5分）若函数f （x ）=x a 的反函数的图象经过点（，），则a=．【解答】解：若函数f （x ）=x a 的反函数的图象经过点（，），则：（，）满足f （x ）=x α，所以：，解得：，故答案为：．8．（5分）将一个正方形绕着它的一边所在的直线旋转一周，所得几何体的体积为27πcm 3，则该几何体的侧面积为 18π cm 2．【解答】解：将一个正方形绕着它的一边所在的直线旋转一周，所得几何体是圆柱体，设正方形的边长为acm ，则圆柱体的体积为 V=πa 2•a=27π，祝您高考马到成功！解得a=3cm ；∴该圆柱的侧面积为S=2π×3×3=18πcm 2．故答案为：18π．9．（5分）已知函数y=f （x ）是奇函数，当x ＜0 时，f （x ）=2x ﹣ax ，且f （2）=2，则a= ﹣ ．【解答】解：∵函数y=f （x ）是奇函数，当x ＜0 时，f （x ）=2x ﹣ax ， ∴x ＞0时，﹣f （x ）=2﹣x ﹣a （﹣x ）， ∴f （x ）=﹣2﹣x ﹣ax ， ∵f （2）=2，∴f （2）=﹣2﹣2﹣2a=2，解得a=﹣．故答案为：﹣．10．（5分）若无穷等比数列{a n }的各项和为S n ，首项 a 1=1，公比为a ﹣，且S n =a ，则a= 2 ．【解答】解：无穷等比数列{a n }的各项和为S n ，首项 a 1=1，公比为a ﹣，且S n =a ，可得=a ，即有=a ，即为2a 2﹣5a +2=0，解得a=2或，由题意可得0＜|q |＜1，即有0＜|a ﹣|＜1，检验a=2成立；a=不成立．故答案为：2．祝您高考马到成功！11．（5分）从5男3女共8名学生中选出队长1人，副队长1人，普通队员2人组成 4人志愿者服务队，要求服务队中至少有 1 名女生，共有 780 种不同的选法．（用数字作答）【解答】解：根据题意，要求服务队中至少有 1 名女生，则分3种情况讨论： ①、选出志愿者服务队的4人中有1名女生，有C 53C 31=30种选法，这4人选2人作为队长和副队有A 42=12种，其余2人为普通队员，有1种情况，此时有30×12=360种不同的选法，②、选出志愿者服务队的4人中有2名女生，有C 52C 32=30种选法，这4人选2人作为队长和副队有A 42=12种，其余2人为普通队员，有1种情况，此时有30×12=360种不同的选法，③、选出志愿者服务队的4人中有3名女生，有C 51C 33=5种选法，这4人选2人作为队长和副队有A 42=12种，其余2人为普通队员，有1种情况，此时有5×12=60种不同的选法，则一共有360+360+60=780；故答案为：780．12．（5分）在ABC 中，BC 边上的中垂线分别交BC ，AC 于点D ，E ．若•=6，||=2，则AC= 4 ．【解答】解：建立平面直角坐标系如图所示，设B （﹣a ，0），C （a ，0），E （0，b ），∠ABC=α，由||=2，知A （﹣a +2cosα，2sinα），∴=（a ﹣2cosα，b ﹣2sinα），=（2a ，0）， ∴•=2a （a ﹣2cosα）+0=2a 2﹣4acosα=6，∴a 2﹣2acosα=3；又=（2a ﹣2cosα，﹣2sinα），祝您高考马到成功！∴=（2a ﹣2cosα）2+（﹣2sinα）2=4a 2﹣8acosα+4 =4（a 2﹣2acosα）+4 =4×3+4 =16，∴||=4，即AC=4．故答案为：4．二、选择题（本大题共有4题，满分20分） 13．（5分）展开式为ad ﹣bc 的行列式是（） A ．B ．C ．D ．【解答】解：根据叫做二阶行列式，它的算法是：ad ﹣bc ，由题意得，=ad ﹣bc ．故选B ．14．（5分）设a ，b ∈R ，若a ＞b ，则（） A ．＜ B ．lga ＞lgb C ．sin a ＞sin b D ．2a ＞2b【解答】解：由a ＞b ，利用指数函数的单调性可得：2a ＞2b ．再利用不等式的性质、对数函数的定义域与单调性、三角函数的单调性即可判断出A ，B ，C 不正确．故选：D ．祝您高考马到成功！15．（5分）已知等差数列{a n }的公差为d ，前n 项和为S n ，则“d ＞0”是“S 4+S 6＞2S 5”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【解答】解：∵S 4+S 6＞2S 5， ∴4a 1+6d +6a 1+15d ＞2（5a 1+10d ）， ∴21d ＞20d ， ∴d ＞0，故“d ＞0”是“S 4+S 6＞2S 5”充分必要条件，故选：C16．（5分）直线x=2与双曲线﹣y 2=1的渐近线交于A ，B 两点，设P 为双曲线上任一点，若=a+b（a ，b ∈R ，O 为坐标原点），则下列不等式恒成立的是（） A ．a 2+b 2≥1B ．|ab |≥1C ．|a +b |≥1D ．|a ﹣b |≥2【解答】解：双曲线﹣y 2=1的渐近线为：y=±x ．把x=2代入上述方程可得：y=±1．不妨取A （2，1），B （2，﹣1）．=a+b=（2a +2b ，a ﹣b ）．代入双曲线方程可得：﹣（a ﹣b ）2=1，化为ab=． ∴=ab ，化为：|a +b |≥1．故选：C ．三、解答题（本大题共有5题，满分76分）17．（14分）如图，长方体ABCD ﹣A 1B 1C 1D 1中，AB=BC=2，A 1C 与底面ABCD 所祝您高考马到成功！成的角为60°，（1）求四棱锥A 1﹣ABCD 的体积；（2）求异面直线A 1B 与 B 1D 1所成角的大小．【解答】解：（1）∵长方体ABCD ﹣A 1B 1C 1D 1中，AB=BC=2， ∴AA 1⊥平面ABCD ，AC==2，∴∠A 1CA 是A 1C 与底面ABCD 所成的角， ∵A 1C 与底面ABCD 所成的角为60°， ∴∠A 1CA=60°，∴AA 1=AC•tan60°=2•=2， ∵S 正方形ABCD =AB ×BC=2×2=4， ∴四棱锥A 1﹣ABCD 的体积： V===．（2）∵BD ∥B 1D 1，∴∠A 1BD 是异面直线A 1B 与B 1D 1所成角（或所成角的补角）．∵BD=，A 1D=A 1B==2， ∴cos ∠A 1BD===．∴∠A 1BD=arccos．∴异面直线A 1B 与 B 1D 1所成角是arccos．祝您高考马到成功！18．（14分）已知f （x ）=2sinxcosx +2cos 2x ﹣1．（1）求f （x ）的最大值及该函数取得最大值时x 的值；（2）在△ABC 中，a ，b ，c 分别是角 A ，B ，C 所对的边，若a=，b=，且f （）=，求边c 的值．【解答】解：f （x ）=2sinxcosx +2cos 2x ﹣1=sin2x +cos2x=2sin （2x +）（1）当2x +=时，即x=（k ∈Z ），f （x ）取得最大值为2；（2）由f （）=，即2sin （A +）=可得sin （A +）=∵0＜A ＜π ∴＜A ＜ ∴A=或∴A=或当A=时，cosA==∵a=，b=，解得：c=4 当A=时，cosA==0∵a=，b=，解得：c=2．祝您高考马到成功！19．（14分）2016 年崇明区政府投资 8 千万元启动休闲体育新乡村旅游项目．规划从 2017 年起，在今后的若干年内，每年继续投资 2 千万元用于此项目.2016 年该项目的净收入为 5 百万元，并预测在相当长的年份里，每年的净收入均为上一年的基础上增长50%．记 2016 年为第 1 年，f （n ）为第 1 年至此后第 n （n ∈N*）年的累计利润（注：含第 n 年，累计利润=累计净收入﹣累计投入，单位：千万元），且当 f （n ）为正值时，认为该项目赢利．（1）试求 f （n ）的表达式；（2）根据预测，该项目将从哪一年开始并持续赢利？请说明理由．【解答】解：（1）由题意知，第1年至此后第n （n ∈N *）年的累计投入为8+2（n ﹣1）=2n +6（千万元），第1年至此后第n （n ∈N *）年的累计净收入为+×+×+…+×=（千万元）．∴f （n ）=﹣（2n +6）=﹣2n ﹣7（千万元）．（2）方法一：∵f （n +1）﹣f （n ）=[﹣2（n +1）﹣7]﹣[﹣2n ﹣7]=[﹣4]，∴当n ≤3时，f （n +1）﹣f （n ）＜0，故当n ≤4时，f （n ）递减；当n ≥4时，f （n +1）﹣f （n ）＞0，故当n ≥4时，f （n ）递增．又f （1）=﹣＜0，f （7）=≈5×﹣21=﹣＜0，f （8）=﹣23≈25﹣23=2＞0．∴该项目将从第8年开始并持续赢利．答：该项目将从2023年开始并持续赢利；方法二：设f （x ）=﹣2x ﹣7（x ≥1），则f′（x ）=，令f'（x ）=0，得=≈=5，∴x ≈4．祝您高考马到成功！从而当x ∈[1，4）时，f'（x ）＜0，f （x ）递减；当x ∈（4，+∞）时，f'（x ）＞0，f （x ）递增．又f （1）=﹣＜0，f （7）=≈5×﹣21=﹣＜0，f （8）=﹣23≈25﹣23=2＞0．∴该项目将从第8年开始并持续赢利．答：该项目将从2023年开始并持续赢利．20．（16分）在平面直角坐标系中，已知椭圆C ：+y 2=1 （a ＞0，a ≠1）的两个焦点分别是F 1，F 2，直线l ：y=kx +m （k ，m ∈R ）与椭圆交于A ，B 两点．（1）若M 为椭圆短轴上的一个顶点，且△MF 1F 2是直角三角形，求a 的值；（2）若k=1，且△OAB 是以O 为直角顶点的直角三角形，求a 与m 满足的关系；（3）若a=2，且k OA •k OB =﹣，求证：△OAB 的面积为定值．【解答】解：（1）∵M 为椭圆短轴上的一个顶点，且△MF 1F 2是直角三角形， ∴△MF 1F 2为等腰直角三角形， ∴OF 1=OM ，当a ＞1时，=1，解得a=，当0＜a ＜1时，=a ，解得a=，（2）当k=1时，y=x +m ，设A （x 1，y 1），（x 2，y 2），由，即（1+a 2）x 2+2a 2mx +a 2m 2﹣a 2=0，∴x 1+x 2=﹣，x 1x 2=，∴y 1y 2=（x 1+m ）（x 2+m ）=x 1x 2+m （x 1+x 2）+m 2=，∵△OAB 是以O 为直角顶点的直角三角形，∴•=0，祝您高考马到成功！∴x 1x 2+y 1y 2=0， ∴+=0，∴a 2m 2﹣a 2+m 2﹣a 2=0 ∴m 2（a 2+1）=2a 2，（3）证明：当a=2时，x 2+4y 2=4，设A （x 1，y 1），（x 2，y 2）， ∵k OA •k OB =﹣， ∴•=﹣，∴x 1x 2=﹣4y 1y 2，由，整理得，（1+4k 2）x 2+8kmx +4m 2﹣4=0．∴x 1+x 2=，x 1x 2=，∴y 1y 2=（kx 1+m ）（kx 2+m ）=k 2x 1x 2+km （x 1+x 2）+m 2 =++m 2=，∴=﹣4×，∴2m 2﹣4k 2=1， ∴|AB |=•=•=2•=∵O 到直线y=kx +m 的距离d==，∴S △OAB =|AB |d==•==1祝您高考马到成功！21．（18分）若存在常数k （k ＞0），使得对定义域D 内的任意x 1，x 2（x 1≠x 2），都有|f （x 1）﹣f （x 2）|≤k |x 1﹣x 2|成立，则称函数f （x ）在其定义域 D 上是“k ﹣利普希兹条件函数”．（1）若函数f （x ）=，（1≤x ≤4）是“k ﹣利普希兹条件函数”，求常数k 的最小值；（2）判断函数f （x ）=log 2x 是否是“2﹣利普希兹条件函数”，若是，请证明，若不是，请说明理由；（3）若y=f （x ）（x ∈R ）是周期为2的“1﹣利普希兹条件函数”，证明：对任意的实数x 1，x 2，都有 |f （x 1）﹣f （x 2）|≤1．【解答】解：（1）若函数f （x ）=，（1≤x ≤4）是“k ﹣利普希兹条件函数”，则对于定义域[1，4]上任意两个x 1，x 2（x 1≠x 2），均有|f （x 1）﹣f （x 2）|≤k |x 1﹣x 2|成立，不妨设x 1＞x 2，则k ≥=恒成立．∵1≤x 2＜x 1≤4，∴＜＜，∴k 的最小值为．（2）f （x ）=log 2x 的定义域为（0，+∞），令x 1=，x 2=，则f （）﹣f （）=log 2﹣log 2=﹣1﹣（﹣2）=1，而2|x 1﹣x 2|=，∴f （x 1）﹣f （x 2）＞2|x 1﹣x 2|， ∴函数f （x ）=log 2x 不是“2﹣利普希兹条件函数”．证明：（3）设f （x ）的最大值为M ，最小值为m ，在一个周期[0，2]内f （a ）=M ，f （b ）=m ，则|f （x 1）﹣f （x 2）|≤M ﹣m=f （a ）﹣f （b ）≤|a ﹣b |．若|a ﹣b |≤1，显然有|f （x 1）﹣f （x 2）|≤|a ﹣b |≤1．若|a ﹣b |＞1，不妨设a ＞b ，则0＜b +2﹣a ＜1，祝您高考马到成功！∴|f（x1）﹣f（x2）|≤M﹣m=f（a）﹣f（b+2）≤|a﹣b﹣2|＜1．综上，|f（x1）﹣f（x2）|≤1．！功成到马考高您祝。

崇明区2020届第一次高考模拟考试数学试卷

高三数学共4页第1页崇明区2020届第一次高考模拟考试试卷数学考生注意：1．本试卷共4页，21道试题，满分150分，考试时间120分钟．2．本试卷分设试卷和答题纸．试卷包括试题与答题要求．作答必须涂（选择题）或写（非选择题）在答题纸上，在试卷上作答一律不得分．3．答卷前，务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号码等相关信息．一、填空题（本大题共有12题，满分54分，其中1～6题每题4分，7～12题每题5分）【考生应在答题纸相应编号的空格内直接填写结果．】1．已知集合0123{}A =，，，，02{|}B x x =<≤，则A B = ．2．不等式21x -<的解集是． 3．半径为1的球的表面积是．4．已知等差数列{}n a 的首项为1，公差为2，则该数列的前项和n S = ． 5．函数()f x =的反函数是．6．计算：= .7．二项式62x x ⎛⎫+ ⎪⎝⎭的展开式中常数项的值等于．8．若双曲线的一个顶点坐标为(3,0)，焦距为10，则它的标准方程是． 9．已知,a b R +∈，若直线230x y ++=与直线(1)2a x by -+=互相垂直，则ab 的最大值等于．10．已知函数()f x 是定义在R 上的周期为2的奇函数．当01x <≤时，3(1)f x x ax =-+，则实数a 的值等于．11．某组委会要从五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作，若其中甲不能从事翻译工作，乙不能从事导游工作，其余三人均能从事这四项工作，则不同的选派方案共有种．12．正方形ABCD 的边长为4，O 是正方形ABCD 的中心，过中心O 的直线l 与边AB 交于点M ，与边CD 交于点N ，P 为平面上一点，满足2(1)OP OB OC λλ=+-，则PM PN ⋅的最小值为．n 112323lim -+∞→+-n n nn n高三数学共4页第2页二、选择题（本大题共有4题，满分20分）【每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．】13．若0a b <<，则下列不等式恒成立的是A ．11a b> B ．a b ->C ．33a b <D ．22a b >14．已知z C ∈，“0z z +=”是“z 为纯虚数”的 A ．充分非必要条件 B ．必要非充要条件C ．充要条件D ．既非充分也非必要条件16．若不等式()sin 06x a b x ππ⎛⎫--+ ⎪⎝⎭≤对[1,1]x ∈-恒成立，则a b +的值等于A ．23B ．56C ．1D ．2三、解答题（本大题共有5题，满分76分）【解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤．】17．（本题满分14分，本题共有2个小题，第(1)小题满分7分，第(2)小题满分7分）在直三棱柱111ABC A B C -中，90ABC ∠=︒，1AB BC ==，12BB =．（1）求异面直线11B C 与1A C 所成角的大小；（2）求点1B 与平面1A BC 的距离．A 1B 1C 1ABC高三数学共4页第3页18．（本题满分14分，本题共有2个小题，第(1)小题满分6分，第(2)小题满分8分）已知函数21()2cos 2f x x x =--. （1）求函数()f x 的最小正周期及单调增区间；（2）设ABC △的内角,,A B C 所对的边分别为,,a b c，且c =()0f C =，若sin 2sin B A =，求,a b 的值．19．（本题满分14分，本题共有2个小题，第(1)小题满分6分，第(2)小题满分8分）某辆汽车以 x 公里/小时速度在高速公路上匀速行驶（考虑到高速公路行车安全要求60120x ≤≤）时，每小时的油耗（所需要的汽油量）为145001005x x ⎛⎫-+ ⎪⎝⎭升．（1）欲使每小时的油耗不超过9升，求 x 的取值范围；（2）求该汽车行驶100 公里的油耗y 关于汽车行驶速度 x 的函数，并求y 的最小值．高三数学共4页第4页20．（本题满分16分，本题共有3个小题，第(1)小题满分4分，第(2)小题满分6分，第(3)小题满分6分）已知椭圆22:14x y Γ+=，其左右顶点分别为A ，B ，上下顶点分别为C ，D ．圆O 是以线段AB 为直径的圆．（1）求圆O 的方程；（2）若点,E F 是椭圆上关于y 轴对称的两个不同的点，直线,CE DF 分别交x 轴于点M N 、，求证：OM ON ⋅为定值；（3）若点P 是椭圆Γ上不同于点A 的点，直线AP 与圆O 的另一个交点为Q ．是否存在点P ，使得13AP PQ =？若存在，求出点P 的坐标，若不存在，说明理由．21．（本题满分18分，本题共有3个小题，第(1)小题满分4分，第(2)小题满分6分，第(3)小题满分8分）已知无穷数列{}n a ，{}n b ，{}n c 满足：对任意的n *∈N ，都有1||||n n n a b c +=-，1||||n n n b c a +=-，1||||n n n c a b +=-．记max{||,||,||}n n n n d a b c =（{}max ,,x y z 表示3个实数,,x y z 中的最大值）．（1）若11a =，12b =，14c =，求4a ，4b ，4c 的值；（2）若11a =，12b =，求满足23d d =的1c 的所有值；（3）设1a ，1b ，1c 是非零整数，且1||a ，1||b ，1||c 互不相等，证明：存在正整数k ，使得数列{}n a ，{}n b ，{}n c 中有且只有一个数列自第k 项起各项均为0．。

2020年上海崇明县高三一模数学试卷

2020年上海崇明县高三一模数学试卷一、填空题（本大题共12小题，1~6每题4分，7~12每题5分，共54分）1.已知集合，，则．2.不等式的解集是．3.半径为的球的表面积是．4.已知等差数列的首项为，公差为，则该数列的前项和．5.函数的反函数是．6.计算：．7.二项式的展开式中常数项的值等于．8.若双曲线的一个顶点坐标为，焦距为，则它的标准方程为．9.已知、，若直线与直线互相垂直，则的最大值等于．10.已知函数是定义在上的周期为的奇函数，当时，，则实数的值等于．11.某组委会要从五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作，若其中甲不能从事翻译工作，乙不能从事导游工作，其余三人均能从事这四项工作，则不同的选派方案共有种．12.正方形的边长为，是正方形的中心，过中心的直线与边交于点，与边交于点，为平面上一点，满足，则的最小值为．二、选择题（本大题共4小题，每小题5分，共20分）13.若，则下列不等式恒成立的是（）．A.B.C.D.14.已知，“”是“为纯虚数”的（）．A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件15.如图，在底面半径和高均为的圆锥中，、是底面圆的两条互相垂直的直径，是母线的中点，已知过与的平面与圆锥侧面的交线是以为顶点的抛物线的一部分，则该抛物线的焦点到圆锥顶点的距离等于（）．A.B.C.D.16.若不等式对上恒成立，则（）．A.B.C.D.三、解答题（本大题共5小题，共76分）（1）（2）17.在直三棱柱中，，，．求异面直线与所成角的大小．求点与平面的距离．（1）（2）18.已知函数．求函数的最大值，并写出取得最大值时的自变量的集合．设的内角、、所对的边分别为、、，且，，若，求、的值．（1）（2）19.某辆汽车以公里/小时速度在高速公路上匀速行驶（考虑到高速公路行车安全要求）时，每小时的油耗（所需要的汽油量）为升．欲使每小时的油耗不超过升，求的取值范围．求该汽车行驶公里的油耗关于汽车行驶速度的函数，并求的最小值．（1）（2）20.已知椭圆，其左右顶点分别为、，上下顶点分别为、，圆是以线段为直径的圆．求圆的方程．若点、是椭圆上关于轴对称的两个不同的点，直线、分别交轴于点、，求证：为定值．【答案】解析:集合，集合，∴．故答案为：．解析:不等式等价于，解得，∴不等式的解集是．故答案为：．解析:由题意，半径为的球的表面积是．故答案为．（3）若点是椭圆上不同于点的点，直线与圆的另一个交点为，是否存在点，使得？若存在，求出点的坐标，若不存在，说明理由．（1）（2）（3）21.已知无穷数列、、满足：对任意的，都有，，，记表示个实数、、中的最大值．若，，，求﹑、的值．若，，求满足的的所有值．设、、是非零实数，且、、互不相等，证明：存在正整数，使得数列、、中有且只有一个数列自第项起各项均为．1.2.3.∵等差数列的首项为，公差为，∴该数列的前项和．故答案为：．5.解析:∵的定义域为，值域为，∴，∴函数的反函数为．综上所述，答案为．6.解析:．7.解析:二项式展开式，通项，令，则，，所以展开式中常数项值为．由题意，，，则，故双曲线的标准方程为．9.解析:直线，变形为，斜率为，∵，，直线，变形为，由直线与直线垂直，则，即，由基本不等式，则（当，时等号成立），∴的最大值为．10.解析:∵是定义在上的周期为的奇函数，∴且，∴当时，，即，则，∵当时，，∴得，故答案为．11.解析:总共有种情况，其中甲从事翻译工作有种情况，乙从事导游工作有种情况，然后甲从事翻译工作同时乙从事导游工作有种情况，∴．解析:设，由向量共线定理，可知点在直线上，为中点，∴，∵，，∴．解析:对于复数，若，不一定为纯虚数，可以为，反之，若为纯虚数，则∴“”是“为纯虚数”的必要非充分条件．故选．解析:将抛物线放入坐标系，如图所示，12.C 13.B 14.D 15.∵，，∴，设抛物线，代入点，可得，∴焦点为，即焦点为中点，设焦点为，则，，∴．故选．解析:方法一：如图，作出函数在上的图象，为使不等式对上恒成立，当且仅当函数的图象经过函数的零点，则由，得，，所以，所以．故选．方法二：令，作出函数在上的图象，B 16.（1）（2）则函数的图象必需经过，两点，则．故选．方法三：当时，，，所以，，即，所以，当时，，，所以，则或，所以，综上．故选．解析:因为，所以就是异面直线与所成的角或补角．在三角形中，，，所以，所以．所以异面直线与所成角的大小是．因为，，所以平面所以设点与平面的距离为，则，由得：．（1）．（2）．17.（1）（2）（1）（2）解析:．函数，当且仅当，时取得最大值，即，，∴的最大值为，取得最大值的取值集合为．由，得，又，所以，得，由及正弦定理，得①，由余弦定理，得②，由①，②解得，．解析:由，得，所以，又因为，所以的取值范围是．设该汽车行驶公里的油耗为升，则：，因为，所以，所以当时，该汽车行驶公里的油耗取得最小值升．（1），集合为．（2），．18.（1）．（2），的最小值．19.（1）．（2）证明见解析．20.（1）（2）（3）解析:由题意，得，，所以圆的方程是．由题意，得，，设，，，则直线的方程是：，所以，同理，因为，所以．显然直线的斜率存在，设其方程为：．代入椭圆方程，得：，设，则，所以，因为圆心到直线的距离，所以，假设存在点，使得，则，所以（*），而方程（*）在实数范围内无解，故原假设错误，即不存在点，使得．（3）不存在，证明见解析．（1），，．（2），，，．21.（1）（2）（3）解析:，，．若，，记，则，，，，，，当时，，，，，由，得，不符合；当时，，，，由，得，符合；当时，，，，由，得，符合；综上，的所有取值是，，，．先证明“存在正整数，使，，中至少有一个为”，假设对任意正整数，，，都不为，由，，是非零整数，且，，互不相等，得，，若对任意，，，都不为，则，即对任意，．当时，，，，所以，，所以，单调递减，由为有限正整数，所以，必存在正整数，使得，矛盾．（3）证明见解析．所以，存在正整数，使，，中至少有一个为．不妨设，且，，，，则，且，否则，若，因为，则必有，矛盾，于是，，，且，所以，，，，依次递推，即有：对，，，，且，此时有且仅有一个数列自第项起各项均为，综上，结论成立．。

上海市崇明区2022—2023年高三一模数学试卷

上海市崇明区2023年高三一模数学试卷一、填空题。

1.已知集合{}{}|04.1,2,3,4,5A x x B =<≤=-,则A B ⋂=2.不等式 2102x x +<-的解集为 3.已知复数2,3,z ai z i =+=+₁₂若z z ₁₂是纯虚数,则实数a = .4.已知对数函数(0,1)a y log x a a =>≠的图像经过点()4,2,则实数a = .5.设等比数列{}n a 满足12131,3a a a a +=--=-,则 4a = .6.已知方程组2168x my mx y +=⎧⎨+=⎩无解,则实数m 的值等于 .7.已知角α的终边与单位圆 221x y += 交于点 1,,2P y ⎛⎫ ⎪⎝⎭ 则sin 2πα⎛⎫+= ⎪⎝⎭8.将半径为2的半圆形纸片卷成一个无盖的圆锥筒，则该圆锥筒的高为 .9.已知函数()2f x x =, 则曲线()y f x =在点()1,1P 处的切线方程是 .10.设函数()sin (0),6f x x k πωω⎛⎫=-+> ⎪⎝⎭ 若 ()3f x f π⎛⎫≤ ⎪⎝⎭对任意的实数x 都成立，则ω的最小取值等于 .11.在边长为2的正六边形ABCDEF 中,点P 为其内部或边界上一点，则 AD BP ⋅的取值范围为 .12.已知椭圆F 1与双曲线F2的离心率互为倒数,且它们有共同的焦点F 1、F 2、P ,是F 1与F 2在第一象限的交点，当126F PF π∠=时,双曲线F 1的离心率等于 .二、选择题。

13.下列函数中，既是奇函数又在区间()0,1上是严格增函数的是( ) .A y x =3 y x =-.lg C y x = D.y sinx =14.设x R ∈,则1“2x x+>”是“1x ≠”的( ) A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件15.设函数()sin ,6f x x π⎛⎫=-⎪⎝⎭若对于任意 5,,62ππα⎡⎤∈--⎢⎥⎣⎦ 在区间[]0,m 上总存在唯一确定的β,使得()()0ff αβ+=,则m 的最小值为( ) .6A π.2B π7.6C π D.π 16.已知曲线C:()3222216x y x y += ,命题p ：曲线C 仅过一个横坐标与纵坐标都是整数的点；命题q ：曲线C 上的点到原点的最大距离是2.则下列说法正确的是( )A.p q 、都是真命题B.p 是真命题，q 是假命题C.p 是假命题，q 是真命题D.p q 、都是假命题三、解答题。

高三数学崇明一模试卷

一、选择题（每题5分，共50分）1. 若函数f(x) = ax^2 + bx + c（a≠0）的图像开口向上，且顶点坐标为（1，2），则下列结论正确的是（）A. a > 0，b > 0，c > 0B. a > 0，b < 0，c > 0C. a < 0，b > 0，c < 0D. a < 0，b < 0，c < 02. 已知数列{an}的通项公式为an = 3n - 2，则数列{an}的前n项和S_n的通项公式是（）A. S_n = (3n^2 - 2n) / 2B. S_n = (3n^2 - 2n) / 2 + nC. S_n = (3n^2 - 2n) / 2 - nD. S_n = (3n^2 - 2n) / 2 + 2n3. 在△ABC中，∠A = 60°，∠B = 45°，则sinC的值为（）A. √3 / 2B. 1 / 2C. √2 / 2D. 3 / 24. 若复数z满足|z - 1| = |z + 1|，则复数z在复平面上的轨迹是（）A. 实轴B. 虚轴C. 圆心在原点，半径为1的圆D. 圆心在(-1,0)，半径为1的圆5. 函数f(x) = |x - 1| + |x + 1|在x≤-1时的导数是（）A. -2B. 0C. 2D. 不存在6. 已知函数f(x) = x^3 - 3x + 2，则f(x)的极值点为（）A. x = -1B. x = 0C. x = 1D. x = 27. 若等差数列{an}的前n项和为S_n，公差为d，首项为a_1，则S_n的表达式为（）A. S_n = (n^2 + n) / 2 a_1B. S_n = (n^2 + n) / 2 (a_1 + a_n)C. S_n = (n^2 + n) / 2 (a_1 - a_n)D. S_n = (n^2 + n) / 2 (a_n - a_1)8. 已知等比数列{an}的公比为q，首项为a_1，若a_1 + a_2 + a_3 = 9，则q的值为（）A. 1B. 3C. -3D. -1/39. 在平面直角坐标系中，点A（2，3）关于直线y=x的对称点为B，则点B的坐标为（）A. (3, 2)B. (2, 3)C. (-3, -2)D. (-2, -3)10. 若不等式|x - 2| ≤ 3的解集为M，则M的长度为（）A. 5B. 4C. 3D. 2二、填空题（每题5分，共50分）11. 函数f(x) = (x - 1)^2 - 4在x=2时的切线斜率为______。

2024届上海市崇明区高三一模数学试卷及参考答案

共4页第1页2023学年第一学期高三第一次模拟考试数学考生注意：1．本试卷共4页，21道试题，满分150分，考试时间120分钟．2．本试卷分设试卷和答题纸．试卷包括试题与答题要求．作答必须涂（选择题）或写（非选择题）在答题纸上，在试卷上作答一律不得分．3．答卷前，务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号码等相关信息．一、填空题（本大题共有12题，满分54分，其中1～6题每题4分，7～12题每题5分）【考生应在答题纸相应编号的空格内直接填写结果．】1．不等式21x -<的解是．2．双曲线2214y x -=的焦距是．3．若复数24(2)i z m m =-++（i 为虚数单位）是纯虚数，则实数m 的值为．4．已知等比数列{}n a 首项11a =，公比2q =，则5S =．5．522x x ⎛⎫+ ⎪⎝⎭的展开式中2x 的系数为．（用数字作答）拉罐包装的饮料．在满足容积要求的情况下，饮料生产商总希望包装材料的成本最低，也就是易拉罐本身的质量最小．某数学兴趣小组对此想法通过数学建模进行验证．为了建立数学模型，他们提出以下3个假设：（1）易拉罐容积相同；（2）易拉罐是一个上下封闭的空心圆柱体；（3）易拉罐的罐顶、罐体和罐底的厚度和材质都相同．你认为以此3个假设所建立的数学模型与实际情况相符吗？若相符，请在以下横线上填写“相符”；若不相符，请选择其中的一个假设给出你的修改意见，并将修改意见填入横线．．11．已知不平行的两个向量,a b 满足1a = ，a b ⋅=．若对任意的t ∈R ，都有2b ta - ≥成立，则b 的最小值等于．共4页第2页12．已知正实数,,,a b c d 满足210a ab -+=，221c d +=，则当22()()a c b d -+-取得最小值时，ab =．二、选择题（本大题共有4题，满分18分，其中13～14题每题4分，15～16题每题5分）【每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得满分，否则一律得零分．】13．已知集合{}23A x x =-≤≤，{}0B x x =>，则A B = （）A ．[]2,3-B ．[]0,3C ．(0,)+∞D ．[)2,-+∞11111q ：过点M 有且只有一个平面与1AA 和11B C 都平行；2q ：过点M 至少可以作两条直线与1AA 和11B C 所在的直线都相交．则以下说法正确的是A ．命题1q 是真命题，命题2q 是假命题B ．命题1q 是假命题，命题2q 是真命题C ．命题1q ，2q都是真命题D ．命题1q ，2q 都是假命题16．若存在实数,a b ，对任意实数[0,1]x ∈，使得不等式33x m ax b x m -++≤≤恒成立，则实数m 的取值范围是（）A．⎫+∞⎪⎪⎣⎭B．⎫+∞⎪⎪⎣⎭C ．⎫+∞⎪⎪⎣⎭D ．⎫+∞⎪⎪⎣⎭三、解答题（本大题共有5题，满分78分）【解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤．】17．（本题满分14分，本题共有2个小题，第(1)小题满分7分，第(2)小题满分7分）如图，四棱锥P ABCD -中，PA ⊥平面ABCD，AB CD ∥，2PA AB AD ===，1CD =，90ADC ∠=︒，E 、F 分别为PB 、AB 的中点．（1）求证：CE ∥平面PAD ；（2）求点B 到平面PCF 的距离．共4页第3页18．（本题满分14分，本题共有2个小题，第(1)小题满分6分，第(2)小题满分8分）在ABC △中，5a =，6b =．（1）若4cos 5B =-，求A 和ABC △外接圆半径R 的值；（2）若ABC △的面积S =c 的值．19．（本题满分14分，本题共有3个小题，第(1)小题满分6分，第(2)小题满分8分）某市2023年元旦及前后共7天与2022年同期的交通高峰期城市道路TPI 的统计数据如下图：（1）从2022年元旦及前后共7天中任取1天，求这一天交通高峰期城市道路拥堵程度为“拥堵”的概率；（2）从2023年元旦及前后共7天中任取3天，将这3天中交通高峰期城市道路TPI 比2022年同日TPI 高的天数记为X ，求所有X 的可能值及其发生的概率．共4页第4页20．（本题满分18分，本题共有3个小题，第(1)小题满分4分，第(2)小题满分6分，第(3)小题满分8分）已知抛物线21:4y x Γ=，22:2y x Γ=，直线l 交抛物线1Γ于点A 、D ，交抛物线2Γ于点B 、C ，其中点A 、B 位于第一象限．（1）若点A 到抛物线1Γ焦点的距离为2，求点A 的坐标；（2）若点A 的坐标为(4,4)，且线段AC 的中点在x 轴上，求原点O 到直线l 的距离；（3）若2AB CD =，求AOD △与BOC △的面积之比．21．（本题满分18分，本题共有3个小题，第(1)小题满分4分，第(2)小题满分6分，第(3)小题满分8分）已知()sin (R 0)f x mx x m m =+∈≠且．（1）若函数()y f x =是实数集R 上的增函数，求实数m 的取值范围；（2）已知数列{}n a 是等差数列（公差0d ≠），()n n b f a =．是否存在数列{}n a 使得数列{}n b 是等差数列？若存在，请写出一个满足条件的数列{}n a ，并证明此时的数列{}n b 是等差数列；若不存在，请说明理由；（3）若1m =，是否存在直线y kx b =+满足：①对任意的x ∈R 都有()f x kx b +≥成立，②存在0x ∈R 使得00()f x kx b =+？若存在，请求出满足条件的直线方程；若不存在，请说明理由．共4页第5页崇明区2023学年第一学期高三第一次模拟考试参考答案及评分标准一、填空题1.（1，3）；2. 3.2；4.31；5.10；6.；7.3；8.9；9.0.42；10.假设2中，易拉罐的顶部类似于圆台；假设3中，易拉罐的罐顶和罐底材质比罐体的材质厚；11.；12.212+.二、选择题13.D ；14.C ；15.A ；16. A.三、解答题17.解（1）证明：取PA 中点G ，连接GE 、GD ，则//GE AB ，12GE AB =，由于//CD AB ，12CD AB =，所以//GE CD ，GE CD =，所以四边形CDGE 是平行四边形，所以//CE GD ，......................................4分由于CE 不在平面PAD 上，DG ⊂平面PAD ，所以CE //平面PAD ；.....................................................................................7分（2）设点B 到平面PCF 的距离为h ，由题意，CF AB ⊥，又PA ⊥平面ABCD ，所以CF PF⊥在RT PAF △中，PF =，所以12PFC S CF PF =⋅=△分由P BCF B PCF V V --=得1133BCF PCF S PA S h⋅=⋅△△所以255h =，即点B 到平面PCF 的距离为255.......................................7分18.解（1）因为4cos 5B =-，()0,B π∈，所以3sin 5B ==...........2分由正弦定理，得2sin sin a b R A B ==，即5623sin 5R A ==，....................................4分所以1sin 2A =，5R =，因为a b <，所以0,2A π⎛⎫∈ ⎪⎝⎭，因此6A π=，5R =..................................................6分（2）由1sin 2ABC S ab C =△得1572274sin 564ABC S C ab ⨯===⨯△，....................2分于是3cos 4C ==±.....................4分当3cos 4C =时，由余弦定理，得222356256164c =+-⨯⨯⨯=.....................6分共4页第6页当3cos 4C =-时，由余弦定理，得2223562561064c ⎛⎫=+-⨯⨯⨯-= ⎪⎝⎭.日TPI 高的天数共有2天，故0,1,2X =.....................2分()3537C 1020C 357P X ====；()215237C C 2041C 357P X ⋅====；()125237C C 512C 357P X ⋅====...........................................................................................8分20.解（1）抛物线24y x =的准线为1x =-，因为点A 到抛物线1Γ焦点的距离为2，所以点A 到抛物线1Γ准线的距离为2，所以点A 的横坐标为1，故点A 的坐标为(1,2).....................4分（2）设00(,)C x y ，则线段AC 的中点坐标为0044(,22x y ++由题意，402y +=，故04y =-，所以(8,4)C -.....................2分所以直线l 的方程为：2120x y +-=.....................4分所以原点O 到直线l 的距离5d ==.....................6分（3）由题意，直线l 的斜率k 显然存在且0k ≠，设直线l 的方程为y kx b =+设11223344(,),(,),(,),(,)A x y D x yB x yC x y 由2AB CD =，得31242()y y y y -=-①，.....................2分由24y x y kx b ⎧=⎨=+⎩，得：204k y y b -+=，所以124y y k +=，124b y y k =同理，342y y k +=，342by y k=.....................4分所以12342()y y y y +=+②，12342y y y y =③由①，②得：23y y =-，代入③得142y y =-，代入②得2434y y =所以4412344442103473AOD BOCy y S y y S y y y y ---===---△△...............................................................8分共4页第7页21.解（1）因为函数()y f x =是实数集R 上的增函数，所以'()cos 0f x m x =+≥对任意的x ∈R 都成立.............................2分因为函数cos y m x =+的最小值为1m -，所以1m ≥.....................4分（2）sin n n n b a ma =+，若{}n b 是等差数列，则212n n n b b b +++=对一切正整数n 成立，即2211sin sin 2sin 2n n n n n n a ma a ma a ma +++++++=+，将212n n n a a a +++=代入化简得21sin sin 2sin n n n a a a +++=，即()()111sin sin 2sin n n n a d a d a +++-++=，展开化简得()12sin cos 10n a d +⋅-=对一切正整数n 成立，所以1sin 0n a +=或cos 1d =，故1n a n π+=或()20,d k k k π=≠∈Z ；......................................................3分注：这里只要给出合适的一个等差数列即可得分当()20,d k k k π=≠∈Z 时，()()11sin sin 1212n n n b a ma a n k m a n k ππ=+=+-++-⎡⎤⎡⎤⎣⎦⎣⎦()1112sin m n k ma a π=-++，所以12n n b b m k π+-=为常数，故{}n b 是等差数列......................................................................6分同理，当n a n π=时，亦可证明数列{}n b 为等差数列.（3）令()(sin )()(1)sin g x x x kx b k x x b=+-+=-+-则当m Z ∈时，(2)2(1)sin 11b bg m k m k kππ+=-+--1k >时，存在m Z ∈使得(2)01bg m kπ+<-，即存在x R ∈使得()f x kx b <+，与题意不符同理，1k <时，存在x R ∈使得()f x kx b <+，与题意不符.......................4分1k =时，()sin g x x b=-当1b >-时，显然存在存在x R ∈使得()0g x <，即存在存在x R ∈使得()f x kx b <+当1b <-时，对任意的x R ∈都有()0g x >，..................................6分当1b =时，存在02x π=-，使得00()=f x kx b +，且对任意的x R ∈都有()0g x ≥，即对任意的x R ∈都有()f x kx b≥+综上，存在直线1y x =-满足题意..................................8分。

2020届上海市崇明区高三上学期期末(一模)数学试题(解析版)

2020届上海市崇明区高三上学期期末（一模）数学试题一、单选题1．若0a b <<,则下列不等式恒成立的是 A ．11a b> B ．a b -> C ．22a b > D ．33a b <【答案】D【解析】∵0a b << ∴设1,1a b =-= 代入可知,,A B C 均不正确对于D ，根据幂函数的性质即可判断正确故选D2．“2p <”是“关于x 的实系数方程210x px ++=有虚数根”的（） A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件【答案】B【解析】先求出关于x 的实系数方程210x px ++=有虚数根的充要条件为：240p =-<，即22p -<<，再由“2p <”与“22p -<<”的关系得解。

【详解】解：关于x 的实系数方程210x px ++=有虚数根的充要条件为：240p =-<，即22p -<<，又“2p <”不能推出“22p -<<”， “22p -<<”能推出“2p <”，即“2p <”是“关于x 的实系数方程210x px ++=有虚数根”的必要不充分条件，故选：B ．【点睛】本题考查了充分条件、必要条件、充要条件及简易逻辑知识，属简单题3．已知向量a 、b 、c 满足0a b c ++=，且222a b c <<，则a b ⋅、b c ⋅、a c ⋅中最小的值是（） A.a b ⋅ B.b c ⋅ C.a c ⋅D.不能确定【答案】B【解析】利用已知条件作差比较可知. 【详解】因为0a b c ++=, 所以()b a c =-+rr r,所以()a b b c b a c ⋅-⋅=⋅-22()()()a c a c a c =-+-=--0>,所以a b b c ⋅>⋅, 同理可得,a c b c ⋅>⋅, 故b c ⋅最小. 故选B . 【点睛】本题考查了平面向量的数量积和比较法比较大小,属于中档题.4．函数()f x x =，()22.g x x x =-+若存在1x ，2x ，⋯，90,2n x ⎡⎤∈⎢⎥⎣⎦，使得()()()()()()()()121121n n n n f x f x f x g x g x g x g x f x --++⋯++=++⋯++，则n的最大值是（） A.11 B.13 C.14 D.18【答案】C【解析】由已知得(22221212(1)[(1)(1)1)n n n x x x x -⎤-=---+-+⋯+-⎦，又1x ，2x ，⋯，90,2n x ⎡⎤∈⎢⎥⎣⎦，可求n 的最大值．【详解】解：()()()()21211212n n n n n f x f x f x g x x x x x x --++⋯++=++⋯++-+，()()()()()()22212112112121n n n n ng x g x g x f x x x x x x x n x ---++⋯++=++⋯+-++⋯++-+，()2222121(1)(1)(1)2(1)n n x x x n x -∴-+-+⋯+-+-=-，(22221212(1)[(1)(1)1)n n n x x x x -⎤∴-=---+-+⋯+-⎦当1211n x x x -==⋯==，92n x =时，2949(2)(1)24max n -=-=， 4924n ∴-≤，又n N ∈，14max n ∴=．故选：C ．【点睛】本题考查参数的最值，配方是关键，考查推理能力和计算能力，属中档题二、填空题5．20lim 31n n n →∞+=+______．【答案】13【解析】将分式2031n n ++ 分子、分母同时除以n ，再利用201lim 0,lim 0n n n n →∞→∞==，可求解．【详解】解：202011lim20101limlim 113130333limn n n n n n n n nn →∞→∞→∞→∞++++====++++ 故答案为：13．【点睛】本题考查了极限的运算，属简单题．6．已知集合{|12}A x x =-<<，{}1,0,1,2,3B =-，则A B =______．【答案】{}0,1【解析】直接利用交集运算得答案．【详解】解：{}0,1A B ⋂=．故答案为：{}0,1．【点睛】本题考查了交集及其运算，是基础题．7．若复数z 满足232z z i +=-，其中i 为虚数单位，则z =______．【答案】12i -【解析】设复数z a bi =+，(a 、b 是实数)，则z a bi =-，代入已知等式，再根据复数相等的含义可得a 、b 的值，从而得到复数z 的值．【详解】解：设z a bi =+，(a 、b 是实数)，则z a bi =-，232z z i +=-，2232a bi a bi i ∴++-=-， 33a ∴=，2b =-，解得1a =，2b =-，则12z i =- 故答案为：12i -．【点睛】本题着重考查了复数的四则运算和复数相等的含义，属于基础题． 8．281()x x-的展开式中x 7的系数为__________.（用数字作答）【答案】56-【解析】试题分析：展开式通项为281631881()()(1)rrr r r r r T C x C x x--+=-=-，令1637r -=，得3r =，所以展开式中7x 的系数为．故答案为56-．【考点】二项式定理【名师点睛】①求特定项系数问题可以分两步完成：第一步是根据所给出的条件（特定项）和通项公式，建立方程来确定指数（求解时要注意二项式系数中n 和r 的隐含条件，即n ，r 均为非负整数，且n≥r ）；第二步是根据所求的指数，再求所要求的项． ②有理项是字母指数为整数的项．解此类问题必须合并通项公式中同一字母的指数，根据具体要求，令其为整数，再根据数的整除性来求解．9．角θ的终边经过点()4,P y ，且3sin 5θ=-，则tan θ=______．【答案】34-【解析】由题意利用任意角的三角函数的定义，求得tan θ的值．【详解】解：角θ的终边经过点()4,P y ，且3sin 5θ=-=，3y ∴=-，则3tan 44y θ==-，故答案为：34-．【点睛】本题主要考查任意角的三角函数的定义，属于基础题．10．在平面直角坐标系xOy 中，已知抛物线24y x =上一点P 到焦点的距离为5，则点P 的横坐标是______．【答案】4【解析】由抛物线定义可知，抛物线上任一点到焦点的距离与到准线的距离是相等的，已知5PF =，则P 到准线的距离也为5，即15x +=，即可求出x ．【详解】解：抛物线242y x px ==，2p ∴=，由抛物线定义可知，抛物线上任一点到焦点的距离与到准线的距离是相等的，15PF x ∴=+=， 4x ∴=，故答案为：4．【点睛】考查了抛物线的定义、焦半径到焦点的距离常转化为到准线的距离求解，属于基础题. 11．圆22240x y x y +-+=的圆心到直线3450x y ++=的距离等于______．【答案】0【解析】先求圆的圆心坐标，利用点到直线的距离公式，求解即可．【详解】解：由已知得圆心为：()1,2P -，由点到直线距离公式得：0d ==，故答案为：0．【点睛】本题以圆为载体考查点到直线的距离公式，考查学生计算能力，是基础题． 12．已知一圆锥的侧面展开图是半径为2的半圆，则该圆锥的体积为 .【答案】π33 【解析】试题分析：设圆锥的底面半径为r ，22⨯=ππr ，解得1=r ，根据勾股定理，圆锥的高等于31222=-，所以圆锥的体积ππ3331312=⨯⨯⨯=V . 【考点】旋转体的体积 13．若函数()2log 1x af x x -=+的反函数的图象过点()3,7-，则a =______．【答案】6【解析】()f x 的反函数图象过点()3,7-，所以原函数()f x 的图象过()7,3-，然后将点()7,3-代入()f x 可解得．【详解】解：()f x 的反函数图象过点()3,7-，所以原函数()f x 的图象过()7,3-，()73f ∴=-，即27log 371a -=-+，3728a--∴=，6a ∴=．故答案为：6 【点睛】本题考查了反函数,属基础题．14．2018年上海春季高考有23所高校招生，如果某3位同学恰好被其中2所高校录取，那么不同的录取方法有______种. 【答案】1518【解析】解决这个问题得分三步完成，第一步把三个学生分成两组，第二步从23所学校中取两个学校，第三步，把学生分到两个学校中，再用乘法原理求解【详解】解：由题意知本题是一个分步计数问题，解决这个问题得分三步完成，第一步把三个学生分成两组，第二步从23所学校中取两个学校，第三步，把学生分到两个学校中，共有12232231518C C A =，故答案为：1518．【点睛】本题考查分步计数问题，本题解题的关键是把完成题目分成三步，看清每一步所包含的结果数，本题是一个基础题．15．设()f x 是定义在R 上的以2为周期的偶函数，在区间[]0,1上单调递减，且满足()1f π=，()22f π=，则不等式组()1212x f x ≤≤⎧≤≤⎨⎩的解集为______．【答案】[]2,82ππ--【解析】根据()f x 是以2为周期的偶函数，并且在[]0,1上单调递减，便可由()1f π=，()22f π=得出()41f π-=，()262f π-=，并且由12x ≤≤得出021x ≤-≤，从而由()12f x ≤≤得出()()()4226f f x f ππ-≤-≤-，进而得出{122624x x ππ≤≤-≤-≤-，解该不等式组即可．【详解】解：()f x 是以2为周期的偶函数，且()f x 在[]0,1上单调递减；∴由()1f π=，()22f π=得，()41f π-=，()262f π-=，且4π-，[]260,1π-∈；由12x ≤≤得，021x ≤-≤；∴由()1212x f x ≤≤⎧≤≤⎨⎩得，()()()124226x f f x f ππ≤≤⎧-≤-≤-⎨⎩；{122624x x ππ≤≤∴-≤-≤-；解得282x ππ-≤≤-；∴原不等式组的解集为[]2,82ππ--．故答案为：[]2,82ππ--．【点睛】考查周期函数和偶函数的定义，以及减函数的定义，不等式的性质．16．已知数列{}n a 满足：①10a =，②对任意的*n N ∈都有1n n a a +>成立．函数()1()sinn n f x x a n=-，[]1,n n x a a +∈满足：对于任意的实数[)0,1m ∈，()n f x m =总有两个不同的根，则{}n a 的通项公式是______．【答案】()12n n n a π-=【解析】利用三角函数的图象与性质、诱导公式、数列的递推关系可得1n n a a n π+-=，再利用“累加求和”方法、等差数列的求和公式即可得出．【详解】解：10a =，当1n =时，()()11sin sin f x x a x =-=，[]20,x a ∈，又对任意的[)0,1m ∈，()1f x m =总有两个不同的根，2a π∴=，()1sin f x x ∴=，[]0,x π∈，2a π=，又()()()2211sinsin cos 222xf x x a x π=-=-=，[]3,x a π∈，对任意的[)0,1m ∈，()1f x m =总有两个不同的根，33a π∴=，又()()()33111sinsin 3sin 333f x x a x ππ=-=-=，[]43,x a π∈，对任意的[)0,1b ∈，()1f x m =总有两个不同的根，46a π∴=，由此可得1n n a a n π+-=，()()()()12111012n n n n n a a a a a a n πππ--∴=+-+⋯+-=++⋯+-=，故答案为：()12n n n a π-=，【点睛】本题考查了三角函数的图象与性质、诱导公式、数列的递推关系、“累加求和”方法、等差数列的求和公式，考查了推理能力与计算能力，属于中档题三、解答题17．如图，设长方体1111ABCD A B C D -中，2AB BC ==，直线1A C 与平面ABCD 所成角为4π．()1求三棱锥1A A BD -的体积；()2求异面直线1A B 与1B C 所成角的大小．【答案】（1）3（2）2arccos 3．【解析】()1转换顶点，以1A 为顶点，易求体积；()12B C 平移至1A D ，化异面直线为共面直线，利用余弦定理求解．【详解】解：()1连接AC ，则1A CA ∠为1A C 与平面ABCD 所成的角，14ACA π∴∠=，2AB BC ==，AC ∴=，1AA ∴=11A A BD A ABD V V --∴=11132AB AD AA =⨯⨯⨯3=()2连接1A D ，易知11//A D B C ，1(BA D ∴∠或其补角)即为所求，连接BD ，在1A DB 中，1A D =，1A B =BD =，由余弦定理得：12cos 3BA D ∠==，12arccos 3BA D ∠=，故异面直线1A B ，1B C 所成角的大小为2arccos 3．【点睛】此题考查了三棱锥体积，异面直线所成角的求法等，难度不大．18．已知函数2()cos sin f x x x x =⋅ ()1求函数()f x 的单调递增区间；()2在锐角ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，若1()2f A =，3a =， 4.b =求ABC △的面积．【答案】（1）5,1212k k ππππ⎡⎤-+⎢⎥⎣⎦；k Z ∈；（2）4+【解析】()1利用二倍角，辅助角公式化简，结合三角函数的单调性即可求解()f x 的单调递增区间；()2根据()12f A =，求解A ，3a =， 4.b =利用余弦定理求解c ，即可求解ABC△的面积．【详解】解：()1函数()21cos sin sin2sin 223f x x x x x x x π⎛⎫=⋅+==+ ⎪⎝⎭令222232k x k πππππ-≤+≤+，得51212k x k ππππ-≤≤+， ()f x ∴的单调递增区间为5,1212k k ππππ⎡⎤-+⎢⎥⎣⎦；k Z ∈； ()2由()12f A =，即1sin 232A π⎛⎫+= ⎪⎝⎭，ABC △是锐角三角形，5236A ππ∴+= 可得4A π=余弦定理：22222243cos 2242b c a c A bc c +-+-===⨯⨯，即270(0)c c -+=>解得：1c =ABC △的面积1sin 42S bc A ==【点睛】本题主要考查三角函数的图象和性质，余弦定理的应用，利用三角函数公式将函数进行化简是解决本题的关键．19．某创业投资公司拟投资开发某种新能源产品，估计能获得25万元~ 1600万元的投资收益，现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加，奖金不超过75万元，同时奖金不超过投资收益的20%．(即:设奖励方案函数模型为y=f (x)时，则公司对函数模型的基本要求是:当x ∈[25，1600]时，①f(x)是增函数;②f (x) ≤75恒成立; ③()5xf x ≤恒成立． (1)判断函数() 1030x f x =+是否符合公司奖励方案函数模型的要求，并说明理由;(2)已知函数()()51g x a =≥符合公司奖励方案函数模型要求，求实数a 的取值范围．【答案】(1) 函数模型()1030xf x =+，不符合公司要求,详见解析(2) [1，2] 【解析】（1）依次验证题干中的条件即可；（2）根据题干得，要满足三个条件，根据三个条件分别列出式子得到a 的范围，取交集即可. 【详解】(1)对于函数模型()1030xf x =+, 当x ∈[25, 1600]时， f (x)是单调递增函数，则f (x) ≤f (1600) ≤75,显然恒成立，若函数()5x f x ≤恒成立，即10305x x +≤,解得x≥60．∴()5xf x ≤不恒成立，综上所述，函数模型()1030xf x =+，满足基本要求①②，但是不满足③，故函数模型()1030xf x =+，不符合公司要求．(2)当x ∈[25，1600]时，()5(1)g x a =≥单调递增，∴最大值(1600)540575g a ==-≤∴2a ≤设()55x g x =≤恒成立，∴22(5)5x a x ≤+恒成立，即225225x a x ≤++, ∵25225xx +≥，当且仅当x=25时取等号，∴a 2≤2+2=4 ∵a ≥1, ∴1≤a ≤2, 故a 的取值范围为[1，2] 【点睛】这个题目考查了函数模型的应用，这类题目关键是选对函数模型，读懂题意，将实际问题转化为数学问题，利用数学知识解决问题.20．已知椭圆Γ：22221(0)x y a b a b +=>>，1B ，2B 分别是椭圆短轴的上下两个端点，1F 是椭圆的左焦点，P 是椭圆上异于点1B ，2B 的点，若112B F B 的边长为4的等边三角形．()1写出椭圆的标准方程；()2当直线1PB 的一个方向向量是()1,1时，求以1PB 为直径的圆的标准方程； ()3设点R 满足：11RB PB ⊥，22RB PB ⊥，求证：12PB B 与12RB B 的面积之比为定值．【答案】（1）221164x y +=；（2）2282128()()5525x y ++-=；（3）证明见解析【解析】()1由112B F B 是边长为4的等边三角形得4a =，进一步求得2b =，则椭圆方程可求；()2由直线1PB 的一个方向向量是()1,1，可得直线1PB 所在直线的斜率1k =，得到直线1PB 的方程，由椭圆方程联立，求得P 点坐标，得到1PB 的中点坐标，再求出1PB ，可得以1PB 为直径的圆的半径，则以1PB 为直径的圆的标准方程可求；() 3方法一、设()00,P x y ，()11,R x y 求出直线1PB 的斜率，进一步得到直线1RB 的斜率，得到直线1RB 的方程，同理求得直线2RB 的方程，联立两直线方程求得R 的横坐标，再结合()00,P x y 在椭圆221164x y +=上可得1x 与0x 的关系，由12121PB B RB B S x S x =求解；方法二、设直线1PB ，2PB 的斜率为k ，得直线1PB 的方程为 2.y kx =+结合11RB PB ⊥，可得直线1RB 的方程为12y x k=-+，把2y kx =+与椭圆方程联立可得021641k x k -=+，再由()00,P x y 在椭圆221164x y +=上，得到220044x y -=-，从而得到200020002241'4y y y k k x x x -+-⋅=⋅==-，得1'.4k k=-结合22RB PB ⊥，可得直线2RB 的方程为4 2.y kx =-与线1RB 的方程联立求得124.41kx k =+再由12121PB B RB B S x S x =求解．【详解】()1解：如图，由112B F B 的边长为4的等边三角形，得4a =，且2b =．∴椭圆的标准方程为221164x y +=； ()2解：直线1PB 的一个方向向量是()1,1，∴直线1PB 所在直线的斜率1k =，则直线1PB 的方程为2y x =+，联立2221164y x x y =+⎧⎪⎨+=⎪⎩，得25160x x +=，解得165P x =-，65P y ∴=-．则1PB 的中点坐标为82,55⎛⎫-⎪⎝⎭，1PB == 则以1PB为直径的圆的半径5r =． ∴以1PB 为直径的圆的标准方程为2282128()()5525x y ++-=；()3证明：方法一、设()00,P x y ，()11,.R x y直线1PB 的斜率为1002PB y k x -=，由11RB PB ⊥，得直线1RB 的斜率为1002RB x k y =-．于是直线1RB 的方程为：0022x y x y =-+-．同理，2RB 的方程为：0022x y x y =--+．联立两直线方程，消去y ，得20104y x x -=．()00,P x y 在椭圆221164x y +=上，22001164x y ∴+=，从而220044x y -=-．14x x ∴=-， 121214PB B RB B S x Sx ∴==．方法二、设直线1PB ，2PB 的斜率为k ，，则直线1PB 的方程为2y kx =+．由11RB PB ⊥，直线1RB 的方程为12y x k=-+，将2y kx =+代入221164x y +=，得()2241160k x kx ++=，P 是椭圆上异于点1B ，2B 的点，00x ∴≠，从而021641kx k -=+． ()00,P x y 在椭圆221164x y +=上，22001164x y ∴+=，从而220044x y -=-．200020002241'4y y y k k x x x -+-∴⋅=⋅==-，得1'4k k=-． 22RB PB ⊥，∴直线2RB 的方程为42y kx =-．联立1242y x k y kx ⎧=-+⎪⎨⎪=-⎩，解得2441k x k =+，即12441k x k =+． 1212201216414441PB B RB B kS x k k Sx k -+∴===+．【点睛】本题考查椭圆方程的求法，考查直线与椭圆的位置关系的综合应用，考查转化思想以及计算能力，是中档题．21．已知数列{}n a ，{}n b 均为各项都不相等的数列，n S 为{}n a 的前n 项和，()*11n n n a b S n N +=+∈．()1若11,2n n a b ==，求4a 的值；()2若{}n a 是公比为()1q q ≠的等比数列，求证：数列11n b q ⎧⎫+⎨⎬-⎩⎭为等比数列；()3若{}n a 的各项都不为零，{}n b 是公差为d 的等差数列，求证：2a ，3a ，⋯，n a ，⋯成等差数列的充要条件是12d =．【答案】（1）8；（2）证明见解析（3）证明见解析【解析】()1直接代入计算即可；()2通过设()111n n a a q q -=≠，利用等比数列的求和公式及11n n n a b S +=+，计算可知n b ，进而化简即得结论；()3通过数列{}n b 是公差为d 的等差数列，对()1n n n n n a b a b d a +--=变形可知111111n n n n n n n n a a b b da a a a d d--+---==----，然后分别证明充分性、必要性即可．【详解】解：()111n n n a b S +=+，11a =，2n n b =， 121111412a a b ++∴===，146132+++ 232114161S a b +++===， 34311461832S a b ++++===，证明：()2设()111n n a a qq -=≠，则()111nn a q S q-=-，11n n n a b S +=+，()()111111111111nn n n nnn a q S a a q q q b a a q q a q +-++-+--∴===-， ()()1111111111111n n n n a a q q a q b q q a q q q a q -+-+-∴+=+=----()11111111n n a q b q q a q +++-∴+=-- 1n nb q b +∴=，(q 为常数) ∴数列11n b q ⎧⎫+⎨⎬-⎩⎭为等比数列， ()3数列{}n b 是公差为d 的等差数列，∴当2n ≥时，()1n n n n n a b a b d a +--=，即()()11n n n n a a b d a +-=-，数列{}n a 的各项都不为零，10n n a a +∴-≠，10d -≠， ∴当2n ≥时，11n nn nb a d a a +=--，当3n ≥时，1111n n n n b a d a a ---=--，两式相减得：当3n ≥时，111111n n n n n n n n a a b b da a a a d d--+---==----．先证充分性：由12d =可知1111n n n n n n a a a a a a -+--=--， ∴当3n ≥时，1111n nn n n na a a a a a --++=--，又0n a ≠，11n n n n a a a a +-∴-=-，即2a ，3a ，⋯，n a ⋯成等差数列；再证必要性：2a ，3a ，⋯，n a ⋯成等差数列， ∴当3n ≥时，11n n n n a a a a +--=-，111111111n n n n n n n n n n n n a a a a d a a a a a a a a d---+---∴-=-==-----，12d ∴=．综上所述，2a ，3a ，⋯，n a ⋯成等差数列的充要条件是12d = 【点睛】本题考查数列的递推式，考查运算求解能力，对表达式的灵活变形是解决本题的关键，注意解题方法的积累，属于难题．。

上海市崇明区2024届高三一模数学试题

一、单选题二、多选题1. 已知函数及其导函数的定义域均为，且，则（）A ．有一个极小值点，一个极大值点B ．有两个极小值点，一个极大值点C ．最多有一个极小值点，无极大值点D ．最多有一个极大值点，无极小值点2.如图，在正方体中，，，分别是，，的中点，有下列四个结论：①与是异面直线；②，，相交于一点；③；④平面．其中所有正确结论的编号是（）A ．①④B ．②④C ．①④D ．②③④3.已知函数，那么（）A ．20B ．12C ．3D ．14. 声音中包含着正弦函数，声音是由于物体的振动产生的能引起听觉的波.每一个音都是由纯音合成的，纯音的数学模型是函数.音有四要素：音调，响度，音长和音色.这都与正弦函数的参数有关.我们一般听到的声音的函数是，对于函数，下列说法正确的是（）A ．是的一个周期B ．关于对称C．是的一个极值点D．关于中心对称5.在等腰直角中，，在边上且满足:,若，则的值为A．B．C．D．6. 已知，，，则，，的大小关系为（）A．B．C．D．7. 化简的值为（）A ．1B ．2C ．4D ．68.，的否定为（）A ．，B ．，C ．，D ．，9. 为了解目前宜兴市高二学生身体素质状况，对某校高二学生进行了体能抽测，得到学生的体育成绩，其中60分及以上为及格，90分及以上为优秀则下列说法正确的是（）参考数据：随机变量，则，，．A ．该校学生体育成绩的方差为10B ．该校学生体育成绩的期望为70C．该校学生体育成绩的及格率不到上海市崇明区2024届高三一模数学试题上海市崇明区2024届高三一模数学试题三、填空题四、解答题D ．该校学生体育成绩不及格的人数和优秀的人数相当10.若函数的定义域为，且，，则（）A．B．为偶函数C．的图象关于点对称D．11. 已知随机变量服从正态分布，则下列结论正确的是（）A ．，B ．若，则C．D ．随机变量满足，则12. “圆幂定理”是平面几何中关于圆的一个重要定理，它包含三个结论，其中一个是相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等.如图，已知圆O 的半径为2，点P 是圆O 内的定点，且，弦AC ､BD 均过点P ，则下列说法正确的是（）A．B ．为定值C．的取值范围是[-2，0]D ．当时，为定值13. 如图，菱形架ABCD 是一种作图工具，由四根长度均为4的直杆用铰链首尾连接而成.已知A ，C 可在带滑槽的直杆上滑动；另一根带滑槽的直杆DH 长度为4，且一端记为H ，另一端用铰链连接在D 处，上述两根带滑槽直杆的交点P 处有一栓子（可在带滑槽的直杆上滑动）.若将H ，B 固定在桌面上，且两点之间距离为2，转动杆HD ，则点P 到点B 距离的最大值为__________.14. 已知展开式中，所有项的二项式系数之和为，则______________．（用数字作答）15. 如图，四面体OABC 的三条棱OA ，OB ，OC 两两垂直，OA=OB=2，OC=3，D 为四面体OABC 外一点．给出下列命题．①不存在点D ，使四面体ABCD 有三个面是直角三角形②不存在点D ，使四面体ABCD 是正三棱锥③存在点D ，使CD 与AB 垂直并且相等④存在无数个点D ，使点O 在四面体ABCD 的外接球面上其中真命题的序号是______________16. 如图，在四棱锥中，底面，四边形为长方形，，点、分别是线段、的中点．（1）证明：平面；（2）在线段上是否存在一点，使得平面，若存在，请指出点的位置，并证明平面；若不存在，请说明理由．17. 安徽新高考改革方案正式公布，根据改革方案，计入高考总分的考试科目共有6门，即“3＋1＋2”，“3”为语文、数学、外语3门全国统一考试科目，不分文理科，使用全国卷，选择性考试科目为思想政治、历史、地理、物理、化学、生物学6门．由考生根据报考高校要求，结合自身特长兴趣，首先在物理和历史中选择1门，再从思想政治、地理、化学、生物学中选择2门．(1)若某学生根据方案从选择性考试科目中随机选择三科，求该生恰好选到政史地的概率；(2)由于物理和历史两科必须选择1科，某校想了解学生选科的需求，随机选取100名学生进行调查，得到如下统计数据，判断是否有99%的把握认为“选科与性别有关”？选择物理选择历史合计男401050女302050合计7030100附表：0.1500.1000.0500.0250.0102.0722.7063.8415.0246.635，．18. 已知函数.（I ）若曲线在上单调递增，求a 的取值范围；（II ）若在区间上存在极大值M ，证明：.19.在三棱锥中，是的中点，，.（1）证明：平面；（2）若，求点到平面的距离.20. 如图,在四棱锥中，平面平面，，，，，点在棱上，且.（Ⅰ）求证：；（Ⅱ）是否存在实数，使得二面角的余弦值为？若存在，求出实数的值；若不存在，请说明理由.21. 已知函数在处的切线方程为(1)求a，b的值；(2)判断的单调性.。

崇明高三数学一摸试卷答案

一、选择题1. 答案：C解析：根据函数的周期性，可以得出函数的最小正周期为2π，因此选项C正确。

2. 答案：A解析：由题意可知，直线与x轴、y轴的交点坐标分别为（-2，0）和（0，3），因此直线方程为3x-2y=0，所以选项A正确。

3. 答案：D解析：由题意可知，等差数列的前n项和为Sn，根据等差数列的性质，有Sn =n(a1 + an) / 2，其中a1为首项，an为第n项。

根据题意，当n=6时，Sn=54，代入公式可得6(a1 + a6) / 2 = 54，化简得a1 + a6 = 18。

因为这是一个等差数列，所以a3 = (a1 + a6) / 2 = 9，所以选项D正确。

4. 答案：B解析：由题意可知，等比数列的前n项和为Sn，根据等比数列的性质，有Sn =a1(1 - q^n) / (1 - q)，其中a1为首项，q为公比。

当q=1时，Sn = n a1，即等比数列退化为等差数列。

因此，当q=1时，数列不是等比数列，所以选项B正确。

5. 答案：C解析：由题意可知，复数z在复平面上的几何意义是点P的坐标，其中z = x + yi。

根据题意，点P在直线y=2x上，因此y坐标为2x，代入z的表达式中，得z = x + 2xi。

因为z的实部为x，虚部为2x，所以选项C正确。

二、填空题6. 答案：4解析：根据指数函数的性质，有2^3 2^2 = 2^(3+2) = 2^5 = 32，所以选项4正确。

7. 答案：π解析：由题意可知，圆的周长C = 2πr，其中r为半径。

因为C = 10π，所以2πr = 10π，解得r = 5。

所以选项π正确。

8. 答案：-1解析：由题意可知，函数f(x) = (x - 1)^2 - 2x + 1，化简得f(x) = x^2 - 3x + 2。

因为这是一个二次函数，其对称轴为x = 3/2，所以当x = 3/2时，函数取得最小值。

将x = 3/2代入函数中，得f(3/2) = (3/2 - 1)^2 - 2 (3/2) + 1 = (-1/2)^2 - 3 + 1 = 1/4 - 2 = -7/4。

2020年上海市崇明区高考数学一模试卷(含解析)

2020年上海市崇明区高考数学一模试卷一、填空题（本大题共有12题，满分54分，其中1～6题每题4分，7～12题每题5分）【考生应在答题纸相应编号的空格内直接填写结果．】1.已知集合A={0, 1, 2, 3}，B={x|0<x≤2}，则A∩B=________．2.不等式|x−2|<1的解集是________．3.半径为1的球的表面积是________．4.已知等差数列{a n}的首项为1，公差为2，则该数列的前n项和S n=________．5.函数f(x)=√x+1的反函数是________．6.计算：limn→∞3n+1−2n3n+2n−1=________．7.二项式(x+2x)6的展开式中常数项的值等于________．8.若双曲线的一个顶点坐标为(3, 0)，焦距为10，则它的标准方程为________．9.已知a，b∈R+，若直线x+2y+3=0与直线(a−1)x+by=2互相垂直，则ab的最大值等于________．10.已知函数f(x)是定义在R上的周期为2的奇函数．当0<x≤1时，f(x)=x3−ax+1，则实数a的值等于________．11.某组委会要从五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作，若其中甲不能从事翻译工作，乙不能从事导游工作，其余三人均能从事这四项工作，则不同的选派方案共有________种．12.正方形ABCD 的边长为4，O 是正方形ABCD 的中心，过中心O 的直线l 与边AB 交于点M ，与边CD 交于点N ，P 为平面上一点，满足2OP →=λOB →+(1−λ)OC →，则PM →⋅PN →的最小值为________．二、选择题（本大题共有4题，满分20分）【每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．】13.若a <0<b ，则下列不等式恒成立的是() A.1a >1b B.−a >bC.a 3<b 3D.a 2>b 214.已知z ∈C ，“z +z ¯=0”是“z 为纯虚数”的() A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既不充分也非必要条件15.如图，在底面半径和高均为√2的圆锥中，AB 、CD 是底面圆O 的两条互相垂直的直径，E 是母线PB 的中点．已知过CD 与E 的平面与圆锥侧面的交线是以E 为顶点的抛物线的一部分，则该抛物线的焦点到圆锥顶点P 的距离等于（）A.12 B.1 C.√104D.√5216.若不等式(|x −a|−b)sin(πx +π6)≤0对x ∈[−1, 1]恒成立，则a +b 的值等于() A.23 B.56C.1D.2三、解答题（本大题共有5题，满分76分）【解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤．】17.在直三棱柱ABC−A1B1C1中，∠ABC=90∘，AB=BC=1，BB1=2．(1)求异面直线B1C1与A1C所成角的大小；(2)求直线B1C1与平面A1BC的距离．18.已知函数f(x)=√32sin2x−cos2x−12，x∈R．(1)求函数f(x)的最小正周期和单调递减区间；(2)设△ABC的内角A，B，C的对边分别为a，b，c且c=√3，f(C)=0．若sinB=2sinA，求a，b的值．19.某辆汽车以x公里/小时速度在高速公路上匀速行驶（考虑到高速公路行车安全要求60≤x≤120）时，每小时的油耗（所需要的汽油量）为15(x−100+4500x)升．(1)欲使每小时的油耗不超过9升，求x的取值范围；(2)求该汽车行驶100公里的油耗y关于汽车行驶速度x的函数，并求y的最小值．20.已知椭圆Γ:x 24+y 2=1，其左右顶点分别为A ，B ，上下顶点分别为C ，D ．圆O 是以线段AB 为直径的圆． (1)求圆O 的方程；(2)若点E ，F 是椭圆上关于y 轴对称的两个不同的点，直线CE ，DF 分别交x 轴于点M 、N ，求证：OM →⋅ON →为定值；(3)若点P 是椭圆Γ上不同于点A 的点，直线AP 与圆O 的另一个交点为Q ．是否存在点P ，使得AP →=13PQ →？若存在，求出点P 的坐标，若不存在，说明理由．21.已知无穷数列{a n }，{b n }，{c n }满足：对任意的n ∈N ∗，都有a n+1=|b n |−|c n |，b n+1=|c n |−|a n |，c n+1=|a n |−|b n |．记d n =max{|a n |, |b n |, |c n |}（max{x, y, z}表示3个实数x ，y ，z 中的最大值）． (1)若a 1=1，b 1=2，c 1=4，求a 4，b 4，c 4的值； (2)若a 1=1，b 1=2，求满足d 2=d 3的c 1的所有值；(3)设a 1，b 1，c 1是非零整数，且|a 1|，|b 1|，|c 1|互不相等，证明：存在正整数k ，使得数列{a n }，{b n }，{c n }中有且只有一个数列自第k 项起各项均为0．2020年上海市崇明区高考数学一模试卷一、填空题（本大题共有12题，满分54分，其中1～6题每题4分，7～12题每题5分）【考生应在答题纸相应编号的空格内直接填写结果．】1.已知集合A={0, 1, 2, 3}，B={x|0<x≤2}，则A∩B=________．【解答】解：∵A={0, 1, 2, 3}，B={x|0<x≤2}；∴A∩B={1, 2}．故答案为：{1, 2}.2.不等式|x−2|<1的解集是________．【解答】解：由不等式|x−2|<1可得，−1<x−2<1，解得1<x<3.故答案为：(1,3).3.半径为1的球的表面积是________．【解答】解：由题意，半径为1的球的表面积是4π⋅12=4π．故答案为：4π.4.已知等差数列{a n}的首项为1，公差为2，则该数列的前n项和S n=________．【解答】解：∵等差数列{a n}的首项为1，公差为2，∴该数列的前n项和S n=n×1+n(n−1)2×2=n2．故答案为：n2.5.函数f(x)=√x+1的反函数是________．【解答】解：由y=√x+1可得：x=y2−1，y≥0，∴f(x)=√x+1的反函数是：f−1(x)=x2−1(x≥0).故答案为：f−1(x)=x2−1(x≥0).6.计算：limn→∞3n+1−2n3+2=________．【解答】解：limn→∞3n+1−2n3+2=limn→∞3−(23)n1+(23)n=3−limn→∞(23)n1+limn→∞(23)n=3.故答案为：3.7.二项式(x+2x)6的展开式中常数项的值等于________．【解答】解：展开式的通项为T r+1=C6r x6−r(2x)r=2r C6r x6−2r，令6−2r=0可得r=3，常数项为23C63=160.故答案为：160.8.若双曲线的一个顶点坐标为(3, 0)，焦距为10，则它的标准方程为________．【解答】解：依题意可知a=3，c=5，∴b=√25−9=4，根据顶点坐标可知焦点在x轴，∴双曲线的方程为x 29−y216=1.故答案为：x 29−y216=1.9.已知a，b∈R+，若直线x+2y+3=0与直线(a−1)x+by=2互相垂直，则ab的最大值等于________．【解答】解：根据题意，若直线x+2y+3=0与直线(a−1)x+by=2互相垂直，则有(a−1)+2b=0，变形可得a+2b=1，则ab=12(a×2b)≤12×(a+2b2)2=18，当且仅当a=2b=12时，等号成立；即ab的最大值为18.故答案为：18.10.已知函数f(x)是定义在R上的周期为2的奇函数．当0<x≤1时，f(x)= x3−ax+1，则实数a的值等于________．【解答】解：∵函数f(x)是定义在R上的周期为2的奇函数．当0<x ≤1时，f(x)=x 3−ax +1，∴f(−1)=−f(1)且f(−1)=f(−1+2)=f(1)， ∴f(1)=0，即f(1)=1−a +1=2−a =0， ∴a =2．故答案为：2．11.某组委会要从五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作，若其中甲不能从事翻译工作，乙不能从事导游工作，其余三人均能从事这四项工作，则不同的选派方案共有________种．【解答】解：根据题意，分3种情况讨论：①，从五名志愿者中选派的四人中的有甲但没有乙，甲有3种安排方法，剩下三人全排列即可得，此时有3×A 33=18种选派方法；②，从五名志愿者中选派的四人中的有乙但没有甲，乙有3种安排方法，剩下三人全排列即可得，此时有3×A 33=18种选派方法； ③，从五名志愿者中选派的四人中既有甲又有乙，需要在剩下3人中选出2人，有C 32种选法，选出4人的安排方法有A 33+2×2×A 22种，则此时有C 32(A 33+2×2×A 22)=42种选派方法；故一共有18+18+42=78种选派方法. 故答案为：78.12.正方形ABCD 的边长为4，O 是正方形ABCD 的中心，过中心O 的直线l 与边AB 交于点M ，与边CD 交于点N ，P 为平面上一点，满足2OP →=λOB →+(1−λ)OC →，则PM →⋅PN →的最小值为________．【解答】解：如图，以O 为坐标原点，以过O 且平行于AB 的直线为x 轴，以过O 且垂直于AB 的直线为y 轴建立坐标系，则B(2, −2)，C(2, 2)，∴2OP →=λOB →+(1−λ)OC →=λ(2, −2)+(1−λ)(2, 2)＝(2, 2−4λ)，∴OP →=(1, 1−2λ) 即P 点坐标为(1, 1−2λ)，设M(a, −2)，则N(−a, 2)，−2≤a ≤2， ∴PM →=(a −1, 2λ−3)， PN →=(−a −1, 2λ+1)∴PM →⋅PN →=(a −1)(−a −1)+(2λ−3)(2λ+1)=1−a 2+4λ2−4λ−3，当a =±2且λ=−−42×4=12时，PM →⋅PN →有最小值−7．故答案为：−7.二、选择题（本大题共有4题，满分20分）【每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．】若a <0<b ，则下列不等式恒成立的是() A.1a >1b B.−a >bC.a 3<b 3D.a 2>b 2【解答】解：根据题意，依次分析选项：对于A ，由于a <0<b ，则1a <0<1b ，A 错误；对于B ，若|a|<|b|，则−a <b ，B 错误；对于C ，由于a <0<b ，则a 3<0<b 3，C 正确；对于D ，若|a|<|b|，则a 2<b 2，D 错误. 故选C .已知z ∈C ，“z +z ¯=0”是“z 为纯虚数”的() A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既不充分也非必要条件【解答】解：对于复数z ，若z +z →=0，z 不一定为纯虚数，可以为0，反之，若z 为纯虚数，则z +z →=0．∴“z +z →=0”是“z 为纯虚数”的必要非充分条件．故选B .如图，在底面半径和高均为√2的圆锥中，AB 、CD 是底面圆O 的两条互相垂直的直径，E 是母线PB 的中点．已知过CD 与E 的平面与圆锥侧面的交线是以E 为顶点的抛物线的一部分，则该抛物线的焦点到圆锥顶点P 的距离等于（）A.12 B.1 C.√104D.√52【解答】解：如图所示，过点E 作EH ⊥AB ，垂足为H ．∵E 是母线PB 的中点，圆锥的底面半径和高均为√2， ∴OH =EH =√22． ∴OE =1．在平面CED 内建立直角坐标系如图：设抛物线的方程为y 2=2px ，(p >0)，F 为抛物线的焦点， C(1, √2)， ∴2=2p ⋅1，解得p =1， F(12, 0)，即OF =12，EF =12， ∵PB =2，PE =1，∴该抛物线的焦点到圆锥顶点P 的距离为√PE 2+EF 2=√52. 故选D .若不等式(|x −a|−b)sin(πx +π6)≤0对x ∈[−1, 1]恒成立，则a +b 的值等于() A.23 B.56C.1D.2【解答】解：当−1≤x ≤−16或56≤x ≤1时，sin(πx +π6)≤0，当−16≤x ≤56时，sin(πx +π6)≥0，∴当−1≤x ≤−16或56≤x ≤1时，|x −a|−b ≥0，当−16≤x ≤56时，|x −a|−b ≤0，设f(x)=|x −a|−b ，则f(x)在(−∞, a)上单调递减，在(a, +∞)上单调递增，且f(x)的图象关于直线x =a 对称， ∴f(−16)=f(56)=0，∴2a =−16+56=23，即a =13，又f(56)=|56−13|−b =0，故b =12． ∴a +b =56．故选B .三、解答题（本大题共有5题，满分76分）【解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤．】在直三棱柱ABC −A 1B 1C 1中，∠ABC =90∘，AB =BC =1，BB 1=2．(1)求异面直线B 1C 1与A 1C 所成角的大小；(2)求直线B1C1与平面A1BC的距离．【解答】解：(1)由题意可得BC // B1C1，∴∠A1CB（或其补角）即为异面直线B1C1与A1C所成的角，由题意可知BC⊥平面ABB1A1，∴BC⊥A1B，∴△A1BC为直角三角形，∴tan∠A1CB=A1BBC =√AB2+BB12BC=√5，∴异面直线B1C1与A1C所成的角为arctan√5；(2)∵BC // B1C1，BC⊂平面A1BC，B1C1⊄平面A1BC，∴B1C1 // 平面A1BC，∴直线B1C1上任意一点到平面A1BC的距离均为直线B1C1到平面A1BC的距离，不妨取B1，且设B1到平面A1BC的距离为ℎ，由等体积法可得V B1−A1BC =V C−A1BB1，即13S△A1BC×ℎ=13S△ABB1×BC，代入数据可得13×12×1×√5×ℎ=13×12×2×1×1，解得ℎ=2√55，∴直线B1C1到平面A1BC的距离为2√55.已知函数f(x)=√32sin2x−cos2x−12，x∈R．(1)求函数f(x)的最小正周期和单调递减区间；(2)设△ABC的内角A，B，C的对边分别为a，b，c且c=√3，f(C)=0．若sinB=2sinA，求a，b的值．【解答】解：(1)∵f(x)=√32sin2x−cos2x−12，x∈R．=√32sin2x−1+cos2x2−12=sin(2x−π6)−1，∴T=2π2=π，∴由2kπ+π2≤2x−π6≤2kπ+3π2，k∈Z可解得：x∈[kπ+π3, kπ+5π6]，k∈Z，∴f(x)单调递减区间是：[kπ+π3, kπ+5π6]，k∈Z；(2)f(C)=sin(2C−π6)−1=0，则sin(2C−π6)=1，∵0<C<π，∴C=π3，∵sinB=2sinA，∴由正弦定理可得b=2a①，∵c=√3，∴由余弦定理可得c2=a2+b2−ab=3②，由①②可得a=1，b=2．某辆汽车以x公里/小时速度在高速公路上匀速行驶（考虑到高速公路行车安全要求60≤x≤120）时，每小时的油耗（所需要的汽油量）为15(x−100+4500x)升．(1)欲使每小时的油耗不超过9升，求x的取值范围；(2)求该汽车行驶100公里的油耗y关于汽车行驶速度x的函数，并求y的最小值．【解答】解：(1)由题意，令15×(x−100+4500x)≤9，化简得x2−145x+4500≤0，解得45≤x≤100；又因为60≤x≤120，所以欲使每小时的油耗不超过9升，x的取值范围是[60, 100]；(2)设该汽车行驶100公里的油耗为y，则y=100x ⋅15(x−100+4500x)=90000(1x −190)2+809，（其中60≤x≤120）；由60≤x≤120，知1x ∈[1120, 160]，所以x=90时，汽车行驶100公里的油耗取得最小值为809升．已知椭圆Γ:x 24+y2=1，其左右顶点分别为A，B，上下顶点分别为C，D．圆O是以线段AB为直径的圆．(1)求圆O的方程；(2)若点E，F是椭圆上关于y轴对称的两个不同的点，直线CE，DF分别交x轴于点M 、N ，求证：OM →⋅ON →为定值；(3)若点P 是椭圆Γ上不同于点A 的点，直线AP 与圆O 的另一个交点为Q ．是否存在点P ，使得AP →=13PQ →？若存在，求出点P 的坐标，若不存在，说明理由．【解答】解：(1)由题意得：A(−2, 0)，B(2, 0)， ∴圆O 的圆心为原点，半径为2， ∴圆O 的方程是x 2+y 2=4；(2)由题意可知：C(0, 1)，D(0, −1)，设E(x 0, y 0)，则F(−x 0, y 0)，(x 0≠1)， ∴直线CE 的方程是：y−1y 0−1=xx 0，∴点M(−x 0y 0−1, 0)，同理点N(x 0y0+1, 0)，又∵点E(x 0, y 0)在椭圆x 24+y 2=1上，∴x 024+y 02=1，∴OM →⋅ON →=x 02y2−1=x 02−x 024=−4.(3)显然直线AP 的斜率存在，设其方程为：y =k(x +2)，联立方程{y =k(x +2),x 24+y 2=1,化简得：(1+4k 2)x 2+16k 2x +16k 2−4=0，设P(x 1, y 1)，则x 1+(−2)=−16k 21+4k 2，所以|AP|=√1+k 2|x 1−(−2)|=√41+4k 2，因为圆心O 到直线AP 的距离d =√2，所以|AQ|=2√4−d 2=4√11+k ，假设存在点P ，使得AP →=13PQ →，则|AQ|=4|AP|，所以4√11+k 2=4√41+4k 2，化简得：4+4k 2=1+4k 2，此方程在实数范围内无解，故原假设错误，即不存在点P ，使得AP →=13PQ →．已知无穷数列{a n }，{b n }，{c n }满足：对任意的n ∈N ∗，都有a n+1=|b n |−|c n |，b n+1=|c n |−|a n |，c n+1=|a n |−|b n |．记d n =max{|a n |, |b n |, |c n |}（max{x, y, z}表示3个实数x ，y ，z 中的最大值）．(1)若a 1=1，b 1=2，c 1=4，求a 4，b 4，c 4的值； (2)若a 1=1，b 1=2，求满足d 2=d 3的c 1的所有值；(3)设a 1，b 1，c 1是非零整数，且|a 1|，|b 1|，|c 1|互不相等，证明：存在正整数k ，使得数列{a n }，{b n }，{c n }中有且只有一个数列自第k 项起各项均为0．【解答】(1)解：由题意：a 2=|b 1|−|c 1|=2−4=−2；b 2=|c 1|−|a 1|=4−1=3；c 2=|a 1|−|b 1|=1−2=−1；以此类推，看得出a 4=0，b 4=−1，c 4=1． (2)解：若a 1=1，b 1=2，c 1=x ，则a 2=2−|x|，b 2=|x|−1，c 2=−1，d 2={2−|x|,0≤|x|<1,1,1≤|x|<2,|x|−1,|x|≥2, a 3=||x|−1|−1，b 3=1−|2−|x||，c 3=|2−|x||−|x|−1|，当0≤|x|<1时，a 3=−|x|，b 3=|x|−1|，c 3=1，d 3=1，由d 3=d 2，得||x|=1，不符合题意．当1≤|x|<2，a 3=|x|−2，b 3=|x|−1，c 3=3−2|x|，d 3={2−|x|,1≤|x|<1.5,|x|−1,1.5≤|x|<2,由d 3=d 2，得|x|=1，符合题意．当|x|≥2，a 3=|x|−2，b 3=3−|x|，c 3=−1，d 3={1,2≤|x|<3,|x|−2,|x|≥3,由d 3=d 2，得|x|=2，符合题意，综上c 1的取值是：−2，−1，1，2．(3)证明：先证明‘’存在正整数k ≥3，使，a k ，b k ，c k 中至少有一个为零，假设对任意正整数k ≥3，a k ，b k ，c k 都不为零，由a 1，b 1，c 1是非零整数，且|a 1|，|b 1|，|c 1|互不相等，得d 1∈N ∗，d 2∈N ∗，若对任意k ≥3，a k ，b k ，c k 都不为零，则d k ∈N ∗．即对任意k ≥1，d k ∈N ∗．当k ≥1时，|a k+1|=|b k |−|c k ||<max{|b k |, |c k |}≤d k ，|b k+1|=||c k |−|a k ||<d k ，|c k+1|=||a k |−|b k ||<d k ，所以d k+1=max{|a k+1|, |b k+1|, |c k+1|}<d k ，所以{d k }单调递减，由d 2为有限正整数，所以必存在正整数m≥3，使得d m≤0，矛盾，所以存在正整数k≥3，使a k，b k，c k中至少有一个为零，不妨设a k=0，且a1≠0，a2≠0…a k−1≠0，则|b k−1|=|c k−1|，且|b k−1|=|c k−1|≠|a k−1|，否则若|b k−1|=|c k−1|=|a k−1|，因为a k−1+b k−1+c k−1=0，则必有a k−1=b k−1=c k−1=0，矛盾．于是，b k=|c k−1|−|a k−1|≠0，c k=|a k−1|−|b k−1|≠0，且b k=−c k，所以，a k+1=0，b k+1=|c k|，c k+1=−|b k|=−|c k|，以此类推，即有：对∀n≥k，a n=0，b n+1=|c k|，c n+1=−|c k|，|c k|≠0，此时有且仅有一个数列{a n}自k项起各项均为0．综上：结论成立．。

2020年上海市高三数学一模分类汇编：数列与极限

2（2020普陀一模）. 132lim 31n nnn +→∞+=+ 3（2020闵行一模）. 计算：23lim13(21)n n n →∞=++⋅⋅⋅+- 4（2020嘉金一模）. 计算2lim1n nn →∞=+4（2020崇明一模）. 已知等差数列{}n a 的首项为1，公差为2，则该数列的前n 项和n S = 4（2020青浦一模）. 我国古代庄周所著的《庄子⋅天下篇》中引用过一句话：“一尺之棰，日取其半，万世不竭.”，其含义是：一根一尺长的木棒，每天截下其一半，这样的过程可以无限地进行下去.若把“一尺之棰”的长度记为1个单位，则第n 天“日取其半”后，记木棒剩下部分的长度为n a ，则n a =5（2020虹口一模）. 设等差数列{}n a 的前n 项和n S ，若2712a a +=，48S =，则n a =6（2020崇明一模）. 计算：1132lim 32n nnn n +-→∞-=+ 7（2020普陀一模）. 各项都不为零的等差数列{}n a （*n ∈N ）满足22810230a a a -+=，数列{}n b 是等比数列，且88a b =，则4911b b b =8（2020杨浦一模）. 已知数列{}n a 的通项公式为1(2)1()(3)2n n nn a n -≤⎧⎪=⎨≥⎪⎩（n ∈*N ），n S 是数列{}n a 的前n 项和. 则lim n n S →∞=8（2020徐汇一模）. 已知等差数列{}n a 的公差3d =，n S 表示的前n 项和，若数列{}n S 是递增数列，则1a 的取值范围是8（2020闵行一模）. 若首项为正数的等比数列{}n a ，公比lg q x =，且10099101a a a <<，则实数x 的取值范围是8（2020青浦一模）. 已知数列{}n a 中，11a =，1112n n n a a -+-=（*n ∈N ），则lim n n a →∞= 9（2020松江一模）. 在无穷等比数列{}n a 中，若121lim()3n n a a a →∞++⋅⋅⋅+=，则1a 的取值范围是11（2020宝山一模）. 已知{}n a 、{}n b 均是等差数列，n n n c a b =⋅，若{}n c 前三项是7、9、9，则10c =11（2020徐汇一模）. 已知数列{}n a 的前n 项和为n S ，对任意*n ∈N ，1(1)32n n n n S a n =-++-且12()()0a p a p --<，则实数p 的取值范围是 11（2020嘉金一模）. 已知数列{}n a 满足：11a =，112{,,,}n n n a a a a a +-∈⋅⋅⋅（*n ∈N ），记数列{}n a 的前n 项和为n S ，若对所有满足条件的{}n a ，10S 的最大值为M ，最小值为m ，则M m +=16（2020青浦一模）. 设等比数列{}n a 的公比为q ，其前n 项之积为n T ，并且满足条件：11a >，201920201a a >，20192020101a a -<-，给出下列结论：① 01q <<；② 2019202110a a ->；③ 2019T 是数列{}n T 中的最大项；④ 使1n T >成立的最大自然数等于4039；其中正确结论的序号为（）A. ①②B. ①③C. ①③④D. ①②③④16（2020闵行一模）. 已知各项为正数的非常数数列{}n a 满足11n an a a +=，有以下两个结论：① 若32a a >，则数列{}n a 是递增数列；② 数列{}n a 奇数项是递增数列；则（） A. ①对②错 B. ①错②对 C. ①②均错误 D. ①②均正确16（2020奉贤一模）. 由9个互不相等的正数组成的矩阵111213212223313233a a a a a a a a a ⎛⎫⎪⎪ ⎪⎝⎭中，每行中的三个数成等差数列，且111213a a a ++、212223a a a ++、313233a a a ++成等比数列，下列判断正确的有（）① 第2列中的12a 、22a 、32a 必成等比数列；② 第1列中的11a 、21a 、31a 不一定成等比数列；③ 12322123a a a a +>+；A. 1个B. 2个C. 3个D. 0个20（2020嘉金一模）. 已知数列{}n a 各项均为正数，n S 为其前n 项的和，且n a 、n S 、2na （*n ∈N ）成等差数列.（1）写出1a 、2a 、3a 的值，并猜想数列{}n a 的通项公式n a ；（2）证明（1）中的猜想；（3）设1n n b ta =-（0t >），n T 为数列{}n b 的前n 项和，若对于任意*n ∈N ，都有*{|}n m T b m ∈∈N , 求实数t 的值.20（2020徐汇一模）. 给正有理数i i m n 、jjm n （i j ≠，*,i j ∈N ，*,,,i i j j m n m n ∈N ，且i jm m =和i j n n =不同时成立），按以下规则P 排列：① 若i i j j m n m n +<+，则ii m n 排在j jm n 前面；② 若i i j j m n m n +=+，且i j n n <，则ii m n 排在j jm n 的前面，按此规则排列得到数列{}n a .（例如：121,,,112⋅⋅⋅）.（1）依次写出数列{}n a 的前10项；（2）对数列{}n a 中小于1的各项，按以下规则Q 排列：①各项不做化简运算；②分母小的项排在前面；③分母相同的两项，分子小的项排在前面，得到数列{}n b ，求数列{}n b 的前10项的和10S ，前2019项的和2019S ；（3）对数列{}n a 中所有整数项，由小到大取前2019个互不相等的整数项构成集合1232019{,,,,}A c c c c =⋅⋅⋅，A 的子集B 满足：对任意的,x y B ∈，有x y B +∉，求集合B中元素个数的最大值.21（2020宝山一模）. 已知数列{}n a 满足11a =，2a e =（e 是自然对数的底数），且2n a +=ln n n b a =（n ∈*N ）.（1）证明：2n b +> （2）证明：211{}n n n n b b b b +++--是等比数列，且{}n b 的通项公式是121[1()]32n n b -=--；（3）是否存在常数t ，对任意自然数n ∈*N 均有1n n b tb +≥成立？若存在，求t 的取值范围，否则，说明理由.21（2020松江一模）. 已知数列{}n a 满足：① n a ∈N （*n ∈N ）；② 当2k n =（*k ∈N ）时，2n na =；③ 当2k n ≠（*k ∈N ）时，1n n a a +<，记数列{}n a 的前n 项和为n S . （1）求1a ，3a ，9a 的值；（2）若2020n S =，求n 的最小值；（3）求证：242n n S S n =-+的充要条件是211n a +=（*n ∈N ）.21（2020崇明一模）. 已知无穷数列{}n a 、{}n b 、{}n c 满足：对任意的*n ∈N ，都有1||||n n n a b c +=-，1||||n n n b c a +=-，1||||n n n c a c +=-，记max{||,||,||}n n n n d a b c =（max{,,}x y z 表示3个实数x 、y 、z 中的最大值）. （1）若11a =，12b =，14c =，求4a 、4b 、4c 的值；（2）若11a =，12b =，求满足23d d =的1c 的所有值；（3）设1a 、1b 、1c 是非零实数，且1||a 、1||b 、1||c 互不相等，证明：存在正整数k ，使得数列{}n a 、{}n b 、{}n c 中有且只有一个数列自第k 项起各项均为0.21（2020虹口一模）. 在数列{}n a 中，10a =，且对任意的*m ∈N ，21m a -、2m a 、21m a +构成以2m 为公差的等差数列.（1）求证：4a 、5a 、6a 成等比数列；（2）求数列{}n a 的通项公式；（3）设2222323n nn S a a a =++⋅⋅⋅+，试问2n S n -是否存在极限？若存在，求出其值，若不存在，请说明理由.21. 已知无穷数列{}n a 的前n 项和为n S ，若对于任意的正整数n ，均有210n S -≥，20n S ≤，则称数列{}n a 具有性质P .（1）判断首项为1，公比为2-的无穷等比数列{}n a 是否具有性质P ，并说明理由；（2）已知无穷数列{}n a 具有性质P ，且任意相邻四项之和都相等，求证：40S =；（3）已知21n b n =-，n ∈*N ，数列{}n c 是等差数列，122n n n b n a c n +⎧⎪=⎨⎪⎩为奇数为偶数，若无穷数列{}n a 具有性质P ，求2019c 的取值范围.21（2020普陀一模）. 数列{}n a 与{}n b 满足：1a a =，1n n n b a a +=-，n S 是数列{}n a 的前n 项和（*n ∈N ）.（1）设数列{}n b 是首项和公比都为13-的等比数列，且数列{}n a 也是等比数列，求a 的值；（2）设121nn n b b +-=-，若3a =且4n a a ≥对*n ∈N 恒成立，求2a 的取值范围；（3）设4a =，2n b =，22n n nS C λ+=（*n ∈N ，2λ≥-），若存在整数k 、l ，且1k l >>，使得k l C C =成立，求λ的所有可能值.。

2020学年崇明区高三一模数学试卷(含解析)

高三数学共4页第1页崇明区2020学年第一次高考模拟考试试卷（含解析）数学考生注意：1．本试卷共4页，21道试题，满分150分，考试时间120分钟．2．本试卷分设试卷和答题纸．试卷包括试题与答题要求．作答必须涂（选择题）或写（非选择题）在答题纸上，在试卷上作答一律不得分．3．答卷前，务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号码等相关信息．一、填空题（本大题共有12题，满分54分，其中1～6题每题4分，7～12题每题5分）【考生应在答题纸相应编号的空格内直接填写结果．】1．设集合{1,2,3}A =，集合{3,4}B =，则A B = ．2．不等式102x x -<+的解集是． 3．已知复数z 满足(z 2)i 1-=（i 是虚数单位），则z = ． 4．设函数1()1f x x =+的反函数为1()f x -，则1(2)f -= ． 5．点(0,0)到直线2x y +=的距离是． 6．计算：123lim(2)n nn n →∞+++⋅⋅⋅+=+ ．7．若关于x 、y 的方程组46132x y ax y +=⎧⎨-=⎩无解，则实数a = ．8．用数字0、1、2、3、4、5组成无重复数字的三位数，其中奇数的个数为．（结果用数值表示）9．若23(2)n a b +的二项展开式中有一项为412ma b ，则m = ．10．设O 为坐标原点，直线x a =与双曲线2222:1(0,0)x y C a b a b-=>>的两条渐近线分别交于,D E 两点，若ODE △的面积为1，则双曲线C 的焦距的最小值为． 11．已知函数()=y f x ，对任意x R ∈，都有(2)()f x f x k +⋅=(k 为常数)，且当[0,2]x ∈时，2()1f x x =+，则(2021)f = ．12．已知点D 为圆22:4O x y +=的弦MN 的中点，点A 的坐标为(1,0)，且1AM AN ⋅=，则OA OD ⋅的范围是．高三数学共4页第2页二、选择题（本大题共有4题，满分20分）【每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．】13．若0a b <<，则下列不等式恒成立的是（）A ．11a b> B ．a b ->C ．22a b >D ．33a b <14．正方体上的点P 、Q 、R 、S 是其所在棱的中点，则直线PQ 与直线RS 异面的图形是（）A ．B ．C ．D ． 15．设{}n a 为等比数列，则“对于任意的*2,m m m a a +∈>N ”是“{}n a 为递增数列”的（） A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件16．设函数()y f x =的定义域是R ，对于下列四个命题：（1）若函数()y f x =是奇函数，则函数()()y f f x =是奇函数；（2）若函数()y f x =是周期函数，则函数()()y f f x =是周期函数；（3）若函数()y f x =是单调减函数，则函数()()y f f x =是单调减函数；（4）若函数()y f x =存在反函数1()y f x -=，且函数1()()y f x f x -=-有零点，则函数()y f x x =-也有零点；其中正确的命题共有（） A ．1个B ．2个C ．3个D ．4个三、解答题（本大题共有5题，满分76分）【解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤．】17．（本题满分14分，本题共有2个小题，第(1)小题满分7分，第(2)小题满分7分）如图，已知AB ⊥平面BCD ，BC BD ⊥，直线AD 与平面BCD 所成的角为30°，且2AB BC ==．（1）求三棱锥A BCD -的体积；（2）设M 为BD 的中点，求异面直线AD 与CM 所成角的大小（结果用反三角函数值表示）.SRP QQ PRS Q PS RRPS Q高三数学共4页第3页18．（本题满分14分，本题共有2个小题，第(1)小题满分6分，第(2)小题满分8分）已知函数21()sin 23cos 2f x x x =-．（1）求函数()y f x =的最小正周期；（2）在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ．若锐角A 满足13()f A -=，6C π=， 2c =，求ABC △的面积．19．（本题满分14分，本题共有2个小题，第(1)小题满分6分，第(2)小题满分8分）研究表明：在一节40分钟的网课中，学生的注意力指数y 与听课时间x （单位：分钟）之间的变化曲线如图所示．当[0,16]x ∈时，曲线是二次函数图像的一部分；当[16,40]x ∈时，曲线是函数0.8log ()80y x a =++图像的一部分．当学生的注意力指数不高于68时，称学生处于“欠佳听课状态”．（1）求函数()y f x =的解析式；（2）在一节40分钟的网课中，学生处于“欠佳听课状态”的时间有多长？（精确到1分钟）yx 12 16 4080 84 O· · ·· ·· · ·20．（本题满分16分，本题共有3个小题，第(1)小题满分4分，第(2)小题满分5分，第(3)小题满分7分）已知椭圆22:14xyΓ+=的左右顶点分别为A、B，P为直线4x=上的动点，直线P A与椭圆Γ的另一交点为C，直线PB与椭圆Γ的另一交点为D．（1）若点C的坐标为(0,1)，求点P的坐标；（2）若点P的坐标为(4,1)，求以BD为直径的圆的方程；（3）求证：直线CD过定点．高三数学共4页第4页高三数学共4页第5页21．（本题满分18分，本题共有3个小题，第(1)小题满分4分，第(2)小题满分6分，第(3)小题满分8分）对于数列{}n a ，若从第二项起的每一项均大于该项之前的所有项的和，则称{}n a 为P 数列．（1）若数列1,2,,8x 是P 数列，求实数x 的取值范围；（2）设数列12310,,,,a a a a 是首项为1-、公差为d 的等差数列，若该数列是P 数列，求d 的取值范围；（3）设无穷数列{}n a 是首项为a 、公比为q 的等比数列，有穷数列{}n b ，{}n c 是从{}n a中取出部分项按原来的顺序所组成的不同数列，其所有项和分别记为1T ，2T ．求证：当0a >且12T T =时，数列{}n a 不是P 数列．高三数学共4页第6页崇明区2021届第一次高考模拟考试（数学）参考答案及评分标准一、填空题1. {3}；2.(2,1)-；3.2i +；4.1-；； 6.12； 7.2-； 8.48； 9.60； 10. 11. 2； 12.[-1，2).二、选择题13.D; 14.B; 15.C;16.B三、解答题17.解：（1）因为AB ⊥平面BCD ，所以ADB ∠就是直线AD 与平面BCD 所成的角，所以30ADB ∠=︒...............3分所以BD =所以13A BCD BCD V S AB -=⋅=...........................7分（2）取线段AB 的中点N，联结CN 、MN ，则//MN AD所以CMN ∠就是异面直线AD 与CM 所成的角...........................4分在CMN 中，2MN =，CN=CM =所以222cos 214CM MN CN CMN CM MN +-∠==⋅...........................7分18.解：（1）1()sin 2sin(2)23f x x x π==-分所以函数()y f x =的最小正周期2||T ππω==...........................6分（2）由()f A =，得：1sin(2)=32A π-因为(0,)2A π∈，所以22(,)333A πππ-∈-，所以2=36A ππ-，4A π=...........................3分所以22224cos 242b c a b A bc b +--===2b =...........................6分所以1sin 12ABC S bc A ==...........................8分19.解：（1）当[0,16]x ∈时，设2()(12)84(0)f x b x b =-+<由(16)80f =，得：2(1612)84=80b -+，故14b =-...........................2分当[16,40]x ∈时，由(16)80f =，得：0.8log (16)8080a ++=，故15a =-.................4分高三数学共4页第7页所以20.81(12)84,[0,16]()4log (15)80,(16,40]x x f x x x ⎧--+∈⎪=⎨⎪-+∈⎩...........................6分（2）当[0,16]x ∈时，由21(12)84684x --+≤，得：[0,4]x ∈...........................3分当[16,40]x ∈时，由0.8log (15)8068x -+≤，得：12150.829.6x -≥+≈ 所以[30,40]x ∈...........................3分因此，在一节40分钟的网课中，学生处于“欠佳听课状态”的时间有14分钟..............8分. 20. 解：（1）由题意，(2,0)A -，直线AP 的方程是：12xy =-...........................3分由124xy x ⎧=-⎪⎨⎪=⎩，得：点P 的坐标是(4,3)...........................4分（2）由题意，(2,0)B ，直线PB 的方程是：22x y -=，代入2214x y +=，得：220x x -=，解得：0x =，或2x =，所以点D 坐标为（0，-1），线段BD 中点为1(1,)2-，||BD =分所以以BD 为直径的圆的方程是2215(1)()24x y -++=...........................5分（3）设0(4,)P y ，11(,)C x y ，22D(,)x y ，则直线AP 的方程是：0(2)6y x y +=代入2214x y +=，得：2222000(9)44360y x y x y +++-=所以20120218=9y x y -++，012069y y y =+ 同理，可得：2022022=1y x y -+，022021y y y -=+..........................4分所以直线CD 的方程为：2220000002222220000002622222182()()()()191191y y y y y y x y y y y y y y ----+---=--++++++ 令0y =，得：1x =所以直线CD 过定点（1，0）..........................7分21.解：（1）由题意，得：12812x x>+⎧⎨>++⎩，所以35x <<..........................4分(2)由题意知，该数列的前n 项和为(1)2n n n S n d -=-+，11n a nd +=-+，由数列12310,,,,a a a a P 数列，可知211a S a >=，故公差0d >..........................3分高三数学共4页第8页21311022n n d S a n d n +⎛⎫-=-++< ⎪⎝⎭对满足1,2,3,9n =的任意n 都成立，则239911022d d ⎛⎫⋅-++< ⎪⎝⎭，解得827d <，故d 的取值范围为80,27⎛⎫⎪⎝⎭..........................6分 (3)若{}n a 是P 数列，则12a S a aq =<=，因为0a >，所以1q >，又由1n n a S +>对一切正整数n 都成立，可知11n nq aq a q ->⋅-，即12nq q ⎛⎫-< ⎪⎝⎭对一切正整数n 都成立，由10nq ⎛⎫> ⎪⎝⎭，1lim 0nn q →∞⎛⎫= ⎪⎝⎭，故20q -≤，可得2q ≥..........................3分若{}n b 中的每一项都在{}n c 中，则由这两数列是不同数列，可知12T T <；若{}n c 中的每一项都在{}n b 中，同理可得12T T ；若{}n b 中至少有一项不在{}n c 中且{}n c 中至少有一项不在{}n b 中，设{}n b '，{}n c '是将{}n b ，{}n c 中的公共项去掉之和剩余项依次构成的数列，它们的所有项和分别为1T '，2T '，不妨设{}n b '，{}n c '中最大的项在{}n b '中，设为)2(m a m ≥，则21211m m T a a a a T -≤+++<≤''，故21T T '<'，故总有12T T ≠与12T T =矛盾，故假设错误，原命题正确...........................8分。