编译原理 第十章 代码优化
代码优化

11. 删除归纳变量(变换循环控制条件) 故可将 if i>= j 在循环中, T2始终与i保 变换成 持T2 := 4*i if T2 >= T4 线性关系, 同时删除 同时T4始终与 i := i+1 := j保持T4 4*j j := j-1 线性关系 两条自赋值 语句
( := , B, , A) (op , B, , A)
改写成 改写成 改写成 改写成 改写成 改写成 改写成
A:=B A:=op B A:=B op C A:=B[C] D[C]:=B if B rop C goto L goto L
(op , B, C, A) (=[], B, C, A) ([]=,B, ,D[C]) (jrop, B, C, L) (j , , , L)
T := a[T ] T9 :=T10 :=] T8 T99 := a[T44] a[T8 a[T2] 2] := 9 T9 a[T := T a[T7] := T9 T10 := T4 T10 := T8 a[T4] := x a[T10] := x a[T4] := x
6. 删除无用代码(删除无用赋值)
(2)有效原则
(3)合算原则
编译前端
代码优化器
代码生成
控制流分析
数据流分析
代码变换
1. 按所处阶段分类
最主要一类优化是在目标代具体的计算机。
另一类重要的优化是在生成目标代码时进行的这 类优化很大程序上依赖于具体的计算机。
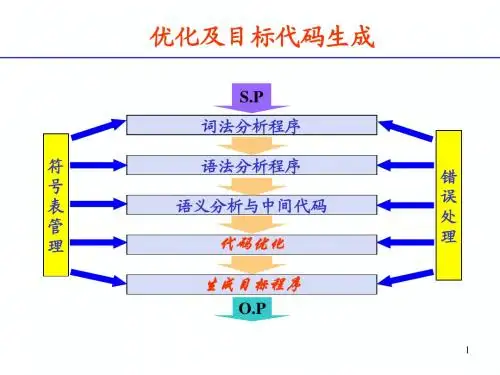
优化可在编译的各个阶段进行
一. 代码优化概念、目的与原则 二. 代码优化器的地位和结构
三. 代码优化分类
四. 代码优化涉及的各个环节
五. 四元式的改写
六. 引例:优化主要方法简介
编译原理chapter9优化

t11 := 4 * i x := a[t11] t12 := 4 * i t13 := 4 * n t14 := a[t13] a[t12] := t14 t15 := 4 * n a[t15] := x
10.2.2 公共子表达式删除
如果表达式E先前已计算,并且从先前的计算到E的再次出现,E中变量的 值没有改变,那么E的这个再次出现称为公共子表达式
(2) j := n
do i = i +1; while(a[i]<v); (3) t1 := 4 * n
do j =j 1;while (a[j]>v); (4) v := a[t1]
if (i >= j) break;
(5) i := i + 1
x=a[i]; a[i]=a[j]; a[j]=x; (6) t2 := 4 * i
}
(7) t3 := a[t2]
10.2 优化的主要种类
本节所用的例子
i = m 1; j = n; v = a[n]; (9) j := j 1
while (1) {
(10) t4 := 4 * j
do i = i +1; while(a[i]<v); (11) t5 := a[t4]
do j =j 1;while (a[j]>v); (12) if t5>v goto (9)
10.2.2 公共子表达式删除
B5 x=a[i]; a[i]=a[j]; a[j]=x;
t6 := 4 * i x := a[t6] t7 := 4 * i t8 := 4 * j t9 := a[t8] a[t7] := t9 t10 := 4 * j a[t10] := x
代码优化

(5) T3:=T2[T1] (6) T4:=T1 (8) T6:=T5[T4] (9) T7:=T3*T6 (10)PROD:=PROD+T7 (11)I:=I+1 (3’) T1:=T1+4 (12)if I<=100 goto (5)
9
2013-8-12
莆田学院许振和
对于这个中间代码段,可用以下六种方法进 行优化:
① 删除多余运算(公共子表达式): 如(3),(6)都用了4*I,而I在(3)(6)之间并没有变化, 所以(6)可以用T4:=T1代替。 ② 代码外提: (4),(7)中的地址运算每次执行时都完全一样,因此 没有必要每循环一次运行一次,可以提到循环体的外面。 ③ 强度削弱: 把乘除运算转换成加减运算,如中间代码块B2中的 T1:=4*I,I每增加1,则T1增加4。所以可以用加法来代 替。经过上述变化,中间代码Ⅰ可以变成Ⅱ的形式。
2013-8-12
莆田学院许振和
12
Ⅲ
(1) (4) (7) (3) PROD:=0 T2:=addr(A)-4 T5:=addr(B)-4 T1:=4 从Ⅰ到Ⅲ,程序运行 结果一点没变,但是少 了:200次乘法、198次 减法,少用了一个存储 单元I和一个临时单元T4。 显然,运算速度大大加 快,占用空间相对减少 了。 以上介绍的是具体采 用的优化措施,根据这 些措施应用的范围不同, 通常把优化分成三个级 别:局部优化,循环优 化和全局优化,以下分 别讨论。
2013-8-12 莆田学院许振和 15
例:求最大公因子 (1) read X (1) read X (2) read Y (2) read Y (3) R:=X mod Y (3) R:=X mod Y (4) if R=0 goto (8) (4) if R=0 goto (8) (5) X:=Y (6) Y:=R (8) write Y (5) X:=Y (7) goto(3) (9) halt (6) Y:=R (8) write Y (7) goto(3) (9) halt
编译原理总结10_优化及目标代码生成
7.1 编译程序考虑的因素
控制结构
一个程序设计语言的控制结构是该语言
在程序运行期间用于改变控制流的语言特征
集合。
5
7.2 运行时的存储分配
编译程序需要为源程序中的数据分配执行时的存储
空间,编译程序从操作系统中申请编译程序计算出的所
需的内存,或编译程序生成在运行时需申请内存的指令。 (1) 确定用来表示某一数据项的内存大小; (2) 使用适当的内存分配策略,实现具体数据的作用 域和生存期;
1.外提不变式:将循环中的不变运算提到循环前面 ,不变运算是指其运算结果不受循环影响的表达式。
2.强度削弱:把程序中执行时间较长的运算替换为 执行时间较短的运算 。 3.删除基本归纳变量:如果循环中对变量I只有唯一 的形如:I = I ± C的赋值,且C为循环不变量,则 称I为循环中的基本归纳变量;删除归纳变量在强度 削弱后进行。
10
7.3 代码优化
优化的基本方法
• 去处冗余
• 削减强度
• 使用更快的指令
11
7.3.1
局部优化
在一个基本块上进行的优化
基本块:程序中一个顺序执行的语句序列, 即一个程序段,它只有一个入口和一个出 口,入口是第一条语句,出口是最后一条 语句。
12
基本块划分方法
(1)确定各个基本块的的入口语句(基本块的第一个语句) ① 语句序列的第一个语句是入口语句; ② 能由条件转移语句或无条件转移语句转到的语句是入口语 句; ③ 紧跟在条件转移语句或无条件转移语句后面的语句是入口 语句。
2
7.1 编译程序考虑的因素
数据结构
一个程序设计语言如允许使用的数组、记录、字符串、表、
栈等形式的数据结构,在编译程序中应为它们提供相应的翻译。
程序设计语言编译原理第三版第10章

§10.2 局部优化
举例:考察下面的三地址代码程序
(1)Read X
(2)Read Y
B1
(3)R:=X mod Y (4)if R=0 goto (8) B2
(5)X:=Y
(6)Y:=R
B3
(7)goto(3)
(8)write Y B4
(9)halt
B1
B2
B3
B4
§10.2 局部优化
3.流图及其生成
标识符(包括常数)-结点 NODE(A)-描述上述对应关系的函数,其值或者是一个结点的编号,
或者无定义
(2)中间代码的三种形式:A:=B A:=op B A:=B op C 或 A:=B[C]
(3)构造算法: ①开始,DAG为空 ②对基本块中每一条中间代码式,依次执行以下步骤:
§10.2 局部优化
步骤: 1.如果NODE(B)无定义,则构造一标记为B的叶结点并定义
NODE(B)为这个结点 如果当前代码是0型,则记NODE(B)的值为n,转4 如果当前代码是1型,则转2(1) 如果当前代码是2型,则(ⅰ)如果NODE(C)无定义,则构造一标 记
为C的叶结点并定义NODE(C)为这个结点;(ⅱ)转2(2)
(1)T0:=3.14 (2)T1:=2*T0 (3)T2:=R+r (4)A:=T1*T2 (5)B:=A (6)T3:=2*T0 (7)T4:=R+r (8)T5:=T3*T4 (9)T6:=R-r (10)B:=T5*T6
(4)代数变换
§10.2 局部优化
二、基本块的DAG表示及其应用
1.基本块的DAG:
一种结点带有下述标记或附加信息的DAG
(1)图的叶结点以一标识符(变量名)或常数作为标记,表示该 结点代表该变量或常数的值。
编译原理课件-代码优化

Wensheng Li BUPT @ 2008
常數合併的實現
在符號表中增加兩個資訊域
–標誌域:指示當前是否存在與該變數相關的常數。 –常數域:如果常數存在,則該域存放的即是與該變數相
應的當前常數值。
常數合併時,注意事項:
–不能將結合律與交換律用於浮點運算式,因為浮點運算 的精度有限,這兩條定律並非是恒真的。
PI:=3.14; D-to-R:= 30P.I01/4117/814084.00;.0
i:=0 10: i:=i+1
... if i<10 goto 10
i:=0 10: i:=0+1
... if i<10 goto 10
... a[i]:=9.0 ... a[j]:=3.0 b:=a[i]
?
7/62
– 所謂等價,指不改變程式的運行結果 – 所謂有效,指目標代碼運行時間短、佔用空間少
基本塊的dag是一種結點上有標記的有向非迴圈圖
– 葉結點由變數名字或常量標記。 – 根據作用到名字上的算符,決定需要名字的左值還是右
值。大多數葉結點代表右值。 – 葉結點代表名字的初值,通常為識別字加上腳標0。 – 內部結點由運算符號標記,代表計算出來的值。 – 圖中各結點可能附加一個或多個識別字,表示這些識別
10.1 優化概述
代碼優化程式的任務
–將前端產生的中間代碼轉換為等價的目標代碼
代碼優化程式的要求
–等價變換 –提高目標代碼的執行速度 –減少目標代碼佔用的空間
代碼優化程式的地位
–目標代碼生成之前的中間代碼優化 –目標代碼生成之後的目標代碼優化
3/62
Wensheng Li BUPT @ 2008
代碼優化程式的位置
编译原理 第10章 代码优化
3、冗余子表达式的消除:在值不发生变化的情 况下,对同一个表达式只需计算一次,再次出现时 直接使用它的值。
例(P199) 有如下 程序段: ① a=b+c; 因为语句2和4之间a 和d没有变化,故应 优化为:
① a=b+c;
② b=a-d; ③ c=b+c; ④ d=b;
10.1 局部优化
基本块的DAG构造算法(续):
(4)若NODE(A)=null,则把A附加到结点n,并令 NODE(A)=n,转(4);否则,先从NODE(A)的附加标识 集中将A删去(注意,若NODE(A)有前驱或NODE(A)是 叶结点,则不能将A删去),然后再把A附加到新的结点 n,并令NODE(A)=n。
10.1 局部优化
基本块的优化技术: 1、常数合并:常数合并是将能在编译时计算出值 的表达式用其相应的值替代。 例(P199)
x=3.14*2
y=2*5*a; z=x+1; 转换成四元 式为: (*,3.14,2,t1) (=,t1,_,x) (*,2,5,t2) (*,t2,a,t3) (=,t3,_,y) (+,x,1,t4) (=,t4,_,z) 常数合并后 的代码如下: (=,6.28,_,x)
例(P212)
优化后
小 结
1、代码优化种类(按优化范围划分): 局部优化、循环优化和全局优化 2、基本块的划分、优化技术(常数合并、 删除无用赋值和冗余子表达式的消除) 和DAG表示 3、循环优化技术:外提循环中的不变表 达式、强度削弱和删除归纳变量
习 题
1. 对下列基本块应用 DAG进行优化: 1. (=,3,,B) 2. (+,A,C,D) 3. (*,A,C,E) 4. (+,D,E,F) 5. (*,B,F,G) 6. (+,A,C,H) 7. (*,A,C,I) 8. (+,H,I,J) 9. (*,B,5,K) 10.(+,K,J,L) 11.(=,L,,M) 2. 对下面程序段画出程 序流图,并进行循环优 化。 I=1; J=10; K=5; L1:X=K*I; Y=J*I; Z=X*Y; I=I+1 if I<100 goto L1;
编译原理:第十章 优化
i:=m-1
j:=n
T1:=4*n
v:=a[T1]
T2]
B2
if T3<v goto B2
10.1 概述
• 优化的三个不同级别:
• 局部优化 • 循环优化
• 全局优化
• 优化的种类:
• 删除多余运算(或称删除公用子表达式) • 代码外提 • 强度消弱 • 变换循环控制条件 • 合并已知量 • 复写传播 • 删除无用赋值
void quicksort (m, n); int m, n;
{ int i, j; int v, x; if (n<=m) return; /* fragment begins here*/ i=m-1; j=n; v=a [n]; while (1) { do i=i+1; while (a [i]<v); do j=j-1; while (a [j]>v); if (i>=j) break; x=a [i]; a[i]=a [j]; a[j]=x; }
if T5>v goto B3
if i>=j goto B6 B4
T6:= T2 x:=T3 T7:= T2 T8:= T4 T9:=T5 a [T2]=T5 T10:= T4 a [T4]= T3 goto B2
B5
T11:= T2 x:=T3
T12:= T2
T13:= T1
T14:= v
a [T2]=v
T4:=4*j
T2:= T2+4
编译原理 第十章 代码优化
第十章代码优化某些编译程序在中间代码或目标代码生成之后要对生成的代码进行优化。
所谓优化,实质上是对代码进行等价变换,使得变换后的代码运行结果与变换前代码运行结果相同,而运行速度加大或占用存储空间少,或两者都有。
优化可在编译的不同阶段进行,对同一阶段,涉及的程序范围也不同,在同一范围内,可进行多种优化。
一般,优化工作阶段可在中间代码生成之后和(或)目标代码生成之后进行。
中间代码的优化是对中间代码进行等价变换。
目标代码的优化是在目标代码生成之后进行的,因为生成的目标代码对应于具体的计算机,因此,这一类优化在很大程度上依赖于具体的机器,我们不做详细讨论。
另外依据优化所涉及的程序范围,又可分为局部优化、循环优化和全局优化三个不同的级别。
局部优化指的是在只有一个入口、一个出口的基本程序块上进行的优化。
循环优化对循环中的代码进行的优化。
全局优化是在整个程序范围内进行的优化。
本章重点:局部优化基本块的DAG表示第一节优化技术简介为了说明问题,我们来看下面这个例子,源程序是:P :=0For I :=1 to 20 doP :=P+A[I]*B[I];经过编译得到的中间代码如图10-1-1所示,这个程序段由B1和B2两个部分组成,B2是一个循环,假定机器按字节编址。
那么,对于这个中间代码段,可进行如下这些优化。
1、删除多余运算(删除公共子表达式)优化的目的在于使目标代码执行速度较快。
图10-1-1中间代码(3)和(6)中都有4*I的运算,而从(3)到(6)没有对I赋值,显然,两次计算机的值是相等的。
所以,(6)的运算是多余的。
我们可以把(6)变换成:T4 :=T1。
这种优化称为删除多余运算或称为删除公共子表达式。
2、代码外提减少循环中代码总数的一个重要办法是代码外提。
这种变换把循环不变运算,即其结果独立于循环执行次数的表达式,提到循环的前面。
使之只在循环外计算一次,上例中,我们可以把(4)和(7)提到循环外。
经过删除多余运算和代码外提后,代码变成图10-1-2。
编译原理-第10章-代码优化
x := t3 t14 := a[t1] a[t2] := t14 a[t1] := x
16
10.1.1公共子表达式删除
B6 x = a[i]; a[i] = a[n]; a[n] = x; a[t1]能否作为公共子表达式? t11 := 4 * i x := a[t11] x := t3 t12 := 4 * i t14 := a[t1] t13 := 4 * n a[t2] := t14 t14 := a[t13] a[t1] := x a[t12] := t14 t15 := 4 * n a[t15] := x
B1
流图
i := i + 1 B2 t2 := 4 * i t3 := a[t2] if t3 < v goto B2
j := j 1 B3 t4 := 4 * j t5 := a[t4] if t5 > v goto B3 if i >= j goto B6 B5
2014-7-6
B4
B6
8
10.1.1公共子表达式删除
15
10.1.1公共子表达式删除
B6 x = a[i]; a[i] = a[n]; a[n] = x; t11 := 4 * i x := a[t11] t12 := 4 * i t13 := 4 * n t14 := a[t13] a[t12] := t14 t15 := 4 * n a[t15] := x
2014-7-6
t6 := 4 * i x := a[t6] t8 := 4 * j t9 := a[t8] a[t6] := t9 a[t8] := x goto B2
x := a[t2] t9 := a[t4] a[t2] := t9 a[t4] := x goto B2 x := t3 a[t2] := t5 a[t4] := x goto B2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十章代码优化某些编译程序在中间代码或目标代码生成之后要对生成的代码进行优化。
所谓优化,实质上是对代码进行等价变换,使得变换后的代码运行结果与变换前代码运行结果相同,而运行速度加大或占用存储空间少,或两者都有。
优化可在编译的不同阶段进行,对同一阶段,涉及的程序范围也不同,在同一范围内,可进行多种优化。
一般,优化工作阶段可在中间代码生成之后和(或)目标代码生成之后进行。
中间代码的优化是对中间代码进行等价变换。
目标代码的优化是在目标代码生成之后进行的,因为生成的目标代码对应于具体的计算机,因此,这一类优化在很大程度上依赖于具体的机器,我们不做详细讨论。
另外依据优化所涉及的程序范围,又可分为局部优化、循环优化和全局优化三个不同的级别。
局部优化指的是在只有一个入口、一个出口的基本程序块上进行的优化。
循环优化对循环中的代码进行的优化。
全局优化是在整个程序范围内进行的优化。
本章重点:局部优化基本块的DAG表示第一节优化技术简介为了说明问题,我们来看下面这个例子,源程序是:P :=0For I :=1 to 20 doP :=P+A[I]*B[I];经过编译得到的中间代码如图10-1-1所示,这个程序段由B1和B2两个部分组成,B2是一个循环,假定机器按字节编址。
那么,对于这个中间代码段,可进行如下这些优化。
1、删除多余运算(删除公共子表达式)优化的目的在于使目标代码执行速度较快。
图10-1-1中间代码(3)和(6)中都有4*I的运算,而从(3)到(6)没有对I赋值,显然,两次计算机的值是相等的。
所以,(6)的运算是多余的。
我们可以把(6)变换成:T4 :=T1。
这种优化称为删除多余运算或称为删除公共子表达式。
2、代码外提减少循环中代码总数的一个重要办法是代码外提。
这种变换把循环不变运算,即其结果独立于循环执行次数的表达式,提到循环的前面。
使之只在循环外计算一次,上例中,我们可以把(4)和(7)提到循环外。
经过删除多余运算和代码外提后,代码变成图10-1-2。
法运算等等。
在图10-1-2的循环中,每循环一次,I的值增1,T1的值与I保持线性关系,每次总是增加4。
因此,我们可以把循环中计算T1值的乘法运算变换成在循环前进行一次乘法运算,而在循环中将其变换成加法运算。
变换后如图10-1-3所示。
4、变换循环控制条件图10-1-3的代码中,I和T1始终保持T1= 4 * I的线性关系,这样可以把(12)的循环控制条件I≤20变换成T1≤80,这样整个程序的运行结果不变。
这种变换称为变换循环控制条件。
经过这一变换后,循环中I的值在循环后不会被引用,四元式(11)可以从循环中删除,这就是我们的目的所在。
5、合并已知量与复写传播图10-1-3中,四元式(3)计算4 * I时,I必为1。
所以(3)中的4 * I的两个运算对象都是编码时的已知量,可在编译时计算出它的值,即(3)可变为T1= 4这种变换称为合并已知量。
图10-1-3中,(6)把T1的值复写到T4中,四元式(8)要引用T4的值,而(6)到(8)之间未改变T4和T1的值,则(8)改为T6 : =T5[T1],之后运算结果保持不变。
这种变换称为复写传播。
图10-1-3经过变换循环控制条件,合并已知量和复写传播等变换后,变为图10-1-4。
6、删除无用赋值在图10-1-4中,(6)对T4赋值,但T4未被引用;另外,(2)和(11)对I赋值,但只有(11)引用I。
所以,只要程序中其它地方不需要引用T4和I,则(6),(2)和(11)对程序的运行结果无任何作用。
我们称之为无用赋值,无用赋值可以从程序中删除,如图10-1-5所示(设(6)(2)(11)为无用赋值)。
比较图10-1-1和图10-1-5可看出,经过优化后的代码的执行效率提高了很多。
当然,实现这些优化的代价也是很大的。
第二节局部优化我们所说的局部优化是指基本块内的优化,所谓基本块,是指程序中一顺序执行语句序列,其中只有一个入口语句和一个出口语句。
执行时只能从其入口语句进入,从其出口语句退出。
对于一个给定的程序,我们可以把它划分为一系列的基本块。
在各基本块的范围内分别进行优化。
一、基本块的划分在介绍基本块的构造之前,我们先定义基本块的入口语句,所谓入口语句,严格地说来就是:1、程序的第一语句;或者,2、条件转移语句或无条件转移语句的转移目标语句;或者,3、紧跟在条件转移语句后面的语句。
有了入口语句的概念之后,我们就可以给出划分中间代码(四元式程序)为基本块的算法,其步骤如下:1、求出四元式程序中各个基本块的入口语句。
2、对每一入口语句,构造其所属的基本块。
它是由该入口语句到下一入口语句(不包括下一入口语句),或到一转移语句(包括该转移语句),或到一停语句(包括该停语句)之间的语句序列组成的。
3、凡未被纳入某一基本块的语句、都是程序中控制流程无法到达的语句,因而也是不会被执行到的语句,我们可以把它们删除。
我们仍以上一节所述的例子来说明,对于图10-1-1中的代码段,由规则1,语句(1)是入口语句,由规则2,语句(3)是入口语句。
由规则3,跟随语句(12)的语句是入口语句,这样,语句(1)和(2)构成一个基本块,语句(3)—(12)构成一个基本块,也即图10-1-1中的B1和B2。
二、基本块的变换很多变换可作用于基本块而不改变它计算的表达式集合,这样的变换对改进代码的质量是很有用的。
有两类重要的局部等价变换可用于基本块,它们是保结构的变换和代数变换。
基本块的主要保结构变换是 1、删除公共子表达式 2、删除无用代码 3、重新命名临时变量 4、交换语句次序对于1和2,我们在第一节已经讨论过,在此简单讨论一下3和4。
重新命名临时变量:假如有语句t : = b + c ,其中t 是临时变量。
如果把这个语句改为u : = b + c , 其中u 是新的临时变量,并且把这个t 的所有引用改成u ,那么基本块的运算结果不变。
交换语句次序:如果基本块有两个相邻的语句: t 1 : = b + c t 2 : = x + y当且仅当x 和y 都不是t 1,b 和c 都不是t 2时我们可以交换这两个语句的次序。
有许多代数变换可以把基本块计算的表达式集合变换成代数等价的集合。
其中有用的变换是那些可以简化表达式或用较快运算代替较慢运算的变换。
例如:x : = x + 0 或 x : = x * 1这样的语句可以从基本块中删除而不改变它计算的表达式集合,又如 x : = y * * 2的指数算符通常要用函数调用来实现,使用代数变换,这个语句可由快速、等价的语句x : = y * y 来代替。
第三节 基本块的DAG 表示这一小节介绍如何应用有向图来进行基本块的优化工作。
先将我们所需使用的DAG 作一说明。
在一个有向图中,我们称任一有向边n i →n j (或表示为有序对(n i ,n j ))中的结点n i 为结点n j 的前驱(父结),结点n j 为结点n i 的后继(子结)。
又称任一有向边序列n 1→n 2, n 2→n 3,…,n k —1→n k 为从结点n 1到结点n k 的一条通路。
如果其中n 1=n k ,则称通路为环路。
该结点序列也记为(n 1 ,n 2,…,n k )。
例如,图10-3-1中有向图的通路(n 2 ,n 2)和(n 3 ,n 4 ,n 3)就是环路。
如果有向图中任一通路都不是环路,则称该有向图为无环路有向图,简称DAG 。
图10-3-2的有向图就是一个DAG 。
在DAG 中,如果(n 1 ,n 2,…, n k )是其中一条通路,则称结点n 1为结点n k 的祖先,结点n k 为结点n 1的后代。
我们这一节中要用到的有向图,是一种其结点带有下述标记或附加信息的DAG :1、图的叶结点,即无后继的结点,以一标识符(变量名)或常数作为标记,表示该结点代表该变量或常数的值。
如果叶结点用来代表某变量A 的地址,则用addr (A )作为该结点的标记。
通常把叶结点上作为标记的标识符加上下标0,以表示它是该变量的初值。
2、图的内部结点,即有后继的结点以一运算符作为标记,表示该结点代表应用该运算符对其后继结点所代表的值进行运算的结果。
3、图中各个结点上可能附加一个或多个标识符,表示这些变量具有该结点所代表的值。
上述这种DAG 可用来描述计算过程,又称描述计算过程的DAG 。
在以下的讨论中,我们简称DAG 。
下面讨论基本块的DAG表示与构造。
一个基本块,可用一个DAG来表示。
下面(图10-3-3)列出各种四元式及相对应的DAG的结点形式。
图中n i为结点编号,结点下面的符号(运算符、标识符或常数)是各结点的标记,各结点右边的标识符是结点的附加标识符。
四元式DAG结点(0)A:=B(:=,B,—,A)(1)A:=op B(op,B,—,A)(2)A:=B op C(op,B,C,A)(3)A:=B [C](=[ ],B[C],—,A)(4)if B rop C goto (s) (jrop, B, C, (S))(5)D[C]:=B ([]=,B,—,D[C])(6)goto(s) (j,—,—,(S))图10-3-3 四元式与DAG结点接着给出一种构造基本的DAG算法。
假设DAG各结点信息将用某种适当的数据结构来存放。
并设有一个标识符(包括常数)与结点的对应表。
NODE(A)是描述这种对应关系的一个函数,它的值或者是一个结点的编号n,或者无定义。
前一个情况代表DAG中存在一个结点n, A是其上的标记或附加标识符。
我们把图10-3-3中各形式的四元式按其对应结点的后继个数分为四类。
其中,四元式(0)称为0型,(1)称为1型;(2)和(3)称为2型;(5)称为3型。
对于3型四元式,由于对数组元素赋值的情形需特殊考虑,因此暂不讨论,对四元式(6)也不涉及,下面是仅含0,1,2型四元式的基本块的DAG构造算法。
首先,DAG为空。
对基本块的每一四元式,依次执行:1、如果NODE(B)无定义,则构造一标记为B的叶结点并定义NODE(B)为这个结点;如果当前四元式是0型,则记NODE(B)的值为n,转4。
如果当前四元式是1型,则转2.(1)。
如果当前四元式是2型,则:(1)如果NODE(C)无定义,则构造一标记为C的叶结点并定义NODE(C)为这个结点,(2)转2.(2)。
2、(1)如果NODE(B)的标记为常数的叶结点,则转2(3),否则转3.(1)。
(2)如果NODE(B)和NODE(C)都是标记为常数的叶结点,则转2.(4),否则转3.(2)。
(3)执行op B(即合并已知量),令得到的新常数为P。
如果NODE(B)是处理当前四元式时新构造出来的结点,则删除它。
如果NODE(P)无定义,则构造一用P做标记的叶结点n。
