钢管订购和运输求解(1)
19569-数学建模-钢管订购和运输 (1)

钢管订购和运输张伟 丁林阁 邓小涛 指导教师:数模组 海军航空工程学院摘要 本模型研究了管道铺设过程中钢管的订购和运输问题,它通过图论和非线性规划的知识建立。
模型使总费用达到最小,很好地解决了向哪个钢厂定货,定货多少,如何运输的问题,并且可以推广到更一般的网络。
同时针对模型中涉及的变量多、求解复杂这一问题,我们对模型进行了适当的简化,大大减少了变量的个数,从而减少了计算量。
一、问题重述要铺设一条1521A A A →→→ 的天然气主管道,可以生产这种主管道钢管的钢厂有721,,S S S 七家。
钢厂的位置,管道的铺设路线,以及从钢厂到铺设地的运输网络(运输网络包括沿管道的公路)均已知。
每个钢厂的钢管价格及其生产能力不全一样,且一个钢厂若要生产这种钢管,至少需要生产500个单位(1千米钢管记为1个单位)。
铁路的运价和公路的运价不一样。
要求在这种情况下,(1)制定一个钢管的订购和运输计划,使总费用最小,并给出总费用。
(2)分析:哪个钢厂钢管的销价的变化对购运计划和总费用影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大,给出相应的数字结果。
(3)如果铺设的管道不是一条线,而是一个树形图,铁路、公路和管道构成网络,就这种更一般的情形给出一种解决办法,并对图二按(1)的要求给出模型和结果。
二、问题的假设在问题所给条件成立的前提下,我们进一步作如下假设: 1. 假设公路运输费用不是整公里的按整公里计算是合理的。
2. 假设沿管道的公路(施工公路)运输费用也为每公里0.1万元(不足整公里部分按整公里计算)。
3. 假设不考虑铁路、公路及施工公路的运输能力限制。
4. 假设运输费用为单程运输的费用,即从出发点到目的地的单程费用,不考虑空车返回的费用。
5. 假设运输费用已包含装卸费用。
关于假设的一点说明:根据上述假设我们认为在铺设管道的过程中每隔一公里,卸下一单位钢管供工人铺设是合理的。
三、符号约定i S :生产主管道钢管的钢厂 ;j A :管道节点 ;1,+j j l :从j A 到1+j A 铺设钢管的路段长度(单位:公里,14,...,1=j ); i s : 钢厂i S 在指定期限内生产钢管的最大数量(单位:单位钢管); i P : 钢厂i S 单位钢管的出厂价格(单位:万元); ij x :从 钢厂i S 运到j A 的钢管数量(单位:单位钢管); ij c :表示1单位钢管从 钢厂i S 到j A 的最小费用(单位:万元); j X :运到j A 的钢管总数(单位:单位钢管); j L : 从j A 往左铺设的钢管总数(单位:单位钢管),j L 为j X 的一部分; j R : 从j A 往右铺设的钢管总数(单位:单位钢管),这里j j j L X R -=; 其中 15,...,1;7,...,1==j i 四、问题分析本问题分两部分:一部分是图论中的最短路径的问题:确定1单位钢管从 钢厂i S 到j A 的最小费用;另一部分是非线性规划问题:求总的最小费用。
钢管订购与运输问题一的数学模型与求解

钢管订购与运输问题一的数学模型与求解
钢管订购与运输问题是一种组合优化问题,它涉及到钢管的订购和运输,旨在找到最佳的订购和运输方案,以最小的成本获得最大的收益。
这个问题通常可以用数学模型来表示。
设 n 个工地需要订购 m 根钢管,钢管订购和运输费用分别为
c1(订购费用)、c2(运输费用),订购钢管的最早时间 t0 为早订购时间,最迟时间为 t1 为晚订购时间,运输时间不计费用。
则钢管订购与运输问题的数学模型可以表示为:
minimize Σi=1~n c1(t1-t0) + Σj=i+1~n c2(t2-t1)
subject to:
t1≤t0
t2≥t1
t1+t2≤t0+30
x1=1, x2=1, ..., xnm=1
其中,x1、x2、...、xnm 是订购钢管的数量,1 表示订购,0 表示不订购。
通过这个数学模型,我们可以制定出钢管订购与运输问题的求解方法,以找到最佳的订购和运输方案。
在实际问题中,我们通常需要对求解结果进行评估和优化,以便找到更加优秀的方案。
因此,钢管订购与运输问题的数学模型和求解方法只是问题的第一步,实际应用中还需要进行进一步的分析和优化。
数学建模钢管订购和运输

数学建模钢管订购和运输(总32页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除钢管的订购和运输优化模型摘要本文建立的多元非线性优化模型。
问题一在保证天然气管道铺设可以顺利实施的情况下,给出了钢管的订购与运输总费用最小的方案。
在求钢管由钢厂运输到站点的费用和铺设钢管时产生的运输费,根据图一,我们通过深度优先遍历的方法对整个图一进行路径搜索,然后根据每条搜索到的路径上的铁路和公路上的不同权重,找到了各个钢厂到各个天然气管道上的站点的最佳路径。
对于整个优化过程我们给出了相关的算法,并用matlab软件编程,经过一系列计算之后,得出了最优的订购与运输方案。
对于问题 1,我们求得的最优解为S钢管销价的变化对购运计划和总费对于问题2我们经过计算比较得出:6S的生产上限的变化购运计划和总费用影响最大。
用影响最大。
1对于问题 3,当天然气管道呈现的是一个树状图的时候,我们得到的最优关键字:非线性优化深度优先遍历最佳路径一、问题重述要铺设一条1521A A A →→→ 的输送天然气的主管道, 如图一所示(见下页)。
经筛选后可以生产这种主管道钢管的钢厂有721,,S S S 。
图中粗线表示铁路,单细线表示公路,双细线表示要铺设的管道(假设沿管道或者原来有公路,或者建有施工公路),圆圈表示火车站,每段铁路、公路和管道旁的阿拉伯数字表示里程(单位km)。
为方便计,1km 主管道钢管称为1单位钢管。
一个钢厂如果承担制造这种钢管,至少需要生产500个单位。
钢厂i S 在指定期限内能生产该钢管的最大数量为i s 个单位,钢管出厂销价1单位钢管为i p i 1 2 3 4 5 6 7 i s80080010002000 2000 2000 3000 i p160 155 155160 155150160 1里程(km) ≤300 301~350351~400 401~450 451~500 运价(万元) 2023262932里程(km) 501~600601~700 701~800 801~900 901~1000 运价(万元)37445055601000km 以上每增加1至100km 运价增加5万元。
钢管订购和运输求解(1)
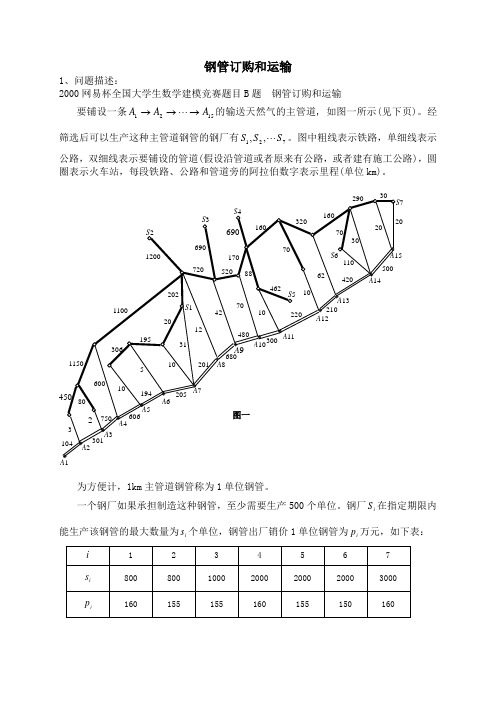
钢管订购和运输1、问题描述:2000网易杯全国大学生数学建模竞赛题目B 题 钢管订购和运输要铺设一条1521A A A →→→ 的输送天然气的主管道, 如图一所示(见下页)。
经筛选后可以生产这种主管道钢管的钢厂有721,,S S S 。
图中粗线表示铁路,单细线表示公路,双细线表示要铺设的管道(假设沿管道或者原来有公路,或者建有施工公路),圆圈表示火车站,每段铁路、公路和管道旁的阿拉伯数字表示里程(单位km)。
为方便计,1km 主管道钢管称为1单位钢管。
一个钢厂如果承担制造这种钢管,至少需要生产500个单位。
钢厂i S 在指定期限内能生产该钢管的最大数量为i s 个单位,钢管出厂销价1单位钢管为i p 万元,如下表:71单位钢管的铁路运价如下表:里程(km) ≤300 301~350 351~400 401~450 451~500 运价(万元) 2023262932里程(km) 501~600 601~700 701~800 801~900 901~1000运价(万元) 3744505560注:1000km 以上每增加1至100km 运价增加5万元。
公路运输费用为1单位钢管每公里0.1万元(不足整公里部分按整公里计算)。
钢管可由铁路、公路运往铺设地点(不只是运到点1521,,,A A A ,而是管道全线)。
(1)请制定一个主管道钢管的订购和运输计划,使总费用最小(给出总费用)。
(2)请就(1)的模型分析:哪个钢厂钢管的销价的变化对购运计划和总费用影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大,并给出相应的数字结果。
(3)如果要铺设的管道不是一条线,而是一个树形图,铁路、公路和管道构成网络,请就这种更一般的情形给出一种解决办法,并对图二按(1)的要求给出模型和结果。
2、运费矩阵的计算模型32 5 80101031 20 1242 701088 10 706270 302030450104 301750 606194205201 680480300 220210 420500600306195202720 690520 170 690462160 320160110 290115011001200A 19130190 260 100A 2A 3 A 4A 5 A 6A 7A 8A 9A 10 A 11A 12A 13 A 14A 15S 1S 2S 3S 4S 5 S 6 7 A 16A 17 A 18 A 20 (A 21)图二问题分析:我们只考虑本题第一问的求解。
钢管的订购及运输优化方案

钢管的订购及运输优化方案钢管是一种常见的工业材料,主要用于建筑、桥梁、机器制造和能源开采等领域。
订购和运输钢管需要考虑多方面因素,如规格、数量、质量、运输距离、运输方式等。
本文将介绍一些钢管订购及运输的优化方案。
一、钢管订购方案1. 确定钢管规格和数量在订购钢管前,首先需要了解工程或项目的具体需求,确定钢管的规格和数量。
不同的工程或项目需要的钢管规格和数量可能会有所不同,选择合适的规格和数量可以避免浪费和损失。
2. 寻找可靠的供应商选择可靠的供应商可以确保钢管的质量和供应稳定性。
可以通过市场调研、参加行业展会或咨询同行业的项目经理、工程师等人员来寻找可靠的供应商。
3. 确定采购合同和交付方式在确定供应商后,需要签订采购合同并确定交付方式。
采购合同要明确规定钢管的规格、数量、价格和交付日期等具体条款,避免误解和纠纷。
交付方式可以选择集装箱运输、散装运输或其他方式,根据具体情况灵活选择。
4. 质量控制为确保钢管的质量,采购方可以要求供应商提供产品质量证明、实际样品或第三方检测报告。
在收到钢管后,可以进行抽检或全检,检查钢管的尺寸、表面状态、壁厚和材质等指标,避免存在不合格品质的钢管进入工程或项目。
二、钢管运输方案1. 选择合适的运输方式钢管的运输可以选择公路运输、铁路运输、水路运输或航空运输等方式。
具体选择哪种方式需要综合考虑运输距离、运输量、运输时间、运输成本及货物安全等各方面因素。
2. 管理运输过程在钢管运输过程中,需要对货车、火车、船舶或飞机等交通工具进行监控,确保运输过程中货物的安全。
可以使用GPS或其他定位技术实时掌握货物的位置和状态,及时处理运输中遇到的问题和风险。
3. 管理卸货和储存在将钢管卸货到工厂、工地或仓库后,需要将其储存到指定位置并标记钢管的规格、数量等信息。
可以采用RFID等智能化技术对钢管进行管理,便于日后的存储和使用。
4. 管理短途运输在项目工期中,可能需要短途运输钢管到具体施工位置。
钢管订购和运输

真实路网示例:节点5696 到节点3006 有三条最短路径。
黑线为第一条,兰线为第二条,红线为第三条,共享部分路段。
利用最短路算法可得最短路(途中红线表示的路径)为:v1→v3→v5→v7。
利用最短路算法可得最短路(途中红线表示的路径)为:v→v→v。
图中各边权值表示相应网线的传输能力。
例如,计算机1与2之间传输信息需要但通过枚举的方法来求解已经很困难了!完整构图为:上图展示了从起点(8,0,0)到终点(4,4,0)不同路径。
两相邻节点之间的边代表一次转移,因此可假设每条边的权值为1。
问题就化成利用最短路算法求得最优解如红线所示。
思考:这个问题仅仅是一个游戏吗?钢厂S 1~S 7节点A 1~A 15铁路公路火车站原有公路施工公路铺设地点管网节点S1→S2的最短距离为1402,路径为S1→S15→S2。
从而S1→S2 的最低运费为85。
S20→S5的最短距离为710,路径为S20→S18→S19→S5。
从而S20→S5 的最低运费为50。
858550铁路线上各节点之间的最低运费示意图新图1.24.21.03.17.01.0于是,我们可以构造出一个新的赋权图 G(V, E),这是一个运输费用图,其中 V 为原图 的顶点集合,E 中每一条边的权值为前面求出 的运费。
图 G 的示意图如下。
对运输费用图 G 再次使用 Floyd 算法,求出 图 G 的最短路。
各 Si 到每个 Aj 的最短路值,就是一个单位 的钢管从钢厂 Si 到管网各个节点 Aj 的最小运输 费用 cij。
最小运价表如表 1 所示。
新图表 1 单位钢管从 Si 到 Aj 的最小运价(单位:万元)S1S2S3S4S5A1170.7000 215.7000 230.7000 260.7000 255.7000A2160.3000 205.3000 220.3000 250.3000 245.3000A3140.2000 190.2000 200.2000 235.2000 225.2000A498.6000171.6000 181.6000 216.6000 206.6000A538.0000111.0000 121.0000 156.0000 146.0000A620.500095.5000105.5000 140.5000 130.5000A73.100086.000096.0000131.0000 121.0000A821.200071.200086.2000116.2000 111.2000A964.2000114.200048.200084.200079.2000A1092.0000142.000082.000062.000057.0000A1196.0000146.000086.000051.000033.0000A12106.0000 156.000096.000061.000051.0000A13121.2000 171.2000 111.200076.200071.2000A14128.0000 178.0000 118.000083.000073.0000A15142.0000 192.0000 132.000097.000087.0000S6 265.7000 255.3000 235.2000 216.6000 156.0000 140.5000 131.0000 121.2000 84.2000 62.0000 51.0000 45.0000 26.2000 11.0000 28.0000S7 275.7000 265.3000 245.2000 226.6000 166.0000 150.5000 141.0000 131.2000 99.2000 76.0000 66.0000 56.0000 38.2000 26.00002.00001.2 整数约束的处理 由于给出的模型是非线性整数规划模型, 因此尚无合适的求解方法。
钢管订购和运输数学建模论文
钢管订购和运输摘要本文建立了一个运输问题的最优化模型。
通过对图(一)的分析,我们首先直观地将路线分成两段,将图分为两个子图建立了模型一, 利用分支定界法求得总费用最优解为1279496万元。
然后对模型一进行优化,得到全线的最优模型二,求得总费用最优解为1278632万元。
通过对最优模型二的分析,我们得出钢厂S1的上限产量和钢厂S6的销价的的变化对运购计划和总费用的影响最大,并给出了数据结果。
我们利用截取和连接的方法将树形图转化成为对线性图进行分析,并给出了一般的解决方法。
对图(二)给出的具体模型,类似与问题一,分别建立了模型三和模型四,求得最优解分别为1408859.4和1403948万元.一、 问题的提出已知有7个钢厂,可生产输送天然气主管道的钢管,用S i 表示(i=1,2,…,7)。
现有15个地点(A 1,A 2,…,A 15),沿着这15个地点铺设一条输送天然气的主管道。
为方便计,1km 主管道称为1单位钢管。
一个钢厂如果承担制造这种钢管,至少需要生产500个单位。
钢厂i S 在指定期限内能生产该钢管的最大数量为i s 个单位,钢管出厂销价1单位钢管为i p 万元,如下表:i1 2 3 4 5 6 7 i s800 800 1000 2000 2000 2000 3000 i p1601551551601551501601单位钢管的铁路运价如下表:里程(km) ≤300 301~350 351~400 401~450 451~500 运价(万元) 2023262932里程(km) 501~600 601~700 701~800 801~900 901~1000运价(万元) 37445055601000km 以上每增加1至100km 运价增加5万元。
公路运输费用为1单位钢管每公里0.1万元(不足整公里部分按整公里计算)。
钢管可由铁路、公路运往铺设地点(不只是运到点1521,,,A A A ,而是管道全线)。
钢管的订购与运输讲述
A j 1
y j1
Aj
yj
A j 1
设
y 是结点 j
A 向右铺设与 j
A 向左铺设之间的交点( j 1
y 1
0,
y15
0 )。
第二方案:也可以考虑在Aj左右各设一个变量!
j 2,3, ,14
2.求单位钢钢管的运输费 用为权的赋权图,再求最短路的权。
d j :相邻点 Aj 与 Aj1 之间的距离;
j 1,2,,14
四、模型的分析、建立、求解
1. 模型的分析与决策变量的设置 根据题目要求,要制定一个主管道钢管的订购
和运输计划,使总费用最小。 先看总费用:总费用由三部分组成: 1) 钢管的订购费。 支付钢厂订购钢管的费用。因为钢厂生产单位钢 管的出厂销价为常量,所以在运费相同的情况下, 应从销价低的钢厂订购钢管。
二、模型假设
1.沿铺设的主管道以有公路或者有施工公路。 2.在主管道上,每公里卸1单位的钢管。 3.公路运输费用为1单位钢管每公里0.1万元(不足整公
里部分按整公里计算) 4.在计算总费用时,只考虑运输费和购买钢管的费用,
而不考虑其他费用。 5.假设钢管在铁路运输路程超过1000km时,铁路每增
加1至100km,1单位钢管的运价增加5万元。
37
44
50
55
60
可考虑将铁路与公路分开考虑。
1) 将铁路图转化成费用图(与Ai对应编号)
将铁路与公路交界的点编号 bj:
图一 中去掉公路得铁路图:
1) 由于钢厂 Si 直接与铁路相连,所以可先求出钢厂 Si 到铁路与公路相交点 bj(对应于 Aj)的最短路径。
计算Si 到bi 的最小费用(与Ai对应编号)
钢管订购与运输
A题 DNA序列分类2000年6月,人类基因组计划中DNA全序列草图完成,预计2001年可以完成精确的全序列图,此后人类将拥有一本记录着自身生老病死及遗传进化的全部信息的“天书”。
这本大自然写成的“天书”是由4个字符A,T,C,G按一定顺序排成的长约30亿的序列,其中没有“断句”也没有标点符号,除了这4个字符表示4种碱基以外,人们对它包含的“内容”知之甚少,难以读懂。
破译这部世界上最巨量信息的“天书”是二十一世纪最重要的任务之一。
在这个目标中,研究DNA全序列具有什么结构,由这4个字符排成的看似随机的序列中隐藏着什么规律,又是解读这部天书的基础,是生物信息学(Bioinformatics)最重要的课题之一。
虽然人类对这部“天书”知之甚少,但也发现了DNA序列中的一些规律性和结构。
例如,在全序列中有一些是用于编码蛋白质的序列片段,即由这4个字符组成的64种不同的3字符串,其中大多数用于编码构成蛋白质的20种氨基酸。
又例如,在不用于编码蛋白质的序列片段中,A和T的含量特别多些,于是以某些碱基特别丰富作为特征去研究DNA序列的结构也取得了一些结果。
此外,利用统计的方法还发现序列的某些片段之间具有相关性,等等。
这些发现让人们相信,DNA序列中存在着局部的和全局性的结构,充分发掘序列的结构对理解DNA全序列是十分有意义的。
目前在这项研究中最普通的思想是省略序列的某些细节,突出特征,然后将其表示成适当的数学对象。
这种被称为粗粒化和模型化的方法往往有助于研究规律性和结构。
作为研究DNA序列的结构的尝试,提出以下对序列集合进行分类的问题:1)下面有20个已知类别的人工制造的序列(见下页),其中序列标号1—10 为A类,11-20为B类。
请从中提取特征,构造分类方法,并用这些已知类别的序列,衡量你的方法是否足够好。
然后用你认为满意的方法,对另外20个未标明类别的人工序列(标号21—40)进行分类,把结果用序号(按从小到大的顺序)标明它们的类别(无法分类的不写入):A类; B类。
钢管的订购及运输优化方案
钢管的订购及运输优化方案一、钢管的订购1.1 需求分析在进行钢管订购之前,首先需要进行需求分析。
钢管的形状、尺寸、材质、用途、数量等方面的需求都需要进行仔细的分析,以确保最终的采购结果符合要求。
1.2 供应商选择在确定钢管的需求后,需要寻找合适的供应商进行订购。
选择供应商要综合考虑各方面因素,包括价格、质量、交期、可靠性等方面。
可以通过询价、对比、调查等手段来寻找合适的供应商。
1.3 合同签订在选择好供应商之后,需要签订合同。
合同中要明确钢管数量、型号、质量标准、交货期限、运输方式、付款方式等内容,规范供应商的行为,确保合同执行的顺利进行。
二、钢管的运输2.1 运输方式选择根据钢管的数量、尺寸、重量、运输距离、要求到达时间等因素,选择合适的运输方式。
常见的运输方式包括铁路、公路、水路、空运等。
2.2 包装方式选择钢管在运输过程中需要进行包装,以保证其不受损坏。
包装方式应根据钢管的特点进行选择,常用的包装方式包括裸装、编织袋、塑料薄膜、木箱等。
2.3 运输路线优化在确定运输方式和包装方式之后,应针对具体的运输路线进行优化。
优化的原则包括缩短运输时间、降低运输成本、提高运输效率等方面。
2.4 运输管理在钢管运输过程中,需要进行运输管理。
管理内容包括钢管的装车、卸货、运输途中的安全监管等方面。
同时,应建立健全的运输记录管理体系,确保运输全程可追溯。
三、钢管订购及运输优化方案为了更好的优化钢管的订购及运输过程,可采取以下措施:3.1 制定钢管需求分析标准建立钢管需求分析的标准化体系,规范钢管订购的流程和细节。
该标准应涵盖钢管的形状、材质、性能、用途、数量等方面,确保符合实际需求。
3.2 建立供应商评价体系通过建立供应商评价体系,以价格、品质、信誉、交期等为考核指标,对供应商进行评价和排名,选用优质和稳定的供应商,确保采购的钢管质量和交货期的稳定。
3.3 采用智能供应链管理系统建立智能供应链管理系统,通过物流信息技术支持物流实时监控、自动化分配、预警预测、异常处理等功能,实现钢管订购及运输全流程的可视化和管理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
钢管订购和运输1、问题描述:2000网易杯全国大学生数学建模竞赛题目B 题 钢管订购和运输要铺设一条1521A A A →→→ 的输送天然气的主管道, 如图一所示(见下页)。
经筛选后可以生产这种主管道钢管的钢厂有721,,S S S 。
图中粗线表示铁路,单细线表示公路,双细线表示要铺设的管道(假设沿管道或者原来有公路,或者建有施工公路),圆圈表示火车站,每段铁路、公路和管道旁的阿拉伯数字表示里程(单位km)。
为方便计,1km 主管道钢管称为1单位钢管。
一个钢厂如果承担制造这种钢管,至少需要生产500个单位。
钢厂i S 在指定期限内能生产该钢管的最大数量为i s 个单位,钢管出厂销价1单位钢管为i p 万元,如下表:71单位钢管的铁路运价如下表:里程(km) ≤300 301~350 351~400 401~450 451~500 运价(万元) 2023262932里程(km) 501~600 601~700 701~800 801~900 901~1000运价(万元) 3744505560注:1000km 以上每增加1至100km 运价增加5万元。
公路运输费用为1单位钢管每公里0.1万元(不足整公里部分按整公里计算)。
钢管可由铁路、公路运往铺设地点(不只是运到点1521,,,A A A ,而是管道全线)。
(1)请制定一个主管道钢管的订购和运输计划,使总费用最小(给出总费用)。
(2)请就(1)的模型分析:哪个钢厂钢管的销价的变化对购运计划和总费用影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大,并给出相应的数字结果。
(3)如果要铺设的管道不是一条线,而是一个树形图,铁路、公路和管道构成网络,请就这种更一般的情形给出一种解决办法,并对图二按(1)的要求给出模型和结果。
2、运费矩阵的计算模型32 5 80101031 20 1242 701088 10 706270 302030450104 301750 606194205201 680480300 220210 420500600306195202720 690520 170 690462160 320160110 290115011001200A 19130190 260 100A 2A 3 A 4A 5 A 6A 7A 8A 9A 10 A 11A 12A 13 A 14A 15S 1S 2S 3S 4S 5 S 6 7 A 16A 17 A 18 A 20 (A 21)图二问题分析:我们只考虑本题第一问的求解。
首先,所有钢管必须要运到天然气主管道铺设线上的节点1521,,,A A A ,然后才能向左或右铺设,因此,必须求出从每个钢管厂721,,S S S (记为i=1,……,7)到每个节点1521,,,A A A (记为j=1,……,15)的每单位钢管最小运费Cij (不妨称为运费矩阵)及其对应的运输方式和线路。
因为题目中没有给出装卸成本,我们简单假设总是采用最经济的运输方式,虽然这个铺设在实际中可能不太接近现实,也就是说,在运输过程中需要多次装卸也是允许的(如铁路转公路,再转铁路,等等)。
自然的想法是运输路线应该是走最短路径,但由于有两种运输和计价方式(铁路和公路),公路运输费用为1单位钢管每公里0.1万元(不足整公里部分按整公里计算),运费是路程的线性函数;然而,铁路运费要通过运输里程查表得到,是一个阶梯函数。
这两种计价方式混合在一起,使得我们不能直接在整个铁路、公路混合的运输网络上计算最短路径作为运输路线,但可以分析分别在铁路、公路网上技计算最短路径,然后换算成相应的费用;最后在整个网络上以两个子网上相应的运费为权,再求一次最短路问题,就可以把它们统一成一个标准的运费矩阵。
铁路子网络:假设铁路运输线应该是走最短路径,而且采用连续路径计价方式一定优于分段计价方式(其实题中数据并不符合这一规定。
例如题中650km 的运价为44万元,而分成300km 和350km 两段计价只需要43万元,这种情况不太符合实际,可能是每题时选择数据的疏忽,我们不过多考虑这种情况)。
这时,我们可以把铁路运输子网独立出来,在这个网络上计算任意两个节点i ,j 之间的最短路径长度dij 1,然后按照这个最短路长度查铁路运价表得到最小费用Cij 1。
在无向网络上求任意两点之间最短路径算法很多,尤其对本题这种弧上的权(距离)全为正数的情况,存在相对比较的算法。
例如,求任意两点之间最短路径的Floyd-Warshall 算法是(可参阅网络优化的有关书籍) (24)这实际上是一种标号算法,其中n 是网络节点数(节点编号为1,2,……,n );wij 是给定的网络上相邻节点i,j 之间的直接距离(i,j 不相邻时取wij 充分大就可以了);u ij (k)可以看成是任意两个节点i,j 之间距离的中间迭代值,(或称为临时编号),即从节点i 到j 但不允许经过其他节点k,k+1,……,n 时的最短距离;自然u ij (k+1)就是i,j 之间的最短距离(或称为永久标号),即dij 1。
下面说明如何用LINGO 软件求最短路。
对图中节点编号(除已经编号的节点si 、Ai 外,在增加编号B1……B17,如图所示)。
实际上如果令铁路运输子网以外的节点间的距离为充分大,就可以把整个铁路、公路网络放在一起考虑。
这样虽然增加了问题的规模,但对于最后将两个网络合并起来考虑是有利的。
所以我们采用这种想法来做。
对于本题,我们设这个充分大的数为BIG=20000(km),显然这已经足够大了。
⎪⎩⎪⎨⎧=+=≠==+.,,1,,},,min{,,,0)()()()1()1()1(n k j i u u u u j i w u u k kj k ik k ij k ijij ij ii相应的LINGO程序如下(简要解释参见程序中的注释语句):model:!铁路运输网的运费计算;SETS:! NOTES表示节点集合;NODES /S1,S2,S3,S4,S5,S6,S7,A1,A2,A3,A4,A5,A6,A7,A8,A9,A10,A11,A12,A13,A14,A15,B1,B2,B3,B4,B5,B6,B7,B8,B9,B10,B11,B12,B13,B14,B15,B16,B17/;! 派生集合ROADS表示的是网络中的直接连接的道路(弧),由于并非所有节点间都有道路直接连接,所以将弧具体列出,这是稀疏集合; ROADS(NODES, NODE S)/! 要铺设的管道;A1,A2 A2,A3 A3,A4 A4,A5 A5,A6 A6,A7 A7,A8 A8,A9 A9,A10 A10,A11A11,A12 A12,A13 A13,A14 A14,A15! 公路网;B1,A2 B2,A3 B5,A4 B4,A5 B6,A6 B7,A7 S1,A7 B8,A8 B9,A9,B10,A10,B11,A11 B13,A12 B15,A13 S6,A14 B16,A14 B17,A15 S7,A15! 铁路网;B1,B3 B2,B3 B3,B5 B4,B6 B6,B7 B7,S1 B5,B8 B8,S1 B8,S2 B8,B9B9,S3 B9,B10 B10,B12 B12,B11 B11,S5 B12,S4 B12,B14 B14,B13B14,B15 B15,B16 B16,S6 B16,B17 B17,S7! 距离W0( i, j) 是节点i到j的直接距离(已知);/: W0;! 属性W表示基本的权矩阵(直接距离,考虑对称性并增加对不相邻弧的考虑), D1(i,j)表示节点i到j的最优行驶路线的路长,C1(i,j)表示节点i到j铁路运输的最小单位运价(万元);LINK(NODES, NODES): W, D1, C1;! 属性U表示迭代过程的权矩阵(临时标号);NNN(Nodes,nodes,nodes):U;ENDSETSDATA:! 针对铁路网计算时,将公路网的距离定为充分大(BIG=20000);BIG=20000;W0 = 20000 20000 20000 20000 20000 20000 20000 20000 20000 20000 20000 20000 20000 2000020000 20000 20000 20000 20000 20000 20000 20000 20000 2000020000 20000 20000 20000 20000 20000 20000450 80 1150 306 195 20 1100 202 1200 720690 520 170 88 462 690 160 70320 160 70 290 30;! 输出费用C1到文本文件中,以备后用;@TEXT(TrainCost.txt)=@writefor(nodes(i): @writefor(nodes(j): @format(c1(i,j),'5.0f')), @newline(1) );ENDDATACALC:! 无向网络,根据给定的直接距离具有对称性,得到初始距离矩阵;@FOR(LINK(i,j)|@IN(ROADS,i,j): W(i,j) = W0(i, j); W(j,i) = W0(i,j); );@FOR(LINK(i,j)|i#eq#j: W(i,j) = 0);! 所有无直接连接的节点间的距离定为充分大;@FOR(LINK(i,j)|i#ne#j #and# #not#@IN(ROADS,i,j) #and##not#@IN(ROADS,j,i): W(i,j) = BIG;W(j,i) = BIG; );!以下三个循环语句就是最短路计算公式(Floyd-Warshall算法);! k=1的初值;@FOR(NNN(i,j,k)|k#eq#1: U(i,j,k) = W(i,j) );!迭代过程;@For(nodes(k)|k#lt#@size(nodes): @FOR(LINK(i,j): U(i,j,k+1) = @if(U(i,j,k) #le# U(i,k,k)+U(k,j,k),U(i,j,k), U(i,k,k)+U(k,j,k))));! 最后一次迭代得到D1;@FOR(NNN(i,j,k)|k#eq#@size(nodes): D1(i,j) =@if(U(i,j,k) #le# U(i,k,k)+U(k,j,k),U(i,j,k), U(i,k,k)+U(k,j,k)) );!以下就是按最短路D1查找相应运费C1的计算公式;@FOR(LINK|D1#eq#0: C1=0);@FOR(LINK|D1#gt#0 #and# D1#le#300: C1=20);@FOR(LINK|D1#gt#300 #and# D1#le#350: C1=23);@FOR(LINK|D1#gt#350 #and# D1#le#400: C1=26);@FOR(LINK|D1#gt#400 #and# D1#le#450: C1=29);@FOR(LINK|D1#gt#450 #and# D1#le#500: C1=32);@FOR(LINK|D1#gt#500 #and# D1#le#600: C1=37);@FOR(LINK|D1#gt#600 #and# D1#le#700: C1=44);@FOR(LINK|D1#gt#700 #and# D1#le#800: C1=50);@FOR(LINK|D1#gt#800 #and# D1#le#900: C1=55);@FOR(LINK|D1#gt#900 #and# D1#le#1000: C1=60);@FOR(LINK|D1#gt#1000: C1 = 60 + 5*@floor(D1/100-10)+@if(@mod(D1,100)#eq#0,0,5) );ENDCALCend其实,这个LINGO模型中的计算过程完全是在计算(CALC)段完成的,所以LINGO很容易就得到了结果,相应的费用存放在文本文件TrainCost.txt中,这是一个39行,每行39个数据的文件,即铁路运输费用。
