视线与水平线的夹角叫做仰角
解直角三角形知识点及跟踪习题

解直角三角形知识点及跟踪习题 考点一、直角三角形的性质1、直角三角形的两个锐角互余可表示如下:∠C=90°⇒∠A+∠B=90°2、在直角三角形中,30°角所对的直角边等于斜边的一半。
∠A=30° 可表示如下: ⇒BC=21AB ∠C=90°3、直角三角形斜边上的中线等于斜边的一半 ∠ACB=90°可表示如下: ⇒CD=21AB=BD=AD D 为AB 的中点 知识点二.三角函数对于锐角A 的每一个确定的值,其对边与斜边、邻边与斜边、邻边与对边的比值也是惟一确定的. 因此这几个比值都是锐角∠A 的函数,记作sin A 、cos A 、tan A 、cot A ,即sin A =斜边的对边A ∠, cos A =斜边的邻边A ∠, tan A =的邻边的对边A A ∠∠, cot A = 的对边的邻边A A ∠∠分别叫做锐角∠A 的正弦、余弦、正切、余切,统称为锐角∠A 的三角函数.知识点三。
锐角三角函数的特征与性质:(1)锐角三角函数的值都是正实数,并且0<sin A <1,0<cos A <1 (2)tan A •cot A =1(3)补充:sin tan cos AAA,cos cot sin AA A (视情况定) (4)补充:已知锐角∠A ,则22sin cos 1AA(视情况定)(5)锐角三角函数的增减性当角度在0°~90°之间变化时,①.正弦值随着角度的增大(或减小)而增大(或减小) ②.余弦值随着角度的增大(或减小)而减小(或增大) ③.正切值随着角度的增大(或减小)而增大(或减小) ④.余切值随着角度的增大(或减小)而减小(或增大 知识点四、一些特殊角的三角函数值三角函数 0° 30°45°60°90° sinα 0 21 22 23 1 cos α 1 23 22 21 0 tan α 0 33 1 3不存在 cot α不存在3133 0︒15020米30米从上往下看,视线与水平线的夹角叫做俯角.(2在修路、挖河、开渠和筑坝时,设计纸上都要注明斜坡的倾斜程度. 如图19.4.5,坡面的铅垂高度(h )和水平长度(l )的比叫做坡面坡度 (或坡比).记作i ,即i =lh . 坡度通常写成1∶m 的形式,如i =1∶6. 坡面与水平面的夹角叫做坡角,记作a ,有i =lh=tan a 显然,坡度越大,坡角a 就越大,坡面就越陡. 知识点六.1.解直角三角形:在直角三角形中,除一个直角外,还有2个角和3条边共5个元素,由已知元素求出未知元素 的过程,叫做解直角三角形。
视线与水平线的夹角叫做仰角

——仰角俯角
平望二中 徐丽美
怎样测学设计了这样一个方案: 先在地面上距塔底B的适当地方, 比如100米的A处,架一个测角 仪,如测角仪高1.52米,那么 从C点可测出∠ECD=27°此时 CD⊥BE, 显然DE+BD即为铁 塔的高。
27°
C
D
sin 27°≈0.45,cos 27°≈0.89, tan 27°≈0.51
.
例题1:如图,AB和CD是同一地面上的两座相距 36米的楼房,在楼AB的楼顶A点测得楼CD的楼 顶C的仰角为45°,楼底D的俯角为30°.求楼 CD的高。
C
A 45° 30°
36
B
D
例题2:在山顶上点D处有一铁塔,在塔顶B 处测得地面上一点A的俯角α=60°,在塔底D 测得点A的俯角β=45°,已知塔高为30米,求 山高CD。
B α
D β
C
A
1.河的对岸有水塔AB, 今在C处测得塔 顶A的仰角为30°,前进 20米到D处, 又测得塔顶A的仰角为60°. 求塔高AB.
A
30°
60°
C
D
B
2.如图,在山脚C处测得山顶A的仰角为 45°,沿着水平地面向前300米到达D点, 在D点测得山顶A的仰角为600 , 求山高 AB。
1.52米
B
100米
A
视线 铅
仰角
垂O
俯角
水平线
线 视线
当从低处观测高处的目标时,视线与水平线 的夹角叫做仰角;
当从高处观测低处的目标时, 视线与水平线 的夹角叫做俯角。
如图,在地面上距塔底B的100米的A 处,架一个测角仪,测角仪高1.52米, 从C点测得仰角∠ECD=27°,求铁 塔的高度。(精确到1米)
视线与水平线的夹角叫做仰角

D β
C
A
1.河的对岸有水塔AB, 今在C处测得塔 顶A的仰角为30°,前进 20米到D处, 又测得塔顶A的仰角为60°. 求塔高AB.
A
30°
60°
C
D
B
2.如图,在山脚C处测得山顶A的仰角为 45°,沿着水平地面向前300米到达D点, 在D点测得山顶A的仰角为600 , 求山高 AB。
A
45° 60°
C
D
B
变式练习:
在山脚C处测得山顶A的仰角为45°, 沿着坡角 为30 °的斜坡前进300米到达D点,在D点测得 山顶A的仰角为600 ,求山高AB。
A
D
F
30°
C
EB
小结:
1.本节例题学习以后,我们可以得到解
直角三角形的两种基本图形:
A
A
B
C
D
B
D
C
2.学会把实际问题转化成数学问题;会用 方程思想解决问题.
怎样测出一座 铁塔的高度呢?
E
张磊同学设计了这样一个方案: 先在地面上距塔底B的适当地方, 比如100米的A处,架一个测角 仪,如测角仪高1.52米,那么 从C点可测出∠ECD=27°此时 CD⊥BE, 显然DE+BD即为铁 塔的高。
27°
C
D
1.52米
B
100米
A
视线 铅
仰角
垂O
俯角
水平线
线 视线
当从低处观测高处的目标时,视线与水平线 的夹角叫做仰角;
当从高处观测低处的目标时, 视线与水平线 的夹角叫做俯角。
如图,在地面上距塔底B的100米的A 处,架一个测角仪,测角仪高1.52米, 从C点测得仰角∠ECD=27°,求铁 塔的高度。(精确到1米)
三角函数应用举例(1)仰角俯角
28.2.2解直角三角形的应用(仰角和俯角)教案
中,
D
设计意图:通过分析题意,引导学生构造直角三角形,把已知条件转化到两个直角三角形里,根据已知的边角条件,恰当地选择锐角三角函数关系,解决实际问题,让学生初步认识到解直角三角形在实际问题中的应用;同时通过
一方面让学生进一步认识到解直角三角形在实际问题中的应用,另一方面,让学生意识到通过设未知数,建立方程也是解决实际问题时常用到
处,看另一栋楼楼顶的俯角为30°,看这
BC有多高?
A
E
尽管实际问题的背景发生了变化,
C E。
解直角三角形(仰角和俯角)讲义

解直角三角形(仰角和俯角)一、知识点讲解1、仰角和俯角的定义:在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角。
二、典例分析利用解直角三角形解决仰角、俯角问题例1 一数学兴趣小组为了测量河对岸树AB的高,在河岸边选择一点C,从C处测得树梢A的仰角为45°,沿BC方向后退10米到点D,再次测得A的仰角为30°,求树高.(结果精确到0.1米,参考数据:≈1.414,≈1.732)变式练习:1、如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为A、50B、51C、50+1D、101第1题第2题第3题2、如图,从坡顶C处测得地面A、B两点的俯角分别为30°、45°,如果此时C处的高度CD为150米,且点A、D、B在同一直线上,则AB两点间距离是米。
3、如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度.站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的距离为9m,则旗杆AB的高度是m(结果保留根号)4、如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,则楼房CD 的高度m(结果保留根号)反馈练习 基础夯实1、如图,某飞机在空中A 处探测到它的正下方地平面上目标C ,此时飞行高度AC =1200m ,从飞机上看地平面 A 、 1200m B 、 1200m C .、 1200m D 、 2400m第1题 第2题 第3题 第4题2、如图,为测量一棵与地面垂直的树OA 的高度,在距离树的底端30米的B 处,测得树顶A 的仰角∠ABO 为α,、 米B D 的仰角为α,从点A 测得点D 的仰角为β,已知甲、乙两建筑物之间的距离为a ,则甲建筑物的高AB 为 。
第02课时 仰角、俯角、方位角

1.(5 分)如图,某地修建高速公路,要从 B 地向 C 地修一座隧道(B,
C 在同一水平面上),为了测量 B,C 两地之间的距离,某工程师乘坐热
气球从 C 地出发,垂直上升 100 m 到达 A 处,在 A 处观察 B 地俯角为
30°,则 B,C 两地之间的距离为( A )
A.100 3 m
B.50 2 m
一、选择题(每小题 6 分,共 12 分)
7.如图,从热气球 C 处测得地面 A,B 两点的俯角分别为 30°,45°,
如果此时热气球 C 处的高度 CD 为 100 米,点 A,D,B 在同一直线上,
则 A,B 两点的距离是( D )
A.200 米
B.200 3 米
C.220 3 米
D.100( 3+1)米
CED=60°,sin∠CED=CCDE ,∴CE= sinC6D0°= 2
3+1.5 3 =(4+
3)
2
≈5.7(米),答:拉线CE的长约为5.7米
11.(14分)(2014·黔东南州)黔东南州某校九年级某班开展数学活 动,小明和小军合作用一副三角板测量学校的旗杆,小明站在B点测得 旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为 30°,已知小明和小军相距(BD)6米,小明的身高(AB)1.5米,小军的身 高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,
三、解答题(共42分) 10.(14分)(2014·钦州)如图,在电线杆CD上的C处引拉线CE,CF 固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米 的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30 °,求拉线CE的长.(结果保留小数点后一位,参考数据: 2 ≈ 1.414, 3≈1.732)
仰角、俯角 方位角概要

A 30˚ 60˚ D X
N1
N
60˚ 30˚
24海里
C
B
答:货轮无触礁危险。
1 某海防哨所(O)发现在它的北偏西30°,距离500m的 A处有一艘船.该船向正东方向航行,经过3分钟到达 哨所东北方向的B处.求这船的航速是每时多少km?
1、解直角三角形的关键是找到与已知和未知相关联
的直角三角形,当图形中没有直角三角形时,要通过 作辅助线构筑直角三角形(作某边上的高是常用的辅 助线);当问题以一个实际问题的形式给出时,要善 于读懂题意,把实际问题化归为直角三角形中的边角 关系。 2、一些解直角三角形的问题往往与其他知识联系, 所以在复习时要形成知识结构,要把解直角三角形作 为一种工具,能在解决各种数学问题时合理运用。
A
B
D
40
C
例2 河对岸有水塔AB.在C处测得塔顶的仰角为 30°,向塔前进12m到达D,在D处测得A的仰 角为45°,求塔高.
3、在山顶上处D有一铁塔,在塔顶B处测得地面上一 点A的俯角α =60o,在塔底D测得点A的俯角β =45o, 已知塔高BD=30米,求山高CD。 B α
D
β
C
A
2、在山脚C处测得山顶A的仰角为45°。问题 如下:(1)沿着水平地面向前300米到达D点, 在D点测得山顶A的仰角为600 , 求山高AB。
A
3x
45° 60°
C
D
x B
旗用的绳子(绳子足够长),王同学拿了 一把卷尺,并且向数学老师借了一把含300 的三角板去度量旗杆的高度。 ( ( 3)此时他的数学老师来了一看,建 2 )若王同学分别在点C、点D处将 ( 1 )若王同学将旗杆上绳子拉成仰角 0、 议王同学只准用卷尺去量,你能给王 旗杆上绳子分别拉成仰角为 60 为 600,如图用卷尺量得BC=4 米,则 同学设计方案完成任务吗? 300,如图量出 CD=8米,你能求出 旗杆 AB的高多少? 旗杆AB的长吗?
仰角俯角和方位角
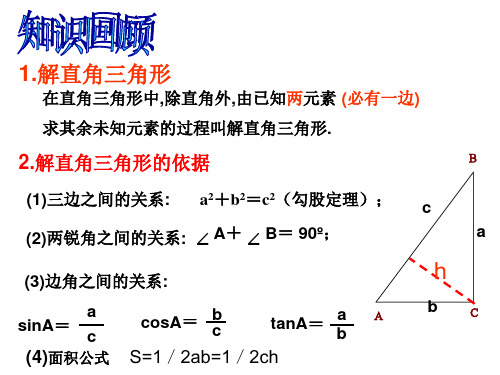
指南或指北的方向线与目标方向线构成小于 900的角,叫做方位角. 如图:点A在O的北偏东30° 点B在点O的南偏西45°(西南方向或南偏西 45°)
北 30° A
西
O 45°
东
B
南
例1. 如图,一艘海轮位于灯塔P的北偏东45°方向,距 离灯塔80海里的A处,它沿正南方向航行一段时间后, 到达位于灯塔P的南偏东30°方向上的B处,这时,海 轮所在的B处距离灯塔P有多远?
B
A
合作与探究
变题1:如图,直升飞机在长400米的跨江大桥 AB的上方P点处,且A、B、O三点在一条直线 上,在大桥的两端测得飞机的仰角分别为30° 和45 °,求飞机的高度PO .
P
答案: (200 3 200) 米
x
O
x
45°
30°
B
400米
A
1、如图,为了测量电线杆的高度AB,在离 电线杆30米的C处,用高1.20米的测角仪CD 测得电线杆顶端B的仰角a=30°,求电线 杆AB的高.
C
60° 45°
A
2km D
B
例3.如图,小岛P的周围20√2海里内有暗礁, 某渔船沿北偏东60°的AM方向航行,在A处测得 小岛P的方向为北偏东30°,距A处40海里,该 渔船若不改变航向,有无触礁的可能?若有, 渔船在A处应再向北偏东偏离多大角度才能脱险?
①弄清已知条件及要求解的问题。 ②画图将实际问题转化为数学问题。 ③寻找解题途径。 ⑷解、答
(2)、如果图中无直角三角形,可适当地作垂 线等辅助线,“化斜为直”,“善于转化”为 解直角三角形问题。 (3)、解直角三角形的有关问题常通过设未知 数、列方程(组)来解,也比较容易。常常设 图形中具有“双重身份”的线段或者是两个三 角形联系密切的特殊线段为未知数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
CD=24米,已知甲同学高1.75米,乙
同学高1.50米, A
请你求树AB
的高度. E M N
F
CB
D
商厦上从A到B悬挂了一条幅,小明和
小红家正好住在商厦对面的家属楼,
小明在四楼D点测得条幅端点A的仰
角为30°端点B的俯角 A
为45°小红在三楼C点 测得端点A的仰角为
商
D
45°端点B的俯角30° 厦
A
D
B
C
AB是一棵古树, 某同学在古树同
侧选取了C,D两点, C处测得树顶
A仰角为60° ,在D处测得树顶A
的仰角为30 °,又量得CD=24米,
已知此同学高1.5米,请你求树AB
的高度.
A
F
EH
D
CB
AB是一古树,甲同学在古树左侧C
处测得树顶A仰角为45°,乙同学
在D处测得树顶A仰角为30°量得
显示,看一栋高楼顶部C的仰角为
60°,看三楼D的仰角为45°C
已知二楼的高度为5 3
米 上升到空中
A时显示,看这栋高楼顶部C的仰角
为30°,看楼底
C
部B的俯角为60°
热气球与高楼 A
的水平距离为
D
12米求这栋楼
BC有多高?
B
变式:热气球的探
测器上升到空中时
显示,观测这栋楼 A
D
顶部的俯角为30°
C
底部的俯角为60°
若楼高为12 3 米,
求此时气球有多高?
B
练习1山CD上有一电视放射塔山高 CD为20米,在B处测得D,A的仰角分 别为45°60°求放射塔AD的高度
A
D
B
C
练习2山CD上有一电视放射塔,放 射塔高100米,在B处测得D,A的仰 角分别为45°60°,求山CD高度
老师站在二楼看到对面大树的顶
点C, 大树在楼的对面15米处,老
师在A处需测出
哪些量,根据哪 些知识就可以求 出大树的高度呢?
C
15米
AA
D
B
仰角和俯角
当视线在水平线
上方,视线与水
平线的夹角叫做 铅
仰角;
直
线
当视线在水平线下
方,视线与水平线
的夹角叫做俯角;
视 线
仰角 俯角
水平线
视 线
例1:热气球的探测器在地面A时
C
CD高3米,你能求出
条幅AB的长吗
B
广场上一充满氢气的气球P挂着广
告悬在空中,甲乙两人站在E,F处
测得气球的仰角分别为30度和45
度,E,F的高度
P
差AB为1m,水平
距离CD=5m,FD
高度为0.5m, E
A
问气球P的
F
B
高度.
CD
小结
