思维特训(二) 巧用乘法运算律
三年级数学思维训练:乘除巧算

三年级数学思维训练:乘除巧算以下是曲#为大家整理的【三年级数学思维训练:乘除巧算】,供大家参考!专题分析:前而我们己介绍了相关加、减法中的巧算,其中“凑整”是巧算中的一种方法,这种方法同样能够使用在乘除计算中。
要提升计算水平,除了加、减、乘、除基本运算要熟练之外,还要掌握一定的运算技巧。
巧算中,经常要用到一些运算定律,例如乘法交换律,乘法结合律,乘法分配律等,灵活使用运算定律,是提升巧算水平的关键。
例1:巧算下面各题。
(1)、25X8 (2)、16X125 (3)、16X25X25 (4)、125X32X25【思路点拨】(1)25X8 (2)16X125=25X (4X2)二(2X8)X125二25X4X2 二2X (8X125)=100X2 =2X1000=200 =2000(3)16X25X25 (4) 125X32X25二(4X4)X25X25 =125X(8X4)X25= (4X25) X (25X4) =(125X8) X (4X25)=100X100 =1000X100=10000 =100000例2:简便运算。
(1) 1304-5 (2) 4200宁25【思路点拨】这里能够使用商不变的性质,即被除数和除数同时扩大或缩小相同的倍数(0除外),商不变,因而:(1) 1304-5 (2) 42004-25=(130X2) 4- (5X2) = (4200X4) 4- (25X4)=2604-10 =168004-100=26 =168例3:计算31X25【思路点拨】题中31不能被4整除,但31可拆成4X7+3,这样就得到(4X7+3) X25,或者把25看做100F4也可求出得数。
31X25 或31X25=(4X7+3) X25 =31X (1004-4)二4X7X25+3X25 =31X1004-4=700+75 =31004-4=775 =775拓展训练:1、计算(1) 125X27X8 (2) 125X4X8X252、速算1、(1)25X12 (2)48X1252、仃)125X16X5 (2) 25X8X5 (3) 32X25X253、简便运算72004-25 36004-25 56004-25 320004-125 4、巧算29X25 17X25 221 X25 322 X255、速算78000 4-125 430004-1252561X25 3753X25。
四年级思维拓展- 速算与巧算(二)

速算与巧算(二)☜知识要点速算与巧算是学习数学、解决生活中数学问题的基础,只有掌握了速算与巧算才能又快又准的计算出正确的结果。
如何掌握此类问题的特征,并能熟练、灵活地加以运用,是研究此类问题所要思考的。
一、运用乘法运算定律巧算1.乘法交换律:a×b=b×a;2.乘法结合律:(a×b)×c=a×(b×c);3.乘法分配律:(a+b)×c=a×c+b×c ,(a-b)×c=a×c-b×c;4.乘法分配律的逆应用:(1)a×c+b×c=(a+b)×c,(2)a×c-b×c=(a-b)×c;【例1】简便计算:(1)(76×25)×4(2)32×25×2×125×5☝思路点拨:我们知道2×5 =10、4×25=100、8×125=1000、16×625=10000.在做乘法运算时我们可以先把相乘能得整十、整百、整千、整万、、、、、、的数相乘再和其它数相乘。
(1)式中有25、4我们可以利用乘法结合律来计算;(2)式有25、125,没有4、8怎么办呢?可以把32分成4×8,这样就可以使计算简便了。
☝标准答案:解:(1)(76×25)×4=76×(25×4)=76×100=7600(2)32×25×2×125×5=8×4×25×2×125×5=(8×125)×(4×25)×(2×5)=1000×100×10=1000000记住这些好朋友:2×5 =10;4×25=100;8×125=1000;16×625=10000,在乘法运算中看到2就要想到5,看到4就要想到25,看到8就要想到125,看到16就要想到625,没有的就想办法从其它数中分解出来!活学巧用1.(176×125)×322.32×25×2×125×689×53.45×32×625☜知识要点特殊的两位数乘以两位数的计算方法:1同头尾补:两个两位数相乘,十位上的数字相同,个位上的数字相加和等于10,这样的两个两位数就称为同头尾补。
三年级数学思维训练:乘除巧算

三年级数学思维训练:乘除巧算以下是###为大家整理的【三年级数学思维训练:乘除巧算】,供大家参考!专题分析:前面我们已介绍了相关加、减法中的巧算,其中“凑整”是巧算中的一种方法,这种方法同样能够使用在乘除计算中。
要提升计算水平,除了加、减、乘、除基本运算要熟练之外,还要掌握一定的运算技巧。
巧算中,经常要用到一些运算定律,例如乘法交换律,乘法结合律,乘法分配律等,灵活使用运算定律,是提升巧算水平的关键。
例1:巧算下面各题。
(1)、25×8 (2)、16×125 (3)、16×25×25 (4)、125×32×25【思路点拨】(1)25×8 (2)16×125=25×(4×2)=(2×8)×125=25×4×2 =2×(8×125)=100×2 =2×1000=200 =2000(3)16×25×25 (4)125×32×25=(4×4)×25×25 =125×(8×4)×25=(4×25)×(25×4) =(125×8)×(4×25)=100×100 =1000×100=10000 =100000例2:简便运算。
(1)130÷5 (2)4200÷25【思路点拨】这里能够使用商不变的性质,即被除数和除数同时扩大或缩小相同的倍数(0除外),商不变,因而:(1)130÷5 (2)4200÷25=(130×2)÷(5×2) =(4200×4)÷(25×4)=260÷10 =16800÷100=26 =168例3:计算31×25【思路点拨】题中31不能被4整除,但31可拆成4×7+3,这样就得到(4×7+3)×25,或者把25看做100÷4也可求出得数。
小学三年级数学思维训练-乘法速算法

专题分析:在日常生活中,有一些按照一定的规律不断重复的现象,如:认得十二生肖,一年有春夏秦东四个季节,一个星期七天等等,称为简单周期问题。
这类问题一般要利用余数的知识来解答。
在研究此类问题时,首先要仔细审题,判断其不断重复出现的规律,找出循环固定数,然后利用除法算式求出余数,最后根据余数得出正确结果。
例1:xx年10月1日是星期一,问10月25日是星期几?【思路导航】我们知道,每星期有7天,也就是说以7天位一个周期不断地重复。
从10月1日到10月25日经过25-1=24(天),24÷7=3(星期)……3(天),说明24天众包括3个星期还多3天,所以从10月1日开始过3个星期,最后一天还是星期一,从这最后一天起在过3天就应是星期四。
25-1=24(天)24÷7=3(星期)……3(天)答:10月25日是星期四。
例2:100个3相乘,积的个位数字是几?【思路导航】我们只需考虑积的个位数的排列规律。
1个3,积的个位数是3,2个3相乘的个位数是9,3个3相乘积的个位数是7,4个3相乘积的个位数是1,5个3相乘积的个位数是3,……可以发现鸡蛋个位数分别以3,9,7,1,不断重复出现,即每4个3记得个位数位一周期。
100÷4=25(个),因此100个3 相乘的记得个位数是第25个周期中的最后一个,即是1。
列式如下:33×3=93×3×3=273×3×3×3=813×3×3×3×3=243···100÷4=25(个)答:积的个位数字是1。
例3:A B C A B C A B……万事如意万事如意……上表中,每一列两个符号组成一组,如第一组“A万”,第二组“B事”,……问第20组是什么?【思路导航】上面一组以“A、B、C”三个字母为一个周期重复出现,下面一行一“万、事、如、意”四个字为一个周期重复出现,要求第20组,必须分别求出上、下两行各是什么符号才行。
三年级数学思维能力提升--乘除法巧算

三年级数学思维能力提升乘除法巧算知识与方法归纳基本特点:乘法巧算中几个常用凑整数:2×5 = 10 4×25 = 100 8×125 = 1000基本方法:(1)去括号和添括号法则在只有乘除运算的算式里,如果括号的前面是“÷”,那么不论是去掉括号或添上括号,括号里面运算符号都要改变,即“×”号变“÷”,“÷”变“×”;如果括号的前面是“×”,那么不论是去掉括号或添上括号,括号里面运算符号都不改变。
例如:① a×(b÷c)= a×b÷c ②a÷(b÷c)= a÷b×c(2)带符号“搬家”在只有乘除运算的算式里,每个数前面的运算符号是这个数的符号。
不论数移动到哪个位置,它前面的运算符号不变。
(3)利用乘法的意义巧算乘法是求几个相同加数的和的简便运算;可以利用乘法的意义,先计算出相同加数的个数,再计算结果,使计算简便。
(4)抵消思想同级运算能抵消的先抵消,就能使计算简便。
典型题讲解例1、用简便方法计算下列各题。
(1)19×25×4 (2)125×27×8 (3)5×25×4×2例2、用简便方法计算下列各题。
(1)125×32 (2)28×25 (3)25×6×64×125练习1、简便计算下列各题。
(1)36×4×25 (2)125×16×5 (3)125×48 ×5例3、简便计算下列各题。
(1)170÷5 (2)2100÷25 (3)35000÷125例4、简便计算下列各题。
(1)3100÷4÷25 (2)12000÷125÷8练习2、简便计算下列各题。
六年级思维训练2 四则运算
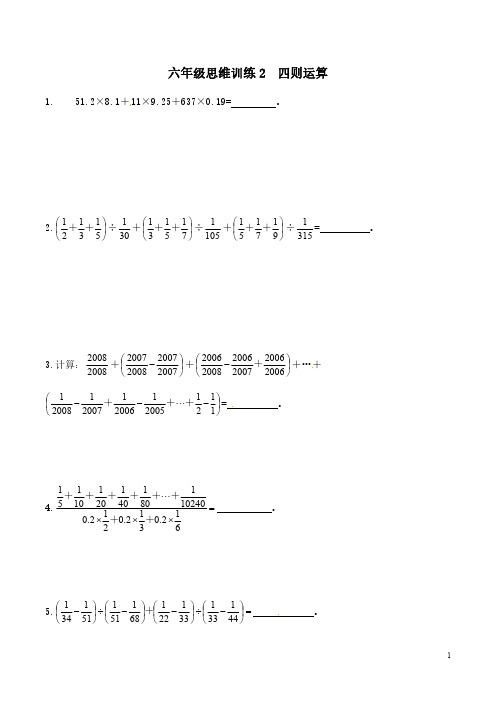
六年级思维训练2四则运算1.51.2×8.1+11×9.25+637×0.19=。
2.⎪⎭⎫ ⎝⎛513121++÷301+⎪⎭⎫ ⎝⎛715131++÷1051+⎪⎭⎫⎝⎛917151+÷3151=。
3.计算:20082008+⎪⎭⎫ ⎝⎛-2007200720082007+⎪⎭⎫⎝⎛-200620062007200620082006++…+⎪⎭⎫⎝⎛---112120051200612007120081+++ =。
4.=⨯⨯⨯612.0312.0212.010240180140120110151+++++++ 。
5.=⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛-441331331221681511511341+。
6.化简:24111359172115258168.132.46124.0155.009.0433851875.3+++÷⎥⎦⎤⎢⎣⎡-⨯⎪⎭⎫ ⎝⎛--÷-⨯⨯。
7.=÷⨯÷-2060452105206020159270020602224。
8.=⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛173327134173327125134173327173327125+++++++。
9.=-0016.01404.0122.0112.011++++。
10.=⨯--2332006620052007。
11.1+2×2+3×4+4×8+5×16+…+11×1024+12×2048=。
12.1×1+2×3+3×5+4×7+…+99×197=。
13.=22222377531+++++ 。
14.=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⨯⎪⎪⎭⎫ ⎝⎛÷⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛22222111818111181811118811118+++。
乘法运算的技巧与策略

乘法运算的技巧与策略乘法是数学中常见且重要的运算之一,广泛应用于各个领域。
掌握乘法运算的技巧与策略不仅可以提高计算速度,也有助于培养学生的逻辑思维和问题解决能力。
本文将分析乘法运算的各种技巧与策略,以帮助读者更好地掌握乘法运算。
1. 分解因数法分解因数法是乘法运算中常用的一种策略,特别适用于大数的乘法。
它的基本思想是将一个较大的数按照其因数的性质进行分解,然后利用分解后的因数分别进行乘法运算。
例如,计算48×9时,可以将48分解成4×12,然后进行乘法运算:4×9=36,12×9=108,再将两个结果相加,即36+108=144,即48×9=144。
2. 估算法估算法是在乘法运算中进行估算的一种策略。
它可以帮助读者快速得到一个接近的结果,以提高计算的效率。
例如,计算73×48可以先估算成70×50,结果为3500。
然后根据估算结果的误差进行调整,得到准确的答案。
3. 变换顺序法变换顺序法是在乘法运算中改变乘法顺序的一种策略。
它可以通过改变乘法的先后顺序,使得计算更加简便。
例如,计算48×9时,可以交换两个数的位置,变为9×48,得到相同的结果144。
通过变换顺序,可以根据计算的便利性选择更加简单的乘法方式。
4. 已知倍数法已知倍数法是乘法运算中利用已知倍数的一种策略。
例如,计算36×25时,可以利用25=5×5的性质,将乘法运算变为36×5×5。
然后通过计算36×5得到180,再将结果乘以5,即180×5=900,得到最终的答案900。
5. 递推法递推法是在乘法运算中通过逐步累加的方式进行计算的一种策略。
例如,计算9×8时,可以从1开始逐步累加乘积,得到9×1=9,9×2=18,9×3=27...直到9×8=72。
小学数学练习题乘法运算的逻辑思维训练

小学数学练习题乘法运算的逻辑思维训练数学是一门需要逻辑思维的学科,而对于小学生来说,培养他们的逻辑思维能力是非常重要的。
乘法运算作为数学中的基础知识,是培养逻辑思维能力的重要途径之一。
本文将通过一系列小学数学练习题,提供乘法运算的逻辑思维训练。
1. 两位数乘一位数的练习题如:23 × 4 = ?解析:这种类型的乘法运算需要学生掌握位数对齐、进位等概念。
在解决这类问题时,学生可以将两位数拆分成个位数和十位数,然后分别与一位数相乘,并将结果相加得出最终答案。
2. 三位数乘一位数的练习题如:456 × 3 = ?解析:这类乘法运算要求学生对进位的掌握更加熟练。
学生可以使用列竖式的方法进行计算,从个位数开始逐位相乘,并将每一步的结果相加,最终得出答案。
3. 两位数乘两位数的练习题如:34 × 56 = ?解析:这种类型的乘法运算需要学生对于乘法分配律的理解和运算符的灵活运用。
学生可以将两个两位数分别拆分成个位数和十位数,然后使用乘法分配律进行计算,并最终将结果相加得出答案。
4. 带有括号的乘法练习题如:(28 × 3) + (5 × 7) = ?解析:这类乘法运算需要学生对于运算顺序的掌握。
学生需要先计算括号内的乘法运算,然后将两个乘法的结果相加得到最终答案。
通过以上乘法运算练习题的训练,可以帮助小学生培养他们的逻辑思维能力。
这种思维能力在解决实际生活中的问题中十分有用,如购物时计算价格、计算零食的数量等。
而且,乘法运算的训练也为学生未来学习更高级的数学知识打下了坚实的基础。
除了练习题,还可以通过一些趣味的数学游戏来训练逻辑思维能力。
比如,给学生一个时间限制,要求他们在规定的时间内解决一定数量的乘法运算题目。
这样的活动可以增强学生的注意力和解决问题的速度,培养他们的逻辑思维能力。
总结起来,小学数学练习题中的乘法运算,可以有效地训练学生的逻辑思维能力。
通过不同难度的练习题,学生可以逐渐提高他们的计算能力和思维敏捷性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思维特训(二) 巧用乘法运算律
方法点津 ·
有理数混合运算是代数运算的基础,一些有特点的运算题目可利用乘法交换律、结合律、正逆用乘法对加法的分配律,达到简化运算、提高正确率的目的.
典题精练 ·
类型一 乘法交换律与结合律
1.计算:(12×32)×(23×43)×(34×54)×…×(20152016×20172016)×(20162017×20182017
). 2.阅读下列材料,回答问题:
(1+12)×(1-13)=32×23
=1; (1+12)×(1+14)×(1-13)×(1-15)=32×54×23×45=(32×23)×(54×45
)=1. 根据以上信息,求出下式的结果:
(1+12)×(1+14)×(1+16)×…×(1+120)×(1-13)×(1-15)×(1-17)×…×(1-121
). 类型二 逆用分配律
3.计算:(23)2×(-112)-(-23)2-12
÷(-1.52). 4.计算:0.7×149-15×(-137)+(-3)×(-14)+59×0.7+47
×15+5×(-25%). 类型三 正逆联用分配律
5.计算:(-321625)×132-(12+23-34-1112
)×(-24). 6.计算:⎝⎛⎭⎫1112-79-518×36-6×1.43+3.93×6.
7.计算:-427×⎝⎛⎭⎫-1112+1047×⎝⎛⎭⎫-1112-⎝⎛⎭⎫-557×⎝⎛⎭⎫-1312+⎝⎛⎭
⎫79-56+34×36. 8.计算:(-512-124-56)×(24×59-24×29+24×23
).
类型四 分配律与乘法交换律、结合律联用
9.计算:(-14-12+23)×|-24|-54
×(-2.5)×(-8). 类型五 运算律的实际应用
10.小豪的爸爸想在他设计的建筑物中绕制三个钢筋圆圈,其半径分别为0.24米、0.37米、0.39米.爸爸想考考小豪,就问小豪:如果制成三个钢筋圆圈各一个,应该买多长的钢筋(精确到0.1米)?小豪眼球一转,马上说出了结果,你能说出其中的奥妙之处吗?
详解详析
1.解:原式=12×(32×23)×(43×34)×(54×45)×…×(20162015×20152016)×(20172016×20162017)×20182017=12
×20182017=10092017
. 2.解:原式=32×54×76×…×2120×23×45×67×…×2021
=(32×23)×(54×45)×(76×67)×…×(2120×2021
) =1×1×1×…×1
=1.
3.解:原式=(23)2×(-112)-(-23)2+12×(23
)2 =(23)2×(-112-1+12
) =-89
. 4.解:原式=0.7×149+59×0.7-15×(-137)+47×15+(-3)×(-14
)+5×(-25%) =0.7×(149+59)-15×(-137-47)+(-14
)×(-3+5) =0.7×2+15×2+2×(-14
) =30.9.
5.解:原式=(-32-1625)×132+12×24+23×24-34×24-1112
×24 =-1-150
+12+16-18-22 =-13150
. 6.
解:原式=1112×36-79×36-518
×36+6×(3.93-1.43) =33-28-10+6×2.5
=-5+15
=10.
7.解:原式=(-
1312)×(-427+1047+557)+79×36-56×36+34×36=-1312
×12+28-30+27=12.
8.解:原式=(-512-124-56)×24×(59-29+23
) =(-512-124-56
)×24×1 =-512×24-124×24-56
×24 =-10-1-20
=-31.
9.解:原式=-14×24-12×24+23×24-54
×(2.5×8) =-6-12+16-25
=-27.
10.解:根据题意,得钢筋的长为2π×0.24+2π×0.37+2π×0.39=2π×(0.24+0.37+0.39)=2π≈6.3(米),
则制成三个钢筋圆圈各一个,应该买约6.3米长的钢筋.。
