成都中考近十年中考数学圆压轴题
2024成都中考数学一轮复习专题 圆的有关位置关系 (含解析)
2024成都中考数学一轮复习专题圆的有关位置关系一、单选题A．25︒B．2．（2023·重庆·统考中考真题）BC=，则OC的长度是（3A．3B．3．（2023·重庆·统考中考真题）∠的度数为（）则BACA．30︒B．A ．23B 5．（2023·四川泸州·统考中考真题）如图，在半圆O 与BC 相切于点E A ．4109B ．8二、填空题6．（2023·浙江嘉兴·统考中考真题）如图，点A 是O 外一点，AB ，AC 分别与O 相切于点B ，C ，点D 在 BDC上，已知50A ∠=︒，则D ∠的度数是___________．7．（2023·黑龙江·统考中考真题）如图，AB 是O 的直径，PA 切O 于点A ，PO 交O 于点C ，连接BC ，若28B ∠=︒，则P ∠=__________︒．8．（2023·湖南·统考中考真题）如图，AD 是O 的直径，AB 是O 的弦，BC 与O 相切于点B ，连接OB ，若65ABC ∠=︒，则BOD ∠的大小为__________．9．（2023·山东滨州上异于点,A B的一点，则10．（2023·浙江宁波·半圆O与BC相切于点AP的长为_____________11．（2023·河南·统考中考真题）OA=，125PA=，则12．（2023·湖北·统考中考真题）如图，在，切于点D，E，连接DE AO13．（2023·湖南·统考中考真题）如图，在半径作圆，当所作的圆与斜边14．（2023·山东烟台在函数(0,ky k x x=>15．（2023·四川·统考中考真题）如图，一点，过点P 向角的两边作垂线，垂足分别为16．（2023·湖南岳阳·统考中考真题）如图，在切点的切线与AB 的延长线交于点（1）若30,A AB ∠=︒=（2）若13CF AF =，则CE AE 17．（2023·上海·统考中考真题）在上，且CD DE =，如果B三、解答题(1)若25EAC ∠=︒，求ACD ∠(2)若2,1OB BD ==，求CE (1)求证：CF 是O 的切线；(2)若直径310,cos 5AD B ==，求FD 的长．20．（2023·江西·统考中考真题）如图，在ABC 中，464AB C =∠=︒，，以AB 为直径的O 与AC 相交于点D ，E 为 ABD 上一点，且40ADE ∠=︒．(1)求 BE的长；(2)若76EAD ∠=︒，求证：CB 为O 的切线．21．（2023·江苏连云港·统考中考真题）如图，在ABC 中，AB AC =，以AB 为直径的O 交边AC 于点D ，连接BD ，过点C 作CE AB ∥．(1)请用无刻度的直尺和圆规作图：过点B 作O 的切线，交CE 于点F ；（不写作法，保留作图痕迹，标明字母）(2)在（1）的条件下，求证：BD BF =．(1)求证：EF 与O 相切；(2)若1sin BF AFE =∠，(1)求证：DE 是O 的切线；(2)若30C ∠=︒，23CD =，求(1)求证：CF 是O 切线；(2)若10AF =，2sin 3F =，求(1)求证：CE 是O 的切线；(2)若6BC =，8AC =，求CE(1)求证：ACD DCB ∽；(2)求证：CD 是O 的切线；(3)若3tan ,105E AC ==，求O 的半径．①过点A 作切线AC ，且4AC =（点C 在A ②连接OC ，交O 于点D ；③连接BD ，与AC 交于点E ．(1)求证：BD 为O 的切线；(2)求AE 的长度．(1)尺规作图：如图，过点P 作出O 的两条切线求写作法和证明）(2)在（1）的条件下，若点D 在O 上（点(1)求证：BC 是O 的切线；(2)若5BD =，tan ADB ∠=30．（2023·福建·统考中考真题）如图，已知ABC 内接于,O CO 的延长线交AB 于点D ，交O 于点E ，交O 的切线AF 于点F ，且AF BC ∥．(1)求证：AO BE ∥；(2)求证：AO 平分BAC ∠．31．（2023·湖北荆州·统考中考真题）如图，在菱形ABCD 中，DH AB ⊥于H ，以DH 为直径的O 分别交AD ，BD 于点E ，F ，连接EF ．(1)求证：①CD 是O 的切线；②DEF DBA ∽；(2)若5AB =，6DB =，求sin DFE ∠．32．（2023·广西·统考中考真题）如图，PO 平分APD ∠，PA 与O 相切于点A ，延长AO 交PD 于点C ，过点O 作OB PD ⊥，垂足为B ．(1)求证：PB 是O 的切线；(2)若O 的半径为4，5OC =，求PA 的长．33．（2023·湖北黄冈·统考中考真题）如图，ABC 中，以AB 为直径的O 交BC 于点D ，DE 是O 的切线，且DE AC ⊥，垂足为E ，延长CA 交O 于点F ．(1)求证：AB AC =；(2)若3,6AE D E ==，求AF 的长．(1)求证：直线CD 是O 的切线；(2)若120ACD ∠=︒，CD =(1)求证：BC 是O 的切线；(2)若2CE =，求图中阴影部分的面积（结果保留(1)求证：直线DE是O的切线；(2)当30F∠=︒时，判断ABM(3)在（2）的条件下，ME= (1)求证：DC是O的切线；(2)若2AE=，1sin3AFD∠=，①求38．（2023·山东枣庄·统考中考真题）如图，AB 为O 的直径，点C 是 AD 的中点，过点C 做射线BD 的垂线，垂足为E ．(1)求证：CE 是O 切线；(2)若34BE AB ==，，求BC 的长；(3)在（2）的条件下，求阴影部分的面积（用含有π的式子表示）．39．（2023·山东临沂·统考中考真题）如图，O 是ABC 的外接圆，BD 是O 的直径，,AB AC AE BC =∥，E 为BD 的延长线与AE 的交点．(1)求证：AE 是O 的切线；(2)若75,2ABC BC ∠=︒=，求 CD的长．的切线；(1)求证：ED是O(2)若,65,AC BD AC CD==>，求BC⋅=⋅，求证：BM (3)若DE AM AC AD的切线；(1)求证：AB是O的半径与菱形的边长之比为(2)已知O(1)试判断直线AB与O的位置关系，并说明理由；(2)若3sin,5B O= 的半径为3，求AC(1)求证：直线AE是O是的切线；(2)若2sin3E=，O的半径为344．（2023·甘肃兰州·统考中考真题）如图，ABC 内接于O ，AB 是O 的直径， BCBD =，DE AC ⊥于点E ，DE 交BF 于点F ，交AB 于点G ，2BOD F ∠=∠，连接BD ．(1)求证：BF 是O 的切线；(2)判断DGB 的形状，并说明理由；(3)当2BD =时，求FG 的长．45．（2023·湖北·统考中考真题）如图，等腰ABC 内接于O ，AB AC =，BD 是边AC 上的中线，过点C 作AB 的平行线交BD 的延长线于点E ，BE 交O 于点F ，连接,AE FC ．(1)求证：AE 为O 的切线；(2)若O 的半径为5，6BC =，求FC 的长．参考答案一、单选题∵AB 切O 于点B ，∴90∠=︒ABO ，∵BD OA ∥，OCD ∠=∴25CDB ∠=︒，【点拨】本题考查了切线的性质，锐角三角函数，勾股定理，掌握切线的性质是解题的关键．3．【答案】B 【分析】连接OC ，先根据圆的切线的性质可得90OCD ∠=︒，从而可得40OCA ∠=︒，再根据等腰三角形的性质即可得．【详解】解：如图，连接OC ，直线CD 与O 相切，OC CD ∴⊥，90OCD ∴∠=︒，50ACD ∠=︒ ，40OCA ∴∠=︒，OA OC = ，40BAC OCA ∴∠=∠=︒，故选：B ．【点拨】本题考查了圆的切线的性质、等腰三角形的性质，熟练掌握圆的切线的性质是解题关键．4．【答案】B 【分析】作CF AB ⊥延长线于F 点，连接DE ，根据圆的基本性质以及切线的性质，分别利用勾股定理求解在Rt DEC △和Rt BFC △，最终得到DE ，即可根据正弦函数的定义求解．【详解】解：如图所示，作CF AB ⊥延长线于F 点，连接DE ，∵AD AB ⊥，AB CD ∥，∴90FAD ADC F ∠=∠=∠=∴四边形ADCF 为矩形，AF ∴AB 为D 的切线，∵90C ∠=︒，8AC =，BC ∴2210AB AC BC =+=∵以AD 为直径的半圆O 与二、填空题∵AB ，AC 分别与O 相切于点∴90ACO ABO ∠=∠=︒，∵50A ∠=︒，∴360909050COB ∠=︒-︒-︒-︒∵ BCBC =，∵PA 切O 于点A ，∴90OAP ∠=︒，∴18034P OAP AOP ∠=︒-∠-∠=︒．故答案为：34．【点拨】此题考查了切线的性质和三角形的外角的性质，三角形内角和定理等知识，解题的关键是熟练掌握以上知识点．8．【答案】50︒【分析】证明90OBC ∠=︒，可得906525OBD ∠=︒-︒=︒，结合OB OA =，证明25A OBA ∠=∠=︒，再利用三角形的外角的性质可得答案．【详解】解：∵BC 与O 相切于点B ，∴90OBC ∠=︒，∵65ABC ∠=︒，∴906525OBD ∠=︒-︒=︒，∵OB OA =，∴25A OBA ∠=∠=︒，∴22550BOD ∠=⨯︒=︒，故答案为：50︒【点拨】本题考查的是圆的切线的性质，等腰三角形的性质，三角形的外角的性质，熟记基本图形的性质是解本题的关键．9．【答案】62︒或118︒【分析】根据切线的性质得到90∠=∠=︒PAO PBO ，根据四边形内角和为360︒，得出AOB ∠，然后根据圆周角定理即可求解．【详解】解：如图所示，连接,AC BC ，当点C 在优弧 AB 上时，∵,PA PB 分别与O 相切于,A B 两点∴90∠=∠=︒PAO PBO ，∵56APB ∠=︒．∵以AE 为直径的半圆O ∴OD BC ⊥，OA OE =∴90ODB ∠=︒设OA OE OD r ===，则=的情况；不存在PD AD综上：AP的长为230或故答案为：230或6．【点拨】本题考查切线的性质，平行线分线段成比例，勾股定理，等腰三角形的定义．熟练掌握切线的性∵OA OB CA CB OC OC =⎧⎪=⎨⎪=⎩,∴OAC OBC ≌，∴90OAC OBC ∠=∠=︒，【点拨】本题主要考查了三角形内切圆，切线长定理，三角形内角和定理，线段垂直平分线的判定，三角形外角的性质，正确作出辅助线是解题的关键．13．【答案】24 5【分析】根据勾股定理，得由90OGC ODC OGH ∠=∠=∠=︒∵45ACB ∠=︒，∴45OHC ∠=︒，∴222OH OG ==，∴222CD DH ==+，同理2PQ PF =，∵2t PE PF =+，∴t PE PQ EQ =+=，当EQ 与O 相切时，EQ 有最大或最小值，同理，t 的最小值为EQ CE CD DE ==-综上，t 的取值范围是22224t ≤≤+故答案为：22224t ≤≤+．【点拨】本题考查了切线的性质，等腰直角三角形的性质，勾股定理，求得∵点C 为 BD的中点，∴ BCCD =，又∵30A ∠=︒，∴2BOC COD A ∠=∠=∠=∵点C 为 BD的中点，∴ BCCD =，∴OC BD ⊥，∵EC 是O 的切线，B过点A，且7AB=，∴e的半径为7，BE过点D，它的半径为r，且CE CD DE r∴=+=，2，=∠=︒BC C3,9022294∴=+=+，BE BC CE r在边AC上，点E在CA延长线上，D由函数图象可知，当即不等式①的解集为同理可得：不等式②则不等式组的解集为又10210 ，<≤r半径r的取值范围是故答案为：10r<≤三、解答题（2）∵CD 是O 的切线，OC 是 ∴90OCD ∠=︒．在Rt OCD △中，∵2,3OC OB OD OB BD ===+=，∴225CD OD OC =-=．∵90OCD AEC ∠=∠=︒，（2）解：∵3,cos 5B ADC B ∠=∠=，∴3cos 5ADC ∠=，∵在Rt ACD 中，3cos 5CD ADC AD∠==∴3cos 106,5CD AD ADC =⋅∠=⨯=（2）证明：如图所示，连接∵76EAD ∠=︒，40ADE ∠=∴180AED EAD =︒--∠∠∴64ABD AED ==︒∠∠，∴BC 是O 的切线．【点拨】本题主要考查了切线的判定，求弧长，圆周角定理，三角形内角和定理等等，正确作出辅助线是解题的关键．21．【答案】(1)见解析(2)见解析【分析】（1）根据尺规作图，过点B 作AB 的垂线，交CE 于点F ，即可求解；（2）根据题意切线的性质以及直径所对的圆周角是直角，证明BDC BFC ∠=∠，根据平行线的性质以及等腰三角形的性质得出BCD BCF =∠，进而证明()AAS BCD BCF ≌ ，即可得证．【详解】（1）解：方法不唯一，如图所示．（2）∵AB AC =，∴A ABC CB =∠∠．又∵CE AB ∥，∴ABC BCF ∠=∠，∴BCF ACB =∠∠．∵点D 在以AB 为直径的圆上，∴90ADB ∠=︒，∴=90BDC ∠︒．又∵BF 为O 的切线，∴90ABF ∠=︒．∵CE AB ∥，∴180BFC ABF ∠+∠=︒，∠∵=BE BE，∴EOB ∵2CAB EAB∠=∠，∴CAB EOB∠=∠，的直径，CD AB，AB为O⊥∴=，BC BDCOB BOD∴∠=∠，∠=∠，BOD DAF2⊥，由（1）得，OC CF，⊥CE AB∴∠=∠=︒，90OCF CEF∵C 为 BD的中点，∴CD BC = ，∴12∠=∠，又∵OA OC =，∴23∠∠=，∵AB 为O 的直径，∴90ADB ∠=︒，∴90∠+∠=︒A ABD ，∵OB OD =，∴ABD ODB ∠=∠，∵AC 是O 的切线，∴OA AC ⊥，∵3OA =，4AC =，∴225OC OA AC =+=，①连接PO，分别以点,P O为圆心，点A，②以点A为圆心，OA为半径画圆，与PE PF即为所求；则直线,上（点（2）如图所示，点D在OPE PF,的半径，∵OA，OD是O=，∴OA OD∠=∠，∴OAD ODA∠，∵AD平分BAC【点拨】本题考查角平分线的定义、平行线的判定与性质、切线的判定、直角三角形的性质、圆周角定理、等边三角形的判定与性质、垂直平分线的判定与性质及扇形的面积公式，熟练掌握相关知识是解题的关键．30．【答案】(1)见解析(2)见解析。
中考压轴题圆的切线证明与计算(中考真题)
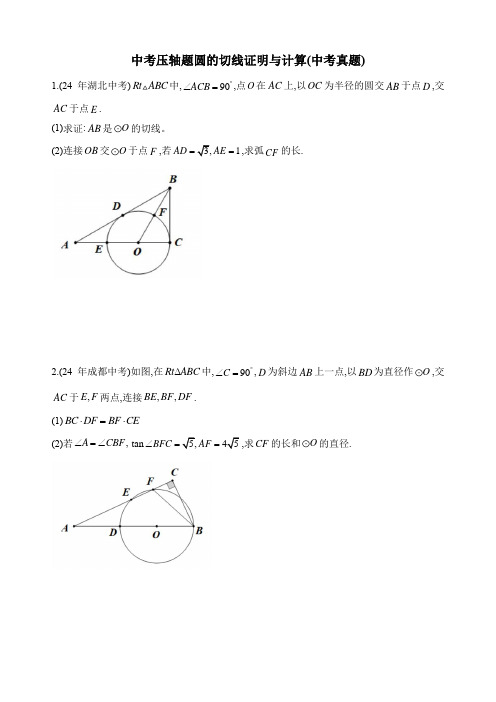
中考压轴题圆的切线证明与计算(中考真题)1.(24年湖北中考)Rt ABC 中,90ACB ︒∠=,点O 在AC 上,以OC 为半径的圆交AB 于点D ,交AC 于点E .(1)求证:AB 是O 的切线。
(2)连接OB 交O 于点F ,若1AD AE ==,求弧CF 的长.2.(24年成都中考)如图,在Rt ABC ∆中,90C ︒∠=,D 为斜边AB 上一点,以BD 为直径作O ,交AC 于,E F 两点,连接,,BE BF DF .(1)BC DF BF CE ⋅=⋅(2)若,A CBF ∠=∠tan BFC AF ∠==,求CF 的长和O 的直径.3.(24年浙江中考)如图,在圆内接四边形ABCD中,AD<AC,ADC BAD∠<∠,延长AD至点E,使AE=AC,延长BA至点F,连结EF,使AFE ADC∠=∠.(1)若60O∠的度数.∠=,CD为直径,求ABDAFE(2)求证:①EF∥BC ②EF=BD.4.(24年辽宁中考)如图,O是ABC的外接圆,AB是O的直径,点D在BC上,AC BD=,E ∠=∠．在BA的延长线上,CEA CAD(1)如图1,求证:CE是O的切线OA=,求BD的长．(2)如图2,若2CEA DAB∠=∠,85.(24年安徽中考)如图,O 是ABC ∆的外接圆,D 是直径AB 上一点,ACD ∠的平分线交AB 于点E ,交O 于另一点,.F FA FE =(1)求证:;CD AB ⊥(2)设FM AB ⊥,垂足为M ,若1OM OE ==,求AC 的长.6.(24年新疆中考)如图,在O 中,AB 是O 的直径,弦CD 交AB 于点E,AD BD =.(1)求证：△ACD ∽△ECB.(2)若AC=3,BC=1,求CE 的长.7.(24年江西中考)如图,AB 是半圆O 的直径,点D 是弦AC 延长线上一点,连接BD BC ，,60D ABC ∠=∠=︒．(1)求证:BD 是半圆O 的切线.(2)当3BC =时,求AC 的长．8.(24年呼伦贝尔中考)如图,在ABC 中,以AB 为直径的O 交BC 于点,D DE AC ⊥,垂足为E ． O 的两条弦,FB FD 相交于点,F DAE BFD ∠∠=．(1)求证:DE 是O 的切线;(2)若30,C CD ∠=︒=,求扇形OBD 的面积．9.(24年扬州中考)在综合实践活动中,“特殊到一般”是一种常用方法,我们可以先研究特殊情况,猜想结论,然后再研究一般情况,证明结论．如图,已知ABC ,CA CB =, O 是ABC 的外接圆,点D 在O 上(AD BD >),连接AD ,BD ,CD ．【特殊化感知】(1)如图1,若60ACB ∠=︒,点D 在AO 延长线上,则AD BD -与CD 的数量关系为________【一般化探究】(2)如图2,若60ACB ∠=︒,点C ,D 在AB 同侧,判断AD BD -与CD 的数量关系并说明理由【拓展性延伸】(3)若ACB α∠=,直接写出AD ,BD ,CD 满足的数量关系．(用含α的式子表示)10.(24年赤峰中考)如图,ABC中,90ACB∠=︒,AC BC=,O经过B,C两点,与斜边AB交于点E,连接CO并延长交AB于点M,交O于点D,过点E作EF CD∥,交AC于点F．(1)求证:EF是O的切线;(2)若BM=,1tan2BCD∠=,求OM的长．11.(24年绥化中考)如图1,O是正方形ABCD对角线上一点,以O为圆心,OC长为半径的O 与AD相切于点E,与AC相交于点F．(1)求证:AB与O相切．(2)若正方形ABCD1,求O的半径．(3)如图2,在(2)的条件下,若点M是半径OC上的一个动点,过点M作MN OC⊥交CE于点N．当:1:4CM FM=时,求CN的长．12.(24年河北中考)已知O的半径为3,弦MN=ABC中.∠=︒==在平面上,先将ABC和O按图1位置摆放(点B与点N重90,3,ABC AB BC合,点A在O上,点C在O内),随后移动ABC,使点B在弦MN上移动,点A始终在O上=．随之移动,设BN x(1)当点B与点N重合时,求劣弧AN的长.(2)当OA MN∥时,如图2,求点B到OA的距离,并求此时x的值.(3)设点O到BC的距离为d．①当点A在劣弧MN上,且过点A的切线与AC垂直时,求d的值.①直接写出d的最小值．13.(24年滨州中考)【教材呈现】现行人教版九年级下册数学教材85页“拓广探索”第14题: 如图,在锐角ABC 中,探究sin a A ,sin b B ,sin c C之间的关系．(提示:分别作AB 和BC 边上的高．)【得出结论】sin sin sin a b c A B C==． 【基础应用】在ABC 中,75B ∠=︒,45C ∠=︒,2BC =,利用以上结论求AB 的长;【推广证明】进一步研究发现,sin sin sin a b c A B C==不仅在锐角三角形中成立,在任意三角形中均成立,并且还满足2sin sin sin a b c R A B C===(R 为ABC 外接圆的半径)． 请利用图1证明:2sin sin sin a b c R A B C ===．【拓展应用】如图2,四边形ABCD 中,2AB =,3BC =,4CD =,90B C ∠=∠=︒．求过A,B,D 三点的圆的半径．14.(24年苏州中考)如图,ABC 中,AB =为AB 中点,BAC BCD ∠=∠cos ADC ∠=. O 是ACD 的外接圆．(1)求BC 的长(2)求O 的半径．15.(24年乐山中考)如图,O 是ABC 的外接圆,AB 为直径,过点C 作O 的切线CD 交BA 延长线于点D,点E 为CB 上一点,且AC CE =．(1)求证:DC AE ∥;(2)若EF 垂直平分OB ,3DA =,求阴影部分的面积．16.(24年武汉中考)如图,ABC ∆为等腰三角形,O 是底边BC 的中点,腰AC 与半圆O 相切于点D ,底边BC 与半圆O 交于E ,F 两点．(1)求证:AB 与半圆O 相切(2)连接OA ．若4CD =,2CF =,求sin OAC ∠的值．17.(24年甘肃武威中考)如图,AB 是O 的直径,BC BD =,点E 在AD 的延长线上,且ADC AEB ∠=∠．(1)求证:BE 是O 的切线;(2)当O 的半径为2,3BC =时,求tan AEB ∠的值．18.(24年深圳中考)如图,在ABD △中,AB BD =,O 为ABD △的外接圆,BE 为O 的切线,AC 为O 的直径,连接DC 并延长交BE 于点E ．(1)求证:DE BE ⊥(2)若AB =5BE =,求O 的半径．19.(24年盐城中考)如图,点C 在以AB 为直径的O 上,过点C 作O 的切线l,过点A 作AD l ⊥,垂足为D,连接AC BC 、．(1)求证:ABC ACD △△∽;(2)若5AC =,4CD =,求O 的半径．20.(24年广西中考)如图,已知O 是ABC ∆的外接圆,AB AC =．点D,E 分别是BC ,AC 的中点,连接DE 并延长至点F,使DE EF =,连接AF ．(1)求证:四边形ABDF 是平行四边形(2)求证:AF 与O 相切(3)若3tan 4BAC ∠=,12BC =,求O 的半径． 21.(24年四川广安中考)如图,点C 在以AB 为直径的O 上,点D 在BA 的延长线上,DCA CBA ∠=∠．(1)求证:DC 是O 的切线;(2)点G 是半径OB 上的点,过点G 作OB 的垂线与BC 交于点F ,与DC 的延长线交于点E ,若4sin 5D =,2DA FG ==,求CE 的长．22.(24年四川南充中考)如图,在O 中,AB 是直径,AE 是弦,点F 是AE 上一点,AF BE =,,AE BF 交于点C,点D 为BF 延长线上一点,且CAD CDA ∠=∠．(1)求证:AD 是O 的切线．(2)若4,BE AD ==求O 的半径长．23.(24年四川泸州中考)如图,ABC ∆是O 的内接三角形,AB 是O 的直径,过点B 作O 的切线与AC 的延长线交于点D,点E 在O 上,AC CE =,CE 交AB 于点F ．(1)求证:CAE D ∠=∠;(2)过点C 作CG AB ⊥于点G,若3OA =,BD =求FG 的长．24.(24年四川德阳中考)已知O 的半径为5,B C 、是O 上两定点,点A 是O 上一动点,且60,BAC BAC ∠=︒∠的平分线交O 于点D ．(1)证明:点D 为BC 上一定点;(2)过点D 作BC 的平行线交AB 的延长线于点F ．①判断DF 与O 的位置关系,并说明理由;①若ABC 为锐角三角形,求DF 的取值范围．25.(24年四川宜宾中考)如图,ABC 内接于O ,10AB AC ==,过点A 作AE BC ∥,交O 的直径BD 的延长线于点E,连接CD ．(1)求证:AE 是O 的切线;(2)若1tan 2ABE ∠=,求CD 和DE 的长．26.(24年内蒙古通辽中考)如图,ABC 中,90ACB ∠=︒,点O 为AC 边上一点,以点O 为圆心,OC 为半径作圆与AB 相切于点D ,连接CD ．(1)求证:2ABC ACD ∠=∠;(2)若8AC =,6BC =,求O 的半径．27.(24年四川达州中考)如图,BD 是O 的直径．四边形ABCD 内接于O ．连接AC ,且AB AC =,以AD 为边作DAF ACD ∠=∠交BD 的延长线于点F ．(1)求证:AF 是O 的切线;(2)过点A 作AE BD ⊥交BD 于点E ．若3CD DE =,求cos ABC ∠的值．28.(24年四川遂宁中考)如图,AB 是O 的直径,AC 是一条弦,点D 是AC 的中点,DN AB ⊥于点E ,交AC 于点F ,连结DB 交AC 于点G ．(1)求证:AF DF =;(2)延长GD 至点M ,使DM DG =,连接AM ．①求证:AM 是O 的切线;①若6DG =,5DF =,求O 的半径．29.(24年包头中考)如图,AB 是O 的直径,,BC BD 是O 的两条弦,点C 与点D 在AB 的两侧,E 是OB 上一点(OE BE >),连接,OC CE ,且2BOC BCE ∠=∠．(1)如图1,若1BE =,CE =求O 的半径;(2)如图2,若2BD OE =,求证:BD OC ∥．(请用两种证法解答)30.(24年四川自贡中考)在Rt ABC △中,90C ∠=︒,O 是ABC 的内切圆,切点分别为D,E,F ．(1)图1中三组相等的线段分别是CE CF =,AF =________,BD =________;若3AC =,4BC =,则O 半径长为________;(2)如图2,延长AC 到点M,使AM AB =,过点M 作MN AB ⊥于点N ．求证:MN 是O 的切线．31.(24年山东枣庄中考)如图,在四边形ABCD 中,AD BC ∥,60DAB ∠=︒,22AB BC AD ===． 以点A 为圆心,以AD 为半径作DE 交AB 于点E ,以点B 为圆心,以BE 为半径作EF 所交BC 于点F ,连接FD 交EF 于另一点G ,连接CG ．(1)求证：CG 为EF 所在圆的切线(2)求图中阴影部分面积．(结果保留π)32.(24年青海中考) 如图,直线AB经过点C,且OA OB=．=,CA CB(1)求证:直线AB是O的切线;(2)若圆的半径为4,30∠=︒,求阴影部分的面积．B中考压轴题圆的切线证明与计算答案1.(24年湖北中考)【答案】(1)略 (2)弧CF 的长为3π2.(24年成都中考)【答案】(1)略(2)CF =;O 的直径为3.(24年浙江中考)【答案】(1)30o (2)证明略4.(24年辽宁中考)【答案】(1)见详解 (2)2π5.(24年安徽中考)【答案】(1)略 (2).6.(24年新疆中考)【答案】(1) 略 (2)CE =.7.(24年江西中考)【答案】(1)见解析 (2)2π8.(24年呼伦贝尔中考)【答案】(1)略 (2)43π 9.(24年扬州中考)【答案】(1)AD BD CD -=.(2)AD BD CD -=(3)当D 在BC 上时,2sin 2CD AD BD α⋅=-.当D 在AB 上时,2sin 2CD AD BD α⋅=+10.(24年赤峰中考)【答案】(1)略 (2)OM =11.(24年绥化中考)【答案】(1)证明略 (2)12.(24年河北中考)【答案】(1)π (2)点B 到OA 的距离为2;3 (3)①3d =2313.(24年滨州中考)【答案】教材呈现:见解析;基础应用:AB =;推广证明:见解析;拓展应用:6R =．14.(24年苏州中考)【答案】(1)4BC = (2)O 的半径为715.(24年乐山中考)【答案】(1)略 (2)3π-16.(24年武汉中考)【答案】(1)略 (2)4517.(24年甘肃武威中考)【答案】(1)略 (2)tan 3AEB ∠=18.(24年深圳中考)【答案】(1)略 (2)19.(24年盐城中考)【答案】(1)略 (2)25620.(24年广西中考)【答案】(1)略 (2)略 (3)1021.(24年四川广安中考)【答案】(1)略 (2)1422.(24年四川南充中考)【答案】(1)略 (2)23.(24年四川泸州中考)【答案】(1)证明略 (2)45 24.(24年四川德阳中考)【答案】(1)证明略(2)①DF 与O 相切,理由见解析;①DF 的取值范围为2DF <<25.(24年四川宜宾中考)【答案】(1)略 (2)CD =DE =． 26.(24年内蒙古通辽中考)【答案】(1)证明略 (2)327.(24年四川达州中考)【答案】(1)证明略 28.(24年四川遂宁中考)【答案】(1)证明略 (2)①证明略,①O 的半径为203． 29.(24年包头中考)【答案】(1)3 (2)略30.(24年四川自贡中考)【答案】(1)AD ;BE ;1 (2)略31.(24年山东枣庄中考)【答案】(1)略 3π32.(24年青海中考) 【答案】(1)详见解析 (2) 83S π=阴影。
中考数学《圆》真题压轴题总汇【附解析】
中考数学《圆》真题压轴题总汇【附解析】1．（2019•阿坝州）如图，AB为⊙O的直径，C为⊙O上的一点，∠BCH＝∠A，∠H＝90°，HB的延长线交⊙O于点D，连接CD．（1）求证：CH是⊙O的切线；（2）若B为DH的中点，求tan D的值．2．（2019•德阳）如图，AB是⊙O的直径，点C为⊙O上一点，OE⊥BC于点H，交⊙O于点E，点D为OE的延长线上一点，DC的延长线与BA的延长线交于点F，且∠BOD＝∠BCD，连结BD、AC、CE．（1）求证：DF为⊙O的切线；（2）过E作EG⊥FD于点G，求证：△CHE≌△CGE；（3）如果AF＝1，sin∠FCA＝，求EG的长．3．（2019•雅安）如图，已知AB是⊙O的直径，AC，BC是⊙O的弦，OE∥AC交BC于E，过点B作⊙O的切线交OE的延长线于点D，连接DC并延长交BA的延长线于点F．（1）求证：DC是⊙O的切线；（2）若∠ABC＝30°，AB＝8，求线段CF的长．4．（2019•内江）AB与⊙O相切于点A，直线l与⊙O相离，OB⊥l于点B，且OB＝5，OB 与⊙O交于点P，AP的延长线交直线l于点C．（1）求证：AB＝BC；（2）若⊙O的半径为3，求线段AP的长；（3）若在⊙O上存在点G，使△GBC是以BC为底边的等腰三角形，求⊙O的半径r的取值范围．5．（2019•广元）如图，AB是⊙O的直径，点P是BA延长线上一点，过点P作⊙O的切线PC，切点是C，过点C作弦CD⊥AB于E，连接CO，CB．（1）求证：PD是⊙O的切线；（2）若AB＝10，tan B＝，求PA的长；（3）试探究线段AB，OE，OP之间的数量关系，并说明理由．6．（2019•成都）如图，AB为⊙O的直径，C，D为圆上的两点，OC∥BD，弦AD，BC相交于点E．（1）求证：＝；（2）若CE＝1，EB＝3，求⊙O的半径；（3）在（2）的条件下，过点C作⊙O的切线，交BA的延长线于点P，过点P作PQ∥CB 交⊙O于F，Q两点（点F在线段PQ上），求PQ的长．7．（2019•资阳）如图，AC是⊙O的直径，PA切⊙O于点A，PB切⊙O于点B，且∠APB＝60°．（1）求∠BAC的度数；（2）若PA＝1，求点O到弦AB的距离．8．（2019•绵阳）如图，AB是⊙O的直径，点C为的中点，CF为⊙O的弦，且CF⊥AB，垂足为E，连接BD交CF于点G，连接CD，AD，BF．（1）求证：△BFG≌△CDG；（2）若AD＝BE＝2，求BF的长．9．（2019•乐山）如图，直线l与⊙O相离，OA⊥l于点A，与⊙O相交于点P，OA＝5．C 是直线l上一点，连结CP并延长交⊙O于另一点B，且AB＝AC．（1）求证：AB是⊙O的切线；（2）若⊙O的半径为3，求线段BP的长．10．（2019•泰州）如图，四边形ABCD内接于⊙O，AC为⊙O的直径，D为的中点，过点D作DE∥AC，交BC的延长线于点E．（1）判断DE与⊙O的位置关系，并说明理由；（2）若⊙O的半径为5，AB＝8，求CE的长．11．（2019•乐山）已知关于x的一元二次方程x2﹣（k+4）x+4k＝0．（1）求证：无论k为任何实数，此方程总有两个实数根；（2）若方程的两个实数根为x1、x2，满足+＝，求k的值；（3）若Rt△ABC的斜边为5，另外两条边的长恰好是方程的两个根x1、x2，求Rt△ABC的内切圆半径．12．（2019•株洲）四边形ABCD是⊙O的圆内接四边形，线段AB是⊙O的直径，连结AC、BD．点H是线段BD上的一点，连结AH、CH，且∠ACH＝∠CBD，AD＝CH，BA的延长线与CD的延长线相交于点P．（1）求证：四边形ADCH是平行四边形；（2）若AC＝BC，PB＝PD，AB+CD＝2（+1）①求证：△DHC为等腰直角三角形；②求CH的长度．13．（2019•巴中）如图，在菱形ABCD中，连结BD、AC交于点O，过点O作OH⊥BC于点H，以点O为圆心，OH为半径的半圆交AC于点M．①求证：DC是⊙O的切线．②若AC＝4MC且AC＝8，求图中阴影部分的面积．③在②的条件下，P是线段BD上的一动点，当PD为何值时，PH+PM的值最小，并求出最小值．14．（2019•广安）如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，AD平分∠BAC，AD 交BC于点D，ED⊥AD交AB于点E，△ADE的外接圆⊙O交AC于点F，连接EF．（1）求证：BC是⊙O的切线；（2）求⊙O的半径r及∠3的正切值．15．（2019•达州）如图，⊙O是△ABC的外接圆，∠BAC的平分线交⊙O于点D，交BC于点E，过点D作直线DF∥BC．（1）判断直线DF与⊙O的位置关系，并说明理由；（2）若AB＝6，AE＝，CE＝，求BD的长．16．（2019•凉山州）如图，点D是以AB为直径的⊙O上一点，过点B作⊙O的切线，交AD的延长线于点C，E是BC的中点，连接DE并延长与AB的延长线交于点F．（1）求证：DF是⊙O的切线；（2）若OB＝BF，EF＝4，求AD的长．17．（2019•遂宁）如图，△ABC内接于⊙O，直径AD交BC于点E，延长AD至点F，使DF ＝2OD，连接FC并延长交过点A的切线于点G，且满足AG∥BC，连接OC，若cos∠BAC＝，BC＝6．（1）求证：∠COD＝∠BAC；（2）求⊙O的半径OC；（3）求证：CF是⊙O的切线．18．（2019•宜宾）如图，线段AB经过⊙O的圆心O，交⊙O于A、C两点，BC＝1，AD为⊙O 的弦，连结BD，∠BAD＝∠ABD＝30°，连结DO并延长交⊙O于点E，连结BE交⊙O于点M．（1）求证：直线BD是⊙O的切线；（2）求⊙O的半径OD的长；（3）求线段BM的长．19．（2019•南充）如图，在△ABC中，以AC为直径的⊙O交AB于点D，连接CD，∠BCD＝∠A．（1）求证：BC是⊙O的切线；（2）若BC＝5，BD＝3，求点O到CD的距离．20．（2019•自贡）如图，⊙O中，弦AB与CD相交于点E，AB＝CD，连接AD、BC．求证：（1）＝；（2）AE＝CE．参考答案1．（1）证明：连接OC，∵AB为⊙O的直径，∴∠ACB＝90°，∴∠ACO+∠BCO＝90°，∵OA＝OC，∠A＝∠ACO，∴∠A+∠BCO＝90°，∵∠A＝∠BCH，∴∠BCH+∠BCO＝90°，∴∠HCO＝90°，∴CH是⊙O的切线；（2）解：∵B为DH的中点，∴设BD＝BH＝x，∴DH＝2x，∵∠A＝∠D，∠A＝∠BCH，∴∠D＝∠BCH，∵∠H＝∠H，∴△DCH∽△CBH，∴＝，∴CH＝＝，∵∠H＝90°，∴tan D＝＝＝．2．（1）证明：如图，连结OC，∵OE⊥BC，∴∠OHB＝90°，∴∠OBH+∠BOD＝90°，∵OB＝OC，∴∠OBH＝∠OCB，∵∠BOD＝∠BCD，∴∠BCD+∠OCB＝90°，∴OC⊥CD，∵点C为⊙O上一点，∴DF为⊙O的切线；（2）解：∵∠OCD＝90°，∴∠ECG+∠OCE＝90°，∵OC＝OE，∴∠OCE＝∠OEC，∴∠ECG+∠OEC＝90°，∵∠OEC+∠HCE＝90°，∴∠ECG＝∠HCE，在△CHE和△CGE中，，∴△CHE≌△CGE（AAS）；（3）解：∵AB是⊙O的直径，∴∠ACB＝90°，∴∠ABC+∠BAC＝90°，∵DF为⊙O的切线，∴∠OCA+∠FCA＝90°，∵OA＝OC，∴∠OAC＝∠OCA，∴∠FCA＝∠ABC，∴sin∠ABC＝sin∠FCA＝，设AC＝a，则AB＝3a，∴BC＝＝＝a，∵∠FCA＝∠ABC，∠AFC＝∠CFB，∴△ACF∽△CFB，∴＝＝＝，∵AF＝1，∴CF＝，∴BF＝＝2，∴BF﹣AF＝AB＝1，∴OC＝，BC＝，∵OE⊥BC，∴CH＝BC＝，∴OH＝＝＝，∴HE＝OE﹣OH＝﹣，∵△CHE≌△CGE，∴EG＝HE＝﹣．3．（1）证明：连接OC，∵OE∥AC，∴∠1＝∠ACB，∵AB是⊙O的直径，∴∠1＝∠ACB＝90°，∴OD⊥BC，由垂径定理得OD垂直平分BC，∴DB＝DC，∴∠DBE＝∠DCE，又∵OC＝OB，∴∠OBE＝∠OCE，即∠DBO＝∠OCD，∵DB为⊙O的切线，OB是半径，∴∠DBO＝90°，∴∠OCD＝∠DBO＝90°，即OC⊥DC，∵OC是⊙O的半径，∴DC是⊙O的切线；（2）解：在Rt△ABC中，∠ABC＝30°，∴∠3＝60°，又OA＝OC，∴△AOC是等边三角形，∴∠COF＝60°，在Rt△COF中，tan∠COF＝，∴CF＝4．4．（1）证明：如图1，连接OA，∵AB与⊙O相切，∴∠OAB＝90°，∴∠OAP+∠BAC＝90°，∵OB⊥l，∴∠BCA+∠BPC＝90°，∵OA＝OP，∴∠OAP＝∠OPA＝∠BPC，∴∠BAC＝∠BCA，∴AB＝BC；（2）解：如图1，连接AO并延长交⊙O于D，连接PD，则∠APD＝90°，∵OB＝5，OP＝3，∴PB＝2，∴BC＝AB＝＝4，在Rt△PBC中，PC＝＝2，∵∠DAP＝∠CPB，∠APD＝∠PBC＝90°，∴△DAP∽△PBC，∴＝，即＝，解得，AP＝；（3）解：如图2，作BC的垂直平分线MN，作OE⊥MN于E，则OE＝BC＝AB＝×，由题意得，⊙O于MN有交点，∴OE≤r，即×≤r，解得，r≥，∵直线l与⊙O相离，∴r＜5，则使△GBC是以BC为底边的等腰三角形，⊙O的半径r的取值范围为：≤r＜5．。
中考数学成都中考数学二诊专题汇编A卷：圆(含答案)压轴题
中考数学专题：圆一．解答题1．如图，在⊙O中，直径AB＝10，tan A＝．（1）求弦AC的长；（2）D是AB延长线上一点，且AB＝kBD，连接CD，若CD与⊙O相切，求k的值；（3）若动点P以3cm/s的速度从A点出发，沿AB方向运动，同时动点Q以cm/s的速度从B点出发沿BC方向运动，设运动时间为t（0＜t＜），连接PQ．当t为何值时，△BPQ为Rt△？2．如图，以△ABC的边AB为直径的⊙O与边AC相交于点D，BC是⊙O的切线，E为BC的中点，连接BD、DE．（1）求DE是⊙O的切线；（2）设△CDE的面积为S1，四边形ABED的面积为S2，若S2＝5S1，求tan∠BAC的值；（3）在（2）的条件下，连接AE，若⊙O的半径为2，求AE的长．3．如图1，AB是⊙O的直径，C是⊙O上一点，CD⊥AB于D，E是BA延长线上一点，连接CE，∠ACE ＝∠ACD，K是线段AO上一点，连接CK并延长交⊙O于点F．（1）求证：CE是⊙O的切线；（2）若AD＝DK，求证：AK•AO＝KB•AE；（3）如图2，若AE＝AK，＝，点G是BC的中点，AG与CF交于点P，连接BP．请猜想P A，PB，PF的数量关系，并证明．4．如图，四边形ABCD内接于⊙O，对角线AC、BD相交于点F，AC是⊙O的直径，延长CB到点E，连接AE，∠BAE＝∠ADB，AN⊥BD，CM⊥BD，垂足分别为点N、M．（1）证明：AE是⊙O的切线；（2）试探究DM与BN的数量关系并证明；（3）若BD＝BC，MN＝2DM，当AE＝时，求OF的长．5．如图，四边形ABCD内接于⊙O，直径AC与弦BD的交点为E，OB∥CD，BH⊥AC，垂足为H，且∠BF A＝∠DBC．（1）求证：BF是⊙O的切线；（2）若BH＝3，求AD的长度；（3）若sin∠DAC＝，求△OBH的面积与四边形OBCD的面积之比．6．如图，△ABC内接于⊙O，AB为⊙O的直径，D为的中点，过D作DF⊥AB于点E，交⊙O于点F，交弦BC于点G，连接CD，BF．（1）求证：△BFG≌△DCG；（2）若AC＝10，BE＝8，求BF的长；（3）在（2）的条件下，P为⊙O上一点，连接BP，CP，弦CP交直径AB于点H，若△BPH与△CPB 相似，求CP的长．7．如图，AB是⊙O的直径，AC是⊙O的切线，连接OC交⊙O于E，过点A作AF⊥OC于F，交⊙O于D，连接DE，BE，BD（1）求证：∠C＝∠BED；（2）若AB＝12，tan∠BED＝，求CF的长．8．AB为⊙O的直径，点C、D为⊙O上的两个点，AD交BC于点F，点E在AB上，DE交BC于点G，且∠DGF＝∠CAB．（1）如图1．求证：DE⊥AB．（2）如图2．若AD平分∠CAB．求证：BC＝2DE．（3）如图3．在（2）的条件下，连接OF，若∠AFO＝45°，AC＝8，求OF的长．9．如图，在△ABC中，AB＝AC＝10，tan∠A＝，点O是线段AC上一动点（不与点A，点C重合），以OC为半径的⊙O与线段BC的另一个交点为D，作DE⊥AB于E．（1）求证：DE是⊙O的切线；（2）当⊙O与AB相切于点F时，求⊙O的半径；（3）在（2）的条件下，连接OB交DE于点M，点G在线段EF上，连接GO．若∠GOM＝45°，求DM和FG的长．10．如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作DF⊥AC，垂足为点F．（1）求证：直线DF是⊙O的切线；（2）求证：BC2＝4CF•AC；（3）若⊙O的半径为2，∠CDF＝15°，求阴影部分的面积．11．如图，△ABC内接于⊙O，且AB为⊙O的直径．∠ACB的平分线交⊙O于点D，过点D作⊙O的切线PD交CA的延长线于点P，过点A作AE⊥CD于点E，过点B作BF⊥CD于点F．（1）求证：DP∥AB；（2）试猜想线段AE，EF，BF之间有何数量关系，并加以证明；（3）若AC＝6，BC＝8，求线段PD的长．12．如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，O是AB边上一点，以点O为圆心，OA长为半径的圆经过点D，作DE⊥AB于点E，延长DE交⊙O于点F，连接FO并延长交⊙O于点G，已知DE＝3，tan∠CDA＝2．（1）求证：BC是⊙O的切线；（2）求证：OA2＝OB•OE；（3）求线段EG的长．13．如图，在△ABC中，∠ACB＝90°，AO平分∠BAC，交BC于点O．以O为圆心，OC为半径作⊙O，分别交AO，BC于点E，F．（1）求证：AB是⊙O的切线；（2）延长AO交⊙O于点D，连接CD，若AD＝2AC，求tan D的值；（3）在（2）的条件下，设⊙O的半径为3，求BC的长．14．如图，在△ABC中，AB＝AC，以边AB为直径的⊙O交边BC于点D，交边AC于点E．过D点作DF ⊥AC于点F．（1）求证：DF是⊙O的切线；（2）求证：CF＝EF；（3）延长FD交边AB的延长线于点G，若EF＝3，BG＝9时，求⊙O的半径及CD的长．15．四边形ABCD是⊙O的圆内接四边形，线段AB是⊙O的直径，连接AC、BD．点H是线段BD上的一点，连接AH、CH，且∠ACH＝∠CBD，AD＝CH，BA的延长线与CD的延长线相交于点P．（1）求证：四边形ADCH是平行四边形；（2）若AC＝BC，PB＝PD，AB+CD＝2（+1）①求证：△DHC为等腰直角三角形；②求CH的长度．16．如图，已知Rt△ABC中，∠ACB＝90°，AC＝，BC＝16．点O在边BC上，以O为圆心，OB为半径的弧经过点A．P是弧AB上的一个动点．（1）求半径OB的长；（2）如果点P是弧AB的中点，联结PC，求∠PCB的正切值；（3）如果BA平分∠PBC，延长BP、CA交于点D，求线段DP的长．17．如图，AB是⊙O的直径，弦CD⊥AB于点E，点P是AB延长线上一点，连接PC交DB的延长线于点F，且∠PFB＝3∠CAB．（1）求证：PC是⊙O的切线；（2）延长AC，DF相交于点G，连接PG，请探究∠CPG和∠CAB的数量关系，并说明理由；（3）若tan∠CAB＝，CF＝5，求⊙O的半径．18．如图，在⊙O的内接△ABC中，∠CAB＝90°，AB＝2AC，过点A作BC的垂线m交⊙O于另一点D，垂足为H，点E为上异于A，B的一个动点，射线BE交直线m于点F，连接AE，连接DE交BC于点G．（1）求证：△FED∽△AEB；（2）若＝，AC＝2，连接CE，求AE的长；（3）在点E运动过程中，若BG＝CG，求tan∠CBF的值．31．如图所示，以△ABC的边AB为直径作⊙O，点C在⊙O上，BD是⊙O的弦，∠A＝∠CBD，过点C作CF⊥AB于点F，交BD于点G过C作CE∥BD交AB的延长线于点E．（1）求证：CE是⊙O的切线；（2）求证：CG＝BG；（3）若∠DBA＝30°，CG＝8，求BE的长．。
2024年中考数学高频压轴题训练——圆的综合题含参考答案
2024年中考数学高频压轴题训练——圆的综合题1．如图，在ABC 中，AB AC =，以AB 为直径的O 分别与,BC AC 交于点,D E ，过点D 作DF AC ⊥，垂足为点F ．（1）求证：直线DF 是O 的切线；（2）求证：24BC CF AC =⋅；（3）若O 的半径为4，15CDF ∠=︒，求阴影部分的面积．2．如图，AB 为⊙O 的直径，点C 是⊙O 上一点，CD 与⊙O 相切于点C ，过点A 作AD ⊥DC ，连接AC ，BC.（1）求证：AC 是∠DAB 的角平分线；（2）若AD ＝2，AB ＝3，求AC 的长.3．如图，在ABC 中，AB AC =，以AB 为直径的O 交BC 于点D ，DE AC ⊥交BA 的延长线于点E ，交AC 于点F ．（1）求证：DE 是O 的切线；（2）若364AC tanE ==，，求AF 的长．4．如图，⊙O 是Rt △ABC 的外接圆，AB 为直径，∠ABC=30°，CD 是⊙O 的切线，ED ⊥AB 于F ，（1）求证：△CDE 是等腰三角形；（2）若AB=4，)21AE =，求证：△OBC ≌△DCE ．5．已知锐角△ABC 内接于圆O ，D 为弧AC 上一点，分别连接AD 、BD 、CD ，且∠ACB ＝90°﹣12∠BAD ．（1）如图1，求证：AB ＝AD ；（2）如图2，在CD 延长线上取点E ，连接AE ，使AE ＝AD ，过E 作EF 垂直BD 的延长线于点F ，过C 作CG ⊥EC 交EF 延长线于点G ，设圆O 半径为r ，求证：EG ＝2r ；（3）如图3，在（2）的条件下，连接DG ，若AC ＝BC ，DE ＝4CD ，当△ACD 的面积为10时，求DG 的长度．6．如图，已知AB 是O 的直径，AC 是O 的弦，点E 在O 外，连接CE ，ACB ∠的平分线交O 于点D .（1）若BCE BAC ∠=∠，求证：CE 是O 的切线；（2）若4AD =，3BC =，求弦AC 的长.7．如图，在Rt △ABC 中，∠ABC ＝90o ，以BC 为直径的半圆⊙O 交AC 于点D ，点E 是AB 的中点，连接DE 并延长，交CB 延长线于点F ．（1）判断直线DF 与⊙O 的位置关系，并说明理由；（2）若CF ＝8，DF ＝4，求⊙O 的半径和AC 的长．8．在平面直角坐标系xOy 中，当图形W 上的点P 的横坐标和纵坐标相等时，则称点P 为图形W 的“梦之点”.（1）已知⊙O 的半径为1.①在点E （1，1），F （22，－22），M(－2，－2)中，⊙O 的“梦之点”为；②若点P 位于⊙O 内部，且为双曲线y =k x （k≠0）的“梦之点”，求k 的取值范围.（2）已知点C 的坐标为（1，t ），⊙C 的半径为，若在⊙C 上存在“梦之点”P ，直接写出t 的取值范围.（3）若二次函数21y ax ax =-+的图象上存在两个“梦之点”()11A x y ，，()22B x y ，，且122x x -=，求二次函数图象的顶点坐标.9．如图，点A 是⊙O 直径BD 延长线上的一点，AC 是⊙O 的切线，C 为切点.AD ＝CD ，（1）求证：AC ＝BC ；（2）若⊙O 的半径为1，求△ABC 的面积.10．如图，△ABC 中，∠ACB ＝90°，BO 为△ABC 的角平分线，以点O 为圆心，OC 为半径作⊙O 与线段AC 交于点D.（1）求证：AB 为⊙O 的切线；（2）若tanA ＝34，AD ＝2，求BO 的长.11．如图①，A 是O 外一点，AB 与O 相切于点B ，AO 的延长线交O 于点C ，过点B 作//BD AC ，交O 于点D ，连接DO ，并延长DO 交O 于点E ，连接AE .已知2BD =，O 的半径为3.（1）求证：AE 是O 的切线；（2）求AE 的长；（3）如图②，若点M 是O 上一点，且3BM =，过A 作//AN BM ，交弧ME 于点N ，连接ME ，交AN 于点G ，连接OG ，则OG 的长度是.12．我们把三角形三边上的高产生的三个垂足组成的三角形称为该三角形的垂足三角形．（1）如图1，△ABC 中，AB ＝AC ＝8，BC ＝6，△DEF 是△ABC 的垂足三角形，求DE 的长．（2）如图2，圆内接三角形ABC 中，AB ＝AC ＝x ，BC ＝6，△ABC 的垂足三角形DEF 的周长为y ．①求y 与x 的关系式；②若△DEF 的周长为19225时，求⊙O 的半径．13．如图，⊙O 是Rt △ABC 的外接圆，∠ABC ＝90°，D 为圆上一点，且B ，D 两点位于AC 异侧，连接BD ，交AC 于E ，点F 为BD 延长线上一点，连接AF ，使得∠DAF ＝∠ABD.（1）求证：AF 为⊙O 的切线；（2）当点D 为EF 的中点时，求证：AD 2＝AO•AE ；（3）在（2）的条件下，若sin ∠BAC ＝13，AF ＝2，求BF 的长.14．如图，△ABC 内接于⊙O ，直径BD 交AC 于E ，过O 作FG ⊥AB ，交AC 于F ，交AB 于H ，交⊙O 于G ．（1）求证：OF•DE=2OE•OH ；（2）若⊙O 的半径为12，且OE ：OF ：OD=2：3：6，求阴影部分的面积．（结果保留根号）15．如图，点P 是圆O 直径CA 延长线上的一点，PB 切圆O 于点B ，点D 是圆上的一点，连接AB ，AD ，BD ，CD ，∠P=30°．（1）求证：PB=BC ；（2）若AD=6，tan∠DCA=34，求BD的长．16．在矩形ABCD中，AB=6，BC=8，BE⊥AC于点E，点O是线段AC上的一点，以AO为半径作圆O 交线段AC于点G，设AO=m．（1）直接写出AE的长：AE=；（2）取BC中点P，连接PE O与△BPE一边所在的直线相切时，求出m的长；（3）设圆O交BE于点F，连接AF并延长交BC于点H．①连接GH，当BF=BH时，求△BFH的面积；②连接DG，当tan∠HFB=3时，直接写出DG的长，DG．17．如图，在Rt△ABC中，∠ACB=90°，∠A=30°，BC=1，以边AC上一点O为圆心，OA为半径的⊙O 经过点B.（1）求⊙O的半径；（2）点P为 AB中点，作PQ⊥AC，垂足为Q，求OQ的长；（3）在(2)的条件下，连接PC ，求tan ∠PCA 的值.18．О 直径12AB cm AM =，和BN 是О 的切线，DC 切О 于点E 且交AM 于点D ，交BN 于点C ，设AD x BC y ==，．（1）求y 与x 之间的关系式；（2）x y ，是关于t 的一元二次方程22300t t m -+=的两个根，求x y ，的值；（3）在（2）的条件下，求COD ∆的面积．19．（1）问题发现：如图1，ABC 内接于半径为4的O ，若60C ∠=︒，则AB =；（2）问题探究：如图2，四边形ABCD 内接于半径为6的O ，若120B ∠=︒，求四边形ABCD 的面积最大值；（3）解决问题：如图3，一块空地由三条直路（线段AD 、AB 、BC ）和一条弧形道路CD 围成，点M 是AB 道路上的一个地铁站口，已知AD BM =1=千米，2AM BC ==千米，60A B ∠=∠=︒，CD 的半径为1千米，市政府准备将这块空地规划为一个公园，主入口在点M 处，另外三个入口分别在点C 、D 、P 处，其中点P 在CD 上，并在公园中修四条慢跑道，即图中的线段DM 、MC 、CP 、PD ，是否存在一种规划方案，使得四条慢跑道总长度（即四边形DMCP 的周长）最大？若存在，求其最大值；若不存在，说明理由.20．在平面直角坐标系xOy 中，给定圆C 和点P ，若过点P 最多可以作出k 条不同的直线，且这些直线被圆C 所截得的线段长度为正整数，则称点P 关于圆C 的特征值为.k 已知圆O 的半径为2，（1）若点M 的坐标为()11，，则经过点M 的直线被圆O 截得的弦长的最小值为，点M 关于圆O 的特征值为；（2）直线y x b =+分别与x ，y 轴交于点A ，B ，若线段AB 上总存在关于圆O 的特征值为4的点，求b 的取值范围；（3）点T 是x 轴正半轴上一点，圆T 的半径为1，点R ，S 分别在圆O 与圆T 上，点R 关于圆T 的特征值记为r ，点S 关于圆O 的特征值记为.s 当点T 在x 轴正轴上运动时，若存在点R ，S ，使得3r s +=，直接写出点T 的横坐标t 的取值范围．21．如图，AB 是⊙O 的直径，DO ⊥AB 于点O ，连接DA 交⊙O 于点C ，过点C 作⊙O 的切线交DO 于点E ，连接BC 交DO 于点F ．（1）求证：CE=EF ；（2）连接AF 并延长，交⊙O 于点G ．填空：①当∠D 的度数为时，四边形ECFG 为菱形；②当∠D 的度数为时，四边形ECOG 为正方形．22．如图，四边形ABCD 内接于O ，O 的半径为4，90ADC AB BC ∠=︒=，，对角线AC 、BD 相交于点P.过点P 分别作PE AD ⊥于点E ，PF CD ⊥于点F.（1）求证：四边形DEPF 为正方形；（2）若 2AD CD =，求正方形DEPF 的边长；（3）设PC的长为x，图中阴影部分的面积为y，求y与x之间的函数关系式，并写出y的最大值.答案解析部分1．【答案】（1）证明：如图所示，连接OD ，∵AB AC =，∴ABC C ∠=∠，而OB OD =，∴ODB ABC C ∠=∠=∠，∵DF AC ⊥，∴90CDF C ∠+∠=︒，∴90CDF ODB ∠+∠=︒，∴90ODF ∠=︒，∴直线DF 是O 的切线（2）证明：连接AD ，则AD BC ⊥，则AB AC =，则12DB DC BC ==，∵90CDF C ∠+∠=︒，90C DAC ∠+∠=︒，∴CDF DCA ∠=∠，而90DFC ADC ∠=∠=︒，∴CFD CDA ∽，∴2CD CF AC =⋅，即24BC CF AC=⋅（3）解：连接OE ，∵15,75CDF C ∠=︒∠=︒，∴30OAE OEA ∠=︒=∠，∴120AOE ∠=︒，11sin 2cos sin 422OAE S AE OE OEA OE OEA OE OEA =⨯∠=⨯⨯∠⨯∠= ，21201643603OAE S OAE S S ππ︒︒=-=⨯-- 阴影部分扇形2．【答案】（1）证明：连接OC，如图，∵CD与⊙O相切于点C，∴∠OCD＝90°，∴∠ACD+∠ACO＝90°，∵AD⊥DC，∴∠ADC＝90°，∴∠ACD+∠DAC＝90°，∴∠ACO＝∠DAC，∵OA＝OC，∴∠OAC＝∠OCA，∴∠DAC＝∠OAC，∴AC是∠DAB的角平分线；（2）∵AB是⊙O的直径，∴∠ACB＝90°，∴∠D＝∠ACB＝90°，∵∠DAC＝∠BAC，∴Rt△ADC∽Rt△ACB，∴AD ACAC AB，∴AC2＝AD•AB＝2×3＝6，∴AC＝3．【答案】（1）证明：如下图，连接OD，∵AB AC =，OB OD =，∴B C ∠=∠，B ODB ∠=∠，∴ODB C ∠=∠，∴//OD AC ，∴ODE CFD ∠∠=，又∵DE AC ⊥，∴90CFD ∠= ，∴90ODE ∠= ，∴DE 是O 的切线．（2）解：∵AC=6，∴11322OD OB AB AC ====，在Rt ODE 中，34OD tanE ED ==，∴4ED =，5OE ==，∴532AE OE OB =-=-=，又∵90AEF OED AFE ODE ∠∠∠∠=== ，，∴AFE ODE ~ ，∴AE AF OE OD =，即2=53AF ，∴65AF =．4．【答案】（1）证明：∵AB 为直径，∴∠ACB=90°，又∠ABC=30°，∴∠BAC=60°，又∵OA=OC ，∴△AOC 是正三角形，又∵CD 是⊙O 的切线，∴∠OCD=90°，∴∠DCE=180°﹣60°﹣90°=30°，又∵ED ⊥AB 于F ，∴∠DEC=90°﹣∠BAC=30°，∴∠DCE=∠DEC ，故△CDE 为等腰三角形（2）证明：在Rt △ABC 中，∵AB=4，AC=AO=2，∴BC ==，而)212CE =+-=，∴BC=CE ，又∵∠OBC=∠OCB=∠DCE=∠DEC=30°，∴△OBC ≌△DCE （ASA ）5．【答案】（1）证明：如图1中，∵∠ADB ＝∠ACB ，∠ACB ＝90°﹣12∠BAD ，∴∠ADB ＝90°﹣12BAD ，∵∠ABD ＝180°﹣∠BAD ﹣（90°﹣12∠BAD ）＝90°﹣12∠BAD ，∴∠ABD ＝∠ADB ，∴AB ＝AD （2）证明：如图2中，连接BE 交AC 于L ，连接AO ，延长AO 交BD 于J ，交BE 于T ，连接CO ，延长CO 交⊙O 于K ，连接BK ．∵AE ＝AD ，∴∠ADE ＝∠AED ，∵∠ADE+∠ADC ＝180°，∠ADC+∠ABC ＝180°，∴∠ADE ＝∠ABC ＝∠AED ，∵AB ＝AD ，∴ AB AD ，∴∠ACB ＝∠ACE ，AJ ⊥BD ，∵AC ＝AC ，∴△ACB ≌△ACE （AAS ），∴CB ＝CE ，∵AB ＝AE ，∴AC ⊥BE ，∴∠ALB ＝∠AJB ＝90°，∵∠ATL ＝∠BTJ ，∴∠TAL ＝∠TBJ ，∵AB ＝AD ＝AE ，∴∠BED ＝12∠BAD ＝∠BAJ ，∵∠EDF ＝∠DBE+∠DEB ，∴∠EDF ＝∠BAC ，∵∠K ＝∠BAC ，∴∠K ＝∠EDF ，∵CG ⊥CE ．EG ⊥BF ，∴∠DFE ＝∠GCG ＝90°，∵∠DEF+∠EDF ＝90°，∠DEF+∠G ＝90°，∴∠G ＝∠EDF ＝∠K ，∵∠CBK ＝∠GCE ＝90°，∴△CBK ≌△ECG （AAS ），∴EG ＝CK ＝2r（3）解：如图3中，在图2的基础上作AH ⊥DE 于H ．∵DE ＝4CD ，∴可以假设CD ＝k ，DE ＝4k ，则CE ＝CB ＝CA ＝5k ，∵AE ＝AD ，AH ⊥DE ，∴DH ＝EH ＝2k ，CH ＝CD+DH ＝3k ，∴AH ＝4k =，AD ＝=∵S △ACD ＝12•CD•AH ＝12•k•4k ＝10，∴k ＝（负根舍弃），∴CD ＝，AC ＝BC ＝EC ＝5，AD ＝AB ＝10，设CK 交AB 于J ，OA ＝OC ＝r ，则BJ ＝AJ ＝5，CJ ＝10==在Rt △AOJ 中，则有r 2＝52+（10﹣r ）2，解得r ＝254，∴EG ＝2r ＝252，∴CG ＝552==∴DG ＝2=6．【答案】（1）证明：连接OC ，∵AB 是O 的直径，∴∠ACB=90︒，∵OA=OC ，∴∠OAC=∠OCA ，∵∠BCE=∠BAC ，∴∠BCE=∠BAC=∠OCA ，∵∠OCA+∠OCB=90︒，∴∠BCE +∠OCB=90︒，∴∠OCE=90︒，∴CE 是⊙O 的切线；（2）解：连接DB ，∵AB 是⊙O 的直径，∴∠ADB=90︒，∵CD 平分∠ACB ，∴ AD DB=，∴AD DB =，∴△ADB 为等腰直角三角形，∴AB ==，∵AB 是⊙O 的直径，∴∠ACB=90︒，∴AC ==．7．【答案】（1）解：相切证明：连接OD ，OE∵点E 是AB 中点，点O 是BC 中点∴OE 是△ABC 的中位线，∴OE ∥AC∴∠1＝∠4，∠2＝∠3∵OC ＝OD ，∴∠3＝∠4，∴∠1＝∠2∵OB ＝OD ，OE ＝OE ，∴△OBE ≌△ODE∴∠ODE ＝∠OBE ＝90o∴OD ⊥DE ，∴直线DF 与⊙O 相切.（2）解：设⊙O 半径为x ，则OD ＝x ，OF ＝8－x在Rt △FOD 中，222OD FD OF +=，∴2224(8)x x +=-，∴x ＝3∴⊙O 半径为3∵∠FBE ＝∠FDO ＝90°，∠F ＝∠F ，∴△FBE ∽△FDO ，∴BF BE DF OD =，∵BF ＝FC －BC ＝2，OD ＝3，DF ＝4，∴BE ＝32，∵点E 是AB 中点，∴AB ＝2BE ＝3在Rt △ABC 中，AC ＝＝8．【答案】（1）F 解：∵⊙O 的半径为1.∴⊙O 的“梦之点”坐标为2222⎛⎫-- ⎪ ⎪⎝⎭和2222⎛ ⎝⎭，.又∵双曲线k y x=（k≠0）与直线y=x 的交点均为圆的“梦之点”，∴将2222⎛⎫-- ⎪ ⎪⎝⎭代入双曲线表达式中，得，1=2k xy =，∵点P 位于⊙O 内部.∴102k <<（2）解：－1≤t≤3（3）解：由“梦之点”定义可得：()11A x x ，，()22B x x ，.则21x ax ax =-+.整理得，()2110ax a x -++=，解得，11x =，21x a=.把两个根代入122x x -=中，即112a -=，解得，11a =-，213a =.当1a =-时，21y x x =-++，其顶点坐标为1524⎛⎫ ⎪⎝⎭，，当13a =时，211133y x x =-+，其顶点坐标为111.212⎛⎫ ⎪⎝⎭，9．【答案】（1）证明：连接OC ，∵AC 为切线，C 为切点，∴∠ACO ＝90°，即∠DCO+∠2＝90°，又∵BD 是直径，∴∠BCD ＝90°，即∠DCO+∠1＝90°，∴∠1＝∠2，∵AD ＝CD ，OB ＝OC ，∴∠A ＝∠2，∠B ＝∠1，∴∠A ＝∠B ，∴AC ＝BC ；（2）解：由题意可得△DCO 是等腰三角形，∵∠CDO ＝∠A+∠2，∠DOC ＝∠B+∠1，∴∠CDO ＝∠DOC ，即△DCO 是等边三角形，∴∠A ＝∠B ＝∠1＝∠2＝30°，CD ＝AD ＝1，∴BC ＝＝＝，在Rt △BCD 中，作CE ⊥AB 于点E ，在Rt △BEC 中，∠B ＝30°，∴CE ＝1BC 2=，BE ＝32，∴S △ABC ＝1AB CE 2⋅＝1324⨯=.10．【答案】（1）证明：过O 作OH ⊥AB 于H ，∵∠ACB ＝90°，∴OC ⊥BC ，∵BO 为△ABC 的角平分线，OH ⊥AB ，∴OH ＝OC ，即OH 为⊙O 的半径，∵OH ⊥AB ，∴AB 为⊙O 的切线；（2）解：设⊙O 的半径为3x ，则OH ＝OD ＝OC ＝3x ，在Rt △AOH 中，∵tanA ＝34，∴OH AH ＝34，∴3x AH ＝34，∴AH ＝4x ，∴AO ＝22OH AH +＝22(3)(4)x x +＝5x ，∵AD ＝2，∴AO ＝OD+AD ＝3x+2，∴3x+2＝5x ，∴x ＝1，∴OA ＝3x+2＝5，OH ＝OD ＝OC ＝3x ＝3，∴AC ＝OA+OC ＝5+3＝8，在Rt △ABC 中，∵tanA ＝BC AC ，∴BC ＝AC•tanA ＝8×34＝6，∴OB ＝22OC BC +＝2236+＝35.11．【答案】（1）证明：连接OB∵AB 与O 相切于点B ，∴OB AB ⊥，∴90OBA ∠=︒∵//BD AC ，∴AOE D ∠=∠，AOB OBD ∠=∠∵OB OD =，∴D OBD ∠=∠，∴AOE AOB ∠=∠，∵OE OB =，OA OA =，∴()SAS AOE AOB ≌∴90OEA OBA ∠=∠=︒∴OE AE⊥又∵点E 在圆上，∴AE 是O 的切线.（2）解：过点O 作OH BD ⊥交BD 于点H .∵OH BD ⊥，O 为圆心，∴112DH BD ==，90OHD ∠=︒在Rt OHD 中，OH ==∵OHD AEO ∠=∠，D AOE ∠=∠，∴AOE ODH∽∴AE OH OE DH=∴2231OH OE AE DH ⨯===（3）12．【答案】（1）解：∵AB ＝AC ，AD ⊥BC ，∴D 是BC 的中点，又∠BEC 是直角，∴DE ＝12BC ＝3．（2）解：①如图，连接CE ，同理（1）可得DE ＝BD ＝DF ＝3，∴∠B ＝∠BED ＝∠ACB ，∴△BDE ∽△BAC ，∴36BE x =，∴BE ＝18x ，∴AE ＝x ﹣18x ，同理可得：AF ＝x ﹣18x，∴AE ＝AF ，∵AB ＝AC ，∴△AEF ∽△ABC ，∴EF AE BC AB =，∴EF ＝6﹣2108x ，∴y ＝12﹣2108x ；②当y ＝19225时，x ＝5，如图，连接AD ，∵AB ＝AC ，∴△ABC 的外心O 在线段AD 上，连接BO ，设⊙O 的半径为r ，则32+（4﹣r ）2＝r 2，∴r ＝258，即⊙O 的半径为258．13．【答案】（1）证明：连接CD .AC 是直径，90ADC ∴∠=︒，90DAC ACD ∴∠+∠=︒，ABD ACD ∠=∠ ，DAF ABC ∠=∠，DAF ACD ∴∠=∠，90DAF DAC ∴∠+∠=︒，90FAC ∴∠=︒，AF ∴为O 的切线（2）证明：90FAE ∠=︒ ，DF DE =，AD DE DF ∴==，DAE AED ∴∠=∠，OA OD = ，DAO ADO ∴∠=∠，ADO AED ∴∠=∠，OAD DAE ∠=∠ ，ADO AED ∴ ∽，∴AD AO AE AD=，2AD AO AE∴=⋅（3）解：如图，过点B 作BJ EC ⊥于J .AC 是直径，90ABC ∴∠=︒，1sin 3BC BAC AC ∴∠==，∴可以假设BC a =，3AC a =，BJ AC ⊥ ，90AJB ∴∠=︒，90BAC ABJ ∴∠+∠=︒，90ABJ CBJ ∠+∠=︒，CBJ BAC ∴∠=∠，1sin sin 3CJ CBJ BAC BC ∴∠=∠==，13CJ a ∴=，223BJ ∴==，DA DE = ，DAE AED CEB ∴∠=∠=∠，DAE CBE ∠=∠ ，CEB CBE ∴∠=∠，CE CB a ∴==，1233EJ EC CJ a a a ∴=-=-=，2AE AC EC a =-=，//AF BJ ，∴AF AE BJ EJ=，∴222233a a =，a ∴=，AE ∴=，3EJ =，3BJ =，6EF ∴==，2BE ==，628BF EF BE ∴=+=+=14．【答案】（1）证明：∵BD 是直径，∴∠DAB=90°．∵FG ⊥AB ，∴DA ∥FO ．∴△FOE ∽△ADE ．∴FO OE AD DE=，即OF•DE=OE•AD ∵O 是BD 的中点，DA ∥OH ，∴AD=2OH∴OF•DE=OE•2OH（2）解：∵⊙O 的半径为12，且OE ：OF ：OD=2：3：6，∴OE=4，ED=8，OF=6代入（1）中OF•DE=OE•AD ，得AD=12．∴OH=12AD=6．在Rt △OHB 中，OB=2OH ，∴∠OBH=30°，∴∠BOH=60°．∴BH=BO•sin60°=122⨯=2OHB GOB 60121=S S =6183602S ππ⨯⨯∴--⨯⨯- 阴影扇形15．【答案】（1）证明：连接OB ，∵PB 是圆O 的切线∴∠OBP=90°∵∠BOP=90°-∠P=90°-30°=60°∵OC=OB∴∠OBC=∠OCB∵∠POB=∠OBC+∠OCB=2∠OCB=60°∴∠OCB=30°=∠P∴PB=BC（2）解：过点A作AE⊥BD于点E ，∴∠AED=∠AEB=90°，∵AC是直径，∴∠ADC=90°在Rt△ADC中，tan∠DCA=634ADDC DC==，解之DC=8∴10 =在Rt△ABC中，∠ACB=30°，∴AB=1110522AC=⨯=在Rt△ADE中，∠ADE=∠ACB=30°∴DE=6×cos30°=AEB=∠ADC，∠ABE=∠ACD∴△ABE∽△CAD∴AB BEAC DC=，即5108BE=解之：BE=4∴DB=DE+BE=16．【答案】（1）AE=18 5（2）解：当圆O与△BPE的BE边相切时，点E和点G重合，则AE⊥BE∴AE是圆O的直径∴m=111892255AE=⨯=；当圆O与△BPE的BP边相切时，切点为F，连接OF∴∠OFC=∠BEC=90°∵∠OCF=∠BCE∴△OFC∽△BCE∴OF OC BE BC=在Rt△ABC中，BE⊥AC∴AB·BC=AC·BE即6×8=10BE解之：BE=245∴102485m m-=解之：m=154;当圆O与△BPE的PE边相切时，交PE的延长线于点F，切点为F，连接OF∴∠OFE=∠BEC=90°∵∠OEF=∠CEP∵点P是Rt△BEC斜边上的中线∴CP=PE∴∠ECP=∠CEP∴∠OEF=∠ECP∴△OFC∽△CBE∴OF OEBE BC=∵圆O的半径为m∴OE=185-m，OF=m∴1852485mm-=解之：m=2720;答：当圆O与△BPE一边所在的直线相切时，95m=，154m=，2720m=（3）过点F作FM⊥AB，过点F作FN⊥BC于点N易证四边形BMFN是矩形∴FN=BM，∵BH=BF∴∠1=∠2,∵∠1=∠5，∠5+∠3=90°，∠2+∠4=90°∴∠3=∠4∴AF平分∠CAB，FE⊥AC，FM⊥AB∴EF=FM在Rt△AEF和Rt△AMF中A=AA=A∴Rt△AEF≌Rt△AMF（HL）∴AE=AM=3.6∴BM=AB-AM=6-3.6=2.4即FN=2.4，∵FM∥BH∴△AFM∽△ABH∴MF AMBH AB=∴3.6365MFBH==，设MF=3x，则BH=BF=5x，在Rt△BMF 中，4x=4x=2.4解之：x=0.6∴BH=5×0.6=3∴S△BFH=11121832255BH FN⋅=⨯⨯=；；1255 17．【答案】（1）解：连接OB，如图，∵OA=OB，∴∠ABO=∠A=30°，∵∠ACB=90°，∠A=30°，∴∠ABC=60°，∴∠OBC=30°，在Rt△OBC中，cosBC OBCOB∠=，即1 cos30OB︒=，解得233 OB=，即⊙O 的半径为23 3（2）解：连接OP，设AB与QP交于点M，∵点P为 AB的中点，∴OP⊥AB，∴∠QPO+∠PMB=90°，∵PQ⊥AC，∴∠A+∠AMQ=90°，又∵∠AMQ=∠PMB，∴∠QPO=∠A=30°，在Rt△OPQ中，sinOQ QPOOP∠=，即sin30233︒=，∴2313323 OQ==（3）解：在Rt△OBC中，∵3OB =，∠OBC=30°，∠ACB=90°∴3sin 30°=3OC OB =⨯，∴233CQ CO OQ =+=，∴tan 2PQ PCA CQ ∠==18．【答案】（1）解：如图，作DF BN ⊥交BC 于F ；AM BN 、与O 切于点A B、AB AM AB BN ∴⊥⊥，．又DF BN ⊥ ，∴BAD ABC BFD ∠=∠=∠=︒，∴四边形ABFD 是矩形，12BF AD x DF AB ∴====，，BC y = ，FC BC BF y x ∴=-=-；DE 切O 于E ，DE DA x CE CB y ∴====，，则DC DE CE x y =+=+，在Rt DFC ∆中，222CD FC DF =+，即222()()12x y y x +=-+，整理为：36y x =，y ∴与x 的函数关系式是36y x=．（2）解：由（1）知36xy =，∵x y ，是方程22300t t m -+=的两个根，∴根据韦达定理知，2m xy =，即72m =；∴原方程为215360t t -+=，解得：12123t t ==，．即=3=12或123x y =⎧⎨=⎩．（3）解：如图，连接OD OE OC ，，，AD BC CD ，，是O 的切线，OE CD AD DE BC CE ∴⊥==，，，AOD ODE OBC COE S S S S ∆∆∆∆∴==，，111==(312)1245222COD COE ODE ABCD S S S S ∆∆∆∴=+⨯⨯+⨯=梯形19．【答案】（1）（2）解：∵∠ABC=120︒,四边形ABCD 内接于O ，∴∠ADC=60︒，∵O 的半径为6，∴由（1）得AC=,如图，连接AC ，作DH ⊥AC,BM ⊥AC,∴四边形ABCD 的面积=111()222AC DH AC BM AC DH BM ⋅⋅+⋅⋅=⋅+,当DH+BM 最大时，四边形ABCD 的面积最大，连接BD ，则BD 是O 的直径，∴BD=2OA=12，BD ⊥AC ，∴四边形ABCD 的面积=111222AC BD ⋅⋅=⨯=.∴四边形ABCD 的面积最大值是（3）解：存在；∵AD BM =1=千米，2AM BC ==千米，60A B ∠=∠=︒，∴△ADM ≌△BMC,∴DM=MC,∠AMD=∠BCM,∵∠BCM+∠BMC=180︒-∠B=120︒，∴∠AMD+∠BMC=120︒，∴∠DMC=60︒，∴△CDM 是等边三角形，∴C 、D 、M 三点共圆，∵点P 在弧CD 上,∴C 、D 、M 、P 四点共圆，∴∠DPC=180︒-∠DMC=120︒，∵CD 弧的半径为1千米，∠DMC=60︒，∴CD=,∵2()0PD PC -≥,∴2()4PD PC PD PC +≥⋅,∴PD PC +≥,∴当PD=PC 时，PD+PC 最大，此时点P 在弧CD 的中点，交DC 于H ,在Rt △DPH 中，∠DHP=90︒,∠DPH=60︒，DH=12DC=32,∴1sin 60DH DP == ，∴四边形DMCP的周长最大值=DM+CM+DP+CP=2+.20．【答案】（1）；3的特征值为4的点，（2）解：设点G是O∴经过一点G且弦长为4(最长弦)的直线有1条，弦长为3的直线有2条，弦长为2的直线有且只有1条， 经过点G的直线被O截得的弦长的最小值为2，=，∴关于O的特征值为4的所有点都在以O为半径的圆周上，=+分别与x，y轴交于点A、B，直线y x b()0，，B b∴-，，()A b∴==，OA OB bOBH∴∠=︒，45b>时，线段AB与以O为半径的圆相切时，点G特征值为4，当0设切点为为H，连接OH，则OH=，∴==OB，∴=b，设以O为半径的圆与y轴正半轴的交点记为1B，OB=，则1当线段AB 与以O 1B 时，可得b =，b ≤≤同理可求当0b <时，b ≤≤，综上，b b b ≤≤-≤（3）当372122t -≤≤+时，存在点R ，S ，使得3r s +=21．【答案】（1）证明：连接OC ，如图，.∵CE 为切线，∴OC ⊥CE ，∴∠OCE=90°，即∠1+∠4=90°∵DO ⊥AB ，∴∠3+∠B=90°，而∠2=∠3，∴∠2+∠B=90°，而OB=OC ，∴∠4=∠B ，∴∠1=∠2，∴CE=FE（2）30°；22.5°22．【答案】（1）证明：∵PE AD ⊥，PF DC ⊥，∴90PED PFD ∠∠==︒，∴90ADC PED PFD ∠∠∠===︒，∴四边形DEPF 是矩形，∵90ADC ∠=︒，∴AC 是圆O 的直径，∴90ABC ∠=︒，∵AB BC =，∴45ACB BCA ∠=∠=︒， AB BC=，∴45ADB CDB ∠=∠=︒，∴45DPE ADB ∠∠==︒，∴PE DE =.∴四边形CEPF 是正方形；（2）解：∵ 2AD CD=，AC 是圆O 的直径，∴ AD 的度数为120︒， AD 的度数为60︒，∴30DAC ∠=︒，60DCA ∠=︒，∴12PE sin DAC AP ∠==，3602PF sin DCA sin PC ∠=︒==，∴2AP PE =，233PC PF =，∵2428AC AP PC r =+==⨯=，正方形DEPF 中，PE PF =，∴23283PF PF +=，∴2PF =.（3）解：在ED 上取点G ，使EG CF =，连接PG ，由（1）得：PE PF =，90GEP PFC ∠∠==︒，∴GPE CPF ≌，∴PG PC x ==，GPE FPC ∠∠=，CEP PFC S S = ，∴阴影部分的面积等于APG ABC S S + ，∵90EPF ∠=︒，∴90APE CPF ∠∠+=︒，∴90GPE APE ∠∠+=︒，即90APG ∠=︒，∵8AC =，∴8AP x =-，∴()11822APG S AP PG x x =⋅=- ，∵ABC 是等腰直角三角形，8AC =，∴AB BC ==，∴2111622ABC S AB ==⨯= ，即阴影部分的面积()()21181642422y x x x =-+=--+，∴当4x =时，y 有最大值，最大值为24.。
成都市中考核心考点 -第五讲压轴题-圆(20题)(A卷)
成都中考核心考点（成都版）简介--只要抓住核心考点，就能拿到卷子上80%的分数在历年的成都中考数学试题中，核心考点虽然只占总考点的20%，却占总分值的80%。
掌握了核心考点，相当于用20%的时间来把握80%的分数，在最短的时间内实现快速提分。
本文共分两轮复习：第一轮过关核心考点聚焦常考考点，五年真题回顾，三年诊断精选。
本文分13讲，由成都市中考数学A卷和B卷难度区分度较大，A卷1-19题较基础，大部分学生都容易掌握，选题主要以中考题和诊断题为主，20题-28题有一定综合性，选题除了中考题和诊断题外，还选择了大量的模拟题和改编题。
第一讲:考点1-考点6，第二讲:考点7-考点10，第三讲:考点11-考点14，第四讲:考点15-考点19，第五讲:考点20，第六讲:考点21，………第十三讲:考点28.（从考点20开始，每个考点一讲）。
第二轮过关B卷攻略专攻B卷重难，五年考点扫描，专题考向攻略。
暂定：B填空7-8讲，应用题1讲，几何综合3讲，抛物线综合5讲考点20：圆的综合命题方向：A 卷20题，2015年以前主要考察三角形和四边形，2015年开始考圆，也就是将20题和27题交换了位置，这意味着加大了三角形和四边形的考察难度，适当降低了圆的考察难度。
主要考察知识点：圆的基本性质定理，结合三角形的全等、相似等，以及平面几何的基本性质（16年考察过角平分线课外补充的性质：三角形一个角的平分线与其对边所成的两条线段与这个角的两边对应成比例）。
五年真题1. (18成都)如图，在Rt ABC ∆中，90C ∠=︒，AD 平分BAC ∠交BC 于点D ，O 为AB 上一点，经过点A ，D 的O ⊙分别交AB ，AC 于点E ，F ，连接OF 交AD 于点G .（1）求证：BC 是O ⊙的切线；（2）设AB x =，AF y =，试用含,x y 的代数式表示线段AD 的长；（3）若8BE =，5sin 13B =，求DG 的长.2. (17成都) 如图，在ABC ∆中，AB AC =，以AB 为直径作圆O ，分别交BC 于点D ，交CA 的延长线于点E ，过点D 作DH AC ⊥于点H ，连接DE 交线段OA 于点F .（1）求证：DH 是圆O 的切线；（2）若AE 为H 的中点，求EFFD的值；（3）若1EA EF ==，求圆O 的半径.3．(16成都)如图，在Rt △ABC 中，∠ABC ＝90°，以CB 为半径作⊙C ，交AC 于点D ，交AC 的延长线于点E ，连接BD ，BE . (1)求证：△ABD ∽△AEB ；(2)当43AB BC =时，求tanE ；(3)在（2）的条件下，作∠BAC 的平分线，与BE 交于点F .若AF ＝2，求⊙C 的半径。
2024成都中考数学第一轮专题复习 圆的有关概念及性质 知识精练(含答案)
2024成都中考数学第一轮专题复习圆的有关概念及性质知识精练基础题1.(2023江西)如图，点A，B，C，D均在直线l上，点P在直线l外，则经过其中任意三个点，最多可画出圆的个数为()A.3B.4C.5D.6第1题图2.(2023广东省卷)如图，AB是⊙O的直径，∠BAC＝50°，则∠D＝()第2题图A.20°B.40°C.50°D.80°3.(2023广元)如图，AB是⊙O的直径，点C，D在⊙O上，连接CD，OD，A C.若∠BOD＝124°，则∠ACD的度数是()A.56°B.33°C.28°D.23°第3题图4.(2023山西)如图，四边形ABCD内接于⊙O，AC，BD为对角线，BD经过圆心O.若∠BAC ＝40°，则∠DBC的度数为()第4题图A.40°B.50°C.60°D.70°5.(2023安徽)如图，正五边形ABCDE内接于⊙O，连接OC，OD，则∠BAE－∠COD＝()A.60°B.54°C.48°D.36°第5题图6.(2023赤峰)如图，圆内接四边形ABCD中，∠BCD＝105°，连接OB，OC，OD，BD，∠BOC＝2∠COD，则∠CBD的度数是()第6题图A.25°B.30°C.35°D.40°7.[新考法—数学文化](2023岳阳)我国古代数学名著《九章算术》中有这样一道题：“今有圆材，径二尺五寸．欲为方版，令厚七寸，问广几何？”结合下图，其大意是：今有圆形材质，直径BD为25寸，要做成方形板材，使其厚度CD达到7寸，则BC的长是() A.674寸 B.25寸C.24寸D.7寸第7题图8.(2023杭州)如图，在⊙O中，半径OA，OB互相垂直，点C在劣弧AB上．若∠ABC＝19°，则∠BAC＝()第8题图A.23°B.24°C.25°D.26°9.(2023广西)赵州桥是当今世界上建造最早，保存最完整的中国古代单孔敞肩石拱桥．如图，主桥拱呈圆弧形，跨度约为37m，拱高约为7m，则赵州桥主桥拱半径R约为()第9题图A.20mB.28mC.35mD.40m10.(2023凉山州)如图，在⊙O中，OA⊥BC，∠ADB＝30°，BC＝23，则OC＝()A.1B.2C.23D.4第10题图11.如图，点A，B，D在⊙O上，CD垂直平分AB于点C.现测得AB＝CD＝16，则圆形宣传图标的半径为()第11题图A.12B.10C.8D.612.如图，在平面直角坐标系中，⊙O的半径为4，弦AB的长为3，过O作OC⊥AB于点C，则OC的长度是________；⊙O内一点D的坐标为(－2，1)，当弦AB绕O点顺时针旋转时，点D到AB的距离的最小值是________．第12题图13.(2023武汉)如图，OA，OB，OC都是⊙O的半径，∠ACB＝2∠BA C.(1)求证：∠AOB＝2∠BOC；(2)若AB＝4，BC＝5，求⊙O的半径．第13题图拔高题14.(2023吉林省卷)如图，AB，AC是⊙O的弦，OB，OC是⊙O的半径，点P为OB上任意一点(点P不与点B重合)，连接CP.若∠BAC＝70°，则∠BPC的度数可能是()A.70°B.105°C.125°D.155°第14题图15.如图，正方形ABCD内接于⊙O，点E为弧AB的中点，连接DE与AB交于点F.若AB＝1，记△ADF的面积为S1，△AEF的面积为S2，则S1S2的值为________．第15题图16.如图，以原点O为圆心的圆交x轴于A，B两点，交y轴的正半轴于点C，且点A的坐标为(－2，0)，D为第一象限内⊙O上的一点，若∠OCD＝75°，则AD的长为________．第16题图参考答案与解析1.D 【解析】本题考查了确定圆的条件及圆的有关定义及性质．∵过不在同一直线上的三个点一定能作一个圆，∴要经过题中所给的3个点画圆，除选定直线l 外的点P 外，再在直线l 上的A ，B ，C ，D 四个点中任选其中2个即可画圆．∵从A ，B ，C ，D 四个点中任选其中2个点的方法可以是AB ，AC ，AD ，BC ，BD ，CD ，共6种，∴最多可以画出圆的个数为6.2.B 【解析】∵AB 是⊙O 的直径，∠BAC ＝50°，∴∠ACB ＝90°，∠B ＝180°－50°－90°＝40°.∵ AC ＝ AC ，∴∠D ＝∠B ＝40°.3.C【解析】∵∠BOD ＝124°，∴∠AOD ＝180°－124°＝56°，∴∠ACD ＝12∠AOD ＝28°.4.B 【解析】∵BD 经过圆心O ，∴∠BCD ＝90°.∵∠BDC ＝∠BAC ＝40°，∴∠DBC ＝90°－∠BDC ＝50°.5.D 【解析】∵五边形ABCDE 是正五边形，∴∠BAE ＝（5－2）×180°5＝108°，∠COD ＝360°5＝72°，∴∠BAE －∠COD ＝108°－72°＝36°.6.A 【解析】∵∠BCD ＝105°，∴∠BAD ＝180°－105°＝75°，∴∠BOD ＝150°.∵∠BOC＝2∠COD ，∴∠COD ＝13∠BOD ＝50°，∴∠CBD ＝12∠COD ＝25°.7.C 【解析】∵BD 是圆的直径，∴∠BCD ＝90°.∵BD ＝25，CD ＝7，∴在Rt △BCD 中，由勾股定理得，BC ＝252－72＝24(寸).8.D 【解析】如解图，连接OC ，∵∠ABC ＝19°，∴∠AOC ＝2∠ABC ＝38°.∵半径OA ，OB 互相垂直，∴∠AOB ＝90°，∴∠BOC ＝90°－38°＝52°，∴∠BAC ＝12∠BOC ＝26°.第8题解图9.B 【解析】如解图，在Rt △OAB 中，由勾股定理，得AO 2＋AB 2＝OB 2，即(R －7)2＋(372)2＝R 2，解得R ≈28(m).第9题解图10.B 【解析】如解图，连接OB ，设OA 交BC 于点E ，∵∠ADB ＝30°，∴∠AOB ＝60°.∵OA ⊥BC ，BC ＝23，∴BE ＝12BC ＝3.在Rt △BOE 中，sin ∠AOB ＝BE OB，∴sin 60°＝3OB ＝32，∴OB ＝2，∴OC ＝2.第10题解图11.B 【解析】如解图，连接OA ，设圆形宣传图标的半径为R ，∵CD 垂直平分AB ，AB＝CD ＝16，∴CD 过点O ，AC ＝BC ＝12AB ＝12×16＝8，∠DCA ＝90°.∵AO ＝OD ＝R ，∴在Rt △AOC 中，由勾股定理，得OC 2＋AC 2＝OA 2，即(16－R )2＋82＝R 2，解得R ＝10，即圆形宣传图标的半径为10.第11题解图12.552；552－5【解析】如解图，连接OB ，∵OC ⊥AB ，∴BC ＝12AB ＝32.由勾股定理，得OC ＝OB 2－BC 2＝552.当OD ⊥AB 时，点D 到AB 的距离最小，由勾股定理，得OD ＝22＋12＝5，∴点D 到AB 的距离的最小值为552－5.第12题解图13.(1)证明：由圆周角定理，得∠ACB ＝12∠AOB ，∠BAC ＝12∠BOC .∵∠ACB ＝2∠BAC ，∴∠AOB ＝2∠BOC ；(2)解：如解图，过点O 作半径OD ⊥AB 于点E ，连接BD .则∠DOB ＝12∠AOB ，AE ＝BE .∵∠AOB ＝2∠BOC ，∴∠DOB ＝∠BOC .∴BD ＝BC .∵AB ＝4，BC ＝5，∴BE ＝2，DB ＝5.在Rt △BDE 中，∵∠DEB ＝90°，∴DE ＝BD 2－BE 2＝1.在Rt △BOE 中，∵∠OEB ＝90°，∴OB 2＝(OB －1)2＋22，∴OB ＝52，即⊙O 的半径是52.第13题解图14.D 【解析】如解图，连接BC ，∵∠BAC ＝70°，∴∠BOC ＝2∠BAC ＝140°.∵OB ＝OC ，∴∠OBC ＝∠OCB ＝180°－140°2＝20°.∵点P 为OB 上任意一点(点P 不与点B 重合)，∴0°<∠OCP <20°.∵∠BPC ＝∠BOC ＋∠OCP ＝140°＋∠OCP ，∴140°<∠BPC <160°，故选D.第14题解图15.2(2＋1)【解析】如解图，连接OE 交AB 于点G ，连接AC .根据垂径定理的推论，得OE ⊥AB ，AG ＝BG .由题意可得，AC 为⊙O 的直径，AC ＝2，则圆的半径是22.根据正方形的性质，得∠OAF ＝45°，∴OG ＝12，EG ＝2－12.∵OE ∥AD ，∴△ADF ∽△GEF ，∴FE FD ＝EG DA ＝2－12.∵△ADF 与△AEF 等高，∴S 1S 2＝S △ADF S △AEF＝DF EF ＝2(2＋1).第15题解图16.23【解析】如解图，连接OD ，BD .∵A (－2，0)，∴OA ＝OB ＝2，∴AB ＝4.∵OC ＝OD ，∴∠OCD ＝∠ODC ＝75°，∴∠DOC ＝180°－2×75°＝30°，∴∠DOB ＝90°－30°＝60°，∴∠DAB ＝12∠DOB ＝30°.∵AB 是⊙O 的直径，∴∠ADB ＝90°，∴AD ＝AB ·cos 30°＝23.第16题解图。
成都市中考核心考点 - 第十二讲 几何类综合压轴题(27题)(B卷)
成都中考核心考点（成都版）简介--只要抓住核心考点，就能拿到卷子上80%的分数在历年的成都中考数学试题中，核心考点虽然只占总考点的20%，却占总分值的80%。
掌握了核心考点，相当于用20%的时间来把握80%的分数，在最短的时间内实现快速提分。
本文共分两轮复习：第一轮过关核心考点聚焦常考考点，五年真题回顾，三年诊断精选。
本文分13讲，由成都市中考数学A卷和B卷难度区分度较大，A卷1-19题较基础，大部分学生都容易掌握，选题主要以中考题和诊断题为主，20题-28题有一定综合性，选题除了中考题和诊断题外，还选择了大量的模拟题和改编题。
第一讲:考点1-考点6，第二讲:考点7-考点10，第三讲:考点11-考点14，第四讲:考点15-考点19，第五讲:考点20，第六讲:考点21，………第十三讲:考点28.（从考点20开始，每个考点一讲）。
第二轮过关B卷攻略专攻B卷重难，五年考点扫描，专题考向攻略。
暂定：B填空7-8讲，应用题1讲，几何综合3讲，抛物线综合5讲考点27、几何图形综合（压轴）命题方向：主要以三角形和四边形为基架，从全等过渡到相似，从定点过渡到动点，求线段、比例、探究数量关系； 五年真题1. (18成都)在Rt ABC ∆中，90ABC ∠=︒，7AB =，2AC =，过点B 作直线//m AC ，将ABC ∆绕点C 顺时针得到A B C ∆′′（点A ，B 的对应点分别为A ′，B ′）射线CA ′，CB ′分别交直线m 于点P ，Q . （1）如图1，当P 与A ′重合时，求ACA ∠′的度数；（2）如图2，设A B ′′与BC 的交点为M ，当M 为A B ′′的中点时，求线段PQ 的长；（3）在旋转过程时，当点,P Q 分别在CA ′，CB ′的延长线上时，试探究四边形PA B Q ′′的面积是否存在最小值.若存在，求出四边形PA B Q ′′的最小面积；若不存在，请说明理由.2．(16成都)如图①，△ABC 中，∠ABC ＝45°，AH ⊥BC 于点H ，点D 在AH 上，且DH ＝CH ，连接BD . (1)求证：BD=AC ；(2)将△BHD 绕点H 旋转，得到△EHF （点B ，D 分别与点E ，F 对应），连接AE .ⅰ）如图②，当点F 落在AC 上时（F 不与C 重合），若BC ＝4，tanC =3,求AE 的长；ⅱ）如图③，当△EHF 是由△BHD 绕点H 逆时针旋转30°得到时，设射线CF 与AE 相交于点G ，连接GH ，试探究线段GH 与EF 之间满足的等量关系，并说明理由。
(完整版)成都市中考近十年中考数学圆压轴题(含答案)
圆【2018 成都中考】如图，在Rt∆ABC 中，∠C = 90︒，AD 平分∠BAC 交BC 于点D ，O 为AB 上一点，经过点A ，D 的⊙O 分别交AB ，AC 于点E ，F ，连接OF 交AD 于点G .（1）求证：BC 是⊙O 的切线；（2）设AB =x ，AF =y ，试用含x, y 的代数式表示线段AD 的长；（3）若BE = 8 ，sin B =513，求DG 的长.【2017 成都中考】如图，在△ABC中，AB=AC，以AB 为直径作圆 O，分别交 BC 于点D，交CA 的延长线于点 E，过点 D 作DH⊥AC于点H，连接 DE 交线段 OA 于点F．（1）求证：DH 是圆O 的切线；（2）若A 为EH 的中点，求的值；（3）若EA=EF=1，求圆 O 的半径．证明：（1）连接OD，如图1，∵OB=OD，∴△ODB 是等腰三角形，∠OBD=∠ODB①，在△ABC 中，∵AB=AC，∴∠ABC=∠ACB②，由①②得：∠ODB=∠OBD=∠ACB，∴OD∥AC，∵DH⊥AC，∴DH⊥OD，∴DH 是圆O 的切线；（2）如图2，在⊙O 中，∵∠E=∠B，∴由（1）可知：∠E=∠B=∠C，∴△EDC 是等腰三角形，∵DH⊥AC，且点A 是EH 中点，设AE=x，EC=4x，则AC=3x，连接AD，则在⊙O 中，∠ADB=90°，AD⊥BD，∵AB=AC，∴D 是BC 的中点，∴OD 是△ABC 的中位线，∴OD∥AC，OD= AC= ×3x= ，∵OD∥AC，∴∠E=∠ODF，在△AEF 和△ODF 中，∵∠E=∠ODF，∠OFD=∠AFE，∴△AEF∽△ODF，∴，∴== ，∴= ；（3）如图2，设⊙O 的半径为r，即OD=OB=r，∵EF=EA，∴∠EFA=∠EAF，∵OD∥EC，∴∠FOD=∠EAF，则∠FOD=∠EAF=∠EFA=∠OFD，∴DF=OD=r，∴DE=DF+EF=r+1，∴BD=CD=DE=r+1，在⊙O 中，∵∠BDE=∠EAB，∴∠BFD=∠EFA=∠EAB=∠BDE，∴BF=BD，△BDF 是等腰三角形，∴BF=BD=r+1，∴AF=AB﹣BF=2OB﹣BF=2r﹣（1+r）=r﹣1，在△BFD 和△EFA 中，∵，∴△BFD∽△EFA，∴，∴= ，解得：r1= ，r2= （舍），综上所述，⊙O 的半径为．【2016 成都中考】如图，在Rt△ABC中，∠ABC=90 °，以 CB 为半径作⊙C，交 AC 于点 D，交 AC 的延长线于点 E，连接 ED， BE．（1 ）求证：△ABD∽△AEB；（2 ）当= 时，求tan E；（3 ）在（ 2 ）的条件下，作∠BAC的平分线，与 BE 交于点 F，若 AF=2 ，求⊙C 的半径．解：（1）∵∠ABC=90°，∴∠ABD=90°﹣∠DBC，由题意知：DE 是直径，∴∠DBE=90°，∴∠E=90°﹣∠BDE，∵BC=CD，∴∠DBC=∠BDE，∴∠ABD=∠E，∵∠A=∠A，∴△ABD∽△AEB；（2）∵AB：BC=4：3，∴设AB=4，BC=3，∴AC= =5，∵BC=CD=3，∴AD=AC﹣CD=5﹣3=2，由（1）可知：△ABD∽△AEB，∴= = ，∴AB2=AD•AE，∴42=2AE，∴AE=8，在Rt△DBE 中tanE= ===；（3）过点F 作FM⊥AE 于点M，∵AB：BC=4：3，∴设AB=4x，BC=3x，∴由（2）可知；AE=8x，AD=2x，∴DE=AE﹣AD=6x，∵AF 平分∠BAC，∴=，∴==，∵tanE= ，∴cosE= ，sinE= ，∴=，∴BE= ，∴EF= BE= ，∴sinE= =，∴MF= ，∵tanE= ，∴ME=2MF= ，∴AM=AE﹣ME= ，∵AF2=AM2+MF2，∴4= + ，∴x=，∴⊙C 的半径为：3x=．【2015 成都中考】如图，在Rt△ABC中，∠ABC=90°，AC 的垂直平分线分别与 AC，BC 及AB 的延长线相较于点D，E，F，且 BF=BC，⊙O 是△BEF 的外接圆，∠EBF 的平分线交 EF 于点 G，交⊙O 于点 H，连接 BD，FH．（1）求证：△ABC≌△EBF；（2）试判断 BD 与⊙O的位置关系，并说明理由；（3）若AB=1，求HG•HB的值．解：（1）由已知条件易得，∠DCE =∠EFB ，∠ABF =∠EBF又BC =BF ，∴ ∆ABC ≅∆EBF （ASA ）（2）BD 与 O 相切。
历年成都中考数学压轴题(二次函数)
（2003*成都）已知二次函数y=x2+bx+c的顶点M在直线y=-4x上，并且图象经过点A（-1，0）．（1）求这个二次函数的解析式；（2）设此二次函数与x轴的另一个交点为B，与y轴的交点为C，求经过M、B、C三点的圆O′的直径长；（3）设圆O′与y轴的另一个交点为N，经过P（-2，0）、N两点的直线为l，则圆心O′是否在直线上，请说明理由．交于点C（0，8），其对称轴为x=1．（1）求此抛物线的解析式；（2）过A、B、C三点作⊙O′与y轴的负半轴交于点D，求经过原点O且与直线AD垂直（垂足为E）的直线OE的方程；（3）设⊙O′与抛物线的另一个交点为P，直线OE与直线BC的交点为Q，直线x=m与抛物线的交点为R，直线x=m与直线OE的交点为S．是否存在整数m，使得以点P、Q、R、S为顶点的四边形为平行四边形？若存在，求出m的值；若不存在，请说明理由．与y轴的正半轴交于点C．如果x1、x2是方程x2-x-6=0的两个根（x1＜x2），且△ABC的面积为15/2（1）求此抛物线的解析式；（2）求直线AC和BC的方程；（3）如果P是线段AC上的一个动点（不与点A、C重合），过点P作直线y=m（m为常数），与直线BC交于点Q，则在x轴上是否存在点R，使得△PQR为等腰直角三角形？若存在，求出点R的坐标；若不存在，请说明理由．（2006*成都）如图，在平面直角坐标系中，已知点B（-22，0），A（m，0）（-2＜m＜0），以AB为边在x轴下方作正方形ABCD，点E是线段OD与正方形ABCD的外接圆除点D以外的另一个交点，连结BE与AD相交于点F.（1）求证：BF＝DO；（2）设直线l是△BDO的边BO的垂直平分线，且与BE相交于点G，若G是△BDO的外心，试求经过B、F、O三点的抛物线的解析表达式；（3）在（2）的条件下，在抛物线上是否存在点P，使该点关于直线BE的对称点在x轴上？若存在，求出所有这样的点的坐标；若不存在，请说明理由.（2007*成都）在平面直角坐标系xOy 中，已知二次函数2(0)y ax bx c a =++≠的图象与x 轴交于A B ，两点（点A 在点B 的左边），与y 轴交于点C ，其顶点的横坐标为1，且过点(23)，和(312)--，．（1）求此二次函数的表达式；（2）若直线:(0)l y kx k =≠与线段BC 交于点D （不与点B C ，重合），则是否存在这样的直线l ，使得以B O D ，，为顶点的三角形与BAC △相似？若存在，求出该直线的函数表达式及点D 的坐标；若不存在，请说明理由；（3）若点P 是位于该二次函数对称轴右边图象上不与顶点重合的任意一点，试比较锐角PCO ∠与ACO ∠的大小（不必证明），并写出此时点P 的横坐标p x 的取值范围．（2013*武汉）如图，点P 是直线l ：y=-2x-2上的点，过点P 的另一条直线m 交抛物线y=x 2于A 、B 两点．（1）若直线m 的解析式为2321+-=x y ，求A 、B 两点的坐标； （2）①若点P 的坐标为（－2，t ），当PA ＝AB 时，请直接写出点A 的坐标；②试证明：对于直线l 上任意给定的一点P ，在抛物线上都能找到点A ，使得PA ＝AB 成立．（3）设直线l 交y 轴于点C ，若△AOB 的外心在边AB 上，且∠BPC ＝∠OCP ，求点P 的坐标．点B．（1）求抛物线的解析式；（2）已知点D（m，m+1）在第一象限的抛物线上，求点D关于直线BC对称的点的坐标；（3）在（2）的条件下连接BD，点P为抛物线上一点且∠DBP=45°，求点P的坐标．与x轴交于另一点B．（1）求此抛物线的解析式；（2）若直线y=kx-1（k≠0）将四边形ABCD面积二等分，求k的值；（3）如图2，过点E（1，-1）作EF⊥x轴于点F，将△AEF绕平面内某点旋转180°后得△MNQ（点M，N，Q分别与点A，E，F对应），使点M，N在抛物线上，求点M，N的坐标．（2007*武汉）如图①，在平面直角坐标系中，Rt △AOB ≌Rt △CDA ，且A(－1，0)、B(0，2)，抛物线y ＝ax 2＋ax －2经过点C 。
成都【数学】中考数学圆的综合解答题压轴题提高专题练习
一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，点P在⊙O的直径AB的延长线上，PC为⊙O的切线，点C为切点，连接AC，过点A作PC的垂线，点D为垂足，AD交⊙O于点E．(1)如图1，求证：∠DAC=∠PAC；(2)如图2，点F（与点C位于直径AB两侧）在⊙O上，BF FA=，连接EF，过点F作AD 的平行线交PC于点G，求证：FG=DE+DG；(3)在(2)的条件下，如图3，若AE=23DG，PO=5，求EF的长．【答案】（1）证明见解析；（2）证明见解析；（3）EF=32．【解析】【分析】（1）连接OC，求出OC∥AD，求出OC⊥PC，根据切线的判定推出即可；（2）连接BE交GF于H，连接OH，求出四边形HGDE是矩形，求出DE=HG，FH=EH，即可得出答案；（3）设OC交HE于M，连接OE、OF，求出∠FHO=∠EHO=45°，根据矩形的性质得出EH∥DG，求出OM=12AE，设OM=a，则HM=a，AE=2a，AE=23DG，DG=3a，求出ME=CD=2a，BM=2a，解直角三角形得出tan∠MBO＝12MOBM=，tanP=12COPO=,设OC=k，则PC=2k，根据OP=5k=5求出k=5，根据勾股定理求出a，即可求出答案．【详解】（1）证明：连接OC，∵PC为⊙O的切线，∴OC⊥PC，∵AD⊥PC，∴OC∥AD，∴∠OCA=∠DAC，∵OC=OA，∴∠PAC=∠OCA，∴∠DAC=∠PAC；（2）证明：连接BE交GF于H，连接OH，∵FG∥AD，∴∠FGD+∠D=180°，∵∠D=90°，∴∠FGD=90°，∵AB为⊙O的直径，∴∠BEA=90°，∴∠BED=90°，∴∠D=∠HGD=∠BED=90°，∴四边形HGDE是矩形，∴DE=GH，DG=HE，∠GHE=90°，∵BF AF=，∴∠HEF=∠FEA=12∠BEA=1902o⨯=45°，∴∠HFE=90°﹣∠HEF=45°，∴∠HEF=∠HFE，∴FH=EH，∴FG=FH+GH=DE+DG；（3）解：设OC交HE于M，连接OE、OF，∵EH=HF，OE=OF，HO=HO，∴△FHO≌△EHO，∴∠FHO=∠EHO=45°，∵四边形GHED是矩形，∴EH∥DG，∴∠OMH=∠OCP=90°，∴∠HOM=90°﹣∠OHM=90°﹣45°=45°，∴∠HOM=∠OHM，∴HM=MO，∵OM⊥BE，∴BM=ME，∴OM=12 AE，设OM=a，则HM=a，AE=2a，AE=23DG，DG=3a，∵∠HGC=∠GCM=∠GHE=90°，∴四边形GHMC是矩形，∴GC=HM=a，DC=DG﹣GC=2a，∵DG=HE，GC=HM，∴ME=CD=2a，BM=2a，在Rt△BOM中，tan∠MBO=122 MO aBM a==，∵EH∥DP，∴∠P=∠MBO，tanP=12 COPO=，设OC=k，则PC=2k，在Rt△POC中，，解得：在Rt△OME中，OM2+ME2=OE2，5a2=5，a=1，∴HE=3a=3，在Rt△HFE中，∠HEF=45°，∴．【点睛】考查了切线的性质，矩形的性质和判定，解直角三角形，勾股定理等知识点，能综合运用性质进行推理是解此题的关键．2．如图，已知AB是⊙O的直径，点C为圆上一点，点D在OC的延长线上，连接DA，交BC的延长线于点E，使得∠DAC=∠B．（1）求证：DA是⊙O切线；（2）求证：△CED∽△ACD；（3）若OA=1，sinD=13，求AE的长．【答案】（1）证明见解析；（22【解析】分析：（1）由圆周角定理和已知条件求出AD⊥AB即可证明DA是⊙O切线；（2）由∠DAC=∠DCE，∠D=∠D可知△DEC∽△DCA；（3）由题意可知AO=1，OD=3，DC=2，由勾股定理可知AD=2，故此可得到DC2=DE•AD，故此可求得DE的长，于是可求得AE的长．详解：（1）∵AB为⊙O的直径，∴∠ACB=90°，∴∠CAB+∠B=90°．∵∠DAC=∠B，∴∠CAB+∠DAC=90°，∴AD⊥AB．∵OA是⊙O半径，∴DA为⊙O的切线；（2）∵OB=OC，∴∠OCB=∠B．∵∠DCE=∠OCB，∴∠DCE=∠B．∵∠DAC=∠B，∴∠DAC=∠DCE．∵∠D=∠D，∴△CED∽△ACD；（3）在Rt△AOD中，OA=1，sin D=13，∴OD=OAsinD=3，∴CD=OD﹣OC=2．∵AD22OD OA-2又∵△CED∽△ACD，∴AD CDCD DE=，∴DE=2CDAD2，∴AE=AD﹣DE222．点睛：本题主要考查的是切线的性质、圆周角定理、勾股定理的应用、相似三角形的性质和判定，证得△DEC∽△DCA是解题的关键．3．如图，已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上，过点C作CD⊥AB，分别交AB、AO的延长线于点D、E，AE交半圆O于点F，连接CF．（1）判断直线DE与半圆O的位置关系，并说明理由；（2）若半圆O的半径为6，求AC的长．【答案】（1）直线CE 与半圆O 相切（2）4π【解析】试题分析：（1）结论：DE 是⊙O 的切线．首先证明△ABO ，△BCO 都是等边三角形，再证明四边形BDCG 是矩形，即可解决问题；（2）只要证明△OCF 是等边三角形即可解决问题，求AC 即可解决问题．试题解析：（1）直线CE 与半圆O 相切，理由如下：∵四边形OABC 是平行四边形，∴AB ∥OC.∵∠D=90°，∴∠OCE=∠D=90°，即OC ⊥DE ，∴直线CE 与半圆O 相切．（2）由（1）可知：∠COF=60°，OC=OF ，∴△OCF 是等边三角形，∴∠AOC=120°∴AC 的长为1206180π⨯⨯=4π.4．已知：AB 是⊙0直径,C 是⊙0外一点,连接BC 交⊙0于点D ，BD=CD,连接AD 、AC ．(1)如图1,求证:∠BAD=∠CAD(2)如图2,过点C 作CF ⊥AB 于点F,交⊙0于点E,延长CF 交⊙0于点G.过点作EH ⊥AG 于点H ，交AB 于点K,求证AK=2OF ；(3)如图3,在(2)的条件下,EH 交AD 于点L,若0K=1,AC=CG,求线段AL 的长.图1 图2 图3【答案】(1)见解析(2)见解析12105【解析】试题分析：（1）由直径所对的圆周角等于90°，得到∠ADB =90°，再证明△ABD ≌△ACD 即可得到结论；（2）连接BE ．由同弧所对的圆周角相等，得到∠GAB =∠BEG ．再证△KFE ≌△BFE ，得到BF =KF =BK ．由OF =OB -BF ，AK =AB -BK ，即可得到结论．（3）连接CO 并延长交AG 于点M ，连接BG ．设∠GAB =α．先证CM 垂直平分AG ，得到AM =GM ，∠AGC +∠GCM =90°．再证∠GAF =∠GCM =α．通过证明△AGB ≌△CMG ，得到BG =GM =12AG ．再证明∠BGC =∠MCG =α．设BF =KF =a ， 可得GF =2a ，AF =4a ． 由OK =1，得到OF =a +1，AK =2（a +1），AF = 3a +2，得到3a +2=4a ，解出a 的值，得到AF ，AB ，GF ，FC 的值．由tanα=tan ∠HAK =12HK AH =， AK =6，可以求出 AH 的长．再由1tan tan 3BAD BCF ∠=∠= ，利用公式tan ∠GAD =tan tan 1tan tan GAF BAD GAF BAD∠+∠-∠⋅∠，得到∠GAD =45°，则AL =2AH ，即可得到结论．试题解析：解：（1）∵AB 为⊙O 的直径，∴∠ADB =90°，∴∠ADC =90°．∵BD =CD ，∠BDA =∠CDA ，AD =AD ，∴△ABD ≌△ACD ，∴∠BAD =∠CAD ．（2）连接BE ．∵BG =BG ，∴∠GAB =∠BEG ．∵CF ⊥AB ，∴∠KFE =90°．∵EH ⊥AG ，∴∠AHE =∠KFE =90°，∠AKH =∠EKF ，∴∠HAK =∠KEF =∠BEF ．∵FE =FE ，∠KFE =∠BFE =90°，∴△KFE ≌△BFE ，∴BF =KF =BK ．∵ OF =OB -BF ，AK =AB -BK ，∴AK =2OF ．（3）连接CO 并延长交AG 于点M ，连接BG ．设∠GAB =α．∵AC =CG ， ∴点C 在AG 的垂直平分线上．∵ OA =OG ，∴点O 在AG 的垂直平分线上， ∴CM 垂直平分AG ，∴AM =GM ，∠AGC +∠GCM =90°．∵AF ⊥CG ，∴∠AGC +∠GAF =90°，∴∠GAF =∠GCM =α．∵AB 为⊙O 的直径，∴∠AGB = 90°，∴∠AGB =∠CMG =90°．∵AB =AC =CG ，∴△AGB ≌△CMG ，∴BG =GM =12AG ．在Rt △AGB 中， 1tan tan 2GB GAB AG α∠=== ． ∵∠AMC =∠AGB = 90°，∴BG ∥CM ， ∴∠BGC =∠MCG =α．设BF =KF =a ， 1tan tan 2BF BGF GF α∠===，∴GF =2a ，1tan tan 2GF GAF AF α∠=== ，AF =4a ．∵OK =1，∴OF =a +1，AK =2OF =2（a +1），∴AF =AK +KF =a +2（a +1）=3a +2，∴3a +2=4a ，∴a =2， AK =6，∴AF =4a =8，AB =AC =CG =10，GF =2a =4，FC =CG -GF =6．∵tanα=tan ∠HAK =12HK AH =，设KH =m ，则AH =2m ，∴AK =22(2)m m +=6，解得：m =655，∴AH =2m =1255．在Rt △BFC 中，1tan 3BF BCF FC ∠== ．∵∠BAD +∠ABD =90°， ∠FBC +∠BCF =90°，∴∠BCF =∠BAD ，1tan tan 3BAD BCF ∠=∠= ，∴tan ∠GAD =tan tan 1tan tan GAF BAD GAF BAD ∠+∠-∠⋅∠=1123111123+=-⨯，∴∠GAD =45°，∴HL=AH ，AL =2AH = 1210．5．对于平面直角坐标系xOy 中的线段MN 和点P ，给出如下定义：点A 是线段MN 上一个动点，过点A 作线段MN 的垂线l ，点P 是垂线l 上的另外一个动点．如果以点P 为旋转中心，将垂线l 沿逆时针方向旋转60°后与线段MN 有公共点，我们就称点P 是线段MN 的“关联点”．如图，M （1，2），N （4，2）．（1） 在点P 1（1，3），P 2（4，0），P 3（3，2）中，线段MN 的“关联点”有 ； （2） 如果点P 在直线1y x =+上，且点P 是线段MN 的“关联点”，求点P 的横坐标x 的取值范围；（3） 如果点P 在以O （1，1-）为圆心，r 为半径的⊙O 上，且点P 是线段MN 的“关联点”，直接写出⊙O 半径r 的取值范围．【答案】（1）P 1和P 3；（2）3311x -≤≤；（3）333 3.r +≤≤ 【解析】【分析】 （1）先根据题意求出点P 的横坐标的范围，再求出P 点的纵坐标范围即可得出结果； （2）由直线y=x+1经过点M （1，2），得出x≥1，设直线y=x+1与P 4N 交于点A ，过点A 作AB ⊥MN 于B ，延长AB 交x 轴于C ，则在△AMN 中，MN=3，∠AMN=45°，∠ANM=30°，设AB=MB=a ，tan ∠ANM=AB BN ，即tan30°=3a a-，求出a 即可得出结果； （3）圆心O 到P 4的距离为r 的最大值，圆心O 到MP 5的距离为r 的最小值，分别求出两个距离即可得出结果．【详解】（1））如图1所示：∵点A 是线段MN 上一个动点，过点A 作线段MN 的垂线l ，点P 是垂线l 上的另外一个动点，M （1，2），N （4，2），∴点P 的横坐标1≤x≤4，∵以点P 为旋转中心，将垂线l 沿逆时针方向旋转60°后与线段MN 有公共点， 当∠MPN=60°时，PM=60MN tan ︒=3=3， 同理P′N=3，∴点P 的纵坐标为2-3或2+3，即纵坐标2-3≤y≤2+3，∴线段MN 的“关联点”有P 1和P 3；故答案为：P 1和P 3；（2）线段MN 的“关联点”P 的位置如图所示，∵ 直线1y x =+经过点M （1，2），∴ x ≥1.设直线1y x =+与P 4N 交于点A .过点A 作AB ⊥MN 于B ，延长AB 交x 轴于C .由题意易知，在△AMN 中，MN = 3，∠AMN = 45°，∠ANM = 30°.设AB = MB = a ，∴ tan AB ANM BN ∠=，即tan303a a ︒=-， 解得333.2a = ∴ 点A 的横坐标为33333111x a --=+=+= ∴331x - 综上 3311x -≤≤（3）点P 在以O （1，-1）为圆心，r 为半径的⊙O 上，且点P 是线段MN 的“关联点”，如图3所示：连接P 4O 交x 轴于点D ，P 4、M 、D 、O 共线，则圆心O 到P 4的距离为r 的最大值，由（1）知：MP 4=NP 5=3， 即OD+DM+MP 4=1+2+3=3+3，圆心O 到MP 5的距离为r 的最小值，作OE ⊥MP 5于E ，连接OP 5，则OE 为r 的最小值，MP 5=225MN NP +=223(3)+=23，OM=OD+DM=1+2=3， △OMP 5的面积=12OE•MP 5=12OM•MN ，即12×OE×23=12×3×3， 解得：OE=33， ∴332≤r≤3+3． 【点睛】本题是圆的综合题，考查了旋转、直角三角形的性质、勾股定理、最值等知识，熟练掌握“关联点”的含义，作出关于MN 的“关联点”图是关键．6．如图，点A ，B ，C ，D ，E 在⊙O 上，AB ⊥CB 于点B ，tanD=3，BC=2，H 为CE 延长线上一点，且AH=10，CH 52=.（1）求证：AH 是⊙O 的切线；（2）若点D 是弧CE 的中点，且AD 交CE 于点F ，求证：HF=HA ；（3）在（2）的条件下，求EF 的长．【答案】（1）证明见解析（2）证明见解析（3102【解析】【分析】（1）连接AC，由AB⊥CB可知AC是⊙O的直径，由圆周角定理可得∠C=∠D，于是得到tanC=3，故此可知AB=6，在Rt△ABC中，由勾股定理得：AC2= 40，从而可得AC2+AH2=CH2，根据勾股定理的逆定理可得AC⊥AH，问题得证；（2）连接DE、BE，由弦切角定理可知∠ABD=∠HAD，由D是CE的中点，可得∠CED=∠EBD，再由圆周角定理可得∠ABE=∠ADE，结合三角形的外角即可证明∠HAF=∠AFH，从而可证得AH=HF；（3）由切割线定理可得EH=2，由（2）可知AF=FH=10，从而可得EF=FH﹣EH=10-2．【详解】（1）如图1所示：连接AC．∵AB⊥CB，∴AC是⊙O的直径，∵∠C=∠D，∴tanC=3，∴AB=3BC=3×2=6，在Rt△ABC中，由勾股定理得：AC2=AB2+BC2=40，又∵AH2=10，CH2=50，∴AC2+AH2=CH2，∴△ACH为直角三角形，∴AC⊥AH，∴AH是圆O的切线；（2）如图2所示：连接DE、BE，∵AH是圆O的切线，∴∠ABD=∠HAD，∵D是CE的中点，∴CD ED，∴∠CED=∠EBD，又∵∠ABE=∠ADE，∴∠ABE+∠EBD=∠ADE+∠CED，∴∠ABD=∠AFE，∴∠HAF=∠AFH，∴AH=HF；（3）由切割线定理可知：AH2=EH•CH，即（10）2=52EH，解得：EH=2，∵由（2）可知AF=FH=10，∴EF=FH﹣EH=10-2．【点睛】本题主要考查圆的综合应用，解答主要应用了切线的判定定理、弦切角定理、切割线定理、圆周角定理、勾股定理、勾股定理的逆定理、三角形的外角的性质等，正确添加辅助线是解题的关键.7．如图，在中，，以为直径作，交边于点，交边于点，过点作的切线，交的延长线于点，交于点．（1）求证：；（2）若，，求的半径．【答案】（1）证明见解析；（2）4．【解析】试题分析：（1）连接AD，根据等腰三角形三线合一即可证明．（2）设⊙O的半径为R，则FO=4+R，FA=4+2R，OD=R，连接OD，由△FOD∽△FAE，得列出方程即可解决问题．试题解析：（1）连接AD，∵AB是直径，∴∠ADB=90°，∵AB=AC，AD⊥BC，∴BD=DC．（2）设⊙O的半径为R，则FO=4+R，FA=4+2R，OD=R，连接OD、∵AB=AC，∴∠ABC=∠C，∵OB=OD，∴∠ABC=∠ODB，∴∠ODB=∠C，∴OD∥AC，∴△FOD∽△FAE，∴，∴，整理得R2﹣R﹣12=0，∴R=4或（﹣3舍弃）．∴⊙O的半径为4．考点：切线的性质、等腰三角形的性质等知识．8．如图，△ABC中，AC＝BC＝10，cosC＝35，点P是AC边上一动点（不与点A、C重合），以PA长为半径的⊙P与边AB的另一个交点为D，过点D作DE⊥CB于点E．（1）当⊙P与边BC相切时，求⊙P的半径．（2）连接BP交DE于点F，设AP的长为x，PF的长为y，求y关于x的函数解析式，并直接写出x的取值范围．（3）在（2）的条件下，当以PE长为直径的⊙Q与⊙P相交于AC边上的点G时，求相交所得的公共弦的长.【答案】（1）409R=;（2）25880320xy x xx=-++;（3）50105-.【解析】【分析】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，即可求解；（2）首先证明PD∥BE，则EB BFPD PF=，即：2024588x yxxxy-+--=，即可求解；（3）证明四边形PDBE为平行四边形，则AG＝EP＝BD，即：AB＝DB+AD＝AG+AD＝45，即可求解．【详解】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，解得：R＝409；（2）在△ABC中，AC＝BC＝10，cosC＝35，设AP＝PD＝x，∠A＝∠ABC＝β，过点B作BH⊥AC，则BH ＝ACsinC ＝8，同理可得：CH ＝6，HA ＝4，AB ＝45，则：tan ∠CAB ＝2，BP ＝228+(4)x -＝2880x x -+， DA ＝25x ，则BD ＝45﹣25x ， 如下图所示，PA ＝PD ，∴∠PAD ＝∠CAB ＝∠CBA ＝β，tanβ＝2，则cosβ5，sinβ5， EB ＝BDcosβ＝（525x ）5＝4﹣25x ， ∴PD ∥BE ， ∴EB BF PD PF =，即：2024588x y x xx -+--=， 整理得：y 25x x 8x 803x 20-++ （3）以EP 为直径作圆Q 如下图所示，两个圆交于点G，则PG＝PQ，即两个圆的半径相等，则两圆另外一个交点为D，GD为相交所得的公共弦，∵点Q是弧GD的中点，∴DG⊥EP，∵AG是圆P的直径，∴∠GDA＝90°，∴EP∥BD，由（2）知，PD∥BC，∴四边形PDBE为平行四边形，∴AG＝EP＝BD，∴AB＝DB+AD＝AG+AD＝5设圆的半径为r，在△ADG中，AD＝2rcosβ5DG5AG＝2r，5＝52r51，则：DG550﹣5相交所得的公共弦的长为50﹣5【点睛】本题考查的是圆知识的综合运用，涉及到解直角三角形、勾股定理等知识，其中（3），要关键是根据题意正确画图，此题用大量的解直角三角形的内容，综合难度很大．9．如图，AB为⊙O的直径，BC为⊙O的弦，过O点作OD⊥BC，交⊙O的切线CD于点D，交⊙O于点E，连接AC、AE，且AE与BC交于点F．（1）连接BD，求证：BD是⊙O的切线；（2）若AF：EF=2：1，求tan∠CAF的值．【答案】（1）证明见解析；（2）3. 【解析】【分析】 （1）根据全等三角形的性质得到∠OBD=∠OCD=90°，根据切线的判定定理即可得到结论； （2）根据已知条件得到AC ∥DE ，设OD 与BC 交于G ，根据平行线分线段成比例定理得到AC ：EG=2：1，EG=12AC ，根据三角形的中位线的性质得到OG=12AC 于是得到AC=OE ，求得∠ABC=30°，即可得到结论．【详解】证明：（1）∵OC=OB ，OD ⊥BC ，∴∠COD=∠BOD ，在△COD 与△BOD 中， OC OB COD BOD OD OD ＝＝＝⎧⎪∠∠⎨⎪⎩，∴△COD ≌△BOD ，∴∠OBD=∠OCD=90°，∴BD 是⊙O 的切线；（2）解：∵AB 为⊙O 的直径，AC ⊥BC ，∵OD ⊥CB ，∴AC ∥DE ，设OD与BC交于G，∵OE∥AC，AF：EF=2：1，∴AC：EG=2：1，即EG=12AC，∵OG∥AC，OA=OB，∴OG=12AC，∵OG+GE=12AC+12AC=AC，∴AC=OE，∴AC=12AB，∴∠ABC=30°，∴∠CAB=60°，∵CE BE=，∴∠CAF=∠EAB=12∠CAB=30°，∴tan∠CAF=tan30°=3．【点睛】本题考查了切线的判定和性质，垂径定理，全等三角形的判定与性质，三角形的中位线的性质，三角函数的定义，正确的识别图形是解题的关键．10．如图，直角坐标系中，直线y kx b=+分别交x,y轴于点A(-8，0)，B(0，6)，C（m,0）是射线AO上一动点，⊙P过B，O，C三点，交直线AB于点D（B，D不重合）.（1）求直线AB的函数表达式.（2）若点D在第一象限，且tan∠ODC=53，求点D的坐标.【答案】（1）364y x=+；（2）D（8825，21625）.【解析】【分析】（1）把A 、B 两点坐标代入y=kx+b 求出k 、b 的值即可；（2）连结BC ，作DE ⊥OC 于点E ，根据圆周角定理可得∠OBC=∠ODC ，由tan ∠ODC=53可求出OC 的长，进而可得AC 的长，利用∠DAC 的三角函数值可求出DE 的长，即可得D 点纵坐标，代入直线AB 解析式求出D 点横坐标即可得答案.【详解】（1）∵A （-8，0）、B （0，6）在y=kx+b 上，∴086k b b =-+⎧⎨=⎩， 解得346k b ⎧=⎪⎨⎪=⎩，∴直线AB 的函数表达式为y=34x+6. (2)连结BC ，作DE ⊥OC 于点E ，∵∠BOC=90°，∴BC 为⊙P 的直径，∴∠ADC=90°，∵∠OBC=∠ODC ，tan ∠ODC=53， ∴OC 5OB 3=， ∵OB=6，OA=8，∴OC=10，AC=18，AB=10， ∵cos ∠DAC=OA AB =45，sin ∠DAC=OB AB =35， 472AD AC cos DAC 1855∠=⋅=⨯=, 723216DE AD sin DAC 5525∠=⋅=⨯=， ∵D 点在直线AB 上， ∴2163x 6254=+， 解得：88x 25=， ∴D （8825，21625）【点睛】本题考查待定系数法求一次函数解析式、圆周角定理及锐角三角函数的定义，熟练掌握直径所对的圆周角等于90°及正切、正弦、余弦等三角函数的定义是解题关键.。
成都四川省成都市中和中学数学圆 几何综合单元测试卷附答案
成都四川省成都市中和中学数学圆几何综合单元测试卷附答案一、初三数学圆易错题压轴题（难）1．在直角坐标系中，A（0，4），B（4，0）．点C从点B出发沿BA方向以每秒2个单位的速度向点A匀速运动，同时点D从点A出发沿AO方向以每秒1个单位的速度向点O 匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点C、D运动的时间是t秒(t>0)．过点C作CE⊥BO于点E，连结CD、DE．⑴当t为何值时，线段CD的长为4；⑵当线段DE与以点O为圆心，半径为的⊙O有两个公共交点时，求t的取值范围；⑶当t为何值时，以C为圆心、CB为半径的⊙C与⑵中的⊙O相切？【答案】(1); (2) 4-＜t≤; (3)或．【解析】试题分析：（1）过点C作CF⊥AD于点F，则CF，DF即可利用t表示出来，在Rt△CFD中利用勾股定理即可得到一个关于t的方程，从而求得t的值；（2）易证四边形ADEC是平行四边形，过点O作OG⊥DE于点G，当线段DE与⊙O相切时，则OG=，在直角△OEG中，OE可以利用t表示，则OG也可以利用t表示出来，当OG＜时，直线与圆相交，据此即可求得t的范围；（3）分两圆外切与内切两种情况进行讨论，当外切时，圆心距等于两半径的和，当内切时，圆心距等于圆C的半径减去圆O的半径，列出方程即可求得t的值．（1）过点C作CF⊥AD于点F，在Rt△AOB中，OA=4，OB=4，∴∠ABO=30°，由题意得：BC=2t，AD=t，∵CE⊥BO，∴在Rt△CEB中，CE=t，EB=t，∵CF⊥AD，AO⊥BO，∴四边形CFOE是矩形，∴OF=CE=t，OE=CF=4-t，在Rt△CFD中，DF2+CF2=CD2，∴（4-t-t）2+（4-t）2=42，即7t2-40t+48=0，解得：t=，t=4，∵0＜t＜4，∴当t=时，线段CD的长是4；（2）过点O作OG⊥DE于点G（如图2），∵AD∥CE，AD=CE=t∴四边形ADEC是平行四边形，∴DE∥AB∴∠GEO=30°，∴OG=OE=（4-t）当线段DE与⊙O相切时，则OG=，∴当（4-t）＜，且t≤4-时，线段DE与⊙O有两个公共交点．∴当 4-＜t≤时，线段DE与⊙O有两个公共交点；（3）当⊙C与⊙O外切时，t=；当⊙C与⊙O内切时，t=；∴当t=或秒时，两圆相切．考点：圆的综合题．2．如图，△ABC内接于⊙O，点D在AB边上，CD与OB交于点E，∠ACD＝∠OBC；（1）如图1，求证：CD⊥AB；（2）如图2，当∠BAC＝∠OBC+∠BCD时，求证：BO平分∠ABC；（3）如图3，在（2）的条件下，作OF⊥BC于点F，交CD于点G，作OH⊥CD于点H，连接FH并延长，交OB于点P，交AB边于点M．若OF＝3，MH＝5，求AC边的长．【答案】（1）见解析；（2）见解析；（3）AC＝48 5【解析】【分析】（1）根据直径所对的圆周角是直角，得出∠FCB=90°，再根据“同弧所对的圆周角相等”得出∠A=∠F，再根据已知条件得∠3=90°，得CD⊥AB；（2）延长BO交AC于K，由已知可得∠A=∠5，由∠A+∠2=90°得∠5+∠2=90°，根据三角形的内角和定理及外角定理得出∠9=∠1得出BO平分∠ABC；（3）延长BO交AC于点K，延长CD交⊙O于点N，联结BN，由条件可得CH=NH，BF=CF，从而HF是△CBN的中位线，HF∥BN，得出∠OEH=∠EHM又由∠OEH+∠EOH=∠EHM+∠OHP=90°可得HM=OB=5，在Rt△OBF中，根据勾股定理可得BF=4，解出BC=8，sin∠OBC=35，所以可得AC=2CK，CK=BC•sin∠OBC=245得AC=48 5.【详解】解：（1）如图1，令∠OBC＝∠1，∠ACD＝∠2延长BO交⊙O于F，连接CF．∵BF是⊙O的直径，∴∠FCB＝90°∴∠1+∠F＝90°，∵弧BC＝弧BC，∴∠A＝∠F又∵∠1＝∠2，∴∠2+∠A＝90°，∴∠3＝90°，∴CD⊥AB（2）如图2，令∠OBC＝∠1，∠BCD＝∠4延长BO交AC于K∵∠A＝∠1+∠4，∠5＝∠1+∠4，∴∠A＝∠5，∵∠A+∠2＝90°，∴∠5+∠2＝90°，∴∠6＝90°∵∠7＝180°﹣∠3＝90°，∴∠6＝∠7，又∵∠5＝∠8，∴∠9＝∠2∵∠2＝∠1，∴∠9＝∠1，∴BO平分∠ABC（3）如图3，延长BO交AC于点K，延长CD交⊙O于点N，联结BN∵OH⊥CN，OF⊥BC∴CH＝NH，BF＝CF∴HF是△CBN的中位线，HF∥BN∴∠FHC＝∠BNC＝∠BAC∵∠BAC＝∠OEH，∠FHC＝∠EHM∴∠OEH＝∠EHM设EM、OE交于点P∵∠OEH+∠EOH＝∠EHM+∠OHP＝90°∴∠EOH＝∠OHP∴OP＝PH∵∠ADC＝∠OHC＝90°∴AD∥OH∴∠PBM＝∠EOH，∠BMP＝∠OHP∴PM＝PB∴PM+PH＝PB+OP∴HM＝OB＝5在Rt△OBF中，根据勾股定理可得BF＝4∴BC＝8，sin∠OBC＝3 5∵∠A+∠ABO＝∠DEB+∠ABO＝90°∴∠AKB+∠CKB＝90°∴OK⊥ACAC＝2CK，CK＝BC•sin∠OBC＝24 5∴AC＝48 5【点睛】此题主要考查了圆的综合应用以及三角形的内角和定理及外角定理和勾股定理、三角函数等知识，理解同弧所对的圆周角相等是解题关键．3．四边形ABCD内接于⊙O，连接AC、BD，2∠BDC+∠ADB＝180°．（1）如图1，求证：AC＝BC；（2）如图2，E为⊙O上一点，AE＝BE，F为AC上一点，DE与BF相交于点T，连接AT，若∠BFC＝∠BDC+12∠ABD，求证：AT平分∠DAB；（3）在（2）的条件下，DT＝TE，AD＝8，BD＝12，求DE的长．【答案】（1）见解析；（2）见解析；（3）2【解析】【分析】（1）只要证明∠CAB=∠CBA即可．（2）如图2中，作TH⊥AD于H，TR⊥BD于R，TL⊥AB于L．想办法证明TL=TH即可解决问题．（3）如图3中，连接EA，EB，作EG⊥AB，TH⊥AD于H，TR⊥BD于R，TL⊥AB于L，AQ⊥BD于Q．证明△EAG≌△TDH（AAS），推出AG=DH，证明Rt△TDR≌Rt△TDH（HL），推出DH=DR，同理可得AL=AH，BR=BL，设DH=x，则AB=2x，由S△ADB=12•BD•AQ=12•AD•h+12•AB•h+12•DB•h，可得AQ=52h，再根据sin∠BDE=sin∠ADE，sin∠AED=sin∠ABD，构建方程组求出m即可解决问题．【详解】解：（1）如图1中，∵四边形ABCD内接于⊙O，∴∠ADC+∠ABC＝180°，即∠ADB+∠BDC+∠ABC＝180°，∵2∠BDC+∠ADB＝180°，∴∠ABC＝∠BDC，∵∠BAC＝∠BDC，∴∠BAC＝∠ABC，∴AC＝BC．（2）如图2中，作TH⊥AD于H，TR⊥BD于R，TL⊥AB于L．∵∠BFC＝∠BAC+∠ABF，∠BAC＝∠BDC，∴∠BFC＝∠BDC+∠ABF，∵∠BFC＝∠BDC+12∠ABD，∴∠ABF＝12∠ABD，∴BT平分∠ABD，∵AE＝BE∴∠ADE＝∠BDE，∴DT平分∠ADB，∵TH⊥AD于H，TR⊥BD于R，TL⊥AB于L．∴TR＝TL，TR＝TH，∴TL＝TH，∴AT平分∠DAB．（3）如图3中，连接EA，EB，作EG⊥AB，TH⊥AD于H，TR⊥BD于R，TL⊥AB于L，AQ⊥BD于Q．∵AE＝BE∴∠EAB＝∠EDB＝∠EDA，AE＝BE，∵∠TAE＝∠EAB+∠TAB，∠ATE＝∠EDA+∠DAT，∴∠TAE＝∠ATE，∴AE＝TE，∵DT＝TE，∴AE＝DT，∵∠AGE＝∠DHT＝90°，∴△EAG≌△TDH（AAS），∴AG＝DH，∵AE＝EB，EG⊥AB，∴AG＝BG，∴2DH＝AB，∵Rt△TDR≌Rt△TDH（HL），∴DH＝DR，同理可得AL=AH，BR＝BL，设DH＝x，则AB＝2x，∵AD＝8，DB＝12，∴AL＝AH＝8﹣x，BR＝12﹣x，AB＝2x＝8﹣x+12﹣x，∴x＝5，∴DH＝5，AB＝10，设TR＝TL＝TH＝h，DT＝m，∵S△ADB=12•BD•AQ=12•AD•h+12•AB•h+12•DB•h，∴12AQ＝（8+12+10）h，∴AQ＝52 h，∵sin∠BDE＝sin ∠ADE，可得hm＝APAD＝AP8，sin∠AED＝sin∠ABD，可得APm＝AQAB＝AQ10＝5210h，∴APm＝52810mAP⋅，解得m＝42或﹣42（舍弃），∴DE＝2m＝82．【点睛】本题属于圆综合题，考查了圆内接四边形的性质，圆周角定理，锐角三角函数，全等三角形的判定和性质，角平分线的性质定理和判定定理等知识，解题的关键是学会添加常用辅助线，学会利用参数构建方程组解决问题，属于中考压轴题．4．如图①、②、③是两个半径都等于2的⊙O1和⊙O2，由重合状态沿水平方向运动到互相外切过程中的三个位置，⊙O1和⊙O2相交于A、B两点，分别连结O1A、O1B、O2A、O2B和AB．(1)如图②，当∠AO1B=120°时，求两圆重叠部分图形的周长l；(2)设∠AO1B的度数为x，两圆重叠部分图形的周长为y，求y关于x的函数关系式，并写出自变量x的取值范围；(3)在(2)中，当重叠部分图形的周长时，则线段O2A所在的直线与⊙O1有何位置关系？请说明理由.除此之外，它们是否还有其它的位置关系？如果有，请直接写出其它位置关系时的x的取值范围.【答案】（1）83π（2）（0≤x≤180）（3）O2A与⊙O1相切；当0≤x≤90和0≤x≤180时，线段O2A所在的直线与⊙O1相交【解析】试题分析：（1）解法一、依对称性得，∠AO2B=∠AO1B=120°,∴解法二、∵O1A=O1B=O2A=O2B∴AO1BO2是菱形∴∠AO2B=∠AO1B=120°∴l=2׈A=(2)∵由（1）知，菱形AO1BO2中∠AO2B=∠AO1B=x度,∴重叠图形的周长, 即（0≤x≤180）(3) 当时，线段O2A所在的直线与⊙O1相切！理由如下：∵，由（2）可知：，解之x=90度∴AO1B=90°,因此菱形AO1BO2是正方形，∴O1AO2=90°,即O2A⊥O1A,而O1A是⊙O1的半径，且A为半径之外端；∴O2A与⊙O1相切．还有如下位置关系：当0≤x≤90和0≤x≤180时，线段O2A所在的直线与⊙O1相交考点：直线与圆的位置关系点评：本题主要考查直线与圆的位置关系，掌握判定直线与圆的位置关系是解本题的关键，会求函数的解析式，本题难度比较大5．如图1，△ABC内接于⊙O，直径AD交BC于点E，延长AD至点F，使DF＝2OD，连接FC并延长交过点A的切线于点G，且满足AG∥BC，连接OC，若cos∠BAC＝13，BC＝8．（1）求证：CF是⊙O的切线；（2）求⊙O的半径OC；（3）如图2，⊙O的弦AH经过半径OC的中点F，连结BH交弦CD于点M，连结FM，试求出FM的长和△AOF的面积．【答案】（1）见解析；（2）32332232【解析】【分析】（1）由DF=2OD，得到OF=3OD=3OC，求得13OE OCOC OF==，推出△COE∽△FOE，根据相似三角形的性质得到∠OCF=∠DEC=90°，于是得到CF 是⊙O 的切线；（2）利用三角函数值，设OE=x ，OC=3x ，得到CE=3，根据勾股定理即可得到答案；（3）连接BD ，根据圆周角定理得到角相等，然后证明△AOF ∽△BDM ，由相似三角形的性质，得到FM 为中位线，即可求出FM 的长度，由相似三角形的性质，以及中线分三角形的面积为两半，即可求出面积.【详解】解：（1） ∵DF ＝2OD ，∴OF ＝3OD ＝3OC ，∴13OE OC OC OF ==， ∵∠COE ＝∠FOC ，∴△COE ∽△FOE ， ∴∠OCF ＝∠DEC ＝90°，∴CF 是⊙O 的切线；（2）∵∠COD ＝∠BAC ，∴cos ∠BAC ＝cos ∠COE ＝13OE OC =， ∴设OE ＝x ，OC ＝3x ，∵BC ＝8，∴CE ＝4，∵CE ⊥AD ，∴OE 2+CE 2＝OC 2，∴x 2+42＝9x 2，∴x ＝2（负值已舍去），∴OC ＝3x ＝32，∴⊙O 的半径OC 为32；（3）如图，连结BD ，由圆周角定理，则∠OAF=∠DBM ，2AOF ADC ∠=∠，∵BC ⊥AD ，∴AC AB =，∴∠ADC=∠ADB ，∴2AOF ADC BDM ∠=∠=∠， ∴△AOF ∽△BDM ；∵点F 是OC 的中点，∴AO ：OF=BD ：DM=2，又∵BD=DC ，∴DM=CM ，∴FM 为中位线，∴FM=322， ∴S △AOF : S △BDM =(32:26)2 34=； ∵111118(322)4222222BDM BCD S S BC DE ∆∆==⨯•=⨯⨯⨯-=； ∴S △AOF =3424⨯=32； 【点睛】本题考查了圆的综合问题，圆周角定理，切线的判定和性质，相似三角形的判定和性质，利用勾股定理求边长，以及三角形中线的性质，解题的关键是熟练掌握所学的定理和性质，运用属性结合的思想进行解题.6．如图，AB 为⊙O 的直径，CD ⊥AB 于点G ，E 是CD 上一点，且BE ＝DE ，延长EB 至点P ，连接CP ，使PC ＝PE ，延长BE 与⊙O 交于点F ，连结BD ，FD ．（1）连结BC ，求证：△BCD ≌△DFB ；（2）求证：PC 是⊙O 的切线；（3）若tan F ＝23，AG ﹣BG ＝533，求ED 的值．【答案】（1）详见解析；（2）详见解析；（3）DE 133 【解析】【分析】 （1）由BE=DE 可知∠CDB=∠FBD ，而∠BFD=∠DCB ，BD 是公共边，结论显然成立． （2）连接OC ，只需证明OC ⊥PC 即可．根据三角形外角知识以及圆心角与圆周角关系可知∠PEC=2∠CDB=∠COB ，由PC=PE 可知∠PCE=∠PEC=∠COB ，注意到AB ⊥CD ，于是∠COB+∠OCG=90°=∠OCG+∠PEC=∠OCP，结论得证．（3）由于∠BCD=∠F，于是tan∠BCD=tanF=23=BGCG，设BG=2x，则CG=3x．注意到AB是直径，连接AC，则∠ACB是直角，由射影定理可知CG2=BG•AG，可得出AG的表达式（用x表示），再根据AG-BG=533求出x的值，从而CG、CB、BD、CD的长度可依次得出，最后利用△DEB∽△DBC列出比例关系算出ED的值．【详解】解：（1）证明：因为BE＝DE，所以∠FBD＝∠CDB，在△BCD和△DFB中：∠BCD＝∠DFB∠CDB＝∠FBDBD＝DB所以△BCD≌△DFB（AAS）．（2）证明：连接OC．因为∠PEC＝∠EDB+∠EBD＝2∠EDB，∠COB＝2∠EDB，所以∠COB＝∠PEC，因为PE＝PC，所以∠PEC＝∠PCE，所以∠PCE＝∠COB，因为AB⊥CD于G，所以∠COB+∠OCG＝90°，所以∠OCG+∠PEC＝90°，即∠OCP＝90°，所以OC⊥PC，所以PC是圆O的切线．（3）因为直径AB⊥弦CD于G，所以BC＝BD，CG＝DG，所以∠BCD＝∠BDC，因为∠F＝∠BCD，tanF＝23，所以∠tan ∠BCD ＝23＝BG CG， 设BG ＝2x ，则CG ＝3x ．连接AC ，则∠ACB ＝90°， 由射影定理可知：CG 2＝AG•BG ，所以AG ＝229922x C x G x G B ==，因为AG ﹣BG ，所以2392x x -=，解得x ＝3，所以BG ＝2x CG ＝3x ＝所以BC =，所以BD ＝BC ＝3， 因为∠EBD ＝∠EDB ＝∠BCD ，所以△DEB ∽△DBC ， 所以BDB DC DE D =，因为CD ＝2CG ＝所以DE ＝2DB CD =． 【点睛】本题为圆的综合题，主要考查了垂径定理，圆心角与圆周角的性质、等腰三角形的性质、全等三角形的判定与性质、切线的判定、射影定理、勾股定理、相似三角形的判定与性质等重要知识点．第（1）、（2）问解答的关键是导角，难度不大，第（3）问解答的要点在于根据射影定理以及条件当中告诉的两个等量关系求出BG 、CG 、BC 、BD 、CD 的值，最后利用“共边子母型相似”（即△DEB ∽△DBC ）列比例方程求解ED ．7．如图．在Rt ABC 中，90ACB ∠=︒，6AC =，10AB =，DE 是ABC 的中位线，连结BD ，点F 是边BC 上的一个动点，连结AF 交BD 于H ，交DE 于G ．(1)当点F 是BC 的中点时，求DH BH的值及GH 的长 (2) 当四边形DCFH 与四边形BEGH 的面积相等时，求CF 的长：(3)如图2．以CF 为直径作O ． ①当O 正好经过点H 时，求证：BD 是O 的切线： ②当DH BH 的值满足什么条件时，O 与线段DE 有且只有一个交点．【答案】（1）12DH BH =，133GH =；（2）83CF =；（3）①见解析；②当32DH BH =或2514DH BH >时，O 与线段DE 有且只有一个交点． 【解析】【分析】（1）根据题意得H 为ABC 的重心，即可得DH BH 的值，由重心和中位线的性质求得16=GH AF ，由勾股定理求得AF 的长，即可得GH 的长； （2）根据图中面积的关系得S 四边形DCFG =DEB S，列出关系式求解即可得CF 的长； （3）根据O 与线段DE 有且只有一个交点，可分两类情况讨论：当O 与DE 相切时，求得DH BH 的值；当O 过点E ，此时是O 与线段DE 有两个交点的临界点，即可得出O 与线段DE 有且只有一个交点时DH BH 满足的条件． 【详解】解：（1）∵DE 是ABC 的中位线，∴,D E 分别是,AC AB 的中点，//DE BC ，又∵点F 是BC 的中点，∴BD 与AF 的交点H 是ABC 的重心， :1:2DH BH ∴=，即12DH BH =；:1:2=HF AH ， ∴13=HF AF ， 在ACF 中，D 为AC 中点，//DE BC ，则//DG CF ，∴DG 为ACF 的中位线，G 为AF 的中点，12∴=GF AF ， 111236∴=-=-=GH GF HF AF AF AF ， 在Rt ABC 中，90ACB ∠=︒，6AC =，10AB =，8BC ∴===， 则142==CF BC ，AF ∴=16∴=⨯=GH ； （2）∵四边形DCFH 与四边形BEGH 的面积相等，∴S 四边形DCFH +DGH S=S 四边形BEGH +DGH S ， 即S 梯形DCFG =DEB S ，∵6AC =，8BC =，DE 是ABC 的中位线，∴3CD =，4DE =， ∵1143622=⋅⋅=⨯⨯=DEB S DE CD ， 设2CF a =，∵DG 为ACF 的中位线， ∴12==DG CF a ， 则S 梯形DCFG ()3(2)622+⋅==+=DG CF CD a a ， 解得：43a =， 823∴==CF a ； （3）①证明：如图2，连结、CH OH ，CF 为O 的直径，O 经过点H ，90∴∠=︒FHC ，∴90∠=∠=︒AHC FHC ，AHC 为直角三角形，D 为AC 的中点，12∴==DH AC CD ， ∠∠∴=DCH DHC ．又OC OH =，∴∠=∠OCH OHC ，∴∠+=∠+OCH DCH OHC DHC ，即90∠=∠=︒DHO ACB ，∴BH BD ⊥，即BD 是O 的切线；②如图3-1，当O 与DE 相切时，O 与线段DE 有且只有一个交点，设O 的半径为r ，圆心O 到DE 的距离为d ，∴当r=d 时，O 与DE 相切， ∵//DE CF ，90ACB ∠=︒，3CD =，∴两平行线、DE CF 之间的距离为3CD =，∴3r =，则6CF =，1862,32=-=-===BF BC CF DG CF ， 由//DE CF 得：DGH BFH ，32DH DG BH BF ∴==； 如图3-2，当O 经过点E 时，连接OE 、OG ，设O 的半径为r ，即==OE OC r ，∵G 为AF 的中点，O 为CF 的中点，∴//OG CD ，∴四边形COGD 为平行四边形，又∵90ACB ∠=︒，∴四边形COGD 为矩形，∴90∠=︒DGO ，则90∠=︒OGE ，OGE 为直角三角形，∴=3=OG CD ，==DG OC r ，则4=-=-GE DE DG r ，由勾股定理得：222+=OG GE OE ，即2223(4)+-=r r ， 解得：258r =，则258==OE OC ，2524==CF r 257258,448∴=-=-===BF BC CF DG OC ，由//DE BC 得：DGH BFH ，252514874∴===DH DG BH BF ， 则当2514DH BH >时，O 与线段DE 有且只有一个交点；综上所述，当32DH BH =或2514DH BH >时，O 与线段DE 有且只有一个交点． 【点睛】 本题属于圆综合题，考查了切线的性质与判定、中位线的性质等知识，解题的关键是灵活添加常用的辅助线，属于中考压轴题．8．如图①②，在平面直角坐标系中，边长为2的等边CDE ∆恰好与坐标系中的OAB ∆重合，现将CDE ∆绕边AB 的中点(G G 点也是DE 的中点），按顺时针方向旋转180︒到△1C DE 的位置．（1）求1C 点的坐标；（2）求经过三点O 、A 、1C 的抛物线的解析式； （3）如图③，G 是以AB 为直径的圆，过B 点作G 的切线与x 轴相交于点F ，求切线BF 的解析式；（4）抛物线上是否存在一点M ，使得:16:3AMF OAB S S ∆∆=．若存在，请求出点M 的坐标；若不存在，请说明理由．【答案】（1）13)C ；（2）2323y x x =；（3）323y x =；（4）1283834,,2,33M M ⎛⎫⎛- ⎪ ⎪ ⎝⎭⎝⎭． 【解析】【分析】（1）利用中心对称图形的性质和等边三角形的性质，可以求出．（2）运用待定系数法，代入二次函数解析式，即可求出．（3）借助切线的性质定理，直角三角形的性质，求出F ，B 的坐标即可求出解析式． （4）当M 在x 轴上方或下方，分两种情况讨论．【详解】解：（1）将等边CDE ∆绕边AB 的中点G 按顺时针方向旋转180︒到△1C DE ， 则有，四边形'OAC B 是菱形，所以1C 的横坐标为3，根据等边CDE ∆的边长是2，利用等边三角形的性质可得13)C ；（2）抛物线过原点(0,0)O ，设抛物线解析式为2y ax bx =+，把(2,0)A，C '代入，得42093a b a b +=⎧⎪⎨+=⎪⎩解得3a =，b = ∴抛物线解析式为233y x x =-；（3）90ABF ∠=︒，60BAF ∠=︒，30AFB ∴∠=︒，又2AB =，4AF ∴=，2OF ∴=， (2,0)F ∴-，设直线BF 的解析式为y kx b =+，把B ，(2,0)F -代入，得20k b k b ⎧+=⎪⎨-+=⎪⎩，解得k =b = ∴直线BF的解析式为33y x =+； （4）①当M 在x轴上方时，存在2()M x ，211:[4)]:[216:322AMF OAB S S ∆∆=⨯⨯⨯=， 得2280x x --=，解得14x =，22x =-，当14x =时，244y ， 当12x =-时，2(2)(2)y =--=1M ∴，2(M -； ②当M 在x轴下方时，不存在，设点2()M x x ，211:[4)]:[216:322AMF OAB S S ∆∆=-⨯⨯⨯=，得2280x x -+=，240b ac -<无解，综上所述，存在点的坐标为183(4,)M ，283(2,)M -． 【点睛】此题主要考查了旋转，等边三角形的性质，菱形的判定和性质，以及待定系数法求解二次函数解析式和切线的性质定理等，能熟练应用相关性质，是解题的关键．9．已知点A 为⊙O 外一点，连接AO ，交⊙O 于点P ，AO=6．点B 为⊙O 上一点，连接BP ，过点A 作CA ⊥AO ，交BP 延长线于点C ，AC=AB ．（1）判断直线AB 与⊙O 的位置关系，并说明理由．（2）若3 PB 的长．（3）若在⊙O 上存在点E ，使△EAC 是以AC 为底的等腰三角形，则⊙O 的半径r 的取值范围是___________． 【答案】（1）AB 与⊙O 相切 ，理由见解析；（2）43PB =3656r ≤< 【解析】【分析】（1）连接OB ，有∠OPB=∠OBP ，又AC=AB ，则∠C=∠ABP ，利用∠CAP=90°，即可得到结论成立；（2）由AB=AC ，利用勾股定理先求出半径，作OH ⊥BP 与H ，利用相似三角形的判定和性质，即可求出PB 的长度；（3）根据题意得出OE=12AC=122216r 2-22162r r -≤，即可求出取值范围．【详解】解：（1）连接OB ，如图：∵OP=OB ，∴∠OPB=∠OBP=∠APC ，∵AC=AB ，∴∠C=∠ABP ，∵AC ⊥AO ，∴∠CAP=90°，∴∠C+∠APC=90°，∴∠ABP+∠OBP=90°，即OB ⊥AB ，∴AB 为切线；（2）∵AB=AC∴22AB AC =，∴2222CP AP OA OB -=-，设半径为r ，则2222(43)(6)6r r --=-解得：r=2；作OH ⊥BP 与H ，则△ACP ∽△HOP ，∴PH OP AP CP=，即443PH = ∴33PH =,∴4323PB PH ==； （3）如图，作出线段AC 的垂直平分线MN ，作OE ⊥MN ，∴四边形AOEM 是矩形，∴OE=AM=12AC=12AB=22162r -； 又∵圆O 与直线MN 有交点，∴OE=22162r r -≤， ∴2262r r -≤，∴22364r r -≤，∴65r ≥， 又∵圆O 与直线AC 相离，∴r ＜6，即656r ≤<． 【点睛】此题主要考查了圆的综合以及切线的判定与性质和勾股定理以及等腰三角形的性质等知识，得出EO 与AB 的关系进而求出r 取值范围是解题关键．10．如图，二次函数y ＝﹣56x 2+bx +c 与x 轴的一个交点A 的坐标为（﹣3，0），以点A 为圆心作圆A ，与该二次函数的图象相交于点B ，C ，点B ，C 的横坐标分别为﹣2，﹣5，连接AB ，AC ，并且满足AB ⊥AC ．（1）求该二次函数的关系式；（2）经过点B 作直线BD ⊥AB ，与x 轴交于点D ，与二次函数的图象交于点E ，连接AE ，请判断△ADE 的形状，并说明理由；（3）若直线y ＝kx +1与圆A 相切，请直接写出k 的值．【答案】（1）y ＝﹣56x 2﹣376x ﹣11；（2）△ADE 是等腰三角形，理由见解析；（3）k 的值为﹣12或2 【解析】【分析】（1）利用三垂线判断出()ACN BAM AAS ∆≅∆，进而得出(2,2)B --，(5,1)C --，最后将点B ，C 坐标代入抛物线解析式中即可得出结论；（2）先判断出ABM BDM ∆∆∽，得出点D 坐标，进而求出直线BD 的解析式，求出点E 坐标，即可得出结论；（3）分两种情况，Ⅰ、切点在x 轴上方，利用三垂线判断出()AQG FPG AAS ∆≅∆，得出AQ PF =，GQ PG =，设成点G 坐标，进而得出3AQ m =+，PF km =，PG m =-，1GQ km =+，即可得出结论；Ⅱ、切点在x 轴下方，同Ⅰ的方法即可得出结论．【详解】解：（1）如图1，过点B 作BM x ⊥轴于M ，过点C 作CN x ⊥轴于N ，90ANC BMA ∴∠=∠=︒，90ABM BAM ∴∠+∠=︒，AC AB ⊥，90CAN BAM ∴∠+∠=︒，ABM CAN ∴∠=∠，A 过点B ，C ，AC AB ∴=，()ACN BAM AAS ∴∆≅∆，2(3)1CN AM ∴==---=，3(5)2BM AN ==---=，(2,2)B∴--，(5,1)C --，点B ，C 在抛物线上，∴54226525516b c b c ⎧-⨯-+=-⎪⎪⎨⎪-⨯-+=-⎪⎩， ∴37611b c ⎧=-⎪⎨⎪=-⎩，∴抛物线的解析式为25371166y x x =---，（2）ADE ∆是等腰三角形，理由如下：如图1，BD AB ⊥，90ABD ∴∠=︒，90ABM DBM ∴∠+∠=︒，过点B 作BM x ⊥轴于M ，90BMD AMB ∴∠=∠=︒，90BDM DBM ∴∠+∠=︒，ABM BDM ∴∠=∠，ABM BDM ∴∆∆∽，∴AM BM BM DM=， ∴122DM=， 4DM ∴=，2()2D ∴,，5AD ∴=，(2,2)B --，∴直线BD 的解析式为112y x =-， 联立，21125371166y x y x x ⎧=-⎪⎪⎨⎪=---⎪⎩， ∴22x y =-⎧⎨=-⎩（舍)或61x y =-⎧⎨=-⎩， (6,4)E ∴--，5AE ∴==，AD AE ∴=，ADE ∴∆是等腰三角形；（3）如图2，点(2,2)B --在A 上，AB ∴ 记直线1y kx =+与y 轴相交于F ，令0x =，则1y =，(0,1)F ∴，1OF ∴=，Ⅰ、当直线1y kx =+与A 的切点在x 轴上方时，记切点为G ，则AG AB ==90AGF ∠=︒，连接AF ，在Rt AOF ∆中，3OA =，1OF =，AF ∴=，在Rt AGF ∆中，根据勾股定理得，FG AG ===，如图2，过点G 作GP y ⊥轴于P ，过点G 作GQ x ⊥轴于Q ，90AQG FPG POQ ∴∠=∠=︒=∠，∴四边形POQG 是矩形，90PGQ ∴∠=︒， FG 是A 的切线，AGQ FGP ∴∠=∠，()AQG FPG AAS ∴∆≅∆，AQ PF ∴=，GQ PG =，设点(,1)G m km +，3AQ m ∴=+，PF km =，PG m =-，1GQ km =+，3m km ∴+=①，1km m +=-②， 联立①②解得，212m k =-⎧⎪⎨=-⎪⎩， Ⅱ、当切点在x 轴下方时，同Ⅰ的方法得，2k =，即：直线1y kx =+与圆A 相切，k 的值为12-或2． 【点睛】此题是二次函数综合题，主考查了待定系数法，三垂线判定两三角形全等，解方程组，判断出FG AG =是解本题的关键．。
2024年中考数学高频压轴题训练——圆-动点问题及参考答案
2024年中考数学高频压轴题训练——圆-动点问题1．“同弧或等弧所对的圆周角相等”，利用这个推论可以解决很多数学问题．（1）【知识理解】如图1，圆O 的内接四边形ACBD 中，60ABC ∠=︒，BC AC =，①BDC ∠=；DAB ∠DCB ∠（填“>”，“=”，“<”）②将D 点绕点B 顺时针旋转60︒得到点E ，则线段DB DC DA ，，的数量关系为．（2）【知识应用】如图2，AB 是圆O 的直径，1tan 2ABC ∠=，猜想DA DB DC ，，的数量关系，并证明；（3）【知识拓展】如图3，已知2AB =，A B ，分别是射线DA DB ，上的两个动点，以AB 为边往外构造等边ABC ，点C 在MDN ∠内部，若120D ∠=︒，直接写出四边形ADBC 面积S 的取值范围．2．如图1，对于PMN 的顶点P 及其对边MN 上的一点Q ，给出如下定义：以P 为圆心，PQ 为半径的圆与直线MN 的公共点都在线段MN 上，则称点Q 为PMN 关于点P 的内联点．在平面直角坐标系xOy 中：（1）如图2，已知点(70)A ，，点B 在直线1y x =+上．①若点(34)B ，，点(30)C ，，则在点O ，C ，A 中，点是AOB 关于点B 的内联点；②若AOB 关于点B 的内联点存在，求点B 纵坐标n 的取值范围；（2）已知点(20)D ，，点(42)E ，，将点D 绕原点O 旋转得到点F ．若EOF 关于点E 的内联点存在，直接写出点F 横坐标m 的取值范围．3．在平面直角坐标系xOy 中，O 的半径为1，对于点A 和线段BC ，给出如下定义：若将线段BC 绕点A 旋转可以得到O 的弦B C ''（B C ''，分别是B C ，的对应点），则称线段BC 是O 的以点A 为中心的“关联线段”．（1）如图，点112233A B C B C B C ，，，，，，的横､纵坐标都是整数．在线段112233B C B C B C ，，中，O 的以点A 为中心的“关联线段”是；（2）ABC 是边长为1的等边三角形，点()0A t ，，其中0t ≠．若BC 是O 的以点A 为中心的“关联线段”，求t 的值；（3）在ABC 中，12AB AC ==，．若BC 是O 的以点A 为中心的“关联线段”，直接写出OA 的最小值和最大值，以及相应的BC 长．4．已知：点C 为⊙O 的直径AB 上一动点，过点C 作CD ⊥AB ，交⊙O 于点D 和点E ，连接AD 、BD ，∠DBA 的角平分线交⊙O 于点F ．（1）若DF ＝BD ，求证：GD ＝GB ；（2）若AB ＝2cm ，在（1）的条件下，求DG 的值；（3）若∠ADB 的角平分线DM 交⊙O 于点M ，交AB 于点N ．当点C 与点O 重合时，AD BD DM+＝；据此猜想，当点C 在AB （不含端点）运动过程中，AD BD DM +的值是否发生改变？若不变，请求其值；若改变，请说明理由．5．在平面直角坐标系xOy 中，O 的半径为1，对于ABC 和直线l 给出如下定义：若ABC 的一条边关于直线l 的对称线段PQ 是O 的弦，则称ABC 是O 的关于直线l 的“关联三角形”，直线l 是“关联轴”．（1）如图1，若ABC 是O 的关于直线l 的“关联三角形”，请画出ABC 与O 的“关联轴”（至少画两条）；（2）若ABC 中，点A 坐标为(23)，，点B 坐标为(41)，，点C 在直线3y x =-+的图像上，存在“关联轴l ”使ABC 是O 的关联三角形，求点C 横坐标的取值范围；（3）已知A ，将点A 向上平移2个单位得到点M ，以M 为圆心MA 为半径画圆，B ，C 为M 上的两点，且2AB =（点B 在点A 右侧），若ABC 与O 的关联轴至少有两条，直接写出OC 的最小值和最大值，以及OC 最大时AC 的长．6．如图，在⊙O 中，AB 为弦，CD 为直径，且AB ⊥CD ，垂足为E ，P 为 AC 上的动点（不与端点重合），连接PD ．（1）求证：∠APD ＝∠BPD ；（2）利用尺规在PD 上找到点I ，使得I 到AB 、AP 的距离相等，连接AD （保留作图痕迹，不写作法）．求证：∠AIP+∠DAI ＝180°；（3）在（2）的条件下，连接IC 、IE ，若∠APB ＝60°，试问：在P 点的移动过程中，IC IE 是否为定值？若是，请求出这个值；若不是，请说明理由．7．在平面直角坐标系xOy 中，已知线段AB 和点P ，给出如下定义：若PA PB =且点P 不在线段AB 上，则称点P 是线段AB 的等腰顶点．特别地，当90APB ∠≥︒时，则称点P 是线段AB 的非锐角等腰顶点．（1）已知点(20)A ，，(42)B ，．①在点(40)C ，，(31)D ，，(15)E -，，(05)F ，中，是线段AB 的等腰顶点的是▲；②若点P 在直线3(0)y kx k =+≠上，且点P 是线段AB 的非锐角等腰顶点，求k 的取值范围；（2）直线33y x =-+与x 轴交于点M ，与y 轴交于点N ．⊙P 的圆心为(0)P t ，，半径为，若⊙P 上存在线段MN 的等腰顶点，请直接写出t 的取值范围．8．在平面直角坐标系xOy中，⊙O的半径为1，T（0，t）为y轴上一点，P为平面上一点．给出如下定义：若在⊙O上存在一点Q，使得△TQP是等腰直角三角形，且∠TQP＝90°，则称点P为⊙O的“等直点”，△TQP为⊙O的“等直三角形”．如图，点A，B，C，D的横、纵坐标都是整数．（1）当t＝2时，在点A，B，C，D中，⊙O的“等直点”是；（2）当t＝3时，若△TQP是⊙O“等直三角形”，且点P，Q都在第一象限，求CPOQ的值．9．综合与实践动手操作利用正方形纸片的折叠开展数学活动．探究体会在正方形折叠过程中，图形与线段的变化及其蕴含的数学思想方法．如图1，点E 为正方形ABCD 的AB 边上的一个动点，3AB =，将正方形ABCD 对折，使点A 与点B 重合，点C 与点D 重合，折痕为MN ．思考探索（1）将正方形ABCD 展平后沿过点C 的直线CE 折叠，使点B 的对应点B '落在MN 上，折痕为EC ，连接DB '，如图2．①点B '在以点E 为圆心，的长为半径的圆上；②B M '=；③DB C ' 为三角形，请证明你的结论．（2）拓展延伸当3AB AE =时，正方形ABCD 沿过点E 的直线l （不过点B ）折叠后，点B 的对应点B '落在正方形ABCD 内部或边上．①ABB ' 面积的最大值为；②连接AB '，点P 为AE 的中点，点Q 在AB '上，连接PQ AQP AB E ∠=∠'，，则2B C PQ '+的最小值为．10．在平面直角坐标系xOy 中，过⊙T （半径为r ）外一点P 引它的一条切线，切点为Q ，若0＜PQ≤2r ，则称点P 为⊙T 的伴随点．（1）当⊙O 的半径为1时，①在点A(4，0)，B(0，)，C(1，)中，⊙O 的伴随点是▲；②点D 在直线y ＝x+3上，且点D 是⊙O 的伴随点，求点D 的横坐标d 的取值范围；（2）⊙M 的圆心为M(m ，0)，半径为2，直线y ＝2x ﹣2与x 轴，y 轴分别交于点E ，F ．若线段EF 上的所有点都是⊙M 的伴随点，直接写出m 的取值范围．11．定义：在平面直角坐标系xOy 中，点P 为图形M 上一点，点Q 为图形N 上一点．若存在OP OQ =，则称图形M 与图形N 关于原点O “平衡”．（1）如图，已知⊙A 是以()1,0为圆心，2为半径的圆，点()1,0C -，()2,1D -，()3,2E ．①在点C ，D ，E 中，与⊙A 关于原点O “平衡”的点是；②点H 为直线y x =-上一点，若点H 与⊙A 关于原点O “平衡”，点H 的横坐标的取值范围为：；（2）如图，已知图形G 是以原点O 为中心，边长为2的正方形．⊙K 的圆心在x 轴上，半径为2．若⊙K 与图形G 关于原点O “平衡”，请直接写出圆心K 的横坐标的取值范围．12．阅读下列材料，并按要求解答相关问题：【思考发现】根据直径所对的圆周角是直角，我们可以推出“如果一条定边所对的角始终为直角，那么所有满足条件的直角顶点组成的图形是以定边为直径的圆或圆弧（直径的两个端点除外）”这一正确的结论．如图1，若AB 是一条定线段，且90APB ∠=︒，则所有满足条件的直角顶点P 组成的图形是定边AB 为直径的O （直径两端点A 、B 除外）（1）已知：如图2，四边形ABCD 是边长为8的正方形，点E 从点B 出发向点C 运动，同时点F 从点C 出发以相同的速度向点D 运动，连接AE ，BF 相交于点P ．①当点E 从点B 运动到点C 的过程中，APB ∠的大小是否发生变化？若发生变化，请说明理由；若不发生变化，请直接写出APB ∠的度数．②当点E 从点B 运动到点C 的过程中，点P 运动的路径是（）A ．线段；B ．弧；C ．半圆；D ．圆③点P 运动的路经长是▲．（2）已知：如图3，在图2的条件下，连接CP ，请直接写出E 、F 运动过程中，CP 的最小值．13．对于平面内的图形1G 和图形2G ，记平面内一点P 到图形1G 上各点的最短距离为1d ，点P 到图形2G 上各点的最短距离为2d ，若12d d =，就称点P 是图形1G 和图形2G 的一个“等距点”．在平面直角坐标系xOy 中，已知点()60A ，，(0B ．（1）在()30R ，，()20S ，，(1T 三点中，点A 和点B 的等距点是；（2）已知直线2y =-．①若点A 和直线2y =-的等距点在x 轴上，则该等距点的坐标为▲；②若直线y a =上存在点A 直线2y =-的等距点，求实数a 的取值范围；（3）记直线AB 为直线1l ，直线2l ：33y x =-，以原点O 为圆心作半径为r 的O ．若O 上有m 个直线1l 和直线2l 的等距点，以及n 个直线1l 和y 轴的等距点（0m ≠，0n ≠），求m n ≠时，求r 的取值范围．14．如图，平面上存在点P 、点M 与线段AB ．若线段AB 上存在一点Q ，使得点M 在以PQ 为直径的圆上，则称点M 为点P 与线段AB 的共圆点．已知点P （0，1），点A （﹣2，﹣1），点B （2，﹣1）．（1）在点O （0，0），C （﹣2，1），D （3，0）中，可以成为点P 与线段AB 的共圆点的是；（2）点K 为x 轴上一点，若点K 为点P 与线段AB 的共圆点，请求出点K 横坐标x K 的取值范围；（3）已知点M （m ，﹣1），若直线y ＝12x +3上存在点P 与线段AM 的共圆点，请直接写出m 的取值范围．15．如图，在ABC 中，AB BC =，30CAB ∠=︒，8AC =，半径为2的O 从点A 开始（如图1）沿直线AB 向右滚动，滚动时始终与直线AB 相切（切点为D ），当O 与ABC 只有一个公共点时滚动停止，作OG AC ⊥于点G ．（1）图1中，O 在AC 边上截得的弦长AE =；（2）当圆心落在AC 上时，如图2，判断BC 与O 的位置关系，并说明理由．（3）在O 滚动过程中，线段OG 的长度随之变化，设AD x =，OG y =，求出y 与x 的函数关系式，并直接写出x 的取值范围．16．在平面直角坐标系xOy 中，给出如下定义：若点P 在图形M 上，点Q 在图形N 上，称线段PQ 长度的最小值为图形M ，N 的“近距离”，记为d(M ，N)，特别地，若图形M ，N 有公共点，规定d(M ，N)＝0．已知：如图，点A(2-，0)，B(0，．（1）如果⊙O 的半径为2，那么d(A ，⊙O)＝，d(B ，⊙O)＝．（2）如果⊙O 的半径为r ，且d （⊙O ，线段AB ）=0，求r 的取值范围；（3）如果C(m ，0)是x 轴上的动点，⊙C 的半径为1，使d （⊙C ，线段AB ）<1，直接写出m 的取值范围．17．在平面直角坐标系xOy 中，对于点()P m n ，，我们称直线y mx n =+为点P 的关联直线.例如，点()24P ，的关联直线为24y x =+．（1）已知点()12A ，．①点A 的关联直线为；②若O 与点A 的关联直线相切，则O 的半径为；（2）已知点()02C ，，点()0.D d ，点M 为直线CD 上的动点．①当2d =时，求点O 到点M 的关联直线的距离的最大值；②以()11T -，为圆心，3为半径作.T 在点M 运动过程中，当点M 的关联直线与T 交于E ，F 两点时，EF 的最小值为4，请直接写出d 的值．18．在平面直角坐标系xOy 中，给定圆C 和点P ，若过点P 最多可以作出k 条不同的直线，且这些直线被圆C 所截得的线段长度为正整数，则称点P 关于圆C 的特征值为.k 已知圆O 的半径为2，（1）若点M 的坐标为()11，，则经过点M 的直线被圆O 截得的弦长的最小值为，点M 关于圆O 的特征值为；（2）直线y x b =+分别与x ，y 轴交于点A ，B ，若线段AB 上总存在关于圆O 的特征值为4的点，求b 的取值范围；（3）点T 是x 轴正半轴上一点，圆T 的半径为1，点R ，S 分别在圆O 与圆T 上，点R 关于圆T 的特征值记为r ，点S 关于圆O 的特征值记为.s 当点T 在x 轴正轴上运动时，若存在点R ，S ，使得3r s +=，直接写出点T 的横坐标t 的取值范围．答案解析部分1．【答案】（1）60︒；=；DC DB DA=+（2）解：在AB 上取一点E ，使ADE BDC ∠=∠，如图所示：∵AB 是圆O 的直径，1tan 2ABC ∠=，∴1tan 2AC ABC BC BC =∠⋅=，∴在Rt ACB 中，52AB BC ==，∵ BD BD =，∴DAB DCB ∠=∠，∵ADE BDC ∠=∠，∴ADE CDB ∽，∴ADAECD CB =，∴AD CB CD AE ⋅=⋅，∵ AD AD =，∴DBA DCA ∠=∠，∵ADE CDE CDB CDE ∠-∠=∠-∠，即ADC BDE ∠=∠，∴BDE CDA ∽，∴BDBECD AC =，∴BD AC CD BE ⋅=⋅，∴()AD CB AC BD CD AE CD BE CD AE BE CD AB⋅+⋅=⋅+⋅=⋅+=⋅，∴AB CD AC DB AD BC ⋅=⋅+⋅，∴122BC CD BC DB AD BC ⋅=⋅+⋅，∴5122CD DB AD ⋅=⋅+，∴5122CD DB AD =+，即2DB AD =+，故答案为：2DB AD =+．（3）解：∵A B ，分别是射线DA DB ，上的两个动点，120D ∠=︒，ABC 是等边三角形，∴四边形ADBC 的两个对角180ADB ACB ∠+∠=︒，∴构造四边形ADBC 的外接圆，∴根据四边形外接圆的性质可得：当点A 和点D 重合时，四边形ADBC 面积S 最小；当CD AB ⊥时，四边形ADBC 面积S 最大，①当点A 和点D 重合时，四边形ADBC 面积S 最小，∵CBD 时等边三角形，且2AB =，∴60CBD ∠=︒，2AB BD BC ===∴1sin 602CBD S BC BD =⋅⋅⋅= ，②当CD AB ⊥时，四边形ADBC 面积S 最大，∵CBD 时等边三角形，且2AB =，∴30ACD ∠=︒，2AC =，∴tan 233AD ACD AC =∠⋅==，∴11232322233ADC S AD DC =⋅⋅=⨯= ，∴23ADC ADBC S S == 四边形；433S <≤．2．【答案】（1）解：①O ，C ②当点B 的坐标为（0，1）时，如图，此时以BO 为半径的B 与线段OA 相切于点O ，∴点O 是OAB 关于点B 的内联点；当点B 移动到在y 轴左侧时，作图发现B 与x 轴有相交，且有一个交点不在线段OA 上，∴不再有OAB 关于点B 的内联点；当点B 的坐标为（7，8）时，以BA 为半径的B 与x 轴相切于点A ，∴点A 是OAB 关于点B 的内联点；当点B 直线x=7的右侧时，以BA 为半径的B 与x 轴相交，且有一个交点不在线段OA 上∴不再有OAB 关于点B 的内联点；综上所述，若AOB 关于点B 的内联点存在，求点B 纵坐标n 的取值范围为18n ≤≤；（2）80m 555m -≤≤≤≤或3．【答案】（1）22B C （2）解：由题意可得：当BC 是O 的以点A 为中心的“关联线段”时，则有AB C '' 是等边三角形，且边长也为1，当点A 在y 轴的正半轴上时，如图所示：设B C ''与y 轴的交点为D ，连接OB '，易得B C y ''⊥轴，∴12B D DC ''==，∴32OD ==，32==，∴OA =，∴t =；当点A 在y 轴的正半轴上时，如图所示：同理可得此时的OA =，∴t =；（3）当1min OA =时，此时BC =；当2max OA =时，此时2BC =．4．【答案】（1）证明：∵CD ⊥直径AB ，∴ BDBE =，∵DF ＝BD ，∴ DFBD =，∴ BEDF =，∴∠1＝∠2，∴DG ＝BG（2）解：∠DBA 的角平分线交⊙O 于点F ，∴∠2＝∠3，由（1）知，∠1＝∠2，∴∠1＝∠2＝∠3，∵∠BCD ＝90°，∴∠1+∠2+∠3＝90°，∴∠1＝∠2＝∠3＝30°，∵AB 是⊙O 的直径，∴∠ADB ＝90°，∴∠4＝90°﹣∠2﹣∠3＝30°，∵AB ＝2，∴BD ＝1，在Rt △BCD 中，∠1＝30°，∴BC ＝12BD ＝12，在Rt △BCG 中，∠3＝30°，∴CG ＝＝6，∴BG ＝2CG ＝33，由（1）知，DG ＝BG ＝33（3）5．【答案】（1）解：如图1，作BM ⊥x 轴，垂足为M ，根据题意AB=AE=EF=BF=，且∠EFO=∠BFM=45°，∴∠EFB=90°，∴四边形ABFE 是正方形，∴边AE ，BF 的中点所在直线就是ABC 与O 的一条“关联轴”；∵O 的半径为1，∴，且∠EFG=90°，∴四边形EFGH 是正方形，∵∠EFG+∠EFB=180°，∴B 、F 、G 三点共线，∴直线EF 是ABC 与O 的一条“关联轴”．（2）解：如图2，根据A （2，3），B （4，1），C （4，1），计算2=，故AB 不能落在圆的内部；过点A 作AN ⊥y 轴，垂足为N ，则AN=2，等于圆的直径，存在“关联轴l ”使ABC 是O 的关联三角形，此时0C x =；作点B 关于x 轴的对称点P ，此时BP=2，等于圆的直径，存在“关联轴l ”使ABC 是O 的关联三角形，此时4C x =，综上所述，点C 横坐标的范围是04C x ≤≤．（3）解：OC 的最小值为2-；OC 最大，根据勾股定理，AC=4.6．【答案】（1）证明：∵直径CD ⊥弦AB ，∴ AD BD=，∴∠APD=∠BPD ；（2）解：如图，作∠BAP 的平分线，交PD 于I ，证：∵AI 平分∠BAP ，∴∠PAI=∠BAI ，∴∠AID=∠APD+∠PAI=∠APD+BAI ，∵ AD BD=，∴∠DAB=∠APD ，∴∠DAI=∠DAB+∠BAI=∠APD+∠BAI ，∴∠AID=∠DAI ，∵∠AIP+∠DAI=180°，∴∠AIP+∠DAI=180°；（3）解：如图2，连接BI ，AC ，OA ，OB ，∵AI 平分∠BAP ，PD 平分∠APB ，∴BI 平分∠ABP ，∠BAI=12∠BAP ，∴∠ABI=12∠ABP ，∵∠APB=60°，∴∠PAB+∠PBA=120°，∴∠BAI+∠ABI=12（∠BAP+∠ABP ）=60°，∴∠AIB=120°，∴点I 的运动轨迹是 AB ，∴DI=DA ，∵∠AOB=2∠APB=120°，∵AD ⊥AB ，∴ AD BD=，∴∠AOB=∠BOD=60°，∵OA=OD ，∴△AOD 是等边三角形，∴AD=AO ，∵CD 是⊙O 的直径，∴∠DAC=90°，∵CD ⊥AB ，∴∠AED=90°，∴∠AED=∠CAD ，∵∠ADC=∠ADE ，∴△ADE ∽△CDA ，∴AD DE CD AD=，∴AD 2=DE•CD ，∵DI′=DI=AD ，∴DI 2=DE•CD ，∵∠I′DE 是公共角，∴△DIE ∽△DCI ，∴2IC CD IE DI==．7．【答案】（1）解：①C(4，0)，E(-1，5)；②（Ⅰ）当点(40)，在直线3y kx =+上时，430k +=，34k =-；（Ⅱ）当点(31)，在直线3y kx =+上时，331k +=，23k =-；（Ⅲ）当点(22)，在直线3y kx =+上时，232k +=，12k =-；结合图象可得3142k -≤≤-且23k ≠-；（2）解：直线333y x =-+与x 轴的交点M 坐标为()30，，与y 轴交点N 的坐标为(03，，∴tan 3NMO ∠=，∴30NMO ∠=︒，如图，作出线段MN 的垂直平分线，如图为两个临界情况：，利用待定系数法求得MN 垂直平分线解析式为y =，∴(0R -，，12230ORQ P RQ ∠=∠=︒，∴1112PR PQ ==，2222P R P Q ==，∴(10P ，(20P -，，∴t -≤<．8．【答案】（1）A 、B 、D（2）解：如图，依题意作⊙O 的“等直三角形”△TQP∴TQ=PQ ，∠TQP=90°过Q 点作MH //x 轴，交y 轴于M 点，过点P 作PH ⊥MH 于H 点∴∠TMQ=∠QHP=90°∴∠TQM+∠MTQ=∠TQM+∠HQP=90°∴∠MTQ=∠HQP∴△TMQ ≌△QHP （AAS ）∴TM=QH ，MQ=HP设Q （x ，y ）∴HM=MQ+QH=MQ+TM=x+3-y ，PH=MQ=x∴P （x-y+3，x+y ）∵C （3，0）∴∵∴CP OQ ．9．【答案】（1）BE ；3332-；等边；证明：B′D=BC CD ==，∴△DB'C 为等边三角形（2）310．【答案】（1）B ，C ；解：②如图2中，设点D 的坐标为(3)d d +，当过点D 的切线长为22r =时，OD ==由两点之间的距离公式得：OD =解得1221d d =-=-，结合图象可知，点D 的横坐标d 的取值范围是21d -≤≤-；（2）解：对于22y x =-当0y =时，220x -=，解得1x =，则点E 的坐标为(10)E ，当0x =时，2y =-，则点F 的坐标为(02)F -，⊙M 的半径为2，⊙M 的圆心为(0)M m ，24r ∴=，OM m=由题意，由以下两种情况：如图3-1中，点M 在点E 的右侧设FT 是⊙M 的切线则有两个临界位置：4FT =和点E 对应的切线长为0当4FT =时，则4OM m FT ===当点E 对应的切线长为0，即2EM =12EM m ∴=-=解得3m =结合图象得，当34m <≤时，线段EF 上的所有点都是⊙M 的伴随点②如图3-2和3-3中，点M 在点E 的左侧则有如下两个临界位置：如图3-2，设ET 是⊙M 的切线，连接MT ，则90MTE ∠=︒当4ET =时，2222245EM MT ET =+=+此时15m -=解得15m =-如图3-3，当⊙M 在直线EF 的左侧与EF 相切时，设切点为T ，连接MT∵(10)(02)E F -，，，∴12OE OF ==，∴22125EF =+=∵EF 是切线∴EF MT⊥∴90MTE FOE ∠=∠=︒∵MET FEO∠=∠∴MTE FOE~ ∴EM MTEF OF =，即22=解得EM =，即1m -=解得1m =-结合图象得，当11m -≤<-时，线段EF 上的所有点都是⊙M 的伴随点综上，m 的取值范围是11m -≤<-或34m <≤．11．【答案】（1）点C 、D ；22H x -≤≤-或22H x ≤≤（2）解： 图形G 是以原点O 为中心，边长为2的正方形，∴原点O 到正方形的最短距离是1d =，最长距离是d =，⊙K 与图形G 关于原点O “平衡”，∴原点O 到⊙K 上一点的距离1d ≤≤，⊙K 的圆心在x 轴上，半径为2，∴当⊙K 在x 轴正半轴时，圆心K 的横坐标的取值范围为：22x -≤≤+，当⊙K 在x 轴负半轴时，圆心K 的横坐标的取值范围为：22x --≤≤，综上所述，圆心K 的横坐标的取值范围22x -≤≤+或22x --≤≤．12．【答案】（1）解：①90°；②B ；③2π（2）解：413．【答案】（1）S(2，0)（2）解：①（4，0）或（8，0）；②如图，设直线y a =上的点Q 为点A 和直线2y =-的等距点，连接QA ，过点Q 作直线2y =-的垂线，垂足为点C ．点Q 为点A 和直线2y =-的等距点，QA QC ∴=．22QA QC ∴=．点Q 在直线y a =上，∴可设点Q 的坐标为()Q x a ，．()()22262x a a ∴-+=--⎡⎤⎣⎦．整理得2123240x x a -+-=．由题意得关于x 的方程2123240x x a -+-=有实数根．()()()212413241610a a ∴∆=--⨯⨯-=+≥．解得1a ≥-．（3）解：如图．直线l 1和直线l 2的等距点在直线l 3：33y x =-+上，直线l 1和y 轴的等距点在直线4l y =+：或33y x =+上，点O 与l 4的距离为32，点O 与l 3的距离为，点O 与l 5的距离为3，当r ＜时，n=0不符合题意，当r=时，m=2，n=0，符合题意，当＜r ＜3时，m=n=2，不符合题意，当r≥3时，m=2，n=3或4，符合题意，综上所述，r=或r≥3.14．【答案】（1）C（2）解：∵P （0，1），点A （﹣2，﹣1），点B （2，﹣1）．∴AP ＝BP ＝＝2，如图2，分别以PA 、PB 为直径作圆，交x 轴于点K 1、K 2、K 3、K 4，∵OP＝OG＝1，OE∥AB，∴PE＝AE＝，∴OE＝12AG＝1，∴K1（﹣1﹣，0），k2（1﹣，0），k3（﹣1，0），k4（1+，0），∵点K为点P与线段AB的共圆点，∴﹣1﹣≤x k≤1﹣或﹣1≤x k≤1+（3）解：分两种情况：①如图3，当M在点A的左侧时，Q为线段AM上一动点，以PQ为直径的圆E与直线y＝12x+3相切于点F，连接EF，则EF⊥FH，当x＝0时，y＝3，当y＝0时，y＝12x+3＝0，x＝﹣6，∴ON＝3，OH＝6，∵tan∠EHF＝ON EFOH FH＝36＝12，设EF＝a，则FH＝2a，EH＝a，∴OE＝6﹣a，Rt △OEP 中，OP ＝1，EP ＝a ，由勾股定理得：EP 2＝OP 2+OE 2，∴2221(6)a =+-，解得：a ＝2+（舍去）或2，∴QG ＝2OE ＝2（6﹣a ）＝﹣3+2，∴m≤3﹣2；②如图4，当M 在点A 的右侧时，Q 为线段AM 上一动点，以PQ 为直径的圆E 与直线y ＝12x+3相切于点F ，连接EF ，则EF ⊥FH ，同理得QG ＝3+2，∴m≥3+2，综上，m 的取值范围是m≤3﹣2或m≥3+215．【答案】（1）2（2）解：BC 与O 相切；理由：如图2，过点O 作OH BC ⊥于H ，连接OD ，∵O 与AB 相切于D ，∴OD AB ⊥，在Rt AOD 中，30BAC ∠=︒，∴24OA OD ==，∵8AC =，∴4OC =，在ABC 中，AB BC =，∴30C BAC ∠=∠=︒，在Rt OHC 中，30C ∠=︒，∴122OH OC OD ===，∴BC 与O 相切，（3）解：①当点O 在AC 的左侧时，连接OD 交AC 于F ，如备用图1，∵O 与AB 相切于D ，∴OD AB ⊥，∵OG AC ⊥，∴30FOG BAC ∠=∠=︒，在Rt FDA 中，tan FD BAC AD ∠=，∴tan 3FD AD BAC x =⋅∠=，∴23OF x =-，在Rt FOG 中，331cos 2322y OG OF FOG ⎛⎫==⋅∠=-⨯-+ ⎪ ⎪⎝⎭，即12y x =-+，此时x 的取值范围为0x ≤≤；②当点O 在AC 的右侧时，连接DO 并延长交AC 于F ，如备用图2，同①的方法得，33FD x =，∴23OF x =-，∵FD AB ⊥，∴90BAC AFD ∠+∠=︒，∴30FOG BAC ∠=∠=︒，在Rt FOG 中，331cos 2322y OG OF FOG x x ⎛⎫==⋅∠=-⨯- ⎪⎪⎝⎭，即12y x =-，此时x 的取值范围为1433x ≤≤．16．【答案】（1）0；2-（2）解：过点O 作OD ⊥AB 于点D ，∵点A(2-，0)，B(0，．∴2OA OB ==，，∴4AB ==，∵1122OA OB AB OD ⋅=⋅，∴112422OD ⨯⨯=⨯⨯∴DO =，∵d （⊙O ，线段AB ）=0，∴当⊙O 的半径等于OD 时最小，当⊙O 的半径等于OB 时最大，∴r r ≤≤（3）43423m -<<-17．【答案】（1）2y x =+（2）解：①当2d =时，()20D ，，设直线CD 的解析式为：y kx b =+，()02C ，，202k b b +=⎧∴⎨=⎩，解得：12k b =-⎧⎨=⎩，∴直线CD 的解析式为：y x =-+，设点M 的坐标为()2m m -+，，∴点M 的关联直线为：()212y mx m m x =-+=-+，∴点M 的关联直线经过定点()12N ，，如图2，过点O 作直线2y mx m =--+的垂线，垂足为H ，连接ON ，ON OH ∴≥，∴当点H与点N重合时，OH最大，即点O到点M的关联直线的距离最大，∴点O到点M=；2 d=②或2 3-18．【答案】（1）；3（2）解：设点G是O的特征值为4的点，∴经过一点G且弦长为4(最长弦)的直线有1条，弦长为3的直线有2条，弦长为2的直线有且只有1条， 经过点G的直线被O截得的弦长的最小值为2，=，∴关于O的特征值为4的所有点都在以O为半径的圆周上，直线y x b=+分别与x，y轴交于点A、B，()0A b∴-，，()B b，，OA OB b∴==，45OBH∴∠=︒，当0b>时，线段AB与以O为半径的圆相切时，点G特征值为4，设切点为为H，连接OH，则OH=，OB∴==，b∴=，设以O 为半径的圆与y 轴正半轴的交点记为1B ，则1OB =，当线段AB 与以O 1B 时，可得b =，b ≤≤同理可求当0b <时，b ≤≤，综上，b b b ≤≤-≤（3）当372122t -≤≤+时，存在点R ，S ，使得3r s +=。
押成都卷第17-18题(圆的综合问题、反比例函数与一次函数综合压轴)(解析版)-备战2024中考数学
押成都卷第17-18题押题方向一：圆的综合问题3年成都真题考点命题趋势2023年成都卷第17题圆周角、相似、正切从近年成都中考来看，圆的综合问题从2022年起就和反比例函数互换了位置，试题难度明显降低，试题以解答题形式呈现，整体难度中上；预计2024年成都卷还将重视圆综合问题（圆的相关概念与定理、相似、勾股、三角函数）的考查。
2022年成都卷第17题圆周角、相似、勾股定理、余弦1．（2023·四川成都·中考真题）如图，以ABC 的边AC 为直径作O ，交BC 边于点D ，过点C 作CE AB ∥交O 于点E ，连接AD DE ，，B ADE ∠=∠．(1)求证：AC BC =；(2)若tan 23B CD ==，，求AB 和DE 的长．【答案】(1)见解析(2)25AB =，25DE =【分析】（1）根据CE AB ∥，得到ACE BAC ∠=∠，再根据同弧所对的圆周角相等，得到ACE ADE B ∠=∠=∠，可证明ABC 是等腰三角形，即可解答；（2）根据直径所对的圆周角为直角，得到tan 2AD B BD ==，设BD x =，根据勾股定理列方程，解得x 的值，即可求出AB ；解法一：过点E 作DC 的垂线段，交DC 的延长线于点F ，证明B ECF ∠=∠，求出,EF DF 的长，根据勾股定理即可解出DE 的长；解法二：连接AE ,得到角相等，进而证得ABC ADE △△∽，根据对应边成比例即可解出DE 的长．【详解】（1）证明：CE AB ∥Q ，BAC ACE ∴∠=∠，BAC ACE ADE ∴∠=∠=∠，B ADE Ð=ÐQ ，B BAC ∴∠=∠，AC BC ∴=；（2）解：设BD x =，AC 是O 的直径，90ADC ADB ∴∠=∠=︒，tan 2B =，2AD BD∴=，即2AD x =，根据（1）中的结论，可得3AC BC BD DC x ==+=+，根据勾股定理，可得222AD DC AC +=，即()()222233x x +=+，解得12x =，20x =（舍去），2BD ∴=，4=AD ,根据勾股定理，可得2225AB AD BD =+=；解法一：如图，过点E 作DC 的垂线段，交DC 的延长线于点F ，CE AB ，ECF B ∴∠=∠，EF CF ⊥ ，tan tan 2ECF B ∴∠=∠=，即2EF CF=，90B BAD ∠+∠=︒ ，90ADE EDF ∠+∠=︒，B ADE ∠=∠，BAD EDF ∴∠=∠，9090DEF EDF BAD B ∴∠=︒-∠=︒-∠=∠，2DF EF∴=，设CF a =，则3DF DC CF a =+=+，2EF a ∴=，可得方程322a a +=，解得1a =，2EF ∴=，4DF =，根据勾股定理，可得2225DE DF EF =+=．解法二：如图，连接AE , B ADE ∠=∠，ACB AED ∠=∠，∴ABC ADE △△∽，∴AB BC AD DE =，又 5BC =，4=AD ，25AB =，∴2554DE=，∴25DE =．【点睛】本题考查了圆周角定理，等腰三角形的判定和性质，相似三角形的判定及性质，平行线的性质，勾股定理，正切，利用等量代换证明相关角相等是解题的关键．2．（2022·四川成都·中考真题）如图，在Rt ABC △中，90ACB ∠=︒，以BC 为直径作⊙O ，交AB 边于点D ，在 CD上取一点E ，使 BE CD =，连接DE ，作射线CE 交AB 边于点F ．(1)求证：A ACF ∠=∠；(2)若8AC =，4cos 5ACF ∠=，求BF 及DE 的长．【答案】(1)见解析(2)BF =5，4225DE =【分析】（1）根据Rt ABC △中，90ACB ∠=︒，得到∠A +∠B =∠ACF +∠BCF =90°，根据 BECD =，得到∠B =∠BCF ，推出∠A =∠ACF ；（2）根据∠B =∠BCF ，∠A =∠ACF ，得到AF =CF ，BF =CF ，推出AF =BF =12AB ，根据4cos cos 5AC ACF A AB ∠===，AC =8，得到AB =10，得到BF =5，根据226BC AB AC =-=，得到3sin 5BC A AB ==，连接CD ，根据BC 是⊙O 的直径，得到∠BDC =90°，推出∠B +∠BCD =90°，推出∠A =∠BCD ，得到3sin 5BD BCD BC ∠==，推出185BD =，得到75DF BF BD =-=，根据∠FDE =∠BCE ，∠B =∠BCE ，得到∠FDE =∠B ，推出DE ∥BC ，得到△FDE ∽△FBC ，推出DE DF BC BF =，得到4225DE =．【详解】（1）解：∵Rt ABC △中，90ACB ∠=︒，∴∠A +∠B =∠ACF +∠BCF =90°，∵ BECD =，∴∠B =∠BCF ，∴∠A =∠ACF ；（2）∵∠B =∠BCF ，∠A =∠ACF ∴AF =CF ，BF =CF ，∴AF =BF =12AB ，∵4cos cos 5AC ACF A AB ∠===，AC =8，∴AB =10，∴BF =5，∵226BC AB AC =-=，∴3sin 5BC A AB ==，连接CD ，∵BC 是⊙O 的直径，∴∠BDC =90°，∴∠B +∠BCD =90°，∴∠A =∠BCD ，∴3sin 5BD BCD BC ∠==，∴185BD =，∴75DF BF BD =-=，∵∠FDE =∠BCE ，∠B =∠BCE ，∴∠FDE =∠B ，∴DE ∥BC ，∴△FDE ∽△FBC ，∴DE DF BC BF =，∴4225DE =．周角定理及推论，运用勾股定理和正弦余弦解直角三角形，相似三角形的判定和性质．1）在证明圆周角相等或弧相等时，通常“由等角找等弧”或“由等弧找等角”；2）当已知圆的直径时，常构造直径所对的圆周角；3）在圆中求角度时，通常需要通过一些圆的性质进行转化。
成都九年级中考数学圆的综合解答题压轴题提高专题练习
成都九年级中考数学圆的综合解答题压轴题提高专题练习一、圆的综合1．如图，在平面直角坐标系xoy中，E（8,0），F(0 , 6)．（1）当G(4，8)时，则∠FGE= °（2）在图中的网格区域内找一点P，使∠FPE=90°且四边形OEPF被过P点的一条直线分割成两部分后，可以拼成一个正方形．要求：写出点P点坐标，画出过P点的分割线并指出分割线（不必说明理由，不写画法）．【答案】（1）90；（2）作图见解析，P（7，7），PH是分割线．【解析】试题分析：（1）根据勾股定理求出△FEG的三边长，根据勾股定理逆定理可判定△FEG是直角三角形，且∠FGE="90" °．（2）一方面，由于∠FPE=90°，从而根据直径所对圆周角直角的性质，点P在以EF为直径的圆上；另一方面，由于四边形OEPF被过P点的一条直线分割成两部分后，可以拼成一个正方形，从而OP是正方形的对角线，即点P在∠FOE的角平分线上，因此可得P（7，7），PH是分割线．试题解析：（1）连接FE，∵E（8,0），F(0 , 6)，G(4，8)，∴根据勾股定理，得FG=，EG=，FE=10．∵，即．∴△FEG是直角三角形，且∠FGE=90 °．（2）作图如下：P（7，7），PH是分割线．考点：1．网格问题；2．勾股定理和逆定理；3．作图（设计）；4．圆周角定理．2．如图，在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.（1）求证：PA是⊙O的切线；（2）过点C作CF⊥AD，垂足为点F，延长CF交AB于点G，若AG•AB=12，求AC的长．【答案】（1）证明见解析（2）3【解析】试题分析：（1）根据圆周角定理得出∠ACD=90°以及利用∠PAC=∠PBA得出∠CAD+∠PAC=90°进而得出答案；（2）首先得出△CAG∽△BAC，进而得出AC2=AG·AB，求出AC即可.试题解析：（1）连接CD,如图,∵AD是⊙O的直径,∴∠ACD=90°,∴∠CAD+∠D=90°，∵∠PAC=∠PBA，∠D=∠PBA，∴∠CAD+∠PAC=90°，即∠PAD=90°，∴PA⊥AD，∴PA是⊙O的切线；（2）∵CF⊥AD，∴∠ACF+∠CAF=90°，∠CAD+∠D=90°，∴∠ACF=∠D，∴∠ACF=∠B，而∠CAG=∠BAC，∴△ACG∽△ABC，∴AC：AB=AG：AC，∴AC2=AG•AB=12，∴AC=23．3．如图，已知在△ABC中，AB=15，AC=20，tanA=12，点P在AB边上，⊙P的半径为定长.当点P与点B重合时，⊙P恰好与AC边相切；当点P与点B不重合时，⊙P与AC边相交于点M和点N．（1）求⊙P的半径；（2）当AP=5△APM与△PCN是否相似，并说明理由．【答案】（1）半径为52）相似，理由见解析.【解析】【分析】（1）如图，作BD⊥AC，垂足为点D，⊙P与边AC相切，则BD就是⊙P的半径，利用解直角三角形得出BD与AD的关系，再利用勾股定理可求得BD的长；（2）如图，过点P作PH⊥AC于点H，作BD⊥AC，垂足为点D，根据垂径定理得出MN=2MH，PM=PN，再利用勾股定理求出PH、AH、MH、MN的长，从而求出AM、NC的长，然后求出AMMP、PNNC的值，得出AMMP=PNNC，利用两边对应成比例且夹角相等的两三角形相似即可证明.【详解】（1）如图，作BD⊥AC，垂足为点D，∵⊙P 与边AC 相切，∴BD 就是⊙P 的半径，在Rt △ABD 中，tanA=1BD 2AD =， 设BD=x ，则AD=2x ，∴x 2+(2x)2=152，解得：5∴半径为5（2）相似，理由见解析，如图，过点P 作PH ⊥AC 于点H ，作BD ⊥AC ，垂足为点D ，∴PH 垂直平分MN ，∴PM=PN ，在Rt △AHP 中，tanA=12PH AH =， 设PH=y ，AH=2y ，y 2+（2y ）2=（52解得：y=6（取正数），∴PH=6，AH=12，在Rt △MPH 中， ()22356-，∴MN=2MH=6，∴AM=AH-MH=12-3=9，NC=AC-MN-AM=20-6-9=5， ∴3535AM MP ==，35PN NC =， ∴AM MP =PN NC， 又∵PM=PN ，∴∠PMN=∠PNM ，∴∠AMP=∠PNC ，∴△AMP ∽△PNC.【点睛】本题考查了解直角三角形、垂径定理、相似三角形的判定与性质等，综合性较强，有一定的难度，正确添加辅助线、灵活应用相关的性质与定理是解题的关键.4．如图，⊙O是△ABC的外接圆，AC为直径，BD＝BA，BE⊥DC交DC的延长线于点E(1) 求证：BE是⊙O的切线(2) 若EC＝1，CD＝3，求cos∠DBA【答案】（1）证明见解析；（2）∠DBA3 5【解析】分析：（1）连接OB，OD，根据线段垂直平分线的判定，证得BF为线段AD的垂直平分线，再根据直径所对的圆周角为直角，得到∠ADC=90°，证得四边形BEDF是矩形，即∠EBF=90°，可得出结论.（2）根据中点的性质求出OF的长，进而得到BF、DE、OB、OD的长，然后根据等角的三角函数求解即可.详解：证明：(1) 连接BO并延长交AD于F，连接OD∵BD＝BA，OA＝OD∴BF为线段AD的垂直平分线∵AC为⊙O的直径∴∠ADC＝90°∵BE⊥DC∴四边形BEDF为矩形∴∠EBF＝90°∴BE是⊙O的切线(2) ∵O、F分别为AC、AD的中点∴OF＝12CD＝32∵BF＝DE＝1＋3＝4∴OB＝OD＝35422-=∴cos∠DBA＝cos∠DOF＝332552OFOD==点睛：此题主要考查了圆的切线的判定与性质，关键是添加合适的辅助线，利用垂径定理和圆周角定理进行解答，注意相等角的关系的转化.5．如图，△ABC内接于⊙O，且AB为⊙O的直径．∠ACB的平分线交⊙O于点D，过点D 作⊙O的切线PD交CA的延长线于点P，过点A作AE⊥CD于点E，过点B作BF⊥CD于点F．（1）求证：DP∥AB；（2）若AC=6，BC=8，求线段PD的长．【答案】详见解析【解析】【分析】（1）连接OD，由AB为⊙O的直径，根据圆周角定理得∠ACB=90°，再由∠ACD=∠BCD=45°，则∠DAB=∠ABD=45°，所以△DAB为等腰直角三角形，所以DO⊥AB，根据切线的性质得OD⊥PD，于是可得到DP∥AB．（2）先根据勾股定理计算出AB=10，由于△DAB为等腰直角三角形，可得到AD5222===△ACE为等腰直角三角形，得到AC6AE CE3222====，在Rt△AED中利用勾股定理计算出DE=42，则CD=72，易证得∴△PDA∽△PCD，得到PD PA AD52PC PD CD72===，所以PA=57PD，PC=75PD，然后利用PC=PA+AC可计算出PD．【详解】解：（1）证明：如图，连接OD，∵AB为⊙O的直径，∴∠ACB=90°．∵∠ACB的平分线交⊙O于点D，∴∠ACD=∠BCD=45°．∴∠DAB=∠ABD=45°．∴△DAB为等腰直角三角形．∴DO⊥AB．∵PD为⊙O的切线，∴OD⊥PD．∴DP∥AB．（2）在Rt△ACB中，，∵△DAB为等腰直角三角形，∴．∵AE⊥CD，∴△ACE为等腰直角三角形．∴．在Rt△AED中，，∴．∵AB∥PD，∴∠PDA=∠DAB=45°．∴∠PAD=∠PCD．又∵∠DPA=∠CPD，∴△PDA∽△PCD．∴．∴PA=75PD，PC=57PD．又∵PC=PA+AC，∴75PD+6=57PD，解得PD=．6．（1）问题背景如图①，BC是⊙O的直径，点A在⊙O上，AB=AC，P为BmC上一动点（不与B，C重合），求证：2PA=PB+PC．小明同学观察到图中自点A出发有三条线段AB，AP，AC，且AB=AC，这就为旋转作了铺垫．于是，小明同学有如下思考过程：第一步：将△PAC绕着点A顺时针旋转90°至△QAB（如图①）；第二步：证明Q，B，P三点共线，进而原题得证．请你根据小明同学的思考过程完成证明过程．（2）类比迁移如图②，⊙O的半径为3，点A，B在⊙O上，C为⊙O内一点，AB=AC，AB⊥AC，垂足为A，求OC的最小值．（3）拓展延伸如图③，⊙O的半径为3，点A，B在⊙O上，C为⊙O内一点，AB=43AC，AB⊥AC，垂足为A，则OC的最小值为．【答案】（1）证明见解析；（2）OC最小值是32﹣3；（3）32．【解析】试题分析：（1）将△PAC绕着点A顺时针旋转90°至△QAB（如图①），只要证明△APQ 是等腰直角三角形即可解决问题；（2）如图②中，连接OA，将△OAC绕点O顺时针旋转90°至△QAB，连接OB，OQ，在△BOQ中，利用三边关系定理即可解决问题；（3）如图③构造相似三角形即可解决问题．作AQ⊥OA，使得AQ=43OA，连接OQ，BQ，OB．由△QAB∽OAC，推出BQ=43OC，当BQ最小时，OC最小；试题解析：（1）将△PAC绕着点A顺时针旋转90°至△QAB（如图①）；∵BC是直径，∴∠BAC=90°，∵AB=AC，∴∠ACB=∠ABC=45°，由旋转可得∠QBA=∠PCA ，∠ACB=∠APB=45°，PC=QB ，∵∠PCA+∠PBA=180°，∴∠QBA+∠PBA=180°，∴Q ，B ，P 三点共线，∴∠QAB+∠BAP=∠BAP+∠PAC=90°，∴QP 2=AP 2+AQ 2=2AP 2，∴QP=2AP=QB+BP=PC+PB ，∴2AP=PC+PB ．（2）如图②中，连接OA ，将△OAC 绕点A 顺时针旋转90°至△QAB ，连接OB ，OQ ，∵AB ⊥AC,∴∠BAC=90°,由旋转可得 QB=OC ，AQ=OA ，∠QAB=∠OAC ，∴∠QAB+∠BAO=∠BAO+∠OAC=90°， ∴在Rt △OAQ 中，OQ=32，AO=3 ，∴在△OQB 中，BQ≥OQ ﹣OB=32﹣3 ， 即OC 最小值是32﹣3；（3）如图③中，作AQ ⊥OA ，使得AQ=43OA ，连接OQ ，BQ ，OB ．∵∠QAO=∠BAC=90°，∠QAB=∠OAC ，∵QA AB OA AC =43， ∴△QAB ∽OAC ，∴BQ=43OC ， 当BQ 最小时，OC 最小，易知OA=3，AQ=4，OQ=5，BQ≥OQ ﹣OB ，∴OQ≥2，]∴BQ 的最小值为2，∴OC 的最小值为34×2=32， 故答案为32． 【点睛】本题主要考查的圆、旋转、相似等知识，能根据题意正确的添加辅助线是解题的关键.7．已知：如图，在四边形ABCD 中，AD ∥BC ．点E 为CD 边上一点，AE 与BE 分别为∠DAB 和∠CBA 的平分线．（1）请你添加一个适当的条件，使得四边形ABCD是平行四边形，并证明你的结论；（2）作线段AB的垂直平分线交AB于点O，并以AB为直径作⊙O（要求：尺规作图，保留作图痕迹，不写作法）；（3）在（2）的条件下，⊙O交边AD于点F，连接BF，交AE于点G，若AE=4，sin∠AGF=45，求⊙O的半径．【答案】（1）当AD=BC时，四边形ABCD是平行四边形，理由见解析；（2）作出相应的图形见解析；（3）圆O的半径为2.5．【解析】分析：（1）添加条件AD=BC，利用一组对边平行且相等的四边形为平行四边形验证即可；（2）作出相应的图形，如图所示；（3）由平行四边形的对边平行得到AD与BC平行，可得同旁内角互补，再由AE与BE为角平分线，可得出AE与BE垂直，利用直径所对的圆周角为直角，得到AF与FB垂直，可得出两锐角互余，根据角平分线性质及等量代换得到∠AGF=∠AEB，根据sin∠AGF的值，确定出sin∠AEB的值，求出AB的长，即可确定出圆的半径．详解：（1）当AD=BC时，四边形ABCD是平行四边形，理由为：证明：∵AD∥BC，AD=BC，∴四边形ABCD为平行四边形；故答案为：AD=BC；（2）作出相应的图形，如图所示；（3）∵AD∥BC，∴∠DAB+∠CBA=180°，∵AE与BE分别为∠DAB与∠CBA的平分线，∴∠EAB+∠EBA=90°，∴∠AEB=90°，∵AB为圆O的直径，点F在圆O上，∴∠AFB=90°，∴∠FAG+∠FGA=90°，∵AE平分∠DAB，∴∠FAG=∠EAB，∴∠AGF=∠ABE，∴sin∠ABE=sin∠AGF=45AE AB =，∵AE=4，∴AB=5，则圆O的半径为2.5．点睛：此题属于圆综合题，涉及的知识有：圆周角定理，平行四边形的判定与性质，角平分线性质，以及锐角三角函数定义，熟练掌握各自的性质及定理是解本题的关键．8．如图，AB为⊙O的直径，DA、DC分别切⊙O于点A，C，且AB=AD．（1）求tan∠AOD的值．（2）AC，OD交于点E，连结BE．①求∠AEB的度数；②连结BD交⊙O于点H，若BC=1，求CH的长．【答案】（1）2；（2）①∠AEB＝135°；②22 CH=【解析】【分析】（1）根据切线的性质可得∠BAD=90°，由题意可得AD=2AO，即可求tan∠AOD的值；（2）①根据切线长定理可得AD=CD，OD平分∠ADC，根据等腰三角形的性质可得DO⊥AC，AE=CE，根据圆周角定理可求∠ACB=90°，即可证∠ABC=∠CAD，根据“AAS”可证△ABC≌△DAE，可得AE=BC=EC，可求∠BEC=45°，即可求∠AEB的度数；②由BC=1，可求AE=EC=1，BE2=∠ABE=∠HBC，可证△ABE∽△HBC，可求CH的长．【详解】（1）∵DA是⊙O切线，∴∠BAD=90°．∵AB=AD，AB=2AO，∴AD=2AO，∴tan∠AODADAO==2；（2）①∵DA、DC分别切⊙O于点A，C，∴AD=CD，OD平分∠ADC，∴DO⊥AC，AE=CE．∵AB是直径，∴∠ACB=90°，∴∠BAC+∠ABC=90°，且∠BAC+∠CAD=90°，∴∠ABC=∠CAD，且AB=AD，∠ACB=∠AED=90°，∴△ABC≌△DAE（AAS），∴CB=AE，∴CE=CB，且∠ACB=90°，∴∠BEC=45°=∠EBC，∴∠AEB=135°．②如图，∵BC=1，且BC=AE=CE，∴AE=EC=BC=1，∴BE2=．∵AD=AB，∠BAD=90°，∴∠ABD=45°，且∠EBC=45°，∴∠ABE=∠HBC，且∠BAC=∠CHB，∴△ABE∽△HBC，∴BC CHEB AE=，即12CH=，∴CH22=．【点睛】本题考查了切线的性质，圆周角定理，锐角三角函数，全等三角形的判定和性质，相似三角形的判定和性质，等腰三角形的性质等知识，灵活运用相关的性质定理、综合运用知识是解题的关键．9．如图，已知AB为⊙O的直径，AB=8，点C和点D是⊙O上关于直线AB对称的两个点，连接OC、AC，且∠BOC＜90°，直线BC和直线AD相交于点E，过点C作直线CG与线段AB的延长线相交于点F，与直线AD相交于点G，且∠GAF＝∠GCE（1）求证：直线CG为⊙O的切线；（2）若点H为线段OB上一点，连接CH，满足CB＝CH，①△CBH∽△OBC②求OH＋HC的最大值【答案】（1）证明见解析；（2）①证明见解析；②5.【解析】分析：（1）由题意可知：∠CAB=∠GAF，由圆的性质可知：∠CAB=∠OCA，所以∠OCA=∠GCE，从而可证明直线CG是⊙O的切线；（2）①由于CB=CH，所以∠CBH=∠CHB，易证∠CBH=∠OCB，从而可证明△CBH∽△OBC；②由△CBH∽△OBC可知：BC HBOC BC＝，所以HB=24BC，由于BC=HC，所以OH+HC=4−24BC +BC ，利用二次函数的性质即可求出OH+HC 的最大值． 详解：（1）由题意可知：∠CAB=∠GAF ，∵AB 是⊙O 的直径，∴∠ACB=90°∵OA=OC ，∴∠CAB=∠OCA ，∴∠OCA+∠OCB=90°，∵∠GAF=∠GCE ，∴∠GCE+∠OCB=∠OCA+∠OCB=90°，∵OC 是⊙O 的半径，∴直线CG 是⊙O 的切线；（2）①∵CB=CH ，∴∠CBH=∠CHB ，∵OB=OC ，∴∠CBH=∠OCB ，∴△CBH ∽△OBC②由△CBH ∽△OBC 可知：BC HB OC BC＝ ∵AB=8，∴BC 2=HB•OC=4HB ，∴HB=24BC ， ∴OH=OB-HB=4-24BC ∵CB=CH ，∴OH+HC=4−24BC +BC ， 当∠BOC=90°，此时∵∠BOC ＜90°，∴0＜BC ＜，令BC=x 则CH=x ，BH=24x ()221142544OH HC x x x ∴+=-++=--+ 当x=2时，∴OH+HC 可取得最大值，最大值为5点睛：本题考查圆的综合问题，涉及二次函数的性质，相似三角形的性质与判定，切线的判定等知识，综合程度较高，需要学生灵活运用所知识．10．如图，PA 切⊙O 于点A ，射线PC 交⊙O 于C 、B 两点，半径OD ⊥BC 于E ，连接BD 、DC 和OA ，DA 交BP 于点F ；（1）求证：∠ADC+∠CBD ＝12∠AOD ； （2）在不添加任何辅助线的情况下，请直接写出图中相等的线段．【答案】（1）详见解析；（2）详见解析；【解析】【分析】()1根据垂径定理得到BD CD =n n ，根据等腰三角形的性质得到()111809022ODA AOD AOD ∠=-∠=-∠o o ，即可得到结论； ()2根据垂径定理得到BE CE =，BD CD =n n ，根据等腰三角形的性质得到ADO OAD ∠=∠，根据切线的性质得到90PAO ∠=o ，求得90OAD DAP ∠+∠=o ，推出PAF PFA ∠=∠，根据等腰三角形的判定定理即可得到结论．【详解】()1证明：OD BC ⊥Q ，BD CD ∴=n n， CBD DCB ∴∠=∠，90DFE EDF ∠+∠=o Q ，90EDF DFE ∴∠=-∠o ，OD OA =Q ，()111809022ODA AOD AOD ∴∠=-∠=-∠o o ， 190902DFE AOD ∴-∠=-∠o o ， 12DEF AOD ∴∠=∠， DFE ADC DCB ADC CBD ∠=∠+∠=∠+∠Q ，12ADC CBD AOD ∴∠+∠=∠；()2解：OD BCQ，⊥n n，BE CE∴=，BD CD=BD CD∴=，Q=，OA OD∴∠=∠，ADO OADe于点A，Q切OPAPAO∴∠=o，90OAD DAP∴∠+∠=o，90Q，∠=∠PFA DFE∴∠+∠=o，90PFA ADO∴∠=∠，PAF PFA∴=．PA PF【点睛】本题考查了切线的性质，等腰三角形的判定和性质，垂径定理，圆周角定理，正确的识别图形是解题的关键．11．如图，⊙O的直径AB＝8，C为圆周上一点，AC＝4，过点C作⊙O的切线l，过点B 作l的垂线BD，垂足为D，BD与⊙O交于点E．（1）求∠AEC的度数；（2）求证：四边形OBEC是菱形．【答案】（1）30°；（2）详见解析.【解析】【分析】（1）易得△AOC是等边三角形，则∠AOC＝60°，根据圆周角定理得到∠AEC＝30°；（2）根据切线的性质得到OC⊥l，则有OC∥BD，再根据直径所对的圆周角为直角得到∠AEB＝90°，则∠EAB＝30°，可证得AB∥CE，得到四边形OBE C为平行四边形，再由OB ＝OC，即可判断四边形OBEC是菱形．【详解】（1）解：在△AOC中，AC＝4，∵AO＝OC＝4，∴△AOC是等边三角形，∴∠AOC ＝60°，∴∠AEC ＝30°；（2）证明：∵OC ⊥l ，BD ⊥l ．∴OC ∥BD ．∴∠ABD ＝∠AOC ＝60°．∵AB 为⊙O 的直径，∴∠AEB ＝90°，∴△AEB 为直角三角形，∠EAB ＝30°．∴∠EAB ＝∠AEC ．∴CE ∥OB ，又∵CO ∥EB∴四边形OBEC 为平行四边形．又∵OB ＝OC ＝4．∴四边形OBEC 是菱形．【点睛】本题考查了切线的性质：圆的切线垂直于过切点的半径．也考查了圆周角定理及其推论以及菱形的判定方法．12．（问题情境）如图1，点E 是平行四边形ABCD 的边AD 上一点，连接BE 、CE ．求证：BCE 1S 2=V S 平行四边形ABCD ．（说明：S 表示面积） 请以“问题情境”为基础，继续下面的探究 （探究应用1）如图2，以平行四边形ABCD 的边AD 为直径作⊙O ，⊙O 与BC 边相切于点H ，与BD 相交于点M ．若AD ＝6，BD ＝y ，AM ＝x ，试求y 与x 之间的函数关系式．（探究应用2）如图3，在图1的基础上，点F 在CD 上，连接AF 、BF ，AF 与CE 相交于点G ，若AF ＝CE ，求证：BG 平分∠AGC ．（迁移拓展）如图4，平行四边形ABCD 中，AB ：BC ＝4：3，∠ABC ＝120°，E 是AB 的中点，F 在BC 上，且BF ：FC ＝2：1，过D 分别作DG ⊥AF 于G ，DH ⊥CE 于H ，请直接写出DG ：DH 的值．【答案】【问题情境】见解析；【探究应用1】18y x=；【探究应用2】见解析；【迁移1927【解析】【分析】（1）作EF ⊥BC 于F ，则S △BCE ＝12BC×EF ，S 平行四边形ABCD ＝BC×EF ，即可得出结论； （2）连接OH ，由切线的性质得出OH ⊥BC ，OH ＝12AD ＝3，求出平行四边形ABCD 的面积＝AD×OH ＝18，由圆周角定理得出AM ⊥BD ，得出△ABD 的面积＝12BD×AM ＝12平行四边形的面积＝9，即可得出结果； （3）作BM ⊥AF 于M ，BN ⊥CE 于N ，同图1得：△ABF 的面积＝△BCE 的面积＝12平行四边形ABCD 的面积，得出12AF×BM ＝12CE×BN ，证出BM ＝BN ，即可得出BG 平分∠AGC ． （4）作AP ⊥BC 于P ，EQ ⊥BC 于Q ，由平行四边形的性质得出∠ABP ＝60°，得出∠BAP ＝30°，设AB ＝4x ，则BC ＝3x ，由直角三角形的性质得出BP ＝12AB ＝2x ，BQ ＝12BE ，AP ＝BP ＝，由已知得出BE ＝2x ，BF ＝2x ，得出BQ ＝x ，EQ x ，PF ＝4x ，QF ＝3x ，QC ＝4x ，由勾股定理求出AF ＝x ，CE，连接DF 、DE ，由三角形的面积关系得出AF×DG ＝CE×DH ，即可得出结果．【详解】（1）证明：作EF ⊥BC 于F ，如图1所示：则S △BCE ＝12BC×EF ，S 平行四边形ABCD ＝BC×EF ， ∴12BCE ABCD S S =V Y ． （2）解：连接OH ，如图2所示：∵⊙O 与BC 边相切于点H ，∴OH ⊥BC ，OH ＝12AD ＝3， ∴平行四边形ABCD 的面积＝AD×OH ＝6×3＝18，∵AD 是⊙O 的直径，∴∠AMD ＝90°，∴AM ⊥BD ，∴△ABD 的面积＝12BD×AM ＝12平行四边形的面积＝9， 即12xy ＝9，∴y 与x 之间的函数关系式y ＝18x ； （3） 证明：作BM ⊥AF 于M ，BN ⊥CE 于N ，如图3所示：同图1得：△ABF 的面积＝△BCE 的面积＝12平行四边形ABCD 的面积， ∴12AF×BM ＝12CE×BN ， ∵AF ＝CE ，∴BM ＝BN ，∴BG 平分∠AGC ． （4）解：作AP ⊥BC 于P ，EQ ⊥BC 于Q ，如图4所示：∵平行四边形ABCD 中，AB ：BC ＝4：3，∠ABC ＝120°，∴∠ABP ＝60°，∴∠BAP ＝30°，设AB ＝4x ，则BC ＝3x ，∴BP ＝12AB ＝2x ，BQ ＝12BE ，AP ＝3BP ＝23x ， ∵E 是AB 的中点，F 在BC 上，且BF ：FC ＝2：1，∴BE ＝2x ，BF ＝2x ，∴BQ ＝x ， ∴EQ ＝3x ，PF ＝4x ，QF ＝3x ，QC ＝4x ，由勾股定理得：AF ＝22AP PF +＝27x ，CE ＝22EQ QC +＝19x ，连接DF 、DE ，则△CDE 的面积＝△ADF 的面积＝12平行四边形ABCD 的面积， ∴AF×DG ＝CE×DH ， ∴DG ：DH ＝CE ：AF ＝19x :27x 19:27=．【点睛】本题是圆的综合题目，考查了圆周角定理、平行四边形的性质、三角形面积公式、含30°角的直角三角形的性质、勾股定理、角平分线的判定等知识；本题综合性强，需要添加辅助线，熟练掌握平行四边形的性质和勾股定理是解题的关键．13．如图，AB 是O e 的直径，DF 切O e 于点D ，BF DF ⊥于F ，过点A 作AC //BF 交BD 的延长线于点C .（1）求证：ABC C ∠∠=；（2）设CA 的延长线交O e 于E BF ，交O e 于G ，若¼DG的度数等于60o ，试简要说明点D 和点E 关于直线AB 对称的理由.【答案】（1）见解析；（2）见解析.【解析】【分析】（1）作辅助线，连接OD ，由DF 为⊙O 的切线，可得OD ⊥DF ，又BF ⊥DF ，AC ∥BF ，所以OD ∥AC ，∠ODB=∠C ，由OB=OD 得∠ABD=∠ODB ，从而可证∠ABC=∠C ；（2）连接OG ，OD ，AD ，由BF ∥OD ，»GD =60°，可求证»BG =»»GD AD ==60°，由平行线的性质及三角形的内角和定理可求出∠OHD=90°，由垂径定理便可得出结论．【详解】（1）连接OD ，∵DF 为⊙O 的切线，∴OD ⊥DF ．∵BF ⊥DF ，AC ∥BF ，∴OD ∥AC ∥BF ．∴∠ODB=∠C ．∵OB=OD，∴∠ABD=∠ODB．∴∠ABC=∠C．（2）连接OG，OD，AD，DE，DE交AB于H，∵BF∥OD，∴∠OBG=∠AOD，∠OGB=∠DOG，∴»»==»BG．GD AD∵»GD=60°，∴»BG=»»==60°，GD AD∴∠ABC=∠C=∠E=30°，∵OD//CE∴∠ODE=∠E=30°．在△ODH中，∠ODE=30°，∠AOD=60°，∴∠OHD=90°，∴AB⊥DE．∴点D和点E关于直线AB对称．【点睛】本题考查的是切线的性质、圆周角定理及垂径定理，解答此题的关键是作出辅助线，利用数形结合解答．14．如图，已知四边形ABCD内接于⊙O，点E在CB的延长线上，连结AC、AE，∠ACB=∠BAE=45°．（1）求证：AE是⊙O的切线；（2）若AB=AD，AC=32tan∠ADC=3，求BE的长．【答案】（1）证明见解析；（2）52BE = 【解析】试题分析：（1）连接OA 、OB ，由圆周角定理得出∠AOB=2∠ACB=90°，由等腰直角三角形的性质得出∠OAB=∠OBA=45°，求出∠OAE=∠OAB+∠BAE=90°,即可得出结论；（2）过点A 作AF ⊥CD 于点F,由AB=AD ，得到∠ACD =∠ACB =45°，在Rt △AFC 中可求得AF ＝3，在Rt △AFD 中求得DF ＝1，所以AB ＝AD ＝10 ，CD = CF +DF =4，再证明△ABE ∽△CDA ，得出BE AB DA CD =，即可求出BE 的长度； 试题解析：（1）证明：连结OA ，OB ，∵∠ACB =45°，∴∠AOB =2∠ACB = 90°，∵OA=OB ，∴∠OAB =∠OBA =45°，∵∠BAE =45°，∴∠OAE =∠OAB +∠BAE =90°，∴OA ⊥AE ．∵点A 在⊙O 上，∴AE 是⊙O 的切线．（2）解：过点A 作AF ⊥CD 于点F ，则∠AFC =∠AFD =90°．∵AB=AD ， ∴AB u u u r =AD u u u r∴∠ACD =∠ACB =45°，在Rt △AFC 中，∵AC =32∠ACF =45°，∴AF=CF=AC ·sin ∠ACF =3，∵在Rt △AFD 中， tan ∠ADC=3AF DF=， ∴DF =1，∴22AB AD==+=，3110且CD= CF+DF=4，∵四边形ABCD内接于⊙O，∴∠ABE=∠CDA，∵∠BAE=∠DCA，∴△ABE∽△CDA，∴BE AB=，DA CD∴10=，410∴5BE=．215．如图，在⊙O中，直径AB垂直弦CD于E，过点A作∠DAF=∠DAB，过点D作AF的垂线，垂足为F，交AB的延长线于点P，连接CO并延长交⊙O于点G，连接EG．（1）求证：DF是⊙O的切线；（2）若AD=DP，OB=3，求»BD的长度；（3）若DE=4，AE=8，求线段EG的长．【答案】（1）证明见解析（2）π（3）13【解析】试题分析：（1）连接OD，由等腰三角形的性质得出∠DAB=∠ADO，再由已知条件得出∠ADO=∠DAF，证出OD∥AF，由已知DF⊥AF，得出DF⊥OD，即可得出结论；（2）易得∠BOD=60°，再由弧长公式求解即可；（3）连接DG，由垂径定理得出DE=CE=4，得出CD=8，由勾股定理求出DG，再由勾股定理求出EG即可．试题解析：（1）证明：连接OD ，如图1所示： ∵OA=OD ，∴∠DAB=∠ADO ，∵∠DAF=∠DAB ，∴∠ADO=∠DAF ，∴OD ∥AF ，又∵DF ⊥AF ，∴DF ⊥OD ，∴DF 是⊙O 的切线；（2）∵AD=DP∴∠P=∠DAF=∠DAB =x 0∴∠P+∠DAF+∠DAB =3x o =90O ∴x 0=300∴∠BOD=60°，∴»BD的长度=π （3）解：连接DG ，如图2所示：∵AB ⊥CD ，∴DE=CE=4，∴CD=DE+CE=8，设OD=OA=x ，则OE=8﹣x ，在Rt △ODE 中，由勾股定理得：OE 2+DE 2=OD 2， 即（8﹣x ）2+42=x 2，解得：x=5，∴CG=2OA=10，∵CG 是⊙O 的直径，∴∠CDG=90°，∴2222108CG CD --， ∴222264DG DE +=+213。
成都市近十年中考数学相似三角形、折叠、几何压轴题
中线、角平分线、垂直平分线、中位线、相似、等量代换、三角函数、旋转、平移【2017成都中考】问题背景：如图1，等腰△ABC中，AB=AC，∠BAC=120°，作AD⊥BC于点D，则D为BC的中点，∠BAD=∠BAC=60°，于是==；迁移应用：如图2，△ABC和△ADE都是等腰三角形，∠BAC=∠DAE=120°，D，E，C三点在同一条直线上，连接BD．①求证：△ADB≌△AEC；②请直接写出线段AD，BD，CD之间的等量关系式；拓展延伸：如图3，在菱形ABCD中，∠ABC=120°，在∠ABC内作射线BM，作点C关于BM 的对称点E，连接AE并延长交BM于点F，连接CE，CF．①证明△CEF是等边三角形；②若AE=5，CE=2，求BF的长．【2016成都中考】如图①，△ABC中，∠ABC=45°，AH⊥BC于点H，点D在AH 上，且DH=CH，连结BD．（1）求证：BD=AC；（2）将△BHD绕点H旋转，得到△EHF（点B，D分别与点E，F对应），连接AE．①如图②，当点F落在AC上时，（F不与C重合），若BC=4，tanC=3，求AE 的长；②如图③，当△EHF是由△BHD绕点H逆时针旋转30°得到时，设射线CF与AE相交于点G，连接GH，试探究线段GH与EF之间满足的等量关系，并说明理由．【2015成都中考】已知AC，EC分别是四边形ABCD和EFDG的对角线，点E在△ABC内，∠CAE+∠CBE=90°．（1）如图①，当四边形ABCD和EFCG均为正方形时，连接BF．（i）求证：△CAE∽△CBF；（ii）若BE=1，AE=2，求CE的长；（2）如图②，当四边形ABCD 和EFCG 均为矩形，且==k 时，若BE=1，AE=2，CE=3，求k 的值；（3）如图③，当四边形ABCD 和EFCG 均为菱形，且∠DAB=∠GEF=45°时，设BE=m ，AE=n ，CE=p ，试探究m ，n ，p 三者之间满足的等量关系．（直接写出结果，不必写出解答过程）【2014成都中考】如图，矩形ABCD 中，AB AD 2=，E 是AD 边上一点，AD n DE 1= （n 为大于2的整数），连接BE ，作BE 的垂直平分线分别交AD 、BC 于点F ，G ，FG 与BE 的交点为O ，连接BF 和EG .（1）试判断四边形BFEG 的形状，并说明理由；（2）当a AB =（a 为常数），3=n 时，求FG 的长；（3）记四边形BFEG 的面积为1S ，矩形ABCD 的面积为2S ，当301721=S S 时，求n 的值.（直接写出结果，不必写出解答过程） 【2013成都中考】如图，点B 在线段AC 上，点D ，E 在AC 同侧，90A C ∠=∠=o ，BD BE ⊥，AD BC =.（1）求证：CE AD AC +=； （2）若3AD =，5CE =，点P 为线段AB 上的动点，连接DP ，作DP PQ ⊥，交直线BE 与点Q ； i ）当点P 与A ，B 两点不重合时，求DP PQ 的值； ii ）当点P 从A 点运动到AC 的中点时，求线段DQ 的中点所经过的路径（线段）长.（直接写出结果，不必写出解答过程）【2012成都中考】如图，△ABC 和△DEF 是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF 的顶点E 与△ABC 的斜边BC 的中点重合．将△DEF 绕点E旋转，旋转过程中，线段DE 与线段AB 相交于点P ，线段EF 与射线CA 相交于点Q ．（1）如图①，当点Q 在线段AC 上，且AP=AQ 时，求证：△BPE ≌△CQE ；（2）如图②，当点Q 在线段CA 的延长线上时，求证：△BPE ∽△CEQ ；并求当BP=a ，BC AF E D OB D图①图②CQ=92a 时，P 、Q 两点间的距离 (用含a 的代数式表示)． 【2011成都中考】如图，已知线段AB∥CD，AD 与B C 相交于点K ，E 是线段AD 上一动点。
中考数学-热点01 与圆有关的计算问题(四川成都专用)(解析版)
热点01与圆有关的计算问题圆得计算是四川成都中考数学的必考考点，常见以选填的形式，主要是求角、长度、面积等问题，一般出现在中考的第7或8题，偶尔也会出现在A 卷填空题中，以简单题为主，但除了常规考法以外，日常练习中多注意新颖题目的考向。
【题型1与圆有关的角度问题】【例1】（2023·四川成都·统考二模）如图，BC 是O 的直径，点,A D 在O 上，若30,ADC ∠=︒则ACB ∠的度数为（）A ．30°B ．40°C ．50°D ．60°【答案】D 【分析】利用圆周角定理求出30,ABC ADC ∠∠==︒再利用三角形角和定理求解即可．【详解】解：BC 是O 的直径，90,CAB ∴∠=︒30,ABC ADC ∠∠==︒ 903060.ACB ∴∠=︒-︒=︒故选：D.【点睛】本题主要考查了圆周角定理，三角形内角和定理等知识，熟练掌握圆周角定理是解此题的关键．A．18︒B．【答案】A【分析】连接OC OB、，再根据圆的性质得BOC∠的度数，根据圆周角定理得【详解】解：如图，连接则有OA OB=，∴OAB OBA∠=∠，根据正多边形的性质可得：∴180 OAB OBA︒-∠=∠=A．41︒B【答案】A【分析】利用圆周角定理求出【详解】解∶∵BOD∠∴1412BCD BOD∠=∠= A．15︒【答案】C【分析】先求出正六边形和正方形的边所对的圆心角，求差可得弦弧所对得圆周角即可．【详解】如图，连接∵四边形AGDH是正方形∴360490AOG∠=︒÷=【题型2与圆有关的长度问题】【答案】1.5【分析】先利用圆周角定理得到BD CD =，则可判断OD 为【详解】解：AB 是O 的直径，∵4AC =，5AB =，BC ∴OD BC ⊥ ，BD CD ∴=，A ．cos36r R =︒C ．2tan36a r =︒【答案】D 【分析】先根据正多边形的性质求出1360725BOC ∴∠=⨯︒=∵OB OC OF BC =，⊥11122BOC ∠∠∴==⨯1A ．233R【答案】A【分析】求出AOD ∠【答案】25【分析】根据题意得5OD =，设【详解】如图，找到半圆的圆心设OE x =，则2EF DE x ==由勾股定理得22225x x +（）=解得25x =．∴5x =（负值舍去）．【题型3与圆有关的面积问题】【答案】184【分析】过点O 作积即为扇形AOB 的面积减去三角形【详解】解：如图，过点 圆心O 到栏杆AB 的距离是5OC ∴=米，OC AB ⊥ ，1sin 2OC OBC OB ∴∠==A．16πB．12π【答案】A【分析】由题意知，S S=阴影扇形【详解】解：由题意知，S=阴影πB A．23（建议用时：30分钟）1．（2023·四川成都·成都实外校考一模）如图，CD 是O 的直径，弦AB CD ⊥，若28CDB ∠=︒，则AOC ∠的度数为（）A ．28︒B ．56︒C ．58︒D ．62︒【答案】B 【分析】根据垂径定理可得 BCAC =，再由圆周角定理，即可求解．【详解】解：∵CD 是O 的直径，弦AB CD ⊥，∴ BCAC =，∴222856AOC CDB ∠=∠=⨯︒=︒．故选：B【点睛】本题主要考查了垂径定理，圆周角定理，熟练掌握垂径定理，圆周角定理是解题的关键．2．（2023·四川成都·模拟预测）如图，ABC 中，3AC =，4BC =，90C ∠=︒，O 为ABC 的内切圆，与三边的切点分别为D 、E 、F ，则O 的面积为___________（结果保留π）（）A ．πB ．2πC ．3πD ．4π【答案】A 【分析】连接OA ，OB ，OC ，OD ，OE ，OF ，设OD OE OF r ===，先由勾股定理求出AB 的长，然后由面积法可求出半径r ，从而根据圆的面积公式可计算出圆的面积．【详解】解：如图，连接OA ，OB ，OC ，OD ，OE ，OF ．设OD OE OF r ===，由勾股定理得 1122AC OF BC OE ⋅+⋅∴()11345322r r r ++=⨯⨯A．5 3π【答案】D【分析】根据圆周角定理可得∠【详解】解：∵OA=OB∴∠ACO=∠CAO，∠A．6【答案】C【分析】延长AO交⊙得BE＝CD，在Rt△ABE 【详解】解：如图，延长则∠AOB+∠BOE＝180又∵∠AOB+∠COD＝∴∠BOE＝∠COD，∴BE＝CD，∵AE为⊙O的直径，∴∠ABE＝90°，A．24πB．12π【答案】B【分析】先根据∠OCA=60°再利用扇形面积公式计算即可．【详解】解：∵∠OCA＝60°∴△OAC是等边三角形，ππ【答案】12π【分析】根据圆周角定理可得出【详解】解：∵ACB∠=∴2120AOB ACB∠=∠=︒∴212061236AOBSπ⨯==扇形故答案为：12π．【点睛】本题考查圆周角定理，扇形面积公式．掌握扇形面积公式为15．（2023·四川成都·校考二模）如图，【答案】40︒/40度【分析】先根据圆周角定理求得可求解．【详解】解：连接OC1【点睛】本题考查圆周角定理、平行线的性质、等腰三角形的性质，熟练掌握圆周角定理和等腰三角形的性质是解答的关键．16．（2023·四川成都·统考二模）如图，已知上一点，连接点D，若P为O【答案】35︒/35度【点睛】本题考查了正多边形和圆、正六边形的性质、解直角三角形；熟练掌握正六边形的性质是解决问题的关键．18．（2023·四川成都·模拟预测）则扇形BOC 的面积为【答案】3π【分析】本题考查的是圆周角定理，扇形面积的计算，掌握圆周角定理、扇形面积公式是解题的关键．根据圆周角定理求出AOB ∠【详解】解：由圆周角定理得，∴18060120BOC ∠=︒-︒=【答案】1或9【分析】由题意知，分E 靠近由垂径定理得132CE CD ==，由勾股定理得，②当E 靠近A 点，同理4OE =【详解】解：由题意知，分E ∵直径10AB =，弦CD AB ⊥，弦∴5OC OB ==，90OEC ∠=︒，由勾股定理得，2OE OC CE =-∴1BE OB OE =-=；②当E 靠近A 点，同理4OE =【答案】36︒/36度【分析】连接OB ，OA ，由多边形是正五边形可求出中心角OAB ∠的度数，利用切线的性质求出【详解】解：连接OB ，OA ，多边形ABCDEF 是正多边形，1(180)542OAB AOB ∴∠=︒-∠=︒． 直线PA 与O 相切于点A ，905436BAP ∴∠=︒-︒=︒．故答案为：36︒．112BD DC BC ∴===，∴ 分别以等边三角形ABC 可知曲边三角形的三个弓形部分面积相等，为∴图形的总面积为233π⎛⨯ ⎝。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
圆
【2017成都中考】如图，在△ABC中，AB=AC，以AB为直径作圆O，分别交BC于点D，交CA的延长线于点E，过点D作DH⊥AC于点H，连接DE交线段OA于点F．
（1）求证：DH是圆O的切线；
的中点，求的值；）若2A为EH（的半径．EA=EF=1，求圆O3（）若
【2016成都中考】如图，在Rt△ABC中，∠ABC=90°，以CB为半径作⊙C，交AC于点D，交AC 的延长线于点E，连接ED，BE．
（1）求证：△ABD∽△AEB；
；时，求tanE（2）当=
C⊙F点，若AF=2，求BE平，作）的2条件下∠BAC的分线，与交于）在（（3 径的
半．
【2015成都中考】如图，在Rt△ABC中，∠ABC=90°，AC的垂直平分线分别与AC，BC及AB的延长线相较于点D，E，F，且BF=BC，⊙O是△BEF的外接圆，∠EBF的平分线交EF于点G，交⊙O于点H，连接BD，FH．
（1）求证：△ABC≌△EBF；
（2）试判断BD与⊙O的位置关系，并说明理由；
（3）若AB=1，求HG?HB的
值．
O的垂线AB，过C作成都中考】如图，在⊙AC=2BC的内接△ABC中，∠ACB=90°，2014【⌒ll 是E.设P交⊙O于另一点D，垂足为上异于 A,C的一个动点，射线AP交，连接于点FAC G.【来源：21·世纪·教育·网】PDPD，交AB于点PC与
；）求证：△PAC∽△PDF1（⌒⌒，求PD2（）若AB=5，的长； = BPAP AG?x tan?AFD?y，）在点（3P，运动过程中，设BGxxy的取值范围）（不要求写出与之间的函数关系式求.
OOBDABCD25?ACr?于点，四边形内接圆⊙2013【成都中考】如图，⊙，的半径CAPABDPDA???H.
为，延长线上的一点，且
OPD的位置关系，并说明理由：）试判断与⊙（1?3?PAAH??ADB tan BD，（2，求）若的长；34ABCD 的面积）的条件下，求四边形. （3）在（2
【2012成都中考】如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F．切点为G，连接AG交CD于K．
（1）求证：KE=GE；
2KG的位置关系，并说明理由；AC与EF（2）若，试判断=KD·GE
323，求AK=FG的长．23 （）在（）的条件下，若sinE= ，5
长为半径作为圆心，OAAC的中点O【2011成都中考】已知：如图，以矩形ABCD的对角线、ACDH 分别与∥D作DHKB，⊥经过OB、D两点，过点B作BK A C，垂足为K。
过⊙O，⊙ H．、、FG、、⊙ABO及CB的延长线相交于点E AE=CK；(1)求证：
1aaa为大于零的常数)，，AD=求BK ((2) 如果AB=3的长：
(3)若F是EG的中点，且DE=6，求⊙O的半径和GH的长．
CABABCCE??Oe FAB是于成都中考】【2010已知：如图，，为直径，内接于
弦，?BCECGCEAD PADBD、、，的中点，连结并延长交分别交的延长线于点于点，连结Q．ACQ?P 的外心；）求证：是（1
3,CF??8tan?ABCCQ的长；（2）若,求42?FPg?PQ)FGFP(．）求证：（ 3
【2009成都中考】如图，Rt△ABC内接于⊙O，AC=BC，∠BAC的平分线AD与⊙0交于点D，与BC 交于点E，延长BD，与AC的延长线交于点F，连结CD，G是CD的中点，连结0G．
F CD的位置关系，写出你的结论并证明； (1)判断0G与
D AE=BF；(2)求证E2)??DE?3(2OG的面积。
，求⊙O3（）若ABO
【2008成都中考】如图，已知⊙O的半径为2，以⊙O的弦AB为直径作⊙M，点C是⊙O优?AB 弧，D、点EM.连结AC、BC，分别与⊙相交于点B上的一个动点（不与点A、点重合）3.
若AB=2连结DE.AD=x（0<x<3）∠tanABC=y，，那么在点C）如果记（DE2的度数；求∠(1)C（）求的长；3DC y. x的运动过程中，试用含的代数式表示。