【管理知识】材料弹性常数E、μ与材料切变模量G的测定(doc 10页)
材料力学 材料切变模量G的测定 实验报告

一. 实验目的1. 两种方法测定金属材料的切变模量G ; 2. 验证圆轴扭转时的虎克定律。
二. 实验仪器和设备1. 微机控制电子万能试验机 2. 扭角仪 3. 电阻应变仪 4. 百分表 5.游标卡尺三. 中碳钢圆轴试件,名义尺寸d=40mm, 材料屈服极限MPa s 360=σ。
四. 实验原理和方法1. 电测法测切变模量G材料在剪切比例极限内,切应力与切应变成正比,γτG = (1)上式中的G 称为材料的切变模量。
由式(1)可以得到:γτ=G (2) 扭角仪百分表H图二 微体变形示意图图三 二向应变花示意图圆轴在剪切比例极限内扭转时,圆轴表面上任意一点处的切应力表达式为:PW T=max τ (3) 由式(1)~(3)得到:γ⋅=P W TG (4) 由于应变片只能直接测出正应变,不能直接测出切应变,故需找出切应变与正应变的关系。
圆轴扭转时,圆轴表面上任意一点处于纯剪切受力状态,根据图二所示正方形微体变形的几何关系可知:454522-=-=εεγ (5)由式(2)~(5)得到:454522εεp p W TW T G -==- (6) 根据上式,实验时,我们在试件表面沿±45o 方向贴应变片(一般贴二向应变花,如图三所示),即可测出材料的切变模量G 。
本实验采用增量法加载,即逐级加载,分别测量在各相同载荷增量∆T 作用下,产生的应变增量∆ε。
于是式(6)写为:454522εε∆⋅∆-=∆⋅∆=-p p W TW T G (7) 根据本实验装置,有a P T ⋅∆=∆ (8)a ——力的作用线至圆轴轴线的距离 最后,我们得到:454522εε∆⋅⋅∆-=∆⋅⋅∆=-p p W aP W a P G (9) 2. 扭角仪测切变模量G 。
等截面圆轴在剪切比例极限内扭转时,若相距为L 的两横截面之间扭矩为常数,则两横截面间的扭转角为:pGI TL=ϕ (10) 由上式可得:pI TLG ϕ=(11) 本实验采用增量法,测量在各相同载荷增量∆T 作用下,产生的转角增量∆φ。
材料弹性常数E、μ的测定——电测法测定弹性模量E和泊松比μ
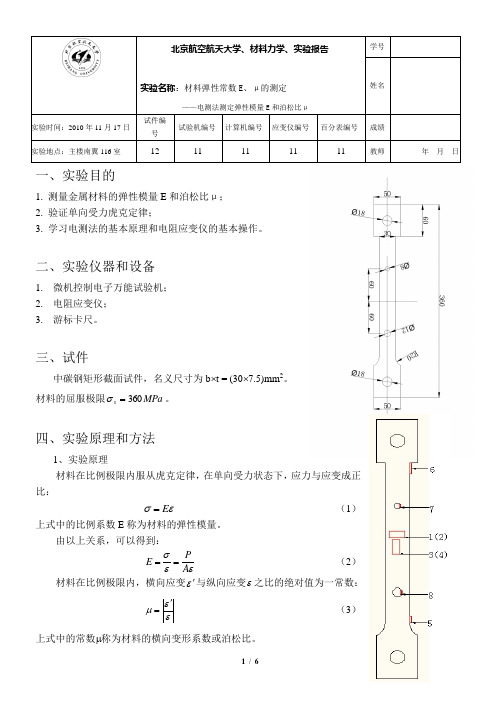
北京航空航天大学、材料力学、实验报告实验名称:材料弹性常数E 、μ的测定——电测法测定弹性模量E 和泊松比μ学号姓名实验时间:2010年11月17日 试件编号试验机编号 计算机编号 应变仪编号百分表编号成绩实验地点:主楼南翼116室12 11 11 11 11教师年 月 日一、实验目的1. 测量金属材料的弹性模量E 和泊松比μ;2. 验证单向受力虎克定律;3. 学习电测法的基本原理和电阻应变仪的基本操作。
二、实验仪器和设备1. 微机控制电子万能试验机;2. 电阻应变仪;3. 游标卡尺。
三、试件中碳钢矩形截面试件,名义尺寸为b ⨯t = (30⨯7.5)mm 2。
材料的屈服极限MPa s 360=σ。
四、实验原理和方法1、实验原理材料在比例极限内服从虎克定律,在单向受力状态下,应力与应变成正比:εσE = (1)上式中的比例系数E 称为材料的弹性模量。
由以上关系,可以得到:PE A σεε== (2)材料在比例极限内,横向应变ε'与纵向应变ε之比的绝对值为一常数:εεμ'=(3) 上式中的常数μ称为材料的横向变形系数或泊松比。
本实验采用增量法,即逐级加载,分别测量在各相同载荷增量∆P 作用下,产生的应变增量∆εi 。
于是式(2)和式(3)分别写为:ii A PE ε∆∆=0 (4) ii i εεμ∆'∆= (5)根据每级载荷得到的E i 和μi ,求平均值:n E E ni i∑==1(6)nni i∑==1μμ (7)以上即为实验所得材料的弹性模量和泊松比。
上式中n 为加载级数。
2、实验方法2.1电测法电测法基本原理:电测法是以电阻应变片为传感器,通过测量应变片电阻的改变量来确定构件应变,并进一步利用胡克定律或广义胡克定律确定相应的应力的实验方法。
试验时,将应变片粘贴在构件表面需测应变的部位,并使应变片的纵向沿需测应变的方向。
当构件该处沿应变片纵向发生正应变时,应变片也产生同样的变形。
弹性模量E和泊松比

00EA A P==εσε弹性模量E 和泊松比µ的测定拉伸试验中得到的屈服极限бb 和强度极限бS ,反映了材料对力的作用的承受能力,而延伸率δ 或截面收缩率ψ,反映了材料缩性变行的能力,为了表示材料在弹性范围内抵抗变行的难易程度,在实际工程结构中,材料弹性模量E 的意义通常是以零件的刚度体现出来的,这是因为一旦零件按应力设计定型,在弹性变形范围内的服役过程中,是以其所受负荷而产生的变性量来判断其刚度的。
一般按引起单为应变的负荷为该零件的刚度,例如,在拉压构件中其刚度为:式中 A 0为零件的横截面积。
由上式可见,要想提高零件的刚度E A 0,亦即要减少零件的弹性变形,可选用高弹性模量的材料和适当加大承载的横截面积,刚度的重要性在于它决定了零件服役时稳定性,对细长杆件和薄壁构件尤为重要。
因此,构件的理论分析和设计计算来说,弹性模量E 是经常要用到的一个重要力学性能指标。
在弹性范围内大多数材料服从虎克定律,即变形与受力成正比。
纵向应力与纵向应变的比例常数就是材料的弹性模量E ,也叫杨氏模量。
横向应变与纵向应变之比值称为泊松比µ,也叫横向变性系数,它是反映材料横向变形的弹性常数。
因此金属才料拉伸时弹性模量E 地测定是材料力学最主要最基本的一个实验,下面用电测法测定低碳钢弹性模量E 和泊松比µ。
(一) (一) 试验目的1.1.用电测方法测定低碳钢的弹性模量E 及泊松比µ;2.2.验证虎克定律;3.3.掌握电测方法的组桥原理与应用。
(二) (二) 试验原理1.测定材料弹性模量E 一般采用比例极限内的拉伸试验,材料在比例极限内服从虎克定律,其荷载与变形关系为:0EA PL L ∆=∆ (1)若已知载荷ΔP 及试件尺寸,只要测得试件伸长ΔL 即可得出弹性模量E 。
(2)由于本试验采用电测法测量,其反映变形测试的数据为应变增量,即(3) 所以(2)成为:)(A L PL E ∆∆∆=0)(L L ∆∆=∆ε(4) 式中: ΔP ——载荷增量,kN ;A 0-----试件的横截面面积,cm为了验证力与变形的线性关心,采用增量法逐级加载,分别测量在相同载荷增量 ΔP 作用下试件所产生的应变增量Δε。
测定材料切变模量G

实验五 测定材料切变模量G一、实验名称测定材料切变模量G 。
二、实验目的1.掌握测定Q235钢切变模量G 的实验方法; 2.熟悉NY-4型扭转测G 仪的使用方法。
三、实验设备及仪器 1.NY-4型扭转测G 仪 2.百分表 3.游标卡尺 四、主要技术指标1. 试样:直径d=10mm ,标距L 0=60-100mm (可调), 材料Q235钢。
2.力臂:长度a=200mm ,产生最大扭矩T=4Nm 。
3.百分表:触点离试样轴线距离b=100mm ,放大倍数K=100格/mm ,用百分表测定扭转的位移。
4. 砝码:4块,每块重5N ,砝码托作初载荷,T 0=0.26Nm ,扭矩增量ΔT=1Nm 。
5.精度:误差不超过5%。
五、实验原理实验时,从F 0到F 4逐级加载,扭矩的每级增量为1Nm 。
每次加载时,相应的扭转角变化量即为ΔT 引起的变形量。
在逐级加载中,如果变形量Δφ基本相等,则表明Δφ与ΔT 为线性关系,符合剪切胡克定律。
完成一次加载过程,可计算得到Δφ的一组数据,实验结束后,求Δφ1到Δφ4的平均值Δφ平,代入剪切胡克定律计算弹性模量。
即pGIT l ⋅∆=∆ϕ六、实验步骤及注意事项1.桌面目视基本水平,把仪器放在桌上(先不加砝码托及砝码)。
2.调整两悬臂杆的位置,大致达到选定标距,固定左旋臂杆,再固定右旋臂杆,调整右横杆,使百分表触头距试样轴线距离b=100mm ,并使表针预先转过十格以上(b 值也可不调,按实际测值计算)。
3.用游标卡尺准确测量标距,作为实际计算用。
4.挂上砝码托,记下百分表的初读数。
5.分四次加砝码,每加一次记录一次表的读数,加砝码时要缓慢放手。
6.实验完毕,卸下砝码。
七、数据记录及计算 1. 原始数据记录 试样标距为L 0= mm 。
分级加载 初载一次加载 二次加载 三次加载 四次加载 百分表读数 S 0=S 1=S 2=S 3=S 4=2. 计算(1)扭转位移的计算分级加载 一次加载 二次加载 三次加载 四次加载 平均值 形变量ΔS 1=ΔS 2=ΔS 3=ΔS 4=ΔS 平=(2)扭转角增量的计算bK S ⋅∆=∆平ϕ其中:K 为百分表的放大倍数(K=100格/mm );b 为百分表触头距轴线的距离(b=100mm )。
高分子材料弹性模量_泊松系数_切变模的测试

应变 (με) 623 587 723 678 596 726 793 692 584 679 668. 1 ±
69. 631 49
弹性模量计 算值 M Pa
7 099 7 545 6 130 6 524 7 426 6 104 5 575 6 397 7 573 5 184 6 555. 7 ±
838. 052 5
表 2 泊松系数测试与计算结果
样号
1 2 3 4
横向应变 (με)
209 196 227 236
纵向应变 (με)
623 587 723 678
泊松系数
0. 335 0. 339 0. 313 0. 348
实验结果表明 ,高分子材料弹性模量为 6 555. 7 ±838. 052 5 M Pa , 泊 松 系 数 为 0. 332 6 ±0. 017 696 ,切变模量为 2 463. 74 ±309. 547 4 M Pa ,材料 为低模量材料 ,其横向变形系数较大 ,大于金属材料 (钢的泊松系数为 0. 27~0. 3) 。
4 讨 论
3 测试结果
弹性模量测试与计算结果见表 1 ,泊松系数测 试与计算结果见表 2 ,切变模量计算结果见表 3 。
表 1 弹性模量测试与计算结果
样号
1 2 3 4 5 6 7 8 9 10
x + SD
应力δ
M Pa 4. 423 4. 429 4. 432 4. 427 4. 426 4. 432 4. 421 4. 427 4. 423 4. 426 4. 426 6 ±
应变电测原理和技术 ,在机械 、电子 、石油 、化 工 、建筑 、国防等各个领域都得到了广泛的应用 。其 具有快捷和测试精度高等特点 。应用应变电测技术 和原理测量试件 、构件结构的应变值 ,严格掌握电阻 应变片的粘贴工艺致关重要 。严格的按照电阻应变 片的粘贴工艺进行贴片 ,是测试取得成功的重要环 节 。为保证测量精度对所使用的测量仪器 ,在使用 前要用应变校准仪进行校准后进行使用才能取得满 意的效果 。
材料切变模量G的测定

材料切变模量G的测定第一篇:材料切变模量G的测定材料切变模量G的测定实验(一)用百分表扭角仪法测定切变模量G一、目的在比例极限内验证扭转时的剪切虎克定律,并测定材料的切变模量G。
二、仪器设备1、多功能组合实验台2、百分表三、试件空心圆管:材料为不锈钢、内径d= 40.2 mm、外径D= 47.14 mm、长度L=420mm四、预习要求:1、阅读第二章中多功能组合实验台工作原理、使用方法以及百分表的工作原理。
五、实验原理与方法实验装置如图3-13所示,加载示意图见图3-14。
试件的一端安装在圆管固定支座上,该端固定不动,另一端可以转动,并在可动端装有一滚珠轴承支座加以支承。
靠近轴承安装一横杆AB,在A点通过加载手轮加载。
这样试件在荷载作用下,仅仅受到纯扭转的作用。
可动端只能产生绕空心圆管轴线方向的角位移。
当试件受到扭转作用时,可动端的横截面转动,此时横杆也转动。
通过百分表(或千分表)测定B点的位移(由于B点转动角很小,B点的位移约等于B点的弧长),这样便可以计算出试件可动端的转角大小 (见图3-15)。
图3-13扭转实验装置图3-14扭转加载示意图图3-15圆管转角示意图根据扭转变形公式∆ϕ=∆B∆TL式中:∆ϕ=;△T=△P×abGIP可计算出切变模量IP=π32(D4-d4)G=∆TL ∆ϕIP施加载荷△P时,试件便受到扭矩△T=△P×a的作用,对试件分级加载,由于各级荷载相等,故相应于每级加载后的读数增量△B也应基本相等(即∆ϕ相等),从而验证了剪切虎克定律。
根据实验中测得的扭转角增量∆ϕ,便可以求出切变模量G。
六、实验步骤1、打开测力仪电源,如果此时数字显示不为“0000”,用螺丝刀将其调整为“0000”。
2、旋转百分表外壳,使大指针指到“0”。
3、顺时针转动加载手轮加载,分四级加载,每级加载200N,一直加到800N(200N→400N→600N→800N)。
每加一级荷载后,读取百分表的读数并记录。
电测法测定材料的弹性模量E和泊松比μ值

电测法测定材料的弹性模量E 和泊松比µ值一、实验目的1. 测定常用金属材料的弹性模量E 和泊松比µ。
2. 验证胡克(Hooke )定律。
二、实验仪器设备和工具1. 组合实验台中拉伸装置2. 力&应变综合参数测试仪3. 游标卡尺、钢板尺三、实验原理和方法试件采用矩形截面试件,电阻应变片布片方式如图3-4。
在试件中央截面上,沿前后两面的轴线方向分别对称的贴一对轴向应变片R1、R1ˊ和一对横向应变片R2、R2ˊ,以测量轴向应变ε和横向应变εˊ。
补偿块P图 3-4 拉伸试件及布片图1. 弹性模量E 的测定由于实验装置和安装初始状态的不稳定性,拉伸曲线的初始阶段往往 是非线性的。
为了尽可能减小测量误差,实验宜从一初载荷P 0(P 0≠0)开始,采用增量法,分级加载,分别测量在各相同载荷增量△P 作用下,产生的应变增量△ε,并求出△ε的平均值。
设试件初始横截面面积为A 0,又因ε=△l/l ,则有E=上式即为增量法测 式中 A 0 — 试件截面面积△ε — 轴向应变增量的平均值2. 泊松比μ的测定利用试件上的横向应变片和纵向应变片合理组桥,为了尽可能减小测量误差,实验宜从一初载荷P 0(P 0≠0)开始,采用增量法,分级加载,分别测量在各相同载荷增量△P 作用下,横向应变增量△εˊ和纵向应变增量△ε。
求出平均值,按定义μ四、实验步骤1. 设计好本实验所需的各类数据表格。
2. 测量试件尺寸。
在试件标距范围内,测量试件三个横截面尺寸,取三处横截面面积的平均值作为试件的横截面面积A 0。
见附表13. 拟订加载方案。
先选取适当的初载荷P 0(一般取P 0 =10% P max 左右),估算P max (该实验载荷范围P max ≤5000N ),分4~6级加载。
4. 根据加载方案,调整好实验加载装置。
5. 按实验要求接好线(为提高测试精度建议采用图3-5d 所示相对桥臂测量方法),调整好仪器,检查整个测试系统是否处于正常工作状态。
实验电测法测定材料弹性模量E、μ

实验一、电测法测定材料弹性模量E、μ一、实验目的1.学习电测方法。
2.电测法测定材料的弹性模量E、μ。
二、实验仪器设备1.弯曲梁实验装置。
2.数字式电阻应变仪。
三、实验装置与实验原理图 1 图 2 1.实验装置见图1和图2,拔下销子3,卸下加载横梁8,卸下传感器9,从传感器上旋下加载压头7,然后将万向接头旋到加载系统5上,再将传感器旋到万向接头上,传感器下端与上夹头连接,下夹头安装在试验机架底座的孔内(注意:螺母不要旋紧,留有一定的活动距离,使其起到万向接头的作用;另外保护试件,以免试件被压弯),接着调整好上、下夹头之间的距离,将E、μ试件放入上、下夹头内,对准孔,插入销子,就可进行试验了。
图 3 图 42.实验原理试件上沿着试件轴向和横向各粘贴两片应变片,补偿块上粘贴四片应变片见图3,按图4接两个测量桥,对试件加载,记录载荷P ,并分别记录测得的轴向应变εP 和横向应变εP /,由公式P A P E ε= 计算出弹性模量E ,由公式 pp εεμ/=计算出泊松比μ。
实验一 电测法测定弹性模量E 和泊松比μ实验日期:: 室温 小组成员 (一)实验目的(二)实验设备、仪器(三)实验记录表1 测定E 和μ实验试件原始尺寸 试件材料宽度 b (mm) 厚度 t(mm)横截面面积A 0 (mm 2)长度 L (mm)152.5(四)结果处理弹性模量: 泊松比:(五)问题讨论1.电测法测定材料的E 和μ值时应测何值?2.电阻应变片的作用是什么?3.写出电阻应变仪的读数应变表达式εd ?4.温度补偿片的作用是什么?5.应变片在电桥中的接线方法有哪两种?6.根据逐级加载时载荷和变形的读数记录,作图验证虎克定律。
P E=εο∆A ∆=εεμ∆∆ O ε实验二、纯弯曲梁正应力电测实验一、实验目的1.电测法测定纯弯曲梁正应力分布规律。
2.验证纯弯曲梁正应力计算公式。
二、实验装置与仪器1.纯弯曲梁实验装置。
2.数字式电阻应变仪。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【管理知识】材料弹性常数E、μ与材料切变模量G的测定(doc 10页)
部门: xxx
时间: xxx
整理范文,仅供参考,可下载自行编辑
实验二 材料弹性常数E 、μ的测定
——电测法测定弹性模量
E 和泊松比μ
预习要求:
1、预习电测法的基本原理;
2、设计本实验的组桥方案;
3、拟定本实验的加载方案;
4、设计本实验所需数据记录表格。
一、实验目的
1. 测量金属材料的弹性模量E 和泊松比μ;
2. 验证单向受力虎克定律;
3. 学习电测法的基本原理和电阻应变仪的基本操作。
二、实验仪器和设备
1. 微机控制电子万能试验机;
2. 电阻应变仪;
3. 游标卡尺。
三、试件
中碳钢矩形截面试件,名义尺寸为b ⨯t = (30⨯7.5)mm 2。
材
料
的
屈
服
极
限
MPa s 360=σ。
四、实验原理和方法
1、实验原理
材料在比例极限内服从虎克定律,在单向受力状态下,应力与应变成正比:
εσE = (1)
图二 实验装置图
图一 试件示意图
b
上式中的比例系数E 称为材料的弹性模量。
由以上关系,可以得到:
ε
εσ0A P E ==
(2) 材料在比例极限内,横向应变ε'与纵向应变ε之比的绝对值为一常数:
ε
εμ'
=
(3) 上式中的常数μ称为材料的横向变形系数或泊松比。
本实验采用增量法,即逐级加载,分别测量在各相同载荷增量∆P 作用下,产生的应变增量∆εi 。
于是式(2)和式(3)分别变为:
i
i A P
E ε∆∆=
0 (4) i
i i εεμ∆'
∆=
(5) 根据每级载荷得到的E i 和μi ,求平均值:
n E E n
i i
∑=
=1
(6)
n
n
i i
∑=
=1μμ (7)
以上即为实验所得材料的弹性模量和泊松比。
上式中n 为加载级数。
2、增量法
增量法可以验证力与变形之间的线性关系,如图三所示。
若各级载荷增量ΔP 相同,相应的应变增量∆ε也应大致相等,这就验证了虎克定律。
利用增量法,还可以判断实验过程是否正确。
若各次测出的应变不按线性规律变化,则说明实验过程存在问题,应进行检查。
采用增量法拟定加载方案时,通常要考虑以下情况:
(1)初载荷可按所用测力计满量程的10%或稍大于此标准来选定;(本次实验试验机采用50KN 的量程) (2)最大载荷的选取应保证试件最大应力值不能大于比例极限,但也不能小于它的一半,一般取屈服载荷的
P P P P 图三 增量法示意图
70%~80%,故通常取最大载荷s P P 8.0max =;
(3)至少有4-6级加载,每级加载后要使应变读数有明显的变化。
五、实验步骤
1. 设计实验所需各类数据表格;
2.
测量试件尺寸;
分别在试件标距两端及中间处测量厚度和宽度,将三处测得横截面面积的算术平均值作为试样原始横截面积 。
3. 拟定加载方案;
4. 试验机准备、试件安装和仪器调整;
5. 确定组桥方式、接线和设置应变仪参数;
6.
检查及试车:
检查以上步骤完成情况,然后预加载荷至最大值,再卸载至初载荷以下,以检查试验机及应变仪是否处于正常状态。
7.
进行试验:
加初载荷,记下此时应变仪的读数或将读数清零。
然后逐级加载,记录每级载荷下各应变片的应变值。
同时注意应变变化是否符合线性规律。
重复该过程至少两到三次,如果数据稳定,重复性好即可。
8. 数据经检验合格后,卸载、关闭电源、拆线并整理所用设备。
六、试验结果处理
1. 在坐标纸上,在εσ—坐标系下描出实验点,然后拟合成直线,以验证虎克定律;
2. 用逐差法(参考公式(4) ~(7))计算弹性模量E 和泊松比μ。
七、思考题
1. 电测法测弹性模量E ,试提出最佳布片方案?
2. 在绘制εσ—图时,如何确定坐标原点?
3. 本实验如果不采用增量法,应如何拟定加载方案?
实验三 材料切变模量G 的测定
预习要求:
1、复习电测法;
2、预习扭角仪和百分表的使用方法。
3、设计本实验的组桥方案;
4、拟定本实验的加载方案;(参照实验二中增量法部分的介绍)
5、设计本实验所需数据记录表格。
一. 实验目的
1. 两种方法测定金属材料的切变模量G ; 2. 验证圆轴扭转时的虎克定律。
二. 实验仪器和设备
1. 微机控制电子万能试验机 2. 扭角仪 3. 电阻应变仪 4. 百分表 5. 游标卡尺
三. 试件
中碳钢圆轴试件,名义尺寸d=40mm, 材料屈服极限MPa s 360=σ。
四. 实验原理和方法
1. 电测法测切变模量G
材料在剪切比例极限内,切应力与切应变成正比,
γτG = (1)
上式中的G 称为材料的切变模量。
由式(1)可以得到:
图一 实验装置图
γ
圆轴在剪切比例极限内扭转时,圆轴表面上任意一点处的切应力表达式为:
P
W T
=
max τ (3) 由式(1)~(3)得到:
γ
⋅=
P W T G (4)
由于应变片只能直接测出正应变,不能直接测出切应变,故需找出切应变与正应变的关系。
圆轴扭转时,圆轴表面上任意一点处于纯剪切受力状态,根据图二所示正方形微体的变形分析可知:
454522-=-=εεγ (5)
由式(2)~(5)得到:
45
45
22εεp p W T
W T G -
==
- (6)
根据上式,实验时,我们在试件表面沿45o 方向贴应变片(一般贴二向应变花,如图三所示),即可测出材料的切变模量G 。
本实验采用增量法加载,即逐级加载,分别测量在各相同载荷增量∆T 作用下,产生的应变增量∆ε。
于是式(6)变为:
45
4522εε∆⋅∆-=∆⋅∆=
-p p W T
W T G (7)
根据本实验装置,有
a P T ⋅∆=∆ (8)
a ——力的作用线至圆轴轴线的距离 最后,我们得到:
45
4522εε∆⋅⋅∆-=∆⋅⋅∆=
-p p W a
P W a P G (9)
2.扭角仪测切变模量G 。
等截面圆轴在剪切比例极限内扭转时,若相距为L 的两横截面之间扭矩为常数,则此梁横截面间的扭转角为:
图二 微体变形示意图
图三 应变花示意图
p
GI 由上式可得:
p
I TL
G ϕ=
(11) 本实验采用增量法,测量在各相同载荷增量∆T 作用下,产生的转角增量∆φ。
于是式(11)变为:
p
I L
T G ⋅∆⋅∆=
ϕ (12)
根据本实验装置,按图四所示原理,可以得到:
b
δ
ϕ∆=
∆ (13) δ——百分表杆移动的距离 b ——百分表杆触点至试件轴的距离 最后,我们得到:
p
I b
L a P G ⋅∆⋅⋅⋅∆=
δ (14)
五、实验步骤
1.设计实验所需各类数据表格; 2.测量试件尺寸 3.拟定加载方案;
4.试验机准备、试件安装和仪器调整; 5.测量实验装置的各种所需尺寸;
6.确定组桥方式、接线、设置应变仪参数; 7.安装扭角仪和百分表; 8.检查及试车;
检查以上步骤完成情况,然后预加一定载荷(一般取试验机量程的15%左右),再卸载,以检查试验机、应变仪、扭角仪和百分表是否处于正常状态。
9.进行试验;
加初载荷,记录此时应变仪的读数或将读数清零,并记录百分表的读数。
逐级加载,记录每级载荷下相应的应变值和百分表的读数。
同时检查应变变化和位移变化是否基本符合线性规律。
实验至少重复三到四遍,如果数据稳定,重复性好即可。
10. 数据检查合格后,卸载、关闭电源、拆线、取下百分表并整理所用设
图四 实测ϕ的示意图。
