材料力学动荷载与循环应力
材料力学13章 动荷载

3.选用弹性模量较低的材料 弹性模量较低的材料,可以增大静位移。但须注意强度问 题。
13-4 循环应力下构件的疲劳强度
1.特征: 1)强度降低:破坏时的名义应力值往 往低于材料在静载作用下的屈服应力; 2)多次循环:构件在交变应力作用下
发生破坏需要经历一定数量的应力 循环; 3)脆性断裂:构件在破坏前没有明显 的塑性变形预兆,即使韧性材料, 也将呈现“突然”的脆性断裂;
4)断口特征:金属材料的疲劳断裂断口上,有明显的光滑区 域与颗粒区域。
一、静荷载与动荷载 实验结果表明,材料在动载荷下的弹性性能基本上与静
载荷下的相同,因此,只要应力不超过比例极限,胡克定律 仍适用于动载荷下的应力、应变的计算、弹性模续也与静载 荷下的数值相同。 二、动载荷类型
根据构件的加速度的性质,动载荷问题可分为三类:
1.一般加速度运动(包括移动加速与转动加速)构件问题。此时不 会引起材料力学性能的改变,该类问题的处理方法是动静法。
水平冲击图示: 重物以一定的速度,沿水平方向冲击弹 性系统。当重物与弹性系统接触后,系统的最大水平位移 如下图所示。
冲击物: 动能改变:Ek=Qv2/2g
势能改变: Ep=0
被冲击物: 应变能改变:
V
1 2
Fd
d
能量方程 动荷因数
1 2
Q2
g
1 2
Qd d
Kd
d s
2
gs
第13章 动荷载
13.1 概述
工程材料力学性能每章重要知识点

第一章1.应力-应变曲线(拉伸力-伸长曲线)。
拉伸力在Fe以下阶段,为弹性变形阶段,到达Fa后,试样开始发生塑性变形,最初试样局部区域产生不均匀屈服塑形变形,曲线上出现平台或锯齿,直至C点结束。
继而进入均匀塑形变形阶段。
达到最大拉伸Fb时,试样在此产生不均匀塑形变形,在局部区域产生缩颈。
最终,在拉伸力Fk处,试样断裂。
2.弹性变形现象及指标弹性变形:是可逆性变形,是金属晶格中原子自平衡位置产生可逆位移的反映。
弹性变形指标:①弹性模量,是产生100%弹性变形所需应力。
②弹性比功(弹性比能、应变比能),表示金属吸收弹性变形功的能力。
③滞弹性:在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象。
④循环韧性:金属材料在交变载荷(振动)下吸收不可逆变形功的能力。
3.塑性变形现象及指标金属材料常见塑性变形方式主要为滑移和孪生。
滑移:金属材料在切应力作用下位错沿滑移面和滑移方向运动而进行切变得过程。
孪生:金属材料在切应力作用下沿特定晶面和特性晶向进行的塑性变形。
塑性变形特点:①各晶粒变形的不同时性和均匀性;②各晶粒变形的相互协调性。
塑性变形指标:⑴屈服强度,屈服强度及金属材料拉伸时,试样在外力不增加(保持恒定)仍能继续伸长时的应力。
屈服现象:金属材料开始产生宏观塑形变形的标志。
屈服现象相关因素:①材料变形前可动位错密度很小;②随塑性变形的发生,位错能快速增殖;③位错的运动速率与外加应力有强烈的依存关系。
屈服现象指标:规定非比例伸长应力;规定残余伸长应力;规定总伸长应力。
影响屈服强度因素:①内在因素:金属本性和晶格类型;晶粒的大小和亚结构;溶质元素;第二相。
②外在因素:温度、应变速率、应力状态。
⑵应变硬化:金属材料阻止继续塑形变形的能力,塑性变形是硬化的原因,硬化是结果。
⑶缩颈:韧性金属材料在拉伸试验时变形集中于局部区域的特殊现象,是应变硬化与截面减小共同作用的结果。
抗拉强度:韧性金属试样拉断过程中最大力所对应的应力。
材料力学 第十四章动荷载及交变应力

2.5m
FNd
2.5m
σ d m ax
M d m ax = = 13 5.4 M P a < [σ ] Wz
梁的强度足够. 梁的强度足够.
二,构件作匀速转动时的应力
轮缘
ω
D
δ
轮幅
y
ω
qd d
D
O
O
m m FNd
O n n FNd x
an=ω2D/2
FNd Aρω 2 D 2 = 4
D Aρω 2 D qd = 1. A.ρω 2 = 2 2 FNd ρω 2 D 2 σd = = = ρ v 2 ≤ [σ ] A 4
di = kd sti Fd = kd P
σ d = kdσ st
动荷因数kd中的st计算:是将冲击物的重量P 动荷因数 中的 计算:是将冲击物的重量 作为静荷载沿冲击方向作用在被冲击构件的冲 击点,引起该点沿冲击方向的位移. 击点,引起该点沿冲击方向的位移.
P
st
l
EA
P h P l
Pd
Δd
如:轮船靠泊时的冲击力 起吊重物时的惯性力
t
构件由动荷载引起的应力和变形称为动应力和动变形. 构件由动荷载引起的应力和变形称为动应力和动变形. 构件在动荷载作用下,同样有强度,刚度和稳定性问题. 构件在动荷载作用下,同样有强度,刚度和稳定性问题. 构件内的应力随时间作交替变化,则称为交变应力. 构件内的应力随时间作交替变化,则称为交变应力.
动荷载作用下构件的材料仍服从虎克定律. 动荷载作用下构件的材料仍服从虎克定律. 构件的材料仍服从虎克定律
§14-2 构件作匀加速直线运动 14和匀速转动时的应力
构件作匀加速直线运动时,内部各质点具有相同的 构件作匀加速直线运动时, 加速度;构件作匀速转动时, 加速度;构件作匀速转动时,内部各质点均具有向 心加速度. 心加速度.
材料力学第九章动荷载和交变应力

kd 1 a g 1 2.5 9.8 1.26
st FNst / A W2 / A 127.3MPa d kd st 160.4MPa 1.05[ ]
∴ 钢索满足强度要求。
2.5m
FNd W2
W2 g
a
2.5m a
W2
2.梁的强度校核
W1
kd 1 a g 1 2.5 9.8 1.26
求σdmax、△Dd。不计梁的自重。 A
解:1.计算静态的△Cst、Mmax和
σstmax
W
h
D
2l / 3 l
C
B
l/3
由 w Fb(l 2 b2 ) x Fb x3
6EIl
6EIl
得
Δ Cst
W
l [l 2 ( l )2]
3
3
6EIl
2l 3
Wl 3
6EIl
( 2l )3 3
4Wl 3 0.19mm 243EI
结论:梁满足强度要求。
三、提高构件抗冲击能力的措施
d kdst Fd kdW d kd st
kd 1
1 2h — —竖向冲击动荷因数
st
kd
v2 水平冲击动荷因数
gst
在静应力不变的情况下,减小动荷系数可以减小冲击应力。
即加大冲击点沿冲击方向的静位移: 被冲击物采用弹性模量低、变形大的材料制作; 或在被冲击物上垫上容易变形的缓冲附件。
W
h C
z Iz = 1130cm4 Wz =141cm3
A
B
1.梁本身的变形
1.5m
1.5m
k
ΔCst1
Wl 3 48EI
0.474mm
2.支座缩短量
第05章 金属的疲劳1

(1)基本特征: 呈现贝壳花样或海滩花样,它是以疲
劳源区为中心,与裂纹扩展方向相垂直的 呈半圆形或扇形的弧形线,又称疲劳弧线。
疲劳弧线是裂纹扩展过程中,其顶端 的应力大小或状态发生变化时,在断裂面 上留下的塑性变形的痕迹。
47
(2)贝纹花样的形成: 是由载荷变动引起的,因为机器运转时
不可避免地常有启动、停歇、偶然过载等, 均可留下塑性变形的痕迹——贝纹线(疲 劳弧线)。
r=-1称为对称循环应力;
r=0(或r=-∽)这种非对称循环又称为 脉动循环。这种载荷是一种最危险的载荷。
r偏离-1越远,应力对称性越差,疲劳 极限越高。
29
(2)循环应力的种类
(交变当)r应=-力1,;即σmin=-σmax时,称为对称循环
当r=0,即σmin=0时,称为脉动循环应力。
2
1、金属疲劳破坏的形成过程 在正常使用机械时,重复的推、拉、扭
或其他的外力情况都会造成机械部件中金 属的疲劳。
这是因为机械受压时,金属中原子的排 列会大大改变,从而使金属原子间的化学 键断裂,导致金属裂开。
3
构件承受交变应力的大小超过一定限 度,并经历了多次的循环重复后,在构件 内部应力最大处或材质薄弱处将产生细微 裂纹(称为疲劳源),这种裂纹随着应力 交变次数增加而不断向四周扩展。
53
(5)不同情况下贝纹线的形状
① 当轴类机件拉压疲劳时, 轴向应力包括拉-拉或拉-压疲劳。它的疲劳
源一般也在表面形成,只有内部有缺陷时才在缺 陷处形成。
54
若表面无应力集中(无缺口),则裂纹因截 面上应力均等而沿截面等速扩展,贝纹线呈一簇 平行的圆弧线;
55
若机件表面存在应力集中(环形缺口), 则因截面表层的应力比中间的高,裂纹沿表层 的扩展快于中间区;高应力时,瞬断区面积相 对较大,疲劳裂纹扩展区面积小,裂纹沿两边 及中间扩展差别不大。
应力-应变循环曲线

应力-应变循环曲线应力-应变循环曲线是材料力学中的重要概念,用来描述材料在循环载荷下的变形行为。
循环载荷是指反复施加在材料上的载荷,应力-应变循环曲线则可用来描述材料在这种交替循环载荷下的应力和应变之间的关系。
本文将详细介绍应力-应变循环曲线的概念、特征和应用。
应力-应变循环曲线通常由两个主要的部分组成:弹性阶段和塑性阶段。
在材料的弹性阶段,应变与应力成正比,即应力和应变满足胡克定律。
材料在这个阶段内,完全恢复了外部加载引起的应变,没有残余应变。
应力-应变曲线在这个阶段呈现出一条直线,斜率代表了材料的弹性模量。
当材料超过了弹性极限,进入了塑性阶段,应力-应变曲线就变成了一个回弹曲线。
在每个循环中,材料会出现一个塑性变形区域,在这个区域内,应变与应力的关系是非线性的。
一般来说,塑性变形区域是由初始的弹性后塑性应变(yield strain)和持续的塑性应变组成。
应力-应变循环曲线的特征还包括屈服点和饱和点。
屈服点是指应力-应变曲线上的一个特殊点,表示了材料的屈服强度。
在屈服点之后,材料会出现明显的应力软化效应,即应力下降。
而饱和点则表示了材料在循环载荷下的最大应变能力。
应力-应变循环曲线的形状和特征会受到多种因素的影响,包括加载速率、温度和材料的微观结构等。
这些因素都会对材料的塑性变形机理和位错运动产生影响。
例如,加载速率的增加会导致材料的强化效应,使得应力-应变曲线呈现出更陡峭的斜率和更高的屈服强度。
而温度的增加则会导致材料的软化效应,使得应力-应变曲线呈现出更平缓的斜率和较低的屈服强度。
应力-应变循环曲线的研究在材料科学和工程领域具有重要的意义。
它不仅可以用来评估材料的力学性能和可靠性,还可以用来设计和优化结构的工作寿命和耐久性。
通过分析应力-应变循环曲线,可以获得材料的弹塑性性质、疲劳特性和损伤行为等信息,有助于提高材料的使用寿命和安全性。
总之,应力-应变循环曲线是描述材料在循环载荷下的力学响应的重要工具。
材料力学应力计算公式

材料力学应力计算公式材料力学应力计算公式主要指按照材料力学原理,预测某一种材料在不同使用情况下所受外力大小和分布状况的公式。
材料力学应力计算通过力学模型和数学方程来预测材料的力学特性,并用数字分析方法根据其力学参数(包括强度、塑性、稳定性和弹性)计算出其受力情况,从而预测出其力学特征。
1、应力计算的基本公式:应力计算的基本公式为:σ=F/A,其中F表示施加在材料上的外力,A表示给定断面上的面积。
2、应变计算的基本公式:应变计算的基本公式为:ε=A/L,其中L表示应力施加前材料的长度,A表示安装施加应力后材料的变形量。
3、体积膨胀热应力计算公式:体积膨胀热应力计算公式为:Δσ=α○ΔT,其中α为材料的热膨胀系数,ΔT表示热膨胀温度差,Δσ表示由热膨胀而引起的材料的应力变化值。
4、拉伸应力计算公式:拉伸应力计算公式为:σ=≈F/Ao,其中F表示施加在材料上的拉伸外力,Ao表示给定断面的面积。
5、压缩应力计算公式:压缩应力计算公式为:σ=-P/A,其中P表示压力,A表示施加压力前的断面积,σ表示施加压力后材料受到的应力。
6、剪切应力计算公式:剪切应力计算公式为:τ=M/I,其中M表示抵抗剪切外力的力矩,I表示断面的惯性矩,τ表示文断面的剪切应力。
7、循环应力计算公式:循环应力计算公式为:σ=±σao/2N,其中N表示经过N次循环后材料仍旧恢复原来状况,σao表示每次循环受到的应力,σ表示经过N次循环后材料受到的应力。
8、疲劳应力计算公式:疲劳应力计算公式为:σf=σa/(2Nf)^m,其中Nf表示发生应力极限疲劳破坏之前经过的循环次数,m为材料的疲劳断裂指数,σf表示发生疲劳破碎的最大应力,σa 表示材料受到的应力。
总之,材料力学应力计算公式是用数学模型和数值分析方法,结合材料的力学参数和外力的情况,对材料在某种外力作用情况下的应力分布情况进行预测,从而得出其力学特性和结构性能,进而决定材料安全性能和可靠性。
第十一、十二章 动荷载和循环应力
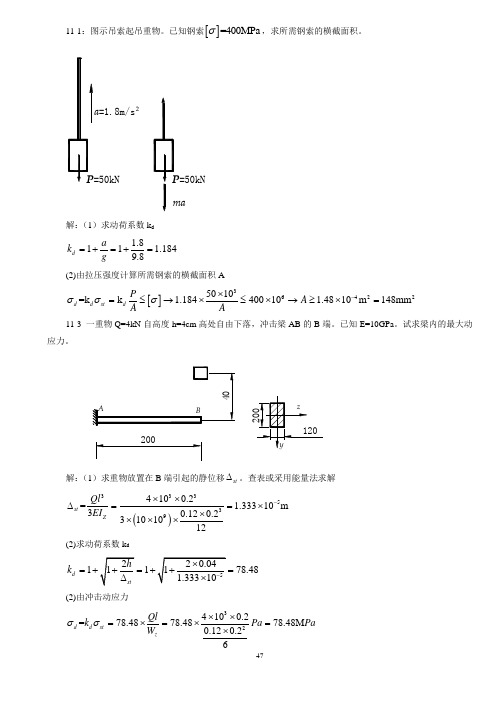
11-1:图示吊索起吊重物。
已知钢索[]=400MPa σ,求所需钢索的横截面积。
2=1.8m/s=50kN解:(1)求动荷系数k d1.811 1.1849.8d a k g =+=+= (2)由拉压强度计算所需钢索的横截面积A[]364225010=k k 1.18440010 1.4810m 148mm d d st d P A A Aσσσ-⨯=≤→⨯≤⨯→≥⨯=11-3 一重物Q=4kN 自高度h=4cm 高处自由下落,冲击梁AB 的B 端。
已知E=10GPa 。
试求梁内的最大动应力。
解:(1)求重物放置在B 端引起的静位移st ∆。
查表或采用能量法求解()3335394100.2= 1.33310m 30.120.23101012st ZQl EI -⨯⨯∆==⨯⨯⨯⨯⨯(2)求动荷系数k d1178.48d k =+=+= (2)由冲击动应力324100.2=78.4878.4878.48M 0.120.26d d st z Ql k Pa Pa W σσ⨯⨯=⨯=⨯=⨯11-4 图示工字钢梁右端置于弹簧上,弹簧常数c=0.8kN/mm,梁的E=200GPa,[]=160MPaσ,重物Q自由下落,求许可下落高度h。
z4433=113010mm=14110mmzzW⨯⨯解:(1)求C截面的静挠度st∆333394-1233-4-3-451021510 =+4822c48200101130101040.810/103.68710+1.56251019.31210mstQl QEI-⨯⨯⨯∆⋅=+⨯⨯⨯⨯⨯⨯⨯=⨯⨯=⨯()()(2)求动荷系数d11k=+=+(3)求危险点在静力荷载时的应力339(510)244Pa=17.73MPa1411010z zQlMW Wσ-⨯⨯===⨯⨯max,j(4)由强度条件求冲击时的许可高度[]17.73160=(10.0612m=612mmd dhkσσσ==⨯≤→+≤max,max,j.11-8 重物Q自H高处自由下落到曲拐上,试按第三强度理论写出危险点的相当应力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例2
§ 10.1 概述
Mechanic of Materials
(5)构件轴向变形 取构件当中一微段 dx
a
m
F
dx
d (L)
Fd (x)dx EA
d (x)
E
dx
d (x)dx
Fd(x)
Fd(x)+dFd
d (x)
Fd (x) A
Fx AL
L l Fx dx FL 0 EAL 2EA
3EI mg 2l 3
v
mgl Wz
3EIm v mg
l
Wz
§10.4 杆件受冲击时的应力和变形
三、求冲击问题的解题步骤
Mechanic of Materials
1、求静位移、静应力
静冲击物静置在被冲击物的冲击位置上,由拉压杆胡克定 理,梁可以查表,求冲击处发生静位移。也可以由能梁法 求解。
(l 2
a2
b2)
1,d
= w1,d
kd 1,st
kd
mgba (l2 6EIl
a2
b2)
§10.4 杆件受冲击时的应力和变形
h
1 1' d
l
动荷因数Kd
kd 1
2h 1 1
st
1
2h mgl 3
3EI
静
荷载 弯矩 应力 强度条件
挠度
Fst mg
M max,st M固 mgl
(1 a )W
d
FT A
g A
(1
a g
) st
静载荷情况下的钢索中的应力: st
例1
讨论 1:
§ 10.1 概述
FT a
Mechanic of Materials
引入:动载荷因数kd
W
kd
1
a g
有:
d kd st
FI
a
(1 )W
d
FT A
g A
(1
5、研究意义
§ 10.1 概述
二、实例 惯性载荷
Mechanic of Materials
§ 10.1 概述
冲击载荷
Mechanic of Materials
§ 10.1 概述
振动载荷(Tacoma大桥共振断裂)
Mechanic of Materials
§ 10.1 概述 交变载荷(交变载荷引起疲劳破坏)
钢索
a
W
例1
§ 10.1 概述
解:(1)对重物进行受力分析
钢索
Mechanic of Materials
惯性力: FI ma
a
(2)沿竖直方向建立
W
FT a W
“平衡方程”: Fy 0 FT W FI 0
FT
ma
mg
(1
a )W g
(3)求动应力若钢索截面积为A
FI
d (x)
d (x)
E
Fx EAL
d (x)
Fd (x) A
Fx AL
Mechanic of Materials
§ 10.1 概述 二、构件作等速转动时的动应力
设圆环以等角速度w 绕通过圆心且垂直
于圆环平面的轴旋转,如图所示(平均直 径D>>厚度t,讨论环内的应力。
w
D
§ 10.1 概述
Mechanic of Materials
h
1
1'
d
§10.4 杆件受冲击时的应力和变形
Mechanic of Materials
在冲击物自由下落的情况下,冲击
物的初速度和末速度为零,故动能
h
没有变化,即:
1
T= 0
1' d
T V Vεd
0
mg (h
d
)
Fd d 2
当重物落到最低点1’时,重物损失 的势能为:
FFNn
x
FN
qd D 2
Ag D2
4g
w2
圆截面上的应力为:
d
FN A
g D2 w2
4g
g v2
g
则强度条件可以写为
:
d
gv 2
g
[ ]
Mechanic of Materials
§10.4 杆件受冲击时的应力和变形
一、构件受冲击时的应力和变形 当运动物体(冲击物)以一定的速度作用在静
Mechanic of Materials
二、冲击问题的特点:
构件受到外力作用的时间很短, v 冲击物的速度在很短的时间内发生 很大的变化,甚至降为0,冲击物得 到一个很大的负加速度 a
a
冲击物
被冲击物
解决冲击问题的方法:近似但偏 于安全的方法--能量法
Mechanic of Materials
§10.4 杆件受冲击时的应力和变形
1 2h ) st
§10.4 杆件受冲击时的应力和变形
l=a+b
mgb a
l
h
1 1' d
b
引用冲击动荷因数Kd
kd 1
1
2h st
1
1
2h
mgba (l 2 a2 b2 )
6EIl
静
冲击
荷载
Fst mg
Fd kdmg
弯矩
M1,st mgab / l
M1,d kd M1,st kd mgab / l
Mechanic of Materials
§ 10.1 概述
一、什么是动载荷,与静荷载的区别。
1、静荷载:
从零开始缓慢地增到终值,然后保持不变的载荷 2、动载荷:
使构件产生明显的加速度的载荷或随时间变化 的载荷。动载荷本质:是惯性力 3、动应力、动变形
构件由于动荷载所引起的应力、变形 4、分类:惯性载荷、冲击载荷、振动载荷、交变载荷
Mechanic of Materials
Mechanic of Materials
§ 10.1 概述
一、构件作等速直线运动时的动应力与动变形 1、此类问题的特点:
加速度保持不变或加速度数值保持不变,即角速度w
=0 2、解决此类问题的方法:
牛顿第二定律 动静法(达朗伯原理)
Mechanic of Materials
§ 10.1 概述
例2: 设有等直杆,长度为L,截面积为A,比 重g,受拉力F的作用,以等加速度a运动,求构件 的应力和变形。(不计摩擦力)
a
m
F
Mechanic of Materials
例2
§ 10.1 概述
a
解:(1)构件加速度:
FF
Fg
m
F
a
m ALg / g ALg
x
(2)构件单位长度qd 上的惯性力(集度):
V=mg ( h + △d)
在冲击过程中,冲击载荷作功等于 梁的变形能,则:
Vd=(Fd △d)/2
而重物以静载荷的方式作用于梁上时,相应的静变形为
△st,在线弹性范围内,载荷和位移成正比,有:
Fd d mg st
d2 2dst 2hst 0
d st (1
1 2T0 mg st
Mechanic of Materials
§10.4 杆件受冲击时的应力和变形
几种常见的冲击动荷因数
4、重物以水平速度v冲击构件:
EA l
v
st
FN l EA
mgl EA
1 mv2 2
1 2
d Fd
1 2
(kd
st
)
(kd
mg
)
kd
v2 g st
st
2、自由落体,已知冲击物在冲击时的速度,那么:
kd 1
1 2h st
1
2 1 gt2
1 2 1
st
1 (gt)2 1 g st
1 v2 gst
3、自由落体,已知冲击物冲击时的初动能:
kd 1
1 2h st
1
1 2 mgh 1 mgst
Mechanic of Materials
第二十八、九讲的内容、要求、重难点 教学内容:
构件作加速直线运动或匀速转动时的动应力计算, 构件受冲击荷载时的动应力计算;交变应力的概念, 交变应力下材料的疲劳破坏,疲劳极限。
教学要求:
1、了解材料疲劳极限曲线、提高疲劳强度措施;
2、理解动荷载和循环应力概念,循环应力的类型;
st,max
st,固(上,下)
mgl Wz
st,max
mgl Wz
1 , st
=
w1
mgl 3 3EI
冲击
Fd kdmg
M固,d kd M固,st kd mgl
d ,max
kd st,max
kd
mgl Wz
d ,max
kd st,max
Mechanic of Materials
由能量守恒:
T V Vεd
T: 冲击物速度降为零所释放出的动能; V: 冲击物接触被冲击物时所减少的势能; Vd: 被冲击物在冲击物速度降为零所增加的变形能。
§10.4 杆件受冲击时的应力和变形
