信号与系统习题集
信号与系统习题给学生
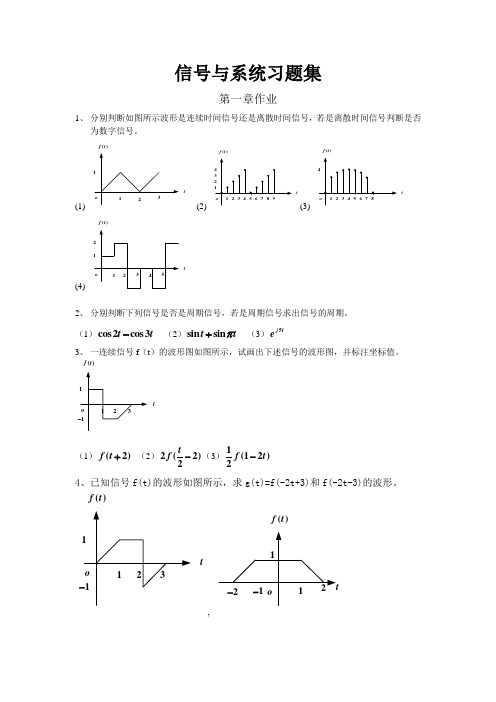
信号与系统习题集第一章作业1、 分别判断如图所示波形是连续时间信号还是离散时间信号，若是离散时间信号判断是否为数字信号。
(1)t()f t (2) t()f t(3) t()f t(4) t()f t2、 分别判断下列信号是否是周期信号，若是周期信号求出信号的周期。
（1）cos 2cos 3t t - （2）sin sin t t π+ （3）5j te3、 一连续信号f （t ）的波形图如图所示，试画出下述信号的波形图，并标注坐标值。
t()f t（1）(2)f t + （2）2(2)2t f -（3）1(12)2f t- 4、已知信号f(t)的波形如图所示，求g(t)=f(-2t+3)和f(-2t-3)的波形。
t()f t,()f t5、写出如图所示的各波形的函数式。
（1）t()f t（2）t()f t-6、画出下列各时间函数的波形。
（1）[](1)(2)t u t u t ---，（2）[](1)(2)(2)t u t u t u t ---+- （3）[](3)()(2)t u t u t --- 7、求下列函数值。
（1）2()()td r te u t dt-⎡⎤=⎣⎦，（2）3()()t r t e t δ-= （3）()cos ()4r t t t dt πδ∞-∞=-⎰，（4）2()()(1)tr t t e t dt δ∞--∞=+-⎰, ( 5 ) 3'()()t r t e t δ=8、画出下列系统的仿真框图。
()()3()2()dr t de t r t e t dt dt+=+ 9、判断下列系统是否为线性的，时不变的，因果的？ （1）()(2)r t e t =- （2）()(3)r t e t = （3）()()(1)r t e t u t =- （4）()()r t te t =第二章作业1、已知系统的电路图如图所示，写出电压()o v t 的微分方程。
()e tR +-()o v t2、已知系统的微分方程和起始状态如下，求齐次解。
信号与系统 高等教育何子述版 课后习题答案
二
g (t )
1
/2
y(t) 11d t / 2t
/ 2t
/2t
当 / 2 /2 t 即t 时
y(t) 0
信 号 与 系 统
习 题 二
t
y(t
)
t
0
t 0 0t
其它
y (t )
t
2) y(t) f (t) h(t) f ( )h(t )d
信
统
2
f[-n]
1
习
.
.
-5 -4 -3 -2 -1 0 1 2 3 4 5 n
题
fo[n]
1
一
... ..
-5 -4 -3 -2 -1 0 1 2 3 4 5 n
1.18 已知连续时间信号 f (t) 如图 p1.18所示。
信
（1）用单位阶跃信号u(t)的延时组合写出信号 f (t) 的
号 与
表达式； （2）求下面各式并画出信号波形。
与
y[n] 2h[n] 2h[n 1] h[n 2] 3h[n 3]
系
2[n 2] 6[n 3] 7[n 4] 7[n 5] 7[n 6] 3[n 7]
统
即y[n] {2,6,7,7,7,3} n 2,3,4,5,6,7
2） F (x) 2 2x x2 3x4
当1 t 0 即t 1时 y(t) 0
号
当0 1 t 2 即1 t 1时
与
h(t)
1
y(t)
1t
cos(
)d
sin(t)
0
系
当2 1 t 4 即1 t 3时
统
1
1
t
1t
y(t) cos( )d 0 1t
信号与系统王明泉第三章习题解答
（4）频域分析法分析系统；
（5）系统的无失真传输；
（6）理想低通滤波器；
（7）系统的物理可实现性；
3.3本章的内容摘要
3.3.1信号的正交分解
两个矢量 和 正交的条件是这两个矢量的点乘为零，即：
如果 和 为相互正交的单位矢量，则 和 就构成了一个二维矢量集，而且是二维空间的完备正交矢量集。也就是说，再也找不到另一个矢量 能满足 。在二维矢量空间中的任一矢量 可以精确地用两个正交矢量 和 的线性组合来表示，有
条件1：在一周期内，如果有间断点存在，则间断点的数目应是有限个。
条件2：在一周期内，极大值和极小值的数目应是有限个。
条件3:在一周期内，信号绝对可积，即
（5）周期信号频谱的特点
第一：离散性，此频谱由不连续的谱线组成，每一条谱线代表一个正弦分量，所以此谱称为不连续谱或离散谱。
第二：谐波性，此频谱的每一条谱线只能出现在基波频率 的整数倍频率上。
(a)周期、连续频谱； (b)周期、离散频谱；
(c)连续、非周期频谱； (d)离散、非周期频谱。
答案：(d)
题7、 的傅里叶变换为
答案：
分析：该题为典型信号的调制形式
题8、 的傅里叶变换为
答案：
分析：根据时移和频移性质即可获得
题9、已知信号 如图所示，且其傅里叶变换为
试确定：
(1)
(2)
(3)
解：
(1)将 向左平移一个单位得到
对于奇谐函数，满足 ，当 为偶数时， ， ；当 为奇数时， ， ，即半波像对称函数的傅里叶级数展开式中只含奇次谐波而不含偶次谐波项。
（4）周期信号傅里叶级数的近似与傅里叶级数的收敛性
一般来说，任意周期函数表示为傅里叶级数时需要无限多项才能完全逼近原函数。但在实际应用中，经常采用有限项级数来代替无限项级数。无穷项与有限项误差平方的平均值定义为均方误差，即 。式中， ， 。研究表明， 越大， 越小，当 时， 。
信号与系统习题集（很有用）
信号与系统习题集（很有⽤）2011《信号与系统》习题集选择题1．图⽰电路的微分⽅程是：（A ）()()()t v t v t v c c =+'2（B ）()()()t v t v t v c c =+'2（C ）()()()t v t v t v c c=+'（D ）()()()t v t v t v c c 2=+'2．f[n]（n-n 0）是 A f[n] B f （n-n 0） C （n-n 0） D （n ）3下列傅⾥叶变换对中错误的是：A ．1)(?δFt B ．222a a eFta +ω?-C ．)(1)(ωδ+ω?Ft uD ．aj t u eFat+ω?-1)(4．下列拉普拉斯变换性质中错误的是A ．时移特性)()(00s F e t t f st L-?-B ．S域微分特性dss dF t tf LC ．时域微分特性)()(s sF dtt df LD ．时域卷积特性)()()()(s H s F t h t f L*5．已知信号f (t )的波形如图所⽰，则f (t )的表达式为 (A)(t ＋1)ε(t) (B)δ(t －1)＋(t －1)ε(t) (C)(t －1)ε(t) (D)δ(t ＋1)＋(t ＋1)ε(t) 6．若系统的起始状态为0，在x （t ）的激励下，所得的响应为（A ）强迫响应；（B ）稳态响应；（C ）暂态响应；（D ）零状态响应。
7．理想不失真传输系统的传输函数H （jω）是（A ）0j t Ke ω- （B ）0tj Ke ω-（C ）0t j Ke ω-[]()()c c u u ωωωω+-- （D ）00j t Ke ω- （00,,,c t k ωω为常数）8.不满⾜)()(n u n 与δ之间满⾜如下关系（A ）∑∞-∞=-=k k n n u )()(δ（B ）∑∞=-=0)()(k k n n u δ（C ）)1()()(--=n u n u n δ（D ）()()(1)n u n u n δ=----9．中图所⽰的离散时间信号⽤单位阶跃信号u[n]表⽰的是 A f[n]=u[n+3]-u[n+1] B f[n]=u[n]-u[n+3](t v ππ--2)(t v R Ω1C F1)(t v cC10 （） 11．图⽰电路的微分⽅程是：（A ）()()()t u t u t u s c c 2=+'（B ）2()()()t u t u t u s c c =+' （C ）()()()t u t u t u s c c=+'2 （D ）()()()t u t u t u s c c=+'12．信号f （t ）变成)121(+t f 的过程为 (A) 先将f （t ）的图形向左移⼀个单位，再时间上展宽1/2倍。
信号系统习题（ＰＤＦ）
1.判断下列系统的线性、时不变性、因果性和记忆性。
（解析P7） ①()10()()dy t y t f t dt += ②()()(10)dy t y t f t dt+=+ ③2()()()dy t t y t f t dt+= ④2()(10)()y t f t f t =++2.判断下列系统的线性、时不变性和因果性。
（解析P7） ①20()()sin ()y t y t t at f t =+ ②()()()y t f t f t b =⋅−3.某系统，当输入为()tδτ−时，输出为()()(3)h t u t u t ττ=−−−，问该系统是否为因果系统？是否为时不变系统？说明理由。
4.下列信号属于功率信号的是（解析P6） ①cos ()tu t ②()teu t − ③()t te u t − ④te−5. 画出函数波形图：2()(1)f t u t =−（指导P12）6.已知()()2(1)(2)(2),f t tu t u t t u t =−−+−−画出()f t 波形。
（指导P13）7.根据1.10图中(32)f t −+的波形，画出()f t 波形。
（指导P18）8.已知()f t 波形波形如例1.11图所示，试画出1(2)2f t −−的波形。
（指导P19）9.已知(52)f t −的波形如图例1.12图所示，求()f t 波形。
（指导P20）10.求下列函数值 ①432'(652)(1)t t t t dt δ∞+++−∫②3'()te d τδττ−−∞∫ ③'2(9)t dt δ+∞−∞−∫（指导P24）11.求信号0.20.3()j n j n x n ee ππ−=+的周期。
（指导P36）12.设()x t 是复指数信号：0()j tx t eΩ=，其角频率为0Ω，基本周期为02T π=Ω。
如果离散时间序列是通过对()x t 以取样间隔s T 进行均匀取样的结果，即00()()s j nT j n s x n x nT e e ωΩ===。
信号与系统习题集(郑君里)
（1） ； （2） ； （3） ； （4） ；
（5） ； （6） ； （7） 。
解：（1）由傅立叶性质有：
；
∴
（2）由傅立叶性质有：
∴
（3）由傅立叶性质有：
∴
（4）由傅立叶性质有：
∴
（5）由傅立叶性质有：
∴
（6）由傅立叶性质有：
∴
（7）由傅立叶性质有：
ae(t) 系统为线性系统
系统为时变系统
当 =0时， ，即系统响应中有 时刻的响应， 系统为非因果系统
（5）激励响应
系统为线性系统
系统为时变系统
系统响应中只有 时刻的响应， 系统为非因果系统
（6）激励响应
系统为非线性系统
系统为时不变系统
系统响应仅于 时刻的激励有关 系统为因果系统
（7）激励响应
系统为线性系统
（1） ；
（2） ；
（3） ；
（4） ；
（5） ；
（6） ；
（7） ；
（8） 。
解：线性系统满足齐次性和叠加性；时不变系统的参数不随时间而变化，即：在同样起始状态下，系统响应与激励施加于系统的时刻无关；因果系统在t0时刻的响应只与t=t0与t<t0时刻的输入有关。
（1）激励响应
e(t)
ae(t) 线性系统
3-41系统如题图3-41所示，
。
（1）（1）为从 无失真恢复 ，求最大抽样间隔 ；
（2）（2）当 时，画出 的幅度谱 。
解：(a)
∴
(b)
∴
(c)
∴
∴
(e)
∴
(f)
∴
3-19求题图3-19所示 的傅立叶逆变换 。
《信号与系统(第四版)》习题详解图文
故f(t)与{c0, c1, …, cN}一一对应。
7
3.3 设
第3章 连续信号与系统的频域分析
试问函数组｛ξ1(t),ξ2(t),ξ3(t),ξ4(t)｝在(0，4)区间上是否 为正交函数组，是否为归一化正交函数组，是否为完备正交函 数组，并用它们的线性组合精确地表示题图 3.2 所示函数f(t)。
题图 3.10
51
第3章 连续信号与系统的频域分析 52
第3章 连续信号与系统的频域分析 53
第3章 连续信号与系统的频域分析 54
第3章 连续信号与系统的频域分析 55
第3章 连续信号与系统的频域分析 56
第3章 连续信号与系统的频域分析 57
第3章 连续信号与系统的频域分析
题解图 3.19-1
8
第3章 连续信号与系统的频域分析
题图 3.2
9
第3章 连续信号与系统的频域分析
解 据ξi(t)的定义式可知ξ1(t)、ξ2(t)、ξ3(t)、ξ4(t)的波形如题 解图3.3-1所示。
题解图 3.3-1
10
不难得到：
第3章 连续信号与系统的频域分析
可知在(0,4)区间ξi(t)为归一化正交函数集,从而有
激励信号为f(t)。试证明系统的响应y(t)=－f(t)。
69
证 因为
第3章 连续信号与系统的频域分析
所以
即
70
系统函数
第3章 连续信号与系统的频域分析
故
因此
71
第3章 连续信号与系统的频域分析
3.23 设f(t)的傅里叶变换为F(jω)，且 试在K≥ωm条件下化简下式：
72
第3章 连续信号与系统的频域分析 73
107
信号与系统奥本海姆习题答案
Chapter 1 Answers1.6 (a).NoBecause when t<0, )(1t x =0.(b).NoBecause only if n=0, ][2n x has valuable.(c).Yes Because ∑∞-∞=--+--+=+k k m n k m n m n x ]}414[]44[{]4[δδ ∑∞-∞=------=k m k n m k n )]}(41[)](4[{δδ ∑∞-∞=----=k k n k n ]}41[]4[{δδ N=4.1.9 (a). T=π/5Because 0w =10, T=2π/10=π/5.(b). Not periodic.Because jt t e e t x --=)(2, while t e -is not periodic, )(2t x is not periodic.(c). N=2Because 0w =7π, N=(2π/0w )*m, and m=7.(d). N=10Because n j j e e n x )5/3(10/343)(ππ=, that is 0w =3π/5, N=(2π/0w )*m, and m=3.(e). Not periodic. Because 0w =3/5, N=(2π/0w )*m=10πm/3 , it ’s not a rational number.1.14 A1=3, t1=0, A2=-3, t2=1 or -1dtt dx )( isSolution: x(t) isBecause ∑∞-∞=-=k k t t g )2()(δ, dt t dx )(=3g(t)-3g(t-1) or dtt dx )(=3g(t)-3g(t+1) 1.15. (a). y[n]=2x[n-2]+5x[n-3]+2x[n-4]Solution:]3[21]2[][222-+-=n x n x n y ]3[21]2[11-+-=n y n y ]}4[4]3[2{21]}3[4]2[2{1111-+-+-+-=n x n x n x n x ]4[2]3[5]2[2111-+-+-=n x n x n xThen, ]4[2]3[5]2[2][-+-+-=n x n x n x n y(b).No. For it ’s linearity.the relationship between ][1n y and ][2n x is the same in-out relationship with (a). you can have a try.1.16. (a). No.For example, when n=0, y[0]=x[0]x[-2]. So the system is memory. (b). y[n]=0.When the input is ][n A δ,then, ]2[][][2-=n n A n y δδ, so y[n]=0. (c). No.For example, when x[n]=0, y[n]=0; when x[n]=][n A δ, y[n]=0. So the system is not invertible.1.17. (a). No.For example, )0()(x y =-π. So it ’s not causal.(b). Yes.Because : ))(sin()(11t x t y = , ))(sin()(22t x t y =))(sin())(sin()()(2121t bx t ax t by t ay +=+1.21. Solution:We have known:(a).(b).(c).(d).1.22. Solution:We have known:(a).(b).(e).(g)1.23. Solution:For )]()([21)}({t x t x t x E v -+= )]()([21)}({t x t x t x O d --= then,(a).(b).(c).1.24.For: ])[][(21]}[{n x n x n x E v -+= ])[][(21]}[{n x n x n x O d --=then,(a).(b).1.25. (a). Periodic. T=π/2.Solution: T=2π/4=π/2.(b). Periodic. T=2.Solution: T=2π/π=2.(d). Periodic. T=0.5. Solution: )}()4{cos()(t u t E t x v π=)}())(4cos()()4{cos(21t u t t u t --+=ππ )}()(){4cos(21t u t u t -+=π )4cos(21t π= So, T=2π/4π=0.51.26. (a). Periodic. N=7Solution: N=m *7/62ππ=7, m=3.(b). Aperriodic.Solution: N=ππm m 16*8/12=, it ’s not rational number.(e). Periodic. N=16 Solution as follow:)62cos(2)8sin()4cos(2][ππππ+-+=n n n n x in this equation,)4cos(2n π, it ’s period is N=2π*m/(π/4)=8, m=1.)8sin(n π, it ’s period is N=2π*m/(π/8)=16, m=1.)62cos(2ππ+-n , it ’s period is N=2π*m/(π/2)=4, m=1. So, the fundamental period of ][n x is N=(8,16,4)=16.1.31. SolutionBecause )()1()(),2()()(113112t x t x t x t x t x t x ++=--=. According to LTI property ,)()1()(),2()()(113112t y t y t y t y t y t y ++=--=Extra problems:Sketch ⎰∞-=t dt t x t y )()(. 1. SupposeSolution:2. SupposeSketch:(1). )]1(2)1()3()[(--+++t t t t g δδδ(2). ∑∞-∞=-k k t t g )2()(δ(2).Chapter 22.1 Solution:Because x[n]=(1 2 0 –1)0, h[n]=(2 0 2)1-, then(a).So, ]4[2]2[2]1[2][4]1[2][1---+-+++=n n n n n n y δδδδδ (b). according to the property of convolutioin:]2[][12+=n y n y(c). ]2[][13+=n y n y][*][][n h n x n y =][][k n h k x k -=∑∞-∞= ∑∞-∞=-+--=k k k n u k u ]2[]2[)21(2 ][211)21()21(][)21(12)2(0222n u n u n n k k --==+-++=-∑ ][])21(1[21n u n +-= the figure of the y[n] is:2.5 Solution:We have known: ⎩⎨⎧≤≤=elsewhere n n x ....090....1][，，, ⎩⎨⎧≤≤=elsewhere N n n h ....00....1][，，,(9≤N ) Then, ]10[][][--=n u n u n x , ]1[][][---=N n u n u n h∑∞-∞=-==k k n u k h n h n x n y ][][][*][][ ∑∞-∞=-------=k k n u k n u N k u k u ])10[][])(1[][(So, y[4] ∑∞-∞=-------=k k u k u N k u k u ])6[]4[])(1[][( ⎪⎪⎩⎪⎪⎨⎧≥≤=∑∑==4,...14, (140)0N N k Nk =5, then 4≥N And y[14] ∑∞-∞=------=k k u k u N k u k u ])4[]14[])(1[][(⎪⎪⎩⎪⎪⎨⎧≥≤=∑∑==14,...114, (1145)5N N k Nk =0, then 5<N ∴4=N2.7 Solution:[][][2]k y n x k g n k ∞=-∞=-∑（a ）[][1]x n n δ=-,[][][2][1][2][2]k k y n x k g n k k g n k g n δ∞∞=-∞=-∞=-=--=-∑∑(b) [][2]x n n δ=-,[][][2][2][2][4]k k y n x k g n k k g n k g n δ∞∞=-∞=-∞=-=--=-∑∑ (c) S is not LTI system..(d) [][]x n u n =,0[][][2][][2][2]k k k y n x k g n k u k g n k g n k ∞∞∞=-∞=-∞==-=-=-∑∑∑2.8 Solution: )]1(2)2([*)()(*)()(+++==t t t x t h t x t y δδ )1(2)2(+++=t x t xThen,That is, ⎪⎪⎪⎩⎪⎪⎪⎨⎧≤<-≤<-+-=-<<-+=others t t t t t t t t y ,........010,....2201,.....41..,.........412,.....3)(2.10 Solution:(a). We know:Then,)()()(αδδ--='t t t h)]()([*)()(*)()(αδδ--='='t t t x t h t x t y )()(α--=t x t xthat is,So, ⎪⎪⎩⎪⎪⎨⎧+≤≤-+≤≤≤≤=others t t t t t t y ,.....011,.....11,....0,.....)(ααααα(b). From the figure of )(t y ', only if 1=α, )(t y ' would contain merely therediscontinuities.2.11 Solution:(a). )(*)]5()3([)(*)()(3t u et u t u t h t x t y t----==⎰⎰∞∞---∞∞--------=ττττττττd t u e u d t u eu t t )()5()()3()(3)(3⎰⎰-------=tt t t d e t u d et u 5)(33)(3)5()3(ττττ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥+-=-<≤-=<=---------⎰⎰⎰5,.......353,.....313.........,.........0315395)(33)(3393)(3t e e d e d e t e d e t tt t t t t t t t ττττττ(b). )(*)]5()3([)(*)/)(()(3t u e t t t h dt t dx t g t ----==δδ)5()3()5(3)3(3---=----t u e t u e t t(c). It ’s obvious that dt t dy t g /)()(=.2.12 Solution∑∑∞-∞=-∞-∞=--=-=k tk tk t t u ek t t u e t y )]3(*)([)3(*)()(δδ∑∞-∞=---=k k t k t u e)3()3(Considering for 30<≤t ,we can obtain33311])3([)(---∞=-∞-∞=--==-=∑∑ee e ek t u e e t y tk k tk kt. (Because k must be negetive ,1)3(=-k t u for 30<≤t ).2.19 Solution:(a). We have known:][]1[21][n x n w n w +-=(1) ][]1[][n w n y n y βα+-=(2)from (1), 21)(1-=E EE Hfrom (2), αβ-=E EE H )(2then, 212212)21(1)21)(()()()(--++-=--==E E E E E E H E H E H ααβαβ∴][]2[2]1[)21(][n x n y n y n y βαα=-+-+-but, ][]1[43]2[81][n x n y n y n y +-+--=∴⎪⎩⎪⎨⎧=⎪⎭⎫ ⎝⎛=+=143)21(:....812βααor ∴⎪⎩⎪⎨⎧==141βα(b). from (a), we know )21)(41()()()(221--==E E E E H E H E H21241-+--=E EE E ∴][)41()21(2][n u n h n n ⎥⎦⎤⎢⎣⎡-=2.20 (a). 1⎰⎰∞∞-∞∞-===1)0cos()cos()()cos()(0dt t t dt t t u δ(b). 0dt t t )3()2sin(5+⎰δπ has value only on 3-=t , but ]5,0[3∉-∴dt t t )3()2sin(5+⎰δπ=0(c). 0⎰⎰---=-641551)2cos()()2cos()1(dt t t u d u πτπττ⎰-'-=64)2cos()(dt t t πδ0|)2(s co ='=t t π 0|)2sin(20=-==t t ππ∑∞-∞=-==k t h kT t t h t x t y )(*)()(*)()(δ∑∞-∞=-=k kT t h )(∴2.27Solution()y A y t dt ∞-∞=⎰,()xA x t dt ∞-∞=⎰,()hA h t dt ∞-∞=⎰.()()*()()()y t x t h t x x t d τττ∞-∞==-⎰()()()()()()()()()(){()}y x hA y t dt x x t d dtx x t dtd x x t dtd x x d d x d x d A A ττττττττττξξτττξξ∞∞∞-∞-∞-∞∞∞∞∞-∞-∞-∞-∞∞∞∞∞-∞-∞-∞-∞==-=-=-===⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰(a) ()()(2)tt y t e x d τττ---∞=-⎰,Let ()()x t t δ=,then ()()y t h t =. So , 2()(2)(2)()(2)()(2)t t t t t h t ed e d e u t τξδττδξξ---------∞-∞=-==-⎰⎰(b) (2)()()*()[(1)(2)]*(2)t y t x t h t u t u t e u t --==+---(2)(2)(1)(2)(2)(2)t t u eu t d u e u t d ττττττττ∞∞-------∞-∞=+------⎰⎰22(2)(2)12(1)(4)t t t t u t e d u t e d ττττ---------=---⎰⎰(2)2(2)212(1)[]|(4)[]|t t t t u t e e u t ee ττ-------=--- (1)(4)[1](1)[1](4)t t e u t e u t ----=-----2.46 SolutionBecause)]1([2)1(]2[)(33-+-=--t u dtde t u e dt d t x dt d t t )1(2)(3)1(2)(333-+-=-+-=--t e t x t e t x t δδ.From LTI property ,we know)1(2)(3)(3-+-→-t h e t y t x dtdwhere )(t h is the impulse response of the system. So ,following equation can be derived.)()1(223t u e t h e t --=-Finally, )1(21)()1(23+=+-t u e e t h t 2.47 SoliutionAccording to the property of the linear time-invariant system: (a). )(2)(*)(2)(*)()(000t y t h t x t h t x t y ===(b). )(*)]2()([)(*)()(00t h t x t x t h t x t y --==)(*)2()(*)(0000t h t x t h t x --=012y(t)t4)2()(00--=t y t y(c). )1()1(*)(*)2()1(*)2()(*)()(00000-=+-=+-==t y t t h t x t h t x t h t x t y δ(d). The condition is not enough.(e). )(*)()(*)()(00t h t x t h t x t y --==τττd t h x )()(00+--=⎰∞∞-)()()(000t y dm m t h m x -=--=⎰∞∞-(f). )()]([)](*)([)(*)()(*)()(000000t y t y t h t x t h t x t h t x t y "=''='--'=-'-'==Extra problems:1. Solute h(t), h[n](1). )()(6)(5)(22t x t y t y dt dt y dtd =++ (2). ]1[][2]1[2]2[+=++++n x n y n y n y Solution:(1). Because 3121)3)(2(1651)(2+-++=++=++=P P P P P P P Hso )()()()3121()(32t u e e t P P t h t t ---=+-++=δ (2). Because )1)(1(1)1(22)(22i E i E EE E E E E E H -+++=++=++=iE Eii E E i -+-+++=1212 so []][)1()1(2][1212][n u i i i k i E E i i E E i n h n n +----=⎪⎪⎪⎪⎭⎫⎝⎛-+-+++=δChapter 33.1 Solution:Fundamental period 8T =.02/8/4ωππ==00000000033113333()224434cos()8sin()44j kt j t j t j t j tk k j t j t j t j tx t a e a e a e a e a e e e je je t t ωωωωωωωωωππ∞----=-∞--==+++=++-=-∑3.2 Solution:for, 10=a , 4/2πj ea --= , 4/2πj ea = , 3/42πj ea --=, 3/42πj ea =n N jk k N k e a n x )/2(][π∑>=<=n j n j n j n j e a e a e a e a a )5/8(4)5/8(4)5/4(2)5/4(20ππππ----++++=n j j n j j n j j n j j e e e e e e e e )5/8(3/)5/8(3/)5/4(4/)5/4(4/221ππππππππ----++++= )358cos(4)454cos(21ππππ++++=n n)6558sin(4)4354sin(21ππππ++++=n n3.3 Solution: for the period of )32cos(t πis 3=T , the period of )35sin(t πis 6=Tso the period of )(t x is 6 , i.e. 3/6/20ππ==w)35sin(4)32cos(2)(t t t x ππ++= )5sin(4)2cos(21200t w t w ++=)(2)(21200005522t w j t w j t w j t w j e e j e e ----++=then, 20=a , 2122==-a a , j a 25=-, j a 25-=3.5 Solution:(1). Because )1()1()(112-+-=t x t x t x , then )(2t x has the same period as )(1t x ,that is 21T T T ==, 12w w =(2). 212111()((1)(1))jkw t jkw tk T T b x t e dt x t x t e dt T--==-+-⎰⎰111111(1)(1)jkw tjkw t T Tx t e dt x t e dt T T --=-+-⎰⎰ 111)(jkw k k jkw k jkw k e a a e a e a -----+=+=3.8 Solution:kt jw k k e a t x 0)(∑∞-∞==while:)(t x is real and odd, then 00=a , k k a a --=2=T , then ππ==2/20wand0=k a for 1>kso kt jw k k e a t x 0)(∑∞-∞==t jw t jw e a e a a 00110++=--)sin(2)(11t a e e a t j t j πππ=-=-for12)(2121212120220==++=-⎰a a a a dt t x∴2/21±=a ∴)sin(2)(t t x π±=3.13 Solution:Fundamental period 8T =.02/8/4ωππ==kt jw k k e a t x 0)(∑∞-∞==∴t jkw k k e jkw H a t y 0)()(0∑∞-∞==0004, 0sin(4)()0, 0k k H jk k k ωωω=⎧==⎨≠⎩ ∴000()()4jkw t k k y t a H jkw e a ∞=-∞==∑Because 48004111()1(1)088T a x t dt dt dt T ==+-=⎰⎰⎰So ()0y t =.kt jw k k e a t x 0)(∑∞-∞==∴t jkw k k e jkw H a t y 0)()(0∑∞-∞== ∴dt e jkw H t y Ta t jkw Tk 0)()(10-⎰=for⎪⎩⎪⎨⎧>≤=100, (0100),.......1)(w w jw H ∴if 0=k a , it needs 1000>kwthat is 12100,........1006/2>>k kππand k is integer, so 8>K3.22 Solution:021)(1110===⎰⎰-tdt dt t x Ta Tdt te dt te dt e t x T a t jk t jk t jkw T k ππ-----⎰⎰⎰===1122112121)(10t jk tde jk ππ--⎰-=1121⎥⎥⎦⎤⎢⎢⎣⎡---=----111121ππππjk e te jk t jk tjk ⎥⎦⎤⎢⎣⎡---+-=--ππππππjk e e e e jk jk jk jk jk )()(21⎥⎦⎤⎢⎣⎡-+-=ππππjk k k jk )sin(2)cos(221[]πππππk jk k j k jk k)1()cos()cos(221-==-=0............≠k404402()()1184416tj tj t t j tt j t H j h t edt ee dte edt e e dtj j ωωωωωωωω∞∞----∞-∞∞----∞===+=+=-++⎰⎰⎰⎰A periodic continous-signal has Fourier Series:. 0()j kt k k x t a e ω∞=-∞=∑T is the fundamental period of ()x t .02/T ωπ=The output of LTI system with inputed ()x t is 00()()jk t k k y t a H jk e ωω∞=-∞=∑Its coefficients of Fourier Series: 0()k k b a H jk ω= (a)()()n x t t n δ∞=-∞=-∑.T=1, 02ωπ=11k a T==. 01/221/21()()1jkw t jk tk T a x t e dt t e dt Tπδ---===⎰⎰ （Note ：If ()()n x t t nT δ∞=-∞=-∑,1k a T=） So 2282(2)16(2)4()k k b a H jk k k πππ===++ (b)()(1)()n n x t t n δ∞=-∞=--∑ .T=2, 0ωπ=,11k a T== 01/23/21/21/2111()()(1)(1)221[1(1)]2jkw t jk tjk t k T k a x t e dt t e dt t e dtT ππδδ----==+--=--⎰⎰⎰So 24[1(1)]()16()k k k b a H jk k ππ--==+, (c) T=1,02ωπ=01/421/4sin()12()jk t jk tk T k a x t e dt e dt Tk ωπππ---===⎰⎰28sin()2()[16(2)]k k k b a H jk k k ππππ==+ 3.35 Solution: T= /7π,02/14T ωπ==.kt jw k k e a t x 0)(∑∞-∞==∴t jkw k k e jkw H a t y 0)()(0∑∞-∞==∴0()k k b a H jkw =for⎩⎨⎧≥=otherwise w jw H ,.......0250,.......1)(,01,. (17)()0,.......k H jkw otherwise ⎧≥⎪=⎨⎪⎩that is 0250250, (14)k k ω<<, and k is integer, so 18....17k or k <≤. Let ()()y t x t =,k k b a =, it needs 0=k a ,for 18....17k or k <≤.3.37 Solution:11()[]()212()21312411511cos 224nj j nj n n n n j nn j nn n j j j H e h n ee ee e e e ωωωωωωωωω∞∞--=-∞=-∞-∞--=-∞=-===+=+=---∑∑∑∑A periodic sequence has Fourier Series:2()[]jk n Nk k N x n a eπ=<>=∑.N is the fundamental period of []x n .The output of LTI system with inputed []x n is 22()[]()jk jk n NNk k N y n a H eeππ=<>=∑.Its coefficients of Fourier Series: 2()jk Nk k b a H eπ=(a)[][4]k x n n k δ∞=-∞=-∑.N=4, 14k a =.So 2314()524cos()44j k Nk k b a H e k ππ==-3165cos()42k b k π=-3.40 Solution: According to the property of fourier series: (a). )2cos(2)cos(20000000t Tka t kw a e a ea a k k t jkw k t jkw k k π==+='- (b). Because 2)()()}({t x t x t x E v -+=}{2k v k k k a E a a a =+='-(c). Because 2)(*)()}({t x t x t x R e +=2*kk k a a a -+='(d). k k k a Tjka jkw a 220)2()(π=='(e). first, the period of )13(-t x is 3T T ='then 3)(1)13(131213120dme m x T dt e t x T a m T jk T t T jk T k +'--'-'-'⎰⎰'=-'='ππTjkk m T jk T T jk T jk m T jk T ea dm e m x T e dm e e m x T πππππ221122211)(1)(1---------=⎥⎦⎤⎢⎣⎡==⎰⎰3.43 (a) Proof:（i ）Because ()x t is odd harmonic ,(2/)()jk T t k k x t a e π∞=-∞=∑,where 0k a = for everynon-zero even k.(2/)()2(2/)(2/)()2T jk T t k k jk jk T tk k jk T tk k T x t a ea e e a e ππππ∞+=-∞∞=-∞∞=-∞+===-∑∑∑It is noticed that k is odd integers or k=0.That means()()2Tx t x t =-+（ii ）Because of ()()2Tx t x t =-+,we get the coefficients of Fourier Series222/200/222(/2)/2/20022/2/200111()()()11()(/2)11()()(1)jk t jk t jk t T T T T T T k T jk t jk t T T T T Tjk t jk t T T k TT a x t e dt x t e dt x t e dtT T T x t e dt x t T e dt T T x t e dt x t e dt T T πππππππ-----+--==+=++=--⎰⎰⎰⎰⎰⎰⎰ 2/21[1(1)]()jk t T kT x t e dt T π-=--⎰It is obvious that 0k a = for every non-zero even k. So ()x t is odd harmonic ,(b)Extra problems:∑∞-∞=-=k kT t t x )()(δ, π=T(1). Consider )(t y , when )(jw H ist(2). Consider )(t y , when )(jw H isSolution:∑∞-∞=-=k kT t t x )()(δ↔π11=T , 220==Tw π(1).kt j k k tjkw k k e k j H a ejkw H a t y 20)2(1)()(0∑∑∞-∞=∞-∞===ππ2=(for k can only has value 0)(2).kt j k k tjkw k k e k j H a e jkw H a t y 20)2(1)()(0∑∑∞-∞=∞-∞===πππte e t j t j 2cos 2)(122=+=- (for k can only has value –1 and 1)。
信号与系统王明泉科学出版社第三章习题解答
左右对t求导，得:
显然， 的指数傅里叶级数为 （式中 ）
3.9求题图3.9所示各信号的傅里叶变换。
题图3.9
解：根据定义
3.10计算下列每个信号的傅里叶变换。
（1） ；（2） ；
（3） ；（4）
（5） ；（6）
解: (1)
(2)
(3)由于
根据卷积乘积性质，得
(4)由于
所以
（5） ,设
第3章傅里叶变换与连续系统的频域分析
3.6本章习题全解
3.1证明函数集 在区间 内是正交函数集。
证明:对任意的自然数n,m (n m),有
=0
证毕
3.2一个由正弦信号合成的信号由下面的等式给出：
（1）画出这个信号的频谱图，表明每个频率成分的复数值。对于每个频率的复振幅，将其实部和虚部分开或者将其幅度和相位分开来画。
图3-19-3
3.21用傅里叶变换法求题图3.21所示周期信号 的傅里叶级数。
题图3.21
解:对x(t)一个周期信号x0(t)的傅里叶变换为
X0(j )=
=
傅里叶级数
3.22求题图3.22所示周期性冲激信号的频谱函数。
题图321-1
3.23已知 的幅频与相频特性如题图3.23所示，求其傅里叶逆变换 。
（a）（b）
题图3.12
解：令傅里叶变换对 ，
（1）根据已知图形可知：
，
已知有
所以
根据傅里叶变换的微积分性质
所以
即
（2） ，
根据（1）的结论得
根据傅里叶变换的微积分性质
所以
即
3.13利用傅里叶变换的对称性求下列信号的频谱函数。
(1) ；(2) ；
信号与系统习题答案第三章
第三章习题基础题3.1 证明cos t , cos(2)t , …, cos()nt (n 为正整数)，在区间(0,2)π的正交集。
它是否是完备集? 解：(积分???)此含数集在(0,2)π为正交集。
又有sin()nt 不属于此含数集02sin()cos()0nt mt dt π=⎰，对于所有的m和n 。
由完备正交函数定义所以此函数集不完备。
3.2 上题的含数集在(0,)π是否为正交集？解：由此可知此含数集在区间(0,)π内是正交的。
3.3实周期信号()f t 在区间(,)22T T-内的能量定义为222()TT E f t dt -=⎰。
如有和信号12()()f t f t +(1)若1()f t 与2()f t 在区间(,)22T T-内相互正交，证明和信号的总能量等于各信号的能量之和;(2)若1()f t 与2()f t 不是相互正交的，求和信号的总能量。
解：(1)和信号f(t)的能量为[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰（少乘以2）由1()f t 与2()f t 在区间内正交可得2122()()0T T f t f t dt -=⎰则有 22221222()()T T T T E f t dt f t dt --=+⎰⎰即此时和信号的总能量等于各信号的能量之和。
和信号的能量为(2)[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰（少乘以2吧？）由1()f t 与2()f t 在区间(,)22T T-内不正交可得 2122()()0T T f t f t dt K -=≠⎰则有2222222212122222()()()()T T T T T T T T E f t dt f t dt K f t dt f t dt ----=++≠+⎰⎰⎰⎰即此时和信号的总能量不等于各信号的能量之和。
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解-第8章 z变换、离散时间系统的z域分
（7）
X
z
1 2
n
u
n
u
n
10
z
n
9 n0
1 2
n
z
n
9 n0
1 2z
n
1
1 2z
1 1
10
z 0
2z
X（z）的零、极点分布图如图 8-2-1（g）所示。
（8）
8 / 75
圣才电子书
十万种考研考证电子书、题库视频学习平
X
z
n台
1 2
圣才电子书
十万种考研考证电子书、题库视频学习平
台
第 8 章 z 变换、离散时间系统的 z 域分析
8.1 复习笔记
从本章开始陆续讨论 Z 变换的定义、性质以及它与拉氏变换、傅氏变换的联系。在此 基础上研究离散时间系统的 z 域分析，给出离散系统的系统函数与频率响应的概念。通过 本章，读者应掌握对于离散时间信号与系统的研究，是先介绍 z 变换，然后引出序列的傅 里叶变换以及离散傅里叶变换（第九章）。
4 / 75
圣才电子书
十万种考研考证电子书、题库视频学习平
台
于实轴的直线映射到 z 平面是负实轴；
（3）在 s 平面上沿虚轴移动对应于 z 平面上沿单位圆周期性旋转，每平移 ωs，则沿
单位圆转一圈。
2．z 变换与拉氏变换表达式
Z
x nT X z zesT X s Z
n
u
n
1 3
n
u
n
z
n
n
（3）
X
z
n
1 3
n
u
n
z
n
n0
信号与系统教程习题解析（前七章）
2e
第2章
连续时间信号
2-1 设有如下函数f t ，试分别画出它们的波形。 (a) f t 2ε t 1 2ε t 2 (b) f t sinπt ∙ ε t ε t 6 解 (a)和(b)的波形如图 p2-1 所示。
2
图 p2-1
2-2 试用阶跃函数的组合表示题 2-2 图所示信号。 解 (a) f t ε t 2ε t 1 ε t 2
信号与系统的频域分析
4-1 求题 4-1 图所示周期信号的三角函数形式的傅里叶级数表示式。
题 4-1(a) 图
解 对于周期锯齿波信号，在周期( 0，T )内可表示为
ft
A T
t
T
At T
A
a
1 T
f t dt
1 T
At T
A dt
A T
t 2T
t
A 2
∵ ω T 2π, ∴ sinnω tdt
cosnω tdt 0
⇒t
2f
t
↔
j
dF ω dω
2F ω
df t dt
↔ jωF ω
⇒
t
df t dt
↔
j
d
jωF ω dω
4-9 对于如题 4-9 图所示的三角波，试求其频谱函数。
13
题 4-9 图
解 过原点的三角波函数是偶函数，其表达式为
ft
A1
|t| τ
,
|t|
0,
|t|
Fω
fte
dt 2
A1
t τ
cosωtdt
2A
1 ω
sinωt|
1 τ
武汉大学信号与系统题库
1-1判断下列信号是否是能量信号，功率信号，或者都不是。
注意这里圆括号和方括号表示其分别对应连续和离散信号，下同。
(1)；(2)；(3)；(4)；(5)；(6)。
解(1) 对于，因此,是能量信号。
(2) 如果是基本周期为的周期信号,则的归一化平均功率与任意时间间隔的的平均功率是相同的，正弦信号是周期为的周期信号，所以的平均功率为因此，是功率信号。
注意，一般情况下，周期信号都是功率信号。
(3) 对，因此，既不是能量信号，也不是功率信号。
(4) 对，根据能量信号定义得因此，是能量信号。
(5) 对，由功率信号定义得因此，是功率信号。
(6) 因为，所以因此，是功率信号。
1-2验证下式：(1) ；(2)。
解可以根据以下等效性质来证明：设是广义函数，则对于所定义的测试函数，当且仅当时，，这就是等效性质。
(1) 对可变的变量,设,则，可以得到以下等式：所以，考虑到是的偶函数，因而有。
(2) 令，由得1-3计算下列积分(1)；(2)；(3)；(4)；(5)。
解(1)(2)(3)(4)(5)1-4如下图所示的系统是(1)无记忆的；(2)因果的；(3)线性的；(4)时不变的；(5)稳定的。
解(1) 由图得，因为输出的值仅取决于输入当前的值，所以系统是无记忆的。
(2) 因为输出不取决于输出将来的值，所以系统是因果的。
(3) 设，则有其中所以系统满足叠加性质，是线性的。
(4) 设，而，因为，所以系统是时变的。
(5) 因为，，若输入是有界的，则输出也是有界的，系统是BIBO稳定的。
1-5如果可以通过观察系统的输出信号来惟一的确定输入信号，则该系统称为可逆的，如下图所示。
试确定以下的系统是否是可逆的，如果是，给出其逆系统。
(1)； (2)；(3)；(4)；(5)。
解(1) 可逆，。
(2) 不可逆。
(3) 可逆，。
(4) 可逆，(5) 不可逆。
1-6 如下图所示的网络中，已知励磁信号为，单位为，电阻（单位），电感（单位）均为常数，电容器是一个伺服机械带动的空气可变电容器，其容量的变化规律为。
信号与系统习题
1,某系统7,4码)()(01201230123456c c c m m m m c c c c c c c ==c 其三位校验位与信息位的关系为：1求对应的生成矩阵和校验矩阵； 2计算该码的最小距离；3列出可纠差错图案和对应的伴随式；4若接收码字R =1110011,求发码;解：1 1000110010001100101110001101G ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦101110011100100111001H ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦2 d min =3 34. RH T=001 接收出错E =0000001 R+E=C = 1110010 发码2.已知(),X Y 的联合概率(),p x y 为： 求()H X ,()H Y ,(),H X Y ,();I X Y 解:(0)2/3p x == (1)1/3p x ==()()(1/3,2/3)H X H Y H === bit/symbol (),(1/3,1/3,1/3)H X Y H == bit/symbol ();()()(,)I X Y H X H Y H X Y =+-= bit/symbol3.一阶齐次马尔可夫信源消息集},,{321a a a X ∈,状态集},,{321S S S S∈,且令3,2,1,==i a S i i ,条件转移概率为01X Y011/31/301/3[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=03121313121141)/(i j S a P ,1画出该马氏链的状态转移图；2计算信源的极限熵; 解：12⎪⎪⎩⎪⎪⎨⎧=++=+=++=++1321323112123312311411332231141w w w w w w w w w w w w w w →⎪⎩⎪⎨⎧===3.03.04.0321w w wHX|S 1 =H 1/4,1/4,1/2=比特/符号HX|S 2=H 1/3,1/3,1/3=比特/符号HX|S 3=H 2/3,1/3= 比特/符号()3|0.4 1.50.3 1.5850.30.918 1.3511Hw H X S i ii ==⨯+⨯+⨯=∑∞=比特/符号 4.若有一信源⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡2.08.021x x P X ,每秒钟发出个信源符号;将此信源的输出符号送入某一个二元信道中进行传输 假设信道是无噪无损的,容量为1bit/二元符号, 而信道每秒钟只传递2个二元符号;（1） 试问信源不通过编码即x 10,x 21在信道中传输 （2） 能否直接与信道连接（3） 若通过适当编码能否在此信道中进行无失真传输 （4） 试构造一种哈夫曼编码两个符号一起编码, （5） 使该信源可以在此信道中无失真传输;解：1不能,此时信源符号通过0,1在信道中传输,二元符号/s>2二元符号/s 2从信息率进行比较, (0.8,0.2)H = < 12可以进行无失真传输 3410.640.16*20.2*3i i i Kp K ===++=∑ 二元符号/2个信源符号此时 2=二元符号/s < 2二元符号/s 5.两个BSC 信道的级联如右图所示：1写出信道转移矩阵； 2求这个信道的信道容量; 解： 16.设随机变量,{21=x x X }1,0{21=Y的联合概率空间为 x 1x 1x 1x 2x 2x 1x 2x 20.64011100101 0.64定义一个新的随机变量Y X Z ⨯=普通乘积（1） 计算熵HX,HY,HZ,HXZ,HYZ,以及HXYZ ；（2） 计算条件熵 HX|Y,HY|X,HX|Z,HZ|X,HY|Z,HZ|Y,HX|YZ,HY|XZ 以及HZ|XY ； （3） 计算平均互信息量IX ；Y,IX ：Z,IY ：Z,IX ；Y|Z,IY ；Z|X 以及IX ：,Z|Y; 解：1 2 37.设二元对称信道的输入概率分布分别为]4/14/3[][=X P ,转移矩阵为[]⎥⎦⎤⎢⎣⎡=3/23/13/13/2|XY P ,（１） 求信道的输入熵,输出熵,平均互信息量； （２） 求信道容量和最佳输入分布； （３） 求信道剩余度; 解：1信道的输入熵4log 4/1)3/4(log 4/3)(22+=X H ；2最佳输入分布为]2/12/1[][=X P ,此时信道的容量为)3/1,3/2(1H C -=3信道的剩余度：);(Y X I C -8.[][]25.025.05.0=X P ,试确定最佳译码规则和极大似然译码规则,并计算出相应的平均差错率;解：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=8/124/112/112/18/124/112/16/14/1][XY P 最佳译码规则：⎪⎩⎪⎨⎧===331211)()()(ab F a b F a b F ,平均差错率为1-1/4-1/6-1/8=11/24；极大似然规则：⎪⎩⎪⎨⎧===332211)()()(ab F a b F a b F ,平均差错率为1-1/4-1/8-1/8=1/2;9.设有一批电阻,按阻值分70%是2k Ω,30%是5k Ω；按功耗分64%是1/8W,36%是1/4W;现已知2k Ω电阻中80%是1/8W,假如得知5k Ω电阻的功耗为1/4W,问获得多少信息量; 解：根据题意有⎥⎦⎤⎢⎣⎡===3.07.05221k r k r R ,⎥⎦⎤⎢⎣⎡===36.064.04/128/11w w W ,8.0)1/1(=r w p 由15/4)2/1()2/1()2()1/1()1()1(=⇒+=r w p r w p r p r w p r p w p 所以15/11)2/1(1)2/2(=-=r w p r w p得知5k Ω电阻的功耗为1/4W,获得的自信息量为=-))2/2((r w p lb10.已知6符号离散信源的出现概率为⎥⎥⎦⎤⎢⎢⎣⎡321321161814121654321a a a a a a ,试计算它的熵、Huffman 编码和费诺编码的码字、平均码长及编码效率; 解：该离散信源的熵为323213232116161881441221)()(61lb lb lb lb lb lb p lb p x H i i i +++++=-=∑== bit/符号11.在图片传输中,每帧约有2106个像素,为了能很好地重现图像,每像素能分256个亮度电平,并假设亮度电平等概分布;试计算每分钟传送两帧图片所需信道的带宽信噪功率比为30dB; 解：每个像素点对应的熵8256log log 22===n H bit/点 2帧图片的信息量bit H N I 7610*2.38*10*2*2**2===单位时间需要的信道容量s bit t I C t /10*3.56010*2.357===由香农信道容量公式Hz SNR C W SNR W C t t 4252210*35.5)10001(log 10*3.5)1(log )1(log ≈+=+=⇒+=12.求右图所示的信道的容量及达到信道容量时的输入分布; 解：由右图可知,该信道的转移概率矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=102/12/101P 可以看到,当该信道的输入分布取⎥⎦⎤⎢⎣⎡=2/102/1)(321a a a X P 时,⎥⎦⎤⎢⎣⎡=2/12/1)(21b bY P 此时2);(2)()/(log)/();(311211lb Y a X I lb b p a b p a bp Y a X I j j jj =====∑=同理可得， 而0);(2==Y a X I ,此分布满足⎩⎨⎧==≠=0);(02);(i i i i p Y x I p lb Y x I ;因此这个信道的容量为X Y b 1b 2a 1a 2a 3C=lb2=1bit/符号,而达到信道容量的输入分布可取⎥⎦⎤⎢⎣⎡=2/102/1)(321a a aX P ; D max =∑==414,3,2,1min i ijij dp ,由于ij i d p 和具有对称性,每个和式结果都为1/2,因此 Dmax= 1/2,13.设离散信源⎥⎥⎦⎤⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡p p p p U U U U u p U 21)1(21)1(2121)(4321其中21≤p 和接收变量V={v1,v2,v3,v4},失真矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=05.05.015.0015.05.0105.015.05.00D ,求D min,D max 、RD min 、RD max 、达到D min 和D max 时的编码器转移概率矩阵P; 解：由于失真矩阵每行每列都只有一个最小值“0”,所以可以达到D min =0,此时对应的信道转移概率矩阵应使得信源的每个输出经过信道转移后失真为0,即选择⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000010000100001P ; RD min = R0= HU = 1-plog p –1-plog1-p = 1+Hp;对应的转移概率矩阵可取任意1列为全1,如⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0001000100010001P ,此时 RD max= R1/2= 0;14.设有一个二进制一阶马尔可夫信源,其信源符号为X ∈0,1,条件概率为p 0/0= p 1/0= p1/1= p 0/1=画出状态图并求出各符号稳态概率;15分15.设输入符号与输出符号为X ＝Y ∈{0,1,2,3},且输入符号等概率分布;设失真函数为汉明失真;求D max 和D min 及RD max 和RD min 20分解：()()()()012314p x p x p x p x ====失真矩阵的每一行都有0,因此D min =016.设随机变量}1,0{},{21==x x X和}1,0{},{21==y y Y 的联合概率空间为定义一个新的随机变量Y X Z ⨯=普通乘积计算熵HX,HY,HZ,HXZ,HYZ,以及HXYZ ；计算条件熵 HX|Y,HY|X,HX|Z,HZ|X,HY|Z,HZ|Y,HX|YZ,HY|XZ 以及HZ|XY ； 计算平均互信息量IX ；Y,IX ：Z,IY ：Z,IX ；Y|Z,IY ；Z|X 以及IX ：,Z|Y; 解：12))3/4(log 4/34log 4/1(2/1))3/4(log 4/34log 4/1(2/1)|(2222+++=Y XH3 )|()();(Y X H X H Y X I -=)|()();(Z X H X H Z X I -=分别为]4/14/3[][=XP ,转移17.设二元对称信道的输入概率分布矩阵为[]⎥⎦⎤⎢⎣⎡=3/23/13/13/2|XY P , 求信道的输入熵,输出熵,平均互信息量；求信道容量和最佳输入分布； 求信道剩余度; 解：1信道的输入熵4log 4/1)3/4(log 4/3)(22+=X H ；2最佳输入分布为]2/12/1[][=X P ,此时信道的容量为)3/1,3/2(1H C -=3信道的剩余度：);(Y X I C-设有ＤＭＣ,其转移矩阵为[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2/16/13/13/12/16/16/13/12/1|X Y P ,若信道输入概率为[][]25.025.05.0=X P ,试确定最佳译码规则和极大似然译码规则,并计算出相应的平均差错率;解：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=8/124/112/112/18/124/112/16/14/1][XY P 最佳译码规则：⎪⎩⎪⎨⎧===331211)()()(a b F a b F a b F ,平均差错率为1-1/4-1/6-1/8=11/24；极大似然规则：⎪⎩⎪⎨⎧===332211)()()(ab F a b F a b F ,平均差错率为1-1/4-1/8-1/8=1/2;一、概念简答题1.什么是平均自信息量与平均互信息,比较一下这两个概念的异同2.简述最大离散熵定理;对于一个有m 个符号的离散信源,其最大熵是多少3.解释信息传输率、信道容量、最佳输入分布的概念,说明平均互信息与信源的概率分布、信道的传递概率间分别是什么关系4.对于一个一般的通信系统,试给出其系统模型框图,并结合此图,解释数据处理定理;5.写出香农公式,并说明其物理意义;当信道带宽为5000Hz,信噪比为30dB 时求信道容量;6.解释无失真变长信源编码定理;7.解释有噪信道编码定理;8.什么是保真度准则 对二元信源,其失真矩阵,求a>0时率失真函数的和9.简述离散信源和连续信源的最大熵定理;10.解释等长信源编码定理和无失真变长信源编码定理,说明对于等长码和变长码,最佳码的每符号平均码长最小为多少编码效率最高可达多少11.解释最小错误概率译码准则,最大似然译码准则和最小距离译码准则,说明三者的关系; 12.设某二元码字C={111000,001011,010110,101110}, ①假设码字等概率分布,计算此码的编码效率②采用最小距离译码准则,当接收序列为110110时,应译成什么码字13.一平稳二元信源,它在任意时间,不论以前发出过什么符号,都按发出符号,求和平均符号熵14.分别说明信源的概率分布和信道转移概率对平均互信息的影响,说明平均互信息与信道容量的关系;15.二元无记忆信源,有求：1某一信源序列由100个二元符号组成,其中有m个“1”,求其自信息量2求100个符号构成的信源序列的熵;16.求以下三个信道的信道容量：,,17.已知一3,1,3卷积码编码器,输入输出关系为：试给出其编码原理框图;18. 简述信源的符号之间的依赖与信源冗余度的关系;19. 简述香农第一编码定理的物理意义20. 什么是最小码距, 以及它和检错纠错能力之间的关系;21. 简述信息的特征22. 简单介绍哈夫曼编码的步骤一、概念简答题每题5分,共40分1.答：平均自信息为表示信源的平均不确定度,也表示平均每个信源消息所提供的信息量;平均互信息表示从Y获得的关于每个X的平均信息量,也表示发X前后Y的平均不确定性减少的量,还表示通信前后整个系统不确定性减少的量;2.答：最大离散熵定理为：离散无记忆信源,等概率分布时熵最大;最大熵值为;3.答：信息传输率R指信道中平均每个符号所能传送的信息量;信道容量是一个信道所能达到的最大信息传输率;信息传输率达到信道容量时所对应的输入概率分布称为最佳输入概率分布;平均互信息是信源概率分布的∩型凸函数,是信道传递概率的U型凸函数;4.答：通信系统模型如下：数据处理定理为：串联信道的输入输出X、Y、Z组成一个马尔可夫链,且有,;说明经数据处理后,一般只会增加信息的损失;5.答：香农公式为,它是高斯加性白噪声信道在单位时间内的信道容量,其值取决于信噪比和带宽;由得,则6.答：只要,当N足够长时,一定存在一种无失真编码;7.答：当R＜C时,只要码长足够长,一定能找到一种编码方法和译码规则,使译码错误概率无穷小;8.答：1保真度准则为：平均失真度不大于允许的失真度;2因为失真矩阵中每行都有一个0,所以有,而;9.答：离散无记忆信源,等概率分布时熵最大;连续信源,峰值功率受限时,均匀分布的熵最大;平均功率受限时,高斯分布的熵最大;均值受限时,指数分布的熵最大;10.答：等长信源编码定理：对于任意,只要,则当L足够长时必可使译码差错;变长信源编码定理：只要,一定存在一种无失真编码;等长码和变长码的最小平均码长均为,编码效率最高可达100%;11.答：最小错误概率译码准则下,将接收序列译为后验概率最大时所对应的码字;最大似然译码准则下,将接收序列译为信道传递概率最大时所对应的码字;最小距离译码准则下,将接收序列译为与其距离最小的码字;三者关系为：输入为等概率分布时,最大似然译码准则等效于最小错误概率译码准则;在二元对称无记忆信道中,最小距离译码准则等效于最大似然译码准则;12.答：12令接收序列为,则有,,,,故接收序列应译为010110;13.答：14.答：平均互信息相对于信源概率分布为上凸函数,相对于信道传递概率分布为下凹函数;平均互信息的最大值为信道容量;15.答：1216.答：P1为一一对应确定信道,因此有;P2为具有归并性能的信道,因此有;P3为具有发散性能的信道,因此有;17.答：18.当信源的符号之间有依赖时,信源输出消息的不确定性减弱;而信源冗余度正是反映信源符号依赖关系的强弱,冗余度越大,依赖关系就越大;19.答：无失真信源编码,编码后尽可能等概率分布, 使每个码元平均信息量最大;从而使信道信息传输率R达到信道容量C, 实现信源与信道理想的统计匹配;20.某一码书C中, 任意两个码字之间汉明距离的最小值称为该码的最小码距Dmin.当已知某线性分组码的最小汉明距离为Dmin,那么这组码最多能检测出e =Dmin-1个码元错误,最多能纠正t =Dmin-1 /2个码元错误;21.答：信息的基本概念在于它的不确定性,任何已确定的事物都不含信息;接收者在收到信息之前,对它的内容是不知道的,所以信息是新知识、新内容;信息是能使认识主体对某一事物的未知性或不确定性减少的有用知识;信息可以产生,也可以消失,同时信息可以被携带、贮存及处理;信息是可以量度的,信息量有多少的差别;22.①将信源消息符号按其出现的概率大小依次排列px1≥px2≥…≥px n②取两个概率最小的符号分别配以0和1,并将这两个概率相加作为一个新符号的概率,与未分配码元的符号重新排队;③对重排后的两个概率最小符号重复步骤2的过程;④继续上述过程,直到最后两个符号配以0和1为止;⑤从最后一级开始,向前返回得到各个信源符号所对应的码元序列,即相应的码字;二、综合题每题10分,共60分1.黑白气象传真图的消息只有黑色和白色两种,求：1 黑色出现的概率为,白色出现的概率为;给出这个只有两个符号的信源X的数学模型;假设图上黑白消息出现前后没有关联,求熵；2 假设黑白消息出现前后有关联,其依赖关系为：,,,,求其熵；3分别求上述两种信源的冗余度,比较它们的大小并说明其物理意义;2.二元对称信道如图; ；1若,,求和； 2求该信道的信道容量和最佳输入分布;3.信源空间为,试分别构造二元和三元霍夫曼码,计算其平均码长和编码效率;4.设有一离散信道,其信道传递矩阵为,并设,试分别按最小错误概率准则与最大似然译码准则确定译码规则,并计算相应的平均错误概率;5.已知一8,5线性分组码的生成矩阵为;求：1输入为全00011和10100时该码的码字；2最小码距;6.设某一信号的信息传输率为s,在带宽为4kHz的高斯信道中传输,噪声功率谱NO=5×10－6mw/Hz;试求：1无差错传输需要的最小输入功率是多少2此时输入信号的最大连续熵是多少写出对应的输入概率密度函数的形式;7.二元平稳马氏链,已知P0/0=,P1/1=,求：1求该马氏信源的符号熵;2每三个符号合成一个来编二进制Huffman码,试建立新信源的模型,给出编码结果;3求每符号对应的平均码长和编码效率;8.设有一离散信道,其信道矩阵为,求：1最佳概率分布2当,时,求平均互信息 信道疑义度3输入为等概率分布时,试写出一译码规则,使平均译码错误率最小,并求此设线性分组码的生成矩阵为,求：1此n,k 码的n= k=,写出此n,k 码的所有码字;2求其对应的一致校验矩阵H;3确定最小码距,问此码能纠几位错列出其能纠错的所有错误图样和对应的伴随式;4若接收码字为000110,用伴随式法求译码结果;设一线性分组码具有一致监督矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=110101100110111000H 1求此分组码n=,k=共有多少码字2求此分组码的生成矩阵G; 3写出此分组码的所有码字;4若接收到码字101001,求出伴随式并给出翻译结果;10.二元对称信道的信道矩阵为,信道传输速度为1500二元符号/秒,设信源为等概率分布,信源消息序列共有13000个二元符号,问：1试计算能否在10秒内将信源消息序列无失真传送完2若信源概率分布为,求无失真传送以上信源消息序列至少需要多长时间11.已知7,4循环码的生成多项式,求：1求该码的编码效率2求其对应的一致校验多项式3写出该码的生成矩阵,校验矩阵;4若消息码式为,求其码字;12.证明：平均互信息量同信息熵之间满足IX;Y=HX+HY-HXY13. 居住在某地区的女孩中有25%是大学生,在女大学生中有75%是身高米以上的,而女孩中身高米以上的占总数的一半;假如我们得知“身高米以上的某女孩是大学生”的消息,问获得多少信息量14. 有两个二元随机变量X 和Y ,它们的联合概率为Y Xx 1=0 x 2=1 y 1=0 1/8 3/8 y 2=13/81/8定义另一随机变量Z = XY 一般乘积,试计算HZ=15. 求以下二个信道的信道容量：, ,16. 已知一个高斯信道,输入信噪比比率为3;频带为3kHz,求最大可能传 送的信息率;若信噪比提高到15,理论上传送同样的信息率所需的频带为 多少17. 设信源为⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡4/34/121x x P X X ,试求1信源的熵、信息含量效率以及冗余度；2求二次扩展信源的概率空间和熵;18. 什么是损失熵、噪声熵什么是无损信道和确定信道如输入输出为s r ⨯,则它们的分别信道容量为多少19. 信源编码的和信道编码的目的是什么20. 什么是香农容量公式为保证足够大的信道容量,可采用哪两种方法21. 什么是限失真信源编码二、综合题1.答：1信源模型为2由得则3119.02log )(121=-=X H γ 1分447.02log )(122=-=∞X H γ 1分12γγ>;说明：当信源的符号之间有依赖时,信源输出消息的不确定性减弱;而信源冗余度正是反映信源符号依赖关系的强弱,冗余度越大,依赖关系就越大;2分2.答：12,最佳输入概率分布为等概率分布;3.答：1二元码的码字依序为：10,11,010,011,1010,1011,1000,1001;平均码长,编码效率2三元码的码字依序为：1,00,02,20,21,22,010,011;平均码长,编码效率4.答：1最小似然译码准则下,有,2最大错误概率准则下,有,26.答：1无错传输时,有即则2在时,最大熵7.答：1由得极限概率：则符号熵为2新信源共8个序列,各序列的概率为信源模型为一种编码结果依信源模型中的序列次序为0,11,1001,1010,1011,10000,100010,10001138.答：1是准对称信道,因此其最佳输入概率分布为;2当,时,有则3此时可用最大似然译码准则,译码规则为且有答：1n=6,k=3,由C=mG可得所有码字为：000000,001011,010110,011101,100101,101110,110011,1110002此码是系统码,由G知,,则3由H可知,其任意2列线性无关,而有3列线性相关,故有,能纠一位错;错误图样E 伴随式100000 101010000 110001000 011000100 100000010 010000001 0014由知E＝010000,则解：1n=6,k=3,共有8个码字;3分2设码字()12345CCCCCCC=由TTHC0=得⎪⎩⎪⎨⎧=⊕⊕⊕=⊕⊕=⊕⊕1353412CCCCCCCCCC3分令监督位为()12CCC,则有⎪⎩⎪⎨⎧⊕=⊕=⊕=34451352CCCCCCCCC3分生成矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1111111112分3所有码字为000000,001101,010011,011110,100110,101011,110101,111000;4分4由TT HRS=得()101=S,2分该码字在第5位发生错误,101001纠正为101011,即译码为1010011分10.答：1信道容量为信源序列信息量为而10秒内信道能传递的信息量为故不能无失真地传送完;2此时信源序列信息量为信息传输率为则11.答：123,而412. 证明：()()()()()()()()()()Y X H X H y x p y x p x p y x p x p y x p y x p Y X I X X Y j i j i Y i j i XYi j i j i -=⎥⎦⎤⎢⎣⎡---==∑∑∑∑∑∑log log log; 2分同理 ()()()X Y H Y H Y X I-=; 1分则 ()()()Y X I Y H X Y H;-=因为 ()()()X Y H X H XY H+= 1分故()()()()Y X I Y H X H XY H;-+=即()()()()XY H Y H X H Y X I-+=; 1分13. 解：设A 表示“大学生”这一事件,B 表示“身高以上”这一事件,则 PA= pB= pB|A= 2分 故 pA|B=pAB/pB=pApB|A/pB== 2分 IA|B== 1分14. 解：Z = XY 的概率分布如下： 15. 答：P 1为一一对应确定信道,因此有; P2为具有归并性能的信道,因此有;16. 答:1 最大可能传送的信息率是Ct = w log 1+ Px/Pn = 3×1000 × log 1+ 3 = 6×1000比特/秒2 17. 解：12二次扩展信源的概率空间为：18. 答：将HX|Y 称为信道},,{|Y P X X Y 的疑义度或损失熵,损失熵为零的信道就是无损信道,信道容量为logr;将HY|X 称为信道},,{|Y P X X Y 的噪声熵,噪声熵为零的信道就是确定信道,信道容量为logs;19. 答：信源编码的作用：1符号变换：使信源的输出符号与信道的输入符号相匹配；2冗余度压缩：是编码之后的新信源概率均匀化,信息含量效率等于或接近于100%; 信道编码的作用：降低平均差错率; 20.答：香农信道容量公式：)1(log )(02BN P B P C SS +=,B 为白噪声的频带限制,0N 为常数,输入Xt 的平均功率受限于S P ;由此,为保证足够大的信道容量,可采用1用频带换信噪比；2用信噪比换频带;21. 答：有失真信源编码的中心任务：在允许的失真范围内把编码的信息率压缩到最小;。
信号与系统课后习题答案
信号与系统课后习题答案《低频电⼦线路》⼀、单选题（每题2分，共28分：双号做双号题，单号做单号题）1.若给PN结两端加正向电压时，空间电荷区将（）A变窄B基本不变C变宽D⽆法确定2.设⼆极管的端电压为 U，则⼆极管的电流与电压之间是（）A正⽐例关系B对数关系C指数关系D⽆关系3.稳压管的稳压区是其⼯作（）A正向导通B反向截⽌C反向击穿D反向导通4.当晶体管⼯作在饱和区时，发射结电压和集电结电压应为 ( ) A前者反偏，后者也反偏B前者反偏，后者正偏C前者正偏，后者反偏D前者正偏，后者也正偏5.在本征半导体中加⼊何种元素可形成N型半导体。
（）A五价B四价C三价D六价6.加⼊何种元素可形成P 型半导体。
（）A五价B四价C三价D六价7.当温度升⾼时，⼆极管的反向饱和电流将（）。
A 增⼤B 不变C 减⼩ D不受温度影响8. 稳压⼆极管两端的电压必须（）它的稳压值Uz 才有导通电流，否则处于截⽌状态。
A 等于 B ⼤于 C ⼩于 D与Uz ⽆关9. ⽤直流电压表测得放⼤电路中某三极管各极电位分别是2V 、6V 、2.7V ，则三个电极分别是（） A （B 、C 、E ） B （C 、B 、E ） C （E 、C 、B ） D（B 、C 、E ）10. 三极管的反向电流I CBO 是由（）形成的。
A 多数载流⼦的扩散运动 B 少数载流⼦的漂移运动 C 多数载流⼦的漂移运动D少数载流⼦的扩散运动11. 晶体三极管⼯作在饱和状态时，集电极电流Ci 将（）。
A 随B i 增加⽽增加 B 随B i 增加⽽减少C 与Bi ⽆关，只决定于eR 和CEuD不变12. 理想⼆极管的正向电阻为( )A A.零 B.⽆穷⼤ C.约⼏千欧 D.约⼏⼗欧13. 放⼤器的输⼊电阻⾼，表明其放⼤微弱信号能⼒（）。
A 强B 弱C ⼀般 D不⼀定14. 某两级放⼤电路，第⼀级电压放⼤倍数为5，第⼆级电压放⼤倍数为20，该放⼤电路的放⼤倍数为（）。
信号与系统习题集
信号与系统 习题1一、填空题1.离散信号()2()k f k k ε=，则该信号的单边Z 变换为 ① 。
2.信号()f t 的傅里叶变换为()F j ω，则(23)f t -的傅里叶变换为 ① 。
3.已知周期信号()cos(230)sin(4+60)f t t t =++，则其周期为 ① s ，基波频率为 ② rad/s 。
4、已知)(1t f 和)(2t f 的波形如下图所示，设)()()(21t f t f t f *=，则=-)1(f ① ，=)0(f ② 。
5、单边拉氏变换())4(22+=s s s F ，其反变换()=t f ① 。
6、一离散系统的传输算子为23)(22+++=E E EE E H ，则系统对应的差分方程为 ① ，单位脉冲响应为 ② 。
二、单项选择题1. 下列说法不正确的是______。
A. 每个物理系统的数学模型都不相同。
B. 同一物理系统在不同的条件下，可以得到不同形式的数学模型。
C. 不同的物理系统经过抽象和近似，有可能得到形式上完全相同的数学模型。
D. 对于较复杂的系统，同一系统模型可有多种不同的数学表现形式。
2. 周期信号f (t )的傅立叶级数中所含有的频率分量是______。
A. 余弦项的奇次谐波，无直流B. 正弦项的奇次谐波，无直流C. 余弦项的偶次谐波，直流D. 正弦项的偶次谐波，直流 3. 当周期矩形信号的脉冲宽度缩小一半时，以下说法正确的是_____。
A. 谱线间隔增加一倍B. 第一个过零点增加一倍C. 幅值不变D. 谱线变成连续的 4. 图3所示的变化过程，依据的是傅立叶变换的_____。
图3A. 时移性 B. 频移性 C. 尺度变换 D. 对称性 5. 对抽样信号进行恢复，需将信号通过_____。
A. 理想带通滤波器B. 理想电源滤波器C. 理想高通滤波器D. 理想低通滤波器 6. 连续周期信号的频谱有_____。
A. 连续性、周期性 B. 连续性、收敛性 C. 离散性、周期性 D. 离散性、收敛性7. 若对)(t f 进行理想取样，其奈奎斯特取样频率为s f ，对)231(-t f 进行取样，其奈奎斯特取样频率为_____。
信号与系统精品课程习题及答案
第一章习题1.函数式x(t)=(1-)[u(t+2)-u(t-2)]cos所表示信号的波形图如图（）(A) (B) (C) (D)2 ．函数式的值为（）（ A ）0 （ B ） 1 （ C ） 2 （ D ）3 ．已知x(3-2) 的波形如图1 所示，则x （t ）的波形应为图（）图1 （A）（B）（C）（D）4.已知信号x[n]波形如图2,信号的波形如图（）图2 （A）（B）(C) (D)5 ．卷积积分等于（）（A）（B）-2 （C）（D）-2 （E）-26 ．卷积和x[n] u[n-2] 等于（）（ A ）（ B ）（ C ）（ D ）（ E ）7 ．计算卷积的结果为（）（ A ）（ B ）（ C ）（ D ）8 ．已知信号x(t) 的波形如图3 所示，则信号的波形如图（）图3 （A）(B)(C) (D) 题九图9 ．已知信号x （t ）如图所示，其表达式为（）(A) (B)(C) (D)10 ．已知x（t)为原始信号，y(t)为变换后的信号,y(t) 的表达式为（）（ A ）（ B ）（ C ）（ D ）11 ．下列函数中（）是周期信号（ A ）（ B ）（ C ）（ D ）（ E ）12 ．函数的基波周期为（）。
（ A ）8 （ B ）12 （ C ）16 （ D ）2413 ．某系统输入—输出关系可表示为，则该系统是（）系统。
（ A ）线性（ B ）时不变（ C ）无记忆（ D ）因果（ E ）稳定14 ．某系统输入—输出关系可表示为，则系统为（）系统。
（ A ）线性（ B ）时不变（ C ）无记忆（ D ）因果（ E ）稳定15．某系统输入—输出关系可表示为,则系统为（）系统。
（ A ）线性（ B ）时不变（ C ）无记忆（ D ）因果（ E ）稳定16.某系统输入—输出关系可表示为，则系统为（）系统。
（ A ）线性（ B ）时不变（ C ）无记忆（ D ）因果（ E ）稳定17 ．某系统输入—输出关系可表示为，则系统为（）系统（ A ）线性（ B ）时不变（ C ）无记忆（ D ）因果（）稳定18 ．下列系统中，（）是可逆系统（A）y[n]=nx[n] （B）y[n]=x[n]x[n-1] （C）y(t)=x(t-4) （D）y(t)=cos[x(t)] （ E ）y[n]=19 ．如图系统的冲激响应为（）（ A ）（ B ）（ C ）（ D ）20 ．某系统的输入x （t ）与输出y （t ）之间有如下关系，则该系统为（）（A）线性时变系统（B）线性非时变系统（C）非线性时变系统（D）非线性非时变系统21 ．一个LTI 系统在零状态条件下激励与响应的波形如图，则对激励的响应的波形（）(A) (B) (C) (D)22. 线形非时变系统的自然（固有）响应就是系统的（）（ A ）零输入响应（ B ）原有的储能作用引起的响应（ C ）零状态响应（ D ）完全的响应中去掉受迫（强制）响应分量后剩余各项之和23 ．零输入响应是（）（ A ）全部自由响应（ B ）部分零状态响应（ C ）部分自由响应（ D ）全响应与强迫响应之差24 ．下列叙述或等式正确的是（）(A) (B)(C)若,则(D)x(t) 和h(t) 是奇函数，则是偶函数25.设是一离散信号,,,则下列说法( )是正确的(A) 若是周期的，则也是周期的(B) 若是周期的，则也是周期的(C) 若是周期的，则也是周期的(D) 若是周期的，则也是周期的26 ．有限长序列经过一个单位序列响应为的离散系统，则零状态响应为（）(A) (B)(C) (D)第二章习题1. 某LTI 连续时间系统具有一定的起始状态，已知激励为x （t ）时全响应，t 0 ，起始状态不变，激励为时，全响应y （t ）＝7e ＋2e ，t 0 ，则系统的零输入响应为（）（ A ）（ B ）（ C ）（ D ）2 ．微分方程的解是连续时间系统的（）(A) 零输入响应(B) 零状态响应(C) 自由响应(D) 瞬态响应（E）全响应3 ．单位阶跃响应是（）(A) 零状态响应(B) 瞬态响应(C) 稳态响应(D) 自由响应(E) 强迫响应4 ．已知系统如图所示，其中h (t) 为积分器，为单位延时器，h (t) 为倒相器，则总系统的冲激响应h (t) 为（）（ A ）（ B ）（ C ）（ D ）5 ．如图所示电路以为响应，其冲激响应h (t) 为（）(A) (B)(C) (D)6. 某LTI 系统如图所示，该系统的微分方程为（）(A ) (B)(C) (D)7 ．已知系统的微分方程, 则求系统单位冲激响应的边界条件h(0 ) 等于（）(A) －1 (B) 0 (C) 2 (D) ＋18 ．已知系统的微分方程则系统的单位冲激响应为（）(A) (B) (C) (D)9 ．已知描述系统的微分方程和初始状态0 值如下；y (0 ) ＝2 ，, , ，则初始条件0 值为（）(A) (B)(C) (D)10 ．已知描述系统的微分方程和初始状态0 值如y(t) ＋6 y (t) ＋8 y (t) ＝x (t) ＋2x (t) ，y (0 ) ＝1 ，y (0 ) ＝2 ，x (t) ＝（t ）则初始条件0 值为（）。
信号与系统考试题及答案
信号与系统考试题及答案第一题：问题描述：什么是信号与系统？答案：信号与系统是电子工程和通信工程中重要的基础学科。
信号是信息的传递载体，可以是电流、电压、声音、图像等形式。
系统是对信号进行处理、传输和控制的装置或网络。
信号与系统的研究内容包括信号的产生、变换、传输、处理和控制等。
第二题：问题描述：信号的分类有哪些？答案：信号可以根据多种特征进行分类。
按照时间域和频率域可以将信号分为连续时间信号和离散时间信号；按照信号的能量和功率可以分为能量信号和功率信号；按照信号的周期性可以分为周期信号和非周期信号；按照信号的波形可以分为正弦信号、方波信号、脉冲信号等。
第三题：问题描述：什么是线性时不变系统？答案：线性时不变系统是信号与系统领域中重要的概念。
线性表示系统满足叠加性原理，即输入信号的线性组合经过系统后，输出信号也是输入信号的线性组合。
时不变表示系统的性质不随时间变化而改变。
线性时不变系统具有许多重要的性质和特点，可以通过线性时不变系统对信号进行处理和分析。
第四题：问题描述：系统的冲激响应有什么作用？答案：系统的冲激响应是描述系统特性的重要参数。
当输入信号为单位冲激函数时，系统的输出即为系统的冲激响应。
通过分析冲激响应可以得到系统的频率响应、幅频特性、相频特性等，从而对系统的性能进行评估和优化。
冲激响应还可以用于系统的卷积运算和信号的滤波等应用。
第五题：问题描述：如何对信号进行采样？答案：信号采样是将连续时间信号转换为离散时间信号的过程。
常用的采样方法包括周期采样和非周期采样。
周期采样是将连续时间信号按照一定的时间间隔进行等间隔采样；非周期采样是在信号上选取一系列采样点，采样点之间的时间间隔可以不相等。
采样频率和采样定理是采样过程中需要考虑的重要因素。
第六题：问题描述：什么是离散傅里叶变换（DFT）？答案：离散傅里叶变换是对离散时间信号进行频域分析的重要工具。
通过计算离散傅里叶变换可以将离散时间信号转换为复数序列，该复数序列包含了信号的频率成分和相位信息。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A.时移性B.频移性C.尺度变换D.对称性
5.对抽样信号进行恢复，需将信号通过_____。
A.理想带通滤波器B.理想电源滤波器
C.理想高通滤波器D.理想低通滤波器
6.连续周期信号的频谱有_____。
A.连续性、周期性B.连续性、收敛性
C.离散性、周期性D.离散性、收敛性
7.若对 进行理想取样，其奈奎斯特取样频率为 ，对 进行取样，其奈奎斯特取样频率为_____。
A. B.
C. D.
5.离散序列 和 如下图所示，设 ，则 ______。
A. -1B.0C. 1D. 3
6.以下特点不属于周期信号频谱的特点。
A．离散性B 谐波性C. 周期性D. 收敛性
7.符号函数 的傅里叶变换等于。
A． B.1C. D.
8.已知某LTI连续系统当激励为 时，系统的零状态响应为 ，零输入响应为 ，全响应为 ，若系统的初始状态不变，激励为 ，系统的全响应 等于。
3
4
5
6
7
8
9
答案
B
C
D
A
C
D
B
C
A
三、画图题
1、（1） ，结果如图1所示
（4分） （4分）
图1 图2
（2）结果如图2所示
2、门函数的幅度谱
（5分）
相位谱
（5分）
3、
（6分）
四、计算题
1．解：因为 ，所以 的傅里叶变换 = （2分）
（2分）
对 进行傅里叶反变换得 （2分）
的傅里叶变换为 （2分）
（1分）
A. B. C. D.
9.拉氏变换在满足条件下，信号的傅立叶变换可以看成是拉氏变换的特例。
A.拉普拉斯变换的收敛域包含虚轴B.拉普拉斯变换的收敛域包含单位圆
C.拉普拉斯变换的收敛域不包含单位圆D.拉普拉斯变换的收敛域不包含虚轴
10.某二阶LTI系统的频率响应 ，则该系统的微分方程形式为______。
二、单项选择题
1.下列说法不正确的是______。
A.每个物理系统的数学模型都不相同。
B.同一物理系统在不同的条件下，可以得到不同形式的数学模型。
C.不同的物理系统经过抽象和近似，有可能得到形式上完全相同的数学模型。
D.对于较复杂的系统，同一系统模型可有多种不同的数学表现形式。
2.周期信号f(t)的傅立叶级数中所含有的频率分量是______。
2.（本小题10分）如图已知系统的微分方程为 ，求系统的单位冲激响应h(t)。
3.如图所示 系统， =12V， =1H， =1F， =3 ， =2 ， =1 。 <0时电路已达稳态， =0时开关S闭合。求 时电压 的零输入响应、零状态响应和完全响应。
习题二参考答案
一、单项选择题
题号
1
2
3
4
5
6
7
8
9
则 ①；
②。
6.化简式子 =①。
7.一系统如下图所示，两个子系统的冲激响应分别为 ， ，则整个系统的冲激响应 =①。
三、画图题
1.连续时间信号 的波形如右图所示，分别画出 和 的波形。
2.已知一LTI系统的系统函数 ，）已知H(s)有两个极点 ，一个零点 ，且系统的冲激响应的终值 。求H(s))的表达式，并判断系统的稳定性。
9.下列傅里叶变换性质中错误的是_____。
A.时间与频率标度
B.时移特性
C.频移特性
D.域相乘特性
三、画图题
1、 和 信号波形如下图所示，计算下列卷积，画出其波形。
(1) ；(2)
2、已知门函数 ，画出其对应的幅度谱和相位谱。
3、画出信号 的波形图。
四、计算题
1.理想低通滤波器具有特性 ，当输入信号分别为 和 时，求系统的响应 和 。
对 进行傅里叶反变换得 （1分）
2. 解：将差分方程转换成算子方程：
（2分）
其传输算子为 （2分）
系统的单位响应为 （2分）
因为 极点 ，所以零输入响应为
结合初始条件 ， ，得 ，所以零输入响应为
（3分）
零状态响应为
（3分）
系统的全响应 （3分）
3.（本小题10分）
解： ，【1分】等效算子电路模型：【3分】
2.描述某离散系统的差分方程为 ，若系统的输入 ，零输入响应初始条件 ， 。试求系统的零输入响应、零状态响应和完全响应。
3.如图4所示电路，已知 ， ， ，画出s域等效模型电路，并 。
习题1参考答案
一、填空题
1. ① 2. ① 3. ① ②24、①-2②-3
5、 ①
6、 ① ②
二、单项选择题
题号
1
2
A.余弦项的奇次谐波，无直流B.正弦项的奇次谐波，无直流
C.余弦项的偶次谐波，直流D.正弦项的偶次谐波，直流
3.当周期矩形信号的脉冲宽度缩小一半时，以下说确的是_____。
A.谱线间隔增加一倍B.第一个过零点增加一倍
C.幅值不变D.谱线变成连续的
4.图3所示的变化过程，依据的是傅立叶变换的_____。
A． B.
C. D.
二、填空题
1、 ①； ②。
2、一个连续因果LTI系统可由微分方程 来描述，则该系统的频率响应的代数式 =①。
3、信号 的傅里叶变换是①，其单边拉普拉斯变换是②。
4.连续系统的系统函数为 ，判断该系统的稳定性：①；一离散系统的系统函数 ，判断该系统的稳定性：②。
5.信号 的波形如图所示，设其傅里叶变换 ，
由： 【2分】
得：
【2分】
带入得全响应： 【2分】
习题二
一、单项选择题
1.单边拉氏变换 ，则其原函数 ______。
A． B. C. D.
2.卷积和 等于。
A. B. C. D.
3.已知信号 ，则该信号的奈奎斯特频率等于。
A. 50HzB. 100HzC. 150HzD. 200Hz
4.LTI连续时间系统输入为 ，冲激响应为 ，则输出为。
信号与系统习题1
一、填空题
1.离散信号 ，则该信号的单边 变换为①。
2.信号 的傅里叶变换为 ，则 的傅里叶变换为①。
3.已知周期信号 ，则其周期为①s，基波频率为②rad/s。
4、已知 和 的波形如下图所示，设 ，则 ①， ②。
5、单边拉氏变换 ，其反变换 ①。
6、一离散系统的传输算子为 ，则系统对应的差分方程为①，单位脉冲响应为②。
10
答案
B
D
B
C
C
C
D
A
A
D
二、填空题
1、 ①5② 2、 ①
A.3 B. C.3( －2)D.
8. 信号f(t)变成 的过程为_____。
A. 先将f(t)的图形向左移一个单位，再时间上展宽1/2倍
B. 先将f(t)的图形向左移一个单位，再时间上展宽1/2倍
C. 先将f(t)的图形向左移一个单位，再时间上展宽1/2倍
D. 先将f(t)的图形向左移一个单位，再时间上展宽1/2倍