春季高考二轮复习--《函数》讲义
届高考数学二轮复习专题一第2讲函数的图象与性质PPT课件

上 页
逻
和定义域.
辑 用 语
2.函数的表示方法:解析法、图象法和列表 法.当一个函数在定义域的不同区间上具有不
下 页
、
同的对应关系时,在不同的定义域区间上的函
函
数解析式也不同,就要用分段函数来表示.分
数
段函数是一个函数.
、
导
数
要点知识整合
热点突破探究 高考动态聚焦
专
题
一 3.函数单调性的判定方法
集 (1)定义法:取值,作差,变形,定号,作答.
、 函
答案:(1)A (2)[12,18]
数
、
导
数
要点知识整合
热点突破探究 高考动态聚焦
专
题
一
题型二 函数的图象
集
合
例2 (2010年高考山东卷)函数y=2x-x2的
与
常
图象大致是( )
用
上 页
逻
辑
下
用
页
语
、
函
数
、
导
数
要点知识整合
热点突破探究 高考动态聚焦
专 题 一
集
合
与 常 用 逻 辑 用
【解析】 由图象可知,y=2x与y=x2的交点 有3个,说明函数y=2x-x2的零点有3个,故 排除B、C选项,当x<x0时,有x2>2x成立,即 y<0,故排除D.
上 页
下 页
语
【答案】 A
、
函
数
、
导
数
要点知识整合
热点突破探究 高考动态聚焦
专
题
一 【题后总结】 作函数图象的基本思想方法大致
集 合
高考数学二轮复习系列课件19《二轮复习-函数》共38页文档

应试策略 1. 高考函数试题,主要有以下几种形式:
(1)函数内容本身的综合,如函数的概念、图象、性质等方面 的综合.
(2)函数与其他知识的综合,如方程、不等式、数列、平面向 量、解析几何等内容与函数的综合,主要体现函数思想的 运用;
(3)与实际问题的综合,主要体现在数学模型的构造和函数关 系的建立.
考题剖析
例1、(2019广东汕头二模)设集合A={x|x<-1或x>1},
B={x|log2x>0},则A∩B=( )
A.{x| x>1}
B.{x|x>0}
C.{x|x<-1}
D.{x|x<-1或x>1}
解:由集合B得x>1 , A∩B={x| x>1},故选(A) 。
[点评]本题主要考查对数函数图象的性质,是函 数与集合结合的试题,难度不大,属基础题。
考题剖析
例2、(2019广东惠州一模)“龟兔赛跑”讲述了这 样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲 起来,睡了一觉,当它醒来时,发现乌龟快到终点 了,于是急忙追赶,但为时已晚,乌龟还是先到达 了终点…用S1、S2分别表示乌龟和兔子所行的路程, t为时间,则下图与故事情节相吻合的是 ( )
考题剖析
考题剖析
例3、(2019广东惠州一模)设f x 1 x ,又记
f 1 x f x ,f k 1 x ff k x ,k 1 ,2 , L 1, x 则 f2008 x
()
A.11
x x
;
B.xx
1 1
; C.x;
D.
1 x
;
解:依题意,计算得:f1x1 1 x x,f2x1 1 ff1 11 x , f3x1 1 ff2 2x x 1 1,f4x1 1 ff3 3x
山东省春季高考数学复习要点——函数

山东省春季高考数学复习要点函数函数的概念一、函数基本概念1. 函数的概念.左义威、值域及概念中对''对应关系"的理解基本题目是判断某种对应关系是否是映射・ 2. 判断两个函数是否是同一函数例1 .下列四组函数,表示同一函数的是A ∙ f(x) = X 与g(x) = (G)-B - /心汀与g(χ)=z例2・下列函数与y = x 具有相同图象的函数是B ・ y = IOg U CI X (a>09a≠ 1)D . y = (√x )^ 3. 判断是否可作为函数的图彖例1 .下图中,可作为函数的y = ∕(x)图象的是例2・下图中,可作为函数的y = /(x)图象的是4. 已知/(x)表达式,求f(ax+b)的表达式;已知f(ax+b)的表达式求门兀)表达式•C. /(X )=∣X ∣与g(χ)n X Λ∈(0,+oc) -X X∈ (→C , 0)D. /(X) = X 与g(x) =疔X c ・ y = -X例 1 .①已知.f(x) = 3x+5 ,求/(2),/(x+l)√(3x+5)√(/(X -I));② 已知")={;;:7 :鳥,求/⑶/(-3),/(/(-3));③ 已知/(x) = 2x+3,g(x) = x-7 ,求f(g(x)),g(f(x))∙例2 .①已知.f(3x) = 6x+7 ,求/(x+l);② 已知/(3x-5) = √+2x -3 ,求/(x), /(2x+l).5. 已知/(g(R)的左义域,求函数g(∕(x))的泄义域.例1 •①已知函数/(Λ+1)的定义域为[-3,4],则函数/(2x)的定义域是 __________________②已知函数f(2x)的定义域是[1,2],则函数/(2Λ)的走义域 ________________ • 6. 求函数的左义域问题.例—Z(X)=λ∕∣2Λ∣-ι,*)=”g(x+i)' /(x)=(x+2)°+緒 例2 ∙ /(x) = √2√-5x-3 , /(x) = √3t -27 ,二、函数表示方法1. 列分段函数的表达式例1 .在国内投寄外埠平信,每封信不超过20g 付邮资80分,超过20g 不超过40g 付邮资160分, 超过40g 不超过60g 付邮资240分,依此类推,每封Xg(OVXG 00)的信应付多少分邮资?(单位: 分)2. 分段函数的计算例2 .已知/(刃彳:二:背,求/(x)>0的解集.例 3. B0]/(X) = IJ (X _I)打红,求门6) •3・分段函数的作图例:例1中函数如何作图?/(x) = λ∕log 05(4x-3)/(x) = 4SinX函数的基本性质1. 函数单调性的槪念;掌握求函数单调性的基本方法及图象特点:例1 •若函数y(χ)是走义在(-ι,ι)上的增函数,且/(1-o)v∕(∕-ι),求满足条件的"的取值 范围・2. 掌握函数奇偶性的概念:掌握判断函数奇偶性的两个基本条件.掌握奇偶函数图象的特点例:判断下列函数的奇偶性基本方法分为定义法和图象法・定义法有两个步骤:第1步:求函数定义域,判断走义域是否关于原点对称;第2步:求/(-%),判断具是否等于・f (兀) 或等于-心).图象法需根据函数图象是否关于原点对称或关于y 轴对称来做判断■例1 .判断下列函数的奇偶性:⑤'/(X)= -~~;———>0Λ6√ ≠ 1) , ® f (X)= >j ∖-x 2 +∖∣x 2 -1'⑦ f (X) = Vl-X + y∣X -∖ CI — 1例2 •设f(x) = a (α≠0),那么子(兀)是A ・奇函数C ・既是奇函数又是偶函数D ・既不是奇函数z 又不是偶函数例3 •设/ (O) = a (a ≠0) I S½∕ (x)可能是 _______ 函数.(填奇偶性)3. 掌握周期函数的概念.例1 .判4. 基本性质综合应用例1 •已知于(兀)是奇函数,且x≥0时f(x) = 2x-F ,则当兀<0时I f(X)的解析式为 ____________① y = Ig(JX2 +] _;V),② y = Ig2 ③ /(x) = SinIXI> ④/(x) = l + -— B •偶函数例2 .已知函数f(X)在R上为奇函数,且在(O,RO)上为减函数,求/(x)在(Y>,0)上的单调性•例3 •已知函数/(兀)在区间(YO,+S)上是奇函数,且在区间(-Oo,0)上y(x) = -F ,试判断函数/ (工)在区间(O, + S)上的单调性并证明你的结论•例4 .已知奇函数门刃,当x>0时,/(x) = x-l ,求f(x)>O的解集.例5 .已知奇函数/(A)(XeR且Eo) , /(3) = 0 ,在(0,乜)上函数为增函数,求①不等式f(x)< O 的解集;②不等式Λ√(ΛJ< O的解集•一元二次函数一、一元二次函数的基本性质泄义域、值域、对称轴、顶点坐标、最值、单调区间、开口方向、奇偶性.1.图象例1 .已知二次函数y = x2 + px + C l顶点在第二象限,则P, g的符号为___________例2 •在同一坐标系中,y = UX -丄与y = UX Z的图象可能是U2.奇偶性例1・已知二次函数)=(加-1)疋+皿_3为偶函数,则该函数的递减区间为___________ ■[0t + ∞)已知函数>∙= (∕π-l)x2+(∕7Γ-iμ-3为偶函数,则加的值为___ ∙(ZH = ±1)二、一元二次函数的对称问题1. /(Λ-x) = ∕(Λ+x)例1 .已知二次函数f(x) = i a2+bx + c若/(-2) = /(4) ,pl®数图象的对称轴为_____________ .已知二次函数f(x) = ax2+hx + c I若/(A)=∕(2-X),则函数图象的对称轴为例2 .已知二次函数>∙=∕(Λ)满足/(4 + x) = ∕(4-x),且/(Λ)= 0的两根为X l f f则Λ1+Λ2= _____ ∙(8)例3 •已知二次函数/(A) = A-2÷,5在(TC,-1]上为减函数,在[-l, + oC)上为增函数,则川的值为________ • (Zn = 2)已知二次函数f(x) = x2+mx-5在(Y),-1]上为减函数f则/H的取值范围是________ . (∕n< 2)2.不求值比较大小例].已知函数f(x) = x2-2x-3 ,不求值比较大小门-2)与/(4),门_2)与门-3) f 川)与/(2)√(4)3.抛物线与X轴交点的问题①韦达定理卜2 -^l I = y∕(x2+ -γi )2 - ^X l X2②利用对称性和两点间距离得两点坐标,再设两点式•=d (尤2>禹)③解方程组{ b _ A-I + X2•~2a 2~例1 .已知函数y = x2+2(∕H +3)X+2∕77-4,该函数图象与X轴有两个不同交点,交点的横坐标分别为α , 0.(1)求P-0|的最小值;(2 )当川为何值时(α-l)2 +(0 — 1)'有最小值,并求其最小值•三、二次函数求最值的问题二次函数求最值可利用配方的方法。
山东春季高考知识点讲解--函数奇偶性

山东春季高考模拟试题---- 根据历年春季高考考试大纲出题 山东春季高考知识点讲解--函数奇偶性(一)主要知识:1.函数的奇偶性的定义;2.奇偶函数的性质:(1)定义域关于原点对称;(2)偶函数的图象关于y 轴对称,奇函数的图象关于原点对称;3.()f x 为偶函数()(||)f x f x ⇔=.4.若奇函数()f x 的定义域包含0,则(0)0f =.(二)主要方法:1.判断函数的奇偶性,首先要研究函数的定义域,有时还要对函数式化简整理,但必须注意使定义域不受影响;2.牢记奇偶函数的图象特征,有助于判断函数的奇偶性;3.判断函数的奇偶性有时可以用定义的等价形式:()()0f x f x ±-=,()1()f x f x =±-. 4.设()f x ,()g x 的定义域分别是12,D D ,那么在它们的公共定义域上:奇+奇=奇,奇⨯奇=偶,偶+偶=偶,偶⨯偶=偶,奇⨯偶=奇.5.注意数形结合思想的应用.(三)例题分析:例1.判断下列各函数的奇偶性:山东春季高考模拟试题---- 根据历年春季高考考试大纲出题 (1)()(f x x =-2)22lg(1)()|2|2x f x x -=--; (3)22(0)()(0)x x x f x x xx ⎧+<⎪=⎨-+>⎪⎩. 解:(1)由101x x+≥-,得定义域为[1,1)-,关于原点不对称,∴()f x 为非奇非偶函数. (2)由2210|2|20x x ⎧->⎪⎨--≠⎪⎩得定义域为(1,0)(0,1)-, ∴22lg(1)()(2)2x f x x -=---22lg(1)x x-=-, ∵2222lg[1()]lg(1)()()x x f x x x ----=-=--()f x = ∴()f x 为偶函数 (3)当0x <时,0x ->,则22()()()()f x x x x x f x -=---=-+=-, 当0x >时,0x -<,则22()()()()f x x x x x f x -=--=--+=-,综上所述,对任意的(,)x ∈-∞+∞,都有()()f x f x -=-,∴()f x 为奇函数.例2.已知函数()f x 对一切,x y R ∈,都有()()()f x y f x f y +=+,(1)求证:()f x 是奇函数;(2)若(3)f a -=,用a 表示(12)f . 解:(1)显然()f x 的定义域是R ,它关于原点对称.在()()()f x y f x f y +=+中,令y x =-,得(0)()()f f x f x =+-,令0x y ==,得(0)(0)(0)f f f =+, ∴(0)0f =,∴()()0f x f x +-=,即()()f x f x -=-, ∴()f x 是奇函数.(2)由(3)f a -=,()()()f x y f x f y +=+及()f x 是奇函数,山东春季高考模拟试题---- 根据历年春季高考考试大纲出题得(12)2(6)4(3)4(3)4f f f f a ===--=-.例3.(1)已知()f x 是R 上的奇函数,且当(0,)x ∈+∞时,()(1f x x =,则()f x的解析式为(10()(10x x f x x x ⎧≥⎪=⎨<⎪⎩. (2) 已知()f x 是偶函数,x R ∈,当0x >时,()f x 为增函数,若120,0x x <>,且12||||x x <,则 ( B )A .12()()f x f x ->-B .12()()f x f x -<-C .12()()f x f x ->-D . 12()()f x f x -<-例4.设a 为实数,函数2()||1f x x x a =+-+,x R ∈.(1)讨论()f x 的奇偶性; (2)求 ()f x 的最小值.解:(1)当0a =时,2()()||1()f x x x f x -=-+-+=,此时()f x 为偶函数; 当0a ≠时,2()1f a a =+,2()2||1f a a a -=++,∴()(),()(),f a f a f a f a -≠-≠-此时函数()f x 既不是奇函数也不是偶函数.(2)①当x a ≤时,函数2213()1()24f x x x a x a =-++=-++, 若12a ≤,则函数()f x 在(,]a -∞上单调递减,∴函数()f x 在(,]a -∞上的最小值为2()1f a a =+; 若12a >,函数()f x 在(,]a -∞上的最小值为13()24f a =+,且1()()2f f a ≤. ②当x a ≥时,函数2213()1()24f x x x a x a =+-+=+-+,山东春季高考模拟试题---- 根据历年春季高考考试大纲出题 若12a ≤-,则函数()f x 在[,)a +∞上的最小值为13()24f a -=-,且1()()2f f a -≤; 若12a >-,则函数()f x 在[,)a +∞上单调递增,∴函数()f x 在[,)a +∞上的最小值2()1f a a =+. 综上,当12a ≤-时,函数()f x 的最小值是34a -,当1122a -<≤时,函数()f x 的最小值是21a +, 当12a >,函数()f x 的最小值是34a +.例5.已知()f x 是定义在实数集R 上的函数,满足(2)()f x f x +=-,且[0,2]x ∈时,2()2f x x x =-, (1)求[2,0]x ∈-时,()f x 的表达式;(2)证明()f x 是R 上的奇函数.。
高考数学第二轮专题复习函数讲义教案
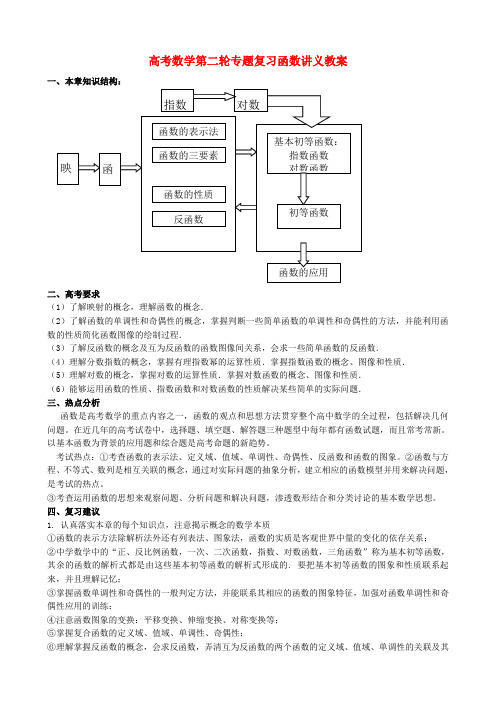
高考数学第二轮专题复习函数讲义教案一、本章知识结构:二、高考要求(1)了解映射的概念,理解函数的概念.(2)了解函数的单调性和奇偶性的概念,掌握判断一些简单函数的单调性和奇偶性的方法,并能利用函数的性质简化函数图像的绘制过程.(3)了解反函数的概念及互为反函数的函数图像间关系,会求一些简单函数的反函数.(4)理解分数指数的概念,掌握有理指数幂的运算性质.掌握指数函数的概念、图像和性质.(5)理解对数的概念,掌握对数的运算性质.掌握对数函数的概念、图像和性质.(6)能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题.三、热点分析函数是高考数学的重点内容之一,函数的观点和思想方法贯穿整个高中数学的全过程,包括解决几何问题。
在近几年的高考试卷中,选择题、填空题、解答题三种题型中每年都有函数试题,而且常考常新。
以基本函数为背景的应用题和综合题是高考命题的新趋势。
考试热点:①考查函数的表示法、定义域、值域、单调性、奇偶性、反函数和函数的图象。
②函数与方程、不等式、数列是相互关联的概念,通过对实际问题的抽象分析,建立相应的函数模型并用来解决问题,是考试的热点。
③考查运用函数的思想来观察问题、分析问题和解决问题,渗透数形结合和分类讨论的基本数学思想。
四、复习建议1. 认真落实本章的每个知识点,注意揭示概念的数学本质①函数的表示方法除解析法外还有列表法、图象法,函数的实质是客观世界中量的变化的依存关系;②中学数学中的“正、反比例函数,一次、二次函数,指数、对数函数,三角函数”称为基本初等函数,其余的函数的解析式都是由这些基本初等函数的解析式形成的. 要把基本初等函数的图象和性质联系起来,并且理解记忆;③掌握函数单调性和奇偶性的一般判定方法,并能联系其相应的函数的图象特征,加强对函数单调性和奇偶性应用的训练;④注意函数图象的变换:平移变换、伸缩变换、对称变换等;⑤掌握复合函数的定义域、值域、单调性、奇偶性;⑥理解掌握反函数的概念,会求反函数,弄清互为反函数的两个函数的定义域、值域、单调性的关联及其图像间的对称关系。
春季高考二轮复习--《三角函数》讲义

第六章《三角函数》例1、(1)设α为第二象限角,其终边上一点为P (m ,5),且cos α=24m ,则sin α的值为________. (2)已知角α的终边在直线y =-3x 上,求10sin α+3cos α的值. 例2、(1)已知cos(π+x )=35,x ∈(π,2π),则tan x =________. (2)已知tan θ=2,则sin 2θ+sin θcos θ-2cos 2θ等于( )A. -43 B. 54 C. -34 D. 45变式训练1、 若α是第二象限角,且tan α=-2,则cos α=( )A. -15 B. -25 C. -55 D. -2552、已知sin α+3cos α3cos α-sin α=5,则sin 2α-sin αcos α的值是( )A. 25 B. -25C. -2D. 2 例3、设tan(π+α)=2,则sin α-π+cos π-αsin π+α-cos π+α等于( )A. 3 B. 13C. 1D. -1 例4、函数f (x )=3sin ⎝ ⎛⎭⎪⎫2x -π6在区间⎣⎢⎡⎦⎥⎤0,π2上的值域为( ) A. ⎣⎢⎡⎦⎥⎤-32,32 B. ⎣⎢⎡⎦⎥⎤-32,3 C. ⎣⎢⎡⎦⎥⎤-332,332 D. ⎣⎢⎡⎦⎥⎤-332,3 例5、(1)求函数y =cos(-2x +π3)的单调递减区间;(2)求函数y =sin(π3-2x )的单调递减区间; 变式训练3、下列区间是函数y =2|cos x |的单调递增区间的是( )A. (0,π)B. ⎝ ⎛⎭⎪⎫-π2,0C. ⎝ ⎛⎭⎪⎫π,32πD. ⎝⎛⎭⎪⎫-π,-π2 4、函数y =2sin(π6-2x )(x ∈[0,π])的增区间是( )A. [0,π3] B. [π12,7π12] C. [π3,5π6]D. [5π6,π] 例6、(1)、将函数y =sin x 的图象向左平移π2个单位,得到函数y =f (x )的图象,则下列说法正确的是( ) A. y =f (x )是奇函数 B. y =f (x )的周期为πC. y =f (x )的图象关于直线x =π2对称D. y =f (x )的图象关于点⎝ ⎛⎭⎪⎫-π2,0对称 (2)、将函数f (x )=sin ωx (其中ω>0)的图象向右平移π4个单位长度,所得图象经过点⎝ ⎛⎭⎪⎫3π4,0,则ω的最小值是( )A. 13 B. 1 C. 53D. 2 变式训练5、函数f (x )=cos(2x +3π2)(x ∈R ),下面结论不正确的是( )A. 函数f (x )的最小正周期为π B. 函数f (x )的一个对称中心是(π2,0) C. 函数f (x )的图象关于直线x =π4对称 D. 函数f (x )是偶函数 6、将函数y =sin ⎝ ⎛⎭⎪⎫2x +π3的图象经过怎样的平移后所得图象关于点⎝ ⎛⎭⎪⎫-π12,0中心对称( ) A. 向右平移π12个单位 B. 向右平移π6个单位 C. 向左平移π12个单位 D. 向左平移π6个单位例7、为了得到函数y =sin(2x +1)的图象,只需把函数y =sin2x 的图象上所有的点( )A. 向左平行移动12个单位B. 向右平行移动12个单位C. 向左平行移动1个单位 D. 向右平行移动1个单位 变式训练7、为了得到函数y =sin(2x -π3)的图象,只需把函数y =sin(2x +π6)的图象( ) A. 向左平移π4个单位长度 B. 向右平移π4个单位长度 C. 向左平移π2个单位长度 D. 向右平移π2个单位长度 例8、(1)计算:3cos10°-1sin170°=( )A. 4 B. 2 C. -2 D. -4(2)计算:3-tan15°1+3tan15°=________. 变式训练9、 (1)求sin7°+cos15°sin8°cos7°-sin15°sin8°的值;(2)化简:sin50°(1+3tan10°); 例9、在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c .若3a =2b ,则2sin 2B -sin 2A sin 2A 的值为( )A -19 B 13 C1D 72变式训练10、在△ABC 中,角A ,B ,C 所对应的边分别为a ,b ,c .已知b cos C +c cos B =2b ,则a b=________.例10、(1)设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若b cos C +c cos B =a sin A ,则△ABC 的形状为( )A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不确定 (2)在△ABC 中,已知a ,b ,c 分别是角A ,B ,C 的对边,若a b =cos B cos A,试确定△ABC 的形状. 变式训练11、在△ABC 中,a ,b ,c 分别为角A ,B ,C 所对的边,若a =2b cos C ,则此三角形一定是( )A. 等腰直角三角形B. 直角三角形C. 等腰三角形D. 等腰三角形或直角三角形12、在△ABC 中,cos 2B 2=a +c 2c(a ,b ,c 分别为角A ,B ,C 的对边),则△ABC 的形状为( ) A .等边三角形 B .直角三角形 C .等腰三角形或直角三角形 D .等腰直角三角形例11、在△ABC 中,A =60°,AC =4,BC =23,则△ABC 的面积等于________.变式训练13、在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c .若c 2=(a -b )2+6,C =π3,则△ABC 的面积是。
山东春考数学二轮复习专题3 函数(一)函数的概念和性质
最高点在对称轴上,所以当 = 时,函数最大值为
03
二 次 函 数
例3
已知二次函数 图像的顶点在直线 = 2 − 1 上,
且 1 = −1, 3 = −1 ,求二次函数的解析式。
1+3
∵ f 1 = −1, f 3 = −1, ∴ 对称轴为 =
a 2
=_ __
+ + = 0(a≠0) 的根,则 1 + 2 =
−
1 2
03
二 次 函 数
例1二次函数y= − 3 − 1 的对称轴是( D)
A. = −1
B. = 1 C. = −2
. 二次函数 =
程为 = −
+ + ≠
函数的概念及其表示
变式训练1 下面函数中,与函数 = − 1是同一个函数的是
A. g
−1
=
C. g =
3
−1
B.g =
3
−1
D.g = 10
( C
2
−1
如果两个函数的定义域和对应法则都相同,则他们表示同一函
数,对应法则相同是指对应法则等价,并非形式完全相同!
( A )
A. -3
B.-1
C. 1
D.3
奇函数:对于函数 定义域内的任意一个, 都有 − =-
02
函
数
的
性
质
变式训练3 已知函数 为偶函数,当 > 0时, = 2 − ,则当 <
0时, 的解析式是( B )
高三二轮复习专题讲座函数与导数ppt课件
3
一、课标、教学要求、考试说明的解读
考试要求: 对知识的考查要求依次分为了解、理解、掌握三个层次 (在下表中分别用A、B、C表示). 了解:要求对所列知识的含义有最基本的认识,并能解 决相关的简单问题. 理解:要求对所列知识有较深刻的认识,并能解决有一 定综合性的问题. 掌握:要求系统地掌握知识的内在联系,并能解决综合 性较强的或较为困难的问题.
4
内
容
要求
函数的有关概念
A
B
C
√
函数的基本性质
√
函
指数与对数
√
指数函数的图象与性质
√
对数函数的图象与性质
√
数
幂函数
√
函数与方程
√
函数模型及其应用
√
导数的概念
√
导
导数的几何意义
√
导数的运算
√
数
利用导数研究函数的单调
√
性与极值
导数在实际问题中的应用
√
5
二、近几年高考试题分析
高考函数与导数试题的命题特点
分析:此 题 的 关 键 是 集正 合 M的 确含 理,所 义 解谓 在 定 义 域 内 x0,使 存得 f在 (x01)f(x0)f(1) 成 立 ,就 是 方 f(x程 1)f(x)f(1)有 实 数 . 解
10
此 题 在 最 初 命,第 题(4时 )个 函 数 不f (是 x) cosx,而 是
7
三、目前学生存在的问题、成因
通过这次期末调研考试,以及一轮复习中反映出的 情况来看,在函数与导数部分主要存在着以下几个 方面的问题: 1.基础知识掌握不牢,该过关的地方还没过关, 主要是由于基本概念不清、运算能力不强; 2.灵活运用知识解决问题的能力不够,主要是由 于对于所学的知识理解不透,不能举一反三; 3.转化与化归的能力较弱,主要是平时解题过程 中不注意对方法的归纳与小结.
2023年职高数学二轮复习——函数
第三章 函 数本章知识点汇总一、求函数定义域类型:①分母≠0 ;② 偶次方根下0≥ ;③ 00≠x x 中: ④ 对数中真数大于0,即0log >x x a 中: ,对数中底数10≠>a a 且。
二、函数单调性(增减性):在单调区间上 ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧<--=∆∆⎪⎩⎪⎨⎧>--=∆∆降图像:从左向右逐渐下定义:减函数:升图像:从左向右逐渐上定义:增函数:0012121212x x y y x y x x y y x y三、函数奇偶性(对称性):*奇偶函数的前提条件: 函数的定义域关于原点对称。
*关于原点对称的定义域常见形式:[],),[],();,()--(;-),(,等,),(;;+∞--∞+∞∞∞+∞--a a a a a a a a①奇函数:)()(x f x f -=-,图像关于原点对称。
②偶函数:)()(x f x f =-,图像关于y 轴对称。
四、函数图像与性质的总结: ①正比例函数:)0(≠=k kx y ,图像过(0,0)点,奇函数。
②一次函数:)0≠+=k b kx y (,(1) 图像过(0,b )点,b 叫直线在y 轴上的截距。
(2) 当b=0时,函数为奇函数。
(3) 当b ≠0时,函数为非奇非偶函数。
(4) K>0时函数为增函数,k<0时为减函数。
•b•bb ••bxyOxyOK > 0,增函数K < 0,减函数xyOK>0,b>0 K>0,b<0K<0,b>0 K<0,b<0③反比例函数:)0(≠=k xky ,奇函数,图像分别在()()上是单调函数。
,或∞+∞-00,0>k 0<k()上是单调递减函数,或∞+∞-00,()()上是单调递增函数,或∞+∞-00,④二次函数:1、一般式:)0(2≠++=a c bx ax y ,时,开口向下。
高三数学二轮复习讲义专题一函数性质与图象
专题一 集合,常用逻辑用语,不等式,函数与导数(讲案)第二讲 函数的基本性质与图象【最新考纲透析】预计时间:3.13---3.18函数与基本初等函数的主要考点是:函数的表示方法、分段函数、函数的定义域和值域、函数的单调性、函数的奇偶性、指数函数与对数函数的图象与性质、幂函数的图象与性质。
本部分一般以选择题或填空题的形式出现,考查的重点是函数的性质和图象的应用,重在检测对该部分的基础知识和基本方法的掌握程度。
复习该部分以基础知识为主,注意培养函数性质和函数图象分析问题和解决问题的能力。
【考点精析】题型一 函数的概念与表示例1 (1)函数21sin()(10)()0x x x f x e x π-⎧-<<=⎨≥⎩,若(1)()2f f a +=,则的所有可能值为( ) A .1,2- B.2- C .1,2- D .1,2(2)根据统计,一名工作组装第x 件某产品所用的时间(单位:分钟)为 ⎪⎪⎩⎪⎪⎨⎧≥<=Ax A c A x x c x f ,,,)((A ,C 为常数)。
已知工人组装第4件产品用时30分钟,组装第A 件产品用时15分钟,那么C 和A 的值分别是A .75,25B .75,16C .60,25D .60,16(3)已知集合A 到集合{}0,1,2,3B =的映射1:1f x x →-,则集合A 中的元素最多有 个。
解析:1:1f x x →-是集合A 到集合B 的映射,∴A 中的每一个元素在集合B 中都应该有象。
令101x =-,该方程无解,所以0无原象,分别令11,2,3,1x =-解得:342,,23x x x =±=±=±。
故集合A 中的元素最多为6个。
(4)如图,已知底角为450的等腰梯形ABCD ,底边BC 长为7cm,腰长为cm ,当一条垂直于底边BC (垂足为F )的直线l 从左至右移动(与梯形ABCD 有公共点)时,直线l 把梯形分成两部分,令BF x =,试写出左边部分的面积y 与x 的函数解析式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章《函数》
例1、函数f (x )=1log 2x -1的定义域为( ) A. (0,2) B. (0,2] C. (2,+∞) D. [2,+∞) 变式训练:1、函数f (x )=1-2x +1
x +3的定义域为( )
A. (-3,0]
B. (-3,1]
C. (-∞,-3)∪(-3,0]
D. (-∞,-3)∪(-3,1] 例2、(1)已知f (x +1x )=x 2+1x 2,求f (x )的解析式; (2)已知f 2(1)x
+=lg x ,求f (x )的解析式; (3)已知f (x )是一次函数,且满足3f (x +1)-2f (x -1)=2x +17,求f (x )的解析式;
变式训练:2、已知函数f 1()x x -=x 2+1x
2,则f (3)=( )A. 8 B. 9 C. 11 D. 10 3、已知f (x )是一次函数,且f [f (x )]=4x +3,求f (x ).
4、已知f (x +1)=x +2x ,求f (x )的解析式.
例3、已知函数f (x )=⎩⎪⎨⎪⎧ a ·2x ,x ≥0,2-x , x <0(a ∈R ),若f [f (-1)]=1,则a =( )A. 14 B. 12
C. 1
D. 2 变式训练:5、设函数f (x )=⎩⎨⎧ x ,x ≥0,-x ,x <0,若f (a )+f (-1)=2,则a =( )
A. -3
B. ±3
C. -1
D. ±1
例4、下列函数中,在区间(0,+∞)上为增函数的是( )
A. y =x +1
B. y =(x -1)2
C. y =2-x
D. y =log 0.5(x +1)
变式训练:6、给定函数①y =12y x =,②12log (1)y x =+,③y =|x -1|,④y =2
x +1.其中在区间(0,1)上单调递减
的函数序号是( ) A. ①② B. ②③ C. ③④ D. ①④
例5、求下列函数的单调区间.f (x )=-x 2
+2|x |+3; (2)212()log (23)f x x x =--+;(3)21()3x x y -=;
变式训练:7、求出下列函数的单调区间.(1)f (x )=|x 2-4x +3|; (2)f (x )=log 2(x 2-1);
例6、(1)若函数f (x )=4x 2-kx -8在区间[5,8]上是单调函数,则k 的取值范围是( )
A. (-∞,40]
B. [40,64]
C. (-∞,40]∪[64,+∞)
D. [64,+∞)
(2)已知函数f (x )=e |x -a |(a 为常数).若f (x )在区间[1,+∞)上是增函数,则a 的取值范围是________.
变式训练:8、如果函数f (x )=ax 2+2x -3在区间(-∞,4)上是单调递增的,则实数a 的取值范围是( )
A. a >-14
B. a ≥-14
C. -14≤a <0
D. -14
≤a ≤0 9、若f (x )=ax +1x +2
在区间(-2,+∞)上是增函数,则a 的取值范围是( ) A. (-2,+∞) B.1
(,)2+∞ C. (-∞,-2) D. 1(,)2-∞
例7、(1)判断下列函数的奇偶性.①f (x )=9-x 2+x 2-9;②f (x )=(x +1) 1-x 1+x ③f (x )=4-x 2
|x +3|-3; (2)、下列函数为奇函数的是( )A. y =2x -12
x B. y =x 3sin x C. y =2cos x +1 D. y =x 2+2x 变式训练10、设函数f (x ),g (x )的定义域都为R ,且f (x )是奇函数,g (x )是偶函数,则下列结论中正确的是( )
A. f (x )g (x )是偶函数
B. |f (x )|g (x )是奇函数
C. f (x )|g (x )|是奇函数
D. |f (x )g (x )|是奇函数
11、判断下列函数的奇偶性.
(1)f (x )=x 2-|x |+1 x ∈[-1,4]; (2)f (x )=ln 2-x 2+x ; (3)f (x )=1a x -1+12
(a >0,且a ≠1); 巩固练习:
1、设函数f (x )=2x +3,g (x +2)=f (x ),则g (x )的表达式是( )
A. g (x )=2x +1
B. g (x )=2x -1
C. g (x )=2x -3
D. g (x )=2x +7
2、函数f (x )=ln(x 2
-x )的定义域为( )
A. (0,1)
B. [0,1]
C. (-∞,0)∪(1,+∞)
D. (-∞,0]∪[1,+∞) 3、设函数f (x )=⎩⎪⎨⎪⎧ x 2+1,x ≤1,2x
,x >1,则f (f (3))等于( )A. 15 B. 3 C. 23 D. 139 4、函数y =x 2-6x +10在区间(2,4)上是( ) A. 递减函数 B. 递增函数 C. 先递减再递增 D. 先递增再递减 5、下列四个函数中,在(0,+∞)上为增函数的是( ) A. f (x )=3-x B. f (x )=x 2-3x C. f (x )=-1x +1
D. f (x )=-|x | 6、已知函数f (x )=1x
在区间[1,2]上的最大值为A ,最小值为B ,则A -B =( ) A. 12 B. -12
C. 1
D. -1 7、下列函数为偶函数的是( )
A. f (x )=x -1
B. f (x )=x 2+x
C. f (x )=2x -2-x
D. f (x )=2x +2-x
8、已知函数f (x )为奇函数,且当x >0时,f (x )=x 2+1x
,则f (-1)=( ) A. -2 B. 0 C. 1 D. 2
9、已知f (x )=ax 2+bx 是定义在[a -1,2a ]上的偶函数,那么a +b 的值是( )
A .-13 B. 13 C. 12 D. -12。
