28.2新人教解直角三角形(第二课时)
人教版数学九年级(下册)28.2解直角三角形及其应用(教案)

最后,课堂总结环节,我发现部分学生对今天所学知识的掌握程度并不理想。这可能是因为在课堂讲解过程中,我没有充分关注学生的反馈,导致他们对知识点的理解不够深刻。为了改善这一状况,我会在今后的教学中,更加关注学生的反应,及时调整教学方法和节奏,确保每位学生都能跟上课程进度。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“解直角三角形在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了直角三角形的基本概念、勾股定理以及正弦、余弦、正切函数的应用。同时,我们也通过实践活动和小组讨论加深了对解直角三角形的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
4.增强学生的数学应用意识,使其认识到数学在生活中的广泛应用,激发学习兴趣,提高数学素养。
三、教学难点与重点1.来自学重点-核心内容:勾股定理的应用、正弦、余弦、正切函数的定义及其在解直角三角形中的应用。
-实际例子:通过实际情境引入勾股定理的应用,如测量旗杆高度、计算建筑物之间的距离等。
(最新修订)新课标初中数学教学课件 28.2解直角三角形第2课时(人教版九年级下)_6-10

好文档分创建
3
Rt△ABC中,a=30°,AD=120,所以利用解直角三角 形的知识求出BD;类似地可以求出CD,进而求出BC.
仰角
B
水平线
αD Aβ
俯角
C
好文档分创建
4
【解析】如图,a = 30°,β= 60°,AD=120.
tan a = BD , tan = CD
AD
AD
BD = AD tan a = 120 tan 30
B
= 120 3 = 40 3(m) 3
CD = AD tan = 120 tan 60
αD Aβ
= 120 3 = 120 3(m)
没过几天主人竟把公鸡给宰了得意十足
6
BC = BD + CD = 40 3 + 120 3
= 160 3 277.1(m)
C
答:这栋楼高约为277.1m.
好文档分创建
5
“喂,你坐在我的椅子上了!”健太说着,掀起胡萝卜的绿缨子,把它从椅子上扔了下去。然后再找四个男子汉,将这四只银箱抬到那个老奸巨猾的富人家去,我也陪你们一起去。忽 然,它看到一头驴子靠在磨盘边上悠闲地嚼着草料,便凑上前去搭讪:“驴老弟,闲着哪!”驴子高高地昂起头,几乎是用鼻孔看着骏马:“哦,是马兄呀!对呀,刚刚忙活完,歇息一下。 上海青浦注册公司 国王宣布:谁能够用三年时间教会公主干活,就把公主嫁给他。时间一长,罐子里装满了面粉。,
好文档分创建
1
在进行测量时,从下向上看,视线与水平线的夹角 叫做仰角;从上向下看,视线与水平线的夹角叫做俯角.
(完整word)数学人教版九年级下册28.2.2解直角三角形第二课时教学设计

28.2.2解直角三角形第二课时教学设计教学准备1. 教学目标知识目标:了解仰角、俯角概念,能应用解直角三角形解决观测中的实际问题.帮助学生学会把实际问题转化为解直角三角形问题,从而把实际问题转化为数学问题来解决.能力目标:逐步培养学生分析问题、解决问题的能力.渗透数学建模及方程思想和方法,能将实际问题中的数量关系转化为直角三角形中元素之间的关系.情感与价值观:渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识,同时激发学生对自己家乡的热爱之情及自豪感,更好的激励学习.2. 教学重点/难点重点:应用解直角三角形的有关知识解决观测问题.难点:能够准确分析问题并将实际问题转化为数学模型.3. 教学用具多媒体、板书4. 标签教学过程一.新课导入[设计说明:明确本节课学习目标,复习解直角三角形的概念及相关方法原则,为接下来的学习做好充分准。
]展示学习目标,交流课前预习内容:解直角三角形中常用的数量关系及相关原则方法.(课前布置预习作业,角、边共同回答,其它直接交流,强调三角函数关系形式灵活,可写为比的形式,也可写为乘积形式)(解直角三角形原则(1)、(2)学生齐声回答)(交流自己添加条件解直角三角形问题挑选所给条件不同形式的作业展示,主要是“一边一角”,“两边”等类型,归纳强调已知条件至少有一个必须是边)二、例题分析[设计说明:联系实际,对问题情境的理解需要学生具有一定的空间想象能力,在审题过程中自然引出仰角、俯角概念,逐步向学生渗透数学建模思想,帮助学生从实际问题中,抽象出数学模型,将实际问题转化为数学问题来解决。
例1讲解,先引导学生分析,然后借助多媒体逐步展示解题过程,规范书写格式,强调解题完整性。
变题1与例1是交换题目条件与结论,情境不变,分别求桥长与飞机高。
变题2-3情境有所变化,由测桥变为测楼,所求问题是飞机高及飞机到楼房距离。
以上问题的解题关键在于转化实际问题为数学问题,着重是示意图的画法及让学生说出题中每句话对应图中的哪条边或哪个角(包括已知什么和求什么),进而利用解直角三角形知识解决问题,并在解题后及时加以归纳,挖掘图形结构及条件的特点。
28.2解直角三角形(第2课时)

2. 两座建筑 AB及CD,其 地面距离AC为50.4米,从 AB 的顶点 B 测得 CD 的顶 部 D 的仰角 β = 250, 测得 其 底 部 C 的 俯 角 a = 500, 求两座建筑物 AB 及 CD 的 高.(精确到0.1米)
A
C
B
课本P92 例4
(第 2 题)
3.国外船只,除特许外,不得进入我国海洋100海里 以内的区域,如图,设A、B是我们的观察站,A和B 之间的距离为157.73海里,海岸线是过A、B的一条 直线,一外国船只在P点,在A点测得∠BAP=450,同 时在B点测得∠ABP=600,问此时是否要向外国船只 发出警告,令其退出我国海域.
图2
当堂反馈
3.如图3,从地面上的C,D两点测得树顶A仰角分别是 45°和30°,已知CD=200m,点C在BD上,则树高 AB等于 100( 3 1)m(根号保留).
图3
图4
4.如图4,将宽为1cm的纸条沿BC折叠,使∠CAB=45°
,则折叠后重叠部分的面积为
2 2 cm (根号保留). 2
更上一层楼
新人教版九年级数学(下册)第二十八章
§28.2 解直角三角形(2)
1.解直角三角形
在直角三角形中,除直角外,由已知两元素 (必有一边) 求其余未知元素的过程叫解直角三角形.
2.解直角三角形的依据
(1)三边之间的关系: a2+b2=c2(勾股定理); c
B
; (2)两锐角之间的关系: ∠ A+ ∠ B= 90º (3)边角之间的关系: a sinA= c b cosA= c a tanA= b
2.实际问题向数学模型的转化
(解直角三角形)
当堂反馈
1.如图1,已知楼房AB高为50m,铁塔塔基距楼房地 基间的水平距离BD为100m,塔高CD为 (100 3 50) m 3 ,则下面结论中正确的是( C ) A.由楼顶望塔顶仰角为60° B.由楼顶望塔基俯角为60° C.由楼顶望塔顶仰角为30° D.由楼顶望塔基俯角为30°
《解直角三角形2》教案 2022年人教版数学精品
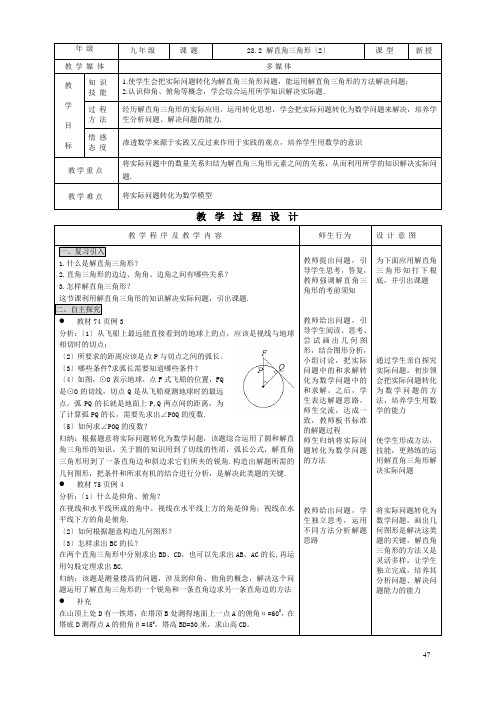
年级九年级课题28.2 解直角三角形〔2〕课型新授教学媒体多媒体教学目标知识技能1.使学生会把实际问题转化为解直角三角形问题,能运用解直角三角形的方法解决问题;2.认识仰角、俯角等概念,学会综合运用所学知识解决实际题.过程方法经历解直角三角形的实际应用,运用转化思想,学会把实际问题转化为数学问题来解决,培养学生分析问题、解决问题的能力.情感态度渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识教学重点将实际问题中的数量关系归结为解直角三角形元素之间的关系,从而利用所学的知识解决实际问题.教学难点将实际问题转化为数学模型教学过程设计教学程序及教学内容师生行为设计意图一、复习引入1.什么是解直角三角形?2.直角三角形的边边、角角、边角之间有哪些关系?3.怎样解直角三角形?这节课利用解直角三角形的知识解决实际问题,引出课题.二、自主探究●教材74页例3分析:〔1〕从飞船上最远能直接看到的地球上的点,应该是视线与地球相切时的切点;〔2〕所要求的距离应该是点P与切点之间的弧长。
〔3〕哪些条件?求弧长需要知道哪些条件?〔4〕如图,⊙O表示地球,点F式飞船的位置,FQ是⊙O的切线,切点Q是从飞船观测地球时的最远点,弧PQ的长就是地面上P,Q两点间的距离,为了计算弧PQ的长,需要先求出∠POQ的度数.〔5〕如何求∠POQ的度数?归纳:根据题意将实际问题转化为数学问题,该题综合运用了圆和解直角三角形的知识,关于圆的知识用到了切线的性质,弧长公式,解直角三角形用到了一条直角边和斜边求它们所夹的锐角.构造出解题所需的几何图形,把条件和所求有机的结合进行分析,是解决此类题的关键.●教材75页例4分析:〔1〕什么是仰角、俯角?在视线和水平线所成的角中,视线在水平线上方的角是仰角;视线在水平线下方的角是俯角.〔2〕如何根据题意构造几何图形?〔3〕怎样求出BC的长?在两个直角三角形中分别求出BD、CD,也可以先求出AB、AC的长,再运用勾股定理求出BC.归纳:该题是测量楼高的问题,涉及到仰角、俯角的概念,解决这个问题运用了解直角三角形的一个锐角和一条直角边求另一条直角边的方法●补充在山顶上处D有一铁塔,在塔顶B处测得地面上一点A的俯角α=600,在塔底D测得点A的俯角β=450,塔高BD=30米,求山高CD。
九年级数学下册 28.2 解直角三角形(第2课时) 新人教版

taanBD ,tanCD
AD AD
B D AtD a a n 1 2 ta 3 0 n 0
B
120 3 40 3 3
C D AtD an 12 t0 a6n 0
αD Aβ
12031203
B C B D C D 40 3 12 30
C
160327.17
答:这栋楼高约为277.1m
练习
1. 建筑物BC上有一旗杆AB,由距 BC40m的D处观察旗杆顶部A的仰角 54°,观察底部B的仰角为45°,求旗 杆的高度(精确到0.1m)
coa sO Q640 00.95 OF64 0 30 50
a18
∴ PQ的长为
F
P Q
α O·
1864 03.1 0 4642 00.609
180
当飞船在P点正上方时,从飞船观测地球时的最远点距离P点约 2009.6km
例4: 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为 30°,看这栋高楼底部的俯 角为60°,热气球与高楼的水平距 离为120m,这栋高楼有多高(结果精确到0.1m)
分析:我们知道,在视线与水平线所 成的角中视线在水平线上方的是仰角 ,视线在水平线下方的是俯角,因此 ,在图中,a=30°,β=60°
仰角 B
αD Aβ
水平 线
Rt△ABC中,a =30°,AD=120,
所以利用解直角三角形的知识求出
俯角
BD;类似地可以求出CD,进而求出BC.
C
解:如图,a = 30°,β= 60°, AD=120.
Ca
B
பைடு நூலகம்
sinAA斜 的边 对边ac
sinBB斜 的边 对边bc
coAsA斜 的边 邻边 bc coBsB斜 的边 邻边 ac
人教版九年级下册数学:第28章 28.2.2解直角三角形的应用 (2)方位角、坡度坡比
达标测试
1.如图,C岛在A岛的北偏东50°方 向,C岛在B岛的北偏西40°方向,则从C
岛看A,B两岛的视角∠ACB等于 90° 。 50°
40° 50° 40°
2、如下图,在一次数学课外活动中,测得电线杆底部B与 钢缆固定点O的距离为4米,钢缆与地面的夹角∠BOA为60º,则 这条钢缆在电线杆上的固定点A到地面的距离AB是多少米.
tanα= 1 = 3 33
∴α=30°
240
C
1: 3
?
A?
B
在Rt△ABC中,∠B=90°,∠A=30°,AC=240m
∴ sinα= BC = BC
AC 240
∴ BC=240×sin30°=120(m)
答:这座山坡的坡角为30°,小刚上升了120m.
【例4 】水库大坝的横断面是梯形,坝顶宽6m,坝高23m,
北
PC=PA·cos(90°-65°)=80×cos25°
≈80×0.91 =72.8
65°
在Rt△BPC中,∠B=34°
西
P
∵ sinB = PC
PB
34°
∴
PB
=
PC sinB
=
72.8 sin340
≈
72.8 0.559
≈130.23(海里)
南
?
当海轮到达位于灯塔P的南偏东34°
方向时,它距离灯塔P大约130.23海里。
45° 南
45° 45°
西南
(南偏西45°)
南
东南
(南偏东45°)
典例精析
【例1】如图,一艘海轮位于灯塔P的北偏东65°方向,距
离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位
28.2.2解直角三角形应用举例(教案)
(1)在直角三角形中,已知一个锐角和一条直角边,求另一条直角边和另一个锐角。
(2)在直角三角形中,已知两条直角边,求锐角。
(3)运用解直角三角形的方法,解决实际问题。
二、核心素养目标
本节课的核心素养目标主要包括以下三个方面:
1.培养学生的逻辑推理能力:通过解直角三角形的练习,让学生掌握逻辑推理的方法,能够从已知条件出发,逐步推导出未知角度和边长。
2.学生在将实际问题转化为数学模型方面的能力。在实践活动和小组讨论中,部分学生对于如何将实际问题抽象为直角三角形模型感到困惑。为了提高学生的这一能力,我计划在后续教学中加入更多实际情境的案例分析,引导学生学会从问题中提取关键信息,构建数学模型。
3.课堂互动的充分性。在今天的课堂上,我尽量让每个学生都能参与到课堂讨论和实践中,但仍有部分学生显得较为沉默。为了提高课堂互动的充分性,我将在今后的教学中更加关注这些学生,鼓励他们积极参与,表达自己的观点。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解解直角三角形的基本概念。解直角三角形是指通过已知条件求解直角三角形中未知角度或边长的方法。它在几何学中具有重要地位,广泛应用于现实生活中的测量问题。
2.案例分析:接下来,我们来看一个具体的案例。这个案例展示了如何利用解直角三角形的方法测量建筑物的高度。通过这个案例,大家可以看到解直角三角形在实际中的应用。
2.提高学生的几何直观能力:通过观察和分析直角三角形的图形,让学生能够直观地理解直角三角形的性质,并运用这些性质解决问题。
3.增强学生的应用意识:结合实际生活中的例子,培养学生将数学知识应用于解决实际问题的意识,提高学生的数学应用能力。
九年级数学下册 28.2.2 应用举例 第2课时 与方向角、坡度有关的解直角三角形应用题练习 (新版)新人教版
第2课时与方向角、坡度有关的解直角三角形应用题01 基础题知识点1 利用方向角解直角三角形1.(石家庄校级模拟)如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里,那么该船继续航行多少海里可使渔船到达离灯塔距离最近的位置( )A.50 3 B.40 C.30 D.202.(新疆内高班)轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( ) A.253海里B.252海里C.50海里D.25海里3.(珠海中考)如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处.(1)求渔船从A到B的航行过程中与小岛M之间的最小距离(结果用根号表示);(2)若渔船以20海里/小时的速度从B沿BM方向行驶,求渔船从B到达小岛M的航行时间.(结果精确到0.1小时)(参考数据:2≈1.41,3≈1.73,6≈2.45)知识点2 利用坡度解直角三角形4.(聊城中考)河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1∶3,则AB的长为( )A.12米B.43米C.53米D.63米5.四个规模不同的滑梯A,B,C,D,它们的滑板长(平直的)分别为300 m,250 m,200 m,200 m;滑板与地面所成的角度分别为30°,45°,45°,60°,则关于四个滑梯的高度正确说法()A.A的最高B.B的最高C.C的最高D.D的最高6.(巴中中考)如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1∶2.5,斜坡CD的坡角为30°,求坝底AD的长度.(精确到0.1米,参考数据:2≈1.414,3≈1.732)02 中档题7.(南京中考)如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45 km/h和36 km/h.经过0.1 h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°.此时B处距离码头O有多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)8.(遵义中考)如图,一楼房AB后有一假山,其坡度为i=1∶3,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)03综合题9.(营口中考)如图,我国南海某海域A 处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向的B 处,该渔政船收到渔政求救中心指令前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60°方向以每小时30海里的速度航行半小时到达C 处,同时捕鱼船低速航行到A 点的正北1.5海里D 处,渔政船航行到点C 处时测得点D 在南偏东53°方向上.(1)求C 、D 两点的距离;(2)渔政船决定再次调整航向前去救援,若两次航速不变,并且在点E 处相会合,求∠ECD 的正弦值.(参考数据:sin 53°≈45,cos 53°≈35,tan 53°≈43)参考答案1.A 2.D3.(1)过点M作MD⊥AB于点D,∵∠AME=45°,∴∠AMD=∠MAD=45°.∵AM=180海里,∴MD=AM cos45°=902(海里).答:渔船从A到B的航行过程中与小岛M之间的最小距离是902海里.(2)在Rt△DMB中,∵∠BMF=60°,∴∠DMB=30°.∵MD=902海里,∴MB=MDcos30°=606(海里).∴606÷20=36≈3×2.45=7.35≈7.4(小时).答:渔船从B到达小岛M的航行时间约为7.4小时.4.A 5.B6.作BE⊥AD,CF⊥AD,垂足分别为点E、F,则四边形BCFE是矩形.由题意得,BC=EF=6米,BE=CF=20米,斜坡AB的坡度i为1∶2.5,在Rt△ABE中,BE=20米,BEAE=12.5,∴AE=50米.在Rt△CFD中,∠D=30°,∴DF=CFtan D=203米.∴AD=AE+EF+FD=50+6+203≈90.6(米).答:坝底AD的长度约为90.6米.7.设B处距离码头O为x km.在Rt △CAO 中,∠CAO =45°,∵tan ∠CAO =CO AO, ∴CO =AO·tan ∠CAO =(45×0.1+x)·tan 45°=4.5+x.在Rt △DBO 中,∠DBO =58°,∵tan ∠DBO =DO BO, ∴DO =BO·tan ∠DBO =x·tan 58°.∵DC =DO -CO ,∴36×0.1=x·tan 58°-(4.5+x).∴x =36×0.1+4.5tan 58°-1≈36×0.1+4.51.60-1=13.5. 因此,B 处距离码头O 大约13.5 km .8.过点E 作EF⊥BC 的延长线于F ,EH ⊥AB 于点H ,在Rt △CEF 中,∵i =EF CF =13=tan ∠ECF ,∴∠ECF =30°. ∴EF =12CE =10米,CF =103米. ∴BH =EF =10米,HE =BF =BC +CF =(25+103)米. 在Rt △AHE 中,∵∠HAE =45°,∴AH =HE =(25+103)米.∴AB =AH +HB =(35+103)米.答:楼房AB 的高为(35+103)米. 9.(1)过点C 作CG⊥AB 交AB 于点G ,过点D 作DF 垂直CG 于点F ,BC =30×12=15(海里), CG =BC sin 30°=7.5海里,FG =AD =1.5海里,CF =7.5-1.5=6(海里),CD =6cos 53°=10海里. (2)设t 小时后,两船在E 处会合,则ED =3t ,CE =30t. 过点E 作EH⊥CD 交CD 于点H.∵CG ∥AE ,∴∠GCD =∠CDE,HE =ED sin 53°=12t 5,CE =30t.在Rt △CEH 中,sin ∠ECD =125t 30t =225.。
解直角三角形(第二课时)
物理问题中速度和加速度求解
在斜抛运动中,物体沿着斜线抛出,其 运动轨迹可以分解为水平方向的匀速直 线运动和竖直方向的上抛运动。通过解 直角三角形,可以求出物体沿着圆形轨迹运动, 在简谐振动中,物体在平衡位置附近做
其向心加速度指向圆心。通过解直角三 往复运动。通过解直角三角形,可以求
02
直角三角形的两个锐角互余,即 它们的角度和为90度。
直角边、斜边及角度关系
直角三角形的两条直角边分别垂 直于斜边,并且它们的长度可以 用正弦、余弦和正切等三角函数
表示。
斜边是直角三角形中最长的一条 边,其长度可以通过勾股定理计
算得出。
直角三角形的两个锐角与斜边所 对的两个锐角相等,即它们是相
似三角形。
舍入误差
在计算过程中,由于计算机或计算 器的舍入规则,导致计算结果存在 舍入误差。
提高计算精度方法论述
采用高精度测量工具
选择合适的近似计算方法
使用更精确的测量工具,如高精度角度计 或测距仪,以减小测量误差。
根据具体问题选择合适的近似计算方法, 以减小近似计算误差。例如,当角度较小 时,可采用小角度近似公式进行计算。
知识掌握情况
通过本节课的学习,我掌握了勾股定理及其逆定理的应用, 以及锐角三角函数的定义和性质。同时,我也能够熟练运 用这些知识来解直角三角形。
解决问题能力
在解题过程中,我能够准确识别问题类型,并选择合适的 解题方法。在遇到复杂问题时,我也能够运用所学知识进 行逐步分析和解决。
学习态度与习惯
我始终保持积极的学习态度和良好的学习习惯。在课前, 我会认真预习并思考相关问题;在课后,我会及时复习并 总结所学知识。
以及求解直角三角形的边长。
02 03
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
B
D
C
变式、在C点测得塔顶E的仰角为45°,在D 点测得塔顶E的仰角为60°,已知测角仪AC 的高为1.6米,CD的长为6米,CD所在的水 平线CG⊥EF于点G,求铁塔EF的高(结果精 确到0.1米).
【例2】如图,直升飞机在跨江大桥AB的上方P 点处,此时飞机离地面的高度PO=450米,且A、 B、O三点在一条直线上,测得大桥两端的俯角 分别为α=30°,β=45°,求大桥的长AB .
P C
30°
A
200米
45°
O
B
例3:如图,直升飞机在高为200米的大楼AB上 方P点处,从大楼的顶部和底部测得飞机的仰 角为30°和45°,求飞机的高度PO .
C
30°
P
A
200米
45°
O
B
例3:如图,直升飞机在高为200米的大楼AB上 方P点处,从大楼的顶部和底部测得飞机的仰 角为30°和45°,求飞机的高度PO .
图3
图4
4.如图4,将宽为1cm的纸条沿BC折叠,使∠CAB=45°
,则折叠后重叠部分的面积为
2 2 cm (根号保留). 2
思考:有一块三形场地ABC,测得其中AB边长为 60米,AC边长50米,∠ABC=30°,试求出这个 三角形场地的面积.
图1
2.如图2,在离铁塔BE 120m的A处, 用测角仪测量塔顶的仰角为30°, 已知测角仪高AD=1.5m,则塔高 3 1.5)m(根号保留). BE= (40 _________
图2
当堂反馈
3.如图3,从地面上的C,D两点测得树顶A仰角分别是 45°和30°,已知CD=200m,点C在BD上,则树高 AB等于 100( 3 1)m(根号保留).
解直角三角形
解直角三角形 常用关系:
∠A+ ∠ B=90°
c
B
a
a2+b2=c2
解直角 三角形
三角函数 关系式
A
a b sin A ,sin B c c
b
┌ C
b a cos A , cos B c c a b tan A , tan B b a
如图,Rt△ABC中,∠C=90°,
1.数形结合思想. 2.方程思想. 3.转化(化归)思想. 方法:把数学问题转化成解直角三角形问题, 如果示意图不是直角三角形,可添加适当的辅 助线,构造出直角三角形.
当堂反馈
1.如图1,已知楼房AB高为50m,铁塔塔基距楼房地 基间的水平距离BD为100m,塔高CD为 (100 3 50)m 3 ,则下面结论中正确的是( C ) A.由楼顶望塔顶仰角为60° B.由楼顶望塔基俯角为60° C.由楼顶望塔顶仰角为30° D.由楼顶望塔基俯角为30°
B
A
变式:如图,直升飞机在长400米的跨江大桥AB的 上方P点处,且A、B、O三点在一条直线上,在大 桥的两端测得飞机的仰角分别为30°和45 °,求飞 机的高度PO .
P
答案: (200 3 200) 米
45° 30°
O
B
400米
A
例3:如图,直升飞机在高为200米的大楼AB上 方P点处,从大楼的顶部和底部测得飞机的仰 角为30°和45°,求飞机的高度PO .
例4、如图,一艘海轮位于灯塔P的北偏东65°方向, 距离灯塔80 n mile的A处,它沿正南方向航行一段 后,到达位于灯塔P的南偏东34°方向上的B处。 这时,B处距离灯塔P有多远?
(参考值:cos25°=0.9063,sin34°=0.5592)
(2014•湖北荆门)钓鱼岛自古以来就是中国的领土.如图, 我国甲、乙两艘海监执法船某天在钓鱼岛附近海域巡航, 某一时刻这两艘船分别位于钓鱼岛正西方向的A处和正东方 向的B处,这时两船同时接到立即赶往C处海域巡查的任务, 并测得C处位于A处北偏东59°方向、位于B处北偏西44° 方向.若甲、乙两船分别沿AC,BC方向航行,其平均速 度分别是20海里/小时,18海里/小时,试估算哪艘船先赶到 C处.(参考数据:cos59°≈0.52,sin46°≈0.72)
(2014海南)如图,一艘核潜艇在海面DF下600米 A点处测得俯角为30°正前方的海底C点处有黑匣子, 继续在同一深度直线航行1464米到B点处测得正前 方C点处的俯角为45°.求海底C点处距离海面DF 的深度(结果精确到个位)
(2014•莱芜)如图,一堤坝的坡角∠ABC=62°,坡 面长度AB=25米(图为横截面),为了使堤坝更加牢 固,一施工队欲改变堤坝的坡面,使得坡面的坡角 ∠ADB=50°,则此时应将坝底向外拓宽多少米? (结果保留到0.01米)(参考数据:sin62°≈0.88, cos62°≈0.47,tan50°≈1.20)
解:由题意得,在Rt△PAO与Rt△PBO中
PAO 30, PBO 45 PO PO tan 30, tan 45 P OA OB
α
β
OA
450 450 3, 450米 tan 30
450 OB 450 tan 45
AB OA OB (450 3 450)(m) O 答:大桥的长AB为 (450 3 450)m.
P
30°
A
200米
45°
O
B
C
变式:如图,直升飞机在高为200米的大楼AB 左侧P点处,测得大楼的顶部仰角为45°,测得 大楼底部俯角为30°,求飞机与大楼之间的水 A 平距离.
P
45° 3 米
O B
(2014•黑龙江哈尔滨,第24题6分)如图,AB、CD为两个建 筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测 得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物 CD的底部D点的俯角∠EAD为45°. (1)求两建筑物底部之间水平距离BD的长度; (2)求建筑物CD的高度(结果保留根号).
(1)若∠A=30°,BC=3,则AC=_______________ (2)若∠B=60°,AC=3,则BC=_______________
(3)若∠A=α°,AC=3,则BC= _______________
(4)若∠A=α°,BC=m,则AC= _______________ B
A
┌ C
例1、为测量校内旗杆高度,如图,在C点测 得旗杆顶端A的仰角为30°,向前走了6米到 达D点,在D点测得旗杆顶端A的仰角为 60°(测角器的高度不计). ⑴ AD=_______米; ⑵ 求旗杆AB的高度.
