河北省张家口市2021年八年级上学期数学期中考试试卷(II)卷
河北省张家口市2021年八年级上学期期中数学试卷(I)卷

河北省张家口市2021年八年级上学期期中数学试卷(I)卷姓名:________ 班级:________ 成绩:________一、选择题 (共8题;共16分)1. (2分) (2018八上·东台月考) 如图,△ACE≌△DBF,若∠E=∠F,AD=8,BC=2,则AB等于()A . 6B . 5C . 3D . 不能确定2. (2分)如图,等腰梯形ABCD的对角线AC、BD相交于O,则图中共有全等三角形()A . 1对B . 2对C . 3对D . 4对3. (2分)如图,△ABC中,AB=AC=13,BC=10,AD是BC边上的中线,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为().A .B . 10C . 12D . 134. (2分)(2017·福州模拟) 下面的四幅简笔画是从文化活动中抽象出来的,其中是轴对称图形的是()A .B .C .D .5. (2分)如图是由边长为1的小正方形组成的网格,△ABC的顶点A,B,C均在格点上,BD⊥AC于点D,则BD的长为()A .B .C .D .6. (2分) (2016九上·罗平开学考) 如图,C,E是直线l两侧的点,以C为圆心,CE长为半径画弧交l于A,B两点,又分别以A,B为圆心,大于 AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,下列结论不一定正确的是()A . CD⊥lB . 点A,B关于直线CD对称C . 点C,D关于直线l对称D . CD平分∠ACB7. (2分)(2017·湖州模拟) 如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数在第一象限的图像经过点B,与OA交于点P,若OA2-AB2=18,则点P的横坐标为()A . 9B . 6C . 3D . 38. (2分) (2016·聊城) 如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为()A . 115°B . 120°C . 130°D . 140°二、填空题. (共8题;共8分)9. (1分) (2017八下·邵阳期末) 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则四边形BDFG的周长为________.10. (1分) (2016八上·江苏期末) 如图,△ABC中,AB=AC=26,BC=20,AD是BC边上的中线,AD=24,F 是AD上的动点,E是AC边上的动点,则CF+EF的最小值为________.11. (1分)(2017·武汉模拟) 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为________ cm.12. (1分) (2017八上·温州月考) 如图所示,AB⊥BC,,CD=5,AD=3,BC=2,则∠A=________度.13. (1分)如图△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,给出下列结论:①DC=DE;②DA平分∠CDE;③DE平分∠ADB;④BE+AC=AB;⑤∠BAC=∠BDE.其中正确的是________ (写序号)14. (1分) (2016八上·淮阴期末) 如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是________.15. (1分)(2018·绥化) 已知等腰三角形的一个外角为,则它的顶角的度数为________.16. (1分) (2016九上·淅川期末) 如图是拦水坝的横断面.斜坡AB的坡度为1:2,BC⊥AE,垂足为点C,AC长为12米,则斜坡AB的长为________米.三、解答题 (共9题;共65分)17. (15分) (2017八上·夏津期中) 如图,(1)写出△ABC的各顶点坐标;(2)画出△ABC关于y轴的对称图形△A1B1C1;(3)写出△ABC关于x轴对称的三角形的各顶点坐标.18. (5分)已知,如图,在四边形ABCD中,BC>BA,∠A+∠C=180°,DE⊥BC,BD平分∠ABC,试说明AD=DC.19. (5分)(2017·官渡模拟) 如图,点A,B,D,E在同一直线上,AD=EB,AC∥EF,∠C=∠F.求证:AC=EF.20. (5分) (2015八下·潮州期中) 在△ABC中,∠B=15°,∠C=90°,AB的垂直平分线交AB于点M,交BC于点N.已知BM=12cm,求AC的长.21. (10分)(2019·南京模拟) 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,且AF=DC,连接CF.(1)求证:D是BC的中点;(2)若∠BAC=90°,求证:四边形ADCF是菱形.22. (5分)(2017·宁波模拟) 如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.(1)如图1,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE是△ABC的一条特异线.(2)如图2,已知BD是△ABC的一条特异线,其中∠A= ,∠ABC为钝角,求出所有可能的∠ABC的度数.(3)如图3,△ABC是一个腰长为2的等腰锐角三角形,且它是特异三角形,若它的顶角度数为整数,请求出其特异线的长度;若它的顶角度数不是整数,请直接写出顶角度数.23. (5分)已知:△ABC中,记∠BAC=α,∠ACB=β.(1)如图1,若AP平分∠BAC,BP,CP分别平分△ABC的外角∠CBM和∠BCN,BD⊥AP于点D,用α的代数式表示∠BPC的度数,用β的代数式表示∠PBD的度数.(2)如图2,若点P为△ABC的三条内角平分线的交点,BD⊥AP于点D,猜想(1)中的两个结论是否发生变化,补全图形并直接写出你的结论.24. (10分) (2019八下·嘉陵期中) 已知:如图,在 ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE 的中点,点G为CD上的一点,连接DF、EG、AG,∠1=∠2。
河北省张家口市2021年八年级上学期数学期中考试试卷(I)卷

河北省张家口市2021年八年级上学期数学期中考试试卷(I)卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)下列长度的三条线段能组成三角形的是()A . 1,2,3B . 2,2,4C . 3,4,5D . 3,4,82. (2分)平行四边形、矩形、菱形、正方形中是轴对称图形的有()个.A . 1B . 2C . 3D . 43. (2分)如图,阴影部分组成的图案既是关于轴成轴对称的图形,又是关于坐标原点成中心对称的图形.若点的坐标是,则点和点的坐标分别为()A .B .C .D .4. (2分)如图,下列条件不能证明△ABD≌△ACD的是()A . BD=DC,AB=ACB . ∠ADB=∠ADC,BD=DCC . ∠B=∠C,∠BAD=∠CADD . ∠B=∠C,BD=DC5. (2分)(2019·温州模拟) 已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示:按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转……连续经过六次旋转.在旋转的过程中,当正方形和正六边形的边重合时,点B,M间的距离可能是()A . 0.5B . 0.7C . ﹣1D . ﹣16. (2分)如图,Rt△ABC中,∠ACB =90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB的度数为()A . 40°B . 30°C . 20°D . 10°7. (2分)如图,△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=8,DE=3,则△BCE的面积等于()B . 8C . 12D . 38. (2分)如图,△ABC≌△DEF.若BC=5cm,BF=7cm,则EC=()A . 1cmB . 2cmC . 3cmD . 4cm9. (2分) (2017八上·涪陵期中) 如图,AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,下列结论正确的有()个①AE= (AB+AD);②∠DAB+∠DCB=180°;③CD=CB;④S△ACE﹣S△BCE=S△ADC;⑤AD=AE.A . 2个B . 3个C . 4个D . 5个10. (2分)(2017·准格尔旗模拟) 如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=()A .C . 3D . +211. (2分)已知ΔABC中,∠A∶∠B∶∠C=3∶7∶8,则ΔABC的形状是()A . 钝角三角形B . 直角三角形C . 锐角三角形D . 都有可能12. (2分) (2019九上·景县期中) 如图,在△ABC中,∠ACB=90°,∠A=20°将△A BC绕点C按逆时针方向旋转得△A′B′C,且点B在A'B′上,CA′交AB于点D,则∠BDC的度数为()A . 40°B . 50°C . 60°D . 70°二、填空题 (共5题;共5分)13. (1分) (2019八上·荣昌期中) 如图,工人师傅制作门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是________.14. (1分) (2017七下·萍乡期末) 如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC=________度.15. (1分) (2016九下·邵阳开学考) 一等腰三角形的两边长分别为4cm和6cm,则其底角的余弦值为________.16. (1分)正三角形、正方形、正六边形都是大家熟悉的特殊多边形,它们有很多共同特征,请写出其中的两点:(1)________;(2)________.17. (1分) (2018八上·硚口期末) 在中,,,点是射线上的一个动点,作,且,连接交射线于点,若,则 ________.三、解答题 (共10题;共85分)18. (5分)(2017·岳阳模拟) 如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.19. (10分) (2018八上·嵩县期末) 已知:如图,OM是∠AOB的平分线,C是OM上一点,且CD⊥OA于D,CE⊥OB于E,AD=EB.求证:AC=CB.20. (5分)在平面直角坐标系中,已知点A(﹣3,1),B(﹣1,0),C(﹣2,﹣1),请在图中画出△ABC,并画出与△ABC关于y轴对称的图形△A1B1C1 ,并写出点A对应点A1的坐标.21. (5分)如图,E,F是▱ABCD的对角线AC上两点,且AE=CF,请你写出图中的一对全等三角形并对其进行证明.22. (10分)已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC,(1)求证:△ABC是等腰三角形;(2)判断点O是否在∠BAC的角平分线上,并说明理由.23. (10分) (2019九上·灵石期中) 如图,在矩形ABCD中,AB=3,AD=6,点E在AD边上,且AE=4,EF⊥BE 交CD于点F .(1)求证:△ABE∽△DEF;(2)求EF的长.24. (10分)(2017·十堰模拟) 将一块正方形和一块等腰直角三角形如图1摆放.(1)如果把图1中的△BCN绕点B逆时针旋转90°,得到图2,则∠GBM=________;(2)将△BEF绕点B旋转.①当M,N分别在AD,CD上(不与A,D,C重合)时,线段AM,MN,NC之间有一个不变的相等关系式,请你写出这个关系式:________;(不用证明)②当点M在AD的延长线上,点N在DC的延长线时(如图3),①中的关系式是否仍然成立?若成立,写出你的结论,并说明理由;若不成立,写出你认为成立的结论,并说明理由.25. (5分) (2019八上·常州期末) 已知:如图,在中,,BE、CD是中线求证:.26. (10分)如图,在矩形ABCD中,AB=4,AD=6,M,N分别是AB,CD的中点,P是AD上的点,且∠PNB=3∠CBN.(1)求证:∠PNM=2∠CBN(2)求线段AP的长27. (15分) (2019八上·宜兴期中) 如图(1)观察推理:如图①,在中, ,直线过点,点在直线的同侧,,垂足分别为 .求证: .(2)类比探究:如图②,在中,,将斜边绕点逆时针旋转90°至,连接,求的面积.(3)拓展提升:如图③,在中,,点在上,且,动点从点沿射线以每秒1个单位长度的速度运动,连接,将线段绕点逆时针旋转120°得到线段 .要使点恰好落在射线上,求点运动的时间 .参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共5题;共5分)13-1、14-1、15-1、16-1、17-1、三、解答题 (共10题;共85分)18-1、19-1、20-1、21-1、22-1、23-1、23-2、24-1、24-2、25-1、26-1、26-2、27-1、27-2、27-3、。
2021-2022学年人教版八年级上学期期中考试数学试卷含答案解析
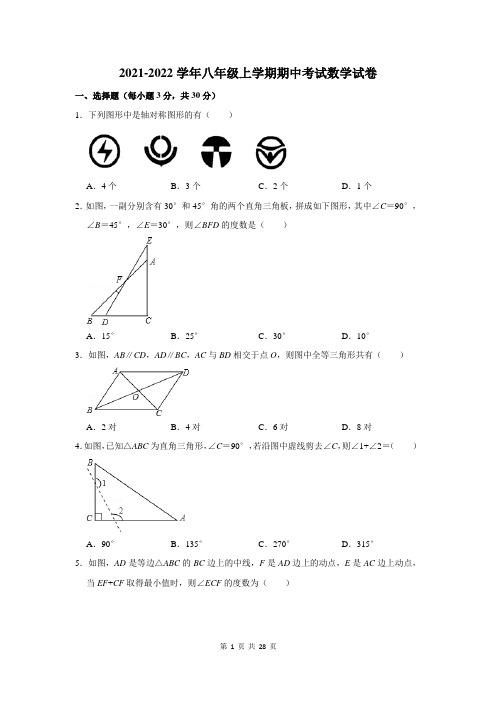
11.小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数为 ,则电子表的实际时刻是.
12.等腰三角形的一个内角为30°,那么其它两个角的度数为.
13.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A=度.
14.如图,在四边形ABCD中,AB∥CD,连接BD,∠ABD=3ቤተ መጻሕፍቲ ባይዱ°,AB=BD,则∠ADC等于.
A.15°B.22.5°C.30°D.45°
6.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE、下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
A.1个B.2个C.3个D.4个
7.在平面直角坐标系中,已知点A(m,3),与点B(4,n)关于y轴对称,那么(m+n)2019的值为( )
A.△DBI和△EIC是等腰三角形
B.I为DE中点
C.△ADE的周长是8
D.∠BIC=115°
10.如图,等腰△ABC的底边BC长为6,面积是36,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
A.6B.10C.15D.16
六、解答题(12分)
27.(12分)如图,△ABC是等边三角形,CF⊥AC交AB的延长线于点F,G为BC的中点,射线AG交CF于D,E在CF上,CE=AD,连接BD,BE.
求证:△BDE是等边三角形
七、解答题(12分)
28.(12分)如图,△ABC和△ADE均为等边三角形,CE,BD相交于点P,连接PA.
3.如图,AB∥CD,AD∥BC,AC与BD相交于点O,则图中全等三角形共有( )
河北省张家口市八年级上学期数学期中考试试卷

河北省张家口市八年级上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、选择题(选择唯一正确的答案填在括号内,每小题3分,共30分) (共10题;共29分)1. (3分)(2020·晋中模拟) 下列图形中,既是轴对称图形,又是中心对称图形的是()A .B .C .D .2. (3分) (2019七下·富宁期中) 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是().A . 两点之间的线段最短B . 长方形的四个角都是直角C . 长方形对边相等D . 三角形具有稳定性3. (3分) (2020八上·永昌期中) 小明从镜子中看到对面电子钟示数如图所示,这时的时刻应是()A . 21:10B . 10:21C . 10:51D . 12:014. (3分)有木条4根,长度分别是12cm,10cm,8cm,4cm.选出其中三根组成首尾相接的三角形,能组成三角形的个数是()A . 1B . 2C . 3D . 45. (3分) (2020八上·南京期末) 若等腰三角形的一个内角为92°,则它的顶角的度数为()A . 92°B . 88°C . 44°D . 88°或44°6. (3分) (2018七下·松北期末) 如图,已知点 D是∠ABC的平分线上一点,点 P在 BD上,PA⊥AB,PC⊥BC,垂足分别为 A,C.下列结论错误的是()A . ∠ADB=∠CDBB . △ABP≌△CBPC . △ABD ≌△CBDD . AD=CP7. (3分) (2020八上·休宁期中) 点与关于x轴的对称,求的值()A .B .C .D .8. (3分) (2017八上·江津期中) 一个多边形内角和是1080°,则这个多边形的对角线条数为()A . 27B . 25C . 22D . 209. (2分) (2019九上·海淀开学考) 已知△ABC(如图1),按图2图3所示的尺规作图痕迹,(不需借助三角形全等)就能推出四边形ABCD是平行四边形的依据是()A . 两组对边分别平行的四边形是平行四边形B . 对角线互相平分的四边形是平行四边形C . 一组对边平行且相等的四边形是平行四边形D . 两组对边分别相等的四边形是平行四边形10. (3分) (2019九上·东台月考) 如图,∠MON=90°,已知△ABC中,AC=BC=13,AB=10,△A BC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的最小距离为()A . 5B . 7C . 12D .二、填空题(每小题3分,共18分) (共6题;共17分)11. (3分) (2020八下·淮安期中) 如图,在矩形ABCD中,∠BOC=120°,则∠BAC=________.12. (3分) (2018八上·佳木斯期中) n边形的每个外角都为24°,则边数n为________ .13. (3分)(2019·呼和浩特) 下面三个命题:底边和顶角对应相等的两个等腰三角形全等;两边及其中一边上的中线对应相等的两个三角形全等;斜边和斜边上的中线对应相等的两个直角三角形全等,其中正确的命题的序号为________.14. (2分) (2016八上·孝南期中) 等腰三角形的两边长分别为3cm和4cm,则它的周长是________ cm.15. (3分) (2020八上·惠州月考) 如图,中,,若沿图中虚线截去,则________.16. (3分)的绝对值是________;﹣3的相反数是________;﹣2的倒数是________;绝对值等于的数是________.三、解答题(本大题52分) (共7题;共52分)17. (6分) (2019八上·大通期中) 如图所示,写出各顶点的坐标以及关于对称的的各顶点坐标,并画出关于对称的 .18. (6分) (2018八上·东台月考) 如图,AE和BD相交于点C,∠A=∠E,AC=EC.求证:△ABC≌△EDC.19. (6分) (2020八上·南京月考) 如图,,为、的平分线的交点,于,且,求与之间的距离.20. (8分) (2020八下·南京期中) 如图,已知正方形 ABCD 的边长为 5,点 E、F 分别在 AD、DC 上,AE =DF=2,BE 与 AF 相交于点 G,点 H 为 BF 的中点,连接 GH,求 GH 的长.21. (8分)(2017·苏州) 如图,在中,,轴,垂足为.反比例函数()的图像经过点,交于点.已知,.(1)若,求的值;(2)连接,若,求的长.22. (8分)(2019·槐荫模拟) 如图,点是线段上任意一点,分别以为边在的同侧作等边和等边,分别连接 .求证: .23. (10分) (2019八上·下陆月考) 如图,A(-t,0)、B(0,t),其中t>0,点C为OA上一点,OD⊥BC 于点D,且∠BCO=45°+∠COD(1)求证:BC平分∠ABO(2)求的值(3)若点P为第三象限内一动点,且∠APO=135°,试问AP和BP是否存在某种确定的位置关系?说明理由参考答案一、选择题(选择唯一正确的答案填在括号内,每小题3分,共30分) (共10题;共29分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:二、填空题(每小题3分,共18分) (共6题;共17分)答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题(本大题52分) (共7题;共52分)答案:17-1、考点:解析:答案:18-1、考点:解析:答案:19-1、考点:解析:答案:20-1、考点:解析:答案:21-1、答案:21-2、考点:解析:答案:22-1、考点:解析:答案:23-1、答案:23-2、答案:23-3、考点:解析:。
2021-2022学年八年级上学期期中考试数学试卷含答案

2021-2022学年八年级上学期期中考试数学试卷
一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,其中是轴对称图形的是()
A.B.C.D.
2.点M(1,2)关于x轴对称的点的坐标为()
A.(﹣1,2)B.(﹣1,﹣2)C.(1,﹣2)D.(2,﹣1)3.下列运算正确的是()
A.a•a2=a2B.(ab)3=ab3C.(a2)3=a6D.a10÷a2=a5 4.等腰三角形的两边长分别为2和7,则它的周长是()
A.9B.11C.16D.11或16
5.下列多项式中能用平方差公式分解因式的是()
A.a2+(﹣b)2B.5m2﹣20mn C.﹣x2﹣y2D.﹣x2+9
6.若x2+8x+m是完全平方式,则m的值为()
A.4B.﹣4C.16D.﹣16
7.如图,△ABC中,AB=AC=15,AB的垂直平分线DE交AC于D,连结BD,若△DBC 的周长为23,则BC的长为()
A.6B.7C.8D.9
8.计算[(﹣a)3]4÷(﹣a4)3的结果是()
A.﹣1B.1C.0D.﹣a
9.如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,∠A =∠ABE,AC=5,BC=3,则BD的长为()
第1 页共23 页。
2021年冀教版八年级数学上册期中试卷及参考答案

2021年冀教版八年级数学上册期中试卷及参考答案 班级: 姓名: 一、选择题(本大题共10小题,每题3分,共30分)1.已知31416181279a b c ===,,,则a b c 、、的大小关系是( )A .a b c >>B .a c b >>C .a b c <<D .b c a >>2.若关于x 的方程3m(x +1)+5=m(3x -1)-5x 的解是负数,则m 的取值范围是( )A .m >-54B .m <-54C .m >54D .m <543.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )A .108°B .90°C .72°D .60°4.□ABCD 中,E 、F 是对角线BD 上不同的两点,下列条件中,不能得出四边形AECF 一定为平行四边形的是( )A .BE=DFB .AE=CFC .AF//CED .∠BAE=∠DCF5.下列各组数中,能作为一个三角形三边边长的是( )A .1,1,2B .1,2,4C .2,3,4D .2,3,56.已知关于x 的不等式组0320x a x ->⎧⎨->⎩的整数解共有5个,则a 的取值范围是( )A .﹣4<a <﹣3B .﹣4≤a <﹣3C .a <﹣3D .﹣4<a <327.下列四个图形中,线段BE 是△ABC 的高的是( )A .B .C .D .8.三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是( )A .90B .120C .135D .1809.如图,在下列条件中,不能证明△ABD ≌△ACD 的是( ).A .BD =DC ,AB =AC B .∠ADB =∠ADC ,BD =DCC .∠B =∠C ,∠BAD =∠CAD D .∠B =∠C ,BD =DC10.如图,在平行四边形ABCD 中,∠ABC 的平分线交AD 于E ,∠BED=150°,则∠A 的大小为( )A .150°B .130°C .120°D .100°二、填空题(本大题共6小题,每小题3分,共18分)116________.2.已知15x x+=,则221x x +=________________. 3.一个正数的平方根分别是1x +和5x -,则x =________.4.如图,已知∠1=75°,将直线m 平行移动到直线n 的位置,则∠2﹣∠3=________°.5.如图,直线y =x +2与直线y =ax +c 相交于点P (m ,3),则关于x 的不等式x +2≤ax +c 的解为__________.6.如图△ABC 中,分别延长边AB 、BC 、CA ,使得BD=AB ,CE=2BC ,AF=3CA ,若△ABC 的面积为1,则△DEF 的面积为________.三、解答题(本大题共6小题,共72分)1.解下列分式方程:(1)32111x x =+-- (2)2531242x x x-=---2.先化简,后求值:(5a 5a (a ﹣2),其中a=12+2.3.已知:关于x 的一元二次方程221(1)204x m x m +++-=.(1)若此方程有两个实数根,求m 的最小整数值;(2)若此方程的两个实数根为1x ,2x ,且满足22211221184x x x m x +=--,求m 的值.4.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.5.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE,已知∠BAC=30°,EF⊥AB,垂足为F,连接DF(1)试说明AC=EF;(2)求证:四边形ADFE是平行四边形.6.为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.(1)求足球和篮球的单价各是多少元?(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?参考答案一、选择题(本大题共10小题,每题3分,共30分)1、A2、A3、C4、B5、C6、B7、D8、D9、D10、C二、填空题(本大题共6小题,每小题3分,共18分)1、22、233、2.4、1055、x≤1.6、18三、解答题(本大题共6小题,共72分)1、(1)x=2;(2)32 x=-2、43、(1)-4;(2)m=34、(1)见解析(2)成立(3)△DEF为等边三角形5、略.6、(1)一个足球的单价103元、一个篮球的单价56元;(2)学校最多可以买9个足球.。
河北省张家口市八年级上学期数学期中考试试卷

河北省张家口市八年级上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共15题;共30分)1. (2分)(2018·菏泽) 下列各数:﹣2,0,,0.020020002…,π,,其中无理数的个数是()A . 4B . 3C . 2D . 12. (2分) (2017七下·永城期末) 实数﹣的绝对值是()A . 2B .C . ﹣D . ﹣3. (2分)当的值为最小值时,a 的取值为()A . -1B . 0C . -D . 14. (2分) (2017八上·安庆期末) 在下列四组点中,可以在同一个正比例函数图象上的一组点是()A . (2,﹣3),(﹣4,6)B . (﹣2,3),(4,6)C . (﹣2,﹣3),(4,﹣6)D . (2,3),(﹣4,6)5. (2分)下列运算正确的是()A .B .C .D .6. (2分) (2019八上·施秉月考) 在平面直角坐标系中,点P(2,-1)关于y轴对称的点的坐标为()A . (2,1)B . (-2,-1)C . (-2,1)D . (-1,2)7. (2分) (2017九·龙华月考) 已知三角形三边的长分别为1、2、x,则x的取值范围在数轴上表示为()A .B .C .D .8. (2分)一个圆桶底面直径为24cm,高32cm,则桶内所能容下的最长木棒为()A . 20cmB . 50cmC . 40cmD . 45cm9. (2分) (2019八下·北京期中) 下列图象不能反映y是x的函数的是()A .B .C .D .10. (2分)如图,在平面直角坐标系中,二次函数y=ax2+mc(a≠0)的图像经过正方形ABOC的三个顶点,且ac=-2,则m的值为()A . 1B . -1C . 2D . -211. (2分)(2018·路北模拟) 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:(1)a=40,m=1;(2)乙的速度是80km/h;(3)甲比乙迟 h到达B地;(4)乙车行驶小时或小时,两车恰好相距50km.正确的个数是()A . 1B . 2C . 3D . 412. (2分) (2019九上·偃师期中) 如果a是一元二次方程x2﹣3x﹣5=0的一个根,那么代数式8﹣a2+3a 的值为()A . 1B . 2C . 3D . 413. (2分) (2017八上·秀洲月考) 以下各点中,在正比例函数y=2x图象上的是()A . (2,1)B . (1,2)C . (—1,2)D . (1,—2)14. (2分)(2017·泊头模拟) 在平面直角坐标系中,点P(x,0)是x轴上一动点,它与坐标原点O的距离为y,则y关于x的函数图象大致是()A .B .C .D .15. (2分)如图抛物线y=ax2+bx+c的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:①2b﹣c=2;②a= ;③ac=b﹣1;④ >0其中正确的个数有()A . 1个B . 2个C . 3个D . 4个二、填空题 (共5题;共5分)16. (1分)(2018·临沂) 计算:|1﹣ |=________.17. (1分) (2018九上·台州期中) 如图,在正方形ABCD中,AB=3,点E , F分别在CD , AD上,CE=DF ,BE , CF相交于点G ,连接DG .点E从点C运动到点D的过程中,DG的最小值为________.18. (1分) (2015八上·南山期末) 如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A,B两地向正北方向匀速直行,他们与A地的距离S(千米)与所行的时间t(小时)之间的函数关系图象如图所示的AC 和BD给出,当他们行走3小时后,他们之间的距离为________千米.19. (1分)已知一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是________ .20. (1分)(2017·杭州模拟) 如图,AB是⊙O的直径,AB=15,AC=9,则tan∠ADC=________.三、解答题 (共8题;共95分)21. (10分)(2019·抚顺模拟) 如图,在平面直角坐标系中,A(﹣1,4),B(﹣4,0),C(﹣1,0).(1)①△A1B1C1与△ABC关于原点O对称,画出△A1B1C1并写出点A1的坐标;②△A2B2C2是△ABC绕原点O顺时针旋转90°得到的,画出△A2B2C2并写出点A2的坐标;(2)连接OA、OA2,在△ABC绕原点O顺时针旋转90°得到的△A2B2C2的过程中,计算线段OA变换到OA2过程中扫过区域的面积是多少?(直接写出答案)22. (20分) (2019八上·郑州期中) 计算(1)(2)× -4× ×(1- )0-()-1(3) (2 -3 )÷ -( - )223. (15分) (2017八下·新野期中) 如图,直线y=kx-3与x轴、y轴分别相交于B、C两点,且OC=2OB(1)求B点的坐标和k的值.(2)若点A(x,y)是直线y=kx-3上在第一象限内的一个动点,当A 在运动的过程中,试写出△AOB的面积S与x的函数关系式,(不要求写出自变量的取值范围).(3)探究:在(2)的条件下①当A运动到什么位置时,△ABO的面积为,并说明理由.②在①成立的情况下,x轴上是否存在一点P,使△AOP是等腰三角形?若存在,请直接写出满足条件的所有P 点的坐标,若不存在,请说明理由.24. (10分) (2017八下·福州期中) 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时血液中含药量最高,达到每毫升6微克,接着就逐步衰减,10小时后血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示,那么成年人规定剂量服药后:(1) y与x之间的函数关系式.(2)如果每毫升血液中含药量在4微克或4微克以上时,治疗疾病才是有效的,那么这个有效时间是多长?25. (10分) (2019七上·余杭期中) 操作探究:已知在纸面上有一数轴(如图所示),(1)折叠纸面,使表示的点1与-1重合,则-2表示的点与________表示的点重合;(2)折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:① 5表示的点与数________表示的点重合;② 表示的点与数________表示的点重合;③若数轴上A、B两点之间距离为9(A在B的左侧),且A、B两点经折叠后重合,此时点A表示的数是________、点B表示的数是________.(3)已知在数轴上点A表示的数是a,点A移动4个单位,此时点A表示的数和a是互为相反数,求a的值。
2021-2022学年八年级上学期期中数学试题(含解析)

∴它的一个底角为(180°−80°)÷2=50°.
故填50.
【点睛】此题主要考查了等腰三角形的性质及三角形内角和定理.通过三角形内角和,列出方程求解是正确解答本题的关键.
10.如图,在△ABC中,AB=5cm,AC=3 cm,BC的垂直平分线交BC于D,交AB于E,连接EC.则△AEC的周长为________cm.
故选C.
【点睛】本题考查等腰三角形的性质、三角形的三边关系,掌握等腰三角形的性质、三角形的三边关系.
6.如图,在∠AOB中,OM平分∠AOB,MA⊥OA,垂足为A,MB⊥OB,垂足为B.若∠MAB=20°,则∠AOB的度数为()
A.20°B.25°C.30°D.40°
【答案】D
【解析】
【分析】根据角的平分线的性质得到MA=MB,从而得到∠AMB=140°,利用四边形内角和定理计算即可.
1.下列四个图形中,不是轴对称图形的为()
A. B. C. D.
2.如图, , , ,则 度数是()
A.35°B.40°C.50°D.60°
3.在△ABC中,∠A=60°,∠B=50°,AB=8,下列条件能得到△ABC≌△DEF的是( )
A.∠D=60°,∠E=50°,DF=8B.∠D=60°,∠F=50°,DE=8
C.∠E=50°,∠F=70°,DE=8D.∠D=60°,∠F=70°,EF=8
【答案】C
【解析】
【分析】显然题中使用ASA证明三角形全等, ,需要保证 ,可以根据三角形内角和定理确定∠F.
【详解】解:∵△ABC≌△DEF,
∴∠B=∠E=50°,∠A=∠D=60°,AB=DE=8,
∴∠F=180°﹣∠E﹣∠D=70°,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北省张家口市2021年八年级上学期数学期中考试试卷(II)卷
姓名:________ 班级:________ 成绩:________
一、单选题 (共8题;共8分)
1. (1分)(2020·阿城模拟) 下列图形中,是轴对称图形,但不是中心对称图形的是()
A .
B .
C .
D .
2. (1分) (2019八上·银川期中) 下列各数:
中无理数的个数是()
A . 3
B . 4
C . 5
D . 6
3. (1分) (2018七上·河口期中) 在△ABC和△A′B′C′中,下列条件:①AB=A′B′,②BC=B′C′,
③AC=A′C′,④∠A=∠A′,⑤∠B=∠B′,⑥∠C=∠C′,不能判定△ABC≌△A′B′C′的是()
A .
B .
C .
D .
4. (1分) (2020八上·淮安期末) 下列四组线段、、,不能组成直角三角形的是()
A .
B .
C .
D .
5. (1分) 2011年,某地区有54310人参加中考,将54310用科学记数法(保留2个有效数字)表示为()
A . 54×103
B . 0.54×105
C . 5.4×104
D . 5.5×104
6. (1分) (2019八上·东莞期中) 如图,若CD是△ABC的中线,AB=10,则AB=()
A . 5
B . 6
C . 8
D . 4
7. (1分) (2020八上·芜湖期末) 如图,是的角平分线,点是上一点,作线段
的垂直平分线交于点,交于点,过点作交于点,连接,若,.则的面积为()
A .
B .
C .
D .
8. (1分) (2020八上·安陆期末) 如图所示,在等边△ABC中,D,E分别是BC,AC的中点,点P是线段AD 上的一个动点,当△PCE的周长最小时,P点的位置在()
A . △ABC的重心处
B . AD的中点处
C . A点处
D . D点处
二、填空题 (共10题;共10分)
9. (1分) (2019七下·河东期末) 若m是的立方根,则m+3=________.
10. (1分) (2016八上·余姚期中) 在等腰△ABC中,AB=AC,∠A=50°,则∠B=________.
11. (1分) (2017七上·大埔期中) 在,-(-3),,中,负数有________个.
12. (1分) (2019八上·宜兴期中) 如图,已知所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为5,则A,B,C,D四个小正方形的面积之和等于________ .
13. (1分) (2017八下·大冶期末) 如图,在直角三角形ABC中,∠ACB=90°,D,E,F分别是AB,AC,BC 的中点,若CD=5,则EF的长为________.
14. (1分) (2018八上·合浦期末) 如图①是的小方格构成的正方形,若将其中的两个小方格涂黑,使得涂黑后的整个图案(含阴影)是轴对称图形,且规定沿正方形对称轴翻折能重合的图案都视为同一种,比如图②中四幅图就视为同一种,则得到不同的图案共有________种.
15. (1分)(2017·福建) 两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于________度.
16. (1分) 9的平方根是________,9的算术平方根是________.
17. (1分) (2015八上·句容期末) 如图,长为12cm的弹性皮筋直放置在x轴上,固定两端A和B,然后把
中点C向上拉升8cm至D点,则弹性皮筋被拉长了________.
18. (1分)(2017·盐城模拟) 如图,点A是双曲线y= 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为________.
三、解答题 (共8题;共13分)
19. (2分) (2019七下·遵义期中) 解方程:
(1)(x﹣3)2+1=26;
(2)﹣=1.
20. (1分) (2019七下·普陀期末) 已知线段a和线段AB(a<AB).
(1)以AB为一边,画△ABC,使AC=a,ÐA=50°,用直尺、圆规作出△ABC边BC的垂直平分线,分别与边AB、BC交于点D、E,联结CD;(不写画法,保留作图痕迹)
(2)在(1)中,如果AB=5,AC=3,那么△ADC的周长等于________.
21. (1分) (2018八上·殷都期中) C、B、E三点在一直线上,AC⊥CB,DE⊥BE,∠ABD=90°,AB=BD,试证明:AC+DE=CE.
22. (1分) (2016八上·顺义期末) 已知:如图,在△ABC中,∠ACB=90°,D是BC的中点,DE∥AC,且DE=AC,若AC=2,AD=4,求四边形ACEB的周长.
23. (1分)如图,在△ABC中,AB=AC,AD⊥BC于D,E是AB上的一点,EF∥AD交CA的延长线于F.
求证:△AEF是等腰三角形.
24. (2分) (2019七下·广安期中) 已知一个正数的平方根是a+3和2a﹣15.
(1)求这个正数.
(2)求的平方根.
25. (3分)(2017·于洪模拟) 两块等腰直角三角板△ABC和△DEC如图摆放,其中∠ACB=∠DCE=90∘,F是DE的中点,H是AE的中点,G是BD的中点.
(1)如图1,若点D.E分别在AC、BC的延长线上,通过观察和测量,猜想FH和FG的数量关系为________和位置关系为________;
(2)将图1中三角板△DEC绕着点C顺时针(逆时针)旋转,旋转角为a(0°<a<180°)以图2和图3的情况为例,其中图2中旋转至点A、C、E在一条直线上时,其余条件均不变,则(1)中的猜想是否还成立,若不成立,请说明理由;若成立,请从图2和图3中选其一证明
(3)在△DEC绕点C按图3方式旋转的过程中,当直线FH经过点C时,若AC=2,CD= ,请直接写出FG 的长.
26. (2分) (2019八上·泰州月考) 如图1,在平面直角坐标系,O为坐标原点,点A(﹣2,0),点B(0,2 ).
(1)直接写求∠BAO的度数;
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1 ,△BA′O 的面积为S2 , S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
参考答案一、单选题 (共8题;共8分)
答案:1-1、
考点:
解析:
答案:2-1、
考点:
解析:
答案:3-1、
考点:
解析:
答案:4-1、考点:
解析:
答案:5-1、考点:
解析:
答案:6-1、考点:
解析:
答案:7-1、考点:
解析:
答案:8-1、考点:
解析:
二、填空题 (共10题;共10分)答案:9-1、
考点:
解析:
答案:10-1、
考点:
解析:
答案:11-1、考点:
解析:
答案:12-1、考点:
解析:
答案:13-1、考点:
解析:
答案:14-1、考点:
解析:
答案:15-1、考点:
解析:
答案:16-1、考点:
解析:
答案:17-1、考点:
解析:
答案:18-1、考点:
解析:
三、解答题 (共8题;共13分)答案:19-1、
答案:19-2、考点:
解析:
答案:20-1、答案:20-2、考点:
解析:
答案:21-1、考点:
解析:
答案:22-1、考点:
解析:
答案:23-1、考点:
解析:
答案:24-1、
答案:24-2、考点:
解析:
答案:25-1、
答案:25-3、考点:
解析:
答案:26-1、答案:26-2、
答案:26-3、
考点:
第21 页共22 页
解析:
第22 页共22 页。
