专题58 三角形中作辅助线造相似(解析版)
专题58 三角形中作辅助线造相似(解析版)

专题58 三角形中作辅助线造相似1、如图1,在△ABC中,AB=AC=10,BC=12.(1)求AC边上的高BH的长;(2)如图2,点D、E分别在边AB、BC上,G、F在边AC上,当四边形DEGF是正方形时,求DE的长.解:(1)过点A作AN⊥BC于N,∵AB=AC=10,BC=12,AN⊥BC,∴BN=CN=6,∴AN===8,∵S△ABC=AC×BH=BC×AN,∴BH==9.6;(2)如图2,设BH与DE交于点M,∵四边形DEGF是正方形,∴DE=EG=DF,DE∥AC,∠EDF=∠DFC=90°,且BH⊥AC,∴四边形DFHM是矩形,∴DF=MH,∵DE∥AC,∴△BDE∽△BAC,∴,∴∴DE=.2、【基础巩固】(1)如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=AD•AB.【尝试应用】(2)如图2,在平行四边形ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF =4,BE=3,求AD的长.【拓展提高】(3)如图3,在菱形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,AC=2EF,∠EDF=∠BAD,AE=2,DF=5,求菱形ABCD的边长.解:(1)证明:∵∠ACD=∠B,∠A=∠A,∴△ADC∽△ACB,∴,∴AC2=AD•AB.(2)∵四边形ABCD是平行四边形,∴AD=BC,∠A=∠C,又∵∠BFE=∠A,∴∠BFE=∠C,又∵∠FBE=∠CBF,∴△BFE∽△BCF,∴,∴BF2=BE•BC,∴BC==,∴AD=.(3)如图,分别延长EF,DC相交于点G,∵四边形ABCD是菱形,∴AB∥DC,∠BAC=∠BAD,∵AC∥EF,∴四边形AEGC为平行四边形,∴AC=EG,CG=AE,∠EAC=∠G,∵∠EDF=∠BAD,∴∠EDF=∠BAC,∴∠EDF=∠G,又∵∠DEF=∠GED,∴△EDF∽△EGD,∴,∴DE2=EF•EG,又∵EG=AC=2EF,∴DE2=2EF2,∴DE=EF,又∵,∴DG=,∴DC=DG﹣CG=5﹣2.3、如图,在平面直角坐标系中,正方形ABOC的两直角边分别在坐标轴的正半轴上,分别过OB,OC的中点D,E作AE,AD的平行线,相交于点F,已知OB=8.(1)求证:四边形AEFD为菱形.(2)求四边形AEFD的面积.(3)若点P在x轴正半轴上(异于点D),点Q在y轴上,平面内是否存在点G,使得以点A,P,Q,G为顶点的四边形与四边形AEFD相似?若存在,求点P的坐标;若不存在,试说明理由.(1)证明:如图1中,∵AE∥DF,AD∥EF,∴四边形AEFD是平行四边形,∵四边形ABCD是正方形,∴AC=AB=OC=OB,∠ACE=∠ABD=90°,∵E,D分别是OC,OB的中点,∴CE=BD,∴△CAE≌△ABD(SAS),∴AE=AD,∴四边形AEFD是菱形.(2)解:如图1中,连接DE.∵S△ADB=S△ACE=×8×4=16,S△EOD=×4×4=8,∴S△AED=S正方形ABOC﹣2S△ABD﹣S△EOD=64﹣2×16﹣8=24,∴S=2S△AED=48.菱形AEFD(3)解:如图1中,连接AF,设AF交DE于K,∵OE=OD=4,OK⊥DE,∴KE=KD,∴OK=KE=KD=2,∵AO=8,∴AK=6,∴AK=3DK,①当AP为菱形的一边,点Q在x轴的上方,有图2,图3两种情形:如图2中,设AG交PQ于H,过点H作HN⊥x轴于N,交AC于M,设AM=t.∵菱形PAQG∽菱形ADFE,∴PH=3AH,∵HN∥OQ,QH=HP,∴ON=NP,∴HN是△PQO的中位线,∴ON=PN=8﹣t,∵∠MAH=∠PHN=90°﹣∠AHM,∠PNH=∠AMH=90°,∴△HMA∽△PNH,∴===,∴HN=3AM=3t,∴MH=MN﹣NH=8﹣3t,∵PN=3MH,∴8﹣t=3(8﹣3t),∴t=2,∴OP=2ON=2(8﹣t)=12,∴P(12,0).如图3中,过点H作HI⊥y轴于I,过点P作PN⊥x轴交IH于N,延长BA交IN于M.同法可证:△AMH∽△HNP,∴===,设MH=t,∴PN=3MH=3t,∴AM=BM﹣AB=3t﹣8,∵HI是△OPQ的中位线,∴OP=2IH,∴HIHN,∴8+t=9t﹣24,∴t=4,∴OP=2HI=2(8+t)=24,∴P(24,0).②当AP为菱形的边,点Q在x轴的下方时,有图4,图5两种情形:如图4中,QH=3PH,过点H作HM⊥OC于M,过D点P作PN⊥MH于N.∵MH是△QAC的中位线,∴MH=AC=4,同法可得:△HPN∽△QHM,∴===,∴PN=HM=,∴OM=PN=,设HN=t,则MQ=3t,∵MQ=MC,∴3t=8﹣,∴t=,∴OP=MN=4+t=,∴点P的坐标为(,0).如图5中,QH=3PH,过点H作HM⊥x轴于M交AC于I,过点Q作QN⊥HM于N.∵IH是△ACQ的中位线,∴CQ=2HI,NQ=CI=4,同法可得:△PMH∽△HNQ,∴===,则MH=NQ=,设PM=t,则HN=3t,∵HN=HI,∴3t=8+,∴t=,∴OP=OM﹣PM=QN﹣PM=4﹣t=,∴P(,0).③如图6中,当AP为菱形的对角线时,有图6一种情形:过点H作HM⊥y轴于于点M,交AB于I,过点P作PN⊥HM于N.∵HI∥x轴,AH=HP,∴AI=IB=4,∴PN=IB=4,同法可得:△PNH∽△HMQ,∴===,∴MH=3PN=12,HI=MH﹣MI=4,∵HI是△ABP的中位线,∴BP=2IH=8,∴OP=OB+BP=16,∴P(16,0),综上所述,满足条件的点P的坐标为(12,0)或(24,0)或(,0)或(,0)或(16,0).4、如图1,在菱形ABCD中,AB=,∠BCD=120°,M为对角线BD上一点(M不与点B、D重合),过点MN∥CD,使得MN=CD,连接CM、AM、BN.(1)当∠DCM=30°时,求DM的长度;(2)如图2,延长BN、DC交于点E,求证:AM•DE=BE•CD;(3)如图3,连接AN,则AM+AN的最小值是.解:(1)如图1,连接AC交BD于O,∵四边形ABCD是菱形,∴AC⊥BD,BD=2OB,CD=BC=AB=,∵∠BCD=120°,∴∠CBD=30°,∴OC=BC=,∴OB=OC=,∴BD=3,∵∠BCD=120°,∠DCM=30°,∴∠BCM=90°,∴CM=BC=1,∴BM=2CM=2,∴DM=BD﹣BM=1;(2)∵四边形ABCD是菱形,∴AB∥CD,AB=CD,∵MN∥CD,MN=CD,∴AB∥MN,AB=MN,∴四边形ABNM是平行四边形,∴AM∥BN,∴∠AMB=∠EBD,∵AB∥CD,∴∠ABM=∠EDB,∴△ABM∽△EDB,∴,∴AM•DE=BE•AB,∵AB=CD,∴AM•DE=BE•CD;(3)如图2,∵四边形ABCD是菱形,∴∠ABD=∠ABC,CD∥AB,∵∠BCD=120°,∴∠ABC=60°,∴∠ABD=30°,连接CN并延长交AB的延长线于P,∵CD∥MN,CD=MN,∴四边形CDMN是平行四边形,∴当点M从点D向B运动时,点N从点C向点P运动(点N的运动轨迹是线段CP),∠APC=∠ABD =30°,由(2)知,四边形ABNM是平行四边形,∴AM=BN,∴AM+AN=AN+BN,而AM+AN最小,即:AN+BN最小,作点B关于CP的对称点B',当点A,N,B'在同一条线上时,AN+BN最小,即:AM+AN的最小值为AB',连接BB',B'P,由对称得,BP=B'P=AB=,∠BPB'=2∠APC=60°,∴△BB'P是等边三角形,B'P过点B'作B'Q⊥BP于Q,∴BQ=B'P=,∴B'Q=BQ=,∴AQ=AB+BQ=,在Rt△AQB'中,根据勾股定理得,AB'==3,即:AM+AN的最小值为3,故答案为3.5、如图,在四边形ABCD中,AB∥DC,BC>AD,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).(1)求证:△ACD∽△BAC;(2)求DC的长;(3)试探究:△BEF可以为等腰三角形吗?若能,求t的值;若不能,请说明理由.(1)证明:∵CD∥AB,∴∠BAC=∠DCA又AC⊥BC,∠ACB=90°,∴∠D=∠ACB=90°,∴△ACD∽△BAC;(2)解:在Rt△ABC中,=8,由(1)知,△ACD∽△BAC,∴,即解得:DC=6.4;(3)能.由运动知,BF=10﹣2t,BE=t,△EFB若为等腰三角形,可分如下三种情况:①当BF=BE时,10﹣2t=t,解得秒.②当EF=EB时,如图,过点E作AB的垂线,垂足为G,则.此时△BEG∽△BAC∴,即,解得:;③当FB=FE时,如图2,过点F作BC的垂线,垂足为H则.此时△BFH∽△BAC∴,即,解得:综上所述:当△EFB为等腰三角形时,t的值为秒或秒或秒.6、如图,在矩形ABCD的边AB上取一点E,连接CE并延长和DA的延长线交于点G,过点E作CG的垂线与CD的延长线交于点H,与DG交于点F,连接GH.(1)当tan∠BEC=2且BC=4时,求CH的长;(2)求证:DF•FG=HF•EF;(3)连接DE,求证:∠CDE=∠CGH.(1)解:在Rt△BCE中,当tan∠BEC=2,∴=2,即=2,解得,BE=2,由勾股定理得,CE===2,∵四边形ABCD为矩形,∴AB∥CD,∴∠ECH=∠BEC,∴tan∠ECH==2,即=2,∴EH=4,∴CH==10;(2)证明:∵∠FEG=∠FDH=90°,∠EFG=∠DFH,∴△EFG∽△DFH,∴=,∴DF•FG=HF•EF;(3)证明:∵△EFG∽△DFH,∴∠CGD=∠CHE,又∠GCD=∠HCE,∴△GCD∽△HCE,∴=,又∠GCD=∠HCE,∴△CDE∽△CGH,∴∠CDE=∠CGH.7、已知,如图,AD是直角三角形ABC斜边上的中线,AE⊥AD,AE交CB的延长线于点E.(1)求证:△BAE∽△ACE;(2)AF⊥BD,垂足为点F,且BE•CE=9,求EF•DE的值.解:(1)∵AD是直角三角形ABC斜边上的中线,∴AD=BD=CD,∴∠C=∠DAC,∵AE⊥AD,∴∠EAD=90°=∠BAC,∴∠EAB=∠DAC,∴∠EAB=∠C,且∠E=∠E,∴△BAE∽△ACE;(2)∵△BAE∽△ACE∴,∴AE2=BE•CE=9,∵∠AFE=∠DAE=90°,∠E=∠E,∴△EAF∽△EFD,∴∴DE•EF=AE2=9.8、如图,在Rt△ABC中,∠A=90°,AB=20cm,AC=15cm,在这个直角三角形内有一个内接正方形,正方形的一边FG在BC上,另两个顶点E、H分别在边AB、AC上.(1)求BC边上的高;(2)求正方形EFGH的边长.解:(1)作AD⊥BC于D,交EH于O,如图所示:∵在Rt△ABC中,∠A=90°,AB=20cm,AC=15cm,∴BC==25(cm),∵BC×AD=AB×AC,∴AD===12(cm);即BC边上的高为12cm;(2)设正方形EFGH的边长为xcm,∵四边形EFGH是正方形,∴EH∥BC,∴∠AEH=∠B,∠AHE=∠C,∴△AEH∽△ABC.∴=,即=,解得:x=,即正方形EFGH的边长为cm.9、如图1,矩形ABCD中,AD=2,AB=3,点E,F分别在边AB,BC上,且BF=FC,连接DE,EF,并以DE,EF为边作▱DEFG.(1)连接DF,求DF的长度;(2)求▱DEFG周长的最小值;(3)当▱DEFG为正方形时(如图2),连接BG,分别交EF,CD于点P、Q,求BP:QG的值.解:(1)如图1所示:∵四边形ABCD是矩形,∠C=90°,AD=BC,AB=DC,∵BF=FC,AD=2;∴FC=1,∵AB=3;∴DC=3,在Rt△DCF中,由勾股定理得,∴DF===;(2)如图1所示:作点F关直线AB的对称点M,连接DM交AB于点N,连接NF,ME,点E在AB上是一个动点,①当点E不与点N重合时点M、E、D可构成一个三角形,∴ME+DE>MD,②当点E与点N重合时点M、E(N)、D在同一条直线上,∴ME+DE=MD由①和②DE+EF的值最小时就是点E与点N重合时,∵MB=BF,∴MB=1,∴MC=3,又∵DC=3,∴△MCD是等腰直角三角形,∴MD===3,∴NF+DN=MD=3,∴l▱DEFG=2(NF+DF)=6;(3)∵▱DEFG为正方形,∴DE=EF,∠DEF=90°,∴∠ADE+∠AED=∠AED+∠BEF=90°,∴∠ADE=∠BEF,∴△ADE≌△BEF(AAS),∴AE=BF=1,BE=AD=2,过点B作BH⊥EF,如图2所示:在Rt△EBF中,由勾股定理得:EF===,∴BH==,又∵△BEF~△FHB,∴=,HF===,在△BPH和△GPF中有:∠BPH=∠GPF,∠BHP=∠GFP,∴△BPH∽△GPF,∴===,∴PF=•HF=,又∵EP+PF=EF,∴EP=﹣=,又∵AB∥BC,EF∥DG,∴∠EBP=∠DQG,∠EPB=∠DGQ,∴△EBP∽△DQG(AA),∴===.10、(1)如图①,在△ABC中,AB=m,AC=n(n>m),点P在边AC上.当AP=时,△APB∽△ABC;(2)如图②,已知△DEF(DE>DF),请用直尺和圆规在直线DF上求作一点Q,使DE是线段DF 和DQ的比例中项.(保留作图痕迹,不写作法)(1)解:∵△APB∽△ABC,∴=,∴=,∴AP=,故答案为.(2)解:作∠DEQ=∠F如图点Q就是所求作的点.11、如图,在矩形ABCD中,已知AD>AB.在边AD上取点E,连结CE.过点E作EF⊥CE,与边AB的延长线交于点F.(1)求证:△AEF∽△DCE.(2)若AB=3,AE=4,DE=6,求线段BF的长.(1)证明:∵四边形ABCD是矩形,∴∠A=∠D=90°,∴∠AEF+∠F=90°∵EF⊥CE,∴∠CED+∠AEF=180°﹣90°=90°,∴∠CED=∠F,又∵∠A=∠D=90°,∴△AFE∽△DEC.(2)∵△AFE∽△DEC,∴=,∵AB=CD=3,AE=4,DE=6,∴=,解得BF=5.答:线段BF的长为5.12、如图,△ABC中,AB=AC,点P为BC边上一动点(不与B,C重合),以AP为边作∠APD=∠ABC,与BC的平行线AD交于点D,与AC交于点E,连结CD.(1)求证:△ABP∽△DAE.(2)已知AB=AC=5,BC=6.设BP=x,CE=y.①求y关于x的函数表达式及自变量x的取值范围;②当S△ACD=时,求CE的值.(1)证明:∵AB=AC,∴∠ABC=∠ACB,∵∠APC=∠ABC+∠BAP,∠APC=∠APD+∠EPC,∠APD=∠ABC,∴∠BAP=∠EPC,∴△ABP∽△PCE,∵BC∥AD,∴△PCE∽△DAE,∴△ABP∽△DAE;(2)解:①∵△ABP∽△PCE,∴=,即=,∴y=﹣x2+x(0<x<6);②∵△ABP∽△DAE,∴=,即=,∴AD=,∵AD∥BC,∴,∵,∴,∴,即13x2+24x﹣100=0,∴x1=2,(舍去)∴.。
相似三角形的辅助线技巧

︵
AHCD 的面积为 21,求△HBC 的面积.
九
【分析】延长 BA 与 CD,两延长线交于点 F,由 CH 垂直于 BF,得到一对直角相等,由
年
CH 为角平分线得到一对角相等,再由 CH 为公共边,利用 ASA 可得出三角形 CFH 与三
级
角形 CBH 全等,由全等三角形的对应边相等得到 CF=CB,且 BH=HF,由 BH=3AH,
1
∴AE= 2AB=1,
∵AB∥DC,
∴△AEM∽△GDM,
∴
=
= ;
(2)∵△ADG 是等腰直角三角形,
∴在 Rt△ADG 中,由勾股定理得:AG= √3 + 3 =3√2,
∵AB∥DC,
15
相似三角形的辅助线技巧
数
【解答】解:
(1)如图,连接 FC、AD.
学
∵点 F 是 AB 的中点,CD=BC,
︵
∴FC 是△ADB 的中位线,
九
1
∴FC= 2AD,
年
∴△EFC∽△EDA,
级
∥
︶
∴
=
∴
= ;
=2,
(2)∵点 F 是 AB 的中点,AB=18,FB=EC,
1
∴EC= 2AB=9.
由(1)知,
=2,则
=2,故 AE=18,
∴AC=AE+EC=18+9=27.
9
相似三角形的辅助线技巧
【点评】本题考查了相似三角形的判定与性质.此类题要注意作平行线,能够根据相似
三角形对应边成比例即可求得线段的比.
2.如图,已知△ABC 的边 AB 上有一点 D,边 BC 的延长线上有一点 E,且 AD=CE.DE
相似三角形添加辅助线的方法举例(有答案)

相似三角形添加辅助线的方法举例例1: 已知:如图,△ABC 中,AB =AC ,BD ⊥AC 于D . 求证: BC 2=2CD ·AC .例2.已知梯形ABCD 中,BC AD //,AD BC 3=,E 是腰AB 上的一点,连结CE(1)如果AB CE ⊥,CD AB =,AE BE 3=,求B ∠的度数;(2)设BCE ∆和四边形AECD 的面积分别为1S 和2S ,且2132S S =,试求AEBE的值例3.如图4-1,已知平行四边ABCD 中,E 是AB 的中点,AD AF 31=,连E 、F 交AC 于G .求AG :AC的值.BC例4、如图4—5,B 为AC 的中点,E 为BD 的中点,则AF :AE=___________.例5、如图4-7,已知平行四边形ABCD 中,对角线AC 、BD 交于O 点,E 为AB 延长线上一点,OE 交BC 于F ,若AB=a ,BC=b ,BE=c ,求BF 的长.例6、已知在△ABC 中,AD 是∠BAC 的平分线.求证:CD BDAC AB.相似三角形添加辅助线的方法举例答案例1: 已知:如图,△ABC 中,AB =AC ,BD ⊥AC 于D . 求证: BC 2=2CD ·AC .分析:欲证 BC 2=2CD ·AC ,只需证BCACCD BC =2.但因为结论中有“2”,无法直接找到它们所在的相似三角形,因此需要结合图形特点及结论形式,通过添加辅助线,对其中某一线段进行倍、分变形,构造出单一线段后,再证明三角形相似.由“2”所放的位置不同,证法也不同.证法一(构造2CD ):如图,在AC 截取DE =DC , ∵BD ⊥AC 于D ,∴BD 是线段CE 的垂直平分线, ∴BC=BE ,∴∠C=∠BEC , 又∵ AB =AC , ∴∠C=∠ABC .∴ △BCE ∽△ACB .∴BC AC CE BC =, ∴BCACCD BC =2 ∴BC 2=2CD ·AC . 证法二(构造2AC ):如图,在CA 的延长线上截取AE =AC ,连结BE , ∵ AB =AC , ∴ AB =AC=AE . ∴∠EBC=90°, 又∵BD ⊥AC .∴∠EBC=∠BDC=∠EDB=90°, ∴∠E=∠DBC , ∴△EBC ∽△BDC∴BC CE CD BC =即BCAC CD BC 2= ∴BC 2=2CD ·AC . 证法三(构造BC 21) :如图,取BC 的中点E ,连结AE ,则EC=BC 21.又∵AB=AC ,∴AE ⊥BC ,∠ACE=∠C ∴∠AEC=∠BDC=90° ∴△ACE ∽△BCD .∴BC AC CD CE =即BCACCD BC=21. ∴BC 2=2CD ·AC . 证法四(构造BC 21):如图,取BC 中点E ,连结DE ,则CE=BC 21. ∵BD ⊥AC ,∴BE=EC=EB ,∴∠EDC=∠C又∵AB=AC ,∴∠ABC=∠C , ∴△ABC ∽△EDC .BCEBCBB C∴EC AC CD BC =J 即BC ACCDBC 21=. ∴BC 2=2CD ·AC .说明:此题充分展示了添加辅助线,构造相似形的方法和技巧.在解题中方法要灵活,思路要开阔.例2.已知梯形ABCD 中,BC AD //,AD BC 3=,E 是腰AB 上的一点,连结CE(1)如果AB CE ⊥,CD AB =,AE BE 3=,求B ∠的度数;(2)设BCE ∆和四边形AECD 的面积分别为1S 和2S ,且2132S S =,试求AEBE的值 (1)设k AE =,则k BE 3=解法1 如图,延长BA 、CD 交于点FBC AD //,AD BC 3=, ∴AF BF 3= k AF 2=,E 为BF 的中点 又BF CE ⊥ CF BC =,又BF CF = B C F ∆为等边三角形 故︒=∠60B解法2如图作AB DF //分别交CE 、CB 于点G 、F 则DF CE ⊥,得平行四边形ABFD 同解法1可证得CDF ∆为等边三角形 故︒=∠=∠601B 解法3 如图作EC AF //交CD 于G ,交BC 的延长线于F 作AB GI //,分别交CE 、BC 于点H 、I 则GI CE ⊥,得矩形AEHGCE AF //3==AEBECF BC ,又AD BC 3= AD CF =,故G 为CD 、AF 的中点 以下同解法1可得CGI ∆是等边三角形 故︒=∠=∠601B 解法4 如图,作CD AF //,交BC 于F ,作CE FG //,交AB 于G ,得平行四边形AFCD ,且AB FG ⊥ 读者可自行证得ABF ∆是等边三角形,故︒=∠60B 解法5 如图延长CE 、DA 交于点F ,作CD AG //,分别交BC 、CE 于点G 、H ,得平行四边形AGCD 可证得A 为FD 的中点,则k AH 2=,故︒=∠601 得ABG ∆为等边三角形,故︒=∠60B 解法6 如图(补形法),读者可自行证明CDF ∆是等边三角形, 得︒=∠=∠60F B(注:此外可用三角形相似、等腰三角形三线合和一、等积法等) (2)设S S BCE 3=∆,则S S AECD 2=四边形 解法1(补形法)如图补成平行四边形ABCF ,连结AC ,则AD DF 2= 设x S ACD =∆,则x S S ACE -=∆2,x S CDF 2=∆ 由ACF ABC S S ∆∆=得, x x x s s 223+=-+,∴s x 45=s x s S ACE 432=-= 4433===∆∆ss S S AE BE ACE BCE解法2(补形法)如图,延长BA 、CD 交于点F ,91=∆∆ABC FAD S SsS S S FAD ABCD FAD 581∆∆==梯形 s S FAD 85=∆,s s s S FEC 821285=+=∆,又s S EBC 3=∆87==∆∆BEC FBC S S BE EF 设m 8=BE ,则m 7=EF ,m 15=BF ,m 5=AFm 2=AE ,4==AEBE解法3(补形法)如图连结AC ,作AC DF //交BA 延长线于点F 连结FC则FAD ∆∽ABC ∆,故AF AB 3=(1)ACF ACD S S ∆∆=,FEC AECD S S ∆=四边形23===∆∆∆AECD BCE FEC BEC S S S S EF BE 四边形 故AF AE AF AE EF BE 33)(332+=+==(2) 由(1)、(2)两式得AE BE 4= 即4=AEBE解法4(割补法)如图连结A 与CD 的中点F 并延长交BC 延长线于点G ,如图,过E 、A 分别作高1h 、2h ,则AD CG =且AECG AECD S S 四边形四边形=,s S S ABCD ABG 5==∆梯形21212153h BG h BC S S ABGEBC⋅⋅⋅⋅==∆∆,又43=BG BC 5421=h h ,54=AB BE ,故4=AEBE 说明 本题综合考查了等腰三角形的性质,相似三角形的判定和性质,解题关键是作辅助线,构造相似三角形.例3.如图4-1,已知平行四边ABCD 中,E 是AB 的中点,AD AF 31=,连E 、F 交AC 于G .求AG :AC的值.解法1: 延长FE 交CB 的延长线于H , ∵ 四边形ABCD 是平行四边形,∴BC AD //,∴ ∠H=∠AFE ,∠DAB=∠HBE又AE=EB ,∴ △AEF ≌△BEH ,即AF=BH ,∵AD AF 31=,∴ BC AF 31=,即CH AF 41=.∵ AD ∥CH ,∠AGF=∠CGH ,∠AFG=∠BHE ,∴ △AFG ∽△CGH .∴ AG :GC=AF :CH ,∴ AG :GC=1:4,∴ AG :AC=1:5.解法2: 如图4—2,延长EF 与CD 的延长线交于M ,由平行四边形ABCD 可知,DC AB //,即AB ∥MC ,∴ AF :FD=AE :MD ,AG :GC=AE :MC . ∵ AD AF 31=,∴ AF :FD=1:2,∴ AE :MD=1:2.∵DC AB AE 2121==.∴ AE :MC=1:4,即AG :GC=1:4,∴ AG :AC=1:5例4、如图4—5,B 为AC 的中点,E 为BD 的中点,则AF :AE=___________.解析:取CF 的中点G ,连接BG .∵ B 为AC 的中点, ∴ BG :AF=1:2,且BG ∥AF ,又E 为BD 的中点, ∴ F 为DG 的中点. ∴ EF :BG=1:2.故EF :AF=1:4,∴ AF :AE=4:3.例5、如图4-7,已知平行四边形ABCD 中,对角线AC 、BD 交于O 点,E 为AB 延长线上一点,OE 交BC 于F ,若AB=a ,BC=b ,BE=c ,求BF 的长.解法1: 过O 点作OM ∥CB 交AB 于M , ∵ O 是AC 中点,OM ∥CB ,∴ M 是AB 的中点,即a MB 21=,∴ OM 是△ABC 的中位线,b BC OM 2121==,且OM ∥BC ,∠EFB=∠EOM ,∠EBF=∠EMO .∴ △BEF ∽△MOE ,∴EM BE OMBF =, 即cacb BF +=221,∴c a bc BF 2+=. 解法2: 如图4-8,延长EO 与AD 交于点G ,则可得△AOG ≌△COF ,∴ AG=FC=b-BF ,∵ BF ∥AG ,∴AE BE AG BF =.即c a cBF b BF +=-, ∵ c a c bBF 2+= ∴ c a bcBF 2+=. 解法3: 延长EO 与CD 的延长线相交于N ,则△BEF 与△CNF 的对应边成比例,即CN BECF BF =. 解得c a bcBF 2+=.例6、已知在△ABC 中,AD 是∠BAC 的平分线.求证:CD BDAC AB =. 分析1 比例线段常由平行线而产生,因而研究比例线段问题,常应注意平行线的作用,在没有平行线时,可以添加平行线而促成比例线段的产生.此题中AD 为△ABC 内角A 的平分线,这里不存在平行线,于是可考虑过定点作某定直线的平行线,添加了这样的辅助线后,就可以利用平行关系找出相应的比例线段,再比较所证的比例式与这个比例式的关系,去探求问题的解决. 证法1: 如图4—9,过C 点作CE ∥AD ,交BA 的延长线于E .在△BCE 中,∵ DA ∥CE ,∴ AE BADCBD =① 又∵ CE ∥AD ,∴ ∠1=∠3,∠2=∠4,且AD 平分∠BAC ,∵ ∠1=∠2,于是∠3=∠4,∴ AC=AE .代入②式得AC ABDCBD =. 分析2 由于BD 、CD 是点D 分BC 而得,故可过分点D 作平行线.证法2: 如图4—10,过D 作DE ∥AC 交AB 于E ,则∠2=∠3.∵ ∠1=∠2,∴ ∠1=∠3. 于是EA=ED .又∵DC BD EA BE =,∴ EA BE ED BE AC AB ==,∴ CD BDAC AB =.分析3 欲证式子左边为AB :AC ,而AB 、AC 不在同一直线上,又不平行,故考虑将AB 转移到与AC 平行的位置.证法3: 如图4—11,过B 作BE ∥AC ,交AD 的延长线于E ,则∠2=∠E .∵ ∠1=∠2,∴ ∠1=∠E ,AB=BE .又∵AC BE DC BD =,∴CD BDAC AB =. 分析4 由于AD 是∠BAC 的平分线,故可过D 分别作AB 、AC 的平行线,构造相似三角形求证. 证法4 如图4—12,过D 点作DE ∥AC 交AB 于E ,DF ∥AB 交AC 于F .易证四边形AEDF 是菱形.则 DE=DF .由△BDE ∽△DFC ,得DE BEDF BE DC BD ==.11 又∵ AC AB DE BE =,∴ DC BD AC AB =.。
全等三角形问题中常见的8种辅助线的作法(有答案)

全等三角形问题中常有的协助线的作法(有答案)总论:全等三角形问题最主要的是结构全等三角形,结构二条边之间的相等,结构二个角之间的相等【三角形协助线做法】图中有角均分线,可向两边作垂线。
也可将图对折看,对称此后关系现。
角均分线平行线,等腰三角形来添。
角均分线加垂线,三线合一试一试看。
线段垂直均分线,常向两头把线连。
要证线段倍与半,延伸缩短可试验。
三角形中两中点,连结则成中位线。
三角形中有中线,延伸中线等中线。
1.等腰三角形“三线合一”法:碰到等腰三角形,可作底边上的高,利用“三线合一”的性质解题2.倍长中线:倍长中线,使延伸线段与原中线长相等,结构全等三角形3.角均分线在三种添协助线4.垂直均分线联络线段两头5.用“截长法”或“补短法” :碰到有二条线段长之和等于第三条线段的长,6.图形补全法:有一个角为60度或120度的把该角添线后组成等边三角形7.角度数为 30、60 度的作垂线法:碰到三角形中的一个角为30 度或 60 度,可以从角一边上一点向角的另一边作垂线,目的是组成30-60-90 的特别直角三角形,而后计算边的长度与角的度数,这样能够获得在数值上相等的二条边或二个角。
从而为证明全等三角形创建边、角之间的相等条件。
8.计算数值法:碰到等腰直角三角形,正方形时,或30-60-90 的特别直角三角形,或40-60-80 的特别直角三角形,常计算边的长度与角的度数,这样能够获得在数值上相等的二条边或二个角,从而为证明全等三角形创建边、角之间的相等条件。
常有协助线的作法有以下几种:最主要的是结构全等三角形,结构二条边之间的相等,二个角之间的相等。
1)碰到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思想模式是全等变换中的“对折”法结构全等三角形.2)碰到三角形的中线,倍长中线,使延伸线段与原中线长相等,结构全等三角形,利用的思想模式是全等变换中的“旋转”法结构全等三角形.3)碰到角均分线在三种添协助线的方法,(1)能够自角均分线上的某一点向角的两边作垂线,利用的思想模式是三角形全等变换中的“对折” ,所考知识点经常是角均分线的性质定理或逆定理.( 2)能够在角均分线上的一点作该角均分线的垂线与角的两边订交,形成一对全等三角形。
初中三角形8种辅助线的作法

初中三角形8种辅助线的作法说到三角形,大家脑袋里第一反应应该就是那三条边和三角形的三个角吧?对,就是这种形状。
那你知道怎么在这些三角形里画出一些特殊的辅助线吗?这些线啊,往往能帮你解决一些看似复杂的问题,让三角形的“奥秘”暴露无遗,简直是数学界的小妙招。
好啦,今天就来聊聊这八种常见的辅助线,保证让你瞬间变身三角形达人!我敢打赌,学会了这些,你会觉得自己就像是三角形里的“魔术师”,每画一条线,都会有新的发现,新的答案。
最简单的辅助线之一就是角平分线。
想象一下,你有一个三角形,某个角很大,你就想把这个角一分为二,变成两个完全一样的小角,咋办呢?对啦,画个角平分线。
它可不是随便一画的,要从角的顶点开始,朝着对边走过去,确保把这个角“平分”成两个一样大的小角。
说白了,角平分线就是帮助我们把角“对半切”的神奇线。
画完后,你会发现,原本难解的问题竟然迎刃而解,想想是不是挺爽的?然后,还有一种叫垂直平分线的辅助线。
别看它名字听起来有点复杂,实际上它就是从三角形的一个边中点出发,垂直地画一条线,直接穿过这个边。
它的作用就像是让三角形中的某一条边被“公平对待”一样,平均分开。
你可以通过这条线,找到三角形的某些对称性,帮助你解决一些难题,尤其是那些涉及到对称性的题目,简直就是救命稻草。
如果你觉得角平分线和垂直平分线还不够酷,那我得给你介绍高线。
它的名字也挺威风的,是不是有种“高大上的感觉”?其实它就是从三角形的一个顶点,垂直地落到对边的延长线上,形成一个直角。
听起来是不是有点高深?但是一旦你学会了高线,你就能解决很多跟直角、面积相关的问题。
这条线虽然看起来简单,但它可以帮助你在一瞬间算出很多复杂的几何问题,简直就是三角形中的秘密武器。
你以为高线已经够神奇了吗?那我再告诉你,中线更是妙不可言。
它从三角形的一个顶点出发,直奔对边的中点,直接把这条边“分成了两半”。
很显然,中线的作用就是帮助你在三角形中找出一个平衡点,很多时候,掌握了中线,你就能找到三角形内心的“宁静”——也就是一些难以捉摸的关系。
相似三角形常用辅助线

又 BD E, C EM EM ECBD
(EM为 中 间 比 ) , BD
AB AC
EF , DF
A B D F A C E F
编辑ppt
20
• 方法二:如图,过D作DN//EC交BC于N
编辑ppt
21
则 有 , B D N B A C ,
B D D N , 即 B D A C A B D N ( 比 例 的 基 本 性 质 ) A BA C
M
C
又 ADN∽ ACF
N A
BE
∴
AN AD ∴ AF AC
AD A FAC A(N 2)
(1)+(2)
A A B A E A D A F A C A M A C A N ( A C A M )
ADNBCM
又
∴ AN=CM
∴ A A B A E A D 编辑 pptF A (A C M C ) M A 2C 36
另外在证明等积式时要先转 化为比例式观察相似关系, 有利于证明
编辑ppt
30
1、如图,梯形ABCD中,AD∥BC,AC、BD 交于O点,BA、CD的延长线交于E点,连结 EO并延长分别交AD、BC于N、M 求证: BM=CM
E
AN AO AD EA AN MC OC BC EB BM
Aj N
B
编辑ppt
A
nF Ey
?5y n
2k
D k Tk C
22 11
练习:
如图,D是△ABC的BC边上的点, BD:DC=2:1,
E是AD的中点, 连结BE并延长交AC于F,
求AF:CF的值.
A
F
E
B 编辑ppt
2023学年八年级数学上册高分突破必练专题(人教版)-等边三角形常考作辅助线法(解析版)

等边三角形常考作辅助线法技巧1:作平行线法技巧2:截长补短法【典例1】(烟台)如图在等边三角形ABC中点E是边AC上一定点点D是直线BC上一动点以DE为一边作等边三角形DEF连接CF.【问题解决】如图1 若点D在边BC上求证:CE+CF=CD;【类比探究】如图2 若点D在边BC的延长线上请探究线段CE CF与CD之间存在怎样的数量关系?并说明理由.【答案】详见解答【解答】【问题解决】证明:在CD上截取CH=CE如图1所示:∵△ABC是等边三角形∴∠ECH=60°∴△CEH是等边三角形∴EH=EC=CH∠CEH=60°∵△DEF是等边三角形∴DE=FE∠DEF=60°∴∠DEH+∠HEF=∠FEC+∠HEF=60°∴∠DEH=∠FEC在△DEH和△FEC中∴△DEH≌△FEC(SAS)∴DH=CF∴CD=CH+DH=CE+CF∴CE+CF=CD;【类比探究】解:线段CE CF与CD之间的等量关系是FC=CD+CE;理由如下:∵△ABC是等边三角形∴∠A=∠B=60°过D作DG∥AB交AC的延长线于点G如图2所示:∵GD∥AB∴∠GDC=∠B=60°∠DGC=∠A=60°∴∠GDC=∠DGC=60°∴△GCD为等边三角形∴DG=CD=CG∠GDC=60°∵△EDF为等边三角形∴ED=DF∠EDF=∠GDC=60°∴∠EDG=∠FDC在△EGD和△FCD中∴△EGD≌△FCD(SAS)∴EG=FC∴FC=EG=CG+CE=CD+CE.【变式1-1】(2020秋•句容市期中)如图在等边三角形ABC中点E是边AC上一定点点D是射线BC上一动点以DE为一边作等边三角形DEF连接CF.【问题解决】如图1 点D与点B重合求证:AE=FC;【类比探究】(1)如图2 点D在边BC上求证:CE+CF=CD;(2)如图3 点D在边BC的延长线上请探究线段CE CF与CD之间存在怎样的数量关系?直接写出你的结论.【答案】详见解答【解答】证明:【问题解决】∵△ABC和△DEF是等边三角形∴AB=BC∠ABC=∠EDC=60°DE=DF∴∠ABC﹣∠EBC=∠EDC﹣∠EBC即∠ABE=∠CBF在△ABE和△CBF中∴△ABE≌△CBF(SAS)∴AE=CF;【类比探究】(1)如图2 在CD上截取CH=CE连接EH∵△ABC是等边三角形∴∠ECH=60°∴△CEH是等边三角形∴EH=EC=CH∠CEH=60°∵△DEF是等边三角形∴DE=FE∠DEF=60°∴∠DEH+∠HEF=∠FEC+∠HEF=60°∴∠DEH=∠FEC在△DEH和△FEC中∴△DEH≌△FEC(SAS)∴DH=CF∴CD=CH+DH=CE+CF∴CE+CF=CD;(2)线段CE CF与CD之间的等量关系是FC=CD+CE;理由如下:∵△ABC是等边三角形∴∠A=∠B=60°过D作DG∥AB交AC的延长线于点G如图3所示:∵GD∥AB∴∠GDC=∠B=60°∠DGC=∠A=60°∴∠GDC=∠DGC=60°∴△GCD为等边三角形∴DG=CD=CG∠GDC=60°∵△EDF为等边三角形∴ED=DF∠EDF=∠GDC=60°∴∠EDG=∠FDC在△EGD和△FCD中∴△EGD≌△FCD(SAS)∴EG=FC∴FC=EG=CG+CE=CD+CE.【变式1-2】(天心区期中)如图在等边△ABC中点D是边AC上一定点点E是直线BC上一动点以DE为一边作等边△DEF连接CF.(1)如图1 若点E在边BC上且DE⊥BC垂足为E求证:CD=2CE;(2)如图1 若点E在边BC上且DE⊥BC垂足为E求证:CE+CF=CD;(3)如图2 若点E在射线CB上请探究线段CE CF与CD之间存在怎样的数量关系?并说明理由.【答案】详见解答【解答】证明:(1)∵△ABC是等边三角形∴∠ACB=60°又∵DE⊥BC∴∠DEC=90°∠EDC=30°∴CD=2CE;(2)∵△DEF是等边三角形∴DE=DF∠EDF=60°∵∠EDC=30°∴∠FDC=30°=∠EDC DC=DC∴△EDC≌△FDC(SAS)∴CE=CF∴CD=2CE=CE+CF;(3)当点E在线段BC上如图2 结论:CD=CE+CF理由如下:如图2 在BC上截取CG=CD连接GD∵∠DCG=60°∴△DCG是等边三角形∴DG=DC∠GDC=60°∵△DEF是等边三角形∴DE=DF∠EDF=60°∵∠GDE+∠EDC=60°=∠EDC+∠CDF∴∠GDE=∠CDF∴△GDE≌△CDF(SAS)∴GE=CF∴CD=CG=CE+EG=CE+CF;当点E在射线BC延长线上如图3 结论:CE=CD+CF理由如下:如图3 在BC上截取CG=CD连接GD∵∠DCG=60°∴△DCG是等边三角形∴DG=DC∠GDC=60°∵△DEF是等边三角形∴DE=DF∠EDF=60°∵∠GDE+∠GDF=60°=∠GDF+∠CDF∴∠GDE=∠CDF∴△GDE≌△CDF(SAS)∴GE=CF∴CE=CG+EG=CD+CF.【典例2】(2020秋•湖南期末)如图△ABC是等边三角形点D、E分别是射线AB、射线CB上的动点点D从点A出发沿射线AB移动点E从点B出发沿BG移动点D、点E同时出发并且运动速度相同.连接CD、DE.(1)如图①当点D移动到线段AB的中点时求证:DE=DC.(2)如图②当点D在线段AB上移动但不是中点时试探索DE与DC之间的数量关系并说明理由.(3)如图③当点D移动到线段AB的延长线上并且ED⊥DC时求∠DEC度数.【答案】详见解答【解答】(1)证明:∵△ABC是等边三角形AD=DB∴∠DCB=∠ACB=30°AD=DB由题意得AD=BE∴BD=BE∴∠BDE=∠BED∵∠BDE+∠BED=∠ABC=60°∴∠BDE=∠BED=30°∴∠DCE=∠BED∴DE=DC.(2)解:DE=DC理由如下:作DF∥AC交BC于F则∠BDF=∠A=60°∠DFB=∠ACB=60°∴△DBF为等边三角形∴DB=DF=BF∠DBF=∠DFB=60°∴FC=AD=BE∠DBE=∠DFC在△DBE和△DFC中∴△DBE≌△DFC(SAS)∴DE=DC;(3)解:在BE上截取BH=BD连接DH∵∠DBH=∠ABC=60°∴△BDH为等边三角形∴DH=DB∠BDH=∠BHD=60°∴∠DHE=∠DBC=120°∵AD=BE BH=BD AB=BC∴HE=BC在△DHE和△DBC中∴△DHE≌△DBC(SAS)∴∠HDE=∠BDC∵∠EDC=90°∠HDB=60°∴∠HDE+∠BDC=30°∴∠HDE=∠BDC=15°∴∠DEC=∠DHC﹣∠HDE=45°.【变式2-1】(道外区期末)如图△ABC中AB=AC点D在AB边上点E在AC的延长线上且CE=BD连接DE交BC于点F.(1)求证:EF=DF;(2)过点D作DG⊥BC垂足为G求证:BC=2FG.【答案】详见解答【解答】证明:(1)过点D作DH∥AC DH交BC于H如图1所示:则∠DHB=∠ACB∠DHF=∠ECF∵AB=AC∴∠B=∠ACB∴∠B=∠DHB∴BD=HD∵CE=BD∴HD=CE在△DHF和△ECF中∴△DHF≌△ECF(AAS)∴EF=DF;(2)如图2 由(1)知:BD=HD∵DG⊥BC∴BG=GH由(1)得:△DHF≌△ECF∴HF=CF∴GH+HF=BH+CH=BC∴BC=2FG.【变式2-2】(东城区期末)(1)老师在课上给出了这样一道题目:如图1 等边△ABC边长为2 过AB边上一点P作PE⊥AC于E Q为BC延长线上一点且AP=CQ连接PQ交AC于D求DE的长.小明同学经过认真思考后认为可以通过过点P作平行线构造等边三角形的方法来解决这个问题.请根据小明同学的思路直接写出DE的长.(2)【类比探究】老师引导同学继续研究:1.等边△ABC边长为2 当P为BA的延长线上一点时作PE⊥CA的延长线于点E Q 为边BC上一点且AP=CQ连接PQ交AC于D.请你在图2中补全图形并求DE的长.2.已知等边△ABC当P为AB的延长线上一点时作PE⊥射线AC于点E Q为②(①BC边上;②BC的延长线上;③CB的延长线上)一点且AP=CQ连接PQ交直线AC于点D能使得DE的长度保持不变.(将答案的编号填在横线上)【答案】详见解答【解答】解:(1)如图过点P作PF∥BC交AC于点F∴∠Q=∠FPD∠APF=∠ABC∠AFP=∠ACB∵△ABC为等边三角形∴∠ABC=∠ACB=∠BAC=60°∴∠APF=∠AFP=∠BAC=60°∴△APF为等边三角形∴AP=AF=PF又∵PE⊥AC∴EF=AF∴PF=AP=CQ又∠PDF=∠CDQ∠Q=∠FPD∴△PDF≌△QDC(AAS)∴FD=CD=FC=(AC﹣AF)∴DE=DF+EF=(AC﹣AF)+AF=AC=1;(2)1、补全的图形如下过点P作PF∥BC交CE的延长线于点F∴∠DQC=∠FPD∠APF=∠ABC∠AFP=∠ACB ∵△ABC为等边三角形∴∠ABC=∠ACB=∠BAC=60°∴∠APF=∠AFP=∠F AP=60°∴△APF为等边三角形∴AP=AF=PF又∵PE⊥AC∴EF=AF∴PF=AP=CQ又∠PDF=∠CDQ∠DQC=∠FPD ∴△PDF≌△QDC(AAS)∴FD=CD=FC=(AC+AF)∴DE=DF﹣EF=(AC+AF)﹣AF=AC=1;2、过点P作PF∥BC交BC的延长线与点F.∴∠DQC=∠FPD∠APF=∠ABC∠AFP=∠ACB∵△ABC为等边三角形∴∠ABC=∠ACB=∠BAC=60°∴∠APF=∠AFP=∠BAC=60°∴△APF为等边三角形∴AP=AF=PF又∵PE⊥AC∴EF=AF∴PF=AP=CQ∠PDF=∠CDQ∠DQC=∠FPD∴△PDF≌△QDC(AAS)∴FD=CD=FC=(AF﹣AC)∴DE=EF﹣DF=(AC+CF)﹣CF=AC=1;答案为②.1.(2021秋•咸丰县期末)如图等边△ABC的边长为12cm D为AC边上一动点E为AB延长线上一动点DE交CB于点P点P为DE中点(1)求证:CD=BE;(2)若DE⊥AC求BP的长.【解答】(1)证明:作DF∥AB交BC于F如图所示:∵△ABC是等边三角形∴∠A=∠ABC=∠C=60°∵DF∥AB∴∠CDF=∠A=60°∠DFC=∠ABC=60°∠DFP=∠EBP ∴△CDF是等边三角形∴CD=DF∵点P为DE中点∴PD=PE在△PDF和△PEB中∴△PDF≌△PEB(AAS)∴DF=BE∴CD=BE;(2)解:∵DE⊥AC∴∠ADE=90°∴∠E=90°﹣∠A=30°∴AD=AE∠BPE=∠ACB﹣∠E=30°=∠E∴BP=BE由(1)得:CD=BE∴BP=BE=CD设BP=x则BE=CD=x AD=12﹣x∵AE=2AD∴12+x=2(12﹣x)解得:x=4即BP的长为4.2.(2021秋•绵竹市期末)在等边△ABC中点E是AB上的动点点E与点A、B不重合点D在CB的延长线上且EC=ED.(1)如图1 若点E是AB的中点求证:BD=AE;(2)如图2 若点E不是AB的中点时(1)中的结论“BD=AE”能否成立?若不成立请直接写出BD与AE数量关系若成立请给予证明.【解答】(1)证明:∵△ABC是等边三角形∴∠ABC=∠ACB=60°∵点E是AB的中点∴CE平分∠ACB AE=BE∴∠BCE=30°∵ED=EC∴∠D=∠BCE=30°.∵∠ABC=∠D+∠BED∴∠BED=30°∴∠D=∠BED∴BD=BE.∴AE=DB.(2)解:AE=DB;理由:过点E作EF∥BC交AC于点F.如图2所示:∴∠AEF=∠ABC∠AFE=∠ACB.∵△ABC是等边三角形∴∠ABC=∠ACB=∠A=60°AB=AC=BC∴∠AEF=∠ABC=60°∠AFE=∠ACB=60°即∠AEF=∠AFE=∠A=60°∴△AEF是等边三角形.∴∠DBE=∠EFC=120°∠D+∠BED=∠FCE+∠ECD=60°∵DE=EC∴∠D=∠ECD∴∠BED=∠ECF.在△DEB和△ECF中∴△DEB≌△ECF(AAS)∴DB=EF∴AE=BD.3.(2020秋•旅顺口区期中)如图在等边三角形ABC中点E是边CA延长线上一点点D是直线BC上一动点以DE为一边作等边三角形DEF连接CF.(1)如图1 若点D在边BC上求证:CE=CF+CD;(2)如图2 若点D在边BC的延长线上请探究线段CE CF与CD之间存在怎样的数量关系并说明理由.【答案】详见解答【解答】(1)证明:在CA上截取CG=CD连接DG如图1所示:∵△ABC和△DEF是等边三角形∴∠B=∠ACB=∠EDF=60°BC=AC DE=DF∵CG=CD∴△CDG是等边三角形∴DG=DC=CG∠GDC=60°=∠EDF∴∠EDG=∠FDC在△DEG和△DFC中∴△DEG≌△DFC(SAS)∴GE=CF∵CE=GE+CG∴CE=CF+CD;(2)解:CD=CF+CE理由如下:在CA的延长线上截取CG=CD连接DG如图2所示:同(1)得:△CDG是等边三角形△DEG≌△DFC(SAS)∴DG=DC=CG GE=CF∵CG=GE+CE∴CD=CF+CE.4.(2020•安徽)如图D是等边△ABC的边AB上一点E是BC延长线上一点CE=DA连接DE交AC于F过D点作DG⊥AC于G点.证明下列结论:(1)AG=AD;(2)DF=EF;(3)S△DGF=S△ADG+S△ECF.【答案】详见解答【解答】证明:(1)∵△ABC是等边三角形∴∠A=60°∵DG⊥AC∴∠AGD=90°∠ADG=30°∴AG=AD;(2)过点D作DH∥BC交AC于点H∴∠ADH=∠B∠AHD=∠ACB∠FDH=∠E∵△ABC是等边三角形∴∠B=∠ACB=∠A=60°∴∠A=∠ADH=∠AHD=60°∴△ADH是等边三角形∴DH=AD∵AD=CE∴DH=CE在△DHF和△ECF中∴△DHF≌△ECF(AAS)∴DF=EF;(3)∵△ABC是等边三角形DG⊥AC∴AG=GH∴S△ADG=S△HDG∵△DHF≌△ECF∴S△DHF=S△ECF∴S△DGF=S△DGH+S△DHF=S△ADG+S△ECF.5.(2020秋•花雨区校级月考)我们在前面曾遇到过这样一道题目:小明与同桌小聪讨论后进行了如下解答:(1)特殊情况探索结论当点E为AB的中点时如图1 确定线段AE与DB的大小关系请你直接写出结论:AE DB(填“>”、“<”或“=”)(2)一般情况证明结论:如图2 过点E作EF∥BC交AC于点F.请你继续完成对以上问题(1)中所填写结论的证明.(3)变式探究:如图3 △ABC是等边三角形D是边BC上一点点E在BA的延长线上且BD=AE此时CE和DE有何数量关系?请画出图形作出判断并说明理【答案】详见解答【解答】解:(1)∵E为等边三角形AB边的中点∴∠ECD=30∵DE=CE∴∠ECD=∠D=30°∵∠DEB=180°﹣∠D﹣∠DBE=30°∴∠DEB=∠D∴BD=BE∴AE=BD.(2)如图2∵在等边三角形ABC中EF∥BC∴BE=CF∵DE=CE∴∠D=∠ECD∵∠D+∠DEB=60°∠ECF+∠ECD=60°∴∠ECF=∠DEB在△CEF和△DBE中∴△CEF≌△DBE(SAS)∴AE=DB.(3)如图3 过D做DF∥AC则△BDF为等边三角形∴BD=BF=DF∵BD=AE∴AB=BF+AF=BD+AF=AE+AF=EF∴AC=EF∵DF∥AC∴∠DFE=∠EAC在△DEF和△ECA中∴△DEF≌△ECA(SAS)∴CE=DE.6.(2020秋•河西区期末)如图△ABC是边长为6的等边三角形P是AC边上一动点由A向C运动(与A、C不重合)Q是CB延长线上一点与点P同时以相同的速度由B 向CB延长线方向运动(Q不与B重合)过P作PE⊥AB于E连接PQ交AB于D.(1)当∠BQD=30°时求AP的长;(2)证明:在运动过程中点D是线段PQ的中点;(3)当运动过程中线段ED的长是否发生变化?如果不变求出线段ED的长;如果变化请说明理由.【解答】(1)解:设AP=x则BQ=x∵∠BQD=30°∠C=60°∴∠QPC=90°∴QC=2PC即x+6=2(6﹣x)解得x=2即AP=2.(2)证明:如图过P点作PF∥BC交AB于F∵PF∥BC∴∠PF A=∠FP A=∠A=60°∴PF=AP=AF∴PF=BQ又∵∠BDQ=∠PDF∠DBQ=∠DFP∴△DQB≌△DPF∴DQ=DP即D为PQ中点(3)运动过程中线段ED的长不发生变化是定值为3 理由:∵PF=AP=AF PE⊥AF∴又∵△DQB≌△DPF∴∴.7.(2020秋•裕华区校级期末)知识链接:将两个含30°角的全等三角尺放在一起让两个30°角合在一起成60°经过拼凑、观察、思考探究出结论“直角三角形中30°角所对的直角边等于斜边的一半”.如图等边三角形ABC的边长为4cm点D从点C出发沿CA向A运动点E从B出发沿AB的延长线BF向右运动已知点D、E都以每秒0.5cm的速度同时开始运动运动过程中DE与BC相交于点P设运动时间为x秒.(1)请直接写出AD长.(用x的代数式表示)(2)当△ADE为直角三角形时运动时间为几秒?(3)求证:在运动过程中点P始终为线段DE的中点.【解答】解:(1)由题意得CD=0.5x则AD=4﹣0.5x;(2)∵△ABC是等边三角形∴AB=BC=AC=4cm∠A=∠ABC=∠C=60°.设x秒时△ADE为直角三角形∴∠ADE=90°BE=0.5x AD=4﹣0.5x AE=4+0.5x∴∠AED=30°∴AE=2AD∴4+0.5x=2(4﹣0.5x)∴x=;答:运动秒后△ADE为直角三角形;(3)如图2 作DG∥AB交BC于点G∴∠GDP=∠BEP∠DGP=∠EBP∠CDG=∠A=60°∠CGD=∠ABC=60°∴∠C=∠CDG=∠CGD∴△CDG是等边三角形∴DG=DC∵DC=BE∴DG=BE.在△DGP和△EBP中∴△DGP≌△EBP(ASA)∴DP=PE∴在运动过程中点P始终为线段DE的中点.8.(2021秋•营口期末)已知A(﹣10 0)以OA为边在第二象限作等边△AOB.(1)求点B的横坐标;(2)如下图点M、N分别为OA、OB边上的动点以MN为边在x轴上方作等边△MNE连结OE当∠EMO=45°时求∠MEO的度数.【解答】解:(1)如图过B作BD⊥OA于点D∵△AOB为等边三角形点A(﹣10 0)∴OA=OB=AB=10 ∠BAO=∠ABO=∠AOB=60°∵BD⊥OA∴AD=OD=OA=×10=5∴点B的横坐标为﹣5;(2)如图2 过点M作MF∥AB交OA于点F∵MF∥AB∴∠MFO=∠BAO=∠AOB=60°∴△MOF为等边三角形∴∠FMO=60°MF=MO∵△MNE是等边三角形∴∠NME=60°MN=ME∴∠FMN+∠NMO=∠NMO+∠OME=60°∴∠FMN=∠OME在△MFN和△MOE中∴△MFN≌△MOE(SAS)∴∠MFN=∠MOE=60°∵∠EMO=45°∴∠MEO=180°﹣∠MOE﹣∠EMO =180°﹣60°﹣45°=75°.。
(完整版)相似三角形中几种常见的辅助线作法(有辅助线)
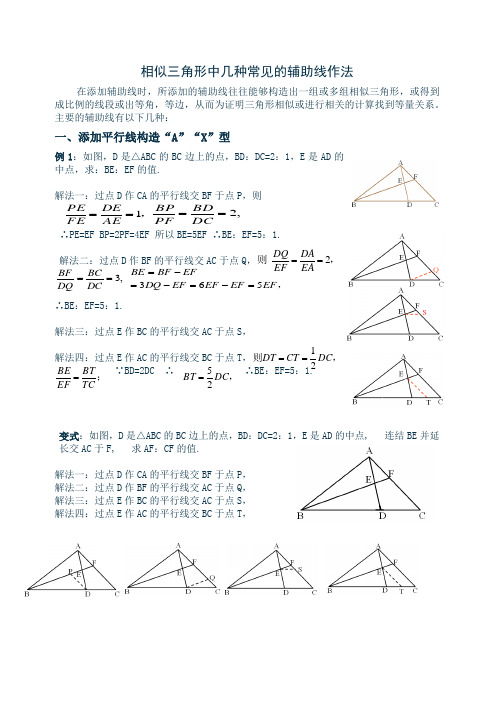
相似三角形中几种常见的辅助线作法在添加辅助线时,所添加的辅助线往往能够构造出一组或多组相似三角形,或得到成比例的线段或出等角,等边,从而为证明三角形相似或进行相关的计算找到等量关系。
主要的辅助线有以下几种:一、添加平行线构造“A ”“X ”型例1:如图,D 是△ABC 的BC 边上的点,BD :DC=2:1,E 是AD 的中点,求:BE :EF 的值.解法一:过点D 作CA 的平行线交BF 于点P ,则∴PE=EF BP=2PF=4EF 所以BE=5EF ∴BE :EF=5:1.解法二:过点D 作BF 的平行线交AC 于点Q ,∴BE :EF=5:1.解法三:过点E 作BC 的平行线交AC 于点S ,解法四:过点E 作AC 的平行线交BC 于点T ,∵BD=2DC ∴ ∴BE :EF=5:1.变式:如图,D 是△ABC 的BC 边上的点,BD :DC=2:1,E 是AD 的中点,连结BE 并延长交AC 于F,求AF :CF 的值.解法一:过点D 作CA 的平行线交BF 于点P , 解法二:过点D 作BF 的平行线交AC 于点Q , 解法三:过点E 作BC 的平行线交AC 于点S , 解法四:过点E 作AC 的平行线交BC 于点T ,,1==AE DE FEPE ,2==DC BD PF BP ,则2==EA DA EF DQ ,3==DCBC DQBF ,EF EF EF EF DQ EF BF BE 563=-=-=-=,则DC CT DT 21==;TC BT EF BE =,DC BT 25=例2:如图,在△ABC 的AB 边和AC 边上各取一点D 和E ,且使AD =AE ,DE 延长线与BC 延长线相交于F ,求证:(证明:过点C 作CG//FD 交AB 于G )例3:如图,△ABC 中,AB<AC ,在AB 、AC 上分别截取BD=CE ,DE ,BC 的延长线相交于点F ,证明:AB ·DF=AC ·EF.分析:证明等积式问题常常化为比例式,再通过相似三角形对应边成比例来证明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)证明:如图1中,
∵AE∥DF,AD∥EF,
∴四边形AEFD是平行四边形,
∵四边形ABCD是正方形,
∴AC=AB=OC=OB,∠ACE=∠ABD=90°,
专题58 三角形中作辅助线造相似
1、如图1,在△ABC中,AB=AC=10,BC=12.
(1)求AC边上的高BH的长;
(2)如图2,点D、E分别在边AB、BC上,G、F在边AC上,当四边形DEGF是正方形时,求DE的长.
解:(1)过点A作AN⊥BC于N,
∵AB=AC=10,BC=12,AN⊥BC,
∴BN=CN=6,
∴AN= = =8,
∵S△ABC= AC×BH= BC×AN,
∴BH= =9.6;
(2)如图2,设BH与DE交于点M,
∵四边形DEGF是正方形,
∴DE=EG=DF,DE∥AC,∠EDF=∠DFC=90°,且BH⊥AC,
∴四边形DFHM是矩形,
∴DF=MH,
∵DE∥AC,
∴△BDE∽△BAC,
∴ ,
∴
∵菱形PAQG∽菱形ADFE,
∴PH=3AH,HN是△PQO的中位线,
∴ON=PN=8﹣t,
∵∠MAH=∠PHN=90°﹣∠AHM,∠PNH=∠AMH=90°,
∴△HMA∽△PNH,
∴ = = = ,
∴HN=3AM=3t,
∴MH=MN﹣NH=8﹣3t,
∵PN=3MH,
∵HI∥x轴,AH=HP,
∴AI=IB=4,
∴PN=IB=4,
同法可得:△PNH∽△HMQ,
∴ = = = ,
∴MH=3PN=12,HI=MH﹣MI=4,
∵HI是△ABP的中位线,
∴BP=2IH=8,
∴OP=OB+BP=16,
∴P(16,0),
综上所述,满足条件的点P的坐标为(12,0)或(24,0)或( ,0)或( ,0)或(16,0).
∵四边形ABCD是菱形,
∴AB∥DC,∠BAC= ∠BAD,
∵AC∥EF,
∴四边形AEGC为平行四边形,
∴AC=EG,CG=AE,∠EAC=∠G,
∵∠EDF= ∠BAD,
∴∠EDF=∠BAC,
∴∠EDF=∠G,
又∵∠DEF=∠GED,
∴△EDF∽△EGD,
∴ ,
∴DE2=EF•EG,
又∵EG=AC=2EF,
∴S菱形AEFD=2S△AED=48.
(3)解:如图1中,连接AF,设AF交DE于K,
∵OE=OD=4,OK⊥DE,
∴KE=KD,
∴OK=KE=KD=2 ,
∵AO=8 ,
∴AK=6 ,
∴AK=3DK,
①当AP为菱形的一边,点Q在x轴的上方,有图2,图3两种情形:
如图2中,设AG交PQ于H,过点H作HN⊥x轴于N,交AC于M,设AM=t.
同法可得:△PMH∽△HNQ,
∴ = = = ,则MH= NQ= ,
设PM=t,则HN=3t,
∵HN=HI,
∴3t=8+ ,
∴t= ,
∴OP=OM﹣PM=QN﹣PM=4﹣t= ,
∴P( ,0).
③如图6中,当AP为菱形的对角线时,有图6一种情形:
过点H作HM⊥y轴于于点M,交AB于I,过点P作PN⊥HM于N.
解:(1)证明:∵∠ACD=∠B,∠A=∠A,
∴△ADC∽△ACB,
∴ ,
∴AC2=AD•AB.
(2)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
又∵∠BFE=∠A,
∴∠BFE=∠C,
又∵∠FBE=∠CBF,
∴△BFE∽△BCF,
∴ ,
∴BF2=BE•BC,
∴BC= = ,
∴AD= .
(3)如图,分别延长EF,DC相交于点G,
∴DE2=2EF2,
∴DE= EF,
又∵ ,
∴DG= ,
∴DC=DG﹣CG=5 ﹣2.
3、如图,在平面直角坐标系中,正方形ABOC的两直角边分别在坐标轴的正半轴上,分别过OB,OC的中点D,E作AE,AD的平行线,相交于点F,已知OB=8.
(1)求证:四边形AEFD为菱形.
(2)求四边形AEFD的面积.
∴OP=2IH,
∴HIHN,
∴8+t=9t﹣24,
∴t=4,
∴OP=2HI=2(8+t)=24,
∴P(24,0).
②当AP为菱形的边,点Q在x轴的下方时,有图4,图5两种情形:
如图4中,QH=3PH,过点H作HM⊥OC于M,过D点P作PN⊥MH于N.
∵MH是△QAC的中位线,
∴MH= AC=4,
同法可得:△HPN∽△QHM,
∴ = = = ,
∴PN= HM= ,
∴OM=PN= ,设HN=t,则MQ=3t,
∵MQ=MC,
∴3t=8﹣ ,
∴t= ,
∴OP=MN=4+t= ,
∴点P的坐标为( ,0).
如图5中,QH=3PH,过点H作HM⊥x轴于M交AC于I,过点Q作QN⊥HM于N.
∵IH是△ACQ的中位线,
∴CQ=2HI,NQ=CI=4,
∴8﹣t=3(8﹣3t),
∴t=2,
∴OP=2ON=2(8﹣t)=12,
∴P(12,0).
如图3中,过点H作HI⊥y轴于I,过点P作PN⊥x轴交IH于N,延长BA交IN于M.
同法可证:△AMH∽△HNP,
∴ = = = ,设MH=t,
∴PN=3MH=3t,
∴AM=BM﹣AB=3t﹣8,
∵HI是△OPQ的中位线,
4、如图1,在菱形ABCD中,AB= ,∠BCD=120°,M为对角线BD上一点(M不与点B、D重合),过点MN∥CD,使得MN=CD,连接CM、AM、BN.
∴DE= .
2、【基础巩固】
(1)如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=AD•AB.
【尝试应用】
(2)如图2,在平行四边形ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF=4,BE=3,求AD的长.
【拓展提高】
(3)如图3,在菱形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,AC=2EF,∠EDF= ∠BAD,AE=2,DF=5,求菱形ABCD的边长.
∵E,D分别是OC,OB的中点,
∴CE=BD,
∴△CAE≌△ABD(SAS),
∴AE=AD,
∴四边形AEFD是菱形.
(2)解:如图1中,连接DE.
∵S△ADB=S△ACE= ×8×4=16,
S△EOD= ×4×4=8,
∴S△AED=S正方形ABOC﹣2S△ABD﹣S△EOD=64﹣2×16﹣8=24,
